Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
THz/Far infrared synchrotron observations of superlattice frequencies in MgB2†
Jose A.
Alarco
 abc,
Bharati
Gupta
abc,
Mahboobeh
Shahbazi
abc,
Bharati
Gupta
abc,
Mahboobeh
Shahbazi
 abc,
Dominique
Appadoo
d and
Ian D. R.
Mackinnon
abc,
Dominique
Appadoo
d and
Ian D. R.
Mackinnon
 *ae
*ae
aCentre for Clean Energy Technologies and Practices, Faculty of Science, Queensland University of Technology, Brisbane, QLD 4001, Australia. E-mail: ian.mackinnon@qut.edu.au
bCentre for Materials Science, Faculty of Science, Queensland University of Technology, Brisbane, QLD 4001, Australia
cSchool of Chemistry and Physics, Faculty of Science, Queensland University of Technology, Brisbane, QLD 4001, Australia
dAustralian Synchrotron, Clayton, VIC, Australia
eSchool of Earth and Atmospheric Sciences, Faculty of Science, Queensland University of Technology, Brisbane, QLD 4001, Australia
First published on 15th October 2021
Abstract
THz/Far Infrared synchrotron absorption experiments on pure and doped MgB2 samples show that the absorption spectral weight at low wavenumber (i.e., <110 cm−1) evolves as the temperature is reduced to 10 K. Distinct spectral peak intensities increase as the temperature of MgB2 and doped MgB2 approaches, and then crosses, the superconducting transition temperature. These experimental data suggest a strong link to superconductivity induced by subtle shifts in structural symmetry. Significant increases in absorption are observed at frequencies that correspond to the superconducting gaps for doped and pure MgB2, and at fractions of these frequency (or energy) values. This low wavenumber spectral transition is consistent with the notion that superlattice frequencies contribute to the optic modes of the MgB2 phonon dispersion and are critical to the superconducting transition for this structure. Key integer ratios are identified in real and reciprocal spaces that link bonding character, Fermi vectors and Fermi surfaces as well as phonon properties with geometric parameters and specific superlattice symmetries for MgB2. Similarly consistent spectral data at low wavenumber are also obtained for carbon doped Mg11B2. Density Functional Theory calculations of superlattice phonon dispersions result in folded mode frequencies that match these observed low wavenumber experiments. These results show that symmetry reductions, largely electronic in character although coupled to vibrations, occur with change in temperature and imply strong links to superconductivity mechanisms.
Introduction
Measurement and analyses of acoustic waves have played a major role in the understanding of superconductivity, particularly for pure elemental metals and ordered intermetallic compounds.1 Acoustic phonons have been key to formulation of concepts for BCS superconductivity,2,3 explanation of isotopic effects4–6 and for other manifestations of superconductivity.1 For example, anomalies in the acoustic phonon dispersions (PDs) of A15 superconducting materials have been correlated with their relatively high superconducting transition temperature (Tc), and attributed to anharmonic effects and/or phonon mode softening.1 While acoustic anomalies have also been partly addressed in higher temperature superconductors of quite different composition,7 attention in recent years has largely shifted to optical phonons, due to evident correlations with electronic band structures and to correspondence of PDs at higher frequencies to optic modes.1 MgB2 is a representative example of this trend, where the optical E2g mode has been extensively implicated in superconductivity.8,9 Furthermore, significant correlations between PD anomalies and the superconducting gap energy have been identified for MgB2 for a wide range of external conditions.10–12Terahertz (THZ) or Far Infrared refers to radiation that covers between the microwave and infrared (IR) regions of the electromagnetic spectrum13 (1 THz = 4.136 meV = 33.356 cm−1). In synchrotrons, where such radiation is generated by electrons moving at relativistic speeds,14 THz radiation or light is highly intense and collimated, so that it finds applications in many fields of research, such as nanoimaging and nano-spectroscopy.15 At energies <400 cm−1, synchrotron radiation flux outperforms conventional thermal sources for data fidelity, making the THz/Far IR region of particular interest for low energy phenomena.16,17 The meV and sub-meV range of THz energy involves the acoustic regions of PDs and the typical energy of superconducting gaps. Previous synchrotron THz experiments on superconductors have been carried out on boron-doped diamond, V3Si (an A15-type intermetallic), MgB2 and isostructural CaAlSi using reflection and transmission modes.17,18 These experiments generally observed broad absorption features that appear to have a temperature dependence correlated with respective Tcs or gap energies.
The THz/Far IR region is also ideal for investigation of superlattice frequencies which are generally located in the low wavenumber range. We have previously observed indications of superlattice periodicities in Raman spectra of MgB219 and YB620 superconductors. Using Density Functional Theory (DFT) to calculate PDs21 and superlattice constructs, which fold the reciprocal space of the original crystal, enables identification of new lower frequency peaks activated for Raman detection. These calculations give a remarkable match to observed small peaks19 at the limit of laboratory detection. Other work by Campi et al.22 implies that a 4× superlattice along the c-axis direction may have been detected in (Mg1−xAlx)B2 by high resolution neutron diffraction.
This article describes detection of low wavenumber signals from MgB2 and C-doped MgB2 superconductors at and below the Tc value. These distinctive changes in spectral intensity occur within the acoustic range of frequencies for the accepted P6/mmm high symmetry of MgB2 and are less evident or absent at higher temperatures (e.g., >100 K). We utilise DFT computation to identify potential superlattice constructs for MgB2 that explain these low frequency observations.
Experimental
Pure MgB2 powders, one synthesized in-house and another outsourced from Sigma Aldrich, as well as a sample of 10% carbon doped Mg11B2 powder (made in-house with 10% C400 and boron 11B isotope) were used for THz/Far IR analysis. The superconducting transitions for these MgB2 samples are shown in Fig. S1 (ESI†). The lattice parameters, transition temperature (Tc) and cell volume for carbon doped Mg11B2 decreased after carbon doping compared to those for pure Mg11B2. Lattice parameters (a = 3.07534(5) Å and c = 3.52318(9) Å) and cell volume (28.857(1) Å3) values obtained using Rietveld refinement as well as Tc are consistent with previous studies of carbon doped MgB2.23 Powders of each sample were thoroughly mixed with polyethylene (PE) powder using a mortar and pestle inside a nitrogen filled glove box, and pressed into small 3 mm diameter, hollow stainless disks, included in a die set from PIKE.25Fine-grained MgB2 is a black powder and so absorbs strongly in the IR region. Because the expected level of absorption from samples under experimental conditions was unknown, a wide range of MgB2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE mixtures were prepared for preliminary analysis. Ratios of MgB2
PE mixtures were prepared for preliminary analysis. Ratios of MgB2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE between 70
PE between 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 50
30, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 35
50, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65, 15
65, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85, 5
85, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95, 4
95, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96 and 3
96 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97 were initially scanned at room temperature to determine optimum ratios for transmission of a signal. Pellets with high ratios of MgB2 did not provide clear transmittance signals; consequently, subsequent work focused on pellets with 4% and 5% MgB2 content.
97 were initially scanned at room temperature to determine optimum ratios for transmission of a signal. Pellets with high ratios of MgB2 did not provide clear transmittance signals; consequently, subsequent work focused on pellets with 4% and 5% MgB2 content.
Images of the He-cryostat and the insertable sample holder for transmission measurements, which are later converted to absorption values, are shown in ESI† (Fig. S2). The THz/Far IR beamline is equipped with a Bruker IFS 125/HR Fourier transform (FT) spectrometer, and for this work, the spectrometer is coupled to a 6 K closed loop pulse-tube (CLPT) cryostat from Cryo-Industries of America. The spectrometer is fitted with a 6 μm multilayer Mylar beam splitter and a Si Bolometer from Infrared Laboratories Ltd equipped with a 13 μm cut-on long-pass cold filter to record the transmittance spectrum between 20–650 cm−1. Spectra are collected at specific temperatures in the range 6 K to 296 K; five separate spectra are collected at each temperature and averaged to improve quality of signal to noise ratios. The OPUS 8.0 software is used for data acquisition and analysis. To deconvolute spectra from sample-PE composites, absorption results for each composite are divided by measurements at the same temperature for PE only under the same conditions.
Calculation procedures
Electronic Band Structure (EBS) and PD calculations are undertaken using Density Functional Theory (DFT) as implemented in the Cambridge Serial Total Energy Package (CASTEP) of Materials Studio (MS) 2017 and 2018.21 All structures are optimized for geometry, including cell parameters, starting from the MgB2 crystal information file (.cif) for P6/mmm group symmetry (No. 191), available in standard databases. Crystal structure visualizations, schematics and bond lengths were generated using Crystal-Maker X version 10.5.3 software based on the MgB2.cif file.Superlattices in the c axis direction are constructed by multiplying the unit cell along the appropriate direction and imposing reduced symmetries to suit the superlattice construction, in line with procedures described in our earlier publications.19,20,26 For higher dimension superlattices (e.g., 4c), where a large computational resource is required for all reciprocal directions, calculations are limited to key, high symmetry reciprocal space directions such as ΓA, ΓK and ΓM. In general, the local density approximation (LDA) and generalized gradient approximation (GGA), with norm-conserving pseudopotentials, are used in separate DFT calculations to provide a measure of computational fidelity.11
The typical setup for calculations uses a Δk value ranging between 0.01 to 0.02 Å−1 (or less; i.e., a grid mesh ranging from 45 × 45 × 30 to 19 × 19 × 14),26 with a plane wave basis set cut-off of 990 eV, an ultra-fine (or better) customized setup to ensure total energy convergence of less than 5 × 10−6 eV per atom, a maximum force of less than 0.01 eV Å−1, a maximum stress of less than 0.02 GPa and maximum displacements of less than 5 × 10−4 Å. These calculation procedures are similar to those previously reported for MgB2 and metal-substituted derivatives of MgB2 (e.g., (Mg1−xMx)B2) where (M = Al, Ti, Sc, Cd, Ba).10,11,28 In general, phonon calculations use a linear approximation method except as annotated where a finite displacement method is used.
Results
Results for THz/Far IR absorption measurements on MgB2 diluted with PE are an important guide to subsequent superlattice calculations which are computationally demanding. Interpretations of these experimental data are supported by results from DFT calculations for a single MgB2 unit cell (with P6/mmm symmetry) and for an MgB2 superlattice with a multiple of the c-lattice parameter.Absorption spectra in the THz region
The absorption spectra for Mg11B2 doped with carbon (10%) and diluted with PE (Mg11B2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PE ratio 5
PE ratio 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
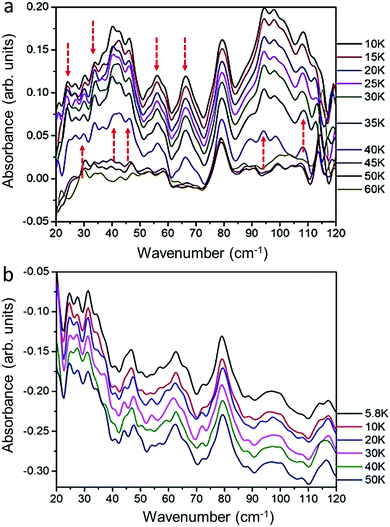
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95) with minimal processing of spectral data is shown in Fig. 1a. Each spectrum at a specific temperature has been offset vertically for visual clarity. New spectral features occur in the low wavenumber region as the sample temperature approaches 40 K, a few degrees above the superconducting transition. In this case, the onset Tc for Mg(11B0.9C0.1)2 is measured at 37.1 K using resistive transition and vibration sample magnetometry (VSM) measurements. Details of onset, mid-point and zero resistance Tc values for both samples are provided in Table S1 (ESI†).
95) with minimal processing of spectral data is shown in Fig. 1a. Each spectrum at a specific temperature has been offset vertically for visual clarity. New spectral features occur in the low wavenumber region as the sample temperature approaches 40 K, a few degrees above the superconducting transition. In this case, the onset Tc for Mg(11B0.9C0.1)2 is measured at 37.1 K using resistive transition and vibration sample magnetometry (VSM) measurements. Details of onset, mid-point and zero resistance Tc values for both samples are provided in Table S1 (ESI†).
Key changes in spectral features between 20 cm−1 and 120 cm−1 are highlighted with dotted red arrows in Fig. 1a. The substantial increase in low wavenumber spectral intensity as well as the appearance of new low frequency peaks at or below 40 K suggests a strong connection to superconductivity. Furthermore, these peaks do not diminish at temperatures below 40 K. As is evident in Fig. 1a, the low wavenumber peaks show strong signal to noise and at similar frequencies at temperatures below Tc. For comparison, Fig. 1b shows the absorption spectra for PE powder obtained under the same temperature and wavenumber ranges and operating conditions as for C-doped Mg11B2 shown in Fig. 1a.
There is a difference in the intensity of peaks obtained on MgB2 and on C-doped Mg11B2 at the same temperature and with the same proportions of intermixed PE. The spectra for C-doped Mg11B2 display features more distinctive than the spectra for MgB2 with reduction in sample temperature. For comparison, the spectra for MgB2 with 5% PE as well as for C-doped Mg11B2 with 4% PE mixture are shown in ESI† (Fig. S3). In both cases, the presence of stronger peaks for T < 40 K is evident (dotted red arrows) but the quality and spectral intensity is not as obvious as shown in Fig. 1a. While spectral signal(s) may be influenced by grain orientation and/or preferential texture(s) induced by sample preparation as well as by the quantity of sample diluted with PE, we note below an additional interpretation for this difference in spectral signal.
Table 1 lists deconvolution peak values, grouped in wavenumber segments, for a range of temperatures below and above Tc for C-doped Mg11B2 as shown in Fig. 1a. Numbering for peaks shown in Table 1 are identified in ESI† Fig. S4. Estimates of peak intensities shown in Table 1 are normalised to the highest FWHM value within each peak dataset. Detailed peak deconvolution results for a range of temperatures (10 K < T < 60 K in 5 K increments) are provided in ESI,† as Table S2.
| Peak no. | Temp. [K] | Wave number [cm−1] | Relative intensity [Arb.] | Peak no. | Temp. [K] | Wave number [cm−1] | Relative intensity [Arb.] |
|---|---|---|---|---|---|---|---|
| 2 | 10 | 26.70 | 54 | 17 | 10 | 79.30 | 100 |
| 20 | 26.62 | 48 | 20 | 79.23 | 88 | ||
| 30 | 26.63 | 60 | 30 | 79.18 | 97 | ||
| 35 | 26.89 | 56 | 35 | 79.23 | 100 | ||
| 40 | 26.82 | 59 | 40 | 79.21 | 83 | ||
| 45 | 26.10 | 100 | 45 | 78.95 | 77 | ||
| 50 | 27.17 | 35 | 50 | 79.00 | 63 | ||
| 60 | 26.91 | 31 | 60 | 78.84 | 78 | ||
| 6 | 10 | 39.92 | 55 | 19 | 10 | 90.15 | 98 |
| 20 | 39.96 | 50 | 20 | 90.27 | 95 | ||
| 30 | 40.24 | 57 | 30 | 90.65 | 81 | ||
| 35 | 39.86 | 55 | 35 | 90.15 | 66 | ||
| 40 | 40.28 | 59 | 40 | 90.83 | 59 | ||
| 45 | 39.44 | 57 | 45 | 90.88 | 54 | ||
| 50 | 39.61 | 50 | 50 | 90.92 | 45 | ||
| 60 | 39.30 | 39 | 60 | 91.41 | 59 | ||
| 11 | 10 | 56.23 | 63 | 22 | 10 | 100.63 | 67 |
| 20 | 56.24 | 58 | 20 | 101.08 | 64 | ||
| 30 | 56.26 | 56 | 30 | 100.91 | 51 | ||
| 35 | 56.32 | 64 | 35 | 100.25 | 75 | ||
| 40 | 56.38 | 53 | 40 | 100.47 | 56 | ||
| 45 | 57.25 | 52 | 45 | 99.17 | 75 | ||
| 50 | 57.15 | 39 | 50 | 100.37 | 37 | ||
| 60 | 57.13 | 37 | 60 | 100.33 | 72 | ||
| 14 | 10 | 66.17 | 77 | 24 | 10 | 108.16 | 93 |
| 20 | 66.12 | 70 | 20 | 107.74 | 100 | ||
| 30 | 66.33 | 87 | 30 | 108.10 | 100 | ||
| 35 | 66.26 | 86 | 35 | 108.50 | 81 | ||
| 40 | 66.18 | 71 | 40 | 108.47 | 67 | ||
| 45 | 67.01 | 94 | 45 | 107.97 | 52 | ||
| 50 | 67.52 | 59 | 50 | 108.04 | 51 | ||
| 60 | 67.81 | 67 | 60 | 107.78 | 100 |
Table 1 lists peaks with relatively high intensities within the wavenumber range 20 cm−1 to 110 cm−1 with change in temperature. Each of these peaks show a consistent wavenumber value between temperatures 60 K to 6 K and, similarly, for all peaks in the THz/Far IR spectra shown in ESI† (Fig. S4 and Table S2). For peaks listed in Table 1, the variation in peak position (i.e., wavenumber value) and the standard deviation from the average peak value (for each temperature) is <0.5 meV. Nevertheless, the relative peak intensities vary with temperature between 6 K and 60 K as shown in Table 1. For example, the peak at 26.7(3) cm−1 shows highest intensity at 45 K, the peak at 79.1(2) cm−1 is highest at 10 K and 35 K and the peak at 108.1(3) cm−1 is highest at 20 K, 30 K and 60 K. These shifts in relative intensity with temperature reflect subtle shifts in either electron density, atom positions or both, with change in temperature. A comparison of the THz/Far IR spectra and deconvoluted peaks for 30 K < T < 40 K, along with numeric identification of peaks referenced in Table 1, is provided in the ESI,† section (Fig. S4).
Phonon dispersions – acoustic region
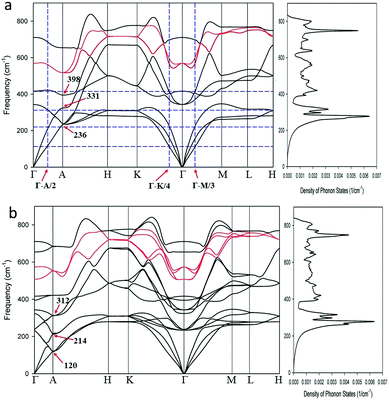
A PD calculation for the unit cell of MgB2 with P6/mmm symmetry is shown in Fig. 2a. The PD displays key features in the optical range including a phonon anomaly associated with the E2g mode (highlighted in red in Fig. 2a) around Γ. This phonon anomaly has been previously discussed by many authors and is well correlated with superconductivity.8–11,26 We provide vertical and horizontal dashed lines in Fig. 2a as guides to highlight specific features in the acoustic region of the PD (i.e., for wavenumbers less than ∼340 cm−1).Note that the lowest optical frequency at the Γ point is ∼340 cm−1. At this point, absorption of electromagnetic radiation will not take place at wavenumbers below this value because the available phonon states for creation or excitation of optical phonons do not exist. Hence, our focus for these absorption experiments is on the acoustic phonon modes and evidence for their presence in superconductors at or below Tc. In Fig. 2a, integer proportions of key reciprocal directions can be identified and are discussed below.
Superlattice calculations – Brillouin zones
Superlattice calculations in this work follow a similar rationale to that used and discussed in our previous publication on laboratory-based Raman microscopy of MgB2.19 In practice, a reduced symmetry to P6/mmm is assigned so that the full supercell describes all symmetry elements. Calculations are carried out for superlattice periods equivalent to 2c, 3c and 4c where c is the c-axis unit cell dimension of the P6/mmm lattice. These calculations utilise a variety of k-grids and LDA and GGA modes in order to achieve self-consistent models at the highest resolution possible for the supercell dimension.Using different k-grid values and LDA and GGA approximations for the same superlattice model, a spread of phonon mode frequencies for the same mode is obtained. These values vary for specific modes at ω < 400 cm−1, for example, frequency differences between 1 cm−1 and 3 cm−1 within the same approximation (LDA or GGA) for different k-grid values and differences between ∼5 cm−1 and 15 cm−1 for comparisons using LDA or GGA functionals for the same k-grid value. Readers are referred to earlier work on key parameter choices for DFT calculations that enable systematic evaluation of meV features pertinent to superconducting materials.27
For many converged calculations, the Density Functional Perturbation Theory (DFPT) approach was utilised. However, the 3c calculation was unable to converge using this DFPT approach presumably due to inappropriate k-grid value27 or insufficient core and/or memory allocation for computation. Consequently, the finite displacement (FD) approach was utilised to achieve convergence for PD calculations for 2c and 3c (Table 2). The relevant PDs for 3c and 4c calculations are shown in Fig. S5 and S6 (ESI†). An example of a converged PD calculated for superlattice period 2c, with Space Group symmetry P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) c2 using a linear approximation for PD calculation is shown in Fig. 2b. Note the folding of reciprocal space in the ΓA direction, which can be visualised by mirror reflecting the dispersion along ΓA in Fig. 2a (i.e., for P6/mmm), with a mirror plane along the dashed vertical line at ΓA/2, which takes dispersion values on the Brillouin Zone (BZ) boundary at A onto the Γ point. While folding of reciprocal space predominantly takes place in the ΓA direction, the bands along KΓ and ΓM are also influenced.
c2 using a linear approximation for PD calculation is shown in Fig. 2b. Note the folding of reciprocal space in the ΓA direction, which can be visualised by mirror reflecting the dispersion along ΓA in Fig. 2a (i.e., for P6/mmm), with a mirror plane along the dashed vertical line at ΓA/2, which takes dispersion values on the Brillouin Zone (BZ) boundary at A onto the Γ point. While folding of reciprocal space predominantly takes place in the ΓA direction, the bands along KΓ and ΓM are also influenced.
| Space group | n × c-axis | ω 1 (at A) | ω 2 (at A) | ω 3 (at A) | Phonon calc’n | Funt’al | Δk value (Å−1) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| (cm−1) | (meV) | (cm−1) | (meV) | (cm−1) | (meV) | |||||
| P6/mmm | 1 | 236 | 29.3 | 331 | 41 | 398 | 49 | Linear | LDA | 0.01 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) c2 c2 |
2 | 120 | 14.9 | 214 | 27 | 312 | 39 | Linear | LDA | 0.013 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) c2 c2 |
2 | 117(12) | 15(2) | 210(5) | 26.0(6) | 303(13) | 38(2) | Finite D | LDA + GGA | 0.01 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
3 | 82 | 10 | 146 | 18 | 232 | 29 | Finite D | LDA | 0.01 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
4 | 59(3) | 7.3(4) | 114(2) | 14.1(3) | 178(7) | 22(1) | Linear | LDA + GGA | 0.01 |
Table 2 lists DFT calculations obtained for the PD of MgB2 with symmetry conditions for three space groups: P6/mmm, P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) c2 and P
c2 and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1. The values for ω1, ω2 and ω3 are for the intersection of the acoustic phonons at the boundary A along ΓA. Values from calculations that utilise the LDA and the GGA functional are averaged in Table 2. Standard deviations for the least significant value are given in parentheses. From Table 2, we note that for increasing value of n (the superlattice along c) the value for ω1 decreases. In general, for n = 2 and n = 4, the lowest intersection of the acoustic phonon at the boundary A (i.e., ω1) is approximately half of the lower order superlattice.
m1. The values for ω1, ω2 and ω3 are for the intersection of the acoustic phonons at the boundary A along ΓA. Values from calculations that utilise the LDA and the GGA functional are averaged in Table 2. Standard deviations for the least significant value are given in parentheses. From Table 2, we note that for increasing value of n (the superlattice along c) the value for ω1 decreases. In general, for n = 2 and n = 4, the lowest intersection of the acoustic phonon at the boundary A (i.e., ω1) is approximately half of the lower order superlattice.
The accuracy of these DFT calculations, and thus, for frequency values, can also be evaluated from Table 2. For example, frequency values determined using an FD method for n = 2 are within standard error of those obtained by a linear approximation at lower DFT resolution (i.e., where the value for Δk is 0.013 A−1).27 We also note that the precision of calculations – as measured by the standard deviations for each frequency in Table 2 for the n = 4 superlattice with P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 symmetry – suggests that this condition is optimum for the MgB2 structure. We show a partial PD for MgB2 with an n = 4c superlattice in Fig. S6 (ESI†).
m1 symmetry – suggests that this condition is optimum for the MgB2 structure. We show a partial PD for MgB2 with an n = 4c superlattice in Fig. S6 (ESI†).
Discussion
Frequencies relevant to the THz/Far IR regions are ideal for investigation of superlattice effects in the low wavenumber range. Wavenumber ranges for standard laboratory Fourier Transform IR (FTIR) and Raman spectroscopy typically extends to about 100 cm−1 or higher. Recent instrumentation advances can extend that limit to lower values for laboratory-based instruments with potential to measure below 50 cm−1.29 Raman signals with low wavenumbers are common in artificial semiconductor nanostructures and can be explained as a result of superlattice periodicity.30–33 This periodicity folds reciprocal space and activates optic modes with phonon frequencies at fractional values of those for the original crystal periodicity.30–33To place these experimental results into perspective, we examine possible mechanisms and evidence for superlattices in MgB2 and similar structures. We then relate the effect of superlattice geometries on subtle variations in electronic properties.
Intrinsic superlattice periodicities – hybridised orbitals
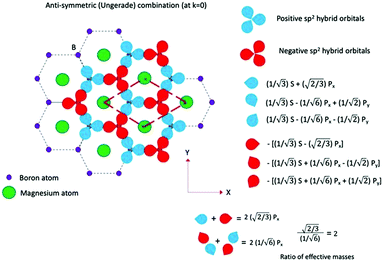
Previous discussion and graphic illustrations show that the electron density responsible for conduction in MgB2 is largely concentrated along B–B covalent bonds.9,27,28 These electronic charges populate σ-bands which correspond to the inverted, approximately parabolic bands30,31 that are degenerate at Γ.Consideration of more than one unit cell as shown schematically for the a–b plane of MgB2 in Fig. 3 (emphasizing hybridisation between boron atoms) provides a convenient means to visualise the relationship of bonding and anti-bonding orbitals in real space. DFT calculations31 of MgB2 band structures identify these σ-bands at Γ as shown in Fig. S7 (ESI†), and through consideration of bonding and anti-bonding orbitals, translates to the hybridized orbital configurations shown in Fig. 3.31
This bonding and anti-bonding orbital character provides a real space physical interpretation for the origin of approximate parameters that define the inverted parabolic construct at Γ in band structure calculations for MgB2.31,32 We have developed these parameters to determine differences between heavy and light effective masses for MgB2 around Γ and for associated bands.32 This interpretation of band structures is well understood for semiconductors with analogous, degenerate σ-bands33–36 and similar principles are utilised in this study. For completeness, we detail an equivalent schematic for sp2 bonding hybridisation within the boron plane(s) of MgB2 in Fig. S8 (ESI†).
The anti-bonding character of σ-bands at Γ is also supported by DFT calculations which show that the energy for these bands is higher at Γ, compared to their energy as the bands circumscribe bonding character at the boundary zone37 (e.g., at M along ΓM or at K along ΓK). At these points on the boundary zones, a change in phase is also expected. In contrast, along the ΓA direction, the σ-band has lower energy at Γ compared to the energy at A, so an opposite condition along the c* direction is expected. In this case, a bonding orbital with pz character at Γ and with antibonding character at A is evident (Fig. S7, ESI†).
One possible interpretation of real space bonding character, consistent with anti-bonding sp2 hybridisation in the boron plane, and with bonding character in the c-direction (at Γ) is schematically illustrated in Fig. 4. In this interpretation, we posit that by considering the bonding–antibonding character of orbital hybridisation in the boron plane and in the c-direction, phase changes resulting in a halving of the c*-direction (or doubling of the c axis lattice parameter) is a minimal requirement to define an appropriate structural periodicity.
With electrons at the Fermi energy (i.e., the conduction electrons) localised along B–B bonds,28 periodicities in real space that are modulated by the orbital character of boron atoms can be identified. These periodicities appear to be correlated to wavelengths associated with Bloch waves. For instance, from a knowledge of the Fermi wavevector, determined from EBS intersections with the Fermi energy and/or their relative distances with respect to the BZ boundary in Fermi surfaces (FS), simple relationships are apparent in reciprocal space. These relationships are demonstrated schematically in Fig. S9 (ESI†). As is readily demonstrated in textbook examples,38,39 these fractional reciprocal space dimensions can be converted to in-plane superlattice modulations and to distances in real space.38,40–42
The average radius of the tubular FS for kz = 0 is ∼1/6 of the distance from the Γ centre point to the M point of the BZ boundary. This radius translates to a wavelength six times the inverse of the reciprocal space distance to the boundary. At reciprocal point A (i.e., kz = π/c), the FS shows an increased radius to ∼1/4 of the ΓM distance. Careful inspection of the parallel FSs (Fig. S9, ESI†) shows that the radius of the outer (heavy effective mass) FS at kz = 0 is approximately identical to the radius of the inner (light effective mass) FS at kz = π/c.
This observation is a key to concepts of electron resonance, whereby conservation of energy and momentum (or wavevector) is inherently guaranteed by a constant value for the Fermi energy and the total momentum of combined Fermi wavevectors. For example, for electrons with states at half the distance to the A point (kz = π/2c), the a* (or x-vector) component of the Fermi wavevector is given by,
| kFx = [(1/4 + 1/6)/2] ΓM = 5/24 ΓM. | (1) |
Two electrons at this state may interact to produce one electron at kz = 0 with kFx = 1/6 ΓM and another at kz = π/c with kFx = 1/4 ΓM. Thus, a mechanism to transfer momentum between a direction fully contained in the a*–b* plane will include energy components in the c* direction(s). In the ΓK direction, different multiplicities exist at kz = 0 and kz = π/c as shown in ESI,† Fig. S9. In this case, further interplay of electrons between the ΓM and ΓK directions is also probable.
We note that integer multiples of the c-axis lattice parameter can be matched to periodicities identified in the hybridisation schematic and in the analysis of average FS radii relative to the BZ boundary. For example, 3c/(31/2a) = 3.5 Å × 3/(3.04 Å × 31/2) = 10.5/5.265 = 1.994 ∼ 2. Such proportionality between c-axis dimensions and in-plane periodicities favours a match between in-plane and perpendicular acoustic vibrations and velocities as discussed in the following section.
Acoustic phonons and lattice dimensions
Above absolute zero, the Bose-Einstein statistical distribution applies to both longitudinal and transverse acoustic phonons in all possible three-dimensional (3D) directions. For the layered hexagonal structure of MgB2, a longitudinal acoustic movement in the a*–b* plane is oriented parallel to transverse acoustic movements along the c* direction and vice versa.Longitudinal vibrations are compression waves and transverse vibrations are shear waves resulting in stronger restoring forces for the former compared to the latter vibrations.43 Appropriate consideration of in-phase (i.e., same sense) movement of the entire unit cell is required for correct analysis of acoustic modes. In contrast, optical modes, or acoustic modes at the BZ boundary, demonstrate an anti-sense (or out of phase) movement. In these latter cases, atoms in the basis set move relative to each other out of phase.43 DFT calculations show that Mg is the major contributor to the PD partial density of states in the acoustic region.10 Thus, movement of Mg atoms will influence the nature of acoustic phonon interactions and, as we will show, are an additional low energy (meV) feature of MgB2 superconducting properties.
Inspection of the PD for MgB2 with P6/mmm symmetry as shown in Fig. 2a, shows that the acoustic transverse and longitudinal frequencies for kz = π/2c (or ΓA/2) display harmonic behaviour up to the second lowest optical mode (i.e., ∼415 cm−1). Furthermore, the two intersecting acoustic phonon frequencies at ΓA/2 show similar values to two other, in-plane high symmetry directions at ΓM and ΓK. Remarkably, these matching values occur at ∼1/3 ΓM and 1/4 ΓK, respectively. In practice, these values are in equivalent reciprocal space positions along the linear sections (i.e., parallel to the Fermi level) of the PD anomaly associated with the E2g mode10–12 as shown by the dotted vertical lines in Fig. 2a.
In Fig. 2a, for a given frequency ω, (e.g., ∼100 cm−1 to ∼110 cm−1), we identify that the k-vector at which the longitudinal acoustic branch along ΓA shows this frequency value is ∼ΓA/4. Accordingly, intersection of this same frequency with the transverse acoustic branch is at ∼ΓA/2. This relationship confirms that wavelengths for the respective acoustic mode wavevectors show inverse proportionality with a ratio ∼2. That is, the longitudinal acoustic velocity is approximately twice the value of the transverse acoustic velocity at the same frequency. This proportion results from the balance of restoring forces along longitudinal and transverse directions. Similar conclusions can be obtained for the ΓM and ΓK directions shown in Fig. 2a.
Our earlier work inferred the presence of partial harmonicity for acoustic PDs.19,44 With this in mind, we note that direct and reciprocal space proportional dimensions favour the occurrence of standing waves in crystalline structures. Such standing waves generate non-dispersive waves in regions where the dispersion curve, ω vs. k, has approximately linear dependence.10,45 In this manner, coincident lattice points for electronic and acoustic waves may serve as nodal points, enabling a degree of tuning and synchronicity between electron and phonon waves that move and interact across the material. However, the observation of superlattice frequencies, which may be difficult to detect but are nevertheless present, may be an indication of minor anharmonicity in MgB2. In such a case, multiples of a single harmonic are required to better approximate anharmonic behaviour.45 Anharmonicity has been reported in several publications46–48 as strongly linked to superconductivity in MgB2; this connection to superlattices is discussed below.
Superlattice signatures
A mechanistic interpretation of DFT calculations for superconductivity can also be gained by further analysis of electron density distributions and Fermi surface topologies.28,49,50 In particular, these features provide detail about the electrons that participate in conduction processes.38,40–42 The deformation potential approach has clearly shown that the conduction electrons in MgB2 largely move in the boron planes, along B–B bonds in response to B atom movements along E2g optical phonon mode displacement patterns.9,28 For acoustic displacements along the boron in-plane directions, stretching of the B–B bonds is also expected to result in deformation potentials. Thus, we may observe a corresponding modulated electron density distribution, or charge density wave, as inferred in our earlier work.28A net electric field pointing along the c-direction is generated because the electron density response to acoustic (and optic vibration) deformation is largely contained within the B–B plane.28 An electric field effect is also generated because electron density modulations retain connection to the periodicity and displacement symmetry of the in-plane longitudinal acoustic wave.51 This electric field imparts a driving force onto the charged Mg layers which donate their valence electrons to the B–B plane.8,9 This effect establishes a strong coupling between acoustic movements in the B–B plane and the perpendicular plane (i.e., the c- or c*-direction). This coupling is largely reflected in the coincidence of velocities along two different directions as noted above. This coincidence of velocities may also guarantee a high degree of coherence and synchronicity that would otherwise not be possible without the influence of acoustic phonon modes.
The fact that we observe absorption of THz/Far IR radiation in spectra of MgB2 at frequencies that include 100–110 cm−1 but also at substantial fractions of these values is essential to our understanding of superconductivity. For instance, these observations indicate that all these low frequencies contribute to the available optic modes of MgB2 that absorb electromagnetic radiation on approaching Tc and at values below Tc. This feature also confirms that superlattices are present in the material, as suggested from our earlier Raman experiments.19,20
Furthermore, these acoustic modes must have a strong connection to superconductivity given that the spectral density largely evolves after crossing Tc. These superlattice signatures are indicative of an overall structural transition with significant electronic involvement which we suggest is connected to the anharmonicity of MgB2.45–48 Small gaps may also be expected in the electronic band structures for superlattices at the new superlattice BZ boundaries.17,19,20,22 We also suggest that previous interpretations of frequencies matching superconducting gap energies in Raman investigations may have mistakenly attributed such observations to pair breaking mechanisms. Pair breaking mechanism(s) can not readily explain observations at fractional values of the presumed pair-breaking (gap) frequencies.
Superlattice formation has been experimentally confirmed in Al-substituted MgB2 by spectroscopy10 and by electron microscopy.52,53 Considering the AlB2-rich end of the substitutional range for this structure type, amplification of the superconducting Tc has been discussed by DiCastro et al.54,55 in terms of a combined effect of tuning the Fermi level and the tensile micro-strain. The importance of a Feshbach shape resonance56–58 and proximity of the chemical potential (or FS) to a topological Lifshitz transition has been extensively discussed by Bianconi50 and constitutes a topic of ongoing interest at SuperStripes conferences. We also note sub-THz reflectivity ratios obtained for CaAlSi, a superconductor (Tc = 6.7 K) isostructural with MgB2, described by Lupi.17 With radiation polarized along the c axis direction, the reflectivity ratio shows a series of peaks between 10 cm−1 and 40 cm−1, particularly for data at 3.5 K and 4.5 K.17 Such modularity of signal(s) below the Tc value for CaAlSi may be indirect evidence for the presence of a lower symmetry superlattice at these temperatures.
The investigation of Al-substituted MgB2 using high resolution neutron diffraction with pair distribution functions by Campi et al.,22 is also a source of relevant structural information. For example, comparison of the c-axis value for (Mg1−xAlx)B2 at superlattice multiples of n (n = 2, 3, 4) showed that when x = 0.5, the superlattice c-axis is an integer multiple of the fundamental unit cell. However, for x = 0.0 (i.e., no Al substitution) and for intermediate values of x, a four times c-axis superlattice for MgB2 diverged from an integer multiple beyond the experimental errors of these high resolution structural determinations.22 These data by Campi et al.22 suggest that MgB2 may exist as a supercell, wherein particular internal distances are shifted slightly from P6/mmm positions.
More recently, Wu et al.59 used transmitted X-ray diffraction measurements with synchrotron radiation to explore electron and hole densities in MgB2 for temperatures 6 K < T < 100 K. Wu et al.59 used a difference electron Fourier method and determined that electron and hole densities develop an asymmetric distribution with respect to the B atomic plane. This asymmetry is accompanied by differentiation of the distances between the B–B plane and adjacent Mg layers, as the temperature approaches and crosses the superconducting transition temperature. We interpret these observations to suggest a change in symmetry of the MgB2 structure occurs as temperature is reduced to Tc and to values below Tc. This change is consistent with a lower, or reduced, symmetry indicative of a superlattice structure.19
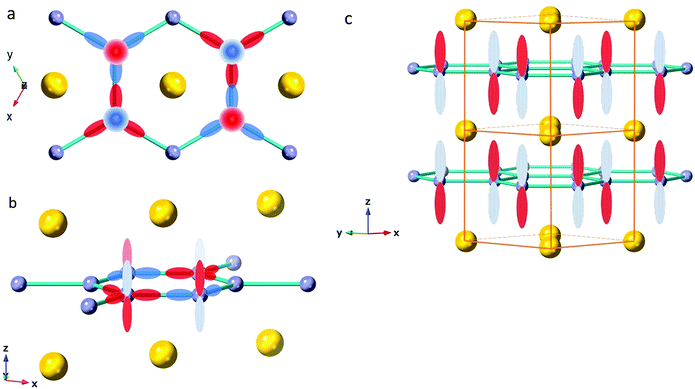
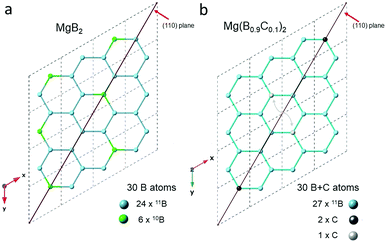
Finally, circumstantial evidence for superlattice formation may be invoked from the enhanced signal strength and distinctive features of the spectra for C-doped Mg11B2 compared with MgB2. Earlier work23,24 established that carbon in Mg(B1−xCx)2 for 0 < x < 0.3 substitutes onto boron sites in the a–b plane. In this study, for which x = 0.10, an ordered distribution of carbon in the a–b plane will disturb the P6/mmm symmetry compared to MgB2 without carbon.
The symmetry of the hexagonal plane is compared in Fig. 5 in which we show ordered arrangements of 30 atoms with nominal P6/mmm symmetry. In Fig. 5a, we show a normal distribution of boron atoms including the natural abundance of both isotopes. In Fig. 5b, we show the presence of 10% C on boron sites in an ordered configuration that requires one C to be alternately on either side of the (110) plane as displayed by the grey coloured atoms (i.e., a mirror plane is removed). This requirement clearly violates P6/mmm symmetry and, we suggest, may be a superlattice configuration with P6mm symmetry as noted in an earlier publication.19 Changes to lower symmetry conditions – induced by a different atom – may accentuate THz signals for C-doped Mg11B2 compared to those obtained for MgB2. These variations in THz spectral signal at low wavenumber for substituted compositions of the AlB2 type structure warrants further detailed understanding.
Analogous band structures
The connection between superlattices and superconductivity of MgB2 and C-doped MgB2 is clearly evident by these THz/Far IR absorption measurements with change in temperature to, and below, Tc. However, there is a similarity of topology between key MgB2 σ-bands and the bands calculated for artificial semiconductor superlattices. In particular, an analogy to semiconductor superlattices perpendicular to the growth direction is encapsulated in corresponding Tight Binding (TB) equations. For example, in the vicinity of the Fermi energy, the approximately inverted parabolic σ-bands can be mathematically expressed using TB equations for layered materials31,60–63 as| En(kx,ky,kz) = E0 −2t⊥cos(ckz) − ℏ2(kx2 + ky2)/2mn | (2) |
For MgB2, the effective masses for the heavy and light holes are typically around mHeff = 0.53–0.59, mLeff = 0.20–0.28, E0 = 0.58–0.6 and t⊥ = 0.092–0.094 eV.9,64,65 Apart from the specific coefficients, the TB equation is identical to the equation used to describe artificial semiconductor superlattices, where c is perpendicular to the superlattice interface (i.e., parallel to the growth direction).66,67
According to these TB equations, electrons move nearly freely in the a–b plane and tunnel across potential barriers in the c-direction.66,67 Since the effective mass in the c-direction is
| meff = ℏ2(∂2E/∂k2)−1, | (3) |
| meff = ℏ2(2c2t⊥cos(ckz)) | (4) |
Hence, meff is undefined (or infinite) when ckz = (2n − 1)π/2(n = 1, 2, 3, …,∞).68 From the gradient of the FS,
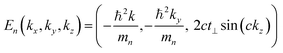 | (5) |
| ckz = (2n − 1)π/2(n = 1, 2, 3, …,∞) |
| ckz = nπ(n = 1, 2, 3, …,∞) |
Under these conditions, it is worth noting that the mid position to the BZ boundary at A for MgB2, with kz = π/2c, is again of significance, but from a different perspective given our analogy to semiconductor superlattices. For example, a well known feature of artificial semiconductor superlattices is that folding of reciprocal spaces for individual semiconductor components is displayed when the combined nanoscale thicknesses of alternating semiconductor materials becomes the new superlattice unit cell dimension.35,66,67,69 Such folding influences many semiconductor properties and is manifest as lower vibration frequencies in Raman and IR spectra.32,35,70,71 This understanding of the BZ condition along Γ–A is consistent with our previous published Raman data on MgB219 and YB6,20 as well as the current synchrotron THz/Far IR observations. Not unreasonably, we also expect that other quasiparticles, or excitations in the meV energy range, observed and extensively investigated for artificial semiconductor superlattices, may influence our understanding of superconductivity in MgB2 and many other materials.
Conclusions
THz/Far IR synchrotron transmission experiments as a function of temperature have been conducted on diluted, pelletised MgB2 and C-doped Mg11B2. Calibrated absorption spectra at low wavenumber display a clear correlation with superconductivity, as sample temperature reduces to near, and then below, Tc. The intensity of the absorption peaks and the overall spectral weight of the THz/Far IR signals increase with lower sample temperature. Strong absorption occurs at wavenumber values that correspond to superconducting gaps for C-doped Mg11B2 and MgB2. Absorption peaks are also observed at substantial fractions of these values, indicating that superlattice frequencies contribute to the PD for these superconductors by introducing new optic modes. DFT calculations using superlattices along the c-axis direction show folded mode frequencies in PDs that match observed experimental absorption values.Analyses of bonding characteristics, Fermi vectors from electronic band structures and Fermi surfaces, PD relations and geometrical parameters, enable identification of integer proportionalities in real and reciprocal spaces that are consistent with subtle shifts in real space symmetry. For example, these analyses indicate that symmetry reductions from P6/mmm, largely electronic in character though coupled to phonon frequencies, occur in MgB2 and C-doped Mg11B2 when cooled near to and below Tc. Such symmetry reductions have strong implications for interpretation of superconducting mechanisms. We reflect on the similarities in our interpretations with physical property manifestations from artificial semiconductor superlattices. The presence of low wavenumber peaks clearly coincident with independently determined superconductor energy gaps for MgB2 and C-doped Mg11B2 suggest that superlattices may be exploited to design new superconductors to achieve desired values of Tc. Analogies with artificial semiconductor superlattices may provide further guidance and inspiration for superconductor materials development.
Author contributions
JAA: conceptualisation, formal analysis, methodology, investigation, supervision, funding acquisition, writing – original, review and editing; BG: formal analysis, investigation, validation and visualization; MS: formal analysis, investigation, resources, validation; DA: investigation, methodology and supervision; IDRM: conceptualisation, formal analysis, funding acquisition, validation, visualization, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to the Australian Synchrotron, ANSTO for awarded merit beamtime. We also acknowledge the Central Analytical Research Facility (CARF) and the e-Research Office, both at QUT, for access to laboratory facilities and to high performance computing and assistance, respectively.References
- P. B. Allen, in Dynamical Properties of Solids, ed. G. K. Horton and A. A. Maradudin, North Holland Publishing Company, 1980, vol. 3, ch. 2 Search PubMed.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175 CrossRef CAS.
- M. Tinkham, Introduction to Superconductivity, McGraw-Hill, New York USA, 1996 Search PubMed.
- E. Maxwell, Phys. Rev., 1950, 78, 477 CrossRef CAS.
- C. Reynolds, B. Serin and L. Nesbitt, Phys. Rev., 1951, 84, 691 CrossRef CAS.
- A. Bill, V. Kresin and S. Wolf, Pair Correlations in Many-Fermion Systems, Springer, 1998, p. 25 Search PubMed.
- R. F. Wood, B. E. Sernelius and A. L. Chernyshev, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 1 CrossRef.
- J. Kortus, I. I. Mazin and K. D. Belashchenko, et al. , Phys. Rev. Lett., 2001, 86, 4656 CrossRef CAS PubMed.
- J. M. An and W. E. Pickett, Phys. Rev. Lett., 2001, 86, 4366 CrossRef CAS PubMed.
- J. A. Alarco, P. C. Talbot and I. D. R. Mackinnon, Phys. Chem. Chem. Phys., 2015, 17, 25090 RSC.
- I. D. R. Mackinnon, P. C. Talbot and J. A. Alarco, Comput. Mater. Sci., 2017, 130, 191 CrossRef CAS.
- J. A. Alarco, P. C. Talbot and I. D. R. Mackinnon, Phys. C, 2017, 536, 11 CrossRef CAS.
- W. Ghann and J. Uddin, Terahertz (THz) Spectroscopy: A Cutting-Edge Technology, InTechOpen, 2016 Search PubMed.
- G. L. Carr, M. C. Martin and W. R. McKinney, et al. , Nature, 2002, 420, 153 CrossRef CAS PubMed.
- O. Khatib, H. A. Bechtel and M. C. Martin, et al. , ACS Photonics, 2018, 5, 2773 CrossRef CAS.
- Y.-L. Mathis, B. Gasharova and D. Moss, J. Bilogical Phys., 2003, 29, 313 CrossRef.
- S. Lupi, in Advances in Condensed Matter Physics, ed. V. V. Moshchalkov, Hindawai Publishing Corporation, 2011, ch. Article ID 816906, p. 9 Search PubMed.
- P. Calvani, S. Lupi and M. Ortolani, et al. , Infrared Phys. Technol., 2008, 51, 429 CrossRef CAS.
- J. A. Alarco, A. Chou and P. C. Talbot, et al. , Phys. Chem. Chem. Phys., 2014, 16, 24443 RSC.
- J. A. Alarco, M. Shahbazi and P. C. Talbot, et al. , J. Raman Spectrosc., 2018, 49, 1985 CrossRef CAS.
- S. J. Clark, M. D. Segall and C. J. Pickard, et al. , Z. Kristallogr., 2005, 220, 567 CAS.
- G. Campi, A. Ricci and A. Bianconi, J. Supercond. Novel Magn., 2012, 25, 1319 CrossRef CAS.
- J. Karpinski, N. D. Zhigadlo and S. Katrych, et al. , Phys. C, 2007, 456, 3 CrossRef CAS.
- J. Karpinski, N. D. Zhigadlo and S. Katrych, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(214507), 1–11 Search PubMed.
- J. C. Grivel and M. Burdusel, Phys. C, 2016, 528, 65 CrossRef CAS.
- J. A. Alarco and I. D. R. Mackinnon, in Phonons in Low Dimensional Structures, ed. V. N. Stavrou, InTech Open, London UK, 2018, ch. 5, p. 75 Search PubMed.
- I. D. R. Mackinnon, A. Almutairi and J. A. Alarco, in Real Perspectives of Fourier Transforms and Current Developments in Superconductivity, ed. J. M. V. Arcos, IntechOpen Ltd., London UK, 2021, ch. 10, p. 1 Search PubMed.
- J. A. Alarco, P. C. Talbot and I. D. R. Mackinnon, Mod. Numer. Sim. Mater. Sci, 2018, 8, 21 CAS.
- H. J. Choi, D. Roundy and H. Sun, et al. , Nature, 2002, 418, 758 CrossRef CAS PubMed.
- D. S. Urch, Orbitals and Symmetry, Penguin Books Ltd, Harmondsworth, Middlesex, England, 1970 Search PubMed.
- A. Almutairi, Electronic Band Structure Equations and Fermi Surface Evolution from 2D Materials to 3D Layered Superconducting Compounds, PhD thesis, Queensland University of Technology, 2019 Search PubMed.
- M. Dresselhaus, G. Dresselhaus and S. B. Cronin, et al., Solid State Properties - From Bulk to Nano, Springer Nature, Berlin, Germany, 2018 Search PubMed.
- J. C. Phillips, Bonds and Bands in Semiconductors, Academic Press, 1973 Search PubMed.
- M. I. Dyakonov, Spin Physics in Semiconductors, Springer, 2nd edn, 2017 Search PubMed.
- in Fundamentals of Semiconductors - Physics and Materials Properties, ed. P. Y. Yu and M. Cardona, Springer, 2010 Search PubMed.
- K. W. Böer and U. W. Pohl, Semiconductor Physics, Springer, 2018 Search PubMed.
- J. Stohr and H. C. Siegmann, Magnetism - From Fundamentals to Nanoscale Dynamics, Springer, 2006 Search PubMed.
- S. L. Altmann, Band Theory of Solids: An Introduction from the Point of View of Symmetry, Clarendon Press, Oxford, 2002 Search PubMed.
- H. Jones, The Theory of Brillouin Zones and Electronic States on Crystals, North-Holland Publishing Company, Amsterdam, 1960 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders, Philadelphia, 1976 Search PubMed.
- C. Kittel, Introduction to solid state physics, Wiley, 2005 Search PubMed.
- J. M. Ziman, Principles of the Theory of Solids, Cambridge University Press Second edn, 1972 Search PubMed.
- J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, Oxford University Press, 1960 Search PubMed.
- J. A. Alarco, P. C. Talbot and I. D. R. Mackinnon, Phys. Chem. Chem. Phys., 2014, 16, 25386 RSC.
- I. G. Main, Vibrations and Waves in Physics, Cambridge University Press, Cambridge, 1979 Search PubMed.
- T. Yildirim, O. Gülseren and J. W. Lynn, et al. , Phys. Rev. Lett., 2001, 87, 037001 CrossRef CAS PubMed.
- M. d’Astuto, M. Calandra and S. Reich, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1 CrossRef.
- A. Y. Liu, I. I. Mazin and J. Kortus, Phys. Rev. Lett., 2001, 87, 087005 CrossRef CAS PubMed.
- J. A. Alarco, A. Almutairi and I. D. R. Mackinnon, J Supercond Nov Magn, 2020, 33, 2287 CrossRef CAS.
- A. Bianconi, J. Supercond. Novel Magn., 2018, 31, 603 CrossRef CAS.
- G. Grüner, Density waves in solids, 1994 Search PubMed.
- H. W. Zandbergen, M. Y. Wu and H. Jiang, et al. , Phys. C, 2002, 366, 221 CrossRef CAS.
- J. Y. Xiang, D. N. Zheng and J. Q. Li, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 214536 CrossRef.
- D. Di Castro, S. Agrestini and G. Campi, et al. , Europhys. Lett., 2002, 58, 278 CrossRef CAS.
- A. Bianconi, S. Agrestini and D. Di Castro, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 174515 CrossRef.
- A. Bianconi, D. Di Castro and S. Agrestini, et al. , J. Phys.: Condens. Matter, 2001, 13, 7383 CrossRef CAS.
- A. Bianconi, J. Supercond.: Incorporating Novel Magnetism, 2005, 18, 626 Search PubMed.
- A. Bianconi, S. Agrestini and A. Bussmann-Holder, J. Supercond., 2004, 17, 205 CrossRef CAS.
- S. Y. Wu, P.-H. Shih and J.-Y. Ji, et al. , Supercond. Sci. Technol., 2016, 29, 045001 CrossRef.
- I. N. Askerzade and B. Tanatar, Phys. C, 2003, 384, 404 CrossRef CAS.
- I. N. Askerzade, J. Korean Phys. Soc., 2004, 45, 475 Search PubMed.
- I. N. Askerzade, Physics - Uspekhi, 2009, 52, 977 CrossRef CAS.
- I. Askerzade, Unconventional Superconductors - Anisotropy and Multiband Effects, Springer-Verlag, Berlin Heidelberg, 2012 Search PubMed.
- Y. Kong, O. V. Dolgov and O. Jepsen, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 1 CrossRef.
- M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1 CrossRef.
- D. K. Ferry, S. M. Goodnick and J. Bird, Transport in Nanostructures, Cambridge University Press, Cambridge, Second edn, 2009 Search PubMed.
- J. D. Patterson and B. C. Bailey, Solid-Sate Physics - Introduction to the Theory, Springer Nature, Cham, Switzerland, Third edn, 2018 Search PubMed.
- L. Solymar and D. Walsh, Electrical Properties of Materials, Oxford University Press, Oxford, United Kingdom, Seventh edn, 2004 Search PubMed.
- M. G. Cottam, Dynamical Properties in Nanostructured and Low-Dimensional Materials, IOP Publishing, London, UK, 2015 Search PubMed.
- M. Cardona, Superlattices and Micrsotructures, 1990, 7, 183 CrossRef CAS.
- V. Davydov, E. Roginskii and Y. Kitaev, et al. , Nanomaterials, 2021, 11, 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03405g |
| This journal is © the Owner Societies 2021 |