The rovibrational Aharonov–Bohm effect
Received
22nd July 2021
, Accepted 13th October 2021
First published on 14th October 2021
Abstract
Another manifestation of the Aharonov–Bohm effect is introduced to chemistry, in fact to nuclear quantum dynamics and high-resolution molecular spectroscopy. As demonstrated, the overall rotation of a symmetric-top molecule influences the dynamics of an internal vibrational motion in a way that is analogous to the presence of a solenoid carrying magnetic flux. To a good approximation, the low-energy rovibrational energy-level structure of the quasistructural molecular ion H+5 can be understood entirely in terms of this effect.
1 Introduction
More than 60 years ago, following the footsteps of Ehrenberg and Siday,1 Aharonov and Bohm2,3 provided a detailed analysis of the significance of electromagnetic potentials in quantum theory. They made the then surprising claim that in the quantum domain these potentials have a physical and measurable effect on charged particles even in regions where the magnetic field vanishes. The findings of Aharonov and Bohm were verified experimentally.4,5 While at the beginning the statements of these studies about fields and potentials may have seemed just counterintuitive curiosities of quantum theory, over the years the Ehrenberg–Siday–Aharonov–Bohm (usually simply referred to as the Aharonov–Bohm) effect, and its various analogues, found application in a number of different fields of molecular sciences. Of particular importance to this study is the so-called molecular Aharonov–Bohm (MAB) effect6–8 within Born–Oppenheimer theory,9,10 in which the conical intersection seam,11,12 corresponding to degenerate electronic states, has an effect on the nuclear motion analogous to the presence of a solenoid carrying magnetic flux. The implications of the MAB effect for both bound states7,8 and scattering events13 have been explored.
We are aware of no indication of the significance of the Aharonov–Bohm effect in nuclear quantum dynamics unrelated to the MAB effect. In this paper we introduce the ‘rovibrational Aharonov–Bohm effect’, occurring in symmetric-top molecules with a separable vibrational degree of freedom (dof). As shown below, the ‘rotational’ dynamics influence the ‘vibrational’ dynamics in a way analogous to the coupling of the selected vibrational motion to the field of a magnetic solenoid. We investigate in detail whether this analogy between rovibrational nuclear dynamics and electromagnetic phenomena can help us to understand high-resolution molecular spectra and the related dynamics of molecules.
The treatment of overall rotations coupled to large-amplitude internal motions (sometimes referred to as contortions14) has been the subject of intensive studies in high-resolution molecular spectroscopy.14–24 Perhaps the most famous among the models is the pioneering Hougen–Bunker–Johns (HBJ) model,17 describing the rotational–contortional dynamics of triatomic molecules with a large-amplitude dof, the bending. There exist reviews14,16,22 on the topic of rotation–contortion–vibration Hamiltonians (the contortions include internal rotation, pseudorotation, inversion, torsion, and bending) and their utilization in the understanding of high-resolution molecular spectra. The different Hamiltonians derived, for example, the approximate principal-axis, internal-axis, and rho-axis ones, are relevant to the present discussion, as they contain different forms of kinetic energy and rotational–vibrational (Coriolis) coupling terms obtained via different rotational transformations. Nevertheless, to the best of our knowledge, the central idea of the present paper, the ‘electromagnetic analogy’ of such Hamiltonians leading to the rovibrational Aharonov–Bohm effect was not considered in these studies.
As an example of a molecular system exhibiting the rovibrational Aharonov–Bohm effect, the low-energy nuclear dynamics of the H+5 molecular cation is considered. First-principles characterization of the dynamics of H+5, as well as of its deuterated derivatives, has been achieved and it offered a number of considerable surprises.25–27 As shown below, the rovibrational Aharonov–Bohm effect dominates the low-energy nuclear dynamics of this quasistructural28 molecular ion, which is approximately a symmetric top with a nearly-free torsional motion.
2 The electromagnetic analogy
Let us start our discussion with the standard spectroscopic four-dimensional (4D) rotation-contortion model Hamiltonian15,16,24,28,29| | Ĥ = Ĥv + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) RRr + RRr + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rv = (a rv = (a![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ2 + ϕ2 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ) + [BĴ2 + (A − B)Ĵz2] − α ) + [BĴ2 + (A − B)Ĵz2] − α![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ϕĴz, ϕĴz, | (1) |
describing the dynamics of a symmetric-top molecule with a torsional (ϕ, period 2π) dof coupled to the rotational dofs. In eqn (1), 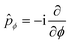 , a depends on the moments of inertia of the internal rotor and of the molecule about the molecular symmetry axis, the potential energy
, a depends on the moments of inertia of the internal rotor and of the molecule about the molecular symmetry axis, the potential energy ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) depends solely on ϕ and typically has multiple minima, the three components of the overall body-fixed angular momentum Ĵ are denoted by Ĵi, A and B are the effective rotational constants of the symmetric top, and α is the rovibrational coupling strength. The various operators appearing in Ĥ of eqn (1) have been grouped, as usual, into the operators Ĥv (vibrational Hamiltonian, containing only ϕ derivatives),
depends solely on ϕ and typically has multiple minima, the three components of the overall body-fixed angular momentum Ĵ are denoted by Ĵi, A and B are the effective rotational constants of the symmetric top, and α is the rovibrational coupling strength. The various operators appearing in Ĥ of eqn (1) have been grouped, as usual, into the operators Ĥv (vibrational Hamiltonian, containing only ϕ derivatives), ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) RRr (rotational Hamiltonian, containing only rotational derivatives), and a rotation–vibration coupling term
RRr (rotational Hamiltonian, containing only rotational derivatives), and a rotation–vibration coupling term ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rv.
rv.
However, this is not the only possible way to group the terms of eqn (1). For example, some authors incorporate the rotation–vibration coupling into the vibrational term to give the rearranged Hamiltonian15,23,24
| | 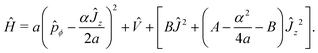 | (2) |
A common next step is to perform the so-called Nielsen transformation,15 which leads to the apparent elimination of the rovibrational coupling. We will discuss the Nielsen transformation shortly. For now, we note that K, related to the projection of the angular momentum onto the molecule-fixed z axis, is a good quantum number. Setting Ĵz = K in eqn (2), we get that
and so the Hamiltonian is given by the sum of a ‘torsional’ Hamiltonian
| | 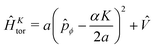 | (4) |
and a rotational kinetic energy contribution, given by
| | 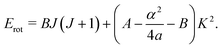 | (5) |
We must point out that ĤKtor, which we are calling the ‘torsional’ Hamiltonian, in fact depends on the rotational quantum number K through the appearance of the operator 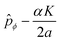 . Essentially, ĤKtor takes the usual kinetic plus potential form, except for the fact that the torsional momentum
. Essentially, ĤKtor takes the usual kinetic plus potential form, except for the fact that the torsional momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ has been ‘modified’ by the replacement
ϕ has been ‘modified’ by the replacement 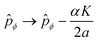 .
.
The key insight is that this is precisely the modification one would make in order to couple the torsional motion to a magnetic field, where 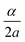 plays the role of an electromagnetic vector potential and K is formally identified with the electric charge. In fact, the Hamiltonian in eqn (4) is of exactly the same form as the Hamiltonian for a particle confined to a ring encircling a solenoid which is carrying magnetic flux,30 just as in the famous Aharonov–Bohm effect. It is as if the rotational dofs induce an effective magnetic field which couples to the torsional motion. We call this the rovibrational Aharonov–Bohm effect. It can be viewed as a special case, for symmetric tops, of the more general influence of rovibrational coupling on vibrational motion through so-called non-Abelian gauge fields (for more information on this general picture, see ref. 31–36).
plays the role of an electromagnetic vector potential and K is formally identified with the electric charge. In fact, the Hamiltonian in eqn (4) is of exactly the same form as the Hamiltonian for a particle confined to a ring encircling a solenoid which is carrying magnetic flux,30 just as in the famous Aharonov–Bohm effect. It is as if the rotational dofs induce an effective magnetic field which couples to the torsional motion. We call this the rovibrational Aharonov–Bohm effect. It can be viewed as a special case, for symmetric tops, of the more general influence of rovibrational coupling on vibrational motion through so-called non-Abelian gauge fields (for more information on this general picture, see ref. 31–36).
As a result, the effect of rovibrational coupling on the torsional motion can be understood by analogy with the familiar effects of a magnetic field. To the best of our knowledge, this is a new perspective on the well-studied Hamiltonian of eqn (1). As we will see, this electromagnetic analogy allows us to get deeper insight into the rovibrational level structure, and reveals properties which are obscured by the usual separation of nuclear-motion Hamiltonians into rotational, vibrational, and rovibrational terms.
2.1 Changes of embedding
Next, let us consider the effect of a change of embedding of the molecule-fixed axes. Suppose that, for our original embedding, we have some rovibrational eigenstate χK(ϕ)|JKM〉 (here, M is related to the projection of the angular momentum onto the space-fixed z axis) with the torsional wavefunction χK satisfying| | | (ĤKtor + Erot)χK = EχK. | (6) |
Imagine now that we change our embedding choice. We only consider embeddings where the body-fixed z-axis is aligned with the symmetry axis of the molecule. At each ϕ, the old and new embedding must be related by a rotation about the body-fixed z-axis by some angle θ(ϕ). With respect to the new embedding, the torsional wavefunction χK will become ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K, where
K, where
| | χK = exp(−iθ(ϕ)K)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K. K. | (7) |
Substituting this relation into eqn (6) gives
| | 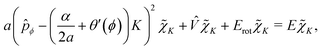 | (8) |
and, by comparison with
eqn (3), we see that the rotational-energy contribution looks exactly the same in the new embedding, and the only change to the torsional Hamiltonian is the shift
| | 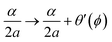 | (9) |
of the electromagnetic vector potential by the
ϕ-derivative of
θ. We recognise this as the usual transformation law for an electromagnetic vector potential under a gauge transformation. Thus, we see that, within the electromagnetic analogy, changes of embedding correspond to electromagnetic gauge transformations.
These considerations reveal that splitting the Hamiltonian into an electromagnetically-coupled vibrational part and a rotational part, as in eqn (2), has a significant advantage: the rotational part becomes independent of the embedding choice. This is to be contrasted with the traditional splitting into vibrational plus rotational plus rovibrational terms [shown in eqn (1)], in which the coefficients in the rotational term (the so-called effective rotational constants) depend on the choice of embedding. The price one pays for this embedding-independence of the rotational term is that the vibrational term depends on the embedding. However, this dependence is only through the inclusion of the electromagnetic vector potential, which simply transforms by a gauge transformation under changes of embedding. In particular, it is obvious from our way of splitting up the Hamiltonian that the rovibrational energy levels are independent of the choice of embedding (as they should be). This is because of the well-known fact that the energy levels of a system coupled to an electromagnetic field are invariant under gauge transformations. In the traditional way of writing the rovibrational Hamiltonian, it is far from obvious that the energy levels do not depend on the choice of embedding. In other words, the traditional way of writing the Hamiltonian obscures the embedding-independence (or the gauge invariance) of the rovibrational energy levels.
2.2 Eliminating rotation–vibration coupling
The electromagnetic analogy gives us insight into the important issue of the “elimination” of rotation–vibration coupling.37 Recall that, under a change of embedding specified by θ(ϕ), the vector potential transforms as in eqn (9). If we can choose our embedding so that the vector potential becomes zero, then clearly the torsional motion will be separated from the rotational motion. This seems possible, since we can just choose 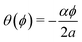 and then eqn (9) tells us that the vector potential will become
and then eqn (9) tells us that the vector potential will become| | 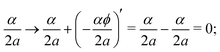 | (10) |
thus, with respect to this new embedding choice, the torsional Hamiltonian becomes| | ĤKtor → a![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ2 + ϕ2 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , , | (11) |
which no longer depends on the rotational quantum number K.
Strictly speaking, however, θ(ϕ) = −αϕ/2a does not give a valid embedding transformation. To see this, first recall that the torsional coordinate ϕ is 2π-periodic. On the other hand, the rotation angles θ(0) and θ(2π) relating the old and new embeddings at ϕ = 0 and ϕ = 2π are not the same, but differ by an angle θ(2π) − θ(0) = −απ/a. In other words, θ does not give a single-valued choice of embedding. As a consequence, the torsional wavefunction in the new embedding [see eqn (7)], ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K, satisfies
K, satisfies
| | ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(2π) = exp(−iαπK/a) K(2π) = exp(−iαπK/a)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0), K(0), | (12) |
and so we see that, while the original torsional wavefunction
χK was 2π-periodic in
ϕ, it becomes necessary to allow for modified boundary conditions,
eqn (12), for the new torsional wavefunction
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K
K. These new boundary conditions ‘compensate’ for the multi-valuedness of the new embedding.
For example, for a molecule composed of two identical rotors (for which it turns out that α/a = 1–see the following section for an example) we have that
| | ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(2π) = exp(−iKπ) K(2π) = exp(−iKπ)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0) = (−1)K K(0) = (−1)K![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0), K(0), | (13) |
or in other words that
χK satisfies periodic/anti-periodic boundary conditions for
K even/odd. So we are able to eliminate the vector potential, if we are prepared to allow non-periodic boundary conditions on the torsional wavefunction.
This ‘multi-valued’ change of embedding which eliminates the vector potential, together with the modified boundary conditions which are required to accommodate it, is essentially the well-known Nielsen transformation referred to earlier. It is also analogous to elimination of the Mead–Truhlar–Berry (MTB) vector potential6 in the context of the molecular Aharonov–Bohm effect, in which the resulting multi-valued nature of the electronic wavefunction leads to modified boundary conditions for the nuclear wavefunction. Specifically, the nuclear wavefunction picks up a minus sign upon encircling a conical intersection of potential energy surfaces, much like how the torsional wavefunction in eqn (13) picks up a minus sign when ϕ goes from 0 to 2π. This analogy with conical intersections will be elaborated on in Section 3.3.
The necessity to modify the boundary conditions, as in eqn (12), is arguably an unpleasant feature of the Nielsen transformation. It is also unnatural from the perspective of the electromagnetic analogy, in which gauge transformations ought to be single-valued. We might ask, therefore, whether it is possible to eliminate the vector potential without having to introduce modified boundary conditions for χK. In other words, can we construct some single-valued change of embedding which transforms the vector potential away? The electromagnetic analogy makes it clear that the answer is generally ‘no’. This is because the electromagnetic vector potential α/2a corresponds to the presence of a magnetic flux and, as is wellknown in the context of the traditional Aharonov–Bohm effect, this magnetic flux generally has a non-trivial effect on the quantum energy levels. It cannot simply be transformed away. The only exception is when α/2a = n ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) is an integer, since then the single-valued embedding transformation θ(ϕ) = −nϕ yields
is an integer, since then the single-valued embedding transformation θ(ϕ) = −nϕ yields
| | 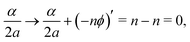 | (14) |
showing that the effect of the corresponding magnetic flux is no different to if there were no magnetic field at all. This is a flux quantization condition, as is familiar in the Aharonov–Bohm effect [see,
e.g., eqn (16) in ref.
30].
To summarize, the vector potential (and, in turn, the coupling between rotations and vibrations) cannot generally be transformed away by a change of embedding. If one is prepared to work with multi-valued embedding transformations, then in a sense the vector potential can be eliminated, but with the price that the torsional wavefunction is no longer 2π-periodic in ϕ. This corresponds to the Nielsen transformation. In what follows, we opt to work with single-valued gauge transformations as this corresponds to the usual perspective taken in electromagnetic theory, and preserves the interpretation of rovibrational coupling in terms of the presence of a magnetic flux.
3 Application to H+5
In this section we show how the rovibrational Aharonov–Bohm effect arises in the context of the unusual rotation–torsion dynamics of the molecular cation H+5.
3.1 1D(ϕ) torsion model
Our starting point is the reduced-dimensionality 1D(ϕ) torsion model25,26,28 developed to understand the low-energy quantum dynamics of H+5. The equilibrium structure of H+5 is depicted in the left panel of Fig. 1. We choose to work in the so-called geometric embedding (GE) of molecule-fixed axes,26 see Fig. 1, with respect to which the positions of the five hydrogen atoms are [see eqn (1) of ref. 26]
r3 = 1/2(−cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −sin ϕ, −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −R)T ϕ, −R)T |
r4 = 1/2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −R)T ϕ, −R)T |
which depend on a torsional coordinate ϕ, which has period 2π, and R is the distance between the midpoints of the two H2 units. Note that here, and throughout this section, we work in units where ħ = mH = r = 1, where mH is the mass of the hydrogen atom and r is the distance between the two hydrogens forming a rotor.
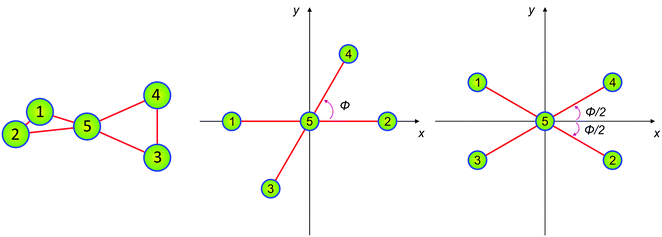 |
| | Fig. 1 Equilibrium structure of the H+5 molecular ion (left panel) and definitions of the geometric (GE, middle panel) and bisector (BE, right panel) embeddings, whereby ϕ corresponds to the torsional coordinate. | |
The time-independent Schrödinger equation for the 1D(ϕ) torsion model takes the form
| | 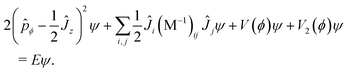 | (16) |
In previous studies this equation has been split into separate rotational, vibrational and rovibrational contributions but here we have grouped the terms as suggested in the mathematical physics literature.
34 In
eqn (16),
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ
ϕ = −i∂/∂
ϕ is the momentum conjugate to the torsional coordinate
ϕ and the
Ĵi are the components of the body-fixed angular momentum, while M is the moment of inertia tensor with respect to the GE molecule-fixed frame, governing the motion along the three rotational dofs, and has the explicit form
| | 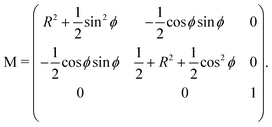 | (17) |
Note that we have allowed for a torsional potential
V(
ϕ) in
eqn (16), which on physical grounds is assumed to satisfy
| | | V(ϕ) = V(−ϕ) = V(ϕ + π) | (18) |
for all
ϕ (recall that
ϕ has period 2π). In addition, the extrapotential term
V2(
ϕ) is a quantum contribution coming from the
ϕ-dependence of the rovibrational
G matrix,
14 which in this case takes the explicit form
| | 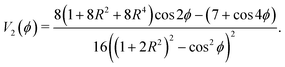 | (19) |
At this point let us pause to interpret the various terms in eqn (16). Broadly speaking, the first term on the left-hand side should be thought of as the torsional kinetic energy; the second term is the rotational kinetic energy; the third term is the torsional potential energy, which has been modified by the extrapotential term V2(ϕ). Note that our grouping of terms in eqn (16) differs from the usual conventions adopted in the nuclear-dynamics literature. For example, note the appearance of the operator 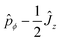 in the first term, reminiscent of the electromagnetic coupling considered in the previous section. We will now make the connection to the previous section, and to the Aharonov–Bohm effect, more explicit.
in the first term, reminiscent of the electromagnetic coupling considered in the previous section. We will now make the connection to the previous section, and to the Aharonov–Bohm effect, more explicit.
3.2 Symmetric-top approximation
For applications to H+5, it is a very good approximation to take R large.25 So let us expand in 1/R. To leading order,| | 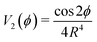 | (20) |
and| | 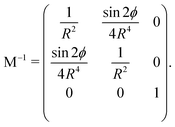 | (21) |
Discarding terms which are of order 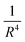 or higher, M−1 becomes diagonal and V2 vanishes and so eqn (16) reduces to
or higher, M−1 becomes diagonal and V2 vanishes and so eqn (16) reduces to| | 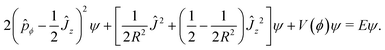 | (22) |
We call this (large-R) approximation the symmetric-top approximation, since the rotational kinetic energy term is now that of a symmetric top. In fact, the Hamiltonian in eqn (22) is of exactly the same form as the Hamiltonian of eqn (2) considered in the previous section, with the particular values
| | 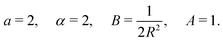 | (23) |
So, by the results of the previous section, the rovibrational energy levels are of the form
where, in this case, the rotational energy contribution is
| | 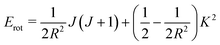 | (25) |
and the torsional energy contribution is an eigenvalue of the torsional Hamiltonian
| | 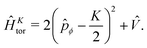 | (26) |
Note that the electromagnetic coupling
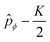
appearing in the torsional Hamiltonian of
eqn (26) takes a particularly simple form, due to the special value of the ratio
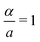
in this case.
We can now take advantage of the electromagnetic analogy to better understand the torsional Hamiltonian of eqn (26), which is simply the Hamiltonian for a charged particle, confined to a ring, encircling a solenoid carrying magnetic flux. The first insight that this analogy gives us is that the torsional energy levels only depend on whether K is even or odd, and not on the precise value of the integer K. We prove this now.
Suppose that Etor is an energy eigenvalue of ĤKtor, with ψ a corresponding eigenstate:
Then consider
ψN: = exp(
iNϕ)
ψ where
N ∈
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif)
. We have that
as can be seen by using the explicit definition of
ĤK+2Ntor given in
eqn (26), together with the definition of
ψN and
eqn (27).
Eqn (28) says that
Etor is also an energy eigenvalue of
ĤK+2Ntor, with
ψN a corresponding eigenstate. In this way we see that the energy levels of
| | | …Ĥ−2tor, Ĥ0tor, Ĥ2tor, Ĥ4tor… | (29) |
are all the same. Similarly,
| | | …Ĥ−3tor, Ĥ−1tor, Ĥ1tor, Ĥ3tor… | (30) |
all have identical energy levels. So, in fact, the energy levels of
ĤKtor are only dependent on whether
K is even or odd, and not on the particular value of the integer
K. In the electromagnetic anology, this can be thought of as a kind of flux quantization condition.
Another property of the Hamiltonian of eqn (26) is that, for K odd, all torsional energy levels are doubly degenerate. This is remarkable, as we might expect the torsional potential energy V to cause a splitting of degenerate levels. For K even, this is precisely what happens – levels which are degenerate for V = 0 are split when V is turned on. However, for K odd, the special value of the magnetic flux carried by the solenoid ensures that the degeneracy of torsional energy levels persists even when V ≠ 0. This doubling of levels is a known effect in electromagnetic theory38 and we give a brief proof here.
Recall that V is symmetric under ϕ → ϕ + π so ĤKtor is also symmetric under ϕ → ϕ + π. As a consequence, we can choose torsional energy eigenstates to be even or odd under ϕ → ϕ + π. Suppose that Etor is an energy eigenvalue of ĤKtor, with ψ a corresponding eigenstate which is even under ϕ → ϕ + π:
Now define a new wavefunction
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
(
ϕ) = exp(
iKϕ)
ψ(−
ϕ). Then direct calculation, remembering that
V is symmetric also under
ϕ → −
ϕ, shows that
| | ĤKtor![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) = Etor = Etor![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) | (32) |
so
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
is also an energy eigenstate with the same energy eigenvalue as
ψ. Note also that
| | ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ + π) = exp(iKϕ + iKπ)ψ(−ϕ − π) = exp(iKπ) (ϕ + π) = exp(iKϕ + iKπ)ψ(−ϕ − π) = exp(iKπ)![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ) = (−1)K (ϕ) = (−1)K![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ) (ϕ) | (33) |
so, if
K is an odd integer, then
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
is odd under
ϕ →
ϕ + π. So we have a pair of degenerate torsional energy eigenstates
ψ and
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
, which are clearly linearly independent because one is even and the other is odd under
ϕ →
ϕ + π. In other words, every even eigenstate automatically comes with an odd partner. By the same argument, every odd eigenstate comes with an even partner and so we see that all levels, for
K odd, are doubly degenerate.
We will come back to these properties shortly to explain how they correspond to well-known properties of the nuclear wavefunction in the presence of conical intersections as studied in the molecular Aharonov–Bohm effect.
In summary, the electromagnetic analogy has given us deeper insight into the energy-level structure of the rovibrational states of H+5. In the general case with non-zero V, states with K even have energy levels
| | 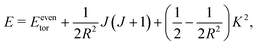 | (34) |
where
Eeventor takes one of a discrete set of non-degenerate torsional energy eigenvalues. States with
K odd have energy levels
| | 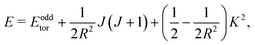 | (35) |
where
Eoddtor takes one of a discrete set of doubly degenerate torsional energy eigenvalues.
H+5 is an example of a system where the rotational and vibrational dofs are strongly coupled, so they cannot be treated independently. This is the reason why the torsional energy levels depend on the rotational quantum number K. However, we have found that the torsional energy levels only depend on K through whether it is even or odd, and not on its precise value. In particular, they only have to be computed for two values of K, say for K = 0 and K = 1, and then all the rovibrational energy levels can be deduced. This is obvious from the perspective of the rovibrational Aharonov–Bohm effect, as a kind of magnetic flux quantization condition. Even more strikingly, every torsional energy level is doubly degenerate for K odd. Again, this double degeneracy is obvious from our new perspective and corresponds to a known electromagnetic effect,38 but it is obscured by the usual decomposition of the rotation–vibration Hamiltonian into rotational, vibrational, and rovibrational coupling terms.
Before finding the rovibrational energy levels, let us elaborate on the connection between the molecular Aharonov–Bohm effect and the rovibrational Aharonov–Bohm effect we are considering here.
3.3 Analogy with conical intersections
For chemists, the most familiar manifestation of the Aharonov–Bohm effect is probably the MAB, in which a nuclear wavefunction encircling a conical intersection of potential energy surfaces picks up a minus sign. In Born–Oppenheimer theory,9,10 one starts by choosing an electronic ground state wavefunction for each nuclear configuration. There is a choice of complex phase involved at each nuclear configuration, since the electronic ground state is only defined up to a phase. Often, we demand that the electronic wavefunction is real-valued (for simplicity, let us imagine our system is time-reversal invariant and that we are ignoring spin–orbit coupling). Then, there is still a choice of phase, but there are only two choices and they differ by a factor of −1 (a phase of π).
Suppose we choose a real-valued electronic ground state wavefunction at some nuclear configuration, and we follow this choice continuously along a closed loop that encircles a conical intersection, all the time requiring our electronic ground state wavefunction to be real valued. As is well known, the wavefunction picks up a phase of π upon returning to the starting point. Single-valuedness of the molecular wavefunction then requires that the nuclear wavefunction also pick up a minus sign. Another way of characterizing this phase choice for the electronic wavefunction is that this is the phase choice for which the MTB vector potential6 vanishes.
In our nuclear-motion problem, we also have a choice: for each value of the torsional coordinate ϕ, we have to choose an embedding of the molecule-fixed axes. We have been working with the GE throughout this section, but we are free to transform to some other embedding by specifying a function θ(ϕ) which gives the rotation about the body-fixed z-axis (the symmetry axis of the symmetric top) which relates the old and the new embedding. Specifying this rotation θ(ϕ) is much like specifying the phase of the electronic ground state wavefunction in Born–Oppenheimer theory.
So let us start at ϕ = 0 and set θ(0) = 0. Now we imagine increasing ϕ and, for each ϕ, choosing θ(ϕ) so that the rotation–vibration coupling vanishes. Note that this choice is analogous to the choice of a real-valued electronic wavefunction in Born–Oppenheimer theory: in the Born–Oppenheimer case the MTB vector potential vanishes, while in this case the vector potential associated with rovibrational coupling vanishes. In this way our original GE is transformed to a new embedding, the bisector embedding (BE), which is depicted in Fig. 1.
It turns out that when we get to ϕ = 2π, the BE embedding has rotated by an angle of π (with respect to the body-fixed z-axis) compared to the BE embedding at ϕ = 0. This rotation by π is just like the phase of π picked up by a real-valued electronic wavefunction upon encircling a conical intersection. Now, what does this rotation by π mean for the quantum states? If our rotational state |JKM〉 has body-fixed angular momentum projection K even, then a rotation by an angle π does nothing to the state and so the state is insensitive to this rotation. If our rotational state has K odd, however, it picks up a minus sign. In turn, for the rovibrational wavefunction to be single-valued, we must have that for K odd the corresponding torsional states pick up a minus sign. This is just as we found in the previous section: elimination of rovibrational coupling is possible, but only if one is prepared to modify the boundary conditions on the torsional wavefunction. With respect to the BE, K even/odd torsional wavefunctions satisfy periodic/anti-periodic boundary conditions. We note that, as a consequence, nuclear motion codes will only yield correct rovibrational energy levels when working in the BE if the boundary conditions are modified compared to the GE.
Thus, the connection between our rovibrational problem and the treatment of conical intersections is clearest when we work with the BE. Let us temporarily adopt this embedding. Then we can make two direct connections between our rovibrational problem and the familiar treatment of conical intersections.
First, for K odd, the torsional wavefunction picks up a minus sign (like when there is a conical intersection) while, for K even, the torsional wavefunction picks up no minus sign (like when there is no conical intersection) under ϕ → ϕ + 2π. This is another way of explaining why the torsional energy levels only depend on whether K is even or odd, and not on the precise value of K. It shows that K even/odd just corresponds to periodic/antiperiodic boundary conditions, i.e. conical intersection/no conical intersection.
Second, it is known that one has to introduce ‘double groups’ to classify nuclear states in the presence of conical intersections,39 and these larger symmetry groups can lead to higher degeneracies than occur in the absence of conical intersections. This can be viewed as the reason for the double degeneracy of K odd torsional energy levels. Indeed, the symmetries of the torsional potential V(ϕ) under ϕ → ϕ + π and ϕ → −ϕ generate a symmetry group for the torsional dynamics isomorphic to C2v, and this group only has one-dimensional irreducible representations (irreps), since it is Abelian. The double group is isomorphic to C4v, a non-Abelian group, with two-dimensional irreps which correspond to the doubly degenerate levels.
3.4 Rovibrational energy-level structure via first-order perturbation theory
Now we return to the calculation of the rovibrational energy levels. As has been argued, we only need to compute the K odd and the K even torsional levels, Eoddtor and Eeventor, respectively, in order to deduce the full rovibrational energy-level structure [see eqn (34) and (35)]. As the torsional potential in the case of H+5 is known to be fairly weak, we can treat the torsional potential by perturbation theory.
3.4.1 The K even case.
The K even levels are simply the energy eigenvalues of the K = 0 torsional Hamiltonian| | Ĥeventor = 2![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 2ϕ + 2ϕ + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) . . | (36) |
We will treat ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) as a small perturbation. Ignoring
as a small perturbation. Ignoring ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , the zeroth order eigenstates can be classified by a
, the zeroth order eigenstates can be classified by a ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalue k ∈
ϕ eigenvalue k ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) and have energy Eeventor = 2k2, so we get the energy eigenvalues
and have energy Eeventor = 2k2, so we get the energy eigenvalues| | | Eeventor/2 = 0, 1, 1, 4, 4, 9, 9,… | (37) |
For small torsional potentials of the form| | 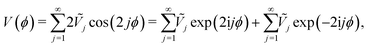 | (38) |
where the Ṽj are the Fourier components of the potential, we have that the matrix element of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) between states with
between states with ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalues k and k′ is
ϕ eigenvalues k and k′ is| | 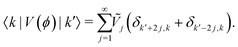 | (39) |
Thus, in the first order of perturbation theory, the perturbed energies are| | 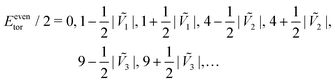 | (40) |
These are our K even torsional energy levels, where Ṽj diminish quickly as j increases. Note that the Eeventor levels are non-degenerate, the potential has split any degeneracies in the zeroth-order levels.
3.4.2 The K odd case.
The K odd levels are the energy eigenvalues of the K = 1 torsional Hamiltonian| | 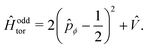 | (41) |
Again, we will treat ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) as a small perturbation. Ignoring
as a small perturbation. Ignoring ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , the zeroth order eigenstates can again be classified by a
, the zeroth order eigenstates can again be classified by a ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalue k ∈
ϕ eigenvalue k ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) and have energy
and have energy 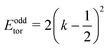 , so we get the energy eigenvalues
, so we get the energy eigenvalues| | | Eoddtor/2 = (1/2)2, (1/2)2, (3/2)2, (3/2)2, (5/2)2, (5/2)2,… | (42) |
with k = 0, 1, −1, 2, −2,3, −3,…. Now we introduce V as in the K even case. However, there is a crucial difference compared to the K even case. It is clear from eqn (39) that the matrix elements of V only connect states k and k′ for which k–k′ is an even integer. On the other hand, degenerate zeroth order levels have k and k′ related by an odd integer. As a result, the first-order corrections are zero and we get, to first order in perturbation theory,| | | Eoddtor/2 = (1/2)2, (1/2)2, (3/2)2, (3/2)2, (5/2)2, (5/2)2,… | (43) |
These are our K odd torsional energy levels. They are all doubly degenerate, the potential does not cause any splitting of degeneracies in the zeroth-order levels. In fact, we know from our earlier discussion that this degeneracy of K odd torsional energy levels is an exact result. Even if we went to higher order in perturbation theory, there would never be any splitting of these levels due to ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) .
.
The resulting rovibrational energy-level pattern, incorporating the rotational kinetic energy Erot as well as these torsional energy levels, is depicted in Fig. 2. For K odd, the torsional levels are doubly degenerate as we have already explained. In addition to this torsional degeneracy, there is a further degeneracy under K → −K so that rovibrational levels with K odd are in fact quadruply degenerate (this K → −K degeneracy occurs because the rotational kinetic energy only depends on |K|, not K, while the torsional energy levels are unchanged under K → −K since K and −K differ by the even integer 2K). Similarly, rovibrational levels with K even are doubly degenerate because of the K → −K degeneracy. The exception to this is when K = 0, yielding non-degenerate levels. So, altogether, states with |K| = 0, 1, 2, 3, 4,… have degeneracies 1, 4, 2, 4, 2,…
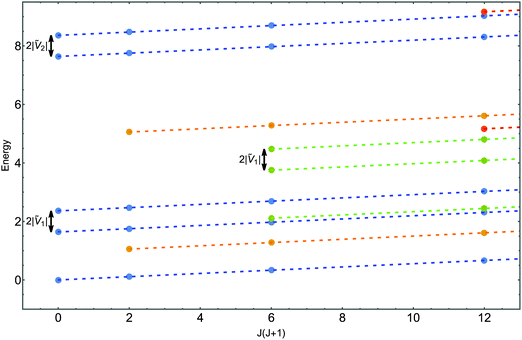 |
| | Fig. 2 Symmetric-top states incorporating torsional splitting. The K = 0 states (blue points) are non-degenerate, the |K| = 1 states (orange points) are quadruply degenerate, the |K| = 2 states (green points) are doubly degenerate and the |K| = 3 states (red points) are quadruply degenerate. The dotted lines all have gradient 1/2R2 to illustrate that the effect of increasing J on the energy levels is simply to translate the energies (as well as allowing more possibilities for K = −J,…, +J). Level splittings due to the torsional potential are indicated with arrows. | |
3.5 Beyond the symmetric-top approximation
Recall that we started our analysis of H+5 with the 1D(ϕ) torsion model, before making an approximation (the large R limit) which yielded a symmetric-top Hamiltonian. This was a very useful approximation, because the symmetric-top Hamiltonian exhibits the rovibrational Aharonov–Bohm effect and can be understood by analogy with motion in an electromagnetic field. It is also a physically reasonable approximation for H+5. We now consider what would happen if we dropped this approximation. The answer is that the quadruple degeneracies we have just found would split into 4 = 2 + 2 and the double degeneracies would split into 2 = 1 + 1.
One way of thinking about these splittings is in terms of the symmetries of the symmetric-top rovibrational Hamiltonian in eqn (22). Firstly, we have rotations about the symmetry axis of the symmetric top which act on the wavefunction as follows:
| | 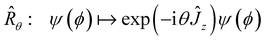 | (44) |
for
θ ∈ [0,2π]. Secondly, we have feasible permutations of the protons, generated by the double transposition
S = (24)(31) and the transposition
Tπ = (21), which act on the wavefunction as follows:
| | 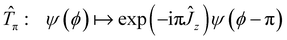 | (45) |
| | 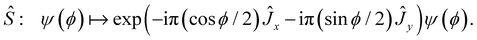 | (46) |
Finally, we have spatial inversion which is carried out by the parity operator:
| | 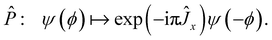 | (47) |
One can check that
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) θ
θ and
Ŝ generate a group 〈
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) θ
θ,
Ŝ〉 ≃
O(2), while
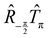
and
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Ŝ
Ŝ generate a group
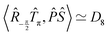
(
D8 is the dihedral group of order 8). These two groups commute with each other, and together generate the symmetry group
| | 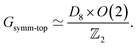 | (48) |
Here, the
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2
2 is generated by a common central element
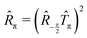
of order 2.
The irreps of Gsymm-top have dimensions 1, 2, and 4. In fact, this is another way of understanding why the rovibrational levels we have found have degeneracies 1, 2, and 4 – they must correspond to irreps of Gsymm-top.
If we drop the symmetric-top approximation, then the only symmetries we expect to have left over are those corresponding to spatial inversion, together with feasible permutations of the identical nuclei. So we only have the subgroup of Gsymm-top which is generated by Ŝ, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π, and
π, and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) . This subgroup is
. This subgroup is
| | G ≃ D8 × ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2 2 | (49) |
,where the
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2
2 factor is generated by parity, while the
D8 factor is generated by the feasible permutations. Note that this group can be identified with
G16 in Bunker's notation.
14
Clearly G sits in Gsymm-top as a subgroup:
The idea is that while, to a good approximation, H
+5 is a symmetric top and has symmetry group
Gsymm-top, in reality this symmetry is actually broken down to the subgroup
G. The irreps of
G have dimensions 1 and 2, there are no four-dimensional irreps. Under restriction to the subgroup
G, it turns out that the four-dimensional irreps of
Gsymm-top split into a sum 4 = 2 + 2 of two-dimensional irreps of
G, and that the two-dimensional irreps of
Gsymm-top split into a sum 2 = 1 + 1 of one-dimensional irreps of
G. These are the (very small) level splittings we would see amongst the degenerate states depicted in
Fig. 2 if we took into account the fact that H
+5 is not strictly a symmetric top.
To illustrate this point further, in Table 1 we reproduce numerical results from ref. 28 for the full 1D(ϕ) torsion model, compared with our perturbation theory analysis of the symmetric-top (Aharonov–Bohm) approximation. For this comparison, we need parameter values. In the units we have adopted so far in this section, for which mH = r = ħ = 1, we take 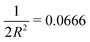 , while the torsional potential Fourier coefficients are given by Ṽ1 = 0.376 and Ṽ2 = −0.016, which corresponds to a torsional barrier of 4Ṽ1 ≈ 1.5. For the comparisons in Table 1, where energies are given in cm−1, our energy unit corresponds to 53.34 cm−1.
, while the torsional potential Fourier coefficients are given by Ṽ1 = 0.376 and Ṽ2 = −0.016, which corresponds to a torsional barrier of 4Ṽ1 ≈ 1.5. For the comparisons in Table 1, where energies are given in cm−1, our energy unit corresponds to 53.34 cm−1.
Table 1 Torsion-rotation energy levels (J ≥ 0) for H+5, calculated from the full 1D(ϕ) torsion model and compared to the symmetric-top (rovibrational Aharonov–Bohm, RAB) approximation. The energy levels are given in units of cm−1 and all levels up to 500 cm−1 are shown
|
J = 0 |
J = 1 |
J = 2 |
J = 3 |
| 1D(ϕ) |
RAB |
|K| |
1D(ϕ) |
RAB |
|K| |
1D(ϕ) |
RAB |
|K| |
1D(ϕ) |
RAB |
|K| |
| 0.00 |
0.00 |
0 |
6.68 |
7.10 |
0 |
20.04 |
21.31 |
0 |
40.09 |
42.62 |
0 |
| 87.93 |
86.62 |
0 |
55.97 |
56.89 |
1 |
69.16 |
71.10 |
1 |
88.95 |
92.41 |
1 |
| 128.26 |
126.74 |
0 |
55.97 |
56.89 |
1 |
69.16 |
71.10 |
1 |
88.95 |
92.41 |
1 |
| 429.10 |
425.87 |
0 |
56.14 |
56.89 |
1 |
69.67 |
71.10 |
1 |
89.97 |
92.41 |
1 |
| 429.35 |
427.57 |
0 |
56.14 |
56.89 |
1 |
69.67 |
71.10 |
1 |
89.97 |
92.41 |
1 |
|
|
|
|
94.61 |
93.73 |
0 |
107.96 |
113.78 |
2 |
127.99 |
135.10 |
2 |
|
|
|
|
134.95 |
133.84 |
0 |
113.35 |
113.78 |
2 |
133.37 |
135.10 |
2 |
|
|
|
|
273.41 |
270.25 |
1 |
113.36 |
107.94 |
0 |
133.40 |
129.25 |
0 |
|
|
|
|
273.41 |
270.25 |
1 |
148.33 |
148.05 |
0 |
168.43 |
169.36 |
0 |
|
|
|
|
273.45 |
270.25 |
1 |
201.28 |
200.41 |
2 |
221.31 |
221.72 |
2 |
|
|
|
|
273.45 |
270.25 |
1 |
201.28 |
200.41 |
2 |
221.31 |
221.72 |
2 |
|
|
|
|
435.78 |
432.97 |
0 |
241.62 |
240.52 |
2 |
261.69 |
221.72 |
2 |
|
|
|
|
436.04 |
434.68 |
0 |
241.62 |
240.52 |
2 |
261.69 |
221.72 |
2 |
|
|
|
|
|
|
|
286.74 |
284.46 |
1 |
276.08 |
277.36 |
3 |
|
|
|
|
|
|
|
286.74 |
284.46 |
1 |
276.08 |
277.36 |
3 |
|
|
|
|
|
|
|
286.86 |
284.46 |
1 |
276.08 |
277.36 |
3 |
|
|
|
|
|
|
|
286.86 |
284.46 |
1 |
276.08 |
277.36 |
3 |
|
|
|
|
|
|
|
449.15 |
447.18 |
0 |
306.74 |
305.77 |
1 |
|
|
|
|
|
|
|
449.40 |
448.89 |
0 |
306.74 |
305.77 |
1 |
|
|
|
|
|
|
|
|
|
|
306.98 |
305.77 |
1 |
|
|
|
|
|
|
|
|
|
|
306.98 |
305.77 |
1 |
|
|
|
|
|
|
|
|
|
|
469.20 |
468.49 |
0 |
|
|
|
|
|
|
|
|
|
|
469.46 |
470.20 |
0 |
|
|
|
|
|
|
|
|
|
|
493.46 |
490.72 |
3 |
|
|
|
|
|
|
|
|
|
|
493.46 |
490.72 |
3 |
|
|
|
|
|
|
|
|
|
|
493.47 |
490.72 |
3 |
|
|
|
|
|
|
|
|
|
|
493.47 |
490.72 |
3 |
Note that K is no longer a good quantum number in the 1D(ϕ) model, but because the symmetric-top symmetry is only slightly broken, it is still useful to label states by |K|, as seen in Table 1. The small splittings 4 = 2 + 2 and 2 = 1 + 1 due to the breaking of the symmetric-top symmetry are evident in Table 1. For example, looking at the J = 3 column, we see that the first row corresponds to a non-degenerate K = 0 level at 42.62 cm−1 in the symmetric-top approximation. The next four rows correspond to a quadruply degenerate |K| = 1 level at 92.41 cm−1 in the symmetric top approximation, which is split as 4 = 2 + 2 into doubly degenerate levels at 88.95 cm−1 and 89.97 cm−1. The next two rows after this correspond to a doubly degenerate |K| = 2 level at 135.10 cm−1 in the symmetric top approximation, which is split as 2 = 1 + 1 into non-degenerate levels at 127.99 cm−1 and 133.37 cm−1.
4 Conclusions
By revisiting the problem of coupling overall rotations with an internal vibrational motion for symmetric-top molecules, we demonstrated that this coupling can be understood by analogy with the famous Aharonov–Bohm effect, with the rotational motion influencing the vibrational motion in a way anologous to the influence of a magnetic solenoid on a charged particle. The effective electric charge is identified with K, the component of the angular momentum along the symmetry axis of the molecule, while the effective magnetic flux carried by the solenoid is proportional to α, the rovibrational coupling strength. In particular, the quantum energy levels associated with the vibrational motion are affected by the rovibrational coupling in a characteristic way familiar from electromagnetic theory.
As an application, we considered the low-energy rovibrational dynamics of H+5, which are known from previous studies to be well-described by a model coupling overall rotations to a single torsional motion. We showed that, since H+5 is approximately a symmetric top, the rovibrational Aharonov–Bohm effect governs the low-energy quantum dynamics of the ion to a good approximation. Moreover, in the case of H+5, the value of the effective magnetic flux carried by the solenoid within this analogy is such that the torsional energy levels only depend on whether K is even or odd, and that all torsional energy levels for K odd are doubly degenerate. These latter effects have analogues in the well-known molecular Aharonov–Bohm effect, in which the presence of a conical intersection of Born–Oppenheimer potential energy surfaces influences the nuclear dynamics through the Mead–Truhlar–Berry vector potential.
The electromagnetic analogy gives us a new way of understanding the rovibrational level structure of symmetric-top molecules, as we have vividly demonstrated for H+5. This gain in understanding is largely due to the fact that changes of embedding of molecule-fixed axes play a transparent role in the electromagnetic analogy, corresponding to gauge transformations. This is to be contrasted with the usual decomposition of the nuclear Hamiltonian into vibrational, rotational and rovibrational terms, in which the behavior under changes of embedding is somewhat obscured.
A natural question is whether these ideas can be extended to the case of asymmetric-top molecules. This can be done, but one has to replace the effective magnetic field which couples to the vibrational dynamics with a so-called non-Abelian gauge field. This perspective on general rotation–vibration coupling is a well-developed subject,31–34 which in a sense reduces to the electromagnetic analogy introduced here in the special case of a symmetric top. An attractive feature of the electromagnetic analogy is that the mathematical ideas involved are already familiar to chemists in the context of the molecular Aharonov–Bohm effect. The non-Abelian fields which arise in the more general case are not as familiar, although we point out that they do in fact have analogues in the chemistry literature. For example, in molecular systems with strong spin–orbit coupling one may be interested in the intersection of two potential energy surfaces, each surface corresponding to a doubly (Kramers) degenerate electronic state. This picture naturally leads to the introduction of a non-Abelian gauge field which couples to the nuclear dynamics, as explored in ref. 8, 40 and 41. We expect that the electromagnetic analogy, and its non-Abelian generalization, will continue to yield new insights in nuclear dynamics.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The work performed received support from NKFIH (grants no. K119658 and K138233) and from the ELTE Institutional Excellence Program (TKP2020-IKA-05).
References
- W. Ehrenberg and R. E. Siday, The refractive index in electron optics and the principles of dynamics, Proc. Phys. Soc., London, Sect. B, 1949, 62, 8 CrossRef.
- Y. Aharonov and D. Bohm, Significance of electromagnetic potential in quantum theory, Phys. Rev., 1959, 115, 485–491 CrossRef.
- Y. Aharonov and D. Bohm, Further considerations on electromagnetic potentials in the quantum theory, Phys. Rev., 1959, 123, 1511–1524 CrossRef.
- A. Tonomura, N. Osakabe, T. Matsuda, T. Kawasaki, J. Endo, S. Yano and H. Yamada, Evidence for Aharonov–Bohm effect with magnetic field completely shielded from electron wave, Phys. Rev. Lett., 1986, 56, 792 CrossRef PubMed.
- A. Tonomura, T. Matsuda, R. Suzuki, A. Fukuhara, N. Osakabe, H. Umezaki, J. Endo, K. Shinagawa, Y. Sugita and H. Fujiwara, Observation of Aharonov–Bohm effect by electron holography, Phys. Rev. Lett., 1982, 48, 1443 CrossRef.
- C. A. Mead and D. G. Truhlar, On the determination of Born–Oppenheimer nuclear motion wave functions including complications due to conical intersections and identical nuclei, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- C. A. Mead, The molecular Aharonov–Bohm effect in bound states, Chem. Phys., 1980, 49, 23–32 CrossRef CAS.
- C. A. Mead, Electronic spin-orbit interaction and the molecular Aharonov–Bohm effect, Chem. Phys., 1980, 49, 33–38 CrossRef CAS.
- M. Born and J. R. Oppenheimer, Zur Quantentheorie der Molekeln, Ann. Phys., 1927, 84, 457–484 CrossRef CAS.
-
M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954 Search PubMed.
- G. Herzberg and H. C. Longuet-Higgins, Intersection of potential energy surfaces in polyatomic molecules, Discuss. Faraday Soc., 1963, 35, 77 RSC.
- D. R. Yarkony, Determining the molecular Aharonov–Bohm phase angle: A rigorous approach employing a molecular properties based adiabatic to diabatic states transformation, J. Chem. Phys., 1999, 110, 701–705 CrossRef CAS.
- B. Zygelman, The molecular Aharonov–Bohm effect redux, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 025102 CrossRef.
-
P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, 2006 Search PubMed.
- H. H. Nielsen, The torsion oscillator-rotator in the quantum mechanics, Phys. Rev., 1932, 40, 445–456 CrossRef CAS.
- C. C. Lin and J. D. Swalen, Internal rotation and microwave spectroscopy, Rev. Mod. Phys., 1959, 31, 841–892 CrossRef CAS.
- J. T. Hougen, P. R. Bunker and J. W. C. Johns, The vibration-rotation problem in triatomic molecules allowing for a large-amplitude bending vibration, J. Mol. Spectrosc., 1970, 34, 136–172 CrossRef CAS.
- P. R. Bunker and J. M. R. Stone, The bending-rotation Hamiltonian for the triatomic molecule and application to HCN and H2O, J. Mol. Spectrosc., 1972, 41, 310–332 CrossRef CAS.
- H. M. Pickett, Vibration-rotation interactions and the choice of rotating axes for polyatomic molecules, J. Chem. Phys., 1972, 56, 1715–1723 CrossRef CAS.
- A. R. Hoy and P. R. Bunker, The effective rotation-bending Hamiltonian of a triatomic molecule, and its application to extreme centrifugal distortion in the water molecule, J. Mol. Spectrosc., 1974, 52, 439–456 CrossRef CAS.
- P. R. Bunker and B. M. Landsberg, The rigid bender and semirigid bender models for the rotation–vibration Hamiltonian, J. Mol. Spectrosc., 1977, 67, 374–385 CrossRef CAS.
- J. T. Hougen, I. Kleiner and M. Godefroid, Selection rules and intensity calculations for a Cs asymmetric top molecule containing a methyl group internal rotor, J. Mol. Spectrosc., 1994, 163, 559–586 CrossRef CAS.
- V. Szalay, A. G. Császár, J. Santos and J. Ortigoso, Rho-axis-system Hamiltonian for molecules with one large amplitude internal motion, J. Chem. Phys., 2003, 118, 6801–6805 CrossRef CAS.
-
A. Bauder, in Handbook of High-resolution Spectroscopy, ed. Quack, M. and Merkt, F., Wiley, Chichester, 2011, vol. 1, pp. 57–116 Search PubMed.
- C. Fábri, J. Sarka and A. G. Császár, Communication: Rigidity of the molecular ion H+5, J. Chem. Phys., 2014, 140, 051101 CrossRef PubMed.
- J. Sarka, C. Fábri, T. Szidarovszky, A. G. Császár, Z. Lin and A. B. McCoy, Modelling rotations, vibrations, and rovibrational couplings in astructural molecules – A case study based on the H+5 molecular ion, Mol. Phys., 2015, 113, 1873–1883 CrossRef CAS.
- J. Sarka and A. G. Császár, Interpretation of the vibrational energy level structure of the astructural molecular ion H+5 and all of its deuterated isotopomers, J. Chem. Phys., 2016, 144, 154309 CrossRef PubMed.
- A. G. Császár, C. Fábri and J. Sarka, Quasistructural molecules, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1432 Search PubMed.
-
W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley, New York, 3rd edn, 1984 Search PubMed.
- E. Merzbacher, Single valuedness of wave functions, Am. J. Phys., 1962, 30, 237–247 CrossRef.
- A. Shapere and F. Wilczek, Self-propulsion at low Reynolds number, Phys. Rev. Lett., 1987, 58, 2051 CrossRef PubMed.
- A. Shapere and F. Wilczek, Gauge kinematics of deformable bodies, Am. J. Phys., 1989, 57, 514 CrossRef.
- A. Guichardet, On rotation and vibration motions of molecules, Ann. I.H.P.: Phys. Theor., 1984, 40, 329–342 CAS.
- R. G. Littlejohn and M. Reinsch, Gauge fields in the separation of rotations and internal motions in the n-body problem, Rev. Mod. Phys., 1997, 69, 213–276 CrossRef.
-
J. I. Rawlinson, Rovibrational Dynamics of Nuclei and Molecules, PhD thesis, University of Cambridge, 2020.
- J. I. Rawlinson, Coriolis terms in Skyrmion quantization, Nucl. Phys. B, 2019, 949, 114800 CrossRef CAS.
- J. Sarka, B. Poirier, V. Szalay and A. G. Császár, On neglecting Coriolis and related couplings in first-principles rovibrational spectroscopy: Considerations of symmetry, accuracy, and simplicity. II. Case studies for H2O isotopologues, H3+, O3, and NH3, Spectrochim. Acta, Part A, 2021, 250, 119164 CrossRef CAS PubMed.
-
D. Tong, Gauge theory, Lecture notes, DAMTP Cambridge, 2018 Search PubMed.
- S. C. Althorpe, General explanation of geometric phase effects in reactive systems: Unwinding the nuclear wave function using simple topology, J. Chem. Phys., 2006, 124, 084105 CrossRef PubMed.
- C. A. Mead, Molecular Kramers degeneracy and non-Abelian adiabatic phase factors, Phys. Rev. Lett., 1987, 59, 161 CrossRef PubMed.
- M. T. Johnsson and I. J. R. Aitchison, The SU(2) instanton and the adiabatic evolution of two Kramers doublets, J. Phys. A: Math. Gen., 1997, 30, 2085 CrossRef.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Csaba
Fábri
*ab,
Csaba
Fábri
 bc and
Attila G.
Császár
bc and
Attila G.
Császár
 bc
bc
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) RRr +
RRr + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rv = (a
rv = (a![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ2 +
ϕ2 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ) + [BĴ2 + (A − B)Ĵz2] − α
) + [BĴ2 + (A − B)Ĵz2] − α![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ϕĴz,
ϕĴz,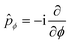 , a depends on the moments of inertia of the internal rotor and of the molecule about the molecular symmetry axis, the potential energy
, a depends on the moments of inertia of the internal rotor and of the molecule about the molecular symmetry axis, the potential energy ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) depends solely on ϕ and typically has multiple minima, the three components of the overall body-fixed angular momentum Ĵ are denoted by Ĵi, A and B are the effective rotational constants of the symmetric top, and α is the rovibrational coupling strength. The various operators appearing in Ĥ of eqn (1) have been grouped, as usual, into the operators Ĥv (vibrational Hamiltonian, containing only ϕ derivatives),
depends solely on ϕ and typically has multiple minima, the three components of the overall body-fixed angular momentum Ĵ are denoted by Ĵi, A and B are the effective rotational constants of the symmetric top, and α is the rovibrational coupling strength. The various operators appearing in Ĥ of eqn (1) have been grouped, as usual, into the operators Ĥv (vibrational Hamiltonian, containing only ϕ derivatives), ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) RRr (rotational Hamiltonian, containing only rotational derivatives), and a rotation–vibration coupling term
RRr (rotational Hamiltonian, containing only rotational derivatives), and a rotation–vibration coupling term ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rv.
rv.
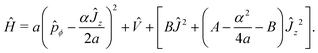
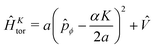
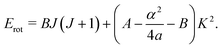
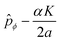 . Essentially, ĤKtor takes the usual kinetic plus potential form, except for the fact that the torsional momentum
. Essentially, ĤKtor takes the usual kinetic plus potential form, except for the fact that the torsional momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ has been ‘modified’ by the replacement
ϕ has been ‘modified’ by the replacement 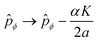 .
.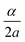 plays the role of an electromagnetic vector potential and K is formally identified with the electric charge. In fact, the Hamiltonian in eqn (4) is of exactly the same form as the Hamiltonian for a particle confined to a ring encircling a solenoid which is carrying magnetic flux,30 just as in the famous Aharonov–Bohm effect. It is as if the rotational dofs induce an effective magnetic field which couples to the torsional motion. We call this the rovibrational Aharonov–Bohm effect. It can be viewed as a special case, for symmetric tops, of the more general influence of rovibrational coupling on vibrational motion through so-called non-Abelian gauge fields (for more information on this general picture, see ref. 31–36).
plays the role of an electromagnetic vector potential and K is formally identified with the electric charge. In fact, the Hamiltonian in eqn (4) is of exactly the same form as the Hamiltonian for a particle confined to a ring encircling a solenoid which is carrying magnetic flux,30 just as in the famous Aharonov–Bohm effect. It is as if the rotational dofs induce an effective magnetic field which couples to the torsional motion. We call this the rovibrational Aharonov–Bohm effect. It can be viewed as a special case, for symmetric tops, of the more general influence of rovibrational coupling on vibrational motion through so-called non-Abelian gauge fields (for more information on this general picture, see ref. 31–36).![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K, where
K, where![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K.
K.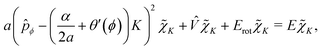
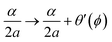
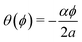 and then eqn (9) tells us that the vector potential will become
and then eqn (9) tells us that the vector potential will become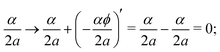
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ2 +
ϕ2 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ,
,![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K, satisfies
K, satisfies![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(2π) = exp(−iαπK/a)
K(2π) = exp(−iαπK/a)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0),
K(0),![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K. These new boundary conditions ‘compensate’ for the multi-valuedness of the new embedding.
K. These new boundary conditions ‘compensate’ for the multi-valuedness of the new embedding.
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(2π) = exp(−iKπ)
K(2π) = exp(−iKπ)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0) = (−1)K
K(0) = (−1)K![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) K(0),
K(0),![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) is an integer, since then the single-valued embedding transformation θ(ϕ) = −nϕ yields
is an integer, since then the single-valued embedding transformation θ(ϕ) = −nϕ yields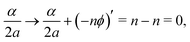
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −sin
ϕ, −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −R)T
ϕ, −R)T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, −R)T
ϕ, −R)T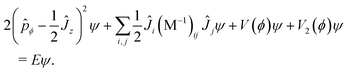
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ = −i∂/∂ϕ is the momentum conjugate to the torsional coordinate ϕ and the Ĵi are the components of the body-fixed angular momentum, while M is the moment of inertia tensor with respect to the GE molecule-fixed frame, governing the motion along the three rotational dofs, and has the explicit form
ϕ = −i∂/∂ϕ is the momentum conjugate to the torsional coordinate ϕ and the Ĵi are the components of the body-fixed angular momentum, while M is the moment of inertia tensor with respect to the GE molecule-fixed frame, governing the motion along the three rotational dofs, and has the explicit form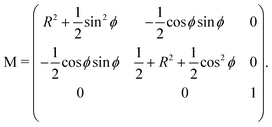
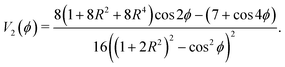
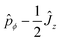 in the first term, reminiscent of the electromagnetic coupling considered in the previous section. We will now make the connection to the previous section, and to the Aharonov–Bohm effect, more explicit.
in the first term, reminiscent of the electromagnetic coupling considered in the previous section. We will now make the connection to the previous section, and to the Aharonov–Bohm effect, more explicit.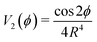
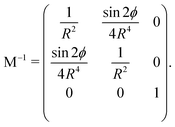
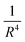 or higher, M−1 becomes diagonal and V2 vanishes and so eqn (16) reduces to
or higher, M−1 becomes diagonal and V2 vanishes and so eqn (16) reduces to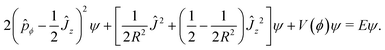
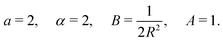
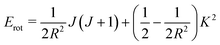
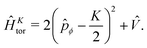
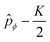 appearing in the torsional Hamiltonian of eqn (26) takes a particularly simple form, due to the special value of the ratio
appearing in the torsional Hamiltonian of eqn (26) takes a particularly simple form, due to the special value of the ratio 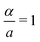 in this case.
in this case.
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) . We have that
. We have that![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ) = exp(iKϕ)ψ(−ϕ). Then direct calculation, remembering that V is symmetric also under ϕ → −ϕ, shows that
(ϕ) = exp(iKϕ)ψ(−ϕ). Then direct calculation, remembering that V is symmetric also under ϕ → −ϕ, shows that![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) = Etor
= Etor![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) is also an energy eigenstate with the same energy eigenvalue as ψ. Note also that
is also an energy eigenstate with the same energy eigenvalue as ψ. Note also that![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ + π) = exp(iKϕ + iKπ)ψ(−ϕ − π) = exp(iKπ)
(ϕ + π) = exp(iKϕ + iKπ)ψ(−ϕ − π) = exp(iKπ)![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ) = (−1)K
(ϕ) = (−1)K![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (ϕ)
(ϕ)![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) is odd under ϕ → ϕ + π. So we have a pair of degenerate torsional energy eigenstates ψ and
is odd under ϕ → ϕ + π. So we have a pair of degenerate torsional energy eigenstates ψ and ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) , which are clearly linearly independent because one is even and the other is odd under ϕ → ϕ + π. In other words, every even eigenstate automatically comes with an odd partner. By the same argument, every odd eigenstate comes with an even partner and so we see that all levels, for K odd, are doubly degenerate.
, which are clearly linearly independent because one is even and the other is odd under ϕ → ϕ + π. In other words, every even eigenstate automatically comes with an odd partner. By the same argument, every odd eigenstate comes with an even partner and so we see that all levels, for K odd, are doubly degenerate.
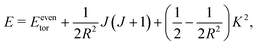
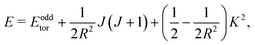
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 2ϕ +
2ϕ + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) .
.![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) as a small perturbation. Ignoring
as a small perturbation. Ignoring ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , the zeroth order eigenstates can be classified by a
, the zeroth order eigenstates can be classified by a ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalue k ∈
ϕ eigenvalue k ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) and have energy Eeventor = 2k2, so we get the energy eigenvalues
and have energy Eeventor = 2k2, so we get the energy eigenvalues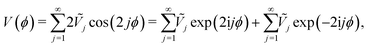
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) between states with
between states with ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalues k and k′ is
ϕ eigenvalues k and k′ is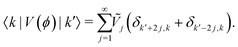
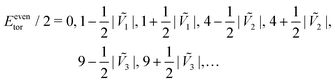
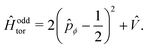
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) as a small perturbation. Ignoring
as a small perturbation. Ignoring ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , the zeroth order eigenstates can again be classified by a
, the zeroth order eigenstates can again be classified by a ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ϕ eigenvalue k ∈
ϕ eigenvalue k ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) and have energy
and have energy 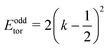 , so we get the energy eigenvalues
, so we get the energy eigenvalues![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) .
.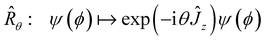
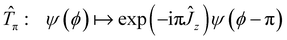
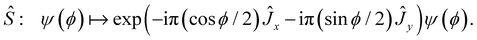
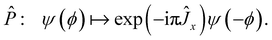
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) θ and Ŝ generate a group 〈
θ and Ŝ generate a group 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) θ,Ŝ〉 ≃ O(2), while
θ,Ŝ〉 ≃ O(2), while 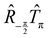 and
and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Ŝ generate a group
Ŝ generate a group 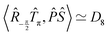 (D8 is the dihedral group of order 8). These two groups commute with each other, and together generate the symmetry group
(D8 is the dihedral group of order 8). These two groups commute with each other, and together generate the symmetry group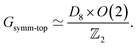
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2 is generated by a common central element
2 is generated by a common central element 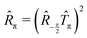 of order 2.
of order 2.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) π, and
π, and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) . This subgroup is
. This subgroup is![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2
2![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2 factor is generated by parity, while the D8 factor is generated by the feasible permutations. Note that this group can be identified with G16 in Bunker's notation.14
2 factor is generated by parity, while the D8 factor is generated by the feasible permutations. Note that this group can be identified with G16 in Bunker's notation.14
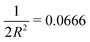 , while the torsional potential Fourier coefficients are given by Ṽ1 = 0.376 and Ṽ2 = −0.016, which corresponds to a torsional barrier of 4Ṽ1 ≈ 1.5. For the comparisons in Table 1, where energies are given in cm−1, our energy unit corresponds to 53.34 cm−1.
, while the torsional potential Fourier coefficients are given by Ṽ1 = 0.376 and Ṽ2 = −0.016, which corresponds to a torsional barrier of 4Ṽ1 ≈ 1.5. For the comparisons in Table 1, where energies are given in cm−1, our energy unit corresponds to 53.34 cm−1.

