Diffusion-enhanced exciton dissociation in single-material organic solar cells

Abstract

Single-material organic solar cells have recently attracted research attention due to their simplicity, morphological robustness and high yield of exciton dissociation. Using α-sexithiophene as a model system, we show that the single-event probability of the exciton dissociation at the boundaries of polycrystalline domains with different molecular orientation is extremely low (∼0.5%), while a high efficiency of charge generation is gained via hundred-fold crossings of the domain boundaries due to the long exciton diffusion length (∼45 nm).

---

Single-material organic solar cells (OSCs) have been used for almost half a century, with early simple devices based on tetracene¹ and chlorophyll-a.^2,3 However, over the years, their power conversion efficiency has increased from 0.01% to an impressive ∼11%,^4–6 owing to improved device architecture and better organic materials. Instead of donor and acceptor materials in the bulk heterojunction (BHJ) architecture⁷ of the most advanced OSCs,^8–10 a single organic material^11–15 is used here as the photoactive layer. Single-material OSCs have recently begun to be revitalized because of their conceptual simplicity^6,11 and significantly improved stability^5,16,17 but also as a playground for the fundamental understanding of exciton dissociation and charge separation mechanisms.^18,19 In such devices, exciton dissociation has been reported to be facilitated by the formation of intermediate inter-molecular charge-transfer (CT) excitons,^20,21 at the homojunction of a single p- and n-type doped organic semiconductor,²² or at the interface of undoped domains with different molecular orientation and packing.^23,24

The latest approach has been thoroughly examined by Dong et al.²³ who demonstrated efficient charge generation at the interfaces of polycrystalline alpha-sexithiophene (α-6T) domains of standing and lying molecular orientations. As a result, inter-domain CT states are formed which mediate the charge generation, finally leading to an external quantum efficiency (EQE) of ∼45%, a short-circuit current density of 3.6 mA cm⁻², a high open-circuit voltage of 1.61 V, and a power conversion efficiency of 2.9%.

While the very mechanism of charge generation at the domain boundaries has been proven beyond any reasonable doubt, a central aspect of the exciton-to-charge conversion remains unaddressed: what is the probability of dissociation upon a single domain boundary crossing event? There are two conceivable scenarios: similar to conventional BHJ OSCs, the probability is close to unity so that a single bounce against the interface suffices to dissociate the exciton into charges – which of course might occur at very different rates.²⁵ The important consequence is that the exciton diffusion length should be of the same order as the domain size – typically, ∼10 nm.^26–28 Alternatively, the probability might be relatively low (say, <1%) but the exciton passes many boundaries along its long diffusional path,²⁹ thereby increasing its accumulated chances to dissociate. The latter scenario may potentially offer an explanation for efficient exciton dissociation under conditions of a small interfacial driving force^25,30 but it also calls for an exciton diffusion length that is well in excess of the domain size.

In this regard, we demonstrate that in fact the second scenario is realized in the case of neat α-6T thin films. We use a combination of precise sample fabrication, the photoluminescence (PL) quenching technique and kinetic Monte-Carlo (KMC) simulations to investigate exciton diffusion and quenching at boundaries of α-6T domains with different molecular orientations. We show that the probability of the single exciton dissociation event at the domain boundary is extremely low (∼0.5%); however, the total share of thereby generated charges is substantial (more than 50% of the initial excitons) because excitons cross domain boundaries hundreds of times. In this case, a high overall dissociation probability is facilitated by the long exciton diffusion length of ∼45 nm.

Samples of α-6T thin films were fabricated by thermal evaporation under vacuum onto quartz substrates (see Section S1 in the ESI† for Samples and Experimental methods). The films showing standing, lying and mixed molecular orientations (Fig. 1a–c) were obtained by varying the deposition conditions and using 2 nm of copper iodide (CuI) as a templating interlayer between the substrate and the α-6T layer. In the mixed-orientation α-6T films, standing and lying molecular orientations co-exist in domains with typical sizes of 10–20 nm as were previously characterized by X-ray scattering.^23,31,32 The difference in the absorption spectra also confirmed the molecular orientation of the α-6T thin films (Fig. S2, ESI†). Fig. 1d and e (open dots) show PL transients of 40 nm thick films with two regular (standing and lying) molecular orientations; similar decay traces with a characteristic time of ∼600 ps are measured. Note that the faster PL decay of lying α-6T reported by Dong et al.²³ is most probably related to the used film thickness of 60 nm under which the lying molecular orientation for the lying film is not preserved, in line with results of Section S11 in the ESI.† In contrast to the standing and lying films, PL in the mixed film decays noticeably faster, at ∼400 ps (Fig. 1f, open dots). A similar acceleration has been previously attributed²³ to exciton quenching at the boundaries between polycrystalline domains with different molecular orientations.

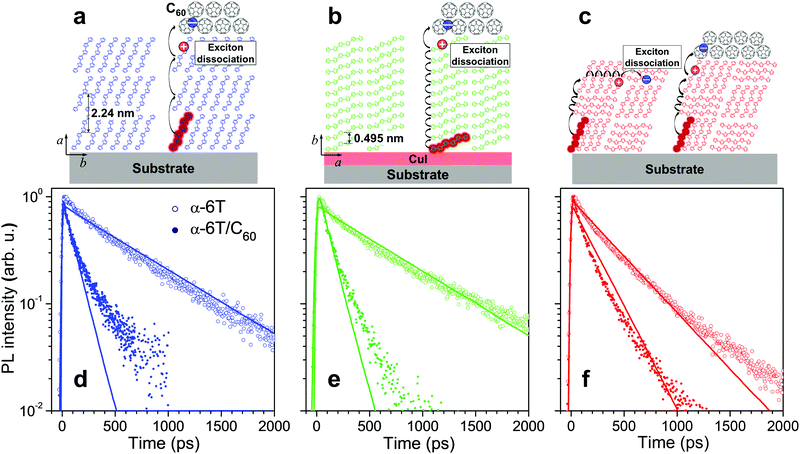Fig. 1 Sketches of molecular stacking (a–c) and time-resolved PL transients (d–f) of the standing (a and d), lying (b and e) and mixed orientation (c and f) α-6T (open dots) and α-6T/C₆₀ heterojunction (filled dots) films under 400 nm excitation. The excitons and their diffusional paths are depicted as red circles and black curve arrows, respectively. The blue and red dots represent electron and hole charge carriers, respectively. The thickness of all neat α-6T films and α-6T in the heterojunction film with mixed orientation is 40 nm; the thickness of α-6T in the heterojunction films with standing and lying α-6T orientations is 20 nm. The transients were obtained by integrating the PL maps measured by a streak-camera (see Fig. S4, ESI†) in the 520–700 nm spectral range. The thick lines show the results of kinetic Monte-Carlo simulations convoluted with the Gaussian apparatus function with standard deviation of σ ≅ 6 ps. C₆₀ stands for a 30 nm thick quenching layer. CuI served as the optically-transparent, 2 nm thick templating layer, used to obtain a lying α-6T orientation. All samples were encapsulated to avoid degradation in air; the data for samples without encapsulation are given in Fig. S8 in the ESI.†

To get hold of the quenching efficiency at the domain boundaries, samples of the standing and lying molecular orientations were fabricated with a thickness of 20 nm, i.e. on the order of the domain size in the mixed orientation film,^23,31,32 and covered at the top with a 30 nm layer of C₆₀. The latter is a strong electron acceptor that quenches the excitons with a high (close to 100%) efficiency.³³ Evidently (Fig. 1d and e; filled dots), the PL from both these samples decays much faster (at ∼100 ps time) than the PL from the sample with mixed orientation, at ∼400 ps (Fig. 1f; open dots). If the probability of the domain boundary quenching had been close to unity, the PL of the mixed-orientation sample would have decayed similarly or even faster than in the standing and lying α-6T/C₆₀ samples because the domain size (estimated as 10–20 nm,^23,31,32) is smaller than the α-6T thickness. The fact that this is not the case incontrovertibly proves that the quenching probability at a single standing/lying α-6T domain boundary is much lower than unity.

A plausible concern in the argument above is whether the excitons in the mixed film maintain their diffusivity similar to that in the standing or lying film. Otherwise, an exciton might be trapped as e.g. a CT exciton²³ at the domain boundary still retains its PL and dissociates into charges at a time scale of 100's of ps.²⁵ To rule out this possibility, we covered the 40 nm thick mixed film with the C₆₀ quenching layer which resulted in a substantial acceleration of the PL transient with a decay time of ∼150 ps (Fig. 1f, filled dots; and Section S13, ESI†). If the excitons had ceased to retain mobility due to trapping at the domain boundaries (or even within a single domain), there would have been very little acceleration of the PL decay because the excitons would have not been able to reach the quenching layer at the top. In contrast, the much faster PL decay was experimentally observed, revealing that excitons in the mixed films retain their mobility to travel through domain boundaries. The exciton–exciton annihilation experiments in the mixed film (see Fig. S14, ESI†) further support the above conclusion.

We can estimate the quenching probability of excitons at the domain boundary more qualitatively in the following simple way. First, we determine the diffusion length (L_D) in the standing and lying films which can be estimated using the equation: , where d_q = 20 nm is the thickness of the α-6T layer in the α-6T/C₆₀ heterojunction sample, T is the exciton lifetime (T ≅ 600 ps as estimated from the PL trace of the 40 nm layer of standing or lying α-6T in Fig. 1), and τ_q is the decay time of PL from the α-6T/C₆₀ layer (≅ 100 ps). Therefore, L_D ≅ 50 nm is in line with the earlier-reported value.³⁴ Next, the hopping time between α-6T molecules can now be calculated as τ_h = (δ²/L_D²)T, where δ ≅ 0.87 nm is the (average) intermolecular distance (calculated as the cubic root from the elementary cell volume of 0.495 × 0.6 × 2.24 nm³, ref. 35 and Fig. S17, ESI†), so that τ_h ≅ 0.18 ps. The number of boundary crossings is calculated using the equation: N = L/d, where L = (δ/τ_h)T_m is the exciton travelling distance (i.e. the sum of the lengths of all segments over which an exciton has travelled), d ≅ 10 nm^23,31,32 is the domain size, and T_m ≅ 400 ps is the diffusion time as obtained from PL decay of the mixed film. Note that the travelling distance L = 1900 nm is not to be confused with an exciton diffusion length L_D ≅ 50 nm, i.e. the distance between initial and final exciton positions. For instance, if the exciton travels back and forth in between two points, the diffusion length is short but the travelling distance is long. Substituting the numerical values, we obtain N ≅ 190. Assuming the total probability of cumulative exciton dissociation as 70% (i.e. approximately the internal quantum efficiency, IQE, which is the measured EQE of 45%²³ divided by absorption by the photoactive layer of ∼0.65), the probability of a single exciton dissociation event amounts to p = 1 − 0.7^1/N ≅ 0.2%. This probability of exciton dissociation at the single crossing of the domain boundary is arguably very low which is compensated by multiple domain boundary crossings because of a long travelling distance (i.e. a long L_D) so that the exciton crosses the domain boundaries many times.

The probability of exciton dissociation at a domain boundary can be obtained more accurately from KMC simulations^36–39 by fitting the KMC simulated transients to the experimental PL transients. First, we obtained parameters of exciton diffusion into different directions, i.e. for standing and lying molecular packings (see more details in Section S16, ESI†). Fig. 2a shows a schematic representation of the KMC simulation for standing and lying α-6T films. In brief, PL transients were calculated in the KMC simulations with the following input parameters: exciton lifetime τ₀, site-to-site hopping time τ_hop, and quenching probability at the α-6T/substrate interface P_substrate. The simulated transients for all samples with different film thicknesses were calculated to best-fit (as judged by a visual inspection) the respective experimental PL transients (Fig. 1d, e and Fig. S18c, d, ESI†). After that, the optimised τ₀, τ_hop and P_substrate (see Table S10, ESI†) were used as the fixed input for the KMC simulation of the mixed α-6T films, with quenching probability at the domain boundaries P_domain as the only varied parameter.

Fig. 2 Schematics of the KMC simulations for standing/lying (a) and mixed-orientation (b) α-6T films. The input parameters in (a) are exciton lifetime τ₀ (with the initial guess obtained from experimental PL transients), site-to-site hopping time τ_hop and quenching probability at the α-6T/substrate interface P_substrate. The only varied parameter in (b) is quenching probability at the domain boundaries P_domain. The input parameters are refined via several iterations of the KMC algorithm.

Table 1 summarizes the exciton diffusion coefficients and lengths. The diffusional coefficients in the a- and b-axis dimensions are quite similar. This is explained by a balance between the distance along the molecular stacking and the exciton hopping rate which depends on the dipole–dipole coupling (see Section S15, ESI†). Similar results have also been previously reported for zinc phthalocyanine⁴⁰ and rubrene.⁴¹ The hopping time in the c-axis dimension of the crystallographic unit cell could not have been directly obtained from experimental data. However, as the coupling energy between two adjacent molecules is similar in both b-axis and c-axis dimensions (see Section S15, ESI†), we set similar diffusion coefficients in both dimensions (D^c ≅ D^b). The three-dimensional diffusion length of 40–50 nm is in good agreement with the previous estimation using the simple model. Such long diffusion length is partially attributed to an extremely low energetic disorder (<4 meV), which excluded exciton cooling due to relaxation to lower energetic states.^37,42

Table 1 Summary of the exciton diffusion coefficients D = δ²/(2τ_hop) (where δ is the hopping distance) in the a- (D^a) and b- (D^b) axis dimensions, and average diffusion lengths 〈L_D〉 in one (1D) and three (3D) dimensions, for different molecular orientations. The average diffusion lengths were obtained from histograms of the exciton displacement (Section S16, ESI)

Molecular orientation	D (nm^2 ps^−1)	1D 〈LD〉 (nm)	3D 〈LD〉 (nm)
a Mean value of diffusion coefficients into three dimensions. b The value is lower than that for the standing and lying molecular orientations because the exciton lifetime is reduced due to exciton dissociation at the domain boundaries.
Standing	D ^a = 2 ± 0.2	28 ± 2	48.5
Lying	D ^b = 1.4 ± 0.4	23 ± 2	40
Mixed	D = 1.6^a	—	35 ± 5^b

---

Next, we modelled the mixed α-6T films as alternative cubic domains of lying and standing molecular orientations with the size of 10–20 nm, based on the reported X-ray diffraction data.^23,31,32 When crossing boundaries of the domains, excitons are quenched with a probability P_domain, which becomes the only fitting parameter (Fig. 2b). From the best fitting (Fig. 1d–f and Fig. S12, ESI†), P_domain was determined as 0.6% and 0.3% for 20 and 10 nm domain sizes, respectively, and the average number of domain boundary crossings amounts to ∼60 and ∼130, respectively (see Fig. S22b, ESI†). Note that the parameters obtained from KMC simulations are reasonably close to those from a simple estimate above, thereby lending support to either approach.

Fig. 3 shows the shares of excitons producing PL and quenched at the domain boundaries and the α-6T/substrate interface as a function of the α-6T thickness. As the α-6T thickness increases, the share of excitons quenched at the domain boundaries increases up to ∼50% for 70 nm thickness, while the share of excitons quenched at the α-6T/substrate interface rapidly decreases. At the same time, the share of excitons producing PL increases from ∼15% to ∼35%. Therefore, a substantial share of excitons dissociate into charges at the domain boundaries despite the low single-event probability. This is consistent with a maximum IQE of 70% (as estimated earlier from EQE of 45% and active layer absorption of 0.65, ref. 23), if we assume negligible exciton losses at the α-6T/substrate interface (∼15% in Fig. 3) in real devices.

Fig. 3 Shares of excitons producing PL (red), dissociated at domain boundaries (green) and quenched at the α-6T/substrate interface (blue) for various α-6T thicknesses as obtained from KMC simulations. The size of the domains is 20 nm.

Finally, we comment on the low values of the single exciton dissociation probability despite a considerable offset of ∼0.4 eV^23,43 between the positions of the frontier orbitals of domains with different molecular orientations. The optical gaps at both sides of the interface are equal as PL spectra do not depend on the particular molecular orientation (see Fig. S6, ESI†). Furthermore, no redshifted CT absorption/PL band⁴⁴ related to inter-domain CT excitons could be detected in mixed orientation α-6T films, indicating that the energy difference between intra- and inter-domain excitons is negligibly small. Therefore, the creation of the inter-domain CT excitons²³ (the first step toward exciton dissociation) competes with inter-domain exciton hopping due to dipole–dipole coupling. The latter wins so that most of the excitons continue diffusing even after having crossed the domain boundary as has been established experimentally (see Section S13, ESI†). Therefore, the envisioned approaches toward improving the efficiency of overall exciton dissociation in single-material OSCs should focus on the increase of either the number of boundary crossings or the dissociation probability at a single-event crossing. The former approach requires OSC materials with long L_D together with minimizing exciton losses at the interfaces. The latter approach calls for an efficient intermediate CT state for charge generation, which might result in voltage losses.

In conclusion, we investigated the exciton diffusion and dissociation at the domain boundaries in α-6T films with different molecular orientations. We obtained an extremely low probability of the single exciton dissociation event at a single domain boundary (∼0.5%). However, as excitons cross domain boundaries hundreds of times due to their long diffusion length, the total share of thereby generated charges is substantial (more than 50% of the initial excitons). This finding directly contributes to the understanding of exciton dissociation in single-material OSCs but might also be applicable to non-fullerene based OSCs with a small driving force.^25,30,45 This also highlights the importance of a long exciton diffusion length, the requirement of which becomes more challenging for solution-processed organic materials and is in contrast to well-ordered evaporated materials considered herein.

Author contributions

Conceptualization: N. V. H. and M. S. P; funding acquisition: K. V. and M. S. P.; investigation: N. V. H. and M. S. P; methodology: N. V. H. and M. S. P.; sample fabrication: N. V. H., V. C. N and L. B.; resources: M. S. P.; supervision: K. V. and M. S. P.; writing: N. V. H. and M. S. P. with contribution from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. V. H. and M. S. P. thank F. de Haan for writing the code for kinetic Monte-Carlo simulations and general laboratory assistance. The SEPOMO network participants (especially D. Beljonne) are acknowledged for numerous discussions. We are indebted to A. A. Bakulin for constructive criticism upon reading the manuscript. N. V. H. thanks K. Leo for hospitality during his secondment stay at Dresden Integrated Center for Applied Physics and Photonic Materials. N. V. H., K. V. and M. S. P. acknowledge funding from the European Union's Horizon 2020 research and innovation program under Marie Sklodowska Curie Grant Agreement No. 722651 (SEPOMO).

References

1. L. E. Lyons and O. M. G. Newman, Aust. J. Chem., 1971, 24, 13–23.
2. C. W. Tang and A. C. Albrecht, J. Chem. Phys., 1975, 62, 2139.
3. C. W. Tang and A. C. Albrecht, Nature, 1975, 254, 507–509.
4. Y. Wu, J. Guo, W. Wang, Z. Chen, Z. Chen, R. Sun, Q. Wu, T. Wang, X. Hao, H. Zhu and J. Min, Joule, 2021, 5, 1–16.
5. G. Feng, J. Li, Y. He, W. Zheng, J. Wang, C. Li, Z. Tang, A. Osvet, N. Li, C. J. Brabec, Y. Yi, H. Yan and W. Li, Joule, 2019, 3, 1765–1781.
6. F. Pierini, M. Lanzi, P. Nakielski, S. Pawlowska, O. Urbanek, K. Zembrzycki and T. A. Kowalewski, Macromolecules, 2017, 50, 4972–4981.
7. G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791.
8. Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515.
9. L. Meng, Y. Zhang, X. Wan, C. Li, X. Zhang, Y. Wang, X. Ke, Z. Xiao, L. Ding, R. Xia, H. L. Yip, Y. Cao and Y. Chen, Science, 2018, 361, 1094–1098.
10. Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275.
11. J. Roncali and I. Grosu, Adv. Sci., 2019, 6, 1801026.
12. A. L. Mannanov, P. S. Savchenko, Y. N. Luponosov, A. N. Solodukhin, S. A. Ponomarenko and D. Y. Paraschuk, Org. Electron., 2020, 78, 105588.
13. Y. Zhang, D. Deng, Q. Wu, Y. Mi, C. Yang, X. Zhang, Y. Yang, W. Zou, J. Zhang, L. Zhu, H. Zhou, X. Liu and Z. Wei, Sol. RRL, 2020, 4, 1900580.
14. M. Marinelli, M. Lanzi, A. Liscio, A. Zanelli, M. Zangoli, F. Di Maria and E. Salatelli, J. Mater. Chem. C, 2020, 8, 4124–4132.
15. S. Liang, X. Jiang, C. Xiao, C. Li, Q. Chen and W. Li, Acc. Chem. Res., 2021, 54, 2227–2237.
16. T. L. Nguyen, T. H. Lee, B. Gautam, S. Y. Park, K. Gundogdu, J. Y. Kim and H. Y. Woo, Adv. Funct. Mater., 2017, 27, 1702474.
17. Y. He, T. Heumüller, W. Lai, G. Feng, A. Classen, X. Du, C. Liu, W. Li, N. Li and C. J. Brabec, Adv. Energy Mater., 2019, 9, 1900409.
18. J.-L. Brédas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1699.
19. O. Inganäs, Adv. Mater., 2018, 30, 1800388.
20. O. V. Kozlov, X. Liu, Y. N. Luponosov, A. N. Solodukhin, V. Y. Toropynina, J. Min, M. I. Buzin, S. M. Peregudova, C. J. Brabec, S. A. Ponomarenko and M. S. Pshenichnikov, J. Phys. Chem. C, 2017, 121, 6424–6435.
21. O. V. Kozlov, Y. N. Luponosov, A. N. Solodukhin, B. Flament, Y. Olivier, R. Lazzaroni, J. Cornil, S. A. Ponomarenko and M. S. Pshenichnikov, Adv. Opt. Mater., 2017, 5, 1700024.
22. S. Izawa, A. Perrot, J. H. Lee and M. Hiramoto, Org. Electron., 2019, 71, 45–49.
23. Y. Dong, V. C. Nikolis, F. Talnack, Y. Chin, J. Benduhn, G. Londi, J. Kublitski, X. Zheng, S. C. B. Mannsfeld, D. Spoltore, L. Muccioli, J. Li, X. Blase, D. Beljonne, J. Kim, A. A. Bakulin, G. D. Avino, J. R. Durrant and K. Vandewal, Nat. Commun., 2020, 11, 4617.
24. F. Kouki, G. Horowitz, F. Garnier and H. Bouchriha, Org. Electron., 2010, 11, 1439–1444.
25. A. Classen, C. L. Chochos, L. Lüer, V. G. Gregoriou, J. Wortmann, A. Osvet, K. Forberich, I. McCulloch, T. Heumüller and C. J. Brabec, Nat. Energy, 2020, 5, 711–719.
26. M. Sim, J. Shin, C. Shim, M. Kim, S. B. Jo, J. H. Kim and K. Cho, J. Phys. Chem. C, 2014, 118, 760–766.
27. G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Rev., 2017, 117, 796–837.
28. Y. Zhang, M. T. Sajjad, O. Blaszczyk, A. J. Parnell, A. Ruseckas, L. A. Serrano, G. Cooke and I. D. W. Samuel, Chem. Mater., 2019, 31, 6548–6557.
29. Y. Firdaus, V. M. Le Corre, S. Karuthedath, W. Liu, A. Markina, W. Huang, S. Chattopadhyay, M. M. Nahid, M. I. Nugraha, Y. Lin, A. Seitkhan, A. Basu, W. Zhang, I. Mcculloch, H. Ade, J. Labram, F. Laquai, D. Andrienko, L. J. A. Koster and T. D. Anthopoulos, Nat. Commun., 2020, 11, 5220.
30. L. Zhu, J. Zhang, Y. Guo, C. Yang, Y. Yi and Z. Wei, Angew. Chem., Int. Ed., 2021, 60, 15348–15353.
31. C. Lorch, R. Banerjee, C. Frank, J. Dieterle, A. Hinderhofer, A. Gerlach and F. Schreiber, J. Phys. Chem. C, 2015, 119, 819–825.
32. U. Hörmann, C. Lorch, A. Hinderhofer, A. Gerlach, M. Gruber, J. Kraus, B. Sykora, S. Grob, T. Linderl, A. Wilke, A. Opitz, R. Hansson, A. S. Anselmo, Y. Ozawa, Y. Nakayama, H. Ishii, N. Koch, E. Moons, F. Schreiber and W. Brütting, J. Phys. Chem. C, 2014, 118, 26462–26470.
33. Y. Ge and J. E. Whitten, Chem. Phys. Lett., 2007, 448, 65–69.
34. A. Mani, J. Schoonman and A. Goossens, J. Phys. Chem. B, 2005, 109, 4829–4836.
35. G. Horowitz, B. Bachet, A. Yassar, P. Lang, F. Demanze, J. L. Fave and F. Gamier, Chem. Mater., 1995, 7, 1337–1341.
36. S. Chandrabose, K. Chen, A. J. Barker, J. J. Sutton, S. K. K. Prasad, J. Zhu, J. Zhou, K. C. Gordon, Z. Xie, X. Zhan and J. M. Hodgkiss, J. Am. Chem. Soc., 2019, 141, 6922–6929.
37. G. M. Akselrod, F. Prins, L. V. Poulikakos, E. M. Y. Lee, M. C. Weidman, A. J. Mork, A. P. Willard, V. Bulović and W. A. Tisdale, Nano Lett., 2014, 14, 3556–3562.
38. M. E. Kcöse, P. Graf, N. Kopidakis, S. E. Shaheen, K. Kim and G. Rumbles, ChemPhysChem, 2009, 10, 3285–3294.
39. B. A. L. Raul, Y. N. Luponosov, W. Yang, N. M. Surin, O. Douhéret, J. Min, T. L. C. Jansen, S. A. Ponomarenko and M. S. Pshenichnikov, Sci. Rep., 2020, 10, 21198.
40. B. P. Rand, D. Cheyns, K. Vasseur, N. C. Giebink, S. Mothy, Y. Yi, V. Coropceanu, D. Beljonne, J. Cornil, J. L. Brédas and J. Genoe, Adv. Funct. Mater., 2012, 22, 2987–2995.
41. P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 017402.
42. A. Serbenta, O. V. Kozlov, G. Portale, P. H. M. Van Loosdrecht and M. S. Pshenichnikov, Sci. Rep., 2016, 6, 36236.
43. S. Duhm, G. Heimel, I. Salzmann, H. Glowatzki, R. L. Johnson, A. Vollmer, J. P. Rabe and N. Koch, Nat. Mater., 2008, 7, 326–332.
44. K. Vandewal, S. Mertens, J. Benduhn and Q. Liu, J. Phys. Chem. Lett., 2020, 11, 129–135.
45. S. M. Menke, A. Cheminal, P. Conaghan, N. A. Ran, N. C. Greehnam, G. C. Bazan, T. Q. Nguyen, A. Rao and R. H. Friend, Nat. Commun., 2018, 9, 277.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods and samples, absorption and PL spectra, PL maps and transients, exciton lifetime, discussions on the exciton mobility at domain boundaries, calculation of dipole–dipole coupling energy, details of kinetic Monte-Carlo simulations and AFM images. See DOI: 10.1039/d1cp03328j

---