Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comparison of methods for the estimation of the enthalpy of formation of rare earth compounds†
Sergio
Sanchez-Segado
 *ab,
Sebastien
Lectez
c,
Animesh
Jha
*ab,
Sebastien
Lectez
c,
Animesh
Jha
 b and
Stephen
Stackhouse
c
b and
Stephen
Stackhouse
c
aDepartment of Chemical and Environmental Engineering, Technical University of Cartagena, Cartagena, 30202, Spain. E-mail: s.sanchezsegado@leeds.ac.uk; sergio.segado@upct.es
bSchool of Chemical and Process Engineering, University of Leeds, Leeds, LS2 9JT, UK. E-mail: a.jha@leeds.ac.uk
cSchool of Earth and Environment, University of Leeds Leeds, LS2 9JT, UK. E-mail: s.stackhouse@leeds.ac.uk
First published on 18th October 2021
Abstract
Rare earth elements are helping drive the global transition towards a greener economy. However, the way in which they are produced is far from being considered green. One of the major obstacles to developing greener production methods and the design of novel processes and materials involving rare earth elements is the limited thermodynamic data available. In the present work, we apply a suite of methods to estimate the enthalpy of formation of several rare earth compounds, including a new method based on a linear relationship, established by the authors. Experimental values of the enthalpy of formation of LnCl3, LnOCl, LnPO4, Ln2O2S, Ln2O2CO3 and NaLnO2 were collated and used to assess the accuracy of the different methods, which were then used to predict values for compounds for which no data exists. It is shown that Mostafa et al.'s group contribution method and the linear relationship proposed by the authors give the lowest mean absolute error (<9%). The volume based thermodynamics (VBT) method yields estimates with absolute mean errors below 16.0% for LnPO4 and Ln2O2S, but above 26.0% for other compounds. Correction of the VBT method using an improved estimate of the Madelung energy for the calculation of the lattice enthalpy decreases the absolute mean error below 12.0% for all compounds except LnPO4. These complementary methods provide options for calculating the enthalpy of formation of rare earth compounds, depending on the experimental data available and desired accuracy.
Introduction
Rare earth elements, commonly called the lanthanides (Ln), are playing a major role in the move towards a more sustainable society, due to their use in green technologies, including electric vehicles and wind turbines.4,5 Rare earth oxycarbonates (Ln2O2CO3) are important for manufacturing high-temperature superconductors, solid oxide fuel cells and permeable membranes; and as alternative catalysts for biodiesel production and dehydrogenation of primary aliphatic alcohols, due to their environmental benefits and process efficiency.6–8 In addition, rare earth oxysulfides (Ln2O2S) are becoming important in the manufacture of red phosphors and oxygen storage, based on the reversible oxidation of sulphur to produce Ln2O2SO4.9–11 The use of rare earth elements in almost all of these applications is linked to their characteristic chemical, magnetic and electronic properties, making their substitution difficult.12The applications discussed above, are pushing the global demand for rare earth compounds, increasing their beneficiation and extraction from ores and recycling from end-of-life products. The current chemical technologies used for extraction of rare earth elements have serious environmental impacts and are energy inefficienct.13,14 In view of this, industry is looking to design novel processes for their extraction and recovery.15–19 For instance, in the early 80s high temperature reactions between Ln2O3 with different sodium compounds was studied, due to the formation of NaLnO2 compounds affecting the swelling behavior of nuclear reactors during the cooling of liquid sodium;20 a similar approach has been applied to recover REEs from waste fluorescent phosphors.21,22 One of the main obstacles inhibiting the design of novel processing routes and synthesis of new rare earth element compounds is the lack of thermodynamic data available, because experimental measurements of their thermodynamic properties are extremely challenging.23
Knowledge of the enthalpies of formation of rare earth element compounds is crucial for calculations of Gibbs free energies and chemical equilibria. Methods exist for predicting these values, but some are only parameterised for a particular set of chemical compounds, while more general methods, based on group contribution, fail to provide a user-friendly mathematical model or the required data is only available for particular compounds of interest.23,24 Other methods rely on the lattice potential energy, from the Born–Haber–Fajans cycle, to calculate enthalpies formation. Born-Lande developed in 1918 an equation to estimate lattice potential energies of binary ionic crystals which was further improved on by Born and Mayer. Kapustinskii developed the previous equations to allow calculation of the lattice potential energy of any simple ionic crystal.25 Jenkins et al.26,27 extended Kapustinskii's equation to link the lattice potential energy with the molecular volume of the crystal unit cell.
In view of this, in the present work, we evaluate a suite of methods for estimating the enthalpy of formation of rare earth compounds, using the rare earth oxides, phosphates, chlorides, oxychlorides, oxysulfides, oxycarbonates and sodium lanthanide oxides as a test set. In particular, we assess the performance of the volume based thermodynamic (VBT) method developed by Glasser and Jenkins2,3 and group contribution method reported by Mostafa and Eakman,1 which were chosen for their ease of use. In addition, we show, for the first time, that a linear relationship exists between ΔH0f(Ln2O3) and ΔH0f(LnSalt), where ΔH0f(Ln2O3) is the enthalpy of formation of the rare earth oxides (Ln2O3) and ΔH0f(LnSalt) is the enthalpy of formation of the rare earth salts under study. If experimental data is available for some rare earth compounds in the series, these can be used to easily estimate values for others.
Crystal structures
Before describing the methodology employed in this work, it is useful to provide a brief description of the crystal structures of the compounds considered.Rare earth sesquioxides (Ln2O3)
Rare earth sesquioxides are polymorphic. At ambient conditions the cubic structure (form C, space group Ia3) is the most thermodynamically stable for all rare earth sesquioxides, with the exception of La2O3, Ce2O3 and Nd2O3.28 In the cubic phase, the rare earth ions are six-coordinate and there are sixteen formula units per unit cell.29,30 For La2O3, Ce2O3 and Nd2O3 a hexagonal structure (form A, space group P32/m) is observed.29 In the hexagonal phase, the rare earth ions are seven-coordinate and there is one formula unit per unit cell. For the light rare earth elements, the thermochemical stability of forms A and C are similar, such that lanthanide sesquioxides with a mixture of both phases can be found at room temperature.31Anhydrous rare earth trichlorides (LnCl3)
Rare earth trichlorides are also polymorphic, presenting three structures at room temperature, depending on atomic number.32 The trichlorides from LaCl3 to GdCl3 are isostructural, having a hexagonal UCl3 structure (space group P63/m) in which rare earth ions are symmetrically coordinated to nine chloride ions.33 The rare earth chlorides from DyCl3 to LuCl3 present a monoclinic YCl3 structure (space group C2/m) in which the chloride ions are arranged in a nearly cubic close packed arrangement, with the rare earth ions located in the octahedral holes formed by alternate pairs of close packed layers of chloride ions.34 TbCl3 has the orthorhombic PuBr3 structure (space group Cmcm), which can be described as triangular prisms in which Tb3+ is eight coordinated, with Tb3+ located at the center and Cl− situated at the corners.35 Rycerz and Gaune-Escard36 investigated the correlation between the thermodynamic properties and crystal structure of rare earth trihalides, using differential scanning calorimetry. They found that TbCl3 was the first compound of the series to present a solid–solid phase transition, pointing out that the structure of TbCl3 depends on the methodology employed for its synthesis, being possible to obtain either the hexagonal (UCl3) or orthorhombic (PuBr3) structure. It is only possible to obtain the hexagonal form of TbCl3, when it is prepared below 640 K.36Rare earth oxychlorides (LnOCl)
Rare earth oxychlorides from LaOCl–HoOCl crystallize in the PbFCl tetragonal crystal structure (space group P4/nmm), meanwhile TmOCl–LuOCl adopt the SmSI hexagonal structure (space group R32/m). ErOCl is dimorphic and can present both structures. The change from tetragonal to hexagonal structure is due to the rearrangement of the chloride ions to reduce the strain present in the tetragonal form, when the ionic radius of the rare earth cation is small enough to allow it.37,38Rare earth phosphates (LnPO4)
Rare earth phosphates change crystal structure with increasing ionic radius. From LaPO4 to GdPO4 they adopt the monoclinic monazite structure (space group P21/n), while from TbPO4 to LuPO4 they adopt the tetragonal xenotime structure (space group I41/amd). Depending on preparation conditions, GdPO4, TbPO4 and DyPO4 can adopt either structure.39 Both structures contain isolated PO43− tetrahedral separated by LnO9 polyhedra for monazite or LnO8 polyhedra for xenotime structure.40Ternary sodium lanthanide oxides (NaLnO2)
All the sodium rare earth oxides have an ordered rocksalt lattice and can present three different crystal structures, depending on the relative size of the Na+ and Ln3+. If the Ln3+ ion is bigger than Na+ (i.e. from La to Gd) the tetragonal α-LiFeO2 structure (space group I41/amd) is found. If the Ln3+ is smaller than Na+, two different structures are possible. The monoclinic β-LiFeO2 structure (space group C2/c) is found from Tb to Er and the hexagonal α-NaFeO2 structure (space group R3m) from Tm to Lu.41,42 Impurities from other Ln3+ ions may alter the structure suggesting polymorphisms in the NaLnO2 series.20Lanthanide oxycarbonates (Ln2O2CO3)
Rare earth oxycarbonates exists in three polymorphic crystalline structures. The tetragonal Type I structure has square Ln2O22+ layers separated by CO32− ions. The type IA is a monoclinic distortion of the type I. The type II structure has hexagonal Ln2O22+ layers separated by CO32− ions.7 The transformation of the type I to the type II structure has been observed for the light lanthanides at temperatures higher than 400 °C, whereas no type II structure has been reported for members beyond Gd.43Lanthanide oxysulfides (Ln2O2S)
Rare earth oxysulfides have a trigonal crystal structure (space group P3m1), with one formula per unit cell. This structure is closely related with the A-type structure of the rare earth sesquioxides and can be described as an alternative stacking of Ln2O22+ and S2− layers.10,53,54Methodology
In this section we outline the various methods used for calculating enthalpies of formation. Example calculations, for LaPO4, are given in the ESI.†Experimental enthalpies of formation
A literature review of the experimental enthalpy of formation values of the different rare earth compounds considered in this work was carried out and their average values are presented in Table 1.| Ln | Ln2O3 | LnCl3 | LnOCl | LnPO4 | Ln2O2CO3a | Ln2O2S | NaLnO2 |
|---|---|---|---|---|---|---|---|
| u.k. = unknown.a Type II oxycarbonates. | |||||||
| La | −1793.8 ± 1.3 | −1072.1 ± 0.9 | −1013.8 ± 4.4 | −1937.2 ± 47.4 | −2388.4 ± 3.5 | −1723.8 ± 9.3 | u.k. |
| Ce | −1799.7 ± 7.1 | −1056.0 ± 3.3 | −1002.3 ± 2.4 | −1949.8 ± 25.5 | u.k. | −1743.0 | −1127.0 |
| Pr | −1812.6 ± 6.7 | −1057.6 ± 1.0 | −1013.6 ± 0.6 | −1969.5 | u.k. | −1742.4 ± 6.8 | u.k. |
| Nd | −1808.2 ± 0.6 | −1041.5 ± 0.4 | −1000.5 ± 0.5 | −1931.9 ± 51.7 | −2382.1 ± 9.4 | −1733.7 ± 19.1 | u.k. |
| Pm | −1811.0 | −1029.3 | u.k. | u.k. | u.k. | −1751.4 | u.k. |
| Sm | −1824.0 ± 1.7 | −1026.4 ± 1.2 | −994.9 ± 4.8 | −1922.2 ± 61.6 | u.k. | −1747.1 ± 18.0 | u.k. |
| Eu | −1658.3 ± 6.0 | −936.8 ± 1.5 | u.k. | −1880.9 ± 14.5 | −2202.4 ± 12.0 | −1578.0 ± 19.5 | u.k. |
| Gd | −1824.5 ± 10.6 | −1007.3 ± 1.9 | −980.8 ± 2.5 | −1924.6 ± 53.2 | u.k. | −1744.2 ± 28.0 | u.k. |
| Tb | −1865.4 ± 0.0 | −1000.1 ± 4.6 | −981.8 ± 5.5 | −1947.8 ± 38.2 | u.k. | −1762.9 ± 13.5 | u.k. |
| Dy | −1863.3 ± 0.6 | −996.6 ± 4.9 | −986.3 ± 2.5 | −1937.9 ± 42.4 | u.k. | −1762.5 ± 20.0 | u.k. |
| Ho | −1881.0 ± 0.5 | −1003.2 ± 5.5 | −996.2 ± 7.4 | −1948.1 ± 33.2 | u.k. | −1774.1 ± 9.5 | u.k. |
| Er | −1898.1 ± 0.6 | −996.8 ± 2.6 | −993.9 ± 5.5 | −1957.0 ± 28.1 | u.k. | −1782.5 ± 2.4 | u.k. |
| Tm | −1888.9 ± 0.6 | −989.8 ± 4.0 | −990.0 ± 1.7 | −1946.8 ± 25.4 | u.k. | −1777.7 ± 10.4 | u.k. |
| Yb | −1821.7 ± 19.3 | −960.3 ± 0.7 | −962.2 ± 0.3 | −1906.1 ± 33.0 | u.k. | −1692.6 | u.k. |
| Lu | −1878.4 ± 0.6 | −966.2 ± 23.4 | −976.8 ± 22.9 | −1948.4 ± 9.9 | u.k. | −1789.2 | u.k. |
Group contribution method
Mostafa et al.1 developed a group contribution (GC) method to estimate the enthalpy of formation (ΔH0f) of solid inorganic salts. It is based on a multiple linear regression analysis, which calculates the contribution of each cation, anion and ligand molecule to the total heat of formation of the inorganic solid. We used this method to estimate the enthalpy of formation of rare earth compounds using the values of the different ionic contributions in ref. 1. The contribution of the ion S2− was estimated as the difference between the contribution of the ligand H2S and two times the contribution of the ion H+ giving a value of 108.8 kJ mol−1.Volume based thermodynamics
The volume based thermodynamics method (VBT), is a range of correlation methods that rely on the volume of the condensed phases to estimate thermodynamic properties.2,3 This method was used to predict the lattice potential energy of rare earth compounds, which was input into the Born–Haber–Fajans cycle (BHFC) to calculate ΔH0f from their individual elements. The lattice potential energy was calculated using the equations proposed by Jenkins and Glasser55,56 | (1) |
 | (2) |
Since the BHFC is an enthalpy cycle, the lattice energy (UPOT) calculated using eqn (1) and (2) was transformed into lattice enthalpy55 using the following expression
 | (3) |
The thermochemical cycles considered in each BHFC are presented in Fig. S1a–f in ESI.† The values of the lattice enthalpy and the standard enthalpies of sublimation, ionization, dissociation, and electronic affinity used in this work can also be found in the ESI.†
Predictions based on lattice energy calculations using EUGEN
EUGEN is a code for calculating Madelung constants of salts,58 and outputs Madelung energies (EMadelung). Madelung energies output from the EUGEN code were used to estimate lattice potential energies (UPOT). Based on the observation of Glasser,59 lattice potential energies were computed using the relation: UPOT = 0.85EMadelung. The factor of 0.85 accounts for the fact that Madelung energies are based on coloumbic interactions alone and neglect other types of interactions, such as van der Waals repulsions. Note that, this relation was used to calculate lattice potential energies for all compounds, with the exception of the trichlorides. For the trichlorides it was found that scaling Madelung energies by a factor of 0.85 led to poor corresponding enthalpies of formation, and so for these compounds lattice potential energies were taken to be Madelung energies, without scaling. This is in keeping with the work of Glasser,59 who reported the Madelung energies and lattice potential energies of LaCl3, and YCl3 to be within 1–2%. Calculated lattice potential energies were then converted to enthalpies using eqn (3) and input into the BHFC to calculate enthalpies of formation.The EUGEN code requires the positions and charges of anions and cations in order to calculate Madelung energies. In our calculations compounds were treated as ionic and charges on anions and cations were taken to be their oxidation number. Of course, the validity this is an approximation decreases with the covalent character of the compound, but calculation of the fractional charges on ions is out of the scope of this study. Using the oxidation number means that the method is kept simple and, as we will show, leads to reasonable results.
The crystal structures of the rare earth oxysulfide and sodium lanthanide oxides were taken from The Materials Project (https://materialsproject.org),60 which contains a database of structures calculated from density functional theory calculations. Due to the absence of some structure for the phosphates, chlorides, and oxychlorides in The Materials Project database, we calculated them ourselves using the density functional theory based VASP code,61,62 with the projector augmented wave method.62–64 The PBEsol exchange–correlation functional65 and an energy cut-off of 1000 eV were used for all calculations. The valence electron configurations for the potentials were: 5s2 5p6 5d1 6s2 for all rare earth elements from La to Sm and 5p6 5d1 6s2 for all rare earth elements from Eu to La (with the 4f electrons frozen in the core); 3s2 3p3 for P; s2 p5 for Cl; and 2s2 2p4 for O. Brillouin zone sampling was carried out using the following Monkhorst–Pack grids:66 phosphates (monazite) 4 × 4 × 4; phosphates (xenotime) 4 × 4 × 4; chlorides (hexagonal) 6 × 6 × 8; chlorides (monoclinic) 4 × 3 × 4; oxychlorides 16 × 16 × 16.
In order to validate the use of the EUGEN code for compounds in our test set, we calculated the lattice potential enthalpies for some similar compounds, e.g. sulfides, chloride and oxides, for which values determined from experimental data exist.67 The crystal structures were taken from The Materials Project (https://materialsproject.org)60 and the charges on ions were taken to be their oxidation number. The results of these calculations are in Table S1 of the ESI.† In general, good agreement is found.
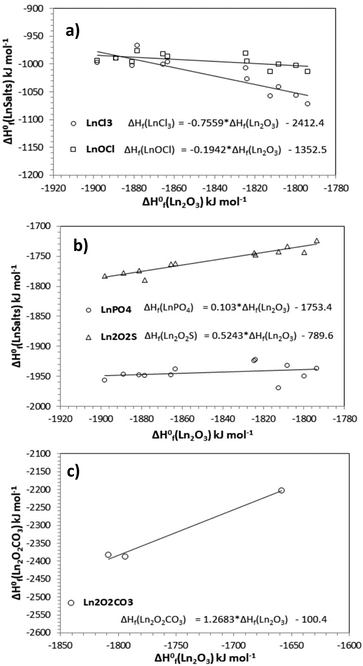
Linear relationship
The correlation between ΔH0f(Ln2O3) and ΔH0f(LnSalt) for our test set of rare earth compounds is presented in Fig. 1a–c using the values given in Table 1. Promethium was excluded from the analysis due to the lack of data for most of the compounds under study. Moreover, from Table 1 the values for europium and ytterbium compounds are anomalous and so were also excluded from our analysis. Glasser68 explained that the anomalous behaviour of europium arises from the ground state of Eu3+ having zero magnetic spin entropy, compared to other trivalent lanthanide ions, which have finite values. The discrepancy between the enthalpies of formation of Lu and Yb compounds are attributed to a fall in the ionization energy of the ion Lu3+ with respect to the Yb3+ due to the fully shielded outer f-electron shell of Yb. To our best knowledge, this is the first time these linear relationships have been reported. They offer a new way to predict the enthalpy of formation of rare earth compounds for which values are known for other rare earth elements in the series.Table 2 shows the statistical descriptors for each regression. As can be observed in Table 2, the r2 values obtained for LnCl3, Ln2O2S and Ln2O2CO3 show a linear dependence between ΔH0f(Ln2O3) and ΔH0f(LnSalt). A poor dependence is observed for LnOCl and LnPO4. However, the F-test carried out at a 99% confidence level, shows that F calc > F critical in all cases indicating that there is a relationship between ΔH0f(Ln2O3) and ΔH0f(LnSalt) in all cases, despite the low r2 values found for LnPO4 and LnOCl.
| LnSalt | r 2 | F calc. | F critical |
|---|---|---|---|
| LnCl3 | 0.7806 | 35.58 | 1.38 × 10−4 |
| LnOCl | 0.3768 | 6.04 | 3.37 × 10−2 |
| LnPO4 | 0.0845 | 0.92 | 3.59 × 10−1 |
| Ln2O2S | 0.9098 | 101.81 | 1.53 × 10−6 |
| Ln2O2CO3 | 0.9864 | 72.40 | 7.44 × 10−2 |
Group contribution method
The values of ΔH0f(LnSalt) calculated using the group contribution method developed by Mostafa et al. are presented in Table S2 (ESI†), where all the values are within 9.0% of available experimental data. Promethium compounds were not calculated because the unknown contribution value for Pm3+. According to the literature review carried out, the type I crystal structure of the oxycarbonates is the most stable at low temperature. However, thermogravimetric studies,8,69 have confirmed the co-existence of type I and type II oxy-carbonates for the light rare earth elements from 400 to 600 °C as a consequence of their polymorphic nature, which suggests that little difference may exist between the enthalpy of formation of the type I and type II oxy-carbonates.No experimental values of the enthalpy of formation were found for the sodium lanthanide oxides. Only Barker et al.70 reported the experimental value of the enthalpy of formation of NaCeO2 as −1127.0 kJ mol−1 at 352 °C, which is within reasonable limits of our estimation using Mostafa's et al. group contribution method.
Volume based thermodynamics
The VBT method relies on accurate determination of molecular volumes to calculate the lattice energy of solid phases. It is important to bear in mind that propagation of uncertainties of ±10% in the molecular volume can lead to ±20% uncertainties in the calculated enthalpy of formation. In addition, the VBT method assumes ionic character of the compounds studied. The values of the ΔH0f(LnSalt) calculated using the volume based thermodynamics are presented in Table S3 (ESI†). As can be observed from Table S3 (ESI†), the average deviation from experimental available data is higher than 14.0%. One of the main reasons for the inaccuracies observed is that the most recent crystal data for the chlorides and oxychlorides are from eighties. In addition, when covalent forces play an important role, eqn (1) and (2) become increasingly unreliable.3 The oxysalts (LnOCl, Ln2O2CO3 and Ln2O2S) and the A-Ln2O3, can be structurally defined as tri or bi-dimensional packing of OLn4 tetrahedra sharing edges that appear as an infinite polymeric complex cation (LnO)nn+ which alternate with sheets of the anions. Considering the OLn4 tetrahedra as the basic structural unit, directional bonding of the oxygen atom might be expected, meaning that a large, but not dominant, covalent contribution may be present in these compounds.71 Similar structural features may apply to the NaLnO2. However, there is little information available in the literature about them.EUGEN calculations
To attempt to improve estimations of enthalpies of formation calculated using the BHFC, electrostatic lattice energies determined using the EUGEN code58 were used as an approximation for lattice potential energies (UPOT) in eqn (3). These lead to significantly improved values, except for the phosphates.Method comparison
In Fig. 2 we present, the absolute error calculated according to eqn (4), for the rare earth chlorides, oxychlorides, oxysulfides and phosphates. When no experimental values were available or the enthalpy of formation could not be predicted by a particular method for some compounds the error was not calculated.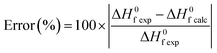 | (4) |
 | ||
| Fig. 2 Comparison between estimated and experimental values of the enthalpy of formation for LnCl3, LnOCl, LnPO4 and Ln2O2S. | ||
The VBT method appears to be unsuitable for estimating the enthalpy of formation of LnCl3 with absolute errors between about 40.0–90.0%. The situation is better for LnOCl and Ln2O2S with absolute errors of about 23.0–28.0% and 12.0–19.0% respectively. For LnPO4, the VBT method shows high variability, with absolute errors of between 0.9 to 26%. The correction of the VBT method carried out using EUGEN to calculate UPOT rather than eqn (1) and (2) improves the estimations of all the compounds except for LnPO4. These differences are attributed to the values of the parameters A and α, which seem to be unsuitable for lanthanide compounds.
Due to scarce experimental values for Ln2O2CO3 and NaLnO2, the group contribution method was taken as a reference for comparison with the other methods, which is presented in Fig. 3. It can be observed that the linear relationship presented in Table 2 for Ln2O2CO3 agrees well with the values predicted using the group contribution method, with absolute errors ranging from 0.6–9.0%. This agreement is excellent, considering that the linear relationship was calculated using the enthalpies of formation of just three of the oxycarbonates, and illustrates the predictive power of the method. The VBT method fails in the prediction of the enthalpy of formation of Ln2O2CO3, because of the important covalent contribution present. It was not possible to predict values for Ln2O2CO3 using the EUGEN code, due to the crystal structure having partial occupancies.
 | ||
| Fig. 3 Comparison between estimated values of the enthalpy of formation with the group contribution, VBT and Madelung methods for Ln2O2CO3 and NaLnO2. | ||
For NaLnO2 discrepancies between 19.0–32.0% are reported when the VBT method is used. Better estimations are achieved when for calculations based on lattice potential energies calculated using the EUGEN code, as shown in Fig. 3.
Conclusions
In this work we have compared several methods for calculating the enthalpies of formation of the rare earth compounds: LnCl3, LnOCl, LnPO4, Ln2O2S, Ln2O2CO3 and NaLnO2. We find that the method of Mostafa et al.1 and our method based on a linear relationship are the most accurate. However, the method of Mostafa et al.1 requires that the contribution of each group is known, while our method based on a linear relationship necessitates that experimental data is available for some of the rare earth compounds. In contrast, the VBT method only requires the molecular volume of a compound, but the accuracy of predicted values is poor when covalent bonding contributions are significant. The calculation of the lattice potential energy using EUGEN instead of eqn (1) and (2) improves the estimation using the BHFC but requires the full crystal structure. This improvement suggests that the value of the parameters α = 139.0 kJ mol−1 and A = 123.0 kJ mol−1 are unsuitable for the compounds studied. Taken together, these methods provide a complementary suite of techniques for predicting the enthalpies of formation of rare earth compounds, depending on the experimental data available and accuracy desired. Our recommendations are as follows. If enthalpies of formation are available for some rare earth compounds in the series, use the linear relationship. If no enthalpies of formation exist, and all group contributions are available, use the method of Mostafa et al.1 Failing this, use the BHFC. If using the BHFC, and the crystal structure is available, calculating the lattice potential energy using the EUGEN code. If only the volume is available, use the VBT method to calculate the lattice potential energy.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support received from the Engineering and Physical Sciences Research Council (EPSRC) (Grants GR/T19889/01 and GR/L95977/01), and Natural Environment Research Council (NERC) (Grants NE/M01147X/1, and NE/L002280/1). Dr Sanchez-Segado acknowledges the support from the European Union's Marie Curie Fellowship grant number 331385 and from The Ministry of Science, Innovation and University of Spain (“Beatriz Galindo” Fellowship BEAGAL18/00079). The authors thank Samuel Tan and Ekaterina I. Izgorodina, for providing the modified version of the EUGEN code.References
- A. T. M. G. Mostafa, J. M. Eakman and S. L. Yarbro, Prediction of Standard Heats and Gibbs Free Energies of Formation of Solid Inorganic Salts from Group Contributions, Ind. Eng. Chem. Res., 1995, 34, 4577–4582 CrossRef CAS.
- L. Glasser and H. D. B. Jenkins, Predictive thermodynamics for condensed phases, Chem. Soc. Rev., 2005, 34, 866 RSC.
- L. Glasser and H. D. B. Jenkins, Predictive thermodynamics for ionic solids and liquids, Phys. Chem. Chem. Phys., 2016, 18, 21226–21240 RSC.
- A. R. Chakhmouradian and F. Wall, Rare Earth Elements: Minerals, Mines, Magnets (and More), Elements, 2012, 8, 333–340 CrossRef CAS.
- A. Golev, M. Scott, P. D. Erskine, S. H. Ali and G. R. Ballantyne, Rare earths supply chains: Current status, constraints and opportunities, Resour. Policy, 2014, 41, 52–59 CrossRef.
- F. Wang, R. Shi, Z.-Q. Liu, P.-J. Shang, X. Pang, S. Shen, Z. Feng, C. Li and W. Shen, Highly Efficient Dehydrogenation of Primary Aliphatic Alcohols Catalyzed by Cu Nanoparticles Dispersed on Rod-Shaped La2O2CO3, ACS Catal., 2013, 3, 890–894 CrossRef CAS.
- A. Olafsen, A.-K. Larsson, H. Fjellvåg and B. C. Hauback, On the Crystal Structure of Ln2O2CO3 II (Ln = La and Nd), J. Solid State Chem., 2001, 158, 14–24 CrossRef CAS.
- A. Olafsen and H. Fjellvåg, Synthesis of rare earth oxide carbonates and thermal stability of Nd2O2CO3 II, J. Mater. Chem., 1999, 9, 2697–2702 RSC.
- X. Wang, J.-G. Li, Q. Zhu, X. Li, X. Sun and Y. Sakka, Facile and green synthesis of (La0.95Eu0.05)2O2S red phosphors with sulfate-ion pillared layered hydroxides as a new type of precursor: controlled hydrothermal processing, phase evolution and photoluminescence, Sci. Technol. Adv. Mater., 2014, 15, 014204 CrossRef CAS PubMed.
- M. Machida, K. Kawamura, K. Ito and K. Ikeue, Large-Capacity Oxygen Storage by Lanthanide Oxysulfate/Oxysulfide Systems, Chem. Mater., 2005, 17, 1487–1492 CrossRef CAS.
- F. Zhao, M. Yuan, W. Zhang and S. Gao, Monodisperse Lanthanide Oxysulfide Nanocrystals, J. Am. Chem. Soc., 2006, 128, 11758–11759 CrossRef CAS PubMed.
- A. R. Jha, Rare Earth Materials, CRC Press, 2014 Search PubMed.
- A. Kumari, R. Panda, M. K. Jha, J. R. Kumar and J. Y. Lee, Process development to recover rare earth metals from monazite mineral: A review, Miner. Eng., 2015, 79, 102–115 CrossRef CAS.
- P. Nuss and M. J. Eckelman, Life Cycle Assessment of Metals: A Scientific Synthesis, PLoS One, 2014, 9, e101298 CrossRef PubMed.
- L. Berry, J. Galvin, V. Agarwal and M. S. Safarzadeh, Alkali pug bake process for the decomposition of monazite concentrates, Miner. Eng., 2017, 109, 32–41 CrossRef CAS.
- K. Binnemans, P. T. Jones, B. Blanpain, T. Van Gerven and Y. Pontikes, Towards zero-waste valorisation of rare-earth-containing industrial process residues: a critical review, J. Cleaner Prod., 2015, 99, 17–38 CrossRef CAS.
- S. Sanchez-Segado, A. Lahiri and A. Jha, Alkali roasting of bomar ilmenite: rare earths recovery and physico-chemical changes, Open Chem., 2015, 13(1), 270–278 Search PubMed.
- T. Makanyire, S. Sanchez-Segado and A. Jha, Separation and recovery of critical metal ions using ionic liquids, Adv. Manuf., 2016, 4, 33–46 CrossRef CAS.
- A. Lahiri and A. Jha, Selective separation of rare earths and impurities from ilmenite ore by addition of K+ and Al3+ ions, Hydrometallurgy, 2009, 95, 254–261 CrossRef CAS.
- M. G. Barker, S. A. Frankham and P. G. Gadd, Polymorphism in some sodium lanthanide-metal ternary oxides of the type NaLnO2, J. Inorg. Nucl. Chem., 1981, 43, 2815–2819 CrossRef CAS.
- Y. Wu, B. Wang, Q. Zhang, R. Li and J. Yu, A novel process for high efficiency recovery of rare earth metals from waste phosphors using a sodium peroxide system, RSC Adv., 2014, 4, 7927 RSC.
- Y. Wu, B. Wang, Q. Zhang, R. Li, C. Sun and W. Wang, Recovery of rare earth elements from waste fluorescent phosphors: Na2O2 molten salt decomposition, J. Mater. Cycles Waste Manage., 2014, 16, 635–641 CrossRef CAS.
- P. J. Spencer, Estimation of thermodynamic data for metallurgical applications, Thermochim. Acta, 1998, 314, 1–21 CrossRef CAS.
- M. Ducros and H. Sannier, Méthode d’estimation des enthalpies de formation et des enthalpies libres de formation des composés inorganiques, Thermochim. Acta, 1992, 196, 27–43 CrossRef CAS.
- S. Kaya and C. Kaya, A Simple Method for the Calculation of Lattice Energies of Inorganic Ionic Crystals Based on the Chemical Hardness, Inorg. Chem., 2015, 54, 8207–8213 CrossRef CAS PubMed.
- H. D. B. Jenkins, H. K. Roobottom, J. Passmore and L. Glasser, Relationships among Ionic Lattice Energies, Molecular (Formula Unit) Volumes, and Thermochemical Radii, Inorg. Chem., 1999, 38, 3609–3620 CrossRef CAS PubMed.
- H. D. B. Jenkins, D. Tudela and L. Glasser, Lattice Potential Energy Estimation for Complex Ionic Salts from Density Measurements, Inorg. Chem., 2002, 41, 2364–2367 CrossRef CAS PubMed.
- S. C. Atkinson, Crystal structures and phase transitions in the rare earth oxides, PhD thesis, University of Salford, 2014 Search PubMed.
- R. S. Roth and S. J. Schneider, Phase equilibria in systems involving the rare-earth oxides. Part I. Polymorphism of the oxides of the trivalent rare-earth ions, J. Res. Natl. Bur. Stand., Sect. A, 1960, 64, 309 CrossRef PubMed.
- G. Adachi and N. Imanaka, The Binary Rare Earth Oxides, Chem. Rev., 1998, 98, 1479–1514 CrossRef CAS PubMed.
- A. Navrotsky, W. Lee, A. Mielewczyk-Gryn, S. V. Ushakov, A. Anderko, H. Wu and R. E. Riman, Thermodynamics of solid phases containing rare earth oxides, J. Chem. Thermodyn., 2015, 88, 126–141 CrossRef CAS.
- G. Garton and P. J. Walker, Polymorphism in the rare-earth trichlorides: Phase equilibria and crystal growth measurements, Mater. Res. Bull., 1982, 17, 1227–1234 CrossRef CAS.
- B. Morosin, Crystal Structures of Anhydrous Rare-Earth Chlorides, J. Chem. Phys., 1968, 49, 3007–3012 CrossRef CAS.
- D. H. Templeton and G. F. Carter, The Crystal Structures of Yttrium Trichloride and Similar Compounds, J. Phys. Chem., 1954, 58, 940–944 CrossRef CAS.
- J. D. Forrester, A. Zalkin, D. H. Templeton and J. C. Wallmann, Crystal Structure of Terbium Trichloride, Inorg. Chem., 1964, 3, 185–188 CrossRef CAS.
- L. Rycerz and M. Gaune-Escard, Lanthanide(III) halides: Thermodynamic properties and their correlation with crystal structure, J. Alloys Compd., 2008, 450, 167–174 CrossRef CAS.
- D. H. Templeton and C. H. Dauben, Crystal Structures of Rare Earth Oxychlorides, J. Am. Chem. Soc., 1953, 75, 6069–6070 CrossRef CAS.
- J. Hölsä, M. Lahtinen, M. Lastusaari, J. Valkonen and J. Viljanen, Stability of Rare-Earth Oxychloride Phases: Bond Valence Study, J. Solid State Chem., 2002, 165, 48–55 CrossRef.
- S. V. Ushakov, K. B. Helean, A. Navrotsky and L. A. Boatner, Thermochemistry of rare-earth orthophosphates, J. Mater. Res., 2001, 16, 2623–2633 CrossRef CAS.
- S. N. Achary, S. Bevara and A. K. Tyagi, Recent progress on synthesis and structural aspects of rare-earth phosphates, Coord. Chem. Rev., 2017, 340, 266–297 CrossRef CAS.
- G. Blasse, Sodium lanthanide oxides NaLnO2, J. Inorg. Nucl. Chem., 1966, 28, 2444–2445 CrossRef CAS.
- Y. Hashimoto, M. Wakeshima and Y. Hinatsu, Magnetic properties of ternary sodium oxides NaLnO2 (Ln = rare earths), J. Solid State Chem., 2003, 176, 266–272 CrossRef CAS.
- R. P. Turcotte, J. O. Sawyer and L. Eyring, Rare earth dioxymonocarbonates and their decomposition, Inorg. Chem., 1969, 8, 238–246 CrossRef CAS.
- V. B. Parker, R. H. Schumm, D. D. Wagman, S. Bailey and W. H. Evans, Selected Values of Chemical Thermodynamic Properties, Tables for the Lanthanide (Rare Earth) Elements, National Bureau of Standards, Maryland, 1973 Search PubMed.
- J. A. Dean, Lange's Handbook of Chemistry, Mc Graw-Hill, New York, 11th edn, 1979 Search PubMed.
- D. R. Lide, Handbook of Chemistry and Physics, CRC Press, Florida, 85th edn, 2003 Search PubMed.
- L. Rycerz and M. Gaune-Escard, Thermodynamics of SmCl3 and TmCl3: Experimental Enthalpy of Fusion and Heat Capacity. Estimation of Thermodynamic Functions up to 1300 K, Z. Naturforsch., A, 2002, 57(1), 79–84 CrossRef CAS.
- L. Rycerz and M. Gaune-Escard, Thermodynamics of EuCl3: Experimental Enthalpy of Fusion and Heat Capacity and Estimation of Thermodynamic Functions up to 1300 K, Z. Naturforsch., A, 2002, 57(9), 79–84 CrossRef CAS.
- R. J. M. Konings, O. Beneš, A. Kovács, D. Manara, D. Sedmidubský, L. Gorokhov, V. S. Iorish, V. Yungman, E. Shenyavskaya and E. Osina, The Thermodynamic Properties of the f -Elements and their Compounds. Part 2. The Lanthanide and Actinide Oxides, J. Phys. Chem. Ref. Data, 2014, 43, 013101 CrossRef.
- R. K. Dwivedi, Determination of the Thermodynamic Properties of Rare Earth-Oxygen-Sulfur Systems at High Temperatures, PhD thesis, Mc Master University, 1982 Search PubMed.
- R. Akila, K. T. Jacob and A. K. Shukla, Gibbs energies of formation of rare earth oxysulfides, Metall. Trans. B, 1987, 18, 163–168 CrossRef.
- A. Roine, 2002. In H.S.C Chemistry for Windows: Chemical Reaction and Equilibrium Software with Extensive Thermodynamical Database, Outokumpu Research Oy, Finland, 2002.
- W. H. Zachariasen, Crystal chemical studies of the 5f-series of elements. VII. The crystal structure of Ce2O2S, La2O2S and Pu2O2S, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1949, 2, 60–62 CrossRef CAS.
- M. Mikami and A. Oshiyama, First-principles band-structure calculation of yttrium oxysulfide, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 8939–8944 CrossRef CAS.
- L. Glasser and L. von Szentpály, Born–Haber–Fajans Cycle Generalized: Linear Energy Relation between Molecules, Crystals, and Metals, J. Am. Chem. Soc., 2006, 128, 12314–12321 CrossRef CAS PubMed.
- L. Glasser and H. D. B. Jenkins, Volume-Based Thermodynamics: A Prescription for Its Application and Usage in Approximation and Prediction of Thermodynamic Data, J. Chem. Eng. Data, 2011, 56, 874–880 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, Volume-Based Thermodynamics: Estimations for 2:2 Salts, Inorg. Chem., 2006, 45, 1754–1756 CrossRef CAS PubMed.
- E. I. Izgorodina, U. L. Bernard, P. M. Dean, J. M. Pringle and D. R. MacFarlane, The Madelung Constant of Organic Salts, Cryst. Growth Des., 2009, 9, 4834–4839 CrossRef CAS.
- L. Glasser, Solid-State Energetics and Electrostatics: Madelung Constants and Madelung Energies, Inorg. Chem., 2012, 51, 2420–2424 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- H. D. B. Jenkins and H. D. B. Roobottom, in Lattice Energies in CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, Boca Raton, 97th edn, 2016, pp. 2097–2105 Search PubMed.
- L. Glasser, Thermodynamic consistencies and anomalies among end-member lanthanoid garnets, J. Chem. Thermodyn., 2014, 78, 93–98 CrossRef CAS.
- A. O. Sjåstad, H. Fjellvåg, K. B. Helean and A. Navrotsky, Enthalpy of formation of Ln2O2CO3 II (Ln = La, Nd, Eu) and thermodynamics of decomposition equilibria, Thermochim. Acta, 2012, 550, 76–82 CrossRef.
- M. G. Barker, S. A. Frankham and P. G. Gadd, The reaction of liquid sodium with the oxides CeO2 and Ce2O3 and the determination of the free energy of formation of NaCeO2 and Na2CeO3, J. Nucl. Mater., 1995, 218, 256–260 CrossRef CAS.
- P. E. Caro, OM4 Tetrahedra linkages and the cationic group (M0)nn+ in rare earth oxides and oxysalts, J. Less-Common Met., 1968, 16, 367–377 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03280a |
| This journal is © the Owner Societies 2021 |