Electrostatic interactions contribute to the control of intramolecular thiol–disulfide isomerization in a protein

Abstract

The roles of structural factors and of electrostatic interactions with the environment on the outcome of thiol–disulfide exchange reactions were investigated in a mutated immunoglobulin domain (I27*) under mechanical stress. An extensive ensemble of molecular dynamics trajectories was generated by means of QM/MM simulations for a total sampling of 5.7 μs. A significant number of thiol–disulfide exchanges were observed, and the Cys32 thiolate preferred to attack Cys55 over Cys24, in agreement with previous experimental and computational studies. The structural features as well as electronic structures of the thiol–disulfide system along the reaction were analyzed, as were the electrostatic interactions with the environment. The previous findings of better accessibility of Cys55 were confirmed. Additionally, the reaction was found to be directed by the electrostatic interactions of the involved sulfur atoms with the molecular environment. The relationships of atomic charges, which stem from the electrostatic interactions, lead to the kinetic preference of the attack on Cys55. Further, QM/MM metadynamics simulations of thiol–disulfide exchange in a small model system with varied artificial external electric potentials revealed changes in reaction kinetics of the same magnitude as in I27*. Therefore, the electrostatic interactions are confirmed to play a role in the regioselectivity of the thiol–disulfide exchange reactions in the protein.

---

1 Introduction

Ubiquitous in proteins, disulfide bonds fulfill many important physiological roles – structural, functional and regulatory. They form between two cysteines on the same or on two different peptide strands, and thus serve as cross-links impacting the stability of the protein structure and the process of folding. Moreover, disulfide bonds may act as catalysts by manipulating other disulfide bonds in substrates or other proteins, like in thioredoxin and glutaredoxin systems¹ or in protein disulfide isomerases.² Recently, it has become evident that they can also regulate the function of proteins or enzymes, i.e. the cleavage or formation of a so-called allosteric disulfide bond can trigger or inhibit the function of a protein.^3,4 For example, the force-dependent binding of platelet proteins to the A1 domain of von Willebrand factor (VWF) in plasma is autoinhibited by the neighboring A2 domain unless an allosteric disulfide bond is cleaved.⁵ In general, disulfide bonds can be cleaved by various mechanisms, and thiol–disulfide exchange is one.

Thiol–disulfide exchange is an S_N2 reaction between a thiolate anion R₁–S⁻ and a disulfide bond R₂–S–S–R₃, which results in a new disulfide bond, either R₁–S–S–R₂ or R₁–S–S–R₃.⁶ Notably, disulfide bonding patterns in proteins are not necessarily static and stable – rather, they can possess a dynamic character and rearrange spontaneously. Intra- or intermolecular shuffling of disulfide bonds can be triggered by mechanical stress, e.g., pulling the disulfide bond into opposite directions, which unfolds the protein and decreases the activation energy for a nucleophilic attack by a free thiolate.^7,8

In a novel approach, Alegre-Cebollada et al. investigated protein unfolding and disulfide isomerization of a mutated I27 immunoglobulin domain (I27*) in real time with force-clamp atomic-force microscopy (AFM).⁹ I27* was engineered to have a disulfide bond between Cys24 and Cys55 and a free reactive cysteine Cys32, see Fig. 1A. Due to a constant pulling force of 250 pN, far below the force necessary to break covalent bonds (above 1 nN),^10,11 the protein unfolded up to the disulfide bond. Residues 25 to 54, including Cys32, were located on a flexible loop which did not stretch because of the disulfide bond, see Fig. 1B. Thus, Cys32 remained in the vicinity of the disulfide bond after the first unfolding step and was able to engage in a nucleophilic attack on Cys24 or Cys55, see Fig. 1C and D. A reaction with Cys55 occurred 3.8 times more frequently than with Cys24. No conclusive explanation of this regioselectivity was found, and it was called for systematic studies on how the reactivity of disulfide bond is affected by their environments.

Fig. 1 Constant pulling force on the termini of the I27* domain (A) leads to unfolding up to the disulfide bond Cys24–Cys55 (B). This uncages Cys32 so that it can perform a nucleophilic attack on Cys24 (C) or Cys55 (D). Sulfur atoms are depicted by yellow balls. (Image created by the authors, based on PDB ID 1WAA.)¹²

To this end, Kolšek et al. carried out force-clamp MD simulations on I27* using a molecular mechanics-based framework that allowed for disulfide bond rearrangements through Monte Carlo-controlled topology exchanges.¹³ This approach reproduced the regioselectivity observed by the experimental AFM setup with the advantage of an atomistic description of the process. In the simulations, Cys55 was more readily spatially accessible for a nucleophilic attack than Cys24, and consequently, it was approached by Cys32 more often, leading to the reaction Cys32 → Cys55 occurring more frequently. Thus, steric factors play an important role in disulfide shuffling.

So do electrostatic interactions. The rate of thiol–disulfide exchange, an S_N2 reaction, depends on the nucleophilicity of the attacking thiolate S_nuc, the electrophilicity of the attacked sulfur S_ctr as well as the stability of the leaving group S_lg.^6,14 These factors are not solely determined by the reactive species themselves; rather, they are affected by the steric and electrostatic interactions with the environment. Notably, the lowest-energy state of a symmetric molecule (R₁ = R₂ = R₃) in the gas phase is a linear trisulfide arrangement with the negative charge delocalized over all three sulfurs.¹⁵ This is reflected by the general observation that thiol–disulfide exchange is best catalyzed by hydrophobic, aprotic environments – conditions in which the charge is quite delocalized.¹⁶ On the other hand, polar solvents induce a localization of the charges, favoring arrangements with separated molecules, a thiolate and a disulfide.

The charge distribution on a thiol–disulfide center – and consequently, the nucleophilicity and the electrophilicity of the sulfur atoms – are modulated not only by the solvent but also by the microenvironment, e.g. the neighboring functional groups or amino acids. Wu et al. demonstrated that ionic residues in close proximity to the reactants have a major impact on disulfide exchange reaction rates.¹⁷ They investigated the reaction between a cysteine as a nucleophile and several small disulfide-bonded peptide homodimers. Net charges ranging from −2 to +2 were introduced in each peptide by putting glutamate or arginine residues in positions adjacent to the disulfide-bonded cysteines. The reactivity showed a linear dependence on the introduced net charges, −2 showing the least and +2 the highest reactivity. Similar effects of the environment on the reactivity were observed in other studies, also.^18–21

This work aims to explain the regioselectivity of the disulfide shuffling in proteins, considering the mutated immunoglobulin domain I27* as an example, providing more detail than the previous work in ref. 13. To this end, we perform 334 QM/MM force-clamp simulations of I27*, with an accumulated sampling of ca.5.7 μs. The QM/MM simulations are set up in order to cover a possible nucleophilic attack of the deprotonated reduced Cys32, located on a flexible loop, on both Cys24 and Cys55. To elucidate the prerequisites for a successful disulfide exchange, we analyze 10 ps prior to the formation of transition state in trajectories where a reaction does take place, and analyze potentials of mean force as function of the sulfur–sulfur distances based on all of the trajectories. Also, we perform QM/MM metadynamics simulation of the two different disulfide exchange reactions in I27* but observe difficult convergence. Finally, we demonstrate the impact of electrostatics on disulfide exchange on the basis of metadynamics simulation of a small model system.

2 Materials and methods

2.1 QM/MM force-clamp simulations of I27*

System setup. We performed 334 QM/MM simulations of an immunoglobulin I27 domain (PDB ID 1WAA),¹² which was engineered to have two oxidized cysteines at positions 24 and 55 forming a disulfide bond and a free reactive cysteine at position 32 by Kolšek et al.¹³ Snapshots from their force-clamp swapping simulations were selected as starting structures. Due to an applied external pulling force on the termini, the protein was already unfolded up to the disulfide bond between S24 and S55. In 160 of the selected structures S32 was closer to S24, and in 174 structures closer to S55. The unfolded termini were removed to reduce the system size and only residues 20 to 65 were kept. The sulfur atom of Cys32 was prepared as an anion to enable a reaction with the disulfide bonded sulfurs. Charge neutrality of the system was achieved by mutating residues 62, 64 and 65 to lysines with xLeap from the AmberTools package²² instead of adding counter ions, which might interfere with the disulfide shuffling. The protein was centered in a rectangular box sized 15.0 × 4.8 × 4.8 nm³ and solvated with 11125 water molecules.

MM equilibration. Prior to QM/MM simulations, the structures were equilibrated with classical force field molecular dynamics using Gromacs 5.0.1 patched with Plumed 2.1.1.^23,24 The AMBER99SB-ILDN forcefield²⁵ and TIP3P water were used. Periodic boundary conditions were employed, and electrostatics were treated with the particle–mesh Ewald method. Lennard-Jones interactions were cut-off at 1 nm and the neighbour list updated every 10 MD steps. The leap-frog integrator was used with a time step of 2 fs. Initial velocities of the atoms were assigned from the Maxwell–Boltzmann distribution at 10 K, and the system was heated up to 300 K linearly over an interval of 10 ps. Subsequently, an NVT equilibration with the Bussi thermostat²⁶ at 300 K was performed over 100 ps, followed by an NPT equilibration with the Parrinello–Rahman barostat²⁷ at 1 bar over 1 ns. During both steps, harmonic position restraints were applied to the heavy atoms of the peptide with a force constant of 1000 kJ mol⁻¹ nm⁻².

QM/MM equilibration. Next, QM/MM equilibrations over 100 ps were performed with Gromacs 5.0.1 including a local DFTB3 implementation,²⁸ additionally patched with Plumed 2.1.1. The QM region comprised the side chains of Cys24, Cys55 and Cys32 up to Cβ. This choice was motivated by the lack of any electronic effects (like, e.g., coordination) to other amino-acid side chains, charge transfer from/to other side chains or other phenomena calling for additional side chains or waters being included in the QM region, and also by the need for efficient computation required to achieve microsecond sampling. Bonds between Cα and Cβ were treated with the link atom approach, i.e. the QM region is capped with a hydrogen atom placed at a fixed position along the bond. In total, the QM region consisted of 15 atoms described with the semi-empirical density functional theory method DFTB3 and 3OB parameters.^29,30 The rest of the system was described with the AMBER99SB-ILDN forcefield²⁵ and TIP3P water. The previously applied positions restraints were lifted and the time steps reduced to 0.5 fs. Temperature and pressure were kept at 300 K and 1 bar with the Nosé–Hoover thermostat and the Parrinello–Rahman barostat, respectively. Additionally, the two centers of mass of the terminal amino acids were pulled away from each other along the x-axis with a constant force of 500 kJ mol⁻¹ nm⁻¹ (830 pN). Electrostatic interactions between the rather localized negative charge of the QM region and the MM system were scaled down by the factor of 0.75 corresponding to the inverse square root of the optical dielectric constant. This is an effective approach to compensate for the missing electronic polarization of the MM environment as recommended by Stuchebrukhov.^31,32

QM/MM production simulation. Finally, the 334 force-clamp simulations were performed over 20 ns each with the same setup. When a disulfide reaction occurred, the simulation stopped due to the protein termini leaving the simulation box at both sides. Thus, instead of a theoretical maximum of ca. 6.68 μs, the total simulation time was ca. 5.7 μs. Snapshots of the trajectories were saved every 0.5 ps.

Analysis. Distances and angles between the sulfurs were measured with Plumed²⁴ in all trajectories. Charges of the QM atoms were calculated with DFTB+.³³ Additionally, the electrostatic potential arising from the MM environment and by the QM sulfur atoms on each QM sulfur atom was calculated.

Images of proteins were created with VMD.³⁴ Plots and histograms were generated with the Python library Matplotlib.^35,36

QM/MM metadynamics. Multiple-walker metadynamics^37–39 QM/MM simulation of the nucleophilic attack of S32 on S24 and S55 was performed to obtain the potentials of mean force of the reactions. In spite of the accumulated sampling of 48 ns, this simulation failed to converge. The setup and results are detailed in the ESI.†

2.2 Metadynamics simulation of disulfide shuffling in a symmetric aqueous model system

We performed QM/MM metadynamics simulations of a system composed of a dimethyl disulfide molecule and a methylthiolate anion using DFTB3 with the 3OB parameter set. An additional, artificial ESP of either −0.5 V, −0.25 V, 0 V, +0.25 V, or +0.5 V was imposed on one of the sulfur atoms. The simulations were performed with a local version of Gromacs 2020 patched with Plumed 2.5.1 and interfaced with DFTB+ 19.1.^24,33,40

Setup. First, the system was put in a rectangular periodic box of 3.0 × 3.0 × 3.0 nm³, solvated with 877 TIP3P waters, and neutralized with one sodium ion. Subsequently, an energy minimization with the steepest descent methods was conducted with GROMACS/DFTB+, followed by an NVT equilibration with the Bussi thermostat at 300 K over 100 ps. For the NVT equilibration the leap frog integrator was used with a time step of 1 fs. Periodic boundary conditions were set and electrostatics were treated with particle–mesh Ewald. Lennard-Jones interactions were cut-off at 1 nm and the neighbour list was updated every 10 MD steps. The 15 atoms of the dimethyl disulfide molecule and methylthiolate were treated with QM and the rest of the system with MM. Electrostatic interactions between the charged QM region and the MM system were scaled down by the factor of 0.75. The sulfur–sulfur distances were restrained to values smaller than 6 Å with a force constant of 100 000 kJ mol⁻¹ nm⁻² to keep the molecules together and to reduce the configurational space for the reaction. Additionally, the distances between the sulfurs and the sodium ion were restrained to values greater than 12 Å with a force constant of 100 000 kJ mol⁻¹ nm⁻².

Metadynamics. Subsequently, the potential of the mean force of the disulfide shuffling was obtained with well-tempered multiple walker metadynamics.^37–39 We used 24 walkers, each simulated for 10 ns at 300 K with the Bussi thermostat and at 1 bar with the Parrinello–Rahman barostat, yielding a total simulation time of 240 ns. All other settings were the same as for the NVT equilibration. The three distances between the sulfurs were used as collective variables (CV) to drive the reactions. A Gaussian potential with an initial height of 0.5 kJ mol⁻¹ and a width of 0.2 Å was deposited every 250 fs along the trajectory. Deposited biases from all other walker were read every 500 fs.

Additional restraints. The configurational space of each reaction was reduced by means of harmonic restraints to S_ctr–S_lg and S_nuc–S_ctr distances above 6 Å with a force constant of 100 000 kJ mol⁻¹ nm⁻¹. Since metadynamics puts biases on both distances, the disulfide bond will extend over time and eventually break even without the sulfur anion S_nuc being close enough for a reaction. Hence, additional restraints were applied to the sum of switching functions applied to the three sulfur–sulfur distances, in order to avoid bond breaking while the sulfur anion is too far away. The switching functions were defined aswith the parameters taking values of r₀ = 2.9 Å, n = 10 and m = 20 for all considered combinations: s(S₁–S₂), s(S₁–S₃) and s(S₂–S₃). The parameters where chosen in such a way that the restraints do not interfere with the formation of the transition state. Whenever the sum of all three switching functions exceeded 1.82, corresponding to a disulfide bond length of ca. 2.3 Å without the sulfur anion nearby, harmonic restraints with a force constant of 20 000 kJ mol⁻¹ nm⁻² set in to avoid any further elongation of the bond.

Also, in pilot metadynamics simulations, the molecules irreversibly reacted to one of several chemically non-sensical species whenever all three sulfur–sulfur distances were very short (below 3 Å), i.e. in a triangular configuration. These structures lie very high in energy and thus are irrelevant for the investigated disulfide shuffling. To prevent such erroneous reactions, restraints were placed on the coordination numbers that were introduced for every sulfur atom as the sum of the switching functions applied to the distances from each of the two other sulfurs, e.g., c(S₃₂) = s(S₃₂–S₂₄) + s(S₃₂–S₅₅). Each of the three coordination numbers was restrained to values below 1.8 with a force constant of 50 000 kJ mol⁻¹ nm⁻², which penalizes triangular structures with short S–S distances. The sum of all three sulfur–sulfur distances was restrained to values above 9 Å with a force constant of 100 000 kJ mol⁻¹ nm⁻², which also prevents the three sulfurs from approaching too closely.

In other high-energy conformations, the sulfur anion came very close to the carbons of the dimethyl disulfide and deprotonated them. Thus, additional restraints were employed to avoid such occurrences. The number of bonded hydrogen atoms was defined as the sum of the switching functions s(C–H) with r₀ = 1.3 Å, n = 45 and m = 90, for each carbon atom separately. Each of these quantities was restrained to values above 2.5 with a force constant of 50 000 kJ mol⁻¹ nm⁻². All non-covalent sulfur–carbon distances were restrained to values above 3 Å with a force constant of 50 000 kJ mol⁻¹ nm⁻². Sulfur–hydrogen distances further than two covalent bonds away, were also restrained to values above 3 Å with a force constant of 50 000 kJ mol⁻¹ nm⁻².

The input files used to carry out these simulations are available in the ESI† as well as on PLUMED-NEST (http://www.plumed-nest.org), the public repository of the PLUMED consortium,⁴¹ as plumID:21.045.

3 Results and discussion

3.1 Detailed view of the approach of the free thiolate

It was previously pointed out that spatial accessibility controls the reactivity on the disulfide bond in I27*. Therefore, it appears necessary to analyze how often and how closely S32 approaches S24 or S55 during the simulations, in detail. To this end, we obtained a 2D histogram of the distances S32–S24 and S32–S55 from all of the 334 QM/MM molecular dynamics simulations. The interval of distances from 2.4 to 30 Å was divided into bins 0.1 Å wide, and the 2D histogram was then converted to a potential of the mean force (PMF). The resulting PMF for S–S distances up to 10 Å is shown in Fig. 2 together with exemplary S–S–S configurations and exemplary pathways. The histogram and PMF over the full range of distances are shown in Fig. S5 (ESI†).

Fig. 2 Potential of the mean force as function of the S32–S24 and S32–S55 distances, with the S24–S55 distance integrated out. Exemplary pathways for a reaction with S24 (orange) and with S55 (light blue) are drawn on the surface coming from large distances (grey). Contour lines are drawn every 2 kJ mol⁻¹.

There are three minima of an equal depth that was set to 0 kJ mol⁻¹. The long, narrow minimum at the upper edge of the energy profile corresponds to nearly-linear S32–S24–S55 configurations, while the similar minimum at the lower edge corresponds to nearly-linear S32–S55–S24 configurations. The third deep minimum is found around the distances S32–S24 and S32–S55 of 7 Å, and corresponds to a triangular configuration with S32 located in similar distances from S55 and S24.

Two shallower minima with free energies of ca. 10 kJ mol⁻¹ are located at the distances S32–S24/S32–S55 of 2.7/5.4 Å and 5.4/2.7 Å. These correspond to the transition state structures of the two disulfide exchange reactions. As such, these should be saddle points on the free energy surface, and the observed shallow minima are an artifact of DFTB3/3OB, which underestimates the energy and overestimates the bond lengths of trisulfide species, as discussed previously.⁴² Nevertheless, this systematic error affects both reactions, S32→S24 and S32→S55, to exactly the same extent, therefore any qualitative conclusions from this study will be unaffected. The height of energy barriers to both reactions is similar, ca. 15 kJ mol⁻¹. A tiny difference in barrier height is expected considering the rather small regioselectivity that was observed in experiments as well as in simulations, however it appears impossible to resolve using free MD simulations like here.

To learn how often S32 approaches S24 or S55, the histogram in Fig. 2A was split into 2 regions, the “upper” region in which S32 is closer to S24, and the “lower” region where S32 is closer to S55. All probabilities in the “upper” region were summed up and converted to a free energy value, and the same was done for the “lower” region; details on this analysis are presented in ESI,† and Fig. S6. We found or in terms of free energy, G_lower–G_upper = −0.8 kJ mol⁻¹. This means that S32 is closer to S55 on average, therefore a reaction may occur more frequently with S55 than with S24, as stated previously in ref. 13 on basis of simpler simulations.

To see how the distances between S32 and the disulfide bond correlate with the length of that bond, histograms of the distances S32–S24 and S32–S55 were generated for different S24–S55 bond lengths observed, see Fig. S7 (ESI†). It appears that S32 is increasingly more likely to be closer to S55 with increasing S24–S55 distance. Viewed from the other side: whenever S32 is closer to S55, a longer S24–S55 bond is favored. Consequently, it may be easier for the system to stretch the bond S24–S55 further to pass to a transition state. By contrast, whenever S32 is closer to S24, a shorter bond is favored, thus a transition state is less likely to form.

3.2 Analysis of observed reactions

QM/MM molecular dynamics captures the experimentally observed regioselectivity. We performed an ensemble of QM/MM force-clamp simulations of I27*, starting from 334 structures generated by Kolšek et al.¹³ The termini of protein chain were pulled in opposite directions with a constant force of 500 kJ mol⁻¹ nm⁻¹ = 830 pN. A disulfide exchange reaction was possible by means of an attack of Cys32, present in the deprotonated thiolate form, on either Cys24 or Cys55. Each simulation was stopped after a disulfide exchange has taken place or after 20 ns, whichever occurred first, and the total simulation time was ca. 5.7 μs.

In spite of the restricted time scale of the QM/MM simulations, a reaction occurred 66 times, with a preference for Cys32 attacking Cys55 (48 reactions) over Cys24 (18 reactions). The preference for Cys32 agrees with the experimental observations, and the Cys55/Cys24 ratio of 2.7 agrees is remarkably similar to the experimental ratio of 3.8. Now, the question arises why one of the reactions is favored over the other. In an attempt to answer this question, we analyzed selected structural and electrostatic parameters in the interval of 10 ps prior to the formation of the transition state in the trajectories where a reaction occurred.

Disulfide shuffling correlates with distances, angles, charges and ESP. In every trajectory in which a disulfide shuffling occurred, the last 10 ps (20 snapshots) before the formation of a transition state were analyzed. The three distances between the sulfurs were measured, as well as the angle between the nucleophilic sulfur anion S32 (S_nuc), the central sulfur under attack (S_ctr), and the respective sulfur of the leaving group (S_lg). In addition, the Mulliken atomic charges of the sulfurs were recorded. To assess the influence of the molecular environment on the outcome of the reaction, the electrostatic potential (ESP) on each of the three QM sulfurs caused by all of the QM and MM atoms was monitored. The temporal course of the described quantities for all of the observed reaction is shown in Fig. 3. The mean values and standard deviations of these quantities are listed in Table 1.

Fig. 3 From top to bottom: Distances and angles between the three sulfur atoms, charges of sulfur atoms, and the electrostatic potential (ESP) on each sulfur atom caused by all of the MM and QM atoms. Each column represents one occurrence of a disulfide shuffling reaction with either S24 (18 times, left) or S55 (48 times, right), showing data from the interval of 10 ps preceding the formation of the transition state. The simulation time of #9 on the left side was shorter than 10 ps. Peaks in the S_nuc–S_ctr distances, sulfur charges, and ESPs resemble structures where the transition state is approached but not fully formed yet.

Table 1 Distances and angles between the three sulfur atoms, charges of sulfur atoms, and electrostatic potentials (ESP) on the sulfur atoms. S24 is S_ctr and S55 is S_lg in the reaction S32→S24; S24 is S_lg and S55 is S_ctr in the reaction S32→S55. All data given as mean value and standard deviation

Reaction	S32→S24	S32→S55
|S32–S24| [Å]	3.78(0.54)	5.48(0.53)
|S32–S55| [Å]	5.65(0.51)	3.68(0.52)
|S24–S55| [Å]	2.14(0.08)	2.14(0.08)
Angle [°]	149(19)	143(18)
Q(S24) [e]	−0.04(0.03)	−0.14(0.04)
Q(S55) [e]	−0.12(0.04)	−0.02(0.04)
Q(S32) [e]	−1.09(0.06)	−1.10(0.05)
ESP(S24) [V]	−2.22(0.35)	−1.91(0.33)
ESP(S55) [V]	−1.94(0.34)	−2.25(0.36)
ESP(S32) [V]	−3.26(0.35)	−3.07(0.36)

---

Distances and angles prior to the reaction. The distance between S_nuc (S32) and the respective attacked sulfur S_ctr (S24 or S55) fluctuates between 3–5 Å whereas S_nuc is further away from the leaving sulfur S_lg, at 4.5–7 Å. The TS is formed as soon as |S_nuc–S_ctr| has decreased to ∼2.75 Å and |S_ctr–S_lg| has increased to ∼2.75 Å, while |S_nuc–S_lg| ∼ 5.4 Å indicating a linear arrangement.⁴² The temporal course of the distances for two example reactions, one with S24 and the other with S32, is shown in Fig. S2 (ESI†) for the section of the trajectory immediately preceding and following the reaction.

The angle S_nuc–S_ctr–S_lg oscillates between 80–180° but this range narrows down to 120–170° right before the formation of TS. At small S32–S24 distances below 3.4 Å, the preferred angle lies between 150–170°, whereas the preferred angle at small S32–S55 distances shows more variance of 120–170°, see also histograms in Fig. S1 (ESI†). Thus, the S–S–S arrangement deviates further from linearity in the 10 ps prior to the disulfide exchange with S55, as compared to the same time frame preceding an exchange with S24. This observed larger flexibility supports the hypothesis that S55 is better accessible for a nucleophilic attack by S32 than S24.¹³

Charges. The target of the S_N2 attack, S_ctr is slightly more positively charged than S_lg in nearly all observed reactions, see Fig. 3. The S32 anion initially has a charge of ca. −1.1 e, and neutralizes as S32 approaches S_ctr gradually. In the transition state, the negative charge is equally distributed between S_nuc and S_lg. By contrast, the charge of S_ctr remains around zero the entire time. All in all, the charges of S32 and the respective S_lg correlate with the distance of the approaching nucleophile, S32, from the target, S_ctr. Also, the negative charge is transferred from S_nuc to S_lg during the reaction directly, without any transient accumulation on S_ctr, which was already observed in previous studies.^43–45

Electrostatic potentials. The electron density on the individual atoms, expressed in terms of atomic charges in DFTB3, is determined to a large extent by the electric field experienced by the atoms. Therefore, in search for the mechanism that controls the disulfide shuffling, it is necessary to analyze the ESP on the sulfur atoms arising from their molecular environment. The ESP on S_ctr and S_lg is substantially negative due to the close proximity of the S32 anion. Since the distance |S_nuc–S_ctr| < |S_nuc–S_lg|, the ESP on S_ctr is generally more negative than on S_lg, with few exceptions. In the transition state, the ESP on the S32 anion decreases as its charge is being transferred to S_lg, and the ESP on S_lg increases. Additional information about the ESP are provided and individual contributions are discussed in the ESI,† text and Fig. S3.

Influence of electrostatics on regioselectivity. As mentioned above, Q(S_ctr) > Q(S_lg), and the negative charges of S_nuc and S_lg are interchanged without accumulating at S_ctr during the reaction. Thus, two assumptions can be made: (i) a more positive Q(S_ctr) favors the nucleophilic attack on S_ctr more; (ii) a more negative Q(S_lg) makes S_lg a better leaving group. These statements may be expressed in terms of ESP, with which the charges correlate. To investigate this, we calculated the differences ΔQ = Q(S_ctr) − Q(S_lg) and ΔESP = ESP(S_lg) − ESP(S_ctr) for both reactions, and took averages over the intervals of 10 ps prior to the formation of the transition state. These results are visualized in Fig. 4, and the complete data are presented in Fig. S4 (ESI†).

Fig. 4 Top: Atomic charges of the sulfur atoms and ESP arising from all of the QM and MM atoms, averaged over the respective ensembles of disulfide exchange reactions as observed in the QM/MM simulations. ESP coded by the radius of balls; charge coded by the outline thickness, scaled down by a factor of 3 for S32 for clarity. Bottom: Averages of charges and ESP represented by differences ΔQ = Q(S_ctr) − Q(S_lg) and ΔESP = ESP(S_lg) − ESP(S_ctr).

It turns out that both ΔQ and ΔESP are larger for the reaction S32→S55. This means that S_ctr is, on average, a somewhat better target of an S_N2 attack, and S_lg is a better leaving group, in that reaction compared to S32→S24. Thus, electrostatic interactions contribute to the observed regioselectivity of the disulfide exchange reaction.

3.3 Effect of external electric potential on the reaction

According to our above analysis of charges and ESP, the polarization of the nucleophile, of the target as well as that of the leaving group dictates whether and how an S_N2 reaction proceeds. The question arises if this polarization of the disulfide is a consequence of or a reason for the preferential attack. The polarization itself is driven by the electrostatic interactions with the surrounding atoms, which may be quantified by the ESP. To investigate how the electrostatics influence disulfide exchange reactions in general, additional QM/MM metadynamics simulations of a model system with an external electrostatic field of varying strength were performed. The system comprised a dimethyl disulfide molecule and a methylthiolate anion in aqueous solution.

An advantage of this small, simple model is that the PMF is completely symmetric as long as no external potential is applied, and this knowledge may be used for a convenient convergence check. In the free energy surface from that simulation (Fig. S11C, ESI†), the minimum energies for bonds between S₁–S₂ and S₁–S₃ are 0 kJ mol⁻¹, and for a bond between S₂–S₃ the energy is 2 kJ mol⁻¹. The energy barriers to the three disulfide exchange reactions lie in the range of 49–52 kJ mol⁻¹. All this illustrates the good convergence of the simulation, with a statistical error of at most 2 kJ mol⁻¹.

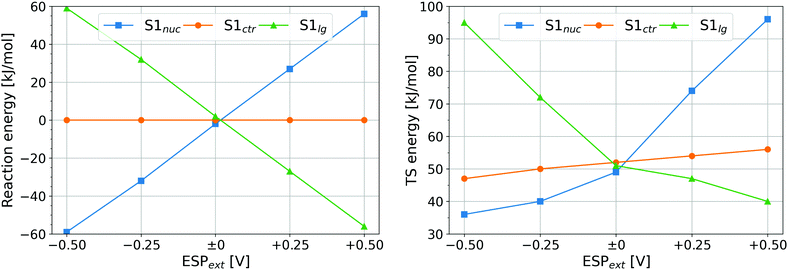
Simulations were performed with an additional, external ESP of −0.50 V, −0.25 V, 0 V, +0.25 V, and +0.50 V, respectively, imposed on the atom S₁; this additional potential will be denoted ESP_ext in the following. The simulation setup was designed to sample all three disulfide bonding patterns: S₁–S₂, S₁–S₃, and S₂–S₃, with the respective remaining sulfur atom in the deprotonated reduced (anionic) state. The reaction energies and height of energy barriers to disulfide shuffling are plotted in Fig. 5. The 2D representations of the PMF expressed as function of the S₁–S₂ and S₁–S₃ distances (with the S₂–S₃ distance integrated out) are shown in Fig. S11 (ESI†) together with exemplary molecular structures, and the numerical values of energy barriers are shown in Table S1 (ESI†).

Fig. 5 Thermodynamics and kinetics of the disulfide exchange reaction in the model system with additional external potential, ESP_ext imposed on atom S₁. Left – reaction energy; right – height of energy barrier. The data points are labeled by the role of S₁ in the reaction. Note: all three respective data points for ESP_ext = 0 V correspond to the same situation.

The reaction energies in Fig. 5 (left) exhibit clear trends. First, ESP_ext applied to the sulfur being attacked, S_ctr, has no influence on the reaction energy because the reactant and the product are identical – one of the disulfide-bonded atoms carries ESP_ext. The other two cases are in fact one: a reaction with ESP_ext on S_nuc is the reverse process to a reaction with ESP_ext on S_lg. Thus, the reaction energy of one equals the negative of the reaction energy of the other. The stabilization or destabilization of the negative charge of the thiolate (which is S_nuc prior to the reaction, and S_lg thereafter) by ESP_ext may be considered to rationalize the numerical value of reaction energies: the contribution to total energy from the interaction of that charge Q(S⁻) with the electrostatic environment (represented here by ESP_ext) is well approximated as E′ = ESP_ext·Q(S⁻). Since Q(S⁻) ≈ −1.1 e always, E′ is a linear function of ESP_ext. As an example, for S₁ being S_nuc and ESP_ext = −0.5 V, E′ = −0.5·(−1.1) eV = +0.55 eV = +53 kJ mol⁻¹, in a good agreement with the actual observation.

The reaction energies are not quite important in the context of the current work, however. Due to the stretching force applied on I27*, the new free thiolate is immediately pulled away from the newly formed disulfide bond as soon as the first disulfide exchange has taken place. Therefore, the energy of the product and the thermodynamics of the reaction do not play any role. The crucial phenomenon will rather be the effect of ESP, or ESP_ext in the study of the model system, on the reaction rates.

Let us turn our attention to the heights of energy barrier in Fig. 5 (right). The barrier heights with ESP_ext on S_nuc or on S_lg change in a way that is very similar to the reaction energies: the barrier is elevated whenever the reaction energy is positive, while lower barriers are seen in cases that have negative reaction energies. This is a simple consequence of the shape of the corresponding energy landscapes as depicted in Fig. S11 (ESI†). Most interesting in the current context will be the case where S₁ is S_ctr because this is the kind of data that we have measured in our simulations of I27*. There is a roughly linear dependence of energy barrier on ESP_ext, with a slope of ca. 10 kJ mol⁻¹ V⁻¹ and positive ESP_ext giving higher barriers. This is explained easily as positive ESP_ext leads to a decrease of charge of S_ctr, which thus becomes a worse nucleophilic target, and the other way around for negative ESP_ext.

It has to be pointed out that a certain ESP_ext applied on S₁ in the model system shall have the same effect on the electronic structure of the disulfide bond as the same value of ΔESP in the simulations of I27*. Recall that the ΔESP values found for the reactions were 0.28 and 0.34 V, respectively. The effect of this difference may be compared to the difference of ESP_ext = 0 and 0.06 V: multiplication by the slope of the dependence of energy barrier on ESP_ext leads to the difference of energy barriers of ca. 0.6 kJ mol⁻¹, which would cause a ratio of reaction rates of ca. 1.3 from Arrhenius' equation. This factor contributes to the above observed ratio of reaction rates of 2.7, while the remainder of this ratio (of ca. 2) is probably due to other effects like spatial accessibility as discussed previously.¹³

4 Conclusion

The disulfide shuffling in the I27* domain was investigated by generating an extensive ensemble of trajectories using unbiased semiempirical QM/MM MD simulation. Of two possible disulfide shuffling reactions, S32→S55 was preferred over S32→S24, in agreement with experimental observations as well as previous computational results.

Next, we asked what structural factors contribute to the preferential attack. The distances and angles between the cysteine sulfur atoms in the trajectories were measured. It was found that S32 can approach S55 over a wider range of angles than S24, therefore S55 is the more easily accessible target of a nucleophilic attack. Further, S32 is located more often closer to S55 than to S24, making a nucleophilic attack on S55 more likely. All that agrees with the previous observations by Kolšek et al.¹³

Clearly, steric factors play a very important role in disulfide shuffling, but this may not be the complete explanation. Rather, electrostatic interactions may contribute to the reaction control. Thus, we decided to analyze the electron density of the trisulfide system as well as electrostatic interactions in the protein, to see if we find any significant effects. Note that electron density is represented by Mulliken atomic charges within DFTB.

S55 in the role of nucleophilic target carried a more positive charge than S24, and S24 carried a more negative charge as a leaving group than S55 did. This means that S55 is the better nucleophilic target, and S24 the better leaving group of the two. The charges were averaged over two separate ensembles of simulations, and thus there is no bias towards the ensemble with a larger number of simulations.

The observed difference of atomic charges may be accounted to the electrostatic potentials on the sulfur atoms caused by the molecular environment (amino acid side chains, peptide backbones and solvent), which are slightly different for each sulfur atom. Consequently, it is the electrostatic effects of the molecular environment that support the reaction S32→S55 more than S32→S24. This is an additional explanation of the outcome of the force-clamp experiments on I27*, in addition to the previous concept of regioselectivity via accessibility.

In terms of the transition state theory, the steric factors make the approach frequency and thus the pre-exponential factor higher for the reaction S32→S55. Also, the different polarization of electron density results in a lower energy barrier for the same reaction. These two effects act in the same direction, favoring the reaction S32→S55.

A possible electrostatic control of regioselectivity was demonstrated on a model system featuring a symmetric free energy landscape of the disulfide exchange reactions. As soon as an external electric potential is imposed on one of the sulfur atoms, the charges of the sulfurs change, and consequently, so do the free energies: a negative applied ESP results in a more positive charge, which makes the touched atom a better nucleophilic target but a worse leaving group. On the other hand, a positive applied ESP results in a more negative charge, making the atom a better leaving group but a worse nucleophilic target.

We provided a quantitative measure of this effect on the reaction energies and barriers. Electrostatic potential arising from the protein and water environment may polarize the disulfide bond slightly, such that the nucleophile attacks one of the sulfur atoms preferentially. Thus, electrostatics may break the symmetry of the disulfide system. This either induces regioselectivity, or contributes to the regioselectivity due to steric factors.

This model study shows how an external electric field affects the kinetics of disulfide shuffling. The magnitude of ESP applied here, in the order of tenths of volt, corresponds to the differences of potentials observed in protein systems like the I27* domain. In a protein, the “external field” arises from the protein and solvent environment – the surrounding amino acid side chains, peptide backbone as well as any water present. Such an electric field brings on a variation of energy barriers of few kJ mol⁻¹. This modulates the reaction rates by a small factor, and it turns out that the kinetics of disulfide shuffling in proteins is affected by electrostatic effects of the close environment of the disulfide moiety.

Active sites of enzymes and other proteins feature perfectly positioned functional groups and patterns of specific interactions. The case of disulfide exchange reaction investigated here is different but still remarkably similar in the working principle: even though there is no real active site, the selectivity of the reaction is still achieved through the interactions with the environment. All of this likely matters for the disulfide exchange reactions as known in proteins like VWF, integrins and others.

Author contributions

T. K., M. E. and F. G. designed research; D. M., M. P. and C. L. G.-F. performed research; D. M. and T. K. analyzed data; D. M., F. G. and T. K. wrote paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the German Science Foundation (DFG) under project GRK 2450, and further by the state of Baden-Württemberg through bwHPC and by the DFG through project INST 40/467-1 FUGG (JUSTUS cluster). Data for this paper, including the trajectories from QM/MM simulations of I27* under mechanical stress and the time series of atomic charges and ESP measured along these trajectories are available from Dryad at https://doi.org/10.5061/dryad.2z34tmpmw.

References

1. A. Holmgren, J. Biol. Chem., 1989, 264, 13963–13966.
2. G. Kozlov, P. Määttänen, D. Y. Thomas and K. Gehring, FEBS J., 2010, 277, 3924–3936.
3. C. Metcalfe, P. Cresswell, L. Ciaccia, B. Thomas and A. N. Barclay, Open Biol., 2011, 1, 110010.
4. J. Chiu and P. J. Hogg, J. Biol. Chem., 2019, 294, 2949–2960.
5. D. Butera, F. Passam, L. Ju, K. M. Cook, H. Woon, C. Aponte-Santamaría, E. Gardiner, A. K. Davis, D. A. Murphy, A. Bronowska, B. M. Luken, C. Baldauf, S. Jackson, R. Andrews, F. Gräter and P. J. Hogg, Sci. Adv., 2018, 4, eaaq1477.
6. T. A. Hamlin, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2018, 19, 1315–1330.
7. G. Bell, Science, 1978, 200, 618–627.
8. W. Li and F. Gräter, J. Am. Chem. Soc., 2010, 132, 16790–16795.
9. J. Alegre-Cebollada, P. Kosuri, J. A. Rivas-Pardo and J. M. Fernández, Nat. Chem., 2011, 3, 882–887.
10. A. P. Wiita, S. R. K. Ainavarapu, H. H. Huang and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7222–7227.
11. M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727–1730.
12. W. Stacklies, M. C. Vega, M. Wilmanns and F. Gräter, PLoS Comput. Biol., 2009, 5, e1000306.
13. K. Kolšek, C. Aponte-Santamaría and F. Gräter, Sci. Rep., 2017, 7, 9858.
14. P. Nagy, Antioxid. Redox Signaling, 2013, 18, 1623–1641.
15. R. D. Bach, O. Dmitrenko and C. Thorpe, J. Org. Chem., 2008, 73, 12–21.
16. R. Singh and G. M. Whitesides, J. Am. Chem. Soc., 1990, 112, 1190–1197.
17. C. Wu, C. Belenda, J.-C. Leroux and M. A. Gauthier, Chem. – Eur. J., 2011, 17, 10064–10070.
18. G. H. Snyder, M. J. Cennerazzo, A. J. Karalis and D. Locey, Biochemistry, 1981, 20, 6509–6519.
19. G. H. Snyder, M. K. Reddy, M. J. Cennerazzo and D. Field, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1983, 749, 219–226.
20. P. J. Britto, L. Knipling and J. Wolff, J. Biol. Chem., 2002, 277, 29018–29027.
21. R. E. Hansen, H. Østergaard and J. R. Winther, Biochemistry, 2005, 44, 5899–5906.
22. AmberTools 1.4 (2010), http://ambermd.org.
23. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
24. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
25. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
26. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
27. S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076.
28. T. Kubař, K. Welke and G. Groenhof, J. Comput. Chem., 2015, 36, 1978–1989.
29. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948.
30. M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354.
31. I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626.
32. B. J. Kirby and P. Jungwirth, J. Phys. Chem. Lett., 2019, 10, 7531–7536.
33. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684.
34. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
35. G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, Scotts Valley, CA, 2009.
36. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
37. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
38. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
39. P. Raiteri, A. Laio, F. L. Gervasio, C. Micheletti and M. Parrinello, J. Phys. Chem. B, 2006, 110, 3533–3539.
40. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25.
41. M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello and The PLUMED consortium, Nat. Methods, 2019, 16, 670–673.
42. M. Putzu, F. Gräter, M. Elstner and T. Kubař, Phys. Chem. Chem. Phys., 2018, 20, 16222–16230.
43. J. M. Wilson, R. J. Bayer and D. J. Hupe, J. Am. Chem. Soc., 1977, 99, 7922–7926.
44. J. A. Pappas, J. Chem. Soc., Perkin Trans. 2, 1979, 67–70.
45. P. A. Fernandes and M. J. Ramos, Chem. – Eur. J., 2004, 10, 257–266.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary Fig. S1–S15; supplementary Table S1; procedure for calculation of electrostatic potentials; metadynamics simulation of disulfide shuffling in I27* – method and results; detailed analysis of system setup; input files for the metadynamics simulation of the model system. See DOI: 10.1039/d1cp03129e

---