Open Access Article
Open Access ArticleSuperparamagnetic nanoparticles with LC polymer brush shell as efficient dopants for ferronematic phases†
Karin
Koch
a,
Matthias
Kundt
a,
Anda
Barkane
a,
Hajnalka
Nadasi
b,
Samira
Webers
 c,
Joachim
Landers
c,
Heiko
Wende
c,
Joachim
Landers
c,
Heiko
Wende
 c,
Alexey
Eremin
c,
Alexey
Eremin
 b and
Annette M.
Schmidt
b and
Annette M.
Schmidt
 *a
*a
aUniversität zu Köln, Department Chemie, Institut für Physikalische Chemie, Luxemburger Str. 116, D-50939 Köln, Germany. E-mail: annette.schmidt@uni-koeln.de
bOtto-von-Guericke-Universität Magdeburg, Institut für Physik, Universitätsplatz 2, D-39016 Magdeburg, Germany
cFaculty of Physics and Center for Nanointegration Duisburg-Essen (CENIDE), Universität Duisburg-Essen, Duisburg, Germany
First published on 26th August 2021
Abstract
Liquid crystal (LC) based magnetic materials consisting of LC hosts doped with functional magnetic nanoparticles enable optical switching of the mesogens at moderate magnetic field strengths and thereby open the pathway for the design of novel smart devices. A promising route for the fabrication of stable ferronematic phases is the attachment of a covalently bound LC polymer shell onto the surface of nanoparticles. With this approach, ferronematic phases based on magnetically blocked particles and the commercial LC 4-cyano-4′-pentylbiphenyl (5CB) liquid crystal were shown to have a sufficient magnetic sensitivity, but the mechanism of the magneto–nematic coupling is unidentified. To get deeper insight into the coupling modes present in these systems, we prepared ferronematic materials based on superparamagnetic particles, which respond to external fields with internal magnetic realignment instead of mechanical rotation. This aims at clarifying whether the hard coupling of the magnetization to the particle's orientation (magnetic blocking) is a necessary component of the magnetization–nematic director coupling mechanism. We herein report the fabrication of a ferronematic phase consisting of surface-functionalized superparamagnetic Fe3O4 particles and 5CB. We characterize the phase behavior and investigate the magneto-optical properties of the new ferronematic phase and compare it to the ferronematic system containing magnetically blocked CoFe2O4 particles to get information about the origin of the magneto–nematic coupling.
Introduction
Liquid crystals (LC) attract considerable interest in science and technology due to the combination of fluidity of liquids with anisotropic optical and mechanical properties as usually found in crystalline solids.1,2 The anisotropies of the dielectric permittivity (Δε) and diamagnetic susceptibility (Δχ) allow the alignment of the LC director using external stimuli such as electric voltage or magnetic fields and is essential for their application in optical devices.1–8 While electric fields are commonly used for such devices over a few decades now, the employment of magnetic fields is less straightforward due to the low magnetic anisotropy of the mesogens requiring relatively high magnetic field strengths. A way to enhance the magnetic response has been developed in the 70s by De Gennes and Brochard. They proposed that doping LC phases with dipolar magnetic nanoparticles (NP) would result in a coupling between the nematic phase and the magnetic particle that enhances the magnetic sensitivity.9 Further quantitative predictions on the effective orientation coupling of the Brochard–de-Gennes theory were derived by Burylov and Raikher.10In the meantime, several potentially ferronematic systems containing spherical and anisotropic magnetic nanoparticles have been discovered and investigated in detail, but the ferronematic coupling is poorly understood.11–36 It became obvious, though, that one of the main obstacles for the realization of a stable ferronematic phase are the strong intermolecular interactions of the mesogens on the one hand, in combination with the strong tendency for agglomeration for the magnetic dopants, on the other hand, prohibiting a stable dispersion in many cases.37 Strategies for the improvement of the compatibility between nanoparticles and the nematic environment are mainly based on utilization of surfactants (e.g. oleic acid) or surface ligands containing mesogenic units, as they exhibit a high chemical compatibility with the employed LC host.13,18,34,36,38–40
In our recent work, we reported a successful fabrication of magnetically blocked CoFe2O4 particles modified with covalently attached mesogenic polymers as doping agents for stable ferronematic systems/dispersions with an enhanced compatibility and magnetic sensitivity.21 We show, that the LC polymer brush effectively promotes the interaction between the magnetic dopants and the LC matrix resulting in a material with novel magneto-optical properties. Additionally, we achieved a quantitative description of the data and determined the surface coupling strength in these systems based on free energy considerations.
From early theoretical predictions of the phenomenon,9,10,41,42 a significant direct magneto–nematic coupling effect between the individual mesogenic molecule orientation and the magnetic stray field of a single magnetic particle is not expected. The exchange energy induced by the magnetic field in the environment of a particle in the respective size range is far lower than kBT and thus readily compensated by thermal motion. Instead, the interactions occur by means of a preferential surface alignment of the mesogens with respect to the surface of a magnetic object. If the latter is geometrically anisotropic (non-spherical), this might lead to a preferential orientation of the particle within the nematic matrix, and the reorientation results in the respective co-alignment of the surrounding mesogens. The magneto–nematic coupling is thus justified by a mechanical or orientational coupling based on a strong anchoring of the LC host molecules with the surface of the NP.9,10,41,42
However, in systems where spherical magnetic nanoparticles are used as dopants, the surface coupling alone does not explain their enhanced magnetic response, as no preferred direction of alignment is induced by a sphere – instead, dependent on their size, spherical nanoparticles usually represent dipolar two-point defects in the nematic phase, where the two disclination points face each other at the surface of the sphere.9,22,43 One feasible explanation could be that under field influence, the magnetic nanoparticles form small anisotropic assemblies, e.g. chains, that play the role of the directing object.12,27,44
In our recent work, the question of the coupling mechanism remained open despite the good quantitative description based on the available theories. However, we suggested the strong enhancement in the experimentally observed magneto–nematic coupling to two main differences between the systems employed in our study as compared to others:
– Excellent compatibilization and colloidal stabilization of the magnetic nanoparticles with their environment by covalent attachment of a mesogen-functionalized polymer brush shell. It can be assumed that the incorporation of surface-attached LC polymer brushes modifies fundamentally the interactions between the dopant surface and the surrounding nematic phase.
– Employment of magnetically blocked cobalt ferrite particles. Their response to a magnetic field occurs thus by mechanical rotation (Brown relaxation, Fig. 1a), which might be relevant.
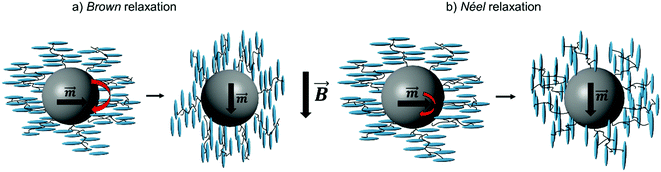 | ||
| Fig. 1 Possible relaxation mechanism of nanoparticles in a magnetic field: Brown and Néel relaxation. | ||
It is the goal of the present study to shed more light on this open question of the coupling mechanism by extending the experiments to otherwise similar, but superparamagnetic particles. Due to their low thermal magnetization reversal barrier, the magnetic moments fluctuate with such fast relaxation times, so that no significant field is expected in the absence of an external field, and thus the relevance of this point is lighted up. Moreover, in an applied external field, the particles do not respond by mechanical rotation, but by relaxation of the magnetic moment of the particle with respect to the crystal lattice (Néel relaxation, Fig. 1b). We thus herein report a ferronematic system based on superparamagnetic Fe3O4 particles with the size, surface functionalization and the magnetic moment comparable with the magnetically blocked particles utilized in our previous work. We explore the magneto-optical behavior of the new ferronematic and compare it to the previous results for more insight into the origin of the magneto–nematic coupling. In addition, we present detailed results on the complementary magnetic and thermomagnetic properties of the systems.
Experimental
Materials and methods
Synthetic procedures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at a concentration of 2 mg of NP per 1 ml of solution. Afterwards, OTS (3.6 mmol per 1 g of Fe3O4) dissolved in ethanol is added dropwise over a period of 10 minutes, the reaction mixture is stirred at ambient temperature for 48 h. The OTS@Fe3O4 are washed repeatedly with acetone by magnetic separation.
1) at a concentration of 2 mg of NP per 1 ml of solution. Afterwards, OTS (3.6 mmol per 1 g of Fe3O4) dissolved in ethanol is added dropwise over a period of 10 minutes, the reaction mixture is stirred at ambient temperature for 48 h. The OTS@Fe3O4 are washed repeatedly with acetone by magnetic separation.
1H-NMR (499 MHz, CDCl3): δ [ppm] = 7.76–7.59 (m, 4H), 7.53 (d, 2H), 6.99 (d, 2H), 5.82 (ddt, 1H), 5.10–4.89 (m, 2H), 4.01 (t, 2H), 2.18–1.96 (m, 2H), 1.94–1.71 (m, 2H), 1.53–1.44 (m, 8H).
Afterwards, the mesogenic polymer is prepared by platinum-catalyzed hydrosilylation reaction between PHMS and 4-cyano-4′-nonenyloxybiphenyl. The obtained polymer shows a functionalization degree of f9OCB = 0.48.
1H-NMR (499 MHz, CDCl3): δ [ppm] = 7.48 (d, J = 70 MHz, 6H, aryl-H), 6.84 (s, 2H, aryl-H), 4.65 (s, 15H, Si-H), 3.85 (s, 2H, O-CH2), 1.67 (s, 2H, alkyl-H), 1.22 (s, 14H, alkyl-H), 0.46 (s, 2H, Si-CH2), 0.10–0.01 (m, 9H, Si-CH3).
Methods
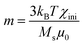 | (1) |
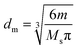 | (2) |
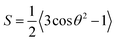 | (3) |
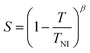 | (4) |
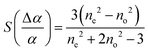 | (5) |
For this method, of the ordinary and the extraordinary refractive indices no and ne are measured as a function of temperature and S is determined by plotting 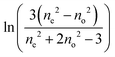 versus
versus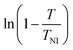 . Using the fact that S = 1 for a virtually fully ordered nematic system, the intercept at T = 0 of the resulting linear plot gives the result for
. Using the fact that S = 1 for a virtually fully ordered nematic system, the intercept at T = 0 of the resulting linear plot gives the result for 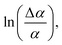 allowing the calculation of S from eqn (5) for every temperature, respectively. The slope of the linear plot gives the value for the critical exponent β.
allowing the calculation of S from eqn (5) for every temperature, respectively. The slope of the linear plot gives the value for the critical exponent β.
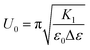 | (6) |
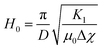 | (7) |
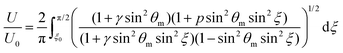 | (8) |
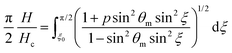 | (9) |
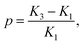 the dielectric anisotropy
the dielectric anisotropy 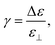 the perpendicular component of the dielectric permittivity ε⊥, Δε = ε‖ − ε⊥,
the perpendicular component of the dielectric permittivity ε⊥, Δε = ε‖ − ε⊥, 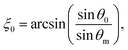 the pretilt angle θ0 between the nematic director and the substrate, the director deflection angle in the midplane of the cell θm, and
the pretilt angle θ0 between the nematic director and the substrate, the director deflection angle in the midplane of the cell θm, and 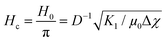 . The equation for the effective dielectric permittivity is
. The equation for the effective dielectric permittivity is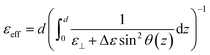 | (10) |
For ferronematic systems, an additional cross-coupling condition is introduced by assuming an effective interaction between the magnetic director of the doping particles, and the director of the nematic phase. Our approach is an adaption of the model developed by Podoliak et al.,52 based on the continuum theory developed by Buylov and Raikher10 and explained in our previous work.21 Here, the free energy in our system is considered as a sum of the elastic deformation energy of the pure nematic LC, the interaction between the nematic director and the magnetic field, the interaction between the magnetic dopants and the magnetic field, and the interaction between the LC and the magnetic nanoparticles (see eqn (11)).
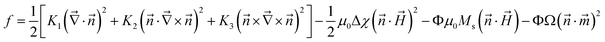 | (11) |
By fitting the data with this model, the dimensionless parameters κ (magnetic parameter) and ω (coupling parameter) are obtained:
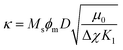 | (12) |
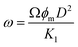 | (13) |
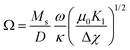 | (14) |
| Ws = Ωd | (15) |
Results and discussion
Preparation and properties of the CoFe2O4 particle cores
After our promising results with magnetically blocked CoFe2O4 particles,21 we investigate the effect of superparamagnetic Fe3O4 particles on the LC phase 5CB to get more information about the magneto–nematic coupling. The surface of the particles is functionalized with a liquid crystalline polymer brush (see Fig. 2) in order to achieve a good compatibilization with the 5CB host. The modified particles are then used as doping agents for 5CB to obtain ferronematic phases. The effect of Fe3O4 on the phase behaviour of 5CB is investigated by measuring the nematic–isotropic transition temperature and the order parameter dependent on particle concentration. The electric and magneto–nematic response is determined by capacitance measurements both in electric and magnetic field and calculation of the magneto–nematic coupling parameter.Synthesis and surface-functionalization of magnetic cores
Fe3O4 nanoparticles are obtained by thermal decomposition of Fe(acac)3 in tri(ethylen glycol) and are electrostatically stabilized in water with citric acid using modified protocols from literature.45,46The size and morphology of the particles is analysed via TEM as shown in Fig. 3. Fe3O4 particles are spherical in shape with a number-averaged diameter of dg = 12.5 nm (σ = 0.13) with σ being the standard deviation of the log normal distribution. The surface-related mean diameter is dA = 12.8 nm (σs = 0.12) and the volume-related mean diameter is dV = 13.0 nm (σs = 0.12) with σs being the standard deviation of the rated mean diameters.
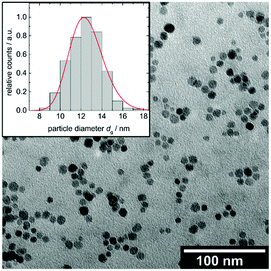 | ||
Fig. 3 TEM image and corresponding size histogram of CA@Fe3O4 nanoparticles with a log normal distribution function ( ). ). | ||
Using our successful approach towards compatibilization of nanoparticles in the LC phase,21 Fe3O4 particles are surface-functionalized with a liquid crystalline polymer brush consisting of a PHMS-based backbone with side chains from 9OCB in a two-step procedure. In the first step, the particles are functionalized with OTS using the procedure of Frickel et al.47 in order to result in surface-attached vinyl groups. Subsequently, the vinyl functionalities are coupled to the remaining Si–H units of 9OCB-PHMS in a platinum-catalyzed hydrosilylation reaction. The success of the coupling reaction which was already discussed for CoFe2O4 in our previous work21 is qualitatively confirmed by ATR-IR spectroscopy (see ESI,† Fig. S1a) by comparing the spectra of the 9OCB-PHMS and carefully washed 9OCB-PHMS@NP after the attachment procedure. More quantitative information on the functionalization is obtained by TGA from the mass loss of carefully dried powders before and after polymer functionalization (Fig. S1b, ESI†). With the mass loss, a specific particle functionality of f9OCB,p = 1.32 mmol g−1 is estimated. Taking into account the particle sizes obtained from TEM and a core density of ρ = 5.2 g cm−3,53 the surface functionalization density σA can be determined to be nearly 13 molecules of 9OCB per nm2. For the fabrication of stable ferronematic phases, 9OCB-PHMS@Fe3O4 dispersed in THF are added to pure 5CB. After evaporation of the solvent, the particles are dispersed by ultrasonication in the isotropic phase at T = 40 °C. By quenching the dispersion in a water bath at room temperature, a stable colloidal ferronematic stock dispersion is obtained.
Magnetic properties of core particles and ferronematic samples
The magnetic properties of the carefully dried core particles and the core particles dispersed in water and 5CB are investigated by vibrating sample magnetometry (VSM). The normalized magnetization curves from powder-based experiments and aqueous solution compared to a magnetization curve of particles dispersed in 5CB are shown in Fig. 4.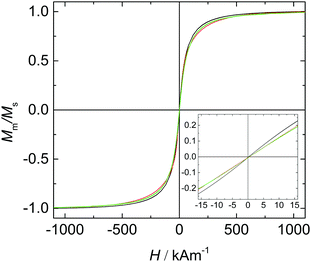 | ||
Fig. 4 Magnetization curves of a dried CA@Fe3O4 particles (—), CA@Fe3O4 particles dispersed in water ( ) and 9OCB-PHMS@Fe3O4 particles in 5CB ( ) and 9OCB-PHMS@Fe3O4 particles in 5CB ( ). ). | ||
The core particles possess a saturation magnetization of Ms = 61.2 A m2 kg−1 which is close to the Ms of CoFe2O4 particles used in our previous work (Ms = 71.4 A m2 kg−1).21 With the magnetic susceptibility χini which is derived from the magnetization curves of the particles dispersed in water, the magnetic moment and the magnetic diameter are determined to be m = 1.17 × 10−19 A m2 and dm = 8.5 nm. Compared to the aqueous solution, the magnetization curve of 9OCB-PHMS@Fe3O4 particles in 5CB shows no significant differences. For dried Fe3O4 nanoparticles no hysteresis but superparamagnetic behaviour can be observed which is in agreement with the results of other works.54
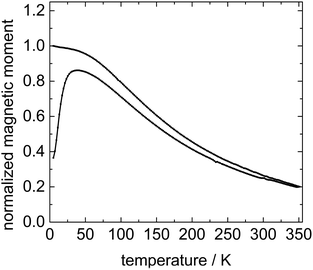
In order to get information about the magnetic relaxation behaviour of the particles in the host matrix 5CB, the ferronematic samples are investigated by temperature-dependent superconducting quantum interference device (SQUID) magnetometry using an applied field of 10 mT. The ZFC–FC magnetization curves of 9OCB-PHMS@Fe3O4 particles in 5CB are depicted exemplary for a concentration of ϕm = 4.7 × 10−4 in Fig. 5.
The zero-field cooled magnetization increases first and then decreases after reaching a maximum at around 45 K which corresponds to the blocking temperature TB. Below this temperature the particles are mainly blocked in terms of Néel relaxation. Moreover, both ZFC and FC curves nearly coincide at high temperatures. Thus, Fe3O4 particles in 5CB predominately are superparamagnetic and relax according to the Néel mechanism which is described with the Néel time τN constant:55
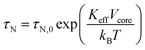 | (16) |
With the blocking temperature TB of Fe3O4 and the effective anisotropy constant Keff = 13 kJ m−3,54 the mean volume of the particles is approximately calculated according eqn (17)
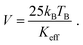 | (17) |
Thermal properties of ferronematic samples
The impact of 9OCB-PHMS@Fe3O4 on the stability of 5CB in dependence on the concentration is investigated with differential scanning calorimetry (DSC). From the two endothermic peaks of the thermograms (see ESI,† Fig. S2) the crystalline to the nematic phase transition temperature TCN and the nematic to the isotropic phase transition temperature TNI are extracted. In. Fig. 6a and b, the difference of the transition temperatures ΔTCN and ΔTNI to 5CB are plotted as a function of the solid doping volume fraction ϕs, respectively.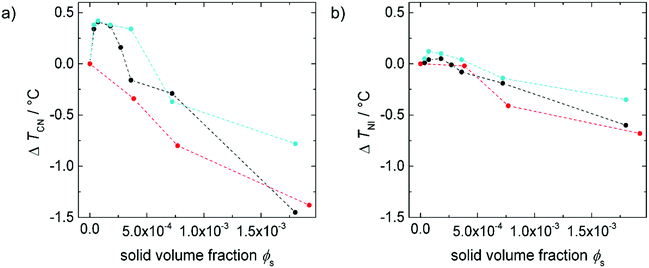 | ||
Fig. 6 Difference of (a) crystal–nematic transition temperature ΔTCN and (b) nematic–isotropic transition temperature ΔTNI of doped 5CB to pure 5CB as a function of magnetic dopant particle volume fraction ϕs with 9OCB-PHMS@Fe3O4 (•), 9OCB-PHMS@CoFe2O4 ( ) and 9OCB-PHMS@SiO2 ( ) and 9OCB-PHMS@SiO2 ( ) as doping agents. The values for 9OCB-PHMS@CoFe2O4 and 9OCB-SiO2 are taken from ref. 21. ) as doping agents. The values for 9OCB-PHMS@CoFe2O4 and 9OCB-SiO2 are taken from ref. 21. | ||
The values for both TCN and TNI increase at small doping fractions and decrease again above a magnetic volume fraction of ϕs = 1.8 × 10−4. In general, the values for the transition temperatures for 5CB doped with 9OCB-PHMS@Fe3O4 are slightly higher. The existence of stable nematic phases for all doping fractions proves a good compatibility between LC phase and nanoparticles as already shown for 9OCB-PHMS@CoFe2O4 and 9OCB-PHMS@SiO2 particles.
Influence of 9OCB-PHMS@NP on order parameter
The order parameters of 5CB doped with the superparamagnetic 9OCB-PHMS@Fe3O4 particles at different solid doping fractions are examined by measuring the refractive indices as a function of temperature and employment of the Haller method. The values for the order parameter as a function of the solid volume fraction ϕs are shown in Fig. 7a. With increasing particle concentration, the order parameter increases. The positive impact on the order parameter of the system further denotes an improved compatibility between nanoparticles and liquid crystalline phase. In Fig. 7b, the critical exponents β for 5CB doped with 9OCB-PHMS@Fe3O4 and with 9OCB-PHMS@CoFe2O4 extracted from the Haller plot are depicted as function of the solid volume ratio ϕs. In general, β is a parameter for the description of the behaviour of S near the phase transition. For pure 5CB, a critical exponent of β = 0.17 is found which is consistent with the value found in literature for this method.56 The nematic–isotropic transition is known to be weakly first-order.57,58 With increasing ϕs the critical exponent β first decreases steeply and then approaches a constant value. This phenomenon can be assigned to the weakly-first order transition becoming more continuous and thus, more akin to second order.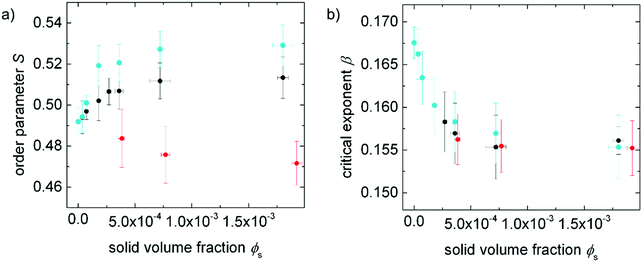 | ||
Fig. 7 (a) Order parameter at a reduced temperature of τ = 0.985 and (b) critical exponent β as a function of solid volume fraction ϕs for 5CB doped with 9OCB-PHMS@Fe3O4 (•), 9OCB-PHMS@CoFe2O4 ( ), and 9OCB-PHMS@SiO2 ( ), and 9OCB-PHMS@SiO2 ( ). The values for 9OCB-PHMS@CoFe2O4 and 9OCB-PHMS@SiO2 are taken from ref. 21. ). The values for 9OCB-PHMS@CoFe2O4 and 9OCB-PHMS@SiO2 are taken from ref. 21. | ||
Capacitance measurement of ferronematics
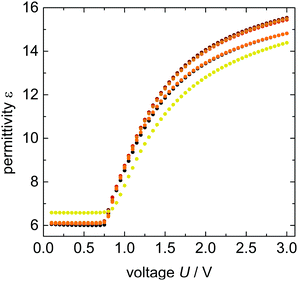
The impact of 9OCB-PHMS@Fe3O4 nanoparticles on the electro and magneto–nematic response is investigated by dielectric spectroscopy measurements in planar aligned sandwich cells as it was done for 9OCB-PHMS@CoFe2O4. The electric transition for 5CB doped with 9OCB-PHMS@Fe3O4 with different magnetic volume ratios are displayed in Fig. 8.In general, the dielectric permittivity as a function of electric field strength exhibits the expected shape. At fields below a critical field amplitude U0 (threshold) the permittivity remains constant with the value of ε⊥. After exceeding the threshold strength, the permittivity increases as the mesogens align in the direction of the electric field. With increasing doping fraction, all curves weakly deviate from the behavior of pure 5CB.
To get more quantitative information, the electric transition data are fitted using eqn (8) and (10) with the elastic constants K1 and K3, the parallel component of the dielectric permittivity, ε‖, and the pretilt angle θ0 between the nematic director and the substrate as fitting parameters.48 The fitting results for the system doped with Fe3O4 are presented in Table 1. The values for U0 and K1 remain nearly constant, with a slight increase for the highest magnetic volume fractions which can be an indication for the presence of particle–particle interaction.
| Φ | U 0/V | ε ‖ | θ 0 | K 1/pN | K 3/pN |
|---|---|---|---|---|---|
| 0 | 0.79 | 17.59 | 3.8 × 10−3 | 6.70 | 7.78 |
| 1.9 × 10−5 | 0.74 | 18.37 | 3.8 × 10−3 | 6.05 | 7.64 |
| 9.4 × 10−5 | 0.75 | 18.26 | 3.8 × 10−3 | 6.05 | 7.34 |
| 1.9 × 10−4 | 0.75 | 18.37 | 3.8 × 10−3 | 6.21 | 7.40 |
| 4.7 × 10−4 | 0.77 | 17.46 | 3.8 × 10−3 | 5.78 | 6.27 |
| 9.4 × 10−4 | 0.84 | 17.53 | 7.2 × 10−3 | 6.77 | 9.45 |
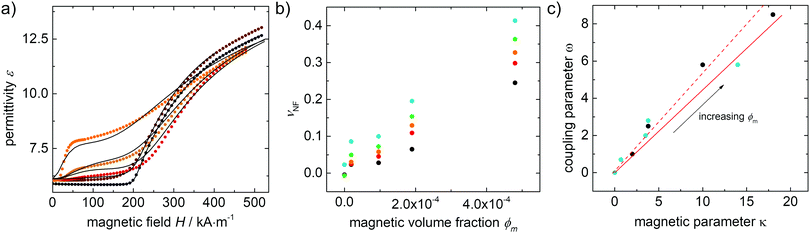
Finally, the magneto–nematic response of the ferronematics is analysed to investigate the effect of superparamagnetic Fe3O4 nanoparticles on the LC phase 5CB. Therefore, the LC sandwich cells are placed in a static magnetic field applied perpendicular to the cell plane and the dielectric permittivity is measured as a function of the magnetic field. The magnetic Fréedericksz transition of 5CB and 5CB doped with 9OCB-PHMS@Fe3O4 in different volume ratios are displayed in Fig. 9a. In the present arrangement, pure 5CB, which is well-explored in literature,59–63 exhibits a transition at H0 = 200 kA m−1. By doping 5CB with 9OCB-PHMS@Fe3O4 the course of the magnetic transition changes drastically with increasing doping fraction. Even at very low concentration of ϕm = 1.9 × 10−5 the graphs do not show the sharp transition typically observed for 5CB. Above a concentration of ϕm = 9.4 × 10−5 the curves additionally feature a shoulder at low magnetic fields. At a magnetic volume fraction of ϕm = 5 × 10−4 a threshold field of only ∼15 kA m−1 or 18 mT is observed. Taking into account the values of ε⊥ which remain nearly constant, the change in the magnetic transition is not caused by weakening of the anchoring at the glass/LC interface but attributed to a strong magneto–nematic coupling. The volume ratio of mesogens oriented in the direction of the magnetic field νNF approximately is obtained using the measured permittivity at a given magnetic field εB, the initial and final permittivity ε⊥ and ε‖ and by using eqn (18)
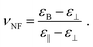 | (18) |
In order to get more information about the magnitudes of the coupling, the experimental data for the ferronematic systems doped with Fe3O4 are analogously fitted with the model based on Burylov and Raikher10 with Δχ and K1 as obtained from the electrical transition simulation, and κ and ω as the fitting parameters. The fitted simulations are given as black lines in Fig. 9a while the obtained fitting parameters ω as a function of the fitting parameter κ is displayed in Fig. 9c.
In general, satisfactory fits are obtained for the present experiments. As expected, κ and ω increase approximately linearly with increasing volume fraction ϕm. With the quotient ω/κ from the slope of ω versus κ being 0.45 we can calculate the effective coupling energy density per particle using eqn (14) to be Ω = 1.17 × 104 N m−2. By taking the particle size into account according to eqn (15), the surface anchoring strength is determined to be Ws = 1.47 × 10−4 J m−2.
Comparison of Fe3O4 and CoFe2O4
In this work, the effect of superparamagnetic Fe3O4 particles on 5CB is investigated in order to compare it with the behaviour of magnetically blocked particles. As for superparamagnetic particles, the mechanical reorientation of the particles in response to the application of a magnetic field is prevented due to magnetic reorientation, further information about the origin of the coupling in such a ferronematic system can be obtained with this approach. For a better compatibilization with 5CB, the particles are modified with LC polymer brushes using our successful approach.21Detailed information about the surface functionalization and magnetic properties of the employed particles are listed in the ESI† (Tables S1 and S2). The synthesized Fe3O4 particles exhibit a comparable size, particle brush, saturation magnetization and magnetic moment to the CoFe2O4 particles used in our previous works. The magnetization curves further reveal a hysteresis and remanence for CoFe2O4 indicating a considerable magnetically blocked state at ambient temperature, while for Fe3O4 no hysteresis is observed. For more information about the magnetic properties, ZFC/FC measurements are performed. Here, for Fe3O4 the superparamagnetic state is confirmed with a blocking temperature of 45 K, but no definite jumps due to the change in mobility of particles because of the melting and crystallization 5CB is observed. In contrast, the ZFC curves of CoFe2O4 particles in 5CB (Fig. S3, ESI†) do not show a maximum and do not coincide with the FC curve as the blocking temperature is not reached within the temperature range of the measurement confirming the magnetically blocked state. Moreover, a characteristic jump in the FC curve can be observed at 308 K which can be attributed to the transition from the isotropic to the nematic phase.
The measurement of thermal properties using DSC proves for both particle types a good stability of the nematic phase. As already observed for 9OCB-PHMS@CoFe2O4, by doping 5CB with 9OCB-PHMS@Fe3O4 the order parameter is increased with increasing doping concentration with slightly higher values for Fe3O4 which can be assigned to a good compatibility between nanoparticles and liquid crystalline phase. In contrast, non-magnetic 9OCB-PHMS@SiO2 particles decrease the order of the system. By performing electric capacitance measurements, the elastic constants K1 and K3 are obtained which remain nearly constant with increasing doping fraction.
Information about the magneto–nematic coupling is obtained by magnetic capacitance measurements. For ferronematic phases doped with 9OCB-PHMS@CoFe2O4, as well as doped with 9OCB-PHMS@Fe3O4, the threshold drastically decreases with respect to particle fraction. In both systems, a measurable magnetic response is obtained at field strengths of ∼15 kA m−1 or 18 mT at magnetic volume fractions of ϕm = 5 × 10−4. Quantitative information about the coupling in the ferronematic systems are determined by an appropriate fitting procedure. Partly unexpected by our initial hypothesis, the magnetic capacitance results of both particle types are qualitatively and quantitatively quite similar (see Table 2), indicating that an analogous effect on the nematic host phase can be achieved as well by doping with magnetically blocked or superparamagnetic particles that are covered with a liquid crystalline polymer brush. This observation indicates that in contrast to our initial hypothesis, a permanent magnetic moment of the dopant particles is not a prerequisite for the observed phenomenon. A major difference in the response to an external magnetic field is that a blocked particle undergoes a mechanical rotation to remagnetize while this is not a requirement for superparamagnetic particles. Accordingly, the mechanical rotation of the particles is not of critical influence for the phenomenon. Instead, we propose the following qualitative mechanistic explanation by individually addressing the different coupling modes present in the systems. Therefore, we approximate roughly the distance dependent magnetic field strength caused by a single dipolar particle of magnetic moment m.
By approximating the particle as a point dipole with a stationary direction and strength, the magnetic flux B of the dipole as a function of the distance to the point dipole rd can be calculated according to eqn (19).
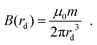 | (19) |
It is verified by work of others that the creation of such a shell drastically changes the situation of interaction.22,43 Without the surface functionalization, the LC host molecules couple directly with the surface of the nanoparticles. As a result, doping with NP leads to the distortion of the nematic phase that is compensated with the formation of defects.9,25 Further it was shown that covalently bound polymer chains on planar surfaces can be manipulated by an external trigger due to the balance of the stretching of the chains and their flexibility.64–66 This phenomenon can be transferred to spherical surfaces, that are functionalized with LC polymer brushes. With this approach, a buffer zone between the host molecules and the particle is established that can minimize the formation of defects. This leads to a high density of mesogens in the area where the magnetic fields lines from the magnetic moment of the particle is dense which further facilitates the alignment. This way, the development of a dipolar defect caused by the particle, as usually reported for spherical particles, might be prevented as already indicated by similar observations.43 We can further propose that the shell is swollen with 5CB molecules from the host liquid crystal to a considerable extend and that also those mesogens are affected by the field (see Table 1). Such a magnetic alignment layer within the host in the particle vicinity is supported also by the observations on the particle influence on the nematic–isotropic transition temperature and on the order parameter that both indicate a stabilizing impact of the dopants on the nematic phase even in the absence of a magnetic field.
While this seems plausible at least for the magnetically blocked particles, our observations made for the superparamagnetic particles only on the first glance contradict the explanation. In the case of superparamagnetic particles, no significant magnetic field is expected in time average. However, in a small external field even for short relaxation times, the particles exhibit on average a preferred orientation along the field axis, which further increases with field strength. Thus, for superparamagnetic particles with a similar magnetic moment m a shell orientation can be expected induced by an external field. This orientation further influences the alignment of the whole matrix by interaction of the polymer-attached mesogens with the adjacent host mesogens. In order to give a precise explanation for the coupling theoretical calculations or more experiments are necessary.
Conclusions
We successfully implemented our concept for the compatibilization of CoFe2O4 to Fe3O4 nanoparticles with nematic liquid crystalline phases to fabricate stable ferronematic materials based on particles with different magnetic relaxation behaviour. The composite materials are based on particles with covalently bound mesogenic polymer and 5CB as LC host.9OCB-PHMS@Fe3O4 particles are synthesized by thermal composition of Fe(acac)3 and subsequent surface functionalization with a liquid crystalline brush. They show similar values for the size, surface functionalization density and magnetic moment compared to 9OCB-PHMS@CoFe2O4. However, CoFe2O4 are magnetically blocked and Fe3O4 particles are superparamagnetic.
The strong compatibilization of 9OCB-PHMS@Fe3O4 in 5CB is proven by DSC. As for CoFe2O4, stable nematic phases with high volume fractions of up to ϕm = 9.6 × 10−4 can be prepared. Moreover, the addition of modified Fe3O4 to 5CB also leads to an increase of the order parameter.
By magneto-optical measurements in planarly aligned cells we could clearly show a considerable influence on the magnetic Fréedericksz transition as already observed for CoFe2O4 as doping agent. The system is sensitive to magnetic fields of the order of tens of milli tesla even for low concentration of ϕm = 4.7 × 10−4. A quantitative analysis and thus, calculation of the effective coupling energy density per particle Ω and the surface anchoring strength Ws is performed with obtained values comparable to CoFe2O4. As for superparamagnetic Fe3O4 particles the orientational coupling due to a mechanical anchoring of the mesogens and the particle surface is excluded, the magneto-optic effects can be induced by a direct coupling over the stray field or the formation of aggregates. Both effects are strengthened by the covalently bound LC polymer brush at the particle surface. However, the origin of this coupling is not fully understood yet.
In general, these hybrid systems are promising material for magnetically driven devices and gaining a deeper insight of the coupling promotes the technical realization and optimization of such devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for financial support from the German Science Foundation (DFG) through the priority program SPP 1681 (SCHM1747/10, STA-425/36-3, and WE2623/7). K. K. acknowledges support by the International Helmholtz Research School of Biophysics and Soft Matter (IHRS BioSoft). K. K. and A. S. acknowledge Dr A. Berkessel for ATR-IR measurements. We also thank Ralf Stannarius for discussion.Notes and references
- D. Demus, J. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Physical Properties of Liquid Crystals, Wiley-VCH Verlag, Weinheim, 2009 Search PubMed.
- J. E. M. Stephen and J. Clarson, Silicone Elastomers, 1996, vol. 12 Search PubMed.
- V. Fréedericks and V. Zolina, Forces causing the orientation of an anisotropic liquid, Kristallographie, 1933, 29, 919–930 Search PubMed.
- F. C. Frank, On the theory of Liquid Crystals, Liq. Cryst., 1958, 1, 19–28 Search PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystal, Phys. Today, 1994, 48, 70 CrossRef.
- S. M. Kelly and M. O. Neill, Handbook of Advanced Electronic and Photonic Materials and Devices, 2001, pp. 1–61 Search PubMed.
- P. R. Romero-Hasler, A. E. Fierro-Armijo, E. A. Soto-Bustamante and A. Meneses-Franco, Synthesis and characterisation of two homologous series of LC acrylic monomers based on phenolic and resorcinic azobenzene groups, Liq. Cryst., 2016, 43, 1804–1812 CrossRef CAS.
- M. Schadt, Liquid crystal materials and liquid crystal displays, Annu. Rev. Mater. Sci., 1997, 27, 305–379 CrossRef CAS.
- F. Brochard and P. de Gennes, Theory of magnetic suspensions in liquid crystals, J. Phys., 1970, 31, 691–708 CrossRef CAS.
- S. V. Burylov and Y. L. Raikher, Macroscopic Properties of Ferronematics Caused by Orientational Interactions on the Particle Surfaces. I. Extended Continuum Model, Mol. Cryst. Liq. Cryst. Sci. Technol., 1995, 258, 107–122 CrossRef CAS.
- P. Kopčanský, M. Koneracká, I. Potočová, M. Timko, L. Tomčo, J. Jadzyn and G. Czechovski, The structural transitions in liquid crystals doped with fine magnetic particles, J. Phys., 2001, 51, 59–63 Search PubMed.
- P. Kopčanský, N. Tomašovičová, V. Gdovinová, M. Timko, N. Éber, T. Tóth-Katona, J. Jadzyn, J. Honkonen and X. Chaud, How to Enhance Sensitivity of Liquid Crystals to External Magnetic Field?, Acta Phys. Pol., A, 2015, 127, 157–162 CrossRef.
- I. Appel, H. Nadasi, C. Reitz, S. Nerea, H. Hahn, A. Eremin, R. Stannarius and S. Behrens, Doping of nematic cyanobiphenyl liquid crystals with mesogen-hybridized magnetic nanoparticles, Phys. Chem. Chem. Phys., 2017, 19, 12127–12135 RSC.
- V. Gdovinová, N. Tomašovičová, N. Éber, T. Tóth-Katona, V. Závišová, M. Timko and P. Kopčanský, Influence of the anisometry of magnetic particles on the isotropic–nematic phase transition, Liq. Cryst., 2014, 41, 1773–1777 CrossRef.
- P. Kopčanský, I. Potočová, M. Timko, M. Koneracká, A. M. G. G. Jansen, J. Jadzyn and G. Czechowski, The structural transitions in ferronematics in combined electric and magnetic fields, J. Magn. Magn. Mater., 2004, 272–276, 2355–2356 CrossRef.
- V. Gdovinová, M. A. Schroer, N. Tomašovičová, I. Appel, S. Behrens, J. Majorošová, J. Kováč, D. I. Svergun and P. Kopčanský, Structuralization of magnetic nanoparticles in 5CB liquid crystals, Soft Matter, 2017, 13, 7890–7896 RSC.
- V. Gdovinová, N. Tomašovičová, N. Éber, P. Salamon, T. Tóth-Katona, V. Závišová, J. Kováč, J. Jadżyn and P. Kopčanský, Ferronematics based on the nematic 6CB in combined electric and magnetic fields, Phase Transitions, 2017, 90, 780–789 CrossRef.
- M. F. Prodanov, O. G. Buluy, E. V. Popova, S. A. Gamzaeva, Y. O. Reznikov and V. V. Vashchenko, Soft Matter Magnetic actuation of a thermodynamically stable colloid of ferromagnetic nanoparticles in a liquid, Soft Matter, 2016, 12, 6601–6609 RSC.
- S. D. Peroukidis and S. H. L. Klapp, Spontaneous ordering of magnetic particles in liquid crystals: from chains to biaxial lamellae, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 010501(R) CrossRef.
- M. Veveričík, P. Bury, P. Kopčanský, M. Timko and V. Závišová, Effect of Magnetic Particles on Structural Changes and Magneto-Optical Behavior of Liquid Crystal, Acta Phys. Pol., A, 2020, 137, 967–969 CrossRef.
- K. Koch, M. Kundt, A. Eremin, H. Nadasi and A. M. Schmidt, Efficient ferronematic coupling with polymer-brush particles, Phys. Chem. Chem. Phys., 2020, 22, 2087–2097 RSC.
- A. Mouhli, H. Ayeb, T. Othman, J. Fresnais, V. Dupuis, I. R. Nemitz, J. S. Pendery, C. Rosenblatt, O. Sandre and E. Lacaze, Influence of a dispersion of magnetic and nonmagnetic nanoparticles on the magnetic Fredericksz transition of the liquid crystal 5CB, Phys. Rev. E, 2017, 96, 012706 CrossRef PubMed.
- A. N. Zakhlevnykh and D. A. Petrov, Weak coupling effects and re-entrant transitions in ferronematic liquid crystals, J. Mol. Liq., 2014, 198, 223–233 CrossRef CAS.
- A. Mertelj, D. Lisjak, M. Drofenik and M. Čopič, Ferromagnetism in suspensions of magnetic platelets in liquid crystal, Nature, 2013, 504, 237–241 CrossRef CAS PubMed.
- A. Mertelj and D. Lisjak, Ferromagnetic nematic liquid crystals, Liq. Cryst. Rev., 2017, 5, 1–33 CrossRef CAS.
- A. Mertelj, N. Osterman, D. Lisjak, M. Čopič, M. Copič and M. Čopič, Magneto-optic and converse magnetoelectric effects in a ferromagnetic liquid crystal, Soft Matter, 2014, 10, 9065–9072 RSC.
- P. Kopčanský, N. Tomašovičová, M. Koneracká, V. Závišová, M. Timko, A. Džarová, A. Šprincová, N. Iber, K. Fodor-Csorba, T. Tóth-Katona, A. Vajda and J. Jadzyn, Structural changes in the 6CHBT liquid crystal doped with spherical, rodlike, and chainlike magnetic particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011702 CrossRef.
- P. Kopčanský, I. Potočová, M. Koneracká, M. Timko, A. G. M. M. Jansen, J. Jadzyn and G. Czechowski, The anchoring of nematic molecules on magnetic particles in some types of ferronematics, J. Magn. Magn. Mater., 2005, 289, 101–104 CrossRef.
- A. N. Zakhlevnykh and D. A. Petrov, Orientational bistability and magneto-optical response in compensated ferronematic liquid crystals, J. Magn. Magn. Mater., 2016, 401, 188–195 CrossRef CAS.
- M. S. Zakerhamidi, S. Shoarinejad and S. Mohammadpour, Fe3O4 nanoparticles effect on dielectric and ordering behaviour of nematic liquid crystal host, J. Mol. Liq., 2013, 191, 3–7 Search PubMed.
- M. Wang, L. He, S. Zorba and Y. Yin, Magnetically actuated liquid crystals, Nano Lett., 2014, 14, 3966–3971 CrossRef CAS PubMed.
- T. Tóth-Katona, P. Salamon, N. Éber, N. Tomašovičová, Z. Mitróová and P. Kopčanský, High concentration ferronematics in low magnetic fields, J. Magn. Magn. Mater., 2014, 372, 117–121 CrossRef.
- B. Matt, K. M. Pondman, S. J. Asshoff, B. ten Haken, B. Fleury and N. Katsonis, Soft Magnets from the Self-Organization of Magnetic Nanoparticles in Twisted Liquid Crystals, Angew. Chem., Int. Ed., 2014, 126, 12654–12658 CrossRef.
- O. Buluy, D. Burseva, M. R. Hakobyan, J. W. Goodby, M. A. Kolosov, Y. Reznikov, R. S. Hakobyan, K. Slyusarenko, M. F. Prodanov and V. Vashchenko, Influence of Surface Treatment of Ferromagnetic Nanoparticles on Properties of Thermotropic Nematic Liquid Crystals, Mol. Cryst. Liq. Cryst., 2012, 560, 149–158 CrossRef CAS.
- O. Buluy, S. Nepijko, V. Reshetnyak, E. Ouskova, V. Zadorozhnii, A. Leonhardt, M. Ritschel, G. Schönhense and Y. Reznikov, Magnetic sensitivity of a dispersion of aggregated ferromagnetic carbon nanotubes in liquid crystals, Soft Matter, 2011, 7, 644–649 RSC.
- I. Appel and S. Behrens, Influence of the particle parameters on the stability of magnetic dopants in a ferrolyotropic suspension, J. Magn. Magn. Mater., 2017, 431, 49–53 CrossRef CAS.
- O. Buchnev, A. Dyadyusha, M. Kaczmarek, V. Reshetnyak and Y. Reznikov, Enhanced two-beam coupling in colloids of ferroelectric nanoparticles in liquid crystals, J. Opt. Soc. Am. B, 2007, 24, 1512–1516 CrossRef CAS.
- S. Saliba, C. Mingotaud, M. L. Kahn and J. D. Marty, Liquid crystalline thermotropic and lyotropic nanohybrids, Nanoscale, 2013, 5, 6641–6661 RSC.
- H. Qi, B. Kinkead, V. M. Marx, H. R. Zhang and T. Hegmann, Miscibility and alignment effects of mixed monolayer cyanobiphenyl liquid-crystal-capped gold nanoparticles in nematic cyanobiphenyl liquid crystal hosts, ChemPhysChem, 2009, 10, 1211–1218 CrossRef CAS PubMed.
- N. Podoliak, O. Buchnev, D. V. Bavykin, A. N. Kulak, M. Kaczmarek and T. J. Sluckin, Magnetite nanorod thermotropic liquid crystal colloids: synthesis, optics and theory, J. Colloid Interface Sci., 2012, 386, 158–166 CrossRef CAS PubMed.
- S. V. Burylov and Y. L. Raikher, Orientation of a solid particle embedded in a monodomain nematic liquid crystal, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 358–367 CrossRef CAS PubMed.
- S. V. Burylov and Y. L. Raikher, Magnetic Fredericksz transition in a ferronematic, J. Magn. Magn. Mater., 1993, 122, 62–65 CrossRef CAS.
- H. Ayeb, M. Derbali, A. Mouhli, T. Soltani, F. Jomni, J. Fresnais and E. Lacaze, Phys. Rev. E, 2020, 102, 052703 CrossRef CAS PubMed.
- M. Hähsler, I. Appel and S. Behrens, Magnetic hybrid materials in liquid crystals, Phys. Sci. Rev., 2020, 20190090 Search PubMed.
- D. Maity, S. N. Kale, R. Kaul-Ghanekar, J. M. Xue and J. Ding, Studies of magnetite nanoparticles synthesized by thermal decomposition of iron(III) acetylacetonate in tri(ethylene glycol), J. Magn. Magn. Mater., 2009, 321, 3093–3098 CrossRef CAS.
- G. A. Van Ewijk, G. J. Vroege and A. P. Philipse, Convenient preparation methods for magnetic colloids, J. Magn. Magn. Mater., 1999, 201, 31–33 CrossRef CAS.
- N. Frickel, R. Messing, T. Gelbrich, A. M. Schmidt and G. Current, Functional Silanes as Surface Modifying Primers for the Preparation of Highly Stable and Well-Defined Magnetic Polymer Hybrids, Langmuir, 2010, 143, 2839–2846 CrossRef PubMed.
- D. Demus, J. Goody, H.-W. Spiess and V. Vill, Handbok of Liquid Crystals, Wiley-VCH, Weinheim, 1998 Search PubMed.
- I. Haller, Thermodynamic and Static Properties of Liquid Crystals, J. Phys. Chem., 1975, 10, 103–118 Search PubMed.
- R. A. Gharde and S. Y. Thakare, Behaviour of Dielectric properties of Liquid Crystal Mixture Doped with Ferroelectric Nanopowder, Int. J. Sci. Res., 2015, 4, 2690–2696 Search PubMed.
- M. F. Vuks, Determination of the Optical Anisotropy of Aromatic Molecules from the Double Refraction of Crystals, Opt. Spectrosc., 1996, 20, 361 Search PubMed.
- N. Podoliak, O. Buchnev, O. Buluy, G. D’Alessandro, M. Kaczmarek, Y. Reznikov and T. J. Sluckin, Macroscopic optical effects in low concentration ferronematics, Soft Matter, 2011, 7, 4742 RSC.
- G. J. Laughlin and J. A. Todd, Evidence for Early Bronze Age tin ore processing, Mater. Charact., 2000, 45, 269–273 CrossRef CAS.
- S. Mosivand, L. M. A. A. Monzon, K. Ackland, I. Kazeminezhad and J. M. D. D. Coey, Structural and magnetic properties of sonoelectrocrystallized magnetite nanoparticles, J. Phys. D: Appl. Phys., 2014, 47, 055001 CrossRef CAS.
- S. Odenbach, Magnetoviscous Effects in Ferrofluids, Springer, Heidelberg, 2002 Search PubMed.
- I. Chirtoc, M. Chirtoc, C. Glorieux and J. Thoen, Determination of the order parameter and its critical exponent for nCB (n = 5–8) liquid crystals from refractive index data Determination of the order parameter and its critical exponent for nCB (n ∼ 5–8) liquid crystals from refractive index dat, Liq. Cryst., 2004, 32, 229–240 CrossRef.
- B. Van Roie, J. Leys, K. Denolf, C. Glorieux, G. Pitsi and J. Thoen, Weakly first-order character of the nematic–isotropic phase transition in liquid crystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041702 CrossRef CAS PubMed.
- G. Cordoyiannis, L. K. Kurihara, L. J. Martinez-Miranda, C. Glorieux and J. Thoen, Effects of magnetic nanoparticles with different surface coating on the phase transitions of octylcyanobiphenyl liquid crystal, Phys. Rev., 2009, 011702 CrossRef.
- J. D. Bunning, T. E. Faber, P. L. Sherrell, J. D. Bunning, T. E. Faber and P. L. Sherrell, The Frank constants of nematic 5CB at atmospheric pressure, J. Phys., 1981, 42, 1175–1182 CrossRef CAS.
- B. J. Frisken, J. F. Carolan, J. A. A. J. Perenboom, G. S. Bates, J. F. Carolan and J. A. A. J. Perenboom, Squid Susceptibility Measurements on 5CB, Mol. Cryst. Liq. Cryst., Lett. Sect., 1985, 3, 57–62 Search PubMed.
- M. Cui and J. R. Kelly, Molecular Crystals and Liquid Crystals Science and Crystals Temperature Dependence of Visco-Elastic Properties of 5CB Temperature Dependence of Visco-Elastic Properties of 5CB, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 31, 49–57 CrossRef.
- A. J. Karn, S. M. Arakelian and Y. R. Shen, Observation of Magnetic Field-Induced First-Order Optical Freederickzs transition in a Nematic film, Phys. Rev. Lett., 1986, 57, 448–451 CrossRef CAS PubMed.
- S.-M. Chen and T.-C. Hsieh, Magnetic field induced Freedericks transition and the dynamic response of nematic liquid-crystal films with a free surface, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 2848–2857 CrossRef CAS.
- B. Peng, J. Rühe and D. Johannsmann, Homogeneously aligned liquid-crystal polymer brushes, Adv. Mater., 2000, 12, 821–824 CrossRef CAS.
- A. Halperin and D. R. M. Williams, Liquid crystalline brushes: an anchoring transition, Europhys. Lett., 1993, 21, 575–580 CrossRef CAS.
- S. Nagano, Surface and interface designs in side-chain liquid crystalline polymer systems for photoalignment, Polym. J., 2018, 50, 1107–1119 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03005a |
| This journal is © the Owner Societies 2021 |