Investigation of alkali and alkaline earth solvation structures in tetraglyme solvent

Abstract

This study compares molecular calculations performed with molecular and periodic codes through an investigation of the solvation structures of alkali and alkaline earth metal ions in tetraglyme solution. The two codes are able to produce equivalent structural and energetic information at the same level of theory, and in the presence of the implicit solvation model or not. This comparison reveals that molecular optimisations can be performed with periodic codes and used directly as input models for interface or electrochemistry calculations in order to preserve the solvent–solute interaction and the cavitation energy. By a rigorous comparison, we have demonstrated that equivalent energetic values can be obtained with the conventional PBE-D3 and the newly developed SCAN-rVV10 functionals. Nevertheless, as far as the vibrational features are concerned and when the molecule possesses a highly conjugated system, the SCAN-rVV10 functional is required to describe the vibrational modes properly. The computed IR/Raman spectra can thus be used as essential information to determine the first solvation shell of metal ions in glyme-based solutions. In tetraglyme solution, the alkali and alkaline earth metal ions exhibit a diverse solvation structure. Small ions like Li⁺ and Mg²⁺ tend to adopt a coordination number of five or six, while larger ions, Na⁺, K⁺, and Ca²⁺, prefer an eight-coordinated environment, and the metal–ligand interaction increases in the order K⁺–O < Na⁺–O < Li⁺–O < Ca²⁺–O < Mg²⁺–O. The solvation spheres play a significant role in the stability and the reactivity of the solvated ions, and can thus be used as input models to construct the solvation structure in more sophisticated electrolytes, such as polyethylene oxide, or perform electrochemical calculations.

---

Introduction

Rechargeable lithium-ion batteries (LIBs) have long been the dominant energy storage system for portable devices due to their high operating voltage and high energy density value.¹ Nonetheless, the unequal distribution of Li resources in the Earth's crust and their increasing price have evoked the development of alternative systems, such as sodium-ion (SIBs),^2–5 potassium-ion (KIBs),⁶ and multivalent ion batteries.^7,8 Among the multivalent ion technologies, magnesium-ion, and calcium-ion batteries are the most promising, thanks to the abundance of Mg and Ca resources, the low potential of the Mg²⁺/Mg and Ca²⁺/Ca redox pairs, and the high theoretical capacity associated with the exchange of two electrons. Even though practical uses of these multivalent ion technologies are still far from reality due to the sluggish kinetics of Mg²⁺ and Ca²⁺ in solid phases and the lack of appropriate electrolytes, on-going research in these areas has led to significant discoveries in the field of chemistry and materials science.^6,8

An essential component of all rechargeable batteries is the electrolyte, which acts as an electronic insulator between the two electrodes but still allows the ionic diffusion process to occur. Most rechargeable LIBs and SIBs employ liquid electrolytes consisting of Li- or Na-containing salts dissolved in a mixture of organic solvents, but polymer and solid-state electrolytes also exist.^9–11 There has been no report on the existence of an optimal electrolyte for multivalent ion batteries.¹² However, most on-going research shows great interest in organic carbonates and the glyme family.^13,14 The glyme family has the general chemical formula of H₃CO(CH₂CH₂O)_nCH₃, with the main representatives being dimethoxylethane (DME) or monoglyme (G1), diglyme (G2), triglyme (G3), or tetraglyme (G4) when n = 1, 2, 3, or 4, respectively. These glyme molecules can be seen as oligomers and prototypes of a more complicated solid electrolyte, known as polyethylene oxide (PEO), which is becoming more and more popular in the scope of all-solid-state batteries. The glyme family exhibits great advantages in practical applications due to their high boiling point and high stability over a wide electrochemical window.^15–19

Despite the great importance of glyme-based electrolytes in the field of batteries, little information can be found on the solvation structure of alkali and alkaline earth metal ions. The stability and reactivity of solvated metal ions strongly depend on the structure of the first coordination sphere, which cannot be ignored in theoretical models. Some attempts have been made to elucidate the solvation structures of these alkali and alkaline earth ions in glyme-based solvents. Among them, Saito et al. proposed a Li⁺ solvation structure in G4 solution determined by neutron total scattering. Fujii's group reported a thorough investigation of the solvation structures of Mg²⁺ in G2 and G3 solutions by combining infrared (IR)/Raman spectroscopy with Density Functional Theory (DFT) calculations. Nonetheless, all the structures proposed in these studies were modelled in the isolated gas phase, which completely ignores the solvent effect on the stability and the local structure of the solvated ions.^20–22 While progress has been achieved by employing an implicit solvent model in the calculation in conjunction with the explicit solvent or electrolyte molecules,^23–26 these studies are still performed at the molecular level, which assumes infinitely dilute solutions. In batteries, liquid electrolytes contain ions at considerable concentrations, and thus short- and long-range electrostatic interactions between the solvated species may be important. These interactions might lead to a significant deviation in the calculated and observed properties, especially in the energetic values. The ion–ion interaction energy that occurs in real solutions can be calculated from Debye–Hückel or extended theories and then added to energetic values obtained from molecular codes as a data post-processing treatment. Nonetheless, the reliability of these models stands only for high dielectric constants where long-range electrostatic interactions do not contribute extensively to the system energetics, which is not the case of glyme-based solutions. In the case of low dielectric constant electrolytes, a concentration-dependent computational model is required, which can be realised through the use of periodic calculations. To that end, a validation step is needed to ensure that both molecular and periodic codes can produce equivalent structural and energetic information under infinite dilution conditions.

This study aims at systematically comparing the structures and the physicochemical properties obtained from molecular modelling performed with the Q-Chem code and periodic modelling performed with the Vienna Ab initio Simulation Package (VASP) code through an investigation of the solvation structure of some important alkali and alkaline earth ions Mⁿ⁺ (M = Li, Na, K, Mg, or Ca) in tetraglyme solutions. The Q-Chem code is chosen for this study as it offers many functionals that are equivalent to those available in the VASP code. The obtained results reveal that equivalent geometric and energetic information can be extracted from the molecular modelling performed in the two codes. As expected, van der Waals interactions have a significant contribution in these systems, and should be included in all calculations. Furthermore, we demonstrate the possibility of combining theoretical DFT calculations with experimental IR spectroscopy to determine ion solvation structures in glyme-based solutions. Furthermore, our analysis shows that solvation energies can be decomposed into competing O–cation bonding and organic skeleton strain energies that present strong evolutions with the cation charge and size. Li⁺ in G4 has a coordination number of five, which is imposed by the tiny size of Li⁺ and the geometry constraint of the G4 ring. Mg²⁺ tends to reside in an octahedral site, while Na⁺, K⁺, and Ca²⁺ prefer a coordination number of eight. The solvation structures in G4 represent those that can exist in more sophisticated glymes, and they can thus be used as starting models to construct the solvation sphere in polyethylene oxide.

Results and discussion

Validity of the calculation approach

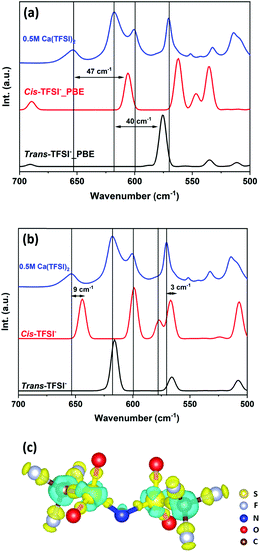
The two computational codes, Q-Chem and VASP, employ many common exchange–correlation functionals, such as the Perdew–Burke–Ernzerhof (PBE) functional, hybrid functional PBE0, and the Strongly Constrained and Appropriately Normed (SCAN) semi-local density functional; nevertheless, Q-Chem utilises Gaussian-type orbitals while VASP uses plane waves as basis sets. In order to verify whether the difference in the choice of basis set may lead to a substantial discrepancy in the structural and energetic values we first compare the enthalpies of the reaction [M(G4)]ⁿ⁺ + G4 → [M(G4)₂]ⁿ⁺ (M = Na, K, Mg, and Ca) calculated with the same functionals, e.g. PBE, PBE-D3, SCAN, and SCAN-rVV10. The calculations were performed in the isolated gas phase and in the presence of the implicit solvent model. Detailed information on the structure of [M(G4)]ⁿ⁺ and [M(G4)₂]ⁿ⁺ is discussed in the following parts. The obtained results show that the two computational codes produce similar structural and energetic information at the same level of theory, irrespective of the solvent conditions (Tables S1–S5, ESI†). The van der Waals interaction contributes significantly to the system energy with the dispersion corrected GGA (PBE-D3) or meta-GGA (SCAN-rVV10) functionals leading to similar solvation spheres. These results validate the performance of the periodic VASP code and its implicit solvent model to reproduce both the geometry and the energy of glyme-based solvation spheres, which can therefore be used as inputs in more complex calculations with a full transferability.

Apart from the energetics of the solvation energy, it is important to check how PBE-D3 and SCAN-rVV10 perform in terms of the vibrational properties, not only for the cations but also for the anions. At this stage, a direct comparison between the theoretical and experimental vibrational spectra of a cation solvated in G4 cannot give any clear conclusion, as the vibrations of G4 molecules in the free and in the complex states might overlap. Furthermore, one does not know whether the PBE-D3 and SCAN-rVV10 functionals can accurately reproduce the vibrational spectra or not. In order to facilitate the discussion, one should choose references whose vibrational spectra are well elucidated and are not interfered with by the solvent's vibrations. Among others, TFSI⁻ salts of alkali and alkaline earth metal ions are widely used in electrolytes for rechargeable batteries. When completely dissolved in G4, TFSI⁻ salts release a considerable amount of solvated cations and free TFSI⁻ anions. In solutions, TFSI⁻ is experimentally found in the form of cis- and trans-isomers and these configurations are determined by the relative positions of the two –CF₃ groups with respect to the S–N–S plane. The trans-TFSI⁻ gives rise to a characteristic deformation mode SO₂ at 618 cm⁻¹, whereas the SO₂ groups in cis-TFSI⁻ have two characteristic vibrations at 600 and 650 cm⁻¹.²⁷ These vibrations lie in the G4-transparent regions and have been the subject of several studies.^27–29 Modelling the TFSI⁻ anion within the DFT framework is not straightforward as it involves highly ionic C–F bonds and a strong conjugation through S=O bonds that can be difficult to capture by standard functionals. This anion is thus an excellent test case. The IR spectra of cis- and trans-TFSI⁻ computed at the PBE-D3 level fail badly to reproduce the IR-active vibrations experimentally observed in the 600–675 cm⁻¹ range (Fig. 1a). All the computed SO₂ deformation modes are down shifted by 40–50 cm⁻¹ compared to the experimental data recorded for a 0.5 M Ca(TFSI)₂/G4 solution (Fig. 1a). On the other hand, the IR spectra computed with the SCAN-rVV10 functional match almost perfectly with the experimental data, with no need to apply any scaling factor (Fig. 1b).

Fig. 1 IR spectra of cis- and trans-TFSI⁻ computed using the (a) PBE-D3 and (b) SCAN-rVV10 functional in the VASP code with the presence of the implicit solvent model, compared to the experimental data recorded for a 0.5 M Ca(TFSI)₂/G4 solution. Vertical lines are added for eye guidance. (c) Charge density difference at an iso-surface density of 3.5 × 10⁻³ electrons Å⁻² of trans-TFSI⁻ calculated with the SCAN-rVV10 and PBE-D3 functionals in the VASP code with the presence of the implicit solvent model. The yellow and blue colours indicate the areas where the electron density is enhanced or depleted for the SCAN-rVV10 functional.

The structures of the cis- and trans-TFSI⁻ anions optimised with the PBE-D3 and SCAN-rVV10 functionals are mostly identical (Table S6, ESI†), showing that the molecular geometry is not the origin of the better description of the IR spectra with the SCAN-rVV10 functional. A charge density difference map is computed for the trans-TFSI⁻, based on the electron densities obtained with the SCAN-rVV10 and PBE-D3 functionals (Fig. 1c). It reveals that the SCAN-rVV10 functional enhances the charge transfer on the S=O and C–F bonds, which increases the bonds’ ionicity and therefore the force constant. Consequently, the vibrational frequencies of S=O bonds, calculated with the SCAN-rVV10 functional, are shifted to higher wavenumbers, leading to a better agreement between the theoretical and experimental values.

In addition to those of TFSI⁻, the IR spectra of [Ca(G4)]²⁺ computed using the PBE-D3 and SCAN-rVV10 functionals are also compared (Fig. S1a, ESI†). The two spectra show slight differences in the relative intensity of some vibrations in the 750–1200 cm⁻¹ range due to the difference in the functionals. Importantly, the wavenumbers computed using the PBE-D3 functional are underestimated by 30–40 cm⁻¹ compared to SCAN-rVV10. The charge density difference map reveals that the SCAN-rVV10 functional increases the charge localisation on the O atom and on the C–C bonds while reducing the hyperconjugation contribution of the C–H bonds (Fig. S1b, ESI†). Like TFSI⁻, the SCAN-rVV10 functional gives a better description of the nature of the chemical bonds in the solvated cations, and thus the chemical bonds’ vibrational modes. The discrepancy in the wavenumber of the vibrations computed using the PBE-D3 and SCAN-rVV10 functionals seems to be more important in TFSI⁻ than in [Ca(G4)]²⁺, e.g. 50–70 cm⁻¹ discrepancy vs. 30–40 cm⁻¹. This points out the tendency of the PBE-D3 functional to overdelocalise the electrons of the TFSI⁻ conjugated system, hence reducing the bond strength and the vibrations’ wavenumber; this overestimation is weaker in [Ca(G4)]²⁺, in which the electrons are much more localised than in TFSI⁻.

These comparisons show that, even though the PBE-D3 and SCAN-rVV10 functionals produce similar structural and energetic information, the SCAN-rVV10 functional is required to accurately describe the material's vibrational structure and the topology of its potential energy surface. In the following sections, all the structural, energetic, and vibrational properties of the solvated ions will be considered, especially for Ca²⁺. Thus, only the results obtained from the SCAN-rVV10 functional in the VASP code will be given unless otherwise specified.

Li⁺ solvation structure

By using neutron total scattering, Saito et al. reported that Li⁺ in G4 solution is surrounded by five oxygens of a G4 molecule at Li–O distances of 1.93, 2.06, 2.09, 2.13, and 2.24 Å. Nonetheless, the authors claimed that the Li⁺ site should be described as deficient five-coordination. The oxygen atom at 2.24 Å was not counted as a coordinating ligand since this distance was slightly greater than the sum of the Shannon radii of Li⁺ and O²⁻. The proposed structure was then modelled using an isolated [Li(G4)]⁺ in the gas phase at the MP2/6-311G(d,p)//HF/6-31G(d) level of theory.³⁰ Nevertheless, it is important to note that the Shannon radii were established from the solid-state database and the ionic radius for a certain ion varies with its coordination: a Li⁺ residing in an octahedral site has a larger ionic size than one in a tetrahedral site (0.76 Å vs. 0.59 Å). The Shannon radius of Li⁺ in a coordination of five is not tabulated, and it is not justifiable to exclude the oxygen at 2.24 Å from the Li⁺ solvation sphere by using the Li⁺ radius in a tetrahedral site. A [Li(G4)]⁺ structural optimisation performed using the SCAN-rVV10 functional in the presence of the implicit solvent model converges to a five-coordinated environment with corresponding Li–O distances of 2.08, 2.12 (×2), 2.14, and 2.18 Å. An alternate model, with the fifth oxygen of the G4 molecule pointing away from Li⁺, is less stable than the five-coordinated structure by 13.9 kJ mol⁻¹ (Fig. 2). This comparison shows that all the five oxygens of a G4 molecule coordinate to the Li⁺ in [Li(G4)]⁺, which is in agreement with the theoretical study of Tsuzuki et al., showing that pentadentate [Li(G4)]⁺ is more stable than the tetradentate one.³¹ The reason for this behaviour is that the tetrahedral site formed by four oxygens of the G4 molecule is greatly distorted (vide infra), which leaves plenty of room for a supplementary bond.

Fig. 2 Optimised structures and the relative energy of the pentadentate and tetradentate [Li(G4)]⁺ calculated with the SCAN-rVV10 functional.

Mg²⁺ solvation structure

The solvation structure of Mg²⁺ in dilute G4 solution has not been reported to the best of our knowledge. Even though the solvation structure of Mg²⁺ in G4 is unknown, it has been reported that Mg²⁺ adopted distorted octahedral coordination and existed as [Mg(G2)₂]²⁺ and [Mg(G3)₂]²⁺ in G2 and G3 solutions, respectively.^20,21 By combining IR spectroscopy and DFT calculations, Fujii et al. proposed that the solvated [Mg(G2)₂]²⁺ ion would exist as a fac-isomer, where the three oxygens of the G2 molecules situate on three vertices of the octahedron's face.²¹ Nonetheless, G2 is a tridentate ligand, and the solvated [Mg(G2)₂]²⁺ can exist as a fac- or mer-isomer, which might exhibit different stability in solution. Structural models for the fac- and mer-[Mg(G2)₂]²⁺ isomers were created and reconsidered in our study. The structural optimisation with the SCAN-rVV10 functional shows that mer-[Mg(G2)₂]²⁺ is more stable than the fac-isomer by 37.7 kJ mol⁻¹ (Fig. S2, ESI†), which would be the favoured isomer to be found in solution. Due to its small size, Mg²⁺ cannot adopt a coordination number greater than six in glyme-based electrolytes. The addition of the seventh oxygen to the coordination sphere of Mg²⁺ would lead to repulsion between the organic chains and destabilize the structure. Consequently, the solvation structures of Mg²⁺ in some of the higher-order glymes are just the derivatives of mer-[Mg(G2)₂]²⁺. In the triglyme molecule, H₃CO(CH₂CH₂O)₃CH₃, there are four oxygens available for the complexation. Mg²⁺ in a G3 solution can achieve octahedral coordination in the form of [3 + 3] by forming the mer-[Mg(G3)₂]²⁺ isomer, where each G3 molecule donates three of its oxygens, as demonstrated in the work of Kimura et al.²⁰

Tetraglyme, H₃CO(CH₂CH₂O)₄CH₃, is a particular case that has a pronounced chelating effect on Mg²⁺. By using Raman spectroscopy, Watkins et al. demonstrated that a low-melting solvate ionic liquid with a G4/Mg(TFSI)₂ ratio of 1/1 had no signature of the Mg–TFSI interaction.³² The absence of the Mg–TFSI vibration in the Raman spectrum implies that Mg²⁺ can be completely solvated in the Mg²⁺/G4 ratio of 1/1; nonetheless, the structure of [Mg(G4)]²⁺ is unknown. The structural optimisation with the SCAN-rVV10 functional shows that Mg²⁺ in [Mg(G4)]²⁺ resides in a distorted pyramidal site with five Mg–O distances of 1.99, 2.01, 2.03, and 2.04 (×2) Å (Fig. 3). Furthermore, the addition reaction of G4 to [Mg(G4)]²⁺ is exothermic (Table S5, ESI†) so that the formation of [Mg(G4)₂]²⁺ could occur easily in a dilute solution. The structural optimisation shows that [Mg(G4)₂]²⁺ would adopt a structure similar to that of mer-[Mg(G2)₂]²⁺, in which two G4 molecules run perpendicular to each other, and each G4 donates three oxygens to form a [3 + 3] coordination site (Fig. 3). By using Raman spectroscopy, Terada et al. suggested that in 0.5 M Mg(TFSI)₂/G4 solution Mg²⁺ ions would exist as [Mg(G4)_y]²⁺ (y > 1), but they did not provide any structural information on this solvation form.³³ Nevertheless, the form that they observed could be the mer-[Mg(G4)₂]²⁺ isomer as described here. In pentaglyme and higher-order glymes, the molecule would have a sufficient amount of oxygen to ensure octahedral coordination for Mg²⁺, and only one molecule will be present in the first coordination sphere of Mg²⁺ (Fig. S3, ESI†). The computational results reveal that the Mg–O interaction and the ring deformation energy in [Mg(G5)]²⁺ are completely comparable to those of mer-[Mg(G4)₂]²⁺ with −1659 vs. −1691 kJ mol⁻¹ for the former and 113 vs. 130 kJ mol⁻¹ for the latter (Fig. S3, ESI†), which promotes the formation of [Mg(G5)]²⁺ in G5 solution.

Fig. 3 Optimised structures of [Mg(G4)]²⁺ and mer-[Mg(G4)₂]²⁺ calculated with the SCAN-rVV10 functional.

Ca²⁺ solvation structure

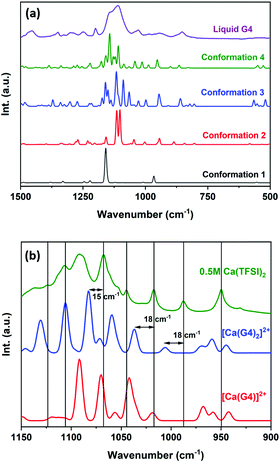
As in the case of Mg²⁺, the solvation structure of Ca²⁺ in G4 solution is unknown. Nonetheless, the G4-chelated structure of Ca²⁺ in the solid phase, such as [Ca(G4)](SCN)₂·H₂O, has been reported in the literature.³⁴ Ca²⁺ in [Ca(G4)](SCN)₂·H₂O has a coordination number of eight, and it resides in the centre of the G4 ring with five Ca–O distances of 2.46, 2.49 (×3), and 2.50 Å. One SCN⁻ ion occupies the coordination site below the ring with a Ca–N distance of 2.49 Å. The other two coordination sites are occupied by one SCN⁻ ion and one H₂O molecule with Ca–N and Ca–O distances of 2.44 and 2.42 Å. By performing extended X-ray absorption fine structure (EXAFS) analysis at the Ca K-edge energy, Hahn et al. reported that solvated Ca²⁺ in G1, G2, and G3 solutions also has a coordination number of eight; nonetheless, there are no refined structures of these solvated ions.³⁵ Due to a lack of relevant information, the Ca²⁺ solvation structure in G4 solution is determined in this study by a combination of IR spectroscopy and DFT calculations.

Several solutions of Ca(TFSI)₂ in tetraglyme with a concentration of 0–0.5 M were prepared to determine the Ca²⁺ solvation structure. The IR spectrum of pure liquid G4 recorded at ambient temperature shows several broad signals (Fig. 4a). In reality, G4 molecules can exist in several conformations in the liquid state due to a small energy barrier for rotation around the C–C and C–O bonds. The computed IR spectra of four representative conformations of G4 (Fig. S4, ESI†) show distinct vibrations for each of them, especially in the range of 1000–1200 cm⁻¹, corresponding to the C–H and C–O bonds’ stretching modes. Nevertheless, the IR signals recorded for liquid G4 are broad due to different G4 conformations. The signal broadening is likely linked to the significant amount of conformations that cannot be resolved by IR spectroscopy and a rapid transformation between different conformations in the liquid state. By comparing the theoretical and experimental IR spectra, one can note that the linear conformation of G4 is not present in a large amount in solution while tilted conformations are the dominant ones. Upon adding Ca(TFSI)₂ in liquid G4, Ca²⁺–G4 complexation occurs together with an increase in the intensity of specific IR lines corresponding to the G4 conformation complexing to Ca²⁺. The IR spectra of Ca(TFSI)₂ in G4 show the appearance of several distinct vibrations in the range of 1000–1200 cm⁻¹ (Fig. 4b), corresponding to the C–H and C–O stretching modes of the G4 conformation complexing to Ca²⁺, thus providing valuable information for the determination of the Ca²⁺ solvation structure. Furthermore, the monotonic evolution in the vibrations’ intensity (Fig. S5, ESI†) implies that the Ca²⁺ solvation structure in G4 is mostly unchanged in the 0.1–0.5 M concentration range.

Fig. 4 (a) Computed IR spectra with the SCAN-rVV10 functional of the four representative conformations of the G4 molecule compared to the experimental spectrum recorded for liquid G4 at ambient temperature. (b) Computed IR spectra with the SCAN-rVV10 functional of [Ca(G4)]²⁺ and mer-[Ca(G4)₂]²⁺ in [4 + 4] solvation coordination as compared to the experimental spectrum acquired for a 0.5 M Ca(TFSI)₂ solution in G4.

The most simple solvation model that can exist is [Ca(G4)]²⁺ as in the case of [Ca(G4)](SCN)₂·H₂O. The optimised structure of [Ca(G4)]²⁺ reveals that the G4 molecule forms a nearly flat ring, where Ca²⁺ fits perfectly in the ring's centre with five Ca–O distances of 2.30, 2.32, 2.33, and 2.37 (×2) Å (Fig. 5); nonetheless, Ca²⁺ in [Ca(G4)]²⁺ is under coordinated. Ca²⁺ in [Ca(G4)](SCN)₂·H₂O attracts other ligands in the structure to coordination sites above and below the G4 ring to achieve a coordination of eight. Therefore, [Ca(G4)]²⁺ might not be the optimum solvation for Ca²⁺ in a G4 solution where a surplus of G4 is available. Furthermore, the addition reaction of G4 to [Ca(G4)]²⁺ is highly exothermic (by −209 kJ mol⁻¹) (Table S5, ESI†), which highly favours the formation of [Ca(G4)₂]²⁺ in solution. Different [Ca(G4)₂]²⁺ solvation models are generated with a coordination number of Ca²⁺ varying from six to eight. The stability of [Ca(G4)₂]²⁺ increases with its coordination number due to a higher number of Ca–O bonds surrounding a Ca²⁺ centre (Fig. 5). The models with more than eight oxygens participating in the Ca²⁺ complexation are unstable, and they converge to a structure with a coordination number of eight during the structural relaxation procedure. Two solvation structures satisfying a coordination number of eight are the [5 + 3] and [4 + 4] models, in which the latter is more stable (Fig. 5).

Fig. 5 Optimised structures of [Ca(G4)]²⁺ and [Ca(G4)₂]²⁺ with the SCAN-rVV10 functional. The relative energy between different forms of [Ca(G4)₂]²⁺ is given for stability comparison.

To confirm the existence of [Ca(G4)₂]²⁺ in the form of [4 + 4] in solution, theoretical IR spectra of [Ca(G4)]²⁺ and [Ca(G4)₂]²⁺ are calculated and compared to the experimental spectrum acquired for a 0.5 M Ca(TFSI)₂ solution. The theoretical IR spectra of [Ca(G4)]²⁺ and [Ca(G4)₂]²⁺ show many similarities, except the vibrations at 1100 and 1150 cm⁻¹, which only exist in [Ca(G4)₂]²⁺ with [4 + 4] coordination (Fig. 4b). The computed IR spectrum of [Ca(G4)₂]²⁺ fits well with the new vibrations observed in a 0.5 M Ca(TFSI)₂ solution (Fig. 4b) with a global shift of 15–18 cm⁻¹ compared to the experimental data. If a small scaling factor of 0.986 is applied, excellent agreement is obtained, which thus confirms the existence of [Ca(G4)₂]²⁺ in the [4 + 4] form (Fig. S6, ESI†). The [Ca(G4)₂]²⁺ structure is quite similar to the mer-[Mg(G2)₂]²⁺ isomer: two G4 chains, wrapping around the Ca²⁺ centre, orient along two perpendicular meridians, just like the Earth's Prime-Meridian and Equator. Only four oxygens of each G4 chain participate in the coordination with the Ca²⁺ centre in the [4 + 4] form. The fifth oxygen on each G4 chain does not participate in the complexation and points away from the Ca²⁺ centre (Fig. 5). This conformation minimises the repulsion between the two G4 chains and ensures the maximum Ca–O interaction. Note that the potential energy surface of the system was not exhaustively sampled because of its complexity, and there might be some undetermined structures that also contribute to the observable properties, though the ones computed therein reasonably reproduce experimental data.

Na⁺ solvation structure

The chemistry of Na⁺ with glymes is very diverse. Na⁺ can form several solvate ionic liquids with different kinds of glyme, such as [Na(G1)₃][TFSI], [Na(G2)₂][TFSI], [Na(G3)][TFSI], and [Na(G3)₂][TFSI]. Furthermore, some of them can be used as stable electrolytes for SIBs.^36,37 Some liquid electrolytes can be crystallised at low temperatures, and their structures have been elucidated by the single-crystal X-ray diffraction technique. When glyme/Na⁺ is 1/1, such as [Na(G3)][TFSI], the glyme molecule encircles Na⁺, and the TFSI⁻ anions fill the coordination sites above and below the ring.³⁶ In [Na(G3)][TFSI], Na⁺ has a coordination of [4 + 3] where the four Na–O bonds with the G3 ring are 2.46, 2.47, 2.50, and 2.56 Å, and the other three coordinated oxygens come from two different TFSI⁻ with Na–O distances of 2.33, 2.42, and 2.43 Å. In [Na(G3)₂][TFSI], two G3 chains wrap around the Na⁺ centre, and the TFSI⁻ anions exist in the crystal in the form of a “solvent-separated ion pair” without any direct interaction with Na⁺.³⁶ It is interesting to note that two G3 chains wrap around Na⁺ in [Na(G3)₂][TFSI], oriented along two perpendicular meridians,³⁶ as in mer-[Ca(G4)₂]²⁺. The actual coordination sphere of Na⁺ in G4 solution has not been determined experimentally. Nevertheless, the coordination number of Na⁺ is already saturated with two G3 molecules in the [4 + 4] form, and no more oxygen can enter the Na⁺ solvation structure. Therefore, it can be predicted that Na⁺ exists in G4 solution in the form of mer-[Na(G4)₂]⁺ (Fig. 6), whose structure is identical to mer-[Ca(G4)₂]²⁺.

Fig. 6 Optimised structures of [M(G4)]⁺ and [M(G4)₂]⁺ (M = Na and K) calculated with the SCAN-rVV10 functional.

K⁺ solvation structure

It has long been know that G4 can dissolve K metal at ambient temperature to result in solvated K⁺ ions;³⁸ nevertheless, little information is known on the solvation structure of K⁺ in G4 or glyme-based solutions. The ionic radius of K⁺ is bigger than Na⁺ and Ca²⁺; hence, the K⁺ solvation structure cannot adopt coordination less than eight. K⁺ in [K(G4)⁺] cannot fit into the G4 cavity and puckers out of the ring, thus creating space for one more G4 molecule to enter its solvation sphere to form [K(G4)₂]⁺ (Fig. 6). In [K(G4)₂]⁺, two G4 chains also run perpendicular to each other to form mer-[K(G4)₂]⁺ with [4 + 4] coordination (Fig. 6). The encapsulation of two G4 chains in the mer-[M(G4)₂]ⁿ⁺ isomer not only reduces the repulsion between the chains but also has great flexibility to adapt to the size of most ions.

Relative stability of solvated [M(G4)_x]ⁿ⁺ complexes and their electrochemical activity

The energy of the M–O bonds involved in a particular solvated [M(G4)_x]ⁿ⁺ complex can be evaluated by the relation , m being the number of M–O bonds and G4 (PCM) being the G4 in a PCM in the same geometry as in the [M(G4)_x]ⁿ⁺ complex to remove any strain effect. The strength of the M–O bonds in [M(G4)_x]ⁿ⁺ decreases in the order E_Mg–O > E_Ca–O > E_Li–O > E_Na–O > E_K–O (Table 1). In this series, the strength of the M–O bonds depends significantly on the charge of the ion. The M–O bonds of divalent ions, e.g. Mg²⁺ and Ca²⁺, are much more stable than monovalent ions, which is expected from a purely electrostatic consideration. Among the ions bearing the same charge, the strength of the M–O bonds depends inversely on the ionic size of the central ion Mⁿ⁺. The larger the size of the central ion, the softer the cation (the lower the charge density), and thus the interaction involved with the hard O-atom in the M–O bonds becomes weaker, as can be seen in the pairs Mg–O vs. Ca–O and Li–O vs. Na–O vs. K–O (Table 1). Compared to a free G4 molecule in the solution, the coordinating G4 molecules in the [M(G4)_x]ⁿ⁺ complexes have to undergo structural reorganization to orient their oxygen atoms to proper positions for the coordination to the central cation, and this structural reorganization induces strain that consumes energy. Nevertheless, the formation of M–O bonds can partially compensate for the energy loss in G4 deformation and favour complexation. The stress is greater on the G4 backbone in [Li(G4)]⁺ (Table 1) due to the tiny size of Li⁺, while energy is gained by a fifth oxygen coordination to the central Li⁺. The comparison between the [M(G4)]ⁿ⁺ (M = Na, K, Mg, and Ca) ion and its [M(G4)₂]ⁿ⁺ counterpart shows that the gain in the total number of M–O interactions stabilizes the di-solvated system over the mono-solvated one (Table 1). In some particular cases, the proportion of the strain energy to the total M–O interaction is reduced in [M(G4)₂]ⁿ⁺, and thus the enthalpy is the dominant factor that promotes the formation of [M(G4)₂]ⁿ⁺ in solution. Nevertheless, the entropy of the system decreases when the second G4 molecule participates in the solvation with [M(G4)]ⁿ⁺ because of the reduction of free molecules in the solvent and the reduction in the possible conformations of the complexing G4. For each [M(G4)]ⁿ⁺/[M(G4)₂]ⁿ⁺ pair, a critical temperature should exist and beyond this point the entropy factor becomes dominant, and favours the mono-solvated [M(G4)]ⁿ⁺.

Table 1 Energy of M–O bonds in solvated [M(G4)_x]ⁿ⁺ (x = 1 or 2) and the energy required for the G4 deformation calculated with the SCAN-rVV10 functional in the VASP code. The coordination number of each central ion is indicated in square brackets

	Total M–O energy (kJ mol^−1)	Energy per M–O bond (kJ mol^−1)	Strain energy for G4 (kJ mol^−1)	Percentage of G4 strain energy compared to M–O energy
[Li(G4)]^+ [5]	−542.8	−108.6	72.6	13.4
[Na(G4)]^+ [5]	−453.4	−90.7	55.6	12.3
[Na(G4)2]^+ [4 + 4]	−569.0	−71.1	55.7	9.8
[K(G4)]^+ [5]	−323.1	−64.6	18.1	5.6
[K(G4)2]^+ [4 + 4]	−434.0	−54.3	44.3	10.2
[Mg(G4)]^2+ [5]	−1529.1	−305.8	100.2	6.6
[Mg(G4)2]^2+ [3 + 3]	−1691.3	−211.4	130.1	7.7
[Ca(G4)]^2+ [5]	−1189.9	−238.0	82.4	6.9
[Ca(G4)2]^2+ [4 + 4]	−1463.0	−182.9	97.5	6.7

---

In terms of electrochemistry, the solutions of Li⁺, Na⁺, and K⁺ in G4 are commonly used as electrolytes for rechargeable batteries, and many of them employ TFSI⁻ sources.^39–43 The facility in the plating and stripping reactions of these monovalent ions in G4 solutions could be linked to the low M⁺–O interaction energy (Table 1). The electrochemical evaluation of Mg(TFSI)₂ in G4 is also known, but it is pretty tricky to perform. The Mg(TFSI)₂/G4 electrolyte must be treated with activated molecular sieves, or additives such as Mg(BH₄)₂ must be used; otherwise, electrode passivation occurs immediately.^33,44 The electrochemical behaviour of diluted Ca(TFSI)₂ in G4 has not been reported; nevertheless, Hahn et al. have conducted a Ca plating and stripping experiment with a 0.5 M Ca(TFSI)₂ solution in G1 and G3.³⁵ In the G1 solution, no reversible Ca electrodeposition and stripping were observed. The authors explained this observation by the fact that most Ca²⁺ ions in 0.5 M Ca(TFSI)₂/G1 exist in the form of a “contact ion pair” with TFSI⁻ and during reduction the coordinated TFSI⁻ ion in the “contact ion pair” becomes susceptible to degradation and then passivates the electrode. By replacing TFSI⁻ with a weaker coordinating anion, e.g. tetrakis(hexafluoroisopropoxy)borate [B(hfip)₄]⁻, all Ca²⁺ ions exist as [Ca(G1)₄]²⁺ and thus the authors succeeded in performing reversible Ca plating and stripping in G1 solution. Nevertheless, the situation in G3 solution is even more complicated. No electrochemical activity is detected for 0.5 M Ca(TFSI)₂ or Ca(BHFIP)₂ in G3, while all the structural analyses show that all Ca²⁺ ions in these solutions only exist as solvated [Ca(G3)₂]²⁺. The same authors speculated that the interaction in [Ca(G3)₂]²⁺ is so strong that desolvation could hardly occur, and the electrode reaction might suffer exceptionally sluggish desolvation kinetics.³⁵ The solvation structure of [Ca(G3)₂]²⁺ shows many similarities to [Ca(G4)₂]²⁺, where Ca²⁺ has a coordination number of [4 + 4], and the mer-isomer is the more stable one. Therefore, one could expect that the electrochemical property of [Ca(G4)₂]²⁺ is similar to that of [Ca(G3)₂]²⁺, which means that Ca²⁺ is strongly solvated in both cases with no reversible Ca plating and stripping reactions regardless of the nature of the anions. In order to promote desolvation and activate the electrochemical property of [Ca(G3)₂]²⁺ and [Ca(G4)₂]²⁺, one should consider all the possibilities to weaken the Ca–O binding energy or reduce the number of solvent molecules present in the first coordination sphere. The following considerations can be taken into account:

• Employing perfluoro-G4 as a solvent or additive: Ca²⁺ in [Ca(G3)₂]²⁺ and [Ca(G4)₂]²⁺ is coordinated by eight oxygens coming from two different G3/G4 molecules, and during the electrode reaction these two molecules have to be desolvated concomitantly. As each G3/G4 chain anchors to Ca²⁺ by four Ca–O bonds and the two molecules wrap around the central ion in a perfect arrangement leaving little space for Ca²⁺ to escape (Fig. 5), the desolvation from [Ca(G3)₂]²⁺ and [Ca(G4)₂]²⁺ would require a high activation energy. In perfluoro-G4, all the hydrogens are replaced by fluorine, and these fluorine atoms possess lone pairs, which can also coordinate to the central ion, and thus a perfluoro-G4 molecule is sufficient to complete the solvation sphere of Ca²⁺ (Fig. 7). Consequently, the desolvation of Ca²⁺ from [Ca(perfluoro_G4)]²⁺ would require the departure of one solvent molecule. Furthermore, the calculations performed at the same dielectric constant value (ε_r = 7.5) show that the Ca–O/F interaction energy in [Ca(perfluoro_G4)]²⁺ is weaker than the Ca–O interaction energy in [Ca(G4)₂]²⁺ (−772 kJ mol⁻¹vs. −1463 kJ mol⁻¹). This interaction energy might be strong enough to promote the dissolution of Ca(TFSI)₂ salt but does not impede the desolvation of [Ca(perfluoro_G4)]²⁺ during the electrode reactions.

Fig. 7 The solvation structure of Ca²⁺ in perfluoro-G4. Ca²⁺ is solvated by five oxygens at Ca–O distances of 2.40–2.98 Å and three fluorines at Ca–F distances of 2.35–2.54 Å.

• Employing [Ca(G4)]²⁺ as an electroactive species. Up to now, we just consider the mer-[Ca(G4)₂]²⁺ isomer, which is the most favourable solvation form of Ca²⁺ in dilute solutions in G4, in all discussions. Ca²⁺ can also exist as [Ca(G4)]²⁺ in G4-deficient conditions or perhaps in an equimolar mixture of Ca(TFSI)₂ and G4. When participating in an electrode reaction, the Ca²⁺ desolvation from [Ca(G4)]²⁺ only requires the rupture of five Ca–O bonds. Moreover, the total Ca–O interaction in [Ca(G4)]²⁺ is weaker than in [Ca(G4)₂]²⁺ (Table 1), which is a great advantage for the use of [Ca(G4)]²⁺. Many studies have shown that when mixed in equimolar conditions at elevated temperature and then cooled down to ambient temperature, solvate structures of [Li(G4)](TFSI), [Na(G4)](TFSI) and [Mg(G4)](TFSI)₂ can be obtained. These compounds are solid at ambient temperature but become liquid at elevated temperature, and they can thus be used as solvents for reactions or electrolytes for batteries.^33,37,45 No such study has been explored for the Ca(TFSI)₂–G4 binary system, which can be the goal for future investigations. Derivatives of G4, obtained by attaching different functional groups on the G4 chain, can also be used to stabilize solvate ionic liquids based on Ca(TFSI)₂. The presence of functional groups might help to reduce the melting point of [Ca(derivative-G4)](TFSI)₂, if existing, making it become liquid at ambient temperature, which is a necessity for a battery electrolyte. Furthermore, these functional groups can also protect G4 from degradation in electrochemical reactions.

These mentioned considerations could be taken into account in the development of new glyme-based electrolytes, especially those for Ca-ion batteries. The solvation energy is an essential factor to the performance of the electrolyte, which should be strong enough to promote the formation of solvated ions but not impede ion desolvation in the electrode reactions.

Conclusions

This study has demonstrated that equivalent conclusions can be extracted from molecular modelling performed with the Q-Chem and VASP codes. Furthermore, the results show that dispersion corrections are required to obtain better structural descriptions and reaction enthalpies. The structures and energetic values computed with the PBE-D3 and SCAN-rVV10 functionals are all equivalent; nevertheless, the SCAN-rVV10 functional is required to obtain accurate information on the topology of the potential energy surface and the phonons. We have also demonstrated the possibility of combining IR spectroscopy with theoretical modelling to identity the solvation structure of Ca²⁺ in G4 solution, which can further be applied to determine solvation structures in other glyme-based solutions. The solvation structures of some alkali and alkaline earth metals in G4 were also revised and compared systematically. Li⁺ has a small size, and [Li(G4)]⁺ exhibits an unusual structure where Li⁺ adopts a coordination number of five. Mg²⁺ exhibits structural flexibility in G4, where it can adopt a five-coordination site, [Mg(G4)]²⁺, in G4-deficient conditions and a six-coordination site, [Mg(G4)₂]²⁺, in dilute solution. Na⁺, K⁺, and Ca²⁺ with large ionic radii tend to adopt eight-coordination sites, and their solvation structures in G4 can all be described by the mer-[M(G4)₂]ⁿ⁺ isomer, where two G4 chains orient themselves on two perpendicular meridians. The solutions of LiTFSI, NaTFSI, KTFSI, and Mg(TFSI)₂ in G4 can be used as electrolytes for rechargeable batteries. The electrochemical activity of Ca(TFSI)₂ in G4 has not been observed, which could be due to the strong Ca–O interaction and the participation of two G4 molecules in the first coordination sphere. Nevertheless, the functionalization of the G4 molecule and the investigation of solvate liquid electrolytes based on Ca(TFSI)₂ and G4 binary mixtures could be the solution to bypass current difficulties. Due to its medium chain length, the G4 molecule has a particular structural property, which is a transition between molecular and polymer glymes. Therefore, the solvation structures in G4 represent those that can exist in more sophisticated glymes, and they can also be used as starting models to construct the solvation sphere in polyethylene oxide. Furthermore, the electrochemical window and the decomposition mechanisms of these glyme-solvated ions can be investigated through interface potential-dependent DFT calculations in upcoming studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the European FET-Open project VIDICAT (Grant Agreement: 829145) including the Post-doctoral Fellowship of L. H. B. N. Part of the computations were performed using HPC resources from GENCI-CINES (grant 2020-A0080910369).

References

1. J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414, 359–367.
2. V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Na-ion batteries, recent advances and present challenges to become low cost energy storage systems, Energy Environ. Sci., 2012, 5, 5884–5901.
3. K. M. Abraham, How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts?, ACS Energy Lett., 2020, 5, 3544–3547.
4. J. M. Tarascon, Na-ion versus Li-ion Batteries: Complementarity Rather than Competitiveness, Joule, 2020, 4, 1616–1620.
5. I. Hasa, S. Mariyappan, D. Saurel and P. Adelhelm, Challenges of today for Na-based batteries of the future: From materials to cell metrics, J. Power Sources, 2021, 482, 228872.
6. Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Promises and Challenges of Next-Generation “Beyond Li-ion” Batteries for Electric Vehicles and Grid Decarbonization, Chem. Rev., 2021, 121, 1623–1669.
7. S. Gheytani, Y. Liang, F. Wu, Y. Jing, H. Dong, K. K. Rao, X. Chi, F. Fang and Y. Yao, An Aqueous Ca-Ion Battery, Adv. Sci., 2017, 4, 1700465.
8. L. Stievano, I. de Meatza, J. Bitenc, C. Cavallo, S. Brutti and M. A. Navarra, Emerging calcium batteries, J. Power Sources, 2021, 482, 228875.
9. I. E. Kelly, J. R. Owen and B. C. H. Steele, Poly(ethylene oxide) electrolytes for operation at near room temperature, J. Power Sources, 1985, 14, 13–21.
10. L. Long, S. Wang, M. Xiao and Y. Meng, Polymer electrolytes for lithium polymer batteries, J. Mater. Chem. A, 2016, 4, 10038–10069.
11. T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291.
12. N. N. Rajput, T. J. Seguin, B. M. Wood, X. Qu and K. A. Persson, Elucidating Solvation Structures for Rational Design of Multivalent Electrolytes—A Review, Springer International Publishing, 2018, vol. 376.
13. J. D. Forero-Saboya, E. Marchante, R. B. Araujo, D. Monti, P. Johansson and A. Ponrouch, Cation Solvation and Physicochemical Properties of Ca Battery Electrolytes, J. Phys. Chem. C, 2019, 123, 29524–29532.
14. J. Forero-Saboya, C. Davoisne, R. Dedryvère, I. Yousef, P. Canepa and A. Ponrouch, Understanding the nature of the passivation layer enabling reversible calcium plating, Energy Environ. Sci., 2020, 13, 3423–3431.
15. N. S. Katorova, S. S. Fedotov, D. P. Rupasov, N. D. Luchinin, B. Delattre, Y. M. Chiang, A. M. Abakumov and K. J. Stevenson, Effect of Concentrated Diglyme-Based Electrolytes on the Electrochemical Performance of Potassium-Ion Batteries, ACS Appl. Energy Mater., 2019, 2, 6051–6059.
16. D. Di Lecce, L. Minnetti, D. Polidoro, V. Marangon and J. Hassoun, Triglyme-based electrolyte for sodium-ion and sodium-sulfur batteries, Ionics, 2019, 25, 3129–3141.
17. D. Di Lecce, L. Carbone, V. Gancitano and J. Hassoun, Rechargeable lithium battery using non-flammable electrolyte based on tetraethylene glycol dimethyl ether and olivine cathodes, J. Power Sources, 2016, 334, 146–153.
18. Y. Orikasa, T. Masese, Y. Koyama, T. Mori, M. Hattori, K. Yamamoto, T. Okado, Z. D. Huang, T. Minato, C. Tassel, J. Kim, Y. Kobayashi, T. Abe, H. Kageyama and Y. Uchimoto, High energy density rechargeable magnesium battery using earth-abundant and non-toxic elements, Sci. Rep., 2014, 4, 1–6.
19. K. V. Nielson, J. Luo and T. L. Liu, Optimizing Calcium Electrolytes by Solvent Manipulation for Calcium Batteries, Batteries Supercaps, 2020, 3, 766–772.
20. T. Kimura, K. Fujii, Y. Sato, M. Morita and N. Yoshimoto, Solvation of Magnesium Ion in Triglyme-Based Electrolyte Solutions, J. Phys. Chem. C, 2015, 119, 18911–18917.
21. K. Fujii, M. Sogawa, N. Yoshimoto and M. Morita, Structural Study on Magnesium Ion Solvation in Diglyme-Based Electrolytes: IR Spectroscopy and DFT Calculations, J. Phys. Chem. B, 2018, 122, 8712–8717.
22. S. Tsuzuki, T. Mandai, S. Suzuki, W. Shinoda, T. Nakamura, T. Morishita, K. Ueno, S. Seki, Y. Umebayashi, K. Dokko and M. Watanabe, Effect of the cation on the stability of cation–glyme complexes and their interactions with the [TFSA]− anion, Phys. Chem. Chem. Phys., 2017, 19, 18262–18272.
23. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways, J. Chem. Phys., 2014, 140, 0–8.
24. N. Lespes and J. S. Filhol, Using Implicit Solvent in Ab Initio Electrochemical Modeling: Investigating Li+/Li Electrochemistry at a Li/Solvent Interface, J. Chem. Theory Comput., 2015, 11, 3375–3382.
25. A. Kopač Lautar, J. Bitenc, T. Rejec, R. Dominko, J. S. Filhol and M. L. Doublet, Electrolyte Reactivity in the Double Layer in Mg Batteries: An Interface Potential-Dependent DFT Study, J. Am. Chem. Soc., 2020, 142, 5146–5153.
26. A. K. Lautar, J. Bitenc, R. Dominko and J. S. Filhol, Building Ab Initio Interface Pourbaix diagrams to Investigate Electrolyte Stability in the Electrochemical Double Layer: Application to magnesium batteries, ACS Appl. Mater. Interfaces, 2021, 13, 8263–8273.
27. J. C. Lassègues, J. Grondin, C. Aupetit and P. Johansson, Spectroscopic identification of the lithium ion transporting species in LiTFSI-doped ionic liquids, J. Phys. Chem. A, 2009, 113, 305–314.
28. M. Herstedt, M. Smirnov, P. Johansson, M. Chami, J. Grondin, L. Servant and J. C. Lassègues, Spectroscopic characterization of the conformational states of the bis(trifluoromethanesulfonyl)imide anion (TFSI−), J. Raman Spectrosc., 2005, 36, 762–770.
29. F. M. Vitucci, F. Trequattrini, O. Palumbo, J.-B. Brubach, P. Roy and A. Paolone, Infrared spectra of bis(trifluoromethanesulfonyl)imide based ionic liquids: Experiments and DFT simulations, Vib. Spectrosc., 2014, 74, 81–87.
30. S. Saito, H. Watanabe, Y. Hayashi, M. Matsugami, S. Tsuzuki, S. Seki, J. N. Canongia Lopes, R. Atkin, K. Ueno, K. Dokko, M. Watanabe, Y. Kameda and Y. Umebayashi, Li+ Local Structure in Li-Tetraglyme Solvate Ionic Liquid Revealed by Neutron Total Scattering Experiments with the 6/7Li Isotopic Substitution Technique, J. Phys. Chem. Lett., 2016, 7, 2832–2837.
31. S. Tsuzuki, W. Shinoda, S. Seki, Y. Umebayashi, K. Yoshida, K. Dokko and M. Watanabe, Intermolecular interactions in Li+-glyme and Li+-glyme-TFSA- complexes: Relationship with physicochemical properties of [Li(glyme)][TFSA] ionic liquids, ChemPhysChem, 2013, 14, 1993–2001.
32. T. Watkins and D. A. Buttry, Determination of Mg²⁺ Speciation in a TFSI⁻-Based Ionic Liquid with and Without Chelating Ethers Using Raman Spectroscopy, J. Phys. Chem. B, 2015, 119, 7003–7014.
33. S. Terada, T. Mandai, S. Suzuki, S. Tsuzuki, K. Watanabe, Y. Kamei, K. Ueno, K. Dokko and M. Watanabe, Thermal and electrochemical stability of tetraglyme-magnesium bis(trifluoromethanesulfonyl)amide complex: Electric field effect of divalent cation on solvate stability, J. Phys. Chem. C, 2016, 120, 1353–1365.
34. Y. Y. Wei, B. Tinant, J. P. Declercq, M. Van Meerssche and J. Dale, Oligoether complexes of alkaline-earth metal ions. I. Structures of 2,5,8,11,14-pentaoxapentadecane (‘tetraglyme’) complexed with calcium, strontium and barium thiocyanates, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 1076–1080.
35. N. T. Hahn, D. M. Driscoll, Z. Yu, G. E. Sterbinsky, L. Cheng, M. Balasubramanian and K. R. Zavadil, Influence of Ether Solvent and Anion Coordination on Electrochemical Behavior in Calcium Battery Electrolytes, ACS Appl. Energy Mater., 2020, 3, 8437–8447.
36. P. Geysens, V. S. Rangasamy, S. Thayumanasundaram, K. Robeyns, L. Van Meervelt, J. P. Locquet, J. Fransaer and K. Binnemans, Solvation Structure of Sodium Bis(fluorosulfonyl)imide-Glyme Solvate Ionic Liquids and Its Influence on Cycling of Na-MNC Cathodes, J. Phys. Chem. B, 2018, 122, 275–289.
37. T. Mandai, R. Nozawa, S. Tsuzuki, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phase diagrams and solvate structures of binary mixtures of glymes and Na salts, J. Phys. Chem. B, 2013, 117, 15072–15085.
38. J. Grobelny, M. Sokól and Z. J. Jedliński, Complexation of potassium cations by tetraglyme and 18-crown-6 as evidenced by 39K NMR spectroscopy, Magn. Reson. Chem., 1991, 29, 679–680.
39. X. Liu, M. Zarrabeitia, B. Qin, G. A. Elia and S. Passerini, Cathode-Electrolyte Interphase in a LiTFSI/Tetraglyme Electrolyte Promoting the Cyclability of V2O5, ACS Appl. Mater. Interfaces, 2020, 12, 54782–54790.
40. X. Liu, G. A. Elia, X. Gao, B. Qin, H. Zhang and S. Passerini, Highly Concentrated KTFSI: Glyme Electrolytes for K/Bilayered-V2O5 Batteries, Batteries Supercaps, 2020, 3, 261–267.
41. R. Zhang, J. Bao, Y. Pan and C. F. Sun, Highly reversible potassium-ion intercalation in tungsten disulfide, Chem. Sci., 2019, 10, 2604–2612.
42. R. Zhang, J. Bao, Y. Wang and C. F. Sun, Concentrated electrolytes stabilize bismuth-potassium batteries, Chem. Sci., 2018, 9, 6193–6198.
43. K. Hashimoto, S. Suzuki, M. L. Thomas, T. Mandai, S. Tsuzuki, K. Dokko and M. Watanabe, Magnesium bis(trifluoromethanesulfonyl)amide complexes with triglyme and asymmetric homologues: Phase behavior, coordination structures and melting point reduction, Phys. Chem. Chem. Phys., 2018, 20, 7998–8007.
44. Z. Ma, M. Kar, C. Xiao, M. Forsyth and D. R. MacFarlane, Electrochemical cycling of Mg in Mg[TFSI]2/tetraglyme electrolytes, Electrochem. Commun., 2017, 78, 29–32.
45. T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Criteria for solvate ionic liquids, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02939h

---