Kinetics of the gas phase reaction of the Criegee intermediate CH₂OO with SO₂ as a function of temperature

Abstract

The kinetics of the gas phase reaction of the Criegee intermediate CH₂OO with SO₂ have been studied as a function of temperature in the range 223–344 K at 85 Torr using flash photolysis of CH₂I₂/O₂/SO₂/N₂ mixtures at 248 nm coupled to time-resolved broadband UV absorption spectroscopy. Measurements were performed under pseudo-first-order conditions with respect to SO₂, revealing a negative temperature dependence. Analysis of experimental results using the Master Equation Solver for Multi-Energy well Reactions (MESMER) indicates that the observed temperature dependence, combined with the reported lack of a pressure dependence in the range 1.5–760 Torr, can be described by a reaction mechanism consisting of the formation of a pre-reaction complex leading to a cyclic secondary ozonide which subsequently decomposes to produce HCHO + SO₃. The temperature dependence can be characterised by k_CH2OO+SO2 = (3.72 ± 0.13) × 10⁻¹¹ (T/298)^{(−2.05±0.38)} cm³ molecule⁻¹ s⁻¹. The observed negative temperature dependence for the title reaction in conjunction with the decrease in water dimer (the main competitor for the Criegee intermediate) concentration at lower temperatures means that Criegee intermediate chemistry can play an enhanced role in SO₂ oxidation in the atmosphere at lower temperatures.

---

Introduction

Criegee intermediates are reactive species produced in the atmosphere following the ozonolysis of unsaturated volatile organic compounds (VOCs) in environments impacted by biogenic and/or anthropogenic emissions.^1,2 The exothermicity associated with ozonolysis reactions leads to the formation of nascent Criegee intermediates with high internal energy, which may undergo either unimolecular decomposition or collisional energy transfer with surrounding gas molecules to form stabilised Criegee intermediates (SCIs). Bimolecular reactions of stabilised Criegee intermediates with atmospheric constituents such as water vapour, water vapour dimers, NO₂, and SO₂ can impact atmospheric budgets of NO_x (NO + NO₂), SO₂, H₂SO₄, sulfate aerosol, and secondary organic aerosol, and thus influence air quality and climate.^3–9 Welz et al.⁴ reported the first direct measurements of SCI kinetics using the photolysis of CH₂I₂ at 248 nm in the presence of O₂ at low pressure (4 Torr) to generate the CH₂OO Criegee intermediate ((R1)-(R2)), coupled with tunable VUV synchrotron photoionisation mass spectrometry (PIMS) to probe CH₂OO:

CH₂I₂ + hν → CH₂I + I (R1)

CH₂I + O₂ → CH₂OO + I (R2)

Welz et al. reported a rate coefficient of (3.9 ± 0.7) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ for the reaction of CH₂OO with SO₂ at 298 K in 4 Torr of He, which is several orders of magnitude larger than previous estimates based on indirect measurements in ozonolysis reactions, with potentially significant impacts on our understanding of SO₂ oxidation in the atmosphere.¹

CH₂OO + SO₂ → HCHO + SO₃ (R3)

Following the work of Welz et al., a number of studies investigating the kinetics of (R3) have been performed at room temperature using the same photochemical source of CH₂OO (i.e. photolysis of CH₂I₂/O₂) but with different spectroscopic techniques used to detect either CH₂OO,^9–14 HCHO formed by reaction (R3),¹¹ or OH as a proxy for CH₂OO.^15,16 A summary of previous measurements of k₃, and techniques employed, is given in Table 1. The pressure dependence of the reaction was investigated by Stone et al.,¹¹ with a pressure independent rate coefficient of k₃ = (3.42 ± 0.42) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ reported over the pressure range 1.5–450 Torr. The good agreement between the results of all the photolytic experiments (Table 1) suggest that the rate coefficient k₃ is relatively well-characterised at room temperature and shows no significant pressure dependence in the range 1.5 to 760 Torr.¹⁷ The current IUPAC recommendations suggest a pressure independent rate coefficient of at 298 K.¹⁷ However, the temperature dependence of the CH₂OO + SO₂ reaction has yet to be reported, with such an investigation necessary to improve the understanding of the mechanism and atmospheric impacts of the reaction between CH₂OO and SO₂.

Table 1 Values for k₃ determined in photolytic experiments using a range of experimental techniques

Reference	Technique	Photolysis wavelength/nm	Temperature/K	Pressure/Torr	Bath gas	k 3/10^−11 cm^3 molecule^−1 s^−1
a LFP = laser flash photolysis of CH2I2 in the presence of O2. b PIMS = photoionisation mass spectrometry monitoring CH2OO. c UV absorption = time-resolved broadband ultraviolet absorption spectroscopy. d LIF = laser induced fluorescence. e CRDS = cavity ring down spectroscopy.
Welz et al. 2012^4	LFP^a/PIMS^b	248	298	4	He	3.9 ± 0.7
Sheps 2013^10	LFP/UV abs^c	266	295	5	He	4.1 ± 0.3
Stone et al. 2014^11	LFP/LIF^d HCHO	355	295	50–450	N2	3.42 ± 0.42
	LFP/PIMS	248	295	1.5	He
Liu et al. 2014^15	LFP/LIF OH	351	295	50–200	Ar	3.53 ± 0.29
Chhantyal-Pun et al. 2015^12	LFP/CRDS^e	355	295	30	N2	3.80 ± 0.04
Huang et al. 2015^13	LFP/UV abs	248	298	30–756	N2	3.57 ± 0.28
Liu et al. 2017^16	LFP/LIF OH	355	300	10	Ar	3.88 ± 0.13
Howes et al. 2019^9	LFP/PIMS	248	295	2	He	3.74 ± 0.43
	LFP/UV abs	248	295	50	N2	3.87 ± 0.45
Qiu and Tonokura^14 2019	LFP/mid-IR abs	266	295	10.4	N2	3.6 ± 0.1

---

Experimental studies employing LIF detection of HCHO produced in (R3)¹¹ suggest that HCHO and thus SO₃ are products of the reaction (R3), with the co-product SO₃ directly observed by PIMS¹⁸ at 4 Torr and transient infrared absorption spectroscopy at 110 and 214 Torr.¹⁹ Theoretical studies also indicate that HCHO and SO₃ are the dominant products under atmospheric conditions, formed via a five-membered secondary ozonide (SOZ) cycloadduct^5,20–22 and thus the SO₂-catalysed isomerisation of CH₂OO to formic acid via SOZ evidenced by Aplincourt and Rui-López²³ is a minor channel of the CH₂OO + SO₂ reaction. Experimental studies using PIMS¹⁸ and transient infrared absorption spectroscopy¹⁹ have not observed the reaction channel producing formic acid, also indicating that this channel is negligible. Vereecken et al.⁵ and Kuwata et al.²² have investigated the potential energy surface for the reaction between CH₂OO and SO₂, combined with Rice–Ramsperger–Kassel–Marcus (RRKM)/master equation simulations to predict product yields, but with contrasting results. Kuwata et al.²² predicted a yield for HCHO + SO₃ of at least 97% at atmospheric pressure, while Vereecken et al.⁵ predicted a yield of 68% HCHO + SO₃ at atmospheric pressure. Both studies report that the reaction is under the low-pressure regime, with negligible stabilisation of the SOZ up to pressures considerably above ambient conditions.^5,22 However, the mechanisms for formation of the SOZ and for the subsequent production of HCHO and SO₃ differ in the two theoretical studies. Vereecken et al.⁵ predicted barrierless formation of the SOZ in the initial CH₂OO + SO₂ encounter, with homolytic cleavage of the O–O bond in the SOZ yielding the biradical OCH₂OS(O)O, which in turn predominantly leads to HCHO and SO₃ by β-scission. The formation of formyl sulfinic acid, HC(=O)OS(=O)OH (15% at 1 atm) and bisoxy diradical, H₂C(O˙)O˙, + SO₂ (17% at 1 atm) by the decomposition of OCH₂OS(O)O was also expected by Vereecken et al.⁵ In contrast, Kuwata et al.²² characterised the barrierless formation of a pre-reaction complex in the first reaction step, which then leads to the SOZ, with the reaction predominantly following a closed-shell pathway involving the direct formation of HCHO + SO₃ from the SOZ by cycloreversion, in qualitative agreement with the earlier studies of Jiang et al.²⁰ and Kurtén et al.²¹ Kuwata et al.²² employed a complex description of the potential energy surface, incorporating two distinct stereochemical pathways owing to the existence of diastereomeric endo and exo conformers of the SOZ. By combining the quantum chemical calculations with statistical rate theory models Kuwata et al.²² predicted that k₃ = (3.68 ± 0.02) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ at 295 K with no statistically significant variation with pressure between 1–760 Torr, in good agreement with the results of the photolytic experiments.

The formation of SO₃ by reaction (R3) indicates that the reaction is potentially significant in the production of H₂SO₄ and sulfate aerosol in the atmosphere. Atmospheric modelling studies have shown that a larger rate coefficient for CH₂OO + SO₂ has a significant impact on sulfate aerosol formation on a regional scale⁶ and on gas phase H₂SO₄ production in forested regions such as a boreal forest in Finland²⁴ and tropical forests.²⁵ However, the modelling results do depend on the competition between the reaction of CH₂OO with SO₂ and that with water vapour/water vapour dimers, with a number of recent studies indicating that the reaction of CH₂OO with water dimers is more important than the CH₂OO + water monomer reaction under atmospheric relevant conditions.^26–29 IUPAC currently recommends a value of (6.4 ± 1.5) × 10⁻¹² cm³ molecule⁻¹ s⁻¹ for the rate coefficient of the CH₂OO + (H₂O)₂ reaction at 298 K, which is four orders of magnitude larger than the rate coefficient of the CH₂OO + H₂O reaction, (2.8 ± 1.1) × 10⁻¹⁶ cm³ molecule⁻¹ s⁻¹.³⁰ Kinetic studies of the CH₂OO + (H₂O)₂ reaction³⁰ have led to the conclusion that the removal of CH₂OO in the troposphere is dominated globally by the reaction with water dimer.² However, the reaction of CH₂OO with SO₂ is fast enough to potentially compete with the CH₂OO + water dimer reaction and impact on SO₂ oxidation in SO₂–rich environments and/or low absolute humidities. As the concentration of water dimer varies strongly with the saturated vapour pressure of water, the competition between SO₂ and water dimers for CH₂OO will be temperature dependent.

In the present work we report the kinetics of the CH₂OO + SO₂ reaction at 85 Torr in the temperature range of 223–344 K using 248 nm photolysis of CH₂I₂/O₂/SO₂/N₂ mixtures under pseudo-first-order conditions with respect to SO₂. Time-resolved broadband UV absorption spectroscopy was employed to monitor CH₂OO directly during the reaction with SO₂. This is the first study of the temperature dependence of the rate coefficient for the CH₂OO + SO₂ reaction.

Experimental

The kinetics of the CH₂OO + SO₂ reaction were studied as a function of temperature using laser flash photolysis of CH₂I₂/O₂/SO₂/N₂ gas mixtures, coupled with time-resolved broadband UV absorption spectroscopy. The experimental apparatus has been described in detail previously^31–33 therefore only a brief description is given here.

Two reaction cells were used, both consisting of a 100 cm long glass tube of 3 cm inner diameter sealed with fused silica windows at both ends. The first cell was jacketed and used for experiments at T ≥ 296 K, in which the temperature was controlled by circulating thermofluid (HUBE6479 DW-therm oil) from a thermoregulator (Huber Unistat 360). The second reaction cell, used for temperatures at T < 296 K, was immersed in a cooling bath of 30% ethane-1,2-diol in methanol and surrounded by 3 cm thick polystyrene for insulation. The temperature for this cell was controlled using a refrigerated immersion chiller (LabPlant Refrigerated Immersion Probe, RP-100CD), with the probe immersed in the cooling mixture and magnetic stirring employed to achieve a constant temperature (within 98%) in the cooling mixture along the cell. Further details of temperature calibrations in the cell are given in the ESI.†

A dilute mixture of SO₂ (Sigma-Aldrich, 99.9%) was prepared manometrically at a known concentration in nitrogen (BOC 99.998%) and stored in a glass bulb. Gases, i.e. SO₂, O₂ (BOC, 99.5%) and the carrier gas N₂, were introduced through calibrated mass flow controllers (MFCs) in a glass mixing manifold. A few percent of the gas mixture was then passed through a bubbler containing liquid CH₂I₂ (Alfa Aesar, 99%) held at constant temperature in an ice bath, which was then mixed with the remaining fraction of the gas and delivered to the reaction cell. The initial concentration of CH₂I₂ in the cell was controlled by a needle valve at the entrance of the bubbler and determined by UV absorption measurements as the average of the concentration in the cell before and after each kinetic run.

The kinetic experiments were performed under pseudo-first-order conditions with respect to SO₂. The initial concentrations were: [SO₂] = (0.6–5.6) × 10¹³ molecule cm⁻³ (typical uncertainties of ∼5%), [CH₂I₂] = (1.0–7.4) × 10¹³ molecule cm⁻³, [O₂] = 7.5 × 10¹⁷ molecule cm⁻³ and [CH₂OO]₀ = (0.4–2.7) × 10¹² molecule cm⁻³.

The total flow rate was 18 slm, giving a residence time in the cell of ∼2 s. The total pressure in the cell was maintained at 85 Torr and measured by a capacitance manometer (MKS Instruments). The chemistry within the cell was initiated by pulsed excimer laser photolysis at 248 nm (KrF, Lambda-Physik CompEx 210) with a laser fluence of 2–6 × 10¹⁶ photon cm⁻² (measured by a Molectron Powermax 500A power meter). The pulse repetition rate was 0.3 Hz to ensure a fresh gas mixture in the cell for each laser pulse.

Absorption of UV/visible radiation during the experiments was monitored using a laser-driven light source (LDLS, Energetiq EQ-99X), which provides ∼10 mW cm⁻² of light between 200 nm and 800 nm. Approximately 10% of the probe light was aligned in a single pass arrangement along the length of the cell, which was used in the temperature calibrations (see ESI†) with the remaining light used for the kinetics measurements aligned in a 7 pass arrangement described previously.^31–33 The total effective pathlength in the multi-pass arrangement, considering the total overlap between the photolysis and probe beams, was determined to be l = (471 ± 50) cm from comparison between the expected depletion of [CH₂I₂] owing to photolysis (Δ[CH₂I₂]), based on the measured concentration of CH₂I₂ and laser fluence in the cell, and Δ[CH₂I₂] × l derived from analysis of the post-photolysis absorption spectra. Further details are given in the ESI.† It should be noted that the value obtained for the total pathlength did not impact the determination of the rate coefficient of the CH₂OO + SO₂ reaction as the kinetic experiments were performed under pseudo-first-order conditions.

The probe beam exiting the reaction cell was passed through a sharp cut-on filter (248 nm RazorEdge ultrasteep long-pass edge filter, Semrock) to minimise the impacts of scattered excimer light and focused onto a fibre optic via a fibre launcher (Elliot Scientific). The output from the fibre optic was directed through a 25 μm slit onto a spectrograph equipped with a diffraction grating of 300 grooves per mm and imaged onto an integrated thermoelectrically cooled charge-coupled device (CCD) detector (FER-SCI-1024BRX, Princeton Instruments), giving spectral resolution of 1 nm (FWHM). The exposure time of the CCD to the light was varied from 10–100 μs. The spectral and temporal information were mapped spatially along the horizontal and vertical directions of the CCD, respectively, as described in detail in our previous work.³³ The photocharge was shifted on the time axis (vertically) from an illuminated region to a storage region with a programmable rate in the range 5.6 μs per row to 35 μs per row. The rapid shift of photocharge on the CCD resulted in an instrument response function, which was included in the analysis of the measured concentration-time profiles as described in the Results section.

Wavelength calibrations were performed by recording the well-known Hg emission spectrum from a low pressure Hg pen-ray lamp (Oriel). Timings of the recording by the camera and the firing of the photolysis laser were controlled by a delay generator (SRS DG535). Intensity data recorded by the camera were typically averaged for 400–800 photolysis shots and transferred to a PC for analysis.

Results

Fig. 1 shows an example of total absorbance recorded following photolysis, with contributions from the absorbance of CH₂I₂, CH₂OO and IO. The absorbance, A(tot)_λ,t, was observed as a function of wavelength (λ) and time (t) and analysed between 300 and 450 nm to determine the changes to concentrations of each species by fitting the reference absorption cross-sections for CH₂OO,³² IO³⁴ and CH₂I₂³⁵ to A(tot)_λ,t at each time point (E1).where I_λ,0 is the average light intensity at wavelength λ prior to photolysis, I_λ,t is the post-photolysis intensity at wavelength λ and time t, σ_i,λ is the cross section of species i at wavelength λ, [i]_t is the concentration of species i at time t, and l is the total pathlength, (471 ± 50) cm.

Fig. 1 Observed absorbance (black), total fit (red), and the individual contributions from CH₂OO (blue), IO (purple) and CH₂I₂ (orange) determined by fitting reference spectra to the measured absorbance using eqn (E1) at t = 1.0 ms following photolysis. For these data, T = 296 K, p = 85 Torr, [O₂] = 7.5 × 10¹⁷ molecule cm⁻³, [CH₂I₂] = 8.0 × 10¹³ molecule cm⁻³, [CH₂OO]₀ = 1.8 × 10¹² molecule cm⁻³ and [SO₂] = 5.0 × 10¹² molecule cm⁻³.

Fig. 2 shows typical concentration–time profiles for CH₂OO, which are given by a convolution of the ‘true’ kinetic decay with an instrument response function (IRF).³³ The IRF is generated by the shift of the photocharge in the time direction of the CCD detector from the illuminated region to the storage region of the CCD (details in the Experimental). The rate coefficient for CH₂I + O₂ (1.7 × 10⁻¹² cm³ molecule⁻¹ s⁻¹)³⁶ and the O₂ concentration (7.5 × 10¹⁷ molecule cm⁻³) employed in this work indicate a time scale of 1–2 μs for the CH₂OO growth following photolysis. However, owing to the IRF, the observed [CH₂OO] increases on a time scale of hundreds of μs before the subsequent decay which occurs on a time scale of 5–10 ms (Fig. 2). Typical concentration-time profiles for CH₂I₂ and IO are given in the ESI.†

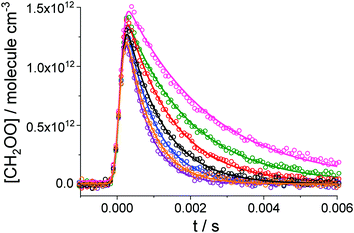Fig. 2 Examples of observations of CH₂OO (open circles) and fit results (solid lines). For this experiment T = 316 K and p = 85 Torr. The initial concentration of the precursor was the same for all the kinetic decays, [CH₂I₂]₀ = 4.2 × 10¹³ molecule cm⁻³, while the initial concentration of SO₂ was varied from one measurement to another: no SO₂ (pink circles), 0.5 × 10¹³ molecule cm⁻³ (green circles), 0.9 × 10¹³ molecule cm⁻³ (red circles), 1.5 × 10¹³ molecule cm⁻³ (black circles), 2.0 × 10¹³ molecule cm⁻³ (blue circles), 2.6 × 10¹³ molecule cm⁻³ (orange circles) and 3.1 × 10¹³ molecule cm⁻³ (purple circles). The global fit to the data using eqn (E4) results in the observed rate coefficients for the CH₂OO reaction with SO₂, k_obs: (435 ± 5) s⁻¹ (pink), (571 ± 5) s⁻¹ (green), (783 ± 7) s⁻¹ (red), (1002 ± 11) s⁻¹ (black), (1261 ± 15) s⁻¹ (blue), (1460 ± 19) s⁻¹ (orange) and (1658 ± 23) s⁻¹ (purple). For these data the IRF parameters are t_c = (7.0 ± 0.1) × 10⁻⁵ s and w = (1.20 ± 0.02) × 10⁻⁴ s. Errors are given at 1σ level.

As the kinetic experiments were performed under pseudo-first-order conditions with respect to SO₂ the decay of [CH₂OO] by reaction with SO₂(R3) is described by an exponential decay (E2).

Here [CH₂OO]_t is the concentration of CH₂OO at time t, [CH₂OO]₀ is the concentration at time zero and k_obs is the observed rate coefficient. The parameter k_obs includes contributions from both the decay rate coefficient of CH₂OO in the absence of SO₂, k_loss and the pseudo-first-order rate coefficient for the reaction of CH₂OO with SO₂, which is given by the product of the bimolecular rate coefficient for the CH₂OO + SO₂ reaction, k₃ and [SO₂] (E3).

k_obs = k_loss + k₃[SO₂] (E3)

where k_loss includes contributions from the first-order coefficient for the loss of CH₂OO by diffusion out of the probe region, the bimolecular rate coefficient for the CH₂OO self-reaction and the bimolecular rate coefficients for the reactions of CH₂OO with other reactive species generated in the CH₂I₂/O₂ photolytic mixture, predominately the reaction of CH₂OO with iodine atoms.³²

The observed temporal behaviour of CH₂OO can be described by a convolution of the exponential decay described by eqn (E2) with the IRF described by a Gaussian centred at time t_c with width w(E4).³³

where erf is the error function encountered in integrating the normal distribution (the normalised form of the Gaussian function).³⁷

Eqn (E4) was employed in the fit to the observed temporal profiles of CH₂OO at each temperature to determine k_obs and the Gaussian parameters t_c and w. The parameters t_c and w are dependent on the exposure time of the CCD detector to the light and the shift rate of the photocharge from the illuminated region to the storage region of the CCD. Concentration-time profiles obtained using the same exposure time and shift rate were fitted globally to determine the parameters t_c and w. Fig. 2 shows an example of the global fit.

Under given conditions the decay rate coefficient of CH₂OO in the absence of SO₂, k_loss is constant, hence a plot of k_obs as a function of [SO₂] is linear with gradient k₃ (eqn (E3)). Typical k_obsvs. [SO₂] plots are shown in Fig. 3 at four different temperatures: 223 K, 270 K, 296 K and 344 K. It can be observed that k₃ decreases with temperature. The plots of k_obs against [SO₂] at all temperatures employed are shown in the ESI.† The values of k₃ determined at all temperatures are shown in Table 2. The temperature dependence of k₃ is shown in Fig. 4.

Fig. 3 k _obs vs. [SO₂] plots at 85 Torr and four different temperatures. The linear fits to the data result in the second order rate coefficients k₃ for each temperature: (6.4 ± 0.3) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ (223 K, dark red), (5.3 ± 0.3) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ (270 K, red), (4.0 ± 0.1) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ (296 K, green) and (3.3 ± 0.1) × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ (344 K, blue). For each temperature [CH₂I₂] was constant: 3.4 × 10¹³ molecule cm⁻³ (dark red), 5.0 × 10¹³ molecule cm⁻³ (red), 4.8 × 10¹³ molecule cm⁻³ (green) and 4.5 × 10¹³ molecule cm⁻³ (blue). Laser fluence: 6.0 × 10¹⁶ photons cm⁻² (dark red), 4.0 × 10¹⁶ photons cm⁻² (red), 4.0 × 10¹⁶ photons cm⁻² (green) and 3.0 × 10¹⁶ photons cm⁻² (blue). Intercepts of the bimolecular plots are noted to decrease with increasing temperature, and are expected to be dominated by the reactions CH₂OO + CH₂OO and CH₂OO + I.³² The rates of these reactions are expected to decrease with increasing temperature and are lower at the lower initial CH₂OO and I concentrations at higher temperatures owing to lower laser fluence used in experiments at higher temperatures.

Table 2 Values for k₃ determined in this work at p = 85 Torr and different temperatures

Temperature/K	k 3/10^−11 cm^3 molecule^−1 s^−1
223	6.4 ± 0.3
259	5.5 ± 0.3
266	4.4 ± 0.3
270	5.3 ± 0.3
275	4.1 ± 0.5
281	4.1 ± 0.1
296	4.0 ± 0.1
316	4.2 ± 0.1
324	3.6 ± 0.2
331	3.4 ± 0.1
340	2.2 ± 0.1
344	3.3 ± 0.1

---

Fig. 4 Temperature dependence of the rate coefficient for the CH₂OO + SO₂ reaction. The data are shown as black circles; error margins are statistical errors at 1σ level. The red line shows the parameterisation of the MESMER result, which gave k₃ = (3.72 ± 0.13) × 10⁻¹¹ (T/298)^{(−2.05±0.38)} cm³ molecule⁻¹ s⁻¹.

Master equation calculations for the temperature dependence of the CH₂OO + SO₂ reaction using the MESMER program

A master equation analysis using the Master Equation Solver for Multi-Energy well Reactions (MESMER) was used to fit the potential energy surface (PES) for (R3) to the experimental rate coefficients. A full description of MESMER is given in previous work.^38–41 MESMER solves the master equation and the subsequent eigenvalue–eigenvector analysis outputs the time profiles of species concentrations together with the phenomenological rate coefficients for the system. The most recent computational study of the CH₂OO + SO₂ by Kuwata et al.²² expanded the understanding of the reaction mechanism by characterising two distinct stereochemical pathways to provide a detailed description of the PES. The authors²² predicted that ∼90–91% of the reaction proceeds through a closed-shell transition structure to form HCHO + SO₃, in qualitative agreement with previous studies,^20,21 with a small contribution (6–7%) of the open-shell mechanism leading to HCHO + SO₃ predicted by Vereecken et al. to be the dominant channel.⁵ The present calculations were based on a potential energy surface shown in Fig. 5, which was obtained by reducing the PES determined by Kuwata et al.²² to the dominant closed-shell mechanism. The reaction first proceeds by the formation of a pre-reaction complex leading to a cyclic secondary ozonide (SOZ). The SOZ subsequently decomposes, producing HCHO + SO₃via two stereochemical pathways arising from the existence of endo and exo conformers of the pre-reaction complex (species 3a and 3b respectively in Fig. 5, using the same notation for the structures given by Kuwata et al.²²) and of the SOZ (species 5a and 5b in Fig. 5). Simulations using MESMER showed that there was no significant loss of accuracy by the reduction in complexity of the PES to that shown in Fig. 5, and that the reduced mechanism dominates the fate of the CH₂OO + SO₂ under all conditions used in the MESMER calculations (T = 223–344 K and p = 2–760 Torr).

Fig. 5 Potential energy surface of the reaction CH₂OO + SO₂ showing the two stereo-chemical pathways proceeding through endo (light blue) and exo conformers (dark blue). Energies (kJ mol⁻¹) of 3a, 3b, TS-4a and TS-4b were generated by MESMER calculations, while the energies of 5a, 5b, TS-7a, TS-7b and the products HCHO and SO₃ were taken from the work of Kuwata et al.²² The energy levels calculated by Kuwata et al.²² for 3a and TS-4a are shown in light red and for 3b and TS-4b are shown in dark red. The notations for intermediates and transitions states are the same as in the work of Kuwata et al.^19,22 Kuwata et al. describe the structures of the species.²²

To characterise the observed negative temperature dependence and the pressure independence in the range 1.5–760 Torr^11,13 of the CH₂OO + SO₂ reaction, the values of k₃ obtained in this work for T = 220–350 K and p = 85 Torr and the 298 K IUPAC recommendation for p = 2–760 Torr, ,³⁰ were fit in MESMER. The inverse Laplace transform (ILT) method was used to describe the barrierless formation of the pre-reaction complexes 3a and 3b, giving a canonical high pressure limiting rate coefficient k^∞ = (5.5 ± 2.0) × 10⁻¹¹ (T/298)^{−(1.0±0.4)} cm³ molecule⁻¹ s⁻¹ for each stereo-chemical pathway. The calculations showed that the cycloaddition transition states TS-4a and TS-4b control the reaction rate and thus the relative energies of TS-4a and TS-4b were floated during the simulations. The energies of the pre-reaction complexes 3a and 3b and the transition states TS-4a and TS-4b were linked⁴² to maintain the same relative differences as those given by Kuwata et al.²² The values calculated by Kuwata et al.²² were used for the relative energies of 5a, 5b, TS-7a, TS-7b and the products HCHO and SO₃. The fit results for k₃ can be parameterised by k₃ = (3.72 ± 0.13) × 10⁻¹¹ (T/298)^{(−2.05±0.38)} cm³ molecule⁻¹ s⁻¹ and are shown in Fig. 4. The fit values for the energies of 3a, 3b, TS-4a and TS-4b (relative to CH₂OO + SO₂) are shown in Fig. 5, which also shows the values calculated by Kuwata et al.²² An agreement within 98% was obtained between the fit energies for 3a, 3b, TS-4a and TS-4b determined by MESMER and the energies predicted by Kuwata et al.,²²i.e. the energies given by MESMER calculations are 0.9 kJ mol⁻¹ more negative than the values of Kuwata et al. (Fig. 5). This small deviation is within the 2.5 kJ mol⁻¹ errors of the MESMER calculations and the errors generated using the multi-coefficient Gaussian-3 quantum chemical method (MCG3) employed by Kuwata et al.²² to determine the energies of 3a, 3b, TS-4a and TS-4b (root-mean-squared error of 6.6 kJ mol⁻¹).⁴³

A negative temperature dependence has also been observed for the reaction of the Criegee intermediate (CH₃)₂COO with SO₂ between 283 and 303 K at 300 Torr following photolysis of (CH₃)₂CI₂/O₂/N₂/SO₂ mixtures at 248 nm coupled with time-resolved UV absorption at 340 nm.⁴⁴ The kinetics of the reaction were characterised by k_{(CH3)2COO+SO2} = (1.36 ± 0.03) × 10⁻¹¹ (T/298)^{(−6.45±0.64)} cm³ molecule⁻¹ s⁻¹, and the dependence on temperature is thus more pronounced than that observed for CH₂OO + SO₂ in the current study, k_CH2OO+SO2 = (3.72 ± 0.13) × 10⁻¹¹ (T/298)^{(−2.05±0.38)} cm³ molecule⁻¹ s⁻¹.

Atmospheric implications

Fig. 6 compares the pseudo-first-order losses of CH₂OO for a range of SO₂ mixing ratios and relative humidities as a function of temperature. Losses to SO₂ are given as k₃[SO₂], using the results for k₃ determined in this work. Losses as a function of relative humidity are given as the product of the current IUPAC recommendation for the temperature dependence of the reaction between CH₂OO and (H₂O)₂^17,28 and the water dimer concentration, which was determined from the saturated vapour pressure of water,⁴⁵ relative humidity, and the equilibrium constant for 2H₂O ⇌ (H₂O)₂.^28,46 Although the reaction with water dimers dominates under most conditions, the reaction of CH₂OO with SO₂ is potentially important in regions with high SO₂ concentrations and low humidity, particularly at low temperatures. Results for k₃ obtained in this work may be useful for the interpretation of field measurements and data obtained in chamber experiments at temperatures away from 298 K.

Fig. 6 Comparison of pseudo-first-order losses for CH₂OO for a range of SO₂ mixing ratios and relative humidities as a function of temperature. Losses for CH₂OO are shown as k[X], where X is SO₂ or (H₂O)₂, and have been determined using results obtained in this work for k(T)[SO₂], with k(T)[(H₂O)₂] determined from current IUPAC recommendations¹⁷ for CH₂OO + (H₂O)₂ kinetics and water dimer concentrations determined from the saturated vapour pressure for water,⁴⁵ relative humidity, and the equilibrium constant for 2H₂O ⇌ (H₂O)₂.^28,46

Conclusions

The kinetics for the reaction between the stabilised Criegee intermediate CH₂OO and SO₂ have been determined as a function of temperature using laser flash photolysis of CH₂I₂/O₂/SO₂/N₂ mixtures at 248 nm coupled to time-resolved broadband UV absorption spectroscopy in the temperature range 223–344 K at a total pressure of 85 Torr. The reaction showed a negative temperature dependence which can be described by k₃ = (3.72 ± 0.13) × 10⁻¹¹ (T/298)^{(−2.05±0.38)} cm³ molecule⁻¹ s⁻¹.

Calculations in MESMER³⁸ using a mechanism based on that proposed by Kuwata et al.²² show that the measured negative temperature dependence and the lack of pressure dependence between 1.5–760 Torr^11,13,30 can be described by the barrierless formation of endo and exo pre-reaction complexes, which lead to endo and exo secondary cyclic ozonides through relatively low barriers. The secondary ozonides further decompose to HCHO + SO₃. The energies of the transition states leading from the pre-reaction complexes to the SOZs were found to be 0.9 kJ mol⁻¹ more negative than those reported in the computational study of Kuwata et al.²² In addition, this work reinforces the prediction that the reaction yield of HCHO + SO₃ at atmospheric pressure is close to 100% and is in agreement with experimental work¹⁹ finding that HCHO + SO₃ are the major products of the reaction.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the Natural Environment Research Council (NERC) for funding (grant references NE/L010798/1 and NE/P012876/1). We would also like to thank K. T. Kuwata for providing details of the calculations on the potential energy surface for CH₂OO + SO₂.

References

1. D. Johnson and G. Marston, The gas-phase ozonolysis of unsaturated volatile organic compounds in the troposphere, Chem. Soc. Rev., 2008, 37(4), 699–716.
2. C. A. Taatjes, Criegee Intermediates: What Direct Production and Detection Can Teach Us About Reactions of Carbonyl Oxides, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, 2017, vol. 68, pp. 183–207.
3. L. Vereecken, Lifting the Veil on an Old Mystery, Science, 2013, 340(6129), 154–155.
4. O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Direct Kinetic Measurements of Criegee Intermediate (CH₂OO) Formed by Reaction of CH₂I with O₂, Science, 2012, 335(6065), 204–207.
5. L. Vereecken, H. Harder and A. Novelli, The reaction of Criegee intermediates with NO, RO₂, and SO₂, and their fate in the atmosphere, Phys. Chem. Chem. Phys., 2012, 14(42), 14682–14695.
6. C. J. Percival, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, D. O. Topping, D. Lowe, S. R. Utembe, A. Bacak, G. McFiggans, M. C. Cooke, P. Xiao, A. T. Archibald, M. E. Jenkin, R. G. Derwent, I. Riipinen, D. W. K. Mok, E. P. F. Lee, J. M. Dyke, C. A. Taatjes and D. E. Shallcross, Regional and global impacts of Criegee intermediates on atmospheric sulphuric acid concentrations and first steps of aerosol formation, Faraday Discuss., 2013, 165, 45–73.
7. R. Chhantyal-Pun, B. Rotavera, M. R. McGillen, M. A. H. Khan, A. J. Eskola, R. L. Caravan, L. Blacker, D. P. Tew, D. L. Osborn, C. J. Percival, C. A. Taatjes, D. E. Shallcross and A. J. Orr-Ewing, Criegee Intermediate Reactions with Carboxylic Acids: A Potential Source of Secondary Organic Aerosol in the Atmosphere. Acs Earth and Space, Chemistry, 2018, 2(8), 833–842.
8. M. A. H. Khan, C. J. Percival, R. L. Caravan, C. A. Taatjes and D. E. Shallcross, Criegee intermediates and their impacts on the troposphere, Environ. Sci.: Processes Impacts, 2018, 20(3), 437–453.
9. N. U. M. Howes, Z. S. Mir, M. A. Blitz, S. Hardman, T. R. Lewis, D. Stone and P. W. Seakins, Kinetic studies of C₁ and C₂ Criegee intermediates with SO₂ using laser flash photolysis coupled with photoionization mass spectrometry and time resolved UV absorption spectroscopy, Phys. Chem. Chem. Phys., 2018, 20(34), 22218–22227.
10. L. Sheps, Absolute Ultraviolet Absorption Spectrum of a Criegee Intermediate CH₂OO. Journal of Physical, Chem. Lett., 2013, 4(24), 4201–4205.
11. D. Stone, M. Blitz, L. Daubney, N. U. M. Howes and P. Seakins, Kinetics of CH₂OO reactions with SO₂, NO₂, NO, H₂O and CH₃CHO as a function of pressure, Phys. Chem. Chem. Phys., 2014, 16(3), 1139–1149.
12. R. Chhantyal-Pun, A. Davey, D. E. Shallcross, C. J. Percival and A. J. Orr-Ewing, A kinetic study of the CH₂OO Criegee intermediate self-reaction, reaction with SO₂ and unimolecular reaction using cavity ring-down spectroscopy, Phys. Chem. Chem. Phys., 2015, 17(5), 3617–3626.
13. H. L. Huang, W. Chao and J. J. M. Lin, Kinetics of a Criegee intermediate that would survive high humidity and may oxidize atmospheric SO₂, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(35), 10857–10862.
14. J. Qiu and K. Tonokura, Detection of the simplest Criegee intermediate CH₂OO in the ν4 band using a continuous wave quantum cascade laser and its kinetics with SO₂ and NO₂, Chem. Phys. Lett.: X, 2019, 2, 100019.
15. Y. D. Liu, K. D. Bayes and S. P. Sander, Measuring Rate Constants for Reactions of the Simplest Criegee Intermediate (CH2OO) by Monitoring the OH Radical, J. Phys. Chem. A, 2014, 118(4), 741–747.
16. Y. Q. Liu, F. H. Liu, S. Y. Liu, D. X. Dai, W. R. Dong and X. M. Yang, A kinetic study of the CH₂OO Criegee intermediate reaction with SO₂, (H₂O)2, CH₂I₂ and I atoms using OH laser induced fluorescence, Phys. Chem. Chem. Phys., 2017, 19(31), 20786–20794.
17. R. A. Cox, M. Ammann, J. N. Crowley, H. Herrmann, M. E. Jenkin, V. F. McNeill, A. Mellouki, J. Troe and T. J. Wallington, Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VII - Criegee intermediates, Atmos. Chem. Phys., 2020, 20(21), 13497–13519.
18. C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. K. W. Mok, D. L. Osborn and C. J. Percival, Direct Measurements of Conformer-Dependent Reactivity of the Criegee Intermediate CH₃CHOO, Science, 2013, 340(6129), 177–180.
19. Y. Y. Wang, M. R. Dash, C. Y. Chung and Y. P. Lee, Detection of transient infrared absorption of SO₃ and 1,3,2-dioxathietane-2,2-dioxide cyc-(CH₂)O(SO₂)O in the reaction CH₂OO+SO₂, J. Chem. Phys., 2018, 148(6), 064301.
20. L. Jiang, Y. S. Xu and A. Z. Ding, Reaction of Stabilized Criegee Intermediates from Ozonolysis of Limonene with Sulfur Dioxide Ab Initio and DFT Study, J. Phys. Chem. A, 2010, 114(47), 12452–12461.
21. T. Kurtén, J. R. Lane, S. Jorgensen and H. G. Kjaergaard, A Computational Study of the Oxidation of SO₂ to SO₃ by Gas-Phase Organic Oxidants, J. Phys. Chem. A, 2011, 115(31), 8669–8681.
22. K. T. Kuwata, E. J. Guinn, M. R. Hermes, J. A. Fernandez, J. M. Mathison and K. Huang, A Computational Re-examination of the Criegee Intermediate-Sulfur Dioxide Reaction, J. Phys. Chem. A, 2015, 119(41), 10316–10335.
23. P. Aplincourt and M. F. Ruiz-López, Theoretical investigation of reaction mechanisms for carboxylic acid formation in the atmosphere, J. Am. Chem. Soc., 2000, 122(37), 8990–8997.
24. A. Novelli, K. Hens, C. T. Ernest, M. Martinez, A. C. Nolscher, V. Sinha, P. Paasonen, T. Petaja, M. Sipila, T. Elste, C. Plass-Dulmer, G. J. Phillips, D. Kubistin, J. Williams, L. Vereecken, J. Lelieveld and H. Harder, Estimating the atmospheric concentration of Criegee intermediates and their possible interference in a FAGE-LIF instrument, Atmos. Chem. Phys., 2017, 17(12), 7807–7826.
25. J. R. Pierce, M. J. Evans, C. E. Scott, S. D. D'Andrea, D. K. Farmer, E. Swietlicki and D. V. Spracklen, Weak global sensitivity of cloud condensation nuclei and the aerosol indirect effect to Criegee + SO₂ chemistry, Atmos. Chem. Phys., 2013, 13(6), 3163–3176.
26. W. Chao, J. T. Hsieh, C. H. Chang and J. J. M. Lin, Direct kinetic measurement of the reaction of the simplest Criegee intermediate with water vapor, Science, 2015, 347(6223), 751–754.
27. T. R. Lewis, M. A. Blitz, D. E. Heard and P. W. Seakins, Direct evidence for a substantive reaction between the Criegee intermediate, CH₂OO, and the water vapour dimer, Phys. Chem. Chem. Phys., 2015, 17(7), 4859–4863.
28. M. C. Smith, C. H. Chang, W. Chao, L. C. Lin, K. Takahashi, K. A. Boering and J. J. M. Lin, Strong Negative Temperature Dependence of the Simplest Criegee Intermediate CH₂OO Reaction with Water Dimer, J. Phys. Chem. Lett., 2015, 6(14), 2708–2713.
29. L. C. Lin, H. T. Chang, C. H. Chang, W. Chao, M. C. Smith, C. H. Chang, J. J. M. Lin and K. Takahashi, Competition between H₂O and (H₂O)₂ reactions with CH₂OO/CH₃CHOO, Phys. Chem. Chem. Phys., 2016, 18(6), 4557–4568.
30. IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation, http://iupac.pole-ether.fr. (accessed 18.06.2021).
31. T. Lewis, D. E. Heard and M. A. Blitz, A novel multiplex absorption spectrometer for time-resolved studies, Rev. Sci. Instrum., 2018, 89(2), 024101.
32. Z. S. Mir, T. R. Lewis, L. Onel, M. A. Blitz, P. W. Seakins and D. Stone, CH₂OO Criegee intermediate UV absorption cross-sections and kinetics of CH₂OO + CH₂OO and CH₂OO + I as a function of pressure, Phys. Chem. Chem. Phys., 2020, 22(17), 9448–9459.
33. L. Onel, M. Blitz, P. Seakins, D. Heard and D. Stone, Kinetics of the Gas Phase Reactions of the Criegee Intermediate CH₂OO with O₃ and IO, J. Phys. Chem. A, 2020, 124(31), 6287–6293.
34. P. Spietz, J. C. G. Martin and J. P. Burrows, Spectroscopic studies of the I₂/O₃ photochemistry - Part 2. Improved spectra of iodine oxides and analysis of the IO absorption spectrum, J. Photochem. Photobiol., A, 2005, 176(1σ3), 50–67.
35. J. B. Burkholder, S. P. Sander, J. P. D. Abbatt, J. R. Barker, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, D. M. Wilmouth and P. H. Wine, Chemical kinetics and photochemical data for use in atmospheric studies - Evaluation No. 18. JPL Publication 15-10: available at: http://jpldataeval.jpl.nasa.gov/, last access: 25 May 2021, 2015.
36. D. Stone, M. Blitz, L. Daubney, T. Ingham and P. Seakins, CH₂OO Criegee biradical yields following photolysis of CH₂I₂ in O₂, Phys. Chem. Chem. Phys., 2013, 15(44), 19119–19124.
37. https://mathworld.wolfram.com/Erf.html. (accessed 18.06.2021).
38. D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER: An Open-Source Master Equation Solver for Multi-Energy Well Reactions, J. Phys. Chem. A, 2012, 116(38), 9545–9560.
39. R. J. Shannon, R. L. Caravan, M. A. Blitz and D. E. Heard, A combined experimental and theoretical study of reactions between the hydroxyl radical and oxygenated hydrocarbons relevant to astrochemical environments, Phys. Chem. Chem. Phys., 2014, 16(8), 3466–3478.
40. D. Stone, K. Au, S. Sime, D. J. Medeiros, M. Blitz, P. W. Seakins, Z. Decker and L. Sheps, Unimolecular decomposition kinetics of the stabilised Criegee intermediates CH₂OO and CD₂OO, Phys. Chem. Chem. Phys., 2018, 20(38), 24940–24954.
41. C. A. Whelan, M. A. Blitz, R. Shannon, L. Onel, J. P. Lockhart, P. W. Seakins and D. Stone, Temperature and Pressure Dependent Kinetics of QOOH Decomposition and Reaction with O2: Experimental and Theoretical Investigations of QOOH Radicals Derived from Cl + (CH₃)₃COOH, J. Phys. Chem. A, 2019, 123(47), 10254–10262.
42. D. J. Medeiros, M. A. Blitz, L. James, T. H. Speak and P. W. Seakins, Kinetics of the Reaction of OH with Isoprene over a Wide Range of Temperature and Pressure Including Direct Observation of Equilibrium with the OH Adducts, J. Phys. Chem. A, 2018, 122(37), 7239–7255.
43. B. J. Lynch and D. G. Truhlar, Robust and affordable multicoefficient methods for thermochemistry and thermochemical kinetics: The MCCM/3 suite and SAC/3, J. Phys. Chem. A, 2003, 107(19), 3898–3906.
44. M. C. Smith, W. Chao, K. Takahashi, K. A. Boering and J. J. M. Lin, Unimolecular Decomposition Rate of the Criegee Intermediate (CH₃)₂COO Measured Directly with UV Absorption Spectroscopy, J. Phys. Chem. A, 2016, 120(27), 4789–4798.
45. NIST/SEMATECH e-Handbook of Statistical Methods. http://www.itl.nist.gov/div898/handbook/ (accessed 18.05.2021).
46. B. Ruscic, Active Thermochemical Tables: Water and Water Dimer, J. Phys. Chem. A, 2013, 117(46), 11940–11953.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02932k

---