Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intercalation/deintercalation of solvated Mg2+ into/from graphite interlayers†
Masahiro
Shimizu
 *,
Atsuhito
Nakahigashi
and
Susumu
Arai
*,
Atsuhito
Nakahigashi
and
Susumu
Arai

Department of Materials Chemistry, Faculty of Engineering, Shinshu University, 4-17-1 Wakasato, Nagano, 380-8553, Japan. E-mail: shimizu@shinshu-u.ac.jp; Fax: +81-26-269-5627; Tel: +81-26-269-5627
First published on 27th July 2021
Abstract
In the development of rechargeable Mg-ion batteries which are not limited by resource constraints, studies on negative electrode materials have been concentrated on efficient Mg-deposition/stripping rather than on insertion/extraction-type active materials, driven by the extremely high theoretical capacity of Mg metal (2205 mA h g−1). This work re-examined the potential of graphite, which is overlooked in electrochemical tests using a two-electrode type cell due to a large overpotential during sluggish Mg-deposition/stripping at the counter electrode caused by the passivation layer. The formation of a graphite intercalation compound (GIC) with a stage structure was demonstrated by the continual application of a constant current without considering the cut-off voltage to eliminate the detrimental impact of the counter electrode, although the intercalant was solvated Mg-ions. The GIC formed during the charging process has a blue tint just like a GIC synthesized by a vapor method. Although there is still issue with the large polarization during the deintercalation of solvated Mg ions, a reversible capacity of approximately 200 mA h g−1 could be achieved in the galvanostatic charge/discharge tests with a current density of 7.44 mA g−1. The results should facilitate future research and development of graphite as a negative electrode material.
Introduction
Rechargeable batteries that rely on Mg ions passing between negative and positive electrodes during charging and discharging are considered to be viable options for achieving high-capacity, low-cost, and large-scale energy storage systems.1–6 There is no doubt that rechargeable batteries will become more important for realizing a low-carbon society that efficiently uses renewable energy, and resource issues associated with battery materials will become more serious as a result. In view of the characteristics and performance required by applications, a diverse range of carrier ions as well as positive and negative electrode materials are required, as illustrated by recent Na-ion7,8 and K-ion9–12 battery developments. The tremendous attention given to energy devices that use of Mg ions has been motivated by the high elemental abundance of Mg (13.9% in the Earth's crust),13 its large specific capacity (2205 mA h g−1; 3833 mA h cm−3), and its inherent lack of dendritic growth.2,14 These favorable characteristics have driven researchers to focus on electrolytes that enable highly efficient and reversible Mg deposition/stripping at the negative electrode,15–20 but this remains challenging due to bottlenecks associated with the irreversible formation of passivation layers on the Mg metal. Apart from Mg metal, the capacities of oxides such as TiO2,21 MgNaTi3O7,22 and Li4Ti5O1223 are relatively small, despite their excellent cycling stabilities. Sn24 and Sb25 cannot easily take/release Mg ions at feasible capacities for a large number of cycles because the large volumetric changes associated with alloying reactions with Mg disintegrate the electrodes. Meanwhile, little importance has been paid to graphite, which is used in current Li-ion battery systems because Mg ions are less likely to intercalate into the interlayer alone; that is, strong Lewis acidity disfavors desolvation of the solvent molecules that surround the Mg ions and thereby results in obstacles for the formation of a binary Mg–graphite intercalation compound (GIC), unlike Li–GIC.26 There are few reports on the use of graphite as a negative electrode material even when its scope is expanded to include ternary Mg–GICs. With respect to ternary Mg–GICs with included solvent molecules, Maeda and Touzain electrochemically synthesized a ternary GIC with a low intercalant content using 0.05 mol dm−3 MgCl2 dissolved in dimethyl sulfoxide (DMSO).27 Xu and Lerner prepared a stage-1 ternary GIC using a vapor-phase synthesis in a simple one-pot approach using Mg metal and ethylenediamine (en);28,29 the GIC contained [Mg2(en)2]2+ as an intercalant, and its detailed composition was determined by thermal analysis and X-ray diffractometry to be [Mg2(en)2.0]C26. Zoidl et al. synthesized imidazole-based Mg-Hückel salt and exhibited that the use of the conductive salt enables intercalation/deintercalation reactions of a graphite electrode as well as reversible Mg-deposition/stripping.30 God and Schmuck et al. showed that the high stage GIC is formed to be able to deliver a specific capacity of 35 mA h g−1 in the electrolyte consisting of magnesium bis(trifluoromethanesulfonyl)amide [Mg(TFSA)2] and N,N-dimethylformamide (DMF) and claimed that Mg2+ is the sole intercalant, although the stage structure was not mentioned.31 They investigated the applicability of electrolyte solutions consisting of Mg(TFSA)2 and various solvents (dimethulacetamide, dimethoxyethane, acetonitrile, sulfolane, etc.) to a graphite electrode. Among them, they found the intercalation reaction in the electrolyte using DMF solvent. The GIC with co-intercalated Mg2+-diethylene glycol dimethyl ether (DEGDME) reported by Kim and Lee et al. has a stage-5 structure and showed a reversible capacity of at least 40 mA h g−1;32 they used a two-electrode cell with Mg metal as the counter electrode to manifest charge/discharge behavior. Passivating surface layers formed on the Mg metal by the electrolyte decomposition tends to block deposition/stripping reactions with a large overpotential,15,33 which may cause the intrinsic properties of active materials to be missed under such conditions. The use of an activated carbon (AC) electrode instead of an Mg metal as the counter electrode maintains the electroneutrality of electrolyte solutions through the storage of anions inside the pores of the AC during the magnesiation (reduction) of the active material, making it possible to evaluate the working electrode with galvanostatic charge–discharge testing.34,35 However, in the measurement system with an insufficient amount of electrolyte, the ionic conductivity affected by the dilution of ion concentration at the electrode/electrolyte interface during charge transfer process cannot be ignored, which complicates the electrochemical measurements. To overcome these problems and to properly determine the capability, we applied a constant current to an electrochemical cell using an Mg metal as the counter electrode, without reference to cut-off voltage/potential. Inspired by God's work,31 we investigate the Mg-ions storage ability of graphite as a guest, using their electrolyte as a reference. Herein, based on the results, we reconsider the potential of graphite as a negative electrode material for Mg-ion batteries.Experimental section
Magnesium bis(trifluoromethanesulfonyl)amide [Mg(TFSA)2; Kishida Chemical Co., Ltd], N,N-dimethylformamide (DMF), methylmagnesium bromide (Grignard Reagent, 12% in tetrahydrofuran, ∼1 mol dm−3 CH3MgBr/THF; Tokyo Chemical Industry Co., Ltd), silver nitrate (AgNO3), tetrabutylammonium perchlorate (TBAP), acetonitrile (AN), polyvinylidene difluoride (PVDF; Sigma-Aldrich), and N-methylpyrrolidone (NMP, Sigma-Aldrich) were purchased. Prior to electrolyte preparation, Mg(TFSA)2 was dried at 120 °C under vacuum for 24 h and the residual water in DMF was removed using 3A molecular sieves in an argon-filled glove box with H2O content of less than 5 ppm and O2 content of less than 1 ppm (UL-800A-SSTM/MF-800; UNICO LTD).The solvation environments of the Mg ions in electrolyte solutions depending on salt concentration was analyzed with a Raman spectroscopy system (LabRAM HR Evolution; HORIBA, Ltd) using the 532 nm line of a diode-pumped solid-state laser at room temperature. We tightly sealed the electrolyte solution in a quartz cell in an argon-filled glove box to prevent exposure to water vapor.
Natural graphite powder (average particle size: 10 μm; SEC Carbon, Ltd) and polyvinylidene difluoride (PVDF) were mixed with N-methyl-2-pyrrolidone (NMP) at a weight ratio of 90/10 wt%. The resulting slurry was uniformly cast onto a Ti current collector using a doctor blade and then dried at 120 °C under vacuum for 5 h. The loaded mass of the active material and electrode thickness were approximately 1.8 mg cm−2 and 20 μm. The electrochemical Mg2+ storage behavior of the graphite was studied using a three-electrode electrochemical cell consisting of a working electrode (∅ 10 mm), a 0.5 mm-thick Mg alloy plate (Mg: 96%, Al: 3%, Zn: 1%, AZ31) as the counter electrode, a reference electrode, an electrolyte, and a glass fiber filter (Whatman GF/A) as the separator. The Mg alloy plate (as the counter electrode) was polished with sandpaper (#120) to remove the surface oxidation layer prior to cell assembly. Since the potential of Mg is known to be unstable in some organic electrolytes due to surface passivation,3,34 we used Ag wire soaked in 0.1 M AgNO3–0.1 M tetrabutylammonium perchlorate/acetonitrile (TBAP/AN) as the reference electrode, which was separated from the main electrolyte by porous Vycor glass (Fig. S1, ESI†). The potential of Ag/Ag+ was converted to the potential of ferrocene/ferrocenium (Fc/Fc+). The electrolyte preparation and cell assembly were carried out within a purge-type glove box filled with an argon atmosphere from which oxygen and water (a dew point below −75 °C) had been removed. For electrochemical impedance spectroscopy, two identical graphite composite electrodes were charged and discharged to assemble a symmetric cell. The impedance analysis was conducted using the symmetric cells in the frequency range of 100 kHz–100 mHz with an amplitude of 5 mV.
Structural changes in the graphite and the formation of the graphite intercalation compound (GIC) under galvanostatic polarization at a current density of 7.44 mA g−1 (0.01C) were tracked using transmission electron microscopy (TEM; HD2300A, Hitachi, Ltd) and X-ray diffractometry (XRD) (SmartLab, Rigaku). In the XRD measurements, the electrochemical cell after the application of a constant current was disassembled, and then the graphite electrode covered with a Kapton film inside an argon-filled glove box. Except when measuring the electrochemical potential of graphite electrodes, two-electrode cells were used to structurally analyze the GIC.
Results and discussion
The uptake of Mg2+ inside the graphite interlayer is categorized according to: (i) the intercalation with desolvation and (ii) the intercalation of solvated ions without desolvation. In the charge transfer reaction that proceeds with the intercalation of solvated ions, the solvation environment has a great influence on the Mg2+ storage capacity. Raman spectra of variously concentrated Mg(TFSA)2/DMF solutions were recorded to understand the local coordination structure of the Mg ions (Fig. S2, ESI†). The Raman band associated with O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N bending and N–CH3 stretching was observed at 659 cm−1, which is assigned to the DMF solvent (free DMF) in the bulk (Fig. 1). With Mg(TFSA)2 at a concentration of 0.25 M or more, new bands associated with DMF participating in the solvation shell (bound DMF) appeared at higher frequencies of 680 and 687.5 cm−1.36 Although the two bands involved with the presence of the [Mg(DMF)x]2+ complexes cannot be identified rigorously at this stage, the later band should be the complexes with a smaller solvation number of DMF, as observed in [Li(DMF)x]+ complexes,37 indeed the latter band was observed to intensify with increasing Mg-salt concentration. It is noteworthy that the bound TFSA anions that participate in the contact ion pair are absent even in the bulk at a concentration of 1.0 M, in which there are fewer DMF molecules available for the solvation shell. This conclusion is supported by the no change in band shift of CF3 bending vibration coupled with the S–N stretching vibration of the TFSA anions, as observed in the Raman spectra (Fig. S3, ESI†).36,38 By using the respective integrated intensity of free DMF (659 cm−1) and bound DMF (680 and 687.5 cm−1), the average solvation number of Mg ions was estimated according to the following equations:39–41
C–N bending and N–CH3 stretching was observed at 659 cm−1, which is assigned to the DMF solvent (free DMF) in the bulk (Fig. 1). With Mg(TFSA)2 at a concentration of 0.25 M or more, new bands associated with DMF participating in the solvation shell (bound DMF) appeared at higher frequencies of 680 and 687.5 cm−1.36 Although the two bands involved with the presence of the [Mg(DMF)x]2+ complexes cannot be identified rigorously at this stage, the later band should be the complexes with a smaller solvation number of DMF, as observed in [Li(DMF)x]+ complexes,37 indeed the latter band was observed to intensify with increasing Mg-salt concentration. It is noteworthy that the bound TFSA anions that participate in the contact ion pair are absent even in the bulk at a concentration of 1.0 M, in which there are fewer DMF molecules available for the solvation shell. This conclusion is supported by the no change in band shift of CF3 bending vibration coupled with the S–N stretching vibration of the TFSA anions, as observed in the Raman spectra (Fig. S3, ESI†).36,38 By using the respective integrated intensity of free DMF (659 cm−1) and bound DMF (680 and 687.5 cm−1), the average solvation number of Mg ions was estimated according to the following equations:39–41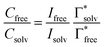 | (1) |
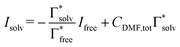 | (2) |
 | (3) |
 and
and 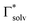 denote the integrated Raman intensities per unit concentration of free DMF (Ifree/Cfree) and bound DMF (Isolv/Csolv), respectively. CMg,tot and CDMF,tot are the total concentration of Mg ion and DMF, respectively. The average solvation numbers of DMF per Mg ion in 0.25, 0.5, 0.75, and 1.0 M solutions were calculated to be 6.0, 5.6, 4.5, and 4.1, respectively. As a result of applying constant reductive current to two-electrode type cells consisting of a graphite composite electrode and an Mg counter electrode with a cutoff voltage of −0.4 V (Fig. S4, ESI†), the charge capacity during reduction decreased in the electrolyte solution with a concentration of 0.75 M or more. We therefore used the 0.5 M electrolyte to explore the potential of graphite as a host material in the subsequent experiments. The water content in the electrolyte was confirmed to be less than 70 ppm by Karl–Fischer titration.
denote the integrated Raman intensities per unit concentration of free DMF (Ifree/Cfree) and bound DMF (Isolv/Csolv), respectively. CMg,tot and CDMF,tot are the total concentration of Mg ion and DMF, respectively. The average solvation numbers of DMF per Mg ion in 0.25, 0.5, 0.75, and 1.0 M solutions were calculated to be 6.0, 5.6, 4.5, and 4.1, respectively. As a result of applying constant reductive current to two-electrode type cells consisting of a graphite composite electrode and an Mg counter electrode with a cutoff voltage of −0.4 V (Fig. S4, ESI†), the charge capacity during reduction decreased in the electrolyte solution with a concentration of 0.75 M or more. We therefore used the 0.5 M electrolyte to explore the potential of graphite as a host material in the subsequent experiments. The water content in the electrolyte was confirmed to be less than 70 ppm by Karl–Fischer titration.
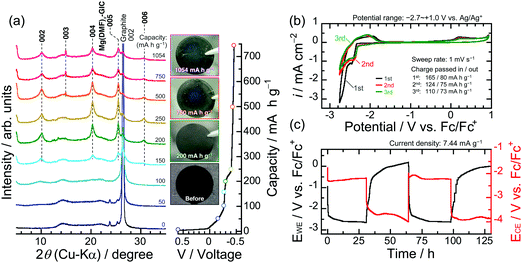
As mentioned earlier, in the case of using a two-electrode type cell without considering the potential of the Mg foil as a counter electrode, it cannot be denied that the function of graphite as a negative electrode material has been overlooked. Structural changes undergone by graphite were carefully followed by ex situ XRD at a constant applied current, until the reductive capacity exceeded 1000 mA h g−1 (which corresponds to 1.34 mol Mg2+ per C6 if the all capacity was expended only in the charge transfer reaction) without a cut-off voltage; that is, under conditions in which the stripping reaction on the Mg counter electrode proceeded sufficiently (Fig. 2a). The graphite exhibited almost no structural change at a capacity of 50 mA h g−1, although the intensity of the 002 diffraction peak of graphite was slightly lower compared to that of the original material. A new broad diffraction peak was observed at 10° at a capacity of 100 mA h g−1; the intensity of this peak became remarkable at a capacity of 150 mA h g−1, while the 002 peak of the graphite was significantly less intense and new diffraction peaks at 20.4°, 25.52°, and 30.56° were observed. A new diffraction peak was observed at 15.0° when the capacity was 500 mA h g−1 or greater. The absence of peaks that correspond to Mg deposits in the XRD patterns, or the blue tint of graphite, which is similar to that of the vapor-phase-synthesized ternary Mg/ethylenediamine–graphite intercalation compound (GIC) reported by Lerner et al.,28,29 suggest that the observed diffraction peaks are due to the formation of a ternary GIC containing DMF as solvation molecules; i.e., Mg(DMF)x–GIC. The diffraction peaks located at 25.52° and 30.56° of the Mg(DMF)x–GIC, which are prominent at 250 mA h g−1, originate from the splitting of the XRD peak caused by the periodic sequence of graphite and intercalant [Mg(DMF)x]2+ planes. When the former and later peaks are assigned as the (00n) and the (00n + 1) indices of stage n and n + 1 GIC structures, the value of n can be calculated with the following equation:42,43
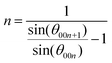 | (4) |
The value of n was calculated to be 4.977, which was labeled as a stage-5 GIC. Consequently, the diffraction peaks at the position of 2θ = 10.1°, 15.0°, 20.4°, 25.52°, and 30.56° are indexed to (002), (003), (004), (005), and (006), respectively, using the above equation. Using the 003- and 005-diffraction angles of the GIC and the 002- and 004-diffractions of graphite, the interlayer space with the intercalant (gallery height) in the c-direction was determined to be 10.87 Å, which is equivalent to 3.24 times the distance (3.35 Å) between graphene sheets devoid of intercalants. Given this significantly extended distance, the intercalant is most likely to be solvated ions of [Mg(DMF)x]2+, rather than Mg ions alone, as opposed to the bare Li ions in a typical electrolyte.26 In addition to this, in light of the crystal and molecule structure of Mg(ClO4)2·DMF analyzed by X-ray diffractometry,44 the solvated Mg ions as the intercalant remain in the electrolyte bulk composition (0.5 M) and are likely to be accompanied by six solvent molecules, that is, the intercalant should be [Mg(DMF)6]2+. Meanwhile, it is noteworthy that Mg neither electrodeposits on the graphite composite nor on the Ti foil in the electrolyte used in this study, even though the voltage of the electrochemical cell was below 0 V and the applied capacity exceeded 250 mA h g−1 (Fig. S5, ESI†). Thus, even considering the possibility that not all of the current capacity was consumed in the GIC formation, the obtained results lead us to conclude that [Mg(DMF)6]2+ intercalates into the interlayers to form ternary GICs with a stage structure.
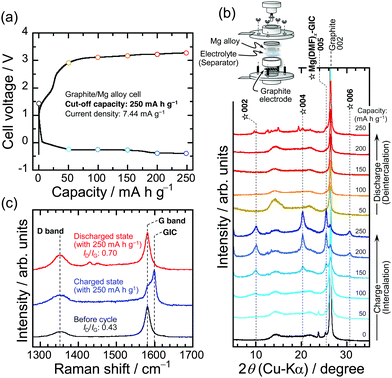
Cyclic voltammetry with an Ag/Ag+ (an Ag wire in 0.1 M AgNO3–0.1 M TBAP/AN) reference electrode at a sweep rate of 1 mV s−1 was used to study the reversibility of the intercalation/deintercalation of [Mg(DMF)6]2+ into/from graphite interlayers (Fig. 2b). Note that the potential of Ag/Ag+ was converted to ferrocene/ferrocenium (Fc/Fc+) in the electrochemical measurements. The current response observed from −2.32 to −2.68 V vs. Fc/Fc+ during sweeping to the cathodic side is attributed to the intercalation of [Mg(DMF)6]2+ to form GICs. The rapid increase in the reduction current below −2.71 V should come from the electrolyte decomposition (Fig. S6, ESI†). The anodic response between −2.14 to −1.51 V and the oxidative current at the broad potential ranges between −0.2 to 0.7 V should be due to the stepwise deintercalation of [Mg(DMF)6]2+ to return to the original graphite structure. At higher potential range, the deintercalation reaction should be accompanied with the oxidative decomposition of the electrolyte on the graphite composite electrode (Fig. S6, ESI†). TEM observation reveals that the thickness of the surface layer is approximately ∼4 nm and it is believed to be composed of inorganic/organic compounds that mainly contain Mg and F (Fig. S7 and S8, ESI†). After the first cycle, the pair of peaks corresponding to the intercalation/deintercalation of the solvated Mg-ions were clearly observed. Focusing on the ternary GIC formed at a capacity of 250 mA h g−1, in which the diffraction peaks of the GIC were prominent compared with those of graphite, the XRD patterns of the graphite electrode were remarkably unchanged as capacity was further increased (Fig. 2a). We monitored the charge–discharge behavior of graphite as a negative electrode material for Mg-ion batteries at a fixed capacity level of 250 mA h g−1 and a constant current density of 7.44 mA g−1 (Fig. 2c). The potential of the graphite composite electrode was −2.6 V vs. Fc/Fc+ when the capacity reached 250 mA h g−1. Two observed potential plateaus from −2.37 to −2.65 V are probably derived from the stepwise formation of ternary Mg(DMF)x–GICs. These plateaus were also detected at the second cycle at the same potentials as in the first cycle. In the desolvation-type reactions such as the intercalation of Li+ alone into graphite interlayers, the range of operating potentials is relatively narrow, whereas the co-intercalation reaction proceeds at wide operating potentials.45 Assuming that the intercalation of Mg2+ alone into graphite interlayers is the desolvation type reaction as reported by God et al.31 and comparing with the results obtained in this work, the range of operating potential in the intercalation/deintercalation of the solvated Mg2+ seems to be wide. This also suggests that the charge/discharge reactions in this case proceed as the co-intercalation/deintercalation type. However, the graphite composite suffered from a large potential hysteresis during discharging. Possible causes for the observed large overpotential are one or more of the following: (i) the ternary Mg(DMF)x–GIC is electrochemically unstable and decomposes during charge–discharge processes, (ii) the surface layers formed by the electrolyte decomposition have a lack of good Mg-ion conductivity, and (iii) the solvated Mg ions inside the graphite layers diffuse extremely slowly. In fact, Calandra and Mauri argued using the density functional theory calculation that MgC6 is energetically unstable against phase separation in Mg and graphite.46 We therefore tracked the structural change in graphite to examine whether or not the capacity of 250 mA h g−1 leading up to the completion of the discharge was consumed for the deintercalation of [Mg(DMF)6]2+.
Fig. 3 exhibits XRD patterns and Raman spectra of the graphite composite electrodes with galvanostatic charge–discharge during the first cycle. The Raman spectrum of graphite showed an additional band at 1599 cm−1 in the charged state at a capacity of 250 mA h g−1, in addition to the E2g mode47 (G band, sp2 graphitic, 1581 cm−1), which is due to the formation of GICs; the graphite electrode had expanded at least 1.33 times by this stage (Fig. 4a–c), although the exact expansion ratio could not be determined due to the relatively sparse electrode mixture prior to charging (Fig. S9, ESI†). Considering the Mg ion radius of ∼72 pm (with coordination number of 6) that is close to the Li ion (∼76 pm) and the two-electron reaction involved in Mg2+,48 the expansion ratio of the electrode in the charged state is great. This is because of the larger size of the intercalant, [Mg(DMF)6]2+, compared to Li+ alone and Mg2+ alone. During the deintercalation process, the 005 diffraction of the GIC had almost disappeared immediately after a discharge capacity of 50 mA h g−1 had been reached, although the position of the 002 of the graphite was not completely returned to the original position as before charging (Fig. S10, ESI†). It suggests that the solid solution with solvated Mg ions intercalated between the graphite interlayers to the extent that no stage structure is formed. The diffraction position gradually shifted to a higher angle with increasing the discharge capacity, and graphite regained its original structure when the capacity reached to 200 mA h g−1. As well as this, the GIC-derived band disappeared at the same time as the G band intensified in the Raman spectrum, that is, the capacity was delivered based on the reversible intercalation/deintercalation of [Mg(DMF)6]2+. At the fully discharged state, the electrode became dense and the thickness resulted in 9.9 μm from 18.34 μm in which the graphite included the intercalants. The phenomenon also indirectly reveals that the formation of the GIC is reversible. Similar changes in the structure and the electrode thickness of the graphite were observed at high current densities, indicating that the diffusion of [Mg(DMF)x]2+ is not fatally sluggish within the host material (not shown here) and is probably not the cause of the large polarization observed during the discharge process. In the case of Li+, which has an ionic size similar to that of Mg2+, the activation energy of the intercalation of the solvated ion is lower compared with that in the intercalation of ion alone accompanied with desolvation and the rapid charge/discharge performance is superior based on the smooth charge transfer reactions though a reversible capacity is reduced.45,49 We plan to study the activation energy of the charge transfer reaction and the diffusion coefficients of solvated Mg2+ inside the graphite structure. Meanwhile, the integrated Raman intensity ratio (ID/IG),47,50 one of the parameters on the crystallinity of carbonaceous material, resulted in 0.43 from 0.70 after the charge/discharge. The TEM images of pristine graphite displayed highly ordered graphene layer stacking with a d-spacing of 3.35 Å, whereas the randomly stacked structure was recognized after the first galvanostatic charge/discharge cycle, as expected based on the Raman spectra (Fig. 4d and e). On the basis of these results, it is plausible to assume that the large polarization observed at the graphite composite electrode during the discharge process is caused by the electrochemical instability of the ternary Mg(DMF)x–GIC and/or the lack of good Mg-ion conductivity through the surface layers formed by electrolyte decomposition. We are currently investigating the details of these causes, with attention given to the binder as well.
It is very interesting to see if the electrochemical formation of GICs achieved in this work also proceeds in a Grignard reagent solution, a typical electrolyte used for efficient Mg-deposition/stripping.51 The Grignard reagent solution of 1 M CH3MgBr/THF was applied to a two-electrode type cell with a graphite composite electrode and Mg alloy as a counter electrode (Fig. 5). In the Grignard electrolyte, the voltage plateau, which corresponds to the Mg deposition, appeared at around 0 V, and there was no change in the diffraction pattern of graphite. The electrolyte of 0.5 M Mg(TFSA)2/DMF enables the formation of GICs, whereas the electrolyte of 1 M CH3MgBr/THF induced the generation of only metallic Mg without the GIC formation. These results reveal that GIC formation depends greatly on the selection of the Mg salt and the electrolyte solvent.
Finally, we performed charge/discharge cycling tests at a current density of 7.44 mA g−1 (0.01C) in the potential range from 0 to −2.65 V vs. Ag/Ag+ (corresponding to −0.06 to −2.71 V vs. Fc/Fc+). Fig. 6a shows the charge/discharge profiles of the graphite composite electrode in 0.5 M Mg(TFSA)2/DMF using a three-electrode type cell. In the first cycle, charge and discharge capacities were 574 and 178 mA h g−1, respectively. The low coulombic efficiency (31%) should be due to the electrolyte decomposition below −2.5 V and the solvated ions that cannot be completely released (Fig. S6, ESI†). We conducted the electrochemical impedance measurements using symmetric cells consisting of two identical graphite composite electrodes which were charged and discharged (Fig. 6b). At the potential of −1.03 V vs. Fc/Fc+ before the charging, one semicircle and a vertical line were detected at a high frequency region, which are assigned to the contact resistance between active materials and the dominant capacitive behavior of the electric double layer formed at the electrode/electrolyte interface, respectively, as typically observed in a Nyquist plot in electric double layer capacitors.52 On the other hand, at the potential of −2.48 V, one semicircle and a slope were confirmed at high and low frequency regions, respectively. Since the top frequency of the semicircle is one order of magnitude lower than that observed before the charging and the electrodes were charged to the potential at which solvated Mg ions were intercalated, it is indicated that the semicircle is mainly the charge transfer resistance associated with the co-intercalation (Fig. S11, ESI†). The slope should be attributed to the diffusion of solvated Mg ions inside the graphite. As clearly shown in the Nyquist plot of the symmetric cell consisting of graphite electrodes charged to −2.6 V corresponding to a capacity of ca. 200 mA h g−1, the diameter of the semicircle decreased with the charging potential. This also supports that the semicircle originates from the charge transfer reaction.49 The semicircle remained even at the upper cut-off potential of −0.06 V, suggesting that the solvated ions are not completely deintercalated from the graphite interlayers. This is also consistent with the lower reversibility in the first cycle (Fig. 6a). At the second cycle, a reversible capacity reached to 194 mA h g−1 and then remained around 180 mA h g−1. The improvement in the reversibility after the second cycle is probably due to the formation of surface layers on graphite that suppresses further electrolyte decomposition while working as the Mg-ion conductor, as observed in the Li-ion batteries system. However, after the end of the 4th cycle (corresponding to ca. 14 days), the cut-off potential in the charge/discharge test could no longer be controlled. Although the reference electrode with a double-junction structure is separated from the main electrolyte by Vycor glass, the electrolyte inside the reference electrode seeped into the main electrolyte and finally disappeared. This is thought to be the reason why the potential did not reach the upper cut-off during the 5th discharging process. The phenomenon was also observed in the reproductive experiments, and it was found that the reference electrode functions for about 14 days under the current conditions. We are investigating the conditions which enables the long-term cycling tests independent of the reference electrode.
Conclusions
In this work, we demonstrated that the ternary Mg(DMF)x–GIC with stage structures can be electrochemically formed by applying a constant current to a graphite composite electrode by not considering the cut-off voltage, that is, the influence of the Mg stripping overvoltage in the counter electrode. The current was consumed in the charge transfer reactions, and the graphite incorporated Mg2+ into its interlayers in the form of a ternary system containing solvated ions and with the capacity, and without going through Mg deposition. The stage structure of the GIC developed at a capacity more than 150 mA h g−1, and the GIC turned blue when the capacity reached to 750 mA h g−1. Importantly, the graphite structure was reversibly changed and solvated Mg2+ could be extracted from the interlayers during the galvanostatic charge–discharge testing to show a reversible capacity of approximately 200 mA h g−1 in the galvanostatic condition with a current density of 7.44 mA g−1. The present study enhances the feasibility of graphite as an alternative to Mg metal, which has received much attention as a negative electrode material for rechargeable Mg-ion batteries. In addition, setting up experimental conditions that are not limited by the counter electrode potential should promote the research and development of Mg-ion storage materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (B) (20H02840) and Early-Career Scientists (18K14317) from the Japan Society for the Promotion of Science (JSPS). The authors also gratefully acknowledge T. Yamakami and J. Inoue for their kind assistance with TEM and SEM observations. Dr M. Shimizu gratefully acknowledge T. Koya, T. Elliot, and Dr S. Uchida for their heartfelt advice.References
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- D. Aurbach, Z. Lu, A. Schechter, Y. Gofe, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727 CrossRef CAS PubMed.
- H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Energy Environ. Sci., 2013, 6, 2265–2279 RSC.
- J. Muldoon, C. B. Bucur and T. Gregory, Chem. Rev., 2014, 114, 11683–11720 CrossRef CAS PubMed.
- Y. Orikasa, T. Masese, Y. Koyama, T. Mori, M. Hattori, K. Yamamoto, T. Okado, Z. D. Huang, T. Minato, C. Tassel, J. Kim, Y. Kobayashi, T. Abe, H. Kageyama and Y. Uchimoto, Sci. Rep., 2014, 4, 5622 CrossRef CAS PubMed.
- R. Mohtadi, M. Matsui, T. S. Arthur and S. J. Hwang, Angew. Chem., Int. Ed., 2012, 51, 9780–9783 CrossRef CAS PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- H. Zhang, I. Hasa and S. Passerini, Adv. Energy Mater., 2018, 8, 1702582 CrossRef.
- Z. Jian, W. Luo and X. Ji, J. Am. Chem. Soc., 2015, 137, 11566–11569 CrossRef CAS PubMed.
- M. Shimizu, T. Koya, A. Nakahigashi, N. Urakami, T. Yamakami and S. Arai, J. Phys. Chem. C, 2020, 124, 13008–13016 CrossRef CAS.
- L. Fan, R. Ma, Q. Zhang, X. Jia and B. Lu, Angew. Chem., Int. Ed., 2019, 58, 10500–10505 CrossRef CAS PubMed.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Adv. Funct. Mater., 2018, 28, 1802938 CrossRef.
- J. W. Morgan and E. Anders, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 6973–6977 CrossRef CAS PubMed.
- M. Matsui, J. Power Sources, 2011, 196, 7048–7055 CrossRef CAS.
- A. Kitada, Y. Kang, K. Matsumoto, K. Fukami, R. Hagiwara and K. Murase, J. Electrochem. Soc., 2015, 162, D389–D396 CrossRef CAS.
- S. B. Son, T. Gao, S. P. Harvey, K. X. Steirer, A. Stokes, A. Norman, C. Wang, A. Cresce, K. Xu and C. Ban, Nat. Chem., 2018, 10, 532–539 CrossRef CAS PubMed.
- K. Shimokawa, H. Matsumoto and T. Ichitsubo, J. Phys. Chem. Lett., 2018, 9, 4732–4737 CrossRef CAS PubMed.
- O. Tutusaus, R. Mohtadi, T. S. Arthur, F. Mizuno, E. G. Nelson and Y. V. Sevryugina, Angew. Chem., Int. Ed., 2015, 54, 7900–7904 CrossRef CAS PubMed.
- J. T. Herb, C. A. Nist-Lund and C. B. Arnold, ACS Energy Lett., 2016, 1, 1227–1232 CrossRef CAS.
- T. Mandai, K. Tatesaka, K. Soh, H. Masu, A. Choudhary, Y. Tateyama, R. Ise, H. Imai, T. Takeguchi and K. Kanamura, Phys. Chem. Chem. Phys., 2019, 21, 12100–12111 RSC.
- Y. Meng, D. Wang, Y. Zhao, R. Lian, Y. Wei, X. Bian, Y. Gao, F. Du, B. Liu and G. Chen, Nanoscale, 2017, 9, 12934–12940 RSC.
- C. Chen, J. Wang, Q. Zhao, Y. Wang and J. Chen, ACS Energy Lett., 2016, 1, 1165–1172 CrossRef CAS.
- N. Wu, Y.-C. Lyu, R.-J. Xiao, X. Yu, Y.-X. Yin, X.-Q. Yang, H. Li, L. Gu and Y.-G. Guo, NPG Asia Mater., 2014, 6, e120 CrossRef CAS.
- N. Singh, T. S. Arthur, C. Ling, M. Matsui and F. Mizuno, Chem. Commun., 2013, 49, 149–151 RSC.
- T. S. Arthur, N. Singh and M. Matsui, Electrochem. Commun., 2012, 16, 103–106 CrossRef CAS.
- R. Fong, U. Y. Sacken and J. R. Dahn, J. Electrochem. Soc., 1990, 137, 2009–2013 CrossRef CAS.
- Y. Maeda and P. Touzain, Electrochim. Acta, 1988, 33, 1493–1497 CrossRef CAS.
- W. Xu and M. M. Lerner, Chem. Mater., 2018, 30, 6930–6935 CrossRef CAS.
- W. Xu, H. Zhang and M. M. Lerner, Inorg. Chem., 2018, 57, 8042–8045 CrossRef CAS PubMed.
- M. Zoidl, C. God, P. Handel, R. Fischer, C. Lenardt, M. Schmuck and T. M. Wrodnigg, J. Electrochem. Soc., 2016, 163, A2461–A2463 CrossRef CAS.
- C. God, B. Bitschnau, K. Kapper, C. Lenardt, M. Schmuck, F. Mautner and S. Koller, RSC Adv., 2017, 7, 14168–14175 RSC.
- D.-M. Kim, S. C. Jung, S. Ha, Y. Kim, Y. Park, J. H. Ryu, Y.-K. Han and K. T. Lee, Chem. Mater., 2018, 30, 3199–3203 CrossRef CAS.
- I. Shterenberg, M. Salama, H. D. Yoo, Y. Gofer, J.-B. Park, Y.-K. Sun and D. Aurbach, J. Electrochem. Soc., 2015, 162, A7118–A7128 CrossRef CAS.
- R. Dugas, J. D. Forero-Saboya and A. Ponrouch, Chem. Mater., 2019, 31, 8613–8628 CrossRef CAS PubMed.
- G. Hasegawa, Y. Akiyama, M. Tanaka, R. Ishikawa, H. Akamatsu, Y. Ikuhara and K. Hayashi, ACS Appl. Energy Mater., 2020, 3, 6824–6833 CrossRef CAS.
- J. D. Forero-Saboya, E. Marchante, R. B. Araujo, D. Monti, P. Johansson and A. Ponrouch, J. Phys. Chem. C, 2019, 123, 29524–29532 CrossRef CAS PubMed.
- K. Fujii, H. Wakamatsu, Y. Todorov, N. Yoshimoto and M. Morita, J. Phys. Chem. C, 2016, 120, 17196–17204 CrossRef CAS.
- G. A. Giffin, A. Moretti, S. Jeong and S. Passerini, J. Phys. Chem. C, 2014, 118, 9966–9973 CrossRef CAS.
- S.-A. Hyodo and K. Okabayashi, Electrochim. Acta, 1989, 34, 1551–1556 CrossRef CAS.
- S.-A. Hyodo and K. Okabayashi, Electrochim. Acta, 1989, 34, 1557–1561 CrossRef CAS.
- M. Shimizu, H. Usui and H. Sakaguchi, Phys. Chem. Chem. Phys., 2015, 18, 5139–5147 RSC.
- J. A. Seel and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 892–898 CrossRef CAS.
- F. M. Alcorn, K. L. Kuntz, D. L. Druffel and S. C. Warren, ACS Appl. Energy Mater., 2018, 1, 5062–5067 CrossRef CAS.
- C. Pulla Rao, A. M. Rao and C. N. R. Rao, Inorg. Chem., 1984, 23, 2080–2085 CrossRef.
- M. Shimizu, T. Koya, M. Umeki and S. Arai, J. Electrochem. Soc., 2018, 165, A3212–A3214 CrossRef CAS.
- M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094507 CrossRef.
- M. S. Dresselhaus and G. Dresselhaus, Adv. Phys., 2006, 30, 139–326 CrossRef.
- Q. Liu, H. Wang, C. Jiang and Y. Tang, Energy Storage Mater., 2019, 23, 566–586 CrossRef.
- T. Abe, H. Fukuda, Y. Iriyama and Z. Ogumi, J. Electrochem. Soc., 2004, 151, A1120–A1123 CrossRef CAS.
- M. Shimizu, T. Ohnuki, T. Ogasawara, T. Banno and S. Arai, RSC Adv., 2019, 9, 21939–21945 RSC.
- D. Aurbach, A. Schechter, M. Moshkovich and Y. Cohen, J. Electrochem. Soc., 2001, 148, A1004–A1014 CrossRef CAS.
- B.-A. Mei, O. Munteshari, J. Lau, B. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 194–206 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Raman spectra of Mg(TFSA)2/DMF; cyclic and liner sweep voltammograms; survey XPS spectra of graphite electrodes; STEM and TEM images of graphite after electrochemical tests, impedance spectra of graphite electrodes during galvanostatic charge/discharge tests (PDF). See DOI: 10.1039/d1cp02895b |
| This journal is © the Owner Societies 2021 |