 Open Access Article
Open Access ArticleCurled cation structures accelerate the dynamics of ionic liquids†
Daniel
Rauber
 *a,
Frederik
Philippi
*a,
Frederik
Philippi
 b,
Björn
Kuttich
c,
Julian
Becker
b,
Björn
Kuttich
c,
Julian
Becker
 b,
Tobias
Kraus
b,
Tobias
Kraus
 ac,
Patricia
Hunt
ac,
Patricia
Hunt
 bd,
Tom
Welton
bd,
Tom
Welton
 b,
Rolf
Hempelmann
b,
Rolf
Hempelmann
 a and
Christopher W. M.
Kay
a and
Christopher W. M.
Kay
 *ae
*ae
aDepartment of Chemistry, Saarland University, Campus B2.2, 66123, Saarbrücken, Germany. E-mail: daniel.rauber@uni-saarland.de
bDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, London W12 0BZ, UK
cINM-Leibniz Institute for New Materials, Campus D2.2, 66123, Saarbrücken, Germany
dSchool of Chemical and Physical Sciences, Victoria University of Wellington, New Zealand
eLondon Centre for Nanotechnology, University College London, 17-19 Gordon Street, London WC1H 0AH, UK. E-mail: c.kay@ucl.ac.uk
First published on 6th September 2021
Abstract
Ionic liquids are modern liquid materials with potential and actual implementation in many advanced technologies. They combine many favourable and modifiable properties but have a major inherent drawback compared to molecular liquids – slower dynamics. In previous studies we found that the dynamics of ionic liquids are significantly accelerated by the introduction of multiple ether side chains into the cations. However, the origin of the improved transport properties, whether as a result of the altered cation conformation or due to the absence of nanostructuring within the liquid as a result of the higher polarity of the ether chains, remained to be clarified. Therefore, we prepared two novel sets of methylammonium based ionic liquids; one set with three ether substituents and another set with three butyl side chains, in order to compare their dynamic properties and liquid structures. Using a range of anions, we show that the dynamics of the ether-substituted cations are systematically and distinctly accelerated. Liquefaction temperatures are lowered and fragilities increased, while at the same time cation–anion distances are slightly larger for the alkylated samples. Furthermore, pronounced liquid nanostructures were not observed. Molecular dynamics simulations demonstrate that the origin of the altered properties of the ether substituted ionic liquids is primarily due to a curled ether chain conformation, in contrast to the alkylated cations where the alkyl chains retain a linear conformation. Thus, the observed structure–property relations can be explained by changes in the geometric shape of the cations, rather than by the absence of a liquid nanostructure. Application of quantum chemical calculations to a simplified model system revealed that intramolecular hydrogen-bonding is responsible for approximately half of the stabilisation of the curled ether-cations, whereas the other half stems from non-specific long-range interactions. These findings give more detailed insights into the structure–property relations of ionic liquids and will guide the development of ionic liquids that do not suffer from slow dynamics.
Introduction
Ionic liquids (ILs) are a remarkable class of materials that bridge the behavioural region between conventional molecular solvents and high temperature molten salts. Due to their unique combination of properties they continue to be the focus of basic scientific research1 and usage in large scale industrial processes.2 Much of the application-oriented research is focused on the implementation of ILs in electrochemical devices such as supercapacitors3 or various types of batteries, including high-voltage Li-ion batteries.4 The efforts to use ILs in electrochemical applications are motivated by the ILs’ inherent conductivity, high electrochemical stability, wide liquid temperature ranges and good dissolution properties for electroactive species.5 Furthermore, they are generally non-volatile and non-flammable, thus offering improved safety compared to conventional organic solvents.5A general advantage of ILs is the possibility to adjust their properties in a targeted manner, for example to address the particular demands of an electrochemical device, a lubricant or for the solvation of biological molecules (such as proteins, cellulose or lignin).6 The number of chemically accessible ionic liquids is estimated to exceed those of molecular solvents by several orders of magnitude.2 Therefore, the search for sophisticated structure–property relations is essential for the development of ILs with optimised properties.
Fundamental investigations are even more vital since it is known that interactions in ILs are more complex than those of non-ionic fluids.6,7 This intricacy is mainly the result of the competition between different interaction types (e.g., hydrogen bonding, Coulomb and van der Waals forces) which span a range of strength and directionality. In addition, other factors such as geometry, ion flexibility as well as structuring on different time and spatial scales need to be considered. Systematic investigations of ILs with different anions, cations or incorporated functional groups are therefore highly important to advance the understanding of these diverse liquid materials and to facilitate further practical implementation.
One of the main limitations of ILs are their high viscosities compared to conventional molecular fluids due to strong and long-range interionic attractions. High viscosities complicate their practical handling and are connected to other important transport properties, such as conductivity. Thus, minimising viscosity is a central goal in the development of novel ILs.
Achieving high conductivities is usually of central interest for electrochemical applications of ILs. The viscosity η of an IL is proportional to the molar conductivity ΛM by the Walden relation given in eqn (1),
| ΛM ∝ (η−1)t | (1) |
 | (2) |
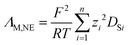 | (3) |
 | (4) |
The quantification of an IL's deviation from an ideally behaving electrolyte is important from a practical point of view to improve the electrolyte conductivity. However, it lacks an underlying theory and is the subject of controversies in the scientific community.9 The deviation from an ideal electrolyte is often attributed to ion-pairing or the formation of ion aggregates. These forms of ion clustering generate formally neutral species that cannot contribute to charge transport, similar to the situation in conventional electrolyte solutions, where ion aggregation/ion paring is a well-known phenomenon.12 The existence of aggregated (overall charge-reduced) species in aprotic ILs is still a scientific controversy and there are both experimental and theoretical studies that support13,14 or oppose15,16 this interpretation.7,17 For hydroxyl-group containing ILs aggregation has even been reported for like-charged ions.18
Frequent reports on differences between diffusion coefficients of ILs measured or simulated on different scales in time and space raise further questions regarding the underlying mechanism of ion aggregation.19 This may be similar to the situation in glass-forming materials where heterogeneous dynamics and relaxation rates are commonly found. Other explanations for the discrepancy between calculated and experimental conductivity propose charge transfer from anion to cation.20,21 This charge transfer leads to non-integer ionic charges and suppressed association of ions with opposite charges.22 Under this interpretation the Nernst–Einstein equation is considered valid and deviations are proposed to be due to close contact of the ions allowing for charge transfer. Feng et al. developed another rationalisation and argued, based upon results from molecular dynamics (MD) simulations, that the Nernst–Einstein equation is valid but that there are free and bound states of ion diffusion.23 These different diffusional states make different contributions to the overall conductivity, in analogy to semiconductors.23
The individual ion diffusion coefficients are commonly measured by NMR spectroscopy (with pulsed or steady magnetic field gradients), where an averaged diffusion over comparatively long timescales (on the order of milliseconds to seconds) is observed. Therefore, different diffusion states or timescale dependent diffusion coefficients might serve as an explanation for why ion aggregation is seen in some experiments, but not in others. Timescale dependent diffusion is supported by both MD simulations and experiments where different types of diffusion, namely subdiffusion on short timescales and Gaussian diffusion on long timescales, are found.24 Recently it was reported that the dynamic properties that ILs share with other glass forming materials, such as subdiffusive behaviour, breakdown of Stokes–Einstein relation and applicability of the Vogel–Fulcher–Tammann equation for the T-dependence of the transport quantities, have their origin in the dynamics of the ion cages intrinsically present in molten salts.25
Furthermore, there are many experimental and computational studies providing evidence for the aggregation of ILs on the nanoscale forming distinct, segregated domains of accumulated non-polar side chains and polar, ionic groups.7,26,27 The formation of this nanoscale structure is driven by a combination of dispersion and solvophobic interactions and is more pronounced for longer alkyl chains. The rigidity of this adopted nanostructure is directly linked to the measured properties, leading to slower dynamics for more persistent structures.28
Despite the dispute in the literature about the interrelations of different transport properties in ILs, their quantification and optimisation are still highly important for further development of and technical implementation of ILs. Quantification of the inter-relationship of transport properties and the development of a better understanding of the underlying transport mechanisms require systematic investigation of ILs. In principle this means the underlying structure of the ILs needs to be rationally varied, one property at a time.1 Systematic investigations of the underlying structure–property relations can be obtained by altering the molecular structures of the ions comprising the IL. For this purpose we synthesised and characterised a series of IL based on the tris(2-methoxyethyl)methylammonium cation [N(2O1)31]+ with different anions. The results were compared to the non-functionalised IL with the tributylmethylammonium cation [N4441]+.
In a previous study, we found that multiple ether substituents attached to ammonium and phosphonium cations lead to a significant increase in the dynamics of the ions.29 However, the origin of the accelerated liquid dynamics remained to be addressed. Possible reasons for the beneficial transport properties could lie in curling of the ether side chains around the cations (found from calculations of the lowest energy geometries and energies for different conformers), or the absence of a rigid nanostructure in these ILs due to the higher polarity of the ether tail compared to the alkyl group. Other investigations in the literature have also revealed that single ether-containing side chains in the cation lead to a curling of the ether chain around the cation center.30–33 It was shown in the mentioned literature reports30–33 and our previous29 investigations that curling prevents the manifestation of a pronounced nanostructure which occurs for ILs with hydrocarbon chains of sufficient length. For the imidazolium systems the formation of the polar-nonpolar domains begins to emerge for hydrocarbon substituent groups larger than butyl.7
The set of ammonium ILs applied here was chosen to obtain insight into the general influence of multiple ether functionalisation and anion choice on transport properties and nanostructure. The structural formula and abbreviations of the investigated ions as well as a visualisation of the investigated properties and their interrelations are shown in Fig. 1. The ammonium cation class is less well investigated than ILs based on imidazolium cations. Nevertheless, ammonium ionic liquids also offer a combination of attractive properties. For example, the ammonium cations have (in general) a higher electrochemical stability than imidazolium cations.34 Moreover, the ammonium cations are cost-efficient in their synthesis, making them attractive candidates for practical applications. Attaching ether groups to the IL cations has been shown to have a beneficial influence on the dynamics of ILs, and also increased the liquid range,35 while thermal and electrochemical stabilities are only minimally effected. Possible applications of multiple ether-containing ammonium ILs include electrolytes for lithium batteries36 and solvents for cellulose.37
The desirable faster dynamics of ILs formed from cations with ether-chains have been assumed to result from an increasing conformational flexibility of the cations.38,39 We will show here that the change in the transport properties results from the altered cation conformations, where the ether chains curls towards the nitrogen centre of the cation. The resulting contracted structures have a significant influence on IL properties: the curling systematically leads to much lower liquefaction temperatures, significantly accelerated dynamics, increased fragilities, higher densities and more diffuse ion coordination compared to the alkylated ammonium ILs. Nevertheless, at the same time no distinct change in liquid nanostructure is observed.
For a formerly studied set of ammonium ionic liquids also comparing the influence of ether and alkyl substitution – but for cations with an additional methylene unit in the side chains – a distinct nanostructure of polar-nonpolar alternation was found for all ILs with the methyltripentyl-ammonium [N5551]+ cation, independent of the anion used.29 Therefore, it was not clear whether the trends in property changes upon introduction of ether groups were the result of the altered cation conformation or stem from the suppression of a nanostructural organisation by the more polar ether groups.
Using a new set of cations, here we are able to resolve the question of whether the different transport, density, and melting properties are mainly the result of the altered liquid structure or the result of altered cation conformation. Herein, we report combined results from scattering experiments and MD simulations that reveal comparable liquid nanostructures and significantly accelerated dynamics, for the curled-ether compared to the linear-alkyl cations. We are thus able to identify the change in the cation conformation (curling vs. linear) as the dominant effect for the distinctly altered properties. Using quantum chemical calculations, we are able to estimate (on a semi-quantitative level) the contributions to stabilisation of the curled cation conformers. Roughly half of the stabilisation stems from intramolecular hydrogen-bonds and half from long range interactions between the methoxy and peripheral alkyl groups.
Materials and methods
Details about the synthesis and characterisation of the ionic liquids are given in the ESI† (Section 1). Sample purity was checked by multinuclear nuclear magnetic resonance (NMR) spectroscopy; the absence of halides in the samples was confirmed by ion chromatography or testing with diluted aqueous silver nitrate solution. All samples were dried in vacuum at 45 °C for at least two days prior to each physicochemical measurement and further handled under inert conditions using Schlenk lines, a glove box and an NMR-port to avoid moisture uptake. Water contents below 100 ppm were determined by Karl–Fischer titration.Physicochemical properties
Thermal transitions and decompositions, dynamic viscosities, specific conductivities and self-diffusion coefficients were measured under inert gas conditions following procedures presented in previous publications.26,35,40 Thermal transitions were determined using dynamic scanning calorimetry (DSC) with sealed aluminium crucibles and slow scan rates of ±1 °C min−1 on a DSC 1 STARe (Mettler Toledo, Gießen, Germany) equipped with liquid nitrogen cooling. Thermal stabilities were investigated by dynamic thermogravimetric analysis (TGA) on a TGA/DSC 1 STARe System (Mettler Toledo, Gießen, Germany) under a nitrogen atmosphere. Decomposition temperatures were obtained with a heating rate of +10 °C min−1 and are given as extrapolated onsets. Density and specific conductivity measurements were performed with an estimated thermal stability of ±0.01 °C using the Proline RP 1845 thermostat bath (LAUDA, Lauda-Königshofen, Germany). The maximal temperature deviation for the dynamic viscosity measurements was ±0.01 °C with an estimated uncertainty in the viscosity of ±1.0% estimated by comparison to commercial viscosity standards and repeated measurements. The uncertainty of the specific conductivity measured by impedance spectroscopy with a commercial conductivity probe consisting of two platinised platinum electrodes (WTW, Weilheim, Germany) with a nominal cell constant of 0.5 cm−1, was ±2%, as estimated by repeated measurements and comparison with conductivity standards. The molar conductivity ΛM was calculated from the obtained specific conductivity κ and density ρ according to eqn (5) | (5) |
Ion self-diffusion coefficients were determined by the pulsed field-gradient stimulated echo (PFGSTE) pulse sequence with bipolar field gradients and longitudinal eddy current delay41,42 on an AVANCE II 400 NMR spectrometer (Bruker, Billerica, USA) with a 5 mm BBFO probe. Cation self-diffusion coefficients were determined using the 1H nucleus, while for the anions the 19F nuclear resonance was used. The temperature-control unit of the NMR spectrometer was calibrated using neat methanol and neat ethylene glycol43 with a temperature accuracy of ±0.2 °C. Gradient calibration was carried out with water purified with a Milli-Q ultrapure water system (Merck KGaA, Darmstadt, Germany) in the insert of a coaxial NMR tube. Vacuum dried ionic liquids were placed in the insert of a coaxial NMR tube which was flame sealed under vacuum using an NMR port. The coaxial inserts were chosen over conventional NMR tubes to minimise the influence of convection and increase temperature stability. The self-diffusion coefficients were determined using the Stejskal-Tanner eqn (6) for the decrease of signal intensity with increasing gradient strength
 | (6) |
All transport properties were fitted using the empirical Vogel–Fulcher–Tammann (VFT) eqn (7) that has its origin in glass physics and is widely used in the field of ILs, since ILs can be classified as fragile glass formers with respect to the T-dependence of their transport properties:44
 | (7) |
The dried samples used for the small angle X-ray scattering (SAXS) measurements were placed in borosilicate capillaries and flame sealed. The measurements were conducted on a Xeuss 2.0 laboratory set-up (Xenocs, Grenoble, France) with a Genix 3D source providing X-rays at the copper Kα-line with a wavelength of λ = 1.54 Å that were registered by a Pilatus 3R 1 M and a Pilatus 100 K detector (Dectris, Baden-Daettwil, Switzerland). Using this setup, scattered intensity was recorded in a range of 0.02 Å−1 < q < 3.02 Å−1 with the scattering vector q = |![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | = 4π
| = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)λ−1 and the scattering angle 2θ. The resulting isotropic 2D scattering patterns were radially averaged into 1D scattering curves and peaks were analysed using Lorentzian line shapes.
sin(θ)λ−1 and the scattering angle 2θ. The resulting isotropic 2D scattering patterns were radially averaged into 1D scattering curves and peaks were analysed using Lorentzian line shapes.
Computational methods
Ab initio and Density Functional Theory (DFT) calculations were carried out using Gaussian 09, Revision E.09.47 Geometry optimisations were performed at the B3LYP-GD3BJ/6-311+G(d,p) level of theory with Grimme D3 dispersion correction48 and Becke–Johnson damping.49 A pruned integration grid with 99 radial and 590 angular points per shell was used. No symmetry constraints were used. The SCF convergence was set to 10−10 RMS change on the density matrix. Tightened optimisation convergence criteria of 2 × 10−6/1 × 10−6 on maximum/RMS force and 6 × 10−6/4 × 10−6 on maximum/RMS displacement. Stationary points were confirmed to be minimum geometries by frequency analysis (absence of imaginary normal modes).To enable parameterisation of the force field: linear [N4441]+, curled [N(2O1)31]+ and linear [N(2O1)31]+ were optimised (see xyz files, given in the ESI†). These minimum geometries were chosen based on a previous conformational study of the relevant backbone dihedral angles.29 Preferred local geometries are (approximately) 60°, 180°, 300° (symmetrically equivalent) for the C–N–C–C dihedral angles, 180° for the C–C–O–C and C–C–C–C dihedral angles, 60° for the N–C–C–O dihedral angle and 180° for the N–C–C–C dihedral angle.29 From these preferred local geometries, C3 symmetrical starting conformers were constructed, which naturally minimises steric clash (in particular of the curled ether side chains). An exception was linear [N(2O1)31]+, for which the N–C–C–O dihedrals were deliberately set to the preferred value for an alkyl side chain (i.e. 180°) rather than that of the ether side chain (i.e. 60°). In addition to the geometries optimised at the B3LYP-GD3BJ/6-311+G(d,p) level of theory, full MP2/cc-pVTZ//B3LYP-GD3BJ/6-311+G(d,p) calculations were also carried out. SCF convergence was tightened to 10−10 RMS change on the density matrix for DFT and 10−11 for MP2 calculations. CHELPG and atomic dipole corrected Hirshfeld charges were calculated for both methods; B3LYP-GD3BJ/6-311+G(d,p) and full MP2/cc-pVTZ//B3LYP-GD3BJ/6-311+G(d,p). Geometries (Fig. S5, ESI†) and partial atomic charges (Tables S18–S20, ESI†) can be found in the ESI† (Section 11).50,51
To study intramolecular interactions, curled [N111(2O1)]+, linear [N111(2O1)]+, curled C111(2O1) and linear C111(2O1) were optimised at the B3LYP-GD3BJ/6-311+G(d,p) level of theory as described above. The structures were selected following the same criteria as outlined for linear [N4441]+, curled [N(2O1)31]+ and linear [N(2O1)31]+. To allow direct comparison, the initial geometries for curled C111(2O1) and linear C111(2O1) were obtained from their (isoelectronic) ammonium counterparts by replacing nitrogen with carbon. Single point HF/cc-pVTZ and full MP2/cc-pVTZ calculations were then performed, with the SCF convergence tightened to 10−11 RMS change on the density matrix.
Natural Bonding Orbitals (NBOs) were calculated with the NBO program (version 6.0).52 Topological analysis of the electron density within the Quantum Theory of Atoms in Molecules (QTAIM) was performed with AIMAll (Version 19.10.12).53 Non-Covalent Interaction (NCI) calculations for the analysis of delocalised intramolecular interactions were performed with the NCIPLOT4 software54 employing a grid spacing of 0.05 Å in each direction of space. Integration of the electron density within volumes enclosed by NCI surfaces was realised with cut-offs of 0.05 a.u. and 0.5 on the electron density and on the reduced electron density gradient, respectively. The results of the NCI calculations were visualised as two-dimensional scatter plots with gnuplot (version 5.2) and as three-dimensional NCI plots with VMD (version 1.9.3 https://doi.org/10.1016/0263-7855(96)00018-5).55 Energy decomposition analysis was used to identify the physical origins of intramolecular interactions. Psi4 (version 1.3.2)56 was used to perform intramolecular Symmetry Adapted Perturbation Theory (SAPT) calculations with the cc-pVTZ basis set to allow for a comparison with relative HF/cc-pVTZ energies. Density fitting was used during SAPT calculations as computation times are reduced while interaction energies do not change significantly.57 Further information on these methods and corresponding results can be found in the ESI† (Section 12).
Classical molecular dynamics (MD) simulations were undertaken. The geometries of [N4441]+ and [N(2O1)31]+, and the corresponding atomic dipole moment corrected Hirshfeld (ADCH) charges at the full MP2/cc-pVTZ//B3LYP-GD3BJ/6-311+G(d,p) level of theory were used as basis to create three forcefields (see Section 11, Tables S17–S19 in the ESI†). Lennard Jones parameters were taken from the literature for methylene and methyl groups,58 the nitrogen atom,59 and the oxygen atom.60 Similarly, we used common values for harmonic bond and angle stretching constants as well as Optimised Potentials for Liquid Simulations (OPLS) parameters for any dihedral involving at least one hydrogen atom.60–62 The remaining three backbone dihedrals (C–N–C–C, C–C–X–C, N–C–C–X with X = C, O) were parameterised in this order by fitting the difference between the ab initio dihedral potential energy scan29 and the classical force field equivalent (with the respective dihedral values zeroed) with the OPLS63 potential. Even with zeroed dihedral coefficients, the classical force field already accounts for some of the non-bonded interactions, which need to be subtracted from the target ab initio potential energy surface before fitting with the OPLS potential.59 Notably, the force field for the [N(2O1)31]+ cation in a linear conformation was obtained by using the ab initio surface of the N–C–C–C scan in [N1114]+ to fit the N–C–C–O dihedral in the classical force field. All force field parameters are given in the ESI,† in separate text files. The format of the force field parameter (.ff) and the geometry (.xyz) files is compatible with fftool. The force field parameters for [NTf2]− are well optimised in the CL&P force field and were kept unchanged.59,64
Classical molecular dynamics simulations were performed using the LAMMPS software package (version 11 Aug 2017).65 The molecular topology was created using fftool66 and packmol,67 1024 ion pairs were packed into cubic boxes of initially 140 Å side length. We used periodic boundary conditions with a particle–particle particle–mesh solver for Coulombic interactions and a relative error in forces of 10−5. Nonbonded (Lennard-Jones and Coulomb) interactions were scaled with 0, 0, or 0.5 between pairs of atoms separated by 1, 2, or 3 bonds, respectively. We used a cutoff of 12 Å for both Lennard-Jones and Coulomb interactions. Lennard-Jones pair coefficients between different atom types were obtained by geometric mixing. All carbon-hydrogen bonds were constrained to their equilibrium values using the SHAKE68 algorithm with a tolerance of 10−4 and a maximum of 20 iterations. Neighbour lists were re-built every time an atom moves more than half the neighbour skin distance of 2 Å. Equations of motion were integrated using the velocity-Verlet algorithm with a timestep of 1 fs. Linear and angular momenta of the box was zeroed every 5000 steps, rescaling the velocities to ensure energy conservation. NVT (NPT) ensembles were realised using a Nosé–Hoover chain thermostat (thermostat and barostat) with a chain length of three, using the Martyna-Tuckerman-Klein correction.69,70 The damping parameters were 100 fs for temperature and 1000 fs for pressure. Details for the equilibration procedure and thermostats used are given in the ESI† (Section 11). Example input files and LAMMPS data files are also provided as ESI.†
The trajectories were analysed using TRAVIS,71,72 prealpha (source code, executable, input files and manual available on github, https://github.com/FPhilippi/prealpha) and VMD.55
Results and discussion
As the thermal and dynamic properties as well as the liquid structure are highly interrelated, (Fig. 1b), a separate discussion is hardly possible and some anticipations are unavoidable. To present the results in a comprehensible way, we chose to start with the thermal and dynamic properties to show that the incorporation of ether side groups into the cations gives ionic liquids with an attractive property combination. Afterwards, we will examine the underlying reason for the altered characteristics of the ether ILs by investigating liquid structure and cation conformation in comparison to the alkyl ones. Finally, we will give the answer as to why the ammoniums with three ether side chains form curled, compressed cation structures affecting dynamics and liquids structure.Thermal properties and density
The broad liquid range of many ionic liquids is an advantage that enables the application of ILs in a very diverse range of environments and conditions. ILs can be superior to standard liquid electrolytes due to their negligible volatility and associated non-flammability. The lower limit of the pure IL's liquid range is determined by its solidification either by vitrification (glass transition) or crystallization into an ordered solid. The upper limit of the IL application temperature is set by thermal degradation, since evaporation for most aprotic ILs is only observed under extreme conditions.73 Dynamic TGA was chosen to estimate the short term thermal stability and to allow for comparison with literature results. The obtained thermal transitions and decomposition temperatures are given in Table 1.| Ionic liquid | T c/°C | T g/°C | T cc/°C | T m/°C | T d /°C | Liquid range/°C |
ρ
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C/g cm−3 °C/g cm−3 |
|---|---|---|---|---|---|---|---|
| a Additional solid–solid transitions at 27 °C (cooling step) and 33 °C (heating step) are observed. | |||||||
| [N(2O1)31][FSI] | — | −85 | — | — | 294 | 379 | 1.317 |
| [N(2O1)31][NTf2] | — | −78 | — | — | 338 | 416 | 1.391 |
| [N(2O1)31][BETI] | — | −73 | — | — | 339 | 412 | 1.457 |
| [N(2O1)31][TSAC] | — | −77 | — | — | 321 | 398 | 1.335 |
| [N(2O1)31][OTf] | — | −67 | −24 | 19 | 311 | 292 | 1.276 |
| [N(2O1)31][TFA] | — | −68 | — | — | 195 | 263 | 1.210 |
| [N4441][FSI] | — | −81 | −24 | 32 | 296 | 264 | 1.178 |
| [N4441][NTf2] | — | −68 | −27 | 27 | 390 | 363 | 1.265 |
| [N4441][BETI] | — | −62 | −12 | 1 | 389 | 388 | 1.351 |
| [N4441][TSAC] | — | −75 | — | — | 351 | 426 | 1.205 |
| [N4441][OTf]a | 83 | — | — | 86 | 355 | 269 | — |
| [N4441][TFA] | — | −56 | −26 | 31 | 208 | 177 | 1.062 |
The structural diversity of ionic liquids makes it hard to predict thermal behaviour since phase transitions can vary significantly even upon slight modifications of the molecular structure. Furthermore, different polymorphs are sometimes found for the ILs crystalline state. Some ionic liquids show considerable (rotational) motion even in the solid state, leading to organic ionic plastic crystals with characteristic solid–solid transitions.74
Suppressed crystallisation and pronounced supercooling in ILs are related to the destabilised crystal lattice of ionic liquids.75 The low lattice energies of ILs are due to the size and shape, as well as the conformational flexibility of the ions which lead to high configurational entropy of the liquid state, affecting both thermal and dynamic properties.76 At the glass transition temperature, Tg, the structural relaxation takes place on long time scales that are not experimentally observable.77
The ammonium ILs studied here can be divided into two classes defined in the literature according to the types of phase transitions that they undergo.78 The first class shows only glass transitions in both cooling and heating traces. The second class forms an amorphous glass upon cooling, while heating causes a cold crystallisation followed by melting. All the ether substituted ammonium ILs, with the exception of tris(2-methoxyethyl)methylammonium triflate [N(2O1)31][OTf], and the alkylated tributylmethylammonium 2,2,2-trifluoro-N-(trifluoromethylsulfonyl)acetamide [N4441][TSAC] belong to the first class with only glass transitions. The second class is found mainly for the alkylated representatives as well as the ether containing triflate IL. [N4441][OTf] is the only sample in this study that belongs to a third class; it crystallised upon cooling and melted upon heating similar to the course usually found for conventional organic salts. This IL also has the highest melting point of all samples, shows nearly no supercooling and undergoes additional solid–solid transitions. Therefore, [N4441][OTf] is overall more comparable to conventional organic salts than to many ILs. As result of the unfavourable thermal characteristics, this particular sample was not investigated any further. Apart from the alkylated [OTf]− sample, all samples are room temperature ionic liquids or can easily be observed and handled in supercooled state at ambient temperature – an important criterion for many applications where ILs are promising.
The observed glass transition temperatures are lower for the [N(2O1)31]+ than for the [N4441]+ ionic liquids. The lowest values for Tg are found for the bis(fluorosulfonyl)imide [FSI]− anion, slightly higher ones for the bis(trifluoromethylsulfony)imide [NTf2]− and [TSAC]− anions, followed by the larger bis(pentafluoroethylsulfonyl)imide [BETI]−. The highest glass transition temperatures are observed for ILs with the non-flexible anions [OTf]− and trifluoroacetate [TFA]−.
The results obtained here are in accordance with general findings of a more entropically favoured liquid state for ions with a large number of possible arrangements (conformational flexibility or ion coordination). This thermodynamic favouring of the liquid state is the result of the increased configurational and conformational entropy. The introduction of multiple ether groups in the cations of ILs leads to lower solidification temperatures as a general trend and usually suppresses crystallisation. The reason for this lies in the ether groups, which lead to less well-defined anion arrangements around the cation, thus to higher configurational flexibility in the liquid state, and eventually lowered liquefaction temperatures. The gain in configurational entropy upon liquefaction due to the ether substitution of ILs is the consequence of the diffuse ion coordination in the liquid state. The increased conformational flexibility of the cations that increases the conformational entropy upon liquefaction due to the higher rotational freedom of the ether chains that has been mentioned in literature to explain the lower liquefaction temperatures of ether containing ILs seems to play only a minor role.79 A further consequence of the higher entropy difference for ether substituted ILs is that crystalline states are often not observed under common experimental conditions.2
The absence of ordered solid states and occurrence of glass formation for the ether substituted ILs is also observed in the DSC measurements here. The only exception in this set are crystalline states observed for the IL with an ether chain [N(2O1)31][OTf], which has a significantly lower melting point than the alkylated analogue. Literature investigations on ammonium IL with two ether groups also revealed the presence of mainly glass transitions.37,80 The impact of changing anion on the liquefaction temperatures for a common cation in this set is less distinct than that of changing cation when there is a common anion. The influence of the cations’ side chains on the entropy of the liquid state seems to be the dominant factor for these samples.
The lowest liquefaction temperatures for ILs with the same cation are found for the highly charge delocalised and flexible imide-type anions. This is again in accordance with higher configurational (charge delocalisation/non-specific interactions) and conformational (structural flexibility of the anion) entropy of the liquid state. For the imide anions the Tg values increase with the anion size, thus follow the trend [FSI]− < [NTf2]− < [BETI]− for both ether and alkyl ILs while for the melting points of the purely hydrocarbon ILs the situation is reversed. This indicates that the glass transition of the samples is mainly influences by the dispersion interaction, while the melting points are decreasing with Coulomb interaction. The absence of an ordered crystalline state for [N4441][TSAC] and the low glass transition temperatures of the [TSAC]−-ILs can be rationalised with the lower degree of symmetry in this amide-type anion compared to the more symmetric [FSI]−, [NTf2]−, and [BETI]−. In accordance with the lower gain in conformational entropy upon liquefaction, the more symmetric, less charge delocalised triflate and trifluoroacetate anions show the highest liquefaction temperatures for a common cation.
The thermal stability as the upper limit of the liquid range from dynamic TGA was higher for the alkylated samples. A slightly lower stability of ether-functionalised ILs compared to isostructural alkylated ones is a common finding in the literature.79,81 All of the investigated ammonium ILs have high thermal stabilities of about 300 °C or higher with the exception of the samples with the [TFA]− anion that decompose around 200 °C. The much lower thermal stability of the ILs with [TFA]− can be rationalised by the higher nucleophilicity of this anion compared to the other anions used here, similar to the trends of thermal stability found in the literature.34 The ILs with the [FSI]− anion have nearly identical thermal stabilities, while the largest difference in thermal stabilities is between the two cations with [NTf2]− reaching 52 °C. The general trend for the Td values of a common cation and varied anions follows the order [TFA]− < [FSI]− < [OTf]− < [TSAC]− < [NTf2]− ≈ [BETI]−.
The largest liquid range in this set was found for [N4441][TSAC], since the IL had only a glass transition and a high decomposition temperature. The widest liquid range for the ether containing ILs was found for [N(2O1)31][NTf2] with a value above 400 °C, while the lowest belonged to [N(2O1)31][TFA] with 263 °C. The overall liquid range for the ether containing ILs with a specific anion is higher than for the comparable alkylated one, with the exception of the [TSAC]− anion, and ranges both far below and far above ambient temperature, making it an overall interesting IL subclass for practical applications.
The densities of the ammonium ionic liquids at 25 °C correlate with the molecular weights of the anions in the order [TFA]− < [OTf]− < [FSI]− < [TSAC]− < [NTf2]− < [BETI]− for both the ether and alkyl substituted ILs. All the ILs with the [N(2O1)31]+ cation show higher densities than the corresponding [N4441]+ samples with the same anion, but the difference decreases with increasing anion weight. The highest ratio is found for the [TFA]− anion paired with the ether IL having an about 14% higher density and the lowest ratio is for the ILs with the [BETI]− anion where the ether-ILs density is only 8% higher. Since the cation molecular weight is quite similar, the higher densities for the [N(2O1)31]+-ILs must be rationalised by structural changes on the molecular level. Since an increased flexibility of the attached side chains induced by ether groups and the increase of free volumes is not in accordance with the observed higher densities of the ether ILs, an alternative explanation is required.
A suitable rationalisation of the ether ILs’ higher densities is the curling of the flexible side chains around the charged central unit of the cation creating more compact, contracted structures as has already been reported in the literature for quaternary ammonium and phosphonium ILs with a single ether substituent.30–33 The hypothesis that denser ether ILs are a result of the compressed cation structure is also supported by the slightly lower cation–anion distances observed from the SAXS measurements shown below. Additional temperature dependent values and linear fitting parameters for the densities are given in the ESI† (Section 2).
To conclude, multiple ether substituents generally increase the overall liquid range of the ammonium ILs by destabilising the crystalline state. This leads to an absence of crystallisation and lower glass transition temperatures for the ether compared to the alkylated analogues. However, decomposition temperatures of the ether ILs are lower and the densities higher than that of the alkylated ILs, slightly reducing the extent of this increase in liquid range.
Viscosity
The viscosity of a liquid is one of its central macroscopic properties and is related to the interactions on microscopic scale. Compared to conventional molecular fluids the viscosities of ILs are about two to three orders of magnitude higher, as a result of the presence of the strong and long-range Coulombic interactions.82 For most applications, ionic liquids with low viscosities are desired, since such representatives show faster dynamics of ions or solutes. Especially for advanced electrochemical applications, low-viscosity ionic liquids are of great interest to fully exploit their intrinsic conductivity that is inversely coupled to their viscosity (eqn (1)). The temperature dependence of the ILs’ viscosity can be well described by the VFT-eqn (7), which is widely applied in the literature for fragile glass-forming materials, as considerable deviations from Arrhenius-type behaviour are frequently found in these types of matter. The obtained fitting parameters and viscosity values at 25 °C for the investigated ammonium ILs are reported in Table 2 and the temperature dependence of the viscosity is shown in Fig. 2. The influence of the threefold ether substitution in the cations is shown in Fig. 3 as the ratio of the viscosity of the alkylated ILs to the ether ILs.| Ionic liquid |
η
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C/mPa s °C/mPa s |
η 0/10−3 mPa s | B/K | T 0/K | δ η |
|---|---|---|---|---|---|
| [N(2O1)31][FSI] | 73.7 | 203.1 | 684.6 | 182.0 | 3.76 |
| [N(2O1)31][NTf2] | 90.5 | 144.6 | 729.6 | 184.9 | 3.95 |
| [N(2O1)31][BETI] | 163.5 | 112.6 | 801.6 | 188.0 | 4.26 |
| [N(2O1)31][TSAC] | 69.7 | 185.7 | 620.5 | 193.5 | 3.21 |
| [N(2O1)31][OTf] | 299.9 | 128.0 | 811.0 | 193.6 | 4.19 |
| [N(2O1)31][TFA] | 205.9 | 148.3 | 746.5 | 194.9 | 3.83 |
| [N4441][FSI] | 399.0 | 100.4 | 1025 | 174.5 | 5.87 |
| [N4441][NTf2] | 555.8 | 65.5 | 1021 | 185.2 | 5.51 |
| [N4441][BETI] | 1186 | 29.7 | 1252 | 180.0 | 6.96 |
| [N4441][TSAC] | 293.0 | 89.6 | 904.7 | 186.4 | 4.85 |
| [N4441][TFA] | 1048 | 51.2 | 1087 | 188.7 | 5.76 |
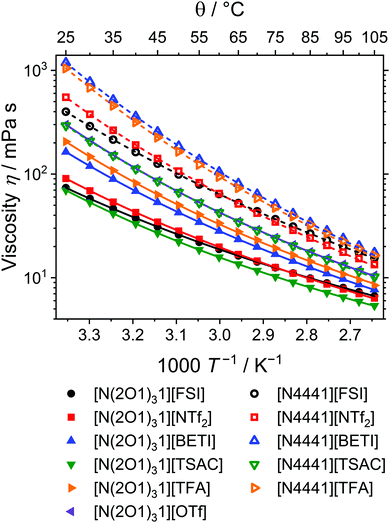 | ||
| Fig. 2 Temperature dependent viscosity of the ionic liquids. Drawn lines are the VFT fits according to eqn (7). Solid lines are the fits of the ether-substituted ILs, while dashed lines are used for the quaternary alkylated ammonium ILs. | ||
 | ||
| Fig. 3 Viscosity ratios of the alkyl (R = 4) and ether (R = 2O1) functionalised ionic liquids showing the significantly lower viscosity of the ether ILs. | ||
Comparing the viscosity values at 25 °C for ILs with the same anion shows that the ether-substituted ILs always have significantly lower viscosities. The lowest viscosity ratio of alkyl to ether was found for the [TSAC]− anion with a value of 4.2 and the highest for the [BETI]− anion being 7.3. The effect of single ether-substitution on viscosity was much lower than that of multiple substituents. For instance, the ratio between ethyldimethylpropylammonium [NTf2]– and the ether substituted analogue ethyldimethyl(2-methoxyethyl)ammonium [NTf2]− is only 1.18.83 Even the ether-IL with the highest viscosity, [N(2O1)31][OTf], has a value comparable to the alkyl IL with the highest fluidity. For the ether ILs, the viscosity values increase in the order [TSAC]− < [FSI]− < [NTf2]− < [BETI]− < [TFA]− < [OTf]−. The viscosity values of the alkylated ILs adopt almost the same ranking with the [BETI]− and [TFA]− samples interchanging. A viscosity of 85 mPa s was reported for a comparable ether ammonium IL where the N-methyl group was replaced by an ethyl group, [N(2O1)32][NTf2].36 This viscosity is similar to that found here for [N(2O1)31][NTf2], which is in the range to be expected as there are no significant structural changes. Even at the highest temperatures investigated here, the viscosities of the ether substituted ammonium ILs were only half the values of the alkylated analogues. In the whole temperature range investigated the order is maintained with the exception of the [FSI]− and [NTf2]− that have a crossover upon temperature increase both for the ether and alkyl ILs. For the ether cation the crossover is around 62 °C while for the totally alkyl cation a value of about 78 °C is found.
The viscosities at 25 °C resembled the trends found for the values of the glass transition temperatures. The lowest viscosities were found for the [FSI]−, [NTf2]− and [TSAC]− anions that have a high flexibility resulting from having different adaptable conformers and pronounced charge delocalisation.39 Similar to the trends of higher glass transition or melting temperatures, the ILs with the rigid, symmetrical and less charge delocalised, but smaller anions, [OTf]− and [TFA]−, show higher viscosities. Comparable findings were reported for ILs based on phosphonium cations with threefold ether-substitution.35 The viscosities that were reported for phosphonium ILs are also lower than for the ammonium cations investigated here.35 Improved transport properties by changing the central atom of quaternary IL cations from N to P is a well-recognised finding that is also valid for totally alkylated species.29,84 The low viscosity for the ILs with the [TSAC]− anion is believed to result from its asymmetric substitution pattern.
At room temperature the imide-type ILs obey a viscosity order similar to their molecular weight and size, thus [FSI]− < [NTf2]− < [BETI]−. However, due to the crossover of the viscosity values, the [NTf2]− ILs have a slightly higher fluidity at higher temperatures. That [FSI]−-based ILs may have higher viscosities than the [NTf2]− ones with the same cation was also found for other systems such as quaternary phosphonium cations.35 The origin of the occasionally higher viscosities for [FSI]− ILs compared to [NTf2]− ILs with the same cation might lie in the smaller ion size of the bis(fluorosulfonyl)imide allowing for better interactions with the bulky cations. The hypothesis of the altered interactions as a result of the reduced anion size is supported by the lower ion distance found for the [FSI]− anion in SAXS experiments (perturbed system including geometrical and specific interaction effects) compared to the ion distance calculated from the individual ion radii (unperturbed system). The proposition that the viscosity crossover of these ions has a molecular origin is also promoted by the finding that the cation self-diffusion coefficients of both the [N(2O1)31]+ and [N4441]+ cations with these anions also have a crossover, as will be shown below. On the other hand the highest viscosity values for [N4441][BETI] can be explained by the high molar mass and large size of the anion.
A general finding in the field of ILs is the pronounced supercooling and formation of amorphous glasses instead of long range ordered crystalline structures. For glass-forming materials the evolution of dynamic properties with temperature is of great interest for both practical applications as well as basic science, since the dynamic properties of glassy matter still lack full understanding.44,85 The kinetics of glass forming liquids are related to thermodynamics through their configurational entropy following the Adam–Gibbs Model75 which was recently demonstrated to be also valid for ionic liquids.76 Using the changes in their viscosities with temperature, glass-forming liquids can be distinguished into strong and fragile. While strong glass formers obey an Arrhenius-type behaviour with constant activation energy, the fragile glass formers follow the VFT-equation and show a growth in the apparent activation energy upon cooling. Strong glass formers therefore show straight lines in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η vs. Tg/T graph (Angell plot) while for the fragile ones curves are found.77,86 The fragility of a liquid can be investigated by both dynamic and calorimetric methods86 and is often quantified by Angell's strength parameter δ (or equivalently the fragility index m).87 Low values of the strength parameter indicate highly fragile liquids, while high values correspond to Arrhenius type behavior.88
η vs. Tg/T graph (Angell plot) while for the fragile ones curves are found.77,86 The fragility of a liquid can be investigated by both dynamic and calorimetric methods86 and is often quantified by Angell's strength parameter δ (or equivalently the fragility index m).87 Low values of the strength parameter indicate highly fragile liquids, while high values correspond to Arrhenius type behavior.88
For a given anion the Angell strength parameter δη is always smaller for the ether-ILs than for the alkylated ones, so that the fragility of the ether-IL is higher than for the ILs without side-chain functionalisation. For ionic liquids with the same cation, the [TSAC]− anion has the highest fragility, while the lowest fragility belongs to the [BETI]− anion. This connection between the propensity for supercooling, glass formation and fragility in ionic liquids has been previously reported.89 All values for δη found for the ionic liquids in this set are very low and in the range of those found for highly fragile organic glass formers.89 In the literature the lower limit for the strength parameter has been given to be about 3.2,89 close to that of multiple ether-substituted ILs. For the prototypical alkylated 1-butyl-3-methyl imidazolium ILs ([C4C1im]+) δη values of 4.65 for the [NTf2]−,87 5.75 for the tetrafluoroborate [BF4]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89 and 6.96 for the hexafluorophosphate [PF6]− anion87 have been reported. The fragilities of these widely used imidazolium salts are thus higher than that of the ether-substituted but the same range as the alkylated ammonium ionic liquids reported here. For the 1-alkyl-3-methyl imidazolium [CxC1im]+ ILs with the [PF6]− anion the strength factor increases with increasing alkyl chain length, where a δη value of 7.81 for the hexyl (x = 6) and a δη value of 8.91 for the octyl chain (x = 8) are given.87
89 and 6.96 for the hexafluorophosphate [PF6]− anion87 have been reported. The fragilities of these widely used imidazolium salts are thus higher than that of the ether-substituted but the same range as the alkylated ammonium ionic liquids reported here. For the 1-alkyl-3-methyl imidazolium [CxC1im]+ ILs with the [PF6]− anion the strength factor increases with increasing alkyl chain length, where a δη value of 7.81 for the hexyl (x = 6) and a δη value of 8.91 for the octyl chain (x = 8) are given.87
Dynamic heterogeneities are believed to be the reason for the generally high fragility of ionic liquids. This behaviour was observed in many simulations and could also offer an answer to the deviation from Nernst–Einstein behaviour.6 Dynamic heterogeneities in ILs were for instance reported by Hu and Margulis who found non-Gaussian diffusion for ionic liquids even at room temperature.90 MD simulations suggest that these are typical properties of ILs as fragile glass formers that stem from the presence of dynamic ion cages,25 thus from a type of molecular order inherently present in all ILs, and not from nanostructures that are often absent.
Fragile liquids have non-directional, dispersive interactions whereas network-forming liquids, such as the prototypical SiO2, fall in the class of strong liquids.85 The trends for the relation of intramolecular interactions and liquid structure to fragility are also observed in literature reports of the ILs, where the fragility decreases with formation or enhancement of a nanostructure, induced by elongation of the alkyl side-chain ([CxC1im][PF6] ILs) and more rigid ions (e.g. [PF6]−vs. [NTf2]−).87 A possible rationalisation of the lower fragilities for the alkylated ammonium ionic liquids might be that they result from the tendency of alkyl chains to aggregate and form non-polar domains. ILs with such networks of alternating polar and nonpolar domains intrinsically have a higher degree of bulk structure, which could result in growth of the strength factor for the [CxC1im][PF6] ILs with increasing x.
It is well established that alkyl-groups in ionic liquids of sufficient length show a tendency to aggregate in nonpolar domains whereby this mesostructure is more pronounced for longer the non-polar side chains. For the case of the [CxC1im][PF6] ILs (as well as many other IL systems7) this has been demonstrated by simulations27 and scattering experiments.91,92 However, this explanation not applicable for this set of ammonium ILs since there is no evidence for nanosegregation in the SAXS patterns. Instead, the higher fragility of the ether ILs can be rationalised by the curled cation conformation. As will be shown from the complementing SAXS data, spatial distribution functions and Coulomb interaction energies, the curled structures adopted by the ether-substituted cations show significantly more isotropic coordination of the anions towards the cations. Therefore, the ions of the ether substituted ILs form more diffuse cages/shells, resulting in less overall structuring on the molecular level. This also manifests in shorter lifetimes of ion cages, as shown below in the faster decay of the non-Gaussian parameter α2. Thus, the overall more diffuse ionic arrangement in the ether-substituted ILs seems to be responsible for their increased fragilities compared to the alkylated analogues. This explanation of less well-defined bulk structures also fits well to the general trends for a single cation with varied anions. Accordingly, ILs with flexible and less symmetric anions which adopt less well-defined alternating structures, tend to have higher fragilities than symmetric and rigid anions, as is found for this set of ammonium ILs and the literature results on [C4C1im]+ ILs with different anions.87,89 However, as the resultant fragilities are a mix of different contributions, only general trends can be derived and individual contributions of the specific cation–anion pair might also be present, which together makes quantitative predictions more complicated.
In summary, attaching ether groups to ammonium cations is in general a valuable tool to increase fluidity and fragility of ionic liquids significantly. The general anion trends for the absolute values of viscosity and fragility resemble those from the thermal phase transition behaviour to a large extent. However, the details in the trends might vary for individual cation–anion combinations due to special characteristics of the combined interaction effects.
Electrochemical properties
As ionic liquids are frequently used in electrochemical applications, their conductivity is one of their most important characteristics. The experimental molar conductivities (eqn (5)) of the ammonium ionic liquids of this set are shown in Fig. 4, while the values for the molar conductivity at 25 °C, the VFT fitting parameters and obtained Angell strength factors for the molar conductivity δΛM are given in Table 3. Experimental values for the specific conductivity and further details can be found in the ESI† (Section 5).| Ionic liquid |
Λ
M
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C/mS cm2 mol−1 °C/mS cm2 mol−1 |
Λ M,0/S cm2 mol−1 | B/K | T 0/K | δ Λ M |
|---|---|---|---|---|---|
| [N(2O1)31][FSI] | 736 | 219.1 | −698.8 | 175.9 | 3.97 |
| [N(2O1)31][NTf2] | 534 | 256.3 | −723.0 | 181.4 | 3.98 |
| [N(2O1)31][BETI] | 261 | 263.8 | −777.7 | 186.0 | 4.18 |
| [N(2O1)31][TSAC] | 657 | 214.9 | −667.3 | 183.2 | 3.64 |
| [N(2O1)31][OTf] | 160 | 279.8 | −834.1 | 186.4 | 4.47 |
| [N(2O1)31][TFA] | 194 | 217.3 | −760.7 | 189.8 | 4.01 |
| [N4441][FSI] | 178 | 416.0 | −960.4 | 174.4 | 5.51 |
| [N4441][NTf2] | 101 | 499.5 | −995.7 | 181.0 | 5.50 |
| [N4441][BETI] | 39.5 | 401.1 | −972.7 | 192.9 | 5.04 |
| [N4441][TSAC] | 165 | 381.2 | −904.8 | 181.4 | 4.99 |
| [N4441][TFA] | 36.1 | 415.2 | −1005 | 190.5 | 5.28 |
In general, the trends in molar conductivity resemble the results obtained for viscosity, which is expected given the connection of the properties via the Walden relation. For the [N(2O1)31]+-cation the conductivity decreases in the same order as the viscosity increases with the exception that the ILs with the highest conductivity, i.e. [TSAC]− and [FSI]−, are interchanged. For the alkylated cation the molar conductivity decreases in the sequence [FSI]− > [TSAC]− > [NTf2]− > [BETI]− > [TFA]−, thus for the imide-type ILs a clear trend with increasing molecular weight is found, while the lowest conductivity belongs to the IL with the smallest molar mass. This again demonstrates that the obtained transport properties are quite sensitive to the geometric and electronic structure of the incorporated ions. The influence of these factors will be further demonstrated to be also valid for the ether-substituted cations compared to the isostructural alkylated cations.
The trends for the strength factors from different transport properties, δη and δΛM, are also comparable. This means that the ether ILs with the highest fragilities are achieved with the [TSAC]− and [FSI]− anions, intermediate fragilities are found for [NTf2]− and [TFA]−, while the highest fragilities belong to ILs with the [BETI]− and [OTf]− anions. For alkylated cations the order of fragilities from the conductivity is somewhat different to the values from the viscosity since the symmetric imide-type ions change their order. Overall, the absolute values of the fragilities by the two different methods deviate less than 10% with the exception of [N(2O1)31][TSAC] and [N4441][BETI].
The Walden plot of the logarithmic fluidity (inverse viscosity) versus the logarithmic molar conductivity yields straight lines for all samples, as shown in Fig. 4b. Details of the fits are given in the ESI† (Section 8). All slopes obtained for these samples are in the range from 0.92 to 0.94 which is in the range of the values commonly reported for ILs. For instance Walden plot slopes of 0.88 to 0.95 are reported for [CxC1im]+ with [BF4]− and [PF6]− anions,93 respectively, while values of 0.90 to 0.97 are found for imidazolium [NTf2]− ILs.94 The intercept of the linear fittings in the Walden plot gives information about which ionic liquids have the highest molar conductivity for the same viscosity, which is also sometimes interpreted in terms of ionicity,95 as is the case with the inverse Haven ratio.9 We found many parallels between the two measures of ionicity. For instance, the ionicity for the two cations by both measures decreases with the size of the symmetrical imide-type anions, thus [FSI]− > [NTf2]− > [BETI]−, the lowest values are obtained for the [TFA]−-ILs and the ionicities at the same temperature are higher for the alkylated samples with the exception of the [TSAC]− representatives. Furthermore, the trends for the ionicities’ dependence on ether functionalisation or type of anion are also quite similar to the results for phosphonium ILs.35,96
All ammonium ionic liquids in this set exhibit electrochemical windows larger than 4.6 V, where alkylated cations showed generally slightly higher decomposition voltages than the ether containing analogues. Details about the stability limits determined by cyclic voltammetry are given in the ESI† (Section 7). The broad voltage range applicable makes the ammonium ILs suitable for many types of batteries where highly stable electrolytes are required.
Diffusive properties
In contrast to viscosity and conductivity, the self-diffusion coefficients give information about the dynamics of individual ions. The measured self-diffusion coefficients DSi, their ratios, the calculated Nernst–Einstein deviation parameters ΔNE and inverse Haven ratios HR−1 as a measure of ionicity are given in Table 4. Due to experimental limitations, the self-diffusion coefficients of [N4441][BETI] and [N4441][TFA] could only be obtained at slightly elevated temperatures (45 °C). However, the values are included for comparison and it should be noted that the inverse Haven ratio HR−1 often shows temperature dependence.9 This temperature dependence is not observed or has only a very minor effect on the ratios of the self-diffusion coefficients as will be shown below, so the DS+/DS− at different temperatures compare well.| Ionic liquid | T/°C | D S+/10−12 m2 s−1 | D S−/10−12 m2 s−1 | D S+/DS− | Δ NE | H R −1 |
|---|---|---|---|---|---|---|
| [N(2O1)31][FSI] | 25 | 13.9 | 17.8 | 0.78 | 0.38 | 0.62 |
| [N(2O1)31][NTf2] | 25 | 11.5 | 11.6 | 0.99 | 0.39 | 0.61 |
| [N(2O1)31][BETI] | 25 | 6.20 | 5.22 | 1.19 | 0.39 | 0.61 |
| [N(2O1)31][TSAC] | 25 | 14.8 | 15.8 | 0.94 | 0.43 | 0.57 |
| [N(2O1)31][OTf] | 25 | 4.23 | 4.25 | 1.00 | 0.50 | 0.50 |
| [N(2O1)31][TFA] | 25 | 4.98 | 5.02 | 0.99 | 0.48 | 0.52 |
| [N4441][FSI] | 25 | 2.78 | 3.82 | 0.73 | 0.28 | 0.72 |
| [N4441][NTf2] | 25 | 1.96 | 2.18 | 0.90 | 0.35 | 0.65 |
| [N4441][BETI] | 45 | 4.61 | 4.64 | 0.99 | 0.48 | 0.52 |
| [N4441][TSAC] | 25 | 3.40 | 3.94 | 0.86 | 0.40 | 0.60 |
| [N4441][TFA] | 45 | 4.85 | 5.07 | 0.95 | 0.55 | 0.45 |
As expected from the other transport properties, the self-diffusion coefficients of both ions for a particular ionic liquid are significantly higher when methylene units in the cation are replaced by oxygen atoms. At the same temperature the cations’ and anions’ self-diffusion coefficients follow the order [TSAC]− > [FSI]− > [NTf2]−, except for the anion self-diffusion coefficients with the [N(2O1)31]+ cation, for which the [FSI]− anion diffuses faster than the [TSAC]− anion. The ratios of the cation to anion self-diffusion coefficient of the same IL are always higher for the ether-cations compared to the alkylated cations with the same anion. This already shows that the increase in the transport properties is mainly a cation effect and to a lesser extent the result of the cation–anion combination. For all ammonium ILs in this work, the diffusion of the cation is slower than the diffusion of the anion, with the exception of [N(2O1)31][BETI]. The ionicities at 25 °C are higher for the alkylated cations, with the largest difference of 0.10 for the [FSI]− anion and the smallest for the [TSAC]− anion with a value of 0.03.
The obtained ionicities for this set of ILs at 25 °C range from 0.57 to 0.72 which is in the range of 0.45 to 0.8 typically found for neat aprotic ionic liquids.9 For ILs with the [C4C1im]+ cation, for instance, values of 0.62 for the [NTf2]−, 0.64 for the [BETI]−, 0.57 for the [OTf]− and 0.52 for the [TFA]− anion have been reported.97 These anion trends for a common cation from the literature reflect the values and trends obtained here for the series of the [N(2O1)31]+ cation quite well. Similar trends and ionicity values are also found for phosphonium ionic liquids that are closer to the ammonium samples in their structure.35,96
To obtain a deeper insight into the temperature dependent movement of the individual ions, temperature dependent self-diffusion was measured for the cations with the anions that show the highest fluidities, [FSI]−, [NTf2]− and [TSAC]−. The plot of the diffusion coefficients is shown in Fig. 5. Similar to the other transport properties, the individual self-diffusion coefficients deviate from Arrhenius behaviour, and obey the VFT equation. The VFT fitting parameters and resulting Angell's strength factors δDSi are given in Table 5. The fragilities arising from both cation and anion self-diffusion coefficients increase upon substitution of methylene units by ether groups. However, there are no further clear trends in the ratios of the fragilities for the same ionic liquid and for the same anion. For comparison the temperature dependent self-diffusion coefficients of [C4C1im][NTf2] yield Angell's strength parameters δDS+ of 7.83 and δDS− of 5.96, calculated from the published data,94 which are in the similar range of the values found for the [N4441]+-ILs here.
| Ionic liquid | i | D Si/10−9 m2 s−1 | B/K | T 0/K | δ D Si |
|---|---|---|---|---|---|
| [N(2O1)31][FSI] | + | 12.46 | −834.9 | 175.1 | 4.77 |
| [N(2O1)31][FSI] | − | 11.84 | −754.4 | 182.1 | 4.14 |
| [N(2O1)31][NTf2] | + | 9.942 | −713.5 | 192.3 | 3.71 |
| [N(2O1)31][NTf2] | − | 10.43 | −722.3 | 191.6 | 3.77 |
| [N(2O1)31][TSAC] | + | 17.28 | −835.4 | 179.3 | 4.66 |
| [N(2O1)31][TSAC] | − | 11.18 | −701.1 | 191.2 | 3.67 |
| [N4441][FSI] | + | 20.68 | −1096 | 175.1 | 6.26 |
| [N4441][FSI] | − | 19.24 | −971.8 | 184.2 | 5.28 |
| [N4441][NTf2] | + | 26.71 | −1084 | 183.5 | 5.91 |
| [N4441][NTf2] | − | 41.04 | −1176 | 177.5 | 6.63 |
| [N4441][TSAC] | + | 50.18 | −1260 | 165.3 | 7.62 |
| [N4441][TSAC] | − | 69.16 | −1318 | 161.7 | 8.15 |
The double logarithmic Stokes–Einstein plot of inverse viscosity versus DSi × T−1, as shown in Fig. 5b, gives straight lines for all the ionic liquids with slopes ranging from 0.987 to 1.020, thus unity (within the measuring accuracy, details on fitting are given in the ESI,† Section 10). For comparison, the series of [CxC1im][NTf2] ILs yielded slopes for Stokes–Einstein plots of 0.92 to 0.97.94 Dynamic heterogeneities have previously been reported to manifest as a stronger increase in viscosities than in diffusion coefficients, thus a breakdown of the Stokes–Einstein relation98 is usually found for supercooled liquids.99 Studies of the temperature dependence of the relaxation rates and transport properties have revealed that the dynamics of ionic liquids are similar to supercooled liquids, even at temperatures that are far above the glass transition.100
The ammonium systems investigated here obey the Stokes–Einstein relation in the temperature range within which the measurements were conducted. This may be interpreted as the absence of pronounced nanostructural or dynamical heterogeneities in the T-range and timescale of the diffusion measurements, which agrees with the findings in the experimental SAXS data and MD simulations. The inherent presence of cage structures in ionic liquids, consisting of ions that are surrounded by ions of opposite charge, is reported to lead to timescale-dependent self-diffusion coefficients101 found by both experiment19 and simulations.25 Therefore, the dynamic heterogeneities and breakdown of the Stokes–Einstein behaviour is expected to be observable only at much lower temperatures or much shorter timescales.
The dependence of ion diffusion on the timescale and the observation of dynamic heterogeneities manifests in the non-Gaussian parameter α2 on short diffusion times. In these time domains, usually in the range of nanoseconds, a subdiffusive behaviour is commonly observed for ionic liquids,102 similar to the result of the MD simulations reported below. Since the self-diffusion coefficients reported here are obtained by NMR-spectroscopy as averaged values on comparable long timescales (range of microseconds), it is very likely that the dynamic heterogeneities simply cannot be probed using this experimental approach. Another rationalisation is that the ammonium systems behave in a more ideal way compared to other ionic liquids cations, such as the imidazolium, where slopes of the Stokes–Einstein plots smaller than unity were found.94 This could be explained by the absence of directed intermolecular interactions such as hydrogen bonding,103 and the closer to spherical shape of the ammonium ions. Further experiments, which are beyond the scope of this work, could clarify whether the Stokes–Einstein relation remains valid for the ammonium ionic liquids in the low T-region and on short timescales, in which the breakdown of the Stokes–Einstein behaviour is reported and dynamic heterogeneities should occur.103,104
The temperature-dependent ratios of the self-diffusion coefficients and the ionicity given as inverse Haven ratio are shown in Fig. 6. While the ratios of the self-diffusion coefficients are independent of temperature within experimental error for all investigated samples, the ionicities of the investigated samples show a slight decrease of 0.09 to 0.14 upon increasing the temperature from 25 to 85 °C. Similar to the occurrence of ionicity itself, its temperature dependence is still heavily disputed.9 For imidazolium systems with [BF4]− and [PF6]− anions a slight change of both the ratios of the self-diffusion coefficients (maximum change of approximately 0.1 in DS+/DS−) and the Nernst–Einstein deviation factor are reported (maximum change of 0.05 in the range of 40 to 80 °C).93 The ionic liquid butyl-trimethyl ammonium [NTf2]−, which is more similar to the samples investigated here, was reported to have an ionicity of 0.66 at about 298 K and showed no clear temperature dependence of HR−1.105 The trends in the T-dependence of the inverse Haven ratios resemble the findings obtained by the Walden plots very well. In the Walden plot, values that are closer to the bisection of the graph (sometimes called ‘ideal KCl line’) are interpreted to correlate with lower deviations from the ideal electrolyte behaviour, thus higher ioncities.9 Similarly, the more negative values of the intercept in the Walden plot linear fits belong to ILs with higher degrees of ion association. This is frequently also interpreted as a measure of ionicity, but some care should be taken about the conclusions drawn.106 However, the trends may still give valuable insight into the interrelations of the transport properties. For these samples, the similar findings for the inverse Haven ratio and the Walden plot specifically mean that the order [FSI]− < [NTf2]− < [TSAC]− as well as [N4441]+ < [N(2O1)31]+ for the deviation from the ideal behaviour are found. Furthermore, both correlations show a slight temperature-dependence towards larger deviations from Nernst–Einstein or Angell–Walden behavior.106
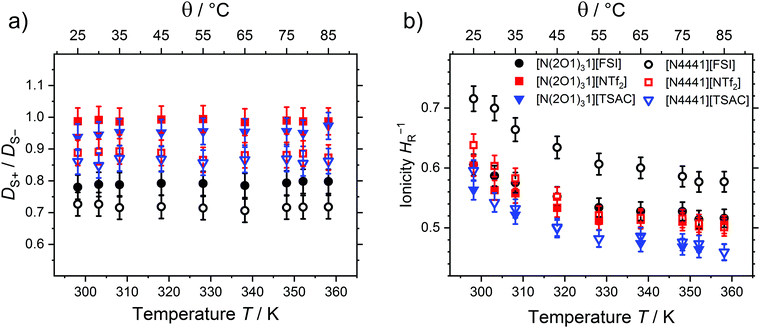 | ||
| Fig. 6 Temperature dependence of (a) the self-diffusion coefficient ratios and (b) the ionicity as inverse Haven ratio. | ||
Using the modified Stokes–Einstein eqn (8) for stick conditions, which correlates the individual self-diffusion coefficients and viscosities with the hydrodynamic radii rh,i (Stokes radii), it is possible to determine the friction an individual ion experiences using the introduction of a correction term f:
 | (8) |
In the case of classical Brownian motion, modelled by a large spherical particle in a continuum, the correction term equals to unity. However, for systems with aggregation or strong interactions, non-spherical particles, as well as for the diffusion of particles that are of similar size to the surrounding medium, such as it is the case for bulk liquids, significant deviations of the correction factor towards lower values are found.107 This deviation from conventional Stokes–Einstein diffusion was also previously reported for several ionic liquid systems based on both molecular dynamics simulations102 and experiments.107 We have calculated the correction factor for the ammonium ionic liquids by taking the ion radii from previous ab initio calculations.21 Both the ab initio and MD calculations gave nearly identical values of the [NTf2]− anion's radius.
The calculated values for the Stokes radius rh,i and correction factors f are given in the ESI† (Section 10) and show only a negligible influence of temperature. The deviations of these ammonium ILs from the conventional Stokes–Einstein relation for both the cation and anion are quite large and the correction factors range from 0.41 to 0.56. The quite large deviations from the Stokes–Einstein relation for each ion results from a combination of the ion's properties and its interaction with the other surrounding ions. The strong, long range intermolecular Coulombic force in the dense ionic medium, quite similar ion sizes and non-perfect spherical ion shapes for these samples therefore lead to quite different conditions as those for which the Stokes–Einstein eqn (8) was derived. However, the obtained values for 6f are close to the values of 4, which then corresponds to the Stokes–Einstein equation for slip conditions. Values for the correction term f of about 0.5 were also reported for other alkylated quaternary ammonium ionic liquids with the [NTf2]− anion108 as well as for quaternary ether-containing ammonium ionic liquids with [NTf2]− and borate-based anions.109 The deviation from the conventional Stokes–Einstein eqn (8) for stick conditions (f = 1) might therefore be the result of the assumptions made in the deviation of the equation that are hardly met for ionic liquids. For a given cation–anion pair the f values are quite similar, indicating the mutual influence of the constituting ions. The weak T-dependence of f is expected given the small changes in densities (max. 4.5%) in the investigated T-range and slopes of the Stokes–Einstein plot that are very close to unity. The virtually constant values for the friction terms of the ions as a function of T are a clear indication that there are no distinct changes of intermolecular interactions, ion conformation or aggregations for a particular IL in the investigated temperature interval. Overall the correction factors for both cation and anion are significantly lower for the ILs with the [N(2O1)31]+ cation compared to [N4441]+. These results can be interpreted as the smaller deviation of the ether-substituted cations from the spherical shape as a result of the curling. This explanation is also in accordance with the finding that correction factors of the [TFA]− anions are significantly higher than the ones for the other ions.
The experimental evidence so far suggests that it is merely the shape of the cation that leads to the accelerated dynamics in ether functionalised cations. We tested this hypothesis further with molecular dynamics simulations. Three simulations with different force fields were set up: [N4441][[NTf2], curled [N(2O1)31][NTf2], and linear [N(2O1)31][NTf2]. The curled [N(2O1)31][NTf2] is the ‘native’ form. For the linear [N(2O1)31][NTf2], the parameterisation of the N–C–C–O dihedral is changed so that the cation preferably adapts an extended conformation, as is the case for pure alkyl chains. The change in the charges is negligible, see the further details in the ESI† (Section 11), and the C–N–C–C and C–C–O–C dihedral angles are fitted to the ‘native’ potential of the 2O1 side chain. Thus, a tracing back of changes in the dynamic properties solely to the shape of the cation as defined by the N–C–C–O dihedral angle becomes possible.
The bulk dynamics can be probed conveniently using the mean squared displacement. The mean squared displacement is proportional to tγ,110eqn (9). The corresponding log–log plot of the mean squared displacement is shown in Fig. 7.
log〈r2(t)〉 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6D + γlog 6D + γlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t | (9) |
It is evident that the bulk behaviour for all three systems transforms from free particle behaviour (ballistic regime, at short timescales) to normal diffusion (Gaussian behaviour/random walk), leading to a slope of 1 in the log–log plot. This transition is largely complete after 3 ns. Fitting the mean squared displacement r2(t) for the cation in curled [N(2O1)31][NTf2] using eqn (9) between 3–7 ns gives γ = 0.97, and γ = 0.99 for 7–15 ns. The changes in the relaxation behaviour are also visible in the non-Gaussian parameter α2, eqn (10).102 The α2 parameter quantifies spatial-temporal heterogenous relaxation, i.e. dynamical heterogeneity, thus type and extent of deviation from Gaussian diffusion. On a timescale of up to 100 ps, α2 increases due to beta relaxation, which is a signature of single particle dynamics.111 On larger timescales, α2 slowly decreases again, approaching zero after approximately 10 ns. This decrease is a signature of collective dynamics, termed alpha relaxation.111 In general, a peak in α2 is interpreted as dynamical heterogeneity, i.e. the presence of spatial domains which relax on different timescales.102,111–114 The α2 peak is less pronounced for the native [N(2O1)31][NTf2] with a curled cation, indicating that the accelerated dynamics for ionic liquids with this cation arise from a more efficient reorganisation of the charge network at intermediate timescales (100 ps).104,115,116
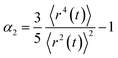 | (10) |
Critically, diffusion of both cations and anions in the simulation with the linear [N(2O1)31]+ cation is much closer to that of [N4441]+ than the curled [N(2O1)31]+, Fig. 7. The diffusion coefficients of the two cations in extended conformation are virtually identical, whereas that of the curled (ether) cation is 2–3 times higher. This is the case for both cations and anions, in both scaled and unscaled simulations, and for both runs, see the ESI† (Section 11, Table S21). Two main conclusions can be drawn from this observation. First, the accelerated dynamics in the [N(2O1)31]+ based ionic liquids is rooted in the shape and size of the cation. Second, the change in shape must influence the structural relaxation in the ionic liquid, since cations and anions are equally affected.
Liquid structure
The liquid structure of ionic liquids is frequently investigated by means of Small Angle X-ray Scattering (SAXS).7,30 They show up to three scattering maxima (‘peaks’) at scattering vectors q below 2 Å−1. The peak at the highest q-values is called the ‘adjacency peak’ and results from correlations between neighbouring atoms, both inter- and intramolecular.30 The adjacency peak (and further peaks at even higher q values) is found for every liquid. At intermediate qvalues of about 0.8 Å−1 the ‘charge peak’ is usually found. This peak is the result of the separation of cations and anions and their arrangement in ion shells in the proximity of counter charged ions. This peak can be absent due to cancellation of peaks and antipeaks, rather than the actual absence of cage-like structures around each single ion which results from the inherent charge separation in ionic liquids.30 For some ILs an additional ‘polarity peak’ is found at low q values, usually in the range of 0.5 Å−1 and lower. Contrary to the adjacency and the charge peak, this ‘prepeak’ is only found for ionic liquids with sufficiently large hydrocarbon segments. It is the result of a larger scale nanostructure consisting of nonpolar, hydrocarbon domains and polar, ionic domains as consequence of the solvophobic interactions between molecular segments with different polarities.The experimental SAXS patterns are displayed in Fig. 8 and fitted peak position as well as calculated real space distances are given in Table 6. For the ionic liquids with ether substituents, only two peaks are observed for all cases, corresponding to the adjacency and polarity peak. For the alkylated cations only very weak polarity peaks are observed. The very faint polarity peaks might be attributed as the beginning of the formation of a nanostructure being only poorly pronounced in the alkylated samples. This is in accordance with the weak signal intensity compared to ionic liquids with clear nanostructure and the small differences in the real space distances of polarity and charge peak. A poorly pronounced polarity peak was also found for other ionic liquids where the longest hydrocarbon chain is a butyl group.117,118 Literature reports on the sample [N4441][NTf2] are in good agreement with our peak analysis where a small shoulder was found as polarity peak at q = 0.63 Å−1, a charge peak at q = 0.78 Å−1 and a adjacency peak at q = 1.37 Å−1.118 The value obtained for the polarity peak of [N4441][NTf2] is consistent with the characteristic size of the nanoscale heterogeneities in [C4C1Im][NTf2] which is given as 9.00 Å.117 Our previous results showed that pentyl groups attached to the ammonium cations are sufficiently long to induce a clear nanostructural organisation that led to a distinct polarity peak with characteristic domain size of 11.11 Å.29 This compares well to the size of the nonpolar domains in the 1-pentyl-3-methylimidazolium ionic liquid [C5C1im][NTf2], reported to be 10.96 Å.117 The similarity of the hydrocarbon domain size is even more remarkable as quite different cations are compared.
 | ||
| Fig. 8 Radially averaged small angle X-ray scattering data at room temperature for (a) the ether substituted and (b) the alkylated ionic liquids. Regions where the polarity, charge and adjacency peaks30 are commonly observed are indicated by colours in the background. An exemplar fit using Lorentzian line shapes is also included. Inset in (b) shows the scattering data for [N4441][NTf2] in comparison to the methyltripentylammonium [N5551][NTf2] IL as investigated in a previous study.29 | ||
| Ionic liquid | Peak position | Real space distance | Ion distances/Å | ||||
|---|---|---|---|---|---|---|---|
| Polarity peak/Å−1 | Charge peak/Å−1 | Adjacency peak/Å−1 | Polarity peak/Å | Charge peak/Å | Adjacency peak/Å | ||
| [N(2O1)31][FSI] | — | 0.87 | 1.40 | — | 7.25 | 4.47 | 7.37 |
| [N(2O1)31][NTf2] | — | 0.80 | 1.32 | — | 7.82 | 4.77 | 7.82 |
| [N(2O1)31][BETI] | — | 0.76 | 1.26 | — | 8.25 | 5.01 | 8.17 |
| [N(2O1)31][TSAC] | — | 0.81 | 1.38 | — | 7.78 | 4.54 | 7.70 |
| [N(2O1)31][OTf] | — | 0.85 | 1.39 | — | 7.40 | 4.53 | 7.19 |
| [N(2O1)31][TFA] | 0.67 | 0.86 | 1.43 | 9.33 | 7.34 | 4.41 | 7.01 |
| [N4441][FSI] | 0.65 | 0.86 | 1.45 | 9.67 | 7.35 | 4.33 | 7.53 |
| [N4441][NTf2] | 0.62 | 0.79 | 1.38 | 10.1 | 7.94 | 4.56 | 7.98 |
| [N4441][BETI] | 0.61 | 0.77 | 1.31 | 10.3 | 8.18 | 4.79 | 8.33 |
| [N4441][TSAC] | 0.62 | 0.80 | 1.43 | 10.1 | 7.89 | 4.40 | 7.86 |
| [N4441][TFA] | 0.62 | 0.83 | 1.45 | 10.1 | 7.57 | 4.32 | 7.17 |
All ionic liquids with the [N4441]+ cation show a more pronounced charge peak compared to the samples with the [N(2O1)31]+ cation. All scattering vectors and corresponding real space distances of the samples are in the same range for the same type of peak. In particular, the real space distances of the adjacency peaks are about 4.5 Å, the charge peaks roughly 8.0 Å and the polarity peaks about 10 Å. The sample with the [TFA]− anion showed only weak charge peaks and the [N(2O1)31][TFA] sample is the only ether-containing sample that showed a polarity peak, but only very weakly pronounced. The weak charge peak for the [TFA]− ILs can be attributed to pronounced cancelling from antipeaks.30 The occurrence of the polarity peak for this ether substituted IL might be the result of geometric or electrostatic factors for this small, relatively charge localised anion. This might result in a competition between the anion and the ether chain oxygen atoms for coordination of the positively charged quaternary centre.
Notwithstanding that the values found for the scattering vectors are in the same range, there are some clear trends visible. All observed charge peaks correspond to real space distances in the order [FSI]− < [TFA]− < [OTf]− < [TSAC]− < [NTf2]− < [BETI]− for a given cation. For the adjacency peaks the same order is obtained, with the exception that [FSI]− and [TFA]− are exchanged. This correlates well with the ion size, at least for the flexible imide-type ILs, with [TFA]− and [OTf]− being exceptions which might result from the rigidity or relative charge asymmetry of these anions. The same order is also found when the polarity peaks of the imide-type alkyl ILs are regarded, i.e. larger anions lead to a larger characteristic size of the nanoscale heterogeneities. The real space distances of all charge and adjacency peaks are slightly smaller for samples with the alkylated cation, with the charge peak of the [BETI]− anion being the sole exception. For the trifluoroacetate ILs, the periodicity of the real-space domains is also smaller for the ether in comparison to the alkylated sample. The slightly shorter real space distances corresponding to the SAXS peaks again hint towards more compact structures of the ILs with ether cations. Despite the cation curling showing only minor differences in the values of the scattering vector it has significant impact on the properties of the ionic liquids as shown above. However, this marked impact is hardly visible in the scattering patterns that at first view seem to be very similar, with no distinct prepeaks indicative of nanoscale structures. For other ILs, nanostructuring was found to be directly connected to transport properties. In general, a more pronounced nanostructure slows down the dynamics. Remarkably, the influence of the cation curling is far less obvious from the SAXS data than the formation of the nanostructure as visualised in the insert of (Fig. 8b). Instead, the influence of the cation conformation on many physico-chemical properties of ILs seems to be greater than the impact of nanostructuring and only becomes more apparent upon comparison with the alkylated counterparts.
We compared the real space distance of the charge peak, thus the cation–anion distance in the liquid (which includes packing effects and free volume), to the expected ‘ideal’ cation–anion distance which is estimated as sum of the two ion radii determined from ab initio calculations (in the gas phase, i.e. without intermolecular interactions or perturbations).21 The results are given in Table 6 and are in good agreement with trends and absolute values found from the SAXS measurements. While the absolute values of the ion distances for the larger ions [TSAC]−, [NTf2]− and [BETI]− are nearly identical, the deviations for the smaller anions are more pronounced. For the [FSI]− anion, the simple addition of (ab initio determined) radii is 0.18 Å larger than that determined from SAXS measurements, whereas the calculated distances for the [OTf]− and [TFA]− anions are smaller than the experimental averaged ion distance by up to 0.33 Å, which is roughly 5% of the distance. The two different directions presumably have their origin in the differences of electronic and geometric structures for the flexible and highly charge delocalised [FSI]− in contrast to the rigid, more charge localised trifluoromethanesulfonate and trifluoroacetate. The qualitative differences between the anions thus manifest in the deviation of the experimental ionic liquid structure from the ideal model of unperturbed, spherical ions.
A main difference in the scattering pattern of the ammonium ILs, which only becomes noticeable when curled and linear cations are at hand, is that the charge and adjacency peaks are broader for the [N(2O1)31]+ cation as evaluated from the full-width at half maximum of the Lorentzian peak fits. These broader charge peaks indicate a greater range of anion cation distances and a more diffuse liquid structure with less-well defined ion coordination. The answer for this finding may lie in the curling of the ether chains around the cation which leads to a more spherical, shielded polar part of the ion and less clear ion coordination. The overall result of cation curling is the less well-defined coordination spheres of the anions around the cation and thus a broadening of the peaks. Evidence for this rationalisation is given by the spatial distribution functions that show blurred anion coordination towards the cation and lower values of the Debye length for the Coulomb stabilisation energy, Fig. 9. The explanation for the broader adjacency peaks is more complicated as it is not possible to separate the intra- and intermolecular contributions. Broader peaks for ether containing IL in comparison to the alkylated analogues were also found in literature results for other cations such as phosphonium and imidazolium.119
 | ||
| Fig. 9 Coulomb interaction energy (E) with respect to the ion–ion distance (r). Dashed lines are the fits according to eqn (10) for r > 10 Å. Lines in the insert show the values of the coulomb interaction energies E0 according to eqn (11). | ||
The SAXS profiles computed from the MD simulations match the experimental ones quite well in shape, peak position of the scattering vector and intensity ratio of the charge to the adjacency peak. The calculated peaks and resulting real space distances for the simulation and plot of the SAXS profiles are given in the ESI† (Section 11, Fig. S6). The maximum deviation of the peak positions computed from the MD simulation to the experimental ones is 4.7%.
The more pronounced localisation of the anions around the alkyl cation is also visible in the spatial distribution function, Fig. 10. For the ether-functionalised cation, the isosurface at 75% of the maximum value occupies a larger volume, thus the anions are more mobile. In contrast, the anions preferably occupy four well-defined sites in a tetrahedral arrangement fitting between the arms of the alkyl chain. In this location the anions minimise the distance to the local positive charge on the cation. Based on the ADCH charges employed in the force field, the positive charge is largely located on the hydrogen atoms geminal to the quaternary ammonium centre. The ADCH charge on the nitrogen atom is essentially neutral (0.055 for the [N4441]+ cation), whereas the charge on each of the hydrogen atoms of the methyl group in the [N4441]+ cation is 0.140.
Electrostatic sum rules allow more detailed insight into the screening behaviour, i.e. the structuring beyond the first shell.120 To this end, ions are treated as monopoles, i.e. as integer point charges located at the centre of charge of the molecular ion. From this approach, an oscillatory screening behaviour consistent with a pronounced shell structure is found, Fig. 9. The oscillatory decaying part (>10 Å) of the Coulomb interaction energy is fitted well by eqn (11).121
 | (11) |
Here, E(r) is the total Coulomb stabilisation energy that the point-like cations and anions experience from all other surrounding point-like ions within a sphere of radius r. Thus, E0 is the required energy to remove and fully separate an ion pair from the bulk, d is the oscillation period, λD is the Debye length, all within the point charge approximation.121 The amplitude A and phase shift φ will not be discussed here, all other quantities are given in Table 7. The asymptotic value for the Coulomb interaction energy E0 is 10 kJ mol−1 less negative for the ionic liquids with the curled ether-functionalised cation ([N(2O1)31][NTf2] curled) compared to both ionic liquids with linear side chains in the cations ([N(2O1)31][NTf2] linear and [N4441][NTf2]). Anions and ether groups compete for the positively charged polar part of the cations, see the next section a detailed discussion of the physical origin. This competition leads to the anions being partly displaced from the region surrounding the positive charge. Albeit small, the difference of 10 kJ mol−1 in E0 is significant, showing that the intermolecular electrostatic interaction is partly replaced with intramolecular interactions, see the next section. Similarly, the oscillation period is slightly larger for the ionic liquid with the curled ether-functionalised cation, since contraction of the ether side chains leads to a larger cation–anion distance, again in line with the anions being expelled from the region surrounding the positive charge.
| [N(2O1)31][NTf2] curled | [N(2O1)31][NTf2] linear | [N4441][NTf2] | |
|---|---|---|---|
| E 0/kJ mol−1 | −359.4(1) | −371.4(1) | −371.0(1) |
| Debye length λD/Å | 9.70(3) | 8.65(3) | 13.12(2) |
| Oscillation period d/Å | 8.464(3) | 8.019(3) | 8.164(1) |
| Amplitude A/kJ mol−1 | 742(4) | 771(4) | 689(1) |
| Phase shift φ | 4.941(4) | 4.838(5) | 4.872(2) |
The Debye length is a measure for the length scale over which electrostatic screening occurs, and is subject to an ongoing discussion in the ionic liquid community.23,122–130 By far the largest Debye length is found for the ionic liquid with the alkyl cation. We interpret this as a direct result of the localisation of ions, see Fig. 10, which reduces the degrees of freedom of the ions to react to local electric fields.
So far, we have identified relationships between ether functionalisation and macroscopic properties. We have furthermore identified the shape of these cations, i.e. the curling of the ether side chains, as the cause of the observed changes. Thus, the last unanswered question is what leads to these changes. A very similar case is the cholinium cation, an ammonium cation between two methylene groups separating an oxygen atom (of the hydroxyl group) from the positively charged cation centre. For the cholinium cation, the curled (gauche) conformation is preferred, which has been attributed to a combination of nonspecific electrostatic interactions between the oxygen atom and the alkyl periphery nitrogen as well as weak hydrogen bonds between oxygen and methylene groups.131,132 Experimental evidence points towards electrostatic interactions being more important in the case of choline.132
Physical origin of the cation curling
Intramolecular interactions were studied by means of electronic structure methods, in order to understand the preference for a curled geometry in the ammonium ions with ether chains [N(2O1)31]+. In addition, two model compounds – [N111(2O1)]+ and C111(2O1) – were investigated. [N111(2O1)]+ reduces the complexity of the system to one ether chain while neutral C111(2O1) allows the influence of the central nitrogen atom and charge to be analysed. All three molecules can adopt both linear and curled structures, Fig. S9 (ESI†), at the B3LYP-GD3BJ/6-311+G(d,p) level of theory. Relative energies, Table S24 (ESI†), indicate that both cations prefer the curled geometry, while the charge neutral analogue is energetically degenerate with respect to the two possible conformations (within the uncertainty of the methods). This observation points towards a significant contribution of the positive charge to the ultimate stabilisation of the curled ether chains in the cations. In the following sections different electronic structure methods were used to elucidate the effect of the central nitrogen atom. Background information on the employed methods can be found in the ESI† (Sections 12.1 through 12.4 and more detailed results are discussed in Section 12.6).Quantum theory of atoms in molecules (QTAIM) molecular graphs, Fig. S10 (ESI†), reveal intramolecular H-bonds between the ether oxygen atoms and hydrogen atoms of methyl groups adjacent to the central nitrogen/carbon atom. All H-bonds were classified as weak on the basis of QTAIM and NBO properties, see ESI† (Section 12.6.1). A small difference in H-bond strength between the two model compounds was found which is not significant enough to explain the difference in relative energies between the two conformations of [N111(2O1)]+ and C111(2O1). The NCI framework allows for a quantitative analysis of attractive and repulsive contributions to non-covalent interactions via Qbind values, see ESI† (Section 12.2). Qbind represents a net measure of non-covalent interactions and is related to the sum of the electron charges connected to attractive and repulsive interactions – the more negative Qbind, the more attractive a given interaction. Qbind is more positive for cations with curled (as opposed to linear) substituents, Table S27 (ESI†). Therefore, the increase in repulsive interactions is more pronounced than the increase in attractive interactions upon curling of the substituent group in the cation. This observation is contrary to the trends in relative energies of the different cation conformations. These findings support the interpretation that H-bonding alone is not the reason for the stabilisation of curled ether functionalised ammonium ions.131,132
Long-range electrostatic interactions seem plausible based on atomic charge distributions, Table S28 (ESI†). The negatively charged oxygen atoms in [N111(2O1)]+ (QQTAIM ≈ −1.03 to −1.06e) should experience electrostatic attraction to the positively charged hydrogen atoms (QQTAIM ≈ 0.06 to 0.09e) on the periphery of the ion. The peripheral hydrogen atoms in C111(2O1) carry negative charges (QQTAIM ≈ −0.01 to −0.03e) indicating a possible electrostatic destabilisation with the negatively charged oxygen atom (QQTAIM ≈ −1.05e) in the curled geometry. In the following section a symmetry-adapted perturbation theory (SAPT) analysis of the importance of long-range electrostatic interactions in the two model compounds is performed.
SAPT quantifies the total non-covalent interactions between two interacting fragments and decomposes the interaction energy in electrostatic, induction, dispersion and exchange contributions. Intramolecular SAPT calculations are only available at a semi-quantitative truncation of SAPT: SAPT(0). SAPT(0) treats the system at the Hartree–Fock level and corrects for dispersive terms (more information on SAPT can be found in ESI,† Section 12.4). Thus, SAPT(0) interaction energies (ESAPT(0)) were compared to relative energies between different conformers at the HF level (Erel,HF, Table S24, ESI†). Intramolecular SAPT calculations require partitioning of the molecule into two interacting fragments (A, B) and one linker fragment (C). [N111(2O1)]+ and C111(2O1) were partitioned according to two schemes: the first one studies the overall interaction between the ether group and the ion/molecule core while the second focusses on intramolecular H-bonding, Fig. S12 (ESI†). Intramolecular SAPT(0) calculations were carried out with the cc-pVTZ basis set.
For [N111(2O1)]+ attractive interactions between the methoxy group and the nitrogen atom with its alkyl periphery almost entirely recover the relative energy difference between curled and linear geometries (Erel,HF = 13 kJ mol−1, ESAPT(0) = −11 kJ mol−1). Comparison of the sum of attractive SAPT(0) contributions in representation (1) (overall stabilisation = −40 kJ mol−1) and representation (2) (stabilisation through H-bonding = −18 kJ mol−1) from Fig. S12 (ESI†) show that intramolecular H-bonding can only account for ≈50% of stabilisation. The other 50% of stabilisation stems from a combination of long-range electrostatic, induction and dispersion interactions between the methoxy group and the alkyl periphery, Fig. S13 (ESI†) (a more detailed explanation of the various SAPT(0) terms is presented in the ESI,† Section 12.6.3). Analogous intramolecular SAPT(0) calculations for C111(2O1) demonstrate that electrostatics between the methoxy group and the carbon-based core are destabilising (Eelst = +5 kJ mol−1), Fig. S13 (ESI†). Additionally, induction and dispersion contributions are less attractive for C111(2O1) (compared to [N111(2O1)]+), which accounts for the reduced stabilisation of the curled geometry. Electrostatic and induction contributions will be dominated by the charge distributions of the interacting fragments. Therefore, intramolecular SAPT(0) and QTAIM atomic charge data complement each other and pinpoint the importance of the overall positive charge, which polarises the hydrogen atoms of the alkyl periphery, for an additional long-range stabilisation of curled ammonium ions with ether functionalisation in the γ-position.
Conclusions
In this study the dynamic and structural properties of a set of ammonium ionic liquids (tris(2-methoxyethyl)methylammonium [N(2O1)3]+ and tributylmethylammonium [N4441]+) with various commonly used anions ([FSI]−, [NTf2]−, [BETI]−, [TSAC]−, [OTf]−, [TFA]−) were examined, with the focus on the influence of ether-substituents in the cation on the structure and dynamics. Many of the properties of the ILs are significantly altered in a beneficial way upon introduction of multiple ether side-chains. Upon substitution of methylene units by oxygen atoms, we observed a systematic lowering of the liquefaction temperatures, pronounced tendency for glass formation, significant acceleration of liquid dynamics and an increase in fragilities as well as densities. However, no distinct changes were visible in the SAXS patterns of the liquid structure, such as significantly altered cation–anion distances or pronounced nano-segregation.We attribute the significant change in liquid characteristics to the altered cation conformation of the ether substituted ILs rather than a change in the liquid nanostructure. Ether cations adopt a curled structure, where the ether chains curl towards the cation centre as a result of intramolecular attraction between the negatively charged ether group and the positively charged core comprised of the ammonium centre and the neighbouring methylene/methyl groups. Quantum chemical methods indicate H-bonding and non-specific long-range attraction have almost equal energy contributions to the cation curling.
MD simulations connect the cation conformation to translational dynamics and thus transport properties. To this end, we compared the diffusion of ionic liquids with (linear) alkylated ammonium cations to those with ether substituents, in both linear and curled conformations. The diffusion of linear ether and alkyl systems was found to be virtually identical, as opposed to the significantly accelerated dynamics obtained for the curled ether system. This result has two implications. First, the curling of the ether functionalisation leads to the experimentally observed macroscopic changes. Second, the presence of the ether group alone (without the curling) is insufficient to explain the differences in macroscopic transport properties. Finally, we showed that the occurrence of the curled cation structures leads to loose coordination of the anion around the cation with less well-defined ion cages/shells.
Overall, the curled conformations of the ether cation have a markedly larger influence on the transport properties of ILs than the formation of nanostructural aggregates. With these results, it is now clear that the highly desirable acceleration of dynamics, which has also been found for other ILs with multiple ether substitution,29,35 is mainly the result of the altered (curled) cation conformation rather than the absence of nanostructure due to the higher polarity of ethers. These findings could enable the design of novel ILs with improved transport properties, thus leading to competitive electrolytes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. P is grateful to Kateryna Goloviznina and Sascha Gehrke for helpful discussions about force field design and classical simulations in LAMMPs. JB thanks the Defence Science and Technology Laboratory (Dstl) for funding his PhD studies. This work is funded by the Imperial President's PhD Scholarship. Computational resources provided by the Imperial College Research Computing Service are gratefully acknowledged. DOI: http://10.14469/hpc/2232.Notes and references
- F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021 RSC.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- S. Pan, M. Yao, J. Zhang, B. Li, C. Xing, X. Song, P. Su and H. Zhang, Front. Chem, 2020, 8, 1–18 CrossRef PubMed.
- T. Rüther, A. I. Bhatt, A. S. Best, K. R. Harris and A. F. Hollenkamp, Batteries Supercaps, 2020, 1–36 Search PubMed.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- K. R. Harris, J. Mol. Liq., 2016, 222, 520–534 CrossRef CAS.
- O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902 CrossRef CAS PubMed.
- A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603–4610 CrossRef CAS.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658 RSC.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- W. Zhao, F. Leroy, B. Heggen, S. Zahn, B. Kirchner, S. Balasubramanian and F. Müller-Plathe, J. Am. Chem. Soc., 2009, 131, 15825–15833 CrossRef CAS PubMed.
- G. W. Driver, Y. Huang, A. Laaksonen, T. Sparrman, Y.-L. Wang and P.-O. Westlund, Phys. Chem. Chem. Phys., 2017, 19, 4975–4988 RSC.
- K. R. Harris, J. Phys. Chem. B, 2016, 120, 12135–12147 CrossRef CAS PubMed.
- B. Kirchner, F. Malberg, D. S. Firaha and O. Hollóczki, J. Phys.: Condens. Matter, 2015, 27, 463002 CrossRef PubMed.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- A. E. Khudozhitkov, J. Neumann, T. Niemann, D. Zaitsau, P. Stange, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 17863–17871 CrossRef CAS PubMed.
- Q. Berrod, F. Ferdeghini, J.-M. Zanotti, P. Judeinstein, D. Lairez, V. García Sakai, O. Czakkel, P. Fouquet and D. Constantin, Sci. Rep., 2017, 7, 2241 CrossRef PubMed.
- F. Philippi, D. Rauber, M. Springborg and R. Hempelmann, J. Phys. Chem. A, 2019, 123(4), 851–861 CrossRef CAS PubMed.
- F. Philippi, A. Quinten, D. Rauber, M. Springborg and R. Hempelmann, J. Phys. Chem. A, 2019, 123, 4188–4200 CrossRef CAS PubMed.
- O. Hollóczki, F. Malberg, T. Welton and B. Kirchner, Phys. Chem. Chem. Phys., 2014, 16, 16880–16890 RSC.
- G. Feng, M. Chen, S. Bi, Z. A. H. Goodwin, E. B. Postnikov, N. Brilliantov, M. Urbakh and A. A. Kornyshev, Phys. Rev. X, 2019, 9, 021024 CAS.
- M. Casalegno, G. Raos, G. B. Appetecchi, S. Passerini, F. Castiglione and A. Mele, J. Phys. Chem. Lett., 2017, 8, 5196–5202 CrossRef CAS PubMed.
- M. Sha, X. Ma, N. Li, F. Luo, G. Zhu and M. D. Fayer, J. Chem. Phys., 2019, 151, 154502 CrossRef PubMed.
- D. Rauber, P. Zhang, V. Huch, T. Kraus and R. Hempelmann, Phys. Chem. Chem. Phys., 2017, 19, 27251–27258 RSC.
- J. N. A. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- S. I. Lall-Ramnarine, M. Zhao, C. Rodriguez, R. Fernandez, N. Zmich, E. D. Fernandez, S. B. Dhiman, E. W. Castner and J. F. Wishart, J. Electrochem. Soc., 2017, 164, H5247–H5262 CrossRef CAS.
- F. Philippi, D. Rauber, B. Kuttich, T. Kraus, C. W. M. Kay, R. Hempelmann, P. A. Hunt and T. Welton, Phys. Chem. Chem. Phys., 2020, 22, 23038–23056 RSC.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- H. K. Kashyap, C. S. Santos, R. P. Daly, J. J. Hettige, N. S. Murthy, H. Shirota, E. W. Castner and C. J. Margulis, J. Phys. Chem. B, 2013, 117, 1130–1135 CrossRef CAS PubMed.
- K. Shimizu, C. E. S. Bernardes, A. Triolo and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256 RSC.
- K. Yoshii, T. Uto, N. Tachikawa and Y. Katayama, Phys. Chem. Chem. Phys., 2020, 22, 19480–19491 RSC.
- Z. Xue, L. Qin, J. Jiang, T. Mu and G. Gao, Phys. Chem. Chem. Phys., 2018, 20, 8382–8402 RSC.
- F. Philippi, D. Rauber, J. Zapp, C. Präsang, D. Scheschkewitz and R. Hempelmann, ChemPhysChem, 2019, 20, 443–455 CrossRef CAS PubMed.
- S. Fang, Y. Jin, L. Yang, S. Hirano, K. Tachibana and S. Katayama, Electrochim. Acta, 2011, 56, 4663–4671 CrossRef CAS.
- Z. Chen, S. Liu, Z. Li, Q. Zhang and Y. Deng, New J. Chem., 2011, 35, 1596 RSC.
- I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingärtner, J. Am. Chem. Soc., 2006, 128, 13427–13434 CrossRef CAS PubMed.
- F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, Chem. Sci., 2020, 11, 6405–6422 RSC.
- D. Rauber, F. Philippi, J. Zapp, G. Kickelbick, H. Natter and R. Hempelmann, RSC Adv., 2018, 8, 41639–41650 RSC.
- D. H. Wu, A. D. Chen and C. S. Johnson, J. Magn. Reson., Ser. A, 1995, 115, 260–264 CrossRef CAS.
- F. Philippi, D. Rauber, J. Zapp and R. Hempelmann, Phys. Chem. Chem. Phys., 2017, 19, 23015–23023 RSC.
- D. S. Raiford, C. L. Fisk and E. D. Becker, Anal. Chem., 1979, 51, 2050–2051 CrossRef CAS.
- P. Sippel, P. Lunkenheimer, S. Krohns, E. Thoms and A. Loidl, Sci. Rep., 2015, 5, 13922 CrossRef CAS PubMed.
- H. W. Hansen, F. Lundin, K. Adrjanowicz, B. Frick, A. Matic and K. Niss, Phys. Chem. Chem. Phys., 2020, 22, 14169–14176 RSC.
- C. A. Angell, R. D. Bressel, J. L. Green, H. Kanno, M. Oguni and E. J. Sare, J. Food Eng., 1994, 22, 115–142 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revis. E.09, Gaussian, Inc., Wallingford CT Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Theor. Comput. Chem., 2012, 11, 163–183 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0. Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013; http://nbo6.chem.wisc.edu/ Search PubMed.
- T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019, http://aim.tkgristmill.com Search PubMed.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, J. Chem. Theory Comput., 2020, 16, 4150–4158 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- S. A. Arnstein and C. D. Sherrill, Phys. Chem. Chem. Phys., 2008, 10, 2646 RSC.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. Kaminski and W. L. Jorgensen, J. Phys. Chem., 1996, 100, 18010–18013 CrossRef CAS.
- R. C. Rizzo and W. L. Jorgensen, J. Am. Chem. Soc., 1999, 121, 4827–4836 CrossRef CAS.
- E. K. Watkins and W. L. Jorgensen, J. Phys. Chem. A, 2001, 105, 4118–4125 CrossRef CAS.
- A. S. L. Gouveia, C. E. S. Bernardes, L. C. Tomé, E. I. Lozinskaya, Y. S. Vygodskii, A. S. Shaplov, J. N. C. Lopes and I. M. Marrucho, Phys. Chem. Chem. Phys., 2017, 19, 29617–29624 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Padua, Z. Gong and K. Goloviznina, https://github.com/agiliopadua/fftool DOI:10.5281/zenodo.18618.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103 CrossRef.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS PubMed.
- V. N. Emel’yanenko, G. Boeck, S. P. Verevkin and R. Ludwig, Chem. – Eur. J., 2014, 20, 11640–11645 CrossRef PubMed.
- J. M. Pringle, P. C. Howlett, D. R. MacFarlane and M. Forsyth, J. Mater. Chem., 2010, 20, 2056 RSC.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139–146 CrossRef CAS.
- S. Cheng, M. Musiał, Z. Wojnarowska and M. Paluch, J. Chem. Phys., 2020, 152, 091101 CrossRef CAS PubMed.
- L. Berthier, M. Ozawa and C. Scalliet, J. Chem. Phys., 2019, 150, 160902 CrossRef PubMed.
- E. Gómez, N. Calvar and Á. Domínguez, Ionic Liquids - Current State of the Art, InTech, 2015, pp. 199–208 Search PubMed.
- S. Tang, G. A. Baker and H. Zhao, Chem. Soc. Rev., 2012, 41, 4030 RSC.
- Y. Jin, J. Zhang, J. Song, Z. Zhang, S. Fang, L. Yang and S. Hirano, J. Power Sources, 2014, 254, 137–147 CrossRef CAS.
- J. Zhang, S. Fang, L. Qu, Y. Jin, L. Yang and S. Hirano, Ind. Eng. Chem. Res., 2014, 53, 16633–16643 CrossRef CAS.
- K. Marsh, J. Boxall and R. Lichtenthaler, Fluid Phase Equilib., 2004, 219, 93–98 CrossRef CAS.
- Z. J. Chen, T. Xue and J.-M. Lee, RSC Adv., 2012, 2, 10564 RSC.
- S. Seki, K. Hayamizu, S. Tsuzuki, K. Fujii, Y. Umebayashi, T. Mitsugi, T. Kobayashi, Y. Ohno, Y. Kobayashi, Y. Mita, H. Miyashiro and S. Ishiguro, Phys. Chem. Chem. Phys., 2009, 11, 3509 RSC.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- P. Lucas, J. Non-Crystalline Solids X, 2019, 4, 100034 CrossRef CAS.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2007, 52, 1080–1085 CrossRef CAS.
- C. A. Angell, Science, 1995, 267, 1924–1935 CrossRef CAS PubMed.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 4372–4377 CrossRef CAS.
- Z. Hu and C. J. Margulis, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 831–836 CrossRef CAS PubMed.
- A. Triolo, O. Russina, B. Fazio, R. Triolo and E. Di Cola, Chem. Phys. Lett., 2008, 457, 362–365 CrossRef CAS.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, T. G. A. Youngs and D. T. Bowron, J. Chem. Phys., 2010, 133, 074510 CrossRef PubMed.
- K. R. Harris and M. Kanakubo, J. Phys. Chem. B, 2016, 120, 12937–12949 CrossRef CAS PubMed.
- K. R. Harris and M. Kanakubo, Phys. Chem. Chem. Phys., 2015, 17, 23977–23993 RSC.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 1784–1788 CrossRef CAS.
- D. Rauber, F. Philippi, J. Zapp, G. Kickelbick, H. Natter and R. Hempelmann, RSC Adv., 2018, 8, 41639–41650 RSC.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- L. M. C. Janssen, Front. Phys., 2018, 6, 1–18 CrossRef.
- M. D. Ediger, Annu. Rev. Phys. Chem., 2000, 51, 99–128 CrossRef CAS PubMed.
- S. Hensel-Bielowka, Z. Wojnarowska, M. Dzida, E. Zorębski, M. Zorębski, M. Geppert-Rybczyńska, T. Peppel, K. Grzybowska, Y. Wang, A. P. Sokolov and M. Paluch, J. Phys. Chem. C, 2015, 119, 20363–20368 CrossRef CAS.
- H. R. Schober and H. L. Peng, Phys. Rev. E, 2016, 93, 052607 CrossRef CAS PubMed.
- T. Köddermann, R. Ludwig and D. Paschek, ChemPhysChem, 2008, 9, 1851–1858 CrossRef PubMed.
- A. Strate, V. Overbeck, V. Lehde, J. Neumann, A.-M. Bonsa, T. Niemann, D. Paschek, D. Michalik and R. Ludwig, Phys. Chem. Chem. Phys., 2018, 20, 5617–5625 RSC.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. Lett., 2020, 11, 2062–2066 CrossRef CAS PubMed.
- H. Tokuda, K. Ishii, M. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833–2839 CrossRef CAS PubMed.
- K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014–7023 CrossRef CAS.
- S. M. Green, M. E. Ries, J. Moffat and T. Budtova, Sci. Rep., 2017, 7, 8968 CrossRef PubMed.
- K. Hayamizu, S. Tsuzuki, S. Seki, K. Fujii, M. Suenaga and Y. Umebayashi, J. Chem. Phys., 2010, 133, 194505 CrossRef PubMed.
- K. Hayamizu, S. Tsuzuki and S. Seki, J. Chem. Eng. Data, 2014, 59, 1944–1954 CrossRef CAS.
- G. Gradenigo, A. Sarracino, D. Villamaina and A. Vulpiani, Acta Phys. Pol., B, 2013, 44, 899 CrossRef CAS.
- W. Kob, C. Donati, S. J. Plimpton, P. H. Poole and S. C. Glotzer, Phys. Rev. Lett., 1997, 79, 2827–2830 CrossRef CAS.
- M. M. Hurley and P. Harrowell, J. Chem. Phys., 1996, 105, 10521–10526 CrossRef CAS.
- S.-H. Chong, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041501 CrossRef PubMed.
- F. Chen, S. W. de Leeuw and M. Forsyth, J. Phys. Chem. Lett., 2013, 4, 4085–4089 CrossRef CAS.
- R. P. Daly, J. C. Araque and C. J. Margulis, J. Chem. Phys., 2017, 147, 061102 CrossRef PubMed.
- J. C. Araque and C. J. Margulis, J. Chem. Phys., 2018, 149, 144503 CrossRef PubMed.
- O. Russina, A. Triolo, L. Gontrani, R. Caminiti, D. Xiao, L. G. Hines Jr, R. A. Bartsch, E. L. Quitevis, N. Pleckhova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121 CrossRef.
- T. Pott and P. Méléard, Phys. Chem. Chem. Phys., 2009, 11, 5469 RSC.
- A. Triolo, O. Russina, R. Caminiti, H. Shirota, H. Y. Lee, C. S. Santos, N. S. Murthy and E. W. Castner, Jr, Chem. Commun., 2012, 48, 4959 RSC.
- J. G. McDaniel and A. Yethiraj, J. Phys. Chem. B, 2019, 123, 3499–3512 CrossRef CAS PubMed.
- P. Keblinski, J. Eggebrecht, D. Wolf and S. R. Phillpot, J. Chem. Phys., 2000, 113, 282–291 CrossRef CAS.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- A. A. Lee, D. Vella, S. Perkin and A. Goriely, J. Phys. Chem. Lett., 2015, 6, 159–163 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- P. Gaddam and W. Ducker, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- R. Kjellander, Phys. Chem. Chem. Phys., 2016, 18, 18985–19000 RSC.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed.
- C. R. Ashworth, R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2016, 18, 18145–18160 RSC.
- Y. Terui, M. Ueyama, S. Satoh and K. Tori, Tetrahedron, 1974, 30, 1465–1471 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on the syntheses and characterisation of the ionic liquids; experimental values for the density, viscosity, specific conductivity, self-diffusion coefficients and electrochemical stability; thermogravimetric analysis plots; calculated values for the molar conductivity, Walden relation, inverse Haven ratio and Stokes–Einstein equation; further details on the molecular dynamics simulations and quantum chemical calculations; force field parameters; topology and LAMMPS input files. See DOI: 10.1039/d1cp02889h |
| This journal is © the Owner Societies 2021 |





