 Open Access Article
Open Access ArticleExploring the validity of the Stokes–Einstein relation in supercooled water using nanomolecular probes†
Sharon
Berkowicz
 and
Fivos
Perakis
and
Fivos
Perakis
 *
*
Department of Physics, AlbaNova University Center, Stockholm University, SE-10691 Stockholm, Sweden. E-mail: f.perakis@fysik.su.se
First published on 31st August 2021
Abstract
The breakdown of Stokes–Einstein relation in liquid water is one of the many anomalies that take place upon cooling and indicates the decoupling of diffusion and viscosity. It is hypothesized that these anomalies manifest due to the appearance of nanometer-scale spatial fluctuations, which become increasingly pronounced in the supercooled regime. Here, we explore the validity of the Stokes–Einstein relation in supercooled water using nanomolecular probes. We capture the diffusive dynamics of the probes using dynamic light scattering and target dynamics at different length scales by varying the probe size, from ≈100 nm silica spheres to molecular-sized polyhydroxylated fullerenes (≈1 nm). We find that all the studied probes, independent of size, display similar diffusive dynamics with an Arrhenius activation energy of ≈23 kJ mol−1. Analysis of the diffusion coefficient further indicates that the probes, independent of their size, experience similar dynamic environment, which coincides with the macroscopic viscosity, while single water molecules effectively experience a comparatively lower viscosity. Finally, we conclude that our results indicate that the Stokes–Einstein relation is preserved for diffusion of probes in supercooled water T ≥ 260 K with size as small as ≈1 nm.
1 Introduction
Water evidently plays a crucial role in natural systems as a solvent, but a complete microscopic understanding of its unique behaviour remains a challenge. Particularly, water's anomalous properties become more pronounced in the supercooled regime, i.e. when cooled below its freezing point while still in the liquid state. These anomalies include for instance the density maximum and the divergence of thermodynamic response functions, such as the isobaric heat capacity and isothermal compressibility.1 However, experimental exploration of the deeply supercooled regime is challenging due to the fast homogeneous ice nucleation. Nevertheless, experiments2–5 as well as molecular dynamics (MD) simulations6 of bulk water have indicated that, microscopically, water fluctuates between two liquid states with distinct local structure – high-density liquid (HDL) and low-density liquid (LDL). It is believed that HDL dominates at high temperatures while the fraction of LDL increases upon cooling and exhibits a higher degree of tetrahedrality.7 It is further known that dynamic quantities exhibit a so-called fragile-to-strong transition in supercooled water around T ≈ 220 K. At this crossover, dynamic observables such as the diffusion coefficient and viscosity, transition from a fragile (super-Arrhenius) to a strong (Arrhenius) behaviour.6 It is hypothesized that this transition may reflect the crossing over from one strong liquid to another, or specifically, from an HDL-dominated regime to an LDL-dominated regime. At ambient pressures, the LDL manifests as spatial fluctuations within the HDL liquid. These spatial fluctuations have been associated with average length scales of 1–2 nm and become increasingly pronounced upon cooling.2,8 They finally reach a maximum along the so-called Widom line9 which has been experimentally resolved in bulk water at TW ≈ 229 K at ambient pressure.2Spatial heterogeneities in liquid water have also been proposed as a possible origin of the decoupling between diffusion and viscosity prevalent in the supercooled regime. In particular, water molecules diffuse significantly faster than what is predicted by the Stokes–Einstein relation, which describes an inverse relationship D ∝ T/η of the diffusion coefficient D and viscosity η. As a result of the anomalous diffusion, the Stokes–Einstein relation breaks down upon cooling.10 Noticeably, this breakdown seems to occur already at ambient temperatures and becomes significant well above the glass transition temperature, in contrast to that observed in other glass-forming liquids.11–13 MD simulations of water indicate indeed that the self-diffusion of water and viscosity are related to different time scales with distinct temperature dependences, namely the hydrogen bond lifetime and the structural α-relaxation time (τα), respectively.14 Moreover, the relationship between the self-diffusion and hydrogen bond lifetime is linked to activated jumping motion of water molecules, giving rise to large angular jumps instead of continuous diffusion.15 An increasing contribution from jump diffusion of water molecules upon cooling was shown in MD simulations to quantitatively describe the deviation from the Stokes–Einstein relation observed in experimental data.16,17 This interpretation is further consistent with a growing fraction of more rigid, tetrahedral liquid structures at lower temperatures associated with LDL, in which activated motion is believed to be more significant.16,18 Hence, the dynamic transition manifested by the fragile-to-strong crossover and the violation of Stokes–Einstein relation in supercooled water are likely highly interconnected, and both linked to spatially heterogeneous dynamics at microscopic level.
Despite the widely discussed connection between the violation of Stokes–Einstein relation and heterogeneities in water, direct experimental evidence is still scarce. As previously mentioned, not all dynamic quantities appear to violate the Stokes–Einstein relation, such as hydrogen bond lifetime, stress relaxation time, and the time scale related to the non-Gaussian parameter, for which the relation is preserved.14 This raises questions regarding which type of dynamics and length scales these different observables are associated with. For instance, is there a critical length scale at which the Stokes–Einstein relation breaks down linked to the domain size of the proposed water heterogeneities? While the decoupling of the diffusive motion of water and bulk viscosity has been thoroughly investigated, highlighting the distinction between microscopic and macroscopic dynamics, its implications and the validity of the Stokes–Einstein relation for the diffusive dynamics of other solutes in water has not received as much attention. Particularly, solute dynamics occur on a variety of length and time scales depending on the solute size, which can be relevant for biological systems. A dynamic crossover in supercooled water has for instance been observed in the atomic mean-squared displacements of proteins and other biomolecules at ≈220 K, in vicinity to the Widom line and the fragile-to-strong transition in bulk water.19 Furthermore, MD simulations of small hydrophobic solutes in supercooled water, ranging from methane to fullerene with van der Waals radii of ≈2–6 Å, found that cage effects and deviations of solute diffusion from Stokes–Einstein relation are significant at ambient temperatures, and become more appreciable upon supercooling.20 Lastly, by using solute size as ruler for spatial heterogeneities in the hydrogen-bond network, a recent study measured the brownian motion of upconverting nanocrystals (20–100 nm) in water, in particular indicating a second dynamic transition at ≈330 K which was attributed to percolation of LDL motifs.21
Here, we measure the dynamics of nanomolecular probes in supercooled water and experimentally explore the effect of probe size on the diffusive dynamics and the validity of the Stokes–Einstein relation. Using dynamic light scattering (DLS) we capture the diffusive dynamics of probes on different length scales, in the order of 100 nm down to the molecular scale of ≈1 nm. By employing water-soluble spherical nanoparticles with similar surface chemistry, in the form of non-functionalized silica spheres and molecular-sized polyhydroxylated fullerenes (PHF), we minimize the difference between probes in terms of shape and water–solute interactions. For each probe size, we analyze the temperature dependence of the diffusive dynamics as well as derive the viscosity based on the Stokes–Einstein relation. Finally, we compare these results with simulations based on Langevin dynamics and corresponding literature data for water self-diffusion and macroscopic viscosity.
2 Methods
2.1 Sample preparation
Stock solutions of silica spheres with bare surface (non-functionalized) in MilliQ water were bought from nanoComposix with specified hydrodynamic radii Rh = 63 nm and Rh = 13.5 nm, respectively. Sample solutions were prepared from the stock solutions by dilution with MilliQ water to a particle concentration of 0.025 vol%.Polyhydroxylated fullerenes (PHF) C60(OH)n·mH2O (n > 40, m > 8) were bought from Sigma-Aldrich (prod. no. 793248). The solid powder was dissolved in MilliQ water in concentrations of 1.2 mg ml−1 (≈0.03 vol%) and vortexed to yield a clear light yellow liquid. In addition, the solution was further dispersed by sonication at 40 kHz for 15 min. Any remains of undissolved large solid particles were removed by filtering the solution through a syringe filter (pore size 0.2 μm).
Cylindrical glass capillaries (inner diameter 4.2 mm, LS Instruments AG) used for DLS measurements were thoroughly cleaned before use by ultrasonication for 45 min in 1% Hellmanex solution, followed by washing several times with MilliQ water and methanol, and finally allowed to air-dry. To minimize contamination by dust particles the cleaning procedure as well as sample preparation were carried out inside a fume hood.
Lastly, volumes of 300 μL of each sample solution were transferred into the pre-cleaned capillaries and ultrasonicated for 15 min prior to DLS measurement, to make sure that the solutions were well-dispersed and to eliminate presence of any air bubbles. In the case of PHF, the samples were allowed to equilibrate until micron-sized aggregates or impurities initially present in the solution had sedimented or dissolved. This step greatly improved the relative scattering signal from single PHF particles versus clusters as well as overall data quality.
2.2 Dynamic light scattering setup and measurements
DLS measurements were performed with a 3D LS spectrometer (LS Instruments AG) equipped with a λ = 660 nm CW laser. In this setup, the sample capillary is immersed in an enclosed bath of decalin connected to an external thermostat which allows control of the sample temperature between 260–300 K. In normal (2D) mode, the scattered light from the sample is re-collimated and detected by two photon detectors mounted on a goniometer arm, covering the momentum transfer Q = 0.002 nm−1 to 0.025 nm−1. Here, Q = 4πn0/λ·sin(θ/2), where λ is the wavelength, θ is the scattering angle and n0 is the solvent refractive index. The measured intensity fluctuations at the two detectors are subsequently pseudo-correlated analogically over time by the integrated correlator. This pseudo cross-correlation minimizes the influence from detector after-pulsing and yields a time resolution of 12.5 ns. Additionally, the DLS setup enables measurement in so-called 3D mode, in which the laser beam is split before the sample and scattered light from the two overlapped beams is simultaneously detected by the two photon detectors. Cross-correlation of the two detector signals results in efficient suppression of eventual contribution from multiple scattering.A total of three and four individually prepared aqueous samples of the Rh = 63 nm and Rh = 13.5 nm silica spheres, respectively, were measured by DLS in 3D mode, and five samples of PHF solution were measured in 2D mode, due the weak scattered signal of the latter. For each sample, the intensity autocorrelation function g2 and scattered intensity at different Q values were recorded as a function of sample temperature. Upon reaching a set temperature, the sample was allowed to thermally equilibrate for 20 min before measurement. Moreover, each configuration (temperature and Q) was consecutively measured 3–5 times with 30 s recordings. Reference measurements of each sample were carried out prior to and after a temperature dependence measurement, in order to determine the particle hydrodynamic radius Rh at a room temperature where the viscosity of water is well-known, as well as to ensure recovery of the system after cooling.
2.3 Data analysis
The temporal intensity autocorrelation function g2 is defined as | (1) |
The measured g2 functions were fitted to mono- or bi-exponential decays of the form
| g2(Q,t) = βe−2t/τ + c, | (2a) |
| g2(Q,t) = β1e−2t/τ1 + β2e−2(t/τ2)γ + c, | (2b) |
In the case of silica spheres, the g2 functions were fitted to the mono-exponential decay given in eqn (2a), whilst in the case of PHF the g2 functions clearly exhibited bi-exponential behaviour with a separable fast (τ1) and slow (τ2) component, which were therefore fitted to eqn (2b). The KWW exponent γ was solely included as a free parameter for the slower component. The latter is motivated by the much improved fit quality which allows to capture the entire shape of the slow component of the g2 decay.
For diffusive motion, the relaxation time constant τ is inversely proportional to the translational diffusion coefficient D with a 1/Q2-dependence:
 | (3) |
Next, we utilized the Stokes–Einstein relation25 (eqn (4)) to examine the probe-solvent interactions and dynamics, as well as the validity of the Stokes–Einstein relation, in two different ways. Firstly, we examined the temperature dependence of the hydrodynamic radius Rh of the spherical probes. Here, Rh was calculated from the probe diffusion coefficient D using the Stokes–Einstein relation and viscosity η based on rheological measurements of water in ref. 26–28, hereon referred to as the macroscopic water viscosity. Secondly, by instead assuming a constant hydrodynamic radius Rh (with Rh determined at room temperature), the viscosity, as experienced by the probes, was derived from the probe diffusion coefficient D and the Stokes–Einstein relation.
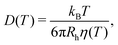 | (4) |
The following equations were used to analyse the temperature dependence of the diffusive dynamics for all the different systems:
(1) The Arrhenius equation empirically describes the temperature dependence of a dynamic property, such as the diffusion coefficient D, by a single activation energy barrier Ea and a pre-exponential factor A with negligible dependence on temperature:29,30
| D(T) = Ae−Ea/kBT | (5) |
(2) Power laws have frequently been used to fit dynamic, as well as thermodynamic properties of supercooled water in order to account for the diverging behaviour. Particularly, such properties of water all seem to diverge towards a singular temperature.31 Herein, we fit diffusion data to the following power law equation:
 | (6) |
3 Results and discussion
3.1 The intensity autocorrelation function
The intensity autocorrelation function g2 at Q = 0.019 nm−1 for different temperatures is shown in Fig. 1 for the two sizes of silica spheres and PHF, respectively. In the case of the silica spheres (Fig. 1A and B), the g2 exhibits mono-exponential decay which slows down with decreasing temperature. The relaxation time constant (τ) of the decay is inversely proportional to Q2, indicative of diffusive motion in the investigated Q-range. We determine the diffusion coefficient D from a global fit to the g2 functions at different Q-values, and calculate the corresponding hydrodynamic radius Rh of the probe particle using the Stokes–Einstein relation and macroscopic water viscosity, as described in Methods. At room temperature, the hydrodynamic radii Rh for the silica spheres are found to be 66 ± 2 nm and 13 ± 1 nm, respectively (see also Table 1). The calculated hydrodynamic radii for the silica spheres are consistent with the producer specifications, 63 nm and 13.5 nm, respectively. The fact that the g2 functions for the silica particles can be well-fitted with single exponential functions and KWW exponents γ = 1, which could otherwise (γ < 1) suggest a broad distribution of relaxation times,24 indicates that the measured dynamics is governed by single particles from a relatively narrow and Gaussian size distribution, where the existence of aggregates only has minor effect. | ||
| Fig. 1 The normalized intensity autocorrelation functions g2 at different temperatures (Q = 0.019 nm−1) in the form of (g2 − c)/β, where β is the total contrast (intercept) and c is the offset. (a) Silica spheres with Rh = 66 nm, (b) silica spheres with Rh = 13 nm and (c) polyhydroxylated fullerenes (PHF) in water. Solid lines indicate exponential fits to the experimental data (dots). Insets: The 1/Q2-dependence of the relaxation time constant τ for the single particles at 296 K and linear fits (dashed lines) according eqn (3). | ||
| Probe | R h (nm) | Arrhenius equation | Power law (fixed m = 2.00) | ||
|---|---|---|---|---|---|
| A (10−8 m2 s−1) | E a (kJ mol−1) | D 0 (10−11 m2 s−1) | T S (K) | ||
| a Determined at room temperature using the Stokes–Einstein relation and macroscopic water viscosity from ref. 26–28. b Based on water self-diffusion data from ref. 39 and 40 in the temperature range 260–298 K. c Based on water self-diffusion data from ref. 39 and 40 in the temperature range 238–318 K. d D SE(T) ∼ T/η(T) where η is the macroscopic water viscosity from ref. 26–28 at temperatures 259–298 K. | |||||
| PHF | 1.4 ± 0.1 | 240 ± 160 | 23.5 ± 1.6 | 140 ± 50 | 221 ± 8 |
| Silica spheres | 13 ± 1 | 21 ± 7 | 23.0 ± 0.9 | 16 ± 2 | 221 ± 4 |
| Silica spheres | 66 ± 2 | 3.8 ± 2.4 | 22.8 ± 1.5 | 3.1 ± 0.5 | 221 ± 4 |
| PHF clusters | 86 ± 9 | 1.9 ± 1.1 | 21.7 ± 1.4 | 2.2 ± 1.4 | 218 ± 14 |
| Water molecules (ref. 39 and 40) | — | 910 ± 410b | 20.5 ± 1.0b | 1500 ± 100c | 215 ± 1c |
| Macroscopic water (ref. 26–28)d | — | — | 23.2 ± 0.6 | — | 221 ± 1 |
Unlike the silica spheres, the PHF solution (Fig. 1C) exhibits a two-component g2 function. These two components can be resolved as they decay on very different time scales, where the fast component decays on a μs to sub-ms time scale while the decay of the slow component is nearly 100 times slower. Similarly to the silica spheres, the fast component is well-described by a single exponential function with a KWW exponent γ = 1, indicating a narrow and Gaussian particle size distribution,24 for which the relaxation time constant (τ1) shows a clear 1/Q2-dependence (see inset Fig. 1C). In contrast, the slow component is best fitted to a stretched exponential function (eqn (2b)) with a KWW exponent γ ≈ 0.6. Moreover, the slow relaxation time constant (τ2) exhibits a 1/Q2-dependence at large Q with a slight positive deviation at the small Q. For this reason, we restricted the Q-range of the global fit described in Methods to the linear region at larger Q. The fitted diffusion coefficients of the fast and slow g2 component correspond to hydrodynamic radii of 1.4 ± 0.1 nm and 86 ± 9 nm, respectively, at room temperature.
We assign the fast and slow component of the PHF g2 function to the dynamics of mainly single PHF molecules and clusters of PHF molecules, respectively. The measured diffusion coefficient of the fast component (1.8 × 10−10 m2 s−1 at 299 K) is indeed consistent with that from simulations of single PHF molecules in water (2.2 × 10−10 m2 s−1 at 300 K).34 In addition, the associated hydrodynamic radius of 1.4 ± 0.1 nm is in agreement with previous experimental characterizations using DLS which have reported hydrodynamic size distributions in the range 0.7–2 nm,35,36 whereas according to simulations, the first hydration shell of the PHF molecule is at 0.7–0.8 nm radial distance from its center-of-mass.34 Larger clusters of PHF in aqueous solution, with preferential sizes in the order of 100 nm, have previously been characterized with DLS and scanning probe microscopy,35–37 as well as with atomic force microscopy and transmission electron microscopy.38 It has also been indicated that the average cluster size of PHF in aqueous solutions depends on concentration and temperature.37,38 The determined hydrodynamic radius of 86 ± 9 nm for the slow component is consistent with the above descriptions of PHF clusters. We also note that the contrast of the fast relative to the slow component of the PHF g2 function increase with Q. At small Q < 0.013 nm−1 the measured dynamics is dominated by the slow component. These observations are consistent with the assignment of the slow PHF component to particles of clustered PHF, since the form factor F(Q,R), where R is the particle radius, for large particles declines faster with Q than for small particles.
As discussed in Methods, the KWW exponent reflects the degree of nonexponentiality of the dynamics in complex systems. Here, we find that the slow PHF component of the g2 is well-captured by using a KWW exponent smaller than 1, i.e. γ ≈ 0.6, yielding a stretched exponential function. The stretching exponent may be attributed to a broad, possibly non-Gaussian, distribution of PHF cluster sizes and/or complex cluster dynamics.23,24 Distinct cluster sizes, but of similar order of magnitude, would give rise to a multitude of relaxation rates on similar time scales that would be difficult to discriminate by analysis of the g2 function. This can be put in contrast to the case of the fast (single PHF) and slow component (large clusters of PHF) which are well separated in time, allowing these two major components to be resolved. The distinct difference in time scale for these two components, rather than a broad distribution, is most likely the result of a preferential range of cluster sizes that form at specific temperature and PHF concentration.37,38
Furthermore, because the scattered intensity for hard spheres scales with R6, the fact that we observe a significant contribution from the fast PHF component indicates that a large portion of the PHF is dispersed on molecular level. This is in line with previous observations which noted that dilute solutions of PHF (0.1 wt%) with similar number of hydroxyl groups (n = 36–44) are highly dispersed, with the vast majority of the dissolved PHF existing as single molecules.35,36 Hence, our results highlights the feasibility to measure fast equilibrium dynamics of molecular probes on the nanoscale and to distinguish between single and clustered molecules in solution by analysis of the intensity autocorrelation function g2, in which the slower cluster dynamics are separated in time from the fast single-molecule dynamics. Since the relative contrast of each component, i.e. the single molecules and clusters, varies with Q in accordance with their form factor, the corresponding relative contributions to the g2 function can be tuned simply by varying the Q-range.
3.2 Diffusive dynamics
In Fig. 2, Arrhenius plots of the probe particles' translational diffusion coefficient are shown as a function of inverse temperature. Specifically, Fig. 2A–D shows that the diffusion coefficient for each probe between T = 260–300 K effectively follows Arrhenius law (eqn (5)) and, with the exception of PHF clusters, all particles exhibit a similar activation energy Ea ≈ 23 kJ mol−1 (see Table 1). This is particularly highlighted in Fig. 2E where the normalized diffusion coefficients for the single particles extensively overlap. One can also see in Fig. 2E that the temperature dependence of water self-diffusion obtained from ref. 39 and 40 deviates from the particle behaviour, which becomes more significant upon cooling. Fits of the water self-diffusion to Arrhenius equation as well as to a power law (eqn (6)) shows that the latter fit is indeed in much better agreement with the data. Nevertheless, the Arrhenius activation energy for water in this temperature range is determined to 20.5 kJ mol−1 (see Table 1) and notably smaller than for the probe particles. | ||
| Fig. 2 (A–D) Arrhenius plots of the translational diffusion coefficient D for different nanomolecular probes as indicated in the legend. (E) Comparison of the diffusion coefficient, multiplied with the hydrodynamic radius Rh, for the probe particles and water molecules (water self-diffusion coefficients from ref. 39 and 40). Fits to Arrhenius equation and power laws in (A–E) are indicated by solid and dashed lines, respectively. | ||
It has been proposed that the fragile behaviour of supercooled water may be attributed to spatially heterogeneous dynamics, involving a gradual transition across the Widom line between two, individually strong liquids with distinct activation energies.9,41 By fitting experimental data for the self-diffusion of water to such a two-state model the two activation energies were determined to 13.0 kJ mol−1, for the liquid dominating at high temperatures, and 36.4 kJ mol−1, for the liquid dominating at low temperatures.41,42 Similar values have also been reported elsewhere, e.g. fits of Arrhenius equation to the self-diffusion of TIP4P water yielded activation energies 19.0 kJ mol−1 and 38.6 kJ mol−1 at high and low temperatures, respectively, between 180–330 K,14 while a similar fit to real water at T > 315 K yielded 15.2 kJ mol−1.43 In the latter case it was in addition proposed that the activation energy value may be related to the H-bond energy.43 Likewise, Arrhenius activation energies of 13 kJ mol−1 and 53 kJ mol−1 were reported based on the experimental bulk viscosity of water at temperatures 240–280 K,10 as well as 14.4 kJ mol−1 for the diffusion of 15 nm gold nanoparticles in water in the temperature range 300–350 K.44 Noticeably, determination of the Arrhenius activation energy strongly depends on the chosen temperature range, since the Arrhenius slope changes continuously in the fragile regime that comprises most of the liquid state below ambient temperatures. We can conclude that our results for the Arrhenius activation energy for probe diffusion in water, Ea ≈ 23 kJ mol−1, as well as for water self-diffusion, 20.5 kJ mol−1, are both concordant with the above previously reported values considering the intermediate temperature range in this study (260–300 K).
Upon further analysis, it is interesting to discuss the difference in the dynamics of the probe particles and water diffusion, as evident in Fig. 2E. The probe diffusion dynamics overall matches that derived from macroscopic water viscosity using the Stokes–Einstein relation, DSE ∼ T/η, as of the similar activation energies in Table 1. We note here that there is a tentative trend of slightly decreasing activation energy with larger particle size, although higher level of accuracy would be required to resolve this trend unambiguously. By contrast, the activation energy for water is significantly smaller and markedly deviates from the above trend of the probe particles. Thus, it seems like individual water molecules diffuse in a different manner than the probe particles examined here, a distinction that appears to be the case on length scales down to the molecular size of PHF, ≈1 nm. If this effect arises from presence of spatial heterogeneities, the length scale of such transient motifs should be comparatively smaller than the size of PHF (≈1 nm). The average fluctuation length scales in bulk water has experimentally been estimated to about 1 nm at ambient temperatures to roughly 2 nm at the Widom line.2,8 Hence, it is possible that PHF molecules might just be large enough to be effectively insensitive to the heterogeneities, at least down to 260 K, i.e. the lower limit of this experiment. Alternatively, the aforementioned coupling of PHF diffusion with macroscopic viscosity in supercooled water, in contrast to that seen for water molecules, may be explained by the temporal as well as spatial and ensemble averaging in the experimental method. For instance, it could be the case that the spatial fluctuations occur on time scales considerably shorter than the experimental time resolution (12.5 ns).14 That is, the measured PHF dynamics reflects the average diffusive motion within a finite time window during which many fluctuations possibly occur, effectively yielding a homogeneous dynamic environment around the PHF molecule. Similar cancellation effects of the spatial heterogeneities could be resulting from spatial (ensemble) averaging over the focal volume of the laser (focus size ≈ 100 μm). Indeed, previous works have indicated that measured heterogeneity in supercooled liquids is highly linked to the relative dynamic time scales of the probe and the host liquid,45,46 as well as by temporal and spatial averaging in the experimental design, which can obscure underlying dynamic and/or spatial heterogeneity.47
The activation process for diffusion can be considered to involve formation of a vacancy in the proximity of the diffusing particle or molecule, which facilitates its mobility. The importance of such pre-solvation processes has for instance been advocated for in the diffusion of small hydrophobic solutes.48 Moreover, the breaking of water H-bonds and creating the vacancy is an energy-driven process and thereby both translational and rotational pre-arrangement is necessary at the present and the future location of the solute in a synchronized fashion. As such, the translation–rotation coupling of the solvent is the key here.48,49 In addition, solutes with geometry and solute–solvent interactions distinct from water molecules presumably require more extensive restructuring of the water network. Such a mechanism could explain why the obtained activation energy for diffusion appears somewhat larger for the probe particles (≈23 kJ mol−1) than for single water molecules (20.5 kJ mol−1). In line with this hypothesis, it has been indicated that the enthalpy to break hydrogen bonds in the hydration shell of hydrophobic solutes is larger than for pure water.50 Furthermore, while larger particles require larger solvent vacancies, the surface-to-volume ratio is smaller, that is, there exists a smaller number of water molecules in the hydration shell relative to the excluded volume. Hence on average, the change in hydrogen bond energy required to accommodate larger particles should be smaller than that required for smaller particles with similar surface chemistry, such as is the case for the probe particles here. This may potentially explain the tentative trend in the probes' activation energy.
Table 1 also presents the results for fits of the diffusion coefficient to a power law equation (eqn (6)). Here, the power law exponent was fixed at m = 2.00 in order to minimise the fitting parameters. This value was chosen based on a power law fit to water self-diffusion over a broader temperature-range (238–318 K), but similar values have previously also been reported.9 Intriguingly, we find that the singularity temperature TS is systematically a few degrees higher for the diffusion of all single probe particles (TS = 221 K), as well as for macroscopic water DSE ∼ T/η (TS = 221 K), than for water self-diffusion (TS = 215 K), although these values appear consistent with previous predictions.51 Similar discrepancies in TS between water self-diffusion, rotational relaxation and macroscopic viscosity has also previously been noted.10 Specifically, TS defines the singular temperature in mode-coupling theory32,33 at which the observable diverges and is often associated with the position of the Widom line.9 It can however be noted that TS here is about 8 K (probe particles) and 14 K (water self-diffusion) lower than the Widom line temperature of bulk water at T ≈ 229 K.2 In accordance with these results, it was previously indicated that the dynamic crossover in water occurs at ≈20 K lower temperature than the Widom line, where the latter is marked by the maximization of thermodynamic response functions.41 In other words, the Widom line defines the thermodynamic crossover, and proposedly the temperature at ambient pressure for which the fractions of the two liquid states, HDL and LDL, are equal. The dynamic crossover, on the other hand, may instead be interpreted as the transition from a fluctuating mixture of HDL and LDL to a strong LDL-dominated liquid at slightly colder temperatures, and is linked to dynamic quantities, such as the diffusion coefficient.41 The occurrence of the dynamic crossover at lower temperature has also been suggested to arise from maxima of dynamic heterogeneities which are distinct from the thermodynamic, or structural, counterpart.41 On the basis of the discrepancy in TS for different dynamic quantities found here and elsewhere,10 the dynamic crossover temperature may additionally depend on the type of dynamic observable. Particularly, this is clearly demonstrated here by the ≈6 K difference in TS for the probe particle diffusion compared to water self-diffusion, which differ only in the type of diffusing species. One can speculate whether this difference originates from the size of the probe in comparison to the transient domains of HDL and LDL, or if this is a result of distinct interactions between the solute and hydration water. For this reason it would be interesting to study this observed phenomenon in more detail also in the deeply supercooled regime (<260 K), where these crossovers seem to take place.
We finally note that the diffusive dynamics of PHF clusters differ slightly from the single particles. Firstly, the clusters seem to exhibit a stronger Arrhenius behaviour (Fig. 2D), and secondly, the Arrhenius activation energy deviates more substantially from the single particles while being closer in value to that of single water molecules. On one hand, these deviations could be accounted for by the large error bars, but on the other hand, this apparent difference in dynamic behaviour could be the result of complex heterogeneous dynamics of the clusters. It was previously shown that PHF clusters are likely transient in nature and that they exhibit a strong concentration and temperature dependence.38 In addition, it has further been indicated that PHF cluster formation at various concentrations exhibit minima at ≈309 K38 which nearly coincides with the isothermal compressibility minimum of water.7 This, as well as the results herein, may be indicative that PHF cluster dynamics is highly sensitive to water dynamics in general. In this context, PHF clusters could be an interesting model system for studying the influence of water on transient cluster formation, a dynamic process which has notably been observed in highly concentrated protein solutions and likely plays an important role in biological systems.52
3.3 Validity of the Stokes–Einstein relation
We test the validity of the Stokes–Einstein relation for the probe particles by plotting the diffusion coefficient as a function of hydrodynamic radius (determined by the Stokes–Einstein relation and macroscopic water viscosity at room temperature). Fig. 3 displays the result at the highest (299 K) and lowest (260 K) measured temperatures together with the corresponding Stokes–Einstein predictions. It can be noted that probe particles with radii across three orders of magnitude (1–100 nm) are consistent with the Stokes–Einstein prediction at both temperatures, within the estimated errors.Thus, the Stokes–Einstein relation appears valid for the solutes examined here, down to nanometer length scales. However, it was previously indicated by MD simulations that deviation from the Stokes–Einstein relation occurs for small hydrophobic solutes, from methane to fullerene, having radii ranging from about 2–6 Å.20 Particularly, the calculated diffusion coefficient increased faster with smaller solute size than the Stokes–Einstein prediction of D ∝ 1/Rh, although the deviation becomes more significant in the supercooled regime.20 Fullerene is only slightly smaller than PHF, wherefore it is possible that the critical solute size at which the Stokes–Einstein relation breaks down is in the same size-range, i.e. ≈1 nm, in agreement with previous estimations.53 It would however be interesting as an outlook to investigate whether differences in particle–water interactions between fullerene (hydrophobic) and PHF (hydrophilic) may play a role in the diffusive dynamics and the Stokes–Einstein validity, e.g. in terms of the applicability of particle–solvent boundary conditions.46,54 Hence, experimentally, one could consider comparing the diffusive dynamics of fullerenes with different surface functionalizations, such as PHF:s with varying degrees of hydroxylation.34 Furthermore, we note that our conclusion about critical particle sizes <1 nm is different from earlier studies, where the diffusion of nanoparticles in water was measured at room temperature.55 In particular, it was indicated that violation of the Stokes–Einstein relation occurs for particles smaller than ≈150 nm, with larger critical particle size at lower particle concentrations. This discrepancy may possibly be related to experimental effects arising from the measurement approach.
By using the Stokes–Einstein relation (eqn (4)), and assuming a constant hydrodynamic radius, we finally derive the viscosity experienced by the probes as a function of temperature. Fig. 4A–C shows the viscosity for the two sizes of silica spheres as well as for single PHF (i.e. only the fast component of the g2 function), respectively. For comparison we also include the macroscopic water viscosity from rheological measurements in ref. 26–28 and the viscosity experienced by single water molecules. The latter is derived from the self-diffusion of water in ref. 39 and 40 using the Stokes–Einstein relation, and is normalized to the well-known value of 1.002 Pas for macroscopic viscosity at 293.15 K. The increasing discrepancy between the macroscopic viscosity and the viscosity derived from the self-diffusion of single water molecules is obvious as water is supercooled, reflecting the breakdown of the Stokes–Einstein relation. On the other hand, all of the probes, even the molecular-sized PHF, yield similar viscosity, i.e. they sense a similar dynamic environment, which overlap well with the macroscopic property. The concordance between the viscosity measured by the probe particles and the macroscopic viscosity, as well as the temperature independence of the hydrodynamic radius (see insets in Fig. 4), again suggest that the Stokes–Einstein relation holds for all particle sizes, including molecular probes (PHF) at nanometer length scales, in the investigated temperature range. By contrast, the viscosity based on water self-diffusion diverges as temperature is lowered, where individual water molecules seem to effectively experience a lower viscosity than the probe particles. The mere fact that the small PHF particle is found to follow the Stokes–Einstein prediction of viscosity in itself confirms the hydrodynamic description of its radius, despite the relatively small solute–solvent size ratio. In the case of individual water molecules, the validity of the Stokes–Einstein relation at high temperatures similarly supports the hydrodynamic description, suggesting that the breakdown of the relation upon supercooling originates from changing dynamics in the supercooled regime.
 | ||
| Fig. 4 Temperature dependence of the viscosity of water as experienced by the different probe particles, assuming a temperature-independent hydrodynamic radius. (A) Silica spheres with Rh = 66 nm, (B) silica spheres with Rh = 13 nm and (C) single PHF molecules. The lines depict the macroscopic viscosity measured by rheology from ref. 26–28 (solid line) and viscosity measured by NMR from ref. 39 (dashed line). Inset: The measured particle hydrodynamic radius Rhversus temperature by using the macroscopic water viscosity from ref. 26–28. | ||
Combined with the agreement of the mean-squared displacement of the probe particles with Langevin dynamics (see ESI†), we conclude that the measured probe particle diffusion is governed by viscous flow, with negligible influence of the sort of activated hopping motion that has been associated with the anomalous self-diffusion of water.16,17 That is, the significant contribution of jump diffusion to the total diffusion of single water molecules may account for the faster water self-diffusion, or inversely, the lower viscosity experienced by diffusing water molecules compared to the probe particles. However, in addition to this kind of activated motion, MD simulations have also suggested that abnormally fast solute diffusion (i.e. large diffusion coefficient D) can arise due to a levitation effect for solutes which are comparable in size to the characteristic voids of the solvent, i.e. dispersion interactions of the solute within the voids lead to a minimum in the solute–solvent friction.56 For diffusion governed by viscous flow, as in Langevin dynamics (see ESI†), the diffusion coefficient is inversely proportional to the solute–solvent friction coefficient ζ = kBT/D, meaning that reduction of the solute–solvent friction is associated with an increase in the diffusion coefficient. Hence, in this picture, water molecules fit ideally inside tetrahedral water cages, which become more prevalent with an increasing fraction of LDL upon supercooling.7,57 On the other hand, from the perspective that activated motion gives rise to the larger D, jump diffusion may similarly become important mainly for such small solutes, which are momentarily trapped and experience strong cage effects. Thereby, the diffusion channel is increasingly governed by the activated jump diffusion with decreasing temperature.16,17 As a result, the jump diffusion takes control to some extent and therefore its reduction with cooling is less pronounced than the increase of viscosity.
4 Summary and conclusions
To summarize, we measured the diffusive dynamics of nanomolecular probes in supercooled water using dynamic light scattering (DLS) and investigated the dependence on temperature (260–300 K) and particle size (1–100 nm), including 100 nm and 20 nm silica spheres, as well as ≈1 nm polyhydroxylated fullerenes (PHF). By analysis of the intensity autocorrelation function g2 we were able to resolve dynamics of single PHF molecules and clusters of PHF. Additionally, PHF clusters show distinct dynamics from that of single PHF molecules which may be a result of complex heterogeneous dynamics.Most importantly, we find that all probe particles display diffusive dynamics with similar Arrhenius activation energies (Ea ≈ 23 kJ mol−1), which are distinct from that of single water molecules (Ea = 20.5 kJ mol−1) but similar to that of macroscopic water, DSE ∼ T/η (Ea = 23.2 kJ mol−1). Furthermore, by applying the Stokes–Einstein relation to the measured diffusion coefficients, all probe particles yield similar viscosity values within the temperature range which coincides with that of macroscopic water, indicating that the probes sense a similar dynamic environment independent of their size, ranging from 100 nm to the molecular-sized PHF (≈1 nm). Individual water molecules, on the other hand, seem to experience an effectively smaller viscosity than the particles. This difference increases upon supercooling, reflecting the violation of Stokes–Einstein relation and the decoupling of water self-diffusion from macroscopic water viscosity.
Based on our results herein we conclude that the probe particle diffusion does not violate Stokes–Einstein relation (down to ≈1 nm particles) and remains coupled to macroscopic water viscosity, suggesting that the relation is preserved in water (T = 260–300 K) down to nanometer length scales. These results suggest that any critical size related to the breakdown of the Stokes–Einstein relation, in the investigated temperature range, is most likely on sub-nanometer length scales, and/or that spatial fluctuations hypothesized to cause the breakdown occur on sub-nanosecond time scales. Finally, the microscopic origin of the violation of Stokes–Einstein relation in supercooled water, and its connection to the fragile-to-strong transition, remains to be further explored in the deeply supercooled regime (T < 260 K) where the spatial heterogeneities proposedly maximizes.2 Supercooling techniques, such as rapid evaporative cooling, allow measurements of liquid water down to T ≈ 227 K,2 which in combination with increased spatial and temporal resolution, e.g. by X-ray photon correlation spectroscopy at X-ray free electron lasers (XFELs),58 may provide the experimental tools to resolve these intriguing phenomena in life's ultimate solvent.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank Mario Reiser for useful discussions and comments on the manuscript. We acknowledge financial support by the Swedish National Research Council (Vetenskapsrådet) under Grant No. 2019-05542 and within the Röntgen-Ångström Cluster Grant No. 2019-06075. We acknowledge support by the MaxWater initiative of the Max-Planck-Gesellschaft and by the Centre for Molecular Water Science (CMWS) at DESY in an Early Science Project.References
- P. G. Debenedetti, J. Phys.: Condens. Matter, 2003, 15, R1669 CrossRef CAS.
- K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, J. P. S. Kim, K. H. Nam, T. Katayama and A. Nilsson, Science, 2017, 358, 1589 CrossRef CAS PubMed.
- K. H. Kim, K. Amann-Winkel, N. Giovambattista, A. Späh, F. Perakis, H. Pathak, M. L. Parada, C. Yang, D. Mariedahl, T. Eklund, T. J. Lane, S. You, S. Jeong, M. Weston, J. H. Lee, I. Eom, M. Kim, J. Park, S. H. Chun, P. H. Poole and A. Nilsson, Science, 2020, 370, 978 CrossRef CAS PubMed.
- H. Pathak, A. Späh, N. Esmaeildoost, J. A. Sellberg, K. H. Kim, F. Perakis, K. Amann-Winkel, M. Ladd-Parada, J. Koliyadu, T. J. Lane, C. Yang, H. T. Lemke, A. R. Oggenfuss, P. J. M. Johnson, Y. Deng, S. Zerdane, R. Mankowsky, P. Beaud and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018379118 CrossRef CAS PubMed.
- F. Perakis, K. Amann-Winkel, F. Lehmkühler, M. Sprung, D. Mariedahl, J. A. Sellberg, A. S. Harshad Pathak, F. Cavalca, D. Schlesinger, A. Ricci, A. Jain, B. Massani, F. Aubree, C. J. Benmore, T. Loerting, G. Grübel, L. G. M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8193 CrossRef CAS.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259 CrossRef CAS PubMed.
- A. Nilsson and L. G. M. Petterson, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamäe, A. P. Lyubartsev, S. Shin, L. G. M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214 CrossRef CAS PubMed.
- L. Xu, P. Kumar, S. V. Buldyrev, S.-H. Chen, P. H. Poole, F. Sciortino and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16558 CrossRef CAS PubMed.
- A. Dehaoui, B. Issenmann and F. Caupin, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12020 CrossRef CAS PubMed.
- I. Chang, F. Fujara, B. Geil, G. Heuberger, T. Mangel and H. Sillescu, J. Non-Cryst. Solids, 1994, 172–174, 248 CrossRef CAS.
- I. Chang and H. Sillescu, J. Phys. Chem. B, 1997, 101, 8794 CrossRef CAS.
- S. F. Swallen, P. A. Bonvallet, R. J. McMahon and M. D. Ediger, Phys. Rev. Lett., 2003, 90, 015901 CrossRef PubMed.
- T. Kawasaki and K. Kim, Sci. Adv., 2017, 3, e1700399 CrossRef PubMed.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832 CrossRef CAS PubMed.
- V. Dubey, S. Erimban, S. Indra and S. Daschakraborty, J. Phys. Chem., 2019, 123, 10089 CrossRef CAS PubMed.
- S. Dueby, V. Dubey and S. Daschakraborty, J. Phys. Chem. B, 2019, 123, 7178 CrossRef CAS PubMed.
- J. C. Palmer, F. Martelli, Y. Liu, R. Car, A. Z. Panagiotopoulos and P. G. Debenedetti, Nature, 2014, 510, 385 CrossRef CAS PubMed.
- S.-H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012 CrossRef CAS PubMed.
- V. Dubey, S. Dueby, S. Erimban and S. Daschakraborty, J. Indian Chem. Soc., 2019, 96, 741 CAS.
- C. D. S. Brites, B. Zhuang, M. L. Debasu, D. Ding, X. Qin, F. E. Maturi, W. W. Y. Lim, D. W. Soh, J. Rocha, Z. Yi, X. Liu and L. D. Carlos, J. Phys. Chem. Lett., 2020, 11, 6704 CrossRef CAS.
- B. Berne and R. Pecora, Dynamic light scattering, Dover Publications, Mineola, 2000 Search PubMed.
- G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80 RSC.
- F. Alvarez, A. Alegria and J. Colmenero, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7306 CrossRef PubMed.
- A. Einstein, Ann. Phys., 1905, 322, 49 Search PubMed.
- J. Hallet, Proc. Phys. Soc., 1963, 82, 1046 CrossRef.
- A. F. Collings and N. Bajenov, Metrologia, 1983, 19, 61 CrossRef CAS.
- J. Kestin, N. Imaishi, S. Nott, J. Nieuwoudt and J. Sengers, Phys. A, 1985, 134, 38 Search PubMed.
- S. A. Arrhenius, Z. Phys. Chem., 1889, 4, 96 CrossRef.
- S. A. Arrhenius, Z. Phys. Chem., 1889, 4, 226 CrossRef.
- R. J. Speedy and C. A. Angell, J. Chem. Phys., 1976, 65, 851 CrossRef CAS.
- E. Leutheusser, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 2765 CrossRef CAS.
- W. Gotze and L. Sjögren, Rep. Prog. Phys., 1992, 55, 241 CrossRef.
- V. V. Chaban and E. E. Fileti, New J. Chem., 2017, 41, 184 RSC.
- K. Kokubo, K. Matsubayashi, H. Tategaki, H. Takada and T. Oshima, ACS Nano, 2008, 2, 327 CrossRef CAS PubMed.
- K. Kokubo, S. Shirakawa, N. Kobayashi, H. Aoshima and T. Oshima, Nano Res., 2011, 4, 204 CrossRef CAS.
- K. N. Semenov, N. A. Charykov and V. N. Keskinov, J. Chem. Eng. Data, 2011, 56, 230 CrossRef CAS.
- M. Vraneš, I. Borišev, A. Tot, S. Armaković, S. Armaković, D. Jović, S. Gadžurić and A. Djordjevic, Phys. Chem. Chem. Phys., 2017, 19, 135 RSC.
- W. S. Price, H. Ide and Y. Arata, J. Phys. Chem. A, 1999, 103, 448 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685 CrossRef CAS.
- J. R. R. Shi and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9447 Search PubMed.
- R. Shi, J. Russo and H. Tanaka, J. Chem. Phys., 2018, 149, 224502 CrossRef PubMed.
- F. Mallamace, C. Corsaro and H. E. Stanley, Sci. Rep., 2012, 2, 993 CrossRef PubMed.
- K. Wong, C. Chen, K. Wei, V. A. L. Roy and S. M. Chathoth, J. Nanopart. Res., 2015, 17, 153 CrossRef.
- R. Zangi and L. J. Kaufman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051501 CrossRef PubMed.
- S. A. Mackowiak, L. M. Leone and L. J. Kaufman, Phys. Chem. Chem. Phys., 2011, 13, 1786 RSC.
- K. Paenga, H. Parka, T. Hoanga and L. J. Kaufman, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4952 CrossRef PubMed.
- S. Indra and S. Daschakraborty, Chem. Phys. Lett., 2017, 685, 322 CrossRef CAS.
- V. Dubey, N. Kumar and S. Daschakraborty, J. Phys. Chem. B, 2018, 122, 7569 CrossRef CAS PubMed.
- K. A. T. Silverstein, A. D. J. Haymet and K. A. Dill, J. Am. Chem. Soc., 2000, 122, 8037 CrossRef CAS.
- F. W. Starr, C. Angell and H. Stanley, Phys. A, 2003, 323, 51 CrossRef CAS.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492 CrossRef CAS PubMed.
- Z. Li, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061204 CrossRef PubMed.
- J. R. Schmidt and J. L. Skinner, J. Phys. Chem. B, 2004, 108, 6767 CrossRef CAS.
- D. Coglitore, S. P. Edwardson, P. Macko, E. A. Patterson and M. Whelan, R. Soc. Open Sci., 2017, 4, 170507 CrossRef PubMed.
- M. Sharma and S. Yashonath, J. Phys. Chem. B, 2006, 110, 17207 CrossRef CAS PubMed.
- G. Camisasca, D. Schlesinger, I. Zhovtobriukh, G. Pitsevich and L. G. M. Pettersson, J. Chem. Phys., 2019, 151, 034508 CrossRef PubMed.
- F. Perakis and C. Gutt, Phys. Chem. Chem. Phys., 2020, 22, 19443 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02866a |
| This journal is © the Owner Societies 2021 |

