Open Access Article
Open Access ArticleOn the nanoscopic structural heterogeneity of liquid n-alkyl carboxylic acids†
Alessandro
Mariani
 ab,
Alessandro
Innocenti
ab,
Alessandro
Innocenti
 ab,
Alberto
Varzi
ab,
Alberto
Varzi
 ab and
Stefano
Passerini
ab and
Stefano
Passerini
 *ab
*ab
aHelmholtz Institute Ulm (HIU), Helmholtzstrasse 11, Ulm 89081, Germany
bKarlsruhe Institute of Technology (KIT), P.O. Box 3640, Karlsruhe 76021, Germany. E-mail: stefano.passerini@kit.edu
First published on 20th August 2021
Abstract
Herein we report the first in-depth structural characterisation of simple linear carboxylic acids with alkyl tail length ranging from one to six carbon atoms. By means of the SWAXS technique, a pronounced nanoscopic heterogeneity evolving along the aliphatic portion of the molecule is highlighted. Via classical molecular dynamics, the origin of such heterogeneity is unambiguously assigned to the existence of aliphatic domains resulting from the self-segregation of the polar and apolar portions of the molecules. Furthermore, the structural correlation of aliphatic-separated polar domains is responsible for observing the so-called “pre-peak” in the SAXS region.
Introduction
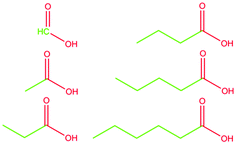
Carboxylic acids are ubiquitous in nature.1–7 They are produced by basically all living organisms as by-products of their methabolism3,8 and are conveniently used in several chemical processes.7,9–12 Despite their seemingly simple molecular structure, carboxylic acids present a pronounced amphiphilicity due to the markedly polar carboxylic group as opposed to the nonpolar alkyl tail. This peculiarity is at the base of the use of their salts as raw materials to produce soaps since antiquity. Surprisingly, though, not much work has been done regarding the structural characterization of such fundamental chemicals. Instead, most studies focus on their hydrogen-bond network (mainly in the solid-state)13–17 or the determination of the crystal structure.18Only a handful of works deal directly with the liquid structural determination,19,20 with only one paper explicitly analysing it21 to an unsatisfactory level, not addressing the heterogeneity of the systems. Such a gap in characterising this important class of compounds is frankly unexpected and needs to be filled. Here we report the structural characterisation of formic acid (methanoic acid, C1OOH), acetic acid (ethanoic acid, C2OOH), propionic acid (propanoic acid, C3OOH), butyric acid (butanoic acid, C4OOH), valeric acid (pentanoic acid, C5OOH), and caproic acid (hexanoic acid, C6OOH). We limit our discussion to short-chained, linear, fully hydrogenated, liquid carboxylic acids (see Fig. 1). This study does not consider effects arising from further complexity, e.g., multiple bonds or a branched skeletal structure. The experimental SWAXS patterns were collected and used to validate the classical molecular dynamics simulations. The models were, in turn, used to extract structural information about the systems. The motivation for this study arises from the much-needed understanding of the structural properties of simple amphiphilic molecules. Such knowledge is of great importance to better understand more complex mechanisms such as protein phase transitions,22,23 ion transport in ionic liquids,24,25 and self-assembling liquid crystals.26
Results and discussion
The experimental and theoretical SWAXS patterns of the n-alkyl carboxylic acids are reported in Fig. 2. | ||
| Fig. 2 Experimental (red, top) and theoretical (blue, bottom) X-ray scattering patterns. The curves are vertically shifted for clarity. | ||
The models reproduce the position and the shape of the experimental peaks excellently. Minor discrepancies arise in the calculated signal intensities, but the difference between the simulation and the experiment is below 5% even in the worst case. All curves, except for the one relative to C1OOH, show an evolving feature at q values below 1 Å−1, indicating a mid-range ordering of the liquid systems. The emerging peak, usually called the “pre-peak”, becomes gradually more intense and left-shifted as the alkyl chain grows, as displayed in Table 1 and Fig. 3.
| System | 100 S(q) [A.U.] | q [Å−1] | r [Å] |
|---|---|---|---|
| C1OOH | N/A | N/A | N/A |
| C2OOH | 6.3 | 0.95 | 6.61 |
| C3OOH | 14.4 | 0.82 | 7.66 |
| C4OOH | 14.8 | 0.70 | 8.98 |
| C5OOH | 17.3 | 0.59 | 10.65 |
| C6OOH | 22.0 | 0.51 | 12.32 |
Such a feature and corresponding behaviour as a function of chain length are uncommon in simple organic liquids, which are usually homogeneous at mid-long scales, presenting flat SAXS patterns below 1 Å−1. Nevertheless, the pre-peak has been reported in markedly amphiphilic systems such as n-alcohols,27–30 and n-aldehydes,31,32 and also in more complex systems like ionic liquids,33–36 deep eutectic solvents,37 and pseudo-ionic liquids.38–40 The trend of the pre-peak position as a function of the alkyl tail length is shown in Fig. 3, together with two tentative fitting lines. The experimental maxima positions were fitted with a linear function (blue line in Fig. 3) and an exponential decay function (red line in Fig. 3). Both the curves showed a satisfactory agreement, with R2 values > 0.98, albeit the exponential fitting was more accurate. To unambiguously determine which function governs the pre-peak position, we calculated the S(q) for the heptanoic, octanoic, and nonanoic acids (C7OOH, C8OOH, and C9OOH, respectively), finding an almost perfect agreement with the value predicted by the exponential decay. The C7–9OOH structure functions and the fitting parameters can be found in Fig. S1 and Table S4 of the ESI.†
The pre-peak position exponentially decaying with the number of carbon atoms in the chain implies that any additional methylene group has a smaller effect on the pre-peak position than the previous methylene addition. In other words, defining Δq as the difference between the pre-peak positions:
 | (1) |
 | (2) |
Such behaviour will be intuitively understood in the following, vide infra.
Although the existence of the pre-peak in simple carboxylic acids was already reported in 2012 by Lajovic et al.,21 the origin of that feature has not been pinpointed so far. In this work, we take advantage of the remarkable quality of our models (Fig. 2) to identify the nature of the pre-peak in this somewhat simple class of molecules. To do so, we calculated some partial structure functions Si,j(q) (Fig. 4). The total X-ray scattering function, S(q), is defined as:
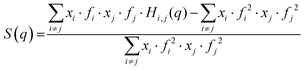 | (3) |
As is clear from eqn (3), it is possible to calculate the partial structure functions by selecting only a subset of the possible i and j pairs, with the constraint that the sum of the partial structure functions obtained for all the possible i,j pairs returns the total structure function S(q), or:
 | (4) |
It should be clear that the partial S(q)s are not experimentally accessible, so they can be confidently extracted only from a model well-representing the real system.
The atom pair selection is straightforwardly made by setting the mole fraction of the undesired atoms to zero in eqn (3), as implemented in the TRAVIS software.41 Practically, this is equivalent to making the undesired atoms transparent to X-rays, thus observing only the scattering pattern originated by the selected atoms in their positions.
We partitioned the structure function in three partial S(q)s following eqn (3). The selected i,j pairs have been chosen to focus on the amphiphilic nature of the molecules, highlighting the effect of the progressively longer alkyl chain. Based on the polar/apolar molecular portions defined in Fig. 1, we calculated the partial structure functions for the polar–polar (P,P), apolar–apolar (A,A), and polar–apolar (P,A) correlations (see Fig. 4). We made the radical decision to consider all the carbon atoms as part of the hydrophobic portion of the molecule (see Fig. 1). However, the overall results would be only slightly affected by considering the carboxylic carbon as part of the hydrophilic portion. Therefore, this decision was made to include C1OOH flawlessly in the analysis. From Fig. 4a, corresponding to the SP,P(q)s, it is immediately evident how the pre-peak originates from this structural correlation. In fact, a feature at q values below 1 Å−1 evolves in the structure function along with the alkyl chain length, passing from the absolute flatness in C1OOH to a rather sharp and well-formed peak in C6OOH, as experimentally observed in the total S(q)s.
Another important clue about the origin of the pre-peak comes from the partial SP,A(q) functions (Fig. 4c). In fact, in the low q region, a progressively more negative contribution to the structure is observed with increasing the alkyl tail length. Such behaviour suggests volume exclusion in the corresponding regions of real space, i.e., mutual self-segregation. The exclusion becomes more pronounced from C1OOH to C6OOH because of the increased hydrophobic character of the molecules, resulting in a more efficient repulsion of the polar portion of adjacent molecules. The same effect is responsible for the increased intensity and sharpness of the pre-peak as the alkyl tail grows.
We would expect SP,P(q) and SA,A(q) to be reasonably similar, given that polar domains are separated by apolar domains and vice versa. Nevertheless, the latter functions are entirely flat in the low q region, as evident from Fig. 4b, suggesting the absence of correlations and volume exclusion at mid-long scales. This is easily explained by the hydrophilic portion of all considered acids being always the same, composed of the carboxylic groups. The corresponding formed polar domains are, thus, relatively small, and their contribution to the structure functions is buried in the main peak at around 1.5 Å−1. In fact, in that q region, the so-called main peak is always observed for any liquid.
Such a peak originates from the first neighbours’ shells. In the case of carboxylic acids, the vastly dominant intermolecular force is the strong intermolecular hydrogen bonding involving the carboxylic groups. On this basis, it is reasonable to expect that the separation induced by the polar domain is always in the q region of the main peak and consequently buried underneath it. The visual inspection of the simulated boxes clarifies the nature of the observations (see Fig. 5).
As the alkyl tail grows, a clear structural evolution appears. The polar portion of the molecules tends to stay together because of the strong intermolecular hydrogen bonding between the carboxylic groups and the lipophobicity towards the alkyl tales. Consequently, two separated domains are generated (only the polar domain is shown in Fig. 5, for clarity). Such domains get more and more physically separated as methylene groups are added to the aliphatic part of the molecule, as hinted by the larger voids separating the red portions in Fig. 5. In other words, the hydrophobic domain acts as a “spacer” between the polar groups of different molecules, modulating the characteristic distance from which the pre-peak in the structure function originates. The segregation is shown in Fig. 6c and schematically represented in Fig. 6d. It is worth noting that the overall structure is bicontinuous, with the polar and apolar domains percolating, reminiscent of the sponge-like structure of some ionic liquids.34 The same conclusion is achieved by calculating the volume of the domains (Fig. S2 in ESI†).
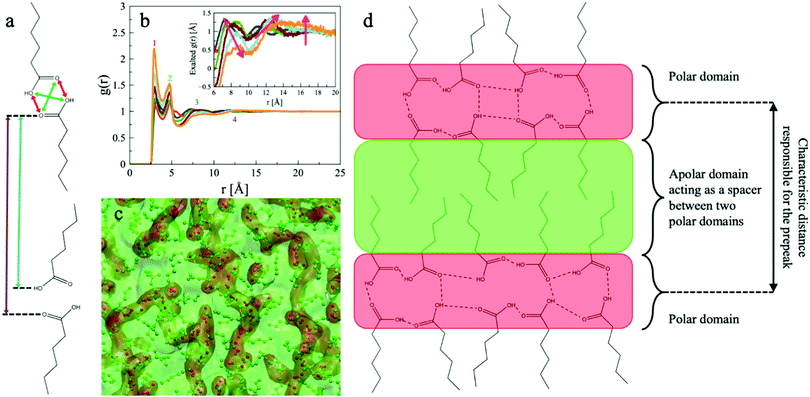 | ||
| Fig. 6 (a) Schematic representation of the characteristic distances originating the peaks observed in the oxygen–oxygen radial distribution function. The colour of the arrows indicates to which peak they are associated. Peak 1 (red), peak 2 (green), peak 3 (cyan), peak 4 (violet). (b) Radial distribution functions for the Oxygen–Oxygen correlation. The inset magnifies the exalted functions (eqn (5)) in the region responsible for the pre-peak. For both panels: C1OOH (blue), C2OOH (red), C3OOH (green), C4OOH (brown), C5OOH (cyan), C6OOH (orange). (c) Snapshot of a region of the simulation box for C6OOH. The polar part is depicted in red, the apolar part is in green. The atoms are displayed as spheres, and the corresponding domains are rendered as space-filling clouds. (d) Schematic representation of the self-segregated domains. | ||
The polar domain size stays roughly constant regardless of the acid considered, which is expected because the polar portion is the same for all six chemicals. Consequently, the occupied volume is also always the same, corresponding to the carboxylic portion of the molecules combined. On the other hand, the apolar domain steadily grows due to the alkyl tail length because more methylene units contribute to the overall apolar portion volume.
Accordingly, the apolar domain growth pushes apart the polar domains (Fig. 6c and d), with the consequential pre-peak shift towards smaller q values.
Finally, by looking at the radial distribution functions (RDFs) of the oxygen atoms it is possible to appreciate, in the real space, the structural correlations responsible for the pre-peak. As expected, the radial distribution functions look somewhat similar, being calculated for the carboxylic oxygen atoms, the same functional group in all the examined molecules. However, two exciting effects are appreciated when focusing on the 6–20 Å region, i.e., the part corresponding to the observed pre-peak. The first (highlighted with the pink arrow on the left of the inset in Fig. 6b) is a progressive loss of correlation in the 6–9 Å region, passing from C1OOH to C6OOH. The intensity loss could be related to increasingly important coiling effects and the side–side interactions of the alkyl tails. Unfortunately, differentiating and quantifying the two effects is not trivial and beyond the scope of the present paper. At the same time, the longer–range bump at 11–18 Å (central and rightmost pink arrows in Fig. 6b inset), even if not dramatically changing, becomes the only peak in this region to be more intense than 1. This means that it becomes the dominant correlation, thus explaining the low q shift of the peak with increasing chain length. To better appreciate the subtle differences in the long–range part of the curves in Fig. 6b, we exalted the RDFs:
| Exalted g(r) = {[g(r) − 1]·r}+1 | (5) |
A possible driving force for the enhanced intensity of the longer-scale correlation is the progressively more pronounced hydrophobicity of the apolar domain. In fact, one has to consider that the self-segregation becomes more effective with longer chains, owing to a more defined and persistent structuration. This interpretation also explains why the pre-peak intensity in Fig. 2 and 4b increases along with the number of methylene groups in the chain, as stated above. Furthermore, as the tail grows, the separation is more effective, enhancing the contrast between the low-electron-density aliphatic region and the high-electron-density polar region and, thus, affecting the intensity of the pre-peak.
Conclusions
In summary, we have here shortly reported the inherent nano-heterogeneity of simple linear n-alkyl carboxylic acids. The experimental SAXS patterns clearly showed an evolving nano-structuration of these ubiquitous compounds, which depends on the length of the alkyl chains. Classical molecular dynamics allowed us to determine the origin of this peak being the aliphatic-mediated distance between polar domains. This conclusion is in line with similar observations in markedly amphiphilic molecules, such as alcohols and ionic liquids. However, the subtle balance between hydrogen bonding, van der Waals forces, and dispersion forces in such simple molecules appears to return pictures much more complicated than one could expect. The pronounced heterogeneity at the nanoscopic level of carboxylic acids could be exploited by using them as a lubricant and explains their excellent properties as solvents. However, a significant limitation is that they remain acids and, albeit weak, could lead to undesired effects during their use.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All the authors thank the support of Helmholtz Association. This research is partially supported by the Bundes Ministerium für Wissenschaft und Forschung (BMWi) research grant “FZK 03ETB003A HiFi-PEFC”.Notes and references
- A. Chebbi and P. Carlier, Carboxylic acids in the troposphere, occurrence, sources, and sinks: a review, Atmos. Environ., 1996, 30, 4233–4249 CrossRef CAS.
- E. Dabek-Zlotorzynska and M. McGrath, Determination of low-molecular-weight carboxylic acids in the ambient air and vehicle emissions: a review, Fresenius’ J. Anal. Chem., 2000, 367, 507–518 CrossRef CAS PubMed.
- C. Skonberg, J. Olsen, K. G. Madsen, S. H. Hansen and M. P. Grillo, Metabolic activation of carboxylic acids, Expert Opin. Drug Metab. Toxicol., 2008, 4, 425–438 CrossRef CAS PubMed.
- M. Casal, S. Paiva, O. Queirós and I. Soares-Silva, Transport of carboxylic acids in yeasts, FEMS Microbiol. Rev., 2008, 32, 974–994 CrossRef CAS PubMed.
- C. S. López-Garzón and A. J. J. Straathof, Recovery of carboxylic acids produced by fermentation, Biotechnol. Adv., 2014, 32, 873–904 CrossRef PubMed.
- V. De Groof, M. Coma, T. Arnot, D. J. Leak and A. B. Lanham, Medium Chain Carboxylic Acids from Complex Organic Feedstocks by Mixed Culture Fermentation, Molecules, 2019, 24, 398 CrossRef PubMed.
- L. Reyes, C. Nikitine, L. Vilcocq and P. Fongarland, Green is the new black–a review of technologies for carboxylic acid recovery from black liquor, Green Chem., 2020, 22, 8097–8115 RSC.
- B. Baena, A. Cifuentes and C. Barbas, Review Analysis of carboxylic acids in biological fluids by capillary electrophoresis, Electrophoresis, 2005, 2622–2636 CrossRef CAS PubMed.
- F. Miller, Carboxylic acids as metal extractants, Talanta, 1974, 21, 685–703 CrossRef CAS PubMed.
- J. C. Petersen and H. Plancher, Quantitative determination of carboxylic acids and their salts and anhydrides in asphalts by selective chemical reactions and differential infrared spectrometry, Anal. Chem., 1981, 53, 786–789 CrossRef CAS.
- P. Domínguez de María, Minimal Hydrolases: organocatalytic Ring-Opening Polymerizations Catalyzed by Naturally Occurring Carboxylic Acids, ChemCatChem, 2010, 2, 487–492 CrossRef.
- M. Pichette Drapeau and L. J. Gooßen, Carboxylic Acids as Directing Groups for C−H Bond Functionalization, Chem. – Eur. J., 2016, 22, 18654–18677 CrossRef CAS PubMed.
- B. H. Meier, F. Graf and R. R. Ernst, Structure and dynamics of intramolecular hydrogen bonds in carboxylic acid dimers: a solid state NMR study, J. Chem. Phys., 1982, 76, 767–774 CrossRef CAS.
- M. C. Etter, Aggregate Structures of Carboxylic Acids and Amides, Isr. J. Chem., 1985, 25, 312–319 CrossRef CAS.
- T. Loerting and K. R. Liedl, Toward Elimination of Discrepancies between Theory and Experiment: double Proton Transfer in Dimers of Carboxylic Acids, J. Am. Chem. Soc., 1998, 120, 12595–12600 CrossRef CAS.
- C. Foces-Foces, A. Echevarría, N. Jagerovic, I. Alkorta, J. Elguero, U. Langer, O. Klein, M. Minguet-Bonvehí and H.-H. Limbach, A Solid-State NMR, X-ray Diffraction, and ab Initio Computational Study of Hydrogen-Bond Structure and Dynamics of Pyrazole-4-Carboxylic Acid Chains, J. Am. Chem. Soc., 2001, 123, 7898–7906 CrossRef CAS PubMed.
- L. Tao, J. Han and F.-M. Tao, Correlations and Predictions of Carboxylic Acid pKa Values Using Intermolecular Structure and Properties of Hydrogen-Bonded Complexes, J. Phys. Chem. A, 2008, 112, 775–782 CrossRef CAS PubMed.
- A. D. Bond, On the crystal structures and melting point alternation of the n-alkyl carboxylic acids, New J. Chem., 2004, 28, 104–114 RSC.
- M. N. Kobrak and K. G. Yager, X-Ray scattering and physicochemical studies of trialkylamine/carboxylic acid mixtures: nanoscale structure in pseudoprotic ionic liquids and related solutions, Phys. Chem. Chem. Phys., 2018, 20, 18639–18646 RSC.
- M. Campetella, F. Cappelluti and L. Gontrani, Medium range interactions evidences in compounds with aliphatic lateral chain: 1-pentanoic acid, 1-pentanol and pentylammonium nitrate as test cases, Chem. Phys. Lett., 2019, 734, 136738 CrossRef CAS.
- A. Lajovic, M. Tomšič and A. Jamnik, Structural Study of Simple Organic Acids by Small-Angle X-Ray Scattering and Monte Carlo Simulations, Acta Chim. Slov., 2012, 59, 520–527 CAS.
- O. Matsarskaia, F. Roosen-Runge and F. Schreiber, Multivalent ions and biomolecules: attempting a comprehensive perspective, ChemPhysChem, 2020, 21, 1742–1767 CrossRef CAS PubMed.
- O. Matsarskaia, S. Da Vela, A. Mariani, Z. Fu, F. Zhang and F. Schreiber, Phase-Separation Kinetics in Protein–Salt Mixtures with Compositionally Tuned Interactions, J. Phys. Chem. B, 2019, 123, 1913–1919 CrossRef CAS PubMed.
- A. Mariani, M. Bonomo, B. Wu, B. Centrella, D. Dini, E. W. Castner and L. Gontrani, Intriguing transport dynamics of ethylammonium nitrate–acetonitrile binary mixtures arising from nano-inhomogeneity, Phys. Chem. Chem. Phys., 2017, 19, 27212–27220 RSC.
- M. Campetella, A. Mariani, C. Sadun, B. Wu, E. W. Castner and L. Gontrani, Structure and dynamics of propylammonium nitrate–acetonitrile mixtures: an intricate multi-scale system probed with experimental and theoretical techniques, J. Chem. Phys., 2018, 148, 134507 CrossRef PubMed.
- O. Francescangeli, M. Pisani, V. Stanić, P. Bruni and T. M. Weiss, Evidence of an inverted hexagonal phase in self-assembled phospholipid–DNA–metal complexes, Europhys. Lett., 2004, 67, 669–675 CrossRef CAS.
- K. S. Vahvaselkä, R. Serimaa, M. Torkkeli, K. S. Vahvaselk, R. Serimaa, M. Torkkeli, B. Y. Kaarlo, S. Vahvaselk, R. Serimaa and M. Torkkeli, Determination of Liquid Structures of the Primary Alcohols Methanol, Ethanol, 1-Propanol, 1-Butanol and 1-Octanol by X-ray Scattering, J. Appl. Crystallogr., 1995, 28, 189–195 CrossRef.
- M. Tomšič, A. Jamnik, G. Fritz-Popovski, O. Glatter and L. Vlček, Structural Properties of Pure Simple Alcohols from Ethanol, Propanol, Butanol, Pentanol, to Hexanol: comparing Monte Carlo Simulations with Experimental SAXS Data, J. Phys. Chem. B, 2007, 111, 1738–1751 CrossRef PubMed.
- A. Mariani, P. Ballirano, F. Angiolari, R. Caminiti and L. Gontrani, Does High Pressure Induce Structural Reorganization in Linear Alcohols? A Computational Answer, ChemPhysChem, 2016, 17, 3023–3029 CrossRef CAS PubMed.
- M. Požar, J. Bolle, C. Sternemann and A. Perera, On the X-ray Scattering Pre-peak of Linear Mono-ols and the Related Microstructure from Computer Simulations, J. Phys. Chem. B, 2020, 124, 8358–8371 CrossRef PubMed.
- I. Pethes, L. Temleitner, M. Tomšič, A. Jamnik and L. Pusztai, X-Ray Diffraction and Computer Simulation Studies of the Structure of Liquid Aliphatic Aldehydes: from Propanal to Nonanal, Phys. Status Solidi, 2018, 255, 1800127 CrossRef.
- I. Pethes, L. Temleitner, M. Tomšič, A. Jamnik and L. Pusztai, Unexpected Composition Dependence of the First Sharp Diffraction Peak in an Alcohol–Aldehyde Liquid Mixture: n-Pentanol and Pentanal, Phys. Status Solidi B, 2018, 255, 1–7 Search PubMed.
- J. N. A. Canongia Lopes and A. A. H. Pádua, Nanostructural Organization in Ionic Liquids, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Pronounced sponge-like nanostructure in propylammonium nitrate, Phys. Chem. Chem. Phys., 2011, 13, 13544 RSC.
- A. Mariani, R. Caminiti, M. Campetella and L. Gontrani, Pressure-induced mesoscopic disorder in protic ionic liquids: first computational study, Phys. Chem. Chem. Phys., 2016, 18, 2297–2302 RSC.
- A. Mariani, M. Campetella, C. Fasolato, M. Daniele, F. Capitani, L. Bencivenni, P. Postorino, S. Lupi, R. Caminiti, L. Gontrani, M. Campetella, C. Fasolato, F. Capitani, P. Postorino, C. Fasolato, M. Daniele, S. Lupi, R. Caminiti, F. Capitani, L. Bencivenni, P. Postorino, S. Lupi, R. Caminiti and L. Gontrani, A joint experimental and computational study on ethylammonium nitrate–ethylene glycol 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. Structural, kinetic, dynamic and spectroscopic properties, J. Mol. Liq., 2017, 226, 2–8 CrossRef CAS.
1 mixture. Structural, kinetic, dynamic and spectroscopic properties, J. Mol. Liq., 2017, 226, 2–8 CrossRef CAS. - A. Malik and H. K. Kashyap, Heterogeneity in hydrophobic deep eutectic solvents: SAXS prepeak and local environments, Phys. Chem. Chem. Phys., 2021, 23, 3915–3924 RSC.
- H. Doi, X. Song, B. Minofar, R. Kanzaki, T. Takamuku and Y. Umebayashi, A new proton conductive liquid with no ions: pseudo-protic ionic liquids, Chem. – Eur. J., 2013, 19, 11522–11526 CrossRef CAS PubMed.
- V. Turco Liveri, D. Lombardo, M. Pochylski and P. Calandra, Molecular association of small amphiphiles: origin of ionic liquid properties in dibutyl phosphate/propylamine binary mixtures, J. Mol. Liq., 2018, 263, 274–281 CrossRef CAS.
- P. Calandra, On the physico-chemical basis of self-nanosegregation giving magnetically-induced birefringence in dibutyl phosphate/bis(2-ethylhexyl) amine systems, J. Mol. Liq., 2020, 310, 113186 CrossRef CAS.
- O. Hollóczki, M. Macchiagodena, H. Weber, M. Thomas, M. Brehm, A. Stark, O. Russina, A. Triolo and B. Kirchner, Triphilic Ionic–Liquid Mixtures: fluorinated and Non-fluorinated Aprotic Ionic–Liquid Mixtures, ChemPhysChem, 2015, 16, 3325–3333 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02846d |
| This journal is © the Owner Societies 2021 |