Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High time resolution measurements of droplet evaporation kinetics and particle crystallisation†
D. A.
Hardy
 a,
J.
Archer
a,
J.
Archer
 a,
P.
Lemaitre
b,
R.
Vehring
c,
J. P.
Reid
a,
P.
Lemaitre
b,
R.
Vehring
c,
J. P.
Reid
 a and
J. S.
Walker
a and
J. S.
Walker
 *a
*a
aSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: jim.walker@bristol.ac.uk
bInstitut de Radioprotection et de Sûreté Nucléaire (IRSN), PSN-RES, SCA, LPMA, Gif sur Yvette, France
cDepartment of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G 2G8, Canada
First published on 11th August 2021
Abstract
A refined technique for observing the complete evaporation behaviour of free-falling droplets, from droplet generation to complete solvent evaporation, with ultra-high time resolution is introduced and benchmarked. High-resolution phase-delay stroboscopic imaging is employed to simultaneously resolve the evolving droplet morphology, geometric and aerodynamic diameters, throughout the evaporative lifetime with a user-controlled < μs timescale. This allows rapid, complex morphological changes, such as crystallisation events, to be clearly observed and the corresponding mechanisms to be inferred. The dried particles are sampled for offline SEM analysis and the observed morphologies compared to the inflight imaging. Density changes can be calculated directly from the deviation between the geometric and aerodynamic diameters. The full capabilities of the new technique are demonstrated by examination of the different evaporation behaviours and crystallisation mechanisms for aqueous sodium chloride droplets evaporating under different ambient relative humidity (RH) conditions. The crystallisation window, defined as the time taken from initial to complete crystallisation, is shown to be RH dependent, extending from 0.03 s at 20% RH and 0.13 s at 40% RH. The different crystallisation mechanisms observed during the experiments are also clearly reflected in the final structure of the dry particles, with multi-crystal structures produced at low RH compared to single-crystal structures at higher RH. It is anticipated that this technique will unlock measurements which explore the evaporation behaviour and crystallisation mechanisms for rapid, complex droplet drying events, and with increasingly non-ideal solutions, relevant to industrial applications.
I. Introduction
Modelling the evaporative drying, phase behaviour, morphology and transport of droplets and aerosol particles is important for many industrial applications, including spray drying, crop spraying, spray painting and droplet vaporisation processes such as fuel injection and combustion in automotive and aerospace engines.1–3 Recent attention has also been paid to the impact of these factors on respiratory disease transmission.4–6 Spray drying, a ubiquitous process in the food and pharmaceutical industries, employs the production of droplets into a heated environment which are dried rapidly to form solid particles.7–13 The processes underlying spray drying can also be applied to understand the properties of airborne particles relevant to various nuclear safety scenarios.14 For example, following the rupture of a heated, pressurised, fission product evaporator radionuclides may be released as a plume of droplets which evaporate rapidly due to the elevated temperatures.15,16 Studies resolving the microphysical behaviour of evaporating droplets can provide important insights into evolving particle size and phase.To quantify the transport of material released in a spray dryer or nuclear accident, and to understand the efficacy of filtration systems, the aerodynamic size of the particles must be understood.17,18 The aerodynamic size depends on physical properties as well as the geometric size. For example, a solid, smooth, spherical particle will sediment more rapidly than a hollow, buckled, non-spherical particle of equivalent mass. The aerodynamic diameter da is defined as the geometric diameter dv of a sphere with density 1 g cm−3 with the same settling velocity as the particle in question. The aerodynamic diameter of a particle falling through a gas can be calculated using eqn (1), where ρ* is the standard density of 1 g cm−3, μ is the dynamic viscosity of the gas medium, g is the acceleration due to gravity and vs is the terminal settling velocity of the particle.
 | (1) |
Droplets formed from a bulk sample by an aerosolization process undergo a brief period of rapid, unsteady evaporation due to an imbalance of heat and mass flux away from the newly formed droplet. However, upon reaching a phase of near-constant heat and mass flux, known as stead-state evaporation, pure solvent droplets evaporate according to a diameter-squared law, defined in eqn (2).19–21 This relates geometric diameter at time t, to the evaporation rate κ and the initial diameter dv0.
| dv(t)2 = dv02 − κt | (2) |
 | (3) |
The dry particle size (at least the point at which a solid crust is formed) and morphology are influenced by the competition between solvent evaporation rate and solute diffusion, represented by the diffusion constant D. This competition is characterised by the Peclét number Pe, defined in eqn (4).23
 | (4) |
To investigate the interplay of drying rate, final particle morphology and aerodynamic size, a suitable instrument would allow observation of the evolving particle morphology throughout the drying process with parallel measurements of geometric diameter and aerodynamic diameter. Finally, sampling of the dry particles produced would allow detailed analysis of the relationship between drying conditions and final dry particle morphology providing a direct comparison to the dry particles produced in industrial applications. Phase transitions and morphological changes in the aerosol phase can occur over short timescales (≪0.1 s), even though full droplet evaporation may take several seconds. In industrial applications droplet evaporation can be exceedingly rapid and, therefore, measurements of the evolving droplet properties are required with a time resolution on the order of milliseconds.
There are a variety of complementary methods for investigating evaporating droplets and the properties of the final dry particles. Studies with droplets deposited on surfaces, often referred to as sessile droplets, or suspended from a wire tip, pendant droplets, are both common, but do not replicate the aerosol phase as the droplets are not free from surface interactions.28 Optical, electrodynamic and acoustic trapping all involve trapping individual aerosol droplets, but do not allow detailed observation of the morphology, especially during crystallisation.29–33 Droplet chain instruments enable studies and observation of the entire droplet drying and particle formation processes free from surface contact, including measurements of droplet optical properties using elastic light scattering, and composition by linear and non-linear Raman scattering.34,35 In addition, they allow high-time resolution observations of the physical and aerodynamic diameter at distinct stages of the evaporative lifetime, from droplet generation to dry particle formation, and dry particles can be collected for further analysis.36
Droplet chain techniques rely upon a droplet source that produces a series of uniform droplets that descend under the influence of gravity or propelled by a gas flow.37 At any moment, each position in the droplet series, or ‘chain’, represents a snapshot of a specific point in the lifetime of a single evaporating droplet. The temporal resolution between snapshots is equivalent to the reciprocal of the frequency of droplets in the chain. One such technique was developed by Baldelli et al. and involved generation and stroboscopic illumination of a droplet chain to observe the evolving aerodynamic size of aqueous cellulose acetate butyrate and sodium nitrate droplets, with ∼20 ms temporal resolution.11,36 Imaging the silhouettes of the droplets allowed the inflight geometric diameter to be calculated and the final dried particle morphologies were analysed using scanning electron microscopy (SEM).
Here, we introduce the Falling Droplet Column (FDC), where the droplet chain technique has been extended to include high resolution imaging and significantly improved temporal resolution. This technique allows detailed images of the evolving morphology to be collected throughout the full evaporative lifetime, from droplet generation to dry particle formation, spanning almost 6 orders of magnitude in time (<1 μs to ∼5 s). The gas phase conditions can be controlled to explore effect of the specific drying conditions on evaporation process and resulting dry particle morphologies. We demonstrate the capabilities of the technique with detailed inflight observations of the different crystallisation mechanisms for inorganic solution droplets evaporating under different environmental conditions.
II. Experimental
A schematic of the FDC instrument is shown in Fig. 1, which also indicates the main analysis techniques. The instrument uses a droplet-on-demand (DoD) dispenser (Microfab, MJ-ABP-01), triggered with a voltage pulse at a regular, user-controlled frequency, to generate a continuous stream of uniform droplets. The stream is dispensed horizontally and directed into a vertical glass column of 4 cm2 inner area and 50 cm long. The droplets rapidly lose their horizontal momentum and fall vertically down the centre of the column, evaporating as they fall. The falling droplets are illuminated by a vertically propagating laser, strobed at the same frequency as the DoD dispenser. This produces the illusion of a visible static ‘chain’ of droplets. An xyz-translational stroboscopic imaging assembly is used to analyse droplets at various positions along the chain. Dry particles formed during the evaporation processes are collected on a glass slide at the bottom of the column and are further analysed using scanning electron microscopy (SEM) imaging. Initially, the droplets are monodisperse with a diameter of 25 to 50 μm depending on the DoD orifice size and pulse sequence parameters (pulse width, frequency, amplitude, etc.); at sampling, the dry particles are typically 5 to 20 μm in size depending on the initial droplet size and composition.The column is isolated from the laboratory environment allowing the internal gas phase conditions to be controlled. A gas flow, formed by combining dry and humidified nitrogen flows in variable proportions, is used to control the relative humidity (RH) inside the column. The gas flow enters at the top of the column and exits near the bottom, with a user-controlled flowrate. The average gas flow speed vG can be calculated using eqn (5), where Q is the volumetric flow rate and A is the cross-sectional area of the glass column.
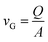 | (5) |
| vs = vy − cGvG | (6) |
Control of the instrument hardware, and all the analysis, is performed electronically from an interfaced PC using a bespoke computer program, written in LabVIEW.
II.a Droplet imaging and position measurement
Brightfield imaging with a high-power LED, strobed at the DoD dispensing frequency with 500 ns pulses is used to analyse the droplet positions along the column. The illuminated droplet image is collected with a long working distance (LWD) objective (Optem 10X M Plan APO LWD) mounted together with an associated zoom lens module (Optem Fusion 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Zoom Detent) and is captured and digitised with a CCD (JAI GO-2400M-USB). The field-of-view of the image is calibrated with a micrometre graticule allowing measured dimensions to be automatically converted from pixels to physical dimensions. The pixel resolution depends on the selected zoom setting, but is typically 0.5–1 μm. Fig. 2 is an example brightfield image of the tip of the DoD dispenser and a freshly dispensed droplet. These images allow the droplet morphology to be observed, as well as the location and physical dimensions to be calculated.
1 Zoom Detent) and is captured and digitised with a CCD (JAI GO-2400M-USB). The field-of-view of the image is calibrated with a micrometre graticule allowing measured dimensions to be automatically converted from pixels to physical dimensions. The pixel resolution depends on the selected zoom setting, but is typically 0.5–1 μm. Fig. 2 is an example brightfield image of the tip of the DoD dispenser and a freshly dispensed droplet. These images allow the droplet morphology to be observed, as well as the location and physical dimensions to be calculated.
Droplets are identified automatically from the brightfield image using an algorithm which makes use of the fact that the edge of the droplet is darker than the background. The greyscale image is binarized against a suitably selected threshold to isolate the droplet shape. A rectangular bounding box is then applied around the droplet allowing the maximum vertical and horizontal dimensions to be retrieved (a and b in Fig. 2). The droplet centre-of-mass is identified from the droplet image, by treating the droplet as a 2-dimensional shape of even density, and used when identifying the droplet location within the image (x and z in Fig. 2). The position of the stroboscopic imaging assembly can be electronically translated to analyse various locations along the droplet chain. The exact horizontal and vertical position of each droplet is calculated by combining the absolute position of the imaging assembly with the relative position of the droplet within the image field-of-view.
II.b Droplet trajectory through the FDC
The trajectory of a droplet through the instrument is characterised by two time-regimes, as shown in Fig. 3. First, there is a period dominated by horizontal motion immediately after the droplet has been dispensed. During this time, the droplet approaches the central vertical axis of the column, decelerating to lose any initial momentum supplied during the dispensing process. The droplet transitions to fall vertically down the centre of the column under the influence of gravity and the gas flow, if present, at a velocity approaching the terminal settling velocity until it either evaporates or reaches the bottom of the instrument and is deposited. In Fig. 3, proportionally sized brightfield images of the droplet are shown for marked time intervals. Note that droplet shape oscillations are also observed early in the droplet lifetime as marked within the first 100 μs.38,39 The inset shows the rapid change in velocity as the droplet decelerates to the terminal settling velocity. The immediate deceleration following droplet generation is discussed in more detail below.II.c Geometric and aerodynamic diameter calculations
Although an initial measurement of the droplet geometric diameter can be taken from the dimensions of the rectangular bounding box from the droplet image, a single value is unrepresentative of the droplet size when non-spherical. This is especially important within the first few 100 μs after droplet generation when the droplet is initially teardrop in shape and then oscillates between oblate and prolate spheroids.39 Instead, a geometric (volume equivalent) diameter dv, defined as the diameter of a sphere with the same volume as the observed particle, is inferred. The estimation of dv assumes the droplet shape is constructed as a series of single-pixel thick cylinders centred on a horizontal axis in the plane of the image. The diameter of each cylinder is taken as the number of pixels occupied by the droplet in the corresponding column of pixels in the image. Then, the droplet volume is the sum of the individual volumes of each cylinder. However, this approach still assumes that each slice is circular about a horizontal axis in the plane of the image, leading to reduced accuracy for non-symmetric or crystalline particles, or if the droplet is not orientated parallel to the plane of the image.The aerodynamic diameter can be calculated directly from a measurement of the terminal settling velocity, as shown in eqn (1). The terminal settling velocity is measured from the spatial and temporal separation between consecutive measurement points in the droplet chain.
II.d Temporal resolution
Traditional evaporation profile measurements made using a droplet chain are limited to a temporal resolution equivalent to the reciprocal of the dispensing frequency. Most DoD dispensers are not recommended for use with dispensing frequencies above ∼100 Hz, which would limit the temporal resolution to >10 ms. However, a further limitation of using a droplet chain is that droplets produced at high frequencies may coalesce as they decelerate. In practice this reduces the maximum dispensing frequency to approximately 20 Hz. In this instrument we use a delay generator (BNC Model 555) to insert a variable delay between the droplet generation pulse and brightfield imaging strobe. Now, rather than the temporal separation between measurements being limited by the dispensing frequency, the measurement limitation is the resolution of the delay generator (10 ns). This method allows quasi-continuous measurements of droplet properties throughout the evaporative lifetime. Importantly, the temporal resolution is not only increased using this approach, but it is also variable. This enables processes that occur over rapid timescales (such as crystallisation) to be probed with much higher temporal resolution than is required for slower processes (such as steady-state evaporation). Variations of this method have been employed to study droplet collisions and short-term dispensing dynamics within the inkjet printing industry, however, the use of this setup to analyse full evaporative lifetimes and crystallisation behaviour is a novel development.40–42II.e Dispensing dynamics
The establishment of a falling droplet chain is underpinned by the controllable and reproducible behaviour of the DoD dispensers. Important for this application is the ‘stopping distance’ of the dispensed droplets.22 This not only defines the approximate distance the DoD dispenser should be positioned from the central vertical axis of the glass column, but also identifies when the dispensed droplets are traveling at their terminal settling velocity. An analysis of the dynamics of the droplets dispensed using a DoD generator with a range of typical pulse voltages is presented in Fig. 4. In these examples the DoD generator was orientated to dispense droplets vertically to clearly show the change in velocity, from high initial velocity to low terminal settling velocity, along a single axis.Droplets are initially dispensed at high velocities and decelerate rapidly until the terminal settling velocity is reached within ∼100 ms, corresponding to a distance-of-travel ∼50 mm or less. At increased pulse voltages the droplets are dispensed faster and travel further before decelerating to terminal settling velocity. Indeed, a droplet dispensed using a 70 V pulse may travel ∼25 mm more than one dispensed using a 40 V pulse.
II.f Droplet chain stability and measurement uncertainty
The instrument relies on the positional stability of the droplet chain to generate complete and reproducible evaporation profile measurements. Factors including electrostatic interactions, internal gas flows and unstable behaviour of the DoD dispensers have the potential to perturb the chain stability. Measurements of the variation in position and diameter across many droplets at sequential points in the lifetime of evaporating water droplets were made to assess the stability of the FDC droplet chain.The environment within the column is assumed to be symmetric about the central vertical axis. Thus, the measured variation in the horizontal position in the plane of the image is taken as equivalent to the horizontal variation perpendicular to the image plane. This positional instability is reflected in an apparent variation in the measured geometric diameter as the droplets move in and out of the focal plane of the imaging assembly. Similarly, instability in the vertical position gives rise to the variation in the measured separation between droplets and therefore uncertainty in the aerodynamic diameter.
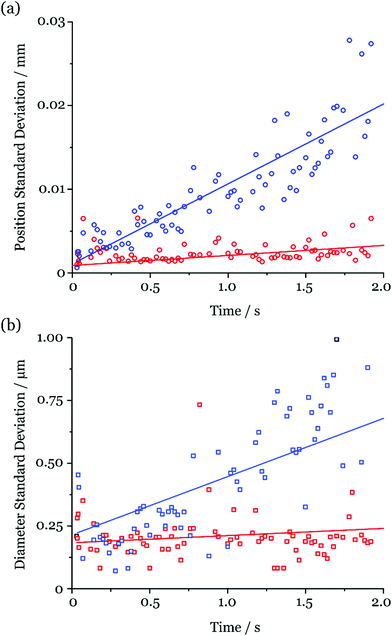
Fig. 5 reports the standard deviation in the measured diameter (geometric and aerodynamic) and position (horizontal and vertical) of 25 droplets at discrete timepoints during the first 2 s of the droplet lifetime (the length of a typical rapid evaporation measurement). These data were collected during the measurements shown in Fig. 3. As can be seen, the measured uncertainties increase with time (i.e. distance along the chain). This is expected, as any small variations between droplet trajectories propagate to larger uncertainties as the droplets travel down the column. However, the uncertainty measured for the geometric diameter does not exceed 0.5 μm and for the aerodynamic diameter generally remains below 1 μm throughout the 2 s window. Intuitively, the increased uncertainty in the aerodynamic diameter can be rationalised when considering that it is calculated using the measured locations of two droplets at different timepoints, both with their own positional instability. These uncertainties are comparable in magnitude to the imaging resolution.
The diameter measurements presented throughout the rest of this work correspond to the mean value from up to 50 droplets recorded at each timepoint with the standard deviation used as a measure of the uncertainty.
III. Results & discussion
III.a Evaporation kinetics measurement validation
Before demonstrating the capability of the instrument for exploring inflight crystallisation mechanisms we first validate the evaporation kinetics measurements by comparing simple solvent evaporation profiles measured using the FDC and Electrodynamic Balance (EDB). The EDB is a well-established technique for performing accurate measurements of the evaporation of single droplets.43Evaporation measurements of ethanol droplets from both EDB and FDC experiments under similar environmental conditions (294 K, ∼0% RH) are reported in Fig. 6a. The timescale is initiated (i.e. t = 0 s) by the DoD dispenser pulse for both experiments and the data clearly show the delay time required before it is possible to capture and observe the droplet size in EDB measurements (∼0.3 s). By comparison, the FDC allows data to be recorded immediately after the droplet is dispensed. Additionally, the initial diameter can be measured directly in the FDC, whereas a significant extrapolation is needed to acquire the same property from the EDB measurements at t = 0 s. The dry environmental conditions for these experiments were specifically selected to compare the performance of the two techniques for monitoring rapid evaporation events. As discussed earlier, each datapoint in an FDC measurement corresponds to the mean value for up to 50 droplets recorded at the same timepoint with the error bars, corresponding to the standard deviation, small enough to be obscured by the datapoints. The spread in the data collected from the EDB highlights the limitations in the measurement of such a rapidly evaporating droplet and indicates that the limits of the technique are being approached.
Fig. 6b presents evaporation profiles for butanol, propanol, ethanol and water measured under equivalent ambient conditions (294 K, ∼0% RH) for both instruments, with linear fits derived from the EDB data shown rather than the raw data. The profiles are displayed as the change in the diameter-squared against time with both axes normalised against the initial diameter for each experiment. This approach allows measurements of droplets with varying initial diameter and different volatilities to be compared on the same graph. The small variations between the FDC and EDB linear fits, reported in Table 1, are consistent within the uncertainty in the temperature and RH measurement attributed to both the FDC (±2 K and ±5% RH) and EDB (±1 K and ±5% RH). An example of the overlap in the uncertainties between the FDC and EDC measurements for water is shown as the shaded blue region in Fig. 6b.
| d 0 2 (FDC)/μm2 | d 0 2 (EDB)/μm2 | κ (FDC)/μm2 s−1 | κ (EDB)/μm2 s−1 | Temperature suppression/K | |
|---|---|---|---|---|---|
| Ethanol | 1140 ± 20 | 2550 ± 60 | 4670 ± 20 | 4700 ± 100 | 18 ± 1 |
| Propanol | 1360 ± 20 | 2380 ± 30 | 4390 ± 90 | 3910 ± 90 | 4 ± 2 |
| Butanol | 1210 ± 7 | 2018 ± 2 | 1428 ± 8 | 1328 ± 2 | 3 ± 1 |
| Water | 1270 ± 40 | 1951 ± 2 | 1215 ± 8 | 1061 ± 2 | 18 ± 2 |
The wet bulb temperature, and therefore the evaporative temperature suppression, was calculated from the evaporation rate for each solvent shown in Fig. 6. This was achieved using the Maxwell definition of the evaporation rate eqn (3), applicable to pure solvents, where the evaporation rate and vapour pressure are expressed as a function of temperature, and varying the droplet temperature until the difference between the calculated and experimental evaporation rates was minimized. The calculated temperature suppressions are shown in Table 1 and the results are consistent with previous measurements of ethanol droplet evaporation performed using the EDB.44–46 The trends in the measured evaporation rates and corresponding temperature suppressions are consistent with the trend in vapour pressure for the individual solvents, as expected.
III.b Crystallisation mechanisms for evaporating NaCl droplets
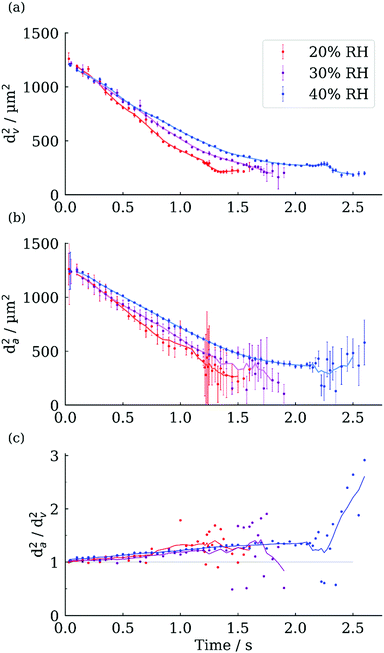
We now demonstrate the capability of the FDC for exploring morphological changes during evaporation, in this case for aqueous NaCl droplets evaporating into a humidity below the efflorescence point (∼45% RH).25Fig. 7 shows the geometric and aerodynamic diameter evaporation profiles for aqueous NaCl droplets of 0.1 initial mass fraction solute (MFS) evaporating into 20%, 30% and 40% RH environments.The initial aerodynamic diameter is slightly larger than the geometric diameter, as expected for a sodium chloride droplet with a density higher than water. For example, the initial density at 40% RH is calculated at 1035 kg m−3, compared to 997 kg m−3 for water, corresponding to a 3.8% increase in the aerodynamic diameter compared to the geometric. As the droplet evaporates and the density increases, the deviation between aerodynamic and geometric diameters also increases (Fig. 7c). Between 0 and 2 s for the 40% RH profile the da2/dv2 ratio increases from 1.04 to 1.4, correlating to an increase in density of ∼360 kg m−3, compared to water. Upon crystallisation both the aerodynamic and geometric diameters decrease. The larger decrease in the aerodynamic diameter reflects a change in the particle morphology (and hence a change in shape factor) alongside the reduction in geometric diameter.
The aerodynamic diameter measurements exhibit significantly larger variability and uncertainty than the geometric diameter, especially after crystallisation (Fig. 7a and b). This could be a true reflection of the differing aerodynamic sizes of the final dry particles, or due to the stochastic nature of the onset of the crystallisation process introducing changes in the separation distance between pairs of droplets, which propagates through the rest of the experiment, remembering that the aerodynamic diameter is measured from the relative positions of two different particles. Although there is no simple method for resolving what is the dominant source of variability in the measured aerodynamic diameter of the dried particles, analysis of the morphology of the dry particles provides an indication of their uniformity.
The evolving evaporation rates for these datasets are shown in more detail in Fig. 8. The general trend is a steady decrease in evaporation rate following droplet generation, deviating away from the d2 law, until the onset of crystallisation. The decrease is most extreme at 40% RH and can be rationalised by considering the difference between the water vapour pressures at the droplet surface and in the gas phase, which govern the evaporation rate. As the water evaporates, the surface concentration of the solute increases which leads to a decrease in the vapour pressure difference and, hence, the evaporation rate. This does not occur as dramatically for droplets evaporating at a lower RH because a significant difference between the vapour pressures is maintained until efflorescence occurs. During crystallisation there is a dramatic increase in the evaporation rate until the solvent loss is complete. Two phenomena contribute to the increase in the evaporation rate during crystallisation. Firstly, the concentration of the supersaturated solution (with highest supersaturation at the droplet surface) reduces rapidly as the solute crystallises, leading to an increase in the vapour pressure at the droplet surface. Secondly, the temperature of the droplet increases as the solute crystallises due to the enthalpy of crystallisation, also increasing the vapour pressure.24 Previous EDB experiments have also observed this short period of increased evaporation rate, and the amount of heat released, corresponding temperature increase and elevated evaporation rate have been shown to correspond well with numerical models.47 This suggests that the temperature increase, calculated as ∼6 K, is the dominant effect increasing the evaporation rate, rather than the decrease in solution concentration. The temperature change ΔT accompanying crystallisation is calculated as follows:
 | (7) |
 | (8) |
 | ||
| Fig. 8 The evolving evaporation rate calculated for aqueous NaCl evaporating at 295 K and 20% RH (red), 30% RH (purple) and 40% RH (blue) The trendlines represent ten-point rolling averages. | ||
 | ||
| Fig. 9 Inflight images of the morphology of evaporating NaCl droplets in environments of 20% (red), 30% (purple) and 40% RH (blue). Enlarged images of final morphologies are inset. | ||
The morphological transition from homogeneous droplet to crystalline dry particle can be clearly seen from the images. Homogeneous droplets are recognised by their symmetrical, circular profile and a distinct dark outer/bright inner appearance. Initial crystallisation is identified by perturbations in the symmetry of the droplet image and the dark outer/bright inner distinction is broken by a mottled appearance, as can be seen at 1.2 s, 1.55 s and 2.15 s for 20%, 30% and 40% RH respectively. During the initial crystallisation stage the image remains circular, indicating the spherical droplets still have a liquid surface, and are referred to as droplets with inclusions.48 Crystal nucleation is expected to occur near the surface of the droplet due to surface enrichment during drying.25,27 After this the droplets lose their spherical nature as the crystals are brought together by the receding liquid surface and begin to define the final morphology of the dry particle. The remaining solvent then continues to evaporate from within the structure until total evaporation has occurred and the final morphology is formed.
Distinct differences in the morphologies of the dry particles formed were observed depending on the environmental RH. Whereas droplets evaporating in 20% and 30% RH produced similarly structured multi-crystal particles, roughly circular in appearance, those evaporating in 40% RH produced single-crystal particles. This behaviour was very reproducible, and images in Fig. 9 were selected to represent typical appearance of these particles. The 40% RH single crystals most commonly nucleated in the bottom half of the droplet, rather than with a stochastic distribution followed by internal settling within the droplet. This contrasts with the crystallisation mechanism observed for sodium benzoate in static pendant droplets, where crystals gradually sank to the bottom of the droplet.49 The crystallising particles also remained aerodynamically stable as they fell, maintaining the same orientation once dry as when first formed.
The dry particle morphologies captured from inflight imaging can be compared with SEM images of the collected particles (Fig. 10). Observations of dry particles collected from the evaporation at 40% RH showed single crystals with opposing square and domed faces (Fig. 10a and b). From the inflight images the domed face originates from the bottom, liquid, curved surface of the droplet. This confirms that the droplet surface can template the crystal structure and corroborates previous observations of externally smooth, round yet fully crystalline spray dried particles.50 The holes seen in the centre of each square face in the SEM images can also be seen from the inflight images. Although the origin of the hole is undetermined at this stage it should be noted that, following surface enrichment during evaporation, the lowest solute concentration would be found toward the centre of the droplet due to depletion as the crystals grow. Crystal growth appears to occur rapidly with the individual crystal morphology determined long before solvent evaporation is complete. The aerodynamic stability of the dry particles formed during this evaporation is highlighted by the fact that the domed faces were only revealed in places where the crystals had tumbled (for example, after landing on other particles). Otherwise, all the crystals were observed to have the same square-face-up orientation. Below 40% RH the dry particles form multi-crystal structures, containing a higher number of crystals as the conditions get dryer (Fig. 10c and d). This may be understood by considering the effect of evaporation rate upon surface concentration; greater evaporation rates lead to increased surface enrichment, corresponding to a higher Péclet number. Increased surface concentration is accompanied with a large increase in nucleation rate, leading to multiple crystals nucleating within a short period and subsequently growing in parallel while the remaining solution evaporates.51 The growth of these crystals are limited by the droplet surface on one face and the less saturated solution towards the centre of the droplet on the opposite face, and so grow preferentially around the circumference of the droplet toward neighbouring crystals. As the SEM images of final morphologies show, the crystals grow until a corner/edge touches a neighbouring crystal, at which point they ‘lock’ the surface of the particle, as is observed by a constant geometric diameter (as seen in Fig. 7). In the case of slow evaporation (higher RH) the low surface enrichment means the nucleation rate is much lower and it is possible for the first nucleating crystal to desaturate the solution sufficiently to supress additional nucleation events. Considering these complex mechanisms with a simple Péclet number alone is not sufficient to explain the morphologies observed. As both the evaporation rate of the droplet and the diffusion rate of the solute vary throughout the evaporation, the Péclet number is strongly time dependent. Furthermore, the establishment of a concentration gradient within the droplet also suggests that there is ambiguity in how the Péclet number is reported, with diffusional transport rates varying throughout the interior of the droplet.25 Despite these complexities, order of magnitude trends in Pé do provide a qualitative understanding of the range of morphologies formed.
 | ||
| Fig. 10 SEM images of particles formed in the FDC. (a and b) 0.1 MFS at 295 K, 40% RH, (c) 0.1 MFS at 295 K, 25% and (d) 0.02 MFS at 318 K 0% RH. | ||
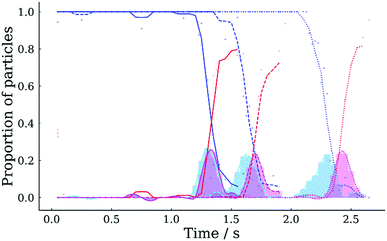
The ability to record many particles at any specific time in the evaporative lifetime allows statistical analyses to be performed of key events, such as crystallisation. Fig. 11 shows the proportion of droplets that have crystallised as a function of time for the three sodium chloride droplet evaporation experiments introduced earlier (i.e. 20% RH, 30% RH and 40% RH). Crystallisation was identified automatically from the image of each droplet using custom software, which applied an ellipse to the droplet shape and calculated the aspect ratio. During the onset of crystallisation the aspect ratio dropped from ∼1 (i.e. for a circle) to a value between 0.4–0.95, depending upon the dry particle morphology. Appropriate aspect ratio thresholds were selected to classify each image as either uncrystallised liquid droplet, droplet with crystal inclusions, or final crystalline morphology. Fig. 11 shows that the majority of droplets (i.e. >50%) achieved final crystalline morphology at 1.4 s, 1.8 s and 2.4 s for 20% RH, 30% RH and 40% RH, respectively. The corresponding aspect ratio data and thresholds used are displayed in Fig. S1 of the ESI.† The process of fitting an ellipse to non-elliptical shapes is a coarse step in the process of automatically detecting morphological changes and can lead to some variation in measured aspect ratio, especially for the crystalline particles, with some failing to be classified as final crystalline morphology. Hence, at the end of experiments shown in Fig. 11, the proportion of final crystalline particles is <1. The cyan and magenta curves show the proportion of droplets transitioning into, and out of, the intermediate state (i.e. droplets with inclusions) described above. The temporal offset between the peaks of these two curves represents the time during which crystal growth and solvent evaporation completes. The length of this transition window is RH dependent, increasing from 0.03 s to 0.13 s as the RH increases from 20% RH to 40% RH in Fig. 11. The transition window is shorter under lower RH conditions due to more the rapid solvent evaporation and parallel growth of many crystals, compared to the higher RH, which produce particles containing fewer crystals.
IV. Conclusions
This work introduces the Falling Droplet Column (FDC) technique, which adds greatly improved temporal resolution and detailed stroboscopic imaging capability to the droplet chain analysis technique. This technique resolves the evolving geometric diameter, aerodynamic diameter and morphology throughout the full evaporative lifetime, from droplet generation to dry particle formation, spanning almost 6 orders of magnitude in time (<1 μs to ∼5 s). Dry particles are collected and further analysed with SEM. The technique is uniquely suited to analysing rapid evaporation processes, such as crystallisation, and the concurrent measurement of aerodynamic diameter and geometric diameter enable changes in droplet density to be inferred.We demonstrate detailed inflight observations of the different crystallisation mechanisms, and resulting dry particle morphologies, for sodium chloride droplets evaporating under different environmental conditions. At 40% RH the slower evaporation rate (lower Peclet number) creates dry particles consisting of large single crystals, which nucleate on the leading face of the droplet. In contrast, dryer conditions (higher Peclet number) produce dry particles composed of multiple smaller crystals distributed around the circumference of the particle. The crystallisation window, the time between initial crystal nucleation and final solvent evaporation, can be clearly resolved. Indeed, subsequent analysis of many droplets at each time point enables accurate statistical analysis of stochastic events, such as crystallisation, to be performed. For example, although the spread in the crystallisation window observed between droplets extended up to ∼0.5 s at 40% RH, the calculated average ranged between 0.03 and 0.13 s for sodium chloride droplets evaporating in 20% RH and 40% RH, respectively.
It is anticipated that the flexibility of the technique, including control over the gas phase conditions, will afford the FDC application to many diverse droplet drying scenarios. This includes the rapid evaporation that occurs in various industrial applications, where the relationship between drying conditions and dry particle morphology, and understanding the dry particle formation mechanisms, may be critical.
Conflicts of interest
There are no conflicts to declare.References
- A. E. Elwardany, S. S. Sazhin and A. Farooq, Modelling of Heating and Evaporation of Gasoline Fuel: Effects of Input Parameters, Fuel, 2013, 966, 1–4 Search PubMed.
- G. Castanet, A. Delconte, F. Lemoine, L. Mees and G. Gréhan, Evaluation of temperature gradients within combusting droplets in linear stream using two colors laser-induced fluorescence, Exp. Fluids, 2005, 39, 431–440 CrossRef CAS.
- F. Wang, J. Yao, S. Yang, R. Liu and J. Jin, A new stationary droplet evaporation model and its validation, Chin. J. Aeronaut., 2017, 30, 1407–1416 CrossRef.
- J. S. Walker, J. Archer, F. K. A. Gregson, S. E. S. Michel, B. R. Bzdek and J. P. Reid, Accurate Representations of the Microphysical Processes Occurring during the Transport of Exhaled Aerosols and Droplets, ACS Cent. Sci., 2021, 7(1), 200–209 CrossRef CAS.
- R. Tellier, Y. Li, B. J. Cowling and J. W. Tang, Recognition of aerosol transmission of infectious agents: A commentary, BMC Infect. Dis., 2019, 19, 1–9 CrossRef.
- X. Xie, Y. Li, A. T. Y. Chwang, P. L. Ho and W. H. Seto, How far droplets can move in indoor environments – revisiting the Wells evaporation–falling curve, Indoor Air, 2007, 17, 211–225 CrossRef CAS PubMed.
- J. J. O’Sullivan, E. A. Norwood, J. A. O’Mahony and A. L. Kelly, Atomisation technologies used in spray drying in the dairy industry: A review, J. Food Eng., 2019, 243, 57–69 CrossRef.
- S. M. Jafari, E. Assadpoor, Y. He and B. Bhandari, Encapsulation efficiency of food flavours and oils during spray drying, Drying Technol., 2008, 26, 816–835 CrossRef.
- G. A. Reineccius, The spray drying of food flavors, Drying Technol., 2004, 22, 1289–1324 CrossRef.
- A. M. Goula and K. G. Adamopoulos, A new technique for spray drying orange juice concentrate, Innovative Food Sci. Emerging Technol., 2010, 11, 342–351 CrossRef CAS.
- A. Baldelli, R. M. Power, R. E. H. Miles, J. P. Reid and R. Vehring, Effect of crystallization kinetics on the properties of spray dried microparticles, Aerosol Sci. Technol., 2016, 50, 693–704 CrossRef CAS.
- A. Ziaee, et al., Spray drying of pharmaceuticals and biopharmaceuticals: Critical parameters and experimental process optimization approaches, Eur. J. Pharm. Sci., 2019, 127, 300–318 CrossRef CAS PubMed.
- N. Grasmeijer, H. de Waard, W. L. J. Hinrichs and H. W. Frijlink, A User-Friendly Model for Spray Drying to Aid Pharmaceutical Product Development, PLoS One, 2013, 8(9), 1–11 CrossRef PubMed.
- A. Baklanov and J. H. Sørensen, Parameterisation of radionuclide deposition in atmospheric long-range transport modelling, Phys. Chem. Earth, Part B Hydrol. Ocean. Atmos., 2001, 26, 787–799 CrossRef.
- ASN, Technical notice: corrosion of fission products concentrating evaporators at La Hague, http://www.french-nuclear-safety.fr/Information/News-releases/Corrosion-of-fission-products-evaporator-concentrators-at-La-Hague (2016).
- C. B. Goodlett, Evaporation and Storage of Liquid Radioactive Waste, Chem. Eng. Prog., 1976, 8, 207–212 Search PubMed.
- IRSN Annual Report 2017. (2017).
- F.-X. Ouf, Impact des aérosols émis lors d’ un incendie sur le confinement des installations nucléaires, 2016 Search PubMed.
- T. Cosgrove, Colloid Science, John Wiley & Sons, 2010 DOI:10.1002/9781444305395.
- G. A. E. Godsave, Studies of the combustion of drops in a fuel spray-the burning of single drops of fuel, Symp. Combust., 1953, 4, 818–830 CrossRef.
- A. H. Lefebvre and J. S. Chin, Steady-state evaporation characteristics of hydrocarbon fuel drops, AIAA J., 1983, 21, 1437–1443 CrossRef.
- W. Hinds, Aerosol Technology, John Wiley & Sons, Inc., 1991 Search PubMed.
- R. Vehring, W. R. Foss and D. Lechuga-Ballesteros, Particle formation in spray drying, J. Aerosol Sci., 2007, 38, 728–746 CrossRef CAS.
- J. Archer, J. S. Walker, F. K. A. Gregson, D. A. Hardy and J. P. Reid, Drying Kinetics and Particle Formation from Dilute Colloidal Suspensions in Aerosol Droplets, Langmuir, 2020, 36(42), 12481–12493 CrossRef CAS.
- F. K. A. Gregson, J. F. Robinson, R. E. H. Miles, C. P. Royall and J. P. Reid, Drying Kinetics of Salt Solution Droplets: Water Evaporation Rates and Crystallization, J. Phys. Chem. B, 2019, 123, 266–276 CrossRef CAS PubMed.
- J. F. Robinson, F. K. A. Gregson, R. E. H. Miles, J. P. Reid and C. P. Royall, Drying kinetics and nucleation in evaporating sodium nitrate aerosols, J. Chem. Phys., 2020, 152, 074503 CrossRef CAS PubMed.
- F. K. A. Gregson, J. F. Robinson, R. E. H. Miles, C. P. Royall and J. P. Reid, Drying and Crystallization of Evaporating Sodium Nitrate Aerosol Droplets, J. Phys. Chem. B, 2020, 124, 6024–6036 CrossRef CAS PubMed.
- R. G. Picknett and R. Bexon, The evaporation of sessile or pendant drops in still air, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- D. R. Burnham and D. McGloin, Holographic optical trapping of aerosol droplets, Opt. Express, 2006, 14, 4175 CrossRef CAS PubMed.
- N. Magome, M. I. Kohira, E. Hayata, S. Mukai and K. Yoshikawa, Optical Trapping of a Growing Water Droplet in Air, J. Phys. Chem. B, 2003, 107, 3988–3990 CrossRef CAS.
- M. D. Cohen, R. C. Flagan and J. H. Seinfeld, Studies of concentrated electrolyte solutions using the electrodynamic balance. 2. Water activities for mixed-electrolyte solutions, J. Phys. Chem., 1987, 91, 4575–4582 CrossRef CAS.
- E. J. Davis, M. F. Buehler and T. L. Ward, The double-ring electrodynamic balance for microparticle characterization, Rev. Sci. Instrum., 1990, 61, 1281–1288 CrossRef CAS.
- J. Lee, et al., Single beam acoustic trapping, Appl. Phys. Lett., 2009, 95, 21–24 Search PubMed.
- C. J. Homer, X. Jiang, T. L. Ward, C. J. Brinker and J. P. Reid, Measurements and simulations of the near-surface composition of evaporating ethanol-water droplets, Phys. Chem. Chem. Phys., 2009, 11, 7780–7791 RSC.
- R. J. Hopkins and J. P. Reid, A comparative study of the mass and heat transfer dynamics of evaporating ethanol/water, methanol/water, and 1-propanol/water aerosol droplets, J. Phys. Chem. B, 2006, 110, 3239–3249 CrossRef CAS PubMed.
- A. Baldelli, M. A. Boraey, D. S. Nobes and R. Vehring, Analysis of the Particle Formation Process of Structured Microparticles, Mol. Pharmaceutics, 2015, 12, 2562–2573 CrossRef CAS.
- C. Sadek, et al., Drying of a single droplet to investigate process–structure–function relationships: a review, Dairy Sci. Technol., 2015, 95, 1–24 CrossRef.
- R. M. Power and J. P. Reid, Probing the micro-rheological properties of aerosol particles using optical tweezers, Rep. Prog. Phys., 2014, 77, 074601 CrossRef.
- R. E. H. Miles, M. W. J. Glerum, H. C. Boyer, J. S. Walker, C. S. Dutcher and B. R. Bzdek, Surface Tensions of Picoliter Droplets with Sub-Millisecond Surface Age, J. Phys. Chem. A, 2019, 123, 3021–3029 CrossRef CAS PubMed.
- K. Anahara and J. Y. Kohno, Initial Collision Process of Two Miscible Droplets, J. Phys. Chem. B, 2017, 121, 9895–9901 CrossRef CAS PubMed.
- Q. V. Nguyen, R. H. Rangel and D. Dunn-Rankin, Measurement and prediction of trajectories and collision of droplets, Int. J. Multiphase Flow, 1991, 17, 159–177 CrossRef CAS.
- J. R. Andrews and M. P. O’Horo, High-speed stroboscopic system for visualization of thermal ink-jet processes, Color Hard Copy Graph. Arts IV, 1995, 2413, 176–181 CAS.
- J. F. Davies, A. E. Haddrell and J. P. Reid, Time-resolved measurements of the evaporation of volatile components from single aerosol droplets, Aerosol Sci. Technol., 2012, 46, 666–677 CrossRef CAS.
- F. K. A. Gregson, M. Ordoubadi, R. E. H. Miles, A. E. Haddrell, D. Barona, D. Lewis, T. Church, R. Vehring and J. P. Reid, Studies of Competing Evaporation Rates of Multiple Volatile Components from a Single Binary-Component Aerosol Droplet, Phys. Chem. Chem. Phys., 2019, 11–13 Search PubMed.
- C. Cai, et al., Comparison of methods for predicting the compositional dependence of the density and refractive index of organic-aqueous aerosols, J. Phys. Chem. A, 2016, 120, 6604–6617 CrossRef CAS.
- Y. Y. Su, A. Marsh, A. E. Haddrell, Z. M. Li and J. P. Reid, Evaporation Kinetics of Polyol Droplets: Determination of Evaporation Coefficients and Diffusion Constants, J. Geophys. Res.: Atmos., 2017, 122, 12317–12334 Search PubMed.
- F. K. A. Gregson, Evaporation Kinetics and Particle Formation from Aerosol Solution Microdroplets, PhD thesis, University of Bristol, School of Chemistry, 2020 Search PubMed.
- A. Haddrell, G. Rovelli, D. Lewis, T. Church and J. Reid, Identifying time-dependent changes in the morphology of an individual aerosol particle from its light scattering pattern, Aerosol Sci. Technol., 2019, 53, 1334–1351 CrossRef CAS.
- D. E. Walton and C. J. Mumford, The morphology of spray-dried particles, The effect of process variables upon the morphology of spray-dried particles, Chem. Eng. Res. Des., 1999, 77, 442–460 CrossRef CAS.
- A. Baldelli and R. Vehring, Analysis of cohesion forces between monodisperse microparticles with rough surfaces, Colloids Surf., A, 2016, 506, 179–189 CrossRef CAS.
- J. Desarnaud, H. Derluyn, J. Carmeliet, D. Bonn and N. Shahidzadeh, Metastability limit for the nucleation of NaCl crystals in confinement, J. Phys. Chem. Lett., 2014, 5, 890–895 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02840e |
| This journal is © the Owner Societies 2021 |