CC-stretched formic acid: isomerisation, dimerisation, and carboxylic acid complexation

Abstract

The cis–trans-isomerism of the propiolic acid monomer (HC≡C–COOH) is examined with linear Raman jet spectroscopy, yielding the first environment-free vibrational band centres of a higher-energy cis-rotamer beyond formic acid (HCOOH) in addition to all fundamentals and a large number of hot and combination/overtone bands of the trans-conformer. Two near-isoenergetic trans-fundamentals of different symmetry (CC=O bend and OH torsion) prove to be a sensitive benchmarking target, as their energetic order is susceptible to the choice of electronic structure method, basis set size, and inclusion of vibrational anharmonicity. For the infrared- and Raman-active C=O stretching fundamentals of the cyclic (C_2h) trans-propiolic acid dimer, resonance couplings are found that in part extend to the C_s-symmetric heterodimer of trans-propiolic and trans-formic acid. Exploratory vibrational perturbation theory (VPT2) calculations show that all perturbing states involve displacements of the OH moieties located on the doubly hydrogen bonded ring. The comparison of the infrared spectra of the propiolic acid dimer and its heterodimer with formic acid to that of several other carboxylic acid dimers from the literature reveals a notable similarity regarding a non-fundamental dimer band around 1800 cm⁻¹, which in most cases is so far unassigned. VPT2 calculations and a simple harmonic model suggest an assignment to a combination vibration of the symmetric and antisymmetric OH torsion.

---

1 Introduction

The spectroscopic characterisation of carboxylic acids and their hydrogen bonded clusters has attracted considerable attention over the years. Carboxylic acids form exceptionally stable doubly hydrogen bonded cyclic dimers in the gas phase¹ (Fig. 1) that are elementary model systems to study concerted proton tunnelling^2,3 and hydrogen bonding^4–6 to name a few aspects that have sparked interest in the past. As the smallest carboxylic acid, the dimer of formic acid (HCOOH) has been most thoroughly examined, both from the experimental^1,3,5,7–12 and theoretical side.^13–18

Fig. 1 The cis- and trans-rotamers of carboxylic acid monomers as well as the global minimum structure of the dimer.

In contrast to the chaotic, resonance broadened O–H stretching spectrum spanning several hundreds of cm⁻¹ that many carboxylic acid dimers seem to share,^7,9,19,20 the vibrational spectrum of the soft modes up to the carbonyl stretching vibration around 1700–1800 cm⁻¹ is less convoluted and more suitable for a systematic vibrational characterisation. Mediated by the hydrogen bonds, these cyclic dimers are centrosymmetric (C_2h) and pairs of identical monomer vibrations are split into so-called Davydov pairs,^21–23 with the symmetric, in-phase combinations of monomer vibrations being exclusively Raman-active and the antisymmetric, out-of-phase combinations being infrared-active. The systematic comparison of the infrared and Raman spectra of several different acids reveals interesting phenomena which to the best of our knowledge have so far not been systematically analysed. In the infrared spectra, for example, a non-fundamental dimer band is observed at a similar band position for formic (1810.6 cm⁻¹),²⁴ acetic (1834.9 cm⁻¹),²⁵ pivalic (1834/1838 cm⁻¹),²⁶ and benzoic acid (1824 cm⁻¹)^27,28 which raises the question of a possible similar origin. For formic acid, it was ascribed to a combination vibration of the two (hindered) OH torsions by Kollipost,²⁴ but for the other acids, it has yet to be assigned. The Raman spectra of several carboxylic acids also exhibit a similarity in this spectral region, namely strong resonance perturbations of the symmetric C=O stretches (cf.ref. 29 and 30). While a combination band was predicted in proximity to the symmetric C=O stretch of the formic acid dimer nearly forty years ago,⁸ conclusive evidence for a potential resonance partner has yet to be provided.

Slightly larger aliphatic, saturated carboxylic acids such as acetic (CH₃COOH) or pivalic acid ((CH₃)₃COOH), in addition to the challenge constituted by their sheer size, significantly complicate routine anharmonic treatments³¹ due to a manifold of internal rotations introduced by the methyl groups.³² Propiolic acid (HC≡C–COOH), as the smallest unsaturated, aliphatic carboxylic acid, constitutes with only seven atoms and fifteen relatively stiff internal degrees of freedom an excellent intermediate between the well studied formic and the larger saturated carboxylic acids. The vibrational spectrum of its dimer has been studied in solid rare gas matrices,^33,34 and in the gas phase using low-resolution infrared¹⁹ and jet-cooled Raman spectroscopy.^29,35 Building on a previous study,²⁹ we will present and scrutinise the vibrational spectrum of the propiolic acid homodimer in the C=O stretching region by means of FTIR and Raman jet spectroscopy and characterise the vibrational spectrum of the formic–propiolic acid heterodimer for the first time, which has been thoroughly investigated with microwave spectroscopy.^36–39 Our results will show how certain features in the C=O stretching spectra of the formic and propiolic acid homo- and heterodimers can qualitatively be understood as perturbations due to vibrational motion of the cyclic ring shared by all three dimers.

One very intriguing feature of the monomers of carboxylic acids is their torsional isomerism that connects the higher-energy cis- and global minimum trans-rotamers (Fig. 1). The first vibrational detection of a cis-carboxylic acid was achieved for formic acid in a cryogenic argon matrix by Pettersson et al. in 1997,⁴⁰ nearly sixty years after the first vibrational characterisation of its trans-form.⁴¹ Ever since, these matrix isolation studies have been extended to a multitude of other acids^34,42–45 and matrix hosts.^44,46–48 One advantage of this technique are the long storing times achievable, which enable the formation of higher-energy conformers via light-induced isomerisation.⁴⁹ In the gas phase, where a comparison with theory is more easily achievable due to the absence of external perturbations, vibrational band positions of the higher-energy cis-carboxylic acids are sparse – a consequence of their low abundance at room temperature (RT). The only higher-energy cis-carboxylic acid where perturbation-free reference data are available to this date is formic acid (0.1% cis-abundance at RT)⁵⁰ with a total of sixteen fundamentals for all four H/D isotopologues.^30,51–53

The propiolic acid monomer has a significantly lower cis–trans-energy difference compared to formic acid, resulting in a room temperature abundance that is an order of magnitude higher (about 1%), yet vibrational data on the cis-rotamer are so far restricted to matrix isolation studies.^34,44 The global minimum trans-rotamer has been examined with low-resolution gas phase infrared spectroscopy,⁵⁴ in the liquid phase with infrared and Raman spectroscopy,⁵⁴ with matrix isolation spectroscopy,^33,34,44 and Raman jet spectroscopy^29,35 focussing mostly on fundamentals. Following the approach that allowed for the detection of cis-formic acid using a heatable Raman jet set-up,^30,52,53 we will present the first perturbation-free vibrational data for cis-propiolic acid in addition to a manifold of vibrational information beyond fundamentals on trans-propiolic acid, highlighting that the torsional isomerism of the propiolic acid monomer as well as its homo- and heterodimer with formic acid can prove to be meaningful reference systems for theory.

2 Experimental and computational methods

The Raman^52,55,56 and FTIR jet spectra⁵⁷ shown throughout this work were recorded with set-ups described in detail in previous publications. Here, only a brief description of their most relevant aspects is given. A comparison of FTIR and Raman jet expansions can be found in ref. 58.

For the Raman jet expansions, propiolic acid (Acros Organics, 98%) was seeded in helium in a temperature controlled saturator (temperature range 15–20 °C) and expanded continuously at reservoir pressures of 400–600 mbar through a temperature-controlled slit nozzle (4 × 0.15 mm²) and feed-line (RT – 190 °C) into an evacuated jet-chamber with background pressures below 1.5 mbar during the expansion. For measurements of the formic–propiolic acid heterodimer, formic acid (Acros Organics, 98+%) was also seeded in helium (saturator temperature of −30 °C) and both acid-in-helium mixtures were premixed in the reservoir prior to the expansion (for further details, see Section S1 in the ESI†). The acid-in-helium expansion is probed at a nozzle distance of 1 mm with a Spectra Physics Millennia eV 532 nm laser operated at 20–24 W. The scattered radiation is collected perpendicular to both the expanding flow and the laser, and is focussed onto the entry slit of a 1 m monochromator, which disperses the radiation onto 1340 pixel columns of a liquid nitrogen cooled CCD camera. Vertical binning is performed along 400 pixel rows. For each spectrum, 6–24 spectra were co-added with exposure times of 300 s. Spectral calibration is carried out with atomic neon and krypton transitions in vacuum.⁵⁹ The experimental uncertainty of the band positions resulting from the spectral calibration and resolving power of the monochromator depends on the spectral range and amounts to about 1–2 cm⁻¹. We therefore assign Raman band position errors of ±2 cm⁻¹ throughout this work.

The polarisation of the incident laser radiation of the Raman set-up is perpendicular ⊥ with respect to the 90° scattering plane.⁵⁵ In some cases, additional measurements with parallel laser polarisation ‖ were carried out to compare these to the ⊥-spectra, which can be used to distinguish totally symmetric from non-totally symmetric modes.⁶⁰ Throughout this work, the higher detection sensitivity of perpendicularly compared to parallelly polarised laser light of the set-up is neglected.⁶¹

Infrared spectra were recorded with a Bruker IFS 66v spectrometer equipped with a globar, a potassium bromide (KBr) beam splitter as well as KBr optics. The IR beam is focussed onto a pulsed supersonic expansion (reservoir pressures of 500–700 mbar) from a 600 mm long and 0.2 mm wide slit nozzle. In contrast to the Raman set-up, the nozzle is not heatable. The distance of IR beam and nozzle amounts to 10 mm in the focal point. For detection of the infrared radiation, a liquid nitrogen cooled mercury cadmium telluride detector is used.

To assist in the interpretation of the recorded vibrational spectra, harmonic Raman scattering cross-sections and anharmonic (VPT2,^62–64 vibrational perturbation theory of second-order) vibrational energies have been computed using Gaussian 16 version A.03.⁶⁵ To solve the electronic Schrödinger equation, several ab initio and DFT methods including MP2,⁶⁶ B3LYP,^67,68 PBE0,⁶⁹ and B2PLYP⁷⁰ were used. For the latter three, Grimme's two-body dispersion correction⁷¹ with Becke–Johnson damping has been employed.⁷²

In the VPT2 calculations, default thresholds for resonance detection were used, but Darling–Dennison resonances were deactivated as low-frequency fundamental energies seem to be very sensitive to the resonance thresholds as implemented in Gaussian 16 (version A.03).⁵⁶ Additional calculations upon inclusion of Darling–Dennison resonances are shown in Fig. S1 in the ESI.† If not further specified, symmetry and very tight optimisation thresholds are used, and in case of DFT calculations the integration grid is set to superfine. To enhance the quality and remove some deficiencies of the harmonic MP2 force field,⁷³ the Hessian is replaced by the corresponding harmonic CCSD(T)-F12a⁷⁴ force field which has been computed using Molpro version 2018.1.^75,76 For the DFT and MP2 calculations, Dunning's correlation consistent aug-cc-pVXZ (aVXZ)⁷⁷ and for CCSD(T)-F12a, explicitly correlated VXZ-F12 basis sets by Peterson et al.⁷⁸ are used. A comprehensive summary of the computational details and used keywords can be found in the ESI† (Tables S1 and S2).

3 The cis–trans isomerism of propiolic acid

3.1 Raman jet spectra

The C_s-symmetric propiolic acid monomer exhibits fifteen vibrational degrees of freedom (Fig. 2), six of which are stretching vibrations ν, five in-plane δ, and four out-of-plane bending vibrations γ. With 11(1) kJ mol⁻¹ (averaged over several methods, see Table S3 in the ESI†), the harmonically calculated energy difference between the cis- and trans-rotamers is about 5 kJ mol⁻¹ smaller than that of the formic acid monomer (exp. 16.3(0.4) kJ mol⁻¹),⁵⁰ resulting in a considerably higher relative cis-abundance of roughly 1% at room temperature. To further elevate the cis-abundance in the supersonic expansion, we use thermal excitation by heating the nozzle and its feed-line up to 190 °C, reaching a maximum of 5–6% of cis-propiolic acid. To characterise the cis- and trans-rotamers, we use linear Raman spectroscopy. The Raman scattering cross-sections in Table 1 show that the stretching vibrations are particularly accessible for Raman spectroscopy, as is also the case for formic acid. An advantage of Raman spectroscopy is that the polarisation of the scattered light can be modulated by variation of the incident laser polarisation. In our set-up, the polarised fraction is maximised when the incident laser polarisation is perpendicular to the scattering plane, the standard setting, and minimised for parallel polarisation.⁵⁶ Non-totally symmetric bands are completely depolarised (depolarisation ratio ρ = 0.75) and therefore persist when the laser polarisation is changed to parallel (except for a numerical value of 7/6, for further details see ref. 60). Totally symmetric bands can have depolarisation values ranging from zero (completely polarised) up to the limiting value of 0.75 (completely depolarised). Bands that significantly decrease in intensity in the parallel spectrum are therefore easily identified as totally symmetric (A′ for the propiolic acid monomer). Hence, the comparison of spectra recorded with parallel and perpendicular laser polarisations can help to distinguish the symmetry of vibrations and will be used to guide assignments throughout this section. Depolarised spectra of the propiolic acid monomer are shown in the ESI† (Fig. S3) and in selected cases in Fig. 3.

Fig. 2 Schematic representation of the fifteen normal modes of trans-propiolic acid alongside their VPT2 band positions (in cm⁻¹, see Table 1). Modes are labelled according to the Herzberg nomenclature. ν₁–ν₁₁ are totally symmetric in-plane (A′) and ν₁₂–ν₁₅ non-totally symmetric out-of-plane vibrations (A′′).

Table 1 Raman and FTIR jet band centres (cm⁻¹) of cis- and trans-propiolic acid together with values from matrix isolation spectroscopy, calculated anharmonic (VPT2) band positions, and harmonic Raman scattering cross-sections (σ_Ra, in 10⁻³⁶ m² sr⁻¹, MP2/aVQZ level). The experimental uncertainty of the Raman jet values amounts to ±2 cm⁻¹. Bands that have not been observed are labelled ‘n.o.’ and bands that have not been investigated ‘n.i.’

Fundamental		trans-Propiolic acid					cis-Propiolic acid
		VPT2^a	σ Ra	Raman jet^b	FTIR jet^b	N2 matrix^c	VPT2^a	σ Ra	Raman jet^b	N2 matrix^c
a Calculated at the MP2/aVQZ level where the Hessian is replaced with the corresponding CCSD(T)-F12a/VTZ-F12 force field. b This work. FTIR spectra are only recorded between 2000–700 cm^−1. c Infrared matrix isolation data from ref. 34 (matrix site 1). d Strong Fermi resonance predicted between ν5 and ν12 + ν14 of trans-propiolic acid. Note that while the assignment inverts when changing the anharmonic MP2 basis set from aVQZ to aVTZ, both calculations predict higher infrared activity for the lower-wavenumber band (cf. Table S4 in the ESI). e Band maxima are listed, see band contours in Fig. S4 in the ESI. The band centre likely corresponds to the dip between both peaks.
A′
ν 1	ν(OH)	3578	99	3578		3534.5	3622	59	3621	3575.5
ν 2	ν(CH)	3330	47	3329		3404.5	3324	47		3298.0
ν 3	ν(C≡C)	2160	340	2143		2147.0, 2142.5	2136	324		2121.0
ν 4	ν(C=O)	1772	114	1764	1765	1750.0, 1748.0	1805	115	1800	1781.0, 1776.5
ν 5	δ(OH)	1361	8	1362	1363	1326.5	1289	15		1248.0
		1299		1302	1303
ν 6	ν(C–O)	1154	15	1154	1154	1152.5	1152	41		n.o.
ν 7	ν(C–C)	814	91	816	816	822.0	820	61		832.0
ν 8	δ(CH)	652	13	654		665.5	667	14		n.o.
ν 9	δ(CC=O)	585	10	584		586.7	584	9		591.0
ν 10	δ(CC–O)	527	19	527		534.5	537	22		n.o.
ν 11	δ(CCC)	178	191	180		n.i.	179	216		n.i.
A′′
ν 12	γ(OCO)	754	1	n.o.	755	760.0	741	3		749.5
ν 13	γ(CH)	682	17	696/688^e		760.0	689	18		703.5
ν 14	γ(OH)	574	21	578/569^e		606.0	476	8		508.0
ν 15	γ(CCC)	229	49	233/225^e		n.i.	230	67		n.i.

---

Fig. 3 Raman jet spectra of propiolic acid in helium recorded at nozzle temperatures between 100–190 °C. The Raman spectra are intensity-scaled to a trans-fundamental (tPr) in the spectrum recorded at 190 °C (red) in each spectral region. cis-Propiolic acid monomer bands are labelled ‘cPr’ and bands corresponding to propiolic acid decomposition products are marked with an asterisk. Additional measurements with parallel laser polarisation (nozzle temperature 100 °C) are shown in green and have been scaled by a factor of 7/6 (see text and ref. 60 for details). Below the Raman spectra, anharmonic VPT2 fundamentals of cPr and tPr and two-quantum states (tPr) calculated at the MP2/aV(T,Q)Z level are shown using harmonic Raman scattering cross-sections. For the VPT2 calculations, the Hessian is replaced with the corresponding CCSD(T)-F12a/VTZ-F12 force field. The symmetry of the vibrations (A′ or A′′) is encoded in the colour shade of the symbols (see legend in panel (B)).

Raman jet spectra of the six stretching vibrations (ν₁–ν₄ and ν₆–ν₇) and other selected spectral regions promising for cis-detection are shown in Fig. 3 for nozzle temperatures between 100–190 °C. The Raman jet spectra of the A′′ fundamentals are shown in the ESI† (Fig. S4). By scaling the spectra recorded at different nozzle temperatures to a known trans-propiolic acid (tPr) fundamental in each spectral region, cluster and hot bands can be distinguished from fundamentals, combination and overtone bands of tPr, as cluster bands decrease in intensity with temperature whereas hot bands increase.⁵² Two types of hot bands are visible in the spectra – isomeric hot bands, i.e., those corresponding to the higher-energy cis-rotamer of propiolic acid (cPr), and non-isomeric hot bands originating from thermally populated vibrational states ν_j in the trans-rotamer. In the context of perturbation theory,⁶² the shift of a non-isomeric hot band ν_i + ν_j − ν_j with respect to the fundamental ν_i amounts to the anharmonic coupling constant x_i,j (2x_i,i for 2ν_i − ν_i). Assuming that the scattering cross-sections of the fundamental ν_i and the hot band ν_i + ν_j − ν_j are similar, the relative intensity of ν_i + ν_j − ν_j with respect to the fundamental reflects the thermal population in ν_j.⁵² Hence, a comparison of band position shifts and intensities with respect to the fundamental in each spectral region can help to distinguish isomeric from non-isomeric hot bands. Below the Raman jet spectra in Fig. 3, CCSD(T)-edited MP2 VPT2 energy levels are plotted, where the MP2 Hessian is replaced with the corresponding CCSD(T)-F12a/VTZ-F12 force field. To visualise convergence of the anharmonic MP2 force field, results using an aVTZ (dashed) and aVQZ basis set (solid lines) are shown. For brevity, we will refer to the CCSD(T)-edited MP2/aVQZ VPT2 calculation as ‘the VPT2’ calculation throughout this section.

The O–H stretching spectrum of propiolic acid is shown in Fig. 3A. It exhibits one fairly strong band of a combination or overtone vibration at 3571(2) cm⁻¹, 7 cm⁻¹ downshifted from the trans-fundamental (3578(2) cm⁻¹). The cis-band is observed upshifted from both at 3621(2) cm⁻¹. Due to the large cis–trans-shift of +43 cm⁻¹ together with a moderate Raman scattering cross-section (cf.Table 1), ν₁ of cis-propiolic acid is one of the most evident cis-assignments. The corresponding formic acid cis–trans-shift is with +67 cm⁻¹ about a third larger.⁵² Close to the trans-propiolic acid band at 3571(2) cm⁻¹, a combination of the C–H stretching vibration ν₂ with the CCC out-of-plane bending vibration ν₁₅ is predicted by the VPT2 calculation (3560 cm⁻¹, A′′ symmetry). However, in line with the high intensity likely caused by resonance interaction with the fundamental, depolarisation measurements reveal A′ symmetry for the band (Fig. S3 in the ESI†). The energetically closest A′-symmetric two-quantum state is predicted at 3528 cm⁻¹ (2ν₄). Thus, an assignment of the band at 3571(2) cm⁻¹ based on the VPT2 calculation is not possible. In the Raman jet spectrum of the formic acid OH stretching vibration, two combination bands were observed downshifted from the trans-OH fundamental. One was attributed to a combination vibration of the C–H stretch with the OCO in-plane bend,⁷⁹ a mode that is distinctly higher in energy in case of propiolic acid due to the stiffer CH stretch. The second combination band was attributed to a state composed of more than two vibrational quanta,⁷⁹ which might also be the case for the trans-propiolic acid band at 3571(2) cm⁻¹. In that context, it is worth pointing to the numerical similarities between the formic and propiolic acid vibrational energy levels with regard to vibrations of the carboxylic –COOH moiety that indicate a possible similar origin for some perturbers in the OH stretching spectra (see note in ref. 80 for further details).

A similarly straightforward cis-assignment as for the OH-stretch of propiolic acid is also feasible for the C=O stretch ν₄, which is shown in Fig. 3D. The cis-band is observed at 1800(2) cm⁻¹, 36 cm⁻¹ upshifted from the trans-fundamental at 1764(2) cm⁻¹. Expectedly, the cis–trans-shift resembles that of formic acid (+41 cm⁻¹).⁵² For the other stretching fundamentals, distinctly smaller cis–trans-shifts are predicted (Table 1), therefore significantly complicating the allocation of isomeric cis-bands.

One such example is the C–H stretch (ν₂) with a predicted cis–trans-shift of solely −6 cm⁻¹. For formic acid, a significantly larger shift of −69 cm⁻¹ was observed⁵² – likely a result of the closer proximity of the OH and CH groups.⁸¹ In the propiolic acid C–H stretching spectrum shown in Fig. 3B, a hot band is observed on the lower-wavenumber shoulder of the trans-fundamental (3329(2) cm⁻¹). Since non-isomeric hot bands originating from thermally populated low-lying vibrational energy levels are also predicted to overlap with ν₂ of cPr (for x_i,j values, see Table S5 in the ESI†), an unambiguous cis-assignment is currently not possible. In addition to this shoulder of the ν₂-fundamental, there is another hot band at 3310(2) cm⁻¹, downshifted by 19 cm⁻¹ from ν₂ (tPr). The largest x_2,j values of the VPT2 calculation for energy levels with significant thermal population are found for the CH in-plane ν₈ (−14.7 cm⁻¹) and out-of-plane bending vibration ν₁₃ (−13.6 cm⁻¹). At the B3LYP-D3(BJ)/aVQZ level, which was shown to perform well for formic acid monomer hot band assignments,⁵² slightly larger values of −19.3 (x_2,8) and −19.0 cm⁻¹ (x_2,13) are obtained, which are compatible with the observed shift. This interpretation of a relatively strong coupling (large x_i,j value) between the CH stretch and corresponding bends matches the findings for formic acid, where a similar experimental shift of −17 cm⁻¹ is observed for the ν₂ hot band originating from the C–H out-of-plane bending vibration.⁷⁹ Therefore, it seems likely that the propiolic acid hot band at 3310(2) cm⁻¹ originates from either one or both of these states.

In the same spectral region (Fig. 3B), three additional bands are observed that exhibit a temperature scaling that differs from that of other (isomeric and non-isomeric) hot bands. In the spectra recorded below 160 °C, these are barely visible but increase significantly in intensity at the highest two nozzle temperatures. This indicates that these bands are due to thermal decomposition of the acid. Due to the steeper intensity-increase of such decomposition bands with temperature, they can be clearly separated from hot bands and therefore do not impair cis-assignments. The most pronounced decomposition band in Fig. 3B at 3372(2) cm⁻¹ corresponds to the CH stretching vibration of acetylene (3372.845(1)⁸²); the other two decomposition bands correspond to its hot bands.⁸² The observation of bands of the second decomposition product CO₂ at 1408(2), 1387(2), 1284(2), and 1264(2) cm⁻¹ (Fig. 3G) further confirms this interpretation and indicates that significant decarboxylation of the acid takes place at temperatures above 130 °C. A full list of all observed acetylene and CO₂ decomposition bands and their assignments can be found in the ESI† (Table S7). Using computed harmonic Raman scattering cross-sections for propiolic acid and acetylene at the MP2/aVQZ level, we can estimate the amount of decarboxylation to about 14% at 190 °C. Under similar conditions and the same temperature range, no decomposition bands are observed in the Raman jet spectrum of formic acid (see ref. 79).

The C≡C stretching vibration ν₃ of propiolic acid is by far the most Raman-active mode of all fifteen fundamentals and the predicted cis–trans-shift is also fairly large (−24 cm⁻¹, cf.Table 1). Therefore one might expect it to be one of the most suitable vibrations for cis-detection. The trans-C≡C stretch band shown in Fig. 3C (2143(2) cm⁻¹), however, is framed by cluster bands on the higher-wavenumber and an extensive hot band structure on the lower-wavenumber side that spans approximately 25 cm⁻¹. In contrast to most other VPT2 fundamentals, which agree with the Raman jet values within the experimental uncertainty (±2 cm⁻¹), the trans-ν₃-band position deviation is particularly large (+17 cm⁻¹). This might be a result of an insufficient description of the electron correlation of the triple bond. As such, the cis-ν₃ band position error might also be significant. In addition, there are a vast number of x_3,j values between 0 and −9 cm⁻¹ (Table S5 in the ESI†), further complicating an allocation of the cis-propiolic acid ν₃-band. Therefore, an assignment is currently not possible. This richness of non-isomeric hot bands afforded by thermal excitation might prove to be very useful in cross-checking assignments of combination and overtone bands, as they are direct probes of anharmonicity.⁷⁹ To fully profit from the large abundance of spectral information contained in these C≡C-stretch Raman jet spectra, further guidance from theory would be particularly useful.

In addition to the broad hot band structure seen in Fig. 3C, there are three A′ bands at 2177(2), 2164(2), and 2110(2) cm⁻¹ that correspond to cold monomer transitions of tPr, i.e., combination or overtone bands. Between 2250 and 2050 cm⁻¹, the VPT2 calculation predicts only one totally symmetric two-quantum state at 2131 cm⁻¹ (ν₅ + ν₇). It therefore seems likely that some of these trans-monomer bands correspond to energy levels involving more than two vibrational quanta.

For the C–O stretch ν₆, an even smaller cis–trans-shift (−2 cm⁻¹) than for the C–H stretch (−6 cm⁻¹) is predicted. Next to the predicted cis-band position, a weak hot band is observed in the spectra (Fig. 3E), which exhibits an intensity that roughly matches the expected cis-intensity with respect to the trans-fundamental at 1154(2) cm⁻¹, considering the Raman scattering cross-sections advantage of the cis- compared to the trans-rotamer (σ_cPr/σ_tPr = 3). As the spectral intensity of the band is very low and there are non-isomeric hot bands with similar predicted shifts x_6,j (Table S5 in the ESI†) and thermal populations, a cis-assignment is not possible. In addition to the hot band, there is another band downshifted from the trans-fundamental at 1118(2) cm⁻¹ that corresponds to a trans-combination or overtone band with a relative intensity of 25% with respect to ν₆ of tPr. The depolarised spectrum confirms that it is of A′ symmetry (Fig. S3 in the ESI†). While the VPT2 calculation predicts two A′ states, 2ν₁₄ and ν₉ + ν₁₀, in close proximity to the band at 1118(2) cm⁻¹, and 2ν₁₄ is even predicted to interact with ν₆via Fermi resonance, no clear assignment can be made, as Fig. 3E shows that the absolute energies of 2ν₁₄ and ν₉ + ν₁₀ are very sensitive to the basis set size of the anharmonic MP2 force field, both seemingly converging towards the band at 1118(2) cm⁻¹.

A substantial basis set sensitivity is also observed for vibrational states in the C–C stretching region (cf.Fig. 3F), yet in contrast to the C–O stretching region, the assignment of anharmonic features in the spectra seems more evident. The trans-fundamental ν₇ is observed at 816(2) cm⁻¹ in the Raman jet spectrum and the cis-band is predicted to be upshifted by 6 cm⁻¹ from it. The prediction coincides with a hot band observed at 822(2) cm⁻¹. However, there are a few non-isomeric hot bands for which a positive spectral shift of up to +4 cm⁻¹ with respect to the fundamental is predicted (cf. Table S5 in the ESI†). While a conclusive assignment of ν₇ of cis-propiolic acid is not possible, the band at 822(2) cm⁻¹ appears to be the most likely candidate considering the good agreement of the other two cis–trans-shifts. Near the trans-fundamental, there are three additional tPr bands at 832(2), 800(2), and 762(2) cm⁻¹ that all correspond to A′-symmetric transitions (Fig. S3 in the ESI†). The best energy matches for the former two are ν₈ + ν₁₁ and ν₁₄ + ν₁₅, respectively. The third band at 762(2) cm⁻¹ is close to the prediction of the OCO out-of-plane bending vibration ν₁₂ (A′′ symmetry) and was assigned to it in a previous Raman jet study by Xue,²⁹ yet ν₁₂ can be ruled out via symmetry and its near-zero Raman scattering cross-section (Table 1). Thus, a more plausible assignment for this band is ν₉ + ν₁₁. As ν₁₂ is predicted to have significant infrared activity (Table S4 in the ESI†) but was not reported in the previous gas phase infrared study by Katon and McDevitt,⁵⁴ we have measured additional FTIR jet spectra between 2000–700 cm⁻¹ (Fig. S2 in the ESI†), where we observe ν₁₂ of trans-propiolic acid at 755 cm⁻¹.

In addition to the stretching vibrations, the VPT2 calculation predicts some A′-symmetric bending vibrations between 1450–500 cm⁻¹ such as the OH (ν₅) and the CC–O bend (ν₁₀) to be promising candidates for cis-detection. The other three A′ fundamentals either have too small cis–trans shifts (ν₉ and ν₁₁) and/or are predicted in spectrally congested regions in the vicinity of broad A′′ fundamentals of trans-propiolic acid (ν₈ and ν₉, cf. Fig. S4, ESI†).

The Raman jet spectrum between 1450–1250 cm⁻¹ is shown in Fig. 3G. In this spectral region, only one propiolic acid fundamental is predicted, namely ν₅. In the peripheries around 1440 and 1270 cm⁻¹ are contributions from clusters that decrease in intensity with temperature and CO₂ bands that increase due to thermal decomposition of the acid. Overall, there are only a few propiolic acid monomer contributions in this spectral region – the band at 1298(2) cm⁻¹, a weak hot band at 1292(2) cm⁻¹, and two broad features centred at 1302(2) and 1362(2) cm⁻¹. ν₅ of trans-propiolic acid is predicted to be near-completely depolarised (ρ = 0.73, cf. Table S4 in the ESI†) and should therefore persist in the spectrum measured with parallel laser polarisation (green in Fig. 3G, multiplied by a factor of 7/6⁶⁰). In the parallel spectrum, the band at 1298(2) cm⁻¹ almost completely vanishes, whereas the broad features at 1362(2) and 1302(2) cm⁻¹ largely persist. The former must therefore correspond to a A′-symmetric combination or overtone band, whereas the fundamental can be assigned to one of the latter two bands. In line with the two potential ν₅ features observed, the VPT2 calculation predicts a near 1 : 1 Fermi resonance between ν₅ (OH in-plane bend) and the ν₁₂ + ν₁₄ (OCO out-of-plane bend and OH torsion) combination band at 1361 and 1299 cm⁻¹, in excellent agreement with experiment. As ν₅ is predicted to have significant infrared activity (cf. Table S4 in the ESI†), we have measured additional infrared spectra which corroborate the assignment (cf. inset in Fig. 3G). An assignment of the non-fundamental A′ band at 1298(2) cm⁻¹ is beyond the reach of this study, as the density of states is quite large in this spectral region. Based on the good agreement of the VPT2 calculation with experiment, one might be inclined to assign the hot band at 1292(2) cm⁻¹ in the Raman spectrum to ν₅ of cPr. However, the overall weak intensity and possible hot band contributions from tPr (x_5,j values ranging from 2 to −17 cm⁻¹) prevent any firm assignment. We note that the predicted infrared intensity of ν₅ of cPr is the highest amongst all cPr fundamentals (cf. Table S4 in the ESI†), so it might be worthwhile to measure the (jet cooled) infrared spectrum at lower concentrations to prevent overlap with cluster contributions (C in the inset of Fig. 3G).

In search of cPr bands, we lastly turn to the spectral region between 610–410 cm⁻¹ which exhibits three broad features (Fig. 3H). Their assignment is straightforward when comparing it with the VPT2 calculation. The band at 527(2) cm⁻¹ can be assigned to the CC–O in-plane bend ν₁₀. As the predicted depolarisation ratio of the A′ vibration (0.73) is close to that of an A′′ band (0.75), it is not surprising that the experimental band mostly persists in the spectrum measured with parallel laser polarisation (green trace in Fig. 3H). On the higher-wavenumber side of ν₁₀ of tPr, there is a hot band at 538(2) cm⁻¹, which matches the predicted band position of ν₁₀ of cis-propiolic acid within the experimental uncertainty. However, the hot band originating from the lowest-energy A′′ fundamental ν₁₀ + ν₁₅ − ν₁₅ is predicted to be upshifted by 6 cm⁻¹ by the VPT2 calculation. With B3LYP-D3(BJ)/aVQZ, an even larger anharmonicity constant x_10,15 of +10 cm⁻¹ is obtained that matches the band centre within the experimental uncertainty. As the expected thermal population of ν₁₅ at the highest nozzle temperature is significant, the hot band at 538(2) cm⁻¹ could also correspond to a trans-propiolic acid hot band.

Between 500–250 cm⁻¹, no fundamental transition of trans-propiolic acid is expected (cf.Table 1). Thus, the tPr band at 455(2) cm⁻¹ in Fig. 3H is likely due to a combination or overtone vibration of the two lowest-energy fundamentals ν₁₁ and ν₁₅. In the spectrum measured with parallel laser polarisation (green in Fig. 3H), only the broad socket of the band persists. Therefore, the band is assigned to the A′-symmetric 2ν₁₅ overtone of trans-propiolic acid, which is predicted at 458 cm⁻¹ by the VPT2 calculation.

Another interesting feature in this spectral region is the broad feature between 600–550 cm⁻¹ with maxima at 584(2), 578(2), and 569(2) cm⁻¹ as well as additional cluster contributions in the spectra recorded at the lowest two nozzle temperatures. From the VPT2 calculation, we expect two tPr fundamentals, ν₉ (A′, ρ = 0.45) and ν₁₄ (A′′, ρ = 0.75), to contribute to it. The depolarised spectrum facilitates the assignment of ν₉ to 584(2) cm⁻¹, as this band nearly vanishes in the parallel spectrum (green trace in Fig. 3H), and an assignment of the two maxima at 578(2) and 569(2) cm⁻¹ to ν₁₄, as these persist. A similar double maximum band shape is observed for the other A′′-symmetric fundamentals ν₁₃ and ν₁₅ (cf. Fig. S4 in the ESI†). It is interesting to note that the energetic order of ν₉ and ν₁₄ seems to be sensitive to subtle perturbations of the environment. The energetic order reported in argon, xenon, and krypton matrices⁴⁴ is the same as in the gas phase, whereas an inverse order is observed in cryogenic nitrogen matrices (cf.Table 1) with ν₁₄ shifted to higher wavenumbers.³⁴ This sensitivity of the energetic order of ν₉ and ν₁₄ also extends to quantum chemical calculations, rendering the ν₉–ν₁₄ energy sequence excellent for benchmarking, which will be explored in the following section.

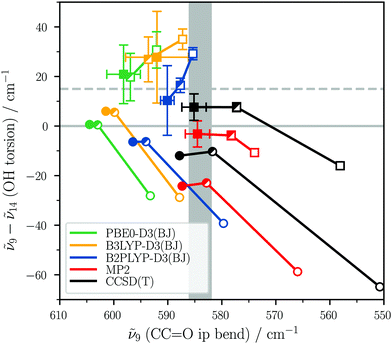
3.2 trans-Propiolic acid benchmark

The predicted energetic order of ν₉ and ν₁₄ of trans-propiolic acid is sensitive to the choice of electronic structure method, basis set, and inclusion of vibrational anharmonicity. This effect is illustrated in Fig. 4, where the ν₉–ν₁₄ shift is plotted against the absolute band position of ν₉ for selected DFT and ab initio methods with (squares) and without (circles) the inclusion of vibrational anharmonicity (VPT2, for coupled-cluster only MP2 corrections). In all VPT2 calculations, Darling-Dennison resonances have been deactivated, as the anharmonic corrections of low-frequency modes seem to be very sensitive to the respective resonance thresholds implemented in Gaussian 16 version A.03 (see also note in ref. 83). The results upon inclusion of these are shown in Fig. S1 in the ESI.†

Fig. 4 Band position shift between the CC=O in-plane bending vibration ν₉ and the OH torsion ν₁₄ plotted against the ν₉ band position for harmonic (circles) and anharmonic VPT2 (squares) vibrational frequency calculations using various electronic structure methods. The basis set size is encoded in the symbol fillings – empty symbols reflect an aVDZ, half-filled an aVTZ, and filled an aVQZ basis set. For coupled-cluster, the corresponding MP2 anharmonic force field is used and the third data point is calculated at the CCSD(T)-F12a/VTZ-F12 level instead of CCSD(T)/aVQZ. Experimental agreement with the ν₉ band position is visualised by the grey area (584 ± 2 cm⁻¹). The experimental upper bound of the shift is indicated by the dashed and the lower bound by the solid line. See text for further details.

In addition to these computational means, the experimental uncertainty of the band positions has to be considered, which is a result of the resolving power of the monochromator and the wavenumber calibration. It amounts to ±2 cm⁻¹ for all experimental band positions and is displayed as a grey area for ν₉ in Fig. 4. As the band position of the OH torsion ν₁₄ cannot be clearly ascertained from the spectrum, agreement with experiment is achieved when the shift is positive. An upper bound for the shift can be estimated by taking the lower-wavenumber maximum of the band at 569 cm⁻¹ as the ν₁₄ band position, which results in a (ν₉–ν₁₄)-shift of +15 cm⁻¹, indicated by a dashed line in Fig. 4, yielding a ‘hard’ (>0) and a ‘soft’ criterium (≤15 cm⁻¹) for agreement with experiment.

As the ν₉–ν₁₄ energetic shift is rather small and DFT VPT2 energies have previously been found to be very sensitive to the calculation settings (see for example Fig. 5 in ref. 52),^84–86 we have averaged the anharmonic vibrational frequency calculations over different settings for each method shown in Fig. 4. The anharmonic force fields were computed with and without symmetry, tight and very tight geometry optimisation thresholds, and for the DFT methods using two different integration grids (ultrafine and superfine). The error bars shown in Fig. 4 correspond to the standard deviation of these eight calculations (four for MP2 and CCSD(T)). For all calculations, a basis set progression from aVDZ to aVQZ has been carried out, with the size encoded in the filling of the symbols (aVDZ □, aVTZ ◩, aVQZ ■).

Fig. 5 Band position deviations of harmonic CCSD(T)-F12a calculations employing a MP2 VPT2 force field with various basis set combinations with respect to CCSD(T)-F12a/VTZ-F12//MP2/aVQZ VPT2 (≡ref) for all fifteen fundamentals of trans-propiolic acid. The basis set combinations are displayed as harmonic//anharmonic. For the ν₅/ν₁₂ + ν₁₄ Fermi resonance, the deviations for both are averaged.

Fig. 4 shows that harmonically (circles), most methods predict the energetic order of the two fundamentals incorrectly. The two exceptions are the PBE0-D3(BJ) and B3LYP-D3(BJ) calculations with the larger aVTZ and aVQZ basis sets. Upon inclusion of vibrational anharmonicity (squares), most methods yield the correct sign for the shift. One exception is MP2 (red), which predicts the correct energetic order only for the aVQZ basis set with the very tight optimisation threshold and C_s symmetry. Generally, the standard deviation of the calculations with different settings (symmetry, optimisation criterion, and DFT integration grid) increases significantly with basis set size and is distinctly larger for the OH torsion than for the CC=O in-plane bend in case of the DFT methods. Similarly large deviations were observed for a benchmark study of formic acid monomer where the OH torsion was also shown to be particularly sensitive to these settings.⁵² Unsurprisingly, the band position of ν₉ is mostly overestimated by the harmonic calculations, which also extends to most VPT2 calculations using DFT. Only MP2 (with very tight optimisation and C_s symmetry) and CCSD(T)-edited VPT2 with large basis sets yield quantitative agreement with experiment for both experimental observables. With only a double-zeta quality basis set, electron correlation of the triple bond is severely underestimated, leading, amongst other things, to a soft force constant for this bond. Overall, it can be concluded that CCSD(T)-edited VPT2 yields the best result for the right reason. Out of the DFT methods, B2PLYP-D3(BJ) performs best with inclusion of vibrational anharmonicity. Similarly good agreement was previously observed for the formic acid monomer.⁵² Harmonically, B3LYP-D3(BJ) with an aVTZ basis set is the best choice. This good performance of harmonic vibrational frequency calculations at the B3LYP-D3(BJ) level for relative quantities has been observed for other carboxylic acids^30,52,87 and various other hydrogen bonded clusters.⁸⁸

In the following section, dimerisation of trans-propiolic acid shall be explored. As seen in Fig. 3 and 4, increasing the basis set size for the harmonic CCSD(T) and the anharmonic MP2 VPT2 force field can yield significant improvement of the anharmonic energy levels. CCSD(T)-F12a/VTZ-F12//MP2/aVQZ VPT2, which was shown to perform particularly well for the propiolic acid monomer, however, is computationally too demanding for the dimers. Therefore, a compromise for the two basis sets (harmonic and anharmonic) needs to be found. This will be explored for the fifteen fundamentals of trans-propiolic acid. For the harmonic force field, the performance of the smaller VDZ-F12 basis is compared to that of VTZ-F12. In case of the anharmonic MP2 force field, aVTZ as well as a split aVTZ + VQZ basis are tested. For the split basis, we use quadruple-zeta basis sets (VQZ) on the carbon atoms and aVTZ on the hydrogen and oxygen atoms. In Fig. 5, the performance of different basis set combinations is compared to the CCSD(T)-F12a/VTZ-F12//MP2/aVQZ reference, which illustrates two important findings: firstly, the difference between the VDZ-F12 and VTZ-F12 basis set for the harmonic CCSD(T)-F12a force field (yellow bars) is reasonably small with differences below 10 cm⁻¹ and a mean absolute deviation of 2.5 cm⁻¹. Notably, the VDZ-F12 basis yields smaller energies compared to the VTZ-F12 results. The second finding is that decreasing the basis set size of the anharmonic MP2 force field (aVTZ) while using CCSD(T)-F12a/VTZ-F12 harmonic wavenumbers yields on average an overestimation of the band positions compared to the MP2/aVQZ VPT2 reference. Fortunately, most of the missing electron correlation (compared to an all-aVQZ basis) seems to be recovered when the basis set size is increased only on the carbon atoms (split basis, green) which significantly reduces the shortcomings of the all-aVTZ basis (mean absolute deviation of 2.8 cm⁻¹ instead of 4.8 cm⁻¹). If both reductions of the basis set size (harmonic and anharmonic) are implemented at the same time (red in Fig. 5), the introduced errors tend to cancel fortuitously, which is reflected in a mean absolute deviation of 2.5 cm⁻¹. We will therefore use CCSD(T)-F12a/VDZ-F12//MP2/aVTZ + VQZ throughout Section 4.

4 Propiolic acid homo- and heterodimers

The vibrations of the C_2h-symmetric doubly hydrogen bonded trans–trans-dimers of carboxylic acids can be divided into four symmetry groups – in-plane vibrations, where the two identical monomer oscillators are either in-phase (A_g) or out-of-phase (B_u), as well as the respective gerade (g) and ungerade (u) out-of-plane vibrations (B_g in-phase and A_u out-of-phase). All gerade vibrations are exclusively Raman- and all ungerade vibrations exclusively infrared-active, rendering the use of both techniques necessary for a full vibrational characterisation of these dimers.

As the OH stretching region of carboxylic acid dimers is notoriously congested with a broad, complicated resonance structure, we focus on the C=O stretching region in the following. Mixed cis–trans- or cis–cis-dimers are not expected to a considerable amount in the jet spectra due to the relatively low abundance of the cis-rotamers in the expansion at the nozzle temperatures explored for the dimer investigation (≤60 °C, resulting in 1–2% of cis-propiolic acid monomer). We will start with the infrared spectrum of the propiolic acid dimer (tPr–tPr) before it is compared to the infrared spectrum of the formic–propiolic acid heterodimer (tF–tPr), followed by an analysis of the Raman spectra of both dimers in Section 4.2. Heterodimers such as (tF–tPr) are no longer centrosymmetric and therefore, the C=O oscillators are not strictly equivalent, yet due to the local inversion symmetry of the carboxylic acid dimer ring, the infrared-activity of the symmetric and the Raman-activity of the antisymmetric C=O stretch are fairly small. As in the monomer section, the vibrational modes are labelled according to the Herzberg nomenclature of the respective dimer. To refer to the two carbonyl stretching vibrations, we introduce the short-hand notation ‘a’ (antisymmetric) and ‘s’ (symmetric) as indices to refer to the infrared- and Raman-active C=O stretching fundamental, respectively, e.g., (tPr–tPr)_a for the infrared-active antisymmetric C=O stretch of the propiolic acid homodimer.

4.1 FTIR jet spectra

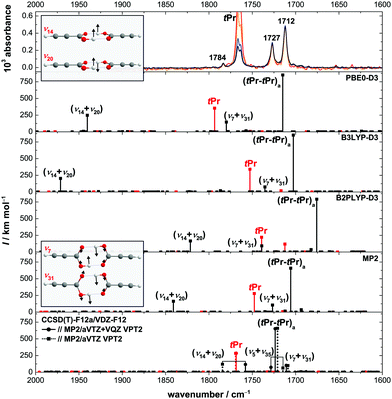
In Fig. 6, intensity-scaled FTIR jet spectra of propiolic acid are shown in the C=O stretching region with increasing concentrations (from red, over orange and blue up to black). The cis-propiolic acid monomer band at 1800 cm⁻¹ is not seen in the infrared spectra due to the overall low intensity of the bands, yet its presence at room temperature is confirmed by the Raman jet spectra, which will be discussed in Section 4.2. In addition to the C=O stretch of the trans-monomer (tPr) at 1765 cm⁻¹, three bands can be seen; two downshifted from the monomer band at 1727 and 1712 cm⁻¹, the latter being approximately twice as intense as the former, and an additional smaller feature upshifted at 1784 cm⁻¹. Considering the overall low acid concentration and identical scaling behaviour of the bands, all three correspond to dimer signals. As only one fundamental of the (tPr–tPr) dimer is expected below the monomer C=O stretch in this spectral region and a higher-energy dimer as the main contributor to these bands seems very unlikely based on the low abundance of higher-energy dimers with respect to the global minimum dimer in supersonic expansions,^32,58 the most likely explanation for the doublet at 1727/1712 cm⁻¹ is a resonance perturbation of the antisymmetric C=O stretching vibration of the global minimum dimer (tPr–tPr)_a (ν₂₈, B_u).

Fig. 6 FTIR jet spectra of propiolic acid in helium with increasing concentrations (from red, over orange, and blue up to black) that are intensity-scaled to the dimer band at 1727 cm⁻¹. Below the spectra, anharmonic (VPT2) calculations of the trans-propiolic acid monomer (red) and dimer (black) are shown using PBE0-D3(BJ), B3LYP-D3(BJ), B2PLYP-D3(BJ), and MP2, all with an aVTZ basis set. Additionally, CCSD(T)-F12a/VDZ-F12//MP2/aVTZ + VQZ VPT2 (solid lines) and CCSD(T)-F12a/VDZ-F12//MP2/aVTZ VPT2 calculations (dotted lines) are shown.

For a closer investigation of potential resonance partners of (tPr–tPr)_a, anharmonic (VPT2) vibrational frequency calculations have been carried out using the same electronic structure methods as for the monomer benchmark (Fig. 4), namely B3LYP-D3(BJ), PBE0-D3(BJ), B2PLYP-D3(BJ), and MP2 all using an aVTZ basis set. Additional CCSD(T)-edited VPT2 results are shown, illustrating the convergence of the anharmonic MP2 force field for an all-aVTZ and the aVTZ + VQZ split basis. The results of the VPT2 calculations are plotted below the FTIR spectra in Fig. 6.

Fig. 6 shows that all methods consistently predict two B_u-symmetric combination vibrations with significant intensity between 2000–1600 cm⁻¹, one in proximity to the antisymmetric C=O stretching fundamental of the dimer (ν₇ + ν₃₁) and one upshifted from the monomer band (ν₁₄ + ν₂₀). The former is a combination of the symmetric (ν₇) and antisymmetric OCO in-plane bending vibration (ν₃₁) and the latter a combination of the symmetric (ν₂₀) and antisymmetric OH torsion (ν₁₄) (see insets of Fig. 6 for schematic representation of the vibrational motion). CCSD(T)-edited VPT2 predicts a third combination state with significant infrared intensity in that spectral region, namely a combination of the symmetric OH in-plane bend and a low-frequency mode that modulates the hydrogen bond length (ν₅ + ν₃₅). The ν₇ + ν₃₁ band position relative to the monomer and cyclic dimer varies across the methods – for all DFT methods, it is predicted closer to the monomer than to the dimer fundamental, with B3LYP-D3(BJ) showing the overall best band position agreement. In case of MP2, the relative distance between ν₇ + ν₃₁ and the antisymmetric C=O stretch (21 cm⁻¹) roughly matches the observed splitting of 15 cm⁻¹ between both bands, but the relative distance with respect to the monomer band as well as the intensity ratio between both bands is too small. An assignment of the 1712/1727 cm⁻¹ doublet to the antisymmetric C=O stretch and ν₇ + ν₃₁ is consistent with the CCSD(T)-edited VPT2 results that predict an energy difference of 13 cm⁻¹ (exp. 15 cm⁻¹, intensity inversely). A firm assignment, however, is currently not possible as the alternative assignment to ν₅ + ν₃₅ cannot be ruled out with the available computational results. Note that except for MP2/aVTZ, which predicts a resonance to ν₇ + ν₃₁, neither DFT nor CCSD(T)-edited VPT2 predicts Fermi resonances involving the antisymmetric C=O stretch when default resonance thresholds are used.

The predicted band position of the second combination vibration with significant intensity (ν₁₄ + ν₂₀) matches the third, smaller dimer feature at 1784 cm⁻¹ within the experimental uncertainty for CCSD(T)-edited VPT2 with the smaller aVTZ basis for the anharmonic force field. However, its band position is not yet converged, as it shifts down significantly (25 cm⁻¹) when changing to the split basis for the anharmonic force field. While MP2 and B2PLYP-D3(BJ) predict ν₁₄ + ν₂₀ slightly higher in energy than CCSD(T)-edited VPT2, particularly large deviations are observed for B3LYP-D3(BJ) and PBE0-D3(BJ). Interestingly, the predicted infrared intensity of ν₁₄ + ν₂₀ is of similar order of magnitude across all methods (87–250 km mol⁻¹, compare to (tPr–tPr)_a in Fig. 6), though the band position difference to the fundamental varies from 268 cm⁻¹ (B3LYP-D3(BJ)) to 37 cm⁻¹ (coupled-cluster), with the smaller band position differences coinciding, perhaps somewhat accidentally, with smaller predicted infrared intensities. Altogether, this relatively high infrared intensity despite fairly large energy differences to the fundamental indicates that ν₁₄ + ν₂₀ may have intrinsic oscillator strength. For formic acid, such a low-intense dimer band upshifted from the monomeric C=O stretching fundamental is also observed in the infrared spectra. In line with the results presented here for the propiolic acid dimer, it was assigned to a combination vibration of the symmetric and antisymmetric OH torsion by Kollipost,²⁴ which is also predicted to exhibit significant oscillator strength.²⁶

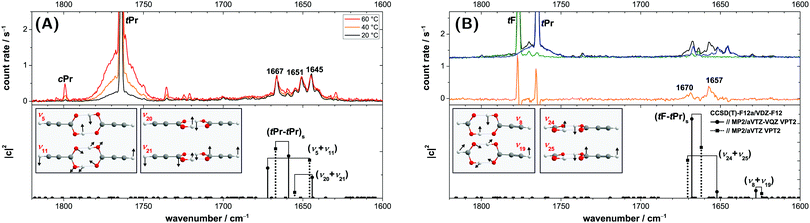
To cross-check this assignment, we look at an intermediate system, i.e., the formic–propiolic acid heterodimer (tF–tPr). FTIR spectra of the mixture of formic and propiolic acid are shown in Fig. 7 alongside predicted band positions of the heterodimer using CCSD(T)-edited VPT2. The FTIR difference spectrum obtained by subtracting monomer-scaled single substance spectra from that of the mixture (orange in Fig. 7) shows one distinct band at 1732 cm⁻¹, which can be clearly attributed to the antisymmetric C=O stretching vibration of the heterodimer (tF–tPr)_a. In addition to the fundamental of the mixed dimer, which agrees within 2 cm⁻¹ with experiment, the VPT2 calculation predicts two combination vibrations of (tF–tPr) with significant infrared intensity between 1820–1600 cm⁻¹, namely ν₂₃ + ν₂₄ and ν₈ + ν₁₈ (cf. insets in Fig. 7 for vibrational motion). ν₂₃ + ν₂₄ corresponds to the aforementioned OH torsion combination vibration and ν₈ + ν₁₈ is predicted to the lower-wavenumber side of the mixed dimer fundamental. In the spectrum of the mixture (black in Fig. 7), there seems to be some intensity in-between the two dimer features of the propiolic acid homodimer, which could correspond to ν₈ + ν₁₈, yet due to the overall low-intensity, no conclusions can be drawn. Close to the predicted band position of the combination vibration of the symmetric and antisymmetric OH torsion (ν₂₃ + ν₂₄), there is a dimer band in the mixed spectrum at 1798 cm⁻¹ (black in Fig. 7, see also Fig. S6 in the ESI†) similar to the dimer band in the propiolic acid homodimer spectrum (1784 cm⁻¹). Interestingly, increasing the basis set size of the anharmonic MP2 force field (all-aVTZ to aVTZ + VQZ) shifts the prediction from 1826 cm⁻¹ to 1788 cm⁻¹ towards experiment (1798 cm⁻¹) whereas the exact opposite is the case for the propiolic acid homodimer (1784 to 1758 cm⁻¹; exp. 1784 cm⁻¹), demonstrating that the anharmonic couplings of this OH torsion combination vibration are not yet fully converged.

Fig. 7 FTIR jet spectrum of the mixture of formic and propiolic acid (black) in helium alongside monomer-scaled single substance spectra (green: formic acid, blue: propiolic acid) and the corresponding difference spectrum (orange). Below the experimental spectra, CCSD(T)-edited MP2 VPT2 band positions of the formic–propiolic acid heterodimer (tF–tPr) are shown alongside anharmonic infrared intensities using an aVTZ and an aVTZ + VQZ split basis.

Such an infrared-active, non-fundamental dimer band upshifted from the monomer is also observed for other acids such as acetic (1834.9 cm⁻¹),²⁵ pivalic (1838/1834 cm⁻¹),²⁶ and benzoic acid (1824 cm⁻¹),^27,28 which for all three acids so far remains unassigned. Considering that the vibrational motion of this OH torsion combination vibration only involves the hydrogen-bonded ring, one would expect it at a similar band position independent of the carboxylic acid substituent, given that it has sufficient oscillator strength or gains it via resonance. As seen for the propiolic acid and formic–propiolic acid dimer, the anharmonic VPT2 band positions of this combination state are not sufficiently converged and the quantitative agreement with experiment varies greatly depending on the basis set chosen for the anharmonic MP2 force field. To further investigate if this combination vibration can plausibly be ascribed to the so far unassigned infrared bands around 1800 cm⁻¹ in the spectra of other carboxylic acid dimers, we turn to a simple harmonic model using B3LYP-D3(BJ) and alternatively explicitly correlated coupled-cluster, assuming similar anharmonic corrections for this vibration across all dimers. In Fig. 8, the sum of the harmonic wavenumbers of the symmetric and antisymmetric OH torsion of the formic, propiolic, acetic, pivalic, and benzoic acid homodimers and selected heterodimers^26,30 is plotted against the experimental band position (for individual results, see Table S8 in the ESI†). One should note that for the formic-acetic and formic-pivalic acid heterodimers (daggers † in Fig. 8), the corresponding normal modes are no longer concerted pair vibrations, but mostly localised OH torsions on each monomer and instead of one, there are two normal vibrations in each case that can be labelled ‘Tor_a’ (cf. Fig. S8 in the ESI†). We therefore average the harmonic wavenumbers of the two respective normal modes. In Fig. 8, it can be clearly seen that for the homodimers (squares) and selected heterodimers (crosses) all points lie on straight lines with different slopes for B3LYP-D3(BJ) and coupled-cluster, strengthening this assignment. For formic acid, deuteration experiments have been carried out by Kollipost,²⁴ showing that such a dimer band is present at a similar band position in the infrared spectrum of DCOOH (1821 cm⁻¹versus 1811 cm⁻¹ for HCOOH), but no dimer band is observed for HCOOD between 1780–1840 cm⁻¹. A systematic extension to the dimers of oxygen-deuterated carboxylic acids therefore seems most promising for verification.

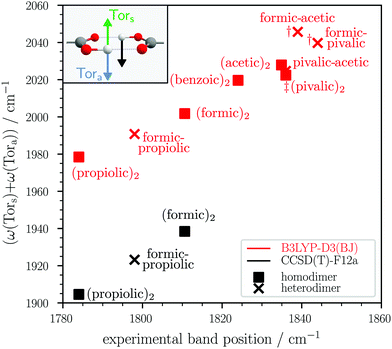Fig. 8 Sum of harmonic B3LYP-D3(BJ)/aVTZ and CCSD(T)-F12a/VDZ-F12 band positions of the symmetric (Tor_s) and antisymmetric OH torsion (Tor_a) for selected homo- and heterodimers plotted against the experimental band position of a non-fundamental dimer feature upshifted from the antisymmetric C=O stretching fundamental in the infrared spectra. The experimental band positions of the dimer bands are taken from ref. 24–27 with the exception of the propiolic acid dimer and the formic–propiolic acid heterodimer (both this work). The † marks dimers where two normal modes contain significant Tor_a character. For these dimers, the Tor_a band position was obtained by averaging over both normal modes (cf. Fig. S8 in the ESI† for further details.) The ‡ indicates that the experimental band shows a double maximum, for which the averaged band position is used (Fig. S7 in the ESI†).

4.2 Raman jet spectra

The Raman jet spectra of the propiolic acid homodimer and its heterodimer with formic acid are displayed in Fig. 9. The Raman-active symmetric C=O stretching fundamental of the homodimer (tPr–tPr)_s (ν₄, A_g) is split into three distinct peaks at 1667, 1651, and 1645 cm⁻¹ with a broad and fine-structured socket spanning approximately 40 cm⁻¹ (Fig. 9A). The corresponding heterodimer band is also resonance split with a doublet observed at 1670/1657 cm⁻¹ and an intensity ratio of 1 : 2 (Fig. 9B). Such symmetric C=O stretching resonances are quite commonly observed for carboxylic acid dimers – the bands of the formic, acetic, and pivalic acid dimer are either resonance split or broadened (see Fig. S5 in the ESI† for comparison of the spectra).³⁰ Conclusive resonance partners, however, have yet to be proposed. Overall, it would be interesting to examine whether there is a connection between these symmetric C=O stretching resonances similar to the OH torsion combination vibration in the infrared spectra discussed in the previous section. A first step in that direction will be taken here by investigating the C=O stretching spectrum of the propiolic acid homodimer and formic–propiolic acid heterodimer.

Fig. 9 (A) Dimer-scaled Raman jet spectra of propiolic acid in helium recorded at increasing nozzle temperatures of 20–60 °C. (B) Raman jet spectrum of the mixture of formic and propiolic acid in helium (black) alongside monomer-scaled single substance spectra (green: formic acid, blue: propiolic acid) and the corresponding difference spectrum (orange), all recorded with the nozzle kept at room temperature. The two artefacts in the Raman difference spectrum are a result of slightly differing monomer band shapes in the mixed and single substance spectra. Below the spectra, CCSD(T)-F12a/VDZ-F12//MP2/aVTZ + VQZ VPT2 band positions are plotted against the squared VCI coefficients of the symmetric C=O stretching vibration of the propiolic acid dimer (tPr–tPr) (A) and the formic–propiolic acid heterodimer (tF–tPr) (B). Additional results using a smaller aVTZ basis set for the anharmonic force field are shown with dotted lines. Squared wavefunction contributions from the C=O stretching fundamental are obtained from diagonalisation of the effective Fermi resonance Hamiltonian set-up by Gaussian 16 with default resonance thresholds.

Below the spectra in Fig. 9, CCSD(T)-edited VPT2 results are shown using default Fermi resonance thresholds and inclusion of two-quantum states. The VPT2 calculations do predict resonances for the homo- (tPr–tPr)_s and heterodimer (tF–tPr)_s C=O stretch. In the absence of anharmonic Raman scattering cross-sections, we inspect the wavefunction overlap with the deperturbed fundamental to check the assignments for plausibility.^89,90 In Fig. 9, the squared wavefunction contribution of the (deperturbed) C=O stretch to the respective eigenstate is plotted against the anharmonic energy after diagonalisation of the effective resonance Hamiltonian for the propiolic acid homo- (Fig. 9A) and the formic–propiolic acid heterodimer (Fig. 9B). The absolute wavenumbers of the three main peaks in the propiolic acid homodimer spectrum (Fig. 9A) at 1667/1651/1645 cm⁻¹ are surprisingly well reproduced by the VPT2 calculations. The assignments to the respective peaks vary between both basis sets used for the anharmonic MP2 force field, but given the experimental near 1 : 1 : 1 intensity, harmonic oscillator labels become insignificant in this context. With the smaller all-aVTZ basis, the triad is predicted at 1667/1655/1646 cm⁻¹, with the larger split basis at 1672/1659/1644 cm⁻¹. While the squared wavefunction coefficients do not quantitatively reproduce the observed intensity pattern, they demonstrate significant delocalisation of the symmetric C=O stretch, as is observed in the Raman jet spectrum. Future fine-tuning should include higher excited states in a variational treatment to account for the fine structure.

For the formic–propiolic acid heterodimer, two main peaks are seen at 1670 and 1657 cm⁻¹ in the Raman jet difference spectrum (orange in Fig. 9B). The VPT2 calculations predict a Fermi resonance between the fundamental (tF–tPr)_s and the combination vibration of the symmetric OH (ν₂₄) and OH/CH out-of-plane bending vibration (ν₂₅) at 1668/1652 cm⁻¹ (aVTZ + VQZ) and 1671/1662 cm⁻¹ (aVTZ) in good agreement with the experimental band positions. Depending on the basis set size of the anharmonic MP2 force field, the resonance between (tF–tPr)_s and ν₂₄ + ν₂₅ is predicted to be either week (aVTZ + VQZ) or strong (all-aVTZ). A third, much weaker perturber is predicted further downshifted from the experimental bands at 1628 cm⁻¹ (aVTZ + VQZ; 1624 cm⁻¹ aVTZ), though is not observed in the spectra. Due to the low acid concentrations used for the measurement of the heterodimer spectra, however, additional weaker mixed dimer bands cannot be excluded.

Altogether, it can be concluded that the VPT2 calculations using default Fermi resonance treatment and including only binary states can predict the experimental band patterns surprisingly well. It is worth noting that the two predicted resonance partners for the homo- and heterodimer are in fact very similar normal modes (cf. normal modes in Fig. 9). Interestingly, all normal modes involved in these resonances almost exclusively comprise displacements of the cyclic ring, particularly (in- and out-of-plane) bending of the hydrogen bonded H atoms. Future work will have to show whether this also extends to the resonance perturbed C=O stretching fundamentals of other carboxylic acid dimers.

5 Conclusions

The torsional isomerism of carboxylic acid monomers is an attractive target for performance tests of quantum chemical calculations, as not only the global minimum trans-form can be scrutinised, but also higher-energy regimes of the potential energy hypersurface, for example the cis-rotamer. In this work, we have extended the cis-vibrational gas phase database, which so far has been limited to formic acid, to the O–H and C=O stretching vibrations of cis-propiolic acid (HC≡C–COOH) using linear Raman jet spectroscopy in combination with thermal excitation. The assignment of other potential cis-propiolic acid bands has to await modelling of the complex hot band structures observed in the Raman jet spectra. A particularly interesting benchmarking target of the trans-rotamer are two near-isoenergetic fundamentals of different symmetry (CC=O bend ν₉ and OH torsion ν₁₄), as the energetic ordering predicted by different electronic structure methods is susceptible to the basis set size and inclusion of vibrational anharmonicity. From the tested methods, B3LYP-D3(BJ) was found to perform best harmonically due to fortuitous error cancellation, whereas MP2 and coupled-cluster show the best agreement with experiment upon inclusion of VPT2 anharmonicity. In addition to the vibrational detection of cis-propiolic acid and updating and completing the record regarding the fifteen trans-fundamentals, a plethora of combination/overtone as well as hot bands of trans-propiolic acid were identified in the Raman jet spectra (band centres in Table S6 in the ESI†), many of which have not been reported in the literature. These newly available experimental reference data call for a close theoretical scrutiny along the lines presented for formic acid.^79,91–94

The systematic comparison of the infrared and Raman jet spectra of the propiolic acid dimer, the formic–propiolic acid dimer as well as other carboxylic acid homo- and heterodimers in the C=O stretching region revealed interesting similarities in their vibrational signature. A weak non-fundamental dimer band that is observed in the propiolic acid (1784 cm⁻¹) and formic–propiolic acid infrared spectrum (1798 cm⁻¹) can be assigned to a combination vibration of the symmetric and antisymmetric (hindered) OH torsion, which has also been observed for the formic acid dimer (1810.6 cm⁻¹).²⁴ A simple harmonic model (Fig. 8) indicates that this combination vibration might be a plausible explanation for the so far unassigned features in the infrared spectra of many other carboxylic acid dimers, such as the benzoic acid,^27,28 the acetic acid,²⁵ and the pivalic acid dimer,^26,30 and the mixed dimers of formic, acetic, and pivalic acid.^26,30 For validation, a systematic experimental extension to the dimers of oxygen-deuterated carboxylic acids is necessary.

As observed for other carboxylic acid dimers,^29,30 the Raman-active symmetric C=O stretching fundamentals of the propiolic acid dimer and its heterodimer with formic acid are strongly perturbed by resonances (see Fig. S5 in the ESI†). In the Raman spectrum of propiolic acid, a broad feature is observed spanning about 40 cm⁻¹ with three distinct peaks, whereas for the corresponding formic–propiolic acid heterodimer, a resonance doublet is observed. CCSD(T)-edited MP2 VPT2 calculations used to guide spectral assignments throughout this work were shown to be able to reproduce the main features in the Raman spectra. In both cases, the calculations clearly illustrate that while the resulting resonance pattern varies, all perturbing states share a notable similarity: all involved normal modes have significant OH in- and out-of-plane bending character. This raises the question of whether the resonance perturbations of the Raman-active C=O stretching fundamentals of other carboxylic acid dimers can also be explained by only a few couplings between the C=O stretch and the (in- and out-of-plane) OH bend in the internal coordinate picture which map onto several vibrations in the normal mode representation (cf. related work by Florio et al.¹³ concerning the OH stretching spectrum of the formic and benzoic acid dimer). The present results call for a similar reduced-dimensional model calculation in the C=O stretching range of the propiolic acid and other carboxylic acid dimers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 388861488/SU121/7-1, 389479699/GRK2455, and 405832858. The authors thank Z. Xue for a preliminary Raman jet study of the trans-propiolic acid monomer and dimer²⁹ and M. A. Suhm for very insightful discussions. A. N. thanks the Fonds der Chemischen Industrie (FCI) for a generous two-year PhD scholarship.

Notes and references

1. F. Kollipost, R. Wugt Larsen, A. V. Domanskaya, M. Nörenberg and M. A. Suhm, J. Chem. Phys., 2012, 136, 151101.
2. D. Luckhaus, J. Phys. Chem. A, 2006, 110, 3151–3158.
3. Ö. Birer and M. Havenith, Annu. Rev. Phys. Chem., 2009, 60, 263–275.
4. A. Almenningen, O. Bastiansen and T. Motzfeldt, Acta Chem. Scand., 1969, 23, 2848–2864.
5. F. Madeja and M. Havenith, J. Chem. Phys., 2002, 117, 7162.
6. V. V. Matylitsky, C. Riehn, M. F. Gelin and B. Brutschy, J. Chem. Phys., 2003, 119, 10553–10562.
7. R. C. Millikan and K. S. Pitzer, J. Am. Chem. Soc., 1958, 80, 3515–3521.
8. J. E. Bertie and K. H. Michaelian, J. Chem. Phys., 1982, 76, 886–894.
9. Y. Maréchal, J. Chem. Phys., 1987, 87, 6344.
10. R. Georges, M. Freytes, D. Hurtmans, I. Kleiner, J. Vander Auwera and M. Herman, Chem. Phys., 2004, 305, 187–196.
11. Z. Xue and M. A. Suhm, J. Chem. Phys., 2009, 131, 54301.
12. A. Olbert-Majkut, J. Ahokas, J. Lundell and M. Pettersson, Chem. Phys. Lett., 2009, 468, 176–183.
13. G. M. Florio, T. S. Zwier, E. M. Myshakin, K. D. Jordan and E. L. Sibert III, J. Chem. Phys., 2003, 118, 1735.
14. G. L. Barnes and E. L. Sibert III, Chem. Phys. Lett., 2008, 460, 42–45.
15. D. Luckhaus, Phys. Chem. Chem. Phys., 2010, 12, 8357–8361.
16. E. Miliordos and S. S. Xantheas, J. Chem. Phys., 2015, 142, 094311.
17. C. Qu and J. M. Bowman, Phys. Chem. Chem. Phys., 2016, 18, 24835–24840.
18. C. Qu and J. M. Bowman, Phys. Chem. Chem. Phys., 2019, 21, 3397–3413.
19. J. Bournay and Y. Maréchal, J. Chem. Phys., 1971, 55, 1230–1235.
20. C. Emmeluth, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2003, 118, 2242.
21. D. Chamma and O. Henri-Rousseau, Chem. Phys., 1999, 248, 53–70.
22. K. Heyne, N. Huse, E. T. J. Nibbering and T. Elsaesser, Chem. Phys. Lett., 2003, 369, 591–596.
23. P. Ottiger, H. Köppel and S. Leutwyler, Chem. Sci., 2015, 6, 6059–6068.
24. F. Kollipost, Schwingungsdynamik in O–H⋯O-verbrückten Aggregaten: FTIR-Spektroskopie vom Nah- bis zum Ferninfraroten, PhD thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2015, see https://hdl.handle.net/11858/00-1735-0000-0023-9644-9.
25. T. Häber, U. Schmitt, C. Emmeluth and M. A. Suhm, Faraday Discuss., 2001, 118, 331–359.
26. K. A. E. Meyer, Carboxylic Acids Under Vibrational Scrutiny: Experimental Reference Data to Benchmark Quantum Chemical Calculations, PhD thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2020, see https://hdl.handle.net/21.11130/00-1735-0000-0005-14BA-3.
27. J. M. Bakker, L. Mac Aleese, G. von Helden and G. Meijer, J. Chem. Phys., 2003, 119, 11180–11185.
28. J. Antony, G. von Helden, G. Meijer and B. Schmidt, J. Chem. Phys., 2005, 123, 014305.
29. Z. Xue, Raman spectroscopy of carboxylic acid and water aggregates, Logos Berlin, Berlin, 2011.
30. K. A. E. Meyer and M. A. Suhm, J. Chem. Phys., 2018, 149, 104307.
31. V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787.
32. S. Oswald, E. Meyer and M. A. Suhm, J. Phys. Chem. A, 2018, 122, 2933–2946.
33. E. M. N. Ndip, Vibrational analysis and ab initio studies of propiolic acid, PhD thesis, Texas Tech University, Lubbock, Texas, 1987, see http://hdl.handle.net/2346/9876.
34. S. Lopes, T. Nikitin and R. Fausto, J. Phys. Chem. A, 2019, 123, 1581–1593.
35. Z. Xue and M. A. Suhm, Mol. Phys., 2010, 108, 2279–2288.
36. A. M. Daly, P. R. Bunker and S. G. Kukolich, J. Chem. Phys., 2010, 132, 201101.
37. A. M. Daly, K. O. Douglass, L. C. Sarkozy, J. L. Neill, M. T. Muckle, D. P. Zaleski, B. H. Pate and S. G. Kukolich, J. Chem. Phys., 2011, 135, 154304.
38. S. G. Kukolich, E. G. Mitchell, S. J. Carey, M. Sun and B. A. Sargus, J. Phys. Chem. A, 2013, 117, 9525–9530.
39. M. Sun, Y. Wang, S. J. Carey, E. G. Mitchell, J. Bowman and S. G. Kukolich, J. Chem. Phys., 2013, 139, 084316.
40. M. Pettersson, J. Lundell, L. Khriachtchev and M. Räsänen, J. Am. Chem. Soc., 1997, 119, 11715–11716.
41. L. G. Bonner and R. Hofstadter, J. Chem. Phys., 1938, 6, 531–534.
42. E. M. S. Maçôas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 16188–16189.
43. E. M. S. Maçôas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Räsänen, Phys. Chem. Chem. Phys., 2005, 7, 743–749.
44. E. Isoniemi, L. Khriachtchev, M. Makkonen and M. Räsänen, J. Phys. Chem. A, 2006, 110, 11479–11487.
45. A. Domanskaya, K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2009, 130, 154509.
46. K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2007, 126, 241102.
47. K. Marushkevich, L. Khriachtchev and M. Räsänen, Phys. Chem. Chem. Phys., 2007, 9, 5748–5751.
48. S. Lopes, R. Fausto and L. Khriachtchev, Mol. Phys., 2019, 117, 1708–1718.
49. L. Khriachtchev, J. Mol. Struct., 2008, 880, 14–22.
50. W. H. Hocking, Z. Naturforsch., A, 1976, 31, 1113–1121.
51. O. I. Baskakov, V.-M. Horneman, J. Lohilahti and S. Alanko, J. Mol. Struct., 2006, 795, 49–53.
52. K. A. E. Meyer and M. A. Suhm, Chem. Sci., 2019, 10, 6285–6294.
53. A. Nejad, M. A. Suhm and K. A. E. Meyer, Phys. Chem. Chem. Phys., 2020, 22, 25492–25501.
54. J. E. Katon and N. T. McDevitt, Spectrochim. Acta, 1965, 21, 1717–1724.
55. T. Forsting and M. Suhm, Curry-Jet SETUP, see DOI: 10.6084/m9.figshare.6395840.v1.
56. M. Gawrilow and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 15303–15311.
57. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
58. K. A. E. Meyer and M. A. Suhm, J. Chem. Phys., 2017, 147, 144305.
59. A. Kramida and Y. Ralchenko, NIST Atomic Spectra Database, NIST Standard Reference Database 78.
60. D. A. Long, The Raman effect: A unified treatment of the theory of Raman scattering by molecules, Wiley, Chichester and New York, 2002.
61. N. O. B. Lüttschwager and M. A. Suhm, Soft Matter, 2014, 10, 4885–4901.
62. H. H. Nielsen, Rev. Mod. Phys., 1951, 23, 90–136.
63. V. Barone, J. Chem. Phys., 2005, 122, 14108.
64. V. Barone, J. Bloino, C. A. Guido and F. Lipparini, Chem. Phys. Lett., 2010, 496, 157–161.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, 2016, Gaussian Inc., Wallingford, CT.
66. M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128.
67. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
68. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
69. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
70. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
71. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
72. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
73. P. R. Franke, J. F. Stanton and G. E. Douberly, J. Phys. Chem. A, 2021, 125, 1301–1324.
74. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
75. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
76. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., MOLPRO, version 2018.1, a package of ab initio programs, 2018, see https://www.molpro.net.
77. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
78. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
79. A. Nejad and E. L. Sibert III, J. Chem. Phys., 2021, 154, 064301.
80. In formic acid, the OH in-plane bend (1306 cm⁻¹) and OH torsion overtone (1220 cm⁻¹) form a strong resonance polyad that includes the C–O stretch (1106 cm⁻¹) at higher energies.⁷⁹ In Section IV.E of ref. 79, it was shown that in the Raman jet spectrum of HCOOH two A′ bands (3609, 3559 cm⁻¹) near the OH stretching fundamental (3570 cm⁻¹) persist upon C-deuteration (3607, 3563 cm⁻¹). C-deuteration narrows down the list of possible perturbing states to the aforementioned three as well as the OCO in-plane bend. At similar wavenumbers near the OH stretching fundamental at 3578 cm⁻¹ (and similar intensity ratios relative to the fundamental), there are three bands in the propiolic acid Raman jet spectrum at 3586, 3582, and 3571 cm⁻¹. Interestingly, the wavenumbers of the –COOH group vibrations are similar in propiolic acid. The OH in-plane bend is doubly degenerate (1362 and 1302 cm⁻¹) and there are indications that the OH torsion overtone (possible assignment 1118 cm⁻¹) is in resonance with the C–O stretching fundamental (1154 cm⁻¹). Indeed, the sum of the three is very similar in formic (1106 + 1220 + 1306 = 3632 cm⁻¹) and propiolic acid (1118 + 1154 + 1302 = 3574 cm⁻¹ or 1118 + 1154 + 1362 = 3634 cm⁻¹), rendering a similar assignment in case of propiolic acid possible.
81. D. Luckhaus, M. Quack and M. Willeke, Z. Phys. Chem., 2000, 214, 1087–1114.
82. H. G. M. Edwards, Spectrochim. Acta, Part A, 1990, 46, 97–106.
83. For all calculations, Darling–Dennison resonances have been deactivated in Gaussian 16, as these lead to instabilities in the low-frequency modes. In a study of 2-methoxyethanol by Gawrilow and Suhm,⁵⁶ the performance of Gaussian 09 and Gaussian 16 was compared showing that the differing standard settings of VPT2 calculations in both program versions (Darling–Dennison resonance thresholds) result in an inferior performance of Gaussian 16 for the low-frequency modes of 2-methoxyethanol. For higher-energy modes of 2-methoxyethanol, such as the OH stretch, similar performance was observed.
84. S. E. Wheeler and K. Houk, J. Chem. Theory Comput., 2010, 6, 395–404.
85. N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303–4325.
86. K. A. E. Meyer, J. A. Davies and A. M. Ellis, Phys. Chem. Chem. Phys., 2020, 22, 9637–9646.
87. A. Nejad, E. Meyer and M. A. Suhm, J. Phys. Chem. Lett., 2020, 11, 5228–5233.
88. S. Oswald and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 18799–18810.
89. H.-R. Dübal and M. Quack, Mol. Phys., 1984, 53, 257–264.
90. H.-R. Dübal and M. Quack, J. Chem. Phys., 1984, 81, 3779.
91. J. Demaison, M. Herman and J. Liévin, J. Chem. Phys., 2007, 126, 164305.
92. D. P. Tew and W. Mizukami, J. Phys. Chem. A, 2016, 120, 9815–9828.
93. F. Richter and P. Carbonnière, J. Chem. Phys., 2018, 148, 064303.
94. A. Aerts, P. Carbonnière, F. Richter and A. Brown, J. Chem. Phys., 2020, 152, 024305.

---

Footnote

† Electronic supplementary information (ESI) available: Depolarised Raman jet spectra of the propiolic acid monomer (including A′′ fundamentals), FTIR jet spectra of the propiolic acid monomer, list of all observed experimental monomer band centres, band positions and assignments of decomposition products, Raman jet spectra of symmetric C=O stretching resonances of carboxylic acid dimers, heterodimer FTIR jet spectra, and further experimental and computational details. See DOI: 10.1039/d1cp02700j

---