QM/MM study of the reactivity of zeolite bound methoxy and carbene groups†
Received
6th June 2021
, Accepted 25th July 2021
First published on 27th July 2021
Abstract
The conversion of methanol-to-hydrocarbons (MTH) is known to occur via an autocatalytic process in zeolites, where framework-bound methoxy species play a pivotal role, especially during catalyst induction. Recent NMR and FT-IR experimental studies suggest that methoxylated zeolites are able to produce hydrocarbons by a mechanism involving carbene migration and association. In order to understand these observations, we have performed QM/MM computational investigations on a range of reaction mechanisms for the reaction of zeolite bound methoxy and carbene groups, which are proposed to initiate hydrocarbon formation in the MTH process. Our simulations demonstrate that it is kinetically unfavourable for methyl species to form on the framework away from the zeolite acid site, and both kinetically and thermodynamically unfavourable for methyl groups to migrate through the framework and aggregate around an acid site. Formation of carbene moieties was considered as an alternative pathway to the formation of C–C bonds; however, the reaction energy for conversion of a methyl to a carbene is unfavourable. Metadynamics simulations help confirm further that methyl species at the framework acid sites would be more reactive towards formed C2+ species, rather than inter-framework migration, and that the role of carbenes in the formation of the first C–C bond will be via a concerted type of mechanism rather than stepwise.
1. Introduction
Reducing the dependence of society on fossil fuel is a priority in current research in chemical sciences, with alternative carbon sources, such as biomass, projected to be significant in achieving the sustainable, environmentally-friendly production of fuels and fine chemicals.1–3 Methanol is a key platform chemical that can be produced from biomass-derived syngas and subsequently converted to a wide range of useful hydrocarbons using zeolite catalysts.4–6 The methanol-to-hydrocarbons (MTH) process is a promising technology for the conversion of methanol to fuel and light olefins, and is now used on industrial scale;3,7 however, controlling the product selectivity and catalyst deactivation remains a challenge.3,7,8 In order to address these challenges, the catalytic mechanism must be understood. The MTH process is known to have an induction period that is characterized by the low reactivity of methanol until certain “hydrocarbon pool” (HP) species are formed, which themselves act as a co-catalyst to produce C–C species,8–10 but even the initial steps during the induction period remain unclear.
Several mechanisms have been proposed for the formation of the first C–C bond, which involve stable compounds (dimethyl ether, methane, formaldehyde) or short life-time intermediates (trimethyl oxonium, carbene). Formaldehyde and methane are present in the reaction mixture and thus have been considered as reaction intermediates when forming the first C–C bond, particularly in the case of ethanol formation, but a very high reaction barrier (183 kJ mol−1) was calculated which led to the discounting of any mechanism involving these intermediates.6 The more favourable oxonium ylide mechanism starts with the formation of trimethyl oxonium (TMO) via the reaction of dimethyl ether with a dimethyl oxonium ion (protonated dimethyl ether); subsequently, TMO is deprotonated by a basic site to form dimethyl oxonium methyl ylide (DOMY), as shown in Scheme 1A, that can undergo a Stevens rearrangement to form methylethyl ether, shown in Scheme 1B, or an intermolecular methylation (Scheme 1C), resulting in the formation of ethylmethyl oxonium ion; however, the inability of the zeolite framework to deprotonate the TMO and stabilise the DOMY made this routes seem unfeasible.11–13
 |
| | Scheme 1 Illustration of oxonium ylide mechanism via TMO to ethene. | |
Another proposed mechanism involves a concerted process whereby abstraction of a hydrogen, from the methyl group of a methanol or DME molecule, by a basic zeolite oxygen, would allow a C–C bond formation with another methanol, DME, trimethyloxonium or zeolite bound methoxy group.11 Computational ONIOM techniques concluded that the energy barrier or the breaking of the covalent C–H bond by the available basic site is considerable (>200 kJ mol−1), which makes this mechanism seem energetically unlikely.6,14 Several other studies15,16 report that pure methylated zeolite and SAPO frameworks (CH3-ZSM-5, CH3-Y, CH3-SAPO-34) have the potential to form a wide range of hydrocarbons (paraffins, olefins, aromatics) once heated over 573 K. Recent studies,17 employing synchrotron based IR techniques, suggested strongly that carbene (:CH2) moieties form from methyl groups, via the deprotonation of a zeolite bound methoxy, followed by either polymerisation to olefins or insertion in to a methanol or DME.11 Theoretical calculations14,18 confirmed that the direct activation energy for carbene formation from methoxy is high (245;14 326 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18), whilst experimental H/D exchange studies showed that C-D bond breaking occurs in H-ZSM-5
18), whilst experimental H/D exchange studies showed that C-D bond breaking occurs in H-ZSM-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 but not in H-SAPO-34,19 which does not completely rule out C–H bond cleavage but rather indicates a limited C–C interaction. Experimental studies involving CH2N2 also showed that the presence of H-ZSM-5 enhances the conversion of CH2N2 to ethene, further indicating that carbene could stabilise in H-ZSM-5.20,21
17 but not in H-SAPO-34,19 which does not completely rule out C–H bond cleavage but rather indicates a limited C–C interaction. Experimental studies involving CH2N2 also showed that the presence of H-ZSM-5 enhances the conversion of CH2N2 to ethene, further indicating that carbene could stabilise in H-ZSM-5.20,21
These current observations provoke several important questions regarding the reaction mechanisms, especially with consideration of the reactivity of H-ZSM-5. A first question concerns the mobility of C1 species within zeolites; any given acid can only convert one methanol, but the framework-bound moieties have to be in the vicinity of each other to react and form higher order hydrocarbons. In this study, we have used computational modelling to examine two potential routes for C1 (methyl or carbene) mobility: (i) the methylation of an Si–O–Si basic site, followed by migration towards a methylated Al–O–Si site; and (ii) the direct migration of a methyl group away from the Al–O–Si active site to a second methylated active site. A second question concerns the conditions that may lead to carbene formation; to address this challenge, we have developed mechanistic models for stable carbene formation and migration on the zeolite framework, which is discussed following the summary of the computational methods employed.
2. Methodology
2.1. QM/MM Model description
The hybrid quantum mechanical/molecular mechanical (QM/MM) approach, available in the Chemshell package,22 is used to calculate energetics, having been used previously in modelling studies that investigated mechanistic processes for catalysis in zeolites.23,24 The approach ensures the correct long-range electrostatics for the active site of interest, whilst also removing the periodic boundary conditions that can hinder charge non-neutral models and/or high-level calculations of large unit cell systems, such as zeolites. Spherical embedded-cluster models of H-ZSM-5 were created from the experimental unit cell of siliceous MFI.25 The embedded-cluster models were centred on a Si tetrahedral (T-)site of interest; MFI has 12 symmetry inequivalent T-sites, and we considered the Al substituent in the T12 position, so as to be at the intersection site of the sinusoidal and straight channels in MFI. The Al positions are difficult to characterise in experiment, and so their positioning in simulations introduces an aspect of selective bias, but some Al positions are commonly assumed more favourable than others, with the T12 site often reported to be substituted.26 Where Al was substituted into the silicate framework, a charge-compensating hydrogen atom is added on an adjacent oxygen in the O26 position, in between two T12 sites, which is referenced as OAl throughout the manuscript; also considered was an OAl* site, where the H was added on the O8 position, between a T12 and a T3 site, with notations as per IZA database.77 In all cases, the Brønsted proton is directed towards the centre of the supercage as this configuration has the highest deprotonation energy,27i.e. most stable, and thus is assumed to be predominant.
The embedded-cluster models are partitioned with a central QM region, which is the chemically active part of our model, and an encapsulating outer MM region, where long-range structural and electrostatic effects are present to ensure correct bulk representation for the high-accuracy QM calculations. All QM atoms were unconstrained during geometry optimisation, whereas two concentric domains were employed in the MM region: an inner MM region where unconstrained atoms can move during a geometry optimisation; and an outer MM region that is frozen to ensure a bulk-like long-range structure, as shown in Fig. S1 of ESI.† In our calculations, the inner and outer MM regions extend from the central T-site to a radius of 10.58 Å (20 a0) and 21.17 Å (40 a0), respectively, and the QM region used herein includes atoms up to the fifth nearest neighbour (the third oxygen atom) from the central T-site. In its entirety, the total number of atoms in the cluster model of the active site is 2165, with 74 QM atoms and 197 inner MM atoms. During QM calculations, the terminal oxygen atoms at the edge of the QM region are saturated with hydrogen atoms: these artificial “link” atoms ensure correct electronic structure for the terminal atoms and do not inadvertently affect the electronic solution of the overall QM calculations, as a bond-dipole correction is added at the boundary to ensure an accurate electrostatic embedding potential.28
Throughout, the QM energy has been calculated using hybrid-DFT with the dispersion corrected Becke 97-3 exchange–correlation (XC) functional, commonly referred to as B97-D,29,30 as provided in the GAMESS-UK code.31 The atomic orbitals are represented using the Ahlrichs and Taylor TZVP Gaussian basis sets.32 The self-consistent field (SCF) convergence criteria was set to an energy change of less than 2.72 × 10−6 eV (1 × 10−7 Hartrees) between SCF iterations.33,34 The MM energy was calculated using DL_POLY,35 employing the forcefield of Hill and Sauer,36,37 with the coordination dependent charges in the original forcefield replaced with fixed point charges of 1.2 and −0.6 e for silicon and oxygen, respectively, as parameterised in the work of Sherwood et al.28 As we have a neutrally charged system, we employed Restricted Hartree–Fock (RHF) conditions in our simulations, corresponding to all spins being paired and overall singlet spin multiplicity.
Geometry optimizations were performed using the ChemShell package,22 in a Cartesian coordinate space, using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm. Structural convergence was deemed complete when the maximum gradient of atoms in the active QM and MM regions was below 0.015 eV Å−1.38–41 Vibrational frequencies were calculated with a task-farmed finite-difference approach,31 allowing us to confirm that geometries correspond to local minima.42,43 The geometrically optimised models were then used to calculate the individual atomic charges using a Mulliken analysis.44 The transition state energies were determined by employing the Nudged Elastic Band (NEB) method,45 in the task-farmed mode, with the reaction path represented by 5 images. For the NEB calculations, only the adsorbate and framework atoms up to the second nearest neighbour framework were free to move, as otherwise a prohibitively large computational cost is encountered; comparison of this approximation against displacement of all atoms in the QM region shows a small difference in the transition state energies (<10 kJ mol−1), which we consider as the error bar going forward. When comparing the energetics involved in the conversion of methanol to methoxy, two models were employed: one where methanol was adsorbed on the T12 site, with methyl pointing towards the active site, and a second with methyl pointing away from the active site. In the case of methanol adsorbed with methyl oriented away from the Al central T-site, the model was reconstructed to maintain the same configuration but with the Al placed at the T11 site, next to the T12 site, i.e. the methanol remained central to the embedded-cluster. This adjustment ensured the optimised methanol had exactly an equivalent QM region and electrostatics. A similar approach was taken for modelling the product state, which consists of methyl and water.
The energy of the deprotonated zeolite is corrected by the addition of the Jost correction,46,47 which accounts for the truncation of the MM polarisation at the end of the first (flexible) MM region. Deprotonation leaves a charge in the QM region of the simulation model (−1), the electrostatic effects of which would be expected to be relatively long-ranging; however, our model prevents polarisation of atoms in the fixed MM region. The Jost correction provides a good estimate of the polarisation energy and is given by:
| |  | (1) |
where
Q is the defect charge,
R is the radius of the total cluster and
ε is the dielectric constant of the material, all in atomic units. The dielectric constant for MFI is taken in this work as 3.38, calculated using classical shell model methods.
48
2.2. Energy analysis
The adsorption energy (Eads) of a sorbate to the zeolite framework is calculated as:| | | Eads = E[ZeOH + Sorbate] − E[ZeOH] − E[Sorbate] | (2) |
where, E[ZeOH], E[Sorbate] and E[ZeOH + Sorbate] are the total energy of the zeolite sorbent, the gas-phase sorbate and the combined guest–host system, respectively, each in their optimised geometry. Due to our use of an atom-centred basis set, it is necessary to include a basis-set-superposition-error (BSSE) for the combined system, which is calculated thus:49| | | EBSSE = (E[ZeOHads + Basis(Sorbateads)] − E[ZeOHads]) + (E[Sorbateads + Basis(ZeOHads)] − E[Sorbateads]) | (3) |
where the term in the first parentheses gives the BSSE (EBSSE) for the framework when including the sorbate orbitals, and the second parentheses gives the EBSSE for the sorbate in the presence of the zeolite orbitals. Thus, in both parts the BSSE is calculated as the difference in energy of the system components (ZeOH and Sorbate) in an adsorbed geometry (denoted with ads), with and without the basis functions (denoted as “Basis”) for the second component of the complete system. e.g. E(ZeOH) is calculated with and without the basis functions of the sorbate present.27EBSSE is included in all energies reported; generally, the error is ≤5 kJ mol−1 for a single adsorbed CH3OH.
In addition to the methylation reaction (Er) and activation (Eact) energies reported here, three other thermodynamic energies are used. First the reaction energy for methyl or carbene to migrate from one bonding oxygen site (OA) to another (OB) is denoted as Emig,
with
EOB and
EOA representing the absolute energies of the methyl bonded to the zeolite framework on Lewis basic sites O
B and O
A, respectively. Secondly, the bonding energy of methyl or carbene to the oxygen bonding site of the zeolite framework is denoted as
Ebond, and is calculated as:
| | | Ebond = EC1-Zeo − EC1 − EZeo- | (5) |
with
EC1-Zeo,
EC1, and
EZeo- representing the absolute energies of the methyl or carbene bonded to the zeolite framework, the gas phase methyl (CH
3+) or carbene (CH
2:) fragments, and the energy of deprotonated zeolite models, respectively. Thirdly, we calculate the carbene formation energy as:
| | | Eformation = ECH2–H − ECH3 | (6) |
with
ECH2–H and
ECH3 representing the absolute energies of the carbene bonded to the protonated zeolite framework model, and methyl bonded to the zeolite framework, respectively.
2.3. Metadynamics simulations
To accelerate the sampling of the carbene/methoxy migration, the metadynamics (MTD) approach was employed.50–52 Dynamic simulations provide a closer replica of the experimental conditions that lead to methoxy conversion to hydrocarbons in experiment. Although the first hydrocarbons are detected after heating at 523 K,16 the simulated temperature was set to 623 K to ensure no heat transfer effects influenced the reactivity. Ab initio molecular dynamics (MD) and metadynamical simulations were performed on the combined system, using 3-dimensional periodic boundary conditions, with the CP2K simulation package (version 6.1).53 The dynamics of the nuclei were governed by the Newtonian equations of motion, in which the potential from the Born–Oppenheimer electronic ground state is inserted. The self-consistent field (SCF) energy was evaluated with DFT using the revPBE functional54 with Grimme D3 dispersion corrections55 and the Gaussian Plane Waves method56 that uses Gaussians as basis sets (DZVP–GTH57) and planewaves (320 Ry cut-off) as an auxiliary basis. The SCF convergence criterion was set to an energy change of less than 1 × 10−5 Hartrees between SCF iterations. In both NPT “production runs” and the NVT metadynamics simulations, the integration time step was set to 0.5 fs. The initial geometry for the NVT metadynamics simulations was taken as the final snapshot of the NPT calibration models, themselves performed on empty zeolite models, with methoxy and carbene inserted into the zeolite pores. The cell parameters, presented in Table S1 of ESI,† were determined from a preliminary isothermal–isobaric (NPT) ensemble simulation of 50 ps on the zeolite cells containing methoxy or carbene, where the number of atoms, temperature (623 K) and external pressure (1 atm) are controlled by a chain of five Nosé–Hoover thermostats58,59 and pressure by the Martina–Tobias–Klein barostat.60
In order to describe the Free Energy Surface (FES) of the methylation pathway, particular parameters were employed that previously gave accurate results for similar MTD simulations of methylation in H-ZSM-5.61–63 Specifically, during the NVT MTD run, two geometric parameters selected to uniquely describe each reaction state, also named collective variables (CVs), were defined by coordination numbers (CN):61
| | 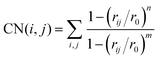 | (7) |
in which
rij is the distance between bonded atoms
i and
j. The parameters
n and
m were set to 6 and 12, respectively. The reference distance,
r0, was chosen to be similar to the transition state distance between atoms
i and
j (2.0 Å). The biased CV is a combination of two CVs, calculated as (CV2–CV1), which permits faster computation without compromising accuracy. The (CV2–CV1) collective variable was biased by adding Gaussian hills every 25 fs. For the methoxy migration case, CV1 is defined by CN(C
Me, O
Z1), which describes the breaking of the C–O bond of the zeolite bound methyl; CV2 is then defined by CN(C
Me, O
Z2) to describe the subsequent formation of the C–O bond between the product methyl moiety and the bonding site external of the zeolite active site. As will be further discussed, carbene bonds with O and Al/Si, so CV1 is defined by CN(C
CH2–O
Z1, Al), which describes the breaking of the C–O and C–Al bonds of the zeolite bound carbene; CV2 is then defined by CN(C
CH2–O
Z2, Si) to describe carbene migration from the active site to the Si–O site. The definition of the collective variables is illustrated schematically in Fig. S2 (ESI
†).
For methyl migration, the width of the Gaussian hills is set to 0.02, and the height is initially 5.0 kJ mol−1. Once the transition state has been identified and crossed twice, the height of the Gaussian hills is halved, which allows more accurate sampling of the activation barrier; this process is repeated until a final hill height of 0.65 kJ mol−1 is used, thus ensuring a refined representation of the energy surface. The metadynamics simulations were deemed complete when a change in the free energy barrier was equal or less than 5 kJ mol−1 between every 500 energy hills added, with the reported errors determined from the minimum and maximum barriers calculated at this point.
During initial MTD simulations, carbene commonly diffused away from the active site to the centre of the pore, or reacted with a neighbouring oxygen to form formaldehyde, and thus the sampling process was limited to Gaussian hills of 1.25 kJ mol−1 height and 0.02 width throughout, with the activation barrier being crossed once only. In addition, to ensure sampling of chemically relevant space with the MTD simulations, restrictions were applied to prevent the carbene from migrating to adjacent oxygen sites connected to Al. In particular, a series of single-sided energy “walls” were applied that extend from the barrier (B) towards larger values of the collective variable (CV3), represented by a quadratic potential k(CV-B)2, with k being a quadratic potential constant. The barrier is applied at CN(CCH2, OAl) = 0.036 (k = 100 Ha), which corresponds to a bond distance of 2 Å. The FES of the reaction was reconstructed from a MTD calculation based on the sum of the spawned Gaussian hills; the free energies of reaction were then calculated as the difference between the lowest energy of the reactant state and the highest of the transition stage. Further details on the methodology and case studies are provided in previous studies.61,64,65
The metadynamics observables, specifically, free energy activation barriers for the forward (ΔFforward) and reverse (ΔFreverse) reactions are determined as:
| | | ΔFforward = FTS − Freactant | (8) |
| | | ΔFreverse = Fproduct − FTS | (9) |
with
FTS,
Freactant and
Fproduct represent the highest energy of the transition state, and lowest energies of the reactant and products states, respectively, on the MTD mapped free energy surface.
3. Results
3.1. Methyl formation and migration
Experimental IR and neutron spectroscopic evidence66–71 suggest that methanol insertion in the zeolite catalyst and adsorption on the Brønsted acid site can lead to the disappearance of the zeolite O–H stretch vibrational band, and the appearance of the bands specific to the zeolite bound methyl group and water. This series of events is widely accepted as being properly described by the nucleophilic substitution framework methoxylation mechanism. Specifically, once multiple methanol molecules adsorb on the acid site, it is proposed23,64,72–74 that the Brønsted proton is spontaneously abstracted by the methanol oxygen, forming a methoxonium molecule (CH3OH2+) or protonated cluster of methanol molecules and a negatively charged zeolite oxygen that acts as a Lewis basic site. Nucleophilic attack of the latter on the methyl group leads to the formation of water and a methylated framework oxygen on the oxygen neighbouring the Al site.
The mobility of methoxylated species is initially investigated considering the association of methanol, and the subsequent methoxylation reaction at an oxygen site coordinated to an Al site (OAl), compared with the association of methanol at an oxygen atom with two silicon atom neighbours (OSi), as shown in Fig. 1.
 |
| | Fig. 1 Active site models, with methyl moiety of methanol oriented towards aluminium (left) and towards silicon (right); and geometric assignment, with Al, Si, O, C and H atoms represented as purple, yellow, red, green, and white. Methoxy bonding sites are denoted as OAl and OSi; Si and Si* are also represented, as referenced in the structural analysis. Optimised bond lengths, marked with dashed lines, are given in Ångstroms. | |
Initially, methanol was adsorbed on the Brønsted acid site with the methyl group oriented either towards the active site, centred on the Al T-site (Fig. 1, left), for the methyl to transfer on to OAl, and away from the active site, centred on the Si T-site (Fig. 1, right), for a methyl transfer on OSi. The optimised structures are similar for the two configurations, with the distances from the zeolite framework to the Brønsted proton and to the methanol molecule being very similar, as well as the Mulliken charge distribution (Table 1); furthermore, the methanol adsorption energies are similar (−120 and −126 kJ mol−1, respectively, Table 1). Previous work23 suggested that the methyl groups do not contribute substantially to the overall adsorption energy of methanol to the framework, with most of the energy attributable to the hydrogen bonding through the hydroxyl group, which the current results support.
Table 1 Summary of results for methanol adsorbed on active sites with methyl oriented towards aluminium (CH3OH·OAl) and silicon (CH3OH·OSi) centres, as shown in Fig. 1, alongside methoxy formation on oxygen closest to aluminium (CH3·H2O·OAl) and silicon (CH3·H2O·OSi). Adsorption energies (Eads), reaction energies (Er) and activation energies (Eact) are given in kJ mol−1; geometric distances (d) and Mulliken charge (q) data are presented in Ångstroms and electronic charge (e), respectively. Further structural and electronic data is provided in Table S2 of the ESI
|
|
E
ads
|
E
r
|
E
act
|
| CH3OH·OAl |
−120 |
49 |
225 |
| CH3OH·OSi |
−126 |
118 |
748 |
|
d (Å) |
OMeOH–HZeO |
OZeO–HZeO |
C–OZeo |
C–OH2O |
| CH3OH·OAl |
1.50 |
1.03 |
— |
— |
| CH3OH·OSi |
1.48 |
1.03 |
|
— |
| CH3·H2O·OAl |
— |
— |
1.48 |
3.14 |
| CH3·H2O·OSi |
— |
— |
1.51 |
3.05 |
|
d (Å) |
OAl |
OSi |
OMeOH |
C |
| CH3OH·OAl |
−0.61 |
— |
−0.53 |
−0.25 |
| CH3OH·OSi |
— |
−0.61 |
−0.52 |
−0.24 |
| CH3·H2O·OAl |
−0.53 |
— |
— |
|
| CH3·H2O·OSi |
— |
−0.49 |
— |
— |
The activation energy for methylating an Al–O–Si site was considered via the mechanism illustrated in Fig. 2, and is calculated to be 225 kJ mol−1, with an overall reaction energy of 49 kJ mol−1. The activation energy is three times higher to methylate a OSi site, i.e. Si–O–Si, with an energy barrier of 748 kJ mol−1 and an overall reaction energy of 118 kJ mol−1 (Table 1). These results make the direct methylation of an oxygen atom away from the Al site both thermodynamically and kinetically infeasible.
 |
| | Fig. 2 Methoxylation reaction path, with the colour scheme the same as Fig. 1. The Brønsted proton is highlighted in blue for clarity. | |
The methylation path (Fig. 2) requires a Brønsted proton to transfer completely from the zeolite active site to the methanol before the dissociation of the CMeOH-OMeOH bond and the formation of water. With the methanol adsorption energies and structures similar for both adsorption configurations considered, one expects the energy to remove the Brønsted proton from the active site to the methanol, in both cases, to be similar in magnitude; thus it may seem surprising that the energy barriers differ so significantly. The initial step of the methylation path, which is the deprotonation of the zeolite, appears not to contribute substantially to the difference in activation barrier between the two cases (which we refer to as methylation “inside” and “outside” of the active site when at the OAl and OSi sites, respectively); therefore, the significant difference in activation energy is due to energetic instability of the methyl fragment when “outside” the environment of the Al, i.e. at an oxygen atom surrounded by silicon, OSi, as opposed to “inside” the environment (i.e. neighbouring) of the aluminium, i.e. OAl. We note, however, that the difference in activation barriers (523 kJ mol−1) is much greater than the stability of the methylated products (69 kJ mol−1), and therefore a more detailed investigation follows in the next section.
3.2. Methyl migration away from the active site
Here we consider the energetics of methyl migration both for isolated methyl groups and for multiple methyl groups at an active site.
3.2.1. Isolated methyl migration.
The energetics associated with the framework-adsorbed methoxy group migrating away from the active site, specifically from OAl to OSi, have been analysed. The bonding sites are presented in Fig. 3.
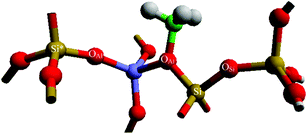 |
| | Fig. 3 Methoxy bonding mode, with colour scheme and labels the same as Fig. 1. OAl and OAl* are highlighted as two possible Al-neighbouring O sites “inside” the active site. | |
The methyl group bonds strongest to the zeolite framework through the C-OAl interaction (Ebond = −635 kJ mol−1) with C–OSi being a slightly weaker interaction (Ebond = −510 kJ mol−1). The reaction energy for methyl transfer (Emig) from OAl to OSi, which is calculated as described in eqn (4), is 126 kJ mol−1. Analysis of the atomic charges and bond lengths for the framework surrounding the methyl moiety are provided in Table 2 (and in more detail in Table S3 of the ESI†). The main structural differences that determine the endothermic reaction energy are over the first nearest neighbours of the methyl group, since the remaining extended structure (to the third nearest neighbour) was similar in both cases. Analysis of the OAl and of OSi methyl bonded models shows that the C–OSi bond is slightly longer (1.52 Å) than the C–OAl distance of 1.48 Å. In addition, the charge on OSi (−0.45 e) is less than on OAl (−0.51 e), when each are bonded to the methyl, showing a reduced charge transfer between the methyl group and the Lewis basic site of the zeolite when the oxygen bonding site is surrounded by Si atoms; thus confirming the methyl is best stabilised adjacent to the Al T-site.
Table 2 Summary of results for methyl (CH3) group bonded on OSi, OAl, and OAl* sites, with migration energy (Emig) for migration from OAl to OSi and from OAl to OAl* as illustrated in Fig. 3 and bonding energy (Ebond), given in kJ mol−1, calculated using equations 4 and 5, respectively, from Section 2.2. Geometric and charge observations are presented in Ångstroms and electronic charge (e), respectively. The methyl bonding sites are highlighted in bold in the charge analysis to aid interpretation
|
|
E
bond
|
E
mig
|
| CH3·OSi |
−510 |
126 |
| CH3·OAl |
−635 |
|
| CH3·OAl* |
−621 |
14 |
|
d (Å) |
OZeo–C |
| CH3·OSi |
1.52 |
| CH3·OAl |
1.47 |
| CH3·OAl* |
1.48 |
|
q (e) |
OSi |
OAl |
OAl* |
C |
| CH3·OSi |
−0.45
|
−0.59 |
−0.59 |
−0.22 |
| CH3·OAl |
−0.50 |
−0.51
|
−0.56 |
−0.25 |
| CH3·OAl* |
−0.49 |
−0.59 |
−0.53
|
−0.30 |
To clarify further the factors influencing the stability of methyl at different framework positions, the energy of transferring a methyl from the OAl site to the most basic other site available, OAl*, was calculated. The methyl bonding energy calculated for OAl* (Ebond = −621 kJ mol−1) is marginally weaker than on OAl (Ebond = −635 kJ mol−1), with the C–OAl* bond of 1.48 Å similar in length to the C–OAl distance (1.47 Å). The reaction energy is much lower (14 kJ mol−1) compared with that for transferring from OAl to OSi (126 kJ mol−1), again illustrating that the methyl group is more stable on the Lewis basic sites that neighbour Al T-sites. In contrast, a more negative charge is present on the methyl carbon when bonded to OAl* (−0.30 e) than when bonded to OAl (−0.25 e), which may contribute to the reduced stability of the methoxy at the OAl* Lewis site.
3.2.2. Neighbouring methyl migration.
To understand how multiple methyl groups might interact, simulations were considered with two methyl groups on the same active site (Fig. 4). The bonding energies of the second methyl groups are ∼250 kJ mol−1 smaller per methyl added (i.e. less strongly bound) than when there is just a single methyl group, highlighting the relative instability of having two methyls in close vicinity. The addition of a methyl moiety at the active site led to a lower energy (81 kJ mol−1) of methyl transfer away from the active site, i.e. “inside” to “outside”, compared to the calculations for an isolated methyl (126 kJ mol−1). This result is mainly attributable to the structural differences of the methyl active site of the single and double methyl models, given in Table 3; specifically, the CAl–OAl bond is slightly longer in the double methyl model, by 0.02 Å, which is due to charge-related electrostatic effects. The higher positive charge on aluminium in the double methyl case (1.07 e) compared to the single methyl case (0.94 e), shows that the addition of a second methyl draws more electronic density from aluminium to the neighbouring oxygen, further lengthening the C–O bonds, as highlighted in Table 3, with further details in the ESI† in Table S4.
 |
| | Fig. 4 Models with an additional second methyl bonded on OAl (left) and OSi (right), alongside a methyl on the OAl* site. The colour scheme is as per Fig. 1. | |
Table 3 Summary of results when two methyl (CH3) groups are bonded on OAl* and OAl (2CH3·OAl) and on OAl* and OSi (2CH3·OSi) sites as illustrated in Fig. 3, with bonding energy (Ebond), and migration energy (Emig) from OSi to OAl, given in kJ mol−1. Geometric and charge observables are presented in Ångstroms and electronic charge (e), respectively. The methyl bonding sites are highlighted in bold
|
|
E
bond
|
E
mig
|
| 2CH3·OSi |
−277 |
81 |
| 2CH3·OAl |
−358 |
— |
|
d (Å) |
OSi–C |
OAl–C |
OAl*–C |
| 2CH3·OSi |
1.52 |
— |
1.48 |
| 2CH3·OAl |
— |
1.49 |
1.49 |
|
q (e) |
OSi |
OAl |
OAl* |
CSi |
CAl |
CAl* |
| 2CH3·OSi |
−0.45
|
−0.60 |
−0.59
|
−0.20 |
— |
−0.29 |
| 2CH3·OAl |
−0.49 |
−0.54
|
−0.55
|
— |
−0.34 |
−0.30 |
The overall conclusion of our analysis is that thermodynamic factors will strongly inhibit the formation of isolated methyl groups at sites other than those surrounding the aluminium active site (i.e. OAl and OAl*), and, as a consequence, migration of methyl groups is unlikely to be prominent in the mechanism for C–C bond formation. Our focus therefore changes to the potential role of carbene species.
3.3. Carbene migration
3.3.1. Carbene bonded on aluminium active site.
Though carbene species have been proposed in experimental studies,17 earlier theoretical studies14,18 showed that the direct formation of carbene from methyl is highly energetically demanding (245;14 326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 kJ mol−1). In order to determine the conditions that could lead to carbene formation from methyl species, and to understand the possible role of carbenes in the production of hydrocarbons, several new models were analysed as illustrated in Fig. 5 and 6.
18 kJ mol−1). In order to determine the conditions that could lead to carbene formation from methyl species, and to understand the possible role of carbenes in the production of hydrocarbons, several new models were analysed as illustrated in Fig. 5 and 6.
 |
| | Fig. 5 Illustrations of reactions considered for methyl bonded on OAl when converted to hydrogen and a carbene bonded between OAl and Al (top) and OAl and Si (bottom). | |
 |
| | Fig. 6 Carbene migration from an Al-coordinated site (A) to an Si-coordinated site (B). The key is as per Fig. 1. | |
The calculated endothermic reaction energies of carbene formation, reported in Table 4, arise mainly from the difficulty of stabilising the carbene fragment on the zeolite framework in a configuration preventing the spontaneous conversion back to methyl (Fig. 5), which was also a challenge reported in other investigations.18 The carbene stabilises between the framework cation and oxygen, bonding to both atoms, in both models considered; the bond distances are: d(Al–C) = 1.95 Å; d(C–OAl) = 1.54 Å (Fig. 6A); and d(Si–C) = 1.89 Å, d(C–OAl) = 1.55 Å (Fig. 6B). The carbene bonding energy is −174 kJ mol−1 for the carbene bonded closer to Al, illustrated in Fig. 6A, and −141 kJ mol−1 for carbene bonded towards Si (Fig. 6B); these bonding energies are substantially weaker than the methyl bonding discussed in Section 3.2 (from −510 to −635 kJ mol−1).
Table 4 Summary of results for a carbene (CH2) moiety bonded in the proximity of Al and Si, and also bonded in the proximity of Si and Si*, with reaction energy (Er), migration energy from Si to Al (Emig), and bonding energy (Ebond) given in kJ mol−1, with geometric and charge data presented in Ångstroms and electronic charge (e), respectively. The specific bonding sites are highlighted in bold and illustrated in Fig. 6. A further detailed geometric and electronic set of observables is provided in Table S5 of ESI
|
|
E
r
|
E
bond
|
E
mig
|
| H·CH2·Si |
317 |
−141 |
34 |
| H·CH2·Al |
283 |
−174 |
|
|
d (Å) |
Al–C |
OAl–C |
Al–OAl |
OAl–Si |
| H·CH2·Si |
1.89 |
1.55 |
1.75 |
1.76 |
| H·CH2·Al |
1.95 |
1.54 |
1.94 |
1.63 |
|
q (e) |
OSi |
OAl |
OAl* |
C |
| H·CH2·Si |
−0.49 |
−0.53
|
−0.53 |
−0.48 |
| H·CH2·Al |
−0.46 |
−0.45
|
−0.45 |
−0.56 |
To determine the influence of the Brønsted proton on the strength of the carbene bond to the zeolite, the two models were optimised without the Brønsted proton present (i.e. for the carbene in isolation). The strength of the carbene-framework bond is calculated to be 20 kJ mol−1 weaker in the absence of the proton from the active site, showing how it aids stability. The carbene bonding energy is noted as exothermic throughout, which ensures the carbene remains stable on the zeolite framework; the energy for carbene migration (34 kJ mol−1) is also significantly less than for the methyl group in Section 3.1, due to the weaker interaction of the carbene with the zeolite framework, leading us to conclude that carbenes are potentially mobile in the zeolite.
3.3.2. Carbene bonded on silicon active site.
Although there is no experimental evidence for the position that carbene might occupy, for completeness, the formation of carbene from a methyl “outside” the active site, i.e. on a Si–O–Si site, was investigated (Fig. 7).
 |
| | Fig. 7 Carbene formation reactions from an OSi bonded methyl, leading to a framework integrated CH2 and Brønsted proton (top) or a framework bonded CH2 and silanol (bottom). | |
For these configurations, the carbene stabilises either “outside” the aluminium active site, or inserts itself in the Si–O bond (Fig. 7 and 8). Whilst the reaction energies are calculated to be endothermic, they are lower than for carbene coordinated “inside” the aluminium active site (Table 5). The carbene is most stable when bonded within the zeolite framework (Fig. 8A), with a reaction energy of 103 kJ mol−1, as opposed to when carbene is positioned outside the lattice (Fig. 8B), with a formation energy of 239 kJ mol−1 (Table 5) similar to previous investigations (245 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14). Since there is no charge neutralisation involved, the positioning of the carbene within the zeolite framework may be a consequence of the framework flexibility. Overall, whilst comparison of the carbene stabilised within the silicate structure (Fig. 8A) with that of carbene being placed closer to the active site (Fig. 8B) shows significant structural and energetic differences, the results are all considerably endothermic, which confirms that neither the Al–O–Si or the Si–O–Si coordination-sites enhance the stability of the carbene moiety.
14). Since there is no charge neutralisation involved, the positioning of the carbene within the zeolite framework may be a consequence of the framework flexibility. Overall, whilst comparison of the carbene stabilised within the silicate structure (Fig. 8A) with that of carbene being placed closer to the active site (Fig. 8B) shows significant structural and energetic differences, the results are all considerably endothermic, which confirms that neither the Al–O–Si or the Si–O–Si coordination-sites enhance the stability of the carbene moiety.
 |
| | Fig. 8 Models of carbene moiety bonded on the OSi site, in the proximity of Si (A) and Si* (B), with a key as per Fig. 1. | |
Table 5 Summary of results for a carbene (CH2) moiety formed from the methyl conversion on OSi, bonded in the proximity of Si and Si* as illustrated in Fig. 8, with reaction energies given in kJ mol−1. Geometric and charge data are presented in Ångstroms and electronic charge (e), respectively. For completeness, a further detailed geometric and electronic set of observables is provided in Table S6 of ESI
|
|
E
r
|
| H·CH2·Si |
103 |
| H·CH2·Si* |
239 |
|
d (Å) |
Si–C |
OSi–C |
Al–OAl |
OAl–Si |
| H·CH2·Si |
1.86 |
1.42 |
1.88 |
1.70 |
| H·CH2·Si* |
1.82 |
1.50 |
1.75 |
1.56 |
|
q (e) |
OSi |
OAl |
C |
| H·CH2·Si |
−0.36
|
−0.64 |
−0.39 |
| H·CH2·Si* |
−0.39
|
−0.56 |
−0.41 |
Previous EPR analysis shows that triplet state species could be present in the “hydrocarbon pool”.11 Thus, the conversion of methoxy to triplet state carbene was also analysed, which led to the determination of a considerably greater carbene reaction energy (526 kJ mol−1) than the singlet state carbene (283 kJ mol−1). As with the formation energies, the triplet carbene migration energy is almost double (79 kJ mol−1) that of the singlet state (34 kJ mol−1), which leads to the conclusion that the triplet carbene species is unlikely to play a role in the C–C formation mechanism.
3.3.3. Metadynamics simulations of free energy barriers for C1 species migration.
Since the migration energy for the singlet state carbene (34 kJ mol−1) was relatively small, metadynamics simulations were carried out, as detailed in Section 2.4, in order to determine the free energy barriers for translation inside the zeolite framework. For completeness, the methyl migration energy was investigated as well with the same procedure, even though the calculated migration energy from the potential energy surface was considerably large (126 kJ mol−1). The free energies of activation obtained for carbene migration (ΔFforward = 212 kJ mol−1; ΔFreverse = −125 kJ mol−1) from the unprotonated active site is considerably smaller than methyl migration (ΔFforward = 357 kJ mol−1; ΔFreverse = −281 kJ mol−1), although still very energetically demanding. By comparing our results to previous studies56 using a similar technical setup to analyse methyl transfer from the active site to olefins, we find that methyl transferring from the active site to ethene (ΔFforward = 123 kJ mol−1), propene (ΔFforward = 112 kJ mol−1) or trans-2-butene (ΔFforward = 108 kJ mol−1),61 is more favourable than framework migration, indicating that, in the presence of the hydrocarbon pool, methyl is unlikely to translate but rather to transfer to olefins. Previous studies proposed ethoxyde as an intermediate,75,76 which could be formed here via a carbene insertion to methoxide, as shown in Fig. 9; however, this reaction route would involve carbene migration, which we have shown to be energetically unfavourable, and thus the formation of ethoxyde via such a carbene/methoxide reaction may be problematic.
 |
| | Fig. 9 Suggested reaction mechanism involving C1 species, specifically, carbene insertion to methoxy forming ethoxyde decomposing to ethene. | |
4. Summary and conclusions
The migration and reaction of C1 species around an active site within the H-ZSM-5 framework was considered by modelling of distinct reaction pathways with accurate QM/MM techniques. The formation of methoxy groups away from the active site is shown to be both kinetically and energetically demanding, leading us to conclude that these species are not present in significant concentrations under reaction conditions in the MTH process. Based on the methanol adsorption energy, we conclude that the rate determining step for methoxylation is the methyl transfer to the active site, rather than the Brønsted proton transfer to methanol. The results suggest that methyl migration would be unlikely within the zeolite; however, due to the small differences in the basicity of the oxygen atoms surrounding the active site needed to stabilise methyl, it could be speculated that a zeolite substituted with gallium or indium may enhance the chances of the methyl forming beyond the active site, due to the higher negative charge present on the adjacent sites.
The direct formation of carbene from methyl is also calculated with our QM/MM techniques, but is also highly energetically demanding; however, due to the strong bonding within the zeolite framework, in the absence of a Brønsted proton, the carbene moiety may have sufficient stability to take part in a concerted reaction with other species. Metadynamics simulations provide evidence for the reactivity of CH3 under realistic MTH conditions, but our results suggest that the methyl moieties will react with formed C2+ species rather than migrate along the zeolite framework, further suggesting that CH3 is unlikely to migrate through the framework to form the initial C–C bond.
Conflicts of interest
There are no conflicts of interest to declare.
Data availability statement
The raw energetics that underpin the work presented are available at DOI: 10.17035/d.2021.0137511663.
Acknowledgements
Computing facilities for this work were provided by ARCCA at Cardiff University, Supercomputing Wales, and through our membership of the UK's HPC Materials Chemistry Consortium (MCC), which is funded by the EPSRC (EP/R029431). We are grateful to Russell Howe and Graham Hutchings for several useful discussions concerning the role of carbenes in MTH; and Veronique Van Speybroeck, Kristof De Wispelaere, and Pieter Cnudde for discussions of metadynamics simulations. SAFN acknowledges the School of Chemistry, Cardiff University for a PhD studentship. AJL acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1).
References
- C. D. Chang and A. J. Silvestri, J. Catal., 1977, 47, 249–259 CrossRef CAS.
-
M. Guisnet and J.-P. Gilson, Zeolites for Cleaner Technologies, Imperial College Press, London, 2002, p. 391 Search PubMed.
- P. Tian, Y. Wei, M. Ye and Z. Liu, ACS Catal., 2015, 5, 1922–1938 CrossRef CAS.
- M. Bjørgen, U. Olsbye, D. Petersen and S. Kolboe, J. Catal., 2004, 221, 1–10 CrossRef.
- I. Yarulina, A. D. Chowdhury, F. Meirer, B. M. Weckhuysen and J. Gascon, Nat. Catal., 2018, 1, 398–411 CrossRef CAS.
- K. Hemelsoet, J. V. der Mynsbrugge, K. D. Wispelaere, M. Waroquier and V. V. Speybroeck, ChemPhysChem, 2013, 14, 1526–1545 CrossRef CAS PubMed.
- U. Olsbye, S. Svelle, M. Bjrgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831 CrossRef CAS.
- J. F. Haw and D. M. Marcus, Top. Catal., 2005, 34, 41–48 CrossRef CAS.
- J. Wang, Y. Wei, J. Li, S. Xu, W. Zhang, Y. He, J. Chen, M. Zhang, A. Zheng, F. Deng, X. Guo and Z. Liu, Catal. Sci. Technol., 2015, 6, 89–97 RSC.
- J. F. Haw, J. B. Nicholas, W. Song, F. Deng, Z. Wang, T. Xu and C. S. Heneghan, J. Am. Chem. Soc., 2000, 122, 4763–4775 CrossRef CAS.
- M. Stöcker, Microporous Mesoporous Mater., 1999, 29, 3–48 CrossRef.
- G. J. Hutchings, F. Gottschalk, M. V. M. Hall and R. Hunter, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 571–583 RSC.
- L. Lin, M. Fan, A. M. Sheveleva, X. Han, Z. Tang, J. H. Carter, I. da Silva, C. M. A. Parlett, F. Tuna, E. J. L. McInnes, G. Sastre, S. Rudić, H. Cavaye, S. F. Parker, Y. Cheng, L. L. Daemen, A. J. Ramirez-Cuesta, M. P. Attfield, Y. Liu, C. C. Tang, B. Han and S. Yang, Nat. Commun., 2021, 12, 822 CrossRef CAS PubMed.
- P. E. Sinclair and C. R. A. Catlow, J. Phys. Chem. B, 1997, 101, 295–298 CrossRef CAS.
- Y. Jiang, M. Hunger and W. Wang, J. Am. Chem. Soc., 2006, 128, 11679–11692 CrossRef CAS.
- W. Wang, A. Buchholz, M. Seiler and M. Hunger, J. Am. Chem. Soc., 2003, 125, 15260–15267 CrossRef CAS PubMed.
- I. B. Minova, S. K. Matam, A. Greenaway, C. R. A. Catlow, M. D. Frogley, G. Cinque, P. A. Wright and R. F. Howe, ACS Catal., 2019, 9, 6564–6570 CrossRef CAS.
- N. Govind, J. Andzelm, K. Reindel and G. Fitzgerald, Int. J. Mol. Sci., 2002, 3, 423–434 CrossRef CAS.
- D. Marcus, K. McLachlan, M. Wildman, J. Ehresmann, P. Kletnieks and J. Haw, Angew. Chem., Int. Ed., 2006, 45, 3133–3136 CrossRef CAS PubMed.
- C. S. Lee and M. M. Wu, J. Chem. Soc., Chem. Commun., 1985, 250 RSC.
- G. J. Hutchings and R. Hunter, Catal. Today, 1990, 6, 279–306 CrossRef CAS.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110 CAS.
- S. A. F. Nastase, A. J. O’Malley, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2019, 21, 2639–2650 RSC.
- J. To, A. A. Sokol, S. A. French and C. R. A. Catlow, J. Phys. Chem. C, 2008, 112, 7173–7185 CrossRef CAS.
- G. Artioli, C. Lamberti and G. L. Marra, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 2–10 CrossRef.
- B. C. Knott, C. T. Nimlos, D. J. Robichaud, M. R. Nimlos, S. Kim and R. Gounder, ACS Catal., 2018, 8, 770–784 CrossRef CAS.
- A. J. O’Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Faraday Discuss., 2016, 188, 235–255 RSC.
- P. Sherwood, A. H. De Vries, S. J. Collins, S. P. Greatbanks, N. A. Burton, M. A. Vincent and I. H. Hillier, Faraday Discuss., 1997, 106, 79–92 RSC.
- T. W. Keal and D. J. Tozer, J. Chem. Phys., 2005, 123, 121103 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- M. F. Guest, I. J. Bush, H. J. Van Dam, P. Sherwood, J. M. H. Thomas, J. H. Van Lenthe, R. W. Havenith and J. Kendrick, Mol. Phys., 2005, 103, 719–747 CrossRef CAS.
- R. Ahlrichs and P. R. Taylor, J. Chim. Phys., 1981, 78, 315–324 CrossRef CAS.
- D. R. Hartree, Math. Proc. Cambridge Philos. Soc., 1928, 24, 426 CrossRef CAS.
- V. Fock, Z. Phys., 1930, 61, 126–148 CrossRef.
- W. Smith, C. W. Yong and P. M. Rodger, Mol. Simul., 2002, 28, 37–41 CrossRef.
- J. R. Hill and J. Sauer, J. Phys. Chem., 1994, 98, 1238–1244 CrossRef CAS.
- J.-R. Hill and J. Sauer, J. Phys. Chem., 1995, 99, 9536–9550 CrossRef CAS.
- C. G. Broyden, Math. Comput., 1970, 24, 365 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647 CrossRef.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. A. Sokol, S. T. Bromley, S. A. French, C. R. A. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712 CrossRef CAS.
- W. Jost, J. Chem. Phys., 1933, 1, 466–475 CrossRef CAS.
- R. Poloni and J. Kim, J. Mater. Chem. C, 2014, 2, 2298–2300 RSC.
- F. B. van Duijneveldt, J. G. C. M. van, D. van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS.
- G. Bussi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2006, 96, 090601 CrossRef PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- K. Yang, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2010, 132, 164117 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- G. Lippert, J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140 Search PubMed.
- S. Goedecker and M. Teter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- J. Van Der Mynsbrugge, S. L. C. Moors, K. De Wispelaere and V. Van Speybroeck, ChemCatChem, 2014, 6, 1906–1918 CrossRef CAS.
- S. L. C. Moors, K. De Wispelaere, J. Van Der Mynsbrugge, M. Waroquier and V. Van Speybroeck, ACS Catal., 2013, 3, 2556–2567 CrossRef CAS.
- K. D. Wispelaere, S. Bailleul and V. V. Speybroeck, Catal. Sci. Technol., 2016, 6, 2686–2705 RSC.
- S. A. F. Nastase, P. Cnudde, L. Vanduyfhuys, K. De Wispelaere, V. Van Speybroeck, C. R. A. Catlow and A. J. Logsdail, ACS Catal., 2020, 10, 8904–8915 CrossRef CAS PubMed.
- S. Bailleul, I. Yarulina, A. E. J. Hoffman, A. Dokania, E. Abou-Hamad, A. D. Chowdhury, G. Pieters, J. Hajek, K. De Wispelaere, M. Waroquier, J. Gascon and V. Van Speybroeck, J. Am. Chem. Soc., 2019, 141(37), 14823–14842 CrossRef CAS PubMed.
- S. K. Matam, R. F. Howe, A. Thetford and R. C. A. Catlow, Chem. Commun., 2018, 54, 12875–12878 RSC.
- A. J. O’Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. García-Sakai and C. R. A. Catlow, Chem. Commun., 2016, 52, 2897–2900 RSC.
- S. G. Izmailova, I. V. Karetina, S. S. Khvoshchev and M. A. Shubaeva, J. Colloid Interface Sci., 1994, 165, 318–324 CrossRef CAS.
- R. von Ballmons, J. B. Higgins and M. M. J. Treacy, Proc. Ninth Int. Zeolite Conf., 1993, 2, 255 Search PubMed.
- A. Zecchina, S. Bordiga, G. Spoto, D. Scarano, G. Spanò and F. Geobaldo, J. Chem. Soc., Faraday Trans., 1996, 92, 4863–4875 RSC.
- S. K. Matam, S. A. F. Nastase, A. J. Logsdail and C. R. A. Catlow, Chem. Sci., 2020, 11, 6805–6814 RSC.
- F. Haase and J. Sauer, J. Am. Chem. Soc., 1995, 117, 3780–3789 CrossRef CAS.
- C. M. Nguyen, M. F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2010, 12, 9481–9493 RSC.
- I. Štich, J. D. Gale, K. Terakura and M. C. Payne, J. Am. Chem. Soc., 1999, 121, 3292–3302 CrossRef.
- G. J. Hutchings, G. W. Watson and D. J. Willock, Microporous Mesoporous Mater., 1999, 29, 67–77 CrossRef CAS.
- Y. Chu, X. Yi, C. Li, X. Sun and A. Zheng, Chem. Sci., 2018, 9, 6470–6479 RSC.
- Ch. Baerlocher and L. B. McCusker, Database of Zeolite Structures, 2021 Search PubMed , http://www.iza-structure.org/databases/.
Footnote |
| † Electronic Supplementary information (ESI) available at DOI: 10.1039/d1cp02535j. Illustrations are provided of the general model of the GM and MM relaxed and fixed regions (Fig. S1), and a schematic of the CV applied in MTD simulations (Fig. S2). Also provided in tabular form is geometric data for the H-ZSM-5 unit cell after NPT simulations (Table S1) and geometric and electronic observables of methanol (Table S2), methoxy (Tables S3 and S4) and carbene models (Tables S5 and S6). |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
C. Richard A.
Catlow
*a and
C. Richard A.
Catlow
 *abc
*abc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18), whilst experimental H/D exchange studies showed that C-D bond breaking occurs in H-ZSM-5
18), whilst experimental H/D exchange studies showed that C-D bond breaking occurs in H-ZSM-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 but not in H-SAPO-34,19 which does not completely rule out C–H bond cleavage but rather indicates a limited C–C interaction. Experimental studies involving CH2N2 also showed that the presence of H-ZSM-5 enhances the conversion of CH2N2 to ethene, further indicating that carbene could stabilise in H-ZSM-5.20,21
17 but not in H-SAPO-34,19 which does not completely rule out C–H bond cleavage but rather indicates a limited C–C interaction. Experimental studies involving CH2N2 also showed that the presence of H-ZSM-5 enhances the conversion of CH2N2 to ethene, further indicating that carbene could stabilise in H-ZSM-5.20,21
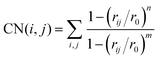



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 kJ mol−1). In order to determine the conditions that could lead to carbene formation from methyl species, and to understand the possible role of carbenes in the production of hydrocarbons, several new models were analysed as illustrated in Fig. 5 and 6.
18 kJ mol−1). In order to determine the conditions that could lead to carbene formation from methyl species, and to understand the possible role of carbenes in the production of hydrocarbons, several new models were analysed as illustrated in Fig. 5 and 6.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14). Since there is no charge neutralisation involved, the positioning of the carbene within the zeolite framework may be a consequence of the framework flexibility. Overall, whilst comparison of the carbene stabilised within the silicate structure (Fig. 8A) with that of carbene being placed closer to the active site (Fig. 8B) shows significant structural and energetic differences, the results are all considerably endothermic, which confirms that neither the Al–O–Si or the Si–O–Si coordination-sites enhance the stability of the carbene moiety.
14). Since there is no charge neutralisation involved, the positioning of the carbene within the zeolite framework may be a consequence of the framework flexibility. Overall, whilst comparison of the carbene stabilised within the silicate structure (Fig. 8A) with that of carbene being placed closer to the active site (Fig. 8B) shows significant structural and energetic differences, the results are all considerably endothermic, which confirms that neither the Al–O–Si or the Si–O–Si coordination-sites enhance the stability of the carbene moiety.



