Aggregation-induced emission leading to two distinct emissive species in the solid-state structure of high-dipole organic chromophores

Abstract

The concept of aggregation-induced emission represents a means to rationalise photoluminescence of usually nonfluorescent excimers in solid-state materials. In this publication, we study the photophysical properties of selected diaminodicyanoquinone (DADQ) derivatives in the solid state using a combined approach of experiment and theory. DADQs are a class of high-dipole organic chromophores promising for applications in non-linear optics and light-harvesting devices. Among the compounds investigated, we find both aggregation-induced emission and aggregation-caused quenching effects rationalised by calculated energy transfer rates. Analysis of fluorescence spectra and lifetime measurements provide the interesting result that (at least) two emissive species seem to contribute to the photophysical properties of DADQs. The main emission peak is notably broadened in the long-wavelength limit and exhibits a blue-shifted shoulder. We employ high-level quantum-chemical methods to validate a molecular approach to a solid-state problem and show that the complex emission features of DADQs can be attributed to a combination of H-type aggregates, monomers, and crystal structure defects.

---

Introduction

Understanding the mechanisms and intricacies related to the optical properties of solid-state materials opens the door towards applications in optoelectronic devices,^1,2 photosensors,^3–5 and bioimaging^6–8 and is therefore of broad interest for chemists, physicists, and material scientists alike. Notably, significant advances have been made in the field of luminescent organic solid-state materials.^9–15 One major drawback encountered in solid-state structures is so-called aggregation-caused quenching (ACQ) of emission promoted by close molecular packing within a crystal often leading to severe reduction of fluorescence quantum yields (QYs).^16–18 Probably the most prominent quenching mechanism in organic crystals involves energy transfer mediated through π–π-stacking in excimers. Quenching mechanisms include Förster resonance energy transfer (FRET) and the short-range Dexter process.^19,20 While the former depends on the potentially far-reaching (>10 Å) interaction of molecular (transition) dipoles, decaying with an R⁻⁶ dependence, the latter is determined by wavefunction overlap which decays much quicker with an exponential dependence on distance. Without the need for resource-demanding high-level quantum-chemical methods, Radhakrishnan and co-workers have developed and successfully applied a model based on the relative orientation and assembly of isolated diaminodicyanoquinones (DADQs) in the solid state to estimate Förster¹⁹ and Dexter²⁰ energy transfer rates and rationalise fluorescence QY trends.²¹

In contrast to ACQ, solid-state materials may also experience QY enhancement due to close molecular packing. In 2001, Luo et al.^22,23 introduced the concept of aggregation-induced emission (AIE) presenting a silole compound which for the first time showed improved QYs upon aggregation in solution. Most commonly, the AIE phenomenon can be attributed to intramolecular torsion-induced emission quenching. Seminal works on this field have been conducted by Gierschner, Park, and others.^24–27 It is, furthermore, didactically meaningful to differentiate AIE from related phenomena such as aggregation-induced emission enhancement (AIEE),²⁸ which describes an increase in fluorescence quantum yields in the solid of already emissive materials in solution. The discovery of AIE luminogens sparked a rapid increase in interest in this topic and many systems were introduced exploiting the AIE idea.^29–31 Approaches to enhance emission in the solid state include the design of materials based on J-aggregates³² and embedded or isolated dimers, which may show diminished non-radiative decay rates due to the rigidity of their microscopic environment.

In this account, we examine the optical properties of selected solid-state DADQ derivatives. DADQs are a class of organic compounds promising for application in non-linear optics and light-harvesting devices due to their large dipole moments, redox activity, and fluorescence properties. We study four C₂ symmetric DADQ derivatives using a combination of fluorescence experiments and state-of-the-art quantum-chemical approaches. Due to an interplay of AIE and ACQ effects, a reverse trend between fluorescence QYs in solution and in the solid state is observed with respect to the substituents. We show that this can be related to the degree of π–π-stacking within the crystals which is furthermore supported by energy transfer rates computed according to the ideas of Radhakrishnan and co-workers.³³

We present an unexpected correlation between fluorescence lifetimes and emission wavelengths in solid-state DADQs. Lifetimes increase with increasing emission wavelength in a way that is incompatible with a two-state system and thus provide a hint for the existence of (at least) one more emissive species. This observation is closely related to dual emission phenomena such as the twisted intramolecular charge-transfer and the interested reader is referred to a recent review by Gierschner et al.³⁴ For two of our compounds, we observe a blue-shifted shoulder of the main emission peak. Additionally, fluorescence intensities are still detectable close to 100 nm beyond the main peak in the long-wavelength region.

We show that instead of computing the optical properties of entire crystal structures, which would necessitate resource-draining evaluation of Greens functions or Bethe–Salpeter equations, a molecular approach based on monomers and dimers embedded in the crystal is sufficient for a proper theoretical analysis. Our protocol is based on a combination of QM/MM (quantum-mechanics/molecular-mechanics) calculations and DFT/MRCI^35–37 (density functional theory/multireference configuration interaction). Finally, we reveal that the main emission peak can be attributed to monomers, while short-wavelength emission associated with much shorter lifetimes are caused by H-type dimers. Lastly, our calculations suggest that long lifetimes measured at the low-energy end of the spectra can be explained by crystal defects.

Results and discussion

Synthesis

The synthesis of compounds 1–4 is illustrated in Scheme 1. The DADQs differ in their amino substituent: 1 for neopentyl, 2 for methyl, and 3 for para-methylbenzoate. Compound 4 is defined by a benzene instead of an ethyl bridge between the nitrogen atoms of the diamino group. All substances were prepared according to literature by coupling 7-pyrrolidino-7,8,8-tricyanoquinomethane (PTCNQ) and the respective diamine.^38,39

Scheme 1 Synthetic route to DADQ derivatives starting from TCNQ by reaction with pyrrolidine and subsequent reaction with the respective primary or secondary diamine. (i) 0.8 eq. pyrrolidine, 70 °C, 4 hours. (ii) 1 eq. of the respective diamine, 70 °C, 2–20 hours. Detailed protocols, yields and characterisation of the compounds can be found in the ESI.†

QY measurements in solution and in the solid state

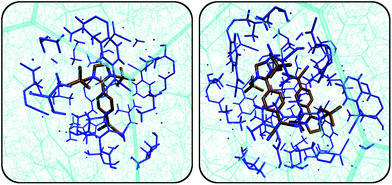
Fig. 1 depicts excerpts of the crystal structures either obtained from X-ray diffraction measurements (1–3) or from a quantum-chemical solid-state optimisation (4) (see Sections S3 and S6 in the ESI† for details). QYs in solution (ACN) and in the solid state are given below the figures. In solution, compound 4 is the only molecule showing high fluorescence QY (92%). The QY differences in solution are related to energetic barriers of intramolecular rotation around the dihedral angles near the dicyano and the amino moieties, as we have shown in an earlier publication.³⁸ Especially rotation of the dicyano moiety provides a mechanism of fluorescence deactivation. In the solid state, this rotational mode is obviously immobilised and cannot contribute to emission quenching (ΔE_rot ≈ 700 kJ mol⁻¹, Fig. S6, ESI†).

Fig. 1 Crystal structure excerpts, QYs in the solid state and in solution (ACN), and selected distances of compounds 1–4. Note that compound 4 was obtained from a periodic DFT calculation at the PBE-D3(BJ) level (see Section S6.2 in the ESI†). The increasing degree of π–π-overlap from 1 to 4 can be appreciated from the decreasing π–π-stacking distance (depicted in green). Hydrogen atoms were omitted for clarity.

Solid-state fluorescence QYs range from 18% for 1 to less than 1% for 4. The QY trend observed in the solid state can be explained by the degree of π–π-stacking in the crystal structures. From the distances listed in Fig. 1, it is clear that there is practically no effective overlap between the π-systems in 1, while molecules in the crystal structure of 4 are efficiently stacked. The plane-to-plane (π–π-stacking) distance decreases quite significantly from 8.3 Å in 1 to 3.1 Å in 4. To account for the difference between 3 and 4, which virtually have the same π–π-stacking distance, the centres of mass (COM) and the centres of the quinone systems (aryl centroids) are taken into account. As can be deduced from the crystal structures, these latter distances are much larger in the case of 3. As we will see later, our observations can be related to energy transfer rates in the spirit of Förster and Dexter modes (Fig. 5 down below).²¹

Dependence of lifetime and emission wavelength

Lifetimes τ for selected emission wavelengths λ_em for compounds 1, 2, and 3 are given in Table 1. A detailed spectroscopic analysis of compound 1 is illustrated in Fig. 2 (Fig. S3 and S4 for 2 and 3, respectively, ESI†). As can be seen in Fig. 2a, there is a strong dependence of τ and λ_em, which is in correlation with the respective emission spectrum (Fig. 2b) and is depicted in Fig. 2c. From Fermis golden rule it can be shown that in a two-level system there should be a linear relationship between τ and λ_em²:⁴⁰

k ∝ τ⁻¹ ∝ ω³M² ∝ ω²f_osc ∝ λ_em⁻² → τ ∝ λ_em² (1)

with radiative rate constant k, vertical excitation energy ω, transition dipole moment M, and oscillator strength f_osc. This relationship is not recovered in our measurements (Fig. 2d). Assuming that the peak splitting in the emission spectrum of compound 1 is not caused by vibronic coupling, we tentatively conclude, that the observed emission properties arise from at least two emissive species. These could either be two different emitting states of the same structure, two different structural motifs in the same emissive electronic state, or two different structures in two different states. While the emission spectrum of compound 1 shows a clear high-energy shoulder, the spectra of compounds 2 and 3 do not unambiguously display a second signal. In their case, the τ against λ_em² plots reveal a similar behaviour as for 1. We note that this is less clear in the case of compound 2, which we attribute to the absence of true H-type aggregates in the solid-state structure, which will be discussed further down below.

Table 1 Solid-state lifetimes in ns of compounds 1–3 measured at different emission wavelengths given in nm in parentheses

1	0.86 (435)	3.60 (495)	4.31 (555)
2	1.20 (410)	2.13 (470)	3.44 (530)
3	0.46 (460)	0.60 (480)	3.95 (500)

---

Fig. 2 Fluorescence properties of 1: (a) lifetime decay measurements at various emission wavelengths ranging from 425 nm to 575 nm, (b) emission spectrum measured after excitation at 375 nm with computed vertical transition insets obtained from DFT/MRCI calculations for an H-type dimer (green) and a monomer (red) scaled according to oscillator strengths, (c) lifetime plotted against emission wavelength, (d) lifetime plotted against squared emission wavelength.

The main emission peak of 1 has a significantly longer lifetime than the high-energy (short wavelength) transition indicating a smaller oscillator strength according to eqn (1). However, their intensities in the emission spectrum are reversed. This may be caused by a larger degree of non-radiative quenching for the high-energy signal. The largest portion of the QY is, hence, unsurprisingly, due to the main peak. A Gaussian curve fit inside the experimental emission spectrum of 1 estimates a contribution of 3% to the overall QY from the high-energy shoulder (Fig. S5, ESI†). In the following sections, we show that these observations can be rationalised by the different optical properties obtained by treating isolated monomers and dimers embedded in the crystal structure. We subsequently apply a combination of energy transfer rate calculations, periodic quantum-chemical methods, and the DFT/MRCI approach to examine the electronic and optical properties of DADQs in the solid state and investigate what may be the origin of the two emitting species.

Spectroscopic studies of single crystals

In addition to the ensemble measurements which are used for the subsequent quantum-chemical calculations, we assessed the emission features of representative single crystals of compounds 1–4 using a custom-made microscopic setup. The resulting emission spectra measured at an excitation wavelength of 405 nm using different crystals of varying size are shown in Fig. 3. The overall similarity of these emission spectra suggests a good homogeneity of the differently sized crystals and the absence of surface and reabsorption effects. The photoluminescence decay kinetics detected in different emission windows (blue tail of the emission band: 435–475 nm, red tail of the emission band: 525–800 nm, whole spectral window covered by dye emission: 435–800 nm), determined by different sets of longpass and shortpass filters, are shown in the lower panels of the figure. These decay curves reveal shorter lifetimes for detection in the blue tail of the emission band of all crystals compared to the respective red tail and with a good match of the decay kinetics derived for different crystals of the same dye. This trend, which is most pronounced for compound 3, varies slightly between the different dyes studied, where the resulting intensity-weighted lifetimes of the analyses of the fitted decay curves are summarised in Table S5 (ESI†). These findings, i.e., the similar emission spectra and the reduced lifetimes in the blue tail of the emission bands, confirm the absence of reabsorption and surface effects for the crystals studied.

Fig. 3 Emission spectra (top) of single crystals of compounds 1–4 under excitation at 405 nm and corresponding normalised fluorescence decay curves (bottom) of representative single crystals (crystal 2 for 1–3, crystal 3 for 4). For the separation of excitation and emission light, a 435 nm longpass dichroic mirror was used.

Energy transfer rates

To elucidate the differences in solid-state fluorescence QYs of compounds 1–4, we calculated energy transfer rates in close relation to long-range Förster and short-range Dexter coupling modes (visualised in Fig. 4). As proposed by Radhakrishnan and co-workers,²¹ Förster rates, k_F, are determined by the relative orientation and distance of the transition dipole moments of two monomers bywhere R connects the centres of mass of the molecules and α₁ and α₂ are the angles between R and the respective transition dipole. In contrast, Dexter energy transfer rates, k_D, depend on the relative orientation and distance of the molecular planes describing the quinone systems and fall off much quicker (exponential versus polynomial decay) since the short-range transfer rate depends on the wavefunction overlap of the two monomers:

k_D ∝ cos(θ) cos(ϕ)e^−r′ = cos(θ) cos(ϕ)e^{−r cos(θ)} (3)

where r and r′ refer to centre of plane distance and the perpendicular distance between the π-planes, respectively. θ defines the angle between the normal vector of the first plane and r, while ϕ describes the interplanar angle between the two π-systems.

Fig. 4 Illustration of the structural parameters determining k_F (left) and k_D (right). For the former, the arrows are aligned with the direction of the transition dipole moments. In the latter, the arrows point in the direction of the normal vectors of the molecules indicated by the blue planes.

While k_F links QYs to intermolecular (transition) dipole–dipole interaction, k_D can be interpreted as a relative measure to estimate energy transfer through π–π-stacking in the crystal. Fig. 5 correlates relative values of k_F and k_D with the solid-state QYs of all compounds. Förster energy transfer is most important for compounds 1 and 2, which show large intermolecular separation and π–π-stacking distances. In comparison, Dexter transfer is most prominent in compounds 3 and 4, which display shorter π–π-stacking distances. We note that the π–π-stacking distance of 4.1 Å in compound 4 may well be overestimated as no crystal structure could be obtained for this substance. The solid-state structure of 4 was instead derived from the crystal data of a similar compound (Fig. S9, ESI†). The dimer motifs yielding the largest Förster and Dexter transfer rates are given in Fig. S8 (ESI†) for all compounds.

Fig. 5 Relative Förster and Dexter energy transfer rates of compounds 1–4 (bars, 4 is set to 1.0) with additional indication of the solid-state QY (black line).

Fig. 5 furthermore reveals that k_F is unsuited to describe experimental differences with respect to compound 3. It seems that regarding π-interactions becomes increasingly important for 3, while it is not yet as essential in 1 and 2. In general, while Dexter modes dominate the immediate environment of the monomers, most important for 3 and 4, Förster interaction likely contributes as well especially at longer ranges due to the slower R⁻⁶ fall-off, which should be the main energy loss mechanism for compounds 1 and 2. Details on how the values were obtained can be found in the ESI† in Section S6.1.

In general, it seems that sterically demanding N-substituents result in more isolated monomer/dimer motifs in the crystal structure, which in turn reduces emission quenching through intermolecular energy transfer. On the other hand, substituents should not be too large, since intramolecular rotations should be prevented as effectively as possible, since they are the most relevant fluorescence deactivation mechanisms in the isolated monomers.³⁸

Please note that this analysis is based on the assumption that the optical properties of DADQs in the solid state can be reduced to the response of a monomer embedded in a crystal environment. In the following, we will refer to this idea as “molecular approach”. In principle, it neglects the possibility of largely delocalised electronic transitions playing an important role in fluorescence experiments. Hence, in the next section, we will justify the molecular approach by analysing the solid-state properties of 1 and 2, for which experimental data for crystal structures, QYs, and lifetimes are available.

A molecular approach to a solid-state problem

Periodic DFT calculations at the PBE-D3(BJ)^41–43 level were conducted to analyse the solid-state structure of compound 1 (see ESI† for 2 and Section S6.2 for computational details). A band gap of 2.31 eV at the PBE level and 3.20 eV using the HSE06⁴⁴ functional (Fig. S10, ESI†) are indicative of a semiconducting material. Calculations at the PBE level produce results in qualitative agreement with the HSE06 level. We note that the latter yields a band gap very similar to the experimentally measured absorption peak of the monomer in solution (3.02 eV in THF³⁸). The bandstructure and the density-of-states (DOS) plots shown in Fig. 6a reveal a molecular, i.e., quite localised, picture of the solid-state electronic structure. The valence band (VB) and conduction band (CB) are energetically separated from the nearest occupied and virtual band by roughly 1.1 eV and 0.7 eV, respectively. A closer look at the VB and CB (Fig. S11, ESI†) shows four interacting bands originating from the four molecules comprising the unit cell. Furthermore, partial charge densities of the VB and CB depicted in Fig. 6b can clearly be interpreted simply as the sum of the in vacuo calculated highest occupied and lowest unoccupied molecular orbitals, respectively (Fig. 6c). All in all, periodic electronic structure calculations present a solid basis for an approach based on small molecular clusters to examine the optical features of DADQs in the solid state.

Fig. 6 (a) Bandstructure (top) and density-of-states (bottom) plots of 1, (b) partial charge densities of the conduction bands (top) and valence band (bottom) with indication of a monomer depicted in red for visual clarity, isovalue of 0.003a₀⁻³, and (c) HOMO and LUMO density plots of a monomer of 1 calculated in vacuo, isovalue of 0.003a₀⁻³. All plots were obtained from calculations employing the PBE functional.

Moreover, to obtain more insight and collect further arguments for (or against) a molecular approach we computed excited states employing the ωB97X-D3⁴⁵ functional within the TD-DFT framework for a tetramer, i.e., the unit cell, and an octamer of compounds 1 and 2, and an additional dodecamer of compound 2. Various dimer conformations were computed for comparison. Larger clusters proved to be unfeasible at this level which prevented us from conducting convergence tests with respect to cluster size. The C-PCM⁴⁶ solvent model was utilised to mimic the dielectric properties of the crystal around the molecular clusters. The dielectric constant and refractive index necessary for the calculations were extracted from the dielectric tensor obtained at the periodic PBE level (Section S6.2 in the ESI† for details). Molecular structures (Fig. S13 and S14), transition energies, and oscillator strengths (Tables S7–S12) are given in the ESI.†

Fig. 7 depicts the difference densities for the excited states with the highest oscillator strengths of an octamer of 1 (S₅) and a dodecamer of 2 (S₁₀). In fact, all electronic transitions are fairly localised on either just a monomer or a dimer resembling an H-type aggregate. This provides a further argument in favour of a molecular approach. Note that in Fig. 7 a transition localised on a monomer (dimer) still involves two (four) molecules, as both the octamer and the dodecamer consist of symmetrically equivalent sub-units. Hence, for clarity, only a part of the clusters is shown.

Fig. 7 Difference densities of the excited states with the highest oscillator strengths in 1 (left, S₅ at 335 nm) and in 2 (right, S₁₀ at 305 nm). Red and blue zones correspond to areas of electron depletion and accumulation, respectively. Hydrogen atoms were omitted for clarity. Isovalue = 0.001a₀⁻³.

Certainly, one must be careful in assessing this approach as no experimental absorption data are available. More importantly, however, emission properties of these larger clusters are currently out of reach as this would necessitate excited-state optimisations requiring massive computational resources with the additional problem of modelling the solid-state environment. Still, our periodic DFT results in combination with localised excited states observed in molecular clusters provide sufficient evidence to justify a molecular approach based on monomers and dimers for the description of the electronic and optical properties of DADQs in the solid state. This comes with the major advantage that emission properties become feasible due to the manageable size of monomers and dimers. This will be exploited in the next part, where we will use a combination of the QM/MM method and DFT/MRCI to assess the absorption and emission properties of compounds 1 and 2.

Rationalising solid-state fluorescence properties

In the previous section, we have established that it is sufficient to examine monomers and dimers of our DADQs embedded in their crystal structure to evaluate their photophysical solid-state properties. We calculated monomers and H- and J-like aggregated dimers embedded in the crystal structure of compound 1 and 2 (Fig. 8 and Fig. S19, ESI†). Since compound 3 essentially only contains H-type aggregates (cf.Fig. 1), J-aggregates are likely to play a subordinated role, if we assume that the mechanisms responsible for the emission properties are similar in all compounds. We employed the ONIOM⁴⁷ scheme to perform a QM/MM optimisation of ground- and excited states using the ωB97XD functional for the high layer and the UFF (universal force field)⁴⁸ for the low layer. Note that the dispersion part of the functional differs from the one used earlier due to limitations of the employed quantum-chemical programme packages. Afterwards, the DFT/MRCI method in combination with the C-PCM model once again using the dielectric constant obtained from the periodic calculations was employed to compute absorption and emission peaks. A similar approach has been used recently for chalcone-based materials.⁴⁹ Due to the non-polarisable force field, state crossings with dark charge-transfer states pose a hypothetical problem. However, excited states in DADQ dimers are of local nature which can be deduced from the difference densities of the S₁ and S₂ states in the H-type dimer displaying the same nodal shape (Fig. S20, ESI†). Details about the DFT/MRCI excited state calculations can be found in Section S6.2 of the ESI.† As can be seen in Table 2, our protocol yields a nice agreement between calculated vertical transitions and experimental emission energies. For compound 1, the main peak at 495 nm is energetically close to the S₁ of the monomer, while the shoulder at 438 nm is near the S₂ of the H-type dimer. Both emission energies differ by less than 7 nm (0.07 eV, vertical transition lines in Fig. 2b above). J-Aggregates can be assumed to only play a minor role for the emission spectrum, presumably in between the main peak and the high-energy (short wavelength) shoulder (Table S14, ESI†). Fig. 9 illustrates the mechanism and shows that excited-state and ground-state structures optimised in a crystal environment differ only very slightly, as expected. For compound 2, the main peak is exactly reproduced by the calculation likely benefitting from fortuitous error cancellation, while the high-energy component of the spectrum cannot be extracted reliably.

Fig. 8 Monomer (left) and H-type dimer (right) of compound 1 embedded in their crystal environments. Hydrogens are omitted for the high layer for clarity. A part of the low layer (dark blue) was allowed to relax during the run. The static low layer is depicted in transparent cyan.

Table 2 Calculated absorption peaks, comparison of calculated and experimental emission wavelengths, emission oscillator strengths and lifetimes of compounds 1 and 2 for monomers (mon) and H-aggregates (H). Absorption and emission wavelengths are given in nm, lifetimes in ns

			λ ^calc.abs	λ ^calc.em	λ ^exp.em	f osc,em	τ exp.
a Extracted from Gaussian fit. b Not reliably extractable.
1	mon	S1	440	488	495	0.81	3.60
	H	S1	404	466	438^a	0.00	0.86
		S2	387	432		1.38
2	mon	S1	412	463	463	0.73	2.13
	H	S1	409	439		0.00	1.19
		S2	392	419		1.38

---

Fig. 9 Excited-state optimisation of 1 in the solid-state: Ground- and excited-state optimised structures are overlaid. Monomer and H-dimer are represented by a cyan to blue and an orange to red colour change, respectively. Solid arrows refer to absorption and emission, while the dashed arrow indicates fluorescence quenching of the H-dimer due to internal conversion. Experimental emission wavelengths are depicted in grey.

As has been addressed earlier, there is a mismatch between emission intensities and fluorescence lifetimes, as shorter lifetimes indicate larger oscillator strengths (eqn (1)) which, in turn, imply larger intensities. In Table 2, we can see that this discrepancy can now be explained by non-radiative fluorescence quenching through internal conversion of the high-energy S₂ of the H-type dimer to its dark S₁ which lies 34 nm (0.2 eV) lower in energy. Technically, emission from the high-lying S₂ violates Kashas rule,⁵⁰ which states that emission originates from the lowest excited state (S₁). However, the two states are very close in energy enabling potentially multiple state crossings or conical intersections that allow for dynamical population exchange. Future analysis would therefore require quantum dynamics which is however not covered in this work.

Depending on the emitting system, the radiative decay pathway of the monomer can vary between quenched or unquenched. We assign the vast majority of the fluorescence QY to the monomers, as those exhibit the largest contribution to the emission according to Table 2. In conclusion, we attribute the general shape of the emission spectrum of 1 to monomers and H-type dimers embedded in the solid-state crystal structure.

One remaining issue is the low-energy (long wavelength) end of the emission spectrum. For compound 1, the longest lifetimes are measured at around 570 nm, almost 80 nm (0.33 eV) red-shifted with respect to the monomer emission peak. This is noteworthy, as lifetime broadening should actually sharpen the signal rather than widening it. Monomers with higher conformational mobility in the crystal should produce larger Stokes shifts and may, thus, explain this observation.

Such structural freedom may be achieved by defects in the solid-state structure. Rather large R-factors of the crystal structures (Table S4, ESI†) support this claim. Hence, we repeated the computational procedure described above for monomers placed inside a defect. As there is no experimental data for the nature of possible defects available, we opted to simply use the cavity formed by the H-type dimer of 1 and put a monomer inside of it. The resulting emission peak is located at 516 nm, red-shifted by 34 nm, making it a potential candidate for the observed long lifetimes near the low-energy end of the emission spectrum. In the most extreme case, without the rigid crystal environment, the monomer loses all of its oscillator strength while constantly increasing the Stokes shift upon relaxation on the S₁ (Fig. 10). We can thus assume, that depending on the size of the defect cavity, the monomer may show small amounts of fluorescence at various emission energies beyond the main emission peak.

Fig. 10 Absorption and emission wavelengths depending on the degree of conformational mobility of the monomer. Left: Completely confined in the crystal, middle: encapsulated inside a dimer cavity, right: “free” inside a dielectric continuum with the same permittivity and refractive index as compound 1 as a solid. Ground- and excited-state optimised structures are overlaid in cyan and blue, respectively.

Conclusion

Using both experimental and computational approaches, we were able to explain the emergence of aggregation-induced emission in an organic crystal system. The solid-state optical properties of four DADQ derivatives were rationalised and the corresponding mechanisms supported by molecular models.

Differences in solid-state fluorescence QYs can be related to the efficiency of π–π-stacking interactions within the crystal which were quantified by energy transfer rate calculations according to Radhakrishnan and co-workers. While benzene-bridged, unsubstituted compound 4 experiences aggregation-caused quenching, dineopentyl-substituted derivative 1 is subject to an aggregation-induced emission effect. Furthermore, lifetime measurements at various emission wavelengths reveal multiple emitting species in compounds 1–3, which we attribute to H-type dimers and monomers, while J-aggregates only play a minor role for the optical properties. Our computational protocol based on QM/MM calculations and the DFT/MRCI method to evaluate the photophysical properties of DADQs in the solid state, may serve as a general approach to study optical problems in organic crystals.

In conclusion, our joint study was able to elucidate a wide range of effects occurring in organic crystals, likely not limited to the DADQ compounds studied here. The results may have implications for the design of organic light emitting compounds.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We thank Tim Küllmey for helpful discussions. The North-German Supercomputing Alliance (Norddeutscher Verbund für Hoch- und Höchstleistungsrechnen) and the computing facilities of Freie Universität Berlin (Zentrale Einrichtung für Datenverarbeitung) are acknowledged for providing computational resources. FW and JPG gratefully acknowledge the Deutsche Forschungsgemeinschaft for financial support through research grant PA 1360/16-1 and project no. 393271229, respectively. URG and NNB gratefully acknowledge financial support by DFG grant RE1203/23-1 and a MI Type 3 Project from BAM.

References

1. M. M. Stylianakis, Nanomaterials, 2020, 10, 520.
2. X. Wang, Y. Cui, T. Li, M. Lei, J. Li and Z. Wei, Adv. Opt. Mater., 2019, 7, 1801274.
3. T. L. Mako, J. M. Racicot and M. Levine, Chem. Rev., 2019, 119, 322–477.
4. R. D. Jansen-van Vuuren, A. Armin, A. K. Pandey, P. L. Burn and P. Meredith, Adv. Mater., 2016, 28, 4766–4802.
5. D. Yang and D. Ma, Adv. Opt. Mater., 2019, 7, 1800522.
6. H.-B. Cheng, Y. Li, B. Z. Tang and J. Yoon, Chem. Soc. Rev., 2020, 49, 21–31.
7. Q. Qi, C. Li, X. Liu, S. Jiang, Z. Xu, R. Lee, M. Zhu, B. Xu and W. Tian, J. Am. Chem. Soc., 2017, 139, 16036–16039.
8. C.-B. Ma, Z.-T. Zhu, H.-X. Wang, X. Huang, X. Zhang, X. Qi, H.-L. Zhang, Y. Zhu, X. Deng, Y. Peng, Y. Han and H. Zhang, Nanoscale, 2015, 7, 10162–10169.
9. J. De, S. P. Gupta, S. Sudheendran Swayamprabha, D. K. Dubey, I. Bala, I. Sarkar, G. Dey, J.-H. Jou, S. Ghosh and S. K. Pal, J. Phys. Chem. C, 2018, 122, 23659–23674.
10. S. Feuillastre, M. Pauton, L. Gao, A. Desmarchelier, A. J. Riives, D. Prim, D. Tondelier, B. Geffroy, G. Muller, G. Clavier and G. Pieters, J. Am. Chem. Soc., 2016, 138, 3990–3993.
11. I. Bala, N. Singh, R. A. K. Yadav, J. De, S. P. Gupta, D. P. Singh, D. K. Dubey, J.-H. Jou, R. Douali and S. K. Pal, J. Mater. Chem. C, 2020, 8, 12485–12494.
12. A. Adak, T. Panda, A. Raveendran, K. S. Bejoymohandas, K. S. Asha, A. P. Prakasham, B. Mukhopadhyay and M. K. Panda, ACS Omega, 2018, 3, 5291–5300.
13. R. Butkute, R. Lygaitis, V. Mimaite, D. Gudeika, D. Volyniuk, G. Sini and J. V. Grazulevicius, Dyes Pigm., 2017, 146, 425–437.
14. S. Mukherjee and P. Thilagar, Angew. Chem., Int. Ed., 2019, 58, 7922–7932.
15. P. Pallavi, V. Kumar, M. W. Hussain and A. Patra, ACS Appl. Mater. Interfaces, 2018, 10, 44696–44705.
16. Y. Huang, J. Xing, Q. Gong, L.-C. Chen, G. Liu, C. Yao, Z. Wang, H.-L. Zhang, Z. Chen and Q. Zhang, Nat. Commun., 2019, 10, 169.
17. W. Z. Yuan, P. Lu, S. Chen, J. W. Y. Lam, Z. Wang, Y. Liu, H. S. Kwok, Y. Ma and B. Z. Tang, Adv. Mater., 2010, 22, 2159–2163.
18. B. Andreiuk, A. Reisch, E. Bernhardt and A. S. Klymchenko, Chem. – Asian J., 2019, 14, 836–846.
19. T. Förster, Ann. Phys., 1948, 437, 55–75.
20. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
21. P. Srujana, P. Sudhakar and T. P. Radhakrishnan, J. Mater. Chem. C, 2018, 6, 9314–9329.
22. J. Luo, Z. Xie, J. W. Y. Lam, L. Cheng, B. Z. Tang, H. Chen, C. Qiu, H. S. Kwok, X. Zhan, Y. Liu and D. Zhu, Chem. Commun., 2001, 1740–1741.
23. Y. Hong, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2011, 40, 5361.
24. J. Gierschner and S. Y. Park, J. Mater. Chem. C, 2013, 1, 5818.
25. J. Gierschner, L. Lüer, B. Milián-Medina, D. Oelkrug and H.-J. Egelhaaf, J. Phys. Chem. Lett., 2013, 4, 2686–2697.
26. J. Shi, L. E. Aguilar Suarez, S.-J. Yoon, S. Varghese, C. Serpa, S. Y. Park, L. Lüer, D. Roca-Sanjuán, B. Milián-Medina and J. Gierschner, J. Phys. Chem. C, 2017, 121, 23166–23183.
27. Z. Guo, C. Yan and W. Zhu, Angew. Chem., Int. Ed., 2020, 59, 9812–9825.
28. B.-K. An, S.-K. Kwon, S.-D. Jung and S. Y. Park, J. Am. Chem. Soc., 2002, 124, 14410–14415.
29. Y. Shen, H. Liu, S. Zhang, Y. Gao, B. Li, Y. Yan, Y. Hu, L. Zhao and B. Yang, J. Mater. Chem. C, 2017, 5, 10061–10067.
30. H. Liu, L. Yao, B. Li, X. Chen, Y. Gao, S. Zhang, W. Li, P. Lu, B. Yang and Y. Ma, Chem. Commun., 2016, 52, 7356–7359.
31. H. Liu, D. Cong, B. Li, L. Ye, Y. Ge, X. Tang, Y. Shen, Y. Wen, J. Wang, C. Zhou and B. Yang, Cryst. Growth Des., 2017, 17, 2945–2949.
32. F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376–3410.
33. P. Srujana and T. P. Radhakrishnan, Chem. – Eur. J., 2018, 24, 1784–1788.
34. J. Gierschner, S. K. Behera and S. Y. Park, Angew. Chem., Int. Ed., 2021, 60, 2–17.
35. I. Lyskov, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2016, 144, 034104.
36. M. Kleinschmidt, C. M. Marian, M. Waletzke and S. Grimme, J. Chem. Phys., 2009, 130, 044708.
37. C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1394.
38. P. Rietsch, F. Witte, S. Sobottka, G. Germer, A. Becker, A. Güttler, B. Sarkar, B. Paulus, U. Resch-Genger and S. Eigler, Angew. Chem., Int. Ed., 2019, 58, 8235–8239.
39. P. Sudhakar and T. P. Radhakrishnan, J. Mater. Chem. C, 2019, 7, 7083–7089.
40. D. Toptygin, J. Fluoresc., 2003, 13, 201–219.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
43. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
44. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
45. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
46. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
47. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363.
48. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
49. M. Dommett, M. Rivera, M. T. H. Smith and R. Crespo-Otero, J. Mater. Chem. C, 2020, 8, 2558–2568.
50. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2051074. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1cp02534a

---