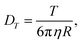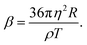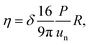Active Brownian particle in homogeneous media of different viscosities: numerical simulations
Received
4th June 2021
, Accepted 2nd July 2021
First published on 26th July 2021
Abstract
Self-propelled colloids, active polymers and membranes, driven (vibrated) granular layers and hybrid synthetic-biological systems are striking examples of systems containing synthetic active Brownian particles. Such particles autonomously convert the available energy of the environment into their own directed mechanical motion. In most studies the self-propelled Brownian particles move in overdamped media. Recently, experiments with Janus particles in a low-pressure plasma have appeared. A distinctive feature of such a medium is an extremely low viscosity at which the inertial effects play a significant role, resulting in underdamped Brownian motion. At present, there is a lack of statistical theory describing the underdamped Brownian motion of self-propelled particles at all time scales. This paper presents the numerical simulation results of active Brownian motion in homogeneous media of different viscosities. The calculations are performed using a mathematical model of a self-propelled Brownian sphere with translational and rotational inertia. The time-dependent mean square displacement and mean linear displacement (the noise-averaged trajectory) of the particle are investigated as a function of medium viscosity, self-propulsion velocity and moment of inertia. Our simulation reveals that the dynamics of a self-propelled spherical particle significantly depends on two independent dimensionless parameters of the particle: the ratio of the self-propulsion velocity to the characteristic thermal velocity and the ratio of the friction coefficient to the rotational diffusion coefficient. The obtained statistical characteristics of active Brownian motion are compared with the known theoretical models in a wide range of medium viscosities. We propose simple corrections to the basic theory of overdamped active Brownian motion, which allow one to calculate the effective diffusion coefficient and the persistence length of a self-propelled Brownian particle in a medium with any dynamic viscosity. The results obtained are discussed in relation to active particles in a colloidal plasma and superfluid helium.
1. Introduction
Active matter is a state of condensed matter, which represents an ensemble of active Brownian nano- or microparticles in a dissipative medium. Such particles autonomously convert the available (chemical, electromagnetic, thermal, etc.) energy of the environment into their own directed mechanical motion.1–11 Many examples of active matter are of biological origin; however, a significant part of the current experimental and theoretical research is devoted to artificial systems: self-propelled colloids, active polymers and membranes, driven (vibrated) granular layers and hybrid synthetic-biological systems. Synthetic active matter is of great fundamental interest in statistical mechanics, opens up new areas in materials science, and has many promising applications: from purely technical to biomedical.2,3
A striking example of a synthetic active particle is the Janus particle.12 It is a bifunctional particle the two parts of which differ in chemical composition and as a result have different surface and/or volume properties. The interaction of the Janus particle with the environment generates a driving force that causes the particle to move itself.
Depending on the parameters of the medium and the particle (and the associated characteristic relaxation times), the active Brownian motion can be underdamped and overdamped.13 In the latter case, inertia does not noticeably effect on the motion of the particle. Most experiments deal with overdamped motion of Janus particles.2,3 Their self-propulsion can be caused, for example, by diffusiophoresis,4,5 thermophoresis,6,7 electrophoresis (electroosmosis)8–10 or bubble thrust,11 depending on the specific mechanism of the “particle–medium” interaction. However, more recently, experimental studies of Janus particles in a low-pressure plasma have appeared.14,15 A distinctive feature of such a medium is an extremely low viscosity at which the inertial effects play a significant role, resulting in underdamped Brownian motion. The driving force of Janus particles in these experiments is the photophoretic force.14,16–18
In most theoretical research, the active Brownian particles are considered to be moving in an overdamped medium.1 However, there is a lack of theory describing underdamped Brownian motion of self-propelled particles. This paper presents the numerical simulation results of active Brownian motion in media of different viscosities. The calculations were performed using a mathematical model of a self-propelled Brownian sphere with translational and rotational inertia. The obtained statistical characteristics of active Brownian motion are compared with the known theoretical models in a wide range of medium viscosities. Simple semiempirical corrections are proposed to the basic theory of overdamped active Brownian motion, which allow one to calculate the effective diffusion coefficient and the persistence length of a self-propelled Brownian particle in media with any dynamic viscosities.
2. Theoretical background
2.1 Basic equations
To demonstrate basic features of the problem, we restrict our analysis here to two spatial dimensions. In this case, a single particle trajectory is described by the particle position vector r(t) = [x, y] and the particle orientation vector n(t) = [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ], where θ(t) is the angle between the x-axis and n, see Fig. 1. Let us assume that due to some driving force acting along n, the particle moves in a medium with a velocity VS = VSn. The direction of n is determined by the random rotation of the particle, the characteristic frequency of which ω is equal to the rotational diffusion coefficient. Neglecting the drag effect of the medium, for purely thermal noise and a spherically symmetric particle of radius R in bulk situations we have
θ], where θ(t) is the angle between the x-axis and n, see Fig. 1. Let us assume that due to some driving force acting along n, the particle moves in a medium with a velocity VS = VSn. The direction of n is determined by the random rotation of the particle, the characteristic frequency of which ω is equal to the rotational diffusion coefficient. Neglecting the drag effect of the medium, for purely thermal noise and a spherically symmetric particle of radius R in bulk situations we have| | 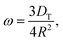 | (1) |
where| | 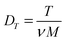 | (2) |
is the translational short-time diffusion coefficient. Here T is the temperature of the medium (expressed in energy units), ν is the friction coefficient of the particle, and M is the particle mass.
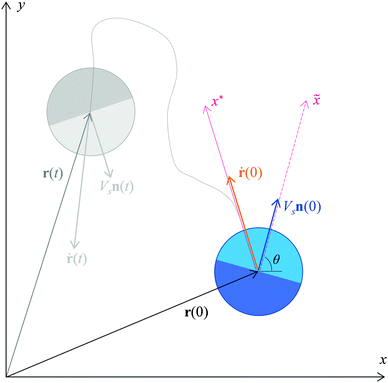 |
| | Fig. 1 Two-dimensional model of a self-propelled Brownian sphere. The ![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) axis is directed along the vector of the particle's self-propulsion velocity at the moment t = 0. The x* axis is directed along the vector of the initial total velocity of the particle. axis is directed along the vector of the particle's self-propulsion velocity at the moment t = 0. The x* axis is directed along the vector of the initial total velocity of the particle. | |
In the absence of deterministic (other internal and external) forces and neglecting the drag effects of the medium, the two-dimensional translational motion of a self-propelled spherical Brownian particle is described by the following Langevin equations:
| | ẍ(t) = −ν[ẋ(t) − VS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] + ξx(t), θ] + ξx(t), | (3a) |
| | ÿ(t) = −ν[ẏ(t) − VS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] + ξy(t), θ] + ξy(t), | (3b) |
where
ξx(
t) and
ξy(
t) are independent delta-correlated Gaussian processes with zero means and autocorrelation functions representing white noise,
i.e., 〈
ξx(0)
ξx(
t)〉 = 〈
ξy(0)
ξy(
t)〉 = 2
Tνδ(
t)/
M.
The random rotation of the particle caused by fluctuations of the tangential component of the momentum transmitted from the environmental particles is described using the following stochastic differential equation:19,20
| | ![[greek theta with two dots above]](https://www.rsc.org/images/entities/i_char_e1a7.gif) (t) = −μ (t) = −μ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) (t) + ξθ(t), (t) + ξθ(t), | (4) |
where
μ =
T/
Iω is the rotational damping rate of the particle with the moment of inertia
I; and
ξθ(
t) is a delta-correlated Gaussian process with 〈
ξθ〉 = 0 and 〈
ξθ(0)
ξθ(
t)〉 = 2
Tμδ(
t)/
I.
In the classical description of Brownian motion, the temperatures corresponding to the translational (3) and rotational (4) noise are assumed to be equal. We stick to this reasonable assumption here. However, note that in some special cases, effective temperatures of the translational and rotational motion may differ, for example: for hot Brownian motion of a heated colloidal particle in a solvent,21 or for a dust grain absorbing the ambient gas.22
2.2 Overdamped Brownian motion of a self-propelled particle
In most theoretical research, active Brownian particles are considered to be moving in an overdamped medium. In this case, it is usually assumed that the left-hand sides of eqn (3) and (4) responsible for inertia are equal to zero, i.e., ẍ(t) = 0, ÿ(t) = 0 and ![[greek theta with two dots above]](https://www.rsc.org/images/entities/i_char_e1a7.gif) (t) = 0. The inertialess Langevin equations provide a quantitative description of the overdamped particle dynamics at the long-time scale (t ≫ ν−1). In particular, the mean square displacement (MSD) of an overdamped self-propelled Brownian particle in an arbitrary direction is described by the following equation:4,23
(t) = 0. The inertialess Langevin equations provide a quantitative description of the overdamped particle dynamics at the long-time scale (t ≫ ν−1). In particular, the mean square displacement (MSD) of an overdamped self-propelled Brownian particle in an arbitrary direction is described by the following equation:4,23| | 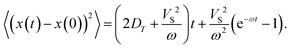 | (5) |
Further, we assume x(0) ≡ 0. Note that eqn (5) is valid for times significantly longer than the momentum relaxation time τp = ν−1. Eqn (5) leads to the following effective (long-time) diffusion coefficient:| |  | (6) |
The first term of eqn (6) is the translational short-time diffusion coefficient (2) associated with passive Brownian motion. The second term represents the contribution from the driving force due to the coupling between translational and rotational motions: it is a well-known solution of the so-called telegraph equation, used to describe a persistent random walk of living cells24 in the absence of velocity fluctuations, i.e., for |ṙ(t)| ≡ VS.
Coupling of rotational diffusion with directed active motion is quantified by the persistence length
| | 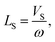 | (7) |
where the inverse rotational diffusion coefficient
ω−1 is a characteristic time scale (the persistence time) during which the particle is more likely to move in a similar direction to its initial orientation. If we direct the
![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif)
axis along the vector of the particle's self-propulsion velocity at
t = 0, as shown in
Fig. 1, then the mean linear displacement (MLD) of an active colloidal particle is described by the following equation:
3,13,23| | 〈![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (t)〉 = LS[1 − e−ωt]. (t)〉 = LS[1 − e−ωt]. | (8) |
This noise-averaged function is also called the ‘average trajectory’
3 or ‘mean position’
23 of the particle.
2.3 Underdamped Brownian motion of a self-propelled particle with inertia
For a correct description of the overdamped Brownian motion at very short time scales (t ≪ τp), the translational inertia must be taken into account. In this limit the well-known Ornstein–Uhlenbeck formula25 describes the MSD of a passive particle (with VS ≡ 0):| | 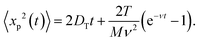 | (9) |
Note that, in contrast to eqn (5), formula (9) is valid at all times of observation. However, there is currently no analytical equation describing the time-dependent MSD for a self-propelled Brownian particle with inertia. In order to correctly describe the underdamped active Brownian motion (even at long-time scales), the rotational inertia must be taken into account.13
Solving the system of eqn (3) and (4) leads to the following generalized form of the effective (long-time) diffusion coefficient:13,26,27
| | 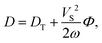 | (10) |
where
Φ is the dimensionless function that depends on the ratio
Iω2/
T and corrects
eqn (6). The asymptotic dependences of
Φ(
Iω2/
T) can be derived analytically for two limits:
26,27| | 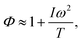 | (11) |
for
Iω2/
T ≪ 1, and
| | 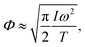 | (12) |
for
Iω2/
T ≫ 1.
In contrast to the diffusion, the effect of inertia on the mean linear displacement and the persistence length of a self-propelled Brownian particle has not been studied at all.
3. Numerical simulation
3.1 Simulation parameters
Hereinafter, for the moment of inertia of a spherical particle relative to the axis of rotation passing through its center of mass the following parameter is used:| | 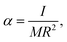 | (13) |
α < 1, which depends on the mass distribution over the volume of the particle (here we assume that the distribution is symmetric with respect to the axis of rotation).
We also introduce two independent dimensionless parameters responsible for the particle dynamics: the inertial delay number13,27
| | 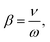 | (14) |
which is the ratio of the friction coefficient to the rotational diffusion coefficient and indicates the inertial delay between the self-propulsion direction and the particle velocity, originating from the finite relaxation times in the system; and the dimensionless self-propulsion velocity
| | 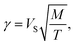 | (15) |
which is the ratio of the self-propulsion velocity to the characteristic thermal velocity. Note that in colloids, the Péclet number is commonly used as a measure of self-propulsion:
3,28,29| | 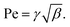 | (16) |
The dynamics of an active Brownian particle was simulated by numerically integrating the equations of motion (3) and (4). Discrete random changes in the velocities of translational and rotational motion were set by 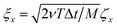 and
and 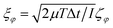 , where Δt is an integration step and ζi is a Gaussian random number with zero mean and unit variance. The integration step Δt was less than 0.05 min[μ−1,ω−1].
, where Δt is an integration step and ζi is a Gaussian random number with zero mean and unit variance. The integration step Δt was less than 0.05 min[μ−1,ω−1].
The calculations were performed for a particle with diameter 2R = 1 μm and mass M = 7.9 × 10−13 g (corresponding to the averaged density ρ = 1.5 g cm−3) in a viscous medium with a temperature T = 0.025 eV. The mass distribution parameter α was varied from 0.01 to 1. The friction coefficient ν was varied in the range from 3.9 to 3.9 × 106 s−1, which, for example, corresponds to a change in pressure from ∼10−1 to ∼ 105 Pa in the argon atmosphere. The Péclet number was in the range from 0.1 to 1000 and the ratio of characteristic frequencies β was in the range from 10−6 to 106. At the initial moment, each particle was located at the origin x(0) = 0, y(0) = 0, and the angle θ(0) represented a uniformly distributed random variable in the range from 0 to 2π.
Fig. 2 shows exemplary trajectories of simulated particles for a fixed Péclet number and different inertial delay numbers. In order to accumulate good statistics, we got up to 106 independent particle trajectories for each set of simulation parameters.
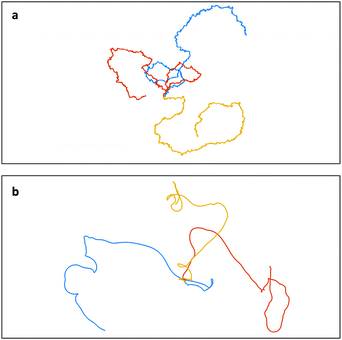 |
| | Fig. 2 Trajectories of three active Brownian particles moving during time τ = 10max[ν−1,ω−1] with a fixed Péclet number (Pe = 10) and different inertial delay numbers: (a) β = 104, (b) β = 10−2. | |
3.2 Results
3.2.1 Mean-square displacement.
To illustrate the numerically calculated MSD of a self-propelled Brownian sphere, Fig. 3 represents the mass transfer functions 〈x2(t)〉/2t for fixed α and various sets of β and γ (or Pe). Note that in comparison with MSD, the mass transfer function has several advantages:30,31 (I) more pronounced transitions between ballistic and diffusion regimes; (II) equality to the effective diffusion coefficient at long observation times. Along with the simulation results, Fig. 3 shows the mass transfer functions for eqn (5) and (9).
 |
| | Fig. 3 Normalized mass transfer functions 〈x2(t)〉/(2tDT) of a self-propelled Brownian particle with α = 2/5 for (a) β = 104, (b) β = 1, (c) β = 10−2 and (blue) Pe = 0.1, (green) Pe = 1, (yellow) Pe = 10, (red) Pe = 100. The symbols show the results of numerical simulation, the thin dotted line plots eqn (8) for the passive particle (γ = 0), the solid bold lines plot eqn (17). Here the time is normalized to the momentum relaxation time τp = ν−1. | |
With a relatively high friction (β ≫ 1, see Fig. 3a) at times t ≪ ω−1, an active Brownian particle moves in the same way as a passive one: motion of both particles is ballistic, i.e., 〈x2(t)〉 ∝ t2, at the shortest time scale t ≪ ν−1; a crossover to a short-time diffusive regime with 〈x2(t)〉 ∝ t occurs at t1 ∼ ν−1. However, at longer time scales, the behavior of active and passive particles differs: there is a second crossover from a short-time diffusive to a propulsive ballistic regime at t2 ∼ γ−2ν−1, and, finally, diffusive motion occurs after the third crossover at t3 ∼ ω−1. Note that similar crossovers have been obtained earlier in theoretical studies of a persistent random walk.23,32 Some crossover corresponding to point t3 was also observed in the experiment with the Janus colloid particle.4
For β ≫ 1 and for all values of Pe (used in the simulations), the numerically calculated MSD of the self-propelled Brownian sphere at all observation times is well described by the following equation:
| | 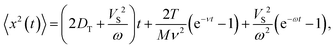 | (17) |
which is a combination of
eqn (5) and (9).
Fig. 3b and c show that when the friction coefficient is comparable or less than the rotational diffusion coefficient, i.e., β ≲ 1, eqn (17) is inapplicable for describing the MSD of an active Brownian particle. In this case, a random walk of an active Brownian particle corresponds to a passive one with some enhanced diffusion coefficient, i.e., D > DT.
Fig. 4 shows the dimensionless correction Φ for the effective (long-time) diffusion coefficient (10) in dependence on the ratio β/α. For numerical data, function Φ was calculated as Φ = 2Pe−2(D/DT − 1), where D = 〈x2(τ)〉/2τ was measured at times τ ≳ 100max[ν−1,ω−1]. For comparison, the plots of eqn (11) and (12) are also presented in Fig. 4 taking into account that Iω2/T ≡ 3α/4β. It is easy to see that eqn (11) is consistent with the simulation results at β/α ≫ 1, and eqn (12) is in satisfactory (but not good) agreement with our simulations at β/α ≪ 1. To approximate the numerical data for all values of α and β, we propose the following expression for the dimensionless correction of the effective diffusion coefficient (see symbols in Fig. 4):
| | 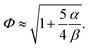 | (18) |
The difference between
eqn (18) and the simulation results shown in
Fig. 4 does not exceed 1.5% which is comparable with the statistical measurement error in the numerical experiment. Substituting
eqn (18) into
eqn (10) in the limit
β/
α → ∞, we obtain
eqn (6). For
β/
α ≪ 1,
eqn (18) provides a better agreement with the simulation results than
eqn (12). In the latter case (in contrast to
eqn (6)), the contribution from the driving force (self-propulsion) to the effective (long-time) diffusion coefficient is independent on the rotational diffusion coefficient:
| | 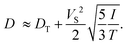 | (19) |
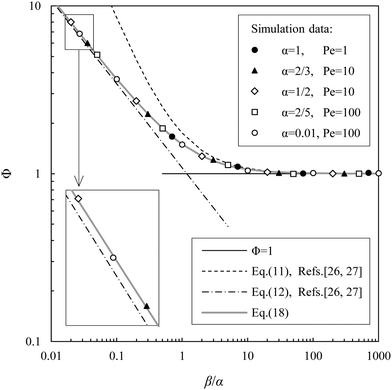 |
| | Fig. 4 Dimensionless correction Φ for the effective (long-time) diffusion coefficient D in dependence on the ratio β/α, see eqn (10). Simulation results for various sets of α and Pe are marked with symbols, and were calculated as Φ = 2Pe−2(D/DT − 1), where D is the average value of MSD(τ) at times τ > 100max[ν−1,ω−1]. | |
Up to this point, we have calculated the MSD for the x-projection. Since the medium is considered homogeneous, then 〈x2〉 = 〈y2〉, and for the particle position vector, we simply get 〈r2(τ)〉 = 2〈x2(τ)〉 = 4Dτ.
3.2.2 Persistent random walk in the direction of the initial driving force.
Fig. 5 represents the mean linear displacement (MLD) of a self-propelled Brownian sphere along the direction of its initial orientation (see ![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) in Fig. 1) which was calculated numerically for fixed α and various sets of (β, γ), and normalized to LS ≡ VS/ω. In addition to the simulation results, Fig. 5 also shows the plot of eqn (8) derived for an overdamped active Brownian particle.13,23 This comparison reveals that eqn (8) is valid only for β/α ≫ 1. The persistence length L of a self-propelled Brownian particle was calculated as an average value of MLD(τ) at times τ ≳ 100max[ν−1,ω−1]. The normalized persistence length L/LS is shown in Fig. 6 in dependence on the inertial delay number β for various sets of α and γ. The numerically obtained values of L/LS turned out to be independent of the dimensionless self-propulsion velocity γ. To fit the numerical data for all values of α and β, we propose the following dimensionless correction for the persistence length of a self-propelled Brownian sphere:
in Fig. 1) which was calculated numerically for fixed α and various sets of (β, γ), and normalized to LS ≡ VS/ω. In addition to the simulation results, Fig. 5 also shows the plot of eqn (8) derived for an overdamped active Brownian particle.13,23 This comparison reveals that eqn (8) is valid only for β/α ≫ 1. The persistence length L of a self-propelled Brownian particle was calculated as an average value of MLD(τ) at times τ ≳ 100max[ν−1,ω−1]. The normalized persistence length L/LS is shown in Fig. 6 in dependence on the inertial delay number β for various sets of α and γ. The numerically obtained values of L/LS turned out to be independent of the dimensionless self-propulsion velocity γ. To fit the numerical data for all values of α and β, we propose the following dimensionless correction for the persistence length of a self-propelled Brownian sphere:| | 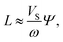 | (20) |
where| | 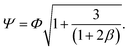 | (21) |
The difference between eqn (21) and the simulation results shown in Fig. 6 is within 5% at β ∼ 1 and does not exceed 2% for large and small values of β. In the limit β → ∞, we get L ≈ LS. And it turns out that for small β, the persistence length of a self-propelled Brownian sphere is independent on the rotational diffusion coefficient:| | 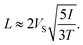 | (22) |
 |
| | Fig. 5 Normalized mean linear displacement 〈![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (t)〉/LS of a self-propelled Brownian sphere (α = 2/5) in the direction of the initial driving force for (blue) β = 104, (green) β = 1, (red) β = 10−2 and (△)γ = 0.1, (◊) γ = 1, (○) γ = 10. The symbols show the results of numerical simulation, the solid gray line plots eqn (8). Here the time is normalized to the inverse coefficient of rotational diffusion ω−1. (t)〉/LS of a self-propelled Brownian sphere (α = 2/5) in the direction of the initial driving force for (blue) β = 104, (green) β = 1, (red) β = 10−2 and (△)γ = 0.1, (◊) γ = 1, (○) γ = 10. The symbols show the results of numerical simulation, the solid gray line plots eqn (8). Here the time is normalized to the inverse coefficient of rotational diffusion ω−1. | |
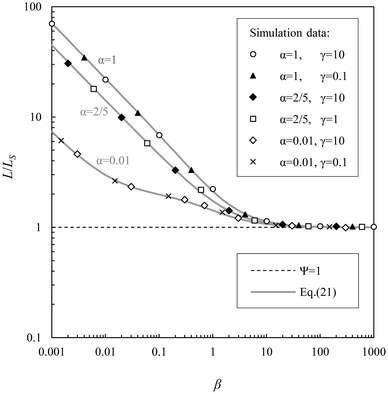 |
| | Fig. 6 Normalized persistence length Lω/VS in dependence on β, where L is an average value of MLD(τ) at times τ > 100max[ν−1,ω−1]. | |
3.2.3 Persistent random walk in the direction of the initial movement.
In the above section, as in previous studies,3,13,23 the mean linear displacement of an active particle was determined along its initial self-propulsion velocity, i.e., along the orientation vector n(0). However, in real experiments with self-propelled spherical particles, it could be difficult to distinguish between the thermal and self-propulsion components of the total particle velocity. In this case, the mean linear displacement could be determined along the direction of the initial total velocity of the particle, i.e., along ṙ(0), as shown in Fig. 1. Here, the mean linear displacement of the simulated particle in the direction of its initial motion (MLD*) was calculated as follows:| | 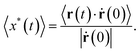 | (23) |
Fig. 7 represents the numerically calculated MLD* of the self-propelled Brownian sphere for fixed α and various sets of β and γ. In addition to the simulation results, Fig. 7 also shows the plots of eqn (8) and theoretical MLD* for a passive Brownian particle, which is written as:| | 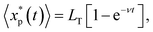 | (24) |
where LT = 〈VT〉ν−1 is the effective persistence length of a passive particle with an initial velocity equal to the arithmetic mean velocity of its Brownian motion in two-dimensional space, i.e., 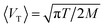 . Fig. 7 reveals that eqn (8) describes the MLD* only for β ≫ 1 and γ ≫ 1.
. Fig. 7 reveals that eqn (8) describes the MLD* only for β ≫ 1 and γ ≫ 1.
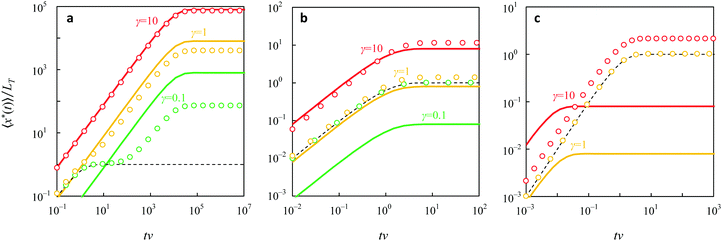 |
| | Fig. 7 Normalized mean linear displacement 〈x*(t)〉/LT of a self-propelled Brownian particle (α = 2/5) in the direction of its initial motion for (a) β = 104, (b) β = 1, (c) β = 10−2 and (green) γ = 0.1, (yellow) γ = 1, (red) γ = 10. The symbols show the results of numerical simulation, the solid bold lines plot eqn (8), and the thin dotted line plots eqn (24) for the passive particle (γ = 0). Here the time is normalized to the momentum relaxation time τp = ν−1. | |
At long observation times (t ≫ max[ν−1,ω−1]) the MLD* function tends to the effective persistence length L* for all values of β and γ. The following simple expression for L* can be used to approximate the numerical data for γ ≲ 1 and all values of β, as well as for β ≫ 1 and all values of γ:
| | | L* ≈ LT + LS(1 + γ−1)−1. | (25) |
The numerically calculated
L* normalized to {
LT +
LS/(1 + 1/
γ)} is plotted in
Fig. 8 as a function of
β and clearly shows the validity range of
eqn (25). For numerical data,
L* was obtained as an average value of MLD*(
τ) at times
τ ≳ 100max[
ν−1,
ω−1]. The effective persistence length of an active particle with low activity (
γ ≪ 1) tends to the persistence length of a passive particle (
i.e.,
L* ≈
LT) only at relatively low friction (
β ≪ 1), and in the opposite case (
β ≫ 1) it depends on the Péclet number:
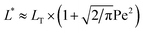
. For strong activity (
γ ≫ 1) and high friction (
β ≫ 1), we get
L* ≈
LS. However, we have not been able to find a simple and physically sound approximation for the effective persistence length of an active particle for
β ≪ 1 and
γ ≫ 1. In this case, additional information on the correlation of the particle velocities caused by two different random processes (
ξx and
ξθ) is required. This is the subject of a separate analytical study and is beyond the scope of this work.
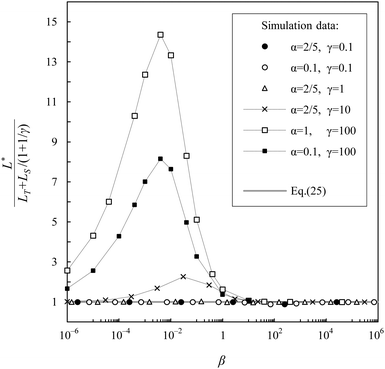 |
| | Fig. 8 The numerically calculated effective persistence length L* normalized to {LT + LS/(1 + 1/γ)} as a function of β. | |
4. Discussion
Fig. 3 and 5 show that the MSD and MLD functions obtained for the same Péclet number and different inertial delay numbers differ markedly. Therefore, the Péclet number cannot be a universal comparative characteristic (measure) of self-propulsion. Our simulation reveals that the MSD and MLD functions of a self-propelled spherical particle with a given mass distribution over its volume (α) significantly depend on two independent dimensionless parameters: the inertial delay number (β) and the dimensionless self-propulsion velocity (γ). Moreover, the ratio of long-time to short-time diffusion coefficients is completely determined by (α, β, γ): from eqn (2), (10) and (18) we get  .
.
For both underdamped and overdamped classical Brownian motion, the inertialess (overdamped) Langevin equation provides a quantitative description of the dynamics of a passive Brownian particle at long time scales (t ≫ ν−1) regardless of the damping rate in the medium. As for active Brownian motion, comparison of the numerically calculated MSD and MLD functions with the existing analytical solutions (5) and (8) clearly shows that the overdamped Langevin equations fail to describe the long-time behavior of an active Brownian particle when its friction coefficient is not so high compared to the rotational diffusion coefficient, i.e., β ≲ 1. For β ≫ 1 the translational inertia of particle's active Brownian motion is important only at the shortest time scale (t ≲ ν−1), while the rotational inertia can be completely neglected. In the opposite case (β ≲ 1), the rotational inertia of an active particle plays an essential role at all time scales.
For overdamped active Brownian motion (β ≫ 1) with a small dimensionless self-propulsion velocity (γ ≪ 1), both the MSD and MLD functions exhibit four consecutive regimes of motion separated by three prominent crossovers (see Fig. 3a and 7a). It should be noted here that in experiments with colloidal particles,2–4,28 the first two crossovers at short and intermediate time scales are beyond the temporal and spatial resolutions of typical observation equipment. As γ increases, the intermediate crossover merges with the others, and for γ ≫ 1, only one crossover is found at t ∼ ω−1. In this limit, the numerically calculated MSD agrees with a persistent random walk of a living cell and a non-living active particle in the absence of velocity fluctuations.24,33
Based on our simulations, we can conclude that a self-propelled particle with a large self-propulsion velocity (γ ≫ 1) and a large inertial delay number (β ≫ 1) behaves like a passive Brownian particle in a medium with significantly less effective friction νeff ∼ ν/β and high temperature Teff ≈ γ2T/2.
As the particle's rotational diffusion increases, motion becomes more random and less directed. For underdamped motion with β/α ≲ 1 and any self-propulsion velocity, we obtain that both the MSD and MLD functions have single crossovers at t1 ∼ ν−1 (see Fig. 3b and 7b). Thus, in the limit β ≪ 1, our simulation does not support the theoretical prediction32 that a single crossover of the MSD function should be at point t1 ∼ ω−1. Our finding is that a random walk of an active Brownian particle in the underdamped limit corresponds to a passive particle in a medium with the same viscosity but with a higher temperature  .
.
In the classical description, the translational diffusion coefficient of a spherical Brownian particle is written as
| | 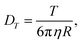 | (26) |
where
η is the dynamic viscosity of a medium. Given
eqn (1), (2) and (26), it is easy to get
| | 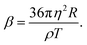 | (27) |
For a typical micron-sized colloidal particle in a liquid medium with a dynamic viscosity of 10−3÷10−1 Pa s at room temperature, we obtain β ∼ 107÷1011. In experiments with laboratory complex plasmas, argon at pressures P ∼ 1÷10 Pa is usually used as a buffer gas.34 In this case, the coefficient of dynamic viscosity can be calculated using the Epstein formula:35
| | 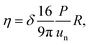 | (28) |
where
δ = 0.5 + π/8 for specular reflection of neutrals from the particle surface and
δ = 1 + π/8 for complete accommodation,
36,37 and
un is the average thermal velocity of neutrals. Taking into account
eqn (28), we find that at low gas pressures,
β is proportional to
P2 and
R3. Thus, in highly rarefied media, the inertial delay number can vary over a wide range. For example,
β ∼ 0.1 for a particle with
R = 10 μm at a pressure of 1 Pa, and
β ∼ 10 for
R = 10 μm and
P = 10 Pa. Here, we assume that
T is equal to room temperature. However, it is worth noting that the kinetic temperature of a single Brownian particle levitating in a gas discharge at room temperature can be higher (usually up to two times).
38–40 With such combinations of experimental parameters, the existing statistical theories developed for the underdamped and overdamped limits of active Brownian motion are inapplicable, see
Fig. 4. These simple estimates show that in experiments with active Brownian particles in rarefied gas media, including weakly ionized plasmas, both overdamped and underdamped motions are possible. The transition from overdamped to underdamped motion is easily accomplished by changing the buffer gas pressure. In addition to Janus particles in a gas-discharge plasma,
14,15 suitable conditions can be realized for self-propelled particle pairs
41,42 formed by the effective nonreciprocal forces of the wake-mediated interaction between microparticles.
43 Another unusual example of underdamped active Brownian motion is the so-called vibrobots, which convert vibrational energy into directed motion using their tilted elastic legs.
27,44
A non-obvious question to ask is what kind of motion would one expect for a self-propelled particle in ‘nonviscous’ fluids.3 A promising example would be the so-called superfluid microswimmer: a Janus particle suspended in superfluid helium self-propels due to the transformation of the superfluid to a normal fluid on the heated side of the particle.45 This situation can arise both in bulk46 and under a free surface of superfluid helium.47 At a temperature of 1.6 K the viscosity of liquid helium is 1.3 × 10−6 Pa s.48 Of course, for a realistic description of particle motion under such conditions, the ‘particle–quantum vortex’ interaction must be taken into account.49 However, using our simple (non-quantum) formalism, we can estimate that the momentum relaxation time of such a particle with R = 10 μm can be τp = (2/9)R2ρ/η ∼ 20 ms and the inertial delay number β can be ∼105. Although this time scale is available for a typical visualization system, instead of both short-time ballistic and diffusion regimes, an enhanced propulsive (ballistic) regime will be observed due to the huge self-propulsion velocity of the Janus particle (γ ≫ 1).45 This directional movement, in turn, can be interrupted by periodic releases of quantum vortices and be limited by the finite dimensions of the experimental setup.
The two-dimensional model for active Brownian motion considered here can be generalized to three spatial dimensions. Taking into account the third dimension in the individual dynamics of a particle, does not bring any new physical effects but can change (by a factor of ≲ 3) the values of the calculated constants.29 In any case, this may become a topic for the next study. And in contrast to the individual dynamics, the collective dynamics can differ significantly for two and three dimensions.1,3,29,34
5. Conclusions
In summary, at present, there is a lack of statistical theory describing underdamped Brownian motion of a self-propelled particle at all time scales. We carried out the numerical simulation of active Brownian motion in media of different viscosities. For this purpose, we used a mathematical model a self-propelled Brownian sphere with translational and rotational inertia. It was shown that in contrast to underdamped passive Brownian motion, the inertialess Langevin equations fail to describe the diffusive regime of underdamped active Brownian motion. The time-dependent mean square displacement and mean linear displacement (the noise-averaged trajectory) of the particle were investigated as a function of medium viscosity, self-propulsion velocity and moment of inertia. It was shown that the Péclet number, which is often used in active colloids, cannot be applied as a comparative characteristic (measure) of self-propulsion of active Brownian particles in media with very different viscosities. Our simulation revealed that the dynamics of a self-propelled Brownian spherical particle with a given mass distribution over its volume significantly depends on two independent dimensionless parameters of the particle: the ratio of the self-propulsion velocity to the characteristic thermal velocity and the ratio of the friction coefficient to the rotational diffusion coefficient.
We propose simple corrections to the basic theory of overdamped active Brownian motion, which allow one to calculate the effective diffusion coefficient and the persistence length of a self-propelled Brownian particle in media with any dynamic viscosities. The obtained corrections perfectly describe the results of numerical simulation over the entire viscosity range. Moreover, in the underdamped limit, our diffusion correction provides a better agreement with the simulation than the correction proposed earlier in ref. 13, 26 and 27.
We also proposed to calculate the mean linear displacement of an active particle not along its initial self-propulsion velocity, but along the initial orientation of the total particle velocity (including its thermal component). This approach is justified, because in real experiments with self-propelled Brownian particles of a spherical shape, it could be difficult to distinguish between the thermal and self-propulsion velocity components. Based on the results of numerical simulation, a simple semiempirical correction was also proposed, which makes it possible to calculate the effective persistence length of a self-propelled Brownian particle in this reference frame.
Our results can be useful for describing motion of self-propelled particles on a vibrating plate or suspended in gaseous media and nonviscous fluids. In particular, laboratory experiments with self-propelled particles in a weakly ionized gas discharge plasma have great potential for studying active Brownian motion since they enable to control the damping rate of the medium over a wide range.
Conflicts of interest
There are no conflicts to declare.
References
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Active brownian particles, Eur. Phys. J.: Spec. Top., 2012, 202(1), 1–162 CAS.
- I. S. Aranson, Active colloids, Phys.-Usp., 2013, 56(1), 79 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88(4), 045006 CrossRef.
- J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Self-motile colloidal particles: from directed propulsion to random walk, Phys. Rev. Lett., 2007, 99(4), 048102 CrossRef PubMed.
- G. Volpe, I. Buttinoni, D. Vogt, H. J. Kümmerer and C. Bechinger, Microswimmers in patterned environments, Soft Matter, 2011, 7(19), 8810–8815 RSC.
- H. R. Jiang, N. Yoshinaga and M. Sano, Active motion of a Janus particle by self-thermophoresis in a defocused laser beam, Phys. Rev. Lett., 2010, 105(26), 268302 CrossRef PubMed.
- R. Golestanian, Debut of a hot “fantastic voyager”, Physics, 2010, 3, 108 CrossRef.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- D. Nishiguchi and M. Sano, Mesoscopic turbulence and local order in Janus particles self-propelling under an ac electric field, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(5), 052309 CrossRef PubMed.
- T. Y. Molotilin, V. Lobaskin and O. I. Vinogradova, Electrophoresis of Janus particles: A molecular dynamics simulation study, J. Chem. Phys., 2016, 145(24), 244704 CrossRef PubMed.
- J. Li, V. V. Singh, S. Sattayasamitsathit, J. Orozco, K. Kaufmann, R. Dong and J. Wang, Water-driven micromotors for rapid photocatalytic degradation of biological and chemical warfare agents, ACS Nano, 2014, 8(11), 11118–11125 CrossRef CAS PubMed.
- A. Walther and A. H. E. Müller, Janus particles: Synthesis, selfassembly, physical properties, and applications, Chem. Rev., 2013, 113, 5194 CrossRef CAS PubMed.
- H. Löwen, Inertial effects of self-propelled particles: From active Brownian to active Langevin motion, J. Chem. Phys., 2020, 152(4), 040901 CrossRef PubMed.
- V. Nosenko, F. Luoni, A. Kaouk, M. Rubin-Zuzic and H. Thomas, Active Janus particles in a complex plasma, Phys. Rev. Res., 2020, 2(3), 033226 CrossRef CAS.
- K. Arkar, M. M. Vasiliev, O. F. Petrov, E. A. Kononov and F. M. Trukhachev, Dynamics of Active Brownian Particles in Plasma, Molecules, 2021, 26(3), 561 CrossRef CAS PubMed.
- C. R. Du, V. Nosenko, H. M. Thomas, A. Müller, A. M. Lipaev, V. I. Molotkov, V. E. Fortov and A. V. Ivlev, Photophoretic force on microparticles in complex plasmas, New J. Phys., 2017, 19, 073015 CrossRef.
- F. Wieben and D. Block, Photophoretic force measurement on microparticles in binary complex plasmas, Phys. Plasmas, 2018, 25, 123705 CrossRef.
- X. G. Koss, O. F. Petrov, K. B. Statsenko and M. M. Vasiliev, Small systems of laser-driven active Brownian particles: Evolution and dynamic entropy, EPL, 2018, 124(4), 45001 CrossRef.
- K. A. Valiev and E. N. Ivanov, “Rotational Brownian motion”, Sov. Phys. – Usp., 1973, 16, 1–16 CrossRef.
- R. Gerling and A. Hüller, Langevin model of the rotational diffusion of molecules, Z. Phys. B: Condens. Matter, 1980, 40(3), 209–217 CrossRef.
- G. Falasco, M. V. Gnann, D. Rings and K. Kroy, Effective temperatures of hot Brownian motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(3), 032131 CrossRef CAS PubMed.
- A. M. Ignatov, S. A. Trigger, S. A. Maiorov and W. Ebeling, Rotational kinetics of absorbing dust grains in neutral gas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(4), 046413 CrossRef CAS PubMed.
- B. ten Hagen, S. van Teeffelen and H. Löwen, Brownian motion of a self-propelled particle, J. Phys.: Condens. Matter, 2011, 23(19), 194119 CrossRef CAS PubMed.
- H. G. Othmer, S. R. Dunbar and W. Alt, Models of dispersal in biological systems, J. Math. Biol., 1988, 26(3), 263–298 CrossRef CAS PubMed.
- G. E. Uhlenbeck and L. S. Ornstein, “On the theory of the Brownian motion,”, Phys. Rev., 1930, 36, 823–841 CrossRef CAS.
- P. K. Ghosh, Y. Li, G. Marchegiani and F. Marchesoni, Communication: Memory effects and active Brownian diffusion, J. Chem. Phys., 2015, 143(21), 211101, DOI:10.1063/1.4936624.
- C. Scholz, S. Jahanshahi, A. Ldov and H. Löwen, Inertial delay of self-propelled particles, Nat. Commun., 2018, 9, 5156 CrossRef PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Physics of microswimmers—single particle motion and collective behavior: A review, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- A. Zöttl and H. Stark, Emergent behavior in active colloids, J. Phys.: Condens. Matter, 2016, 28(25), 253001 CrossRef.
-
A. A. Ovchinnikov, S. F. Timashev and A. A. Belyi, Kinetics of Diffusion-Controlled Chemical Processes, Nova Science, Commack, NY, 1989 Search PubMed.
- O. S. Vaulina, X. G. Adamovich, O. F. Petrov and V. E. Fortov, Evolution of the mass-transfer processes in nonideal dissipative systems. I. Numerical simulation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(6), 066403 CrossRef CAS PubMed.
- F. Peruani and L. G. Morelli, Self-propelled particles with fluctuating speed and direction of motion in two dimensions, Phys. Rev. Lett., 2007, 99(1), 010602 CrossRef PubMed.
-
A. Mikhailov and D. Meinköhn, Self-motion in physico-chemical systems far from thermal equilibrium, Stochastic Dynamics, Springer, Berlin, Heidelberg, 1997, pp. 334–345 Search PubMed.
-
V. E. Fortov and G. E. Morfill, Complex and Dusty Plasmas: From Laboratory to Space, CRC Press, Boca Raton, 2009 Search PubMed.
- P. S. Epstein, On the resistance experienced by spheres in their motion through gases, Phys. Rev., 1924, 23(6), 710 CrossRef CAS.
-
N. A. Fuchs, The mechanics of aerosols, Dover, New York, 1964 Search PubMed.
-
E. M. Lifshitz and L. P. Pitaevskii, Physical kinetics, Butterworth Heinemann, 1981 Search PubMed.
- C. Schmidt and A. Piel, Stochastic heating of a single Brownian particle by charge fluctuations in a radio-frequency produced plasma sheath, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(4), 043106 CrossRef PubMed.
- J. Kong, K. Qiao, L. S. Matthews and T. W. Hyde, Temperature measurement of a dust particle in a RF plasma GEC reference cell, J. Plasma Phys., 2016, 82, 905820505 CrossRef.
- M. Rubin-Zuzic, V. Nosenko, S. Zhdanov, A. Ivlev, H. Thomas, S. Khrapak and L. Couedel, Single particle dynamics in a radio-frequency produced plasma sheath, AIP Conf. Proc., 2018, 1925, 020023 CrossRef.
- V. Nosenko, S. K. Zhdanov, H. M. Thomas, J. Carmona-Reyes and T. W. Hyde, Spontaneous formation and spin of particle pairs in a single-layer complex plasma crystal, EPL, 2015, 112(4), 45003 CrossRef.
- J. Bartnick, A. Kaiser, H. Löwen and A. V. Ivlev, Emerging activity in bilayered dispersions with wake-mediated interactions, J. Chem. Phys., 2016, 144(22), 224901 CrossRef PubMed.
- E. A. Lisin, O. F. Petrov, E. A. Sametov, O. S. Vaulina, K. B. Statsenko, M. M. Vasiliev, J. Carmona-Reyes and T. W. Hyde, Experimental study of the nonreciprocal effective interactions between microparticles in an anisotropic plasma, Sci. Rep., 2020, 10, 13653 CrossRef CAS PubMed.
- L. Giomi, N. Hawley-Weld and L. Mahadevan, Swarming, swirling and stasis in sequestered bristle-bots, Proc. R. Soc. A, 2013, 469(2151), 20120637 CrossRef.
- G. V. Kolmakov and I. S. Aranson, Superfluid swimmers, Phys. Rev. Res., 2021, 3(1), 013188 CrossRef CAS.
- G. P. Bewley, K. R. Sreenivasan and D. P. Lathrop, Particles for tracing turbulent liquid helium, Exp. Fluids, 2008, 44(6), 887–896 CrossRef CAS.
- P. Moroshkin, P. Leiderer, K. Kono, S. Inui and M. Tsubota, Dynamics of the vortex-particle complexes bound to the free surface of superfluid helium, Phys. Rev. Lett., 2019, 122(17), 174502 CrossRef CAS PubMed.
- R. J. Donnelly and C. F. Barenghi, The observed properties of liquid helium at the saturated vapor pressure, J. Phys. Chem. Ref. Data, 1998, 27(6), 1217–1274 CrossRef CAS.
- Y. A. Sergeev, C. F. Barenghi and D. Kivotides, Motion of micron-size particles in turbulent helium II, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(18), 184506 CrossRef.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
O. S.
Vaulina
,
I. I.
Lisina
and
O. F.
Petrov
*,
O. S.
Vaulina
,
I. I.
Lisina
and
O. F.
Petrov
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ], where θ(t) is the angle between the x-axis and n, see Fig. 1. Let us assume that due to some driving force acting along n, the particle moves in a medium with a velocity VS = VSn. The direction of n is determined by the random rotation of the particle, the characteristic frequency of which ω is equal to the rotational diffusion coefficient. Neglecting the drag effect of the medium, for purely thermal noise and a spherically symmetric particle of radius R in bulk situations we have
θ], where θ(t) is the angle between the x-axis and n, see Fig. 1. Let us assume that due to some driving force acting along n, the particle moves in a medium with a velocity VS = VSn. The direction of n is determined by the random rotation of the particle, the characteristic frequency of which ω is equal to the rotational diffusion coefficient. Neglecting the drag effect of the medium, for purely thermal noise and a spherically symmetric particle of radius R in bulk situations we have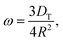
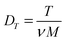
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] + ξx(t),
θ] + ξx(t),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] + ξy(t),
θ] + ξy(t),![[greek theta with two dots above]](https://www.rsc.org/images/entities/i_char_e1a7.gif) (t) = −μ
(t) = −μ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) (t) + ξθ(t),
(t) + ξθ(t),![[greek theta with two dots above]](https://www.rsc.org/images/entities/i_char_e1a7.gif) (t) = 0. The inertialess Langevin equations provide a quantitative description of the overdamped particle dynamics at the long-time scale (t ≫ ν−1). In particular, the mean square displacement (MSD) of an overdamped self-propelled Brownian particle in an arbitrary direction is described by the following equation:4,23
(t) = 0. The inertialess Langevin equations provide a quantitative description of the overdamped particle dynamics at the long-time scale (t ≫ ν−1). In particular, the mean square displacement (MSD) of an overdamped self-propelled Brownian particle in an arbitrary direction is described by the following equation:4,23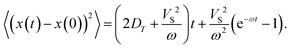

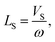
![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) axis along the vector of the particle's self-propulsion velocity at t = 0, as shown in Fig. 1, then the mean linear displacement (MLD) of an active colloidal particle is described by the following equation:3,13,23
axis along the vector of the particle's self-propulsion velocity at t = 0, as shown in Fig. 1, then the mean linear displacement (MLD) of an active colloidal particle is described by the following equation:3,13,23![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (t)〉 = LS[1 − e−ωt].
(t)〉 = LS[1 − e−ωt].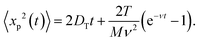
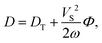
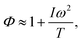
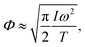
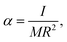
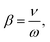
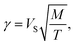
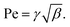
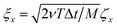 and
and 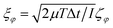 , where Δt is an integration step and ζi is a Gaussian random number with zero mean and unit variance. The integration step Δt was less than 0.05 min[μ−1,ω−1].
, where Δt is an integration step and ζi is a Gaussian random number with zero mean and unit variance. The integration step Δt was less than 0.05 min[μ−1,ω−1].

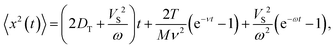
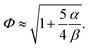
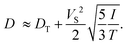

![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) in Fig. 1) which was calculated numerically for fixed α and various sets of (β, γ), and normalized to LS ≡ VS/ω. In addition to the simulation results, Fig. 5 also shows the plot of eqn (8) derived for an overdamped active Brownian particle.13,23 This comparison reveals that eqn (8) is valid only for β/α ≫ 1. The persistence length L of a self-propelled Brownian particle was calculated as an average value of MLD(τ) at times τ ≳ 100max[ν−1,ω−1]. The normalized persistence length L/LS is shown in Fig. 6 in dependence on the inertial delay number β for various sets of α and γ. The numerically obtained values of L/LS turned out to be independent of the dimensionless self-propulsion velocity γ. To fit the numerical data for all values of α and β, we propose the following dimensionless correction for the persistence length of a self-propelled Brownian sphere:
in Fig. 1) which was calculated numerically for fixed α and various sets of (β, γ), and normalized to LS ≡ VS/ω. In addition to the simulation results, Fig. 5 also shows the plot of eqn (8) derived for an overdamped active Brownian particle.13,23 This comparison reveals that eqn (8) is valid only for β/α ≫ 1. The persistence length L of a self-propelled Brownian particle was calculated as an average value of MLD(τ) at times τ ≳ 100max[ν−1,ω−1]. The normalized persistence length L/LS is shown in Fig. 6 in dependence on the inertial delay number β for various sets of α and γ. The numerically obtained values of L/LS turned out to be independent of the dimensionless self-propulsion velocity γ. To fit the numerical data for all values of α and β, we propose the following dimensionless correction for the persistence length of a self-propelled Brownian sphere: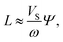
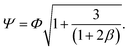
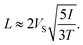

![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (t)〉/LS of a self-propelled Brownian sphere (α = 2/5) in the direction of the initial driving force for (blue) β = 104, (green) β = 1, (red) β = 10−2 and (△)γ = 0.1, (◊) γ = 1, (○) γ = 10. The symbols show the results of numerical simulation, the solid gray line plots eqn (8). Here the time is normalized to the inverse coefficient of rotational diffusion ω−1.
(t)〉/LS of a self-propelled Brownian sphere (α = 2/5) in the direction of the initial driving force for (blue) β = 104, (green) β = 1, (red) β = 10−2 and (△)γ = 0.1, (◊) γ = 1, (○) γ = 10. The symbols show the results of numerical simulation, the solid gray line plots eqn (8). Here the time is normalized to the inverse coefficient of rotational diffusion ω−1.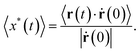
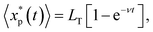
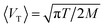 . Fig. 7 reveals that eqn (8) describes the MLD* only for β ≫ 1 and γ ≫ 1.
. Fig. 7 reveals that eqn (8) describes the MLD* only for β ≫ 1 and γ ≫ 1.

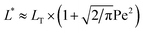 . For strong activity (γ ≫ 1) and high friction (β ≫ 1), we get L* ≈ LS. However, we have not been able to find a simple and physically sound approximation for the effective persistence length of an active particle for β ≪ 1 and γ ≫ 1. In this case, additional information on the correlation of the particle velocities caused by two different random processes (ξx and ξθ) is required. This is the subject of a separate analytical study and is beyond the scope of this work.
. For strong activity (γ ≫ 1) and high friction (β ≫ 1), we get L* ≈ LS. However, we have not been able to find a simple and physically sound approximation for the effective persistence length of an active particle for β ≪ 1 and γ ≫ 1. In this case, additional information on the correlation of the particle velocities caused by two different random processes (ξx and ξθ) is required. This is the subject of a separate analytical study and is beyond the scope of this work.
 .
.
 .
.