Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dipolar repulsion in α-halocarbonyl compounds revisited†
Daniela
Rodrigues Silva
 ab,
Lucas
de Azevedo Santos
ab,
Lucas
de Azevedo Santos
 ab,
Trevor A.
Hamlin
ab,
Trevor A.
Hamlin
 a,
F. Matthias
Bickelhaupt
a,
F. Matthias
Bickelhaupt
 *ac,
Matheus
P. Freitas
*ac,
Matheus
P. Freitas
 *b and
Célia
Fonseca Guerra
*b and
Célia
Fonseca Guerra
 *ad
*ad
aDepartment of Theoretical Chemistry, Amsterdam Institute of Molecular and Life Sciences (AIMMS), Amsterdam Center for Multiscale Modeling (ACMM), Vrije Universiteit Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands. E-mail: f.m.bickelhaupt@vu.nl; c.fonsecaguerra@vu.nl
bDepartamento de Química, Instituto de Ciências Naturais, Universidade Federal de Lavras, 37200-900, Lavras, MG, Brazil. E-mail: matheus@ufla.br
cInstitute for Molecules and Materials (IMM), Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands
dLeiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, Einsteinweg 55, 2333 CC Leiden, The Netherlands
First published on 1st September 2021
Abstract
The concept of dipolar repulsion has been widely used to explain several phenomena in organic chemistry, including the conformational preferences of carbonyl compounds. This model, in which atoms and bonds are viewed as point charges and dipole moment vectors, respectively, is however oversimplified. To provide a causal model rooted in quantitative molecular orbital theory, we have analyzed the rotational isomerism of haloacetaldehydes OHC–CH2X (X = F, Cl, Br, I), using relativistic density functional theory. We have found that the overall trend in the rotational energy profiles is set by the combined effects of Pauli repulsion (introducing a barrier around gauche that separates minima at syn and anti), orbital interactions (which can pull the anti minimum towards anticlinal to maximize hyperconjugation), and electrostatic interactions. Only for X = F, not for X = Cl–I, electrostatic interactions push the preference from syn to anti. Our bonding analyses show how this trend is related to the compact nature of F versus the more diffuse nature of the heavier halogens.
Introduction
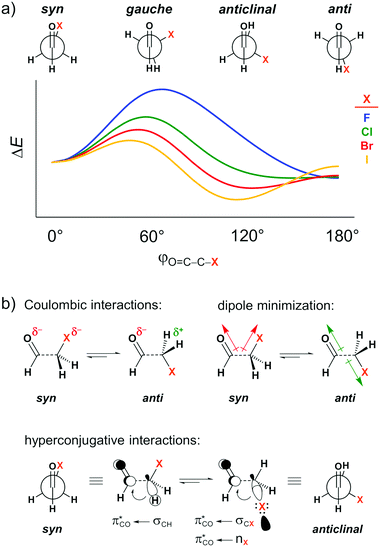
The carbonyl group is one of the most common functional groups in organic chemistry. Its unique chemistry renders the carbonyl group a site for a wide spectrum of chemical transformations1 and interactions2 that govern the structure of important biological systems, such as proteins,3 and nucleic acids.4 Attempts to understand and rationalize the structure and properties of compounds bearing a carbonyl group abound.5 In particular, the forces underlying their conformational preferences, and the resulting influence on their physical, chemical, and biological properties, have intrigued organic chemists for decades.6Several theoretical7 and experimental8 studies have explored the conformational landscape of haloacetaldehydes OHC–CH2X (X = F, Cl, Br, I) as archetypal model systems to investigate the main intramolecular interactions involving the carbonyl group. The rotation around the C–C bond in these systems results in the energy profile schematically illustrated in Fig. 1a. The relative conformational stability has typically been ascribed to dipolar interactions, that is, the syn conformer (i.e., φO=C–C–X = 0°) experiences a strong electrostatic repulsion between the partially negatively charged oxygen and halogen atoms, which shifts the conformational equilibrium to anti (i.e., φO=C–C–X = 180°; see Coulombic interactions in Fig. 1b).7a This is equivalent to the explanation that the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–X bond dipoles in the O
C and C–X bond dipoles in the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–X arrangement achieve the most or least unfavorable dipole–dipole interaction in the case of maximum (syn) or minimal (anti) overall dipole moment (see dipole minimization in Fig. 1b).9 The same rationalization has also been used to explain conformational energies in other systems containing polar groups, such as in the anomeric effect.10 Additionally, for heavier haloacetaldehydes, it is argued that the global energy minimum gradually shifts from the anti to the anticlinal conformation (i.e., φO=C–C–X = 120°) because of the better donor ability of the σCX orbital to engage in stabilizing orbital interaction with the π*CO orbital of the carbonyl group as X goes from F to I (see hyperconjugative interactions in Fig. 1b).7a,11
C–C–X arrangement achieve the most or least unfavorable dipole–dipole interaction in the case of maximum (syn) or minimal (anti) overall dipole moment (see dipole minimization in Fig. 1b).9 The same rationalization has also been used to explain conformational energies in other systems containing polar groups, such as in the anomeric effect.10 Additionally, for heavier haloacetaldehydes, it is argued that the global energy minimum gradually shifts from the anti to the anticlinal conformation (i.e., φO=C–C–X = 120°) because of the better donor ability of the σCX orbital to engage in stabilizing orbital interaction with the π*CO orbital of the carbonyl group as X goes from F to I (see hyperconjugative interactions in Fig. 1b).7a,11
 | ||
| Fig. 1 (a) Stationary points in the energy profile for rotation around the C–C bond of haloacetaldehydes and (b) intramolecular interactions used to rationalize the conformational preferences. | ||
The above concept of dipolar repulsion depicts the electrostatic interaction as deriving from the sum of pairwise interactions between atoms that follows Coulomb's law for the respective point charges; this same representation can also be found in organic chemistry textbooks.12 However, the validity of such an oversimplified picture, the treatment of atoms as point charges, has been questioned in the literature. It can lead to incorrect predictions in, for instance, rationalizing the factors governing the conformational preferences of small organic molecules,13 chemical bonding,14 and non-covalent interactions.15 Molecules are characterized by a more complex charge distribution of nuclei and a 3-dimensional electron charge density that, more often than not, does not behave as a collection of point charges.14b For example, some diatomic molecules, such as N2 and O2, would not be bound without the contribution from the attractive electrostatic component,14a while the negative end of the dipole moment vector of the CO molecule lies on the partially positively charged carbon because the σ C–O HOMO has a large, lone-pair like lobe, colinear with, and pointing away from, the CO molecule.16
In this work, we have, therefore, analyzed the rotational isomerism of haloacetaldehydes OHC–CH2X (X = F, Cl, Br, and I, see Fig. 1) within the framework of quantitative Kohn–Sham molecular orbital (KS-MO) theory to reveal the physical mechanism behind the conformational preferences. In particular, we have investigated the role of dipolar repulsion as compared to other features in the bonding mechanism. Our bonding analyses show how the overall trend in the rotational energy profiles is set by the combined effects of Pauli repulsion, orbital interactions, and electrostatic interactions. Pauli repulsion, as will be explained, introduces a rotational barrier around gauche which separates minima at syn and anti. In addition, orbital interactions can pull the anti minimum towards a more anticlinal conformation to maximize hyperconjugation. And, only for X = F, not for X = Cl–I, electrostatic interactions push the preference from syn to anti. Our results furthermore reveal how this trend in electrostatic interactions is related to the compact nature of F, which shows behavior that is reminiscent of a partially negative point charge that has Coulomb repulsion with the partially negative O. At variance, the more diffuse nature of the heavier halogens X = Cl–I causes a more pronounced overlap of charge densities between O and X, which goes with a breakdown of the point-charge picture. The most striking consequence is a net stabilizing electrostatic interaction due to the reduced repulsion between the overlapping O and X densities in combination with significant stabilization of these densities by the nuclei of the other atom.
Methods
Computational details
All calculations were performed using the Amsterdam Density Functional (ADF) software package.17 The geometry of the stationary points and energy profile along rotation around the C–C bond of the haloacetaldehydes OHC–CH2X (X = F, Cl, Br, and I) were calculated using relativistic, dispersion-corrected density functional theory at ZORA-BP86-D3(BJ)/QZ4P. This approach comprises the generalized-gradient approximation of Becke (B) and Perdew (P86)18 augmented by Grimme's D3 dispersion correction19 using the damping function proposed by Becke and Johnson.20 Scalar relativistic effects are accounted for using the zeroth-order regular approximation (ZORA).21 Molecular orbitals (MO) were expanded in a large uncontracted set of Slater type orbitals (STOs) containing diffuse functions: QZ4P.22 The basis set is of quadruple-ζ quality augmented with polarization functions, i.e., two 2p and two 3d sets on H, two 3d and two 4f sets on C, O, F; three 3d and two 4f sets on Cl, two 4d and three 4f sets on Br, one 5d and three 4f sets on I. All electrons were included in the variational process, i.e., no frozen core approximation was applied. The accuracies of the fitting scheme (ZLM fit23a for all computations except the decomposition of the electrostatic interaction term, as shown in eqn (3), which, for technical reasons, was performed with the STO fitting scheme23b) and the integration grid (Becke grid)24 were set to ‘VERY GOOD’. All optimized structures were confirmed to be true minima (no imaginary frequencies) or transition states (only one imaginary frequency) through vibrational analyses.25The BP86-D3(BJ) functional has been previously shown to accurately reproduce the rotational profiles of 1,2-disubstituted ethanes.26 Herein, we have computed additional high-level relativistic CCSD(T) reference data (see Table S1 in the ESI†). Comparison with our ZORA-BP86-D3(BJ)/QZ4P results confirms that trends in homolytic C–C bond dissociation energies and, importantly, conformational preferences of haloacetaldehydes computed with our DFT approach agree well with those from the ab initio benchmark CCSD(T).
Activation strain model and energy decomposition analysis
To understand how the OHC–CH2X bonding mechanism determines conformational preferences, we have analyzed this bond explicitly for all four haloacetaldehydes in terms of two open-shell fragments, OHC˙ and CH2X˙, forming a C–C electron-pair bond (see Fig. 2) in various conformations (i.e., by varying the φO=C–C–X dihedral angle from 0° to 180°). The overall bond energy ΔE has been divided into two major components using the activation strain model (ASM),27 ΔEstrain and ΔEint, and projected these values onto φO=C–C–X [eqn (1)].| ΔE = ΔEstrain + ΔEint | (1) |
 | ||
| Fig. 2 Schematic MO diagram for the formation of the syn-haloacetaldehydes OHC–CH2X (X = F, Cl, Br, I) from two open-shell fragments, OHC˙ and CH2X˙, along with the fragment molecular orbitals (FMO) depicted as quantitative 3D plots (isovalue = 0.04 a.u.) for the representative syn-chloroacetaldehyde, computed at ZORA-BP86-D3(BJ)/QZ4P. Note that the overlap between the closed-shell 1π OHC˙ and 3σ CH2X˙ orbitals (in red) builds up from φO=C–C–X = 0° to 90° and causes the central rotational barrier (see Fig. 4). | ||
In this equation, the strain energy ΔEstrain results from the distortion of the two open-shell fragments from their equilibrium structure to the geometry they acquire in the overall molecule, and ΔEint is the actual interaction between the deformed fragments. The interaction energy ΔEint was further decomposed using canonical energy decomposition analysis for open-shell fragments (EDA)28 into four physically meaningful energy terms [eqn (2)]:
| ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp | (2) |
The ΔVelstat term corresponds to classical electrostatic interaction between the unperturbed charge distributions of the (deformed) fragments and is usually attractive. The ΔVelstat term can be further divided into four components [eqn (3)]:28a
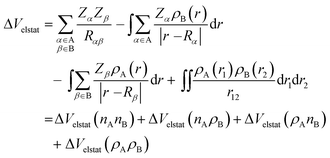 | (3) |
The steric Pauli repulsion ΔEPauli comprises the destabilizing interaction between occupied closed-shell orbitals of both fragments due to the Pauli principle. The stabilizing orbital interactions ΔEoi accounts for electron-pair bonding, charge transfer (i.e., donor–acceptor interactions between occupied orbitals on one fragment and unoccupied orbitals on the other fragment), and polarization (i.e., empty-occupied orbital mixing on one fragment due to the presence of the other fragment). The dispersion energy ΔEdisp corresponds to the dispersion corrections as introduced by Grimme et al.19
For the purpose of clarity, all above-mentioned energy terms along rotation around the C–C bond are considered relative to the syn conformation (i.e., φO=C–C–X = 0°) and represented as a ΔΔE. To facilitate the analyses, the ASM and EDA were performed using the PyFrag 2019 program.29
Results and discussion
Rotational energy profiles
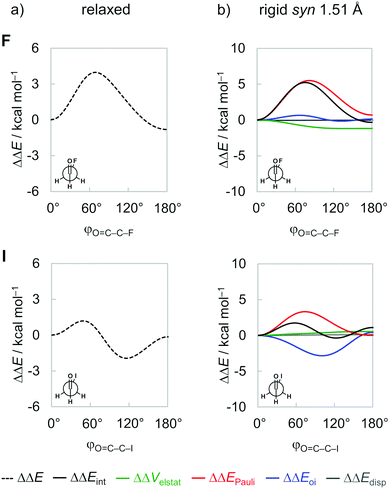
The energy profiles for half a rotation around the C–C bond, that is, from φO=C–C–X = 0° to 180°, of the fluoro and iodoacetaldehydes from our ZORA-BP86-D3(BJ)/QZ4P calculations are given in Fig. 3 (full data on all model systems can be found in Fig. S1 in the ESI†). Note that only half a rotation is shown because the energy profile from 180° to 360° mirrors the one from 0° to 180°. From Fig. 3a, we note the well-known energy profile of these systems which features two minimum-energy conformations: (i) one is always the syn conformer and (ii) the second one gradually changes its geometric character from anti to anticlinal, as X goes from F to I. This latter conformer is the global energy minimum in all cases, in line with earlier reports in the literature.8 Furthermore, the energy profile for half a rotation of the fluoroacetaldehyde has a onefold rotational barrier with one energy maximum around the gauche orientation (i.e., φO=C–C–X = 70°), whereas the iodoacetaldehyde has a twofold rotational barrier with energy maxima at the gauche and anti-conformations.To understand the origin of the conformational energy differences, the various contributors to the bond energy along internal rotation around the C–C bond were analyzed by applying the activation strain model (ASM)27 with canonical energy decomposition analysis (EDA,28 see Methods section). At this point, it is important to emphasize that the energy components are highly dependent on the geometry and the distance between the fragments.27a In previous studies,26 we have shown that the interpretation of fully relaxed rotational energy profiles (i.e., where all geometrical parameters are flexible to optimize during rotation) can be misleading because they comprise both, the change in the interaction terms due to the mutual reorientation of the two fragments along the internal rotation as well as the change in the interaction terms due to geometrical relaxation in response to the former changes. Along the relaxed rotation around the C–C bond of 1,2-dihaloethanes, the C–C distance expands or contracts as a result of the steric Pauli repulsion experienced in each conformation.26 When the C–C bond is shorter, the various orbital and electrostatic interactions are maximized, and the opposite occurs when the C–C bond is longer. Therefore, the changes manifested in the interaction energy components are just a consequence of the C–C bond distance variation. Similar behavior is observed in the relaxed rotation of the haloacetaldehydes studied herein (see Fig. S2, ESI†). Thus, to properly identify causalities in rotational profiles, it is necessary to perform the analysis at a rigid rotation around the C–C bond, that is, where all geometry parameters but the φO=C–C–X torsion angle are kept unchanged. To this end, we take the syn conformer of each haloacetaldehyde at its equilibrium geometry and rotate it with fixed C–C bond length and OHC˙ and CH2X˙ geometries to the anti-conformation. To compare all molecules on a more equal footing, the rotation of all haloacetaldehydes is performed from the same C–C distance set to 1.51 Å (as in the conformer with the shortest C–C bond length, i.e., the syn-iodoacetaldehyde; see Fig. 3b). We note that, although physically plausible, our choices of geometrical constraints might seem somewhat arbitrary. We have, therefore, verified that all trends and conclusions that play a role in the following discussion are not affected if other plausible choices of fragment geometry and C–C distance are made. The same overall trend is found if the rigid rotation is performed from their equilibrium syn or anti geometries or in a longer C–C bond length (see Fig. S3, ESI†).
Inspection of the EDA plots in Fig. 3b reveals three major features about the rotational isomerism of haloacetaldehydes: (i) a barrier around gauche because of an increased steric Pauli repulsion ΔΔEPauli (red curve) that separates anti and syn energy minima; (ii) the global energy minimum shifts from anti to anticlinal as X goes from F to I to maximize stabilizing orbital interactions ΔΔEoi (blue curve); and (iii) the only contribution from electrostatic interactions ΔΔVelstat (green curve) is to stabilize the anti-form for X = F. Note that the dispersion energy ΔΔEdisp (grey curve) remains nearly constant upon rotation around the C–C bond and, therefore, does not contribute to the overall trend in the rotational energy profiles. We recall that all energy terms are represented as a ΔΔE relative to the syn conformer. Thus, the strain energy ΔEstrain vanishes in this analysis because it is constant for geometrically frozen fragments; that is, ΔΔEstrain is zero and ΔΔEint = ΔΔE. The absolute energy values of the main conformations are provided in Table S2 in ESI.† In the following, we address each one of the abovementioned features and their underlying physical mechanism individually.
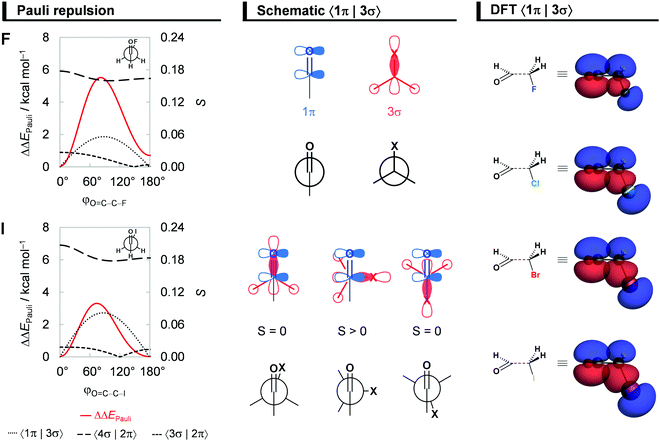
Steric Pauli repulsion and rotational barriers
Our analysis of rotational energy profiles reveals that steric Pauli repulsion ΔΔEPauli is the dominant term behind main rotational trends, namely, the central rotational barrier and the fact that both anti (for heavier halogens hyperconjugation pulls anti towards anticlinal, vide infra) and syn are energy minimum conformers. This is one more example that highlights the important role of steric Pauli repulsion in controlling rotational landscapes of organic molecules.26,30 As seen from Fig. 3b, ΔΔEPauli is a minimum at the syn and anti-conformations and goes to a maximum when the OHC˙ and CH2X˙ fragments are nearly perpendicular (i.e., φO=C–C–X is ca. 70–80°). The most significant closed-shell–closed-shell overlap contributing to the trend in ΔΔEPauli arises between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π-bonding OHC˙ FMO with the C–X σ-bonding CH2X˙ FMO, that is, 〈1π|3σ〉. The MO diagram with the valence orbitals of the OHC˙ and CH2X˙ fragments is provided in Fig. 2 and the 〈1π|3σ〉 overlap is illustrated in more detail in Fig. 4. Note that 〈1π|3σ〉 is zero at the syn and anti-conformations as the 3σ orbital of CH2X˙ overlaps symmetrically with the nodal plane region of the 1π orbital of OHC˙ (see Fig. 4; see also Fig. S4 for the orbital overlap depicted as 3D plots, ESI†). But, as the dihedral angle φO=C–C–X is rotated in between, 〈1π|3σ〉 deviates from zero and achieves a maximum around 90° (see Fig. 4). This maximum becomes larger and the effect is more pronounced as the 3σ orbital becomes more diffuse, i.e., for heavier halogens X. For example, at φO=C–C–X = 90°, 〈1π|3σ〉 varies from a value of 0.06 to 0.08 along X = F to I (see Fig. 4). Similar behavior is found for the 〈1π|2π〉 and 〈3σ|1π〉 overlap integrals (see Fig. S5, ESI†).
O π-bonding OHC˙ FMO with the C–X σ-bonding CH2X˙ FMO, that is, 〈1π|3σ〉. The MO diagram with the valence orbitals of the OHC˙ and CH2X˙ fragments is provided in Fig. 2 and the 〈1π|3σ〉 overlap is illustrated in more detail in Fig. 4. Note that 〈1π|3σ〉 is zero at the syn and anti-conformations as the 3σ orbital of CH2X˙ overlaps symmetrically with the nodal plane region of the 1π orbital of OHC˙ (see Fig. 4; see also Fig. S4 for the orbital overlap depicted as 3D plots, ESI†). But, as the dihedral angle φO=C–C–X is rotated in between, 〈1π|3σ〉 deviates from zero and achieves a maximum around 90° (see Fig. 4). This maximum becomes larger and the effect is more pronounced as the 3σ orbital becomes more diffuse, i.e., for heavier halogens X. For example, at φO=C–C–X = 90°, 〈1π|3σ〉 varies from a value of 0.06 to 0.08 along X = F to I (see Fig. 4). Similar behavior is found for the 〈1π|2π〉 and 〈3σ|1π〉 overlap integrals (see Fig. S5, ESI†).
It is interesting to observe that ΔΔEPauli along rotation around the C–C bond favors the syn conformer, where the most electron-rich atoms on each fragment are in closest proximity. The reason for this is twofold. Firstly, the overlap between FMOs that possess O and X lone-pair character, 〈3σ|2π〉 and 〈4σ|2π〉, expected to give a more destabilizing ΔΔEPauli at the syn, only slightly changes upon rotation around the C–C bond (see Fig. 4). This is because the overlapping region is largest in between the two carbons, on the C–C bond region, and, therefore, varies less as a function of the φO=C–C–X torsional angle (see Fig. S4 for the 3D plots of 〈3σ|2π〉 and 〈4σ|2π〉, ESI†). Secondly, the 3π* orbital, one of the main contributors to the Pauli repulsion in the rotational barrier of 1,2-dihaloethanes,26 is actually empty in the OHC˙ fragment (see Fig. 2) and, thus, 〈3π*|3π*〉 does not give rise to any Pauli repulsion between the OHC˙ and CH2X˙ fragments. Therefore, the trends in steric Pauli repulsion of haloacetaldehydes stem mostly from the 〈1π|3σ〉 overlap integral (Fig. 4), which is zero at the syn and anti-conformations.
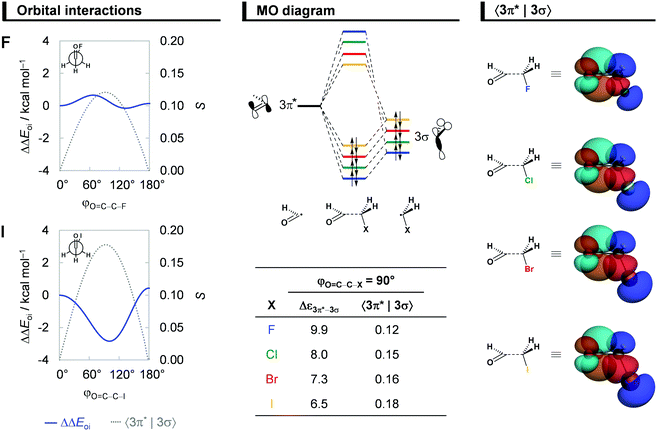
Hyperconjugative interactions
Next, we comment on the role of orbital (hyperconjugative) interactions ΔΔEoi to the conformational energies. In agreement with previous reports in the literature,7a,11 the hyperconjugation becomes increasingly more stabilizing at the anticlinal conformer for heavier haloacetaldehydes (see Fig. 5). This is the reason why the global energy minimum conformation gradually shifts from anti to anticlinal as X goes from F to I. The stabilization due to ΔΔEoi results predominantly from a charge transfer into the empty C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding OHC˙ FMO from the occupied C–X σ-bonding CH2X˙ FMO, that is, the 3π*–3σ interaction (see Fig. 5). Additional but less stabilizing contribution from the 3π*–2π interaction is given in Fig. S5 and Table S3 (ESI†). These orbital interactions are more stabilizing for the iodoacetaldehyde because of both smaller orbital energy gap and larger orbital overlap (e.g., Δε3π*–3σ = 9.9 and 6.5 eV, and 〈3π*|3σ〉 = 0.12 and 0.18 for X = F and I, respectively). As the electronegativity of the halogen atom decreases from F to I,31 the 3σ orbital becomes higher in energy, which leads to a smaller energy gap with the 3π* orbital of OHC˙. The associated 〈3π*|3σ〉 orbital overlap is largest at φO=C–C–X = 90° (Fig. 5; see Fig. S5 in ESI† for data along the rotation of the C–C bond) and increases as the 3σ orbital becomes more diffuse, due to the larger np atomic orbital of heavier halogen atoms. These findings consolidate earlier studies on the role of hyperconjugative orbital interactions.7a,11
O π*-antibonding OHC˙ FMO from the occupied C–X σ-bonding CH2X˙ FMO, that is, the 3π*–3σ interaction (see Fig. 5). Additional but less stabilizing contribution from the 3π*–2π interaction is given in Fig. S5 and Table S3 (ESI†). These orbital interactions are more stabilizing for the iodoacetaldehyde because of both smaller orbital energy gap and larger orbital overlap (e.g., Δε3π*–3σ = 9.9 and 6.5 eV, and 〈3π*|3σ〉 = 0.12 and 0.18 for X = F and I, respectively). As the electronegativity of the halogen atom decreases from F to I,31 the 3σ orbital becomes higher in energy, which leads to a smaller energy gap with the 3π* orbital of OHC˙. The associated 〈3π*|3σ〉 orbital overlap is largest at φO=C–C–X = 90° (Fig. 5; see Fig. S5 in ESI† for data along the rotation of the C–C bond) and increases as the 3σ orbital becomes more diffuse, due to the larger np atomic orbital of heavier halogen atoms. These findings consolidate earlier studies on the role of hyperconjugative orbital interactions.7a,11
Electrostatic interactions and dipolar repulsion
Finally, we address the small role of electrostatic interactions ΔΔVelstat to the rotational energy profiles, which, for X = F and I, favors anti and syn, respectively (see Fig. 3b). As will become clear in the following, this difference in preference originates from the small, compact nature of fluorine and the large, more diffuse nature of iodine. The small nucleus and compact electron density render the fluorine atom a point-charge-like behavior, which gradually fades as one goes down group 17 in the periodic table. The large nucleus and more diffuse electron density of the iodine atom result in more electrostatic attraction with the electron density and nucleus of the oxygen atom, respectively, as well as less repulsion between electron densities compared to point charges. This results in the rotational trends mentioned above, that is, along the ΔΔVelstat curve, the anti is preferred for X = F to reduce electrostatic repulsion, whereas the opposite is observed for X = I, the preference shifts to syn to enhance electrostatic attraction.To specifically evaluate the magnitude of the electrostatic interaction between the oxygen and halogen atoms, we approach the OHC˙ and CH2X˙ fragments not by forming a C–C electron-pair bond, but along the O⋯X distance (where X = F and I), as shown in Fig. 6a and b. The ΔVelstat energy becomes repulsive only at a very short internuclear distance (rO⋯X < 0.8 Å), which stems mostly from the nuclei–nuclei repulsion.14b Note that the physical nature of the charge densities is different from point charges, and the former yields less electrostatic repulsion than the latter.14a Furthermore, ΔVelstat is less stabilizing for X = F than X = I all along the O⋯X distance, even at their rO⋯X distance in the corresponding haloacetaldehydes (see vertical lines in Fig. 6a). The same overall trend is observed if one analyzes the electrostatic interaction by approaching the OHC˙ and CH2X˙ fragments along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯X–C bond axis (see Fig. S6, ESI†). This can be traced back to the electrostatic interaction between the bare O˙˙ and X˙ atoms in their triplet and doublet valence configuration, respectively (see Fig. S7, ESI†). The overlap between electron densities and nuclei of the OHC˙ and CH2X˙ fragments is better for X = I because the electron density of the iodine atom is more diffuse and its nucleus is larger than the fluorine atom (Fig. 6d), resulting in stronger electrostatic attraction with the oxygen atom (Fig. 6c). Therefore, the electrostatic interaction ΔVelstat between OHC˙ and CH2X˙ is predominantly attractive and increases in magnitude from X = F to I, leading to a breakdown of the point-charge picture.
O⋯X–C bond axis (see Fig. S6, ESI†). This can be traced back to the electrostatic interaction between the bare O˙˙ and X˙ atoms in their triplet and doublet valence configuration, respectively (see Fig. S7, ESI†). The overlap between electron densities and nuclei of the OHC˙ and CH2X˙ fragments is better for X = I because the electron density of the iodine atom is more diffuse and its nucleus is larger than the fluorine atom (Fig. 6d), resulting in stronger electrostatic attraction with the oxygen atom (Fig. 6c). Therefore, the electrostatic interaction ΔVelstat between OHC˙ and CH2X˙ is predominantly attractive and increases in magnitude from X = F to I, leading to a breakdown of the point-charge picture.
However, at short distances, even the compact fluorine atom can deviate from point-charge behavior. Along the series of haloacetaldehydes, this can be achieved by artificially shortening the C–X bond length and, therefore, the O⋯X separation. Table 1 shows the ΔΔVelstat energy of the syn relative to the anti-conformation. We recall that ΔVelstat is predominantly attractive and, therefore, positive (i.e., less stabilizing) values of ΔΔVelstat indicate that syn is electrostatically less favorable than anti, whereas negative (i.e., more stabilizing) values of ΔΔVelstat denote the opposite. By decreasing the O⋯X distance, the overlap between electron densities and nuclei of OHC˙ and CH2X˙ becomes more effective, resulting in more stabilizing electrostatics at the syn conformer for all haloacetaldehydes (see Table 1, column “C–X –0.3 Å”). This is further corroborated by the fact that the anti preference dominates with the elongation of the C–X bond length and, therefore, of the O⋯X distance (see Table 1, column “C–X +0.3 Å”). At a longer O⋯X separation, ΔVelstat becomes less stabilizing, which shifts the electrostatic preference to anti. Thus, the electrostatic preference for syn or anti depends on the balance between the attractive and repulsive components of ΔVelstat (see eqn (3) and Fig. S5 in ESI†). For X = I, ΔVelstat is strongly stabilizing and prefers to be syn to maximize the overlap between the electron density on one with the nuclei on the other of the OHC˙ and CH2X˙ fragments. For X = F, on the other hand, the electrostatic attraction is weaker than for X = I and does not compensate for the electrostatic repulsion between nuclei and between densities on either fragment at syn, therefore, shifting the preference to anti (see Tables S2 and S4 for absolute and relative values, respectively, ESI†). The oversimplified concept of dipolar repulsion does not capture this interplay of electrostatic interactions. At variance with this rationale, the point-charge-like behavior of the fluorine atom along the ΔΔVelstat curve is not due to a larger electrostatic repulsion, but instead stems from the attractive electrostatic components that are less stabilizing than for larger halogens.
Conclusions
The overall rotational energy profile of haloacetaldehydes OHC–CH2X (X = F, Cl, Br, and I) is set by an interplay of steric Pauli repulsion, which causes a barrier separating syn- and anti-minima, orbital interactions, which pull the anti-minimum towards anticlinal in order to optimize hyperconjugative overlap, and electrostatic interactions, which drive the preference to anti only in the case of X = F. This follows from our detailed analyses based on relativistic dispersion-corrected density functional theory at ZORA-BP86-D3(BJ)/QZ4P.The results of our quantitative Kohn–Sham molecular orbital theory analyses reveal that steric Pauli repulsion is the causal term giving rise to the central rotation barrier between syn- and anti-minima, which reaches a maximum when the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–X bonds are nearly perpendicular, due to the maximum overlap in the four–electron interaction between the filled π orbital of the carbonyl group with the filled σ orbital of the halogenated methyl fragment. This closed-shell–closed-shell orbital overlap is zero at the syn and anti-conformations because the CH2X˙ σ orbital overlaps symmetrically with the nodal plane region of the OHC˙ π orbital. Therefore, Pauli repulsion is also the reason why the syn is an energy minimum conformer for all haloacetaldehydes. The global energy minimum, on the other hand, gradually shifts from anti to anticlinal as X goes from F to I because of the more stabilizing orbital interactions in the latter, in line with the currently accepted rationale. As the halogen atom increases in size, the orbital overlap becomes larger, and the orbital energy gap becomes smaller for the charge transfer to the empty π* orbital of the carbonyl group from the filled σ orbital of the halogenated methyl.
O and C–X bonds are nearly perpendicular, due to the maximum overlap in the four–electron interaction between the filled π orbital of the carbonyl group with the filled σ orbital of the halogenated methyl fragment. This closed-shell–closed-shell orbital overlap is zero at the syn and anti-conformations because the CH2X˙ σ orbital overlaps symmetrically with the nodal plane region of the OHC˙ π orbital. Therefore, Pauli repulsion is also the reason why the syn is an energy minimum conformer for all haloacetaldehydes. The global energy minimum, on the other hand, gradually shifts from anti to anticlinal as X goes from F to I because of the more stabilizing orbital interactions in the latter, in line with the currently accepted rationale. As the halogen atom increases in size, the orbital overlap becomes larger, and the orbital energy gap becomes smaller for the charge transfer to the empty π* orbital of the carbonyl group from the filled σ orbital of the halogenated methyl.
Electrostatic interactions are intuitively seen as the repulsion or attraction between atoms with partial charges of the same or opposite signs, respectively. As such, they are often represented as the sum of pairwise interactions that follows Coulomb's law for the respective point charges, which is the center of the concept of dipolar repulsion. We show that this oversimplified view is, however, only valid for compact atoms, in our model systems, the second-row fluorine atom. As the halogen atom increases in size and becomes more diffuse, it deviates more from the behavior of point charge to an atomic charge distribution. This results in a net stabilizing electrostatic interaction between O and X arising from both less repulsion between overlapping densities and more attraction between overlapping density and nucleus. Therefore, while the electrostatic energy favors anti for X = F to reduce O(ρ−)⋯(ρ−)F and O(⊕)⋯(⊕)F repulsions, it favors syn for X = I to enhance O(⊕)⋯(ρ−)I and O(ρ−)⋯(⊕)I attractions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the Netherlands Organization for Scientific Research (NWO), the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), and the Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) for financial support.Notes and references
- J. Clayden, N. Greevs and S. G. Warren, Organic Chemistry, Oxford University Press, Oxford, 2012 Search PubMed.
- R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838 CrossRef CAS PubMed.
- (a) L. Pauling, R. B. Corey and H. R. Branson, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 205 CrossRef CAS PubMed; (b) L. Pauling and R. B. Corey, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 729 CrossRef CAS PubMed.
- (a) C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem. – Eur. J., 1999, 5, 3581 CrossRef; (b) J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737 CrossRef CAS PubMed.
- (a) T. K. Dickens and S. Warren, Chemistry of the Carbonyl Group: A Step-by-Step Approach to Understanding Organic Reaction Mechanisms, John Wiley & Sons, Hoboken, 2018 Search PubMed; (b) J. Jones, Core Carbonyl Chemistry, Oxford University Press Inc., New York, 1997 Search PubMed.
- See, for instance: (a) K. B. Muchowska, D. J. Pascoe, S. Borsley, I. V. Smolyar, I. K. Mati, C. Adam, G. S. Nichol, K. B. Ling and S. L. Cockroft, Angew. Chem., Int. Ed., 2020, 59, 14602 ( Angew. Chem. , 2020 , 132 , 14710 ) CrossRef CAS PubMed; (b) D. Rodrigues Silva, L. A. Zeoly, R. A. Cormanich, C. Fonseca Guerra and M. P. Freitas, Eur. J. Org. Chem., 2020, 884 CrossRef; (c) G. Pattison, Beilstein J. Org. Chem., 2017, 13, 2915 CrossRef CAS PubMed; (d) F. A. Martins, J. M. Silla and M. P. Freitas, Beilstein J. Org. Chem., 2017, 13, 1781 CrossRef CAS PubMed; (e) R. A. Cormanich, L. C. Ducati, C. F. Tormena and R. Rittner, Chem. Phys., 2013, 421, 32 CrossRef CAS; (f) K. B. Wiberg, Acc. Chem. Res., 1999, 32, 922 CrossRef CAS , and references cited therein; (g) J. I. Seeman, Chem. Rev., 1983, 83, 83 CrossRef CAS; (h) N. L. Allinger, J. Allinger and M. A. DaRooge, J. Am. Chem. Soc., 1964, 86, 4061 CrossRef CAS.
- For selected theoretical studies, see: (a) R. M. Pontes, B. C. Fiorin and E. A. Basso, Chem. Phys. Lett., 2004, 395, 205 CrossRef CAS; (b) G. Frenking, K. F. Köhler and M. T. Reetz, Tetrahedron, 1994, 50, 11197 CrossRef; (c) H. V. Phan and J. R. Durig, J. Mol. Struct., 1990, 209, 333 CrossRef; (d) J. R. Durig, H. V. Phan and T. S. Little, J. Mol. Struct., 1989, 202, 143 CrossRef.
- For representative experimental studies, see: (a) R. J. Abraham, A. D. Jones, M. A. Warne, R. Rittner and C. F. Tormena, J. Chem. Soc., Perkin Trans. 2, 1996, 533 RSC; (b) S. Dyngeseth, H. Schei and K. Hagen, J. Mol. Struct., 1983, 102, 45 CrossRef CAS; (c) T. B. Malloy Jr. and L. A. Carreira, J. Chem. Phys., 1977, 66, 4246 CrossRef; (d) R. G. Ford, J. Chem. Phys., 1976, 65, 354 CrossRef CAS; (e) G. J. Karabatsos and D. J. Fenoglio, J. Am. Chem. Soc., 1969, 91, 1124 CrossRef CAS; (f) L. J. Bellamy and R. L. Williams, J. Chem. Soc., 1957, 0, 4294 RSC.
- E. Juaristi and G. Cuevas, The anomeric effect, CRC Press Inc., Boca Raton, 1995 Search PubMed.
- (a) K. B. Wiberg, W. F. Bailey, K. M. Lambert and Z. D. Stempel, J. Org. Chem., 2018, 83, 5242 CrossRef CAS PubMed; (b) C. M. Filloux, Angew. Chem., Int. Ed., 2015, 54, 8880 ( Angew. Chem. , 2015 , 127 , 9006 ) CrossRef CAS PubMed; (c) Y. Mo, Nat. Chem., 2010, 2, 666 CrossRef CAS PubMed; (d) C. Wang, F. Ying, W. Wu and Y. Mo, J. Org. Chem., 2014, 79, 1571 CrossRef CAS PubMed.
- J. V. Coelho, M. P. Freitas and T. C. Ramalho, Struct. Chem., 2008, 19, 671 CrossRef CAS.
- E. L. Eliel, S. H. Wilen and L. N. Mander, Stereochemistry of Organic Compounds, John Wiley & Sons Inc., New York, 1994 Search PubMed.
- (a) E. Solel, M. Ruth and P. R. Schreiner, J. Org. Chem., 2021, 86, 7701 CrossRef CAS PubMed; (b) M. Baranac-Stojanović, RSC Adv., 2014, 4, 43834 RSC.
- (a) G. Frenking and F. M. Bickelhaupt, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 121–158 CrossRef; (b) A. Krapp, F. M. Bickelhaupt and G. Frenking, Chem. – Eur. J., 2006, 12, 9196 CrossRef CAS PubMed; (c) A. Kovács, C. Esterhuysen and G. Frenking, Chem. – Eur. J., 2005, 11, 1813 CrossRef PubMed; (d) C. Esterhuysen and G. Frenking, Theor. Chem. Acc., 2004, 111, 381 Search PubMed.
- (a) P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2008, 14, 659 CrossRef CAS PubMed; (b) S. C. C. van der Lubbe, F. Zaccaria, X. Sun and C. Fonseca Guerra, J. Am. Chem. Soc., 2019, 141, 4878 CrossRef CAS PubMed.
- See, for example: (a) C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189 CrossRef PubMed; (b) F. M. Bickelhaupt, J. K. Nagle and W. L. Klemm, J. Phys. Chem. A, 2008, 112, 2437 CrossRef CAS PubMed , and references therein; (c) S. C. C. van der Lubbe, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, Chem. – Eur. J., 2020, 26, 15690 CrossRef CAS PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed; (c) ADF2017.103, SCM Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- (a) E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281 CrossRef CAS; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- (a) M. Franchini, P. H. T. Philipsen, E. van Lenthe and L. Visscher, J. Chem. Theory Comput., 2014, 10, 1994 CrossRef CAS PubMed; (b) E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41 CrossRef CAS.
- M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819 CrossRef CAS PubMed.
- (a) A. Bérces, R. M. Dickson, L. Fan, H. Jacobsen, D. Swerhone and T. Ziegler, Comput. Phys. Commun., 1997, 100, 247 CrossRef; (b) H. Jacobsen, A. Bérces, D. P. Swerhone and T. Ziegler, Comput. Phys. Commun., 1997, 100, 263 CrossRef CAS; (c) S. K. Wolff, Int. J. Quantum Chem., 2005, 104, 645 CrossRef CAS.
- D. Rodrigues Silva, L. de Azevedo Santos, T. A. Hamlin, C. Fonseca Guerra, M. P. Freitas and F. M. Bickelhaupt, ChemPhysChem, 2021, 22, 641 CrossRef CAS PubMed.
- (a) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protocol., 2020, 15, 649 CrossRef CAS PubMed; (b) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 ( Angew. Chem. , 2017 , 129 , 10204 ) CrossRef CAS PubMed; (c) L. P. Wolters and F. M. Bickelhaupt, WIREs Comput. Mol. Sci., 2015, 5, 324 CrossRef CAS PubMed; (d) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC; (e) W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118 RSC; (f) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114 CrossRef CAS.
- (a) T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analysis, ed. S. Grabowsky, De Gruyter, Berlin, 2021, pp. 199–212 Search PubMed; (b) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, pp. 1–86 Search PubMed; (c) R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432 CrossRef CAS PubMed; (d) F. M. Bickelhaupt, N. M. M. Nibbering, E. M. van Wezenbeek and E. J. Baerends, J. Phys. Chem., 1992, 96, 4864 CrossRef CAS.
- (a) W.-J. van Zeist, C. Fonseca Guerra and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 312 CrossRef CAS PubMed; (b) X. Sun, T. M. Soini, J. Poater, T. A. Hamlin and F. M. Bickelhaupt, J. Comput. Chem., 2019, 40, 2227 CrossRef CAS PubMed; (c) PyFrag 2007–2020, X. Sun, T. Soini, L. P. Wolters, W.-J. van Zeist, C. Fonseca Guerra, T. A. Hamlin and F. M. Bickelhaupt, Vrije Universiteit Amsterdam, The Netherlands.
- (a) Y. Mo, W. Wu, L. Song, M. Lin, Q. Zhang and J. Gao, Angew. Chem., Int. Ed., 2004, 43, 1986 ( Angew. Chem. , 2004 , 116 , 2020 ) CrossRef CAS PubMed; (b) Y. Mo and J. Gao, Acc. Chem. Res., 2007, 40, 113 CrossRef CAS PubMed; (c) Z. Chen, C. Corminboeuf and Y. Mo, J. Phys. Chem. A, 2014, 118, 5743 CrossRef CAS PubMed; (d) F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183 ( Angew. Chem. , 2003 , 115 , 4315 ) CrossRef CAS PubMed.
- (a) L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1960 Search PubMed; (b) A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational results, Cartesian coordinates, and energies of the stationary points in the energy profiles for rotation around the C–C bond of haloacetaldehydes. See DOI: 10.1039/d1cp02502c |
| This journal is © the Owner Societies 2021 |