Origin of asynchronicity in Diels–Alder reactions

Abstract

Asynchronicity in Diels–Alder reactions plays a crucial role in determining the height of the reaction barrier. Currently, the origin of asynchronicity is ascribed to the stronger orbital interaction between the diene and the terminal carbon of an asymmetric dienophile, which shortens the corresponding newly formed C–C bond and hence induces asynchronicity in the reaction. Here, we show, using the activation strain model and Kohn–Sham molecular orbital theory at ZORA-BP86/TZ2P, that this rationale behind asynchronicity is incorrect. We, in fact, found that following a more asynchronous reaction mode costs favorable HOMO–LUMO orbital overlap and, therefore, weakens (not strengthens) these orbital interactions. Instead, it is the Pauli repulsion that induces asynchronicity in Diels–Alder reactions. An asynchronous reaction pathway also lowers repulsive occupied–occupied orbital overlap which, therefore, reduces the unfavorable Pauli repulsion. As soon as this mechanism of reducing Pauli repulsion dominates, the reaction begins to deviate from synchronicity and adopts an asynchronous mode. The eventual degree of asynchronicity, as observed in the transition state of a Diels–Alder reaction, is ultimately achieved when the gain in stability, as a response to the reduced Pauli repulsion, balances with the loss of favorable orbital interactions.

---

1. Introduction

Nearly one century after its discovery, the Diels–Alder (DA) cycloaddition reaction is still one of the most useful transformations in chemistry. This is ultimately due to the ability of the DA reaction to produce densely functionalized six-membered rings, with up to four stereocenters, in a single reaction step with high atom efficiency.^1–3 This specific reaction, therefore, has been widely utilized towards the synthesis of a vast number of target compounds, including complex natural products and molecular species with potential applications in material sciences and medicinal chemistry.⁴

Lewis acids (LA) that bind to the dienophile are efficient catalysts of the DA reaction.⁵ This enhanced reactivity is traditionally attributed to the lowering of the LUMO of the activated dienophile, resulting in a smaller HOMO_diene–LUMO_dienophile energy gap and hence more favorable orbital interactions.⁶ In our previous work, however, we have shown that this rationale behind Lewis acid-catalyzed DA reactions is incorrect.⁷ Our analyses showed that Lewis acids indeed lower the LUMO_dienophile but do not enhance the total orbital interaction, because the strengthening of the normal electron demand HOMO_diene–LUMO_dienophile interaction is counteracted by the weakening of the inverse electron demand LUMO_diene–HOMO_dienophile interaction. Instead, we established that the increase in reaction rate is originating from a significant reduction of closed-shell Pauli repulsion between the occupied π-molecular orbitals of the reactants. The binding of a LA to the dienophile not only reduces the Pauli repulsion by polarizing the occupied π-orbital density on the C=C double bond of the dienophile away from the approaching diene but also by inducing asynchronicity through the asymmetry in the π-electronic system (vide infra). In addition, the asynchronicity also results in less pressure on the reactants to deform and, thus, less destabilizing activation strain, which leads to an additional lowering of the reaction barrier. Besides LA-catalyzed Diels–Alder reactions, it was found that this mode of catalysis is active in a myriad of other catalyzed organic transformations,⁸ such as aza-Michael addition reactions,^8a aromatic Diels–Alder reactions,^8b and cyclohexene oxide ring-opening reactions,^8c and we, therefore, have coined the concept of Pauli-lowering catalysis to describe this mode of catalysis.⁹

The degree of asynchronicity of a DA reaction, that is, the difference in length between the newly forming C⋯C bonds in the transition state, plays a crucial role in determining the height of the reaction barrier. As previously mentioned, a more asynchronous DA reaction, i.e., a DA reaction with a larger difference in length between the newly forming C⋯C bonds in the transition state leads to both a less destabilizing Pauli repulsion and a reduced activation strain, which, ultimately, manifests into a lower reaction barrier. It is, therefore, essential to understand why and to which extent DA reactions become asynchronous. Various studies have attempted to elucidate the origin of asynchronicity in Diels–Alder reactions.¹⁰ The most well-accepted rationale is by Houk et al., who explained the asynchronicity in DA reaction between 1,3-butadiene and acrolein based on frontier molecular orbital (FMO) theory and ascribed this phenomenon to the magnitude of the molecular orbital (MO) coefficients of the LUMO_acrolein on the C=C double bond.¹¹ The larger MO-coefficient of the LUMO_acrolein on the β-carbon makes this terminal carbon more electrophilic than the α-carbon, which has a smaller MO-coefficient. As a result, the greater overlap between HOMO_{1,3-butadiene}–LUMO_acrolein at the β-carbon of acrolein leads to a shorter bond and, thus, an asynchronous DA reaction. In contrast, we found in our recent studies on LA-catalyzed DA reactions that these reactions tend to be asynchronous in order to reduce the otherwise highly destabilizing Pauli repulsion.^7b,d Despite recent advances on elucidating the mechanism behind asynchronicity in DA reactions, little quantitative data is available regarding the physical factors that control whether and to which extent a DA reaction wants to be asynchronous.

In this work, we have performed an in-depth theoretical study to unravel the physical mechanism behind asynchronicity of Diels–Alder reactions. To this end, we have analyzed and compared the Diels–Alder reaction between 1,3-butadiene (B) and acrylaldehyde (O–LA) with the analogous reaction catalyzed by different Lewis acids, namely, AlCl₃, Li⁺, and H⁺, using relativistic density functional theory (DFT) at ZORA-BP86/TZ2P (Scheme 1). These Lewis acid catalysts were selected due to their ability to make the Diels–Alder reaction more asynchronous. The activation strain model (ASM)¹² of reactivity in combination with Kohn–Sham molecular orbital (KS-MO)¹³ theory and the matching canonical energy decomposition analysis (EDA)¹⁴ were employed to gain quantitative insights into the origin of asynchronicity in these Diels–Alder reactions. This computational approach has been proven to be reliable for the understanding of fundamental processes in organic chemistry.^7,8,15

Scheme 1 The uncatalyzed and Lewis acid-catalyzed Diels–Alder reactions between 1,3-butadiene (B) and acrylaldehyde (O–LA) that were computationally studied.

2. Computational method

2.1 Computational details

All calculations were performed using the Amsterdam Density Functional (ADF2019.102) software package.¹⁶ The generalized gradient approximation (GGA) functional BP86 was used for all computations and analyses.¹⁷ The basis set employed, denoted TZ2P,¹⁸ is of triple-ζ quality and is augmented with two sets of polarization functions on each atom. Scalar relativistic effects are accounted for using the zeroth-order regular approximation (ZORA).¹⁹ This level of theory has been proven to be accurate in calculating the relative trends in reaction barriers and energies as well as for performing the activation strain and energy decomposition analyses for cycloaddition reactions.^7,20 The accuracies of the fit scheme (Zlm fit)^21a and the integration grid (Becke grid)^21b were set to VERYGOOD. Equilibrium and transition state geometries were verified by means of vibrational analysis, to assess the nature of all structures: for minima, no imaginary frequencies were found, whereas transition states present a single imaginary frequency. Furthermore, the character of the normal mode associated with the imaginary frequency was analyzed to ensure that the correct transition state was found, i.e., the formation of the two C–C bonds between 1,3-butadiene (B) and acrylaldehyde (O–LA). A conformational search has been performed to ensure that the structures are in their lowest energy conformation. The potential energy surfaces of the studied Diels–Alder reactions were obtained by performing intrinsic reaction coordinate (IRC) calculations.²² The acquired potential energy surfaces were analyzed using the PyFrag 2019 program.²³ Optimized structures were illustrated using CYLview.²⁴

2.2 Activation strain model and energy decomposition analysis

The activation strain model of reactivity (ASM,¹² also known as the distortion/interaction model²⁵), is a fragment-based approach based on the idea that the energy of a reacting system, i.e., the potential energy surface, can be described with respect to, and understood in terms of the characteristics of the original reactants. It considers the rigidity of the reactants as well as the extent to which the reactants must deform during the reaction plus their capability to interact as the reaction proceeds. In this model, we decompose the total energy, ΔE(ζ), into the strain and interaction energy, ΔE_strain(ζ) and ΔE_int(ζ), respectively, along the IRC which is projected onto a reaction coordinate ζ that is critically involved in the transformation, vide infra (eqn (1)).

ΔE(ζ) = ΔE_strain(ζ) + ΔE_int(ζ) (1)

In this equation, the strain energy, ΔE_strain(ζ), is the penalty that needs to be paid in order to deform the reactants from their equilibrium structure to the geometry they adopt during the reaction at point ζ of the reaction coordinate. On the other hand, the interaction energy, ΔE_int(ζ), accounts for all mutual chemical interactions that occur between the deformed fragments along the reaction coordinate.

The interaction energy between the deformed reactants is further analyzed by means of the canonical energy decomposition analysis (EDA).¹⁴ The EDA decomposes the ΔE_int(ζ) into the following three physically meaningful energy terms (eqn (2)):

ΔE_int(ζ) = ΔV_elstat(ζ) + ΔE_Pauli(ζ) + ΔE_oi(ζ) (2)

Herein, ΔV_elstat(ζ) is the classical electrostatic interaction between the unperturbed charge distributions of the (deformed) reactants and is usually attractive. The Pauli repulsion, ΔE_Pauli(ζ), comprises the destabilizing interaction between occupied closed-shell orbitals of both fragments due to Pauli's exclusion principle. The orbital interaction energy, ΔE_oi(ζ), accounts for polarization and charge transfer between the fragments, such as HOMO–LUMO interactions. A detailed, step-by-step guide on how to perform and interpret the ASM and EDA can be found in ref. 12a.

In both the activation strain and accompanied energy decomposition diagrams, the intrinsic reaction coordinate (IRC) is projected onto the shortest of the two newly forming C⋯C bonds between 1,3-butadiene (B) and acrylaldehyde (O–LA). This critical reaction coordinate undergoes a well-defined change during the reaction from the reactant complex via the transition state to the cycloadduct and is shown to be a valid reaction coordinate for studying cycloadditions.^7,26

3. Results and discussion

The reaction profiles of the uncatalyzed and Lewis acid-catalyzed Diels–Alder (DA) reaction between 1,3-butadiene (B) and acrylaldehyde (O–LA), together with their transition state structures (intermediate structure for O–H⁺) are shown in Fig. 1. Note that all dienophiles studied in this work are in the s-trans conformation, which is the most stable conformation of the dienophiles (Fig. S1, ESI†).²⁷ In analogy with previous studies,⁷ we establish that Lewis acids not only significantly lower the reaction barrier but also make the DA reaction more asynchronous. As expected, the uncatalyzed reaction (O) has the highest reaction barrier, namely, 12.2 kcal mol⁻¹, and follows the least concerted asynchronous reaction mode (Δr^TS_C⋯C = 0.46 Å, where Δr^TS_C⋯C refers to the difference between the newly forming C⋯C bond lengths in the transition state). Binding a Lewis acid to acrylaldehyde lowers the DA reaction barriers to 3.5 kcal mol⁻¹ for O–AlCl₃ and −1.9 kcal mol⁻¹ (2.2 kcal mol⁻¹ with respect to preceding reactant complex 3-RC) for O–Li⁺ and significantly increases the degree of asynchronicity of these reactions (O–AlCl₃: Δr^TS_C⋯C = 0.78 Å, O–Li⁺: Δr^TS_C⋯C = 0.91 Å). Strikingly, the DA reaction catalyzed by H⁺ follows a stepwise reaction pathway, which can be seen as an extreme case of asynchronicity, whereby the formation of the first C–C bond between the terminal carbon of B and the β-carbon of O–H⁺ is barrierless. The formation of the second C–C bond, i.e., ring closure, goes with a reaction barrier at −19.5 kcal mol⁻¹ (0.5 kcal mol⁻¹ with respect to preceding intermediate 4-Int). These results already indicate that the degree of asynchronicity of a DA reaction has a profound effect on the height of the reaction barrier.

Fig. 1 (a) Reaction profiles (in kcal mol⁻¹) and (b) transition state structures (intermediate structure for O–H⁺) with newly forming bond lengths (in Å) and degree of asynchronicity (Δr^TS_C⋯C) of the uncatalyzed and Lewis acid-catalyzed Diels–Alder reaction between 1,3-butadiene (B) and acrylaldehyde (O–LA), computed at ZORA-BP86/TZ2P.

Next, we examine the physical factors leading to the enhanced reactivity of the LA-catalyzed compared to the uncatalyzed Diels–Alder reactions, by applying the activation strain model (ASM) of reactivity.¹²Table 1 shows the results of the activation strain analyses at consistent, transition state-like geometries with a C_B⋯C_β bond length between B and O–LA of 2.118 Å (see ESI,† Fig. S2 for complete activation strain and energy decomposition analysis diagrams). Performing this analysis at a consistent point along the reaction coordinate (near all transition state structures), rather than on the individual transition state structures alone, ensures that the results are not skewed by the position, earlier or later, of the transition state.^12,20 Note that for O–H⁺ the barrierless formation of the first C–C bond is analyzed.²⁸ The trend in total energies at the consistent geometry, ΔE*, in Table 1 follows that of the actual reaction barriers ΔE^‡, namely, the uncatalyzed reaction (O) goes with the highest, i.e., least stabilizing, total energy, while binding of AlCl₃ (O–AlCl₃) lowers the energy to 1.5 kcal mol⁻¹ which then further drops to −1.9 kcal mol⁻¹ and −16.4 kcal mol⁻¹ for O–Li⁺ and O–H⁺, respectively. The acceleration of the LA-catalyzed reactions, i.e., lower reaction barriers, originates from both a consistently less destabilizing strain energy and a more stabilizing interaction energy.

Table 1 Activation strain and energy decomposition analyses (in kcal mol⁻¹) of the uncatalyzed and Lewis acid-catalyzed Diels–Alder reactions between B and O–LA^ab

O–LA	ΔE*	ΔEstrain	ΔEint	ΔVelstat	ΔEPauli	ΔEoi
a Analyses at consistent transition state-like geometries with a CB⋯Cβ bond length between B and O–LA of 2.118 Å at ZORA-BP86/TZ2P. b See ESI Fig. S2 for complete activation strain and energy decomposition analysis diagrams.
O	12.1	19.3	−7.2	−38.9	82.9	−51.5
O–AlCl3	1.5	14.9	−13.4	−34.5	73.5	−52.4
O–Li^+	−1.9	13.5	−15.4	−31.3	68.1	−52.2
O–H^+	−16.4	12.3	−28.7	−28.2	62.0	−62.5

---

The trend in strain energy can be explained by looking at the degree of asynchronicity (O: Δr^TS_C⋯C = 0.46 Å, O–AlCl₃: Δr^TS_C⋯C = 0.78 Å, O–Li⁺: Δr^TS_C⋯C = 0.91 Å, O–H⁺: Δr^TS_C⋯C = stepwise). The more asynchronous the reaction, the lower the degree of deformation of the reactants in the saddle-point region of the reaction's PES since the C_B⋯C_α bond forms behind of the C_B⋯C_β bond, resulting in a less destabilizing strain energy. Note that, in the case of the stepwise Diels–Alder reaction with O–H⁺, the C_B⋯C_α bond is not formed at all in the first step which, ultimately, leads to even less deformation in the reactants and hence the least destabilizing strain energy. To understand why the interaction energy becomes increasingly more stabilizing from O to O–H⁺, we applied the energy decomposition analysis (EDA).¹⁴ In line with our previous studies,⁷ we find that the reduced Pauli repulsion is the main actor behind the more stabilizing interaction energy for the LA-catalyzed compared to the uncatalyzed DA reaction, going from 82.9 kcal mol⁻¹ for O to 62.0 kcal mol⁻¹ for O–H⁺. Interestingly, the reaction involving O–H⁺ also benefits from more stabilizing orbital interactions, while the orbital interactions of both O–AlCl₃ and O–Li⁺ are nearly equivalent to the uncatalyzed analog. The electrostatic interaction, on the other hand, shows an opposite trend, namely, the uncatalyzed reaction goes with the most stabilizing electrostatic interaction, and is, therefore, not responsible for the observed reactivity trend.

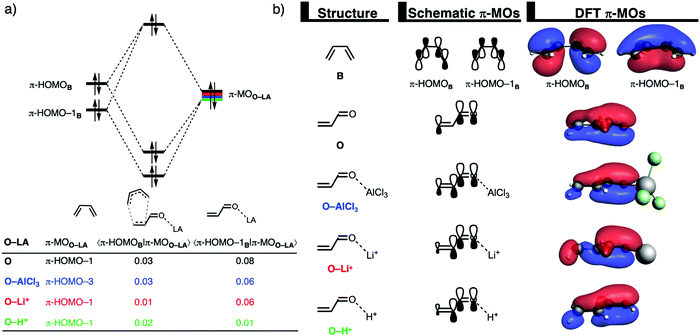
The origin of the less destabilizing Pauli repulsion for the LA-catalyzed compared to the uncatalyzed Diels–Alder reaction is further investigated by performing a Kohn–Sham molecular orbital (KS-MO) analysis.^13,29 The occupied molecular orbitals of B and O, O–AlCl₃, O–Li⁺, and O–H⁺ were quantified at consistent geometries with a C_B⋯C_β bond length between B and O–LA of 2.118 Å. The most important occupied π-MOs of the dienophiles that are decisive for the trend in Pauli repulsion are the π-HOMO–1 of O, O–Li⁺, and O–H⁺ and the π-HOMO–3 of O–AlCl₃. Note that these π-MOs are of the same type for each of the different O–LA dienophiles in that they have all 2p_z atomic orbitals (AOs) on the carbon and oxygen atoms in-phase. The occupied orbitals of B involved in this repulsive orbital interaction are the π-HOMO and π-HOMO−1, where the former has a nodal plane between the 2p_z AOs of the middle two carbon atoms while, for the latter, all 2p_z AOs are in-phase. The orbital overlap between the π-HOMO_B and π-HOMO–1_B and the occupied π-MOs of O–LA are the largest and, therefore, most destabilizing for O (S = 0.03 and 0.08) and the smallest and least destabilizing for O–H⁺ (S = 0.02 and 0.01; see Fig. 2a). Binding of a LA to O polarizes, due to the strong donor–acceptor interaction (Table S1, ESI†), the occupied π-MO_O–LA located on the C=C double bond of the dienophile away from the incoming B which, in turn, decreases the occupied–occupied orbital overlap and hence the Pauli repulsion.

Fig. 2 (a) Molecular orbital diagram and the most significant occupied orbital overlaps of the uncatalyzed and Lewis acid-catalyzed Diels–Alder reactions between B and O–LA; and (b) key occupied orbitals (isovalue = 0.03 Bohr^−3/2), computed at consistent transition state-like geometries with a C_B⋯C_β bond length between B and O–LA of 2.118 Å at ZORA-BP86/TZ2P.

In addition, the difference in reaction mode, that is, the degree of asynchronicity, also plays a significant role in the reduction of occupied–occupied orbital overlap. A more asynchronous reaction, i.e., the DA reaction catalyzed by AlCl₃ and Li⁺, has, due to the longer C_B⋯C_α bond, a reduced repulsive orbital overlap at the α-carbon of O–LA, manifesting in less Pauli repulsion between B and O–LA. This effect is further amplified when the DA reaction is stepwise, in the case of O–H⁺, because, along this reaction pathway, the reactants are oriented in a way that no repulsive occupied–occupied orbital overlap can occur between the filled orbitals of B and the 2p_z AO on the α-carbon of O–LA. This driving force behind Lewis acid catalysis confirms our previous analyses of Lewis acid and iminium ion-catalyzed Diels–Alder, Michael addition, and ring-opening reactions,^7,8 and again demonstrate the generality of the concept of Pauli-lowering catalysis.⁹

Next, we address why only the LA-catalyzed DA reaction involving O–H⁺ experiences more stabilizing orbital interactions compared to the uncatalyzed reaction, while the reactions catalyzed by AlCl₃ and Li⁺ do not. In line with the textbook rationale behind Lewis acid catalysis,⁶ binding of a Lewis acid to the dienophile strengthens the normal electron demand (NED) interaction by lowering the π-LUMO_O–LA, but the LA catalyst simultaneously weakens the inverse electron demand (IED) interaction by stabilizing the π-MO_O–LA and hence increasing the π-LUMO_B–π-MO_O–LA energy gap. By performing a Kohn–Sham molecular orbital (KS-MO) analysis on consistent geometries with a C_B⋯C_β bond length between B and O–LA of 2.118 Å,^13,29 we found that the π-LUMO_O–LA lowers in energy significantly more pronouncedly than in the case of the neutral uncatalyzed reaction, from –3.5 eV for the uncatalyzed reaction to –10.4 eV for the H⁺-catalyzed reaction (Fig. 3a). The stabilization of the π-LUMO_O–LA and hence reduction of the π-MO_B–π-LUMO_O–LA gap is, therefore, significant enough to overcome the loss of favorable π-HOMO_B–π-LUMO_O–LA orbital overlap, which results from the more asynchronous reaction mode, and hence results in a more favorable NED interaction for the LA-catalyzed reactions. In addition, the NED interaction, namely, that between π-HOMO−1_B and π-LUMO_O–LA, also becomes stronger, due to both a smaller orbital energy gap and an enhanced orbital overlap. The π-HOMO−1_B has a phase mismatch with the π-LUMO_O–LA and hence only a small net orbital overlap. This phase mismatch, however, becomes less severe when the reaction becomes more asynchronous, such as in the case of O–H⁺, and the π-HOMO−1_B–π-LUMO_O–LA interaction, therefore, starts to contribute to the total NED interaction. As mentioned above, binding of a LA stabilizes all orbitals of O–LA, thus, also the key occupied π-MO_O–LA from −7.5 eV for the uncatalyzed reaction to –13.9 eV for the H⁺-catalyzed reaction, yielding an increase of the π-LUMO_B–π-MO_O–LA energy gap. This, together with a reduced orbital overlap as a result of a more asynchronous reaction mode, weakens the IED interaction for the LA-catalyzed compared to the uncatalyzed DA reaction. For the reaction catalyzed by H⁺, the enhancement of the NED interaction prevails over the reduction of the IED interaction, which, ultimately, results in more stabilizing orbital interactions than the uncatalyzed reaction. The reactions catalyzed by AlCl₃ and Li⁺, on the other hand, do not engage in stronger orbital interactions, because the gain in NED interaction becomes effectively compensated by the loss of IED interaction, resulting in orbital interactions that are nearly identical to the uncatalyzed reaction.

Fig. 3 Molecular orbital diagrams with key orbital overlaps and energies for (a) the normal electron demand (NED) π-MO_B–π-LUMO_O–LA interactions; and (b) inverse electron demand (IED) π-LUMO_B–π-MO_O–LA interactions of the uncatalyzed and Lewis acid-catalyzed Diels–Alder reactions between B and O–LA, computed at consistent transition state-like geometries with a C_B⋯C_β bond length between B and O–LA of 2.118 Å at ZORA-BP86/TZ2P.

As described above, the reaction mode is a crucial factor for the kinetics of Diels–Alder reactions, because a larger degree of asynchronicity results in a lower reaction barrier due to a reduction of the destabilizing activation strain and Pauli repulsion. Understanding the origin of asynchronicity in Diels–Alder reactions is, therefore, essential for understanding and designing reactivity trends. To that end, we analyzed and compared Diels–Alder reaction pathways that were artificially constraint to be synchronous, asynchronous to various degrees, up till the point at which they turn from concerted asynchronous to stepwise. This approach allows us to rationalize (i) the origin of asynchronicity, and (ii) the driving force behind the degree of asynchronicity.

In Fig. 4, we focus on the activation strain diagram (ASD) of the uncatalyzed Diels–Alder reaction between B and O, which is a moderately asynchronous reaction with a degree of asynchronicity of Δr^TS_C⋯C = 0.46 Å. We have artificially constraint this reaction to be synchronous (Δr^TS_C⋯C = 0.00 Å), increasingly more asynchronous (Δr^TS_C⋯C = 0.19 Å, 0.42 Å, 0.62 Å, 0.82 Å, and 1.02 Å), and stepwise (Δr^TS_C⋯C = stepwise). Note that the ASDs of the artificially constraint reaction pathways of O–AlCl₃, O–Li⁺, and O–H⁺ follow the same trends and can be found in ESI,† Fig. S4–S6. The reaction barrier lowers when going from a synchronous to an asynchronous DA reaction with a degree of asynchronicity of 0.42 Å (Fig. 4a), which is close to the actual degree of asynchronicity of the reaction between B and O. By further amplifying the degree of asynchronicity, the reaction barrier increases to such an extent that the stepwise reaction pathway becomes an up-hill reaction without a kinetically stable intermediate, that is, the species in which the first C–C bond is formed would spontaneously fall back to the reactants. As previously discussed, the more asynchronous reaction yields the least destabilizing strain energy (Fig. 4b), because the C_B⋯C_α bond forms behind of the C_B⋯C_β bond, resulting in less geometrical deformation. Thus, from a strain energy perspective, DA reactions prefer to be as asynchronous as possible. This effect, however, becomes compensated by the dramatic loss of stabilizing interaction energy, when the DA reaction becomes asynchronous (Fig. 4c). It is, therefore, the interaction energy that determines whether and to which extent a DA reaction becomes asynchronous.

Fig. 4 Activation strain analyses: (a) total energy, (b) strain energy, and (c) interaction energy; and energy decomposition analyses: (d) Pauli repulsion, (e) electrostatic interaction, and (f) orbital interactions, of the artificially constraint synchronous, asynchronous, and stepwise Diels–Alder reaction modes (rxn mode) between B and O, where the transition states are indicated with a dot and the energy values are projected onto the shorter newly forming a C_B⋯C_β bond, computed at ZORA-BP86/TZ2P.

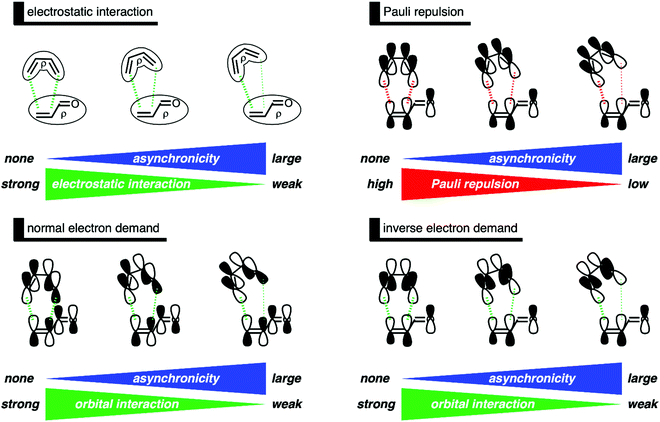
Next, we turn to the EDA to get a more detailed insight into how the interaction energy determines the degree of asynchronicity. In contrast with the current rationale that ascribes the origin of asynchronicity to enhanced orbital interactions between the diene and the β-carbon of the dienophile,¹¹ we found that the reduction of Pauli repulsion is the actual driving force behind the asynchronicity. The synchronous reaction pathway goes with the most destabilizing Pauli repulsion, which the reaction can relieve by increasing the degree of asynchronicity (Fig. 4d). However, the loss of destabilizing Pauli repulsion will converge when the DA reaction reaches a degree of asynchronicity of 0.62 Å. Thus, increasing the degree of asynchronicity beyond 0.62 Å will not lead to an additional stabilization of the DA reaction between B and O. The orbital interactions, and to a lesser extent the electrostatic interactions, do not benefit from a more asynchronous reaction mode (Fig. 4e and f), since both energy terms become consistently less stabilizing when the DA reaction becomes more asynchronous. Thus, asynchronicity arises when the associated reduction in Pauli repulsion is able to overcome the unfavorable loss in stabilizing orbital interactions. And the eventual degree of asynchronicity, as observed in the transition state, is achieved when the gain in stability, as a response to the reduced Pauli repulsion, balances with the loss of favorable orbital and electrostatic interactions. It is, therefore, the delicate interplay between the reduction of unfavorable Pauli repulsion and the loss of favorable orbital and, to a lesser extent, electrostatic interactions that determine the degree of asynchronicity in Diels–Alder reactions, which is, in the case of B and O at 0.46 Å.

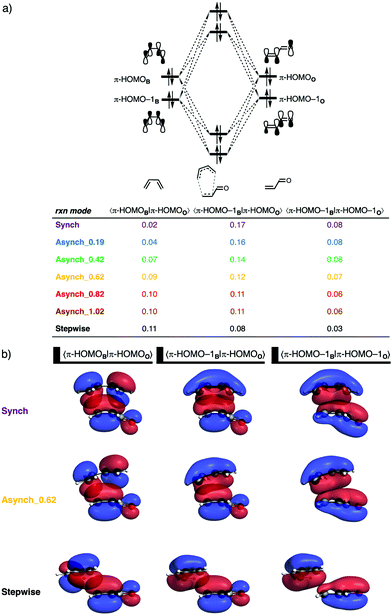
The origin of the reduction in destabilizing Pauli repulsion when the reaction pathway becomes more asynchronous is further investigated by performing a KS-MO analysis. The occupied molecular orbitals of B and O, which determine the trend in Pauli repulsion, were quantified on consistent geometries with a C_B⋯C_β bond length between B and O of 2.186 Å. The most important occupied orbitals of B are the π-HOMO and π-HOMO−1, where the former has a nodal plane between the 2p_z AOs of the middle two carbon atoms, while, for the latter, all 2p_z AOs are in-phase. The participating orbitals on O are the π-HOMO, where the 2p_z AOs on the C=C double bond are out-of-phase with the 2p_z AO of the carbonyl oxygen, and π-HOMO−1, where all 2p_z AOs of the carbon and oxygen atoms are in-phase. As expected, the occupied–occupied orbital overlaps between 〈π-HOMO–1_B|π-HOMO_O〉 and 〈π-HOMO–1_B|π-HOMO–1_O〉 decrease when the DA reaction pathway follows a more asynchronous reaction pathway, from S = 0.17 and 0.08 for the synchronous reaction pathway to S = 0.08 and 0.03 for the stepwise reaction pathway (Fig. 5a). We can trace this reduction in orbital overlap back to the longer C_B⋯C_α bond distance, which, effectively, leads to less occupied–occupied orbital overlap at the α-carbon of the dienophile when the reaction becomes more asynchronous and hence results in a reduction of Pauli repulsion (Fig. 5b). Interestingly, this reduction of destabilizing Pauli repulsion becomes counteracted by the occupied–occupied orbital overlap between 〈π-HOMO_B|π-HOMO_O〉, which becomes increasingly larger and hence more destabilizing. The π-HOMO_B has a nodal plane between the 2p_z AOs of the middle two carbon atoms and, therefore, engages, when following the synchronous reaction pathway, in an in-phase and out-of-phase overlap with π-HOMO_O, resulting in much orbital overlap cancellation and thus a total orbital overlap of only 0.02 (Fig. 5b). When the reaction pathway becomes more asynchronous, or even stepwise, the out-of-phase orbital overlap diminishes (Fig. 5b), which increases the total orbital overlap of 〈π-HOMO_B|π-HOMO_O〉 to 0.11 for the stepwise reaction. The loss of destabilizing 〈π-HOMO−1_B|π-HOMO_O〉 and 〈π-HOMO−1_B|π-HOMO−1_O〉 orbital overlap becomes, when the reaction pathway increases the degree of asynchronicity beyond 0.62 Å, effectively compensated by the gain in destabilizing orbital overlap between 〈π-HOMO_B|π-HOMO_O〉 resulting in the above-mentioned convergence of reduction in Pauli repulsion when the reaction pathway exceeds the degree of asynchronicity of 0.62 Å. As we will show later, the extent to which the destabilizing occupied–occupied orbital overlap and hence Pauli repulsion reduces, when the DA reaction becomes asynchronous, is highly dependent on the asymmetry in the occupied π-orbitals on the C=C double bond of O–LA.

Fig. 5 (a) Orbital interaction diagram and the most significant occupied orbital overlaps of the artificially constraint synchronous, asynchronous, and stepwise Diels–Alder reaction between B and O; and (b) key occupied–occupied overlapping orbitals (isovalue = 0.03 Bohr^−3/2), computed at consistent transition state-like geometries with a C_B⋯C_β bond length between B and O of 2.186 Å at ZORA-BP86/TZ2P.

After having established the origin of the less destabilizing Pauli repulsion in more asynchronous DA reactions, we want to address why the current rationale behind asynchronicity is incorrect.¹¹ In other words, why does the asynchronous DA reaction pathway not benefit from more stabilizing orbital interactions. In contrast with the current rationale, a more asynchronous reaction pathway leads to a weakening, not a strengthening, of both the normal electron demand (NED) and inverse electron demand (IED) orbital interactions (Fig. 6). Therefore, neither NED nor IED orbital interactions can be the reason behind the occurrence of an asynchronous reaction mode. An increasing degree of asynchronicity not only reduces the favorable orbital overlap, for both the NED and IED, but also increases the orbital energy gap. The loss of orbital overlap can be traced back to the longer C_B⋯C_α bond distance when the reaction becomes more asynchronous, which results in less favorable orbital overlap between B and the α-carbon of O. The increased orbital energy gap is related to the reduced geometrical deformation of the reactants along a more asynchronous reaction pathway. Larger geometrical deformation in the reactants, such as along the synchronous reaction pathway, result in a more significant destabilization of the π-HOMOs and a larger stabilization of the π-LUMOs of the individual reactants, which, in turn, leads to a smaller NED and IED π-HOMO–π-LUMO energy gap. These two effects, the loss of favorable orbital overlap and enlargement of π-HOMO–π-LUMO energy gap, result in consistently less stabilizing orbital interactions when the DA reaction between B and O becomes more asynchronous.

Fig. 6 Orbital interaction diagrams with key orbital overlaps and energies for (a) the normal electron demand (NED) π-HOMO_B–π-LUMO_O interactions; and (b) inverse electron demand (IED) π-LUMO_B–π-HOMO_O interactions of the artificially constraint synchronous and asynchronous Diels–Alder reaction between B and O, computed at consistent transition state-like geometries with a C_B⋯C_β bond length between B and O of 2.186 Å at ZORA-BP86/TZ2P.

In summary, asynchronicity in Diels–Alder reactions originates from the interplay between the reduction of destabilizing Pauli repulsion and the maximization of stabilizing orbital interactions (Fig. 7). When the DA reaction becomes asynchronous, it is liberated, due to a longer C_B⋯C_α bond distance, from destabilizing occupied–occupied orbital overlap at the α-carbon of the dienophile and hence Pauli repulsion. However, in contrast with the current rationale,¹¹ the elongation of the C_B⋯C_α bond also leads to less stabilizing orbital interactions, because of the reduction of both favorable normal electron demand and inverse electron demand orbital overlap. Thus, in the event that the mechanism of reducing Pauli repulsion dominates, the Diels–Alder reaction begins to deviate from synchronicity and adopts an asynchronous mode. The eventual degree of asynchronicity in the transition state is achieved when the gain in stability, as a response to the reduced Pauli repulsion, balances with the loss of favorable orbital interactions.

Fig. 7 Schematic summary of the effect of asynchronicity on the electrostatic interactions, Pauli repulsion, and orbital interactions of the Diels–Alder reaction between B and O, where the dashed lines indicate the stabilizing (green) and destabilizing (red) interactions.

Finally, we want to understand how exactly our model DA reactions achieve their particular, different degrees of asynchronicity (vide supra). By comparing the two extremes, that is, the moderately asynchronous reaction between O and B and the extremely asynchronous reaction between O–Li⁺ and B (O: Δr^TS_C⋯C = 0.46 Å; O–Li⁺: Δr^TS_C⋯C = 0.91 Å), we aim to establish the origin of the differences in reaction mode (Fig. S7, ESI†). The reaction involving O–Li⁺ goes via a larger degree of asynchronicity because it benefits from a larger reduction of destabilizing Pauli repulsion when the reaction pathway becomes increasingly more asynchronous than the reaction with O. In addition, O–Li⁺ also suffers less from a loss in stabilizing orbital interactions when the reaction becomes more asynchronous because of: (i) a less severe loss of NED orbital overlap 〈π-HOMO_B|π-HOMO_O–Li⁺〉 and; (ii) a more pronounced gain in additional NED orbital interaction, i.e., between π-HOMO and π-LUMO_O–Li⁺ (Fig. 6 and Fig. S8, S9, ESI†). Both effects can be traced back to the larger asymmetry in the orbital amplitudes on the α- and β-carbon atoms of LUMOs of O–Li⁺ compared to O (Fig. S10, ESI†). Thus, the equilibrium between the reduction of destabilizing Pauli repulsion and the loss of stabilizing orbital and electrostatic interactions, which eventually determines the degree of asynchronicity, lies for the DA reaction with O–Li⁺ at a significantly more asynchronous reaction mode than for the uncatalyzed analog. Note that we found that the same phenomena cause the difference in reaction mode when we compare the DA reaction involving O and O–H⁺, i.e., concerted asynchronous versus stepwise reaction (Figs. S11–S14, ESI†).

The differences in reduction of Pauli repulsion between the uncatalyzed and Li⁺-catalyzed DA reaction, upon making the reaction more asynchronous, are further analyzed by performing a Kohn–Sham molecular orbital analysis. Comparing the occupied–occupied orbital overlaps of O and O–Li⁺ with B, that determine the trend in reduction of Pauli repulsion, reveals that O–Li⁺ benefits from (i) a larger reduction of destabilizing 〈π-HOMO–1_B|π-HOMO–1_O–Li⁺〉 orbital overlap; and (ii) a lesser build-up of repulsive 〈π-HOMO_B|π-HOMO_O–Li⁺〉 orbital overlap compared to O when the reaction becomes more asynchronous (Fig. 5 and Fig. S15, ESI†). These differences can directly be related to the orbital amplitudes of these key orbitals on the α- and β-carbon atoms of O and O–Li⁺. Fig. 8 shows the MO-coefficients of the 2p_z AOs on the α- and β-carbon atoms of the key π-MOs of O and O–Li⁺. As discussed elsewhere,^8a binding of a LA induces a polarization of the π-MOs located on the C=C double bond towards the LA, due to the strong donor–acceptor interaction between LA and the dienophile, (Table S1, ESI†) yielding a larger asymmetry in the π-MOs on the C=C double bond of the dienophile. Consequently, the smaller orbital amplitudes on the β-carbon of the occupied π-HOMO and π-HOMO−1 orbitals of O–Li⁺ (e.g., π-HOMO_O–Li⁺: 0.49 on C^βversus 0.56 on C^α) compared to O (e.g., π-HOMO_O: 0.54 on C^βversus 0.52 on C^α) will, in turn, overlap less with the occupied orbitals of B and hence result in a larger reduction of destabilizing Pauli repulsion if the DA reaction follows a more asynchronous reaction mode. Thus, a large asymmetry in the π-MOs on the C=C double bond of the dienophile causes the equilibrium between the reduction of Pauli repulsion and the loss of stabilizing orbital interactions to shift to a larger degree of asynchronicity.

Fig. 8 Key occupied π-MOs (isovalue = 0.03 Bohr^−3/2) computed at the equilibrium structures of (a) O and (b) O–Li⁺, where the MO-coefficients of the carbon and oxygen 2p_z atomic orbitals, contributing to the occupied orbitals, are shown in the schematic π-MOs, computed at ZORA-BP86/TZ2P.

4. Conclusions

Asynchronicity in Lewis-acid (LA)-catalyzed Diels–Alder reactions of 1,3-butadiene (B) with acrylaldehyde (O–LA) is induced by the accompanying lowering of Pauli repulsion of the occupied π-orbitals of B with the asymmetric occupied π orbitals of O–LA, and not because of the widely accepted picture of more favorable orbital interactions. In fact, we show that donor–acceptor orbital interactions become even less stabilizing in the asynchronous reaction mode and always favor synchronicity. These and other findings emerge from detailed quantum chemical analyses based on the activation strain model and Kohn–Sham molecular orbital theory.

The rate enhancement upon going from the uncatalyzed to LA-catalyzed Diels–Alder reaction is exclusively caused by the diminished two-center four-electron Pauli repulsion between the occupied π-orbitals of B and O–LA and not the enhanced orbital interactions as commonly accepted. The LA catalyst polarizes, due to donor–acceptor interactions, the occupied π-orbitals of the dienophile away from its reactive C=C double bond which hence results in less destabilizing occupied–occupied orbital overlap with the incoming B. However, the orbital interactions are not strengthened by the LA catalyst, because the gain in normal electron demand HOMO_diene–LUMO_dienophile interaction becomes effectively compensated by the loss of inverse electron demand LUMO_diene–HOMO_dienophile interaction. One exception is O–H⁺, in which, interestingly, the LUMO is lowered to such a significant extent that this reaction benefits, besides from the Pauli-lowering catalysis mechanism, also from LUMO-lowering catalysis.

The LA catalyst also alters the DA reaction mode by amplifying the asynchronicity of the reaction, which has additional reaction barrier lowering consequences, namely, (i) less destabilizing activation strain in the transition state; and (ii) reduced occupied–occupied orbital overlap and hence Pauli repulsion. Asynchronicity in DA reactions is exclusively caused by the reduction of Pauli repulsion, because by following an asynchronous reaction mode, Diels–Alder reactions reduce, as a result of the larger degree of asymmetry in the two newly forming C⋯C bonds, the occupied–occupied orbital overlap between B and the α-carbon side of O–LA and hence the destabilizing Pauli repulsion. However, following a more asynchronous reaction pathway also leads, in contrast with the current rationale, to a significant weakening (not strengthening) of stabilizing orbital interactions, since the elongation of the C_B⋯C_α bond results in less favorable HOMO–LUMO orbital overlap. Thus, the degree of asynchronicity, as observed in the transition state of a Diels–Alder reaction, is achieved when the gain in stability, due to the reduced occupied–occupied orbital overlap (i.e., reduction of Pauli repulsion), dominates the loss of favorable orbital interactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank The Netherlands Organization for Scientific Research (NWO) and the Dutch Astrochemistry Network (DAN) for financial support. This work was carried out on the Dutch national e-infrastructure with the support of SURF cooperative.

Notes and references

1. O. Diels and K. Alder, Justus Liebigs Ann. Chem., 1928, 460, 98.
2. (a) F. Fringuelli and A. Taticchi, The Diels-Alder Reaction: Selected Practical Methods, Wiley, Hoboken, NJ, 2002; (b) S. Sankararaman, Pericyclic Reactions – A Textbook: Reactions, Applications and Theory, Wiley, Weinheim, 2005; (c) M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, Wiley, New York, 2013.
3. J.-A. Funel and S. Abele, 52 , Angew. Chem., Int. Ed., 2013, 3822 ( Angew. Chem. , 2013 , 125 , 3912 ).
4. For reviews on the application of Diels-Alder reactions, see: (a) W. Carruthers, Cycloaddition Reactions in Organic Synthesis, Pergamon Press, Oxford, UK, 1990; (b) K.-I. Takao, R. Munakata and K.-I. Tadano, Chem. Rev., 2005, 105, 4779; (c) M. Juhl and D. Tanner, Chem. Soc. Rev., 2009, 38, 2983; (d) K. C. Nicolaou, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668; (e) H. B. Kagan and O. Riant, Chem. Rev., 1992, 92, 1007; (f) C. O. Kappe, S. S. Murphree and A. Padwa, Tetrahedron, 1997, 53, 14179.
5. (a) U. Pindur, G. Lutz and C. Otto, Chem. Rev., 1993, 93, 741; (b) F. Fringuelli, O. Piermatti, F. Pizz and L. Vaccaro, Eur. J. Org. Chem., 2001, 439.
6. (a) K. N. Houk, Acc. Chem. Res., 1975, 8, 361; (b) M. J. R. Dewar, Molecular Orbital Theory for Organic Chemists, McGraw-Hill, New York, 1969; (c) W. T. Borden, Modern Molecular Orbital Theory for Organic Chemists, Prentice-Hall, Englewood Cliffs, New Jersey, 1975; (d) I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley, New Jersey, 2009.
7. (a) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201 ( Angew. Chem. , 2020 , 132 , 6260 ); (b) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Chem. Sci., 2020, 11, 8105; (c) P. Vermeeren, T. A. Hamlin, F. M. Bickelhaupt and I. Fernández, Chem. – Eur. J., 2021, 27, 5180; (d) P. Vermeeren, M. Dalla Tiezza, M. van Dongen, I. Fernández, F. M. Bickelhaupt and T. A. Hamlin, Chem. – Eur. J., 2021, 27, 10620; (e) S. Portela, J. J. Cabrera-Trujillo and I. Fernández, J. Org. Chem., 2021, 86, 5317; (f) S. Yu, F. M. Bickelhaupt and T. A. Hamlin, ChemistryOpen, 2021, 10, 784.
8. (a) T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922 ( Angew. Chem. , 2019 , 131 , 9015 ); (b) P. Vermeeren, F. Brinkhuis, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Asian J., 2020, 15, 1167; (c) T. Hansen, P. Vermeeren, R. Yoshisada, D. V. Filippov, G. A. van der Marel, J. D. C. Codée and T. A. Hamlin, J. Org. Chem., 2021, 86, 3565; (d) H. Gao, L. Hu, Y. Hu, X. Lv, Y.-B. Wu and G. Lu, Catal. Sci. Technol., 2021, 11, 4417; (e) L. Hu, H. Gao, Y. Hu, X. Lv, Y.-B. Wu and G. Lu, Chem. Commun., 2021, 57, 6412.
9. T. A. Hamlin, F. M. Bickelhaupt and I. Fernández, Acc. Chem. Res., 2021, 54, 1972.
10. (a) D. Yepes, O. Donoso-Tauda, P. Pérez, J. S. Murray, P. Politzer and P. Jaque, Phys. Chem. Chem. Phys., 2013, 15, 7311; (b) D. Yepes, J. S. Murray, P. Pérez, L. R. Domingo, P. Politzer and P. Jaque, Phys. Chem. Chem. Phys., 2014, 16, 6726; (c) A. M. Sarotti and Org Biomol, Chem, 2014, 12, 187; (d) J. S. Murray, D. Yepes, P. Jaque and P. Politzer, Comput. Theor. Chem., 2015, 1053, 270; (e) D. Yepes, J. Munarriz, D. l’Anson, J. Contreras-Garcia and P. Jaque, J. Phys. Chem., 2020, 124, 1959; (f) I. Tuvi-Arad and D. Avnit, J. Org. Chem., 2011, 76, 4973; (g) B. R. Beno, K. N. Houk and D. A. Singleton, J. Am. Chem. Soc., 1996, 118, 9984.
11. (a) R. J. Loncharich, F. K. Brown and K. N. Houk, J. Org. Chem., 1989, 54, 1129; (b) D. M. Birney and K. N. Houk, J. Am. Chem. Soc., 1990, 112, 4127.
12. For a step-by-step protocol, see: (a) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649 For reviews, see: ; (b) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114; (c) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953; (d) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 ( Angew. Chem. , 2017 , 129 , 10204 ); (e) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880.
13. R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432.
14. For an overview of the EDA method, see: (a) T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analysis, ed. S. Grabowsky, De Gruyter, Berlin, 2021, pp. 199–212 For a detailed overview of the EDA method, see; (b) F. M. Bickelhaupt and E. J. Baerends, inReviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, Hoboken, 2000, pp. 1–86.
15. See, for instance: (a) P. Vermeeren, M. T. Doppert, F. M. Bickelhaupt and T. A. Hamlin, Chem. Sci., 2021, 21, 4526; (b) P. Vermeeren, T. Hansen, P. Jansen, M. Swart, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2020, 26, 15538; (c) T. Hansen, P. Vermeeren, F. M. Bickelhaupt and T. A. Hamlin, Angew. Chem., 2021, 133, 21008 ( Angew. Chem., Int. Ed. , 2021 , 60 , 20840 ); (d) O. Larrañga and A. de Cózar, ChemistryOpen, 2019, 8, 49; (e) J. J. Cabrera-Trujillo and I. Fernández, Chem. – Eur. J, 2018, 24, 17823.
16. (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391; (c) E. J. Baerends, et al., ADF, SCM, Theoretical Chemistry, Vrije Universiteit Amsterdam, The Netherlands, 2019, p. 102, http://www.scm.com.
17. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
18. E. van Lenthe and E. J. Baerends, J. Chem. Phys., 2003, 24, 1142.
19. (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783; (c) E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943.
20. T. A. Hamlin, D. Svatunek, S. Yu, L. Ridder, I. Infante, L. Visscher and F. M. Bickelhaupt, Eur. J. Org. Chem., 2019, 378.
21. (a) M. Franchini, P. H. T. Philipsen, E. van Lenthe and L. Visscher, J. Chem. Theory Comput., 2014, 10, 1994; (b) M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819.
22. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363; (b) L. Deng, T. Ziegler and L. Fan, J. Chem. Phys., 1993, 99, 3823; (c) L. Deng and T. Ziegler, Int. J. Quantum Chem., 1994, 52, 731.
23. (a) X. Sun, T. M. Soini, J. Poater, T. A. Hamlin and F. M. Bickelhaupt, J. Comput. Chem., 2019, 40, 2227; (b) X. Sun, T. Soini, L. P. Wolters, W.-J. van Zeist, C. Fonseca Guerra, T. A. Hamlin and F. M. Bickelhaupt, PyFrag, Theoretical Chemistry, Vrije Universiteit Amsterdam, The Netherlands, 2019.
24. C. Y. Legault, CYLview20, Université de Sherbrooke, 2020, http://www.cylview.org.
25. (a) D. H. Ess and K. Houk, J. Am. Chem. Soc., 2007, 129, 10646; (b) D. H. Ess and K. Houk, J. Am. Chem. Soc., 2008, 130, 10187.
26. (a) I. Fernández, Chem. Sci., 2020, 11, 3769; (b) I. Fernández, Phys. Chem. Chem. Phys., 2014, 16, 7662.
27. (a) R. F. Childs, D. L. Mulholland and A. Nixon, Can. J. Chem., 1982, 60, 801; (b) R. F. Childs, D. L. Mulholland and A. Nixon, Can. J. Chem., 1982, 60, 809; (c) D. Yepes, P. Pérez, P. Jaque and I. Fernández, Org. Chem. Front., 2017, 4, 1390.
28. The potential energy surface of the barrierless formation of the first C–C bond between B and O–H⁺ is acquired by performing a linear transit calculation (also known as a relaxed scan calculation), wherein the newly formed C–C bond in 4-Int is systematically elongated in 20 equidistant steps from 1.66 Å to 3.00 Å. At each step, the atomic coordinates are optimized, except for the coordinates of the carbon atoms involved in the newly formed C–C bond.
29. T. A. Albright, J. K. Burdett and W. H. Wangbo, Orbital Interactions in Chemistry, Wiley, New York, 2013.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02456f

---