Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Local energy decomposition analysis and molecular properties of encapsulated methane in fullerene (CH4@C60)†
Aleksander
Jaworski
 * and
Niklas
Hedin
* and
Niklas
Hedin

Department of Materials and Environmental Chemistry, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: aleksander.jaworski@mmk.su.se
First published on 1st September 2021
Abstract
Methane has been successfully encapsulated within cages of C60 fullerene, which is an appropriate model system to study confinement effects. Its chemistry and physics are also relevant for theoretical model descriptions. Here we provide insights into intermolecular interactions and predicted spectroscopic responses of the CH4@C60 complex and compared them with results from other methods and with data from the literature. Local energy decomposition analysis (LED) within the domain-based local pair natural orbital coupled cluster singles, doubles, and perturbative triples (DLPNO-CCSD(T)) framework was used, and an efficient protocol for studies of endohedral complexes of fullerenes is proposed. This approach allowed us to assess energies in relation to electronic and geometric preparation, electrostatics, exchange, and London dispersion for the CH4@C60 endohedral complex. The calculated stabilization energy of CH4 inside the C60 fullerene was −13.5 kcal mol−1 and its magnitude was significantly larger than the latent heat of evaporation of CH4. Evaluation of vibrational frequencies and polarizabilities of the CH4@C60 complex revealed that the infrared (IR) and Raman bands of the endohedral CH4 were essentially “silent” due to the dielectric screening effect of C60, which acted as a molecular Faraday cage. Absorption spectra in the UV-vis domain and ionization potentials of C60 and CH4@C60 were predicted. They were almost identical. The calculated 1H/13C NMR shifts and spin–spin coupling constants were in very good agreement with experimental data. In addition, reference DLPNO-CCSD(T) interaction energies for complexes with noble gases (Ng@C60; Ng = He, Ne, Ar, Kr) were calculated. The values were compared with those derived from supramolecular MP2/SCS-MP2 calculations and estimates with London-type formulas by Pyykkö and coworkers [Phys. Chem. Chem. Phys., 2010, 12, 6187–6203], and with values derived from DFT-based symmetry-adapted perturbation theory (DFT-SAPT) by Hesselmann & Korona [Phys. Chem. Chem. Phys., 2011, 13, 732–743]. Selected points at the potential energy surface of the endohedral He2@C60 trimer were considered. In contrast to previous theoretical attempts with the DFT/MP2/SCS-MP2/DFT-SAPT methods, our calculations at the DLPNO-CCSD(T) level of theory predicted the He2@C60 trimer to be thermodynamically stable, which is in agreement with experimental observations.
Introduction
Carbon displays rich chemistry and physics with a variety of molecular allotropes, including common graphite and diamond, but also fullerenes, carbon nanotubes, and graphene.1–4 The most investigated fullerene is the C60 “Buckminsterfullerene” composed of 20 hexagons and 12 pentagons of sp2-hybridized carbon atoms fused into a pseudosphere with a ∼7 Å diameter, as displayed in Fig. 1. C60 occurs in trace amounts on Earth in carbon-rich rocks and soot.5,6 It has also been observed in micrometeorite impact residue on the NASA Long Duration Exposure Facility orbiter,7 which indicates that it either survived impact at nominal encounter velocity of orbital debris (∼11 km s−1),8 or was created in situ in space. Fullerenes isolated from meteorites revealed encapsulated atoms of noble gases with a 3He/4He isotope ratio of clearly extraterrestrial origin.9 Moreover, analyses of the 2019 data collected by the NASA/ESA Hubble Space Telescope confirmed spectral features of the ionized C+60 species in diffuse interstellar bands making it the largest molecule observed in space and indicating that fullerenes might play an important role in interstellar chemistry.10,11The properties and chemistry of C60 have been studied; for example, the wave-particle duality was experimentally observed for C60.12 Methods for preparation and separation have been established,13,14 and possibilities to encapsulate atoms and molecules inside the fullerene cage were recognized soon after its discovery.15 C60 endohedral complexes with metal ions, noble gases, H2, N2, and H2O have been prepared by high-energy collisions of ionized fullerene species, harsh conditions of high temperature and pressure, electric arc, or by organic synthesis methods called molecular surgery.16–19 The successful synthesis of an endohedral complex with CH4 was reported in 2019 by Whitby and coworkers.20 Methane is the largest, and the first organic molecule to be encapsulated in the C60 fullerene, and this complex denoted as CH4@C60 is the main object of this study.
There is no obvious direct route to measure the stabilization energy in fullerene endohedral complexes and obtain insights into the interaction mechanisms. Experimental observations in this respect have been limited to assessing the efficiency/probability of the given complex to be formed, and the main focus has been on spectroscopic and diffraction studies in relation to unusual physical properties of the encapsulated species.21–23 Substantial theoretical efforts have been directed to studies of C60 endohedral complexes and associated intermolecular interactions. Pioneering ab initio studies by Jerzy Cioslowski24–26 at the Hartree–Fock (HF) level of theory were expanded by studies of Bühl et al.,27,28 Patchkovskii et al.,29 Darzynkiewicz et al.,30 and Autschbach et al.31 among others,32–37 where density functional theory (DFT) and second-order Møller–Plesset perturbation theory (MP2) were used. However, within the supramolecular approach with the interaction energy being the arithmetic relation of related energies (Eint = EAB − (EA + EB)), DFT is essentially blind to long-range dispersion. This limitation has typically been addressed by using empirical correction schemes for the dispersion contributions.38–42 MP2 is the lowest ab initio method that accounts for “real” dispersion effects but it is unbalanced and its performances for weak, noncovalent interactions are modest and system dependent.43 Symmetry-adapted perturbation theory (SAPT) with monomer description at the DFT level (DFT-SAPT) developed by Krzysztof Szalewicz and coworkers is an alternative approach to account for dispersion contributions.44–46 Within SAPT, the interaction energy is obtained as a sum of physical contributions, free from basis set superposition error (BSSE).47 Hence, the most reliable stabilization energies for C60 endohedral complexes so far have been obtained with DFT-SAPT by Hesselmann and Korona.48,49 In parallel developments, approximate London-type formulas have been derived by Pyykkö and coworkers for the estimation of dispersion interaction in endohedral systems.50,51
Attractive dispersion interactions between nonpolar species such as C60 and CH4 (or noble gases) are purely quantum mechanical and originate from instantaneous effects of dynamical electron correlation.52 For systems of chemical interest that can be correctly described by a single reference wave function, the most robust (and still tractable) way of introducing electron correlation is the coupled cluster singles, doubles, and perturbative triples CCSD(T) method.53 It is the “gold standard” of quantum chemistry. However, a canonical implementation of the CCSD(T) model exhibits a seventh-order scaling with the system size, which results in tremendous computational expenses when considering systems larger than 15–25 atoms. Frank Neese and coworkers have recently developed an efficient implementation of the domain-based local pair natural orbital coupled cluster method (DLPNO-CCSD(T)).54–56 Briefly, in the DLPNO-CCSD(T) approach the correlation energy is expressed as a sum of electron pair correlation energies, which enables the distinction between the “weak pairs” with negligible contributions to the total correlation energy and the “strong pairs” that constitute the dominant, desired part. In this way, the “weak pairs” can be treated with a computationally more efficient second-order perturbation theory, whereas only the essential “strong pairs” are subjected to an accurate coupled cluster treatment, which greatly reduces the computational complexity. With appropriately selected pair-selection thresholds, this model is capable of recovering 99.9% of the correlation energy of its canonical counterpart. It reproduces the CCSD(T) results within a chemical accuracy at substantially reduced computational efforts.57,58 This approach extends the possibility of obtaining accurate ab initio energies to systems for which only DFT has been applicable so far.59,60 Moreover, using a local energy decomposition (LED) protocol allows for a physical meaningful decomposition of the interaction energy within the DLPNO-CCSD(T) framework.52,61,62
In this study, the goal was to provide an accurate interaction energy decomposition for the CH4@C60 complex and the encapsulation energy barrier using the DLPNO-CCSD(T) method. This approach is not biased by the parametrization inherent to the DFT models, including the type of exchange–correlation approximation and dispersion correction scheme. The reference interaction energies for endohedral complexes with noble gases were provided and compared with results by Pyykkö et al. and Hesselmann and Korona.49–51
Methods
The counterpoise-corrected interaction energy of molecular fragments X and Y can be expressed as:61 | (1) |
The electronic interaction energy ΔEint is decomposed within the following DLPNO-CCSD(T)-LED decomposition scheme:
 | (2) |
Computational details
All calculations were performed with the ORCA code63,64 using a very tight convergence tolerance of 1 × 10−9Eh. The evaluation of Coulomb and exchange integrals was accelerated with the RIJCOSX approximation65 with the def2/J Coulomb-fitting basis set66 and tightened grid (GridX5; a further increase was verified to have a negligible effect). Geometry optimizations were converged to very tight thresholds (VeryTightOpt setting) using the revised PBE “revPBE” exchange–correlation DFT approximation67,68 together with atom-pairwise dispersion correction based on tight binding partial charges (D4).42 The polarization-consistent segmented pcseg-1 basis set,69 and the increased DFT integration grid (Grid5 NoFinalGrid) were used. The choice of the revPBE model was based on its performance in a recent and thorough benchmark study (best among the computationally efficient gradient-corrected GGA functionals).70 To confirm the global energy minima at the potential energy surfaces, and to evaluate vibrational IR and Raman spectra, Hessians, and dipole polarizabilities were calculated. The transition state search involved many consecutive computations of the Hessians towards the first-order saddle point. Thereby computational efforts were reduced by using the smaller pcseg-0 basis set for atoms of aryl groups for the open-cage models. Cartesian coordinates of the models are provided in the ESI.† DLPNO-CCSD(T) calculations were performed with a Foster-Boys localization scheme, a full MP2 guess, and T0 perturbative triples correction based on semicanonical approximation (the difference with respect to the iterative T1 algorithm was verified to be small; see the ESI†).71 Correlation-consistent cc-pVXZ (X = D, T, Q, 5) orbital basis sets72–74 were employed together with the corresponding cc-pVXZ/C auxiliary basis sets.75 The chosen PNO truncation thresholds are discussed in the results and discussion section. Computations were performed on a cluster node equipped with two Intel Xeon® Gold® 6126 CPUs (2.6 GHz; 12-core) and 256 GB of RAM.Results and discussion
The choice of PNO truncation thresholds and basis sets
To facilitate accuracy control in a user-friendly manner, the authors of the DLPNO-CCSD(T) method have implemented three levels of predefined PNO truncation thresholds. These levels converge towards the method limit at increasing computational cost: LoosePNO, NormalPNO, and TightPNO.57 The first two offer sufficient accuracy for most applications (<0.5 kcal mol−1 deviation for the evaluations of total energy with respect to the CCSD(T) reference),57 but for analysis of weak intermolecular interactions, the TightPNO setting should be used. This ensures that the electron pairs that dominate the interaction are being treated at the coupled cluster level.61 However, fullerenes are challenging for local coupled cluster methods. The large number of (long-range) π–π interactions in the highly delocalized π-system of fullerenes render calculations with the TightPNO setting and accurate basis sets very demanding.58,76,77 The DLPNO-CCSD(T) in its current implementation is formally a linear-scaling method when considering the iterative part, but the RI-PNO integral transformations on large systems add substantial prefactors to the total computation times, which in turn limit the feasibility, also due to the memory and disk space requirements. Therefore, based on test calculations for the CH4⋯C6H6 dimer (Fig. 2), which is expected to exhibit a similar nature of noncovalent interactions to those in the CH4@C60 complex, we used a multilevel approach as proposed by Sparta et al.59 Within the multilevel DLPNO approach the test CH4⋯C6H6 system was divided into CH4 and C6H6 fragments. By this division, the intrafragment electron pairs with their orbitals entirely localized on one molecular fragment could be separated from those that gave rise to intermolecular interactions.59 In Table 1, dispersion interaction and time used for the DLPNO-CCSD(T)-LED calculations for the CH4⋯C6H6 dimer are presented (total interaction energies as well as the ΔEnon-disp and ΔEC-(T)int terms are included in the ESI†). We monitored the convergence of the energy component for the dispersion interaction (ECdisp) since it depends solely on the treatment of the electron correlation, and therefore is critically sensitive to the truncation thresholds of the PNO and the (in)completeness of the basis set. By using a TightPNO setting for both intrafragment and interfragment pairs, smooth convergence towards the limit of a complete basis set (CBS) was observed (see Fig. 2). The dispersion interaction energy essentially converged at the TightPNO/cc-pVQZ level. Unfortunately, this setup would involve prohibitive computational costs when applied to endohedral fullerene complexes. Therefore, for routine applications, we propose a more tractable multilevel DLPNO scheme. In this scheme, the truncation thresholds for the intrafragment PNO for the guest (in this case CH4) and for a troublesome delocalized π-system (C6H6, C60) are reduced to the NormalPNO and LoosePNO, respectively, whereas the critical interfragment pairs are subjected to an accurate TightPNO evaluation. Together with the combination of the cc-pVQZ/cc-pVTZ basis sets, the multilevel scheme proposed in the last row in Table 1 offers massive computational savings without compromising accuracy to any significant extent. For a test conducted for the CH4⋯C6H6 dimer, this approach recovered >95% of the dispersion interaction energy when compared to the TightPNO/CBS reference, while being only twice as expensive as the TightPNO/cc-pVDZ calculation. The contribution from weak pairs to the ECdisp was less than 4% throughout the calculations presented in Table 1. Moreover, the related interaction energies compared well with previously reported accurate ab initio calculated energies for the CH4⋯C6H6 dimer. When using the proposed multilevel DLPNO-CCSD(T) setup, a total interaction energy ΔEint = −1.34 kcal mol−1 was calculated, which agreed very well with the CCSD(T)/aug-cc-pVTZ result of −1.39 kcal mol−1 by Ringer et al.80 The estimated dispersion contribution of −2.03 kcal mol−1 at the SAPT2/aug-cc-pVDZ level of theory by Ringer et al.80 was close to our value of −2.22 kcal mol−1. The above indicates that the multilevel DLPNO-CCSD(T) setup tailored for substantially more demanding calculations on endohedral complexes of fullerenes is robust. | ||
| Fig. 2 (a) Molecular geometry of the CH4⋯C6H6 dimer optimized at the revPBE-D4/pcseg-1 level of theory. (b) Basis set convergence for the DLPNO-CCSD(T)-LED dispersion interaction energy component ECdisp using TightPNO settings. Open circles correspond to the calculation with the multilevel scheme proposed in the last row of Table 1. | ||
| Inter CH4⋯C6H6 | Intra CH4 | Intra C6H6 | Basis set CH4 | Basis set C6H6 | E Cdisp | Time factorc |
|---|---|---|---|---|---|---|
| a TightPNO: TCutPairs = 10−5, TCutDO = 5 × 10−3, TCutPNO = 1.00 × 10−6, TCutMKN = 10−3; NormalPNO: TCutPairs = 10−4, TCutDO = 1 × 10−2, TCutPNO = 3.33 × 10−7, TCutMKN = 10−3; LoosePNO: TCutPairs = 10−3, TCutDO = 2 × 10−2, TCutPNO = 1.00 × 10−7, TCutMKN = 10−3; see ref. 57. b Estimated from cc-pVXZ (X = T, Q, 5) results using an extrapolation scheme by Helgaker et al.78,79 c Time estimates based on computations using 8 cores of the Intel® Xeon® Gold 6126 CPU and 256 GB of RAM. Calculations were run in competition with other processes on the cluster, so there might be fluctuations in the computation time estimates. | ||||||
| TightPNO | TightPNO | TightPNO | CBS | CBS | −2.31 | ×112 |
| TightPNO | TightPNO | TightPNO | cc-pV5Z | cc-pV5Z | −2.30 | ×85 |
| TightPNO | TightPNO | TightPNO | cc-pVQZ | cc-pVQZ | −2.28 | ×21 |
| TightPNO | TightPNO | TightPNO | cc-pVTZ | cc-pVTZ | −2.14 | ×6 |
| TightPNO | TightPNO | TightPNO | cc-pVDZ | cc-pVDZ | −1.55 | ×1 |
| TightPNO | NormalPNO | LoosePNO | cc-pVQZ | cc-pVTZ | −2.22 | ×2 |
DLPNO-CCSD(T)-LED analysis of the CH4@C60
In Table 2 the corresponding bond lengths of energy-optimized geometries of the CH4, C60, and CH4@C60 endohedral complex are shown. As a consequence of Ih symmetry, the C60 fullerene molecular structure is defined by the two distinct C–C distances r1 and r2 that originate from the bonds between fused pentagons and hexagons (r1) and the shorter ones between two hexagons (r2). The energy-optimized model of C60 exhibited excellent agreement with experimental bond length estimates. For r1 the deviation was <0.005 Å, and r2 coincided with the empirical C–C distance. This indicated that the revPBE-D4/pcseg-1 level of theory was capable of delivering robust models of fullerene systems.For comparison, reported geometries of C60 optimized at the (ab initio) HF and MP2 levels of theory have revealed considerable deviations of C–C bond lengths,35,36 whereas previous tests of different DFT approximations have not included dispersion corrections.35,36 Of note, at the revPBE-D4/pcseg-1 level of theory the geometries of both CH4 and C60 remained essentially unchanged upon formation of the CH4@C60 endohedral complex. We note however that in our DFT optimized model of CH4 the C–H bond length was overestimated by ∼0.01 Å, and did not correspond to an energy minimum at the coupled cluster level of theory, for which the equilibrium C–H distance was shorter and closer to the experimental estimate. The encapsulation of CH4 in C60 is associated with a tiny shortening (<0.001 Å) of the C–H bond lengths. Therefore, the total DLPNO-CCSD(T) energy of the CH4 molecule calculated at molecular geometry corresponding to that in the CH4@C60 complex was lower compared to that for the isolated CH4. Although this effect was very small and had no implications on the evaluation of the electronic interaction energy ΔEint in the CH4@C60 complex, it would lead to an unphysical lowering of the “deformation energy”, the ΔEgeo-prep term in eqn (1). Therefore, to provide the most realistic values the evaluation of ΔEgeo-prep included only the contribution from the deformation of the C60 cage.
In Fig. 3, interaction energy contributions are presented from the DLPNO-CCSD(T)-LED analysis of the CH4@C60 endohedral complex. The total interaction energy for the complex is represented as a sum of seven physical contributions: ΔEHFel-prep, Eelstat, Eexch, ΔECnon-disp, ECdisp, ΔEC-(T)int, and ΔEgeo-prep (according to eqn (1) and (2)). The large and positive electronic preparation term ΔEHFel-prep = +81.22 kcal mol−1 is counteracted by attractive contributions due to electrostatics and exchange (Eelstat = −39.73 kcal mol−1, Eexch = −21.00 kcal mol−1). However, the summed components of the interaction energy at the Hartree–Fock level (ΔEHFel-prep + Eelstat + Eexch) resulted in substantially repulsive interaction of ΔEHFint = +20.49 kcal mol−1. This value was basically identical to the value calculated by Pyykkö and coworkers at the HF/def2-QZVPP level of theory (the same as the +20.50 kcal mol−1).51 This summation can be regarded as an estimate of the extent of steric repulsion.50 It is noteworthy that CH4@C60 is predicted to be unstable also by DFT if empirical dispersion corrections are not used.32,33 The non-dispersive correction due to electron correlation was small and repulsive (ΔECnon-disp = +1.00 kcal mol−1). As expected, London dispersion is the dominant intermolecular interaction mechanism. The magnitude of the ECdisp term of −29.96 kcal mol−1 was larger than the substantially repulsive Hartree–Fock interaction and the ΔECnon-disp correction, resulting in an endohedral complex stabilization by −8.47 kcal mol−1. However, a further attractive correction came from the contribution from perturbative triple excitations ΔEC-(T)int that stabilized the complex by an additional estimated contribution of −5.03 kcal mol−1. The correction from perturbative triples was important, given that it increased the net binding energy in the complex by nearly 60% (from −8.47 to −13.50 kcal mol−1; see the inset in Fig. 3). Therefore, the final electronic interaction energy at the DLPNO-CCSD(T)/cc-pVQZ(CH4)/cc-pVTZ(C60) level of theory for the CH4@C60 endohedral complex was −13.50 kcal mol−1. The geometry preparation (“deformation energy”) term was very small (ΔEgeo-prep = +0.03 kcal mol−1). C60 is a rigid molecule and encapsulation of the CH4 guest had a negligible effect on its geometry (see Table 2). Our reference stabilization energy of ΔE = −13.47 kcal mol−1 was compared with the best reported estimates. For the CH4@C60 complex, the most robust results have been reported by Pyykkö and coworkers.51 In that study interaction energies were obtained with supramolecular MP2 and its spin component scaled counterpart (SCS-MP2). Calculations were performed with the def2-TZVPP and def2-QZVPP basis sets, interaction energies were corrected for basis set superposition error and extrapolated to the complete basis set limit. The obtained MP2 interaction energy of −21.37 kcal mol−1 was clearly overestimated. The value obtained with SCS-MP2 (−11.97 kcal mol−1) was closer to the coupled cluster reference, but underestimated. These calculated interaction energies followed the pattern observed in previously reported benchmark calculations. For the CH4⋯C6H6 dimer, MP2 overestimates the CCSD(T) interaction energy, as was shown by Ringer et al.,80 and for the endohedral CH4@C60 complex, this overestimation seems to be even more pronounced. The same trend of deviation was observed by Pyykkö and coworkers for dimers composed of atoms of noble gases and benzene (Ng⋯C6H6), where MP2 overestimated the CCSD(T) reference interaction energies significantly, whereas SCS-MP2 was generally much closer to coupled cluster results, but consistently underestimated the interaction.51
Pyykkö and coworkers have also developed London-type formulas to estimate dispersion interaction energies in endohedral systems.50,51 The input parameters to these formulas such as ionization potentials and polarizabilities can be readily computed at the DFT level. Using the data from the study of Pyykkö and coworkers51 (Table 17, equations 69 + 86) the dispersion energy estimate of −17.33 kcal mol−1 was obtained for the CH4@C60 complex. This energy was much smaller than for the DLPNO-CCSD(T)-LED (−29.96 kcal mol−1), and would not overcome the steric repulsion estimate of +20.49 kcal mol−1, and the complex would not be estimated to be stabilized in that description.
In Fig. 4, energies are shown in relation to the energy barrier of CH4 insertion through the orifice of the open-cage C60. The model of open-fullerene is designed to match the molecule used by Whitby and coworkers20 in their successful synthesis of the CH4@C60 endohedral complex. The insertion energy barrier was calculated at the DLPNO-CCSD(T)/cc-pVQZ(CH4)/cc-pVDZ(open-fullerene) level of theory and was significant (ΔE = +19.81 kcal mol−1), and in agreement with experimental observations that high pressure and elevated temperature conditions (1645 atm, 190 °C for 22 h) are necessary to achieve a high degree of CH4 insertion.20 It is noteworthy that the electronic repulsive interaction at the orifice ΔEint = +9.19 kcal mol−1 amounted to only less than half of the insertion energy barrier. The remaining geometry preparation term corresponded to the energy needed to deform the open-cage fullerene from its equilibrium geometry to the one optimal for CH4 insertion (ΔEgeo-prep = +10.62 kcal mol−1). After insertion, the CH4 molecule is predicted to be stabilized inside the open-fullerene cage by ΔE = −10.16 kcal mol−1.
Spectroscopic properties of CH4@C60 in IR and UV-Vis
Harmonic vibrational frequencies of the endohedral CH4@C60 complex have been computed at the level of GGA and hybrid DFT approximations without using dispersion corrections,32,33 and at the Hartree–Fock level of theory.34 Hence, those frequencies were evaluated on structures corresponding to energy minima in a situation where London dispersion interactions had not been accounted for. In those studies the intensities in the resulting calculated IR and Raman spectra were not discussed as well. Therefore, we calculated the harmonic vibrational frequencies together with the respective IR absorption coefficients and Raman scattering factors for CH4, C60, and the CH4@C60 complex at the revPBE-D4/pcseg-1 level of theory. Related frequencies, absorption coefficients and scattering factors are presented in Table 3.| CH4 | C60 | CH4@C60 |
|---|---|---|
| a See ref. 83. b Only the respective IR/Raman active modes (A, S ≥ 0.1) are shown. c From ref. 84 and 85. | ||
| ν/A | 502 (527)/23.4 | 501/22.0 |
| 579 (577)/14.1 | 581/13.7 | |
| 1201 (1183)/9.5 | 1201/8.9 | |
| 1287 (1367)/19.9 | 1296/0.3 | |
| 1304/0.3 | ||
| 1332/0.3 | ||
| 1456 (1428)/13.8 | 1457/13.4 | |
| 3107 (3157)/15.7 | 3218/0.1 | |
| 3220/0.1 | ||
| 3223/0.1 | ||
| ν/S | 258 (273)/25.4 | 263/24.2 |
| 416 (437)/0.4 | 421/0.4 | |
| 488 (496)/152.7 | 491/149.7 | |
| 664 (710)/0.2 | 664/0.2 | |
| 775 (774)/9.0 | 775/9.0 | |
| 1108 (1099)/14.7 | 1108/12.7 | |
| 1264 (1250)/22.3 | 1264/19.6 | |
| 1287 (1367)/0.8 | 1296/0.7 | |
| 1304/0.7 | ||
| 1332/0.7 | ||
| 1444 (1428)/2.9 | 1444/2.7 | |
| 1496 (1470)/365.0 | 1496/348.4 | |
| 1506 (1583)/21.4 | 1534/1.3 | |
| 1581 (1575)/59.1 | 1580/52.4 | |
| 2972 (3026)/160.1 | 3075/2.3 | |
| 3107 (3157)/69.2 | 3218/0.5 | |
| 3220/0.5 | ||
| 3223/0.3 | ||
The calculated vibrational frequencies of C60 were in very good agreement with experimental data and virtually unchanged upon CH4 encapsulation. This situation was in agreement with the experimental IR spectrum of H2O@C60, where the vibrational frequencies of the fullerene cage were the same as those of the free C60.19 The calculated IR absorption coefficients and Raman scattering factors (for the fullerene cage) were predicted to be slightly affected by CH4 encapsulation and resulted on average in a <5% loss in spectral intensity. Frequencies of the encapsulated CH4 on the other hand were blue shifted with respect to the free CH4 molecule, and were in agreement with previous theoretical predictions.33,34 Our results suggested that the triple degeneracy of the asymmetric bending and stretching IR modes (1287 and 3107 cm−1) of CH4 was partially removed due to the interaction with the cage. However, what was the most important, for both IR and Raman a substantial loss in spectral intensities for the encapsulated CH4 was revealed. This intensity loss was in line with experimental IR spectra of the CH4@open-fullerene complex, where vibrations of the CH4 could not be observed.37 In addition, vibrational features of the H2O were very weak in the experimental IR spectrum of H2O@C60, and the potential screening effect of the fullerene cage was indicated.19,86 Dielectric measurements conducted at low temperature and IR spectra of H2O@C60 collected at liquid helium temperature have revealed that the dipole moment of the encapsulated H2O was 0.5 ± 0.1 D,87,88 which is about 25% of free H2O molecules (in agreement with theoretical predictions89). A very similar extent of dipole moment reduction has been observed for HF in HF@C60 as well.90
The fullerene cage protects encapsulated species from the influence of the external electric field, and acts as a molecular Faraday cage.91,92 Such a screening effect can be assessed by calculating a difference between the dipole polarizability (α) of an endohedral complex, and the sum of polarizabilities of an isolated guest and the empty fullerene:93
| Δα = α(X@C60) − [α(X) + α(C60)] | (3) |
 | (4) |
The electronic excited state energies and absorption in the UV-vis domain were calculated at the CAM-B3LYP/cc-pVTZ level of theory with a time-dependent DFT (TD-DFT) within the efficient sTD-DFT implementation of Bannwarth and Grimme.102 Transition energies, wavelengths, and oscillator strengths for C60 and CH4@C60 are shown in Table 5.
| C60 | CH4@C60 | ||||
|---|---|---|---|---|---|
| E | λ | f osc | E | λ | f osc |
| a Transitions with oscillator strengths fosc > 0.01 are shown. | |||||
| 3.86 | 322 | 0.151 | 3.86 | 322 | 0.149 |
| 4.14 | 300 | 0.384 | 4.14 | 300 | 0.379 |
| 5.31 | 231 | 1.922 | 5.37 | 231 | 1.919 |
| 6.28 | 198 | 0.228 | 6.28 | 198 | 0.222 |
| 6.63 | 187 | 1.907 | 6.63 | 187 | 1.905 |
| 7.38 | 168 | 0.407 | 7.38 | 168 | 0.378 |
| 7.62 | 163 | 0.013 | 7.62 | 163 | 0.013 |
The predicted spectroscopic characteristics of C60 and CH4@C60 were almost identical in the UV-vis range. Both entities exhibited the same transition energies. The oscillator strengths were marginally lower for the complex compared to the empty fullerene. These results were in agreement with experimental observations for C60 and H2O@C60. They display close to identical UV-vis spectra, despite revealing a slightly lower absorption for the complex.19 The data in Table 5 compare favorably with the experimental UV-vis spectrum of C60 in the gas phase.103 The set of three most intense bands at 187/231/300 nm that reveal oscillator strengths of 1.907/1.922/0.384 correspond to the experimentally observed transitions at 205/257/330 nm that exhibit extinction coefficients of 4.8/3.5/0.9 (105 L mole−1 cm−1).103 Hence, the pattern of UV-vis bands correlated well between theoretical predictions and the experimentally observed spectra, however, transition energies were overestimated (too short wavelengths) at the TD-DFT level of theory.
Because of the rich chemistry of the ionized fullerene species (Cn+60; n = 1, 2, 3), it is interesting to compare the ionization potentials of the C60 and its endohedral complex. Ionized fullerenes exhibit a diversity of ionization mechanisms and a variety of reactions with potential implications to chemistry in the interstellar medium.104 The vertical ionization energies (VIE) for C60 and CH4@C60 were calculated at the CAM-B3LYP/Sadlej-pVTZ level of theory according to:
| VIE = En+cation − E0neutral; n = 1, 2, 3 | (5) |
NMR properties of the CH4@C60
Fullerenes constitute the only known allotrope of carbon that can be dissolved in organic solvents at room temperature.106 Therefore, high resolution liquid-state NMR spectra of C60 and its endohedral complexes can be measured in common NMR solvents.107,108 Whitby and coworkers collected and analyzed 1H and 13C NMR spectra of the CH4@C60 complex dissolved in 1,2-dichlorobenzene.20 For prediction of such spectra with quantum chemistry methods, a robust model including subtle interactions of the fullerene cage with solvent molecules is important. Hence, we constructed systems composed of the C60 and CH4@C60 explicitly solvated by 25 molecules of 1,2-dichlorobenzene, whereas solvent effects at the outer sphere were accounted implicitly by a polarizable continuum model (PCM) assuming a dielectric constant ε = 9.93. The initial configuration was obtained with the Packmol software,109 and the coordinates were energy optimized at the revPBE-D4/pcseg-1(CH4,C60)/pcseg-0(C6H4Cl2) level of theory up to the energy change of <5 × 10−6Eh; see Fig. 5.The 1H and 13C nuclear magnetic shielding tensors110,111 (σ; assessed with the GIAO approach112) and indirect nuclear spin–spin coupling constants (J) were calculated at the level of PBE0 DFT approximation.113 The calculations were performed with segmented pcS-1 and pcJ-1 basis sets, which have been specifically developed to provide fast convergence towards the Kohn–Sham limit for NMR shieldings and spin–spin couplings.114,115 The chosen setup represents a reasonable compromise for the calculations of 1H/13C NMR parameters when compared to more accurate methods given the size of the system.116,117 For solvent molecules, the pcseg-0 basis set was used. The calculations of NMR observables involved all electrons (no frozen core) and very tight grids (GridX8 Grid7). The calculated isotropic 1H/13C NMR shielding:
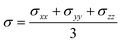 | (6) |
 | (7) |
 and
and  represent the calculated shielding and experimental shift of the reference, respectively. The CH4 molecule was used as a reference since its proton and carbon chemical shifts measured in the gas phase are available.118 Shifts of chemically equivalent atoms were averaged. Spin–spin coupling constants were represented as a sum of four physical contributions: the Fermi contact (FC), spin-dipole (SD), paramagnetic spin–orbit (PSO), and diamagnetic spin–orbit (DSO) terms.
represent the calculated shielding and experimental shift of the reference, respectively. The CH4 molecule was used as a reference since its proton and carbon chemical shifts measured in the gas phase are available.118 Shifts of chemically equivalent atoms were averaged. Spin–spin coupling constants were represented as a sum of four physical contributions: the Fermi contact (FC), spin-dipole (SD), paramagnetic spin–orbit (PSO), and diamagnetic spin–orbit (DSO) terms.
The calculated 1H and 13C NMR chemical shifts as well as the 1H–13C spin–spin couplings presented in Table 7 revealed very good agreement with experimental data. For protons in the CH4 molecule, the change in chemical shift (Δδ) upon encapsulation in C60 was predicted to be −7.54 ppm, which compared very well to −7.88 ppm observed in an experiment.20 This change on encapsulation is associated with the NMR shielding inside the fullerene cage, where the locally induced magnetic fields counteract the applied external field of the NMR instrument. The corresponding effect for the 13C in CH4 was slightly smaller, as revealed by the calculated and experimental Δδ values of −5.87 and −4.98 ppm, respectively. For carbon atoms of the fullerene cage, the presence of endohedral CH4 results in a deshielding of the 13C NMR signal. Therefore, this effect is opposite to that observed for the 13CH4 inside the cage. The calculated 13C deshielding of the cage of +0.51 ppm was in excellent agreement with the experimental value of +0.52 ppm.20 The spin–spin coupling constant 1JHC in the CH4 was dominated by the Fermi-contact (FC) mechanism. The calculated coupling strength of 1JHC = 126.4 Hz for the free CH4 was close to the experimental value of 125.3 Hz.119 Encapsulation of CH4 in C60 had little effect on the 1JHC, and the calculated value of 124.1 Hz was very close to the experimentally determined 124.3 Hz.20 Therefore, our theoretical model predicts correctly the sign and the small magnitude of the ΔJ. The small change of the coupling was consistent with negligible deformation of the CH4 geometry upon encapsulation.
| CH4 | C60 | CH4@C60 | |
|---|---|---|---|
| a From ref. 20, 118 and 119. | |||
C1![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 4 4 |
|||
| δ | Ref (2.17) | −5.37 (−5.71) | |
| Δδ | −7.54 (−7.88) | ||
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) H4 H4 |
|||
| δ | Ref (−8.65) | −14.52 (−13.63) | |
| Δδ | −5.87 (−4.98) | ||
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) 60 60 |
|||
| δ | 143.99 (142.68) | 144.50 (143.20) | |
| Δδ | +0.51 (+0.52) | ||
| 1 J HC(FC) | 124.4 | 121.4 | |
| 1 J HC(SD) | 0.2 | 0.2 | |
| 1 J HC(PSO) | 1.6 | 0.5 | |
| 1 J HC(DSO) | 0.2 | 2.0 | |
| 1 J HC | 126.4 (125.3) | 124.1 (124.3) | |
| ΔJ | −2.3 (−1.0) | ||
Complexes with noble gases Ng@C60 (Ng = He, Ne, Ar, Kr)
The efficient DLPNO-CCSD(T) setup designed for probing intermolecular interactions in the CH4@C60 complex was also used to obtain reference interaction energies for endohedral complexes with atoms of noble gases (Ng@C60; He, Ne, Ar, Kr). Hence, in this section, we compared our coupled cluster results to previously reported estimates at lower levels of theory. In Table 8, interaction energies (ΔEint) calculated at the DLPNO-CCSD(T)/cc-pVQZ(Ng)/cc-pVTZ(C60) level of theory are presented together with values from the MP2/SCS-MP2 calculations by Pyykkö and coworkers,51 and from the DFT-SAPT calculations by Hesselmann and Korona.49 The MP2 method exhibited the most unbalanced performance. The associated interaction energies for He was too low with this method, for Ne they were quite reasonable (accidentally), but those for Ar and Kr were severely overestimated. These trends resembled those observed for values derived with the MP2 method for the CH4@C60 complex. The spin component scaled variant (SCS-MP2) displayed an improved description. Although interaction energies for He and Ne were too low, the result for Ar was close to the coupled cluster reference, and the overestimation for Kr was not as severe as with the MP2. The situation with the DFT-SAPT results was more complex and somewhat difficult to judge. On the one hand, all interaction energies for these systems obtained with the DFT-SAPT were consistently underestimated when compared to the DLPNO-CCSD(T) values. On the other hand, the performance of the DFT-SAPT was consistent and well balanced across the He, Ne, Ar, and Kr complexes. This complexity became apparent when the results of DLPNO-CCSD(T) were plotted against the DFT-SAPT counterpart in Fig. 6a. The correlation between the two approaches was very good, despite the consistently underestimated interaction energies by the latter. For comparison, the correlation with the SCS-MP2 data shown in panel b was much worse and significantly less convincing.| Method | He | Ne | Ar | Kr |
|---|---|---|---|---|
| a Two-point extrapolation to the CBS limit based on the def2-TZVPP/def2-QZVPP basis sets; results from ref. 51. b DFT-SAPT calculations with the PBEac functional, aug-cc-pVDZ(He,Ne), aug-cc-pVTZ(Ar,Kr), and TZVP(C) basis sets; results from ref. 49. | ||||
| MP2 | −2.63 | −5.40 | −19.49 | −26.80 |
| SCS-MP2 | −1.86 | −3.75 | −12.92 | −16.98 |
| DFT-SAPT | −1.58 | −2.85 | −7.87 | −8.26 |
| DLPNO-CCSD(T) | −4.97 | −6.56 | −12.30 | −13.39 |
 | ||
| Fig. 6 Interaction energies (ΔEint) calculated at the DLPNO-CCSD(T)/cc-pVQZ(Ng)/cc-pVTZ(C60) level of theory plotted against the results from DFT-SAPT (a),49 and supramolecular SCS-MP2 (b).51 The grey line corresponds to the ideal correlation y = x, and the red line to the linear regression fit. | ||
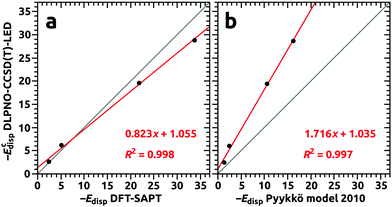
In Table 9, estimations of dispersion contributions to the interaction energy for the Ng@C60 complexes are presented for different methods of calculations. The dispersion contributions (ECdisp) from the DLPNO-CCSD(T)-LED were in good agreement with the dispersion components from the DFT-SAPT for all four considered complexes. Hence, it was concluded that the DFT-SAPT compared favorably to the DLPNO-CCSD(T)-LED for prediction of the dispersion interaction in fullerene complexes. This favorable comparison for DFT-SAPT is illustrated in Fig. 7a where results of DLPNO-CCSD(T) and DFT-SAPT are plotted against each other. Therefore, the too low interaction energies obtained with the DFT-SAPT for the complexes with noble gases did not originate from an inappropriate description of the dispersive part of the interaction, but resulted from deficiencies in the remaining components of the interaction energy. Analysis with DLPNO-CCSD(T)-LED revealed significant contributions from perturbative triples (ΔEC-(T)int), and yet, for small guests (He, Ne) for which repulsive interaction at the Hartree–Fock level (ΔEHFel-prep + Eelstat + Eexch) is small, the non-dispersive corrections due to electron correlation (ΔECnon-disp) were attractive.
| Method | He | Ne | Ar | Kr |
|---|---|---|---|---|
| a Results with London-type formula for dispersion interaction in endohedral systems, model 2007 from Table 2 column 5 in ref. 50, model 2010 equations 69 + 72 from ref. 51. b DFT-SAPT results from ref. 49. | ||||
| Pyykkö model 2007 | −1.31 | −2.44 | −9.22 | −13.40 |
| Pyykkö model 2010 | −1.31 | −2.48 | −10.53 | −16.27 |
| DFT-SAPT (disp) | −2.57 | −5.28 | −21.96 | −33.89 |
| DLPNO-CCSD(T)-LED | ||||
| ΔEHFel-prep | +2.38 | +10.65 | +52.47 | +97.34 |
| E elstat | −1.13 | −7.09 | −32.44 | −61.25 |
| E exch | −0.69 | −2.05 | −10.75 | −18.97 |
| ΔECnon-disp | −2.30 | −1.02 | +0.98 | +2.14 |
| E Cdisp | −2.45 | −6.05 | −19.45 | −28.68 |
| ΔEC-(T)int | −0.78 | −0.99 | −3.11 | −3.97 |
 | ||
| Fig. 7 Dispersion interaction energy ECdisp from DLPNO-CCSD(T)-LED decomposition compared to that obtained with the DFT-SAPT (a),49 and (b) with the London-type formula by Pyykkö.51 The grey line corresponds to the ideal correlation y = x, and the red line to the linear regression fit. | ||
The dispersion interaction as predicted with London-type formulas by Pyykkö and coworkers were substantially underestimated when compared to the DLPNO-CCSD(T)-LED results, although a linear trend with the latter was revealed; see Table 9 and Fig. 7b. This underestimation indicates that the sum of the dipole–dipole and quadrupole–quadrupole terms in the “Pyykkö model 2010” (eqn 69 + 72 from ref. 51) was not sufficient, and that it is necessary to include higher order multipole–multipole contributions to obtain better agreement with high-level quantum chemistry methods.49,51
The He2@C60 trimer
The existence of the He2@C60 trimer, where two helium atoms are encapsulated inside the C60 was discovered with 3He NMR by Rabinovitz and coworkers.120 The observed He2@C60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He@C60 ratio of 1
He@C60 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 was 10 times smaller than that for He2@C70
200 was 10 times smaller than that for He2@C70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He@C70 (1
He@C70 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20). This reduction suggests that the smaller cavity of C60 was significantly less suited for the encapsulation of two He atoms as compared to the C70 fullerene.
20). This reduction suggests that the smaller cavity of C60 was significantly less suited for the encapsulation of two He atoms as compared to the C70 fullerene.
The stability of the He2@C60 trimer was studied with quantum chemistry methods by Darzynkiewicz & Scuseria,30 Krapp & Franking,121 and Hesselmann & Korona.49 However, all methods applied, including DFT, MP2, SCS-MP2, and DFT-SAPT predicted repulsive interaction in the range from +1.13 to +10.23 kcal mol−1, depending on the method and the basis sets used. Hence, theoretical investigations reported so far suggest that He2@C60 is thermodynamically unstable towards loss of the noble gas atom, in stark contrast to the experimental observation.
To gain insight into this challenging system and confront the discrepancy between theory and experiment with the DLPNO-CCSD(T) approach, a relaxed potential energy surface scan at the revPBE-D4/pcseg-1 level of theory was performed for the He2@C60. The He–He distance was sampled with a 0.02 Å increment, and for each step all other coordinates were subjected to unconstrained optimization. Subsequently, single-point DLPNO-CCSD(T) calculations were performed on the resulting geometries to locate the “true” energy minimum; see Fig. 8.
At the DLPNO-CCSD(T)/cc-pVQZ(He)/cc-pVTZ(C60) level of theory, the equilibrium He–He distance inside C60 was 1.94 Å. This distance was not only substantially shorter than that of 3.00 Å calculated for the free He2 dimer, but it corresponded to a clearly repulsive regime for the latter. Our result was close to the value of 1.95 Å obtained by Krapp & Franking121 at the DFT BP86/TZVPP level, and slightly shorter than 1.98 Å estimated by Kryachko et al. at the DFT M062X/6-31G(d) level.122 In agreement with the analysis in the latter work, we observed that the He2 dimer inside the C60 was fractionally ionized by +0.0141 |e| (Mulliken charge). The corresponding effect for the case of a single He atom in the He@C60 complex was +0.0036 |e|; hence, comparably smaller. Note that the interaction well for the isolated He2 dimer was relatively shallow, whereas the relation of potential energy change upon He–He distance variation was very steep for the He2@C60 trimer.
For the equilibrium distance rHe–He = 1.94 Å inside C60 the stabilization energy ΔEint of the He2@C60 trimer:
| ΔEint = EXYZXYZ(XYZ) − (EXYZX(XYZ) + EXYZY(XYZ) + EXYZZ(XYZ)) | (8) |
Comparison of the DLPNO-CCSD(T) and HFLD approaches
Recently the “Hartree–Fock + London dispersion” (HFLD) approach was introduced by Bistoni and coworkers123 as an efficient alternative to the DLPNO-CCSD(T) method when considering large molecular systems. Within the HFLD approach the interaction energy can be written as:| ΔEint = ΔEHFint + ECdisp | (9) |
| Method | He | Ne | Ar | Kr | CH4 |
|---|---|---|---|---|---|
| a HFLD computations were performed with the same setup as the DLPNO-CCSD(T) counterparts (i.e. with TightPNO interfragment truncation thresholds). | |||||
| HFLD | |||||
| ΔEint | −1.85 | −3.65 | −12.55 | −14.25 | −11.28 |
| E Cdisp | −2.40 | −5.16 | −21.82 | −31.35 | −31.77 |
| DLPNO-CCSD(T) | |||||
| ΔEint | −4.97 | −6.56 | −12.30 | −13.39 | −13.50 |
| E Cdisp | −2.45 | −6.05 | −19.45 | −28.68 | −29.96 |
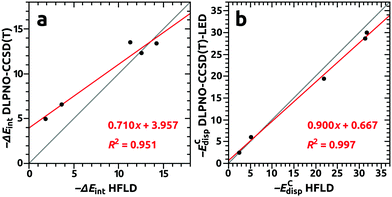
Two observations can be made: (i) the data revealed a rather moderate accuracy of the HFLD method for the total interaction energies when compared to the DLPNO-CCSD(T) (see Fig. 9 panel a), which in turn indicated that the ΔECnon-disp and ΔEC-(T)int contributions are important for an accurate description of endohedral fullerene complexes, (ii) the agreement for dispersion interaction components ECdisp obtained with the HFLD and DLPNO-CCSD(T)-LED approaches was very good (see Fig. 9 panel b). This agreement suggests that the HFLD scheme can be used as a nonempirical quantum mechanical method to obtain reliable estimates of the dispersion interaction contribution for large systems, where the accurate DLPNO-CCSD(T) treatment is no longer affordable.
Conclusions
The reference interaction energies for endohedral complexes of the C60 fullerene with He, Ne, Ar, Kr, and CH4 were calculated at the DLPNO-CCSD(T) level of theory and decomposed into physical contributions with the LED scheme. An accurate and efficient multilevel DLPNO-CCSD(T) setup was proposed, which was applicable to routine studies of endohedral complexes of C60 and larger fullerenes. Calculated molecular properties of the CH4@C60 complex revealed that the IR and Raman bands of the endohedral CH4 were essentially “silent” due to the dielectric screening effect of the C60, which acted as a molecular Faraday cage. Absorption spectra in the UV-vis and ionization potentials of C60 and CH4@C60 were predicted to be almost the same. Calculated 1H/13C NMR shifts and spin–spin coupling constants were in very good agreement with experimental data. Lastly, selected points at the potential energy surface of the endohedral He2@C60 trimer were calculated at the DLPNO-CCSD(T) level of theory. In contrast to previous theoretical studies with DFT, MP2, SCS-MP2, and DFT-SAPT, where all these methods predicted the He2@C60 to be thermodynamically unstable towards the loss of the noble gas atom, our calculations predicted the He2@C60 to be stable, which is in agreement with experimental observations. Therefore, the case of the He2@C60 trimer clearly indicated that the DLPNO-CCSD(T) level of theory is indispensable in studies of weakly interacting systems and should be used whenever applicable.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computational resources of the Department of Materials and Environmental Chemistry, Stockholm University, are acknowledged.Notes and references
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 Search PubMed.
- S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605 Search PubMed.
- D. S. Bethune, C. H. Kiang, M. S. de Vries, G. Gorman, R. Savoy, J. Vazquez and R. Beyers, Nature, 1993, 363, 605–607 Search PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, A. A. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 Search PubMed.
- P. R. Buseck, S. J. Tsipursky and R. Hettich, Science, 1992, 257, 215–217 Search PubMed.
- J. B. Howard, J. T. McKinnon, Y. Makarovsky, A. L. Lafleur and M. E. Johnson, Nature, 1991, 352, 139–141 Search PubMed.
- F. R. di Brozolo, T. E. Bunch, R. H. Fleming and J. Macklin, Nature, 1994, 369, 37–40 Search PubMed.
- D. J. Kessler, J. Spacecr. Rockets, 1991, 28, 347–351 Search PubMed.
- L. Becker, R. J. Poreda and T. J. Bunch, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 2979–2983 Search PubMed.
- P. Ehrenfreund and B. H. Foing, Adv. Space Res., 1997, 19, 1033–1042 Search PubMed.
- M. A. Cordiner, H. Linnartz, N. L. J. Cox, J. Cami, F. Najarro, C. R. Proffitt, R. Lallement, P. Ehrenfreund, B. H. Foing, T. R. Gull, P. J. Sarre and S. B. Charnley, Astrophys. J., Lett., 2019, 875, 1–7 Search PubMed.
- M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw and A. Anton Zeilinger, Nature, 1999, 401, 680–682 Search PubMed.
- W. Krätschmer, D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354–358 Search PubMed.
- D. S. Bethune, R. D. Johnson, J. R. Salem, M. S. de Vries and C. S. Yannoni, Nature, 1993, 366, 123–128 Search PubMed.
- J. R. Heath, S. C. O'Brien, Q. Zhang, Y. Liu, R. F. Curl, H. W. Kroto, F. K. Tittel and R. E. Smalley, J. Am. Chem. Soc., 1985, 107, 7779–7780 Search PubMed.
- T. Akasaka and S. Nagase, Endofullerenes: A New Family of Carbon Clusters, Kluwer Academic, Dodrecht, Netherlands, 2002 Search PubMed.
- T. Suetsuna, N. Dragoe, W. Harneit, A. Weidinger, H. Shimotani, S. Ito, H. Takagi and K. Kitazawa, Chem. – Eur. J., 2002, 22, 5079–5083 Search PubMed.
- K. Komatsu, M. Murata and Y. Murata, Science, 2005, 307, 238–240 Search PubMed.
- K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616 Search PubMed.
- S. Bloodworth, G. Sitinova, S. Alom, S. Vidal, G. R. Bacanu, S. J. Elliott, M. E. Light, J. M. Herniman, G. J. Langley, M. H. Levitt and R. J. Whitby, Angew. Chem., Int. Ed., 2019, 58, 5038–5043 Search PubMed.
- M. H. Levitt, Philos. Trans. R. Soc., A, 2013, 371, 20120429 Search PubMed.
- Z. Bačić, J. Chem. Phys., 2018, 149, 100901 Search PubMed.
- P. M. Felker and Z. Bačić, J. Chem. Phys., 2020, 152, 014108 Search PubMed.
- J. Cioslowski, J. Am. Chem. Soc., 1991, 113, 4139–4141 Search PubMed.
- J. Cioslowski, J. Am. Chem. Soc., 1994, 116, 3619–3620 Search PubMed.
- J. Cioslowski, Chem. Phys. Lett., 1994, 227, 361–364 Search PubMed.
- M. Bühl, W. Thiel, H. Jiao, P. von Ragué Schleyer, M. Saunders and F. A. L. Anet, J. Am. Chem. Soc., 1994, 116, 6005–6006 Search PubMed.
- M. Bühl, S. Patchkovskii and W. Thiel, Chem. Phys. Lett., 1997, 275, 14–18 Search PubMed.
- S. Patchkovskii and W. Thiel, J. Am. Chem. Soc., 1996, 118, 7164–7172 Search PubMed.
- R. B. Darzynkiewicz and G. E. Scuseria, J. Phys. Chem. A, 1997, 101, 7141–7144 Search PubMed.
- J. Autschbach and E. Zurek, J. Phys. Chem. A, 2003, 107, 4967–4972 Search PubMed.
- O. Charkin, N. Klimenko, D. Charkin and A. Mebel, Russ. J. Inorg. Chem., 2004, 49, 868–880 Search PubMed.
- A. Rehaman, L. Gagliardi and P. Pyykkö, Int. J. Quantum Chem., 2006, 107, 1162–1169 Search PubMed.
- O. Shameema, C. N. Ramachandran and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 2–4 Search PubMed.
- M. Straka and J. Vaara, J. Phys. Chem. A, 2006, 110, 12338–12341 Search PubMed.
- M. Straka, P. Lantto and J. Vaara, J. Phys. Chem. A, 2008, 112, 2658–2668 Search PubMed.
- K. E. Whitener, R. J. Cross, M. Saunders, I. Sho-ichi, S. Murata, N. Mizorogi and S. Nagase, J. Am. Chem. Soc., 2009, 131, 6338–6339 Search PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 Search PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 Search PubMed.
- K. E. Riley, J. A. Platts, J. Řezáč, P. Hobza and J. G. Hill, J. Phys. Chem. A, 2012, 116, 4159–4169 Search PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 Search PubMed.
- A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103 Search PubMed.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 Search PubMed.
- T. Korona, A. Hesselmann and H. Dodziuk, J. Chem. Theory Comput., 2009, 5, 1585–1596 Search PubMed.
- A. Hesselmann and T. Korona, Phys. Chem. Chem. Phys., 2011, 13, 732–743 Search PubMed.
- P. Pyykkö, C. Wang, M. Straka and J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 2954–2958 Search PubMed.
- C. Wang, M. Straka and P. Pyykkö, Phys. Chem. Chem. Phys., 2010, 12, 6187–6203 Search PubMed.
- G. Bistoni, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1–22 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 Search PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 Search PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 Search PubMed.
- C. Riplinger, P. Pinski, E. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 Search PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 Search PubMed.
- D. Liakos, Y. Guo and F. Neese, J. Phys. Chem. A, 2020, 124, 90–100 Search PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, J. Chem. Theory Comput., 2017, 13, 3198–3207 Search PubMed.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824 Search PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 Search PubMed.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 215–228 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 73–78 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 Search PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 15, 3865 Search PubMed.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 Search PubMed.
- F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 Search PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 Search PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov and F. Neese, J. Chem. Phys., 2018, 148, 011101 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 Search PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 Search PubMed.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667 Search PubMed.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 Search PubMed.
- F. Calbo, J. C. Sancho-García, E. Ortí and J. Aragó, J. Comput. Chem., 2017, 38, 1869–1878 Search PubMed.
- L. Gyevi-Nagy, M. A. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2021, 17, 860–878 Search PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 Search PubMed.
- V. Vasilyev, Comput. Theor. Chem., 2017, 1115, 1–3 Search PubMed.
- A. L. Ringer, M. S. Figgs, M. O. Sinnokrot and C. D. Sherill, J. Phys. Chem. A, 2006, 110, 10822–10828 Search PubMed.
- H. Hollenstein, R. R. Marquardt, M. Quack and M. A. Suhm, J. Chem. Phys., 1994, 101, 3588–3602 Search PubMed.
- K. Hedberg, L. Hedberg, D. S. Bethune, C. A. Brown, H. C. Dorn, R. D. Johnson and M. de Vries, Science, 1991, 254, 410–412 Search PubMed.
- J. Neugebauer, M. Reiher, C. Kind and B. A. Hess, J. Comput. Chem., 2002, 23, 895–910 Search PubMed.
- R. D. Amos, J. Chem. Soc., Faraday Trans., 1987, 83, 1595–1607 Search PubMed.
- D. S. Bethune, G. Meijer, W. C. Tang, H. J. Rosen, W. G. Golden, H. Seki, C. A. Brown and M. S. de Vries, Chem. Phys. Lett., 1991, 179, 181–186 Search PubMed.
- K. Yagi and D. Watanabe, Int. J. Quantum Chem., 2009, 109, 2080–2090 Search PubMed.
- B. Meier, S. Mamone, M. Concistré, J. Alonso-Valdesueiro, A. Krachmalnicoff, R. Whitby and M. Levitt, Nat. Commun., 2015, 6, 8112 Search PubMed.
- A. Shugai, U. Nagel, Y. Murata, Y. Li, S. Mamone, A. Krachmalnicoff, S. Alom, R. J. Whitby, M. H. Levitt and T. Rõõm, J. Chem. Phys., 2021, 154, 124311 Search PubMed.
- B. Ensing, F. Costanzo and P. L. Silvestrelli, J. Phys. Chem. A, 2012, 116, 12184–12188 Search PubMed.
- A. Krachmalnicoff, R. Bounds, S. Mamone, S. Alom, M. Concistrè, B. Meier, K. Kouřil, M. E. Light, M. R. Johnson, S. Rols, A. J. Horsewill, A. Shugai, U. Nagel, T. Rõõm, M. H. Carravetta, M. Levitt and R. J. Whitby, Nat. Chem., 2016, 8, 953–957 Search PubMed.
- P. Delaney and J. C. Greer, Appl. Phys. Lett., 2004, 84, 431–433 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Chem. Sci., 2013, 4, 2349–2356 Search PubMed.
- D. S. Sabirov, Fullerenes, Nanotubes, Carbon Nanostruct., 2020, 28, 71–77 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 Search PubMed.
- G. Skrzyński, K. Radula-Janik, T. Kupka and T. Pluta, J. Phys. Chem. A, 2019, 123, 9753–9762 Search PubMed.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 Search PubMed.
- A. J. Sadlej, Collect. Czech. Chem. Commun., 1988, 53, 1995–2016 Search PubMed.
- A. J. Sadlej, Theor. Chim. Acta, 1992, 83, 351–366 Search PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 Search PubMed.
- U. Hohm and K. Kerl, Mol. Phys., 1990, 69, 803–817 Search PubMed.
- A. Ballard, K. Bonin and J. Lauderback, J. Chem. Phys., 2000, 113, 5732–5735 Search PubMed.
- C. Bannwarth and S. Grimme, Comput. Theor. Chem., 2014, 1040, 45–53 Search PubMed.
- S. Dai, L. M. Toth, G. D. Del Cul and D. H. Metcalf, J. Chem. Phys., 1994, 101, 4470 Search PubMed.
- D. K. Böhme, Philos. Trans. R. Soc., A, 2016, 374, 20150321 Search PubMed.
- A. V. Pogulay, R. R. Abzalimov, S. K. Nasibullaev, A. S. Lobach, T. Drewello and Y. V. Vasil'ev, Int. J. Mass Spectrom., 2004, 233, 165–172 Search PubMed.
- R. S. Ruoff, D. S. Tse, R. Malhotra and D. C. Lorents, J. Phys. Chem., 1993, 97, 3379–3383 Search PubMed.
- M. Saunders, H. A. Jiménez-Vázquez, R. J. Cross, S. Mroczkowski, D. I. Freedberg and F. A. L. Anet, Nature, 1994, 367, 256 Search PubMed.
- M. S. Syamala, R. J. Cross and M. Saunders, J. Am. Chem. Soc., 2002, 124, 6216–6219 Search PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 Search PubMed.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699 Search PubMed.
- T. Helgaker, M. Jaszuński and K. Ruud, Chem. Rev., 1999, 99, 293–352 Search PubMed.
- K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 Search PubMed.
- F. Jensen, Theor. Chem. Acc., 2010, 126, 371–382 Search PubMed.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 Search PubMed.
- T. Kupka, M. Nieradka, M. Stachów, T. Pluta, P. Nowak, H. Kjær, J. Kongsted and J. Kaminsky, J. Phys. Chem. A, 2012, 116, 3728–3738 Search PubMed.
- P. Rzepka, Z. Bacsik, A. J. Pell, N. Hedin and A. Jaworski, J. Phys. Chem. C, 2019, 123, 21497–21503 Search PubMed.
- A. Antušek, K. Jackowski, M. Jaszuński, W. Makulski and M. Wilczek, Chem. Phys. Lett., 2005, 411, 111–116 Search PubMed.
- B. Bennett and W. T. Raynes, Mol. Phys., 1987, 61, 1423–1430 Search PubMed.
- T. Sternfeld, R. E. Hoffman, M. Saunders, R. J. Cross, M. S. Syamala and M. Rabinovitz, J. Am. Chem. Soc., 2002, 124, 8786–8787 Search PubMed.
- A. Krapp and G. Frenking, Chem. – Eur. J., 2007, 13, 8256–8270 Search PubMed.
- T. Y. Nikolaienko, E. S. Kryachko and G. A. Dolgonos, J. Comput. Chem., 2018, 39, 1090–1102 Search PubMed.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 5894–5907 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Convergence tests, Cartesian coordinates of the models. See DOI: 10.1039/d1cp02333k |
| This journal is © the Owner Societies 2021 |