The role of electric field, peripheral chains, and magnetic effects on significant ¹H upfield shifts of the encapsulated molecules in chalcogen-bonded capsules

Abstract

The chalcogen-bonded homo-cavitand and hetero-cavitand A_Y+A_Y′ capsules (Y, Y′ = Se, Te), as well as their encapsulated complexes with one or two guest molecules have been studied theoretically via density functional theory (DFT), while the ¹H NMR spectra of the homo-cavitand encapsulated complexes (in A_Se+A_Se) have been measured experimentally. There is excellent agreement between theoretical and experimental spectra. In all cases, we found significant ¹H upfield shifts which are more intense in the A_Se+A_Se cage compared to the A_Te+A_Te and A_Se+A_Te cages. The non-uniform electron distribution which gives rise to an inherent electric field and a non-zero electric dipole moment of the encapsulated complexes, the induced electric field effects, the magnetic anisotropy which is enhanced due to the polarizability of chalcogen atoms, and the peripheral chains, which are responsible for the solubility of the cages, increase the upfield shifts of ¹H of the encapsulated molecules; the peripheral chains lead to an increase of the upfield shifts by up to 1.8 ppm for H of the rim and up to 1.2 ppm for the terminal H in the interior of the cage. Hence, substantial ¹H upfield chemical shifts of the guests in these capsules are consequences of (i) the enhanced aromaticity of the walls of the capsules due to the polarizability of chalcogen atoms, (ii) the induced and inherent electric field effects, and (iii) the peripheral chains.

---

1 Introduction

Noncovalent interactions were first considered by van der Waals in 1873.¹ Nowadays, the importance of the role of the intermolecular noncovalent interactions is not in question, even though they are both weaker and less directional than covalent bonds. Chalcogen bonding (ChB) is a net attractive noncovalent σ-hole based interaction between an electrophilic region associated with a chalcogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity.^2–8 These interactions arise from the anisotropy in the surface electrostatic potential on chalcogen atoms and they are more intense in the heavier atoms.^7–10 This anisotropy gives rise to their directional nature, which differentiates chalcogen bonding from hydrogen bonding. Experimentally, the chalcogen bonds can be studied directly by multinuclear solid-state magnetic resonance and vibrational spectroscopy.¹¹ In general, there is an increasing interest in chalcogen bonding because they collectively play a dominant role in the synthesis, catalysis, and design of materials.^2,3,10–12 However, there are still some open questions regarding the chalcogen bonding: how is the NMR response affected by chalcogen bonding? Can such a response be used as a predictor value? How can this NMR response be related to other NMR responses corresponding to different non-covalent interactions such as hydrogen bonds?¹¹ The main aim of the present work is to add useful physical insight on this type of bonding and to give answers to the above questions.

The first purely chalcogen-bonded supramolecular capsules were formed via dimerization of 2,1,3-benzotelluradiazole and 2,1,3-benzothiadiazole cavitands.⁴ Chalcogen bonding examples in water are rare,¹² perhaps because the donors and acceptors of hydrogen bonding in water can compete with those involved in chalcogen bonding. However, recently we reported the use of chalcogen (Se) bonding to form container assemblies that are stable in water.⁵ Hydrophobic forces and hydrogen-bonding attractions between guest molecules stabilized the assemblies in the presence of the competing effects of water. It is interesting that the cavitand walls impart an unusually high magnetic anisotropy to the capsule environment, as it was shown both experimentally via¹H NMR spectroscopy and theoretically via DFT calculations. As a result, important ¹H upfield shifts in the encapsulated molecules were observed. Moreover, the chalcogen bonding in a series of chalcogen bonded container capsules (A_X+A_X), where X = O, S, Se, and Te, and in their encapsulation complexes with n-C₉H₂₀ was examined.⁷ We found that different factors contribute to the observed magnetic anisotropy of the capsule's interior: for the Te capsule the most important factor is Te's large polarizability; for the O analogue the inductive effects produced by the electro-negative nature of the O and N heteroatoms; and for the S and Se capsules, the polarizability of the heteroatoms combines with electric field effects. However, there are some questions regarding which factors are more important, i.e., electric field effects or magnetic effects for the ¹H upfield shifts, and whether there exist any additional factors that can affect the upfield shifts. Another question is: can hetero-cavitands based on chalcogen bonding be formed as well as of homocavitands? Are there significant ¹H upfield shifts in this case? Note also that the hetero cavitands can show which effect is more important for the ¹H upfield shifts, electric field effects or magnetic effects since they have an inherent dipole moment.

In consideration of the above questions, here we study theoretically the chalcogen-bonded homo-cavitand and hetero-cavitand A_Y+A_Y′ capsules (Y, Y′ = Se, Te), namely, resorcin[4]arene cavitands containing 2,1,3-benzoselenadia-zole and/or 2,1,3-benzotelluradiazole motifs which are dimerized to supramolecular capsules by chalcogen bonding. Additionally, their encapsulated complexes with nonane and with homodimers and heterodimers of n-C₄H₉X, where X = Br and I, are studied. All calculations are carried out employing density functional theory (DFT). Additionally, the ¹H NMR spectra of the chalcogen-bonded homo-cavitands and their encapsulated complexes with halides and ketones were measured experimentally and calculated theoretically. The present work aims to (i) rationalize the electric field effects versus magnetic effects and (ii) to find if the electric field effects (dipole moment, electric field isotropic and anisotropic polarizabilities, charge distributions) or magnetic effects (magnetic isotropy and anisotropy) are more important for the ¹H upfield shifts. Additionally, the present study also examines the role of peripheral chains in aromaticity and in magnetic effects in the rim of the cavitands of the cages.

2 Methodology

2.1. Experimental details

All analytical grade solvents and reagents purchased from commercial sources were used without further purification. SeO₂ was purchased from Energy Chemical Company Ltd, Shanghai China. D₂O was used as NMR analysis solvent. ¹H NMR analyses were performed using Bruker AVANCE III HD 600 MHz spectrophotometer. Positive ions high-resolution mass analyses were performed on Bruker micrOTOF II machine. Cavitand 1 was prepared using our previously reported protocol.⁵

1 mM, 0.5 mL of 1 in D₂O was taken in an NMR tube and excess of pure cyclic ketone or pure alkyl halide (∼0.5 μL or ∼0.5 mg) was added to the tube, it was shaken well to mix the guest in water. The sample was sonicated for 1 h at r.t. and analyzed by ¹H NMR spectroscopy at r.t.

2.2. Computational details

The chalcogen-bonded homo-cavitand and hetero-cavitand A_Y+A_Y′ capsules (Y, Y′ = Se, Te), as well as their encapsulated complexes with homodimers and heterodimers of n-C₄H₉X, where X = Br and I, Fig. 1, are calculated at the M06-2X¹³/6-31G(d,p)¹⁴//M06-2X/LANL2DZ¹⁵ level of theory. The structures are fully optimized at M06-2X/LANL2DZ and the calculation of frequencies shows that they are true minima. Two types of A_Y are used, which differ only in the R_1,2 chains, i.e., A_Y(R₁ = CH₃) and A′_Y(R₂ = CH₂CH₂CH₂Cl) for each Y = Se and Te. Additionally, the encapsulation of alkane in A_Y+A_Y′ capsules, where Y, Y′ = Se, Te and R₁ = CH₃ and R₂ = CH₂CH₂CH₂Cl are studied. Based on our previous studies,⁷ where the application of larger basis sets and other functionals were examined, this level of theory was considered as adequate for the study of molecule encapsulation. Specifically, it has been shown that the M06-2X/6-31G(d,p) methodology provided similar results to the M06-2X/6-311+G(d,p) methodology, where a larger basis set is employed.^7b Due to the large size of the studied species up to 300 atoms, it is not feasible the use of ab initio methodologies such as MP2 and CCSD methodologies. Thus, the properties of part of the walls of the capsules, i.e., furazan and its substituted with Se and Te atoms, were calculated via the MP2, CCSD and DFT (B3LYP, M06-2X, PBE0) methodologies in conjunction with the 6-311+G(d,p) and 6-31G(d,p) basis sets. Our conclusion was that the M06-2X/6-31G(d,p) methodology predicts well geometries, charges, dipole moments, isotropic/anisotropic electric field polarizabilities, and magnetic isotropy/anisotropy, comparing to the MP2 and CCSD methodologies.

Fig. 1 A_Y and A′_Y cavitands, A_Y+A_Y and A′_Y+A′_Y cages, where, A_Y(R = R₁) and A′_Y(R = R₂) and Y = Se, Te.

The binding energies of the homo-cavitand and hetero-cavitand A_Y+A_Y′ capsules, of homodimers and heterodimers RX–RX′, as well as the binding energies of their encapsulated complexes with RX–RX′, are calculated. In all interaction energies and dimerization energies presented here, the basis set superposition error (BSSE) corrections have been considered using the counterpoise procedure.¹⁶ An analysis of the many-body interaction energy terms is performed corrected for the BSSE;¹⁷ the terms, i.e., 2-body, 3-body and deformation (D), are given in the ESI.† This analysis offers insight into the stabilization of the 3-body and 4-body system, i.e., 2 cavitands + guest and 2 cavitands + 2 guests, respectively. Additionally, information is gained on the possible distortion required for the formation of the encapsulated complexes. Dipole moments, dipole electric field isotropic and anisotropic polarizabilities, ¹H NMR spectra, contour plots of magnetic isotropy and anisotropy in the whole cavity, are calculated. NMR shielding tensors have been computed with the Gauge-Independent Atomic Orbital (GIAO) method.¹⁸ Finally, the Nucleus-Independent Chemical Shifts (NICS) are computed and used as aromaticity indexes.¹⁹ All calculations are carried out with the aid of the Gaussian16 program.²⁰

3 Results and discussion

3.1. Experimental details

The conformations of cavitands i.e., vase, kite, dimeric kite or velcrand²¹ depend on several conditions including temperature, solvent and presence or absence of a metal ions.^22–24 The vase form (A_Se) is the only receptive form which was found to hold complementary sized hydrophobic guest in the cavity.⁵ It is recognized from its methine protons chemical shift. We found 1 in kite conformation in water, while by the addition of a hydrophobic guest,^5,25,26 we observed transformation to vase (A_Se) form that dimerized to a capsule (A_Se+A_Se) by taking one or two gest molecules in the space. For smaller guest we observed 2+2 while for bigger sized guests we got 1+1 host–guest capsular complexes. Cyclic ketone and haloalkanes as amphiphilic or hydrophobic guests showed occupation of the space of the capsule formed by A_Se in water.

A tendency for capsule formation (A_Se+A_Se) was observed in the presence of amphiphilic molecules including cyclic ketones and terminal monoalkylhalides. Smaller sized ketones (cyclobutanone and cyclopentanone) could not form host–guest complexes, it should be due to their smaller size and even two molecules did not occupy enough space of the capsule to result dimeric assembly A_Se+A_Se, while cyclohexanone to octanone formed 2+2 host–guest capsular assembly (Scheme 1). Similarly small sized alkyl halides (butyl to pentylhalides) formed 2+2 host–guest capsular complexes, showing two molecules of these guest satisfied the minimum volume occupation barrier of the space to result a stable capsular assembly. We also found mixed binding pattern for 1-iodopentane i.e., in some capsule iodide occupied the deepest position, while in the other terminal methyl group was observed in the deepest resorcinarene ring. 1-Halohexane could not bind, similarly 1-chloroheptane and 1-bromoheptane also did not form host–guest complexes showing these molecules in 2+2 or 2+1 host–guest ratios could not satisfy the inner space occupation demand of the capsule. In turn 1-iodoheptane bound well and formed 2+1 host guest capsular complex showing the size of the iodine was bigger enough to stabilize the dimeric capsule as compared to 1-chlor- or 1-bromoheptane. 1-Halooctane to 1-halononane all formed 2+1 stable host–guest capsules. We observed the same peculiar high magnetic anisotropy⁷ for these guests inside A_Se+A_Se capsule as compared to the hydrogen-bonded capsules reported earlier.^27,28 The terminal methyl (–CH₃) groups of each alkyl halide guest appeared at −3.5 to −3.7 ppm (or −Δδ 4.3 to 4.5 ppm), while −Δδ for the middle methylene was 3.9 to 4.1 ppm, see Fig. 2. Below, these peculiar high upfield shifts are analyzed.

Scheme 1 1+1 host–guest cavitand and 2+2 and 2+1 host–guest Capsules.

Fig. 2 Comparative ¹H NMR spectra of A_Se+A_Se in the presence of these guest; smaller guest cyclic ketone and 4–5 carbons alkylhalides formed 2+2 capsules while bigger sized guest from haloheptane to halononane formed 1+1 capsules.

3.2. Theoretical section

3.2.1. Geometries and binding energies. The calculated cavitands A_Y, the homo-cavitand and hetero-cavitand cages A_Y+A_Y′ capsules (Y, Y′ = Se, Te), are depicted in Fig. 1. Two types of A_Y are used, which differ only in the R_1,2 chains (R₁ = CH₃ and R₂ = CH₂CH₂CH₂Cl) for each Y, Y = Se and Te. The encapsulated complexes C₄H₉X+C₄H₉X′@A_Y+A_Y′ and C₉H₂₀@A_Y+A_Y′, where X, X′ = Br, I and Y, Y′ = Se, Te, are depicted in Fig. 2 and Fig. S2, S3 of ESI.†

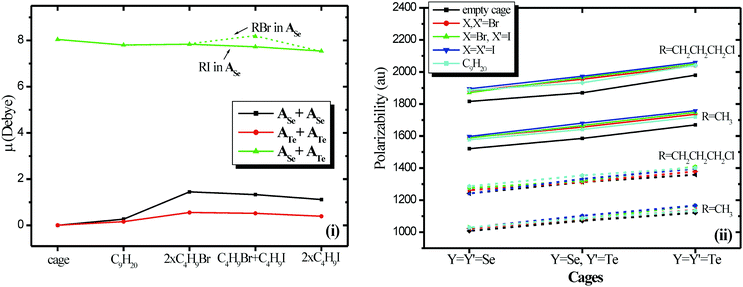
Comparing the size of cages and the encapsulated cages, see Table 1, all have similar sizes about 9.7 × 9.7 × 16.7 Å, however, the free or encapsulated A_Te+A_Te cage, has the shortest N⋯Y bonds on average and as a result it is the smallest cage. Note that the N⋯Te bonds are the strongest ones. Within the same cage, the N⋯Y bonds are increased on the average according to the ordering n-C₉H₂₀ < RBr + RBr < RBr + RI < RI + RI. Regarding the encapsulated halide dimers, the shortest distance between Br atoms is observed in A_Te+A_Te cage, which is the cage with the smallest cavity, the shortest distance between I atoms is observed in A_Se+A_Se cage, which is the cage with the larger cavity and thus they can fit better, since the repulsion between I is larger than Br atoms. The shortest distance between I and Br atoms is observed in A_Se+A_Te cage, which is the cage with the mediate cavity, note that the RI it fit better in the A_Te cavitand. Thus, the RI + RI fits better in the largest cavity, the RBr + RBr in the smallest cavity, while RB + RI in the intermediate cavity. It should be mentioned that the alkane halides prefer to be encapsulated with the halide at the rim of the cage.²⁹ It is very interesting that while, the cages are similar and the sizes of the alkane and of the two halogenoalkanes are similar, the encapsulated molecules affect the cages according to their type or to the corresponding halogen atom.

Table 1 Size of the calculated capsules and encapsulated complexes and interaction bond distances in Å. Experimental values are given in parenthesis

Capsule	Size (x × y × z)	N⋯Y	X–X
a Single-crystal X-ray structure, R = C4H8Cl; ref. 28. b X-Ray crystal structure but including two benzene molecules @ATe+ATe; N⋯X = 2.6–2.9 Å and R = C6H13; ref. 4.
ASe+ASe	9.80 × 9.80 × 16.72	2.838(2.94–3.04)^a
ASe+ATe	9.72 × 9.80 × 16.65	2.733, 2.755
ATe+ATe	9.65 × 9.65 × 16.60	2.491–2.778
RBr+RBr@ASe+ASe	9.15 × 10.46 × 16.71	2.794–2.911	3.669
RBr+RI@ASe+ASe	8.96 × 10.71 × 16.75	2.799–2.934	3.777
RI+RI@ASe+ASe	9.02 × 10.80 × 16.75	2.810–2.970	3.869
C9H20@ASe+ASe	9.42 × 10.12 × 16.74	2.769–2.857
	9.66 × 9.72 × 16.75
RBr+RBr@ASe+ATe	9.24 × 10.37 × 16.69(Se)	2.667–2.852	3.609
	9.16 × 10.39 × 16.69(Te)
RBr+RI@ASe+ATe	9.36 × 10.28 × 16.71(Se)	2.681–2.850	3.730
	8.94 × 10.65 × 16.70(Te)
RI+RBr@ASe+ATe	9.28 × 10.40 × 16.66(Se)	2.702–2.886	3.743
	9.07 × 10.57 × 16.69(Te)
RI+RI@ASe+ATe	9.73 × 9.83 × 16.78(Se)	2.632–2.867	3.958
	8.56 × 10.89 × 16.76(Te)
C9H20@ASe+ATe	9.46 × 10.06 × 16.67(Se)	2.659–2.767
	9.61 × 9.67 × 16.66(Te)
RBr+RBr@ATe+ATe	9.07 × 10.32 × 16.63	2.444–2.918(2-6–2.9)^b	3.544
RBr+RI@ATe+ATe	8.98 × 10.34 × 16.72	2.403–3.054	3.823
RI+RI@ATe+ATe	8.81 × 10.56 × 16.72	2.404–3.104	3.900
C9H20@ATe+ATe	9.57 × 9.67 × 16.64	2.436–2.839
	9.50 × 9.71 × 16.64

---

The BSSE corrected binding energies ΔE of the homo-cavitand and hetero-cavitand cages are −1.80 eV (A_Se+A_Se), −2.77 eV (A_Se+A_Te), −4.60 eV (A_Te+A_Te) and they are attributed to the N⋯X chalcogen bonds, see Table 2. It is of interest that the A_Se+A_Te cage has a smaller binding energy of −2.77 eV than the average of the binding energies of the homo-cavitands of ∼−3.2 eV and this results from the fact that in A_Te+A_Te shorter N⋯Te bonds are formed than A_Se+A_Te, see Table 1. The binding energies ΔE₁ of the nonane with cages range from −0.83 eV to −0.94 eV and the corresponding ΔE₁ values of the alkyl-halide dimers range from −0.83 eV to −1.05 eV. For both cases, the largest value is observed in the A_Se+A_Se cage, see Table 2. The binding energies of the free homodimers and heterodimers of RX are about −0.22 eV (see Table 2) and they result for the H⋯X interactions. In the cages, the deformation energy of the halide dimers, def5 of Table 2, range from 0.21 eV to 0.33 eV, showing that the geometry of the encapsulated dimers differs a lot from the free ones. Their interaction energy is up to −0.08 eV (2B₃: 2Body term which corresponds to the interaction between the encapsulated halides), i.e., the dimers are weakly bound within the cage, only one or two very weak H⋯X is formed, while in free RX–RX′ dimers four weak hydrogen bonds are formed with bond distances at ∼3 Å, see Fig. 3. However, hydrogen bonds are formed with the walls of the cavitands which stabilized the encapsulation, by up to −0.5 eV, see below. The deformation energy of the cages with respect to un-capsulated cages, def1, are very small, showing that their structure is not deformed by the encapsulation, except for RI + RI@A_Se+A_Te, RBr + RI@A_Te+A_Te, and RI + RI@A_Te+A_Te, where the inclusion of RI pushes the walls of the cages.

Table 2 BSSE corrected binding energies ΔE (eV), deformation energy (Def), 2-body (2B), 3-body (3B) terms in eV at M06-2X/6-31G(d,p)//M06-2X/LANL2DZ level of theory

	ΔE1^a	2B^a	ΔE2^b	def1^a	def2^a	def3^b	def4^b		ΔE	2B		ΔE	2B	Def.^c
a ΔE and 2B with respect to cage + nonane; def1: deformation energy of the cage, def2: deformation energy of the nonane. b ΔE2 with respect to two cavitands + nonane; def3, def4: deformation energy of the cavitands. c Total deformation energy. d ΔE1 and 2B with respect to cage + RX dimer; def1: deformation energy of the cage, def5: deformation energy of the RX dimer. e ΔE2 with respect to cage + RX + RX′; 2B1: 2-body term of the cage + 1st guest; 2B2: 2-body term of the cage + 2nd guest; 2B3: 2-body term of the two guests; def6 and def7: deformation energy of each RX. f ΔE3 with respect to the two cavitands + RX + RX′; def3, def4: deformation energy of each cavitand.
C9H20@ASe+ASe	−0.94	−0.95	−2.67	0.00	0.01	0.34	0.36	2RBr	−0.23	−0.24	ASe+ASe	−1.80	−2.51	0.72
C9H20@ASe+ATe	−0.83	−0.97	−3.57	0.03	0.11	0.53	0.64	RBr+RI	−0.22	−0.23	ASe+ATe	−2.77	−3.94	1.17
C9H20@ATe+ATe	−0.85	−1.01	−5.42	0.05	0.12	1.15	1.15	2RI	−0.22	−0.23	ATe+ATe	−4.60	−6.84	2.23

---

	ΔE1^d	2B^d	ΔE2^e	2B1^e	2B2^e	2B3^e	3B^e	ΔE3^f	def1^d	def3^f	def4^f	def5^d	def6^e	def7^e
RBr-RBr@ASe+ASe	−0.87	−1.19	−1.19	−0.35	−0.34	−0.08	−0.52	−2.96	0.00	0.30	0.30	0.33	0.05	0.05
RBr-RI@ASe+ASe	−0.97	−1.23	−1.22	−0.41	−0.25	−0.06	−0.57	−2.96	0.01	0.29	0.28	0.25	0.03	0.04
RI-RI@ASe+ASe	−1.05	−1.28	−1.28	−0.32	−0.31	−0.06	−0.65	−3.03	0.01	0.28	0.28	0.22	0.02	0.02
RBr-RBr@ASe+ATe	−0.98	−1.27	−1.17	−0.34	−0.42	−0.06	−0.44	−3.93	0.01	0.46	0.57	0.29	0.04	0.05
RBr-RI@ASe+ATe	−0.98	−1.30	−1.23	−0.48	−0.26	−0.06	−0.53	−3.98	0.03	0.58	0.46	0.26	0.03	0.04
RI-RBr@ASe+ATe	−1.00	−1.37	−1.24	−0.43	−0.34	0.00	−0.53	−4.00	0.01	0.45	0.55	0.31	0.02	0.04
RI-RI@ASe+ATe	−0.93	−1.31	−1.23	−0.34	−0.39	−0.08	−0.63	−3.97	0.16	0.50	0.64	0.21	0.03	0.03
RBr-RBr@ATe+ATe	−0.83	−1.33	−1.19	−0.45	−0.46	−0.03	−0.40	−5.80	0.06	1.02	1.03	0.33	0.05	0.05
RBrRI@ATe+ATe	−0.89	−1.39	−1.08	−0.36	−0.52	−0.07	−0.45	−5.68	0.19	1.15	1.15	0.31	0.06	0.07
RI + RI@ATe+ATe	−0.87	−1.19	−1.12	−0.43	−0.44	−0.07	−0.52	−5.72	0.24	1.15	1.16	0.26	0.05	0.05

---

Fig. 3 Calculated A_Y+A_Y′ capsules, alkyl-halides dimers, and encapsulated C₄H₉X+C₄H₉X′@A_Y+A_Y′ and C₉H₂₀@A_Y+A_Y′ complexes, where X, X′ = Br, I; Y, Y′ = Se, Te; A_Y(R = R₁ = CH₃) and A′_Y(R = R₂ = CH₂CH₂CH₂Cl) from two points of view.

The ΔE₂ values with respect to the cages + two halides range from −1.08 to −1.28 eV, while the interaction of the cages with each one halide, i.e., 2B₁ and 2B₂ 2-body terms, range from −0.3 to −0.5 eV, see Table 2 and Fig. 4. It is of interest that the 3-body term (3B), which corresponds to the energy gained by the existence of the three parts (cage + halide + halide) after the subtraction of the two-body interactions, is up to −0.65 eV showing that the whole system is stabilized by the simultaneous presence of the three parts. Finally, the ΔE₃ values with respect to the two cavitands + two halides range from −2.96 to −5.80 eV, see Table 2 and Fig. 4. The largest values are observed in Te cages, since the N⋯Te are the strongest bonds. The deformation energy of the cavitands in the cage with respect to the free cavitands range from 0.28 (A_Se) to 1.16 (A_Te) eV because in the A_Te+A_Te cage the cavitands are more stressed because of the strongest N⋯Te bonds. Finally, it should be noted that the RI prefers energetically to be encapsulated in the A_TeA_Te cage or at least in the A_Te cavitand.

Fig. 4 (i) BSSE corrected dissociation energy, ΔE₁(cage + dimer or alkane), ΔE₂(cage + RX + RX′) ΔE₃(2 cavitands + RX + RX′ or alkane); (ii) 2-body term, 2B(cage + dimer or alkane), 2B₁ and 2B₂(cage + RX), 2B₃(RX +RX′) and 3-body term 3B (cage + RX +RX′), (iii) deformation energy of the cages (def1), cavitands (def3, def4), dimers (def5) and monomers (def6, def7), see Table 2.

3.2.2. Properties. Dipole moments, dipole electric field isotropic and anisotropic polarizabilities, charges via the Mulliken, charge model 5 (CM5) and natural bond orbital (NBO) analyses of the cages and encapsulated complexes (cf.Fig. 1 and 2) are given in Tables S1 and S2 of ESI.† The dipole moments μ of the encapsulated complexes are depicted in Fig. 5. The A_Se+A_Te cage has a dipole moment of 8.04 Debye due to different chalcogen atoms of the cavitands. The encapsulation of the molecules influences the dipole moments of the encapsulated complexes and mainly this of the A_Se+A_Se cage when the alkane halides are enclosed. The dipole electric field isotropic and anisotropic polarizabilities are depicted in Fig. 5. The replacement of the peripheral chain of R₁ = CH₃ with R₂ = CH₂CH₂CH₂Cl results in an increasement of both isotropic and anisotropic polarizabilities. The increase is about 15% and 17%, respectively and it affects the ¹H NMR upfield shifts of the encapsulated molecules, see below. The isotropic are larger than anisotropic polarizabilities by about 34% for the A_Y+A_Y′ cage and they reach to about 58% for the A′_Y+A′_Y′ cages. Regarding the charges, all population analyses show that Te is more positively charged than Se, as it is expected.

Fig. 5 (i) Dipole moments μ of the encapsulated complexes with respect to the encapsulated contents. (ii) Isotropic (solid lines) and anisotropic (dot lines) polarizabilities of the encapsulated RX + RX′@A_Y+A_Y′ complexes with respect to the cages at M06-2X/6-31G(d,p) for two R₁ and R₂ chains.

However, it is of interest that the Se atoms are more positively charged in A_Se+A_Te than A_Se+A_se, and Te is more positively charged in A_Te+A_Te than A_Se+A_Te.

The HOMO (H) and LUMO(L) molecular orbitals (MO) of all encapsulated complexes are mainly located on the chalcogen atoms and partially in the cases of halides encapsulated molecules and on halogen, see Fig. 6(i). In the cases of homo-cavitands the charge distribution is more symmetrically located in the H MO, cf.Fig. 6(ii) and (iii). Finally, the H–L gap is significantly larger in A_Se+A_Se, than in A_Se+A_Te, and in A_Te+A_Te see Fig. 7 and Table S8 of ESI.† This shows that the electrons are more localized in the Se cages than in the other two cages and as a result, there are more intense electric field effects in the Se cages. Finally, it should be noted that a correlation between aromaticity and H–L gap has been reported before in the case of the polycyclic aromatic hydrocarbons.³⁰

Fig. 6 Molecular HOMO and LUMO MO of C₄H₉I+C₄H₉I@A_Se+A_Te, n-C₉H₂₀ @A_Se+A_Te, and n-C₉H₂₀ @A_Te+A_Te complexes at M06-2X/6-31G(d,p)_{C,H,O,N,Se,Br}/LANL2TZ_I,Te.

Fig. 7 ¹H NMR shifts (ppm) of the 1-C₄H₉Br, 1-C₄H₉I and n-C₉H₂₀ compounds encapsulated and in solvent at M06-2X/6-31G(d,p). Average ¹H NMR shifts for the same C and for the symmetric C atom (n-C₉H₂₀); A(R₁ = CH₃); A′(R₂ = CH₂CH₂CH₂Cl).

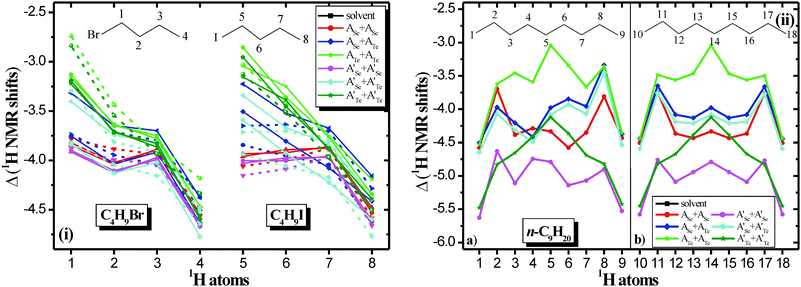
The experimental ¹H NMR spectra and the computed ¹H NMR spectra of the encapsulated complexes are given in Fig. 8 and in Fig. S9–S15 and S25–S51 of ESI.† The computed ¹H NMR chemical shifts of the guest in solvent and encapsulated are given in Tables S3–S6 of ESI† and they are shown in Fig. 8. As previously inferred,^5,7 the ¹H upfield chemical shifts are a consequence of the enhanced aromaticity of the walls of the capsules and the inductive effects are also important for the upfield chemical shifts; they are affected not only by the magnetic anisotropy, but also by steric and electric field effects.⁷ Moreover, it should be noted that weak hydrogen bond interactions are formed between the hydrogen atoms of encapsulated atoms with the N atoms of the cage, i.e., HCH⋯N hydrogen bonds, resulting in H atoms of the same C atom having slightly different chemical shifts. In other words, the environment in the capsule is not strictly cylindrical. For the homo-cavitand capsule of Te, where the two cavitands are strongly bonded and the cavity is more cylindrical, very small deviations are observed in the chemical shifts for the nonane, while for the two halides this symmetry is distorted and the deviations in the shifts are larger.

Fig. 8 ¹H NMR shifts (ppm) of the 1-C₄H₉Br, 1-C₄H₉I and n-C₉H₂₀ compounds encapsulated and in solvent at M06-2X/6-31G(d,p). Average ¹H NMR shifts for the same C and for the symmetric C atom (n-C₉H₂₀); A(R₁ = CH₃); A′(R₂ = CH₂CH₂CH₂Cl).

As it is shown in Fig. 8, there are significant upfield peaks for the H atoms of encapsulated molecules up to −3.7 ppm for the halogenoalkanes and up to −4.6 ppm for the alkane. These values are in excellent agreement with the present experimental values. For instance, in A′_Se+A′_Se the theoretical (experimental) peaks of the encapsulated C₄H₉Br and C₄H₉I range from −0.7 to −3.7 (−0.6 to −3.6) ppm and −1.0 to −3.7 (−0.7 to −3.6) ppm, respectively, see Fig. 8 and Table S4, Fig. S39 and S46 of ESI.† The most upfield peaks are found for the H atoms in the interior of the cage and not in the rim, which also has been observed in other carriers;³¹ however, here there are significant relative upfield shifts for all ¹H NMR peaks of the encapsulated molecules with respect to the molecules in solvent is (ppm), see Fig. 9. The relative (Δδ) ¹H NMR peaks of encapsulated molecules on the rim range from −2.7 (@A_Te+A_Te) to −3.9 ppm (@A′_Se+A′_Se) for the C₄H₉Br, form −2.9 (@A_Te+A_Te) to −4.2 ppm (@A′_Se+A′_Se) for the C₄H₉I, and form −3.0 (@A_Te+A_Te) to −4.8 ppm (@A′_Se+A′_Se) for the C₉H₂₀, while in the interior they range from −4.2 (@A_TeA_Te) to −4.8 ppm (@A′_Se+A′_Te) for the C₄H₉Br, form −4.2 (@A_Se+A_Te) to −4.8 ppm (@A′_Se+A′_Te) for the C₄H₉I, and form −4.4 (@A_Te+A_Te) to −5.6 ppm (@A′_Se+A′_Se) for the C₉H₂₀. These values are in excellent agreement with experimental values, i.e., the terminal methyl (–CH₃) groups of each alkyl halide guest appeared experimental Δδ = −4.3 to −4.5 ppm and theoretical Δδ = −4.2 to −4.8 ppm in A′_Se+A′_Se cage.

Fig. 9 (i) Relative shifts of ¹H NMR shifts (ppm) of the 1-C₄H₉Br and 1-C₄H₉I encapsulated compounds with respect to the free ones at M06-2X/6-31G(d,p). Average ¹H NMR shifts for the same C; A(R = CH₃); A′(R = CH₂CH₂CH₂Cl). (ii) Relative shifts of ¹H NMR shifts (ppm) of the n-C₉H₂₀ encapsulated compound with respect to the free compound at M06-2X/6-31G(d,p). (a) Average ¹H NMR shifts for the same C; (b) average ¹H NMR shifts for the same C and for the symmetric C atom; A(R₁ = CH₃); A′(R₂ = CH₂CH₂CH₂Cl).

Thus, the H atoms (–CH₂X) present more upfield shifts for iodide than bromide alkane, while in the interior the shifts are the same for both halides. Finally, it is of interest to note the effect of the peripheral chains, where the replacement of peripheral chain –CH₃ with –CH₂CH₂CH₂Cl results in an increase of the relevant upfield peaks of ¹H up to 1.8 ppm in the rim and up to 1.2 ppm in the interior. Moreover, at the rim, for all encapsulated molecules, the replacement of the peripheral chains results in a more intense ¹H upfield shifts in homo-cavitands than hetero-cavitands; specifically, in the A′_Se+A′_Se cage, the largest shifts are observed. In the case of nonane, the shifts are increased significantly in the homo-cavitands A′_Se+A′_Se and A′_Te+A′_Te comparing to halides, see Fig. 9. Finally, the small increase of the relevant upfield shifts, which are observed in the hetero-cavitand A′_Se+A′_Te cage, is attributed to the fact that the A_Se+A_Te cage has already a large dipole moment and as a result inherent electric field. Thus, the replacement of the peripheral chain does not influence the cage significantly. In other words, the electric field already exists and results in similar large shifts with or without the replacement of the peripheral chains.

It should be noted in passing that as the chalcogen bonding results in ¹H NMR upfield shifts, Se and Te solid-state NMR studies of cocrystals also establish correlations between the NMR parameters of selenium and tellurium and the local chalcogen bonding geometry.¹¹ Typically, stronger chalcogen bonds result in a decrease in the span of the chalcogen chemical shift tensor. These bonds alone produce consistent and predictable effects (e.g., the chalcogen chemical shift decreases as the chalcogen bond is shortened), while red shifts of the Se–C stretching wavenumber are observed. Finally, capsules present special interest owning to the fact that NMR shifts in capsules can be more intense than those in simple bridged aromatic dimers due to (i) the multiple chalcogen bonds that are formed between the two cavitands and (ii) the formed cavity which may induce special properties to the encapsulated guests.

Contours of the magnetic isotropy and anisotropy of A_Y+A_Y′ cages on the XY plane at distances R = 0–6 Å from the center of mass of the capsule along the main Z axis of the capsule are depicted in Fig. 10 and in Fig. S21 and S22 of ESI.† Similarly, the Nucleus-Independent Chemical Shifts (NICS) aromaticity indexes are depicted in Fig. S23 of the ESI,† where a NICS-xyz scan has been carried out. Note that the NICS-scan identifies local and global ring currents in (poly)cyclic aromatic hydrocarbons and predicts their properties both qualitatively and quantitatively, see^32,33 and references therein. All A_X+A_X′ cages, present unusually high magnetic anisotropy, see Fig. 10, equal to their magnetic isotropy; compare Fig. S13 and S14 of ESI.† In the contour plots, the empty space of the cavity is clearly shown. In nonane, its central >CH₂ is located at Z = 0 and the terminal –CH₃ is close to Z = 6, while in halides, the adjacent H atoms to halogen are located near to Z = 2 and their terminal H are located at about Z = 6 Å. The larger Δδ shifts are obtained in the terminal H atoms, where the magnetic anisotropy is larger than in Z = 0 and Z = 2 Å, see Fig. 10 and Fig. S22 of ESI.† Finally, comparing the three different cages, the A_Se+A_Se cage presents denser magnetic isotropy and anisotropy (see Fig. S21 and S22 of the ESI†) and more negative NICS values, see Fig. S23 of ESI† than the other two cages; and as a result, there are larger Δδ shifts of ¹H NMR, peaks, see Fig. 9. The more negative NICS values show enhanced electron density, which shields the protons of the guests and as a result significant upfield shifts are observed.

Fig. 10 Magnetic anisotropy of A_X+A_X complexes, where X = O, S, Se and Te. Contour on the XY plane at distances R from the center of the cage along the main Z axis of the cage.

To sum up, here for the first time, hetero-cavitand chalcogen cages are considered. These cages are ideal cages for checking the electric field effects, due to their inherent electric dipole moment, on ¹H NMR upfield shifts. We found that the electron charge distribution of the cages, their resulting electric dipole moments, the polarizability of chalcogens, and the peripheral chains can affect the ¹H NMR peaks. Overall, the ¹H upfield shifts are more intense in the A_Se+A_Se cage compared to the A_Se+A_Te and A_Te+A_Te cages since the chalcogen bonds are the least strong, the cavity is less cylindric resulting in the encapsulated species being situated in a less uniform electric field which increases the electric field effects. Consequently, dipole moments of the encapsulated complexes in A_Se+A_Se are affected the most, while the HOMO electrons are more localized in the Se cages than in the other two cages. Moreover, the peripheral chains can induce electric field effects resulting in an increase of the ¹H NMR upfield shifts in the cage. This effect is more intense in the case where the inherent electric field is uniform. Finally, the polarizability of the chalcogen atoms contributes to the enhanced aromaticity of the cavity's walls and affects the ¹H NMR upfield shifts.

4 Summary and conclusions

The chalcogen-bonded homo-cavitand and hetero-cavitand A_Y+A_Y′ capsules (Y, Y′ = Se, Te), as well as their encapsulated complexes with nonane and with two halogenoalkanes (n-C₄H₉X, where X = Br and I) have been studied theoretically via density functional theory (DFT). Additionally, the ¹H NMR spectra of the homo-cavitands capsules of Se have been measured experimentally. The main aim of this work is to study influence of the electric field effects and the magnetic effects on the ¹H upfield shifts of the encapsulated molecules.

The binding energies with respect to the cages and two halides range from −1.08 to −1.28 eV. The halide dimers are weakly bound within the cage. However, hydrogen bonds are formed with the walls of the cavitands which stabilized the encapsulation, by up to −0.5 eV. It is of interest that the energy gained by the existence of the three parts (cage + halide + halide) after the subtraction of the two body interactions, is up to −0.65 eV showing that the whole system is stabilized by the simultaneous presence of the three parts. Finally, the ΔE₃ values with respect to the two cavitands + two halides range from −2.96 to −5.80 eV.

It was found both theoretically and experimentally, that the ¹H NMR peaks of the encapsulated molecules are significantly upfield in cages with respect the un-capsulated ones. Generally, the upfield chemical shifts are a consequence of the enhanced aromaticity of the walls of the capsules. Here we analyzed the three factors that enhance the upfield shifts, i.e., (i) charges: inherent and induced electric field effects leading to non-zero dipole moments and local electron charge distributions of the cage; (ii) polarizability: the enhanced polarizability of chalcogen atoms contributes to enhanced aromaticity of the cavity's walls; (iii) peripheral chains which are responsible for the solubility of the cages.

In all cages, significant upfield shifts are found because of the enhanced aromaticity caused by magnetic anisotropy and polarizability of the chalcogen atoms. The enhanced electron density in the cages shields the protons of the guests and as a result significant upfield shifts are observed. The ¹H upfield shifts are more intense in the A_Se+A_Se cage compared to the A_Se+A_Te and A_Te+A_Te cages because in the Te capsule, the upfield shifts result mainly from Te's significant large polarizability, while in Se capsule it results from both large Se polarizability and electric field effects. In the A_Se+A_Se cage, the chalcogen bonds are the least strong and the encapsulated species are situated in a less uniform electric field increasing the electric field effects, while in the A_Te+A_Te cage, the chalcogen bonds are energetically the strongest bonds with the shortest bond distances resulting in a smaller cavity and more cylindrical; so, the encapsulated species are situated in a more uniform field with smaller inherent electric field effects.

The peripheral chain (–CH₂CH₂CH₂Cl) leads to an increase of upfield shifts of H of the encapsulated molecules up to 1.2 ppm for the terminal H and up to 1.8 ppm for the central H next to the chalcogen bonds. Both charge distributions and polarizabilities are responsible for the ¹H NMR up-field chemical shifts. However, in the case of the hetero-cavitand A_Se+A_Te and A′_Se+A′_Te cages, the replacement of the peripheral chain does not influence a lot their inherent electric field, i.e., it is already significant, and as a result additional increase in the ¹H NMR up-field chemical shifts is very small.

To sum up, the upfield shifts are a consequence of the enhanced aromaticity due to magnetic anisotropy of the walls of the capsules and of the inherent and inductive electric field effects. We end up that the influence of the electric field effects could of equal importance to magnetic field effects. Overall, the present work adds useful physical insight in chalcogen bonding and its effects which are particularly important due to the increasing research interest in this type of bonding.

Author contributions

Conceptualization (all), methodology (all), investigation (DT: calculations, FUR: expt), writing (DT, FUR: expt), editing & review (DT, IDT, GT).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DT acknowledges the National and Kapodistrian University of Athens, Special Accounts for Research Grants for supporting this work through the project “SONFM” (KE 17034). YY thanks the National Natural Science Foundation of China (No. 21801164 and 22071144), Shanghai University (No. 13-G210-19-230) and the Program for Professor of Special Appointment (Dongfang Scholarship) of the Shanghai Education Committee.

Notes and references

1. J. D. van der Waals, Over de Continuiteit Van der Gas-en Vloeistoftoestand, 1873.
2. J. Y. C. Lim, I. Marques, A. L. Thompson, K. E. Christensen, V. Félix and P. D. Beer, Chalcogen Bonding Macrocycles and [2]Rotaxanes for Anion Recognition, J. Am. Chem. Soc., 2017, 139, 3122–3133.
3. K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Chalcogen bonding in synthesis, catalysis and design of materials, Dalton Trans., 2017, 46, 10121–10138.
4. L.-J. Riwar, N. Trapp, K. Root, R. Zenobi and F. Diederich, Supramolecular Capsules: Strong versus Weak Chalcogen Bonding, Angew. Chem., Int. Ed., 2018, 57, 17259–17264.
5. F.-Ur Rahman, D. Tzeli, I. Petsalakis, G. Theodorakopoulos, P. Ballester, J. Rebek, Jr. and Y. Yu, Chalcogen Bonding and Hydrophobic Effects Force Molecules into Small Spaces, J. Am. Chem. Soc., 2020, 135, 5876–5883.
6. Y.-J. Zhu, Y. Gao, M.-M. Tang, J. Rebek Jr and Y. Yu, Dimeric capsules self-assembled through halogen and chalcogen bonding, Chem. Commun., 2021, 57, 1543–1549.
7. (a) D. Tzeli, I. D. Petsalakis, G. Theodorakopoulos, F.-U. Rahman, P. Ballester, J. Rebek Jr and Y. Yu, Aromaticity and Chemical Bonding of Chalcogen-bonded capsules featuring enhanced magnetic anisotropy, ChemPhysChem, 2020, 21, 2187–2195; (b) D. Tzeli, I. D. Petsalakis and G. Theodorakopoulos, Compression in encapsulated carboxylic acid homodimers, Chem. Phys. Lett., 2013, 573, 48–55.
8. A. J. Peloquin, C. D. McMillen, S. T. Iacono and W. T. Pennington, Halogen and Chalcogen Bonding Between the Triphenylphosphine Chalcogenides (Ph₃P = E; E = O,S,Se) and Iodofluorobenzenes, ChemPlusChem, 2021, 86, 549–557.
9. P. Politzer, J. S. Murray and T. Clark, Halogen bonding and other σ-hole interactions: a perspective, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
10. (a) W. Zierkiewicz, R. Wysokiński, M. Michalczyka and S. Scheiner, Chalcogen bonding of two ligands to hypervalent YF4 (Y = S, Se, Te, Po), Phys. Chem. Chem. Phys., 2019, 21, 20829–20839; (b) X. Zhang, N. Sakai and S. Matile, Methyl Scanning for Mechanochemical Chalcogen-Bonding Cascade Switches, ChemistryOpen, 2020, 9, e1900288.
11. (a) V. Kumar, Y. Xu, C. Leroy and D. L. Bryce, Direct investigation of chalcogen bonds by multinuclear solid-state magnetic resonance and vibrational spectroscopy, Phys. Chem. Chem. Phys., 2020, 22, 3817–3824; (b) V. Kumar, Y. Xu and D. L. Bryce, Double Chalcogen Bonds: Crystal Engineering Stratagems via Diffraction and Multinuclear Solid-State Magnetic Resonance Spectroscopy, Chem. – Eur. J., 2020, 26, 3275–3286.
12. R. L. Spicer, A. D. Stergiou, T. A. Young, F. Duarte, M. D. Symes and P. J. Lusby, Host–Guest-Induced Electron Transfer Triggers Radical-Cation Catalysis, J. Am. Chem. Soc., 2020, 142, 2134–2139.
13. (a) Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241; (b) Y. Zhao and D. G. Truhlar, Density Functionals with Broad Applicability in Chemistry, Acc. Chem. Res., 2008, 41, 157–167.
14. (a) P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222; (b) M. M. Francl, W. J. Petro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods. XXIII. A polarization type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654–3665; (c) V. Rassolov, J. A. Pople, M. Ratnerand and T. L. Windus, 6-31G* basis set for atoms K through Zn, J. Chem. Phys., 1988, 109, 1223–1229.
15. (a) P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, J. Chem. Phys., 1985, 82, 299–310; (b) L. E. Roy, P. J. Hay and R. L. Martin, Revised Basis Sets for the LANL Effective Core Potentials, J. Chem. Theory Comput., 2008, 4, 1029–1031.
16. S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566.
17. D. Tzeli, A. Mavridis and S. S. Xantheas, First principles Examination of the Acetylene-Water clusters, HCCH-(H₂O)x, x = 2, 3, and 4, J. Phys. Chem. A, 2002, 106, 11327–11337.
18. (a) F. London, The quantic theory of inter-atomic currents in aromatic combinations, J. Phys. Radium, 1937, 8, 397–409; (b) J. R. Cheeseman, G. M. Trucks, T. A. Keith and M. J. Frisch, A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors, J. Chem. Phys., 1996, 104, 5497–5509.
19. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
21. D. J. Cram, H. J. Choi, J. A. Bryant and C. B. Knobler, Solvophobic and entropic driving forces for forming velcraplexes, which are 4-fold, lock-key dimers in organic media, J. Am. Chem. Soc., 1992, 114, 7748–7765.
22. P. J. Skinner, A. G. Cheetham, A. Beeby, V. Gramlich and F. Diederich, Conformational switching of resorcin[4]arene cavitands by protonation, preliminary communication, Helv. Chim. Acta, 2001, 84, 2146–2153.
23. V. A. Azov, B. Jaun and F. Diederich, NMR investigations into the vase-Kite conformational switching of resorcin[4]arene cavitands, Helv. Chim. Acta, 2004, 87, 449–462.
24. M. Frei, F. Marotti and F. Diederich, Zn(II)-induced conformational control of amphiphilic cavitands in Langmuir monolayers, Chem. Commun., 2004, 1362–1363.
25. K. D. Zhang, D. Ajami and J. Rebek, Hydrogen-bonded capsules in water, J. Am. Chem. Soc., 2013, 135, 18064–18066.
26. F.-U. Rahman, H.-N. Feng and Y. Yu, A new water-soluble cavitand with deeper guest binding properties, Org. Chem. Front., 2019, 6, 998–1001.
27. K. Tiefenbacher, K. Zhang, D. Ajami and J. Rebek, Robust hydrogen-bonded capsules with stability in competitive media, J. Phys. Org. Chem., 2015, 28, 187–190.
28. A. Scarso, L. Trembleau and J. Rebek, Encapsulation induces helical folding of alkanes, Angew. Chem., 2003, 115, 5657–5660.
29. I. D. Petsalakis, D. Tzeli, G. Theodorakopoulos and J. Rebek Jr, Theoretical investigation on the binding of alkyl halides and cyclohexyl halides in water-soluble cavitands, Chem. Phys. Lett., 2019, 728, 174–180.
30. R. Gershoni-Poranne, A. P. Rahalkarb and A. Stanger, The predictive power of aromaticity: quantitative correlation between aromaticity and ionization potentials and HOMO–LUMO gaps in oligomers of benzene, pyrrole, furan, and thiophene, Phys. Chem. Chem. Phys., 2018, 20, 14808–14817.
31. H. S. Ashbaugh, B. C. Gibb and P. Suating, Cavitand Complexes in Aqueous Solution: Collaborative Experimental and Computational Studies of the Wetting, Assembly, and Function of Nanoscopic Bowls in Water, J. Phys. Chem. B, 2021, 125, 3253–3268.
32. D. Tzeli and P. G. Tsoungas, N,N- and N,O-6-membered Ring peri-Annelation in Naphthalene. Is it a Heteroring or merely a peri-Heterobridge?, ChemistrySelect, 2021, 6, 951–961.
33. R. Gershoni-Poranne and A. Stanger, The NICS-XY-Scan: Identification of Local and Global Ring Currents in Multi-Ring Systems, Chem. – Eur. J., 2014, 20, 5673–5688.

---

Footnote

† Electronic supplementary information (ESI) available: Geometries, many body analyses of the binding energies, dipole moments, charges on the chalcogen, dipole electric field isotropic and anisotropic electric field polarizabilities, ¹H NMR spectra, contour plots of magnetic isotropy and anisotropy and NICS indexes of A_X + A_X′. See DOI: 10.1039/d1cp02277f

---