First hyperpolarizability of water at the air–vapor interface: a QM/MM study questions standard experimental approximations

Abstract

Surface Second-Harmonic Generation (S-SHG) experiments provide a unique approach to probe interfaces. One important issue for S-SHG is how to interpret the S-SHG intensities at the molecular level. Established frameworks commonly assume that each molecule emits light according to an average molecular hyperpolarizability tensor β(−2ω,ω,ω). However, for water molecules, this first hyperpolarizability is known to be extremely sensitive to their environment. We have investigated the molecular first hyperpolarizability of water molecules within the liquid–vapor interface, using a quantum description with explicit, inhomogeneous electrostatic embedding. The resulting average molecular first hyperpolarizability tensor depends on the distance relative to the interface, and it practically respects the Kleinman symmetry everywhere in the liquid. Within this numerical approach, based on the dipolar approximation, the water layer contributing to the Surface Second Harmonic Generation (S-SHG) intensity is less than a nanometer. The results reported here question standard interpretations based on a single, averaged hyperpolarizability for all molecules at the interface. Not only the molecular first hyperpolarizability tensor significantly depends on the distance relative to the interface, but it is also correlated to the molecular orientation. Such hyperpolarizability fluctuations may impact the S-SHG intensity emitted by an aqueous interface.

---

1 Introduction

Liquid water is ubiquitous on Earth; understanding the properties of its interfaces with other media is essential for many fields of physics, chemistry, and biology. Surface analytical tools have been developed to obtain information on the molecular organization at interfaces; in particular, non-linear optical techniques such as Surface Second Harmonic Generation (S-SHG) and Surface Sum Frequency Generation (S-SFG) are increasingly used to probe biological materials at interfaces,^1–3 and to investigate the molecular structure of liquid–gas,^4–9 liquid–liquid^10,11 or liquid–solid^12–16 interfaces. The SHG is an optical process whereby two photons at a fundamental frequency are converted into one photon at twice the fundamental frequency, i.e. the harmonic frequency. Coherent SHG techniques are surface-sensitive because of the cancellation of the SHG process within centrosymmetric media like bulk liquids¹⁷. Moreover, the SHG response is strongly dependent on the molecular arrangement and the molecular electrostatic environments,^18,19 so that S-SHG has become a useful tool for probing molecular structure^1,20,21 or surface electrostatics.^{2,8,9,12,14,22–24} However, linking the experimental S-SHG intensity to interface molecular structure often remains a challenge, for which different experimental characterizations,^9,11 theoretical developments,^17,25 and molecular modeling^26–28 can benefit from each others.^10,29–32

The interpretation of the S-SHG signal of the water/air interface has been a subject of debate for decades.^9,10,33 Efforts have been made to assess the contribution of the interface (local) contribution of “the Bonded Interface Layer” (BIL) and the one of bulk electric quadrupole and magnetic dipole contributions to the SHG signal appearing in the diffuse layer (DL).^9,27

For a neat water/air interface, Dalstein et al.⁹ and Zhang et al.³³ attribute the signal to the BIL, i.e. the layer where the inversion symmetry is broken by the interface-specific structure. Typically, under the electric dipole approximation, this contribution to the quadratic surface susceptibility tensor χ⁽²⁾ is modeled as a sum of the molecular hyperpolarizability tensors β(−2ω,ω,ω)ⁿ, where n is not a power notation, but an index running over the molecules.^10,33 To express χ⁽²⁾ in the laboratory frame, one takes into account the orientation of the nth-molecule via the matrix Rⁿ of its molecular coordinate system {a,b,c} in the laboratory frame .^10,33 To interpret the S-SHG signal of the water/air interface in terms of interface structure using this formalism, one therefore needs to know the hyperpolarizabilities of individual water molecules.³³ Moreover, one considers that the signal can be interpreted in terms of molecular hyperpolarizability. The decomposition of the non linear optical response of a cluster into a sum of molecular properties is not obvious,³⁶ since intermolecular interactions may strongly impact non linear optical properties (for a recent example see ref. 37). In the special case of water, Maroulis³⁸ or Liang et al.³⁹ compared the polarizabilities and/or hyperpolarizabilities of dimers to the sum of the properties of the individual molecules. Their results indicate that the single-molecule summation is a reasonable first step.

The molecular hyperpolarizability is commonly assumed to be the same for all the water molecules of a given phase, and respecting the molecular symmetry group C_2v. These hypotheses permit to extract from the susceptibilities the mean molecular orientation – via the orientation matrices.^4,20 However, it is known that solvation has a substantial effect on the measured hyperpolarizability of water molecules, and the liquid environment breaks the C_2v symmetry.^36,39–43 To reach quantitative interpretation of S-SHG signal of aqueous interfaces, the water hyperpolarizability must be known, precisely at these interfaces.

In particular, the origin of the failure of Kleinman symmetry observed experimentally for the neat air/water interface (χ⁽²⁾_ZXX ≠ χ⁽²⁾_XZX, for example) is debated.^33,44,45 It was attributed by Zhang et al. to the asymmetry of the molecular hyperpolarizability, for instance to β_aca ≠ β_caa or β_bcb ≠ β_cbb, where the c-axis is along the water dipole moment.³³ A symmetry breaking of the hyperpolarizability tensor β indeed exists for water in the gas phase,^10,33 but to our knowledge, it has been reported neither in the bulk liquid, nor at the interface.

In this article, we report theoretical chemistry calculations of the molecular hyperpolarizability of water molecules nearby the interface, and discuss the results in terms of the S-SHG measurements. Liquid water is a difficult system for computational modeling in general, and for the prediction of electric properties in particular because of the extended H-bond network.^46,47 Modeling the molecular environment as homogeneous dielectric material is not sufficient to reproduce the sign change of water hyperpolarizability from the gas phase to the liquid phase.⁴⁸ Here, we propose a sequential Quantum Mechanical/Molecular Mechanics (QM/MM) approach to provide new insights on the contribution of water molecular hyperpolarizability to the S-SHG signal of the liquid–vapor interface, see Fig. 1.

Fig. 1 Scheme of the numerical procedure (performed by the home-made software FROG). (a) Molecular dynamics snapshot of the water liquid–vapor simulation within a box of 5 × 5 × 40 nm³. (b) Zoom on the interface and on one water molecule at a given time step. (c) A single water molecule with its electrostatic environment, within a radius R_c, used for quantum mechanics calculation of individual hyperpolarizabilities. Average hyperpolarizability profiles are obtained as a function of the coordinate normal to the interface (Z) by selecting and analyzing molecules within 0.1 nm-thick slices. Pictures were prepared using VMD³⁴ and Inkscape³⁵ softwares.

Such methods have been successful to describe the impact of solvation on the optical properties of NLO-dyes,^28,49–54 and on other non-resonant molecules.^{39,41–43,55–57} First, a classical molecular description of the structure of the liquid–vapor water interface is obtained using Molecular Dynamics (MD) simulations. Then, the frequency dependent β(−2ω,ω,ω) of each water molecule at the interface is computed using a QM description within an electrostatic embedding framework⁵⁸ to mimic the condensed phase environment.

In Section 2, we present the MD and QM methods and justify some important calculation parameters. In Section 3, we report our results concerning the interface structure, and the evolution of the hyperpolarizability components when the water molecule gets close to the liquid–vapor interface.

2 Method description and validation

2.1 Molecular mechanics simulations and analysis

LAMMPS⁵⁹ V.11.08.2017 is used to perform the MD simulation along with the rigid TIP4P/2005 water force field.⁶⁰ Using equilibrated bulk configurations, 9000 rigid TIP4P/2005 water molecules are placed in a simulation box (5 × 5 × 40 nm³) to form a water film, about 10 nm thick, see Fig. 1(a). Thanks to the sufficient film thickness, the middle part of the fluid film well mimics bulk water. Periodic boundary conditions were applied in all three directions, so that the simulation is actually that of a multi-film system, but the vacuum layer of 30 nm is thick enough to neglect interactions between the water interfaces. The target temperature is 300 K using a Nose–Hoover thermostat with the period of the temperature fluctuations set to τ = 0.4 ps. 3 ns of NVT equilibration is performed before the 20 ns NVT production run with a time step of 2 fs. The center of mass of the whole system is fixed every timestep. Both electrostatic and Lennard-Jones intermolecular interactions are computed using the long-range PPPM formalism.^61,62 Neighbor lists were updated every timesteps with a radius of 1 nm.

To compute the structural properties of the simulated system, such as the molecular orientations or the hyperpolarizabilities, a home-made Python software FROG is used, using the module MDAnalysis.⁶³ Local composition and molecular orientation are computed along with the hydrogen bond (H-bond) network. The H-bond analysis uses the geometric criteria from Pezzotti et al., i.e. an H-bond is present if the distance O(–H)⋯O is smaller than 3.2 Å and the angle O–H⋯O is in the range of [140–220]°.²⁷ For the bulk phase, we obtain 3.37 H-bonds per water molecule, to be compared to the value obtained by Pezzotti et al. of 3.4.²⁷ The structural properties such as densities and H-bond numbers are averaged over time and space to produce profiles, as precised below.

2.2 Space averaging

In the system, two liquid–vapor interfaces are present, but we shall focus on a single interface here, see Fig. 1(b). The average position of the interface is supposed to be planar, parallel to the {X,Y} plane. To calculate profiles along the Z-direction, the various properties are averaged over the molecules belonging to 0.1 nm-thick slices normal to the Z direction. In the following, the profiles are plotted as function of the “altitude” ΔZ = Z − Z₀ relative to the average position of the interface Z₀. To calculate the error-bars, we have estimated space-correlations within each slice, see ESI,† for details (Section S1.3).

2.3 Response properties within density functional theory

The QM/MM workflow was handled by our software FROG that reads the MD trajectories and writes input files for the QM calculations, to compute NLO properties within the PE framework.⁵¹ After the hyperpolarizability calculations have been performed, FROG analyses the individual QM outputs and computes the altitude-dependent distribution of the hyperpolarizability (see Section S1.1 of ESI†).

Hyperpolarizability calculations. Calculations of the static and dynamic NLO responses of water at the interface were performed at the density functional theory (DFT) CAM-B3LYP⁶⁴/d-aug-cc-pVTZ⁶⁵ level using the DALTON software,⁶⁶ release 2018.2 package. DFT presents inaccuracies that we discuss in the following, but its computational efficiency, necessary for a proper QM/MM sampling of several thousands of calculations, was the reason of our choice.

Concerning the basis, large sets including polarization and diffuse functions are necessary to obtain reliable hyperpolarizabilities.^67,68 The Dunning's correlation consistent (cc) basis sets,^65,69,70 in particular d-aug-cc-VTZ basis set is commonly used for water.^10,39,42,71 It can be considered as a very good compromise between efficiency and accuracy for the present QM/MM applications that has been used for water molecules in the gas and liquid bulk phases. For an isolated water molecule, Sections S1.2.1 and S1.2.2 of ESI,† show the convergence of DFT approaches relative to basis set.

Concerning the functional, CAM-B3LYP is a range-separated hybrid functional which adds long-range correction using the Coulomb-attenuating method and includes 19% of HF exchange at short-range and 65% at long-range.⁶⁴ It is expected to provide reliable results for the non linear optical properties of medium-size molecules.^72,73 While it is true that DFT/CAM-B3LYP is not very accurate to compute cross section at resonant frequency,⁷⁴ the present work investigates SHG response for the fundamental frequency of 800 nm, i.e. in the non-resonant case, where no excited state is populated. For water, the excitation energies of the first states are around 7–10 eV, corresponding to a fundamental wavelength about 300 nm. Even if the excitation wavelength of interest in our article is 800 nm, these states should still contribute to the SHG response. CAM-B3LYP seems a reasonable choice, since it performs best to predict the cross section and the frequency compared to other DFT functionals.⁷⁴ For single water molecules, the use of long-range-corrected functionals permits to obtain DFT hyperpolarizabilities in reasonable accordance with CCSD/d-aug-cc-pVTZ results: the typical absolute difference is 1.3 a.u., averaged over non-zero hyperpolarizability components (see Table S1, ESI† and ref. therein^67,75). Finally, since the QM/MM approach involves an electrostatic environment, the second hyperpolarizability γ plays an important role. Besalú-Sala et al. have showed recently that CAM-B3LYP is among the best choices regarding the second hyperpolarizability of water.⁷³

The first hyperpolarizability is extracted using the frequency-dependent quadratic response scheme.⁷⁶ The hyperpolarizability values are given within the T convention,⁷⁷ in atomic units. Frequency-dependent calculations were carried out using an incident wavelength λ of 800 nm, and compared to the results for a static field (λ → ∞). The vibrational contribution to the first hyperpolarizability is neglected. This contribution is typically of 10% for water in the gas phase.⁷¹

QM/MM embedding. To model the liquid phase effect, an electrostatic environment is considered. The QM system is always composed of a single water molecule, surrounded by point charges representing the neighboring water molecules. The typical size of the electrostatic environment is defined by R_c. To preserve the electroneutrality of the whole system, only complete molecules are included in the electrostatic environment. If a neighbor molecule posses at least one atom in radius R_c around the center of mass of the target water molecule, the whole molecule is included in the electrostatic environment. This heterogeneous and discrete solvation model is still in active development.^{51,58,78–80} Even if potential improvement can be gained using more accurate electrostatic description of the neighbors⁷⁸ or the calculation of the local effective field,⁵¹ we have used a point charge description (PE0 scheme in DALTON) of the electrostatic environment fully coherent with the MD simulation protocol. This ensures consistency within the QM embedding and the MD structures and provides a first robust and simple calculation.

To characterize the effect of the MM embedding, we have calculated the electrostatic field generated by the point charges on the QM water molecule. More precisely, this electrostatic field is calculated at the position of the negative charge in the TIP4P/2005 force field −0.15 Å away from the oxygen atom, along the dipole vector.

Validation of the QM/MM method for bulk liquid water. The averages and standard deviations of the β components with CAM-B3LYP/d-aug-pVTZ for water in liquid water are compared to the values of Liang et al.³⁹ in Table 1 (see Table S2 of ESI,† for all components). Both calculation schemes use the TIP4P/2005 rigid force field and the basis set d-aug-pVTZ. Liang et al. have used couple-cluster calculation, while we have used DFT. The bulk hyperpolarizability values differ from the ones of Liang et al. by 0.2 to 1 a.u., but the main features of the hyperpolarizability of solvated water are well reproduced by our scheme: (i) the hyperpolarizability of water in bulk liquid is very different from the one of water in the gas phase, with a change of sign of β_ccc, β_bcc and β_cbc; (ii) the component β_ccc remains the most important in absolute value; (iii) the standard deviations of the hyperpolarizability distributions are very large, often similar to the average values, (iv) the tensor respects the C_2v symmetry on average, but it is generally not the case for the hyperpolarizability of individual water molecules within their anisotropic environments. Moreover, our results for the first hyperpolarizability of water in bulk match well the ones obtained with the a polarizable environment (PE1 level) by Osted et al.⁴² This is in qualitative accordance with the results by Liang et al.,³⁹ who have shown the small impact of the water flexibility on β values for water in bulk phase.

Table 1 Molecular hyperpolarizability β(−2ω,ω,ω) in the gas and bulk liquid water phases. Hyperpolarizabilities are in a.u. and the excitation wavelength λ is in nm. For the liquid phase, the mean values are presented along with the distribution width in brackets. Table S1 of ESI reports the other components, which average to 0

λ	Gas		Liquid
	∞^a	800^a	∞^b	∞^a	800^a
a This work, using DFT-CAM-B3LYP/d-aug-pVTZ level within the PE-0 response scheme using the charges of the TIP4P-2005 force field. The values for the liquid are averages over 48 000 configurations obtained from 32 MD frames separated from 20 ps, with an electrostatic environment built up to Rc = 2 nm around the target molecule. b Combined coupled cluster/molecular mechanics (CC/MM) method by Liang et al.^39
β caa	−10.6	−12.5	−2.1 [1.1]	−1.9 [1.0]	−1.9 [1.1]
β aca	−10.6	−12.4	−2.1 [1.1]	−1.9 [1.0]	−2.0 [1.1]
β cbb	−4.2	−5.0	1.6 [1.8]	2.6 [1.7]	2.7 [2.0]
β bcb	−4.2	−7.4	1.6 [1.8]	2.6 [1.7]	2.3 [2.1]
β ccc	−12.1	−15.3	3.0 [3.0]	3.9 [2.8]	4.0 [3.1]

---

Based on these results, the rest of the work concerning the interface was done using the CAM-B3LYP functional and the d-aug-cc-VTZ basis set.

Impact of electrostatic environment radius (R_c). To choose the value for R_c, the convergence of the hyperpolarizability relative to it has been performed for the water molecules belonging to the 0.1 nm-thick slice at the altitude ΔZ = −0.06 nm. This altitude has been chosen because it is typical of the interface: for this altitude, the structural properties differ strongly from the bulk ones while the density remains large enough to obtain precise averages. Moreover, due to the large number of molecules with a net orientation, this slice is expected to contribute strongly to the second harmonic response of the interface. The convergence of 〈β_ccc〉 relative to R_c is illustrated by Fig. 2, where 〈·〉 denotes here an average over the molecules at the chosen altitude (in this case, 4294 molecules extracted from 80 MD frames separated from 20 ps).

Fig. 2 Convergence of the averaged molecular first hyperpolarizability component 〈β_ccc〉 relative to the environment cutoff radius R_c, for molecules at the altitude ΔZ = −0.06 ± 0.05 nm. The percentage of the relative absolute error |〈β_ccc〉 − 〈β_ccc〉⁰|/〈β_ccc〉⁰ is plotted with a log. scale, where the reference value 〈β_ccc〉⁰ is obtained for R_c = 5 nm. The dashed line represents an error of 1%. See ESI,† Fig. S7 for other β components.

A radius of about 2 nm is needed to reach a relative error below 1%, i.e. 0.1 atomic unit (dashed line on Fig. 2). The convergence is similar for molecules selected in the bulk phase (see Fig. S6 of ESI†). Therefore, in the following, the neighborhood is built up to a distance R_c = 2.3 nm. This result highlights that the hyperpolarizability is sensitive to the electrostatic environment up to several nanometers: for aqueous interfaces in general, the S-SHG signal of the BIL might be influenced indirectly by the structure and composition of a thicker interfacial layer. Indeed, special care should be granted to the choice of the electrostatic embedding description for QM/MM SHG studies.^51,78

2.4 Time averaging of hyperpolarizability

The hyperpolarizability profiles are obtained from the analysis of N_f selected frames of the MD trajectory, separated from a time span Δt. This Section presents our methods to choose Δt and N_f.

Hyperpolarizability time autocorrelation. To avoid time-correlation in the hyperpolarizabilities, one waits for a given time span Δt between treated MD frames. To choose this time span, we have calculated the autocorrelation function of the hyperpolarizability tensors of two arbitrary molecules chosen either in the bulk phase, or at the interface. For this particular test, 1000 configurations of these two molecules are treated, every δt = 0.2 ps, with the same functional and basis as for the rest of the study (CAM-B3LYP/d-aug-pVTZ), with an electrostatic embedding up to R_c = 2 nm. The autocorrelation function (AC) is defined as:for Δt in range 0 to 200δt, T = 800δt and [small beta, Greek, tilde]_ijk(t) = β_ijk(t) − 〈β_ijk〉. In order to represent the contribution of all the components, a “total autocorrelation” (TAC) function is defined:The normalized TAC (TAC(Δt)/TAC(0)) is plotted in Fig. 3. In the interface region, as in the bulk region, the autocorrelation time of the hyperpolarizability of a single water molecule nearby the interface is of the order of a few picoseconds. This is coherent with the value used for the β calculation in bulk phase in ref. 42 (1 ps) and for properties of larger molecules in ref. 79 (10 ps). Finally, we have exploited the MD configurations obtained every Δt = 20 ps of simulation, which is also larger than the surface tension autocorrelation time.⁸¹

Fig. 3 Time auto-correlation (TAC) of the fluctuations of the beta tensor of a single molecule, either in the bulk phase (blue solid line), or at the interface (orange solid line), averaged over the components as defined by eqn (2). The ordinate axis follows a logarithmic scale. The dashed line represents a TAC of 5%.

Hyperpolarizability time convergence. To choose the total number of treated frames N_f, we have calculated the average hyperpolarizability obtained as a function of N_f for the typical altitude of ΔZ = −0.06 nm. Fig. 4 depicts the non-zero components, relatively to our reference (80 frames, i.e. 4294 configurations).

Fig. 4 Relative deviation of the average β components as a function of the number of QM calculations, for the typical altitude of ΔZ − Z₀ = −0.06 ± 0.05 nm. The relative deviation (in %) is calculated with respect to the reference value obtained using the 4294 molecular configurations obtained for N_f = 80 selected MD frames. The dashed lines represent a deviation of 5%.

Approximately 4200 configurations are needed to obtain relative deviation of the order of 2% at this typical altitude. These correspond to the N_f = 80 selected MD frames, which was chosen for the rest of the study, for all altitudes. Fig. S5 of ESI† reports the evolution for the other components, that converge towards zero, and the conclusions are the same.

For a fixed number of frames N_f, the number of QM calculations included in the hyperpolarizability average of a given slice is proportional to the density in this slice. Therefore, the hyperpolarizability averages are less precise for altitudes where the density is lower.

3 Results and discussion

3.1 Interface structure from classical molecular dynamics simulations

In a first step, the structure of the liquid–vapor interface has been obtained from the analysis of one interface in an MD simulation of a water film surrounded by vapor, see Fig. 1(a and b).

We discuss here the density profile and the water dipole orientation profile displayed in Fig. 5(b). The density decreases progressively from the bulk value to zero with a profile close to a hyperbolic tangent shape.⁸² Its inflection point permits to define an absolute position Z₀ for the interface, and the distance relative to it (ΔZ = Z − Z₀) that is called “altitude” here.

Fig. 5 (a) Definition of the molecular frame {a,b,c} and of the angle θ = (c,Z) characterizing the orientation of the water dipole moment with respect to the interface normal Z-axis. (b) Water density profile (black circles) and 〈cos θ〉 profile (gray squares) as a function of the altitude. The solid black line is proportional to a hyperbolic tangent function fitted onto the density profile. The error bars are calculated using eqn (S3) of ESI.†

The projection of the water dipole c-axis on the interface normal (Z), illustrated by Fig. 5(a), is particularly relevant for the interpretation of the S-SHG intensities. Indeed, the C_∞ symmetry of the interface, associated to an expected C_2v symmetry of the water hyperpolarizability tensor, yields surface susceptibility components expressed as linear combinations of 〈β_ijk(cos θ)^l〉 where θ is the (c,Z) angle^33,83 and l is 1 or 3. For example, if one focuses on the χ⁽²⁾_ZZZ element (the dominant one, according to experimental observations on the water–air interface¹⁰):

χ⁽²⁾_ZZZ ∝ 〈β_⊥ cos θ〉 + 〈(β_ccc − β_⊥)cos³ θ〉, (3)

where 〈·〉 defines the average over molecules and

β_⊥ = (β_caa + β_cbb + 2β_aca+ 2β_bcb)/2. (4)

Section S4 of ESI† recalls the complete expressions.

The profile of 〈cos θ〉 is therefore plotted in Fig. 5(b) as a function of the altitude. The region where a net orientation appears, i.e. 〈cos θ〉 ≠ 0, spotlights the BIL and the thickness of the layer which should contribute to the S-SHG signal. Noticeably, the net water orientation appears few Angstroms further away from the interface than the density drop. The deviation for the H-bond network relative to the bulk occurs at a similar altitude (see Fig. S3 of ESI†).

Moreover, 〈cos θ〉 provides structural information: the negative values indicate that the dipole moment of the water molecule points on average with the hydrogens towards the bulk phase. But this propensity is weak, and the dipole moment of the water molecule in the most external water layers is preferentially close to parallel to the interface plane (see Fig. S4 of ESI†). These results agree with previous studies.^10,47,84

To guide the interpretation, we have divided the system into 3 regions shown in Fig. 5: bulk (in purple), interface (in cyan) and vapor (in white). The limit between the bulk and interface is fixed at the altitude where 〈cos θ〉 significantly deviates from its bulk value. The edge of the vapor area is defined where the density reaches 5% of the bulk value. In practice, we have limited the vapor region at the point where accurate statistical averaging over the number of water molecules became difficult because of too small densities.

3.2 Water hyperpolarizabilities from quantum mechanics/molecular mechanics (QM/MM) calculations

The second step consists in computing, for each MD snapshot, the molecular hyperpolarizability β(2ω,ω,ω) of all water molecules. After justifying several calculation parameters (see Section 2.3), we discuss here the molecular hyperpolarizability components as a function of the altitude.

First, the average hyperpolarizability tensor respects the C_2v symmetry at the interface. Note that this was already true in the bulk (see Table S2 of ESI†). Indeed, the C_2v-forbidden β components remain negligible (less than 0.3 a.u. in average) throughout the whole interface (see Fig. 6). All these values average to zero in the region where the density is large enough to obtain precise results, but their fluctuations are strong, as already noted by Liang et al.³⁹ for the bulk phase. Concerning the non-vanishing hyperpolarizability components, Fig. 7 shows that they start to deviate from their bulk values roughly at the same altitude as the density, molecular orientation or H-bond network.

Fig. 6 Averages of the hyperpolarizability β(−2ω,ω,ω) as a function of the altitude, in the molecular frame {a,b,c}, for the C_2v-forbidden components. The exciting wavelength is 800 nm. Errors bars are calculated using eqn (S3) of ESI.†

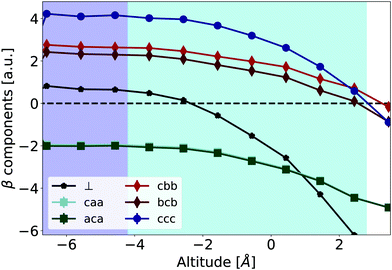Fig. 7 Averages of the components of the hyperpolarizability β(−2ω,ω,ω) as a function of the altitude, in the molecular frame {a,b,c}, for an exciting wavelength of 800 nm. β_caa and β_aca are indistinguishable. β_⊥ is defined by eqn (4). The errors bars, calculated using eqn (S3) of ESI,† are smaller than the symbols.

Concerning the frequency dispersion, characterized for example by the difference between 〈β_cbb〉 and 〈β_bcb〉, it is much smaller in the water bulk phase (≃0.5 a.u.) than in the vacuum phase (≃2.5 a.u., see Table 1). In the interface region, the frequency dispersion remains weak, and the Kleinman symmetry is practically respected, i.e. 〈β_caa〉 = 〈β_aca〉 and 〈β_cbb〉 ≃ 〈β_bcb〉. Therefore, within our methodology, the Kleinman symmetry breaking observed experimentally seems difficult to be explained solely by the individual dipolar molecular responses (see Section S4.3 of ESI†). Our calculations do not take into account the effective field (cavity field) effect, which is beyond the scope of this work. However, since the dispersion of the water polarizability between 800 and 400 nm is very small,¹⁰ it should not affect much our conclusion. More precise QM/MD calculations, local effective field effects, collective effects, or quadrupolar contributions should be further explored to explain this behavior.

The evolutions of individual components are relatively modest, and the hyperpolarizability tensor remains closer to the bulk one than to the gas one. Indeed, similarly to the structural properties depicted in Fig. 5, the electric field generated by the point-charge environment differs from the bulk one in the interface area. However, its projection along the molecular c-axis loses only about 30% of its bulk value. This can be seen on Fig. 8 that shows the electrostatic field generated by the point-charged environment on the central water molecule, projected along the c-molecular axis. We attribute this strong remaining field to the presence of close neighbors, and H-bonds, even for the most external layer of water molecules,⁴⁷ see Fig. S3 of ESI.†

Fig. 8 Electrostatic field generated by the environment along the molecular c-axis throughout the interface. In insert the electrostatic field distribution. The environment is built up to R_c = 2 nm. The average values of the electric field along the a and b-axis remain null across the interface – data not shown.

3.3 Link with surface-second harmonic generation (S-SHG)

Even if the variations of individual molecular hyperpolarizability components could be considered as weak, the evolution of β_ccc and β_⊥ is significant for the S-SHG interpretation. Whereas β_ccc is dominant in the bulk (4.0 vs. 0.5 a.u.), at the altitude of 0.04 nm, β_ccc and β_⊥ have opposite values so that (β_ccc − β_⊥) vanishes. The ratio of the two components of eqn (3) is strongly modulated by the altitude. This questions some frameworks used to analyze S-SHG signals, in which the ratio between β_ccc and β_⊥ is typically considered as constant throughout the interface (see for example Section S4.4 of ESI†).

Further, we tackle an even more basic question: can the β tensor distribution be replaced by a single, average value at a given altitude? In the dipolar approximation, one may write the susceptibility χ⁽²⁾ as proportional to the average over molecular configurations of the product of the rotational matrix R with the β tensor. In practice, it is often assumed that all molecules can be described by a single hyperpolarizability tensor 〈β_ijk〉, and that the fluctuations of the hyperpolarizability tensor and the molecular orientation are uncorrelated, i.e. 〈β_ijk cos^l θ〉 = 〈β_ijk〉〈cos^l θ〉. In our data, such equalities do not hold: Fig. 9 illustrates it for eqn (3), where the contributions of β_⊥ and β_ccc to χ⁽²⁾_ZZZ are calculated either taking into account the fluctuations, or using the average β tensor and average orientation at each altitude (see Section S4.2 of ESI,† for details). The difference between the two curves emphasizes correlations between the molecular orientation and molecular hyperpolarizabilities at the interface.

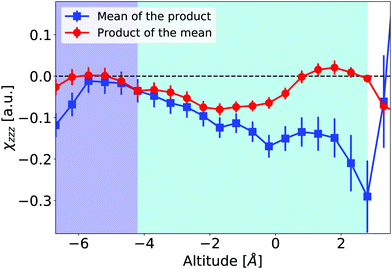Fig. 9 χ ⁽²⁾ _ZZZ as a function of altitude calculated using the right hand side of eqn (3) in 0.1 nm-thick slices. Either the correlations between hyperpolarizability and orientation are considered (blue squares, using 〈β_ijk cos^lθ〉), or they are neglected (red circles, using 〈cos^l θ〉〈β_ijk〉).

In Fig. 9, χ⁽²⁾ is expected to vanish in the bulk region. The deviations relative to zero in this area indicate that the convergence relative to sampling is not completely achieved. Indeed, the configuration-convergence study presented in Fig. 4 is focused on the hyperpolarizability components β. Since the χ⁽²⁾ elements also include molecular orientations, their convergence is more demanding. However, at the interface, the differences between the two ways of calculating χ⁽²⁾ on our data exceed these errors.

We conclude that orientation/hyperpolarizability correlations may be relevant to interpret quantitatively S-SHG intensities. Such correlations have been mentioned by Champagne and co-workers in a more complex system, composed of an organic dye embedded in a lipid bilayer,⁸⁵ and we show here that these may appear even at the neat liquid–vapor interface of pure water.

4 Conclusions

To summarize, a QM/MD approach was applied at the water liquid–vapor interface, to compute first hyperpolarizabilities of individual water molecules within the very specific environment where the S-SHG signal is generated. There is still a lot of room for improving the accuracy of the QM/MM approach (QM framework, electronic delocalization on several molecules, environment polarizability, long range electrostatic effects, local field factors,…), but qualitative results emerge. Within our approach, the dipolar contribution to the NLO response appears in a molecular layer of about half a nanometer thickness, where both the molecular orientation and the hyperpolarizability significantly differ from the bulk ones. The molecular first hyperpolarizabilities depend on the molecular environment up to radii larger than 2 nm, so that the S-SHG is very sensitive to the electrostatic properties of the interface. The hyperpolarizability tensor elements calculated in our PE approach almost respect the Kleinman symmetry, both in the bulk water phase and at the liquid–vapor interface, so that the Kleinman symmetry breaking observed experimentally may not originate in individual dipolar molecular response. The variations of the hyperpolarizability within the interface have an impact on the relative weights of its different components. Finally, we spotlight that the calculated molecular hyperpolarizabilities and molecular orientations are correlated: single average values for the molecular hyperpolarizability tensor and orientation are not sufficient to describe the entire distribution of molecular responses. The hyperpolarizability cannot be considered as constant for all water molecules at the liquid–vapor interface. More generally, this work indicates that one may need to consider different water populations at the interface to interpret the dipolar contributions to the surface second harmonic generation of aqueous interfaces. These hyperpolarizability fluctuations revealed at the neat air/water interface may also be relevant in more complex systems and could be more generally considered in quantitative interpretations of S-SHG experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thanks Zacharie Behel for his help during the writing of FROG. We gratefully acknowledge support from the PSMN (Pôle Scientifique de Modélisation Numérique) of the Ecole Normale Supérieure de Lyon for the computing resources.

Notes and references

1. E. Donohue, S. Khorsand, G. Mercado, K. M. Varney, P. T. Wilder, W. Yu, A. D. MacKerell, P. Alexander, Q. N. Van, B. Moree, A. G. Stephen, D. J. Weber, J. Salafsky and F. McCormick, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17290–17297.
2. A. C. McGeachy, E. R. Caudill, D. Liang, Q. Cui, J. A. Pedersen and F. Geiger, Chem. Sci., 2018, 9, 4285–4298.
3. G. Licari, J. S. Beckwith, S. Soleimanpour, S. Matile and E. Vauthey, Phys. Chem. Chem. Phys., 2018, 20, 9328–9336.
4. H.-T. Bian, R.-R. Feng, Y. Guo and H.-F. Wang, J. Chem. Phys., 2009, 130, 134709.
5. H. C. Allen, N. N. Casillas-Ituarte, M. R. Sierra-Hernandez, X. Chen and C. Y. Tang, Phys. Chem. Chem. Phys., 2009, 11, 5538–5549.
6. M. Sulpizi, M. Salanne, M. Sprik and M.-P. Gaigeot, J. Phys. Chem. Lett., 2012, 4, 83–87.
7. Y. Chen, H. I. Okur, N. Gomopoulos, C. Macias-Romero, P. S. Cremer, P. B. Petersen, G. Tocci, D. M. Wilkins, C. Liang, M. Ceriotti and S. Roke, Sci. Adv., 2016, 2, 1–9.
8. P. E. Ohno, H. Chang, A. P. Spencer, Y. Liu, M. D. Boamah, H.-F. Wang and F. M. Geiger, J. Phys. Chem. Lett., 2019, 10, 2328–2334.
9. L. Dalstein, K.-Y. Chiang and Y.-C. Wen, J. Phys. Chem. Lett., 2019, 10, 5200–5205.
10. T. T. Pham, A. Jonchère, J. F. Dufrêche, P. F. Brevet and O. Diat, J. Chem. Phys., 2017, 146, 144701.
11. L. B. Dreier, C. Bernhard, G. Gonella, E. H. Backus and M. Bonn, J. Phys. Chem. Lett., 2018, 9, 5685–5691.
12. R. K. Campen, A. K. Pymer, S. Nihonyanagi and E. Borguet, J. Phys. Chem. C, 2010, 114, 18465–18473.
13. S. Xu, S. Xing, S.-S. Pei, V. Ivanišev, R. Lynden-Bell and S. Baldelli, J. Phys. Chem. C, 2015, 119, 26009–26019.
14. A. Marchioro, M. Bischoff, C. Lütgebaucks, D. Biriukov, M. Předota and S. Roke, J. Phys. Chem. C, 2019, 123, 20393–20404.
15. J. H. Raberg, J. Vatamanu, S. J. Harris, C. H. van Oversteeg, A. Ramos, O. Borodin and T. Cuk, J. Phys. Chem. Lett., 2019, 10, 3381–3389.
16. S. Pezzotti, D. R. Galimberti and M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2019, 21, 22188–22202.
17. Y. Shen, Annu. Rev. Phys. Chem., 1989, 40, 327–350.
18. N. A. Murugan, R. Apostolov, Z. Rinkevicius, J. Kongsted, E. Lindahl and H. Ågren, J. Am. Chem. Soc., 2013, 135, 13590–13597.
19. G. C. Gschwend, M. Kazmierczak, A. J. Olaya, P.-F. Brevet and H. H. Girault, Chem. Sci., 2019, 10, 7633–7640.
20. H.-T. Bian, R.-R. Feng, Y.-Y. Xu, Y. Guo and H.-F. Wang, Phys. Chem. Chem. Phys., 2008, 10, 4920–4931.
21. Q. Wei, D. Zhou and H. Bian, Phys. Chem. Chem. Phys., 2018, 20, 11758–11767.
22. S. Ong, X. Zhao and K. B. Eisenthal, Chem. Phys. Lett., 1992, 191, 327–335.
23. Y. Liu, E. C. Yan, X. Zhao and K. B. Eisenthal, Langmuir, 2001, 17, 2063–2066.
24. G. C. Gschwend, A. Olaya and H. H. Girault, Chem. Sci., 2020, 11, 10807–10813.
25. A. G. F. de Beer and S. Roke, J. Chem. Phys., 2010, 132, 234702.
26. G. Tocci, C. Liang, D. M. Wilkins, S. Roke and M. Ceriotti, J. Phys. Chem. Lett., 2016, 7, 4311–4316.
27. S. Pezzotti, D. R. Galimberti, Y. R. Shen and M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2018, 20, 5190–5199.
28. C. Bouquiaux, C. Tonnelé, F. Castet and B. Champagne, J. Phys. Chem. B, 2020, 124, 2101–2109.
29. S. Roke, ChemPhysChem, 2009, 10, 1380–1388.
30. M. N. Nasir, E. Benichou, C. Loison, I. Russier-Antoine, F. Besson and P.-F. Brevet, Phys. Chem. Chem. Phys., 2013, 15, 19919–19924.
31. C. Loison, M. N. Nasir, E. Benichou, F. Besson and P.-F. Brevet, Phys. Chem. Chem. Phys., 2014, 16, 2136–2148.
32. R. Hartkamp, A.-L. Biance, L. Fu, J.-F. Dufrêche, O. Bonhomme and L. Joly, Curr. Opin. Colloid Interface Sci., 2018, 37, 101–114.
33. W.-K. Zhang, D.-S. Zheng, Y.-Y. Xu, H.-T. Bian, Y. Guo and H.-F. Wang, J. Chem. Phys., 2005, 123, 224713.
34. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
35. http://www.inkscape.org/ .
36. I. Harczuk, O. Vahtras and H. Ågren, Phys. Chem. Chem. Phys., 2016, 18, 8710–8722.
37. T. N. Ramos, F. Castet and B. Champagne, J. Phys. Chem. B, 2021, 125, 3386–3397.
38. G. Maroulis, J. Chem. Phys., 2000, 113, 1813–1820.
39. C. Liang, G. Tocci, D. M. Wilkins, A. Grisafi, S. Roke and M. Ceriotti, Phys. Rev. B, 2017, 96, 1–6.
40. P. Kaatz, E. A. Donley and D. P. Shelton, J. Chem. Phys., 1998, 108, 849–856.
41. T. D. Poulsen, P. R. Ogilby and K. V. Mikkelsen, J. Chem. Phys., 2001, 115, 7843–7851.
42. A. Osted, J. Kongsted, K. V. Mikkelsen, P. O. Åstrand and O. Christiansen, J. Chem. Phys., 2006, 124, 124503.
43. C. B. Nielsen, O. Christiansen, K. V. Mikkelsen and J. Kongsted, J. Chem. Phys., 2007, 126, 154112.
44. P. Guyot-Sionnest and Y. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7985.
45. C. A. Dailey, B. J. Burke and G. J. Simpson, Chem. Phys. Lett., 2004, 390, 8–13.
46. J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2004, 120, 3787–3798.
47. S. Pezzotti, D. R. Galimberti and M. P. Gaigeot, J. Phys. Chem. Lett., 2017, 8, 3133–3141.
48. K. V. Mikkelsen, Y. Luo, H. Ågren and P. Jørgensen, J. Chem. Phys., 1995, 102, 9362–9367.
49. K. Garrett, X. Sosa Vazquez, S. B. Egri, J. Wilmer, L. E. Johnson, B. H. Robinson and C. M. Isborn, J. Chem. Theory Comput., 2014, 10, 3821–3831.
50. S. Osella, N. A. Murugan, N. K. Jena and S. Knippenberg, J. Chem. Theory Comput., 2016, 12, 6169–6181.
51. N. H. List, H. J. A. Jensen and J. Kongsted, Phys. Chem. Chem. Phys., 2016, 18, 10070–10080.
52. G. Licari, L. Cwiklik, P. Jungwirth and E. Vauthey, Langmuir, 2017, 33, 3373–3383.
53. M. De Wergifosse, E. Botek, E. De Meulenaere, K. Clays and B. Champagne, J. Phys. Chem. B, 2018, 122, 4993–5005.
54. C. Tonnelé, B. Champagne, L. Muccioli and F. Castet, Chem. Mater., 2019, 31, 6759–6769.
55. M. H. Cardenuto and B. Champagne, Phys. Chem. Chem. Phys., 2015, 17, 23634–23642.
56. M. de Wergifosse, F. Castet and B. Champagne, J. Chem. Phys., 2015, 142, 194102.
57. P. Beaujean and B. Champagne, Theor. Chem. Acc., 2018, 137, 50.
58. C. Steinmann, P. Reinholdt, M. S. Nørby, J. Kongsted and J. M. H. Olsen, Int. J. Quantum Chem., 2019, 119, e25717.
59. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
60. J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
61. R. E. Isele-Holder, W. Mitchell and A. E. Ismail, J. Chem. Phys., 2012, 137, 174107.
62. R. E. Isele-Holder, W. Mitchell, J. R. Hammond, A. Kohlmeyer and A. E. Ismail, J. Chem. Theory Comput., 2013, 9, 5412–5420.
63. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
64. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2008, 393, 51–57.
65. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
66. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani and P. Dahle, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
67. J. R. Hammond and K. Kowalski, J. Chem. Phys., 2009, 130, 194108.
68. F. Castet, E. Bogdan, A. Plaquet, L. Ducasse, B. Champagne and V. Rodriguez, J. Chem. Phys., 2012, 136, 024506.
69. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
70. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988.
71. P. Beaujean and B. Champagne, J. Chem. Phys., 2019, 151, 064303.
72. F. Castet and B. Champagne, J. Chem. Theory Comput., 2012, 8, 2044–2052.
73. P. Besalú-Sala, S. P. Sitkiewicz, P. Salvador, E. Matito and J. M. Luis, Phys. Chem. Chem. Phys., 2020, 22, 11871–11880.
74. M. J. Paterson, O. Christiansen, F. Pawłowski, P. Jørgensen, C. Hättig, T. Helgaker and P. Sałek, J. Chem. Phys., 2006, 124, 054322.
75. P. Beaujean and B. Champagne, J. Chem. Phys., 2016, 145, 044311.
76. P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, J. Chem. Phys., 2002, 117, 9630–9645.
77. A. Willetts, J. E. Rice, D. M. Burland and D. P. Shelton, J. Chem. Phys., 1992, 97, 7590–7599.
78. M. T. Beerepoot, A. H. Steindal, N. H. List, J. Kongsted and J. M. H. Olsen, J. Chem. Theory Comput., 2016, 12, 1684–1695.
79. E. R. Kjellgren, J. M. Haugaard Olsen and J. Kongsted, J. Chem. Theory Comput., 2018, 14, 4309–4319.
80. A. Marefat Khah, P. Reinholdt, J. M. H. Olsen, J. Kongsted and C. Hattig, J. Chem. Theory Comput., 2020, 16, 1373–1381.
81. G. Le Breton and L. Joly, J. Chem. Phys., 2020, 152, 241102.
82. W. Bu, D. Kim and D. Vaknin, J. Phys. Chem. C, 2014, 118, 12405–12409.
83. P.-F. Brevet, Surface Second Harmonic Generation, PPUR Presses Polytechniques, 1997.
84. W. Gan, D. Wu, Z. Zhang, R. R. Feng and H. F. Wang, J. Chem. Phys., 2006, 124, 114705.
85. C. Bouquiaux, C. Tonnelé, F. Castet and B. Champagne, J. Phys. Chem. B, 2020, 124, 2101–2109.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the QM/MD method and comparison with literature, MD structural analysis, molecular water hyperpolarizability analysis in the bulk and at the liquid/vapor interface, susceptibility expressions for the study of molecular orientation/β correlations. See DOI: 10.1039/d1cp02258j

---