Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining steady state and temperature jump IR spectroscopy to investigate the allosteric effects of ligand binding to dsDNA†
Jessica
Dale
a,
C. Peter
Howe
 a,
Hedvika
Toncrova‡
b,
Robby
Fritzsch
c,
Gregory M.
Greetham
d,
Ian P.
Clark
d,
Michael
Towrie
d,
Anthony W.
Parker
a,
Hedvika
Toncrova‡
b,
Robby
Fritzsch
c,
Gregory M.
Greetham
d,
Ian P.
Clark
d,
Michael
Towrie
d,
Anthony W.
Parker
 d,
Thomas C.
McLeish
d,
Thomas C.
McLeish
 *e and
Neil T.
Hunt
*e and
Neil T.
Hunt
 *a
*a
aDepartment of Chemistry and York Biomedical Research Institute, University of York, Heslington, York YO10 5DD, UK. E-mail: neil.hunt@york.ac.uk
bDepartment of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK
cDepartment of Physics, SUPA, University of Strathclyde, Glasgow, G4 0NG, UK
dSTFC Central Laser Facility, Research Complex at Harwell, Rutherford Appleton Laboratory, Harwell Campus, Didcot, OX11 0QX, UK
eDepartment of Physics, University of York, Heslington, York YO10 5DD, UK. E-mail: tom.mcleish@york.ac.uk
First published on 7th July 2021
Abstract
Changes in the structural dynamics of double stranded (ds)DNA upon ligand binding have been linked to the mechanism of allostery without conformational change, but direct experimental evidence remains elusive. To address this, a combination of steady state infrared (IR) absorption spectroscopy and ultrafast temperature jump IR absorption measurements has been used to quantify the extent of fast (∼100 ns) fluctuations in (ds)DNA·Hoechst 33258 complexes at a range of temperatures. Exploiting the direct link between vibrational band intensities and base stacking shows that the absolute magnitude of the change in absorbance caused by fast structural fluctuations following the temperature jump is only weakly dependent on the starting temperature of the sample. The observed fast dynamics are some two orders of magnitude faster than strand separation and associated with all points along the 10-base pair duplex d(GCATATATCC). Binding the Hoechst 33258 ligand causes a small but consistent reduction in the extent of these fast fluctuations of base pairs located outside of the ligand binding region. These observations point to a ligand-induced reduction in the flexibility of the dsDNA near the binding site, consistent with an estimated allosteric propagation length of 15 Å, about 5 base pairs, which agrees well with both molecular simulation and coarse-grained statistical mechanics models of allostery leading to cooperative ligand binding.
Introduction
The role that structural dynamics have in influencing biomolecular interactions is complex and multifaceted. This is particularly true when considering large species such as proteins or sequences of nucleic acids that exhibit dynamics in solution covering a wide range of time and length scales. An open question relates to the way that fast local dynamics, for example emanating from hydrogen bond motion or solvent exchange, influence those occurring over larger spatial scales and at much slower rates, such as domain reorganization or strand separation.Here, we investigate the fast structural fluctuations of double-stranded (ds)DNA, inspired by the suggestion that changes in the structural dynamics of the DNA duplex upon ligand binding can dictate the cooperative binding of a second ligand to a remote point on the dsDNA sequence.1–3 Instances where it has not been possible to attribute such cooperative binding to changes in structure of the DNA or to ligand–ligand interactions, so-called allostery without conformational change, have led to the concept of allosteric effects being mediated by ligand-induced changes in the dynamics of the DNA.4 Such allosteric effects are widespread in biological systems involving local binding to proteins as well as DNA5 while allosteric control of the binding of small molecules to specific DNA sequences has been implicated in gene therapy applications inter alia.6–18
Experimental detection of ligand-induced changes in the type of thermally-activated dynamics that might underpin allosteric phenomena is challenging,19,20 but an opportunity presents itself in the case of short oligodeoxynucleotide (ODN) sequences because the full range of structural dynamics leading up to the melting transition of dsDNA can be captured in a single experiment using time-resolved temperature jump (T-jump) spectroscopy methods.21–28 Such experiments employ a short duration laser pulse tuned to an absorption band of the solvent to induce a sudden temperature rise, followed by a time delayed probe, which follows the response of the ODN to the change in temperature over timescales from nanoseconds to milliseconds. Use of infrared (IR) wavelength probes provides a level of base specific insight by allowing observation of separate signals from AT and GC base pairs.21,22,27,28 Furthermore, the temperature rise that can be induced by the T-jump is typically limited to <15 °C, giving the opportunity to examine the response of the DNA over a range of starting temperatures with varying proximity to the melting transition.
T-jump methods have been applied to observe the base-specific melting dynamics of short strands of dsDNA showing that melting takes place in tens of microseconds with fast dynamics occurring on 100 ns timescales that have been assigned to end fraying.21,22,27–31 Temperature jump studies of the binding of the archetypal minor groove binding ligand Hoechst 33258 (H33258) to dsDNA sequences featuring a central AT-rich binding site (Fig. S1, ESI†) with GC-rich end sections showed that melting of the whole strand was slowed by more than an order of magnitude in time upon ligand binding to the central region.27,28 A marked suppression of the extent of the fast dynamic motion in the central binding site accompanied this change while the timescales of these dynamics decreased slightly upon ligand binding.27,28
The precise impact that the ligand has on the dynamics of bases remote from the binding site, as would be implicated in allosteric models, remains unclear however, as both a suppression of the dynamic behavior27 and a destabilization of the bases near to the binding site by the ligand have been reported.28 Previous work applying NMR spectroscopy and molecular dynamics simulations point to H33258 binding inducing a more rigid, less dynamic dsDNA structure with evidence that this restriction in dynamics extends beyond the specific binding region.4,32–34
Here, we attempt to clarify the allosteric impact of H33258 on the fast structural dynamics of dsDNA. We extend our recent work on the melting behavior of DNA·H33258 complexes27 by combining fast temperature-jump IR absorption spectroscopy measurements with temperature-dependent steady state IR absorption measurements in a quantitative fashion. The intensities of bands in the IR absorption spectrum of dsDNA respond sensitively to changes in base stacking35 and so allow for base-pair specific interrogation of DNA dynamics via a metric that is common to both T-jump IR and steady state measurements. We demonstrate that by using changes in absorbance under equilibrium conditions as a benchmark for time resolved non-equilibrium measurements, the relative contributions of pre-melting and melting dynamics can be ascertained as a function of starting temperature (T0). We show that fast pre-melting dynamics (100 ns) contribute a change in absorbance that is only weakly dependent on T0. This is in stark contrast to the signal due to strand melting (10 μs), which increases significantly as the melting temperature (Tm) of the dsDNA is approached. The result is that, although the fraction of the T-jump signal due to fast processes is strongly T0-dependent, its absolute contribution is small and near-constant.
From our experiments, we show that binding of H33258 to AT-rich dsDNA leads to a small but consistent restriction in fast structural fluctuations of bases located outside of the binding region. By considering our experimental results in the context of both molecular simulation and coarse-grained statistical mechanics models, we show that the experimental measurements are in agreement with accepted models of allostery without conformational change.4,32
Experimental
DNA
DNA oligomer 5′-GCATATATCC-3′ and its complementary sequence (ODN1) were purchased as salt free, lyophilised solids from Eurogentec. All other chemicals were purchased from Sigma-Aldrich and used without further purification. In all cases, the dsDNA concentration was 10 mM in a deuterated Tris buffer (100 mM Tris, 100 mM NaCl, pD 7.0). Solutions containing H33258 were prepared by annealing the dsDNA with the ligand in equimolar ratio. The high affinities shown by H33258 for this sequence means that there is no appreciable amount of free DNA.36 It is noted that, at the concentrations studied there is no contribution from the ligand to the spectra reported.IR absorption spectroscopy
Measurements of dsDNA melting were performed on a Nicolet iS10 Spectrometer (Thermo Fisher Scientific) at a frequency resolution of 4 cm−1. The sample temperature was adjusted by a temperature-controlled liquid cell with resistive heating accurate to ±1 °C. For all infrared spectroscopy experiments, including T-jump measurements, the sample was held between two, 2 mm thick CaF2 windows separated by a 6 μm thick spacer.T-jump spectroscopy
The T-jump pump, mid-IR probe spectrometer used for DNA melting experiments has been described previously along with T-jump calibration methods and identical procedures were followed.27,37 T-jump excitation pulses were produced at a repetition rate of 1 kHz using a home-built Nd:YAG-pumped optical parametric oscillator (OPO). The ∼4 ns-duration pulses produced had a maximum energy of 70 μJ at 2660 cm−1, resonant with the high frequency wing of the OD stretching vibration of D2O, enabling a T-jump of ∼9 °C while avoiding complete absorption of the pump radiation by the solvent. The T-jump pulse train was optically chopped to give a repetition rate of 0.5 kHz. Mid-IR probe pulses were generated by an amplified Ti:sapphire laser system pumping an optical parametric amplifier equipped with difference frequency mixing of the signal and idler outputs. The pulse duration and center frequency of the mid-IR pulses were 50 fs and 1630 cm−1 respectively; the latter was coincident with the characteristic base vibrational modes of dsDNA. The difference between the 10 kHz repetition rate of the Ti:sapphire laser and the 0.5 kHz repetition rate of the T-jump pump pulses, combined with the use of an electronic delay to control the relative pulse timings of the pump and probe laser systems, enabled collection of T-jump pump-IR probe spectra at time delays (τpp) from 1 ns to 2 ms.37Results and discussion
Previous studies have determined a Tm value for ODN1 of 60 °C, while addition of the H33258 ligand causes Tm to rise by 15 °C.27 This change in Tm upon ligand binding means that the spectral effects of strand melting will be observed at different temperatures for the two samples. This also means that, for T-jump measurements producing a ∼9 °C increase in temperature, experiments with the same value of T0 will capture different extents of melting for ODN1 and ODN1·H33258. It is important that this is allowed for in any subsequent analysis and so we present data as a function of T0 − Tm, where T0 indicates the starting temperature of the sample for a T-jump measurement (i.e. prior to the T-jump pulse) or the steady state temperature of the spectral measurement in IR absorption spectroscopy respectively.IR absorption spectroscopy
Infrared absorption spectra of ODN1 and ODN1·H33258 samples as a function of T0 − Tm (Fig. 1(a) and Fig. S2, ESI†) show clear changes in both the intensity and position of the absorption bands. The spectra and their response to increases in temperature have been widely studied, identifying the effects of strand separation at elevated temperature.38Fig. 1(b) reports the results as difference spectra relative to T0 − Tm = −25 °C and we focus on the behavior of the modes near 1575 and 1622 cm−1 (gold and purple boxes in Fig. 1 and Fig. S1, ESI†), both undergoing increases in amplitude as the temperature rises. The 1575 cm−1 band is assignable to a ring vibration mode of guanine, while the 1622 cm−1 band arises from a similar mode of adenine.38,39 The increase in amplitude of the bands is caused by the loss of base stacking during melting or disruption of the double helix structure, meaning that these two bands provide base specific markers of structural changes for GC (1575 cm−1) and AT (1622 cm−1) base pairs respectively.38 Use of a narrow spectral window for analysis also allows separation of the rising AT-band (Fig. 1(a) purple box) from the impact of broadening of the large 1660 cm−1 band, containing multiple contributions, which occurs with increased temperature, which can be seen in the difference spectra (Fig. 1(b), purple/blue). The behavior of the AT and GC marker modes is consistent with the reported melting temperatures of ODN1 and ODN1·H33258, displaying sigmoidal temperature dependence with mid-points at T0 − Tm = 0 °C in both cases (Fig. 1(c), and Fig. S2, ESI†).T-jump IR spectroscopy – direct comparisons with equilibrium data
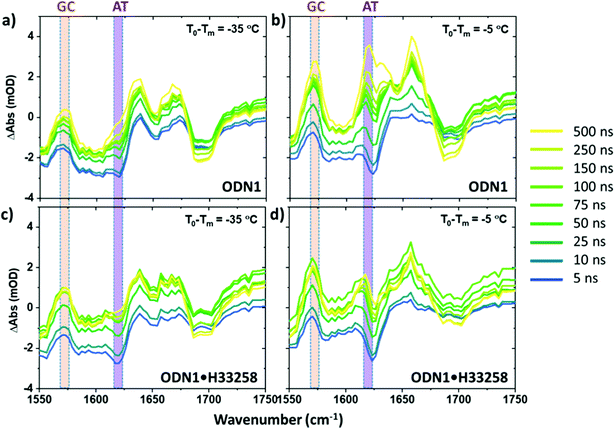
Fast T-jump IR spectra of ODN1 (Fig. 1(d) and 2) and ODN1·H33258 (Fig. S2 and S3, ESI†) have been reported previously.27 The data obtained for ODN1 at T0 − Tm = −5 °C (Fig. 1(d)) showed clear increases in IR absorbance at the wavenumber positions of the GC and AT marker modes following the T-jump pulse, peaking at time delays between 10 and 50 μs (Fig. 1(d), green), which closely mirror those observed in the IR absorption difference spectra (Fig. 1(b)). These were assigned previously to the effects of strand melting and have been shown to follow stretched-exponential rising dynamics with timescales of 20–30 μs.27 Similar spectra were obtained for ODN1·H33258 (Fig. S2, ESI†) where it was observed that the melting dynamics were slowed down by up to two orders of magnitude, in agreement with other recent studies.28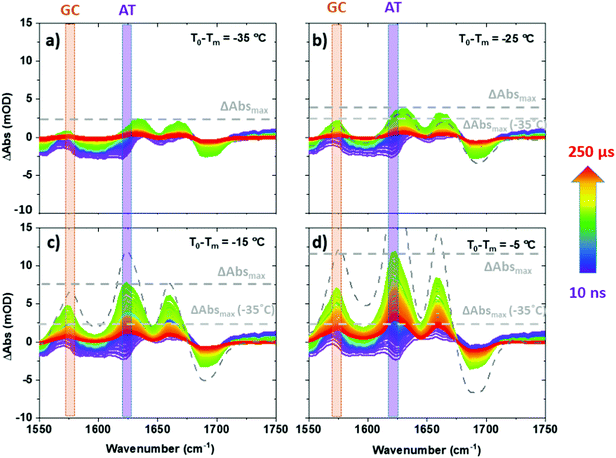 | ||
| Fig. 2 T-jump IR spectra of ODN1 obtained as a function of T-jump-probe delay time from 10 ns to 250 μs. Spectra were obtained at initial temperatures (T0 − Tm) of (a) −35 °C, (b) −25 °C, (c) −15 °C and (d) −5 °C. Equilibrium difference IR absorption data at corresponding temperatures from Fig. 1(b) are shown using grey dashed lines. | ||
In this article, we extend previous reports of the melting dynamics of DNA·ligand complexes by using equilibrium, or steady state IR absorption spectra (Fig. 1 and Fig. S2, ESI†) as a quantitative benchmark for the changes in absorbance obtained from non-equilibrium T-jump IR measurements (Fig. 2 and Fig. S3, ESI†). We begin with a detailed discussion of the approach with reference to dsDNA (ODN1) before applying it to understand the dynamic impact of ligand binding.
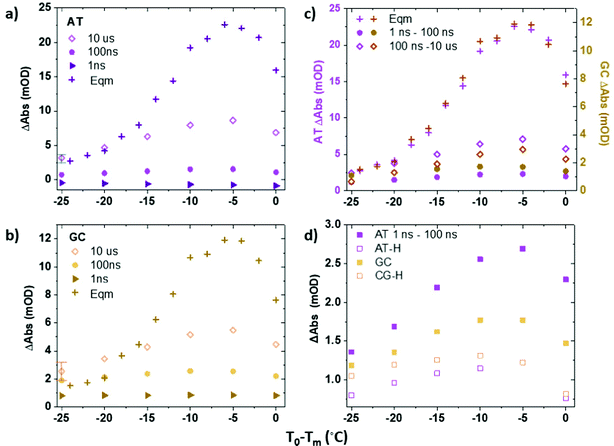
Examining T-jump IR spectra obtained as a function of T0 for ODN1 shows that the magnitude of the maximum change in absorbance of the AT and GC marker modes varies strongly with T0. For example, the maximum change in absorbance observed for the AT marker mode of ODN1 (ΔAbsmax, Fig. 2) increases from ∼2 mOD when T0 − Tm = −35 °C (Fig. 2(a)) to ∼12 mOD when T0 − Tm = −5 °C (Fig. 2(d)); note for the T0 − Tm = −5 °C measurement the T-jump pulse provides a sufficient increase to raise the temperature above the DNA melting temperature.
Subtracting equilibrium IR absorption spectra at a temperature, T0, from that obtained at T0 + 10 °C (equivalent to the T-jump achieved by the non-equilibrium experiment27,37) provides a measurement of the change in absorbance of each marker mode of the dsDNA sample that occurs if the sample is allowed to re-equilibrate at the higher temperature. As all steady state and T-jump IR data were recorded under the same sample conditions (path length and concentration), this is equal to the maximum absorbance change that could be measured in the non-equilibrium experiment. The ability to perform such a comparison arises from the fact that both the equilibrium and non-equilibrium experiments measure changes in DNA absorbance.
Fig. 3(a and b) plot the change in absorbance of the two marker modes (AT, Fig. 3(a); GC, Fig. 3(b)) obtained via IR absorption (Fig. 3(a and b), crosses) and T-jump IR spectra (Fig. 3(a and b), diamonds) as a function of T0 − Tm. A T-jump-probe delay time of 10 μs, close to the peak intensity of the signals in the non-equilibrium experiment, was used for consistency. The relative change of the peaks in the T-jump IR experiment (Fig. 3(a and b), diamonds) follow the same trend with T0 − Tm as the equilibrium absorbance changes (crosses), peaking at T0 − Tm = −5 °C. The result being consistent with the previous assignment of changes in absorbance on 10 μs timescales to the melting of the dsDNA in response to the T-jump. The change in absorbance increases in size as Tm is approached as would be expected from the rate of change of the sigmoidal function which describes dsDNA melting (Fig. 1(c)).
Although the changes in absorbance of the T-jump IR spectra at 10 μs and the steady state IR absorption measurements have the same dependence on T0 − Tm, the two signals are not of equal magnitude. The discrepancy is due to the competing effects of DNA melting and cooling occurring in the T-jump measurement, which occur on similar timescales.27,37 For example; at T0 − Tm = −5 °C, the non-equilibrium T-jump measurement captures around 40% of the full change in absorbance observed in both AT and GC marker modes when measured under equilibrium conditions at this temperature (Fig. 3(a and b)). If the rise in temperature brought about by the T-jump was sustained for a longer period and homogeneous across the cell, the absolute size of the melting signal would be expected to increase, however this is not the case here because, as stated, the timescales of melting and recovery have been shown to be comparable.21,22,27 This reduction in observed spectral change in the T-jump measurement also explains why the magnitude of the maximum T-jump IR signals obtained for ODN1·H33258 (Fig. S3, ESI†), although the same spectral shape as those of ODN1, are much smaller. The delayed melting caused by binding of the ligand moves more of the increase in absorbance due to strand melting outside of the accessible temporal window of the non-equilibrium T-jump experiment.27
We note that for large negative values of T0 − Tm (Fig. 3(a and b)), when T0 is far from the melting temperature, the magnitude of the 10 μs T-jump signal (diamonds) is significantly reduced, correlating with the lesser degree of melting induced by the temperature jump of ∼10 °C. At temperatures where T0 − Tm = −25 °C the magnitude of the 10 μs T-jump signal is, within error, equal to that expected from the equilibrium measurements (Fig. 3(a and b)). Furthermore, examination of the T-jump spectra far from Tm (Fig. 2(a and b)) shows that, although the band pattern observed is similar to that near Tm, the responses of the AT and GC marker modes are significantly smaller. This is because the spectral signature of strand melting becomes less dominant and we conclude the spectral pattern that arises at lower T0 − Tm is not from melting but from the impact that the temperature increase has on the DNA modes. These signatures are present at early T-jump-probe delay times and we term these fast pre-melting fluctuations.
Fast pre-melting fluctuations
Having identified the spectral contributions due to melting in the T-jump data, we now turn to scrutinize the temperature dependence of the dynamics of ODN1 at much earlier T-jump-probe delay times. On these timescales, any contribution from duplex melting, which occurs on tens of microsecond timescales, is absent from the spectra (Fig. 4(a and b)). Despite this lack of melting, T-jump spectra of ODN1 obtained at pump–probe time delays below 10 ns (Fig. 4(a and b), blue) contain changes. These arise from what is effectively an instantaneous response of the vibrational modes of DNA to the rapid heating of the solvent caused by T-jump pulse. The origin is likely to relate to rapid changes in solvation of the DNA as the water temperature increases. The spectral pattern contained in these datasets is remarkably constant in terms of both amplitude and position of the peaks as T0 varies, although it has been shown to vary slightly with T0 − Tm in accordance with the concentration ratio of single-stranded to double stranded DNA present in the sample at a given T0. The latter is simply a consequence of differences in the spectra of ss and dsDNA and has been discussed elsewhere.27As the T-jump-probe time delay increases towards 100 ns (Fig. 4(a and b), green), the spectra undergo changes in amplitude at the positions of the marker bands for AT and GC base pairs. The GC mode shows an instantaneous increase in amplitude relative to the baseline but then continues to increase in amplitude, relative to the baseline, towards 100 ns and beyond. In the case of the AT marker mode, the initial impact of the temperature jump is to decrease absorbance at this frequency before the signal rises during the first 100 ns following the T-jump. The rising feature is visible as a growing shoulder in Fig. 4(a) and is somewhat more prominent in Fig. 4(b), which was obtained at higher T0 (vide infra). The change in the AT marker band amplitude is further exemplified by a time trace of the AT band intensity in Fig. S4 (ESI†). The increase in amplitude of the GC and AT marker bands on fast timescales implies that changes that have the same spectral impact as melting, namely reduction in base stacking leading to increases in amplitude of the GC and AT marker modes, are occurring within 100 ns of the T-jump, but it is important to re-iterate that the DNA has not melted on these timescales. These observations are consistent with previous reports.27
To analyze these fast dynamics in more detail, we quantify the magnitude of the changes in absorbance due to fast motion as a function of T0via the magnitude of the GC and AT marker modes at T-jump-probe time delays of 1 ns (Fig. 3(a and b), triangles) and 100 ns (circles). In each case, the effect of the changing baseline, which arises from thermal effects in the solvent and is of comparable magnitude to the peak heights in some regions of the spectrum, has been accounted for. In the case of both the GC and AT modes, the rise in signal by 100 ns relative to the baseline is on the order of 1–2 mOD. It is important to note that, although small, this is larger than would be expected if it were a contribution from the rising melting signal, which arrives some two orders of magnitude later in time. The changes in intensity of the bands across the time window from 1 ns to 50 μs are consistent with the fact that fitting the time-dependence of the melting signal requires bi-exponential functions and include a term with dynamics occurring on 100 ns timescales.21,22,27
These fast (100 ns) dynamics have been assigned to end fraying processes,21,22,27 though it is hard to be definitive, because the origin of the signals is the same spectroscopic signature as is assigned to melting (Fig. 2, 4 and Fig. S3, ESI†), namely an increase in band intensity, which is generally assigned to a disruption of base stacking.35,40 The fact that both the central AT bases of ODN1, as well as the terminal GC bases have similar 100 ns dynamics indicates that the rise in absorbance must be assigned to fast structural dynamics occurring both at the ends and in the center of the strand. Thus, the similarities suggest that they relate to perturbations of the whole double helix that impact on base stacking.
Further insight can be obtained by comparing the magnitude of the 100 ns component of the T-jump data to equilibrium IR measurements. In principle, the IR absorption change for a given increase in temperature obtained at equilibrium is equal to the maximum rise in absorbance obtained following the T-jump. As discussed above, this is not the case here because the full extent of the melting signal is not accessible, however the cooling of the sample post-T-jump over the first 100 ns in this experiment is less than 20% and so the amplitude measured at 100 ns is not appreciably affected by this cooling.27,37 Moreover, comparing the 100 ns change in absorbance from the T-jump experiment directly to the steady state IR absorption measurement provides a more robust form of analysis by removing any systematic errors caused by referencing to the T0-dependent non-equilibrium signal. As we have shown above, the maximum size of the T-jump signal is strongly influenced by melting and changes significantly with T0 and so provides a potentially unreliable benchmark for fast dynamics. The ability to compare T-jump and IR absorption data in this way arises from the fact that both the equilibrium and non-equilibrium experiments measure the same absolute changes in DNA absorbance.
Fig. 3(c) shows a comparison of the rises in the AT and GC signals over two time-windows, from 1–100 ns and 100 ns–10 μs. Inspection of Fig. 3(c) shows that the magnitude of the rise in absorbance over the first 100 ns following the T-jump is only weakly dependent upon T0 − Tm. Although in the case of both the AT and the GC bands there is an increase as T0 nears Tm, the increase is significantly less than what is observed in the 100 ns–10 μs melting signal. This is also visible by comparing Fig. 4(a and b), where the response of the two marker modes on 100 ns timescales is larger at T0 − Tm = −5 °C than at −35 °C, but still within the few mOD range, whereas melting induces a change of >20 mOD.
This finding shows once again that the changes in the IR absorbance of both GC and AT marker bands under equilibrium conditions is dominated near the melting temperature by changes caused by melting. At more negative values of T0 − Tm the contribution due to melting falls significantly but the 1–100 ns signal stays largely constant in terms of absolute size. When T0 − Tm = −25 °C the rise in signal between 1–100 ns accounts for 70% of the equilibrium change in absorbance of the AT marker mode and 60% of that of the GC mode (Fig. 3(c)). When T0 − Tm = −5 °C this falls to 16 and 10% respectively, despite the fact that the absolute magnitude of the 1–100 ns rise has increased slightly from ∼1 to ∼2 mOD (Fig. 3(c)). Crucially, this shows that 100 ns fluctuations of the DNA structure are present even in the absence of any later melting behavior.
The conclusion that the rise in absorbance due to 100 ns timescale dynamics is only weakly dependent upon T0 − Tm is an important result. Our data shows that the impact of temperature on the magnitude of the signal due to fast (100 ns) structural fluctuations is small and that it comprises an absolute contribution to the change in absorbance as Tm is approached, irrespective of whether the measurement is performed under equilibrium or non-equilibrium conditions. Given that the magnitude of the changes in absorbance measured are in the few mOD range, while the melting of the full dsDNA molecule (as opposed to the signal change in a 10 °C step) leads to a change of ∼20 and 40 mOD for GC and AT modes respectively (Fig. 1(a–c)), it must be concluded that a small fraction of bases within the ensemble are perturbed at a given time. This is consistent with a model proposed by molecular dynamics simulations in which rapid transient perturbations of the duplex structure on significantly faster timescales than melting will cycle from non-perturbed to perturbed and back many times before a melting event occurs.41 Based on the change in absorbance that we have measured here, the average is clearly a situation with a small amount of perturbation. The observation of a relative lack of T0 dependence is also consistent with reports of barrierless end fraying in very short sequences and a clear separation between fast structural dynamics and melting.21
It is also instructive to compare the relative magnitudes of the 1–100 ns rise in absorbance for the AT and GC modes (Fig. 3 and 4). Although there are fewer GC base pairs than AT in the ODN1 sequence and the overall change in the GC mode amplitude upon full melting is smaller than that of the AT mode (Fig. 1), in both equilibrium and non-equilibrium measurements, the 1–100 ns rise in absorbance in the T-jump IR data is consistently proportionately larger for GC than for the AT band (Fig. 3(c)). This suggests that fast perturbations of the GC base pairs are occurring to a greater extent, i.e. that they involve a greater proportion of the available GC base pairs, than for AT base pairs. This is perhaps to be expected, given that the GC base pairs appear at the ends of the ODN1 sequence and the AT base pairs in the center, indicating greater perturbation at the ends of the strand. This result is consistent with some contribution from end fraying to the general assignment of fast perturbation discussed above. This result also suggests that bubble formation in the AT-rich region of these short strands is not significant.
Quantifying the impact of ligand binding on fast dynamics
Having discussed the fast dynamics observed for the ODN1 sample in comparison with equilibrium IR measurements, we compare those for DNA with those for DNA·H33258 complex. It was described above that the microsecond changes in absorbance due to melting are suppressed in the ODN1·H33258 T-jump spectra, due to the change in melting timescales. However, a direct comparison of the behavior on 100 ns timescales is well within the reach of the T-jump experiments performed here. Indeed, it has been shown by separate studies that the faster pre-melting dynamics are slightly accelerated when dsDNA is bound to H33258.27,28 The comparison of the magnitudes of the 1–100 ns rising signal for AT and GC modes for ODN1 and ODN1·H33258 samples are shown in Fig. 3(d) and the relevant spectral data is shown in Fig. 4(c and d). The impact of the ligand is most striking for the AT band, which shows a significant reduction (∼60% at T0 − Tm = −5 °C, Fig. 3(d)) in the amplitude of the 100 ns signal upon ligand binding (cf.Fig. 4(a and b) with Fig. 4(c and d)). Indeed, its contribution to the T-jump spectrum becomes hard to resolve. This is consistent with previous studies showing a suppression of these dynamics by ligand binding and indicates that the ligand has a strong effect on bases directly in the binding region as would be expected.27 Once again, it is important to stress that any spectrally observed effect of H33258 binding is too large to be attributable to the slowing down in melting that has been reported for ODN1·H33258 complexes.The 100 ns rise of the GC marker band in the ODN1·H33258 complex, which relates to any allosteric effect of the ligand, also shows a reduction in amplitude (Fig. 3(d) and 4(c, d)). However, the effect is much smaller than that observed for the AT band (∼35% at T0 − Tm = −5 °C, Fig. 4(d)). A more detailed comparison of GC band behavior between 5 and 100 ns is shown in Fig. S5 and S6 (ESI†) alongside a comparison of the melting curves for the ODN1 and ODN1·H33258 sequences. In particular the latter shows that the slight flattening of the melting curve for ODN1·H33258 relative to ODN1 should make these samples more responsive to the temperature jump when T0 is far from Tm, whereas the reverse is observed. Repeated measurements showed that the signal is small and approaches the uncertainty of the experiment, but the suppression is observed consistently and in more than one DNA sequence.27 Based on this, we conclude that there is likely to be a small reduction in the magnitude of these fast perturbations of the DNA structure when bound to H33258, but that the impact is small outside of the binding region of the ligand.
A fluctuation-transmission interpretation of DNA allostery
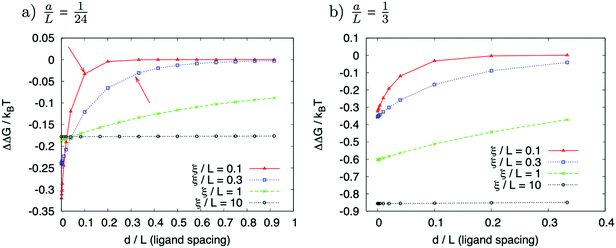
The allosteric effects of ligand binding (see e.g.Fig. 4 and 3(c) comparing the relative 100 ns perturbations of AT and GC marker bands) are consistent with both molecular simulation and coarse-grained statistical mechanics models of allostery without conformational change. Under this mechanism by which local binding on DNA affects the amplitude of structural fluctuations distant from the binding site, the non-locality is generated via thermally activated normal modes of the biopolymer.1,5,42 A similar mechanism has been identified for proteins.1,5If the decrease in the change of absorbance (ΔAbs) on ligand binding, between the AT and CG pairs, is taken to be due to a finite propagation length of allosteric binding along DNA (consistent with modelling, as below), then this length, ξ, can be estimated from the data assuming
| ΔAbs(x) = ΔAbs(0)e−|x|/ξ | (1) |
The simplest structure of a coarse-grained Hamiltonian consistent with down-chain allostery contains both local elasticity (first term in eqn (2)) as well as stiffness (second term in eqn (2)):1
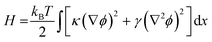 | (2) |
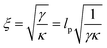 | (3) |
A slightly more sophisticated model of DNA allostery recognized that the helical structure induces the dynamical mode of groove-width breathing, as well as down-chain bending and stretching.33 So two fields of displacement should be present in a model at the level of (2), but which additionally respects this new, internal mode.
Fig. 5 represents an elastic network model (discrete) representation of such a model, in which the two strands support down-chain elasticity k, and inter-strand elasticity λ. This may be transformed into a continuous model of the type of (2), now interpreted in terms of two fields, f(x) the inter-strand separation, and g(x) the mean strand displacement:33
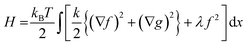 | (4) |
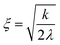 | (5) |
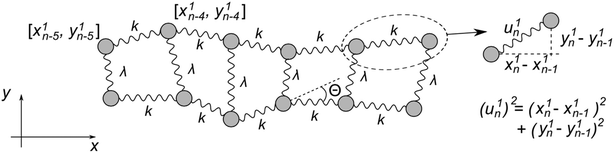 | ||
| Fig. 5 Discrete version of an ENM model for DNA that contains groove-breathing as well as down-chain stretching. | ||
Finally, these experimental observations and coarse-grained models are also consistent with atomistic simulations of allosteric correlations of structural fluctuations in DNA.34 This work carefully investigated the form of allosteric interaction of binders at varying separations on simulations of duplex DNA of up to 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, and recorded the correlation of dynamics as a function of separation, which is itself the cause of fluctuation-allostery. Rather than the monotonic correlation function of the coarse-grained models discussed above, they found, in detail, a damped-oscillatory form, but an exponential-decay length of propagation of allosteric interaction of comparable magnitude to the value of 5 b.p. derived from this work (the reported value of ref. 34 was ∼10 b.p.), especially when compared to the much longer persistence length.
000 atoms, and recorded the correlation of dynamics as a function of separation, which is itself the cause of fluctuation-allostery. Rather than the monotonic correlation function of the coarse-grained models discussed above, they found, in detail, a damped-oscillatory form, but an exponential-decay length of propagation of allosteric interaction of comparable magnitude to the value of 5 b.p. derived from this work (the reported value of ref. 34 was ∼10 b.p.), especially when compared to the much longer persistence length.
Taken together, the results of the analysis of experimental data alongside the outcomes of a range of different computational methods point to ligand-induced suppression of dynamic motion of the double helix being a viable mechanism for allosteric communication. The examination of T-jump IR measurements in the context of steady state IR absorption data, provides a means to separate melting dynamics from faster thermally-activated motions as well as providing base specific insight. This combination could therefore provide a useful means for testing these results and theories further, such as, for example probing the base specific dynamics in systems featuring two cooperatively bound ligands.
Conclusions
Overall, the comparison of non-equilibrium measurements with steady state IR absorption data shows that the fast pre-melting fluctuations of dsDNA are small but somewhat more prevalent at the ends of the sequence. The major impact of the ligand is felt in the binding region with bases outside of this region showing moderately suppressed dynamic behavior on 100 ns timescales.The findings reported here are consistent with our previous measurements,27 with results from NMR experiments4 and from MD simulations,4,32 where it was concluded that rigidification of the DNA structure caused by ligand binding extends outside of the binding region and provides a means of allosteric communication that, in another example of the same effect, promotes cooperative binding of a second H33258 molecule nearby.4,32 Our experimental results are also consistent with the findings of a number of coarse-grained and atomistic models of allosteric propagation in DNA.33,34,44
The conclusions drawn from this work contrast with recent reports of a strong destabilization of GC bases adjacent to the site of H33258 binding to a similar dsDNA sequence.28 It is therefore important to consider the benefits of comparing T-jump spectroscopy to equilibrium data as we do here. For example, we have demonstrated that measuring non-equilibrium, time resolved measurements at a range of T0 values leads to significant changes in the nature of the data obtained. For example, when T0 − Tm is small and negative (i.e. close to Tm) the spectral changes on 10 μs timescales due to melting are significantly larger than those on 100 ns timescales, which we termed fast pre-melting fluctuations. In contrast, when T0 − Tm is large and negative (i.e. far below Tm) the melting signal reduces in magnitude dramatically, while the signal from fast dynamics remains largely constant. As can be seen in Fig. 3(c), at T0 − Tm = −25 °C, the change in absorbance of the GC and AT marker modes in the T-jump experiment is comprised nearly entirely of the 100 ns contribution. In other words, the peak T-jump signal is almost present by 100 ns. Crucially, this does not indicate an increase in pre-melting perturbation, because, as we show here, the absolute magnitude of the 100 ns signal is almost the same as it is near to Tm, so the fraction of DNA bases involved in the pre-melting fluctuations must also be similar. Rather, the fact that the signal changes induced by melting at this temperature are small compared to the changes observed at early T-jump-probe times, mean that the fast dynamics dominate. This means that any analysis of DNA melting that compares magnitudes of fast perturbations needs to be carried out in a way that is independent of the size of the melting signal, either by maintaining a constant T0 − Tm if full melting is reached, or by comparing absolute magnitudes. This is a particularly problematic issue when considering ligand binding because the ligand increases the stability of the DNA duplex. Comparing measurements obtained at the same T0 will lead to a reduced signal due to melting being observed in the more thermally-stable sample (the DNA·ligand complex) and we show that this could lead to the appearance of an increase in pre-melting dynamics upon ligand binding, but not an actual increase.28 Using quantitative comparisons of T-jump IR with equilibrium spectroscopy data however, we have shown that the pre-melting perturbations of ODN1·H33258 are small, nearly temperature independent and suppressed in the binding region. In the case of base pairs adjacent to the binding region the impact is small but favors moderate suppression of the extent of the perturbation, albeit with a slight acceleration of the rate, consistent with existing models of allosteric communication.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Funding from STFC is gratefully acknowledged for programme access to the Central Laser Facility ULTRA spectrometer. RF gratefully acknowledges studentship support from the University of Strathclyde.References
- T. C. B. McLeish, T. L. Rodgers and M. R. Wilson, Allostery without conformation change: Modelling protein dynamics at multiple scales, Phys. Biol., 2013, 10(5), 056004 CrossRef CAS PubMed.
- A. Cooper and D. T. F. Dryden, Allostery without conformational change – a plausible model, Eur. Biophys. J. Biophys. Lett., 1984, 11(2), 103–109 CrossRef CAS PubMed.
- J. Monod, J. Wyman and J. P. Changeux, On nature of allosteric transitions – a plausible model, J. Mol. Biol., 1965, 12(1), 88–118 CrossRef CAS PubMed.
- S. A. Harris, E. Gavathiotis, M. S. Searle, M. Orozco and C. A. Laughton, Cooperativity in drug–DNA recognition: A molecular dynamics study, J. Am. Chem. Soc., 2001, 123(50), 12658–12663 CrossRef CAS PubMed.
- S. J. Wodak, E. Paci, N. V. Dokholyan, I. N. Berezovsky, A. Horovitz, J. Li, V. J. Hilser, I. Behar, J. Karanicolas, G. Stock, P. Hamm, R. H. Stote, J. Eberhardt, Y. Chebaro, A. Dejaegere, M. Cecchini, J. P. Changeux, P. G. Bolhuis, J. Vreede, P. Faccioli, S. Orioli, R. Ravasio, L. Yen, C. Brito, M. Wyart, P. Gkeka, I. Rivalta, G. Palermo, J. A. McCammon, J. Panecka-Hofman, R. C. Wade, A. Di Pizio, M. Y. Niv, R. Nussinov, C. J. Tsai, H. Jang, D. Padhorny, D. Kozakov and T. McLeish, Allostery in its many disguises: From theory to applications, Structure, 2019, 27(4), 566–578 CrossRef CAS PubMed.
- K. Aman, G. Padroni, J. A. Parkinson, T. Welte and G. A. Burley, Structural and kinetic profiling of allosteric modulation of duplex DNA induced by DNA-binding polyamide analogues, Chem. – Eur. J., 2019, 25(11), 2757–2763 CrossRef CAS PubMed.
- G. Padroni, J. A. Parkinson, K. R. Fox and G. A. Burley, Structural basis of DNA duplex distortion induced by thiazole-containing hairpin polyamides, Nucleic Acids Res., 2018, 46(1), 42–53 CrossRef CAS PubMed.
- N. G. Nickols, J. O. Szablowski, A. E. Hargrove, B. C. Li, J. A. Raskatov and P. B. Dervan, Activity of a Py-Im polyamide targeted to the estrogen response element, Mol. Cancer Ther., 2013, 12(5), 675–684 CrossRef CAS PubMed.
- D. M. Chenoweth and P. B. Dervan, Structural basis for cyclic Py-Im polyamide allosteric inhibition of nuclear receptor binding, J. Am. Chem. Soc., 2010, 132(41), 14521–14529 CrossRef CAS PubMed.
- E. H. Yao, N. Fukuda, T. Ueno, H. Matsuda, K. Matsumoto, H. Nagase, Y. Matsumoto, A. Takasaka, K. Serie, H. Sugiyama and T. Sawamura, Novel gene silencer pyrrole-imidazole polyamide targeting lectin-like oxidized low-density lipoprotein receptor-1 attenuates restenosis of the artery after injury, Hypertension, 2008, 52(1), 86–92 CrossRef CAS PubMed.
- C. F. Hsu and P. B. Dervan, Quantitating the concentration of Py-Im polyamide-fluorescein conjugates in live cells, Bioorg. Med. Chem. Lett., 2008, 18(22), 5851–5855 CrossRef CAS PubMed.
- N. G. Nickols, C. S. Jacobs, M. E. Farkas and P. B. Dervan, Modulating hypoxia-inducible transcription by disrupting the HIF-1-DNA interface, ACS Chem. Biol., 2007, 2(8), 561–571 CrossRef CAS PubMed.
- N. G. Nickols and P. B. Dervan, Suppression of androgen receptor-mediated gene expression by a sequence-specific DNA-binding polyamide, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(25), 10418–10423 CrossRef CAS PubMed.
- Y. Kageyama, H. Sugiyama, H. Ayame, A. Iwai, Y. Fujii, L. E. Huang, S. Kizaka-Kondoh, M. Hiraoka and K. Kihara, Suppression of VEGF transcription in renal cell carcinoma cells by pyrrole-imidazole hairpin polyamides targeting the hypoxia responsive element, Acta Oncol., 2006, 45(3), 317–324 CrossRef CAS PubMed.
- N. Fukuda, T. Ueno, Y. Tahira, H. Ayame, W. Zhang, T. Bando, H. Sugiyama, S. Saito, K. Matsumoto, H. Mugishima and K. Serie, Development of gene silencing pyrrole-imidazole polyamide targeting the TGF-beta 1 promoter for treatment of progressive renal diseases, J. Am. Soc. Nephrol., 2006, 17(2), 422–432 CrossRef PubMed.
- B. Z. Olenyuk, G. J. Zhang, J. M. Klco, N. G. Nickols, W. G. Kaelin and P. B. Dervan, Inhibition of vascular endothelial growth factor with a sequence-specific hypoxia response element antagonist, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(48), 16768–16773 CrossRef CAS PubMed.
- P. B. Dervan and B. S. Edelson, Recognition of the DNA minor groove by pyrrole-imidazole polyamides, Curr. Opin. Struct. Biol., 2003, 13(3), 284–299 CrossRef CAS PubMed.
- J. M. Gottesfeld, C. Melander, R. K. Suto, H. Raviol, K. Luger and P. B. Dervan, Sequence-specific recognition of DNA in the nucleosome by pyrrole-imidazole polyamides, J. Mol. Biol., 2001, 309(3), 615–629 CrossRef CAS PubMed.
- B. Buchli, S. A. Waldauer, R. Walser, M. L. Donten, R. Pfister, N. Blochliger, S. Steiner, A. Caflisch, O. Zerbe and P. Hamm, Kinetic response of a photoperturbed allosteric protein, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(29), 11725–11730 CrossRef CAS PubMed.
- J. M. Schmidt-Engler, L. Blankenburg, R. Zangl, J. Hoffmann, N. Morgner and J. Bredenbeck, Local dynamics of the photo-switchable protein PYP in ground and signalling state probed by 2D-IR spectroscopy of –SCN labels, Phys. Chem. Chem. Phys., 2020, 22(40), 22963–22972 RSC.
- P. J. Sanstead and A. Tokmakoff, Direct observation of activated kinetics and downhill dynamics in DNA dehybridization, J. Phys. Chem. B, 2018, 122(12), 3088–3100 CrossRef CAS PubMed.
- P. J. Sanstead, P. Stevenson and A. Tokmakoff, Sequence-dependent mechanism of DNA oligonucleotide dehybridization resolved through infrared spectroscopy, J. Am. Chem. Soc., 2016, 138(36), 11792–11801 CrossRef CAS PubMed.
- R. Narayanan, L. Zhu, Y. Velmurugu, J. Roca, S. V. Kuznetsov, G. Prehna, L. J. Lapidus and A. Ansari, Exploring the energy landscape of nucleic acid hairpins using laser temperature-jump and microfluidic mixing, J. Am. Chem. Soc., 2012, 134(46), 18952–18963 CrossRef CAS PubMed.
- A. L. Stancik and E. B. Brauns, Rearrangement of partially ordered stacked conformations contributes to the rugged energy landscape of a small RNA hairpin, Biochemistry, 2008, 47(41), 10834–10840 CrossRef CAS PubMed.
- S. V. Kuznetsov, S. Sugimura, P. Vivas, D. M. Crothers and A. Ansari, Direct observation of DNA bending/unbending kinetics in complex with. DNA-bending protein IHF, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(49), 18515–18520 CrossRef CAS PubMed.
- E. B. Brauns and R. B. Dyer, Time-resolved infrared spectroscopy of RNA folding, Biophys. J., 2005, 89(5), 3523–3530 CrossRef CAS PubMed.
- R. Fritzsch, G. M. Greetham, I. P. Clark, L. Minnes, M. Towrie, A. W. Parker and N. T. Hunt, Monitoring base-specific dynamics during melting of DNA ligand complexes using temperature-jump time-resolved infrared spectroscopy, J. Phys. Chem. B, 2019, 123(29), 6188–6199 CrossRef CAS PubMed.
- X.-X. Zhang, S. L. Brantley, S. A. Corcelli and A. Tokmakoff, DNA minor-groove binder Hoechst 33258 destabilizes base-pairing adjacent to its binding site, Commun. Biol., 2020, 3, 525 CrossRef CAS PubMed.
- P. J. Sanstead, B. Ashwood, Q. Dai, C. He and A. Tokmakoff, Oxidized derivatives of 5-methylcytosine alter the stability and dehybridization dynamics of duplex DNA, J. Phys. Chem. B, 2020, 124(7), 1160–1174 CrossRef CAS PubMed.
- B. Ashwood, P. J. Sanstead, Q. Dai, C. He and A. Tokmakoff, 5-Carboxylcytosine and cytosine protonation distinctly alter the stability and dehybridization dynamics of the DNA duplex, J. Phys. Chem. B, 2020, 124(4), 627–640 CrossRef CAS PubMed.
- R. J. Menssen and A. Tokmakoff, Length-dependent melting kinetics of short DNA oligonucleotides using temperature-jump IR spectroscopy, J. Phys. Chem. B, 2019, 123(4), 756–767 CrossRef CAS PubMed.
- B. Fresch and F. Remacle, Atomistic account of structural and dynamical changes induced by small binders in the double helix of a short DNA, Phys. Chem. Chem. Phys., 2014, 16(27), 14070–14082 RSC.
- H. Toncrova, Coarse-grained models of biomolecule dynamics and allostery, PhD thesis, University of Leeds, 2011.
- A. Balaceanu, A. Perez, P. D. Dans and M. Orozco, Allosterism and signal transfer in DNA, Nucleic Acids Res., 2018, 46(15), 7554–7565 CrossRef CAS PubMed.
- G. Hithell, P. M. Donaldson, G. M. Greetham, M. Towrie, A. W. Parker, G. A. Burley and N. T. Hunt, Effect of oligomer length on vibrational coupling and energy relaxation in double-stranded DNA, Chem. Phys., 2018, 512, 154–164 CrossRef CAS.
- F. G. Loontiens, P. Regenfuss, A. Zechel, L. Dumortier and R. M. Clegg, Binding characteristics of Hoechst-33258 with calf thymus DNA, POLY d(A–T), and d(CCGGAATTCCGG) – multiple stoichiometries and determination of tight-binding with a wide spectrum of site affinities, Biochemistry, 1990, 29(38), 9029–9039 CrossRef CAS PubMed.
- G. M. Greetham, I. P. Clark, B. Young, R. Fritsch, L. Minnes, N. T. Hunt and M. Towrie, Time-resolved temperature-jump infrared spectroscopy at a high repetition rate, Appl. Spectrosc., 2020, 74(6), 720–727 CrossRef CAS PubMed.
- M. Banyay, M. Sarkar and A. Graslund, A library of IR bands of nucleic acids in solution, Biophys. Chem., 2003, 104(2), 477–488 CrossRef CAS PubMed.
- C. S. Peng, K. C. Jones and A. Tokmakoff, Anharmonic vibrational modes of nucleic acid bases revealed by 2D IR spectroscopy, J. Am. Chem. Soc., 2011, 133(39), 15650–15660 CrossRef CAS PubMed.
- G. W. Doorley, M. Wojdyla, G. W. Watson, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, Tracking DNA excited states by picosecond-time-resolved infrared spectroscopy: Signature band for a charge-transfer excited state in stacked adenine-thymine systems, J. Phys. Chem. Lett., 2013, 4(16), 2739–2744 CrossRef CAS.
- J. A. Bueren-Calabuig, C. Giraudon, C. M. Galmarini, J. M. Egly and F. Gago, Temperature-induced melting of double-stranded DNA in the absence and presence of covalently bonded antitumour drugs: Insight from molecular dynamics simulations, Nucleic Acids Res., 2011, 39(18), 8248–8257 CrossRef CAS PubMed.
- S. Brinkers, H. R. C. Dietrich, F. H. de Groote, I. T. Young and B. Rieger, The persistence length of double stranded DNA determined using dark field tethered particle motion, J. Chem. Phys., 2009, 130(21), 215105 CrossRef PubMed.
- C. R. Kissinger, B. S. Liu, E. Martinblanco, T. B. Kornberg and C. O. Pabo, Crystal-structure of an engrailed homeodomain-DNA complex at 2.8A resolution – a framework for understanding homeodomain-DNA interactions, Cell, 1990, 63(3), 579–590 CrossRef CAS.
- R. J. Hawkins and T. C. B. McLeish, Coupling of global and local vibrational modes in dynamic allostery of proteins, Biophys. J., 2006, 91(6), 2055–2062 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02233d |
| ‡ Current address: 5 Gwyneth Rd, Oxford OX4 4QH, UK. |
| This journal is © the Owner Societies 2021 |