Screening of transition metal doped copper clusters for CO₂ activation

Abstract

Activation of CO₂ is the first step towards its reduction to more useful chemicals. Here we systematically investigate the CO₂ activation mechanism on Cu₃X (X is a first-row transition metal atom) using density functional theory computations. The CO₂ adsorption energies and the activation mechanisms depend strongly on the selected dopant. The dopant electronegativity, the HOMO–LUMO gap and the overlap of the frontier molecular orbitals control the CO₂ dissociation efficiency. Our calculations reveal that early transition metal-doped (Sc, Ti, V) clusters exhibit a high CO₂ adsorption energy, a low activation barrier for its dissociation, and a facile regeneration of the clusters. Thus, early transition metal-doped copper clusters, particularly Cu₃Sc, may be efficient catalysts for the carbon capture and utilization process.

---

Introduction

Due to the increased carbon dioxide emission from fossil fuel combustion, CO₂ reduction is an urgent problem for our society. The rise of its atmospheric concentration leads to the severe problems of global warming and the decrease of the hydrosphere pH.^1–8 To mitigate these and also solve the inevitable depletion of the fossil fuels, the capture of the CO₂ and its storage or recycling to industrially applicable chemical compounds (e.g. methanol) is a possible solution.^1,7,9–14 Although CO₂ hydrogenation to methanol is thermodynamically feasible, in practice this reaction is hindered by the high kinetic barriers.¹⁵ Thus, a suitable catalyst is necessary to facilitate the reaction. Depending on the energy source, thermal,¹⁶ electrochemical,^17,18 and photochemical^19,20 catalysts are distinguished. It is well known from the seminal work of Hori et al. that copper surfaces catalyse the CO₂ electroreduction to methane and various other small hydrocarbons.¹⁷ Methanol is industrially produced by thermal catalysis from synthesis gas, containing CO, CO₂, and H₂, using a Cu/ZnO/Al₂O₃ catalyst at high pressure (between 10 and 100 bar).²¹

Since the late 1990s, nanocatalysis has also become a very actively researched field.^22,23 In particular, it is well known since the work of Haruta et al., and subsequently from others, that small clusters can exhibit unexpectedly high catalytic activity.^24,25 Specific reactivity at the nanoscale may provide special properties that are not achievable with standard macroscale materials (e.g. huge specific surface area, size dependent electronic structure, etc.).²⁶

Due to their well-defined compositions and precise geometric structures, gas-phase clusters are excellent model systems to investigate the reactions at active sites of complex catalysts.^27–29 With the help of gas-phase model systems it was possible to uncover reaction mechanisms and the role of cluster size,^30,31 geometry,^32,33 dopant atoms,^34,35 and the charge state.^27,36,37

Transition- and noble metal-based catalysts are among the most studied CO₂ reduction catalysts, partly because of their relative stability under reaction conditions and the various synergistic effects that can be achieved by combining different metals. In particular, copper exhibits a promising activity,^38–43 particularly in organic bond-coupling reactions⁴⁴ and the hydrogenation of carbonate to methanol.⁴⁵

Copper is one of the most promising metals for CO₂ reduction. Copper catalysts of various sizes and types are widely used for the hydrogenation of CO₂ to methanol and show exceptional activity and very good methanol selectivity for low temperature CO₂ hydrogenation.^46,47 Various copper surfaces (111, 211) and copper clusters Cu_n (n = 13, 15, 19, 55, 79) have also been studied, of which n = 19 was found to be the most active for CO₂ dissociation.⁴⁸ The mechanism of the metal-mediated reduction of CO₂ to CO was investigated using DFT computations.^49–52

Cationic copper clusters can, depending on their size, facilitate dissociative H₂ adsorption, an important step in CO₂ hydrogenation.^53,54

The catalytic effect of copper nanoparticles and clusters deposited on the ZnO surface is outstanding.⁵⁵ It was shown that the deposited clusters are much more active than the conventional industrial catalysts.⁵⁶ Experiments and density functional theory (DFT) calculations showed that Cu₄ clusters exhibit high activity and a low activation barrier for CO₂ reduction to methanol^57,58 and methane.⁵⁹ Further tuning of the CO₂ reduction activity of various catalysts is in the frontier of interest.

Several studies have investigated the effect of the cluster size and support on the reactivity towards CO₂. Alumina surface deposited copper clusters exhibit non-monotonous size dependent activity (Cu₄/Al₂O₃ > Cu₂₀/Al₂O₃ > Cu₃/Al₂O₃) for the CO₂ reduction to methanol.⁶⁰ Similarly, high methanol synthesis activity was observed for Cu₄ clusters deposited on a Fe₂O₃ surface.⁶¹ It was shown that due to electron transfer from the catalyst to the CO₂ molecule, Cu_x/TiO₂ (x = 1–5) promotes CO₂ activation in all cases compared to the pure TiO₂ system.^62,63 These results highlight the synergistic effects between clusters and their support. According to computational studies graphene-supported Cu₄ clusters are promising for electrocatalysis,⁶⁴ while experiments showed that carbon-supported copper clusters are highly active catalysts for CO₂ reduction.⁶⁵

For small (111)-like facets (Cu₁₃, Cu₅₅) the hydrocarbon production is favourable, while synergetic effect between (100)- and (111)-like facets (Cu₃₈, Cu₇₉) favours CO production.⁶⁶ Cu₃, Cu₅, and Cu₄, Cu₆ exhibit similar CO₂ reduction mechanisms. The rate-determining step is the cleavage of the adsorbed OH in the first case, while it is the proton–electron transfer to the adsorbed CO for the latter one.⁶⁷ The redox behaviour of Cu₅ and Cu₂₀, and the effect of CO₂ also has been investigated.⁶⁸ CO₂ adsorbs more strongly on Cu₅ than on Cu₂₀ and larger nanoparticles, and forms bicarbonate in solution. This explains the high electrochemical CO₂ reduction activity of Cu₅.

The composition dependence of the catalytic activity of doped clusters is less studied. It was shown that chalcogen doping of copper clusters lowers the activation barrier and enhances the selectivity for electrochemical CO₂ reduction to methane.⁶⁹ A combined spectroscopy and computational study of gas-phase Mn_xO_y⁺ (x = 2–5, y ≥ x) showed linear binding of CO₂ and only a small change in the CO₂ electronic structure. Therefore, Mn-oxide does not seem to be a suitable material for CO₂ activation.⁷⁰ Experimental studies showed, that gas-phase Pt, Pd, Cu and Pd–Cu bimetallic hydride cluster anions can catalyse the formation of formate and formic acid from CO₂.^71–74 CO₂ reduction on cationic titanium hydride complexes [LTiH]⁺ (L = cyclopentadyenil, O) showed ligand-dependent CO₂ reduction pathways. These clearly indicate, that the product selectivity can be tuned by the composition.⁷⁵ The study of CO₂ hydrogenation to methanol and formate on Pd₆M (M = Cu, Ni, Pt, Rh) showed that the dopants can reduce the activation barriers, thus enhancing the catalytic activity.⁷⁶ The Ni dopant was found to be especially active. It was observed that doped clusters tend to be more selective toward formate than to CO, thus leading to methanol or methane formation. These clusters were found to be more active than the Cu(111) surface. CO₂ adsorption and dissociation were studied on Ni₄M clusters, with M = Ni, Mo, Sc, or Y. With the exception of the Mo dopant, the Ni₄M clusters promote CO₂ dissociation with the Sc-doped cluster being the most active.⁷⁷ Another DFT study showed that Sc and other early 3d transition metal atoms are promising dopants for CO₂ activation on [MMgO₂]^+/0/− clusters, while in contrast late 3d transition metals are favored for methane activation.⁷⁸ It was found that the atomic d orbitals of the metals atoms play an important role in the CO₂ activation, because the electron transfer takes place from the metal's d orbital to the unoccupied σ orbital of CO₂.⁷⁹ Gas-phase pure platinum clusters exhibited size-dependent CO₂ activation.⁸⁰ CO₂ adsorption on gas-phase Cu_4−xPt_x (x = 0–4) was investigated using DFT calculations. High adsorption energies (from −78 to −158 kJ mol⁻¹) and CO₂ adsorption in a bent mode were found,⁸¹ and could be explained by charge transfer towards the cluster's LUMO.⁸² Based on the reversible structural transformation, the optimal strength of the interaction between the cluster and the adsorbent, and the low CO₂ dissociation barrier, Cu₃Pt is a promising catalyst.⁸¹ It was shown, that Ni- or Pd-doped Cu₄ clusters exhibit higher adsorption energy and promote the CO₂ activation, because the dopant enhances the charge transfer between the cluster and the adsorbent.⁸³ Although none of these clusters decrease the CO₂ dissociation barrier. Zr-doped copper clusters made the CO₂ dissociation also possible and Cu₃Zr was found to be especially active. The HOMO–LUMO gap and the charge of the adsorbed CO₂ molecule were found to be the most important factors to determine the catalytic activity.⁸⁴

While doping has been applied to fine-tune and improve the activity of metal clusters, a systematic investigation of the effect of the different dopants for CO₂ activation is not yet available. The goal of this work is a comprehensive investigation of the effect of the first-row transition metal dopants (X) for the CO₂ activation by small copper clusters. We selected the Cu₃X clusters for this study because it was experimentally shown that Cu₄/Al₂O₃ is effective for CO₂ reduction to methanol⁵⁷ and because computational studies indicated that the Pt-,⁸¹ Ni-,⁸³ and Zr-⁸⁴doped four-atomic copper clusters are effective for CO₂ activation.

Computational methods

Density functional theory computations were carried out using the Q-Chem 5.3 program package.⁸⁵ The structures were preoptimized using the TPSSh/def2-TZVP method,^86,87 while the most stable structures were reoptimized using the TPSSh/def2-TZVP+D3 level of theory. This method was selected after a benchmarking analysis of the effect of the basis set size and the level of correlation (up to CCSD(T)/def2-QZVPPD reference) for the relative energies of different molecules and radicals bound to Cu₄ (see Fig. S1 and S2 and Table S1 in ESI† for details). For each structure a stability analysis was performed to ensure that the SCF procedure converged to a minimum with respect to the molecular orbital coefficients. Subsequently, the harmonic vibrational frequencies were determined to confirm that the minima and transition structures have zero and one imaginary frequencies, respectively. Intrinsic reaction coordinates were computed starting from the transition structures.

We selected seven initial structural isomers (rhombohedral, tetrahedral etc. see the ESI† for details of the most stable isomers) and performed geometry optimizations using possible multiplicities of 1 to 7 and 2 to 8 for clusters with an even and an odd number of electrons, respectively. After the identification of low energy bare metal clusters (up to ∼50 kJ mol⁻¹ above the lowest energy structure), CO₂ adsorption in different binding modes (O–Cu bond, O–X bond, C–Cu bond, C–X bond, ring, etc.) and structures with dissociated CO₂ were systematically investigated to locate the intermediates and products of the CO₂ activation reaction, as described in ref. 88. Subsequently, we explored the full reaction pathways.

Finally, we analysed the electronic structure using the Frontier Molecular Orbitals, Natural Charges,^89,90 Wiberg bond indexes, and the Energy Decomposition Analysis based on the Absolutely Localized Molecular Orbitals (ALMO-EDA).⁹¹

Reaction energies are computed with reference to the lowest energy bare gas phase clusters and the CO₂ molecule. Free energies were computed at a pressure of 1 atm and at various temperatures using the Tamkin library.⁹²

Results

1. Geometry and electronic structure of bare clusters

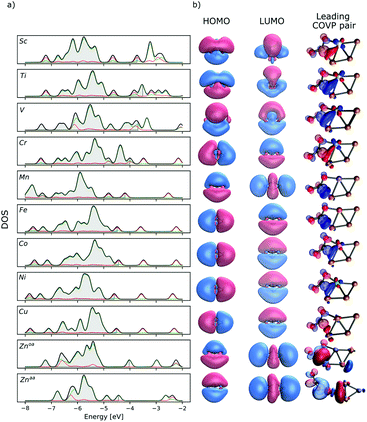
The lowest energy isomers of the Cu₃X clusters (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn) are depicted in Fig. 1. Except for Zn, their total atomization energies (the energy change during the dissociation of the clusters to separated atoms in their most stable spin states) are similar to that of the Cu₄ (see Fig. S7 in the ESI†). As Al₂O₃-deposited Cu₄ clusters were successfully applied to hydrogenate the CO₂ to methanol,⁵⁷ we expect that the doped clusters are also stable synthetic targets.

Fig. 1 Lowest energy structures of the bare Cu₃X clusters, the CO₂ entrance adducts/complexes, the intact CO₂ adducts, and the lowest energy structures of Cu₃X–CO₂. Spin multiplicities of the clusters are indicated in the superscripts. Notations: oa – obtuse apex, aa – acute apex.

The obtained lowest energy structures for Cu₃Sc and Cu₃V are consistent with previous results.^93,94 All lowest energy Cu₃X clusters have planar rhombus shapes. The frontier orbitals of the Cu₃X clusters are consistent with the phenomenological shell model (PSM)^95,96 as each copper atom contributes 1 valence electron, while the transition metal dopants contribute 2 to 4 itinerant electrons, resulting in 1s²p^2–5 electronic structures. Consistently, the LUMOs of most clusters correspond to a p orbital in the PSM (Fig. 2). It is interesting to note that the HOMO and the LUMO indicate a partially filled D shell in the case of manganese doping. This is explained by the hybridization of the shell orbitals with the d atomic orbitals of manganese.⁹⁷ A similar LUMO shape is observed for Cu₃Zn.

Fig. 2 (a) Total (black line) and partial (red and green lines for the s and d atomic orbital contributions, respectively) Density of States (DOS). Shaded areas show the occupied orbitals. For open shell clusters, the majority spin DOS is shown. (b) The frontier orbitals of Cu₃X and the main Complementary occupied-virtual pairs (COVP). In the COVP pairs solid and transparent surfaces indicate the donor and acceptor part of each pair, respectively.

Generally, the dopant atom prefers the high coordination, obtuse apex position. The only exception is the Zn, where the acute apex doped isomer is ∼10 kJ mol⁻¹ more stable. Although in this case the CO₂ dissociation is thermodynamically unfavoured. Because of this and for consistent comparison we only discuss the obtuse apex case. The Wiberg bond-indices (Table 1) show highly dopant-dependent partial covalent bonds between the dopant atom and the adjacent copper atoms. The Cu–X bonds are the strongest in the case of early transition metals (X = Sc, Ti or V) and the weakest in the case of X = Mn and Zn.

Table 1 Natural atomic charges and Wiberg bond-indices in the lowest energy isomers of Cu₃X

X	Charge of X	Charge of Cuoa	Charge of Cuaa	Bond length of Cuoa–X [Å]	Bond length of Cuaa–X [Å]	Wiberg bond index of Cuoa–X	Wiberg bond index of Cuaa–X
a aa and oa refer to acute apex and obtuse apex positions, respectively (Fig. 1).
Sc	0.50	−0.17	−0.16	2.55	2.48	0.82	0.77
Ti	0.39	0.04	−0.22	2.53	2.57	0.42	0.51
V	0.26	0.14	−0.20	2.51	2.57	0.39	0.46
Cr	0.40	0.18	−0.29	2.43	2.58	0.42	0.27
Mn	0.46	0.04	−0.21	2.51	2.53	0.15	0.31
Fe	0.34	0.19	−0.27	2.34	2.45	0.50	0.36
Co	0.28	0.25	−0.26	2.31	2.43	0.47	0.34
Ni	0.29	0.26	−0.28	2.40	2.28	0.48	0.32
Cu	0.27	0.27	−0.27	2.41	2.28	0.45	0.30
Zn^oa,^a	0.42	0.02	−0.22	2.42	2.41	0.14	0.28
Zn^aa,^a	0.22	−0.11	0.00	2.45	4.14	0.19	0.29

---

The variation of the Cu–X bond indices can be explained by the electron donation from copper 3d atomic orbitals to the partially filled valence 3d orbitals of the dopant, which was shown to lead to high coordination scandium-doped copper clusters.⁹⁴ On the other hand, zinc has a fully occupied 3d shell and electron donation is only possible to the less favoured Zn 4p orbitals. This idea is consistent with the small difference between the stabilities of the low-coordinated zinc at the acute apex or the higher coordinated zinc at the obtuse apex position.

The partial atomic charges depend considerably on the dopant atom and at the obtuse apex dopant position they are generally in line with the dopant electronegativities. Thus, not only the electron donation to the unoccupied 3d atomic orbitals of the dopant, but also polarization effects determine the partial atomic charges. This is well reflected in the calculated density of states of the bare clusters (Fig. 2).

The variation of the magnetic moments of Cu₃X follows similar trend to that of the free transition metal atoms: Cr and Mn dopants lead to the largest magnetic moments (see the ESI† for details).

2. CO₂ adsorption and activation mechanism

Possible geometries of the different CO₂ adducts were systematically investigated (lowest energy structures are depicted in Fig. 1; additional structures are available in the ESI†) and the CO₂ dissociation reaction pathways are shown in Fig. 3.

Fig. 3 The reaction pathways for CO₂ activation on Cu₃X. Superscripts indicate the spin multiplicities of the different structures along the reaction paths. Shaded areas indicate the transition states.

We analyse three classes of CO₂ adducts: (i) entrance complexes that can be reached from the Cu₃X and CO₂ reactants without an energy barrier, (ii) intact CO₂ adducts that contain non-dissociated CO₂, and (iii) the lowest energy CO₂ adducts are the thermodynamically most stable among the located Cu₃X–CO₂ isomers.

CO₂ adsorption quenches the magnetic moment of Sc-, Ti- and V-doped clusters and partially also for Mn, thus spin–flip should take place during the CO₂ activation (see the ESI† for the details). However, the spin–orbit coupling is relatively weak in the case of the first-row transition metals, thus, we expect that the chemical reactions are much faster than the spin relaxation. Hence, the spin–flip is expected to take place in the reaction product and the reaction proceeds on the high-spin potential energy surface. Therefore, we computed the reaction paths using the initial spin state of the cluster. The only exception is the Cu₃Sc, where the singlet and triplet states of the bare cluster are quasi-degenerate, but the all the singlet Cu₃Sc–CO₂ entrance adducts are significantly more stable. Therefore, we explored the reaction path on the singlet potential energy surface, while the most stable spin states are discussed in the ESI.†

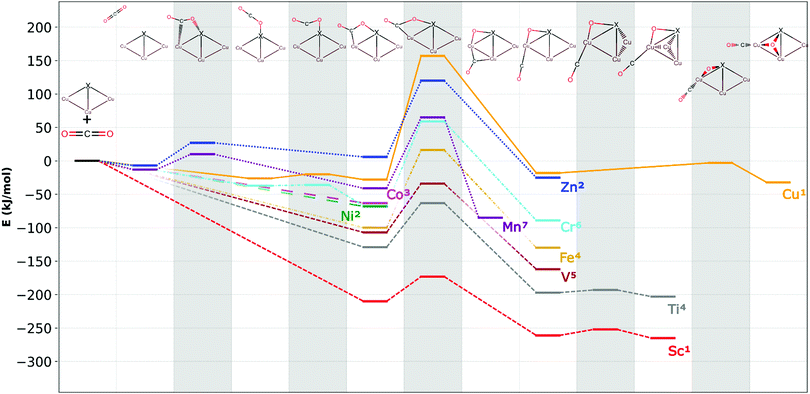
Fig. 3 shows the dopant-dependent trends in the CO₂ reactivities of Cu₃X clusters. Generally, early transition metal Cu₃X clusters yield thermodynamically more stable intermediates and products as well as lower transition state energies than the late transition metal Cu₃X clusters. This opens the way towards fine-tuning the reactivity with an appropriate dopant.

The entrance complex geometries depend on the dopant type. There are three different CO₂ adsorption modes in Fig. 3. In case of X = Sc, Ti, V, Fe, Co, or Ni the CO₂ molecule binds to the clusters without an energy barrier in a di-σ mode, i.e., the molecule bends and forms formal oxygen–dopant and carbon–copper bonds.

In the case of Mn or Zn dopants, the adsorption is preceded by a van der Waals complex and the subsequent stabilization to a di-σ structure is hindered by an energy barrier. For X = Cr or Cu, the intact, linear CO₂ binds to the cluster without an energy barrier, while very small barriers of 6 kJ mol⁻¹ and 1 kJ mol⁻¹, respectively lead the di-σ structures.

The barrier following the di-σ structure is the highest in all the reaction paths. This shows that the di-σ structure plays a central role in the reaction path of all the dopants.

The geometric structures of the most stable adducts depend considerably on the dopant atom type. In case of Cu₃Co and Cu₃Ni, the intact CO₂ adduct is the most stable, while in all other cases CO₂ dissociates to CO and a formal oxide ion. In the dissociated product the CO binds at the acute apex position in all doped clusters and oxygen is in a bridge position above the adjacent copper-dopant edge.

Based on the similarities of the reaction paths, the dopants can be classified into four categories:

Type I – scandium, titanium, and vanadium (short-dashed line in Fig. 3): the entrance complex is the lowest energy intact CO₂ structure with a di-σ binding mode. This is formed from the reactants without an energy barrier. The cluster-CO₂ adduct then isomerizes to a tetrahedral geometry. Here, the dopant atom locates at one of the apexes of the tetrahedral structure and not the oxide ion, as observed in Cu₄. All the barriers are submerged, implying a facile CO₂ dissociation reaction. The dissociated CO forms thermodynamically stable adduct with the cluster, thus its desorption and the cluster catalyst regeneration will be investigated in Section 4.

Type II – manganese and zinc (dotted line in Fig. 3): CO₂ forms only weak van der Waals complexes in the case of Mn and Zn at the obtuse apex position. Subsequently, low barriers lead to the di-σ structure with intact CO₂. This structure is unstable in the Zn-doped and metastable in the Mn-doped case that is energetically stabilized during the subsequent reaction step. The CO₂ dissociation is hindered by energy barriers with the transition state energy being well above that of the reactants. Moreover, in the case of acute apex positioned Cu₃Zn^aa the CO₂ dissociation is thermodynamically unfavoured.

Type III – chromium and iron (dash-dotted line in Fig. 3): in case of Fe the initial CO₂ adsorption is similar to the Type I and Type IV dopants, where the intact CO₂ adduct formation is barrierless and the final product involves dissociated CO with a formal oxide ion in bridge position on rhombus shape cluster. In both the chromium and iron case, the rate determining step is the CO₂ dissociation with a transition state lying somewhat higher in energy than the reactants. The preceding reaction barrier that exists in the Cr case is very small and does not make a qualitative difference between the chemical behaviour of Cr and Fe dopants.

Type IV – cobalt and nickel (long-dashed line in Fig. 3): in contrast to copper, no adsorption barrier was found for the clusters doped with Co and Ni and the most stable product is the di-σ structure with intact CO₂. However, in contrast to pure Cu₄, CO₂ dissociation is thermodynamically unfavoured.

3. Electronic structure analysis

The bent shape of the CO₂ molecule and the atomic charges (Table 2) in the most stable intact adduct with di-σ structure (third column in Fig. 1) indicate its activation and significant charge transfer from the cluster to the molecule. Depending on the dopant, the carbon–oxygen bond orders decrease from 1.91 in the free CO₂ molecule to 1.10–1.50 in the intactly bound CO₂. The negative charge of the oxygen atoms imply a carboxyl group (Table 2). This negative charge is compensated mainly by the dopant atom.

Table 2 Dopant atom charges in the di-σ structure of Cu₃X for different dopants in unit of the elementary charge e; O–X, Cu–C, and C–O Wiberg indices; and CO₂ dissociation barriers in kJ mol⁻¹

Dopant	CO2 charge [e]	Dopant charge [e]	O–X bond index	Cu–C bond index	Cu–X bond index	Dissociating C–O bond index	CO2 dissociation barrier [kJ mol^−1]
Sc	−1.00	1.04	0.60	0.25	0.47	1.10	37
Ti	−0.84	0.58	0.49	0.35	0.33	1.20	67
V	−0.81	0.50	0.42	0.36	0.33	1.29	73
Cr	−0.71	0.55	0.28	0.38	0.25	1.42	126
Mn	−0.89	0.96	0.25	0.42	0.05	1.21	107
Fe	−0.77	0.64	0.27	0.29	0.36	1.39	117
Co	−0.72	0.50	0.25	0.30	0.34	1.45	—
Ni	−0.66	0.37	0.25	0.30	0.33	1.50	—
Cu	−0.59	0.45	0.13	0.40	0.13	1.50	185
Zn	−0.90	0.96	0.16	0.44	0.03	1.25	115

---

To investigate the electronic structure origin of the charge transfer between the cluster and the carbon-dioxide in the different cluster-CO₂ adducts, the charge transfer energy was decomposed to contributions from Complementary Occupied Virtual Pairs (COVPs) (Fig. 2 and 4, see the ESI† for the details). In case of the intact adducts, the most significant COVP of the most stable intact CO₂ adduct shows electron donation from the cluster HOMO to the CO₂ LUMO (Fig. 2). As the CO₂ LUMO is antibonding, electron donation to this orbital explains the weakened carbon–oxygen bond and the bent shape of the CO₂ molecule. On the other hand, the back-donation from the CO₂ HOMO to the cluster LUMO is generally small and a notable effect is observed only in the case of scandium doping (Fig. 4).

Fig. 4 (a) Reaction energies of Cu₃X-CO₂ compared to the pure cluster and free CO₂, (b) charge transfer energies due to electron donation from the cluster to the CO₂ or back-donation in the opposite direction, and (c) frontier orbital energies of the most stable intact CO₂–cluster adducts.

This is in line with the observed negative charge of the adsorbed CO₂. The dopant dependent contribution of valence s and d orbitals to the HOMOs/SOMOs (Fig. 2) are also reflected in the shape of the donor part of the COVPs. The SOMOs of Mn and Fe have small contributions from the valence s orbitals, thus the donor COVPs have clear, localized d characters, while in the early transition metal doped Cu₃X with itinerant d electrons and high contributions from the valence s orbitals to the SOMOs, large, delocalized lobes on the donor part of the COVP clearly show the role of the hybridization of s and d atomic orbitals. Also, the HOMO/SOMO energies of the early transition metal-doped clusters are higher than those of clusters doped with the other transition metal dopants. This reduces the energy difference between the CO₂ LUMO and the cluster HOMO. In addition to that, the shape of the LUMO (Fig. 2) clearly imply favourable overlap with the CO₂ HOMO in case of early transition metals. This is in line with the slightly increased back-donation, especially in the case of Sc. These contribute to the higher binding energy in the case of early transition metals.

On the other hand, the overlap of the frontier orbitals of Cu₃Mn and Cu₃Zn with those of the CO₂ molecule, and the increased energy gap between the cluster HOMO and CO₂ LUMO explain the small energy barriers up to ∼30 kJ mol⁻¹ in these cases from the entrance complex to the more stable di-σ structure.

The energies of the HOMOs/SOMOs decrease gradually from Sc to Zn, thus their energy differences to that of the CO₂ LUMO increase. This is in line with the decreased stability of the intermediates and the products with the atomic number.

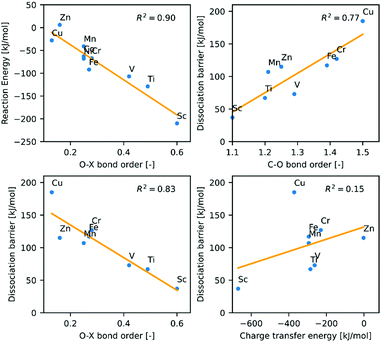
The di-σ adducts with bent, intact CO₂ are the key structures to interpret the reaction mechanism, as their properties directly correlate with the CO₂ binding energy and the dissociation activation energy (Fig. 5). The oxygen-dopant bond index decreases with the mass of the dopant atom X, while the carbon-copper bond index follows the opposite trend. It is well visible that O–X bond order correlates both with the CO₂ adsorption energy and also with the activation energy corresponding to its dissociation. It follows from the figure that the lower the O–X bond index, the less stable the intact CO₂ adduct is and the higher the energy barrier for CO₂ dissociation. As discussed above, the changes of the bond orders are due to electron donation from the cluster HOMO to the CO₂ LUMO, but the correlation between the charge transfer energy and the activation energy is weak. On the other hand, the good correlation between the O–X bond orders and the activation energy of the CO₂ dissociation clearly show that the strong bonds between the cluster and the CO₂ enhance the activation of CO₂.

Fig. 5 Correlation between the O–X and C–O bond orders and charge transfer energy corresponding to electron donation in the di-σ adduct with the reaction energies and dissociation barriers corresponding to CO₂ dissociation. The orange lines are linear trendlines. Coefficients of determination are given in the top right corners.

Similarly, to the Cu₄ case, the atoms in the shorter diagonal bears a partially positive charge in all of the doped Cu₃X clusters (Table 1). However, the electronegativity of the dopant atom plays an important role, as the nucleophilic attack will also take place more easily and the O–X bond will be stronger (Table 2) and structure with bent CO₂ is greatly stabilized in the case of the lower electronegativity early transition metal dopants. The Wiberg indices show that the O–X bond is the weakest in the case of the Zn- or Mn-doped clusters (Table 2), so the dopant Mn and Zn atoms with relatively low electronegativity will be polarized not towards the oxygen but towards the adjacent copper atom. This effect is so strong that while the electronegativities of Sc and Ti are 1.36 and 1.54, the partial charges of the dopant atoms are 1.04 and 0.58, respectively. For Mn and Zn, which electronegativities are 1.55 and 1.65 and the partial charges equal to 0.96 in both cases (Table 2). Therefore, compared to other doped clusters, the bond strength between the more electron-rich Cu atom and C increases significantly and in return the C–X bond strength decreases (Table 2). This indicates a reduced donation interaction, which weakens the C–O bond to a lesser extent than in the Type I dopants. This leads to slightly higher dissociation barrier than for Sc, Ti, V, but still lower than in the Cu₄ case.

In the Cu₃Cr and Cu₃Fe cases, large overlap is possible between the frontier orbitals, which is beneficial to strengthen the O–X bond. But, since the Cr and Fe have relatively high electronegativities (1.66 for Cr; 1.83 for Fe,), the dopant is less polarized, which has a weakening effect. Thus, intermediate strength O–X bond is formed between the dopant atoms and the CO₂. In line, the C–O bond is weakened to a lesser extent than in the Type II case.

4. General considerations for CO₂ reduction

Finally, we summarize the most important factors for the selection of the most suitable doped cluster catalyst.

The very first of these is the relative stability and formation of the di-σ structure. For Zn, Mn, Cu and Cr dopants, an energy barrier precedes the formation of this structure. However, this barrier is relatively low, less than 35 kJ mol⁻¹. The reaction energy of the intermediate plays an important role, since the released energy can be used to overcome the dissociation barrier, and the more stable our structure, the easier it can be realized in practice. This reaction energy is shown in Fig. 4. Based on these, Sc, Ti, and V are the most promising.

The second factor is the height of the dissociation barrier (Fig. 5). Sc, Ti and V have the lowest of these, while it is the highest in the case of the pure copper cluster. The third important factor is the relative stability of the final product, i.e. the reaction energy (Fig. 4). This is also favourable for the Sc-, V- and Ti-doped clusters.

Thus, the early transition metals of Type I are the most promising dopant atoms, as they lead to the smallest dissociation barriers and at the same time give the most stable structures. However, an over-stabilized product of the CO₂ dissociation can also hinder the elimination of the product from the cluster surface, i.e. the cluster cannot be regenerated. For this reason, we must also study the CO desorption energy.

Our study has shown that in each of the cases discussed here, the CO desorption from the final structure proceeds without an energy barrier. Fig. 6 shows a relatively weak dopant dependence of the CO desorption energy. This could be interpreted by the fact that the CO binds to the opposite side of the cluster as the dopant. Among the different dopants, Type I leads to the lowest desorption energies and it is lowest in the case of the Ti dopant. On the other hand, the pure copper cluster has the highest CO desorption energy.

Fig. 6 CO desorption energy from the Cu₃XO(CO) clusters. The oxide-cluster reduction energy is calculated based on the following reaction: Cu₃XO + H₂ → Cu₃X + H₂O stable dissociated CO₂ product was not found for Co and Ni.

Finally, the Cu₃XO cluster must be reduced to close the catalytic cycle. While the exploration of the detailed, multistep reduction mechanism is beyond the scope of our present article, we studied the thermodynamic driving force according to Cu₃XO + H₂ → Cu₃X + H₂O. The reduction energy shows a strong dopant-dependence with most favoured reduction in Cu and Zn and least in Sc (Fig. 6).

In summary, early transition metals are favourable dopants to facilitate the CO₂ dissociation, however the regeneration of the catalyst is difficult. Nevertheless, the energy gain from the CO₂ dissociation is high, so it can cover large part of the regeneration energy. Thus, early transition metal-doped Cu₃X clusters are promising catalysts in the gas phase.

On the other hand, CO₂ dissociation is hindered with high energy barriers in late transition metal dopants, but the regeneration of the catalyst is facile. Transition metals from the middle of the row (Mn or Cr) represent a promising balance.

Finally, we investigated the effect of the finite temperature by computing the Gibbs-free energies from 300 K to 800 K for several intermediates and products of Cu₃Sc (see the ESI† for details). As expected, due to the entropy effects, the relative Gibbs-free energies of the adducts increase with temperature. However, the adducts are all still highly stable thermodynamically, even at the highest temperature. On the other hand, the high temperature facilitates the regeneration of the catalyst, as the dissociation of the CO product and the reduction of the oxide are both favored. Only ∼100 kJ mol⁻¹ Gibbs-free energy is necessary to regenerate the catalyst.

Conclusions

In summary, we found strongly dopant-dependent reaction energies, reaction mechanisms, dissociation barriers for CO₂ and less dopant-dependent desorption energies for CO during the CO₂ activation with first row transition metal doped Cu₃X clusters. However, based on similar properties of some dopants, the reaction mechanisms of these clusters could be grouped into four categories.

The low electronegativity dopants of Type I, i.e., early transition metals (Sc, Ti, V) lead to small HOMO–LUMO gaps and relatively high overlaps between the frontier molecular orbitals of the doped cluster and the molecule. This results in barrier-free CO₂ adsorption in di-σ binding mode, low dissociation barriers, and notably high thermodynamic stability of the adducts. These make the early transition metals very promising dopants for CO₂ activation.

In the Type II electron-rich transition metal- (Mn, Zn) doped clusters, we observed very weak binding between the oxygen and the dopant due to a large HOMO–LUMO gap and small overlap between the frontier molecular orbitals of the doped cluster and the CO₂. These lead to lower activation barriers for CO₂ dissociation compared to the pure Cu₄ cluster, but still higher than that in the Type I clusters.

The frontier orbitals of Type III metal (X = Cr, Fe) doped Cu₃X clusters have high overlaps with those of the CO₂, however due to their relatively high electronegativities the O–X bond is less polarized and thus CO₂ adsorbs relatively weakly, and the dissociation barriers are high.

For Ni and Co doped clusters (Type IV), dissociation of CO₂ is thermodynamically unfavourable, thus the intact CO₂ structure is formed. Nevertheless, the bent structure of the molecule and its negative charge clearly shows that it is activated.

Our work has shown that early transition metal dopants facilitate the CO₂ binding and can reduce the CO₂ dissociation barrier, thereby promoting CO₂ activation and reduction to CO. This highlights the potential of doping effects and motivates further studies to develop new CO₂ reduction catalysts, to investigate further reduction to C1 or C2 product, and study the effect of the surface deposition on these doped copper clusters.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the KU Leuven–Budapest University of Technology and Economics joint research funding (CELSA/18/032). This research has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement no. 955650 (CATCHY).

References

1. W. Wang, Y. Himeda, J. Muckerman, G. Manbeck and E. Fujita, Chem. Rev., 2015, 115, 12936–12973.
2. P. Nejat, F. Jomehzadeh, M. Taheri, M. Gohari and M. Majid, Renewable Sustainable Energy Rev., 2015, 43, 843–862.
3. H. Arakawa, M. Aresta, J. Armor, M. Barteau, E. Beckman, A. Bell and W. Tumas, Chem. Rev., 2001, 101, 953–996.
4. N. Lewis and D. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
5. M. Aresta and A. Dibenedetto, Dalton Trans., 2007, 2975–2992.
6. A. Appel, J. Bercaw, A. Bocarsly, H. Dobbek, D. DuBois, M. Dupuis, J. Ferry, E. Fujita, R. Hille, P. Kenis, C. Kerfeld, R. Morris, C. Peden, A. Portis, S. Ragsdale, T. Rauchfuss, J. Reek, L. Seefeldt, R. Thauer and G. Waldrop, Chem. Rev., 2013, 113, 6621–6658.
7. M. Aresta, A. Dibenedetto and A. Angelini, Chem. Rev., 2014, 114, 1709–1742.
8. A. Harriman, Philos. Trans. R. Soc., A, 2013, 371, 20110415.
9. D. Darensbourg, Chem. Rev., 2007, 107, 2388–2410.
10. G. Olah, G. Prakash and A. Goeppert, J. Am. Chem. Soc., 2011, 133, 12881–12898.
11. M. Peters, B. Köhler, W. Kuckshinrichs, W. Leitner, P. Markewitz and T. Müller, ChemSusChem, 2011, 4, 1216–1240.
12. P. Markewitz, W. Kuckshinrichs, W. Leitner, J. Linssen, P. Zapp, R. Bongartz, A. Schreiber and T. Müller, Energy Environ. Sci., 2012, 5, 7281–7305.
13. E. Kondratenko, G. Mul, J. Baltrusaitis, G. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135.
14. I. Ganesh, Renewable Sustainable Energy Rev., 2014, 31, 221–257.
15. D. Talbi and E. Herbst, Astron. Astrophys., 2002, 386, 1139–1142.
16. M. Porosoff, B. Yan and J. Chen, Energy Environ. Sci., 2016, 9, 62–73.
17. Y. Hori, I. Takahashi, O. Koga and N. Hoshi, J. Mol. Catal. A: Chem., 2003, 199, 39–47.
18. R. Kortlever, J. Shen, K. Schouten, F. Calle-Vallejo and M. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082.
19. Y. Kuramochi, O. Ishitani and H. Ishida, Coord. Chem. Rev., 2018, 373, 333–356.
20. E. Kondratenko, G. Mul, J. Baltrusaitis, G. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135.
21. K. C. Waugh, Catal. Today, 1992, 15, 51–75.
22. S. Thomas, ChemCatChem, 2010, 2, 127–132.
23. D. Astruc, Nanopart. Catal., 2008, 16, 1–48.
24. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408.
25. G. Hutchings, J. Catal., 1985, 96, 292–295.
26. K. Klabunde, Nanoscale materials in chemistry, Wiley, Hoboken, NJ, 2009.
27. T. Bligaard and J. Nørskov, Electrochim. Acta, 2007, 52, 5512–5516.
28. J. Nørskov, T. Bligaard, J. Rossmeisl and C. Christensen, Nat. Chem., 2009, 1, 37–46.
29. J. Kleis, J. Greeley, N. Romero, V. Morozov, H. Falsig, A. Larsen, J. Lu, J. Mortensen, M. Dułak, K. Thygesen, J. Nørskov and K. Jacobsen, Catal. Lett., 2011, 141, 1067–1071.
30. S. Zhao, R. Jin, H. Abroshan, C. Zeng, H. Zhang, S. House, E. Gottlieb, H. Kim, J. Yang and R. Jin, J. Am. Chem. Soc., 2017, 139, 1077–1080.
31. F. Schweinberger, M. Berr, M. Döblinger, C. Wolff, K. Sanwald, A. Crampton, C. Ridge, F. Jäckel, J. Feldmann, M. Tschurl and U. Heiz, J. Am. Chem. Soc., 2013, 135, 13262–13265.
32. S. Zhao, N. Austin, M. Li, Y. Song, S. House, S. Bernhard, J. Yang, G. Mpourmpakis and R. Jin, ACS Catal., 2018, 8, 4996–5001.
33. T. Imaoka, H. Kitazawa, W. Chun and K. Yamamoto, Angew. Chem., Int. Ed., 2015, 54, 9810–9815.
34. S. Xie, H. Tsunoyama, W. Kurashige, Y. Negishi and T. Tsukuda, ACS Catal., 2012, 2, 1519–1523.
35. H. Qian, D. Jiang, G. Li, C. Gayathri, A. Das, R. Gil and R. Jin, J. Am. Chem. Soc., 2012, 134, 16159–16162.
36. H. Tsunoyama, N. Ichikuni, H. Sakurai and T. Tsukuda, J. Am. Chem. Soc., 2009, 131, 7086–7093.
37. A. von Weber, E. Baxter, S. Proch, M. Kane, M. Rosenfelder, H. White and S. Anderson, Phys. Chem. Chem. Phys., 2015, 17, 17601–17610.
38. S. Lang, T. Bernhardt, D. Kiawi, J. Bakker, R. Barnett and U. Landman, Angew. Chem., 2015, 127, 15328–15332.
39. W. Wang, S. Wang, X. Ma and J. Gong, Chem. Soc. Rev., 2011, 40, 3703–3727.
40. P. Jessop, T. Ikariya and R. Noyori, Chem. Rev., 1995, 95, 259–272.
41. S. Vukojević, O. Trapp, J. Grunwaldt, C. Kiener and F. Schüth, Angew. Chem., Int. Ed., 2005, 44, 7978–7981.
42. D. Bazin, D. Guillaume, C. Pichon, D. Uzio and S. Lopez, Oil Gas Sci. Technol., 2005, 60, 801–813.
43. D. Wang, A. Villa, F. Porta, L. Prati and D. Su, J. Phys. Chem. C, 2008, 112, 8617–8622.
44. J. Oliver-Messeguer, L. Liu, S. García-García, C. Canós-Giménez, I. Domínguez, R. Gavara, A. Doménech-Carbó, P. Concepción, A. Leyva-Pérez and A. Corma, J. Am. Chem. Soc., 2015, 137, 3894–3900.
45. M. Tamura, T. Kitanaka, Y. Nakagawa and K. Tomishige, ACS Catal., 2015, 6, 376–380.
46. H. Arakawa, J. Dubois and K. Sayama, Energy Convers. Manage., 1992, 33, 521–528.
47. M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B. Kniep, M. Tovar, R. Fischer, J. Norskov and R. Schlogl, Science, 2012, 336, 893–897.
48. X. Zhang, J. Liu, B. Zijlstra, I. Filot, Z. Zhou, S. Sun and E. Hensen, Nano Energy, 2018, 43, 200–209.
49. H. Schwarz, Coord. Chem. Rev., 2017, 334, 112–123.
50. B. Szyja, D. Smykowski, J. Szczygieł, E. Hensen and E. Pidko, ChemCatChem, 2016, 8, 2500–2507.
51. G. Yan, Z. Gao, M. Zhao, K. Ma, Z. Ding, W. Yang and X. Ding, Mol. Catal., 2020, 497, 111205.
52. G. Yan, Z. Gao, M. Zhao, W. Yang and X. Ding, Appl. Surf. Sci., 2020, 517, 146200.
53. O. Lushchikova, D. Huitema, P. López-Tarifa, L. Visscher, Z. Jamshidi and J. Bakker, J. Phys. Chem. Lett., 2019, 10, 2151–2155.
54. O. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848.
55. A. Karelovic and P. Ruiz, Catal. Sci. Technol., 2015, 5, 869–881.
56. F. Studt, I. Sharafutdinov, F. Abild-Pedersen, C. Elkjær, J. Hummelshøj, S. Dahl, I. Chorkendorff and J. Nørskov, Nat. Chem., 2014, 6, 320–324.
57. C. Liu, B. Yang, E. Tyo, S. Seifert, J. DeBartolo, B. von Issendorff, P. Zapol, S. Vajda and L. Curtiss, J. Am. Chem. Soc., 2015, 137, 8676–8679.
58. X. Nie, M. Esopi, M. Janik and A. Asthagiri, Angew. Chem., 2013, 125, 2519–2522.
59. A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. Kolipaka, C. Piazzoni, S. Seifert, V. Bonačić-Koutecký, A. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 6210–6224.
60. B. Yang, C. Liu, A. Halder, E. Tyo, A. Martinson, S. Seifert, P. Zapol, L. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412.
61. B. Yang, X. Yu, A. Halder, X. Zhang, X. Zhou, G. Mannie, E. Tyo, M. Pellin, S. Seifert, D. Su and S. Vajda, ACS Sustainable Chem. Eng., 2019, 7, 14435–14442.
62. S. Iyemperumal and N. Deskins, Phys. Chem. Chem. Phys., 2017, 19, 28788–28807.
63. P. López-Caballero, A. Hauser and M. Pilar de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
64. C. Liu, H. He, P. Zapol and L. Curtiss, Phys. Chem. Chem. Phys., 2014, 16, 26584–26599.
65. H. Xu, D. Rebollar, H. He, L. Chong, Y. Liu, C. Liu, C. Sun, T. Li, J. Muntean, R. Winans, D. Liu and T. Xu, Nat. Energy, 2020, 5, 623–632.
66. Y. Bu, M. Zhao, G. Zhang, X. Zhang, W. Gao and Q. Jiang, ChemElectroChem, 2019, 6, 1831–1837.
67. R. Raju, P. Rodriguez and R. Johnston, J. Phys. Chem. C, 2019, 123, 14591–14609.
68. R. Passalacqua, S. Parathoner, G. Centi, A. Halder, E. Tyo, B. Yang, S. Seifert and S. Vajda, Catal. Sci. Technol., 2016, 6, 6977–6985.
69. Q. Zhang, Q. Zhao, X. Liang, X. Wang, F. Ma, B. Suo, W. Zou, H. Han, Q. Song, Q. Wu, Y. Li and H. Zhu, Int. J. Hydrogen Energy, 2018, 43, 9935–9942.
70. N. Zimmermann, T. Bernhardt, J. Bakker, R. Barnett, U. Landman and S. Lang, J. Phys. Chem. A, 2020, 124, 1561–1566.
71. X. Zhang, G. Liu, K. Meiwes-Broer, G. Ganteför and K. Bowen, Angew. Chem., Int. Ed., 2016, 55, 9644–9647.
72. G. Liu, Z. Zhu, M. Marshall, M. Blankenhorn and K. Bowen, J. Phys. Chem. A, 2021, 125, 1747–1753.
73. Y. Liu, L. Jiang, X. Li, L. Wang, J. Chen and S. He, J. Phys. Chem. C, 2018, 122, 19379–19384.
74. G. Liu, P. Poths, X. Zhang, Z. Zhu, M. Marshall, M. Blankenhorn, A. Alexandrova and K. Bowen, J. Am. Chem. Soc., 2020, 142, 7930–7936.
75. S. Tang, N. Rijs, J. Li, M. Schlangen and H. Schwarz, Chem. – Eur. J., 2015, 21, 8483–8490.
76. A. Saputro, A. Maulana, F. Fathurrahman, G. Shukri, M. Mahyuddin, M. Agusta, T. Wungu and H. Dipojono, Int. J. Hydrogen Energy, 2021, 46, 14418–14428.
77. A. Pangh, Catal. Commun., 2021, 149, 106245.
78. J. Li, P. González-Navarrete, M. Schlangen and H. Schwarz, Chem. – Eur. J., 2015, 21, 7780–7789.
79. Q. Tang, F. Shi, K. Li, W. Ji, J. Leszczynski, A. Russell, E. Eddings, Z. Shen and M. Fan, Fuel, 2020, 280, 118446.
80. A. Green, J. Justen, W. Schöllkopf, A. Gentleman, A. Fielicke and S. Mackenzie, Angew. Chem., Int. Ed., 2018, 57, 14822–14826.
81. L. Gálvez-González, J. Juárez-Sánchez, R. Pacheco-Contreras, I. Garzón, L. Paz-Borbón and A. Posada-Amarillas, Phys. Chem. Chem. Phys., 2018, 20, 17071–17080.
82. Y. Wang, K. Wiberg and N. Werstiuk, J. Phys. Chem. A, 2007, 111, 3592–3601.
83. A. Alvarez-Garcia, E. Flórez, A. Moreno and C. Jimenez-Orozco, Mol. Catal., 2020, 484, 110733.
84. M. Sharma, K. Mondal, T. Ghanty and A. Banerjee, J. Phys. Chem. A, 2021, 125, 2558–2572.
85. Y. Shao, Z. Gan, E. Epifanovsky, A. Gilbert, M. Wormit, J. Kussmann and V. Rassolov, Mol. Phys., 2015, 113, 184–215.
86. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
87. F. Liu, E. Proynov, J. Yu, T. Furlani and J. Kong, J. Chem. Phys., 2012, 137, 114104.
88. G. Hou, E. Faragó, D. Buzsáki, L. Nyulászi, T. Höltzl and E. Janssens, Angew. Chem., Int. Ed., 2021, 60, 4756–4763.
89. A. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
90. E. Glendening, C. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
91. R. Khaliullin, E. Cobar, R. Lochan, A. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765.
92. A. Ghysels, T. Verstraelen, K. Hemelsoet, M. Waroquier and V. Van Speybroeck, J. Chem. Inf. Model., 2010, 50, 1736–1750.
93. D. Die, B. Zheng, L. Zhao, Q. Zhu and Z. Zhao, Sci. Rep., 2016, 6, 1–13.
94. T. Höltzl, N. Veldeman, J. De Haeck, T. Veszprémi, P. Lievens and M. Nguyen, Chem. – Eur. J., 2009, 15, 3970–3982.
95. W. Knight, K. Clemenger, W. de Heer, W. Saunders, M. Chou and M. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143.
96. E. Janssens, H. Tanaka, S. Neukermans, R. Silverans and P. Lievens, New J. Phys., 2003, 5, 46.
97. T. Höltzl, P. Lievens, T. Veszprémi and M. Nguyen, J. Phys. Chem. C, 2009, 113, 21016–21018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02220b

---