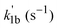An experimental and master-equation modeling study of the kinetics of the reaction between resonance-stabilized (CH₃)₂CCHCH₂ radical and molecular oxygen

Abstract

The kinetics of the reaction between resonance-stabilized (CH₃)₂CCHCH₂ radical (R) and O₂ has been investigated using photoionization mass spectrometry, and master equation (ME) simulations were performed to support the experimental results. The kinetic measurements of the (CH₃)₂CCHCH₂ + O₂ reaction (1) were carried out at low helium bath-gas pressures (0.2–5.7 Torr) and over a wide temperature range (238–660 K). Under low temperature (238–298 K) conditions, the pressure-dependent bimolecular association reaction R + O₂ → ROO determines kinetics, until at an intermediate temperature range (325–373 K) the ROO adduct becomes thermally unstable and increasingly dissociates back to the reactants with increasing temperature. The initial association of O₂ with (CH₃)₂CCHCH₂ radical occurs on two distinct sites: terminal 1(t) and non-terminal 1(nt) sites on R, leading to the barrierless formation of ROO_(t) and ROO_(nt) adducts, respectively. Important for autoignition modelling of olefinic compounds, bimolecular reaction channels appear to open for the R + O₂ reaction at high temperatures (T > 500 K) and pressure-independent bimolecular rate coefficients of reaction (1) with a weak positive temperature dependence, (2.8–4.6) × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹, were measured in the temperature range of 500–660 K. At a temperature of 501 K, a product signal of reaction (1) was observed at m/z = 68, probably originating from isoprene. To explore the reaction mechanism of reaction (1), quantum chemical calculations and ME simulations were performed. According to the ME simulations, without any adjustment to energies, the most important and second most important product channels at the high temperatures are isoprene + HO₂ (yield > 91%) and (2R/S)-3-methyl-1,2-epoxybut-3-ene + OH (yield < 8%). After modest adjustments to ROO_(t) and ROO_(nt) well-depths (∼0.7 kcal mol⁻¹ each) and barrier height for the transition state associated with the kinetically most dominant channel, R + O₂ → isoprene + HO₂ (∼2.2 kcal mol⁻¹), the ME model was able to reproduce the experimental findings. Modified Arrhenius expressions for the kinetically important reaction channels are enclosed to facilitate the use of current results in combustion models.

---

Introduction

Olefins are important fuel constituents and combustion intermediates and contribute significantly to the gross global fossil fuel consumption.^1,2 Olefins contain one or more C=C double bond in their molecular structure, which results in high thermal stability under combustion conditions. This, combined with high thermal stability of radicals formed from olefins, partly explains the soot-forming propensity of olefins under fuel-rich combustion conditions.^3–5 In addition to soot formation affinity, autoignition chemistry and oxidation kinetics of olefins and olefinic radicals differ significantly from those of similar-size alkanes and alkyl radicals.⁶ Recently, olefin flame chemistry,^7–9 pyrolysis,^10,11 ignition delay times,^12–15 and oxidation in jet-stirred-reactor (JSR)^16–18 experiments have received attention. However, little is still known experimentally about the oxidation kinetics of olefinic hydrocarbon radicals larger than allyl^19,20 and methyl-vinyl²¹ (i.e. >C₃), which can be expected to play an important role in autoignition and oxidation of real fuels under low-temperature-combustion (LTC) conditions. Real scarcity exists on kinetic oxidation experiments of allyl-type, resonance-stabilized radicals larger than 1- and 2-methylallyl radicals (i.e. >C₄).^22,23

In this work, we focus on the oxidation kinetics of the allyl-type, resonance-stabilized (CH₃)₂CCHCH₂ (2-methylbut-3-en-2-yl) radical. A potential source of this radical is a H-atom abstraction from 2-methyl-2-butene (2M2B) as well as pyrolysis and decomposition reactions of larger olefinic fuel constituents. 2M2B is a potential surrogate fuel for the combustion modeling of real fuels. As discussed by Westbrook et al.,¹⁶ under typical combustion conditions H-atom abstraction reactions of small radical species (e.g. H, O, OH, CH₃, CH₃OO etc.) from 2M2B is an important, if not crucial, route to initiate 2M2B oxidation. These reactions abstract H-atoms by breaking weak allylic C–H bonds (BDE ∼89 kcal mol⁻¹) much more likely than the stronger vinylic C–H bond (BDE ∼108 kcal mol⁻¹), resulting in production of two distinct allyl-type pentenyl radicals, as shown in Scheme 1.

Scheme 1 Two allyl-type pentenyl radicals, CH₂(CH₃)CCHCH₃ and (CH₃)₂CCHCH₂, produced via H-atom abstraction reactions from 2-methyl-2-butene (2M2B).

Both these allyl-type radicals, CH₂(CH₃)CCHCH₃ and (CH₃)₂CCHCH₂, are resonantly stabilized. Their (and allyl-type radical R_A in general) reaction with molecular oxygen (O₂) has a characteristically shallow R_A + O₂ → R_AOO barrierless association reaction well-depth (∼20 kcal mol^−1 19,24 compared to ∼40 kcal mol⁻¹ for vinyl-type radicals^25,26). This enables thermal decomposition of the R_AOO adduct back to the reactants to start to compete with the forward association reaction already at relatively low temperatures, establishing the chemical equilibrium R_A + O₂ ⇌ R_AOO. Upon increasing temperature, this may eventually lead to conditions with almost no net reaction, until a new reaction channel for the R_A + O₂ reaction, potentially, but not necessarily, becomes accessible at higher temperatures. For example, even at temperatures as high as 700 K, only an upper limit of 2 × 10⁻¹⁶ cm³ molecule⁻¹ s⁻¹ for the bimolecular rate coefficient of the CH₃CHCHCH₂ + O₂ reaction has been measured.²² In their JSR measurements of 2M2B oxidation in the temperature range 600–1100 K and at about 1 atm pressure with residence time 1.5 s, Westbrook et al.¹⁶ observed only a little reactivity below 800 K, above which a rapid increase in the fuel consumption was observed. Under LTC conditions (500 < T < 1000 K), one may typically expect a fuel-radical + O₂ reaction to constitute the major sink reaction of fuel-radical until unimolecular thermal decomposition reactions become accessible. However, in case of allyl-type radicals this is not necessarily the case (as discussed above for the CH₃CHCHCH₂ + O₂ reaction), and for this reason kinetic oxidation experiments with still larger C₅ allyl-type radicals are of great importance.

In this work, we have studied the kinetics of the (CH₃)₂CCHCH₂ (R) + O₂ reaction (1) over a wide 238–660 K temperature range and at low pressures (0.2–5.7 Torr), as well as thermochemistry of the (CH₃)₂CCHCH₂ + O₂ (CH₃)₂CCHCH₂OO reaction (1a,−1a) in a narrower temperature range using photoionization mass spectrometry.

As shown in Scheme (2), the resonance hybrid structure of the (CH₃)₂CCHCH₂ radical is composed of two resonance structures. The association of O₂ with either the terminal (t) or non-terminal (nt) radical site of the (CH₃)₂CCHCH₂ radical generates ROO_(t) and ROO_(nt) adducts, respectively, conveniently denoted as (CH₃)₂CCHCH₂OO in reaction (1a,−1a).

Scheme 2 Resonance structures contributing to the resonance hybrid structure of the (CH₃)₂CCHCH₂ radical.

The kinetic measurements performed in this work were focused on providing accurate bimolecular rate coefficient and equilibrium constant data of reaction (1). Subsequently, high-level quantum chemistry calculations and master equation (ME) modeling of reaction (1) were performed to complement the measured bimolecular rate coefficient and thermochemistry data.

Experimental

Experiments were performed using a laminar flow-reactor coupled with a photoionization mass spectrometer (PIMS). A thorough description of the employed PIMS apparatus has been presented previously,²⁷ so only the specific details concerning the current measurements are discussed here.

Photolysis of 1-bromo-3-methyl-2-butene or 1-chloro-3-methyl-2-butene precursor at 248 nm radiation was performed using MPB ASX-750 or Coherent COMPex 201F excimer laser, respectively, to achieve a homogeneous [(CH₃)₂CCHCH₂] along the flow-reactor axis.

(CH₃)₂CCHCH₂Br + hν_{248 nm} → (CH₃)₂CCHCH₂ + Br (P1a)

→ Other products (P1b)

(CH₃)₂CCHCH₂Cl + hν_{248 nm} → (CH₃)₂CCHCH₂ + Cl (P2a)

→ Other products (P2b)

The measurements presented in this study were primarily conducted using the bromide precursor, while the chloride precursor, which has a higher BDE(C–Cl) compared to BDE(C–Br), was principally used to show that the kinetic results do not depend on the selected photolytic precursor. Due to the smaller absorption cross-section of (CH₃)₂CCHCH₂Cl at 248 nm in comparison to (CH₃)₂CCHCH₂Br, experiments using the chloride precursor required higher [(CH₃)₂CCHCH₂Cl] and higher laser fluences [∼170 mJ cm⁻²] than measurements using the bromide precursor, where lower precursor concentrations and laser fluences [∼17–50 mJ cm⁻²] were used. We estimate that [(CH₃)₂CCHCH₂]_t=0 ≤ 3 × 10¹¹ cm⁻³ in the kinetic measurements using either precursor.

Producing the same (CH₃)₂CCHCH₂ radical by photolysing two different precursors, (CH₃)₂CCHCH₂Br and (CH₃)₂CCHCH₂Cl, with the same 248 nm energy photons enables to some extent testing a potential isomerization of nascent (CH₃)₂CCHCH₂ radicals immediately after photolysis before their thermalization. Fig. 1 presents relative enthalpies (ΔH_(298K)) of the various (CH₃)₂CCHCH₂ radical isomers and the transition states (TS) connecting them as well as maximum internal energies of the radicals after 248 nm photolysis of (CH₃)₂CCHCH₂Br and (CH₃)₂CCHCH₂Cl precursors (full horizontal lines), all calculated at the MN15/cc-pVTZ level in this work. In a recent study by this group, Döntgen et al.²⁴ investigated the kinetics of the CH₂CHCHCH₂CH₃ + O₂ reaction and utilized 248 nm photolysis of BrCH₂CHCHCH₂CH₃ and ClCH₂CHCHCH₂CH₃ precursors for radical production. They performed time-dependent density functional theory calculations for electronic excitation energies of the bromide and chloride precursors and concluded that the total vibrational excitation of the CH₂CHCHCH₂CH₃ radical after photolysis is about 15.0 and 13.4 kcal mol⁻¹ for the bromide and chloride precursors, respectively. Both these energies were significantly below the ∼37 kcal mol⁻¹ energy required for the lowest-energy CH₂CHCHCH₂CH₃ → CH₃CHCHCHCH₃ isomerization in the system, showing that in those experiments only one isomer was produced during photolysis. Considering the very close similarity between those and the current experiments, i.e. the same photolysis energy and especially very similar photolytic precursors (e.g. BrCH₂CHCHCH₂CH₃vs. (CH₃)₂CCHCH₂Br and ClCH₂CHCHCH₂CH₃vs. (CH₃)₂CCHCH₂Cl), we estimate that the post-photolysis vibrational excitation of the (CH₃)₂CCHCH₂ radical is also about 15.0 and 13.4 kcal mol⁻¹ for the bromide and chloride precursors, respectively. Both these values, which contain some uncertainty due to the above estimation, are significantly below the calculated energy of the lowest isomerization transition state, TS1 = 38.9 kcal mol⁻¹, see Fig. 1. The experimental conditions and the results of the kinetic measurements using chlorine and bromine precursors are presented in Tables 2–4.

Fig. 1 Relative enthalpies (ΔH_(298K)) of the various (CH₃)₂CCHCH₂ radical isomers and the connecting transition states (TS) calculated at the MN15/cc-pVTZ level. The colored horizontal lines represent the difference between the 248 nm photon energy and the calculated BDE of Br–C and Cl–C bonds for (CH₃)₂CCHCH₂Br (BDE_{(MN15/cc-pVTZ)} = 55.1 kcal mol⁻¹) and (CH₃)₂CCHCH₂Cl (BDE_{(MN15/cc-pVTZ)} = 68.4 kcal mol⁻¹) precursors, respectively. The red, shaded area shows our best estimate on excitation energy of the (CH₃)₂CCHCH₂ radicals after photolysis of (CH₃)₂CCHCH₂Br and (CH₃)₂CCHCH₂Cl precursors at 248 nm wavelength, respectively. The optimized geometries and ΔH_(298K) values of the stationary points are given in the ESI† (see Fig. S1).

The reaction mixture flowing through the temperature-controlled flow-reactor consisted of a mainly inert bath-gas (Helium > 97%) along with radical precursor ((CH₃)₂CCHCH₂Br < 0.02%, (CH₃)₂CCHCH₂Cl < 0.05%) and molecular oxygen ([O₂] < 3%). In the high-temperature measurements a significantly higher amount of O₂ (<51%) was used. Depending upon the temperature and pressure conditions employed during the measurements, different combinations of reactor tube sizes and coatings were used (see also Tables 2–4 caption): Pyrex-glass reactor (i.d. = 1.65 cm) with polydimethylsiloxane (PDMS) or halocarbon wax (HW) coating, stainless steel reactor (i.d. = 1.7 cm or 0.8 cm) with HW coating, and quartz reactor (i.d. = 0.85 cm) with boric oxide coating. A set temperature of the reaction zone was maintained within a uniformity of ±2 K using a PID controller.

The observed kinetics of the (CH₃)₂CCHCH₂ + O₂ reaction (1) at different temperatures can be characterized as follows.

Here, reaction (1a) represents the association reaction between the (CH₃)₂CCHCH₂ radical and O₂ leading to the formation of (CH₃)₂CCHCH₂OO adducts. This reaction is important at low temperatures, 238–298 K. Reactions (1a,−1a) are important in the intermediate temperature range (325–373 K), where adducts become thermally unstable and a kinetic equilibrium is established between the forward bimolecular (CH₃)₂CCHCH₂ + O₂ reaction and the unimolecular dissociation of (CH₃)₂CCHCH₂OO adducts back to the reactants. Phenomenological reaction (1b) corresponds to new reaction channels that open for (CH₃)₂CCHCH₂ + O₂ reaction at high temperatures (>500 K).

Apart from the reaction with O₂, two other reactions that contribute to the (CH₃)₂CCHCH₂ radical decay under experimental conditions are heterogeneous wall losses and second order radical-radical decay processes.

R + R → Products (B)

Contribution due to reaction (B) was minimized by reducing the laser intensity and/or photolytic precursor concentration until the measured decay rate was strictly single-exponential. Depending upon the temperature range of interest, different reactor coatings (i.e. PDMS, HW or boric oxide) were employed for minimizing the heterogeneous wall-decay rate coefficients (k^(R)_wall) of the (CH₃)₂CCHCH₂ radical.

The detection of the (CH₃)₂CCHCH₂ radical decay profiles for reaction (1) was performed using the PIMS. The radiation of energy 8.44 eV from a microwave-discharge of 6% xenon in a helium-mixture with a sapphire window to cut-off higher energy photons was used to ionize (CH₃)₂CCHCH₂ radicals present in the reaction mixture. Potential products of reaction (1b) were searched utilizing ionization radiation from a H₂-lamp (discharge of H₂ gas with an MgF₂ window to produce radiation at around 10.2 eV). Ions formed were mass selected by a quadrupole mass spectrometer followed by the detection using an electron multiplier. Radical ion (CH₃)₂CCHCH₂⁺ was detected at its parent mass at m/z = 69. A temporal ion decay signal was recorded from 10 ms before to 50 ms after each laser pulse, and accumulated for 3000–15000 repetitions before transferring to a PC for further analysis.

A nonlinear least-squares-fitting method was used for fitting the observed (CH₃)₂CCHCH₂ radical decay profiles. For reactions (1a) and (1b) the measured radical decay profiles were fitted using the single-exponential expression: . Here, is directly related to the bimolecular rate coefficients of the reaction (1a; k_1a) and (1b; k_1b) via relation: 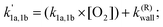B is the background signal, and [R₀] and [R_t] are proportional to the initial (t = 0) and temporal radical concentration, respectively. Under conditions where kinetic equilibrium is established, a decay profile of a resonantly stabilized radical with two non-similar resonance structures follows, in principle, a tri-exponential behavior. However, following the scheme proposed by Knyazev et al.²² for the kinetics of the CH₃CHCHCH₂ + O₂ reaction, such tri-exponential behavior can be fitted with a bi-exponential expression, [R_t] = B + Ce^−λ₁t + De^−λ₂t, which effectively leads to averaging the kinetic behavior of the two radical sites. Subsequently, the obtained fitted parameters (i.e. C, D, λ₁, λ₂) are used to calculate the forward (k_1a) and backward (k_−1a) rate coefficients of reaction (1a,−1a) using the following equations.

k_−1a = λ₁ + λ₂ − (k_1a[O₂]) − k^(R)_wall − k^(ROO)_irr. (E2)

Here, k^(ROO)_irr. represents the rate coefficients for irreversible first-order decay processes (including heterogeneous wall losses) related to ROO adducts, and is calculated using expression (E3).

The values for equilibrium-constants (K_eq) of reaction (1a,−1a) were calculated using expression (E4).

Here, the standard pressure term (P°) is introduced to the (E4) for satisfying the definition of equilibrium-constant being a dimensionless quantity. The species involved are assumed to have an ideal gas behavior and their standard states are chosen at 1 bar pressure (i.e. P° = 1 bar), at a specified temperature. R is the gas constant and N_A is the Avogadro's constant.

Before use, 1-bromo-3-methyl-2-butene (Sigma-Aldrich, purity >95%) and 1-chloro-3-methyl-2-butene (Sigma-Aldrich, purity >95%) were degassed by several freeze–pump–thaw cycles. Helium (Messer-Griesheim purity of 99.9996%) and O₂ (Aga, purity of 99.998%) were used as supplied.

Computational methods and master equation simulations

We used the MN15 functional²⁸ with the Def2TZVP basis set²⁹ to locate the stationary points on the potential energy surface (PES) of reaction (1). The same level of theory was used to determine harmonic frequencies and to perform one-dimensional hindered rotor scans (5 degree increments). The harmonic frequencies were scaled³⁰ by a factor of 0.979 to partially account for anharmonic effects. Single-point energies were calculated for many of the stationary points at the ROHF-CCSD(T) level of theory using the cc-pVDZ, cc-pVTZ, and cc-pVQZ basis sets.³¹ The Hartree–Fock and correlation energies of the species were extrapolated to the complete basis set limit using relations (E5) and (E6), respectively.^32,33

E_HF(X) = E^CBS_HF + B_HF e^−a_HFX (E5)

E_corr(X) = E^CBS_corr + B_corrX_corr^−a (E6)

Here X is 2, 3, and 4 for the basis sets cc-pVDZ, cc-pVTZ, and cc-pVQZ, respectively and the E^CBS, B, and a parameters are obtained by solving a system of three equations. The MN15/Def2TZVP and ROHF-CCSD(T)/CBS calculations were performed with Gaussian 16.³⁴

Multireference methods were used to evaluate the energies of some stationary points. We used the CASPT2 method with the cc-pVTZ and cc-pVQZ basis sets. For multireference calculations, we extrapolated the complete basis set (ΔE^CBS_total) limit energy difference from the following relation.³⁵

ΔE^CBS_total = ΔE_cc-pVQZ − ((ΔE_cc-pVTZ − ΔE_cc-pVQZ) × 0.69) (E7)

The ORCA software package (program version 4.2.0)³⁶ was employed in these calculations using the default CASSCF/CASPT2 settings. Notably, we did not use IPEA or level shifts. In a recent publication, Zobel et al. questioned the validity of the IPEA shift.³⁷ In their investigation of excitation energies of organic molecules, they found that the ideal value of the IPEA shift correlated both with the size of the molecule and the basis set that was being used. Thus, the idea of there being an average IPEA shift value that improves the results for most systems seems unreasonable. Furthermore, for the benchmark set they were testing, they found that using the standard IPEA shift of 0.25 resulted in poorer agreement with experiment than not using an IPEA shift. Level shifts are typically used to avoid problems with intruder states. In our calculations, reference weights were between 0.7–0.8, so intruder states should not be a problem and, therefore, level shifts are not needed. Details on active space selections are given in the results and discussion section.

In order to complement the measured bimolecular rate coefficients (k_1a, k_1b), ME simulations were performed on the associated PES. ME simulations were done using MESMER code (version 6.1)³⁸ incorporating 1-D energy-grained ME treatment. Coupling between external and internal rotations can be treated classically, although potential coupling between internal rotors is not explicitly treated.

Since there are no well-defined transition states for the barrierless R + O₂ → ROO association reactions,²⁴ we used the inverse-Laplace transform (ILT) method implemented in MESMER to compute the number of states of the variational transition states. The expression MESMER transforms is the modified Arrhenius expression of the canonical (high-pressure) association reaction rate coefficient. The Arrhenius parameters in the expression can be optimized using experimental data.

Here, k_∞(T) is the rate coefficient at the high pressure limit, T is temperature, and T_ref (=300 K) is the reference temperature. A, m and E_a are the pre-exponential factor, modified Arrhenius parameter and activation energy, respectively. Note that since reaction (1a) is considered to be a barrierless reaction, the activation energy in (E8) is approximated to be zero (i.e. E_a = 0). Microcanonical rate coefficients are calculated using RRKM theory.

MESMER utilizes a single-exponential-down model (E9) to account for the energy transfer via collisions between bath gas (i.e. helium in our case) and modelled species.

Here, 〈ΔE_down〉 corresponds to an average energy transferred from a higher energy grain to a lower energy grain in a single collision, and is used to calculate the associated collisional energy transfer probabilities. The 〈ΔE_down,ref〉 and n are the independent parameters representing the value of 〈ΔE_down〉 at some reference temperature (T_ref = 300 K) and the temperature dependence of the 〈ΔE_down〉, respectively. The Lennard-Jones (L-J) potential model was used for obtaining the collision frequencies governing the energetics of collisions between bath-gas and modelled species. The L-J parameters used for helium bath-gas and the modeled species are shown in Table 1.

Table 1 L-J parameters for Helium bath-gas³⁹ and C₅H₉O₂ intermediates

Species	ε (K)	σ (Å)
Helium	10.2	2.55
C5H9O2 intermediates	463	6.53

---

We used the online resources of Cantherm⁴⁰ to estimate the L-J parameters of (CH₃)₂CCHCH₂OOH (2-methylbut-3-ene-2-peroxol) and HOO(CH₃)₂CCHCH₂ (3-methylbut-2-ene-1-peroxol) with the Joback method. We averaged these values and assigned them to the C₅H₉O₂ intermediates.

An energy grain size of 75 cm⁻¹ was used in all MESMER simulations. The quantum-mechanical tunneling corrections for elementary steps involving intra-molecular H-atom transfer were modelled using Eckart potential energy barriers.

Subsequently, using the experimental data as input, MESMER optimizes the fitting parameters for the modified Arrhenius eqn (E8) (i.e. parameters A and m) and the collisional energy transfer model (i.e. parameters 〈ΔE_down,ref〉 and n), by minimizing the value of χ²(k_1a(exp.) − k_1a(calc.))² using a built-in Levenberg–Marquardt fitting algorithm (non-linear least-squares fitting method). The optimized ME model may then be used to extrapolate the kinetics of reaction (1) to experimentally inaccessible temperature and pressure conditions.

Results and discussion

The results of the kinetics measurements of the (CH₃)₂CCHCH₂ + O₂ reaction (1) are categorized into low, intermediate, and high temperature region based on their kinetic behavior in the employed overall temperature range 238–660 K of the current work.

Low and intermediate temperature range

As can be seen in Fig. 2, the (CH₃)₂CCHCH₂ radical decay kinetics at 298 K and below in the low temperature range (238–298 K) is single-exponential and is governed by the forward reaction (1a), (CH₃)₂CCHCH₂ + O₂ → (CH₃)₂CCHCH₂OO. In the intermediate temperature range (325–373 K), the dissociation of (CH₃)₂CCHCH₂OO adducts back to reactants (reaction (−1a)) becomes increasingly important and results in the bi-exponential behavior of the observed (CH₃)₂CCHCH₂ radical decay signals.

Fig. 2 A comparative plot for the measured (CH₃)₂CCHCH₂ radical decay signals obtained at three different temperatures at low (238–298 K) and intermediate (325–373 K) temperature ranges, reflecting the increasing importance of (CH₃)₂CCHCH₂OO adduct dissociation back to the reactants (via reaction (−1a)) above 298 K temperature.

A typical bimolecular plot for reaction (1a) in the low temperature range is shown in Fig. 3 and the plot represents the measured pseudo-first-order rate coefficients as a function of the employed molecular oxygen concentration, [O₂].

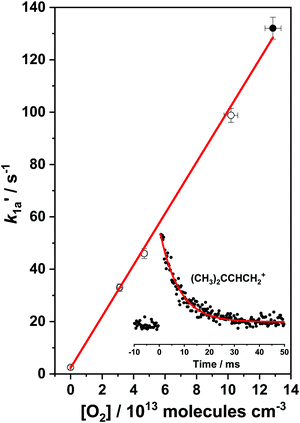Fig. 3 A bimolecular plot of the (CH₃)₂CCHCH₂ + O₂ → (CH₃)₂CCHCH₂OO association reaction (1a) measured at T = 298 K and P = 1.2 Torr. A typical (CH₃)₂CCHCH₂ radical decay profile (, filled circle) for reaction (1a) is shown on the lower right corner of the plot. Statistical uncertainties shown are 1σ.

We were not able to observe a (CH₃)₂CCHCH₂OO adduct (m/z = 101) formation signal, because ions of peroxy radicals (apart from CH₃OO radical) are generally not stable and may instead dissociatively ionize to produce the parent radical ion (i.e. (CH₃)₂CCHCH₂⁺ radical ion in the current case) among other products.⁴¹ For this reason, in our kinetic experiments we have utilized a low photon energy, 8.44 eV, radiation for ionization of (CH₃)₂CCHCH₂ radical (m/z = 69) and avoided any dissociative ionization of (CH₃)₂CCHCH₂OO adducts to the m/z = 69 of the parent radical. This can be clearly observed from Fig. 2, where the signal at m/z = 69 from the (CH₃)₂CCHCH₂ radical measured at 298 K decays back to the baseline.

For the low temperature range experiments, the measured pressure-dependent bimolecular rate coefficients (k_1a) of reaction (1a) are shown in Table 2. Experiments were mainly performed using the (CH₃)₂CCHCH₂Br photolytic precursor. A few measurements using chloride precursor show that the measured k_1a values are independent of the precursor used (i.e. (CH₃)₂CCHCH₂Br or (CH₃)₂CCHCH₂Cl).

Table 2 The experimental conditions and results of the low temperature range kinetics measurements for reaction (1a).^a Statistical uncertainties shown are 1σ

T (K)	P He (Torr)	[He]/10^16 (cm^−3)	[Pr]/10^12 (cm^−3)	[O2]/10^13 (cm^−3)		k ^(R)wall ^b (s^−1)	k ^(R)wall ^c (s^−1)	k 1a/10^−12 (cm^3 molecule^−1 s^−1)
a Xe-lamp with a sapphire window was used for detection as well as stainless steel reactor (i.d. = 1.7 cm) with halocarbon wax coating, unless otherwise stated. b Average of the measured wall rates for the (CH3)2CCHCH2 radical. c Wall rates determined from the linear fit y-axis intercepts of the bimolecular plots for reaction (1a). d Stainless steel reactor (i.d. = 0.8 cm) with halocarbon wax coating. e 1-Chloro-3-methyl-2-butene precursor was used for the production of (CH3)2CCHCH2 radical utilizing pyrex-glass reactor (i.d. = 1.65 cm) with halocarbon wax coating.
238	0.22	0.89	0.30	2.32–6.81	47.9–119.2	5.5 ± 0.8	5.5 ± 1.5	1.70 ± 0.09
238	0.40	1.62	0.27	1.45–4.65	38.2–94.3	5.1 ± 0.9	5.5 ± 1.1	2.06 ± 0.08
238	0.81	3.29	0.25	0.95–3.01	33.2–79.3	4.0 ± 0.6	4.2 ± 0.7	2.56 ± 0.09
238^d	2.39	9.70	1.87	2.68–5.13	109.6–167.8	19.7 ± 1.2	19.8 ± 0.9	2.97 ± 0.13
238^d	3.66	14.85	2.99	2.31–5.33	120.3–202.1	21.8 ± 1.2	22.4 ± 2.7	3.55 ± 0.16
268	0.20	0.72	0.25	4.11–15.06	43.6–129.0	4.1 ± 0.8	4.3 ± 0.8	0.85 ± 0.03
268	0.40	1.44	0.40	1.63–6.82	19.5–76.1	2.2 ± 0.9	2.1 ± 0.4	1.07 ± 0.02
268	0.81	2.92	0.39	1.11–4.96	25.2–79.9	3.5 ± 0.7	3.5 ± 0.7	1.54 ± 0.06
268^e	1.21	4.36	19.4	4.84–10.46	80.3–184.0	8.8 ± 2.6	8.5 ± 2.1	1.62 ± 0.09
268^d	2.68	9.66	3.03	2.16–8.36	69.5–185.7	19.8 ± 1.2	21.9 ± 3.6	1.97 ± 0.11
268^d	4.12	14.85	3.06	2.55–6.06	86.0–160.3	24.3 ± 1.3	24.2 ± 3.0	2.21 ± 0.12
298	0.31	1.00	0.35	4.28–12.52	17.1–60.2	2.8 ± 0.7	2.5 ± 0.8	0.45 ± 0.02
298	0.60	1.94	0.32	2.82–12.65	24.0–91.7	4.4 ± 0.7	4.4 ± 0.7	0.67 ± 0.02
298	1.20	3.89	0.32	3.11–12.85	33.0–132.1	2.5 ± 0.6	2.4 ± 0.6	0.97 ± 0.02
298^e	1.20	3.89	16.9	4.55–12.28	53.4–134.2	3.7 ± 1.9	3.8 ± 0.7	1.02 ± 0.02
298^d	2.99	9.69	0.84	3.63–25.91	74.9–297.6	17.4 ± 1.0	18.4 ± 2.2	1.19 ± 0.08
298^d	4.57	14.81	1.68	4.25–11.33	81.1–164.7	15.8 ± 0.7	16.4 ± 2.1	1.40 ± 0.06

---

For the intermediate temperature range, the observed forward and backward rate coefficients of reactions (1a) and (−1a), along with respective natural logarithm of the equilibrium constants (ln(K_eq)) are given in Table 3. The results of the intermediate temperature range measurements are also independent of the precursor ((CH₃)₂CCHCH₂Br or (CH₃)₂CCHCH₂Cl) used. The returned values of the fitting parameters associated with fitting the bi-exponential expression [R_t] = B + Ce^−λ₁t + De^−λ₂t to the decay traces are given in the ESI† (see Table S1).

Table 3 The experimental conditions and results of the intermediate temperature range measurements for reaction (1a,−1a).^a Statistical uncertainties shown are 1σ

T (K)	P He (Torr)	[He]/10^16 (cm^−3)	[O2]/10^14 (cm^−3)	k ^(R)wall ^b (s^−1)	k ^(ROO)irr. ^c (s^−1)	k 1a/10^−14 (cm^3 molecule^−1 s^−1)	k −1a (s^−1)	ln(Keq)^d
a Xe-lamp with a sapphire window was used for detection as well as Pyrex-glass reactor (i.d. = 1.65 cm) with polydimethylsiloxane (PDMS) coating, unless otherwise stated. b Average of the measured wall rates for the (CH3)2CCHCH2 radical. c Rate coefficients for irreversible first-order decay processes of ROO adducts, determined from the bi-exponential fit performed to the observed (CH3)2CCHCH2 radical decay profiles. d Natural logarithmic of the measured Keq values. e 1-Chloro-3-methyl-2-butene precursor was used for the production of the (CH3)2CCHCH2 radical as well as Pyrex-glass reactor (i.d. = 1.65 cm) with halocarbon wax coating. f Stainless steel reactor (i.d. = 0.8 cm) with halocarbon wax coating.
325	0.86	2.56	2.99	13.8 ± 0.3	15.4 ± 1.5	48.7 ± 6.4	15.0 ± 4.7	13.49 ± 0.34
325	0.86	2.56	4.83	14.0 ± 0.3	18.1 ± 1.8	44.8 ± 5.9	15.6 ± 6.4	13.37 ± 0.43
330	0.88	2.58	5.37	14.6 ± 0.3	18.8 ± 2.2	43.0 ± 5.6	21.7 ± 10.3	12.98 ± 0.49
335	0.90	2.59	4.36	12.3 ± 0.2	11.8 ± 1.1	35.8 ± 4.5	24.4 ± 5.2	12.67 ± 0.25
337	0.90	2.58	4.88	13.5 ± 0.3	15.7 ± 1.4	35.1 ± 4.5	33.3 ± 8.2	12.33 ± 0.28
338	0.91	2.60	5.17	17.7 ± 0.3	17.2 ± 1.5	34.1 ± 4.3	31.5 ± 7.8	12.35 ± 0.28
344	0.92	2.58	5.01	15.5 ± 0.3	17.7 ± 1.1	31.1 ± 3.9	49.6 ± 7.5	11.79 ± 0.20
348	0.94	2.61	5.35	15.0 ± 0.5	16.5 ± 1.1	26.0 ± 3.2	56.7 ± 7.8	11.47 ± 0.19
353	0.96	2.63	5.73	13.2 ± 0.5	20.0 ± 4.4	19.5 ± 3.3	63.2 ± 25.7	11.05 ± 0.44
356	0.96	2.60	5.22	12.9 ± 0.4	19.5 ± 1.8	21.8 ± 2.8	98.5 ± 13.9	10.71 ± 0.19
356^e	1.22	3.31	7.39	9.8 ± 2.1	7.4 ± 5.1	24.4 ± 11.3	100.8 ± 76.9	10.80 ± 1.09
358	0.97	2.62	6.37	14.6 ± 0.5	15.1 ± 5.9	21.7 ± 5.7	116.6 ± 66.7	10.54 ± 0.63
361	0.48	1.28	5.58	12.6 ± 0.3	20.5 ± 2.2	15.6 ± 3.9	79.5 ± 12.7	10.58 ± 0.30
361	0.96	2.57	7.17	13.8 ± 0.3	16.1 ± 1.5	21.3 ± 2.8	124.8 ± 17.8	10.44 ± 0.19
361^e	1.22	3.26	7.21	9.9 ± 2.0	7.9 ± 4.8	18.2 ± 8.1	116.1 ± 85.4	10.36 ± 1.02
361^f	3.61	9.66	6.57	15.9 ± 0.9	33.1 ± 14.9	13.5 ± 4.1	103.4 ± 67.8	10.17 ± 0.72
361^f	5.58	14.93	4.72	17.5 ± 1.1	39.6 ± 21.2	19.5 ± 7.1	128.5 ± 95.0	10.32 ± 0.82
362	0.97	2.59	5.20	12.6 ± 0.3	21.4 ± 2.8	22.3 ± 3.3	153.7 ± 25.7	10.27 ± 0.22
367	0.71	1.87	6.45	13.3 ± 0.5	19.2 ± 4.4	17.7 ± 3.9	167.7 ± 44.6	9.95 ± 0.35
373	0.76	1.97	4.66	14.2 ± 0.4	19.2 ± 5.9	21.7 ± 5.7	264.8 ± 71.0	9.67 ± 0.38
373	1.21	3.13	6.48	12.4 ± 0.5	20.8 ± 6.0	17.5 ± 3.9	282.2 ± 75.3	9.40 ± 0.35

---

The stated uncertainties of the k_1a values in the low temperature range (Table 2) originate from linear fits to the data and are somewhat smaller than the uncertainties of the k_1a values in the intermediate temperature range (Table 3), where the bi-exponential expression described above is fitted to the data and the stated uncertainties originate from using an error propagation method and eqn (E1). The stated uncertainties of the k_−1a values in the intermediate temperature range (Table 3) are obtained using an error propagation method and eqn (E2). The uncertainties of the k_−1a values are larger than those of the k_1a values.

The overall uncertainty (accuracy) of the k_1a values presented in Table 2 is estimated to be about ±25%. This estimation is composed of several sources of uncertainties. The above discussed fitting uncertainties are the single most important sources, while uncertainties to determine reactant concentrations and uncertainties in measuring temperature and pressure of the reaction zone also play a role. Overall uncertainties of the k_1a and k_−1a values in the intermediate temperature range are difficult to estimate.

High temperature range

Once the temperature is increased well above the intermediate temperature range, a new, considerably slower reaction channel appears to open for the (CH₃)₂CCHCH₂ + O₂ reaction, becoming measurable at about 500 K with the current apparatus. Bimolecular rate coefficients of the (CH₃)₂CCHCH₂ + O₂ reaction, k_1b, were then measured over a temperature range of 500–660 K. The upper limit of 660 K temperature originates from the thermal stability of the (CH₃)₂CCHCH₂Br radical precursor in the reactor. A bimolecular plot obtained for reaction (1b) is shown in Fig. 4. The measured bimolecular rate coefficients of reaction (1b) in the temperature range 500–660 K are given in Table 4. The values of k_1b appear to be independent of total pressure.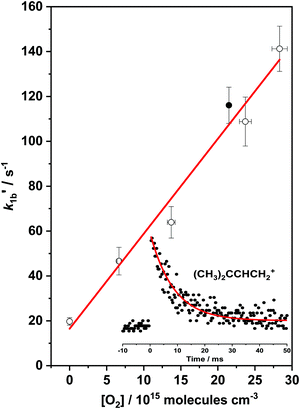

Fig. 4 A bimolecular plot for (CH₃)₂CCHCH₂ + O₂ → products reaction (1b), measured at T = 550 K and P = 2.92 Torr. The lower right corner of the plot presents the (CH₃)₂CCHCH₂ radical decay profile under conditions of the filled circle in the plot. The uncertainties shown are 1σ.

Table 4 The experimental conditions and results of the bimolecular rate coefficient measurements of reaction (1b).^a Statistical uncertainties shown are 1σ

T (K)	P He (Torr)	[He]/10^16 (cm^−3)	[Pr]/10^12 (cm^−3)	[O2]/10^15 (cm^−3)		k ^(R)wall ^b (s^−1)	k ^(R)wall ^c (s^−1)	k 1b/10^−15 (cm^3 molecule^−1 s^−1)
a Xe-lamp with a sapphire window was used for detection as well as quartz reactor (i.d. = 0.85 cm) with boric acid coating. b Average of the measured wall rates for the (CH3)2CCHCH2 radical. c Wall rates determined from the linear fit y-axis intercepts of the bimolecular plots for reaction (1b).
501	2.90	5.59	1.25	7.41–29.17	72.8–120.1	29.6 ± 2.3	33.3 ± 4.1	2.82 ± 0.44
502	2.94	5.66	2.71	9.84–47.43	82.1–185.5	44.6 ± 1.9	45.0 ± 1.2	3.08 ± 0.14
550	2.92	5.13	1.31	6.66–28.32	46.6–141.3	19.7 ± 1.7	18.7 ± 2.7	4.23 ± 0.35
579	1.83	3.05	2.48	3.95–7.52	20.6–33.6	5.2 ± 0.4	5.22 ± 0.1	3.75 ± 0.10
660	5.67	8.30	4.38	7.26–23.28	56.8–103.3	9.1 ± 1.2	9.5 ± 1.9	4.62 ± 0.43

---

Measuring kinetics as slow as reaction (1b) with k_1b ≈ 3–5 × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹ in this work requires significant amounts of O₂ (<51% of the total reaction mixture) to be added to the reaction mixture. This results in high total pressure in the reaction zone (P_total < 7.8 Torr) and high oxygen content of the reaction mixture, which altogether causes high pressures in the vacuum chamber containing the quadrupole mass spectrometer (P_QMS-chamber). In fact, conditions (i.e. P_QMS-chamber) of the kinetic measurements of reaction (1b) were at or even beyond the upper limit of pressure that our PIMS setup can tolerate. In addition, at T > 500 K, presumably heterogeneous wall-effects started to have an influence on the measured values, causing some additional uncertainty on the respective k_1b values. There is some more discussion on this in the ESI† (see Fig. S2). Taking into account the abovementioned additional uncertainty sources at T > 500 K, including the uncertainties in the temperature and pressure measurements in the reaction zone as well as the fitting uncertainties, the overall uncertainty (=accuracy) in the k_1b values presented in Table 4 is estimated to be the factor of two (upper = 2 × k_1b, lower = 0.5 × k_1b).

Measurements were also conducted to detect possible products of reaction (1b). Our quantum chemistry calculations (see next section), suggest isoprene (m/z = 68) + HO₂ (m/z = 33) to be the major product channel of reaction (1b). Our PIMS apparatus is unable to detect HO₂ radical, mainly due to its high ionization energy IE(HO₂) ≈ 11.4 eV.⁴² Utilizing H₂-lamp for ionization radiation, a product formation signal was observed at m/z = 68, see Fig. 5. However, a fast, almost immediate product formation signal at m/z = 68 was observed also in the absence of [O₂], originating, almost certainly, from the photolysis of the radical precursor (CH₃)₂CCHCH₂Br. For this reason, two consecutive measurements were performed, the first one in the absence and the second one in the presence of O₂, see Fig. 5(a). The signal without O₂ was then subtracted from the signal with O₂ present, giving a product formation signal at m/z = 68 originating only from reaction (1b), see Fig. 5(b). The product formation signal at m/z = 68 was fitted using the expression where, I_t(P⁺) is the temporal product ion signal and I₀(P⁺) the signal value for the channel yield × [R]₀ as t → ∞. The term was treated as an independent parameter and the fitting process returned the value see the fit in Fig. 5(b). This value agrees well within the stated 1σ-uncertainty with the value obtained from fitting the corresponding (CH₃)₂CCHCH₂ radical decay profile shown in Fig. 5(c). This shows that under utilized pseudo-first-order conditions, signal at m/z = 68 originates from reaction (1b). As already mentioned, high values of P_QMS-chamber reduces detection sensitivity of the PIMS apparatus, which is evident from the product ion signals presented in the Fig. 5.

Fig. 5 The product formation and corresponding radical decay profiles for the (CH₃)₂CCHCH₂ + O₂ → products reaction (1b), measured at T = 501 K, P = 2.9 Torr. The top most panel (a) depicts the product ion formation signals observed at m/z = 68. The filled blue and red circles represent the product ion formation signals when [O₂] = 0 cm⁻³ and 2.2 × 10¹⁶ cm⁻³, respectively. The middle panel (b) shows the difference between the product ion formation signals observed at [O₂] = 2.2 × 10¹⁶ cm⁻³ and [O₂] = 0 cm⁻³. The corresponding (CH₃)₂CCHCH₂ radical decay profile measured at [O₂] = 2.2 × 10¹⁶ cm⁻³ is shown on the bottom panel (c).

The measured values of k_1b exhibit weak, positive temperature dependence. Current results show that in the temperature range of 500–660 K, the k_1b values are in the range of (2.82–4.62) × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹. These values are comparable to the bimolecular rate coefficient k(753 K) = 3.49 × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹ measured by Baldwin et al.²³ for the kinetics of the CH₂CHCHCH₂CH₃ + O₂ → CH₂ = CHCH = CHCH₃ + HO₂ reaction channel at 753 K, and about 10 times faster than an upper-limit of bimolecular rate coefficient of the CH₃CHCHCH₂ + O₂ reaction measured at 700 K by Knyazev et al.²² In addition, current results are an order of 10³ times faster than the bimolecular rate coefficient measured for allyl-radical + O₂ reaction at a temperature of 673 K.²⁰ We are not aware of any previous measurements of bimolecular rate coefficients of the (CH₃)₂CCHCH₂ + O₂ reaction.

The Arrhenius plot for the forward bimolecular rate coefficients of the (CH₃)₂CCHCH₂ + O₂ reaction, k_1a and k_1b, measured in this work at the overall temperature range of (238–660) K, is presented in Fig. 6. This plot is both striking and revealing. It shows that in both the low- and intermediate temperature ranges the (CH₃)₂CCHCH₂ + O₂ reaction shows negative temperature and positive pressure dependence and is faster than the allyl + O₂ reaction¹⁹ but comparable to the CH₂CHCHCH₂CH₃ + O₂ reaction²⁴ at 298 K. Upon increasing temperature to about 500 K, the rate coefficient of the (CH₃)₂CCHCH₂ + O₂ reaction decreases by almost two orders of magnitude. The temperature dependence also changes from negative to positive and the rate coefficient becomes pressure-independent. Next, we use computational methods to better understand the kinetics and mechanism behind the observed behavior of the (CH₃)₂CCHCH₂ + O₂ reaction.

Fig. 6 An Arrhenius-type plot for the bimolecular rate coefficients of the (CH₃)₂CCHCH₂ + O₂ reaction (1) measured in this work. The presented dataset encompasses the employed temperature range of 238–660 K and bath-gas pressures 0.2–5.7 Torr, respectively. Filled and blank circles indicate the experiments conducted using brominated ((CH₃)₂CCHCH₂Br) and chlorinated ((CH₃)₂CCHCH₂Cl) photolytic precursors, respectively.

Quantum chemistry

The results of our quantum chemical calculations along with the geometries of the stationary points of reaction (1) are provided in the ESI† (Tables S2 and S3). Based on the MN15/Def2TZVP energies, reaction channels that have barriers over 12 kcal mol⁻¹ (relative to the reactants R + O₂) were omitted from additional analysis as kinetically unimportant. The remaining channels were further investigated with the ROHF-CCSD(T)/CBS method. It was discovered that the lowest energy reaction channel leads to the formation of 2-methylbut-1,3-diene (isoprene) and hydroperoxyl radical from the non-terminal peroxyl radical (ROO_(nt)) by concerted elimination. At slightly higher energy appears the reaction channel that leads to the (2R/S)-3-methyl-1,2-epoxybut-3-ene and hydroxyl radical. However, both of these channels have barriers that are over 6 kcal mol⁻¹ above the energy of the reactants. With barriers this high the experimental high-temperature rate coefficients would be under-predicted by several orders of magnitude. We were quite certain we had managed to locate all the important reaction channels, so we started to question the accuracy of our ROHF-CCSD(T)/CBS calculations. To check whether multi-reference methods would need to be used, we recalculated the energetics of the low-energy reaction channels with the CASPT2/CBS method. Note that the T1 diagnostics were generally acceptable for the kinetically important transition state structures (below 0.03). The details of the CASPT2 calculations are given separately for each reaction channel.

ROO_(nt) → CH₂C(CH₃)CHCH₂ + HO₂ (P1)

This is a single-step reaction where isoprene + HO₂ products are formed from ROO_(nt) by concerted elimination (see Fig. 8). Similar to the ROHF-CCSD(T)/CBS calculations, CASPT2/CBS calculations predict this channel to have the lowest reaction barrier. ROHF-CCSD(T)/CBS calculations have a barrier of 26.3 kcal mol⁻¹ above the energy of the ROO_(nt). CASPT2/CBS calculations with a 13,11 active space reduce the barrier to 22.8 kcal mol⁻¹. The active space consists of the lone electron pairs of the oxygen atoms (4,2), the bonding and anti-bonding C–O and O–O σ orbitals (4,4), the bonding and anti-bonding π orbitals of the C=C bond (2,2), the radical orbital on the terminal oxygen atom (1,1), and the bonding and anti-bonding electron orbitals of the C–H bond where the hydrogen is abstracted (2,2). The CASPT2 barrier is 3.5 kcal mol⁻¹ lower in energy than the ROHF-CCSD(T) one and is much more consistent with the experimental observations. However, we cannot rule out that this is fortuitous. Nonetheless, an energy difference this large between the CASPT2 and ROHF-CCSD(T) calculations is interesting, especially since the T1 diagnostic (0.029) would suggest that a single-reference approach should be appropriate. It is possible that there is a concerted elimination channel from the terminal peroxyl radical (ROO_(t)) that produces isoprene in its cis-form. We were, however, unable to locate the transition state structure for such a process, but we cannot rule out its existence.

ROO_(t) → CH₂C(CH₃)CH(O)CH₂ + HO (P3)

This is a two-step reaction. First ROO_(t) internally abstracts a hydrogen from an allylic position (see Fig. 8). Then the oxygen bonded to a carbon atom reacts with the allylic system to form a C–O σ-bond. As this happens, the O–O σ-bond is broken. The final products are (2R/S)-3-methyl-1,2-epoxybut-3-ene and hydroxyl radical (P3). Two possible transition state structures were found for the hydrogen abstraction which are not rotamers. The ROHF-CCSD(T) calculations set these transition state structures 23.9 kcal mol⁻¹ and 24.0 kcal mol⁻¹ above the energy of the peroxyl radical and the T1 diagnostics are acceptable, 0.024 and 0.022. For the latter step, the transition state structure is 19.6 kcal mol⁻¹ above the energy of the peroxyl radical, although the T1 diagnostic is already moderately high, 0.041. The CASPT2 calculations with a 9,9 active space reduce the relative energies to 22.1 and 22.2 kcal mol⁻¹ (hydrogen abstraction transition state structures) and 12.4 kcal mol⁻¹ (ring-forming/OH eliminating transition state structure). The active space consists of the bonding and anti-bonding C–O and O–O σ-orbitals (4,4), the bonding and anti-bonding π-orbitals of the C=C bond (2,2), the radical orbital on the terminal oxygen atom (1,1), and the bonding and anti-bonding C–H σ-orbital of the hydrogen that is abstracted (2,2). The lone pair electron orbitals of the oxygens are almost fully occupied and were left out of the active space. The hydrogen abstraction reactions are the kinetic bottleneck and the CASPT2 calculations reduce the barriers by around 2 kcal mol⁻¹. However, the CASPT2 and ROHF-CCSD(T) energies are within the expected uncertainties of these methods. For the latter transition structure, CASPT2 reduces the energy by over 7 kcal mol⁻¹. This is already a significant change, although somewhat expected as the T1 diagnostic is moderately high (0.041).

Five-membered ring channel (products P4 and P6)

This reaction channel proceeds by either the terminal (ROO_(t)) or non-terminal (ROO_(nt)) peroxy-radical reacting internally with the carbon–carbon double bond to form a five-membered ring (see Fig. 8). The O–O bond then breaks and either propan-2-one and 1,2-epoxyethyl P4 or methanal and 2-methyl-1,2-epoxyprop-1-yl P6 are formed. The ring-forming transition state structures have acceptable T1 diagnostics (<0.03) and ROHF-CCSD(T) calculations predict the barriers 27–31 kcal mol⁻¹ above the energy of ROO_(nt). Only preliminary ROHF-CCSD(T) calculations were performed for the ring-breaking transition state structures because the T1 diagnostics are above 0.05. CASPT2 calculations reduce the relative energies of the ring-forming transition structures by 2–3 kcal mol⁻¹. The CASPT2 relative energies for the ring-breaking transition state structures are 27.0 kcal mol⁻¹ P4 and 25.5 kcal mol⁻¹ P6, respectively. An active space of 7,7 was used in these calculations. The orbitals are the bonding and anti-bonding O–O and C–O σ orbitals (4,4), the bonding and anti-bonding π orbitals of the C=C bond (2,2), and the radical orbital on the terminal oxygen atom (1,1). Again, we observe that CASPT2 calculations reduce the barrier heights. This reaction channel has barriers that are several kcal mol⁻¹ higher in energy than the (P1) channel and is not expected to be kinetically important.

Four-membered ring channel (products P2, P4, P6, P7)

The peroxyl radicals can react with the double bond also to form four-membered rings, which can subsequently form products by either breaking the O–O or the C–C bond (see Table S2, ESI†). In these reactions multi-reference behavior was more apparent and ROHF-CCSD(T) calculations were not carried out systematically. A 9,9 active space was chosen to explore the energetics of these reactions. The orbitals are the bonding and anti-bonding O–O and C–O orbitals (4,4), the bonding and anti-bonding π orbitals of the C=C bond (2,2), the radical orbital on the terminal oxygen atom (1,1), and the bonding and anti-bonding orbitals of the C–C bond that is present in the four-membered ring. As one would expect, the barriers in the four-membered ring channel are noticeably higher in energy than the barriers in the five-membered ring channel and for this reason the four-membered ring channel is not expected to be kinetically important.

We observe that CASPT2 calculations systematically predict lower barriers in comparison to ROHF-CCSD(T) calculations. Significant reductions in barrier heights are observed even in cases where the T1 diagnostic suggest that a single-reference method is suitable. The obvious question is which energies should we trust? The ROHF-CCSD(T) method produces more reliable results when a single-reference approach is suitable, and for the many important transition state structures the T1 diagnostics suggest that such an approach is suitable. However, we are confident in our experimental findings, which strongly suggest that the ROHF-CCSD(T) energies (barriers) are too high and that the CASTP2 energies are more reasonable. If the CASPT2 energies are indeed more correct, it may indicate that the T1 diagnostic alone is a less reliable measure of the multi-reference character present in the studied species. Although we are more inclined to trust the CASPT2 energies, we cannot entirely rule out the possibility that the ROHF-CCSD(T) energies are reliable, in which case we have simply failed to locate low-energy reaction channel(s). For ME simulations, we decided to use ROHF-CCSD(T) energies for the peroxyl radicals (ROO_(t), ROO_(nt) well-depths) and for the products. CASPT2 energies are used for everything else. To simplify the simulations, we left out all reaction channels with a barrier higher than 8 kcal mol⁻¹ above the energy of the reactants.

ME simulation results

As discussed in the experimental section, under conditions where kinetic equilibrium is established (e.g. reactions (1a) and (−1a)), a decay profile of a resonance-stabilized radical with two non-similar resonance structures follows, in principle, a tri-exponential behavior, but can be fitted with a double-exponential expression. This double-exponential fit yields “average” values for the forward and reverse rate coefficients and can be used to compute an “average” equilibrium constant value. Such results of the double-exponential fits to the measured radical decays at an intermediate temperature range are given in Table 3. However, our quantum chemistry calculations revealed that the ROO_(t) well depth is around 2.5 kcal mol⁻¹ more shallow than the ROO_(nt) well depth. Simulations further revealed that at 325 K, the lowest temperature of our equilibrium constant measurements, the equilibrium population of the ROO_(t) is already below 3% (i.e. [ROO_(t)]/([ROO_(t)] + [ROO_(nt)]) < 0.03). Therefore, the kinetic traces measured in the intermediate temperature range (325–373 K) can be described almost entirely by the kinetic behavior of the R + O₂ ⇌ ROO_(nt) reaction channel.

In our modeling effort, we first used our experimental low- and intermediate-temperature kinetic data to obtain the optimal values for the ROO well-depths as well as for both the exponential-down collision energy transfer (E9) and modified Arrhenius expression (E8) parameters. For the barrierless association reaction channels R + O₂ ⇌ ROO_(t) and R + O₂ ⇌ ROO_(nt), MESMER returned the following modified Arrhenius expressions at the high-pressure limit (E_a in (E8) was set = 0): and , respectively. The optimized 〈ΔE_down〉 parameters are presented by the following expression: . See also Table 5 for these values. For helium bath-gas, the obtained 〈ΔE_down〉 parameters (i.e. 〈ΔE_down,ref〉 = 166 cm⁻¹, n = 0.1), lies within their typical limits.³⁸

Table 5 The MESMER optimized 〈ΔE_down〉 and the modified Arrhenius equation parameters at the high-pressure limit for the reaction channels R + O₂ ⇌ ROO_(t) and R + O₂ ⇌ ROO_(nt)

〈ΔEdown,ref〉 (cm^−1)	n	A R + O2 ⇌ ROO(t) (cm^3 molecule^−1 s^−1)	A R + O2 ⇌ ROO(nt) (cm^3 molecule^−1 s^−1)	m R + O2 ⇌ ROO(t)	m R + O2 ⇌ ROO(nt)
166	0.1	1.17 × 10^−12	2.34 × 10^−12	(−1.06)	(−1.04)

---

In the fitting process, the energy difference between ROO_(nt) and ROO_(t) well-depths was constrained to remain equal to the energy difference obtained from ROHF-CCSD(T)/CBS calculations. The fitted ROO well-depths are 0.72 kcal mol⁻¹ shallower than the computed ones, but are within estimated computational uncertainty (∼1 kcal mol⁻¹).

As shown in Fig. 7, the measured values of average ln(K_eq) at the intermediate temperature range are plotted alongside the calculated channel-specific ln(K_eq) values of reaction channels R + O₂ ⇌ ROO_(t) and R + O₂ ⇌ ROO_(nt). For a given temperature range, MESMER uses NASA-polynomials for generating the temperature dependent standard thermodynamic quantities, such as standard enthalpy (H°)_T, entropy (S°)_T and Gibbs free energy (G°)_T, for different reaction species. These standard thermodynamic quantities are then used for calculating the ln(K_eq) values for each reaction channel independently. The thermodynamic MESMER output file contains the standard thermodynamic quantities of a particular species in their zero-point energy corrected form e.g.. This enables us to locate the changes in the calculated channel specific ln(K_eq) values with respect to the fitted ROO well-depths. Interestingly, the more shallow ROO_(nt) and ROO_(t) well-depths (by 0.72 kcal mol⁻¹ each) returned by the fitting process, give the ln(K_eq) values for reaction channel R + O₂ ⇌ ROO_(nt) that are equivalent to the measured average ln(K_eq) values, see Fig. 7. This strongly suggests that the kinetic traces measured in the intermediate temperature range are almost entirely due to the R + O₂ ⇌ ROO_(nt) reaction channel.

Fig. 7 The ln(K_eq) values of the R + O₂ ⇌ ROO reactions (1a,−1a), R = (CH₃)₂CCHCH₂, plotted as a function of temperature. Experimental results are given as symbols and computational MESMER results as lines. Filled and blank circles indicate the experiments conducted with brominated ((CH₃)₂CCHCH₂Br) and chlorinated ((CH₃)₂CCHCH₂Cl) precursors, respectively.

Incorporating 0.72 kcal mol⁻¹ (shallower) correction to the ROO_(nt) and ROO_(t) well-depths provides the standard reaction enthalpies for reaction channels R + O₂ ⇌ ROO_(t) and R + O₂ ⇌ ROO_(nt) to be (−17.1) kcal mol⁻¹ and (−20.0) kcal mol⁻¹, respectively.

The potential energy profile utilized in the ME simulations of reaction (1), already including the 0.72 kcal mol⁻¹ correction to the ROO well-depths, is shown in Fig. 8. The product energies are from ROHF-CCSD(T)/CBS calculations and all the other energies, apart from the ROO well-depths, are from CASPT2 calculations.

Fig. 8 The simplified potential energy profile for the R + O₂ ⇌ reaction (R = (CH₃)₂CCHCH₂) used in our ME simulations. Energies are in kcal mol⁻¹. The reported Int1T (ROO_(t)) and Int1NT (ROO_(nt)) energies include the correction of 0.72 kcal mol⁻¹. The rest of the energies are either from ROHF-CCSD(T)/CBS//MN15/Def2TZVP or CASPT2/CBS//MN15/Def2TZVP calculations. The optimized geometries, T1 diagnostic values and single point energies of the stationary points are given in the ESI† (see Tables S2–S3).

Measured bimolecular rate coefficients of reaction (1a) at three temperatures along with the results of constrained ME simulations performed over a wide pressure range are shown in Fig. 9. As can be seen, a reasonably good agreement with the experimental results is obtained.

Fig. 9 The bimolecular rate coefficients of reaction (1a), R + O₂ → ROO_(t,nt), R = (CH₃)₂CCHCH₂, plotted as a function of pressure at three temperatures. The symbols depict the experimental results and the lines show the results of ME simulations. The optimized modified Arrhenius equation parameters at the high-pressure limit and 〈ΔE_down〉 parameters are shown on the lower right corner. Filled and blank circles indicate the experiments conducted with brominated ((CH₃)₂CCHCH₂Br) and chlorinated ((CH₃)₂CCHCH₂Cl) precursors, respectively.

While the constrained ME model is able to reproduce the experimental kinetic data in the low-temperature range, the simulated bimolecular rate coefficients in the high-temperature range are a factor of 5–9 times lower than the respective experimental k_1b values. To remedy this, we lowered the barrier height of transition state (TS1NTP1) associated with the kinetically most dominant channel R + O₂ → isoprene + HO₂ by ∼2.2 kcal mol⁻¹. This adjustment is within the expected uncertainty of the CASPTP2/CBS calculations.

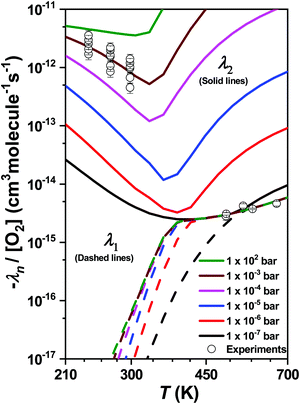
During our ME simulations, we discovered that under most pressure conditions there is a one-to-one correspondence between an eigenvalue λ₁ and the high-temperature bimolecular rate coefficients k_1b at T > 450 K. This correspondence was checked at different temperatures and pressures by manually performing single-exponential fits to simulated decay profiles. Similarly, we also observed that an eigenvalue λ₂ corresponds to the bimolecular rate coefficients measured in the low temperature range (T < 300 K). The pressure and temperature dependent behavior of λ₁ and λ₂ is illustrated in Fig. 10. Interestingly, under extremely low pressure conditions (P ∼ 1 × 10⁻⁷ bar) there is a nearly seamless transition from λ₁ to λ₂ upon increasing temperature. Above this pressure, there exists a narrow transition region (∼300–450 K) where the kinetic behavior of the system cannot be described by a single eigenvalue. In this region multi-dimensional decays are observed.

Fig. 10 The chemically significant eigenvalues λ₁ (dashed lines) and λ₂ (solid lines) plotted as a function of temperature and pressure. The symbols depict results of the measurements. ROO_(t) and ROO_(nt) well-depths were shallowed by ∼0.72 kcal mol⁻¹ each and the barrier height for the transition state (TS1NTP1) associated with channel R + O₂ → isoprene + HO₂ (P1) was lowered by ∼2.2 kcal mol⁻¹.

We multiply −λ₁/[O₂] with the calculated branching ratios of different product channels to obtain channel-specific bimolecular rate coefficients at T > 450 K. Arrhenius fits were then performed to obtain the results in a form that is usable in autoignition and combustion models. The channel specific Arrhenius fit parameters are reported in Table 6.

Table 6 Arrhenius expression parameters for different product channels of (CH₃)₂CCHCH₂ + O₂ → products, reaction (1b), in the high temperature range

Reaction channel (T = 450–2000 K)
	A (cm^3 molecule^−1 s^−1)	m	E a (kcal mol^−1)
TS1NTP1 lowered by ∼2.2 kcal mol^−1
R + O2 → P1	1.46 × 10^−19	1.71	0.78
Transition states unadjusted
R + O2 → P1	2.87 × 10^−20	1.91	2.46
R + O2 → P3	2.09 × 10^−28	3.76	−2.53
R + O2 → P4	3.56 × 10^−18	0.79	7.02
R + O2 → P6	3.18 × 10^−18	0.77	5.51

---

The Arrhenius expressions of Table 6 fit closely the results of ME simulations of bimolecular reaction channels leading to products P1, P3, P4, and P6, which are shown in Fig. 11(a). Among all the channels studied in this work, (CH₃)₂CCHCH₂ + O₂ → isoprene + HO₂ (P1) is overwhelmingly the dominating one with a yield >91% or so without any adjustment to the stationary-point energies. This corroborates our assignment of product formation signal observed at m/z = 68 (see Fig. 5) originating from isoprene. The second most important channel is (2R/S)-3-methyl-1,2-epoxybut-3-ene + OH (P3) with yield <8%. In Fig. 11(b), the ME simulated k_1b values obtained for different channels are compared to the current experimental k_1b values. Clearly, an adjustment to stationary-point energy, here to TS1NTP1, is required to reach agreement with the experimental results. Also shown in Fig. 11(b) are the bimolecular rate coefficients of the (CH₃)₂CCHCH₂ + O₂ → isoprene + HO₂ (P1) reaction channel used by Westbrook et al.¹⁶ in their kinetic modeling study of 2M2B oxidation. Apparently, the current ME simulated k_1b values obtained for the respective (CH₃)₂CCHCH₂ + O₂ → P1 reaction channel only intersect with the results of Westbrook et al. at around T ∼ 1600 K, and diverge sharply for temperatures above and especially below 1600 K. The MESMER input file ((CH₃)₂CCHCH₂.xml) used for ME modeling is available in the ESI.†

Fig. 11 The graph (a) shows the results of ME simulations of different product channels of reaction k_1b (solid lines) as well as their respective Arrhenius fits (dashed lines) given in Table 6. The graph (b) depicts the same results of ME simulations as in (a), compared with our experimental k_1b values (symbols). The graph (b) also shows the rate-coefficients of the (CH₃)₂CCHCH₂ + O₂ → isoprene + HO₂ (P1) bimolecular reaction channel estimated by Westbrook et al.¹⁶ in their 2M2B oxidation study.

Probably the main outcome of the current, combined experimental and theoretical study of the allylic C₅ radical reaction (CH₃)₂CCHCH₂ + O₂ is that larger (>C₄) allylic radicals seem to be more reactive with respect to O₂ under low-temperature combustion (LTC) conditions (T < 1000 K) than is currently believed. However, more work is certainly needed on oxidation kinetics of allylic radicals under LTC conditions to better understand their effects on autoignition behavior of fuel–air mixtures containing alkenes. Similar to this work, investigating oxidation kinetics of different allylic C₅ (and larger) radical isomers experimentally (and theoretically) over a wide temperature range would be valuable. Also, it would be highly useful to have photolysis-initiated product studies of alkene oxidation experiments available that have been performed under LTC conditions.

Conclusion

In this work, we have performed the first direct kinetic measurements of the (CH₃)₂CCHCH₂ + O₂ reaction over a wide temperature range (238–660 K) at low pressures (0.2–5.7 Torr) using photoionization mass spectrometry. Under combustion conditions, the (CH₃)₂CCHCH₂ radical (R) may be produced in H-atom abstraction reactions from 2-methyl-2-butene ((CH₃)₂CCHCH₃) or in decomposition reactions of larger olefinic fuel constituents. The resonance-stabilized (CH₃)₂CCHCH₂ radical has terminal and non-terminal radical sites available for association with molecular oxygen (O₂), resulting in the formation of ROO_(t) and ROO_(nt) adducts, respectively. At low temperatures (238–298 K), the kinetics of reaction (1) is governed by the R + O₂ → ROO adduct formation, exhibiting a typical negative temperature and positive pressure dependence behavior. At the intermediate temperatures (325–373 K), kinetics of equilibrium R + O₂ ⇌ ROO reaction is measured and experimental equilibrium constant ln(K_eq) values are determined. Master equation (ME) simulations and concomitant CCSD(T) and CASPT2 potential energy profile calculations of reaction (1) were performed to support experimental observations. After making a modest adjustment to the ROO_(t) and ROO_(nt) well-depths (∼0.7 kcal mol⁻¹ each), the ME model was able to reproduce the R + O₂ kinetics measured at low and intermediate temperatures. Interestingly, simulations reveal that the kinetics of the R + O₂ ⇌ ROO equilibrium reaction measured at intermediate temperature ranges is almost entirely dominated by the R + O₂ ⇌ ROO_(nt) reaction channel. Probably the most important outcome of the current work was the observation and subsequent measurements of significantly faster kinetics of the R + O₂ reaction (1) at high temperatures than combustion models currently expect. The measured bimolecular rate coefficients k_1b = (2.8–4.6) × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹ in the range 500–660 K are pressure-independent and exhibit a weak positive temperature dependence. ME simulations were also performed to calculate kinetics at high temperatures. However, without any corrections to the calculated stationary point energies, ME simulations of the R + O₂ reaction suggest about a factor of 5–9 times slower kinetics than the measured k_1b values. The ME simulations suggest isoprene (2-methylbut-1,3-diene) + HO₂ to be the major product channel of the (CH₃)₂CCHCH₂ + O₂ reaction (1) at high temperatures. In the kinetic experiments, a product formation signal was observed at m/z = 68, which was assigned to originate from isoprene. After a reasonable correction (∼2.2 kcal mol⁻¹) to the CASPT2 energy of the transition-state pertaining to the channel R + O₂ → isoprene + HO₂, a good agreement between the respective ME simulated k_1b values and the measured k_1b values is observed.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. P. J. and A. J. E. acknowledge support from the Academy of Finland, grant numbers 294042, 319353, 325250, and 288377. P. S. acknowledges support from the BiofCFD project of the INNO INDIGO ERA-Net S&T Energy 2016 bio-based energy program funded by the Academy of Finland, grant number 311967. T. T. P. acknowledges support from the Doctoral Programme in Chemistry and Molecular Sciences of the University of Helsinki. The authors wish to acknowledge the CSC-IT Center for Science, Finland, for computational resources.

References

1. D. Y. Goswami and F. Kreith, Handbook of Energy Efficiency and Renewable Energy, CRC Press, Boca Raton, 2007.
2. D. M. Alonso, J. Q. Bond, J. C. Serrano-Ruiz and J. A. Dumesic, Green Chem., 2010, 12, 992–999.
3. S. C. Moldoveanu, Pyrolysis of Organic Molecules: Applications to Health and Environmental issues. Elsevier, Amsterdam, 2009.
4. C. K. Law, Combustion Physics, Cambridge University Press, Cambridge, 2010.
5. I. Glassman, R. A. Yetter and N. G. Glumac, Combustion, Academic Press, Cambridge, 5th edn, 2014.
6. C. K. Westbrook, M. Mehl, W. J. Pitz and M. Sjöberg, Combust. Flame, 2017, 175, 2–15.
7. L. Ruwe, K. Moshammer, N. Hansen and K. Kohse-Höinghaus, Combust. Flame, 2017, 175, 34–46.
8. L. Ruwe, L. Cai, K. Moshammer, N. Hansen, H. Pitsch and K. Kohse–Höinghaus, Combust. Flame, 2019, 206, 411–423.
9. K. Moshammer, L. Seidel, Y. Wang, H. Selim, S. M. Sarathy, F. Mauss and N. Hansen, Proc. Combust. Inst., 2017, 36, 947–955.
10. S. S. Nagaraja, J. Liang, S. Dong, S. Panigrahy, A. Sahu, G. Kukkadapu, S. W. Wagnon, W. J. Pitz and H. J. Curran, Combust. Flame, 2020, 219, 456–466.
11. S. S. Nagaraja, G. Kukkadapu, S. Panigrahy, J. Liang, H. Lu, W. J. Pitz and H. J. Curran, Int, J. Chem. Kinet., 2020, 52, 964–978.
12. C.-W. Zhou, Y. Li, U. Burke, C. Banyon, K. P. Somers, S. Ding, S. Khan, J. W. Hargis, T. Sikes, O. Mathieu, E. L. Petersen, M. AlAbbad, A. Farooq, Y. Pan, Y. Zhang, Z. Huang, J. Lopez, Z. Loparo, S. S. Vasu and H. J. Curran, Combust. Flame, 2018, 197, 423–438.
13. C.-W. Zhou, Y. Li, E. O'Connor, K. P. Somers, S. Thion, C. Keesee, O. Mathieu, E. L. Petersen, T. A. DeVerter, M. A. Oehlschlaeger, G. Kukkadapu, C.-J. Sung, M. Alrefae, F. Khaled, A. Farooq, P. Dirrenberger, P.-A. Glaude, F. Battin-Leclerc, J. Santner, Y. Ju, T. Held, F. M. Haas, F. L. Dryer and H. J. Curran, Combust. Flame, 2016, 167, 353–379.
14. W. K. Metcalfe, W. J. Pitz, H. J. Curran, J. M. Simmie and C. K. Westbrook, Proc. Combust. Inst., 2007, 31, 377–384.
15. F. Arafin, A. Laich, E. Ninnemann, R. Greene, R. K. Rahman and S. S. Vasu, Int, J. Chem. Kinet., 2020, 52, 739–751.
16. C. K. Westbrook, W. J. Pitz, M. Mehl, P.-A. Glaude, O. Herbinet, S. Bax, F. Battin-Leclerc, O. Mathieu and E. L. Petersen, J. Bugler and H. J. Curran, J. Phys. Chem. A, 2015, 119, 7462–7480.
17. X. Meng, A. Rodriguez, O. Herbinet, T. Wang and F. Battin-Leclerc, Combust. Flame, 2017, 181, 283–299.
18. F. Battin-Leclerc, A. Rodriguez, B. Husson, O. Herbinet, P.-A. Glaude, Z. Wang, Z. Cheng and F. Qi, J. Phys. Chem. A, 2014, 118, 673–683.
19. M. P. Rissanen, D. Amedro, A. J. Eskola, T. Kurten and R. S. Timonen, J. Phys. Chem. A, 2012, 116, 3969–3978.
20. Z. H. Lodhi and R. W. Walker, J. Chem. Soc., 1991, 87, 2361–2365.
21. S. P. Joshi, T. T. Pekkanen, R. S. Timonen, G. Lendvay and A. J. Eskola, J. Phys. Chem. A, 2019, 123, 999–1006.
22. V. D. Knyazev and I. R. Slagle, J. Phys. Chem. A, 1998, 102, 8932–8940.
23. R. R. Baldwin, J. P. Bennett and R. W. Walker, J. Chem. Soc., 1980, 76, 2396–2412.
24. M. Döntgen, T. T. Pekkanen, S. P. Joshi, R. S. Timonen and A. J. Eskola, J. Phys. Chem. A, 2019, 123, 7897–7910.
25. C. F. Goldsmith, L. B. Harding, Y. Georgievskii, J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2015, 119, 7766–7779.
26. X. Chen and C. F. Goldsmith, J. Phys. Chem. A, 2017, 121, 9173–9184.
27. A. J. Eskola and R. S. Timonen, Phys. Chem. Chem. Phys., 2003, 5, 2557–2561.
28. S. Y. Haoyu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. Database of Frequency Scale Factors for Electronic Model Chemistries (Version 3 Beta 2), https://comp.chem.umn.edu/freqscale/version3b2.htm, accessed June 2020.
31. T. H. Dunning, Chem. Phys., 1989, 90, 1007–1023.
32. A. Halkier, T. Helgaker, P. Jrgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446.
33. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
35. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
36. F. J. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
37. J. P. Zobel, J. J. Nogueira and L. González, Chem. Sci., 2017, 8, 1482–1499.
38. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
39. B. E. Poling, J. M. Prausnitz and J. P. O’Connell, The Properties of Gases and Liquids, McGraw-Hill, New York, 5th edn, 2001.
40. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225.
41. G. Meloni, P. Zou, S. J. Klippenstein, M. Ahmed, S. R. Leone, C. A. Taatjes and D. L. Osborn, J. Am. Chem. Soc., 2006, 128, 13559–13567.
42. L. G. Dodson, L. Shen, J. D. Savee, N. C. Eddingsaas, O. Welz, C. A. Taatjes, D. L. Osborn, S. P. Sander and M. Okumura, J. Phys. Chem. A, 2015, 119, 1279–1291.

---

Footnote

† Electronic supplementary information (ESI) available: The optimized geometries and ΔH_(298K) values of the stationary points associated with the isomerization of (CH₃)₂CCHCH₂ radical, bi-exponential fitting parameters for intermediate temperature range measurements, determination of experimental uncertainty in the high-temperature range measurements, energies of the stationary points associated with reaction (1) along with their T1 diagnostic values and optimized geometries, and the MESMER input file ((CH₃)₂CCHCH₂.xml), are provided in the electronic supplementary information. See DOI: 10.1039/d1cp02210e

---