Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A method for calculating temperature-dependent photodissociation cross sections and rates†
Marco
Pezzella
 *,
Sergei N.
Yurchenko
*,
Sergei N.
Yurchenko
 and
Jonathan
Tennyson
and
Jonathan
Tennyson

Department of Physics & Astronomy, University College London, London WC1E 6BT, UK. E-mail: j.tennyson@ucl.ac.uk
First published on 20th July 2021
Abstract
The destruction of molecules by photodissociation plays a major role in many radiation-rich environments, including the evolution of the atmospheres of exoplanets, which often exist close to UV-rich stars. Most current photodissociation calculations and databases assume T = 0 K, which is inadequate for hot exoplanets and stars. A method is developed for computing photodissociation spectra of diatomic molecules as a function of temperature exploiting bound state variational nuclear motion program Duo and post-processing program ExoCross. Discrete transition intensities are spread out to represent a continuous photodissociation spectrum either by Gaussian smoothing or by averaging calculations over a range of different grid sizes. Our approach is tested on four different chemical species (HCl, HF, NaCl and BeH+), showing its ability to reproduce photodissociation cross sections and rates computed with other approaches and experiment. The temperature dependence of photodissociation cross sections and rates is studies showing strong temperature variation of the photodissociation cross sections.
1 Introduction
Photochemistry substantially impacts the atmospheric composition of planets and exoplanets with consequences for the chemical compositions, radiative transfer, thermal structure, and dynamics of the atmospheres. This is particularly true for the many exoplanets that have been discovered orbiting near their host stars as these planets exists in UV-rich environments.1–4 Of course, it is exactly the planets which experience high UV fluxes where the molecules are also hot and hence vibrationally and rotationally excited. Modelling and understanding the atmospheres of such planets therefore requires temperature-dependent photodissociation cross sections. Measurements of photodissociation cross sections of molecules at higher temperatures have been performed1 but these studies struggle to reach the temperatures needed for the top of hot atmospheres (T > 1000 K).Current state-of-the-art for calculation of photodissociation cross sections for astronomical studies often use simplified (harmonic) ground state wavefunctions.5 This model is appropriate for the cold molecules such as those found in the interstellar medium (ISM) but inadequate for hot environments such as the atmospheres of exoplanets. Here we present a novel methodology aimed at resolving this problem. Similarly, there are standard databases of photodissociation cross sections studies of the ISM6,7 but these only contain data for molecules at interstellar temperatures, often assumed to be 0 K.
There is a long history of theoretical treatments of photodissociation,8 but it is only recently that cross section calculations have begun to seriously consider the effects of temperature9 and even then the effects of rotational excitation appears to have been largely ignored.
The ExoMol project was designed to produce comprehensive line lists of bound–bound transitions for molecules in hot atmospheres.10 The ExoMol database provides such line lists for a large range of molecules deemed to be important in exoplanets and elsewhere.11 As part of the ExoMol project a series of nuclear motion codes have been developed or enhanced to give results which are both comprehensive and accurate.12 Here we concentrate on one of the programs, Duo.13 Duo solves the bound–bound diatomic nuclear motion problem by explicit solution of the nuclear motion Schrödinger equation and allows for treatment of spin–orbit and other coupling effects14 as well avoided and allowed curve crossings.15 The treatment we propose here is based on extending Duo to treat the bound–free problem of photodissociation. This will allow temperature effects to be fully captured; our procedure can also provide the requisite data for modelling the effect of photodissociation in environments where non-local thermodynamic equilibrium (non-LTE) is important. Such data are not obtainable with current experimental procedures. We note that photodissociation itself is likely to prove to be a major driver of non-LTE regimes.
Duo has already been adapted for the study of continuum (free–free) states within an R-matrix formalism with a particular focus on the treatment of ultracold collisions.16 Here we propose a rather more radical approach where the continuum is only modelled using a (finite) inner region and photodissociation cross sections or rates are extracted from the results. This approach avoids the need for computationally expensive treatment of the long-range wavefunctions making studies over many rotational states easy and fast. The approach allows the full photoabsorption problem, i.e., bound–bound and bound–free transitions, to be treated within a single formalism and on an equal footing.
2 Theory and methods
2.1 Theoretical background
Our treatment of the diatomic photoabsorption problem, which includes both bound–bound transitions and bound–free (photodissociation) transitions is based on the diatomic code Duo.13 Duo uses a variational procedure to find solutions to the multistate rovibronic nuclear motion problem allowing for treatment of spin–orbit and other couplings.14 Duo has been extensively used to provide accurate line lists for challenging bound–bound problems.17–22 The present implementation uses Duo to solve the nuclear motion Schrödinger equation and then post-processing program ExoCross23 to produce photodissociation cross sections and rates, and, optionally, to distinguish between bound–bound and bound–free transitions. Duo initially uses a grid basis set to solve the rotationless one-dimensional Schrödinger equation separately for each electronic state Γ: | (1) |
The transition dipole moment curves, 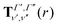 between two vibronic states
between two vibronic states  and
and  are expressed as:
are expressed as:
 | (2) |
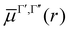 as the electronic dipole moment vector and are used for evaluating the intensity of the transitions.
as the electronic dipole moment vector and are used for evaluating the intensity of the transitions.
The vibrational wavefunction are then combined with suitable angular functions in a Hund's case a representation, to provide a basis set for each total angular momentum quantum number, J. These basis sets are used to solve the full Hamiltonian, that couples rovibronic states ψJi belonging to different electronic states and different values of the angular momenta J. Additional terms can be added to take into account non-adiabatic couplings between curves,15 and allow for spin–orbit and other similar couplings. Only transitions f ← i that obey the electric dipole moment selection rules parity changes and
| ΔJ = Jf − Ji = 0, ±1 | (3) |
The intensity If←i of a given bound–bound transition also depends on the rotational number of the initial (Ji) and final (Jf) states and on the temperature (T):
 | (4) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi is the transition wavenumber (cm−1),
fi is the transition wavenumber (cm−1),  is the term value (cm−1),
is the term value (cm−1),  is the second radiations constant (cm K−1); h is the Planck constant, c the speed of light, kB the Boltzmann constant; gtoti is the total nuclear statistical weight factor
is the second radiations constant (cm K−1); h is the Planck constant, c the speed of light, kB the Boltzmann constant; gtoti is the total nuclear statistical weight factor| gtoti = gnsi(2Ji + 1), |
 | (5) |
The intensity is the integral of the cross section σfi over an absorption line:
 | (6) |
By introducing a line profile f![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi(
fi(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), σfi(
), σfi(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) can be defined as
) can be defined as
σfi(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) = If←if ) = If←if![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi( fi(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), ), | (7) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) fi(
fi(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) is an integrable function which is normalized to unity.
) is an integrable function which is normalized to unity.
The bound–free photodissociation process is characterized by the excitation from a bound electronic state, usually the electronic ground state, to an unbound rovibronic level of an excited state. The radial wavefunctions of these dissociative states are described by a sinusoidal wavefunction at the asymptotic limit. Here we adapt eqn (4) to cover both bound–bound and bound–free processes. We note that the self-absorption term in eqn (4), given by −e−c2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi/T, is probably not needed for bound–free transitions26 but in practice will be negligible for the short wavelength processes considered here. A future refinement will be to remove this term for bound–free processes.
fi/T, is probably not needed for bound–free transitions26 but in practice will be negligible for the short wavelength processes considered here. A future refinement will be to remove this term for bound–free processes.
2.2 Continuum cross section calculations
Duo is designed to provide discrete solutions for bound electronic systems of diatomics. Here we present a robust approach to use Duo for computing temperature-dependent photo-dissociation spectra of diatomics representing bound–free transitions. To this end, a coupled set of Schrödinger equations for the system containing bound and unbound PECs is solved on the basis of bound vibrational functions ϕΓ from eqn (1). The discrete eigenvalues Ẽi and eigenfunctions ψJi are then used to generate line intensities viaeqn (4). This gives a photodissociation spectrum which is represented by clusters of discrete, high intensity lines, separated by regions where there is no intensity, see Fig. 1. To recover the continuum nature of the spectrum we apply a smoothing function to the cross sections, computed using the ExoCross program.23 | ||
| Fig. 1 Cross sections generated using a Gaussian with HWHM of 10 cm−1 for HCl and HF from a single run in Duo (black) and with the stabilization method (red). Our calculations are performed at 100 K. | ||
We have tested two smoothing functions included into the SciPy27 package. The first method consists in interpolating the spectrum with knots equally distributed along the wavelengths. The second method consist of applying a normalized Gaussian smoothing function to each grid point. The Gaussian line profile is given by:28
 | (8) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi is the line centre and αD is the Gaussian half width at half maximum (HWHM).
fi is the line centre and αD is the Gaussian half width at half maximum (HWHM).
The HWHM of the Gaussian line profile is used for regulating the cross section height. Optimal values for the HWHMs depend strongly on the molecule under analysis, with values between 2000 cm−1 and 3000 cm−1 for hydrogen halides (see Section 3.1), and 75 cm−1 in case of high temperature cross sections for BeH+ (Section 3.3). The appropriate HWHM depends on several factors including the size and density of the grid used, which determines the number of discrete transitions given by Duo, and the temperature as the large number of lines at elevated temperatures leads to dense spectra making further smoothing beyond the initial 10 cm−1 broadening unnecessary. Both methods are designed to conserve the integrated intensity and the photodissociation rates with respect to the initial transition intensities.
Some excited potentials support a few bound vibrational states. These states manifest themselves in a photoabsorption spectrum as a series of bound–bound transitions at longer wavelengths than the transitions to those states which are responsible for photodissociation. It is therefore important to be able distinguishing bound–free transitions from bound–bound ones. Here we adopt an approach that has some similarities to the stabilization method of Taylor and co-workers.29–31 In our case, the Duo calculations are repeated using different grid sizes which are varied by a few tenths of an Å. Each calculation results in temperature-depended cross sections, which are then averaged to produce our final photodissociation cross sections. The individual cross sections are obtained using a Gaussian line profile of HWHM = 10 cm−1. These repeated calculations smear out the bound–free transitions, possibly leading to results that are more easily smoothed to give continuum cross sections, but leave bound–bound transitions in the same place allowing them to be readily identified. Photodisocciation cross sections generated using the stabilization method are illustrated in Fig. 1.
If one only wants photodissociation cross sections or rates, bound–bound contributions need to be identified and discounted. Identification of bound–bound transitions is facilitated by using the stabilization method as they always occur with the same transition frequency when the box size is varied. The photodissociation spectrum can be recovered by calculating the overall photoabsorption spectrum and then subtracting the bound–bound transitions contribution. An alternative approach consists of summing photodissociation cross sections evaluated for each single state in turn excluding the bound contributions. Results of these two methods are compared in Section 3.3.
2.3 Photodissociation rates
For many purposes photodissociation rates are used instead of cross sections; for example, rates are used for modelling the abundance and the evolution of species in space.32,33 The rates provide a useful quantity to test the validity of our approach for the molecules we study. The photodissociation rate k of a molecule dissociated by a field with a flux F(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) between the wavelengths
) between the wavelengths ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 and
1 and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 is expressed as:
2 is expressed as: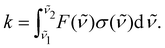 | (9) |
There are several standard fluxes used to produce appropriate rates. Here we concentrate on the flux appropriate for the interstellar medium (ISM) since this is widely used by the databases to which we want to compare. Future work will consider a variety of stellar fluxes. Photodissociation rates are calculated using the interstellar radiation field (ISRF).34–36 The ISRF has been fitted to an analytical expression for wavelengths between 91.2 nm and 200 nm, and was expressed as:
| F(λ) = 3.2028 × 1013λ−3 − 5.1542 × 1015λ−4 + 2.0546 × 1017λ−5 | (10) |
| F(λ) = 3.67 × 104λ0.7. | (11) |
3 Results
Our approach is tested for three different system types. The first consists of the A1Π ← X1Σ+ photodissociation from the vibrational ground state for two hydrogen halides: HCl and HF. The second system is NaCl and its photodissociation as a function of temperature. With the third system, BeH+, we compare the results from our method with recently published calculations. All calculations are carried using a 8 core Intel local machine with 32 GB of RAM using available potential energy and transition dipole curves.3.1 HCl and HF
HCl and HF are characterized by the presence of a repulsive A1Π excited state. The A1Π← X1Σ+ electronic transition leads to the immediate photodissociation into two neutral fragments H(2S) + X(2P), where X is F or Cl. Photodissociation arising from these electronic transitions was chosen as an initial test of our methodology.For HCl we used the X1Σ+ and the A1Π potentials taken from Alexander et al.37 and the A1Π ← X1Σ+ transition dipole moment from Givertz and Balint-Kurti.38 For HF the X1Σ+, A1Π potentials and the A1Π ← X1Σ+ transition dipole moments of HF are taken from Brown and Balint-Kurti.39 For both molecules, vibrational wavefunctions were built for J = 0, between 0.5 Å and 3.0 Å. Transitions from the vibrational ground state of the X1Σ+ state to the A1Π state were considered for a temperature of T = 100 K, which required J up to 16 for HCl and up to 11 for HF. Calculations were also performed with the time-dependent Schrödinger code PHOTO, developed by Balint-Kurti et al.,40 which only considers states with J = 0 and is hence useful for a low temperature comparison.
Fig. 1 presents photodissociation cross sections of HCl and HF computed using the stabilization approach for T = 100 K. The black lines in Fig. 1 show the intensity of the discretised transitions to the continuum obtained running a single calculation with Duo and ExoCross on a grid of 2001 points ranging from 0.5 Å to 3.00 Å. These spectra of HCl and HF consist in clusters of discrete lines, characterized by high values of σ(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), separated by regions where σ(
), separated by regions where σ(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) = 0. The red curves in Fig. 1 show the spectra calculated with the stabilization method extending the original grid from 2.50 Å to 2.60 Å with steps of 0.001 Å, obtained by averaging 100 individual cross sections, each computed using the Gaussian line profile with HWHM = 10 cm−1. The final spectrum consists of a discrete spectrum overlapped to a continuum background. The magnitude of the cross section for the discrete spectrum obtained with this procedure is 20 times smaller the peaks in the black curves of Fig. 1.
) = 0. The red curves in Fig. 1 show the spectra calculated with the stabilization method extending the original grid from 2.50 Å to 2.60 Å with steps of 0.001 Å, obtained by averaging 100 individual cross sections, each computed using the Gaussian line profile with HWHM = 10 cm−1. The final spectrum consists of a discrete spectrum overlapped to a continuum background. The magnitude of the cross section for the discrete spectrum obtained with this procedure is 20 times smaller the peaks in the black curves of Fig. 1.
Now we apply the Gaussian smoothing method to produce the T = 100 K photodissociation cross sections of HCl as described above. These are compared to experimental results41–43 and to the results from PHOTO40 with the numerical results are reported in Table 2 and plotted in Fig. 2. The Gaussian smoothing model with HWHM of 1800 cm−1 produces cross sections with σmax = 3.55 × 10−18 cm2 molecule−1, while the interpolation scheme (with knots at every 5 nm) leads to a higher value of σmax = 4.13 × 10−18 cm2 molecule−1, but within the upper limits reported by Inn.41 The peak position (λmax) is overestimated by 3 Å with respect to PHOTO and experiments. Our photodissociation rates calculated for ISRF before and after smoothing give the same value of k = 2.29 × 10−10 s−1 at T = 100 K. The photodissociation rates differ between our model and PHOTO only by the 4%.
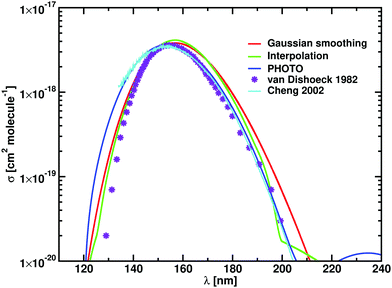 | ||
| Fig. 2 Photodissociation cross sections of HCl, numerical values are in Table 2. Results from Duo and ExoCross with the Gaussian smoothing are plotted in red, with the interpolation in green. Calculations carried with PHOTO are blue, the data from van Dishoeck et al. in violet,44 and the experimental data in cyan.43 Our calculations are performed at 100 K. | ||
The experimental HCl photodissociation cross section shows an asymmetry at short wavelengths, see Fig. 2, due to a non-adiabatic coupling between the A1Π and the C1Π states.43 The maximum of the cross section is found at λmax = 153.0 nm, with σmax = 3.53 × 10−18 cm2 molecule−1. The computer model of van Dishoeck et al.44 overestimates λmax by 2.3 nm with respect to the experiments and estimates a photodissociation rate of k = 2.1 × 10−10 s−1. The time dependent Schrödinger code PHOTO estimates the photodissociation rate of k = 2.188 × 10−10 s−1.
Three different types of basis functions were tested in Duo, corresponding to Sinc DVR, Lobatto and the 5 point finite differences; Table 1 shows the corresponding values of λmax, σmax as well as of the integrated intensity I. The calculations were performed on a grid of 601 points. The Lobatto wavefunctions lead to the largest difference from the other methods, especially in case of HF. For this molecule we observe a shift of the maximum cross section peak λmax of 2.08 nm and an overestimation of the cross section maximum of the order of 18%. All further calculations in this work are performed using the sync DVR basis function.
| Sinc DVR | Lobatto | 5 pt differences | |
|---|---|---|---|
| HCl | |||
| λ max | 155.21 | 154.29 | 155.37 |
| σ max | 1.47 × 10−16 | 1.72 × 10−16 | 1.47 × 10−16 |
| I | 4.84 × 10−14 | 4.81 × 10−14 | 4.84 × 10−14 |
| Q | 5.64 | 5.68 | 5.64 |
| HF | |||
| λ max | 119.90 | 121.98 | 119.91 |
| σ max | 1.33 × 10−16 | 1.46 × 10−16 | 1.33 × 10−16 |
| I | 4.30 × 10−14 | 4.19 × 10−14 | 4.30 × 10−14 |
| Q | 15.31 | 15.46 | 15.31 |
| Model | λ max | σ max | k |
|---|---|---|---|
| Experimental41 | 153.00 ± 0.05 | 3.82 ± 0.38 × 10−18 | — |
| Experimental42 | 153.90 ± 0.05 | 3.28 ± 0.49 × 10−18 | — |
| Experimental43 | 153.90 ± 0.02 | 3.53 ± 0.18 × 10−18 | — |
| van Dishoeck et al.44 | 154.4 | 3.5 × 10−18 | 2.1 × 10−10 |
| PHOTO | 153.63 | 3.644 × 10−18 | 2.188 × 10−10 |
| Raw data | 155.21 | 1.472 × 10−16 | 2.289 × 10−10 |
| Gaussian smooth | 156.76 | 3.553 × 10−18 | 2.290 × 10−10 |
| Interpolation | 156.88 | 4.135 × 10−18 | 2.290 × 10−10 |
There is a weak dependence of the cross section on the number of grid points. Increasing the size from 251 to 4001 points, for both HCl and HF, there is an increase of 0.6% in σmax and of 0.3% in λmax.
The theoretical and experimental photodissociation cross sections of HF are compared in Fig. 3. The shape of the HF photodissociation cross section is symmetric, with measured values of λmax varying between 119.8 and 121.7 nm.45,46σmax also varies greatly between the two experiments, from 6 × 10−18 cm2 molecule−1 given by Hitchcock et al.45 to 3.3 × 10−18 cm2 molecule−1 given by Nee et al.46 Previous computational results39 agree with the results of Nee et al.46
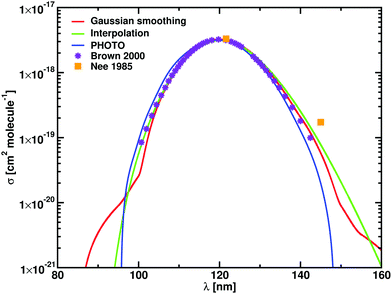 | ||
| Fig. 3 Cross sections for HF for computational models presented in Table 3. Gaussian smoothing results are in red, results of interpolation in green, and calculation performed with PHOTO in blue; the calculations of Brown and Balint-Kurti39 are in violet. The Gaussian smoothing model is sensitive to the high energy tail shown in Fig. 1. | ||
Our λmax for HF at T = 100 K agrees with Hitchcock et al.45 The spectrum from Duo and ExoCross show a high energy tail at 90 nm (see Fig. 3), that is reproduced in the Gaussian smoothing model with a HWHM of 2700 cm−1. Our photodissociation rates (1.173 × 10−10 s−1) agree within an uncertainty of 4% with the rates calculated by Brown and Balint-Kurti39 and our calculations using PHOTO. Table 3 compares calculated and experimental values of λmax, σmax and k.
| Model | λ max | σ max | k |
|---|---|---|---|
| Experiment45 | 119.81 ± 0.06 | 6 ± 1 × 10−18 | — |
| Experiment46 | 121.7 ± 0.3 | 3.3 ± 0.3 × 10−18 | — |
| Brown39 | 121.6 | 3.10 × 10−18 | 1.148 × 10−10 |
| PHOTO | 119.479 | 3.156 × 10−18 | 1.129 × 10−10 |
| Raw data | 119.800 | 1.330 × 10−16 | 1.173 × 10−10 |
| Gaussian smoothing | 120.197 | 3.128 × 10−18 | 1.173 × 10−10 |
| Interpolation | 120.006 | 3.254 × 10−18 | 1.173 × 10−10 |
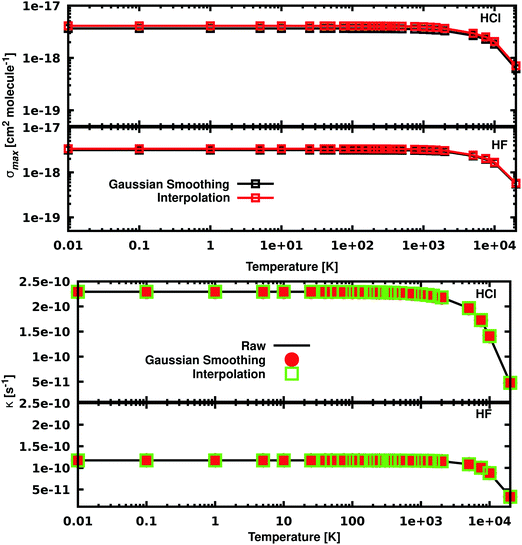
The temperature dependence of σmax and k is reported in Fig. 4. For temperatures below 1000 K, σmax is constant and it starts decreasing at higher temperatures. In the case of HCl, at 0.01 K σmax = 3.53 × 10−18 cm2 molecule−1 and decreases to σmax = 4.77 × 10−19 cm2 molecule−1 at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for the Gaussian smoothing model. The same trend is observed for HF, with σmax = 3.13 × 10−18 at 0.01 K and σmax = 5.50 × 10−19 at 20
000 K for the Gaussian smoothing model. The same trend is observed for HF, with σmax = 3.13 × 10−18 at 0.01 K and σmax = 5.50 × 10−19 at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The bottom part of Fig. 4 shows that photodissociation rates for HCl and HF with the expected decrease when temperature increases. The figure shows near perfect agreement, within the 0.2%, between the rates calculated using the raw, unsmoothed data from ExoCross and the two smoothing models.
000 K. The bottom part of Fig. 4 shows that photodissociation rates for HCl and HF with the expected decrease when temperature increases. The figure shows near perfect agreement, within the 0.2%, between the rates calculated using the raw, unsmoothed data from ExoCross and the two smoothing models.
The temperature increase leads to an increase of population of the excited (bound) rovibrational states of the lower, ground electronic state. As a consequence, the photodissociation spectrum has a more dense character forming featureless spectral background even without extra smoothing applied. Fig. 5 shows the unsmoothed and Gaussian smoothed cross section for HCl at different temperatures: the two of them present the same shape for temperatures equal to or higher than 2000 K.
3.2 NaCl
Experimental photodissociation cross sections for NaCl have been reported for T = 300 K Na + + Cl− dissociation products,47 and at T = 1123 K for the neutral dissociation products.48 The photodissociation spectrum above 200 nm comprises two contributions from the A1Π ← X1Σ+ and the B1Σ+ ←X1Σ+ transitions. At low temperatures, both bands form distinct, observable structures, as shown in Silver et al.,47 while they merge at higher temperatures: the cross section at 1123 K shows a maximum at λ = 236 nm with σ = 3.5 ± 0.3 × 10−17 cm2.48Our calculations are performed using the potential energy curves, dipole moments and couplings from the ExoMol study of Barton et al.,49 where they were used to calculate the X1Σ+ state rovibrational spectrum. As part of the current work, we have produced components required for modelling the electronic A–X and B–X spectra using the MRCI/aug-cc-pVQZ ab initio level of theory as implemented in MOLPRO.50 This includes the PECs X1Σ+, A1Π and B1Σ+, the transition dipole moment curves A–X and B–X and an electronic angular momentum coupling curve between the A and B state. The active space was selected to be (10, 4, 4, 0) with (4, 2, 2, 0) closed orbitals.
For temperatures below 1000 K, transitions up to J = 100 are used; this is extended to J = 291 for higher temperatures. A 1001 point grid with points between 1.5 Å and 5 Å is used, selecting 60 vibrations states for the X1Σ+ states, 150 for the A1Π and 120 for the B1Σ+. The electronic angular momentum coupling curve ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) x is considered between the X1Σ+ and the A1Π states. The calculated photodissociation cross sections of NaCl for different temperatures are plotted in Fig. 6 with the corresponding λmax and σmax values tabulated in Table 4. A direct comparison between our calculations and experimental cross sections of NaCl at 1123 K are shown in Fig. 7. Our calculations reproduce the two peak structure in the NaCl cross sections and the disappearance of the lower energy peak at high temperatures. The photodissociation band A1Π ← X1Σ+ is very distinct at T = 100 K, T = 300 K, T = 500 K, turning a into shoulder at T = 750 K. It is submerged by the B1Σ+ ← X1Σ+ band at higher temperatures. For the analysis presented in Table 4, their contributions for T ≥ 1200 K were separated as indicated by an asterisk. The B1Σ+ ← X1Σ+ transition shows a blue shift of 1.71 nm and a decrease of the cross section from 19.1 × 10−16 to 2.67 × 10−17 over the 100–1500 K interval. A direct comparison between the cross sections at 300 K of Silver et al.47 is not possible, due to the different final states. The photodissociation rate for the ISRF field shows almost no temperature dependence, passing from 9.24 × 10−10 s−1 at T = 100 K to 9.26 × 10−10 s−1 at T = 1500 K.
x is considered between the X1Σ+ and the A1Π states. The calculated photodissociation cross sections of NaCl for different temperatures are plotted in Fig. 6 with the corresponding λmax and σmax values tabulated in Table 4. A direct comparison between our calculations and experimental cross sections of NaCl at 1123 K are shown in Fig. 7. Our calculations reproduce the two peak structure in the NaCl cross sections and the disappearance of the lower energy peak at high temperatures. The photodissociation band A1Π ← X1Σ+ is very distinct at T = 100 K, T = 300 K, T = 500 K, turning a into shoulder at T = 750 K. It is submerged by the B1Σ+ ← X1Σ+ band at higher temperatures. For the analysis presented in Table 4, their contributions for T ≥ 1200 K were separated as indicated by an asterisk. The B1Σ+ ← X1Σ+ transition shows a blue shift of 1.71 nm and a decrease of the cross section from 19.1 × 10−16 to 2.67 × 10−17 over the 100–1500 K interval. A direct comparison between the cross sections at 300 K of Silver et al.47 is not possible, due to the different final states. The photodissociation rate for the ISRF field shows almost no temperature dependence, passing from 9.24 × 10−10 s−1 at T = 100 K to 9.26 × 10−10 s−1 at T = 1500 K.
| Temperature [K] | λ B←Xmax [nm] | σ B←Xmax [cm2 molecule−1] | λ A←Xmax [nm] | σ A←Xmax [cm2 molecule−1] | k [s−1] |
|---|---|---|---|---|---|
| 100 | 235.53 | 1.91 × 10−16 | 254.29 | 7.16 × 10−17 | 9.23 × 10−10 |
| 300 | 235.53 | 8.51 × 10−17 | 254.29 | 3.38 × 10−17 | 9.23 × 10−10 |
| 500 | 235.53 | 5.62 × 10−17 | 254.31 | 2.46 × 10−17 | 9.23 × 10−10 |
| 750 | 235.53 | 4.13 × 10− 17 | 254.33 | 2.15 × 10− 18 | 9.24 × 10− 10 |
| 1200* | 233.82 | 3.05 × 10−17 | 254.32 | 1.26 × 10− 17 | 9.26 × 10− 9 |
| 1500* | 233.82 | 2.67 × 10−17 | 254.33 | 1.07 × 10−17 | 9.26 × 10−10 |
 | ||
| Fig. 7 Photodissociation cross section of NaCl at T = 1123 K. Results for our calculations after Gaussian smoothing (HWHM = 100 cm−1) is in black, while the experimental values from Davidovits and Brodhead48 are plotted in red. | ||
The experimental T = 1123 K cross section by Davidovits and Brodhead48 (see Fig. 7) shows a feature from the C1Π ← X1Σ+ band at shorter wavelengths, which is not present in our model. The smoothed curve is characterized by λmax = 233.82 nm versus the experimental value of λmax = 236 nm with a cross section of 3.17 × 10−17 cm2 molecule−1, within the uncertainty range of the experimental results.
3.3 BeH+
Beryllium is the lightest stable nuclide not synthesized in the Big Bang, and it is a probe to study the early Universe structure and evolution.51,52 The hydrogenated species BeH+ finds application in plasma and nuclear physics.53,54 The potential energy curves, transition dipole moments, spectroscopic data and photodissociation cross sections of BeH+ covering the X1Σ+, A1Σ+, B1Π, C1Σ+ states at 1800 K, 4500 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K and 20
000 K and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K have been reported by Xu et al.55 and Yang et al.56 The photodissociation spectrum of BeH+ comprises two peaks, the first from the A1Σ+, B1Π ← X1Σ+ bands that correlates with the Be+(2p) + H(1s), and the second one from the C1Σ+ ← X1Σ+ band, which correlates with the Be(2s2) + H+ asymptote. All the three excited electronic states support bound vibrational states: 23 for A1Σ+, 13 for B1Π, and 7 for C1Σ+.
000 K have been reported by Xu et al.55 and Yang et al.56 The photodissociation spectrum of BeH+ comprises two peaks, the first from the A1Σ+, B1Π ← X1Σ+ bands that correlates with the Be+(2p) + H(1s), and the second one from the C1Σ+ ← X1Σ+ band, which correlates with the Be(2s2) + H+ asymptote. All the three excited electronic states support bound vibrational states: 23 for A1Σ+, 13 for B1Π, and 7 for C1Σ+.
The coupled system of Schrödinger equations is solved using Duo with PECs of BeH+ from Xu et al.55 on a grid of 4001 points between 0.5 and 6.0 Å, evaluating 400 vibrational states (both bound and unbound) for X1Σ+, 393 for A1Σ+, 391 for B1Π, and 381 for C1Σ+, imposing Emax = 998![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 841 cm−1. The X1Σ+ state can hold 20 bound vibrational states with the rotational excitations ranging up to Jmax = 56. The photodissociation intensities were computed using Xu et al.'s transition dipole moment curves. For all temperatures, Jmax = 32 was used chosen as to maximize the agreement with the calculations of Yang et al.56
841 cm−1. The X1Σ+ state can hold 20 bound vibrational states with the rotational excitations ranging up to Jmax = 56. The photodissociation intensities were computed using Xu et al.'s transition dipole moment curves. For all temperatures, Jmax = 32 was used chosen as to maximize the agreement with the calculations of Yang et al.56
Fig. 9 shows an example of how the photodissociation cross section of BeH+ is recovered from the photoabsoption spectrum on top of the PECs involved. The bound–free transitions are given by dashed arrows, while the bound–bound transitions are depicted by the straight arrows. The inset in the figure shows the photoabsorption spectrum calculated at T = 1800 K. An estimate of the photodissociation cross section directly excluding the bound–bound contributions leads to the same trend as the previous method. Fig. 10 show the outcome of the two methods compared with the results from Yang et al.56 in Panel A, the absolute difference between our two approaches is shown in Panel B. The greatest differences encountered at the boundaries, while the relative difference between the two methods is of the order of the 5 × 10−4, making them equivalent for our purposes.
 | ||
| Fig. 8 Difference in partition functions between Xu et al.55 and this work (ΔQ) as function of temperature, expressed in terms of percentage with respect to our (ExoCross) values. For temperatures below 7500 K, the difference between the two models is within the 2%, which increases at higher temperatures, with our model having higher values. The red dot points show the temperatures for which the photodissociation cross section are simulated. | ||
 | ||
| Fig. 9 The main plot shows the BeH+ PECs from Xu et al.55 The solid vertical arrows show examples of bound–bound transitions, while the dashed vertical arrows represent bound–free transitions. An example of the photoabsorption spectrum at 1800 K is given in the inset: photodissociation is represented by the black curve, while each component of the bound–bound spectrum is represented by the colour of the final state in the main plot. A Gaussian smoothing model with HWHM = 75 cm−1 is used. | ||
 | ||
| Fig. 10 Panel A: photodissociation cross sections of BeH+ calculated at T = 1800 K, with two different approaches: in method 1, the complete photoabsorption spectrum is calculated and then the bound contributions are removed; in method 2 the single state photodissociation cross sections are calculated separately and then they are summed together. Panel B: the difference between method 1 and method 2 is plotted. Data from Yang et al.56 are plotted in red. A Gaussian smoothing model with HWHM = 75 cm− 1 is used. | ||
The photodissociation cross sections form two peaks with maxima at λ = 172.31 nm and λ = 96.01 nm. As the temperature increases, the height of the two peaks decreases alongside a flattening of the regions between the cross sections. In Fig. 9, our computed spectra (black) are compared with the values of Yang et al.56 (red) for T = 1800 K, 4500 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K and 20
000 K and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The photodissociation spectral contributions are obtained by subtracting the bound–bound components from the total photoabsorption spectrum, as shown in Fig. 9. The shapes and positions of the cross sections are the same in Yang et al.56 and our model, but our model consistently gives lower cross sections (Fig. 11). This discrepancy is directly proportional to the temperature. An important contribution to the discrepancy between our results and those of Yang et al.56 is the differences in the partition functions used. This difference is small for temperatures below 4500 K, where the two partition sums differ by about the 2% but is important for 10
000 K. The photodissociation spectral contributions are obtained by subtracting the bound–bound components from the total photoabsorption spectrum, as shown in Fig. 9. The shapes and positions of the cross sections are the same in Yang et al.56 and our model, but our model consistently gives lower cross sections (Fig. 11). This discrepancy is directly proportional to the temperature. An important contribution to the discrepancy between our results and those of Yang et al.56 is the differences in the partition functions used. This difference is small for temperatures below 4500 K, where the two partition sums differ by about the 2% but is important for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, where our partition function 10% bigger, and for 20
000 K, where our partition function 10% bigger, and for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, where our partition function is 30% bigger. Fig. 8 shows the difference of partition functions as function of the temperature; we believe ours to be more accurate (Fig. 11).
000 K, where our partition function is 30% bigger. Fig. 8 shows the difference of partition functions as function of the temperature; we believe ours to be more accurate (Fig. 11).
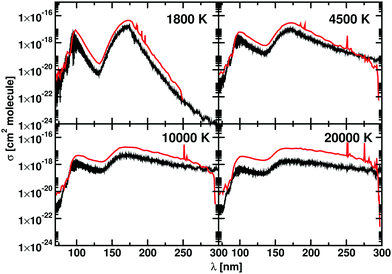 | ||
Fig. 11 Photodissociation cross sections for BeH+: our calculations are in black, the data from Yang et al.56 are in red. Each panel shows a different temperature: 1800 K, 4500 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, and 20 000 K, and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. A Gaussian smoothing model with HWHM = 75 cm−1 is used. 000 K. A Gaussian smoothing model with HWHM = 75 cm−1 is used. | ||
4 Conclusions
In this paper we develop a methodology which is suitable for the calculation of temperature-dependent photodissociation cross sections for diatomic molecules of arbitrary complexity. The methodology involves a solution of the coupled system of Schrödinger equations using bound vibrational basis functions and construction of pseudo-bound, temperature dependent cross-sections. For pure continuum cases, the photodissociation cross sections are generated using one of our smoothing approaches (Gaussian broadening or interpolation scheme). For hybrid, bound/free spectra, we use a stabilization method with averaged cross sections. We have tested the algorithm on a number of systems (HCl, HF, NaCl and BeH+) containing both pure repulsive excited state potential curves and ones which support bound states. Agreement, within understandable limits, is found between published data and our calculations for all molecules examined. Our plan is to include theoretical temperature-dependent photodissociation cross sections of HCl, HF, NaCl and BeH+ into the ExoMol data base, as part of the ExoMol project.11 Results of these studies, after some improvements of the corresponding spectroscopic models, will be published elsewhere.A major motivation for the developments presented here is the need to provide temperature-dependent photodissociation cross sections for polyatomic molecules such water and CO2. We note that the DVR3D program suite57 has already been extended to provide rovibronic dipole transition intensities58 and to use Lobatto shape functions59 meaning that many of the developments for exploiting our proposed procedure are in place. However, for systems with more than two atoms, the identification of dissociative coordinates also becomes important.59 We plan to extend our calculations of photodissociation cross sections and rates to triatomic and larger molecules. This will require us to develop a rigorous procedure appropriate for multichannel systems.
Data availability
Working examples of the input files used for generating the photodissociation cross sections and rates, together with the analysis tool are available as ESI† in the ESI.zip archive. A working version of Duo and ExoCross, which can be downloaded from the ExoMol github area, are required in order to run the input files. The file analysis.ipyn can be opened using Jupyter Notebook.The directory duo-input contains the following input files that can be run using Duo, in order to create the initial state and transition files:
1 http://HCl-X-A.com, http://HF-X-A.com: input files for the A1Π← X1Σ+ band.
2 http://NaCl-Duo.com: input file for the A1Π ← X1Σ+ and the B1Σ+ ← X1Σ+s bands.
3 http://BeHp-X-A-Zhang.com, http://BeHp-X-B-Zhang.comhttp://BeHp-X-C-Zhang.com.
The directory analysis contains the files required for calculating the cross sections and photodissociation rates:
1 hcl-2000.0.states and hcl-2000.0.trans: output from DUO calculation of HCl.
2 xsec-T2000.0.com: ExoCross input file needed for generating the raw absorption cross sections at T = 2000 K assuming the Gaussian profile of HWHM = 10 cm− 1.
3 http://hcl-2000.0.xsec: output from xsec-T2000.0.com.
4 http://analysis.ipyn: analysis script for recovering the smoothed photodissociation cross section and the ISRF rates. All smoothing processes are included.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Olivia Venot for helpful discussions over the course of this work and Gabriel Balint-Kurti for making the code PHOTO available. This work was funded by ERC Advanced Investigator Project 883830 and by the STFC Project ST/R000476/1. The authors acknowledge the use of the UCL Legion High Performance Computing Facility (Myriad@UCL) and associated support services in the completion of this work, along with the Cambridge Service for Data Driven Discovery (CSD3), part of which is operated by the University of Cambridge Research Computing on behalf of the STFC DiRAC HPC Facility (http://www.dirac.ac.uk). The DiRAC component of CSD3 was funded by BEIS capital funding via STFC capital grants ST/P002307/1 and ST/R002452/1 and STFC operations grant ST/R00689X/1. DiRAC is part of the National e-Infrastructure.Notes and references
- O. Venot, M. Rocchetto, S. Carl, A. R. Hashim and L. Decin, Astrophys. J., 2016, 830, 77 CrossRef.
- M. A. Badhan, E. T. Wolf, R. K. Kopparapu, G. Arney, E. M.-R. Kempton, D. Deming and S. D. Domagal-Goldman, Astrophys. J., 2019, 887, 34 CrossRef CAS.
- B. Fleury, M. S. Gudipati, B. L. Henderson and M. Swain, Astrophys. J., 2019, 871, 158 CrossRef CAS.
- N. K. Lewis, H. R. Wakeford, R. J. MacDonald, J. M. Goyal, D. K. Sing, J. Barstow, D. Powell, T. Kataria, I. Mishra, M. S. Marley, N. E. Batalha, J. I. Moses, P. Gao, T. J. Wilson, K. L. Chubb, T. Mikal-Evans, N. Nikolov, N. Pirzkal, J. J. Spake, K. B. Stevenson, J. Valenti and X. Zhang, Astrophys. J., 2020, 902, L19 CrossRef CAS.
- R. Valiev, A. Berezhnoy, I. Gritsenko, B. Merzlikin, V. Cherepanov, T. Kurten and C. Wöhler, Astron. Astrophys., 2020, 633, A39 CrossRef CAS.
- A. N. Heays, A. D. Bosman and E. F. van Dishoeck, Astron. Astrophys., 2017, 602, A105 CrossRef.
- A. Noelle, A. C. Vandaele, J. Martin-Torres, C. Yuan, B. N. Rajasekhar, A. Fahr, G. K. Hartmann, D. Lary, Y.-P. Lee, P. Limao-Vieira, R. Locht, K. McNeill, J. J. Orlando, F. Salama and R. P. Wayne, J. Quant. Spectrosc. Radiat. Transfer, 2020, 253, 107056 CrossRef CAS PubMed.
- R. Schinke, Photodissociation Dynamics, Cambridge University Press, 1993 Search PubMed.
- S. Y. Grebenshchikov, J. CO2 Util., 2016, 15, 32–40 CrossRef CAS.
- J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2012, 425, 21–33 CrossRef CAS.
- J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, V. H. J. Clark, K. L. Chubb, E. K. Conway, A. Dewan, M. N. Gorman, C. Hill, A. E. Lynas-Gray, T. Mellor, L. K. McKemmish, A. Owens, O. L. Polyansky, M. Semenov, W. Somogyi, G. Tinetti, A. Upadhyay, I. Waldmann, Y. Wang, S. Wright and O. P. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2020, 255, 107228 CrossRef CAS.
- J. Tennyson and S. N. Yurchenko, Int. J. Quantum Chem., 2017, 117, 92–103 CrossRef CAS.
- S. N. Yurchenko, L. Lodi, J. Tennyson and A. V. Stolyarov, Comput. Phys. Commun., 2016, 202, 262–275 CrossRef CAS.
- J. Tennyson, L. Lodi, L. K. McKemmish and S. N. Yurchenko, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 102001 CrossRef.
- Q. Qu, B. Cooper, S. N. Yurchenko and J. Tennyson, J. Chem. Phys., 2021, 154, 074112 CrossRef CAS PubMed.
- T. Rivlin, L. K. McKemmish, K. E. Spinlove and J. Tennyson, Mol. Phys., 2019, 117, 3158–3170 CrossRef CAS.
- A. T. Patrascu, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2015, 449, 3613–3619 CrossRef CAS.
- S. N. Yurchenko, A. Blissett, U. Asari, M. Vasilios, C. Hill and J. Tennyson, Mon. Not. R. Astron. Soc., 2016, 456, 4524–4532 CrossRef CAS.
- S. N. Yurchenko, I. Szabo, E. Pyatenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2018, 480, 3397–3411 CrossRef CAS.
- L. K. McKemmish, T. Masseron, J. Hoeijmakers, V. V. Pérez-Mesa, S. L. Grimm, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2019, 488, 2836–2854 CrossRef CAS.
- S. N. Yurchenko, A. N. Smirnov, V. G. Solomonik and J. Tennyson, Phys. Chem. Chem. Phys., 2019, 21, 22794–22810 RSC.
- Q. Qu, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2021, 504, 5768–5777 CrossRef.
- S. N. Yurchenko, A. F. Al-Refaie and J. Tennyson, Astron. Astrophys., 2018, 614, A131 CrossRef.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- D. E. Manolopoulos, Numerical Grid Methods and Their Application to Schrödinge's Equation, Springer, 1993, pp. 57–68 Search PubMed.
- R. J. Le Roy, R. G. Macdonald and G. Burns, J. Chem. Phys., 1976, 65, 1485–1500 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- C. Hill, S. N. Yurchenko and J. Tennyson, Icarus, 2013, 226, 1673–1677 CrossRef CAS.
- A. U. Hazi and H. S. Taylor, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 1, 1109 CrossRef.
- V. A. Mandelshtam, T. R. Ravuri and H. S. Taylor, Phys. Rev. Lett., 1993, 70, 1932 CrossRef CAS PubMed.
- Z. Bacic and J. Simons, J. Phys. Chem., 1982, 86, 1192–1200 CrossRef CAS.
- V. Wakelam, E. Herbst, J.-C. Loison, I. W. M. Smith, V. Chandrasekaran, B. Pavone, N. G. Adams, M.-C. Bacchus-Montabonel, A. Bergeat, K. Béroff, V. M. Bierbaum, M. Chabot, A. Dalgarno, E. F. van Dishoeck, A. Faure, W. D. Geppert, D. Gerlich, D. Galli, E. Hebrard, F. Hersant, K. M. Hickson, P. Honvault, S. J. Klippenstein, S. Le Picard, G. Nyman, P. Pernot, S. Schlemmer, F. Selsis, I. R. Sims, D. Talbi, J. Tennyson, J. Troe, R. Wester and L. Wiesenfeld, Astrophys. J., Suppl. Ser., 2012, 199, 21 CrossRef.
- V. Wakelam, J.-C. Loison, E. Herbst, B. Pavone, A. Bergeat, K. Béroff, M. Chabot, A. F. W. D. Geppert, D. Gerlich, P. Gratier, N. Harada, K. M. Hickson, P. Honvault, S. J. Klippenstein, S. Le Picard, G. Nyman, M. Ruaud, S. Schlemmer, I. R. Sims, D. Talbi, J. Tennyson and R. Wester, Astrophys. J., Suppl. Ser., 2015, 217, 20 CrossRef.
- B. T. Draine, Astrophys. J., Suppl. Ser., 1978, 36, 595–619 CrossRef CAS.
- E. F. van Dishoeck and J. H. Black, Astrophys. J., 1982, 258, 533–547 CrossRef CAS.
- L. C. Lee, Astrophys. J., 1984, 282, 172–177 CrossRef CAS.
- M. H. Alexander, B. Pouilly and T. Duhoo, J. Chem. Phys., 1993, 99, 1752–1764 CrossRef CAS.
- S. C. Givertz and G. G. Balint-Kurti, J. Chem. Soc., Faraday Trans., 1986, 82, 1231–1242 RSC.
- A. Brown and G. G. Balint-Kurti, J. Chem. Phys., 2000, 113, 1870–1878 CrossRef CAS.
- G. G. Balint-Kurti, S. P. Mort and C. C. Marston, Comput. Phys. Commun., 1993, 74, 289–296 CrossRef CAS.
- E. C. Y. Inn, J. Atmos. Sci., 1975, 32, 2375–2377 CrossRef CAS.
- J. B. Nee, M. Suto and L. C. Lee, J. Chem. Phys., 1986, 85, 719–724 CrossRef CAS.
- B.-M. Cheng, C.-Y. Chung, M. Bahou, Y.-P. Lee and L. C. Lee, J. Chem. Phys., 2002, 117, 4293–4298 CrossRef CAS.
- E. F. van Dishoeck, M. C. van Hemert and A. Dalgarno, J. Chem. Phys., 1982, 77, 3693–3702 CrossRef CAS.
- A. P. Hitchcock, G. R. J. Williams, C. E. Brion and P. W. Langhoff, Chem. Phys., 1984, 88, 65–80 CrossRef CAS.
- J. B. Nee, M. Suto and L. C. Lee, J. Phys. B: At., Mol. Opt. Phys., 1985, 18, L293–L294 CrossRef CAS.
- J. A. Silver, D. R. Worsnop, A. Freedman and C. E. Kolb, J. Chem. Phys., 1986, 84, 4378–4384 CrossRef CAS.
- P. Davidovits and D. C. Brodhead, J. Chem. Phys., 1967, 46, 2968–2973 CrossRef CAS.
- E. J. Barton, C. Chiu, S. Golpayegani, S. N. Yurchenko, J. Tennyson, D. J. Frohman and P. F. Bernath, Mon. Not. R. Astron. Soc., 2014, 442, 1821–1829 CrossRef CAS.
- H. J. Werner, P. J. Knowles, R. Lindh, F. R. Manby and M. Schütz, MOLPRO, a package of ab initio programs, 2010, see http://www.molpro.net/ Search PubMed.
- F. Primas, P. Molaro, P. Bonifacio and V. Hill, Astron. Astrophys., 2000, 362, 666–672 CAS.
- M. Pinsonneault, S. D. Kawaler and P. Demarque, Astrophys. J., Suppl. Ser., 1990, 74, 501–550 CrossRef CAS.
- R. Celiberto, R. K. Janev and D. Reiter, Plasma Phys. Controlled Fusion, 2012, 54, 035012 CrossRef.
- V. Laporta, K. Chakrabarti, R. Celiberto, R. K. Janev, J. Z. Mezei, S. Niyonzima, J. Tennyson and I. F. Schneider, Plasma Phys. Controlled Fusion, 2017, 59, 045008 CrossRef.
- X.-S. Xu, A.-Q. Dai, Y.-G. Peng, Y. Wu and J.-G. Wang, J. Quant. Spectrosc. Radiat. Transfer, 2018, 206, 172–179 CrossRef CAS.
- Y. K. Yang, Y. Cheng, Y. G. Peng, Y. Wu, J. G. Wang, Y. Z. Qu and S. B. Zhang, J. Quant. Spectrosc. Radiat. Transfer, 2020, 254, 107203 CrossRef CAS.
- J. Tennyson, M. A. Kostin, P. Barletta, G. J. Harris, O. L. Polyansky, J. Ramanlal and N. F. Zobov, Comput. Phys. Commun., 2004, 163, 85–116 CrossRef.
- E. J. Zak and J. Tennyson, J. Chem. Phys., 2017, 147, 094305 CrossRef PubMed.
- L. K. McKemmish and J. Tennyson, Philos. Trans. R. Soc., A, 2019, 377, 20180409 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ESI.zip, containing example of inputs and analysis scripts used in this work. See DOI: 10.1039/d1cp02162a |
| This journal is © the Owner Societies 2021 |