 Open Access Article
Open Access ArticleRegression and clustering algorithms for AgCu nanoalloys: from mixing energy predictions to structure recognition†
Cesare
Roncaglia
 a,
Daniele
Rapetti
a and
Riccardo
Ferrando
a,
Daniele
Rapetti
a and
Riccardo
Ferrando
 *b
*b
aDipartimento di Fisica dell'Università di Genova, via Dodecaneso 33, Genova 16146, Italy
bDipartimento di Fisica dell'Università di Genova, via Dodecaneso 33, Genova 16146, Italy. E-mail: ferrando@fisica.unige.it
First published on 11th October 2021
Abstract
The lowest-energy structures of AgCu nanoalloys are searched for by global optimization algorithms for sizes 100 and 200 atoms depending on composition. Even though the AgCu system is very weakly miscible in macroscopic samples, the mixing energy for these nanoalloys turns out to be clearly negative for both sizes, a result which is attributed to the stabilization of non-crystalline Cu@Ag core–shell structures at the nanoscale. The mixing energy is a quantity nowadays unknown in its functional form, so that its prediction may take advantage of machine learning techniques. A support vector regressor is then implemented to successfully predict the mixing energy of AgCu nanoalloys of both sizes. Moreover, with the help of unsupervised learning algorithms, it is shown that the automatic classification of such nanoalloys into different physically meaningful structural families is indeed possible. Finally, thanks to the harmonic superposition approximation, the temperature-dependent probabilities of such structural families are calculated.
1 Introduction
Since the understanding of their wide range of applications, ranging from catalysis1,2 to data storage,3 plasmonics,4 biomedicine,5 water purification6 and others, nanoparticles (NPs) have been studied rather extensively in recent years. For this reason, both experimental and theoretical efforts have been made in order to understand the physical and chemical properties of such systems.7 In particular, the obstacles inherent to the theoretical study of a system of a finite number of atoms are often tackled with the help of computer simulations (e.g. global optimization techniques8 and molecular dynamics simulations9), which are nowadays an essential partner of experiments.Only in the past few years, also Machine Learning has been proposed as an effective tool to investigate and solve some problems related to the modeling of nanoparticles,10 such as energy landscape exploration11,12 and dynamic predictions via force field reconstruction,13 but also binding energy14 and free energy15 predictions, and atom classification.16 In a very broad general depiction, machine learning algorithms can be divided in two large classes: supervised and unsupervised learning algorithms. The first class deals with data sets consisting of both input and output data, and tries to establish a relation between these sets for fitting or classification purposes. The second class deals with unlabelled data, i.e. only input data, and tries to work out a specific task such as clustering the data into separate sets, feature selection or dimensionality reduction.
Here in particular we decided to implement both supervised and unsupervised learning algorithms, showing indeed their ability to capture different interesting properties of our data set. It is in fact known that a regression algorithm is capable of detecting subtle relationships between input and output data, whereas a clustering algorithm can identify subgroups of an ensemble without any prior knowledge. Our data sets were collected by global optimization searches of the lowest-energy structures of AgCu nanoalloys of sizes N = 100 and N = 200 atoms, for different compositions. Machine learning algorithms were then trained in order to make predictions of the mixing energy, a quantity not known in its functional form, and also to find structural families without any previous classification. Finally, we calculated probabilities for such different structural families as a function of temperature by means of the Harmonic Superposition Approximation (HSA).17–19
AgCu nanoalloys are important for a different number of remarkable reasons. In general, the bi-metallic nature of nanoalloys allows to enrich their range of applicability in real life situations, since the chemical ordering of equilibrium and out of equilibrium structures will induce different desirable properties, missing most of the times in their single metal counterparts. For example, AgCu nanoalloys have shown interesting plasmonic,20 electrical,21 antibacterial22 and catalytic23 properties, but also applications in corrosion resistance24 and solar cells.25 The interest in the theoretical modeling of such nanoalloys is therefore motivated by this impressive variety of experimental results.
AgCu is a weakly miscible system in bulk samples,26 with positive (endothermic) mixing energy. However, global optimization studies of small nanoalloys (of 34 and 38 atoms)27 showed that the mixing energy at the nanoscale is negative in the whole composition range. It is therefore interesting to check whether this behaviour persists at larger sizes such as those considered in this article (100 and 200 atoms).
The material is organized as follows. The second section includes a brief explanation of the theoretical methods, including Machine Learning (ML) and global optimizations algorithms, as well as more specific topics such as Common Neighbor Analysis (CNA) and Harmonic Superposition Approximation (HSA). The third section is entirely dedicated to the results of the applications of such methods to AgCu nanoalloys of 100 and 200 atoms. Finally in the fourth and last section, the conclusions can be found.
A note on terminology. In order to avoid confusion, aggregates of atoms will be referred to as nanoparticles or nanoalloys. On the other hand, the term cluster will be used to denote a set of nanoparticle structures which are grouped together by a clustering algorithm working in the space of suitable order parameters (i.e. of structural descriptors).
2 Models and methods
2.1 Atomistic force field
Interactions between NPs were modelled by an atomistic potential, in the form proposed by Gupta28 and by Rosato et al.,29 which can be derived from the second moment approximation to the tight-binding model.30 The potential energy E is the sum of one-atom contributions Ej containing a bonding (Ebj) and a repulsive part (Erj): | (1) |
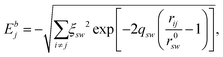 | (2) |
 | (3) |
| p | q | A (eV) | ξ (eV) | r 0 (Å) | r c1 (Å) | r c2 (Å) | |
|---|---|---|---|---|---|---|---|
| Ag–Ag | 10.85 | 3.18 | 0.1031 | 1.1895 | 2.89 | 4.08707719 | 5.00562683 |
| Cu–Cu | 10.55 | 2.43 | 0.0894 | 1.2799 | 2.56 | 3.62038672 | 4.43405007 |
| Ag–Cu | 10.70 | 2.805 | 0.0977 | 1.2275 | 2.725 | 4.08707719 | 4.43405007 |
This interaction potential has been used previously to model the structures of AgCu nanoalloys and compared to Density Functional Theory (DFT) calculations and experimental results,32–35 obtaining quite good agreement with DFT data on the behaviour of the composition-dependent excess energy and on the structures of lowest-energy magic polyicosahedra of sizes 34, 38 and 45,32 on the energetics of the placement of Cu impurities in Ag icosahedra and truncated octahedra (see ref. 7, Tables 5.1 and 5.3), on the relative stability of Mackay, anti-Mackay and chiral Cu@Ag icosahedral structures (see ref. 33). Moreover, the agreement between the predictions of this model and the experimentally observed structures is quite good34 as discussed in ref. 35. Therefore we believe that this model, although approximate, is able to catch the relevant structural aspects of AgCu nanoalloys, with the advantage of allowing such a thorough exploration of the nanoalloy energy landscape that would be unfeasible by DFT calculations.
2.2 Global optimization and data collection
Each data set consisted of nanoparticle structures obtained by global optimization searches. Therefore, all structures considered in the following correspond to local minima in the energy landscape, and, where specified, to global minima (that are the lowest-energy local minima). These searches were made by the Basin Hopping (BH) algorithm,36 using our own code.37–39 For each composition, three independent simulations of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 BH steps each were made, using different seeds and parameters. Generally speaking, each of these three simulations had different proportions for Brownian, exchange, shake and bonds moves.37,38 Two simulations over three were using a single Monte Carlo walker (standard BH algorithm), whereas the third simulation used three different walkers running in parallel (parallel excited walker algorithm37). The use of different global optimization algorithms usually allows a more thorough exploration of the energy landscape.37
000 BH steps each were made, using different seeds and parameters. Generally speaking, each of these three simulations had different proportions for Brownian, exchange, shake and bonds moves.37,38 Two simulations over three were using a single Monte Carlo walker (standard BH algorithm), whereas the third simulation used three different walkers running in parallel (parallel excited walker algorithm37). The use of different global optimization algorithms usually allows a more thorough exploration of the energy landscape.37
The mixing energy Emix7 was used to analyze the energetic stability of the nanoalloys depending on composition. Emix is defined as follows
 | (4) |
| NE(m, n) < mE(N, 0) + nE(0, N) | (5) |
Each nanoparticle structure was described with the aid of two other parameters, coming from the Common Neighbor Analysis40 (CNA). For each pair of nearest-neighbor atoms, the CNA defines a signature consisting of a triplet of integer numbers rst:
• r – the number of common nearest neighbors of the pair.
• s – the number of bonds between those r atoms.
• t – the length of the longest chain of bonds that can be made out of the s bonds present.
For a given nanoalloy and signature, we define its signature order parameter as the number of nearest-neighbor pairs presenting such signature divided by the total number of nearest-neighbor pairs in the nanoalloy. Some typical signatures are shown in Fig. 1. In particular, here we decided to use first a two-dimensional description based on the (555, 422) pair of signatures, and the to compare the results to those obtained by means of different choices of the variables.
2.3 Machine learning models
In order to find a suitable approximation of the mixing energy, regression models were trained and tested. For a classification of nanoalloys into structural families, unsupervised learning algorithms were also implemented. Both tasks were achieved thanks to the open source software Scikit-Learn.41 | (6) |
where ε and C are two positive hyperparameters and k(xi, xj) is a kernel function. The parameters that have to be found by the algorithm are αi and
 for each i. Here we used the radial basis function (RBF) kernel, that is k(xi, xj) = e−γ||xi−xj||2. The constant γ is the third positive hyperparameter. Given a set of hyperparameters and a solution to the minimization problem
for each i. Here we used the radial basis function (RBF) kernel, that is k(xi, xj) = e−γ||xi−xj||2. The constant γ is the third positive hyperparameter. Given a set of hyperparameters and a solution to the minimization problem 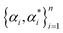 , the functional relation between x and y can be expressed as
, the functional relation between x and y can be expressed as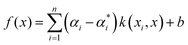 | (7) |
 | (8) |
 | (9) |
 | (10) |
BIC = log(n)p − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) | (11) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) is the maximized value of the likelihood function. The optimal value of K is the one that minimizes the BIC.
is the maximized value of the likelihood function. The optimal value of K is the one that minimizes the BIC.
2.4 Harmonic superposition approximation (HSA)
Probabilities for nanoparticles as a function of temperature were calculated thanks to the Harmonic Superposition Approximation.17,18 Given a pool of nmin structures that locally minimize the potential energy surface for a fixed number of atoms N, this framework allows to calculate the probability of each structure. For a local minimum s with potential energy Es, it is assumed that the partition function can be decomposed into translational, rotational and vibrational terms: | (12) |
 | (13) |
 | (14) |
 | (15) |
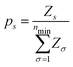 | (16) |
3 Results
In Sections 3.1 and 3.2 we report the results of both regression and clustering algorithms applied to the global minima found by our global optimization searches for sizes N = 100, and N = 200. For N = 100, the data set consists of the global minima of AgmCun for all compositions, i.e. for m = 0, 1, 2,…,100. For size 200, where calculations are more cumbersome, the data set consists of the global minima of AgmCun with even m, i.e. m = 0, 2, 4,….,200. The global minima were searched for by the BH algorithm, which has proven its efficiency in the optimization of AgCu nanoalloy structures.33,52–54 For both N = 100 and 200 we provide the results for the regression of the mixing energy, as given in eqn (4), as well as for the clustering of the data sets in different structural families. Such structural families are then described in terms of their main geometrical features and chemical ordering.In Section 3.3, we discuss different possible choices of the order parameters for the application of the clustering algorithms. Finally, in Section 3.4, we consider a specific composition, Ag64Cu36. For that composition we consider a set of low-energy local minima collected by our BH searches, we use the clustering algorithm to separate these structures into families, and we calculate the temperature-dependent probability of the families by means of the HSA.
3.1 N = 100
The mixing energy, as a function of the number of silver atoms m is shown in Fig. 2. The mixing energy is negative in the whole composition range. Its profile is evidently rather complicated, with different stationary points. | ||
| Fig. 2 (A) Mixing energies calculated after global optimization. (B) SVR (20% test) predictions for every composition, along with mixing energies calculated from global optimization. | ||
For a selected set of compositions, we checked the behavior of the mixing energy by DFT calculations. The DFT results (reported in the ESI†) are in good agreement with those of the Gupta potential, confirming the overall behavior of the mixing energy, and even giving somewhat more negative values. The negative values of the mixing energy in nanoalloys such as AgCu, AgNi, AgCo, AuCo and others was attributed to the efficient stress relaxation achieved by core@shell structures in which the element with lower surface energy and larger atomic size is segregating at the surface.35 The DFT data confirm this result and show that, at least for AgCu, the electronic effects not included in the Gupta model, such as directional terms in bonding between atoms or charge transfer, are likely to be of minor importance.
For this size, the mixing energy is calculated for every possible composition, so that in principle there is a complete knowledge about this function. However, for larger nanoalloys (as we shall see later) it can be difficult and rather expensive to compute the mixing energy for every possible composition, since it requires a full global optimization for each composition, so that in principle it is useful to have a method capable of making predictions where they are needed, i.e. on “unseen” data.
To make such predictions, we trained and tested a SVR splitting randomly the data set into an 80% training set and a 20% test set, using the number of silver atoms m as the only variable. In order to avoid overfitting, hyperparameters were tuned from the following ensemble, which spans different orders of magnitudes, after 5-fold cross validation:
Rtraining2 = 0.999825![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rtest2 = 0.999657 Rtest2 = 0.999657 |
| Rtraining2 = 0.999875 Rtest2 = 0.999468 |
When the data set is represented in the two dimensional space given by the 422 and 555 CNA signatures, all nanoalloys automatically separate into different groups. However, it is still not clear at this stage how many are there, as shown in Fig. 3A. After K-means is implemented, and the silhouette score is plotted as a function of the number of clusters K, one obtains the plot given in Fig. 4A. The optimal number of clusters, according to this criterion, is then K = 7. The Voronoi tessellation, along with each cluster center, is shown in Fig. 3B. A representative structure for each family can be found in Fig. 4B. Further details and images are given in the ESI.† Here we give a description of the different structural families found, specifying the number of silver atoms m.
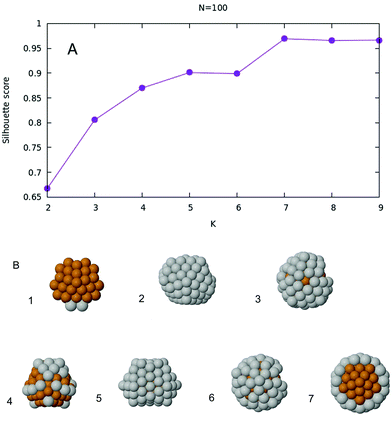 | ||
| Fig. 4 (A) Silhouette score as a function of K for the case N = 100. (B) Seven representative structures, one for each family. Labels are referred to Fig. 3B. The seven structures have 2, 82, 62, 23, 72, 56 and 45 silver atoms respectively. | ||
• (1) m = 0–4, m = 100
These are the only six structures with Marks decahedral55 symmetry.
• (2) m = 79–83
Five asymmetric icosahedral structures.
• (3) m = 59–66
These eight nanoalloys have a 55-atom perfect Mackay icosahedron covered by an incomplete Mackay crust, which is slightly distorted and presents a small rotation.
• (4) m = 5–34, m = 84–99
These forty six structures, which compose the largest cluster, have icosahedral symmetry. They are basically composed of a 55-atom perfect Mackay icosahedron covered with an incomplete Mackay icosahedral shell (which is part of the surface of the 147-atom icosahedron). However, even if they share this common feature, there are two subgroups that can be identified. The first subgroup is that of m = 5–34, where the silver atoms are at the nanoalloy surface, typically occupying icosahedral vertices and the external shell. The second subgroup can be identified with the remaining nanoalloys. Those structures have all of their copper atoms in the core, typically forming part of the 13-atom perfect icosahedron.
• (5) m = 67–78
These twelve structures are polyicosahedra32 resulting from three joined 55-atom icosahedra sharing some atoms. The third icosahedron is incomplete because of an insufficient total number of atoms.
• (6) m = 54–58
These five structures are again core–shell as those in group 4. However their crust is of anti-Mackay type.33 Moreover, they have part of such crust removed at the boundary and some silver atoms are placed at the fivefold vertices. We remark that this small deviation (their 422 signature differs 0.0262 from the seventh group) was detected by the clustering algorithm.
• (7) m = 35–53
All nineteen these structures are similar for their icosahedral symmetry to those already described in group 4 and 6, however they have the 55 perfect Mackay icosahedron covered with a partial anti-Mackay crust to form a ball-and-cup structure.56 Perfect symmetry is achieved when m = 45.
With very few exceptions, the global minima of 100-atom particles belong to some type of icosahedral family. Exceptions are found at a few extreme Cu-rich compositions and for pure Ag, where the best structures are decahedral. All structures with the lowest mixing energy are icosahedral, and the best ones (belonging to clusters 3, 6 and 7) present a 55-atom Mackay icosahedron covered either by a Mackay or an anti-Mackay incomplete shell. These results show that icosahedral and polyicosahedral structures take advantage from stress relaxation in Cu@Ag structures much more efficiently than decahedral ones.
We note also that the transition between neighboring clusters of structures often corresponds to a change in slope or to an inflexion point in the mixing energy curve (see the ESI,† Fig. S2).
3.2 N = 200
The mixing energy profile, as a function of m (the number of silver atoms), along side with the SVR fit is shown in Fig. 5. The behaviour is similar to the first case, that is rather complicated. Mixing energy values are again negative, with very few exceptions that are found in the extreme Ag-rich limit, where there are some slightly positive values. The model was trained on the 80% of the data, and tested on the remaining 20%. The same set of hyperparameters for the case N = 100 was considered during 5-fold cross validation. The best triplet was found to be given by γ = 0.001, C = 50 and ε = 0.01. As before, the model was finally trained on the full training set, and tested on the test set, with the following scores:| Rtraining2 = 0.999013 Rtest2 = 0.997736 |
| Rtraining2 = 0.999591 Rtest2 = 0.998537 |
 | ||
| Fig. 5 Mixing energy profile for AgCu nanoalloys with N = 200 atoms in total, and SVR fit for the case of 80–20 split. | ||
The representation of these nanoalloys in the same two dimensional space described by the 422 and 55 CNA signatures is given in Fig. 6A.
When K-means is implemented, and the silhouette score is plotted as a function of the number of clusters K, one obtains the plot given in Fig. 7A. The optimal number of clusters, according to this criterion, is then K = 5. The Voronoi tessellation, along with each cluster center, is shown in Fig. 6B. A representative structure for each family is shown in Fig. 7B. Further details and images are given in the ESI.† The different structural families can be described as follows
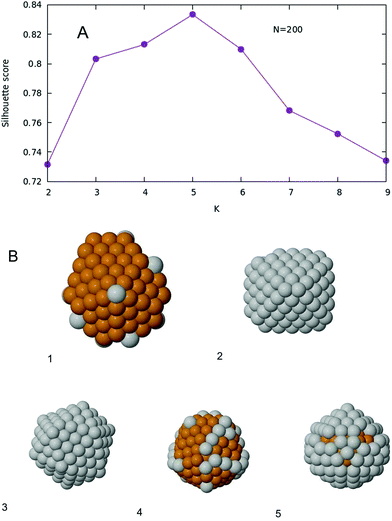 | ||
| Fig. 7 (A) Silhouette score as a function of K for the case N = 200. (B) Five representative structures, one for each family. Labels are referred to Fig. 6B. The five structures have 10, 106, 168, 42 and 80 silver atoms respectively. | ||
• (1) m = 0–30, m = 196–200
Marks decahedra. In Cu-rich decahedra, Ag atoms fill the vertices first, then they start filling (100) facets. In Ag-rich decahedra, the few Cu are atoms placed in the fivefold axis.
• (2) m = 104–108
Core–shell FCC–HCP fragments.
• (3) m = 160–174
Core–shell asymmetric icosahedra.
• (4) m = 32–54, m = 102, m = 110–152, m = 176–194
Incomplete core–shell structures, with a Cu icosahedron of N = 147 atoms covered by a Mackay Ag crust. Ag atoms initially fill the vertices, and later the edges. Finally they become part of the surface of the core 147 icosahedron. Again as in the case with N = 100, this is the largest cluster of structures.
• (5) m = 56–100, m = 154–158
As group (4), but with an anti-Mackay crust.
Also for size 200, a vast majority of global minima is of icosahedral structure. The exceptions are the decahedra found for Ag-rich and Cu-rich compositions and few FCC–HCP structures at intermediate compositions. These results confirm the key role of stress relaxation in determining the most stable structures also at this larger size of 200 atoms.
3.3 Alternative choices for the clustering of structures
Here we analyze how clustering into structural families is sensitive to the choice of the nanoparticle descriptors, i.e. of our 555, 422 and 421 variables. This analysis was made by K-means, which was applied to different choices of variables besides the (522, 422) choice used so far.First of all, we applied the clustering algorithms in the three-dimensional (3D) space of (555, 422, 421) signatures. Then we applied clustering in the spaces of two signatures at a time: (555, 421) and (422, 421) besides (555, 422), and finally to 1D spaces of one signature at a time, i.e. (555), (422) and (421) separately. We compared all clustering choices finding the following results:
– For size 100, only the pair (555, 422) was able to reproduce exactly the same clustering as the 3D description, while (555, 421) and (422, 421) were giving somewhat different clusters. On the other hand, the clustering obtained by 1D descriptions was significantly different.
– For size 200, only the pair (422, 421) was able to reproduce the same clustering as the 3D description. At variance with the (555, 422) description, (422, 421) gave six clusters instead of five, due to the splitting of cluster 4 of Section 3.2 into two new clusters corresponding to Cu-rich and Ag-rich parts. These two parts differ by a small distortion of the Ag crust in the Ag-rich part which eliminates the few 421 signatures that are present in Cu-rich nanoparticles.
From these results it turns out that (555, 422) and (422, 421) are the best choices to capture the physically relevant clusters of the full 3D description. However we note that the (422, 421) pair would be unable to separate well nanoparticles with fivefold symmetries and nanoparticles with extended hcp domains or several stacking faults. The latter were not present in our samples of global minima for sizes 100 and 200, but they may appear in samples including also higher energy isomers. For this reason we prefer the (555, 422) pair as the most useful 2D description. We note that this procedure of selecting the minimal set of variables for clustering of structures can be generalized to multi-dimensional cases including many CNA signatures and also other variables. Work in this direction is in progress.
3.4 Analysis of N = 100, m = 64, n = 36
Here we consider a specific composition for N = 100, Ag64Cu36, which is in the composition range with the lowest mixing energy. Here we consider all structures collected in the output of our three BH searches. This does not correspond to the much larger set of all visited structures during optimization, because these structures were collected by dividing the space of the 422 signature into small intervals of width 0.01 for the first two simulations and 0.002 for the third and looking for the lowest-energy structure for each interval. In total, our pool consists of 309 structures. In the usual (555, 422) 2D space given by the CNA signatures, the structures are arranged as shown in Fig. 8A. Given the nature of such representation (evidently more complicated than the previous two cases), we used the Gaussian mixture model in order to find a separation into structural families, because the Gaussian mixture model allows clusters to have ellipsoidal shapes (a more general and flexible hypothesis with respect to the hard tessellation found by K-means). The BIC and silhouette scores are then plotted as a function of the number of mixture components, K, in Fig. 9(A) and (B). The minimum of the BIC scores dictates that the optimal separation happens when the number of components is seven. This optimal number is confirmed by the silhouette score which shows a local maximum at K = 7. However we must recall that the silhouette score is less and less representative as the elongation of clusters increases. Apparently then, there is a clear distinction between seven different structural families. However, after manual inspection, one finds out that the first three clusters on the left (i.e. the orange, purple and red one) comprehend a large variety of amorphous structures, making very difficult the distinction between them, even for human eye. The reason behind this is that the pool of structures is composed of various local minima, among which a large part (in fact the majority) is very high in energy with respect to the global minimum, and thus represents a sort of noise of non-relevant structures. A simple way to overcome this obstacle is to put an energy cutoff. | ||
| Fig. 8 (A) Data set representation in the two dimensional space of 422 and 555 order parameters. (B) Gaussian mixture model plot with centers and contours for K = 7 distributions. | ||
 | ||
| Fig. 9 (A) BIC and (B) silhouette scores for both full and reduced data sets. In (A) the curve for the reduced data set has the y-axis range given on the right part of the plot. | ||
If we consider only structures which differ at most 0.5 eV from the global minimum, we obtain another representation of such nanoalloys, as shown in Fig. 10A.
With such restriction, the amount of structures reduces to 90. BIC and silhouette score suggest (as expected) four clusters to be the optimal subdivision of the reduced data set, as shown in Fig. 9(A) and (B). A representative structure for each family is instead depicted in Fig. 11.
 | ||
| Fig. 11 Representative structures for the four clusters of Fig. 10B. Top left is an icosahedron with a Mackay crust (black cluster), top right is an icosahedron with mixed Mackay and anti-Mackay crust (yellow cluster), bottom left is an icosahedron with full anti-Mackay crust (purple cluster) and finally bottom right is a polyicosahedron (red cluster). | ||
When the HSA is implemented, the probability for these four structural families as a function of temperature can be calculated, as shown in Fig. 12. Specifically, the relative probability P of family ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is given by
is given by
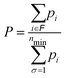 | (17) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , while the sum in the denominator extends to the minima of all families considered in the calculation. The probabilities pi of individual minima are given by eqn (16). In this way we can compute the probability for each motif as a function of temperature. The black curve in Fig. 12 suggests that the icosahedron with Mackay crust is the most favorite structural family (i.e. the most probable) in the relevant interval of temperature from 0 to 500 K (after which AgCu nanoalloys start melting their surface), coherently with the previous discussion on the structural properties of global minima at all compositions for AgCu nanoalloys with N = 100 atoms in total. Icosahedra with anti-Mackay crust are ranked second (purple curve), whereas mixed crust (yellow) and polyicosahedra (red) are ranked respectively third and fourth.
, while the sum in the denominator extends to the minima of all families considered in the calculation. The probabilities pi of individual minima are given by eqn (16). In this way we can compute the probability for each motif as a function of temperature. The black curve in Fig. 12 suggests that the icosahedron with Mackay crust is the most favorite structural family (i.e. the most probable) in the relevant interval of temperature from 0 to 500 K (after which AgCu nanoalloys start melting their surface), coherently with the previous discussion on the structural properties of global minima at all compositions for AgCu nanoalloys with N = 100 atoms in total. Icosahedra with anti-Mackay crust are ranked second (purple curve), whereas mixed crust (yellow) and polyicosahedra (red) are ranked respectively third and fourth.
 | ||
| Fig. 12 Probability P of the different structural families as a function of temperature in the range 200–600 K. P is calculated by eqn (17). The curves refer to icosahedra with Mackay crust (black), icosahedra with mixed Mackay and anti-Mackay crust (yellow), icosahedra with full anti-Mackay crust (purple) and polyicosahedra (red). The colors correspond to those of the clusters of Fig. 10B, while representative structures are given in Fig. 11. | ||
4 Conclusions
In this article, the lowest-energy structures of AgCu nanoalloys of sizes N = 100 and 200 were searched for by the Basin Hopping global optimization algorithm. For N = 100, all compositions were considered, whereas for N = 200 we optimized one composition over two. These searches revealed a rich variety of structural motifs and a non-parabolic behaviour of the mixing energy.The mixing energy was found to be negative, for all compositions at size 100 and for the vast majority of compositions of size 200, with very few slightly positive values in the extreme Ag-rich limit. We attribute the negative values of the mixing energy to the possibility of forming non-crystalline structures with core shell Cu@Ag chemical ordering, which is the optimal chemical ordering due to the larger size and lower surface energy of Ag compared to Cu. This chemical ordering, which is possible at the nanoscale with no counterpart in the bulk limit, allows an efficient stress relaxation which helps in stabilizing nanoalloy structures with respect to elemental nanoparticles.32,35 In fact, the structures with the lowest mixing energy are found in the composition range where the inner part and the surface layer are almost completely made of Cu and Ag atoms, respectively. The most efficient stress relaxation is achieved by structures of the icosahedral or polyicosahedral families, even for sizes, such as 100 and 200, that are far from icosahedral magic numbers. The stabilization of icosahedra by stress relaxation was already found for nanoparticles of sizes below 50 atoms, in several systems (AgCo, AgNi, AgCu and others).27,32,35 Here we have shown that stress relaxation is still very effective in stabilizing icosahedral structures at significantly larger sizes, and for wide composition intervals.
The global optimization data were used as a benchmark for the use of machine-learning techniques with the aim of answering to the following questions:
1. Is it possible to accurately fit the mixing energy by a suitable expression?
2. Is it possible to automatically group the nanoalloy structures into physically meaningful families?
As regards question 1, our calculations showed that the SVR algorithm is able to produce very accurate fits, for both N = 100 and N = 200. These results indicate that the same procedure is likely to produce accurate functions for interpolating the mixing energy also in cases in which the search of the global minima for all compositions might be very cumbersome (think for example about nanoalloys of sizes 500 or 1000), so that interpolating on the basis of the results of a limited set of compositions may be quite useful. We note also that the interpolation procedure by the SVR method includes a cross-validation of the result of the fitting that allows to determine the reliability of the fit itself.
As regards question 2, thanks to the clustering algorithms, we successfully divided each data set in distinct groups, thus underlying the variety of structural families present in AgCu nanoalloys of size N = 100 and N = 200 atoms. In particular we found that even without a previous manual classification of such nanoalloys, it is still possible to recover a physically meaningful as well as detailed separation into different clusters of structures. This result was achieved also thanks to the clever description given by the CNA signatures, which made possible the success of the two algorithms used, in a two dimensional space. We remark the importance of our choice of using unsupervised learning algorithms, for it would be surely possible to train a supervised classification model on a manually labelled data set, but more time consuming and, at some point, subjective. In order to cluster the data sets of the global minima for N = 100 and 200, we used K-means which produced a hard partition (Voronoi tessellation) of the two dimensional space of the two order parameters relative to 422 and 555 signatures. The classification obtained by the (555, 422) pair was compared also to those obtained by using other CNA sets of variables, discussing how the classification depended on the choice of the set.
A different algorithm, the Gaussian mixture model, was instead used to perform the same task on a slightly more complicated case, that is the one offered by the two dimensional representation of some of the local minima found in the global minimization of Ag64Cu36. Here the superior flexibility of such algorithm with respect to K-means was crucial to find a good separation into clusters.
The usefulness of the clustering of the minima of Ag64Cu36 was then demonstrated by calculating the equilibrium probabilities of the different structural families depending on temperature. Finally, we note that the approaches developed in this work do not rely on any specific feature of the AgCu system, so that they can be easily used to treat other nanoalloys.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the project “Dipartimento di Eccellenza” of the Physics, from the project PRIN2017 UTFROM of the Italian Ministry of University and Research, and from the International Research Network Nanoalloys of CNRS.Notes and references
- C. D. Abernethy, G. M. Codd, M. D. Spicer and M. K. Taylor, J. Am. Chem. Soc., 2003, 125, 1128–1129 CrossRef CAS PubMed.
- M. B. Gawande, A. Goswami, F.-X. Felpin, T. Asefa, X. Huang, R. Silva, X. Zou, R. Zboril and R. S. Varma, Chem. Rev., 2016, 116, 3722–3811 CrossRef CAS PubMed.
- H. Ditlbacher, J. R. Krenn, B. Lamprecht, A. Leitner and F. R. Aussenegg, Opt. Lett., 2000, 25, 563–565 CrossRef CAS.
- K. B. Mogensen and K. Kneipp, J. Phys. Chem. C, 2014, 118, 28075–28083 CrossRef CAS.
- K. McNamara and S. A. M. Tofail, Adv. Phys.: X, 2017, 2, 54–88 CAS.
- E. Kowalska, M. Endo, Z. Wei, K. Wang and M. Janczarek, Nanoscale Materials in Water Purification, Elsevier, 2019, pp. 553–579 Search PubMed.
- R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, 2016 Search PubMed.
- R. Ferrando, J. Nanopart. Res., 2018, 20, 179 CrossRef.
- D. Frenkel and B. Smit, Understanding Molecular Simulation from Algorithms to Applications, Academic Press, 2002 Search PubMed.
- K. Takahashi and L. Takahashi, J. Phys. Chem. Lett., 2019, 10, 4063–4068 CrossRef CAS.
- P. C. Jennings, S. Lysgaard, J. S. Hummelshøj, T. Vegge and T. Bligaard, npj Comput. Mater., 2019, 5, 46 CrossRef.
- G. R. Weal, S. M. McIntyre and A. L. Garden, J. Chem. Inf. Model., 2021, 61, 1732–1744 CrossRef CAS.
- C. Zeni, K. Rossi, A. Glielmo and F. Baletto, Adv. Phys.: X, 2019, 4, 1654919 CAS.
- R. Jinnouchi, H. Hirata and R. Asahi, J. Phys. Chem. C, 2017, 121, 26397–26405 CrossRef.
- X. Mao, L. Wang, Y. Xu, P. Wang, Y. Li and J. Zhao, npj Comput. Mater., 2021, 7, 46 CrossRef CAS.
- H. Kurban, Chem. Phys., 2021, 545, 111143 CrossRef CAS.
- J. P. K. Doye and F. Calvo, Phys. Rev. Lett., 2001, 86, 3570–3573 CrossRef CAS PubMed.
- D. J. Wales, Energy Landscapes, Cambridge University Press, 2003 Search PubMed.
- E. Panizon and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205417 CrossRef.
- M. Pellarin, M. Broyer, J. Lermé, M.-A. Lebeault, J. Ramade and E. Cottancin, Phys. Chem. Chem. Phys., 2016, 18, 4121–4133 RSC.
- M. Sharma, R. Buchner, W. Scharmach, V. Papavassiliou and M. Swihart, Aerosol Sci. Technol., 2013, 47, 858–866 CrossRef CAS.
- M. Taner Camci, N. Sayar Atasoy, I. Yulug and S. Suzer, J. Mater. Chem., 2011, 21, 13150–13154 RSC.
- S. Piccinin, S. Zafeiratos, C. Stampfl, T. W. Hansen, M. Hävecker, D. Teschner, V. I. Bukhtiyarov, F. Girgsdies, A. Knop-Gericke, R. Schlögl and M. Scheffler, Phys. Rev. Lett., 2010, 104, 035503 CrossRef.
- N. Bahremandi Tolou, M. Fathi, A. Monshi, V. Mortazavi and F. Shirani, Dent. Res. J., 2011, 8, S43–S50 Search PubMed.
- D. Bansal, J. Sekhon and S. Verma, Plasmonics, 2013, 143–150 Search PubMed.
- P. R. Subramanian and J. H. Perepezko, J. Phase Equilib., 1993, 14, 62–75 CrossRef CAS.
- A. Rapallo, G. Rossi, R. Ferrando, A. Fortunelli, B. C. Curley, L. D. Lloyd, G. M. Tarbuck and R. L. Johnston, J. Chem. Phys., 2005, 122, 194308 CrossRef.
- R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265 CrossRef CAS.
- V. Rosato, M. Guillopé and B. Legrand, Philos. Mag. A, 1989, 59, 321 CrossRef.
- F. Cyrot-Lackmann and F. Ducastelle, Phys. Rev. B: Condens. Matter Mater. Phys., 1971, 4, 2406–2412 CrossRef.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2003, 90, 135504 CrossRef CAS.
- G. Rossi, A. Rapallo, C. Mottet, A. Fortunelli, F. Baletto and R. Ferrando, Phys. Rev. Lett., 2004, 93, 105503 CrossRef CAS PubMed.
- D. Bochicchio and R. Ferrando, Nano Lett., 2010, 10, 4211–4216 CrossRef CAS PubMed.
- C. Langlois, Z. Y. Li, J. Yuan, D. Alloyeau, J. Nelayah, D. Bochicchio, R. Ferrando and C. Ricolleau, Nanoscale, 2012, 4, 3381–3388 RSC.
- R. Ferrando, J. Phys.: Condens. Matter, 2015, 27, 013003 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- G. Rossi and R. Ferrando, J. Phys.: Condens. Matter, 2009, 21, 084208 CrossRef CAS.
- G. Rossi and R. Ferrando, Comput. Theor. Chem., 2017, 1107, 66–73 CrossRef CAS.
- J. Pirart, A. Front, D. Rapetti, C. Andreazza-Vignolle, P. Andreazza, C. Mottet and R. Ferrando, Nat. Commun., 2019, 10, 1982 CrossRef CAS PubMed.
- D. Faken and H. Jónsson, Comput. Mater. Sci., 1994, 2, 279–286 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Springer, 2009 Search PubMed.
- H. Drucker, C. J. C. Burges, L. Kaufman, A. Smola and V. Vapnik, Advances in Neural Information Processing Systems, 1997 Search PubMed.
- V. N. Vapnik, The Nature of Statistical Learning Theory, Springer, 1999 Search PubMed.
- A. J. Smola and B. Schölkopf, Stat. Comput., 2004, 14, 199–222 CrossRef.
- C.-C. Chang and C.-J. Lin, ACM Trans. Intell. Syst. Technol., 2011, 2, 27 Search PubMed.
- Y. S. Abu-Mostafa, M. Magdon-Ismail and H.-T. Lin, Learning From Data, AMLbook.com, 2012 Search PubMed.
- S. Lloyd, IEEE Trans. Inf. Theory, 1982, 28, 129–137 CrossRef.
- K. P. Murphy, Machine Learning: A Probabilistic Perspective, The MIT Press, 2012 Search PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 Search PubMed.
- A. Géron, Hands-On Machine Learning with Scikit-Learn, Keras, and Tensorflow, O'Reilly, 2019 Search PubMed.
- D. Nelli and R. Ferrando, Nanoscale, 2019, 11, 13040–13050 RSC.
- M. Settem, J. Alloys Compd., 2020, 844, 155816 CrossRef CAS.
- M. Settem and A. K. Kanjarla, Comput. Mater. Sci., 2020, 184, 109822 CrossRef CAS.
- L. D. Marks, Rep. Prog. Phys., 1994, 57, 603–649 CrossRef CAS.
- S. Nunez and R. L. Johnston, J. Phys. Chem. C, 2010, 114, 13255–13266 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Parameters of the machine learning fit. Details on nanoalloy structural families. See DOI: 10.1039/d1cp02143e |
| This journal is © the Owner Societies 2021 |






