 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simple models for the quick estimation of ground state hydrogen tunneling splittings in alcohols and other compounds†
Robert
Medel

Institute of Physical Chemistry, University of Goettingen, Tammannstr. 6, 37077 Goettingen, Germany. E-mail: rmedel@gwdg.de
First published on 15th July 2021
Abstract
Models for the quick estimation of energy splittings caused by coherent tunneling of hydrogen atoms are evaluated with available experimental data for alcohols and improvements are proposed. The discussed models are mathematically simple and require only results from routine quantum chemical computations, i.e. hybrid DFT calculation of the equilibrium geometry and the transition state within the harmonic approximation. A benchmark of experimental splittings spanning four orders of magnitude for 27 alcohol species is captured by three evaluated models with a mean symmetric deviation factor of 1.7, 1.5 and 1.4, respectively, i.e. the calculated values deviate on average by this factor in either direction. Limitations of the models are explored with alcohols featuring uncommon properties, such as an inverted conformational energy sequence, a very light molecular frame, an elevated torsional frequency, or a coupling with a second internal degree of freedom. If the splitting of either the protiated or deuterated form of an alcohol is already experimentally determined, the one of the second isotopolog can be estimated by three additional models with a mean symmetric deviation factor of 1.14, 1.19 and 1.15, respectively. It is shown that this can be achieved with a novel approach without any quantum chemical calculation by directly correlating experimental splittings of isotopologs across related species. This is also demonstrated for other classes of compounds with hydrogen tunneling, such as amines, thiols, and phenols. Furthermore, it is found that the isotope effect can even be anticipated without any further knowledge about the system solely from the size of either splitting with a mean symmetric deviation factor of 1.3. This is based on an extensive sample of 77 pairs of splittings spanning eight orders of magnitude for isotopologs of chemically diverse compounds.
1 Introduction
In quantum mechanics atoms (and entire molecular groups)1,2 can tunnel coherently back and forth between degenerate positions,3 with the tunneling frequency depending on the separating barrier, the mass of the atom and the attempt frequency of the associated small-amplitude vibration. This phenomenon manifests itself in a splitting of the energy levels of the system which enables the accurate determination of quantum dynamics by time-independent spectroscopy. However, spectral assignment can be seriously complicated by the presence of these tunneling splittings,4 especially if multiple tunneling interactions occur.5–8 One example is the to date unassigned microwave spectrum of cyclopentanol, quote: ‘despite being a small, volatile, readily available, and easily measurable species’.9 This is due to splittings from the pseudorotation of the ring10 and possibly from the internal rotation of the hydroxy group. But once understood, the spectroscopic pattern provides valuable information about parts of the potential energy surface (PES) distant from the equilibrium geometry which is probed by the tunneling.11 As examples of direct application, the transitions between the tunneling states of the textbook example ammonia were the basis for the realization of the first atomic clock12 and the first maser.13The vast energy range of splittings can be illustrated for the tunneling of hydrogen, which is the most prevalent chemical element in atom tunneling due to its light mass and ubiquity in nature. When the vibrational zero-point level of the small-amplitude motion is close to the top of the barrier, splittings can be in the order of 100 cm−1hc.14–19 In contrast, the perhaps smallest splitting resolved so far in the deep tunneling regime is more than eight orders of magnitudes smaller with 4.6 × 10−7 cm−1hc (14 kHz h).20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡ The delocalization between enantiomeric conformations and configurations is expected to be ultimately limited by quenching from the minuscule asymmetry introduced by parity violation, for molecules with light atoms calculated down to about 10−15 cm−1hc.21
‡ The delocalization between enantiomeric conformations and configurations is expected to be ultimately limited by quenching from the minuscule asymmetry introduced by parity violation, for molecules with light atoms calculated down to about 10−15 cm−1hc.21
Theory provides an important synergy for spectral assignment and interpretation, but the strong dependence of tunneling on details of a large part of the electronic PES as well as on the treatment of quantum nuclear motion22 provides serious challenges. Due to their tunneling rates being accurately determinable by spectroscopy, systems with coherent tunneling offer an attractive experimental benchmark23 for theory. Refined methods and models can be applied subsequently to tunneling contributions to (or even tunneling control of)24 chemical reactions in which reactants and products are not isoenergetic.25 Sophisticated techniques for the accurate calculation of tunneling splittings have been developed.26–29 However, these approaches are mathematically very complex and often require the full PES, or at least a considerable part of it, to be computed with wave function-based methods with high-level treatment of electron correlation.30 More affordable and somewhat more accessible, but also more approximate, are models which explore the tunneling along a one-dimensional pathway.31–33 For the latter the release of software is acknowledged which makes the computation of half-lives for tunneling reactions broadly accessible.34
From the perspective of a spectroscopist (such as the author of the present article), a supplementation with even more approximate methods for quickly and straightforwardly attainable estimations is desirable. Even if they are only robust perhaps to the correct order of magnitude, similar to a Fermi estimate,35 they already allow to assess whether tunneling might qualify as a plausible explanation for an unexpected spectral splitting.36 If positive, more sophisticated, but also more laborious, follow-up investigations can be justified. Such estimates also enable to choose a spectroscopic method with an appropriate energy range and resolution in the first place, if the characterization of tunneling dynamics is the goal.37
The aim of the present article is to highlight, evaluate, improve and expand on some models used in the literature. The discussed approaches have in common that they require only input from routine quantum chemical computations, i.e. calculation of the equilibrium geometry and the transition state within the double-harmonic approximation. The needed quantities can be computed with hybrid DFT methods with decent accuracy in a matter of minutes for medium-sized molecules. Due to their mathematical simplicity, the models themselves can be applied as well within minutes by the user, not requiring further software beyond a spreadsheet program. As it will be shown, one could even do a calculation on the back of an envelope for the expected change of a given tunneling splitting upon hydrogen isotope substitution.
The models are tested, and in part adjusted, with reported experimental tunneling splittings of monohydric alcohols as a benchmark. With alcohols being among the most common classes of organic compounds, accurate values for splittings are available in the literature for a considerable number of species. They are only rivaled in quantity by reported cases of nitrogen inversion,38 dynamics in molecular complexes of water39,40 as well as internal rotation in methyl41 and ammonium compounds.41,42 From a model building and benchmarking perspective, analyzing a group of distinct but still related species enables to distinguish between fortuitous and systematic model performance, while it allows at the same time to exploit similarities for model simplification. Still, some black sheep in the alcohol family with special characteristics help to recognize the limitations of (over-)simplified models.
2 Torsional dynamics in alcohols
Alcohols are compounds with a hydroxy group –OH bound to a saturated carbon atom R3C–.43 Molecular structures, names and abbreviations of the species investigated in detail in this work are given in Fig. 1. | ||
| Fig. 1 Optimized (gauche−) structures, names and abbreviations of alcohols investigated in detail in this work. From left to right and from top to bottom the experimental tunneling splitting of the respective main isotopolog decreases (for 1-methylcyclohexanol estimates44 are used). | ||
By torsion around the C–O-bond, and possibly other bonds in the molecular frame, alcohols can interconvert between different conformations. Typically, staggered arrangements correspond to minima on the PES and eclipsed structures to transition states. If all three substituents are identical R1 = R2 = R3, so that the molecular frame has C3v or C3 symmetry, all three conformations are identical as well. Examples are methanol and tert-butyl alcohol. The torsional wave functions are then delocalized equally over all three potential wells and due to tunneling the vibrational ground state is split in an energetically lower A state and a higher doubly degenerate E state.
With one unique substituent R1 ≠ R2 = R3 and a frame of Cs symmetry, two enantiomeric gauche τ(R1COH) ≈ ±60° conformers and a diastereomeric trans τ(R1COH) = 180° conformer result. The tunneling interaction between the two gauche wave functions leads to an energetically lower symmetric, with respect to spatial parity inversion, and an upper antisymmetric delocalized combination. In the majority of cases the gauche conformers are energetically lower than the trans conformer. A central concept of this work is to take advantage of this by assuming that the hydrogen atom dominantly tunnels through the narrow cis barrier (Δτ ≈ 120°) and only negligibly through the wide trans part (Δτ ≈ 240°) of the torsional potential. Instead of having to calculate and analyze the entire torsional potential, the problem is thus reduced to the treatment of a symmetric acyclic double-well potential. From this solution the splitting for a symmetric cyclic triple-well potential can be obtained as well by multiplication with a factor of 3/2.45
Notable exceptions with an inverted conformational energy sequence are found in otherwise unfunctionalized primary alcohols,46,47 such as ethanol,48 and in certain tertiary alcohols, such as 1-methylcyclohexanol with the hydroxy group in an equatorial position.44 Here the calculated (nominal) gauche wave functions have a non-negligible amplitude in the trans potential well,44,48,49 which is not the case for the wave functions of alcohols with the more common conformational energy sequence.44,49,50 For ethanol it was found that treating the cyclic torsional potential as acyclic, effectively blocking tunneling through the cis barrier, still leaves a calculated tunneling splitting of about one third of the cyclic treatment.49 It will be tested whether reasonable estimates for ethanol and equatorial 1-methylcyclohexanol can be obtained nevertheless by taking only the cis barrier into account.
For most alcohols the tunneling can be reasonably approximated as an internal rotation of the hydroxy group relative to a rigid molecular frame. Known exceptions are benzyl alcohol1 and its derivatives.51–54 Here the internal rotations of the hydroxy group and the phenyl ring are strongly coupled. This can be anticipated already from the structural comparison of the connected enantiomeric minima (Fig. 2). Even though the effective tunneling mass is expected to be far heavier, the shallow barrier still leads to a small but resolved tunneling splitting in benzyl alcohol.1 The situation is further complicated by the presence of four degenerate minima connected by different tunneling pathways. Ring substitution enables the modulation of the tunneling rate between specific pairs or to quench it by a lowering of the symmetry.54 The models will be tested on the parent benzyl alcohol.
3 Computational methods
Density functional computations were carried out with the Gaussian 09 Rev. E.01 program package.55 The B3LYP56–59 functional with Grimme's D3 dispersion correction with two-body terms and Becke–Johnson damping60 was employed. The minimally augmented may-cc-pVTZ basis set,61 the ultrafine integration grid, very tight convergence criteria and no density fitting were used. The Hessian was evaluated in the double-harmonic approximation. Minima were confirmed by the absence and transition states by the presence of exactly one imaginary frequency. The C–O torsional character of the latter was checked by visual inspection using GaussView 6.0.16. For illustrative purposes, in addition a relaxed scan of the R1COH dihedral τ in 1° steps for propargyl alcohol was carried out with tight convergence criteria. Example inputs for reproduction and for the application of the models to further alcohols are available in the ESI.†Assumptions and approximations used in the discussed models throughout this article are that the tunneling in alcohols follows a single trajectory along the minimum energy path of the local torsional mode with the other vibrational modes contributing adiabatically to the barrier. The electronic barrier height Vel is calculated by taking the difference of the electronic energies between the cis transition state and the gauche minimum geometry through eqn (1). This barrier height is corrected by the difference of the vibrational zero-point energies, excluding the respective torsional wavenumbers ωi and ω0, to obtain V0 through eqn (2). The output of quantum chemistry software provides the total zero-point energy of the F vibrational modes ωj, excluding by default the imaginary wavenumber ωi of the transition state, while the torsional zero-point energy E0 of the minimum conformation needs to be manually subtracted (eqn (3)). Not excluding or re-adding the torsional zero-point energy results instead in an effective barrier height V0 − E0 with the width 2τ0. These quantities are illustrated in Fig. 3.
| Vel = Eel(TS) − Eel(min) | (1) |
 | (2) |
 | (3) |
 | (4) |
 | ||
| Fig. 3 Relevant part of the torsional potential for propargyl alcohol with different quantities illustrated. The calculated electronic potential, the calculated harmonic torsional zero-point vibrational energy and the experimental tunneling splitting62 are to scale. | ||
4 Computational results
Obtained barrier heights, without and with zero-point corrections for different isotopologs, are listed in Table 1. The zero-point correction is found to alter the barrier heights only by a few percent. Where available, computed values are compared with barrier heights estimated from models utilizing microwave and far-infrared spectroscopy results. Excellent agreement is found for the most accurately known barrier heights of methanol, both for the absolute values as well as for the small differences between the four considered isotopologs. The barrier of tert-butyl alcohol is likely calculated slightly too shallow; a scenario for a lower height was discussed, though.71 Discrepancies for alcohols with lower symmetry, and therefore more complicated potential shapes, tend to be larger. This should not be blamed solely on deficits in the employed electronic structure method and the vibrational treatment. Unlike tunneling splittings, barrier heights are not directly observable quantities. Their estimation tends to depend strongly on the utilized experimental information (splittings, torsional transitions, conformational differences, etc.) and its weighting. Different model assumptions are used, e.g. whether potentials for isotopologs are taken to be different or identical, whether the effective tunneling mass is assumed to be constant or to depend on the torsional coordinate, etc.11 This is reflected by the often considerable discrepancies between different experimentally derived estimations for some alcohols in Table 1. The largest difference percentage-wise is found for propargyl alcohol, with a calculated barrier height of about 200 cm−1hc, in contrast to an experimentally derived one of (90 ± 10) cm−1hc.63 For the estimation of the latter a barrier width at the base of (118 ± 6)° was assumed, while the calculated width is only 99°. Both a shallow broad and a high narrow barrier can explain the same tunneling splitting, highlighting one source of error for simple models.| Alcohol | ΔH(exp) | ΔD(exp) | V H(exp) | V D(exp) | V 0,H | V 0,D | V el | ω 0,H | ω 0,D | ω i,H | ω i,D | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HCCCH2OH | 2.2 × 10+1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 62 |
7.162 | 90 ± 1063 | 90 ± 1063 | 204 | 198 | 199 | 265 | 201 | 250i | 190i | 1.74 |
| CH3OH | 9.164 | 2.665 | 37466 | 36665 | 369 | 363 | 345 | 291 | 231 | 295i | 235i | 1.58 |
| CD3OH | 7.264 | 1.567,68 | 37069 | 36268 | 366 | 358 | 345 | 276 | 212 | 280i | 216i | 1.68 |
| NCCCCH2OH | 4.670 | 352 | 315 | 353 | 286 | 211 | 292i | 222i | 1.73 | |||
| tBuOH | 3.871 | 44371 | 424 | 412 | 404 | 270 | 193 | 289i | 215i | 1.82 | ||
| NCCH2OH | 3.872 | 5.6 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73 73 |
270 ± 5073 | 270 ± 5073 | 394 | 386 | 390 | 292 | 219 | 301i | 229i | 1.73 |
| 43374 | ||||||||||||
| MeCyOH eq | 6.1 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
320 ± 1044 | 368 | 354 | 351 | 268 | 191 | 275i | 204i | 1.81 | ||
| MeCyOH ax | 5.2 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
356 ± 1044 | 385 | 371 | 363 | 266 | 189 | 273i | 202i | 1.83 | ||
| EtOH | 3.275 | 5.7 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
40975 | 40975 | 419 | 409 | 397 | 276 | 204 | 302i | 228i | 1.83 |
| 39976 | 36176 | |||||||||||
| 37377 | 36577 | |||||||||||
| MeOCH2OH | 3.078 | 479 | 477 | 496 | 322 | 241 | 328i | 248i | 1.76 | |||
| CyOH eq | 1.750 | 37750 | 419 | 409 | 413 | 269 | 195 | 270i | 200i | 1.81 | ||
| iPrOH | 1.679 | 1.5 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 79 |
54079 | 54979 | 461 | 447 | 443 | 286 | 198 | 282i | 210i | 1.81 |
| 53879 | 53879 | |||||||||||
| 60480 | 60480 | |||||||||||
| AllOH | 4.7 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81 81 |
3.1 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81 81 |
55881 | 55881 | 589 | 578 | 602 | 303 | 220 | 355i | 263i | 1.82 |
| CF3CH2OH | 2.0 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
7.0 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
76382 | 72082 | 783 | 773 | 774 | 341 | 255 | 383i | 283i | 1.83 |
| 60376 | 44076 | |||||||||||
| cPrOH | 1.4 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83 83 |
5.5 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83 83 |
660 ± 13083 | 660 ± 13083 | 721 | 711 | 735 | 303 | 224 | 336i | 252i | 1.78 |
| Vi-cPrOH | 7.6 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 84 |
2.4 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 84 |
890 ± 25084 | 890 ± 25084 | 818 | 800 | 837 | 315 | 220 | 387i | 288i | 1.81 |
| FCH2OH | 5.9 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 85 |
1103 | 1104 | 1144 | 387 | 290 | 433i | 330i | 1.72 | |||
| BnOH | 1.6 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
4.6 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2801 | 2801 | 317 | 310 | 287 | 301 | 227 | 245i | 189i | 1.69 |
Some ambiguity arises as well in the estimation of the torsional wavenumber ω0 in the normal mode picture. It is assumed that the tunneling coordinate is represented by the minimum energy path of the torsional local mode, but some alcohols have one or multiple skeletal vibrations of similar frequency. Coupling between them leads to several normal modes possessing some torsional character. From these the vibration with the strongest torsional character is selected, judged by visual inspections using GaussView 6.0.16 and helped by the high infrared activity of the torsion. For a few cases two normal modes with very similar torsional character are found, here the averaged value is used. The obtained torsional wavenumbers are not too different between most alcohols, in a range of 265–315 cm−1. However, this window is exceeded by alcohols with strongly electronegative substituents: methoxymethanol (322 cm−1), 2,2,2-trifluoroethanol (341 cm−1) and fluoromethanol (387 cm−1). This can be attributed to the anomeric effect86 providing an additional restoring force already to small deflections out of the minimum geometry.
In the limit of the remainder of the molecule becoming infinitely heavier than the hydroxy hydrogen, the torsional moment of inertia (acting as the effective tunneling mass μ) is expected to converge towards a constant value (reduced mass concept). This asymptotic value approximately doubles upon deuteration. Information about how close the investigated alcohols are to this limit can be extracted from the torsional wavenumbers. With the force (torque) constants being isotope-independent, one obtains in the harmonic approximation the ratio of the effective masses r = μD/μH = ωH2/ωD2. Due to being decoupled, the imaginary torsional wavenumbers of the transition states are more reliable for this analysis than those of the gauche conformers. Calculated ratios fall in a range of 1.68–1.83, with the notable exception of methanol with a protiated methyl group. The ratio for CH3OH/D is substantially smaller with 1.58 (experimental: 1.59),68 indicating another special case to keep an eye on. In methanol the motion can be described with similar merit as tunneling of the hydroxy hydrogen relative to the methyl group as well as tunneling of the methyl hydrogen atoms relative to the hydroxy group. This is reflected by substantial decreases of both the experimental tunneling splitting (from 9.1 to 7.3 cm−1hc)64 and the calculated imaginary wavenumber (from 295i to 280i cm−1) upon deuteration of the methyl hydrogen atoms. In contrast, these quantities change only very slightly for ethanol upon deuteration of the methylene hydrogens, from 3.2 to 3.1 cm−1hc87 and from 302i to 300i cm−1, respectively.
One particularly interesting pair of isotopologs is CH3OH/CD3OD. The calculated ratio is 1.86 (experimental: 1.87)68 – slightly higher than for the hydroxy deuteration of the heavier alcohols, but still falling substantially short of the ideal value of 2, despite all substituents at the heavy atoms doubled in mass. This can be explained by the carbon or/and oxygen the nucleus being located slightly off the torsional axis.88 A ratio of about 1.99 is calculated between CH3OH and the hypothetical CD332OD as well as between CH3999OH and CD3999OD. Experimentally it is found as well that oxygen isotope substitution has a small and carbon isotope substitution only a minuscule impact on the torsional moment of inertia.89
5 Evaluation of model performance
The performance of models are evaluated and compared with the mean symmetric deviation factor (MSDF),90 redefined in eqn (5). | (5) |
6 Simple models for the estimation of tunneling splittings through quantum chemical calculations
6.1 Eckart barrier model
One of the few realistic barrier shapes, for which an analytical solution for tunneling is available, is the symmetric Eckart barrier.91 One can obtain92 within the WKB approximation93–95eqn (6) to conveniently estimate tunneling splittings from quantities obtained directly from routine calculations – under the assumption that the barrier shape in the investigated system is similar to the Eckart idealization. | (6) |
 from an improved WKB connection scheme.96 This increases calculated splittings by about 7.5%. This model was applied to evaluate the contribution of tunneling to the isomerism rates in cyclobutadiene97 and cis-l,3-pentadiene,98 gave a reasonable estimate for the splitting in malonaldehyde,92 and helped to distinguish between tunneling pathways in 1,3-propanediol.99 It was also used in reverse to estimate the barrier height from the observed splitting in the benzoic acid dimer.100 However, the model was also criticized for large and unpredictable errors due to wrong tunneling distances and incomplete description of zero-point effects.101
from an improved WKB connection scheme.96 This increases calculated splittings by about 7.5%. This model was applied to evaluate the contribution of tunneling to the isomerism rates in cyclobutadiene97 and cis-l,3-pentadiene,98 gave a reasonable estimate for the splitting in malonaldehyde,92 and helped to distinguish between tunneling pathways in 1,3-propanediol.99 It was also used in reverse to estimate the barrier height from the observed splitting in the benzoic acid dimer.100 However, the model was also criticized for large and unpredictable errors due to wrong tunneling distances and incomplete description of zero-point effects.101
The correlation between experimental and calculated tunneling splittings for alcohols through the Eckart Barrier Model using B3LYP-D3(BJ)/may-cc-pVTZ is shown in Fig. 4. Considering that not a single parameter was adjusted to experimental data (at least beyond the DFT functional), the descriptive quality of the Eckart Barrier Model is found to be very decent. For n = 27 considered splittings MSDF = 1.75 is reached, meaning the model is on average by this factor off target in either direction. The maximum symmetric devation factor MAX is found for fluoromethanol with an underestimation of factor 4.9. There is a tendency to underestimations, which appears to become more pronounced for small splittings and the heavy isotopolog(s) of each alcohol. An additional model for the prediction of the isotope effect, which exploits the observation that isotopologs have similar over- or underestimations, is elaborated in the ESI.†
 | ||
| Fig. 4 Correlation between experimental and calculated tunneling splittings according to the symmetric Eckart barrier model through eqn (6). The diagonal line represents perfect agreement. | ||
Excluded from this evaluation, however, is benzyl alcohol for whose isotopologs overestimations by about a factor of 500 and 300, respectively, are obtained. When the tunneling pathway does not correspond at least approximately to a single normal mode coordinate, the Eckart Barrier Model breaks down. Here, a two-dimensional approach is more appropriate for the complex tunneling motion in this alcohol.102
6.2 Barrier height model
In a recent article, Buschmann et al. investigated the rotational spectrum of acetone cyanohydrin (2-cyanopropan-2-ol).74 The tunneling splitting could not be determined, due to it exceeding the spectral range, but an estimate was needed as a fitting parameter. Therefore, the authors correlated for some protiated alcohols the logarithmized tunneling splittings (mostly experimental, but also some estimated) with reported experimentally derived barrier heights. A linear regression yielded eqn (7) which can be converted into eqn (8).| ln(ΔH/GHz h) = −0.00730·(V0,H/cm−1hc) + 7.17 | (7) |
| lg(ΔH/cm−1hc) = − 0.00317·(V0,H/cm−1hc) + 1.64 | (8) |
The procedure of Buschmann et al. includes the implicit assumption that the experimentally derived barrier heights (used for the adjustment of the model parameters) and the calculated ones (used in the application of the model) are both accurate enough to be comparable. As it was found in Section 4, this needed agreement is not seldom lacking. This suggests to instead correlate consistently experimental tunneling splittings with barrier heights calculated with a fixed theoretical method. The adjustment of the model parameters by linear regression then also allows to partially compensate possible weaknesses of the theoretical method, e.g. if there were a trend to under- or overestimation. The inclusion of more alcohols in the training set should also improve robustness.
By doing so, one obtains the correlation shown in Fig. 5. The linear regression for protiated alcohols, excluding only BnOH, is represented by a red solid line. The obtained parameters, given in eqn (9), are not too dissimilar to the one derived by Buschmann et al. in eqn (8).
| lg(ΔH/cm−1hc) = −0.00315·(V0,H/cm−1hc) + 1.77 | (9) |
The model is straightforwardly expanded to deuterated alcohols with a separate regression (blue solid line in Fig. 5, eqn (10)).
| lg(ΔD/cm−1hc) = −0.00570·(V0,D/cm−1hc) + 1.96 | (10) |
What can be anticipated at this point: if there are linear relationships between lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔH and V0,H as well as between lg
ΔH and V0,H as well as between lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔD and V0,D, and in addition V0,H ≈ V0,D is valid, then there is also a direct linear connection between lg
ΔD and V0,D, and in addition V0,H ≈ V0,D is valid, then there is also a direct linear connection between lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔH and lg
ΔH and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔD to be expected. This idea will be revisited when the isotope effect will be analyzed.
ΔD to be expected. This idea will be revisited when the isotope effect will be analyzed.
While the Eckart Barrier Models employs individual calculated values for ω0 and ωi to connect barrier heights with splittings, the Barrier Height Model uses instead two times two adjusted parameters. No justification for the somewhat unusual linear connection between lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ and V0 was given by Buschmann et al. For carboxylic acid dimers,103 three-dimensional rotors in crystals104 and also some alcohols105 models were proposed which correlate logarithmized tunneling splittings not with the barrier heights themselves but instead with their square roots. This can be theoretically substantiated on the change of the tunneling splitting when vertically scaling a potential.104,106 Nevertheless, tests on the alcohol data indicate that the correlations with the square roots and the unpotentiated barrier heights are almost equally good.
Δ and V0 was given by Buschmann et al. For carboxylic acid dimers,103 three-dimensional rotors in crystals104 and also some alcohols105 models were proposed which correlate logarithmized tunneling splittings not with the barrier heights themselves but instead with their square roots. This can be theoretically substantiated on the change of the tunneling splitting when vertically scaling a potential.104,106 Nevertheless, tests on the alcohol data indicate that the correlations with the square roots and the unpotentiated barrier heights are almost equally good.
Some conclusions about other assumptions needed for the model can be drawn from comparing with eqn (11), which was first derived by Dennison and Uhlenbeck for the treatment of the inversion of ammonia.107 The equation was amended here by using the simplification of an averaged value for  , moving it outside the integral, as well as again improving the pre-exponential factor.96
, moving it outside the integral, as well as again improving the pre-exponential factor.96
 | (11) |
| μj ≈ μk | (12) |
| ω0,j ≈ ω0,k | (13) |
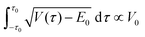 | (14) |
6.3 Restricted barrier height model
By inspection of Fig. 5 one notices that among the strongest outliers are the alcohols which, according to the calculations, do not conform well to the assumptions of similar tunneling mass and similar torsional wavenumber (eqn (12) and (13)). The exclusion of these alcohols – CH3OH/D (unusually low μ) as well as MeOCH2OH, CF3CH2OH/D and FCH2OH (unusually high ω0) – changes the regression parameters for protiated alcohols noticeably and improves the MSDF drastically. These alternative linear regressions (Restricted Barrier Height Model) are represented by dotted lines in Fig. 5 and their results are given in eqn (15) and (16).| lg(ΔH/cm−1hc) = −0.00407·(V0,H/cm−1hc) + 2.12 | (15) |
| lg(ΔD/cm−1hc) = −0.00589·(V0,D/cm−1hc) + 1.98 | (16) |
Deviating from Buschmann et al., the non-alcohol methyl hydroperoxide108 was not included in the updated version of the Barrier Height Model. It shares some similarities to alcohols, e.g. two enantiomeric conformers interconvertible trough an internal rotation of a hydroxy group by about 120°, but its calculated torsional wavenumber is far lower (176 cm−1 compared to about 300 cm−1). Consequently, the tunneling splitting is strongly overestimated by the Restricted Barrier Height Model.
6.4 Effective barrier height model
The main weakness of the Barrier Height Model is that it does not capture alcohols with somewhat unusual torsional wavenumber well. To remedy this, one can try to account for its role in the attempt frequency and in the zero-point energy. The latter reduces the effective barrier height the hydrogen atom has to tunnel through, making V0 − E0 a more obvious quantity than V0 for correlation with the splitting.The integral in eqn (11) can be re-expressed by the square root of the height of the barrier above the vibrational zero-point level  multiplied by the width of the barrier 2τ0 between the classical turning points of the attempt vibration and by a parameter σ describing the shape of the barrier (eqn (17)).109
multiplied by the width of the barrier 2τ0 between the classical turning points of the attempt vibration and by a parameter σ describing the shape of the barrier (eqn (17)).109
 | (17) |
 | (18) |
 were constant across alcohols and both the WKB approximation and the calculations were perfect, one would expect
were constant across alcohols and both the WKB approximation and the calculations were perfect, one would expect  to be directly proportional to
to be directly proportional to  . Unsurprisingly, this ideal scenario is not realized. Nevertheless, allowing somewhat more empirically an intercept different from zero enables a decent linear description, as shown in Fig. 6. The results of the regressions are given in eqn (19) and (20).
. Unsurprisingly, this ideal scenario is not realized. Nevertheless, allowing somewhat more empirically an intercept different from zero enables a decent linear description, as shown in Fig. 6. The results of the regressions are given in eqn (19) and (20). | (19) |
 | (20) |
 | ||
| Fig. 6 Correlation between experimental tunneling splittings divided by the calculated attempt wavenumbers and the square root of the calculated effective barrier heights according to the Effective Barrier Height Model (eqn (18)). The solid lines represent linear regressions for all alcohols but BnOH/D, separate for protiated (red) and deuterated (blue) alcohols. | ||
7 Simple models for the estimation of tunneling splittings through the isotope effect
Isotopic substitution is the most important experimental approach to verify that an observed splitting is indeed caused by tunneling of one (or multiple) suspected atom(s). The reduction of the splitting by deuteration enables in some cases its determination in the first place, either by moving transitions into an accessible spectral region4,110 or by increasing the thermal population of the upper tunneling state.44 Observed isotope effects for hydrogen tunneling, defined as IE = ΔH/ΔD, are as low as about 2 for some compounds15,18,19 but reach at least 459 for others.20 The ability to predict the size of the isotope effect makes it possible to judge which spectral range and resolution will be needed for the measurement of the other isotopolog to confirm that the tunneling interpretation is correct.The most important effects of deuteration of the hydroxy group are:
• The increased mass reduces the ability to penetrate the torsional barrier.
• The lowered torsional wavenumber leads to less frequent attempts to do so.
• The lowered torsional zero-point energy increases both the height as well as the width of the effective barrier.
• The dependence of the vibrational energy for other modes on the tunneling coordinate results in a (slightly) altered potential.
While these effects might be captured at least qualitatively by simple models based on the harmonic approximation, one also has to keep vibrational anharmonicity beyond the tunneling in mind as a potential spoiler for all but the most sophisticated models. Anharmonic effects will further change vibrational energies but also the effective structure. For example, the vibrationally averaged OH bond length will shrink from deuteration, further affecting the torsional moment of inertia. While for many alcohols the anharmonicity of the OH oscillator appears to be very similar,111 this is not the case for hydrogen bonded systems. Here, geometrical alterations, such as the (reverse) Ubbelohde effect,112,113 can lead to counter-intuitive changes, such as an increase of the splitting upon deuteration.2,114 Even a switch between qualitatively different structures was reported.115
7.1 Mass scaling model
In their classic textbook,116 Townes and Schawlow estimated the isotope effect on the inversion splitting of ammonia upon full deuteration with a simple scheme. They calculated the exponential argument in eqn (11) for NH3, using ΔH = 0.8 cm−1hc and ω0,H = 950 cm−1, and scaled it by to estimate the exponential argument for ND3 and therefrom the isotope effect. Their scheme can be generalized with eqn (21).
to estimate the exponential argument for ND3 and therefrom the isotope effect. Their scheme can be generalized with eqn (21). | (21) |
 | (22) |
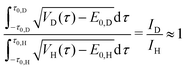 | (23) |
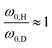 | (24) |
 . This scheme was also applied to estimate the isotope effect on a spectral splitting of oxadisulfane, again underestimating it by a factor of 1.4.119 Similar underestimations are yet again found when applied to all alcohols but benzyl alcohol. This deficit can be blamed on the complete neglect of the isotope impact on the small-amplitude motion (eqn (24)). As an improvement, the attempt wavenumber in the pre-exponential factor can also be scaled, following eqn (22), by
. This scheme was also applied to estimate the isotope effect on a spectral splitting of oxadisulfane, again underestimating it by a factor of 1.4.119 Similar underestimations are yet again found when applied to all alcohols but benzyl alcohol. This deficit can be blamed on the complete neglect of the isotope impact on the small-amplitude motion (eqn (24)). As an improvement, the attempt wavenumber in the pre-exponential factor can also be scaled, following eqn (22), by 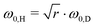 . This leads to eqn (25) as well as its counterpart eqn (26) when starting from the deuterated isotopolog.
. This leads to eqn (25) as well as its counterpart eqn (26) when starting from the deuterated isotopolog. | (25) |
 | (26) |
 , as in the Effective Barrier Height Model, with calculated ratios between 1.02 and 1.17.
, as in the Effective Barrier Height Model, with calculated ratios between 1.02 and 1.17.
 | ||
| Fig. 7 Correlation between the experimental tunneling splittings of deuterated alcohols and those calculated from their lighter isotopologs by the Mass Scaling Model through eqn (25) with r = 2 and ID/IH = 1. The diagonal line represents perfect agreement. | ||
7.2 Direct Correlation Model
Instead of trying to estimate ω0,H, r and ID/IH by quantum chemistry, one can extract optimal global parameters from experimental data of other alcohols. One way to do this systematically is rearranging eqn (25) to obtain eqn (27) and its equivalent eqn (28). | (27) |
 | (28) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔD and lg
ΔD and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔH. Such a connection was already anticipated from the performance of the Barrier Height Model. This is now confirmed by inspection of the direct correlation between the experimental values of the two quantities in Fig. 8. The result of the regression is given in eqn (29).
ΔH. Such a connection was already anticipated from the performance of the Barrier Height Model. This is now confirmed by inspection of the direct correlation between the experimental values of the two quantities in Fig. 8. The result of the regression is given in eqn (29).| lg(ΔD/cm−1hc) = 1.46·lg(ΔH/cm−1hc) − 1.03 | (29) |
 | ||
| Fig. 8 Correlation between the experimental tunneling splittings of deuterated and protiated alcohols. The data points represented by empty squares are not included in the linear regression, with the result given in eqn (29). | ||
To my knowledge and surprise, it appears that this correlation was not analyzed before, neither for alcohols nor for any other series of compounds. The natural expectation that two related compounds with similar tunneling splittings should retain this similarity after isotopic substitution was occasionally mentioned, but I am not aware that this was ever used for quantitative inter- or extrapolation.
As expected from the Mass Scaling Model, the slope  is found to be close to
is found to be close to  . Inserting this term into the expression for the intercept and solving for ω0,H leads to eqn (30). This equation allows to obtain a rough estimate for a typical attempt wavenumber and therefore a check for the consistency of the quantum chemical results for the torsional wavenumbers used in the other models.
. Inserting this term into the expression for the intercept and solving for ω0,H leads to eqn (30). This equation allows to obtain a rough estimate for a typical attempt wavenumber and therefore a check for the consistency of the quantum chemical results for the torsional wavenumbers used in the other models.
 | (30) |
The outlier of benzyl alcohol in this correlation between purely experimental values further confirms that its tunneling dynamics is very different from the one in the other alcohols. BnOD has a similar tunneling frequency as cPrOD. While protiation speeds up tunneling by a factor of 3.6 for the former, it is a factor of 25 for the latter.
Interestingly, reported isotope effects for two cases of torsional tunneling in diols4,20 and three cases in phenols120,121 are captured by eqn (29) similarly well (MSDF = 1.09, MAX = 1.15) – even though this involves an extrapolation to splittings several orders of magnitude smaller. For phenols with their cyclic double-minimum potential this requires a symmetry correction of the splittings by a factor of 1/2 to again correspond to the acyclic double-minimum situation. This finding suggests a glance at other compounds to check how universal the Direct Correlation Model might be applied.
As one example, the result for nitrogen inversion is shown in Fig. 9 and the result of the regression is given in eqn (31).
| lg(ΔD/cm−1hc) = 1.37·lg(ΔH/cm−1hc) − 1.10 | (31) |
 | ||
| Fig. 9 Correlation between the experimental inversion splittings of fully N-deuterated and N-protiated amines and amides. The outlier from vinylamine is not considered in the regression, whose result is given in eqn (31). The value of the inversion splitting of deuterated vinylamine has been questioned before.122,123 Based on the regression a value of about 15 cm−1hc is expected, instead of the 37 cm−1hc from the assignments. Predictions in the literature are 10 and 15 cm−1hc.122,123 Used values with references are available in the ESI.† | ||
Further series of hydrogen tunneling compounds found to be well described the model are thiols and crystalline compounds containing methyl groups. It appears to be valid as well for phenols, solid solutions of hydrogen in metals as well as systems with a transfer along a hydrogen bond (e.g. malonaldehyde). However, for the last mentioned examples this is based on only three data points each and requires further verification. Graphs and regressions for these series are available in the ESI.† The results of the regressions are overall not too dissimilar, this suggests to push the concept further and attempt a Universal Direct Correlation Model.
7.3 Universal direct correlation model
A total of 77 isotopologic pairs of tunneling splittings are collated from the literature for systems for which it is plausible that they represent cases of dominant hydrogen tunneling. This extensive but not exhaustive list contains very diverse systems of isolated molecules, molecular complexes, molecular crystals and solid solutions of hydrogen in metals. It is available in the ESI.† To presuppose minimal knowledge about the systems, no symmetry corrections to splittings are applied. While there is some expected scatter, the correlation shown in Fig. 10 can overall still be well described over the full range of eight orders of magnitude by the linear regression given in eqn (32).| lg(ΔD/cm−1hc) = 1.38·lg(ΔH/cm−1hc) − 1.12 | (32) |
 | ||
| Fig. 10 Correlation for 77 isotopologic pairs of experimental splittings from hydrogen tunneling in chemically diverse systems. The regression parameters are given in eqn (32), the used values with references in Table 1 and in the ESI.† | ||
Overall, the Universal Direct Correlation Model offers through eqn (32) a reasonable estimate for the isotope effect even if the tunneling pathway is unclear, so that quantities needed for other models are ambiguous or not computable. However, it requires the assumption that the dynamics are dominated by hydrogen tunneling. Observed isotope effects far smaller than estimated through the (Universal) Direct Correlation Model might be used as an indicator for substantial participation of other atoms than the substituted hydrogen atom(s). For mono-126 and dideuteration127 of ammonia deviations from eqn (31) by a factor of 7 respectively 3 are obtained, reflecting the equal participation of all three hydrogen atoms in the main isotopolog. For benzyl alcohol the IE is by a factor of 20 smaller than expected from eqn (29). For the water pyrazine complex114 the increase in the tunneling splitting upon substitution of the non-hydrogen bonded water hydrogen is by a factor of 83 smaller than anticipated from eqn (32). This reflects the strong non-linearity of the hydrogen bond in this complex and thus the substantial participation of the oxygen atom in the tunneling for the internal rotation about the hydrogen bond, as it is also supported by the effect from 16O → 18O substitution.
8 Predictions for additional alcohols
Every model has to prove its value not only by describing already known data, but also by successfully anticipating yet unknown. Predictions for some alcohols are given in Table 2. The first seven rows are attempts to fill the white spaces for isotopologs in Table 1. For MeCyOH ax and eq the predictions agree well with those from ref. 44.| Alcohol | EBM | BHM | RBHM | EBHM | MSM | DCM | SEBM (ESI) | Literature |
|---|---|---|---|---|---|---|---|---|
| (6) | (9) and (10) | (15) and (16) | (19) and (20) | (25) and (26) | (29) | (S3) and (S4) | ||
| NCCCCH2OD | 1.7 | 1.4 | 1.3 | 1.6 | 9.0 × 10−1 | 8.5 × 10−1 | 1.7 | |
| tBuOD | 2.0 × 10−1 | 6.1 × 10−1 | 5.4 × 10−1 | 3.9 × 10−1 | 6.0 × 10−1 | 5.4 × 10−1 | 4.1 × 10−1 | |
| MeCyOH eq | 3.2 | 4.0 | 4.2 | 3.6 | 3.4 | 3.6 | 4.1 | 3.444 |
| MeCyOH ax | 2.4 | 3.6 | 3.6 | 2.9 | 3.0 | 3.2 | 4.2 | 3.444 |
| MeOCH2OD | (2.0 × 10−1) | (1.7 × 10−1) | (1.5 × 10−1) | (1.8 × 10−1) | 4.8 × 10−1 | 4.7 × 10−1 | 3.6 × 10−1 | |
| CyOD eq | 9.5 × 10−2 | 4.2 × 10−1 | 3.7 × 10−1 | 2.7 × 10−1 | 2.4 × 10−1 | 2.1 × 10−1 | 1.7 × 10−1 | |
| FCH2OD | (1.5 × 10−4) | (4.6 × 10−5) | (3.0 × 10−5) | (3.5 × 10−4) | 1.7 × 10−3 | 1.5 × 10−3 | 1.0 × 10−3 | |
| NCCMe2OH | 1.6 | 1.9 | 1.6 | 1.9 | 1.774 | |||
| NCCMe2OD | 1.3 × 10−1 | 2.0 × 10−1 | 1.7 × 10−1 | 2.1 × 10−1 | ||||
| 1PrOH | 2.2 | 2.8 | 2.6 | 2.2 | ||||
| 1PrOD | 2.1 × 10−1 | 4.3 × 10−1 | 3.8 × 10−1 | 2.8 × 10−1 | ||||
| 1BuOH | 2.6 | 3.0 | 2.8 | 2.5 | 6.0 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
|||
| 1BuOD | 2.6 × 10−1 | 5.0 × 10−1 | 4.4 × 10−1 | 3.3 × 10−1 | 3.4 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
For acetone cyanohydrin NCCMe2OH the literature prediction by Buschmann et al. is supported as well. In this case the predictions are based on very similar underlying quantum chemical calculations, but are in good agreement with an adjusted indirect experimental estimate.74
For the respective conformer of 1-propanol and 1-butanol with eligible backbone symmetry the tunneling states were assigned, but so far the size of the respective splitting could not be determined.47,128 Very recently, Kawashima et al. searched for the tunneling transitions of 1BuOD in the 1 GHz (≙0.03 cm−1) region based on their prediction of this size.47 Due to the lack of success they suppose the splitting might actually be at least ten times larger. This appears to be a sensible supposition considering that EtOD has a splitting of 0.57 cm−1hc.75 The extension of the alkyl chain is calculated to have only a small impact on the torsional properties. Consequently, the predictions obtained here are similar to ethanol and one order of magnitude larger than the one by Kawashima et al. In analogy, the splittings of ethanethiol,129 1-propanethiol130 and 1-butanethiol47 are similar to each other as well.
9 Conclusions and outlook
In the present article it was demonstrated that ground state splittings caused by hydrogen tunneling in alcohols can be captured, and therefore expectedly predicted, by simple models using quantities from routine quantum chemical calculations on a broadly affordable hybrid DFT level in the harmonic approximation. From benchmarking with experimental data one can expect predictions to deviate on average by less than a factor of two and to be widely robust within the correct order of magnitude. This enables the zeroth-order assessment of a complex molecular property with minimal effort. In the light of some extensive approximations used, results should be checked by experiment and more rigorous models, though. More detailed benchmarking metrics, a spreadsheet for the convenient application of the proposed models as well as example inputs for necessary quantum chemical calculations are provided in the ESI.†For alcohols with a typical harmonic torsional wavenumber (265–315 cm−1) the Restricted Barrier Height Model is recommended, which correlates splittings with cis barrier heights while assuming similar moments of inertia and torsional wavenumbers between alcohols. Electronegative substituents are found to elevate the torsional wavenumber, its explicit consideration in the Effective Barrier Height Model reduces deviations for affected alcohols.
It is hard to judge to what extent the remaining deviations originate from the model assumptions and from the approximations of the used quantum chemical level. The estimation of the torsional wavenumber from the harmonic normal mode treatment might be a major source of error and thus a good starting point for improvement.31 In this context, it might be interesting to explore the performance of more sophisticated methods and models on the collated benchmark data as well as to investigate whether the proposed simple models might be applied as well to other series of compounds.
The latter was done with success already for the Direct Correlation Model, which does not require any quantum chemical input at all. This model represents a novel approach to predict isotope effects from purely experimental data by directly correlating logarithmized tunneling splittings of deuterated and protiated isotopologs across different compounds. It was found to be applicable to an extensive and diverse experimental data set of coherent hydrogen tunneling.
As a showstopper for the simple models was identified, though, a strong coupling with a second internal degree of freedom, as in benzyl alcohol. However, it should in principle be possible to anticipate such a situation in advance with the calculations.
The splittings of ethanol and equatorial 1-methylcyclohexanol are not captured noticeably worse than those of other alcohols, this indicates that in theses cases the impact of the partial delocalization of the gauche wave functions into the trans potential well is smaller than other causes of deviations for the models. The approximation to only consider tunneling through the narrow cis barrier, based on the ‘width trumps height principle’,24 might break down, though, for alcohols with a much lower gauche/trans than cis barrier, such as isobutanol.47 Work has begun to account for the whole torsional potential without sacrificing affordability and accessibility too much. Such an approach promises to capture more alcohols, to investigate the cooperation (or competition?) between different tunneling pathways and to explore the impact of introduced asymmetry.
It is hoped that the present article encourages the spectroscopic characterization of further alcohols and other systems with tunneling dynamics, as well as the benchmarking of other models on a wider experimental basis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Early versions of the Restricted Barrier Height Model and the Direct Correlation Model for alcohols were published before in German language as part of the doctoral thesis of the author.105 This project was partly funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 271107160/SPP1807. The benchmarking aspect has profited from the environment provided by the local research training group BENCh (DFG – 389479699/GRK2455). Computational resources from the GWDG and helpful discussions with J. R. Springborn and M. A. Suhm are acknowledged. This publication was supported financially by the Open Access Grant Program of the DFG and the Open Access Publication Fund of the University of Göttingen.References
- K. A. Utzat, R. K. Bohn, J. A. Montgomery, H. H. Michels and W. Caminati, J. Phys. Chem. A, 2010, 114, 6913–6916 CrossRef CAS PubMed.
- L. Evangelisti, L. Spada, W. Li, S. Blanco, J. C. López, A. Lesarri, J.-U. Grabow and W. Caminati, Phys. Chem. Chem. Phys., 2017, 19, 204–209 RSC.
- M. Quack and G. Seyfang, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, 2021, pp. 231–282 Search PubMed.
- D. Christen, L. Coudert, R. Suenram and F. Lovas, J. Mol. Spectrosc., 1995, 172, 57–77 CrossRef CAS.
- E. Fischer and I. Botskor, J. Mol. Spectrosc., 1984, 104, 226–247 CrossRef CAS.
- M. Schnell and J.-U. Grabow, Angew. Chem., Int. Ed., 2006, 45, 3465–3470 CrossRef CAS PubMed.
- H. J. Wörner, X. Qian and F. Merkt, J. Chem. Phys., 2007, 126, 144305 CrossRef.
- J. O. Richardson, S. C. Althorpe and D. J. Wales, J. Chem. Phys., 2011, 135, 124109 CrossRef PubMed.
- P. B. Carrol, Laboratory and Astronomical Rotational Spectroscopy, PhD thesis, California Institute of Technology, 2018 Search PubMed.
- D. G. Melnik, S. Gopalakrishnan, T. A. Miller and F. C. De Lucia, J. Chem. Phys., 2003, 118, 3589–3599 CrossRef CAS.
- D. G. Lister, J. N. Macdonald and N. L. Owen, Internal rotation and inversion: An introduction to large amplitude motions in molecules, Academic Press, London, New York, 1978 Search PubMed.
- H. Lyons, Sci. Am., 1957, 71–82 CrossRef.
- J. P. Gordon, H. J. Zeiger and C. H. Townes, Phys. Rev., 1955, 99, 1264–1274 CrossRef CAS.
- Z. N. Vealey, L. Foguel and P. H. Vaccaro, J. Phys. Chem. Lett., 2018, 9, 4949–4954 CrossRef CAS PubMed.
- Y. Kume, D. Amino and T. Asaji, J. Mol. Struct., 2013, 1043, 1–6 CrossRef CAS.
- S. Yu, B. J. Drouin, J. C. Pearson and H. M. Pickett, Astrophys. J. Suppl. Ser., 2009, 180, 119–124 CrossRef CAS.
- S. Willitsch, U. Hollenstein and F. Merkt, J. Chem. Phys., 2004, 120, 1761–1774 CrossRef CAS PubMed.
- Z. Kisiel, A. C. Legon and D. J. Millen, Proc. R. Soc. London, Ser. A, 1982, 381, 419–442 CAS.
- R. Kydd, Spectrochim. Acta, Part A, 1979, 35, 409–413 CrossRef.
- L. Evangelisti, Q. Gou, L. Spada, G. Feng and W. Caminati, Chem. Phys. Lett., 2013, 556, 55–58 CrossRef CAS.
- R. Berger, M. Quack, A. Sieben and M. Willeke, Helv. Chim. Acta, 2003, 86, 4048–4060 CrossRef CAS.
- A. G. Császár, C. Fábri, T. Szidarovszky, E. Mátyus, T. Furtenbacher and G. Czakó, Phys. Chem. Chem. Phys., 2012, 14, 1085–1106 RSC.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 15276–15283 CrossRef CAS.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 158–168 Search PubMed.
- J. O. Richardson and S. C. Althorpe, J. Chem. Phys., 2011, 134, 054109 CrossRef PubMed.
- M. Schröder, F. Gatti and H.-D. Meyer, J. Chem. Phys., 2011, 134, 234307 CrossRef.
- J. K. Gregory and D. C. Clary, J. Chem. Phys., 1995, 102, 7817–7829 CrossRef CAS.
- N. Shida, P. F. Barbara and J. Almlöf, J. Chem. Phys., 1991, 94, 3633–3643 CrossRef CAS.
- C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. Lett., 2021, 12, 4902–4909 CrossRef CAS PubMed.
- T. A. H. Burd and D. C. Clary, J. Chem. Theory Comput., 2020, 16, 3486–3493 CrossRef CAS PubMed.
- Y. Watanabe, T. Taketsugu and D. J. Wales, J. Chem. Phys., 2004, 120, 5993–5999 CrossRef CAS.
- C. S. Tautermann, A. F. Voegele, T. Loerting and K. R. Liedl, J. Chem. Phys., 2002, 117, 1967–1974 CrossRef CAS.
- H. Quanz and P. R. Schreiner, J. Comput. Chem., 2019, 40, 543–547 CrossRef CAS PubMed.
- R. Nityananda, Resonance, 2014, 19, 73–81 CrossRef CAS.
- K. Suma, Y. Sumiyoshi and Y. Endo, J. Am. Chem. Soc., 2005, 127, 14998–14999 CrossRef CAS PubMed.
- R. S. Berry, J. Chem. Phys., 1960, 32, 933–938 CrossRef CAS.
- J. M. Lehn, Dynamic Stereochemistry, Springer-Verlag, Berlin/Heidelberg, 1970, vol. 15/3, pp. 311–377 Search PubMed.
- L. Evangelisti and W. Caminati, Phys. Chem. Chem. Phys., 2010, 12, 14433 RSC.
- F. N. Keutsch and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10533–10540 CrossRef CAS.
- M. Prager and A. Heidemann, Chem. Rev., 1997, 97, 2933–2966 CrossRef CAS PubMed.
- D. Smith, Chem. Rev., 1994, 94, 1567–1584 CrossRef CAS.
- G. P. Moss, P. A. S. Smith and D. Tavernier, Pure Appl. Chem., 1995, 67, 1307–1375 Search PubMed.
- W. Li, L. Spada, L. Evangelisti and W. Caminati, J. Phys. Chem. A, 2016, 120, 4338–4342 CrossRef CAS PubMed.
- R. Isnard and J. Gilchrist, Chem. Phys., 1980, 52, 405–413 CrossRef CAS.
- T. N. Wassermann, P. Zielke, J. J. Lee, C. Cézard and M. A. Suhm, J. Phys. Chem. A, 2007, 111, 7437–7448 CrossRef CAS PubMed.
- Y. Kawashima, Y. Tanaka, T. Uzuyama and E. Hirota, J. Phys. Chem. A, 2021, 125, 1166–1183 CrossRef CAS.
- J. C. Pearson, K. V. L. N. Sastry, E. Herbst and F. C. De Lucia, Astrophys. J., 1997, 480, 420–431 CrossRef CAS.
- U. Kuenzer and T. S. Hofer, Chem. Phys. Lett., 2019, 728, 195–200 CrossRef CAS.
- M. Juanes, W. Li, L. Spada, L. Evangelisti, A. Lesarri and W. Caminati, Phys. Chem. Chem. Phys., 2019, 21, 3676–3682 RSC.
- S. Tang, Z. Xia, A. Maris and W. Caminati, Chem. Phys. Lett., 2010, 498, 52–55 CrossRef CAS.
- R. G. Bird, A. E. Nikolaev and D. W. Pratt, J. Phys. Chem. A, 2011, 115, 11369–11377 CrossRef CAS PubMed.
- L. Evangelisti, Q. Gou, G. Feng and W. Caminati, Mol. Phys., 2013, 111, 1994–1998 CrossRef CAS.
- L. Evangelisti and W. Caminati, Chem. Phys. Lett. X, 2019, 1, 100004 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, K. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc. Technical report, 2009 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- J. Pearson and B. Drouin, J. Mol. Spectrosc., 2005, 234, 149–156 CrossRef CAS.
- E. Hirota, J. Mol. Spectrosc., 1968, 26, 335–350 CrossRef CAS.
- G. Moruzzi, L. Xu, R. Lees, B. Winnewisser and M. Winnewisser, J. Mol. Spectrosc., 1994, 167, 156–175 CrossRef CAS.
- I. Mukhopadhyay, Y. Duan and K. Takagi, Spectrochim. Acta, Part A, 1998, 54, 1325–1335 CrossRef.
- L. Xu and J. Hougen, J. Mol. Spectrosc., 1995, 173, 540–551 CrossRef CAS.
- E. L. Sibert and J. Castillo-Chará, J. Chem. Phys., 2005, 122, 194306 CrossRef PubMed.
- L.-H. Xu, H. Müller, F. van der Tak and S. Thorwirth, J. Mol. Spectrosc., 2004, 228, 220–229 CrossRef CAS.
- M. Walsh, L.-H. Xu and R. Lees, J. Mol. Spectrosc., 1998, 188, 85–93 CrossRef CAS.
- R. A. Motiyenko, L. Margulès, M. L. Senent and J.-C. Guillemin, J. Phys. Chem. A, 2018, 122, 3163–3169 CrossRef CAS PubMed.
- E. Cohen, B. Drouin, E. Valenzuela, R. Woods, W. Caminati, A. Maris and S. Melandri, J. Mol. Spectrosc., 2010, 260, 77–83 CrossRef CAS.
- L. Margulès, B. A. McGuire, M. L. Senent, R. A. Motiyenko, A. Remijan and J. C. Guillemin, Astron. Astrophys., 2017, 601, A50 CrossRef.
- G. Cazzoli, D. G. Lister and A. M. Mirri, J. Chem. Soc., Faraday Trans. 2, 1973, 569 RSC.
- P. Buschmann, K. G. Lengsfeld, K. Aydt, M. K. Jahn, S. Herbers, M. J. Travers, H. V. L. Nguyen and J.-U. Grabow, J. Mol. Spectrosc., 2020, 373, 111372 CrossRef CAS.
- R. K. Kakar and C. R. Quade, J. Chem. Phys., 1980, 72, 4300–4307 CrossRef CAS.
- J. Durig and R. Larsen, J. Mol. Struct., 1990, 238, 195–222 CrossRef CAS.
- C. Quade, M. Liu and C. F. Liu, J. Mol. Spectrosc., 2000, 201, 319–320 CrossRef CAS.
- R. A. Motiyenko, L. Margulès, D. Despois and J.-C. Guillemin, Phys. Chem. Chem. Phys., 2018, 20, 5509–5516 RSC.
- E. Hirota and Y. Kawashima, J. Mol. Spectrosc., 2001, 207, 243–253 CrossRef CAS PubMed.
- F. Inagaki, I. Harada and T. Shimanouchi, J. Mol. Spectrosc., 1973, 46, 381–396 CrossRef CAS.
- S. Melandri, P. G. Favero and W. Caminati, Chem. Phys. Lett., 1994, 223, 541–545 CrossRef CAS.
- L.-H. Xu, G. T. Fraser, F. J. Lovas, R. D. Suenram, C. W. Gillies, H. E. Warner and J. Z. Gillies, J. Chem. Phys., 1995, 103, 9541–9548 CrossRef CAS.
- J. N. Macdonald, D. Norbury and J. Sheridan, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1365 RSC.
- A. Leonov, K.-M. Marstokk, A. de Meijere and H. Møllendal, J. Phys. Chem. A, 2000, 104, 4421–4428 CrossRef CAS.
- R. Suenram, F. Lovas and H. Pickett, J. Mol. Spectrosc., 1986, 119, 446–455 CrossRef CAS.
- H. Roohi and A. Ebrahimi, THEOCHEM, 2005, 726, 141–148 CrossRef CAS.
- C. F. Su and C. Quade, J. Mol. Spectrosc., 2000, 199, 34–39 CrossRef CAS PubMed.
- E. Flood, P. Pulay and J. E. Boggs, J. Am. Chem. Soc., 1977, 99, 5570–5574 CrossRef CAS.
- J. Fisher, G. Paciga, L.-H. Xu, S. Zhao, G. Moruzzi and R. Lees, J. Mol. Spectrosc., 2007, 245, 7–20 CrossRef CAS.
- M. Hunger and P. Döll, Hydrol. Earth Syst. Sci., 2008, 12, 841–861 CrossRef.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- J. Bicerano, H. F. Schaefer and W. H. Miller, J. Am. Chem. Soc., 1983, 105, 2550–2553 CrossRef CAS.
- G. Wentzel, Z. Phys., 1926, 38, 518–529 CrossRef.
- H. A. Kramers, Z. Phys., 1926, 39, 828–840 CrossRef.
- L. Brillouin, C. R. Hebd. Seances Acad. Sci., 1926, 183, 24–26 Search PubMed.
- A. Garg, Am. J. Phys., 2000, 68, 430–437 CrossRef.
- M. J. S. Dewar, K. M. Merz and J. J. P. Stewart, J. Am. Chem. Soc., 1984, 106, 4040–4041 CrossRef CAS.
- G. J. M. Dormans and H. M. Buck, J. Am. Chem. Soc., 1986, 108, 3253–3258 CrossRef CAS.
- D. F. Plusquellic, F. J. Lovas, B. H. Pate, J. L. Neill, M. T. Muckle and A. J. Remijan, J. Phys. Chem. A, 2009, 113, 12911–12918 CrossRef CAS PubMed.
- I. Kalkman, C. Vu, M. Schmitt and W. L. Meerts, ChemPhysChem, 2008, 9, 1788–1797 CrossRef CAS PubMed.
- F. Zerbetto and M. Z. Zgierski, Chem. Phys., 1989, 130, 45–54 CrossRef CAS.
- T. V. Alves, L. Simón-Carballido, F. R. Ornellas and A. Fernández-Ramos, Phys. Chem. Chem. Phys., 2016, 18, 8945–8953 RSC.
- C. S. Tautermann, A. F. Voegele and K. R. Liedl, J. Chem. Phys., 2004, 120, 631–637 CrossRef CAS.
- G. Voll and A. Huller, Can. J. Chem., 1988, 66, 925–937 CrossRef CAS.
- R. Medel, Schwingungsspektroskopische Untersuchungen zur Chiralitätserkennung und Torsionsdynamik bei Alkoholen, PhD dissertation, Georg-August-Universität Göttingen, 2020 Search PubMed.
- R. Berger, M. Gottselig, M. Quack and M. Willeke, Angew. Chem., Int. Ed., 2001, 40, 4195–4198 CrossRef CAS PubMed.
- D. M. Dennison and G. E. Uhlenbeck, Phys. Rev., 1932, 41, 313–321 CrossRef CAS.
- M. Tyblewski, T.-K. Ha, R. Meyer, A. Bauder and C. E. Blom, J. Chem. Phys., 1992, 97, 6168–6180 CrossRef CAS.
- A. Vdovin, J. Sepioł, N. Urbańska, M. Pietraszkiewicz, A. Mordziński and J. Waluk, J. Am. Chem. Soc., 2006, 128, 2577–2586 CrossRef CAS PubMed.
- N. W. Larsen and L. Schulz, J. Mol. Struct., 2009, 10 Search PubMed.
- R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2021, 23, 5629–5643 RSC.
- A. R. Ubbelohde and K. J. Gallagher, Acta Crystallogr., 1955, 8, 71–83 CrossRef CAS.
- S. Tang, I. Majerz and W. Caminati, Phys. Chem. Chem. Phys., 2011, 13, 9137 RSC.
- W. Caminati, L. B. Favero, P. G. Favero, A. Maris and S. Melandri, Angew. Chem., Int. Ed., 1998, 37, 792–795 CrossRef CAS.
- B. M. Giuliano and W. Caminati, Angew. Chem., Int. Ed., 2005, 44, 603–606 CrossRef CAS PubMed.
- C. H. Townes and A. L. Schawlow, Microwave spectroscopy, Dover Publications, New York, McGraw-Hill, 1975, corrected republication of the first edition, 1955 edition Search PubMed.
- Š. Urban, V. Špirko, D. Papoušek, J. Kauppinen, S. Belov, L. Gershtein and A. Krupnov, J. Mol. Spectrosc., 1981, 88, 274–292 CrossRef.
- L. Fusina, G. di Lonardo and J. Johns, J. Mol. Spectrosc., 1985, 112, 211–221 CrossRef CAS.
- S. Brünken, M. Behnke, S. Thorwirth, K. M. Yamada, T. Giesen, F. Lewen, J. Hahn and G. Winnewisser, J. Mol. Struct., 2005, 742, 237–242 CrossRef.
- N. Larsen and F. Nicolaisen, J. Mol. Struct., 1974, 22, 29–43 CrossRef CAS.
- N. Larsen, J. Mol. Struct., 1986, 144, 83–99 CrossRef CAS.
- Y. Hamada, N. Sato and M. Tsuboi, J. Mol. Spectrosc., 1987, 124, 172–178 CrossRef CAS.
- R. Brown, P. Godfrey, B. Kleibomer, A. Pierlot and D. McNaughton, J. Mol. Spectrosc., 1990, 142, 195–204 CrossRef CAS.
- S. L. Baughcum, Z. Smith, E. B. Wilson and R. W. Duerst, J. Am. Chem. Soc., 1984, 106, 2260–2265 CrossRef CAS.
- N. W. Larsen and T. Steinarsson, J. Mol. Spectrosc., 1987, 123, 405–425 CrossRef CAS.
- V. Job, S. Kartha, K. Singh and V. Kartha, J. Mol. Spectrosc., 1987, 126, 290–306 CrossRef CAS.
- S. Kartha, K. Singh, V. Job and V. Kartha, J. Mol. Spectrosc., 1988, 129, 86–98 CrossRef CAS.
- A. A. Abdurakhmanov and G. I. Ismailzade, J. Struct. Chem., 1987, 28, 238–243 CrossRef.
- J. Nakagawa, K. Kuwada and M. Hayashi, Bull. Chem. Soc. Jpn., 1976, 49, 3420–3432 CrossRef CAS.
- J. Nakagawa and M. Hayashi, J. Mol. Spectrosc., 1981, 85, 327–340 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Example inputs and outputs, a spreadsheet for the application of the models, lists of splittings and correlation graphs for other compounds, calculations on further alcohols, discussion of evaluation metrics. See DOI: 10.1039/d1cp02115j |
| ‡ Tunnel splittings and other energy differences will be given throughout this article in units of cm−1hc to facilitate the comparison with vibrational wavenumbers in cm−1. Useful conversion factors to other common energy units, rounded to two leading digits, are: 1 cm−1hc ≈ 30 GHz h ≈ 120 μeV ≈ 12 J mol−1NA−1 ≈ 2.9 cal mol−1NA−1. |
| This journal is © the Owner Societies 2021 |



