 Open Access Article
Open Access ArticleUniversal description of steric hindrance in flexible polymer gels†
Manuel
Quesada-Pérez
 a,
José Alberto
Maroto-Centeno
a,
José Alberto
Maroto-Centeno
 a,
María del Mar
Ramos-Tejada
a,
María del Mar
Ramos-Tejada
 a and
Alberto
Martín-Molina
a and
Alberto
Martín-Molina
 *bc
*bc
aDepartamento de Física, Escuela Politécnica Superior de Linares, Universidad de Jaén, Linares, 23700, Jaén, Spain
bDepartamento de Física Aplicada, Universidad de Granada, Campus de Fuentenueva s/n, Granada 18071, Spain. E-mail: almartin@ugr.es
cInstituto Carlos I de Física Teórica y Computacional, Universidad de Granada, Campus de Fuentenueva s/n, Granada 18071, Spain
First published on 28th June 2021
Abstract
In this work, the long-time diffusion of a solute in a chemically crosslinked and flexible hydrogel is computed from a bead-spring model of a polymeric network to assess the effect of steric obstruction. The relative diffusivities obtained for a wide variety of systems can be described by an exponential decay depending on a parameter that differs from that employed for rigid gels. The mathematical expression derived here can approximately predict the diffusivity in flexible gels if steric hindrance is the mechanism ruling diffusion.
Diffusion in crosslinked gels plays a key role in many industrial, technological and biological processes. For instance, the comprehension of the parameters involved in diffusion is essential in separation processes such as size exclusion chromatography.1 In many instances, the accurate prediction of drug release kinetics from gels and microgels also relies on the precise knowledge of the diffusion coefficient of the solute.2–4 On the other hand, biopolymer-based hydrogels such as mucus or the extracellular matrix act as protective barriers against pathogens and toxic agents.5 In spite of their relevance, the physical mechanisms that explain why only certain particles can permeate such barriers are not fully understood yet. In addition, particle diffusion is the cornerstone of microrheology since rheological properties are intimately related to the long- and short-time diffusion coefficients. In fact, from a microscopic viewpoint, both diffusion and microrheology are based on the knowledge of the mean square displacement (MSD) of a tracer particle. For solute particles diffusing in a liquid, Einstein found that the MSD (〈r2〉) is a linear function of time t:
| 〈Δr2〉 = 6Dt | (1) |
Diffusion in gels has drawn the attention of many theorists, who have developed a lot of expressions to predict diffusion coefficients from different models, which were reviewed by Amsden6 and Masaro et al.7 at the late nineties. Some of these theories focus on steric hindrance (or obstruction). According to them, polymer chains are thought of as fixed and impenetrable obstacles that slow down the diffusive motion of the solute.
From the early nineties, researchers began to use a new and powerful tool to address different issues related to diffusion in gels: computer simulations.8,9 In fact, many researchers have simulated diffusive processes in gel-like systems since then. Most of them modelled gels as rigid structures of different geometry (see references in ref. 8 and 10). In particular, Johansson and Löfroth assessed the effect of steric hindrance on the long-time coefficient diffusion for rigid gels and concluded that most of their results merge into a mater curve when they are represented as a function of α = φ(1 + Rs/Rp)2, where φ is the polymer volume fraction, Rs is the solute radius and Rp is the radius of the polymeric fibers (or chains).11 The functional form of this master curve was a slightly compressed exponential decay:
| D/D0 = exp(−0.84α1.09) | (2) |
A few flexible gel-like structures have also been simulated. Some authors have employed a system made of spheres initially placed at the nodes of a cubic lattice and connected to their nearest neighbors by harmonic potentials.12–14 It should be stressed, however, that polymeric chains are not explicitly included in these simulations. In fact, some researchers have recently simulated solute diffusion in gels considering explicitly flexible polymeric chains through the bead-spring model.15–17 Their model was quite similar to the bead-spring model employed by some researchers to study the swelling of polyelectrolyte gels in the early 2000.18–20 This model was able to justify some experimental behaviors reported for microgels synthesized from tetrafunctional crosslinkers21 and served as reference to test different mean-field theories on gels.22–24 In addition, this model has been employed in simulations of nanogels.25,26 More recently, the bead-spring model has also been used within coarse-grained Langevin simulations to study how the cross-link ratio of polymer networks controls the solute partitioning, diffusion and permeability of flexible and regular polymeric networks.27 Therein, the authors revealed how the diffusion in collapsed gels strongly depends on the flexibility of the polymers. In this sense, implicit-solvent coarse-grained simulations together with scaling theories have been used by the same group to study penetrant transport through semi-flexible polymer networks.28
According to the preceding paragraphs, our main goal is to find out to what extent the steric obstruction in gels made of flexible polymer chains can be described in terms of a single function (like eqn (2)). To explicitly consider the flexibility of the polymer backbone, the bead-spring model of gel was employed. Accordingly, the solvent is a continuum and each monomeric unit that forms the polymeric chain is modeled as a sphere of radius Rm. The radius of the monomeric units is expected to be almost identical to the radius of the molecule of the monomer. In turn, this parameter can be estimated from the molecular weight (Mm) and the density (ρm) of the corresponding monomer as 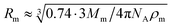 , where NA is Avogadro's number. In the simulations performed for this study, a radius of 0.3 nm has been used for monomeric units and crosslinkers. This value is close to the mean radius estimated for several monomers, such as vinyl acetate, N-vinyl-2-pyrrolidone, N-isopropylacrylamide and ethylene glycol.29
, where NA is Avogadro's number. In the simulations performed for this study, a radius of 0.3 nm has been used for monomeric units and crosslinkers. This value is close to the mean radius estimated for several monomers, such as vinyl acetate, N-vinyl-2-pyrrolidone, N-isopropylacrylamide and ethylene glycol.29
In an ideal polymeric network, each chain is composed of the same number of monomeric units (Nmu). To simulate flexible chains, these monomers are connected through a harmonic potential:
| ue(r) = 0.5ke(r − r0)2 | (3) |
The excluded volume effects between any pair of particles (solute, monomeric units or crosslinkers) are taken into account through the Weeks–Chandler–Andersen (WCA) potential:
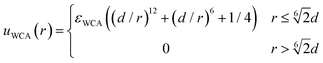 | (4) |
As the reader can imagine, the whole gel cannot be simulated. Simulations are restricted to a unit cell, which is replicated periodically in the three spatial directions. Periodic boundary conditions are applied. The unit cell contains 16 chains connected by 8 crosslinkers and the solute particle. Simulations were performed at constant volume, temperature, and number of particles (canonical ensemble). The number of particles is determined by the number of monomeric units per chain. The volume of the simulation cell was adjusted to reproduce the polymer volume fraction desired in every simulation.
All the particles included in the simulation cell move according to the Brownian Dynamics (BD) algorithm. In the absence of hydrodynamic interactions, the m-component (m can be x, y or z) of the displacement of particle i during a time step Δt is given by:30
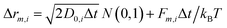 | (5) |
The MSD (required for the computation of the diffusion coefficient from eqn (1)) was calculated averaging on 300 independent trajectories of the solute particle (only one solute particle was used in our simulations to avoid the effect of concentration on the diffusion coefficient). Its displacement was sampled every 30 ps for 30 ns. Consequently, 2 × 105 moves per particle were executed in every trajectory. It should be also mentioned that, before collecting data for statistical purposes, the polymer network was equilibrated through 1 × 105 moves per particle. The longtime diffusion coefficient (D) was computed fitting 〈r2〉/6t to the exponential decay D + Ae−t/τ, where A and τ are also adjustable parameters. An example of fit is provided as ESI† (see Fig. SI-2 in ESI†). The error bars of some diffusion coefficients were estimated as the standard deviation of three independent runs. Although this work is focused on the long-time diffusive behavior, the MSD can provide valuable information on diffusive phenomena at other time scales, such as anomalous diffusion,33,34 recently observed in mucin hydrogels.35 The presence of anomalous diffusion in the simulations performed here is also briefly commented in ESI.†
The simulations performed in this work can be grouped into five series, which are summarized in Table 1. The values of the polymer volume fraction (φ), number of monomeric units per chain (Nmu), solute radius (Rs) and absolute temperature (T) employed in each simulation can be found in Table 1. These values are inspired by real systems. In fact, series 3–5 try to reproduce the conditions of experiments carried out by Hagel et al.36 (series 3 and 4) and Majer and Southan32 (series 5) with hydrogels made of poly(ethylene glycol) diacrylate (PEGDA). Hagel et al. measured the diffusion coefficient of monodisperse dextran particles with diameters ranging from 1.9 to 2.6 nm,36 whereas Majer and Southan measured the diffusion coefficient of adenosine triphosphate (ATP) in twelve hydrogels with polymer volume fractions ranging from 0.06 to 0.30.32 The Nmu-value corresponding to the hydrogel employed by Hagel et al. was adjusted trying to reproduce the mesh sizes reported for different polymer volume fractions. On the other hand, the Nmu-values corresponding to the hydrogels synthesized by Majer and Southan were computed from the molecular weight between crosslinks (Mc), which in turn can be estimated from data provided by Majer and Southan applying a modified version of the Flory–Rhener equation (see ref. 32 for further details). Table 1 also includes the degree of crosslinking (defined here as the ratio of crosslinking molecules to the total number of monomeric units).
| Series | Polymer volume fraction (φ) | Solute radius (Rs, nm) | Number of monomers per chain (Nmu) | Degree of crosslinking | Temperature (K) |
|---|---|---|---|---|---|
| 1 | 0.01, 0.03, 0.05, 0.08, 0.11, 0.14 | 1.0 | 25 | 0.020 | 293 |
| 2 | 0.08 | 1.00, 1.27, 1.53, 1.69, 1.90 | 25 | 0.020 | 293 |
| 3 | 0.03 | 1.00, 1.27, 1.53, 1.69, 1.90, 2.20 | 40 | 0.012 | 298 |
| 4 | 0.05 | 1.00, 1.27, 1.53, 1.69, 1.90, 2.20 | 40 | 0.012 | 298 |
| 5 | 0.03 | 0.633 | 69 | 0.007 | 293 |
| 0.06 | 33 | 0.015 | |||
| 0.06 | 53 | 0.009 | |||
| 0.07 | 21 | 0.023 | |||
| 0.09 | 30 | 0.016 | |||
| 0.09 | 42 | 0.012 | |||
| 0.10 | 6 | 0.077 | |||
| 0.13 | 14 | 0.034 | |||
| 0.13 | 23 | 0.021 | |||
| 0.16 | 13 | 0.037 | |||
| 0.20 | 4 | 0.111 | |||
| 0.30 | 2 | 0.200 |
As can be inferred from Table 1, the gels simulated here comprise wide ranges of φ (0.01–0.30), Nmu (2–69) and degree of crosslinking (0.007–0.200). In addition, it is worth mentioning that series 5 includes three pairs of gels with the same volume fraction (0.06, 0.09 and 0.13) but different Nmu-values. Concerning the solute, the largest radius is 2.20 nm and this includes a wide variety of molecules or macromolecules of biotechnological interest, such as urea, glucose, caffeine, myoglobin, lysozyme or α-lactalbumin (their radii can be found in ref. 6).
Fig. 1 shows the relative diffusivity (D/D0, where D and D0 stand for the longtime diffusion coefficient of the solute inside the gel and its free diffusion coefficient, respectively) of the five series of simulation data (see Table 1) as a function of α = φ(1 + Rs/Rm)2. In the estimation of α it was assumed that Rp ≈ Rm because we are dealing with polymer chains, whose thickness is of the order of the monomer diameter. As can be concluded, these data do not merge into a master curve. This obviously means that solute diffusion in flexible gels is not governed by the parameter ruling diffusion in rigid networks.
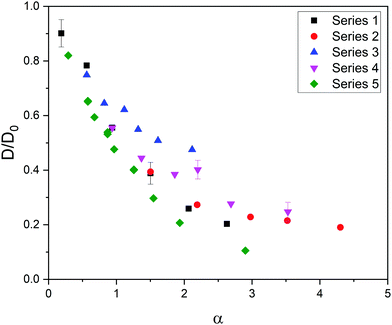 | ||
| Fig. 1 Relative diffusivity corresponding to five series of data as a function of α = φ(1 + Rs/Rm)2. The error bars of a few cases are shown to exemplify the uncertainty in the relative diffusivity. | ||
Luckily, the five series of relative diffusivity approximately collapse onto a master curve when they are represented as a function of a new dimensionless parameter, β, defined as β = φ(1 + Rs/Rm)1.3. This is illustrated in Fig. 2. As can be easily seen, the exponent of (1 + Rs/Rm) in β is smaller than in α. This means that the relative importance of size (compared to the polymer volume fraction) in steric hindrance is smaller in flexible gels.
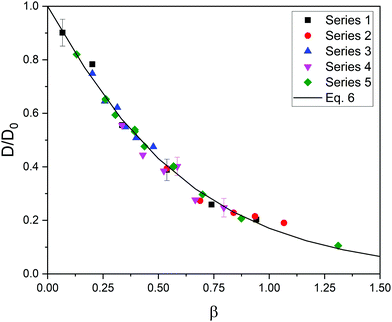 | ||
| Fig. 2 Relative diffusivity corresponding to five series of data as a function of β = φ(1 + Rs/Rm)1.3. The best fit obtained from eqn (6) is also plotted (solid line). The error bars of a few cases are shown to exemplify the uncertainty in the relative diffusivity. | ||
After having found a master curve introducing a new dimensionless parameter, the data of Fig. 2 were fitted to the function:
| D/D0 = exp(−Aβe) | (6) |
In any case, it should be mentioned that Fig. 2 and the parameters of eqn (6) were obtained from simulations in which the elastic constant remained fixed (ke = 0.4 N m−1). As preliminary work, simulations with elastic constants ranging from 0.04 to 0.4 N m−1 were carried out. No important effects were found on the diffusion coefficient. However, this coefficient and the definition of β might depend on the rigidity of the network for ke-values outside that range.
At this point, it is worth finding out to what extent real systems also obey eqn (6). To tackle this task, we have used five series of experimental diffusivities. Three of them inspired our own simulations (dextran particles in PEGDA-based gels at φ = 0.03 and φ = 0.05,36 ATP in PEGDA-based gels32). The relative diffusivities measured for them are plotted in Fig. 3. This figure also displays diffusivities corresponding to ribonuclease (RNase) and urea in polyacrylamide (PAAm) gels37,38 as a function of β. Rm and Rs are required to estimate this parameter. As mentioned previously, the radius of different monomers (estimated as 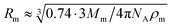 ) is of the order of 0.3 nm. This is also the case of ethylene glycol and acrylamide. In relation to Rm, it should also be stressed that it was not considered an adjustable parameter. The solute radius is 2.0 nm for RNase37 and 0.2 nm for urea.38 As can be seen in Fig. 3, the diffusivities of these five series are located very close to the prediction of eqn (6). For β > 1, the experimental values seem to be slightly greater than those predicted by eqn (6). This suggests that simulations might underestimate the diffusion coefficient of large solutes. In any case, the advantage of using β with real systems can be illustrated plotting their relative diffusivities as a function of α. This is shown in Fig. SI-5 (ESI†).
) is of the order of 0.3 nm. This is also the case of ethylene glycol and acrylamide. In relation to Rm, it should also be stressed that it was not considered an adjustable parameter. The solute radius is 2.0 nm for RNase37 and 0.2 nm for urea.38 As can be seen in Fig. 3, the diffusivities of these five series are located very close to the prediction of eqn (6). For β > 1, the experimental values seem to be slightly greater than those predicted by eqn (6). This suggests that simulations might underestimate the diffusion coefficient of large solutes. In any case, the advantage of using β with real systems can be illustrated plotting their relative diffusivities as a function of α. This is shown in Fig. SI-5 (ESI†).
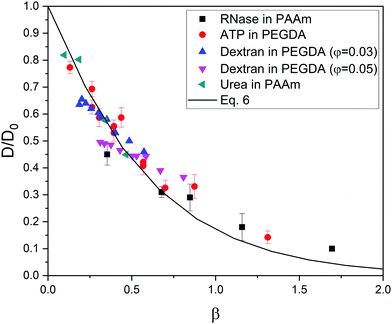 | ||
| Fig. 3 Relative diffusivity corresponding to real gel/solute systems as a function of β = φ(1 + Rs/Rm)1.3. The prediction obtained from eqn (6) is also plotted (solid line). These diffusivities (and their error bars) were extracted from ref. 32,36,37,38. | ||
In addition, we should keep in mind that the only solute/gel interaction considered in the bead-spring model used here is the purely steric one. Consequently, the predictions of eqn (6) might significantly deviate from the real ones if other interactions are present. For instance, previous simulations performed within rigid gel-like systems suggest that electrostatic interactions can play a fundamental role, particularly when solute and gel are oppositely charged.31,39–44 But, in the presence of additional interactions, eqn (6) might be used in combination with other expressions quantifying their effects. In fact, obstruction theories have been previously combined with hydrodynamic theories in the case of rigid gels.6
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for funding from “Consejería de Economía, Conocimiento, Empresas y Universidad, Junta de Andalucía, Programa Operativo FEDER Andalucía 2014–2020”, Project PY20_00138. In addition, A. M.-M. thanks the financial support by the “Consejería de Conocimiento, Investigación y Universidad, Junta de Andalucía” and European Regional Development Fund (ERDF), Project SOMM17/6105/UGR. M. M. R.-T. also thanks the financial support by Ministerio de Ciencia e Innovación, Projects PGC2018-098770-B-I00 and PID2020-116615RA-I00.References
- J. J. Hermans, Role of diffusion in gel permeation chromatography, J. Polym. Sci., Part A-2, 1968, 6, 1217–1226 CrossRef CAS.
- N. A. Peppas, P. Bures, W. Leobandung and H. Ichikawa, Hydrogels in pharmaceutical formulations, Eur. J. Pharm. Biopharm., 2000, 50, 27–46 CrossRef CAS PubMed.
- J. Siepmann and F. Siepmann, Modeling of diffusion controlled drug delivery, J. Controlled Release, 2012, 161, 351–362 CrossRef CAS PubMed.
- T. Casalini and G. Perale, From Microscale to Macroscale: nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery, Gels, 2019, 5, 28 CrossRef CAS PubMed.
- C. P. Goodrich, M. P. Brenner and K. Ribbeck, Enhanced diffusion by binding to the crosslinks of a polymer gel, Nat. Commun., 2018, 9, 4348 CrossRef PubMed.
- B. Amsden, Solute diffusion within hydrogels. Mechanisms and models, Macromolecules, 1998, 31, 8382–8395 CrossRef CAS.
- L. Masaro and X. X. Zhu, Physical models of diffusion for polymer solutions, gels and solids, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- M. Quesada-Pérez and A. Martín-Molina, Solute diffusion in gels: thirty years of simulations, Adv. Colloid Interface Sci., 2021, 287, 102320 CrossRef PubMed.
- T. Casalini, Not only in silico drug discovery: molecular modeling towards in silico drug delivery formulations, J. Controlled Release, 2021, 332, 390–417 CrossRef CAS PubMed.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Modeling of stimuli-responsive nanoreactors: rational rate control towards the design of colloidal enzymes, Mol. Syst. Des. Eng., 2020, 5, 602–619 RSC.
- L. Johansson and J. LLöfroth, Diffusion and interaction in gels and solutions. 4. Hard sphere Brownian dynamics simulations, J. Chem. Phys., 1993, 98, 7471–7479 CrossRef CAS.
- P. Licinio and A. V. Teixeira, Anomalous diffusion of ideal polymer networks, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 631–634 CrossRef CAS.
- H. Zhou and S. B. Chen, Brownian dynamics simulation of tracer diffusion in a cross-linked network, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021801 CrossRef PubMed.
- D. Sandrin, D. Wagner, C. E. Sitta, R. Thoma, S. Felekyan, H. E. Hermes, C. Janiak, N. De Sousa Amadeu, R. Kühnemuth, H. Löwen, S. U. Egelhaaf and C. A. M. Seidel, Diffusion of macromolecules in a polymer hydrogel: from microscopic to macroscopic scales, Phys. Chem. Chem. Phys., 2016, 18, 12860–12876 RSC.
- N. Kamerlin and C. Elvingson, Tracer diffusion in a polymer gel: simulations of static and dynamic 3D networks using spherical boundary conditions, J. Phys.: Condens. Matter, 2016, 28, 475101 CrossRef PubMed.
- Y. Chen, R. Ma, X. Qian, R. Zhang, X. Huang, H. Xu, M. Zhou and J. Liu, Nanoparticle Mobility within Permanently Cross-Linked Polymer Networks, Macromolecules, 2020, 53, 4172–4184 CrossRef CAS.
- H. Cho, H. Kim, B. Sung and J. Kim, Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: a Brownian Dynamics Simulation Study, Polymers, 2020, 12, 2067 CrossRef CAS PubMed.
- S. Schneider and P. Linse, Monte Carlo simulation of defect-free cross-linked polyelectrolyte gels, J. Phys. Chem. B, 2003, 107, 8030–8040 CrossRef CAS.
- B. A. Mann, R. Everaers, C. Holm and K. Kremer, Scaling in polyelectrolyte networks, Europhys. Lett., 2004, 67, 786–792 CrossRef CAS.
- B. A. Mann, C. Holm and K. Kremer, Swelling of polyelectrolyte networks, J. Chem. Phys., 2005, 122, 154903 CrossRef PubMed.
- M. Quesada-Pérez, J. Ramos, J. Forcada and A. Martín-Molina, Computer simulations of thermo-sensitive microgels: quantitative comparison with experimental swelling data, J. Chem. Phys., 2012, 136, 244903 CrossRef PubMed.
- S. Ahualli, A. Martín-Molina and M. Quesada-Pérez, Excluded volume effects on ionic partitioning in gels and microgels: a simulation study, Phys. Chem. Chem. Phys., 2014, 16, 25483–25491 RSC.
- P. Kosovan, T. Richter and C. Holm, Modeling of Polyelectrolyte Gels in Equilibrium with Salt Solutions, Macromolecules, 2015, 48, 7698–7708 CrossRef CAS.
- O. Rud, T. Richter, O. Borisov, C. Holm and P. Kosovan, A self-consistent mean-field model for polyelectrolyte gels, Soft Matter, 2017, 13, 3264–3274 RSC.
- L. Rovigatti, N. Gnan, L. Tavagnacco, A. J. Moreno and E. Zaccarelli, Numerical modelling of non-ionic microgels: an overview, Soft Matter, 2019, 15, 1108–1119 RSC.
- A. Martín-Molina and M. Quesada-Pérez, A review of coarse-grained simulations of nanogel and microgel particles, J. Mol. Liq., 2019, 280, 374–381 CrossRef.
- S. Milster, W. K. Kim, M. Kanduč and J. Dzubiella, Tuning the permeability of regular polymeric networks by the cross-link ratio, J. Chem. Phys., 2021, 154, 154902 CrossRef CAS PubMed.
- W. K. Kim, R. Chudoba, S. Milster, R. Roa, M. Kanduč and J. Dzubiella, Tuning the selective permeability of polydisperse polymer networks, Soft Matter, 2020, 16, 8144–8154 RSC.
- M. Quesada-Pérez, I. Adroher-Benítez and J. A. Maroto-Centeno, Size-exclusion partitioning of neutral solutes in crosslinked polymer networks: a Monte Carlo simulation study, J. Chem. Phys., 2014, 140, 204910 CrossRef PubMed.
- D. L. Ermak, A computer simulation of charged particles in solution. I. Technique and equilibrium properties, J. Chem. Phys., 1975, 62, 4189–4196 CrossRef CAS.
- L. Johansson, U. Skantze and J. E. Löfroth, Diffusion and interaction in gels and solutions. 6. Charged systems, J. Phys. Chem., 1993, 97, 9817–9824 CrossRef CAS.
- G. Majer and A. Southan, Adenosine triphosphate diffusion through poly(ethylene glycol) diacrylate hydrogels can be tuned by cross-link density as measured by PFG-NMR, J. Chem. Phys., 2017, 146, 225101 CrossRef PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- S. K. Ghosh, A. G. Cherstvy and R. Metzler, Non-universal tracer diffusion in crowded media of non-inert obstacles, Phys. Chem. Chem. Phys., 2015, 17, 1847–1858 RSC.
- A. G. Cherstvy, S. Thapa, C. E. Wagner and R. Metzler, Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels, Soft Matter, 2019, 15, 2526–2551 RSC.
- V. Hagel, T. Haraszti and H. Boehm, Diffusion and interaction in PEG-DA hydrogels, Biointerphases, 2013, 8, 1–9 CrossRef.
- J. Tong and J. L. Anderson, Partitioning and diffusion of proteins and linear polymers in polyacrylamide gels, Biophys. J., 1996, 70, 1505–1513 CrossRef CAS.
- M. L. White and G. H. Dorion, Diffusion in a crosslinked acrylamide polymer gel, J. Polym. Sci., 1961, 55, 731–740 CrossRef CAS.
- T. Miyata, A. Endo, T. Ohmori, M. Nakaiwa, M. Kendo, K. Kurumada and M. Tanigaki, Brownian Dynamics Simulation Study of Self-Diffusion of a Charged Particle in Swollen Counter-Charged Hydrogel Modeled as Cubic Lattice, J. Chem. Eng. Jpn., 2002, 35, 640–648 CrossRef CAS.
- T. Miyata, Brownian dynamics simulation of self-diffusion of ionic large solute molecule in modeled polyelectrolyte gel, J. Phys. Soc. Jpn., 2012, 81, 1–7 CrossRef.
- X. Zhang, J. Hansing, R. R. Netz and J. E. Derouchey, Particle transport through hydrogels is charge asymmetric, Biophys. J., 2015, 108, 530–539 CrossRef CAS PubMed.
- J. Hansing, C. Ciemer, W. K. Kim, X. Zhang, J. E. DeRouchey and R. R. Netz, Nanoparticle filtering in charged hydrogels: effects of particle size, charge asymmetry and salt concentration, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 53 CrossRef PubMed.
- J. Hansing, J. R. Duke, E. B. Fryman, J. E. DeRouchey and R. R. Netz, Particle Diffusion in Polymeric Hydrogels with Mixed Attractive and Repulsive Interactions, Nano Lett., 2018, 18, 5248–5256 CrossRef CAS PubMed.
- J. Hansing and R. R. Netz, Hydrodynamic Effects on Particle Diffusion in Polymeric Hydrogels with Steric and Electrostatic Particle-Gel Interactions, Macromolecules, 2018, 51, 7608–7620 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02113c |
| This journal is © the Owner Societies 2021 |
