Determining chemical exchange rate constants in nanoemulsions using nuclear magnetic resonance†
Received
11th May 2021
, Accepted 16th August 2021
First published on 26th August 2021
Abstract
In this work, the second-order kinetics of molecules exchanging between chemically distinct microenvironments, such as those found in nanoemulsions, is studied using nuclear magnetic resonance (NMR). A unique aspect of NMR exchange studies in nanoemulsions is that the difference in molecular resonance frequencies between the two phases, which determines whether the exchange is fast, intermediate, or slow on the NMR timescale, can depend upon the emulsion droplet composition, which is also determined by the kinetic exchange constants themselves. Within the fast-exchange regime, changes in resonance frequencies and line widths with dilution were used to extract the exchange rate constants from the NMR spectra in a manner analogous to determining the kinetic parameters in NMR ligand binding experiments. As a demonstration, the kinetic exchange parameters of isoflurane release from an emulsification of isoflurane and perflurotributylamine (FC43) were determined using NMR dilution and diffusion studies.
I Introduction
Emulsions are an important class of soft materials1 that are often found in foods, such as butter, milk, and salad dressings, and in industrial processes, such as in the extraction, transport, and refinement of petroleum and associated products. Emulsions typically consist of two immiscible phases where one phase is broken up into droplets that are homogeneously dispersed throughout the other phase. Characterization of an emulsion's size distribution, composition, and rheological properties are carried out using a variety of techniques, such as optical2–4 and electron microscopies,5,6 and nuclear magnetic resonance (NMR)7–9 to name just a few.
One important application of emulsions is their use as nanocarriers of pharmaceuticals.10,11 In this case, a drug, which typically comprises a sizable composition fraction of an emulsion droplet, can exchange between hydrophobic emulsion droplets and an aqueous phase. This is depicted in Fig. 1 and by the following kinetic processes:
| |  | (1) |
In
eqn (1),
A denotes a molecule, such as a drug, in the aqueous phase while
AEmul denotes an
A molecule in an emulsion droplet, which is denoted by Emul. The forward process of an
A molecule entering an emulsion droplet is modeled by second-order kinetics with a rate constant
kF, while the reverse process of an
A molecule leaving an emulsion droplet is modeled by first-order kinetics with a rate constant
kB. The total exchange rate constant,
kexch =
kF[Emul] +
kB, defines a timescale of drug exchange between aqueous and organic phases given by

, where [Emul] denotes the sample molar concentration of emulsion droplets.
 |
| | Fig. 1 An illustration of the equilibrium in eqn (1) depicting A molecules in an aqueous phase exchanging with AEmul molecules in a spherical emulsion droplet. | |
A variety of techniques have been used to study the exchange dynamics in eqn (1), such as dialysis and related methods,12 electrochemical techniques,13 and flow cytometry.14 NMR has also been used15 to study the kinetics in eqn (1). Since most NMR studies are performed under equilibrium conditions, differences between an A and AEmul molecule's physical properties, such as self-diffusion coefficients,16,17 and/or NMR spectral parameters, such as chemical shifts, spin–spin couplings, and transverse (T2) and longitudinal (T1) spin relaxation times,18,19 are required in order to determine kF and kB in eqn (1).
The Bloch–McConnell equations20 are typically used to model the effects of chemical exchange on an NMR spectrum. In general, the solutions to the Bloch–McConnell equations can be understood by simply comparing kexch to the effective difference in physical and/or NMR parameters between A molecules in the aqueous and organic phases. Consider the situation when there is a difference in the A and AEmul NMR resonance frequency, Δω = ωA − ωAEmul ≠ 0. In this case, |Δω|−1 determines an effective NMR timescale in which the dynamics can be classified as being in either the (τexch ≫ |Δω|−1) slow-, (τexch ∼ |Δω|−1) intermediate-, or (τexch ≪ |Δω|−1) fast-exchange regimes.21–23 In all of the above exchange regimes, |Δω| is usually taken to be constant. However, a small amount of A molecules entering or leaving an emulsion droplet can dramatically alter the composition and chemical environment within a droplet. Since kF and kB in eqn (1) determine the partitioning of A molecules between the emulsion droplets and the aqueous phase, both ωAEmul and hence Δω will also depend upon kF and kB. While traditional EXSY experiments24 could still be used to obtain the kinetic parameters in eqn (1) if the dynamics were in the slow-exchange regime, determination of kF and kB in the fast-exchange when Δω depends upon those very rate constants would be much more challenging and has not been previously addressed.
In this work, the theory for determining the kinetic parameters of a molecule exchanging between emulsion droplets and an aqueous phase within the fast-exchange regime when |Δω| depends explicitly on kF and kB in eqn (1) is presented. This is accomplished by first (I) calibrating the composition-dependence of an A molecule's chemical shift within the emulsion droplet using a local composition model,25 and then (II) using dilution experiments to modify the forward rate of A molecules entering an emulsion droplet in eqn (1). From (I) and (II), the kinetic rate constants within the fast-exchange regime can be determined from the observed chemical shifts and line widths using simple algebraic expressions that are presented in this work. As a demonstration, the theory and methodology developed in this work are applied to the problem of determining the kinetic exchange parameters of the anesthetic isoflurane in an emulsification of isoflurane in perflurotributylamine (FC43).
II Theory
If the system in eqn (1) is at equilibrium, the forward and reverse rates are equal, which gives:| | 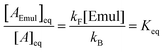 | (2) |
where [A]eq and [AEmul]eq denote the equilibrium sample molar concentrations of A in the aqueous and organic phases, respectively. For a solution with a total A concentration of [A]tot = [A]eq+ [AEmul]eq:| |  | (3) |
where ProbAaq,eq([Emul]) and 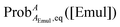 are the equilibrium probabilities that an A molecule is in either the aqueous or organic phases, respectively.
are the equilibrium probabilities that an A molecule is in either the aqueous or organic phases, respectively.
Consider a simple  –acquire NMR experiment applied to a system at equilibrium and described by eqn (1). The NMR signal or free induction decay, FID(t), is proportional to the total transverse magnetization as a function of time after the initial
–acquire NMR experiment applied to a system at equilibrium and described by eqn (1). The NMR signal or free induction decay, FID(t), is proportional to the total transverse magnetization as a function of time after the initial  –pulse, FID(t) ∝ Mtot,+(t) = MA,+(t) + MAEmul,+(t) where MA,+(t) = MA,X(t) + iMA,Y(t) and MAEmul,+(t) = MAEmul,X(t) + iMAEmul,Y(t) represent the total transverse A magnetization in the aqueous and organic phases, respectively. The dynamics of both MA,+(t) and MAEmul,+(t) can be calculated using the Bloch–McConnell equations:20
–pulse, FID(t) ∝ Mtot,+(t) = MA,+(t) + MAEmul,+(t) where MA,+(t) = MA,X(t) + iMA,Y(t) and MAEmul,+(t) = MAEmul,X(t) + iMAEmul,Y(t) represent the total transverse A magnetization in the aqueous and organic phases, respectively. The dynamics of both MA,+(t) and MAEmul,+(t) can be calculated using the Bloch–McConnell equations:20
| | 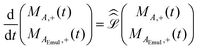 | (4) |
where
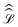
is the evolution superoperator given by:
| |  | (5) |
where
ωA and
ωAEmul are the
A resonance frequencies (in radians per second) in the aqueous and organic phases, respectively, while

and
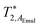
are the effective
A transverse spin relaxation times in the aqueous and organic phases, respectively.
The formal solution to eqn (4) with initial conditions MA,+(0) = ProbAaq,eq([Emul]) and  can be written as:
can be written as:
| |  | (6) |
The eigenvalues of  , which are denoted by λ+ and λ−, determine both the observed resonance frequencies
, which are denoted by λ+ and λ−, determine both the observed resonance frequencies  and line widths
and line widths  after Fourier transformation of the FID(t) and are given by:
after Fourier transformation of the FID(t) and are given by:
| |  | (7) |
where
ωΣ =
ωA +
ωAEmul,

,

, and Δ
k =
kF[Emul] −
kB.
II.A Fast-exchange regime
In the fast-exchange regime, the resonance at ν−obs would have a line width of  that is often broadened beyond the point of practical detection. Thus only the resonance at ωobs ≡ ω+obs = Real[λ+] is typically observed in the spectrum, which is given up to order k−1exch by:
that is often broadened beyond the point of practical detection. Thus only the resonance at ωobs ≡ ω+obs = Real[λ+] is typically observed in the spectrum, which is given up to order k−1exch by:| |  | (8) |
In eqn (8), ωobs is simply the weighted average of the A resonance frequencies in the aqueous and organic phases, which is the expected result in the fast-exchange regime.21 Similarly, the observed line width,  , is given up to order k−1exch by:
, is given up to order k−1exch by:
| |  | (9) |
where

represents the weighted average of the effective transverse relaxation rates in the aqueous and organic phases in the absence of exchange, and
| |  | (10) |
is the effective transverse relaxation rate due solely to chemical exchange within the fast-exchange limit.
21
In principle, both  and kexch can be determined from
and kexch can be determined from  and ωobs. If ωAEmul is known, then from eqn (8):
and ωobs. If ωAEmul is known, then from eqn (8):
| |  | (11) |
However, if
ωAEmul depends upon the composition of the emulsion droplets and hence

,
e.g.,
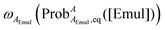
, then

at a given [Emul] could still be determined from
eqn (8) by minimizing:
| |  | (12) |
If an
A molecule contains
Nnuclei > 1 chemically distinct NMR-active nuclei, then

can be found by minimizing
eqn (12) over all such nuclei that are observed in the NMR spectrum:
| |  | (13) |
Once  is known, kexch can be determined from
is known, kexch can be determined from  in eqn (9) for each observed nuclei:
in eqn (9) for each observed nuclei:
| | 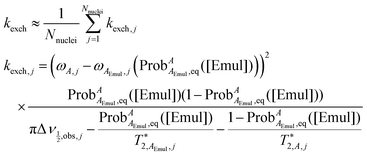 | (14) |
Using 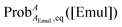 determined from eqn (13) and kexch determined from eqn (14), kF and kB at a given [Emul] are given by:
determined from eqn (13) and kexch determined from eqn (14), kF and kB at a given [Emul] are given by:
| | 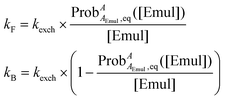 | (15) |
III Experimental
III.A Emulsion preparation and characterization
Isoflurane in a perfluorotributylamine solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was emulsified in saline (20% v/v hydrophobic phase) by temperature controlled high pressure (15
1 v/v) was emulsified in saline (20% v/v hydrophobic phase) by temperature controlled high pressure (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi) homogenization using the ShearJet™ HL60 from Dyhydromatics (Maynard, MA, USA) as was previously reported.26 The surfactants, pluronic F68 and F127, were used in a 1
000 psi) homogenization using the ShearJet™ HL60 from Dyhydromatics (Maynard, MA, USA) as was previously reported.26 The surfactants, pluronic F68 and F127, were used in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to stabilize the emulsion droplets. The particle size of the emulsion droplets was characterized using dynamic light scattering (DLS). From prior studies of similar emulsions,27 dilutions greater than 40× were needed to remove particle–particle interactions and multiple scattering in order to accurately measure the hydrodynamic radius of the emulsion droplets, rEmul. From DLS measurements at 100× dilution, rEmul = (74.7 ± 0.7) nm. The undiluted emulsion had an initial concentration of emulsion droplets of [Emul] ≈ 172.8 nM and an initial isoflurane concentration of [Iso]tot = (660 ± 15) mM that was determined from high performance liquid chromatography.
1 ratio to stabilize the emulsion droplets. The particle size of the emulsion droplets was characterized using dynamic light scattering (DLS). From prior studies of similar emulsions,27 dilutions greater than 40× were needed to remove particle–particle interactions and multiple scattering in order to accurately measure the hydrodynamic radius of the emulsion droplets, rEmul. From DLS measurements at 100× dilution, rEmul = (74.7 ± 0.7) nm. The undiluted emulsion had an initial concentration of emulsion droplets of [Emul] ≈ 172.8 nM and an initial isoflurane concentration of [Iso]tot = (660 ± 15) mM that was determined from high performance liquid chromatography.
III.B NMR dilution studies
VWR Signature™ Ergonomic High-Performance Pipettors were used to transfer a calculated amount of a stock solution of undiluted emulsion and an isoflurane saturated saline D2O solution into an NMR tube. Three replicates of each solution were prepared and measured by NMR within 12 hours of sample preparation. Experiments on a series of diluted emulsion samples were performed on a 300 MHz Bruker AVANCE NEO spectrometer with an automatic sample changer. All proton spectra were acquired with the pulse sequence “zgcpgppr” available in the Bruker library using a 50 Hz presaturation pulse applied to suppress the residual water signal. The following acquisition parameters were used in the dilution experiments: a repetition time of 30 s, a dwell time of 333 μs (corresponding to a spectral width of 10 ppm), and an acquisition time of 3 s. In all experiments, the transmitter frequency was set to the water resonance, and the number of scans (NS) was varied for different dilutions to achieve a desired signal-to-noise ratio with NS ≤ 512.
To obtain the isoflurane chemical shift calibration curves in an isoflurane/FC43 mixture as a function of isoflurane volume fraction, isoflurane/FC43 mixtures with an isoflurane volume fraction ranging from 10% to 100% were prepared and measured immediately in a coaxial NMR tube with the inner tube containing D2O for locking. All proton spectra for the calibration curves were acquired with the pulse sequence “zg” using a 322 μs dwell time, a 3 s acquisition, a 50 s relaxation delay, and NS = 1.
Finally, both δα/βobs and  were determined as follows: the Bloch equations were used to simulate the spectrum at each dilution by treating signals from the Hα and Hβ resonances (Fig. 2a) as a quartet and a doublet of doublets, respectively. In the simulations, the chemical shifts (δα/β), spin–spin couplings constants (JαHF and JβHF,1 and JβHF,2), and the effective transverse relaxation times
were determined as follows: the Bloch equations were used to simulate the spectrum at each dilution by treating signals from the Hα and Hβ resonances (Fig. 2a) as a quartet and a doublet of doublets, respectively. In the simulations, the chemical shifts (δα/β), spin–spin couplings constants (JαHF and JβHF,1 and JβHF,2), and the effective transverse relaxation times  were varied in order to minimize the absolute difference between the simulated and experimental spectra. From these simulations, both δα/βobs ≈ δα/βoptimal and
were varied in order to minimize the absolute difference between the simulated and experimental spectra. From these simulations, both δα/βobs ≈ δα/βoptimal and  were determined, which were then used to determine kF and kB using eqn (15). It should be noted that differences in line widths for the individual peaks within a multiplet were not captured by this procedure (an example of this procedure for a single trial is given in ESI†).
were determined, which were then used to determine kF and kB using eqn (15). It should be noted that differences in line widths for the individual peaks within a multiplet were not captured by this procedure (an example of this procedure for a single trial is given in ESI†).
 |
| | Fig. 2 (a) Chemical shifts of the (blue) Hβ and (red) Hα spins of isoflurane in a bulk mixture of isoflurane and FC43 as a function of isoflurane volume fraction, ϕFC43/IsoIso. Experimental observations are denoted by asterisks while the solid curves represent the best fits to eqn (16) and (17) at T = 298 K with λFC43,Iso − λIso,Iso = 1220 J mol−1, δβ,∞FC43/Iso = 6.02 ppm, and δα,∞FC43/Iso = 5.69 ppm. (b) In an emulsion, the observed chemical shifts (δα/βobs, solid lines) as a function of [Emul] are shown in addition to δα/βEmul calculated using the calibration curves in Fig. 2a and the NMR-derived kF and kB given in Fig. 4. The error bars represent ± a standard deviation after averaging over three replicates. | |
III.C NMR diffusion studies
All diffusion measurements were acquired on a 400 MHz Bruker spectrometer using a stimulated echo with bipolar gradient and longitudinal eddy current delay sequence,28 which is given in Fig. 5a and was implemented using the “ledbpgp2s” pulse program in the Bruker library. Experiments were performed using 16 constant time gradients with varying amplitude (g) in order to map the diffusion decay curves of the FC43 and isoflurane resonances. Different NS, gradient pulse lengths (δ), and diffusion times (Δ) were used to measure the self-diffusion coefficients of isoflurane (using 1H NMR) and FC43 in emulsion droplets (using 19F NMR) in order to achieve a desired signal to noise ratio. A 322 μs dwell time, a total acquisition time of 1.5 s, a gradient stabilization delay of τ = 200 μs, an LED time of ΔLED = 5 ms, and smoothed square shaped pulsed field gradients were used in the diffusion studies. From prior studies,27 the self-diffusion coefficient of isoflurane in pure saline solution was DIso,aq = (9.7 ± 0.5) × 10−6 cm2 s−1 while in a (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) isoflurane/FC43 solution, isoflurane and FC43 had self-diffusion coefficients of DIso,Iso/FC43 = (20.34 ± 0.06) × 10−6 cm2 s−1 and DFC43,Iso/FC43 = (8.86 ± 0.03) × 10−6 cm2 s−1, respectively.
1 v/v) isoflurane/FC43 solution, isoflurane and FC43 had self-diffusion coefficients of DIso,Iso/FC43 = (20.34 ± 0.06) × 10−6 cm2 s−1 and DFC43,Iso/FC43 = (8.86 ± 0.03) × 10−6 cm2 s−1, respectively.
IV Results and discussion
In this section, the theory and methodology developed in Section II is applied to the problem of characterizing isoflurane exchange in an emulsification of isoflurane and FC43. The results are organized as follows: in Section IV.A, the composition dependence of the isoflurane chemical shifts in an isoflurane/FC43 mixture is presented, which is then used in Section IV.B to determine the isoflurane exchange parameters in an emulsion using NMR dilution experiments. In Section IV.C, NMR diffusion studies of both isoflurane and FC43 are provided, which is followed by Section IV.D with a comparison between two different models used in the Bloch–McConnell simulations in which the isoflurane chemical shifts in an emulsion droplet were either fixed or changed with the droplet composition. Finally in Section IV.E, a discussion of the apparent crossover between “crowded” and “lifetime-limited” regimes in NMR dilution experiments and the effects of this crossover on the NMR-determined values of kB are discussed.
IV.A Calibration of isoflurane chemical shifts in an isoflurane/FC43 solution
As shown in Fig. 2, isoflurane consists of two 1H spins, Hα and Hβ, that are only coupled via scalar spin–spin interactions to neighboring 19F nuclei in the CF3 and CF2 group, respectively (the experimentally determined J-couplings and chemical shifts in saline and in FC43 are given in Table 1). As shown in Fig. 2a, the Hα and Hβ chemical shifts in a solution of FC43 and isoflurane, δαFC43/Iso and δβFC43/Iso, respectively, were found to depend upon the volume fraction of isoflurane in the mixture,  . In this case, the ϕFC43/IsoIso-dependence of δα/βFC43/Iso could be fit to a local composition model25 (solid curves in Fig. 2a) given by:
. In this case, the ϕFC43/IsoIso-dependence of δα/βFC43/Iso could be fit to a local composition model25 (solid curves in Fig. 2a) given by:| |  | (16) |
| |  | (17) |
where  ,
,  is proportional to ratio of the difference between the FC43–isoflurane and isoflurane–isoflurane intermolecular interaction energies to thermal energy at a temperature T, δαIso = 6.146 ppm and δβIso = 6.494 ppm are the chemical shifts in pure isoflurane, and δα/β,∞FC43/Iso are the isoflurane chemical shifts at infinite dilution in FC43.
is proportional to ratio of the difference between the FC43–isoflurane and isoflurane–isoflurane intermolecular interaction energies to thermal energy at a temperature T, δαIso = 6.146 ppm and δβIso = 6.494 ppm are the chemical shifts in pure isoflurane, and δα/β,∞FC43/Iso are the isoflurane chemical shifts at infinite dilution in FC43.
Table 1 Experimentally determined spectral parameters for isoflurane in saline and in an emulsion droplet
| Parameter |
Hαaq |
Hβaq |
HαEmul |
HβEmul |
|
Determined from the isoflurane in saline spectrum [spectrum (12) in Fig. 3].
Determined from the first emulsion dilution spectrum [spectrum (1) in Fig. 3].
Determined from the undiluted emulsion.
|
|
δ (ppm) |
6.80a |
6.701a |
Eqn (20)
|
Eqn (21)
|
|
J
HF (Hz) |
4.3a |
71.1a |
4.0b |
(70.3, 72.2)b |
 (ms) (ms) |
373.1a |
385.9a |
144.4b |
169.9b |
|
T
1 (s) |
11.20a |
8.76a |
2.37c |
2.18b |
In Fig. 2a, δα/β,∞FC43/Iso and λFC43,Iso − λIso,Iso were determined by minimizing the least square error between the observed chemical shifts in an FC43/isoflurane solution and those predicted by eqn (16) and (17), where the best-fit parameters at T = 298 K were found to be λFC43,Iso − λIso,Iso = 1.220 kJ mol−1, δα,∞FC43/Iso = 6.02 ppm and δβ,∞FC43/Iso = 5.69 ppm. The positive value for λFC43,Iso − λIso,Iso indicated that the FC43–isoflurane intermolecular interaction energies were slightly less favorable than the isoflurane–isoflurane intermolecular interaction energies.
IV.B NMR measurements and determination of kF and kB in an isoflurane/FC43 emulsion
The exchange of isoflurane from an emulsification of isoflurane in FC43 was modeled analogously to the equilibrium in eqn (1):| |  | (18) |
where “Iso” and “IsoEmul” denote isoflurane molecules in the aqueous phase and in an emulsion droplet, respectively. As noted in the previous section, a solution of isoflurane and FC43 behaves non-ideally due to differences in isoflurane–isoflurane and isoflurane–FC43 intermolecular interaction energies. The volume fraction of isoflurane in an emulsion droplet, ϕOrgIso, can be calculated from the probability of isoflurane to be in an emulsion droplet,  :
:| |  | (19) |
where [Iso]tot is the total isoflurane concentration in a volume Vtot, VFC43 is the total FC43 volume, and VIsom = 0.123329 L mol−1 is the molar volume of isoflurane at T = 298 K.
The chemical shifts of the isoflurane resonances in an emulsion droplet were modeled by:
| | | δαEmul(ϕOrgIso) = δαFC43/Iso(ϕOrgIso) + δEmuloffset | (20) |
| | | δβEmul(ϕOrgIso) = δβFC43/Iso(ϕOrgIso) + δEmuloffset | (21) |
where
δα/βFC43/Iso(
ϕOrgIso) are the isoflurane chemical shifts in an FC43/isoflurane mixture given in
eqn (16) and (17) and evaluated at
ϕOrgIso given in
eqn (18). A small offset,
δEmuloffset, which was taken to be the same at all dilutions, was included in
eqn (20) and (21) to account for the change in magnetic susceptibility going from a bulk isoflurane/FC43 mixture to an isoflurane/FC43 mixture confined to small, spherical droplets stabilized by surfactants. From the dilution experiments, it was found that
δEmuloffset = −(0.0920 ± 0.0002) ppm.
The chemical shifts and transverse relaxation times for isoflurane in the aqueous phase, δαaq and δβaq and  and
and  , respectively, were determined from an isoflurane saturated saline solution while
, respectively, were determined from an isoflurane saturated saline solution while  and
and  were determined from the first emulsion dilution. These parameters are given in Table 1. As discussed earlier, the effect of exchange on an NMR spectrum depends upon the relative magnitude of kexch compared to the absolute frequency differences between the two phases, |Δωα/β(ϕOrgIso)| = γB0|δα/βaq − δα/βEmul(ϕOrgIso)|, where γ is the gyromagnetic ratio, and B0 is the magnitude of the large, static magnetic field. It is important to emphasize that a unique aspect of modeling chemical exchange for the equilibrium in eqn (18) is that |Δωα/β| depends upon ϕOrgIso and hence kexch [eqn (19)].
were determined from the first emulsion dilution. These parameters are given in Table 1. As discussed earlier, the effect of exchange on an NMR spectrum depends upon the relative magnitude of kexch compared to the absolute frequency differences between the two phases, |Δωα/β(ϕOrgIso)| = γB0|δα/βaq − δα/βEmul(ϕOrgIso)|, where γ is the gyromagnetic ratio, and B0 is the magnitude of the large, static magnetic field. It is important to emphasize that a unique aspect of modeling chemical exchange for the equilibrium in eqn (18) is that |Δωα/β| depends upon ϕOrgIso and hence kexch [eqn (19)].
To extract kF and kB, a series of dilution experiments of the emulsion were performed. The dilution spectra for one replicate are shown in Fig. 3, where both  and να/βobs changed with dilution. Both να/βobs, which is given by the solid curves in Fig. 2b, and
and να/βobs changed with dilution. Both να/βobs, which is given by the solid curves in Fig. 2b, and 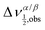 , which is given in ESI,† were used along with δα/βEmul(ϕOrgIso) in eqn (20) and (21) to determine ProbIsoEmul,eq([Emul]) from eqn (13). Both ProbIsoEmul,eq([Emul]) and
, which is given in ESI,† were used along with δα/βEmul(ϕOrgIso) in eqn (20) and (21) to determine ProbIsoEmul,eq([Emul]) from eqn (13). Both ProbIsoEmul,eq([Emul]) and  were then used to calculate kexch in eqn (14). From kexch, both kF and kB at each [Emul] were determined using eqn (15) and are given in Fig. 4. The uncertainties in kF and kB in Fig. 4 mainly reflect variations between replicates since kexch,α and kexch,β were generally within 2–13% of each other after the second dilution. While |Δωα/β| increased with increasing dilution as shown in Fig. 2b, the exchange of isoflurane in the emulsion was always within the fast-exchange regime21–23 since kexch ≫ |Δωα/β| over the entire dilution range. As a result, the isoflurane spectra in Fig. 3 contained only one set of isoflurane resonances.
were then used to calculate kexch in eqn (14). From kexch, both kF and kB at each [Emul] were determined using eqn (15) and are given in Fig. 4. The uncertainties in kF and kB in Fig. 4 mainly reflect variations between replicates since kexch,α and kexch,β were generally within 2–13% of each other after the second dilution. While |Δωα/β| increased with increasing dilution as shown in Fig. 2b, the exchange of isoflurane in the emulsion was always within the fast-exchange regime21–23 since kexch ≫ |Δωα/β| over the entire dilution range. As a result, the isoflurane spectra in Fig. 3 contained only one set of isoflurane resonances.
 |
| | Fig. 3 (blue) Experimental 1H NMR dilution spectra of isoflurane in an emulsion along with the (red) theoretical spectra calculated using the Bloch–McConnell equations20 (the green spectra represent the difference between experimental and simulated spectra). The spectra are labeled from (1) to (12) in order of increasing dilution of an initial emulsion with [Emul]0 = 172.8 nM. For dilutions (1) to (12), [Emul] was given by 148 nM, 86.4 nM, 27.6 nM, 17.3 nM, 10.4 nM, 6.9 nM, 3.5 nM, 2.7 nM, 1.7 nM, 1.0 nM, 0.7 nM, and 0 nM (corresponding to isoflurane in saline), and with corresponding scaling factors applied to the spectra given by ×1.0, ×2.5, ×30, ×121, ×277, ×461, ×583, ×597, ×469, ×365, ×355, and ×220, respectively. By modeling δα/βobs and  as a function of [Emul], both kF and kB in eqn (15) were determined and used as input in the Bloch–McConnell simulations (red spectra). as a function of [Emul], both kF and kB in eqn (15) were determined and used as input in the Bloch–McConnell simulations (red spectra). | |
 |
| | Fig. 4 The NMR determined kF and kB in eqn (18) as a function of [Emul] determined using δα/βobs,  , and eqn (15). The error bars represent ± a standard deviation after averaging the rate constants determined from both the Hα and Hβ resonances of isoflurane over three emulsion replicates. (a) As [Emul] decreased, kB increased by about a factor of 3 while (b) kF was on the same order of magnitude as the corresponding Smoluchowski diffusion-limited bimolecular rate constant,29kdiff = 5.47 × 1011 M−1 s−1, which is represented by a dashed line. , and eqn (15). The error bars represent ± a standard deviation after averaging the rate constants determined from both the Hα and Hβ resonances of isoflurane over three emulsion replicates. (a) As [Emul] decreased, kB increased by about a factor of 3 while (b) kF was on the same order of magnitude as the corresponding Smoluchowski diffusion-limited bimolecular rate constant,29kdiff = 5.47 × 1011 M−1 s−1, which is represented by a dashed line. | |
Using the values of kF and kB in Fig. 4, the theoretical spectra for the dilution experiments were also calculated from the Bloch–McConnell equations (red spectra in Fig. 3) (see ESI† for more details on the Bloch–McConnell simulations). The absolute differences between the simulated and observed δα/βobs and  in Fig. 3 were (0.0026 ± 0.0020) ppm and (0.29 ± 0.24) Hz, respectively, with the largest differences between the calculated and experimental spectra (the green spectra in Fig. 3) occurring at both the lowest and highest dilutions. The application of the Bloch–McConnell equations was well justified since for timescales on the order of the inverse of the frequency difference,
in Fig. 3 were (0.0026 ± 0.0020) ppm and (0.29 ± 0.24) Hz, respectively, with the largest differences between the calculated and experimental spectra (the green spectra in Fig. 3) occurring at both the lowest and highest dilutions. The application of the Bloch–McConnell equations was well justified since for timescales on the order of the inverse of the frequency difference,  , the root mean square displacement of isoflurane due to diffusion in the aqueous phase was
, the root mean square displacement of isoflurane due to diffusion in the aqueous phase was  , which was larger than the average separation between emulsion droplets, which ranged from 0.1–1.2 μm over the range of [Emul] studied in this work. The behavior of the isoflurane spectra with increasing dilution in Fig. 3 was similar to prior observations in ligand binding NMR titration experiments30 where a maximum in
, which was larger than the average separation between emulsion droplets, which ranged from 0.1–1.2 μm over the range of [Emul] studied in this work. The behavior of the isoflurane spectra with increasing dilution in Fig. 3 was similar to prior observations in ligand binding NMR titration experiments30 where a maximum in  occurs at a ligand concentration such that the forward binding rate is half the ligand release rate, i.e.,
occurs at a ligand concentration such that the forward binding rate is half the ligand release rate, i.e.,  . Due to the ϕOrgIso-dependence of δα/βEmul(ϕOrgIso), the maximal
. Due to the ϕOrgIso-dependence of δα/βEmul(ϕOrgIso), the maximal  in Fig. 3 occurred at a slightly larger emulsion concentration,
in Fig. 3 occurred at a slightly larger emulsion concentration,  .
.
IV.C Self-diffusion measurements
The self-diffusion coefficients for both isoflurane and FC43 were found by fitting the experimental diffusion data (Fig. 5b, blue dots) acquired using the pulse sequence in Fig. 5a to the standard diffusion decay curve:31| | 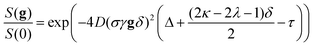 | (22) |
where γ is the gyromagnetic ratio for a given nucleus (1H or 19F), D is the self-diffusion coefficient, δ is the gradient pulse length, τ is the gradient stabilization delay, Δ is the diffusion time, and σ, κ, and λ are numerical factors that are determined by the pulsed gradient pulse shape31 [for the smoothed rectangular gradient pulses used in this work31,  ,
,  , and
, and  ]. The self-diffusion coefficients of isoflurane were always over an order of magnitude larger than those of FC43 as shown in Fig. 5b. Furthermore, both isoflurane's and FC43's self-diffusion coefficients increased with increasing dilution as shown in Fig. 5c.
]. The self-diffusion coefficients of isoflurane were always over an order of magnitude larger than those of FC43 as shown in Fig. 5b. Furthermore, both isoflurane's and FC43's self-diffusion coefficients increased with increasing dilution as shown in Fig. 5c.
 |
| | Fig. 5 Diffusion studies for a series of emulsion dilutions. (a) Stimulated echo with bipolar gradient sequence28 using smoothed rectangular gradient pulses of length δ, where τ = 200 μs is the gradient stabilization delay, Δ is the diffusion time, and ΔLED = 5 ms is the LED time (values of Δ and δ are given in (b)). (b) Experimental (blue asterisks) decay curves as a function of gradient strength, g, along with the (red curves) best fits to eqn (22) for (left) isoflurane and (right) FC43. (c) Plots of the observed self-diffusion coefficients for isoflurane and FC43 vs. [Emul], where the error bars represent ± a standard deviation. | |
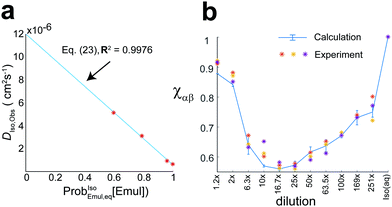
The isoflurane decay curves could always be fit to eqn (22) using a single self-diffusion coefficient, supporting the observation that isoflurane exchange was in the fast-exchange regime. As such, the observed isoflurane self-diffusion coefficient over the dilution range shown in Fig. 6a, DIso,obs, was found to be given by the average diffusion coefficient for a molecule exchanging between an aqueous phase and emulsion droplets in the fast-exchange regime:
| |  | (23) |
where Prob
IsoEmul,eq([Emul]) was calculated using the NMR-determined
kB and
kF given in
Fig. 4,
DIso,Emul is the self-diffusion coefficient of isoflurane within an emulsion droplet, and
D∞Iso,saline is the predicted self-diffusion coefficient of isoflurane in saline at infinite emulsion dilution,
i.e., [Emul] → 0. Note that from the fit to
eqn (23) in
Fig. 6a,
D∞Iso,saline = 1.20 × 10
−5 cm
2 s
−1, which was about 24% larger than the self-diffusion coefficient of isoflurane measured in pure saline,
DIso,aq = 9.7 × 10
−6 cm
2 s
−1.
 |
| | Fig. 6 (a) The observed isoflurane diffusion coefficient, DIso,obs as a function of ProbIsoEmul,eq([Emul]) for data taken from Fig. 5c. A fit to eqn (23) (blue line) gave D∞Iso,saline = 1.20 × 10−5 cm2 s−1 and DIso,Emul = 5.88 × 10−7 cm2 s−1. (b) Change in the ratio of Hα and Hβ NMR signal intensity, χαβ, for different dilutions and averaged over three replicates. Asterisks represent experiment data, while the solid-blue curve represents the predicted χαβ from the Bloch–McConnell equations using kF and kB given in Fig. 4, with error bars representing ±standard deviation. The observation that χαβ < 1 was due to both the water presaturation pulse and changing δα/βobs with dilution. In pure saline [Iso(aq), rightmost], χαβ = 1. | |
Additionally, the ratio of NMR signal intensities for the Hα and Hβ resonances,  , was also found to change with dilution as shown in Fig. 6b. The differential attenuation of the Hα and Hβ signals, which led to χαβ < 1, was the result of both the presaturation pulse used to suppress the water signal and changing δα/βobs with dilution. The behavior of χαβ for different dilutions could also be calculated (solid blue curve in Fig. 6b) using the Bloch–McConnell equations with the NMR-determined kB and kF given in Fig. 4.
, was also found to change with dilution as shown in Fig. 6b. The differential attenuation of the Hα and Hβ signals, which led to χαβ < 1, was the result of both the presaturation pulse used to suppress the water signal and changing δα/βobs with dilution. The behavior of χαβ for different dilutions could also be calculated (solid blue curve in Fig. 6b) using the Bloch–McConnell equations with the NMR-determined kB and kF given in Fig. 4.
IV.D Comparing exchange models with either changing or fixed δα/βEmul
While the model with δα/βEmul changing with ϕOrgIso [eqn (20) and (21)] was shown to be consistent with the experimental results in Fig. 3 and 6, an alternative model where δα/βEmul did not change with ϕOrgIso was also found to be consistent with these experimental results too (see ESI† for more details). However, the NMR-determined kB and kF from both models were still within an order of magnitude from each other, kF ≈ 1011 M−1 s−1 and kB ≈ 104 s−1, while exhibiting a similar [Emul]-dependence. This naturally leads to the question as to whether these two models can be experimentally distinguished from one another?
One way to distinguish between the two models was to utilize the [Iso]tot-dependence of ϕOrgIso in eqn (19). For the model used in Fig. 3 and 6, both δαEmul(ϕOrgIso) [eqn (20)] and δβEmul(ϕOrgIso) [eqn (21)] explicitly depended upon ϕOrgIso and hence on [Iso]tot. If [Iso]tot increased, both δαEmul and δβEmul in this model would experience a downfield shift due to increasing ϕOrgIso (Fig. 2a). However, for the model in which δα/βEmul was fixed, no spectral shifts with changing [Iso]tot would be observed. In Fig. 7a, the experimental spectrum (blue) of the inner resonances of the Hβ multiplet in an initial sample containing 500 μL of a 10× emulsion dilution is shown (solid) in addition to the spectra in which nominally (dotted) 1 μL and (dashed) 2 μL of pure isoflurane was added directly to the NMR tube, resulting in a slight increase in [Iso]tot from 0.0967 M up to 0.1289 M. As a result of increasing [Iso]tot, the experimental spectra exhibited a slight downfield shift. In Fig. 7 (middle inset), the water resonance frequency did not change with changing [Iso]tot, indicating that the observed isoflurane shifts were not global in nature. The results from numerical simulations of the (Fig. 7a, red spectra) using the Bloch–McConnell equations with δα/βEmul(ϕOrgIso) in eqn (20) and (21) showed a similar downfield shift, whereas the spectra from simulations with fixed δα/βEmul remained roughly the same as shown in Fig. 7b. In the simulations, kF and kB were determined from να/βobs and  for an initial 10× dilution (solid), which gave either [Fig. 7a] kF = 5.12 × 1011 M−1 s−1 and kB = 5.96 × 103 s−1 or [Fig. 7b] kF = 4.31 × 1011 M−1 s−1 and kB = 3.80 × 103 s−1 for fixed δαEmul = 5.83 ppm and δβEmul = 6.19 ppm.
for an initial 10× dilution (solid), which gave either [Fig. 7a] kF = 5.12 × 1011 M−1 s−1 and kB = 5.96 × 103 s−1 or [Fig. 7b] kF = 4.31 × 1011 M−1 s−1 and kB = 3.80 × 103 s−1 for fixed δαEmul = 5.83 ppm and δβEmul = 6.19 ppm.
 |
| | Fig. 7 Effects of [Iso]tot on an NMR spectrum. The (blue) experimental spectrum for the inner transitions of the Hβ multiplet are shown for different [Iso]tot caused by titrating pure isoflurane into an initial 500 μL sample of 10× a diluted emulsion. Experimentally, the isoflurane resonances shifted downfield with increasing [Iso]tot. [middle inset] The residual H2O resonance frequency was unchanged with changing [Iso]tot, indicating that the observed downfield shift was local and not global in nature. (a) Simulated spectra from the Bloch–McConnell equations using δα/βEmul(ϕOrgIso) in eqn (20) and (21) exhibited a similar downfield shift while (b) simulations with fixed δαEmul = 5.83 ppm and δβEmul = 6.19 ppm did not. (c) Better agreement between simulation and experiment was found if it was assumed that smaller volumes of isoflurane were titrated than in a [0.76 μL and 1.28 μL vs. 1 μL and 2 μL]. (d) For comparison, the corresponding simulated spectra using fixed δα/βEmul also did not exhibit a downfield shift. In the Bloch–McConnell simulations, either (a and c) kF = 5.12 × 1011 M−1 s−1 and kB = 5.96 × 103 s−1 or (b and d) kF = 4.31 × 1011 M−1 s−1 and kB = 3.80 × 103 s−1 were used. | |
The simulated spectra in Fig. 7a exhibited similar downfield shifts as the experimental spectra, albeit with larger predicted shifts than what was experimentally observed. As shown in Fig. 7c, however, better agreement between simulation and experiment could be achieved if it was assumed that the actual titrated volumes of isoflurane were slightly smaller than the nominal values of 1 μL and 2 μL assumed in Fig. 7a, in this case (dotted) 0.75 μL and (dashed) 1.28 μL. The possibility that the actual amounts of isoflurane added were less than 1 μL and 2 μL seems physically justified due to the ineffectiveness of accurately titrating such small volumes directly into an NMR tube. For comparison, the simulated spectra for fixed δα/βEmul using the same values of [Iso]tot assumed in Fig. 7c are shown in Fig. 7d, where no significant spectral changes were observed with changing [Iso]tot. Overall, the results in Fig. 7 support the use of δα/βEmul(ϕOrgIso) in eqn (20) and (21) in modeling isoflurane exchange in these nanoemulsions.
It should be noted that both kF and kB in Fig. 4 were calculated using eqn (15) under the assumption that the chemical shifts, δα/βaq and δα/βEmul([Emul]), and the effective transverse relaxation times,  and
and  , were always described over the entire dilution range by the expressions given in Table 1. Experimentally, small differences in magnetic field inhomogeneity between samples are expected to introduce small variations in
, were always described over the entire dilution range by the expressions given in Table 1. Experimentally, small differences in magnetic field inhomogeneity between samples are expected to introduce small variations in  . Furthermore, it is possible that the chemical shifts,
. Furthermore, it is possible that the chemical shifts,  s, and the effective 1H–19F spin–spin interactions could also be changing with dilution in a manner that is not taken into account using the model described above. For example, while the spin–spin couplings and chemical shifts (up to a global shift of δEmuloffset) derived from the isoflurane spectrum at high [Emul] (low dilutions) were similar to those of isoflurane in pure FC43 since ProbEmul,eq([Emul]) ≈ 1, the spectral parameters of isoflurane in the aqueous phase could possibly differ from their isotropic values in pure saline [Table 1] due to anisotropic interactions, such as dipolar couplings32 and chemical shift anisotropy,33 that are not fully averaged away due to the partial ordering of isoflurane in concentrated emulsion samples. With dilution, these contributions would decrease to zero as the spin–spin couplings and chemical shifts approached their isotropic values in the aqueous phase given in Table 1. Furthermore, the intrinsic transverse relaxation times in both the emulsion droplets and aqueous phase could also change with dilution (say due to changes in partial ordering and/or some, yet unidentified mechanism). Further investigations employing additional experimental methods, such as magic-angle spinning, could be used to better characterize the contributions of anisotropic interactions in emulsions. For the system studied in this work, however, both the dilution spectra in Fig. 3 and the diffusion data in Fig. 6 a provided orthogonal measurements that were consistent with the above model using the spectral parameters in Table 1, suggesting that anisotropic interactions, if present, did not significantly affect the NMR-determined kF and kB values give in Fig. 4. More details about the tolerances of the NMR-determined kF and kB rate constants to errors or changes to
s, and the effective 1H–19F spin–spin interactions could also be changing with dilution in a manner that is not taken into account using the model described above. For example, while the spin–spin couplings and chemical shifts (up to a global shift of δEmuloffset) derived from the isoflurane spectrum at high [Emul] (low dilutions) were similar to those of isoflurane in pure FC43 since ProbEmul,eq([Emul]) ≈ 1, the spectral parameters of isoflurane in the aqueous phase could possibly differ from their isotropic values in pure saline [Table 1] due to anisotropic interactions, such as dipolar couplings32 and chemical shift anisotropy,33 that are not fully averaged away due to the partial ordering of isoflurane in concentrated emulsion samples. With dilution, these contributions would decrease to zero as the spin–spin couplings and chemical shifts approached their isotropic values in the aqueous phase given in Table 1. Furthermore, the intrinsic transverse relaxation times in both the emulsion droplets and aqueous phase could also change with dilution (say due to changes in partial ordering and/or some, yet unidentified mechanism). Further investigations employing additional experimental methods, such as magic-angle spinning, could be used to better characterize the contributions of anisotropic interactions in emulsions. For the system studied in this work, however, both the dilution spectra in Fig. 3 and the diffusion data in Fig. 6 a provided orthogonal measurements that were consistent with the above model using the spectral parameters in Table 1, suggesting that anisotropic interactions, if present, did not significantly affect the NMR-determined kF and kB values give in Fig. 4. More details about the tolerances of the NMR-determined kF and kB rate constants to errors or changes to  and δα/β are provided in ESI.†
and δα/β are provided in ESI.†
IV.E “Crowded” vs. “lifetime-limited” regimes
In this section, the effects of emulsion droplet crowding on the NMR-determined kF and kB shown in Fig. 4 will be addressed. Earlier theoretical work34,35 predicted that bimolecular rate constants should increase with increasing volume fraction of spherical emulsion droplets, which can be calculated by:| | 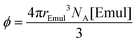 | (24) |
where NA is Avogadro's number. While kF increased slightly with increasing [Emul] in Fig. 4b, the increase was much smaller than predicted34,35 from prior theoretical work (see ESI† for more information). Furthermore, kF was on the same order of magnitude as the Smoluchowski diffusion-limited bimolecular rate constant,29kdiff = 4πrEmulDIso,aq. NA = 5.47 × 1011 M−1 s−1 (Fig. 4b, dashed line). This suggests that the rate of isoflurane entering an emulsion droplet was diffusion-limited.
As shown in Fig. 4a, on the other hand, the NMR-determined kB changed dramatically with [Emul], increasing by roughly a factor of three for dilutions up to 50×. For dilutions greater than 50×, kB appeared to be roughly constant at kB ≈ (1.05 ± 0.07) × 104 s−1. This behavior in kB could possibly be related to the observation that dilutions greater than 40× were needed to reduce particle–particle interactions in emulsions in order to accurately measure rEmul using DLS. However, the observed behavior for kB shown in Fig. 4 a could also be due to the effects of “crowding” on the NMR-determined kB. To see this, consider a thought experiment where we label isoflurane molecules within a given emulsion droplet at t = 0 and monitor their positions in time (these isofluranes are represented by red circles in Fig. 8). The average residence lifetime for an isoflurane molecule to stay within the same emulsion droplet that they were in at t = 0 is given by  . After a time τ = τEmullifetime, only e−1 ≈ 36.8% of isoflurane molecules will still reside in the same emulsion droplet they were in at t = 0. Those isoflurane molecules that left an emulsion droplet during the time τ = τEmullifetime would be expected to diffuse from the surface of the emulsion droplet by an average diffusion length, LD, given by:
. After a time τ = τEmullifetime, only e−1 ≈ 36.8% of isoflurane molecules will still reside in the same emulsion droplet they were in at t = 0. Those isoflurane molecules that left an emulsion droplet during the time τ = τEmullifetime would be expected to diffuse from the surface of the emulsion droplet by an average diffusion length, LD, given by:
| |  | (25) |
 |
| | Fig. 8 The effects of crowding on the apparent reverse rate constant in eqn (18) determined from NMR, kEffectiveB. Isoflurane molecules within a central emulsion droplet at t = 0 are represented by red circles. (a) Depiction of the “lifetime-limited regime” where LD < Rnn. In this case, the residence lifetime of isoflurane molecules to be found in an emulsion droplet is the same as the residence lifetime of isoflurane molecules to remain in a given emulsion droplet, τobs = τEmullifetime. (b) Depiction of the “crowded-regime” when LD > Rnn. In this case, the observed residence lifetime of isoflurane to be in any emulsion droplet is greater than the actual residence lifetime to remain in a given droplet, i.e., τobs > τEmullifetime. (c) Plot of the experimental Rnn (green curve with black asterisks denoting Rnn calculated from eqn (26)) and LD (blue curve with red asterisks denoting LD calculated from eqn (25) using the kB values in Fig. 4a) vs. the total organic phase volume fraction, ϕ in eqn (24). A dashed box is drawn around the crossover between “crowded” and “lifetime-limited regimes”, which is shown more clearly in (d). The “lifetime-limited regime” occurs for ϕ ≤ 0.0029, in which case, the NMR-determined kB would correspond to the actual release rate constant of isoflurane from emulsion droplets. | |
Isoflurane molecules that were released from an emulsion droplet will not enter a different emulsion droplet during the time τEmullifetime as long as LD is smaller than the shortest distance between neighboring emulsion droplets, Rnn, which is given by:
| | 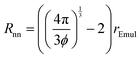 | (26) |
When LD < Rnn, which we refer to as the “lifetime-limited” regime and is depicted in Fig. 8a, the residence lifetime of isoflurane molecules remaining in any emulsion droplet is just given by τobs = τEmullifetime. In this case, the NMR-determined kB value would correspond to the actual kB value.
For LD > Rnn, however, isoflurane molecules leaving an emulsion droplet would be able to diffuse and reenter neighboring droplets within a time τEmullifetime. This situation, which we refer to as the “crowded regime”, is depicted in Fig. 8b. While the residence lifetime of an isoflurane molecule in a given emulsion droplet is still τEmullifetime as illustrated in Fig. 8, the apparent lifetime for an isoflurane molecule to remain in any emulsion droplet is longer as a result of isoflurane molecules diffusing into neighboring emulsion droplets, i.e.,  . Since NMR is sensitive to the lifetime of isoflurane in different chemical environments overall, the observed isoflurane release rate constant determined by NMR, kEffectiveB, would be smaller in the “crowded-regime” than the true isoflurane release rate constant, kEffectiveB < kB.
. Since NMR is sensitive to the lifetime of isoflurane in different chemical environments overall, the observed isoflurane release rate constant determined by NMR, kEffectiveB, would be smaller in the “crowded-regime” than the true isoflurane release rate constant, kEffectiveB < kB.
In Fig. 8c, the (blue curve) calculated LD distances using the apparent kEffectiveB values given in Fig. 4a as input in eqn (25) and the (green curve) calculated Rnn distances using eqn (26) are both plotted as a function of ϕ. A crossover between the “crowded regime” (LD > Rnn) and the “lifetime-limited regime” (LD < Rnn) is observed around ϕ = 0.0029 (corresponding to a 50× dilution and denoted by the dashed box in Fig. 8c, which is shown more clearly in Fig. 8d). This crossover also corresponded to a dilution when kEffectiveB in Fig. 4a became relatively constant, i.e., kEffectiveB ≈ kB. While the above qualitative arguments could explain the observed [Emul]-dependence of kB in Fig. 4a, calculations explicitly taking into account crowding effects and the diffusion of isoflurane between aqueous phase and multiple emulsion droplets36–38 could provide further support that the crossover between “crowded-” and “lifetime-limited” regimes affects the NMR determination of the actual kinetic parameters in emulsions.
V Conclusions
The theory for determining the kinetic parameters describing molecules exchanging between emulsion droplets and an aqueous phase using the Bloch–McConnell equations was presented. Simple algebraic expressions were provided from which the kinetic parameters could be determined from the measured line widths and resonance frequencies of the exchanging molecule. As a demonstration, a series of dilution experiments were used to determine the kinetic exchange parameters of isoflurane in an emulsification of isoflurane and FC43. The isoflurane exchange was found to always be within the fast exchange regime, with a forward rate constant of isoflurane entering an emulsion droplet being on the same order of magnitude as the theoretical Smoluchowski diffusion-limited rate constant, indicating that isoflurane entering an emulsion droplet was diffusion-limited. The NMR-determined reverse rate “constant” for isoflurane release from emulsion droplets was shown to increase by a factor of three for dilution up to 50×, after which kB appeared relatively constant. It was argued that this behavior was a result of a crossover between “crowded-” and “lifetime-limited” regimes, whereby the NMR-determined kB would correspond to the actual reverse rate constant only in the “lifetime-limited” regime. A small, downfield frequency shift of the isoflurane resonances with increasing [Iso]tot was also observed and provided experimental evidence in support of composition-dependence of the isoflurane chemical shifts used in the Bloch–McConnell simulations. The theory and methodology presented in this work should provide more insight into the interpretation of NMR spectra in exchanging systems where composition effects can be important, such as in nanoemulsions, hydrogels, etc. Compared to more traditional techniques, NMR exchange studies could provide alternative methods to more accurately characterize drug release rates in nanocarrier systems.27
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Research reported in this manuscript was supported by funding from the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health under award number R01DK116875, the Diabetes Research Institute Foundation, the National Science Foundation under CHE-1626015 and CHE-1807724, and the University of Miami Center for Computational Science. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Notes and references
- F. Goodarzi and S. Zendehboudi, Can. J. Chem. Eng., 2019, 97, 281–309 CrossRef CAS.
-
D. A. Weitz and D. J. Pine, Dynamic Light Scattering: The Method and Some Applications, Clarendon Press, 1st edn, 1993 Search PubMed.
- P. S. Denkova, S. Tcholakova, N. D. Denkov, K. D. Danov, B. Campbell, C. Shawl and D. Kim, Langmuir, 2004, 20, 11402–11413 CrossRef CAS PubMed.
- P. Jokela, P. D. I. Fletcher, R. Aveyard and J.-R. Lu, J. Colloid Interface Sci., 1990, 134, 417–426 CrossRef CAS.
- B. P. Binks and M. Kirkland, Phys. Chem. Chem. Phys., 2002, 4, 3727–3733 RSC.
- V. Klang, N. B. Matsko, C. Valenta and F. Hofer, Micron, 2012, 43, 85–103 CrossRef CAS PubMed.
- G. J. W. Goudappel, J. P. M. van Duynhoven and M. M. W. Mooren, J. Colloid Interface Sci., 2001, 239, 535–542 CrossRef CAS PubMed.
- M. L. Johns and K. G. Hollingsworth, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 51–70 CrossRef CAS.
- M. L. Johns, Curr. Opin. Colloid Interface Sci., 2009, 14, 178–183 CrossRef CAS.
- K. B. Sutradhar and M. L. Amin, Eur. J. Nanomed., 2013, 5, 97–110 Search PubMed.
- Y. Singh, J. G. Meher, K. Raval, F. A. Khan, M. Chaurasia, N. K. Jain and M. K. Chourasia, J. Controlled Release, 2017, 252, 28–49 CrossRef CAS PubMed.
- M. Levy and S. Benita, Int. J. Pharm., 1990, 66, 29–37 CrossRef CAS.
- L. Mora, K. Y. Chumbimuni-Torres, C. Clawson, L. Hernandez, L. Zhang and J. Wang, J. Controlled Release, 2009, 140, 69–73 CrossRef CAS PubMed.
- S. Petersen, A. Fahr and H. Bunjes, Mol. Pharmaceutics, 2010, 7, 350–363 CrossRef CAS PubMed.
- V. Agrahari, J. Meng, S. Purohit, N. Oyler and B.-B. Youan, J. Pharm. Sci., 2017, 106, 3005–3015 CrossRef CAS PubMed.
- K. I. Momot, P. W. Kuchel, B. E. Chapman, P. Deo and D. Whittaker, Langmuir, 2003, 19, 2088–2095 CrossRef CAS.
- K. I. Momot and P. W. Kuchel, Concepts Magn. Reson., Part A, 2003, 19A, 51–64 CrossRef CAS.
- M. J. Hey and F. Al-Sagheer, Langmuir, 1994, 10, 1370–1376 CrossRef CAS.
- J. Wolber, I. J. Rowland, M. O. Leach and A. Bifone, Mag. Res. Med., 1999, 41, 442–449 CrossRef CAS.
- H. M. McConnell, J. Chem. Phys., 1958, 28, 430–431 CrossRef CAS.
- H. S. Gutowsky and A. Saika, J. Chem. Phys., 1953, 21, 1688–1694 CrossRef CAS.
- A. D. Bain, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS.
- A. G. Palmer and H. Koss, Methods Enzymol., 2019, 615, 177–236 CAS.
- J. Jeener, B. H. Meier, P. Bachmann and R. R. Ernst, J. Chem. Phys., 1979, 71, 4546–4553 CrossRef CAS.
- D. Deng, H. Li, J. Yao and S. Han, Chem. Phys. Lett., 2003, 376, 125–129 CrossRef CAS.
- C. A. Fraker, A. J. Mendez, L. Inverardi, C. Ricordi and C. L. Stabler, Colloids Surf., B, 2012, 98, 26–35 CrossRef CAS.
-
Z. Gong, M. H. Tootoonchi, C. A. Fraker and J. D. Walls, Int. J. Pharm., submitted Search PubMed.
- S. J. Gibbs and C. S. Johnson, J. Mag. Res., 1991, 93, 395–402 Search PubMed.
- M. von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- L. Fielding, Prog. Nucl. Mag. Res., 2007, 51, 219–242 CrossRef CAS.
- D. Sinnaeve, Concepts Magn. Reson., Part A, 2012, 40, 39–65 CrossRef.
- T. I. Igumenova, U. Brath, M. Akke and A. G. Palmer, J. Am. Chem. Soc., 2007, 129, 13396–13397 CrossRef CAS PubMed.
- P. Vallurpalli, D. F. Hansen and L. E. Kay, J. Am. Chem. Soc., 2008, 130, 2734–2735 CrossRef PubMed.
- R. A. Reck and S. Prager, J. Chem. Phys., 1965, 42, 3027–3032 CrossRef CAS.
- B. U. Felderhof and J. M. Deutch, J. Chem. Phys., 1976, 64, 4551–4558 CrossRef CAS.
- P. S. Belton and B. P. Hills, Mol. Phys., 1987, 61, 999–1018 CrossRef CAS.
- P. S. Belton and B. P. Hills, Mol. Phys., 1988, 65, 313–326 CrossRef CAS.
- M. R. Gherase, J. C. Wallace, A. R. Cross and G. E. Santyr, J. Chem. Phys., 2006, 125, 044906 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Brief descriptions of sample preparation and characterization and additional information of the NMR experiments. See DOI: 10.1039/d1cp02077c |
| ‡ These authors contributed equally to this work. |
| § Co-senior author. |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Mohammad Hossein
Tootoonchi‡
a,
Mohammad Hossein
Tootoonchi‡
 b,
Christopher A.
Fraker§
b and
Jamie D.
Walls
b,
Christopher A.
Fraker§
b and
Jamie D.
Walls
 *a
*a

 , where [Emul] denotes the sample molar concentration of emulsion droplets.
, where [Emul] denotes the sample molar concentration of emulsion droplets.

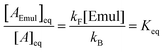

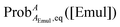 are the equilibrium probabilities that an A molecule is in either the aqueous or organic phases, respectively.
are the equilibrium probabilities that an A molecule is in either the aqueous or organic phases, respectively.
 –acquire NMR experiment applied to a system at equilibrium and described by eqn (1). The NMR signal or free induction decay, FID(t), is proportional to the total transverse magnetization as a function of time after the initial
–acquire NMR experiment applied to a system at equilibrium and described by eqn (1). The NMR signal or free induction decay, FID(t), is proportional to the total transverse magnetization as a function of time after the initial  –pulse, FID(t) ∝ Mtot,+(t) = MA,+(t) + MAEmul,+(t) where MA,+(t) = MA,X(t) + iMA,Y(t) and MAEmul,+(t) = MAEmul,X(t) + iMAEmul,Y(t) represent the total transverse A magnetization in the aqueous and organic phases, respectively. The dynamics of both MA,+(t) and MAEmul,+(t) can be calculated using the Bloch–McConnell equations:20
–pulse, FID(t) ∝ Mtot,+(t) = MA,+(t) + MAEmul,+(t) where MA,+(t) = MA,X(t) + iMA,Y(t) and MAEmul,+(t) = MAEmul,X(t) + iMAEmul,Y(t) represent the total transverse A magnetization in the aqueous and organic phases, respectively. The dynamics of both MA,+(t) and MAEmul,+(t) can be calculated using the Bloch–McConnell equations:20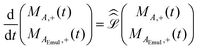
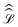 is the evolution superoperator given by:
is the evolution superoperator given by:
 and
and 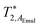 are the effective A transverse spin relaxation times in the aqueous and organic phases, respectively.
are the effective A transverse spin relaxation times in the aqueous and organic phases, respectively.
 can be written as:
can be written as:
 , which are denoted by λ+ and λ−, determine both the observed resonance frequencies
, which are denoted by λ+ and λ−, determine both the observed resonance frequencies  and line widths
and line widths  after Fourier transformation of the FID(t) and are given by:
after Fourier transformation of the FID(t) and are given by:
 ,
,  , and Δk = kF[Emul] − kB.
, and Δk = kF[Emul] − kB.
 that is often broadened beyond the point of practical detection. Thus only the resonance at ωobs ≡ ω+obs = Real[λ+] is typically observed in the spectrum, which is given up to order k−1exch by:
that is often broadened beyond the point of practical detection. Thus only the resonance at ωobs ≡ ω+obs = Real[λ+] is typically observed in the spectrum, which is given up to order k−1exch by:
 , is given up to order k−1exch by:
, is given up to order k−1exch by:
 represents the weighted average of the effective transverse relaxation rates in the aqueous and organic phases in the absence of exchange, and
represents the weighted average of the effective transverse relaxation rates in the aqueous and organic phases in the absence of exchange, and
 and kexch can be determined from
and kexch can be determined from  and ωobs. If ωAEmul is known, then from eqn (8):
and ωobs. If ωAEmul is known, then from eqn (8):
 , e.g.,
, e.g., 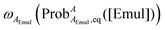 , then
, then  at a given [Emul] could still be determined from eqn (8) by minimizing:
at a given [Emul] could still be determined from eqn (8) by minimizing:
 can be found by minimizing eqn (12) over all such nuclei that are observed in the NMR spectrum:
can be found by minimizing eqn (12) over all such nuclei that are observed in the NMR spectrum:
 is known, kexch can be determined from
is known, kexch can be determined from  in eqn (9) for each observed nuclei:
in eqn (9) for each observed nuclei:
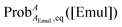 determined from eqn (13) and kexch determined from eqn (14), kF and kB at a given [Emul] are given by:
determined from eqn (13) and kexch determined from eqn (14), kF and kB at a given [Emul] are given by:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was emulsified in saline (20% v/v hydrophobic phase) by temperature controlled high pressure (15
1 v/v) was emulsified in saline (20% v/v hydrophobic phase) by temperature controlled high pressure (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi) homogenization using the ShearJet™ HL60 from Dyhydromatics (Maynard, MA, USA) as was previously reported.26 The surfactants, pluronic F68 and F127, were used in a 1
000 psi) homogenization using the ShearJet™ HL60 from Dyhydromatics (Maynard, MA, USA) as was previously reported.26 The surfactants, pluronic F68 and F127, were used in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to stabilize the emulsion droplets. The particle size of the emulsion droplets was characterized using dynamic light scattering (DLS). From prior studies of similar emulsions,27 dilutions greater than 40× were needed to remove particle–particle interactions and multiple scattering in order to accurately measure the hydrodynamic radius of the emulsion droplets, rEmul. From DLS measurements at 100× dilution, rEmul = (74.7 ± 0.7) nm. The undiluted emulsion had an initial concentration of emulsion droplets of [Emul] ≈ 172.8 nM and an initial isoflurane concentration of [Iso]tot = (660 ± 15) mM that was determined from high performance liquid chromatography.
1 ratio to stabilize the emulsion droplets. The particle size of the emulsion droplets was characterized using dynamic light scattering (DLS). From prior studies of similar emulsions,27 dilutions greater than 40× were needed to remove particle–particle interactions and multiple scattering in order to accurately measure the hydrodynamic radius of the emulsion droplets, rEmul. From DLS measurements at 100× dilution, rEmul = (74.7 ± 0.7) nm. The undiluted emulsion had an initial concentration of emulsion droplets of [Emul] ≈ 172.8 nM and an initial isoflurane concentration of [Iso]tot = (660 ± 15) mM that was determined from high performance liquid chromatography.
 were determined as follows: the Bloch equations were used to simulate the spectrum at each dilution by treating signals from the Hα and Hβ resonances (Fig. 2a) as a quartet and a doublet of doublets, respectively. In the simulations, the chemical shifts (δα/β), spin–spin couplings constants (JαHF and JβHF,1 and JβHF,2), and the effective transverse relaxation times
were determined as follows: the Bloch equations were used to simulate the spectrum at each dilution by treating signals from the Hα and Hβ resonances (Fig. 2a) as a quartet and a doublet of doublets, respectively. In the simulations, the chemical shifts (δα/β), spin–spin couplings constants (JαHF and JβHF,1 and JβHF,2), and the effective transverse relaxation times  were varied in order to minimize the absolute difference between the simulated and experimental spectra. From these simulations, both δα/βobs ≈ δα/βoptimal and
were varied in order to minimize the absolute difference between the simulated and experimental spectra. From these simulations, both δα/βobs ≈ δα/βoptimal and  were determined, which were then used to determine kF and kB using eqn (15). It should be noted that differences in line widths for the individual peaks within a multiplet were not captured by this procedure (an example of this procedure for a single trial is given in ESI†).
were determined, which were then used to determine kF and kB using eqn (15). It should be noted that differences in line widths for the individual peaks within a multiplet were not captured by this procedure (an example of this procedure for a single trial is given in ESI†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) isoflurane/FC43 solution, isoflurane and FC43 had self-diffusion coefficients of DIso,Iso/FC43 = (20.34 ± 0.06) × 10−6 cm2 s−1 and DFC43,Iso/FC43 = (8.86 ± 0.03) × 10−6 cm2 s−1, respectively.
1 v/v) isoflurane/FC43 solution, isoflurane and FC43 had self-diffusion coefficients of DIso,Iso/FC43 = (20.34 ± 0.06) × 10−6 cm2 s−1 and DFC43,Iso/FC43 = (8.86 ± 0.03) × 10−6 cm2 s−1, respectively.
 . In this case, the ϕFC43/IsoIso-dependence of δα/βFC43/Iso could be fit to a local composition model25 (solid curves in Fig. 2a) given by:
. In this case, the ϕFC43/IsoIso-dependence of δα/βFC43/Iso could be fit to a local composition model25 (solid curves in Fig. 2a) given by:

 ,
,  is proportional to ratio of the difference between the FC43–isoflurane and isoflurane–isoflurane intermolecular interaction energies to thermal energy at a temperature T, δαIso = 6.146 ppm and δβIso = 6.494 ppm are the chemical shifts in pure isoflurane, and δα/β,∞FC43/Iso are the isoflurane chemical shifts at infinite dilution in FC43.
is proportional to ratio of the difference between the FC43–isoflurane and isoflurane–isoflurane intermolecular interaction energies to thermal energy at a temperature T, δαIso = 6.146 ppm and δβIso = 6.494 ppm are the chemical shifts in pure isoflurane, and δα/β,∞FC43/Iso are the isoflurane chemical shifts at infinite dilution in FC43.
 (ms)
(ms)
 :
:
 and
and  , respectively, were determined from an isoflurane saturated saline solution while
, respectively, were determined from an isoflurane saturated saline solution while  and
and  were determined from the first emulsion dilution. These parameters are given in Table 1. As discussed earlier, the effect of exchange on an NMR spectrum depends upon the relative magnitude of kexch compared to the absolute frequency differences between the two phases, |Δωα/β(ϕOrgIso)| = γB0|δα/βaq − δα/βEmul(ϕOrgIso)|, where γ is the gyromagnetic ratio, and B0 is the magnitude of the large, static magnetic field. It is important to emphasize that a unique aspect of modeling chemical exchange for the equilibrium in eqn (18) is that |Δωα/β| depends upon ϕOrgIso and hence kexch [eqn (19)].
were determined from the first emulsion dilution. These parameters are given in Table 1. As discussed earlier, the effect of exchange on an NMR spectrum depends upon the relative magnitude of kexch compared to the absolute frequency differences between the two phases, |Δωα/β(ϕOrgIso)| = γB0|δα/βaq − δα/βEmul(ϕOrgIso)|, where γ is the gyromagnetic ratio, and B0 is the magnitude of the large, static magnetic field. It is important to emphasize that a unique aspect of modeling chemical exchange for the equilibrium in eqn (18) is that |Δωα/β| depends upon ϕOrgIso and hence kexch [eqn (19)]. and να/βobs changed with dilution. Both να/βobs, which is given by the solid curves in Fig. 2b, and
and να/βobs changed with dilution. Both να/βobs, which is given by the solid curves in Fig. 2b, and 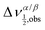 , which is given in ESI,† were used along with δα/βEmul(ϕOrgIso) in eqn (20) and (21) to determine ProbIsoEmul,eq([Emul]) from eqn (13). Both ProbIsoEmul,eq([Emul]) and
, which is given in ESI,† were used along with δα/βEmul(ϕOrgIso) in eqn (20) and (21) to determine ProbIsoEmul,eq([Emul]) from eqn (13). Both ProbIsoEmul,eq([Emul]) and  were then used to calculate kexch in eqn (14). From kexch, both kF and kB at each [Emul] were determined using eqn (15) and are given in Fig. 4. The uncertainties in kF and kB in Fig. 4 mainly reflect variations between replicates since kexch,α and kexch,β were generally within 2–13% of each other after the second dilution. While |Δωα/β| increased with increasing dilution as shown in Fig. 2b, the exchange of isoflurane in the emulsion was always within the fast-exchange regime21–23 since kexch ≫ |Δωα/β| over the entire dilution range. As a result, the isoflurane spectra in Fig. 3 contained only one set of isoflurane resonances.
were then used to calculate kexch in eqn (14). From kexch, both kF and kB at each [Emul] were determined using eqn (15) and are given in Fig. 4. The uncertainties in kF and kB in Fig. 4 mainly reflect variations between replicates since kexch,α and kexch,β were generally within 2–13% of each other after the second dilution. While |Δωα/β| increased with increasing dilution as shown in Fig. 2b, the exchange of isoflurane in the emulsion was always within the fast-exchange regime21–23 since kexch ≫ |Δωα/β| over the entire dilution range. As a result, the isoflurane spectra in Fig. 3 contained only one set of isoflurane resonances.
 as a function of [Emul], both kF and kB in eqn (15) were determined and used as input in the Bloch–McConnell simulations (red spectra).
as a function of [Emul], both kF and kB in eqn (15) were determined and used as input in the Bloch–McConnell simulations (red spectra).
 , and eqn (15). The error bars represent ± a standard deviation after averaging the rate constants determined from both the Hα and Hβ resonances of isoflurane over three emulsion replicates. (a) As [Emul] decreased, kB increased by about a factor of 3 while (b) kF was on the same order of magnitude as the corresponding Smoluchowski diffusion-limited bimolecular rate constant,29kdiff = 5.47 × 1011 M−1 s−1, which is represented by a dashed line.
, and eqn (15). The error bars represent ± a standard deviation after averaging the rate constants determined from both the Hα and Hβ resonances of isoflurane over three emulsion replicates. (a) As [Emul] decreased, kB increased by about a factor of 3 while (b) kF was on the same order of magnitude as the corresponding Smoluchowski diffusion-limited bimolecular rate constant,29kdiff = 5.47 × 1011 M−1 s−1, which is represented by a dashed line. in Fig. 3 were (0.0026 ± 0.0020) ppm and (0.29 ± 0.24) Hz, respectively, with the largest differences between the calculated and experimental spectra (the green spectra in Fig. 3) occurring at both the lowest and highest dilutions. The application of the Bloch–McConnell equations was well justified since for timescales on the order of the inverse of the frequency difference,
in Fig. 3 were (0.0026 ± 0.0020) ppm and (0.29 ± 0.24) Hz, respectively, with the largest differences between the calculated and experimental spectra (the green spectra in Fig. 3) occurring at both the lowest and highest dilutions. The application of the Bloch–McConnell equations was well justified since for timescales on the order of the inverse of the frequency difference,  , the root mean square displacement of isoflurane due to diffusion in the aqueous phase was
, the root mean square displacement of isoflurane due to diffusion in the aqueous phase was  , which was larger than the average separation between emulsion droplets, which ranged from 0.1–1.2 μm over the range of [Emul] studied in this work. The behavior of the isoflurane spectra with increasing dilution in Fig. 3 was similar to prior observations in ligand binding NMR titration experiments30 where a maximum in
, which was larger than the average separation between emulsion droplets, which ranged from 0.1–1.2 μm over the range of [Emul] studied in this work. The behavior of the isoflurane spectra with increasing dilution in Fig. 3 was similar to prior observations in ligand binding NMR titration experiments30 where a maximum in  occurs at a ligand concentration such that the forward binding rate is half the ligand release rate, i.e.,
occurs at a ligand concentration such that the forward binding rate is half the ligand release rate, i.e.,  . Due to the ϕOrgIso-dependence of δα/βEmul(ϕOrgIso), the maximal
. Due to the ϕOrgIso-dependence of δα/βEmul(ϕOrgIso), the maximal  in Fig. 3 occurred at a slightly larger emulsion concentration,
in Fig. 3 occurred at a slightly larger emulsion concentration,  .
.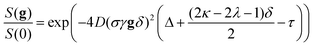
 ,
,  , and
, and  ]. The self-diffusion coefficients of isoflurane were always over an order of magnitude larger than those of FC43 as shown in Fig. 5b. Furthermore, both isoflurane's and FC43's self-diffusion coefficients increased with increasing dilution as shown in Fig. 5c.
]. The self-diffusion coefficients of isoflurane were always over an order of magnitude larger than those of FC43 as shown in Fig. 5b. Furthermore, both isoflurane's and FC43's self-diffusion coefficients increased with increasing dilution as shown in Fig. 5c.



 , was also found to change with dilution as shown in Fig. 6b. The differential attenuation of the Hα and Hβ signals, which led to χαβ < 1, was the result of both the presaturation pulse used to suppress the water signal and changing δα/βobs with dilution. The behavior of χαβ for different dilutions could also be calculated (solid blue curve in Fig. 6b) using the Bloch–McConnell equations with the NMR-determined kB and kF given in Fig. 4.
, was also found to change with dilution as shown in Fig. 6b. The differential attenuation of the Hα and Hβ signals, which led to χαβ < 1, was the result of both the presaturation pulse used to suppress the water signal and changing δα/βobs with dilution. The behavior of χαβ for different dilutions could also be calculated (solid blue curve in Fig. 6b) using the Bloch–McConnell equations with the NMR-determined kB and kF given in Fig. 4. for an initial 10× dilution (solid), which gave either [Fig. 7a] kF = 5.12 × 1011 M−1 s−1 and kB = 5.96 × 103 s−1 or [Fig. 7b] kF = 4.31 × 1011 M−1 s−1 and kB = 3.80 × 103 s−1 for fixed δαEmul = 5.83 ppm and δβEmul = 6.19 ppm.
for an initial 10× dilution (solid), which gave either [Fig. 7a] kF = 5.12 × 1011 M−1 s−1 and kB = 5.96 × 103 s−1 or [Fig. 7b] kF = 4.31 × 1011 M−1 s−1 and kB = 3.80 × 103 s−1 for fixed δαEmul = 5.83 ppm and δβEmul = 6.19 ppm.
 and
and  , were always described over the entire dilution range by the expressions given in Table 1. Experimentally, small differences in magnetic field inhomogeneity between samples are expected to introduce small variations in
, were always described over the entire dilution range by the expressions given in Table 1. Experimentally, small differences in magnetic field inhomogeneity between samples are expected to introduce small variations in  . Furthermore, it is possible that the chemical shifts,
. Furthermore, it is possible that the chemical shifts,  s, and the effective 1H–19F spin–spin interactions could also be changing with dilution in a manner that is not taken into account using the model described above. For example, while the spin–spin couplings and chemical shifts (up to a global shift of δEmuloffset) derived from the isoflurane spectrum at high [Emul] (low dilutions) were similar to those of isoflurane in pure FC43 since ProbEmul,eq([Emul]) ≈ 1, the spectral parameters of isoflurane in the aqueous phase could possibly differ from their isotropic values in pure saline [Table 1] due to anisotropic interactions, such as dipolar couplings32 and chemical shift anisotropy,33 that are not fully averaged away due to the partial ordering of isoflurane in concentrated emulsion samples. With dilution, these contributions would decrease to zero as the spin–spin couplings and chemical shifts approached their isotropic values in the aqueous phase given in Table 1. Furthermore, the intrinsic transverse relaxation times in both the emulsion droplets and aqueous phase could also change with dilution (say due to changes in partial ordering and/or some, yet unidentified mechanism). Further investigations employing additional experimental methods, such as magic-angle spinning, could be used to better characterize the contributions of anisotropic interactions in emulsions. For the system studied in this work, however, both the dilution spectra in Fig. 3 and the diffusion data in Fig. 6 a provided orthogonal measurements that were consistent with the above model using the spectral parameters in Table 1, suggesting that anisotropic interactions, if present, did not significantly affect the NMR-determined kF and kB values give in Fig. 4. More details about the tolerances of the NMR-determined kF and kB rate constants to errors or changes to
s, and the effective 1H–19F spin–spin interactions could also be changing with dilution in a manner that is not taken into account using the model described above. For example, while the spin–spin couplings and chemical shifts (up to a global shift of δEmuloffset) derived from the isoflurane spectrum at high [Emul] (low dilutions) were similar to those of isoflurane in pure FC43 since ProbEmul,eq([Emul]) ≈ 1, the spectral parameters of isoflurane in the aqueous phase could possibly differ from their isotropic values in pure saline [Table 1] due to anisotropic interactions, such as dipolar couplings32 and chemical shift anisotropy,33 that are not fully averaged away due to the partial ordering of isoflurane in concentrated emulsion samples. With dilution, these contributions would decrease to zero as the spin–spin couplings and chemical shifts approached their isotropic values in the aqueous phase given in Table 1. Furthermore, the intrinsic transverse relaxation times in both the emulsion droplets and aqueous phase could also change with dilution (say due to changes in partial ordering and/or some, yet unidentified mechanism). Further investigations employing additional experimental methods, such as magic-angle spinning, could be used to better characterize the contributions of anisotropic interactions in emulsions. For the system studied in this work, however, both the dilution spectra in Fig. 3 and the diffusion data in Fig. 6 a provided orthogonal measurements that were consistent with the above model using the spectral parameters in Table 1, suggesting that anisotropic interactions, if present, did not significantly affect the NMR-determined kF and kB values give in Fig. 4. More details about the tolerances of the NMR-determined kF and kB rate constants to errors or changes to  and δα/β are provided in ESI.†
and δα/β are provided in ESI.†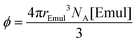
 . After a time τ = τEmullifetime, only e−1 ≈ 36.8% of isoflurane molecules will still reside in the same emulsion droplet they were in at t = 0. Those isoflurane molecules that left an emulsion droplet during the time τ = τEmullifetime would be expected to diffuse from the surface of the emulsion droplet by an average diffusion length, LD, given by:
. After a time τ = τEmullifetime, only e−1 ≈ 36.8% of isoflurane molecules will still reside in the same emulsion droplet they were in at t = 0. Those isoflurane molecules that left an emulsion droplet during the time τ = τEmullifetime would be expected to diffuse from the surface of the emulsion droplet by an average diffusion length, LD, given by:

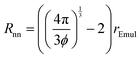
 . Since NMR is sensitive to the lifetime of isoflurane in different chemical environments overall, the observed isoflurane release rate constant determined by NMR, kEffectiveB, would be smaller in the “crowded-regime” than the true isoflurane release rate constant, kEffectiveB < kB.
. Since NMR is sensitive to the lifetime of isoflurane in different chemical environments overall, the observed isoflurane release rate constant determined by NMR, kEffectiveB, would be smaller in the “crowded-regime” than the true isoflurane release rate constant, kEffectiveB < kB.