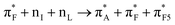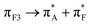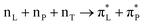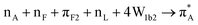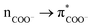Anchoring of a hydrophobic heptapeptide (AFILPTG) on silica facilitates peptide unfolding at the abiotic–biotic interface

Abstract

A hydrophobic heptapeptide, with sequence AFILPTG, as part of a phage capsid protein binds effectively to silica particles carrying negative charge. Here, we explore the silica binding activity of the sequence as a short polypeptide with polar N and C terminals. To describe the structural changes that occur on binding, we fit experimental infrared, Raman and circular dichroism data for a number of structures simulated in the full configuration space of the hepta-peptide using replica exchange molecular dynamics. Quantum chemistry was used to compute normal modes of infrared and Raman spectra and establish a relationship to structures from MD data. To interpret the circular dichroism data, instead of empirical factoring of optical activity into helical/sheet/random components, we exploit natural transition orbital theory and specify the contributions of backbone amide units, side chain functional groups, water, sodium ions and silica to the observed transitions. Computed optical responses suggest a less folded backbone and importance of the N-terminal when close to silica. We further discuss the thermodynamics of the interplay of charged and hydrophobic moieties of the polypeptide on association with the silica surface. The outcomes of this study may assist in the engineering of novel artificial bio-silica heterostructures.

---

Introduction

Short polypeptides (less than 30 amino acids) offer an extensive playground for structural variability and functionalization, both of which are important for contemporary pharmacology and micro-engineering.^1,2 There is much interest in polypeptides that have the capacity to associate with mineral components: beside possible practical benefits, bio-mineral structural organization is a wide-ranging curiosity. Indeed, since the early days of evolution,³ development of inorganic structural elements has been both essential and necessary for the functioning of micro-organisms, plants and animals.^4–8

In recent years, the phage display technique⁹ has been used for identification of primary sequences capable of associating with different materials.^10,11 The technique makes use of short polypeptides (typically 7 or 12 amino acids) genetically fused to the surface coat proteins of bacteriophages that are then exposed to a molecule or material of interest. In a typical phage display procedure, libraries of phage containing millions of different surface polypeptide primary sequences are incubated with the material, the phages that associate with the target are isolated, the DNA amplified and sequenced to identify the peptide binders. Typically, multiple rounds, up to 5 are required to isolate ‘strong’ binders. Using this approach, in a previous study, we determined a number of silica specific polypeptides.¹² However, it is clear that phage identification of mineral-specific primary sequences is just the first step towards the development of predictable bio-mineral structural organization. Mastering bio-silica engineering requires building systematic knowledge to correlate primary sequences with structure–function properties at bio–mineral interfaces according to full configurational structural space.

Prediction of structure in relatively short polypeptides in configuration spaces of increasing order is a challenge. Balance is needed between local (relative orientation of adjacent residues) and long–range interactions. In recent years, assisted with artificial intelligence, prediction of structure has progressed from Q₃ {helix, strand, coil}^13,14 to Q₈ {3₁₀ helix, α-helix, π-helix, β-strand, bridge, turn, bend, others} space.^15,16 For now, however, artificial intelligence is currently not able to explain neither the electric nor entropic aspects of interactions in bio-mineral composites. For structural analysis in such systems experimental techniques are of critical importance. At the same time, we cannot expect diffraction techniques, as well as, for example, NMR to be effective in providing detailed structural information on bio-mineral composites based on relatively short polypeptides. This is due to disorder, motional spectral broadening and deficiency in through-space coupling in the case of relatively short sequences. In this respect, methods of optical spectroscopy may complement structural studies in such systems.

In a recent publication¹⁷ we adopted predictions of classical simulations and quantum chemistry to address structural properties of a hydrophilic LDHSLHS (LD) polypeptide – one of several sequences we determined to be silica specific.¹² In particular, we took advantage of the non-coincidence of infrared and Raman responses¹⁸ to extract the major (beta-like central region with helix-twisted terminals) and the minor secondary structural conformations of the LDHSLHS polypeptide at its interface with amorphous silica nanoparticles in an aqueous environment, and alone in water. Exploring thermodynamics of interactions with the surface we inferred dominance of electrostatic interactions between the polypeptide and silica modulated by diffusion of Na⁺ ions.

The importance of polar and ionic interactions for this particular polypeptide is reasonable since at pH = 7 the LD polypeptide is hydrophilic according to its GRAVY value of −0.557¹⁹ and shows a relatively low hydrophobicity of 10.71: here, we compute hydrophobicity using the Peptide Analyzing Tool (ThermoFisher website), derived from analysis of retention times by Reversed-Phase High-Performance Liquid Chromatography of Peptides.²⁰ In this respect it is interesting to explore the structure and mechanisms of binding of another silica active AFILPTG (AF) polypeptide.¹² Compared to the LDHSLHS case, the AF polypeptide lacks histidines. Also, it includes isoleucine and leucine, which provide hydrophobic and sterically bulky character in the middle structural region. This hydrophobic core is flanked by aromatic phenylalanine and compact alanine on one side and hydrophilic threonine and glycine on the other side. The structurally constrained proline sits between the hydrophobic and polar sides of the polypeptide. Accordingly, at pH = 7, the AF system is expected to demonstrate relatively high hydrophobicity of 26.42²⁰ and a corresponding GRAVY value of +1.46.¹⁹

To address structure and mechanisms of interactions of the AF polypeptide when next to silica, here, we elaborate further the approach we introduced previously.¹⁷ Specifically, in the present study (a) we use replica exchange molecular dynamics (REMD)^21,22 to sample configurational space for initial structural guesses; (b) we combine optical responses sensitive to skeletal motions (infrared and Raman) with circular dichroism (CD) which is sensitive to electronic and magnetic components; and (c) we combine experimental data with quantum chemical (DFT) studies of relevant structural cases of the peptide in water and in the presence of silica to extract plausible structural conformations and discuss the thermodynamics of binding.

Experimental

Synthesis

Synthesis of silica nanoparticles is according to a modified Stöber method.^23,24 In our studies we use 100 ± 6 nm radius particles. We determine the sizes of silica narticles by dynamic light scattering Zetasizer Nano-S, Malvern Instruments, Malvern, UK. To measure optical absorption of silica nanoparticles in the mid-infrared spectral range, we exchange the solvent for Deuterium Oxide using a rotary evaporator IKA RV10/HB10 basic, Sigma-Aldrich Co., St. Louis, MO, USA, operated at 60–80 °C under reduced pressure to remove the solvent after each hydration step. As for previous studies, the polypeptide is synthesized using a Liberty Blue Liberty Blue Automated Microwave Peptide Synthesizer (CEM Corporation, Buckingham, UK). The general procedure is described elsewhere.²⁵ We remove the trifluoroacetic acid left after reverse phase HPLC by lyophilizing the acquired substance under low pH (pD). Prior to optical studies, we add NaCl to the aqueous solutions to maintain a sodium ion concentration about 100 mM. We conduct measurements under pH(pD) = 7: hence, we cannot exclude a minor contribution of protonated C-terminals.

Spectroscopy

We conduct FTIR and polarization sensitive ATR-FTIR studies using a Nicolet 6700 FTIR spectrometer and an Attenuated Total Reflection (ATR) unit Model 0055290, Thermo Electron (now, Thermo Fisher Scientific) equipped with BaF₂ holographic wire grid polarizers WP25H-B, Thorlabs Ltd, Ely UK. The spectral resolution used was 1 cm⁻¹. The polarisation sensitive ATR-FTIR spectra confirm the isotropic character of the prepared samples. The concentrations of the polypeptide for FTIR and ATR-FTIR measurements were about 20 mM and 0.5 mM, respectively. Even though, the FTIR studies are conducted for samples in Deuterium Oxide, a residual amount of normal water remains. This provides a non-negligible contribution to HOD bending modes centred at about 1467 cm⁻¹,^26,27 which we subtract out. Due to the potential for ambiguity upon subtraction, we use dashed lines in the spectral region around 1467 cm⁻¹ (see Fig. 1).

Fig. 1 Protocol for structural analysis. A: FTIR spectra of AFILPTG polypeptide in deuterium oxide, when alone (black line) and in the presence of SiO₂ nanoparticles (red line). B: Raman spectra of AFILPTG polypeptide in deuterium oxide, when alone (blue line) and in the presence of SiO₂ nanoparticles (orange line). B: CD spectra of AFILPTG polypeptide in deuterium oxide, when alone (green line) and in the presence of SiO₂ nanoparticles (magenta line). AA–CC: Simultaneous spectral fit of FTIR, Raman and CD spectra.

We measure Raman spectral dispersions using a DXR microscope station from Thermo Fisher Scientific, Madison, WI 53711. The spectra are taken using 530 nm excitation radiation of 10 mW. The 25 micron confocal slit provides spectral resolution of 2 cm⁻¹. Raman spectra are taken from liquid droplets deposited solutions on an unprotected gold mirror, PFSQ05-03-M03 (Thorlabs), without any cover. For structural analysis comparing CD response we utilised spectral responses as reported previously.²⁸

Isothermal titration calorimetry (ITC)

Isothermal titration calorimetry (ITC) studies were performed using a Malvern MicroCal VP instrument, Malvern, UK. In particular, peptide and silica nanoparticles were dispersed in either type 1 water (H₂O) or in 200 mM NaCl saline solution at a pH of 7.4 to prepare 1 mM and 0.1 mM stock solutions, respectively. The cell temperature and the reference power were 25 °C and 15 μcal s⁻¹, respectively. A stirring speed of 307 rpm was used to maintain nanoparticles in suspension. The time delay between injections was 30 minutes to allow equilibrium to be reached after each Injection. Each experiment had a total duration of around 8.5 hours and was repeated at least in duplicate to ensure reproducibility of the results. To obtain the values for the association constant a linear fitting was used, while enthalpy was taken from the amplitude of the data.

General Outline of Structural Analysis Protocol

Fig. 1 (left) presents the logic flow chart we follow to extract structural properties. Briefly, we use REMD to try sampling full configurational space and extract plausible structural variances. Then, after exploring the dihedral angles of the backbone, the dihedral angles of the side groups, and the statistical weights of the structural realizations, we take representative and diverse structural cases for MD simulations in water, in the presence of Na⁺, Cl⁻ ions and silica slabs.^29,30 From the MD simulations, we extract representative structures with explicit first neighbour water and silica, when present. We describe the criteria to extract MD simulated structures next to silica in a separate section below. Using the extracted systems, we compute normal modes, infrared and Raman intensities and electronic properties using density functional theory (DFT). Finally, we tune the weightings of the sets of infrared, Raman and circular dichroism spectra computed for the representative structure to best match the detected optical responses. Normalized weights are the probabilities for the structural realizations which would fit (or not) the experimental results.

Replica exchange and molecular dynamics in water

Compared to our previous report on structural behaviour of the LD polypeptide,¹⁷ here, we make additional efforts to try sampling full configurational space of the polypeptide when in water. For this purpose, we conduct replica exchange molecular dynamics (REMD) with the CHARMM force field in NAMD environment^21,31 using the generalized Born implicit solvent model with a “soft” cut-off (12 Å) to speed up computation.²² The REMD simulations are conducted in implicit water: solvent friction is added via a Langevin friction term (10 ps⁻¹). A 15 Å cut-off is used for long-range interactions and a time step of 2 fs. REMD is run for 20 ns per sample (total of 960 ns) with the temperatures exchanged every 0.2 ps. Statistical analysis is performed using the MMTSB toolbox,³² with a k-means clustering algorithm (cluster distance 2 Å). Forty-eight replicas of strands with initial configuration are simulated at temperatures between 300 and 800 K. The higher temperatures are used for fast conformational search and overcoming kinetic trapping in the REMD scheme. Representative structures are chosen from the lowest temperature replica (300 K). To approach quantum chemistry of these structures when in explicit water, next, we re-equilibrate the respresentative structures from REMD in explicit water using classical MD with the CHARMM force field in NAMD environment.³¹

Next, for the selected (by REMD) structures we conducted MD simulations with explicit solvent molecules. In the MD simulations, we employed a spherical cutoff of 12 A, which accurately accounts for the Lennard-Jones interactions. We used a summation of Coulomb interactions with the Particle Mesh Ewald (PME) method in high accuracy (10⁻⁶) as implemented in the NAMD program. The size of the simulation box was approximately 3.5 × 3.5 × 10.0 nm², including the polypeptide of 106 atoms, 1600 water molecules, and a six layered α-cristobalite silica slab, which contains 672 silicon atoms. For the water molecules, the flexible SPC model was used. The simulation box lateral size of approximately of 3.5 nm was about twice the length of the peptides, avoiding effects from 3D periodicity, and the height of the box sufficient to allow unrestrained binding (the 10 nm height consists of slightly over 2 nm for the silica slab and about 8 nm for the water/solution slab). The force field was CHARMM, which included accurate parameters for silica surfaces and for the peptides according to the Interface Force Field (IFF) and a Surface Model Database available on line (bionanostructures.com). Agreement of experimentally measured free energies of binding and computed free energies of binding by steered molecular dynamics within ±1 kcal mol⁻¹ (about 10% uncertainty) was previously shown ref. 29.

Simulations of selected structures are conducted with silica surfaces using the IFF update, while 9% and 18% of ≡SiOH groups are ionized to ≡SiO^− 29,30 where the extent of ionization is taken as a proxy for the pH at the surface of the silica. Specifically, in a prior publication,³⁰ we described a wide range of experimental data (surface titration, zeta potentials, pK values of silicic acid and of various types of silica surfaces) to justify the ionization states for a comprehensive range of conditions. 9% ionization represents a pH of ca. 5 and 18% ionization represents a pH ca. 7 and in experimental studies we showed that binding of the peptide to silica was similar at both pH values²⁹ Accordingly, further in this article, we use the notations AF-91 and AF-82 for the structural extracts from these systems for surfaces having two distinct levels of ionization being 9% and 18% respectively.¹⁷ Charge compensation of the simulation boxes is accomplished adding the corresponding number of Na⁺ ions. Initial secondary structures are prepared as a minimum energy realization upon thermalisation of a polypeptide of a random secondary structure in water. Five AF-82 and three AF-91 trajectories were conducted.³⁰ Extraction of representative structural cases was conducted by reviewing 3200 selected molecular arrangements generated along the simulations: more details are provided in the ESI.†

Representative structural cases

Representative structural cases were chosen to fulfil several criteria: that at least one atom of the polypeptide would be no further than 3 angstroms from the average height of the H atoms of the Si–OH groups at the surface, and that the (Φ, Ψ) angular pairs for the five of the seven residues of the polypeptide would be unique. The structural extractions were conducted using home-written Wolfram Mathematica code, as reported previously,¹⁷ to sample from the MD box (i) the coordinates of the atoms of the polypeptide, (ii) the water molecules and Na⁺ within 3 angstroms from any atom of the polypeptide, and (iii) the segment of the first layer of the silicon oxide under a perimeter determined by the outer area of the polypeptide at the considered contact. In the case where several contacts are considered, the extracted silicon oxide segment would include all the perimeters at the considered contacts.

After extraction of the representative structures from the classical simulations, we edit the atomic composition. In particular, we remove Si atoms which are not involved in rings. If necessary, as extraction from MD box requires cutting Si–O bonds, we hydroxylate the Silicon atoms to complete their valence shells. We remove water molecules that are not involved in hydrogen bonding, and try to decrease the number of water molecules as much as we can. A smaller number of atoms allows faster DFT but, preserving water molecules is necessary to describe the role of first neighbour solvent (as predicted by classic simulations) and for quantum chemistry geometry optimization avoiding structural changes without any constraints. The latter is important to avoid imaginary frequences for the normal modes commuted using quantum chemistry.

Quantum chemistry: DFT

The optimization, normal mode analysis and calculations of optical electronic properties are conducted using density functional theory (DFT) implemented in the Gaussian 09 package.³³ Since there are a large number of atoms in the extracted systems; to approach fitting of the experimental data on a realistic time scale we employ restricted B3LYP hybrid functional^34,35 and 6-31G* basis sets. For the optimizations we use the Berny Algorithm³⁶ as implemented in the Gaussian 09 package.³³ Next, using “Freq” protocol we computed force constants, vibrational frequencies, and intensities. By default, the force constants are determined by single numerical differentiation for methods for which only first derivatives are available, and by double numerical differentiation for those methods for which only energies are available. Vibrational frequencies are computed by determining the second derivatives of the energy with respect to the Cartesian nuclear coordinates and then transforming to mass-weighted coordinates.

We explore molecular vibrations and Raman responses in a frequency range from 1350 to 1750 cm⁻¹. This spectral range is too wide to use one scaling factor for the calculated normal modes. To address this, as we introduced previously,¹⁷ we adopt a linear scaling function 1.0909ω_nm − 230 to map the frequencies of the calculated normal modes, ω_nm, in the indicated spectral range.

After DFT studies for structures at silica, we remove atoms specific to silica and fill the voids with water molecules to conduct DFT studies on the same peptide structure but in an aqueous environment. This is to describe properties of the polypeptide when in an aqueous environment either before or after binding to the surface. We conduct quantum chemistry using three types of structural extracts: (1) six cases in water extracted from REMD-MD simulations; (2) seven cases when next to silica in water with Na⁺ as extracted from the five AF-82 and the three AF-91 trajectories; (3) seven cases derived from the cases when next to silica but where silica atoms are replaced with water: see ESI.† Accordingly, in this report we use notation for the cases according to the preparation. For example, case 91_3:09 means that the structure was extracted from the nineth snapshot from the third MD simulation at silica, where 9% of ≡SiOH groups were ionized to ≡SiO⁻. When we discuss properties of polypeptides originally extracted with silica but where silica was replaced with water, we use a notation such as 82_4:50w, for example.

Time dependent DFT

We use the well established time-dependent DFT method to compute CD spectra. The approximations of the method were described, for example by Bauernschmitt and Ahlrichs.³⁷

NTO theory and circular dichroism

Motivated by Koopmans' theorem,³⁸ we address the challenge of describing the electronic and magnetic changes responsible for optical activities adopting natural transition orbital (NTO) theory.³⁹ We provide representations of electronic redistributions upon optical excitations and transform the computed transition density matrix³⁸ to represent “particle” or “electron” and “hole” orbital components involved in the electronic transitions. Pairs of such orbital components constitute the so-called natural transition orbitals.⁴⁰ By visualizing NTOs of the electronic transitions responsible for optical density in the chosen spectral range we provide a rigorous, up to the level of theory used, description of the electronic components that govern spectral responses in the spectral range. To plot electronic spectral dispersions according to TD-DFT predictions, we take convolutions with Lorentzian line-shape with full width at half maximum of 50 cm⁻¹.

Results

In Fig. 1A–C we present FTIR and Raman spectra and CD dispersions for the hydrophobic AFILPTG polypeptide when in aqueous (D₂O) environment alone and in presence of SiO₂ nanoparticles. The experimental Raman and infrared responses demonstrate that, comparing when in water, the Amide and CH modes of the polypeptide are redshifted when in the presence of silica. Circular dichroism data suggests that when the polypeptide is in the presence of silica its electronic states show stronger optical activities at 200 and 220 nm. At the same time, when at the mineral interface, circular dichroism responses at 190 and 230 nm become weaker.

Following the structural extraction protocol as described in the Material and Methods, in Fig. 1AA–CC we present theoretical fits of the observed spectral responses using Infrared, Raman and CD dispersions computed for 13 representative structural cases in water and 7 representative structural cases next to silica: see ESI.† In Fig. 3 and 4 we present the spectral sets of the structural cases which are used to fit the experimental data. To explain the observed spectral responses in water, we consider two main structures 82_4:50w and 82_3:150w with probabilities 0.37 and 0.36, respectively. Additionally, we identify two minor structural arrangements 82_4:300w and MD3 that contribute equally with a probability of 0.14. For the peptide at silica we select the structural cases 91_3:09 and 82_2:50 as the main structural configurations with probabilities of 0.42 and 0.25, respectively. Additionally, we propose the involvement of two minor structural forms 82_3:150 and 82_4:50 with probabilities 0.22 and 0.11, respectively. To visualise anticipated structural tendencies, in Fig. 2 (at the left side) we suggest backbone Ramachandran characteristics of the extracted cases and, at the right side, graphical co-alignments of the main structures under the two environments.

Fig. 2 Left: Dihedral angles of the five residues (from the N-terminal to the C-terminal) in the expanded region of the Ramachandran angular space for the extracted backbones to explain experimental results in water (blue line), and in the presence of silica nanoparticles (red line). Cyan and purple circles indicate the dihedral angles for the first (from the N terminal) residue. Right: Graphical co-alignments of the structures under the two modelled environments.

Assignment of infrared and Raman spectra

First we discuss skeletal dynamics specific to the structures in water. Using theory predictions, we assign the experimentally observed main spectral feature at 1670 cm⁻¹ to Amide I stretching delocalized over the phenylalanine (−), isoleucine (+) and leucine (+) carbonyls of the aqueous 82_4:50w: mode 708 in Fig. 3. Here, the signs in brackets are to highlight that displacements of the Ile and Leu carbonyls are in phase, but π-shifted in respect to displacement of the phenylalanine carbonyl. In Ramachandran space, the structures of the phenylalanine and isoleucine residues explore the region bordering on the angular space of an α helical system, while the rest of the residues towards the C-terminal resemble β-sheet but are strongly folded in respect to the Φ dimension: see Fig. 2 (left side). The experimentally observed spectral shoulder at 1685 cm⁻¹ includes contributions of Amide I mode 607 of 82_3:150w that includes A(−)F(+)I(+) displacements, and a very delocalized mode 539 A(+)F(+)L(+)P(−)T(+) of 82_4:300w, where the main displacements are on the alanine and threonine carbonyls. The contributing residues of the former conformer explore the structural space of β-sheet which is strongly folded in respect to the Φ dimension. The backbone of 82_4:300w has helical and β-sheet motifs at the flanks of the N and C terminals, respectively.

In the higher frequency range, according to our DFT studies, we assign resonances in the frequency range above 1700 cm⁻¹ to stretching modes, which involve terminal groups (alanine and threonine) when not optimally hydrogen bonded. Also, as described in the Materials and Methods, for the chosen pH, (ca. 7) we cannot exclude some contribution of CO stretching of protonated C-terminals at 1720 cm⁻¹. At the lower frequency side, the distinct Raman mode at about 1610 cm⁻¹ is due to in-plane symmetric CH bend/CC stretching of the phenylalanine side group: for example, see the image of mode 603 atomic displacements specific to 82_3:150w at the right side of Fig. 3. Finally, here, it is interesting to note that theory predicts peculiar infrared active low-frequency Amide II modes at 1460 cm⁻¹ for 82_3:150w (mode 150) and 82_4:300w (mode 526) when the backbone displacements admix with the CC stretching of the side groups of the proline and phenylalanine residues.

Fig. 3 Left-top: Experimental Raman and FTIR spectra for the AF polypeptide in water (blue lines); DFT predictions of the responses of the AF structural cases computed in water (purple lines), which provide fittings as shown in Fig. 1. Left-bottom: Experimental Raman and FTIR spectra for the AF polypeptide when next to silica (red lines); DFT predictions (orange lines) for the AF structural cases computed next to silica, which provide fitting as shown in Fig. 1. Right: Computed atomic displacements of the normal modes to explain FTIR and Raman spectra of the AF polypeptide in water (top) and when exposed to silica nanoparticles (bottom).

Fig. 4 Left-top: Experimental CD spectrum for the AF polypeptide in water (blue lines); DFT predictions of the responses of the AF structural cases computed in water (purple lines), which provide fittings as shown in Fig. 1. Left-bottom: Experimental CD spectrum for the AF polypeptide when next to silica (red lines); DFT predictions (orange lines) for the structural cases computed next to silica, which provide fitting as shown in Fig. 1. Right: NTO pairs to explain main electronic, FTIR and Raman spectra of the AF polypeptide in water (top) and when exposed to silica nanoparticles (bottom). In ESI,† we provide images for all the pairs as we numerate in the spectra at the left-side panels.

When at the silica interface, we assign the experimentally observed red-shifted (compared to when in water) spectral feature at 1650 cm⁻¹ to two Amide I stretching modes of 91_3:09. One is mode 848 (see Fig. 3) delocalized as F(+)I(−)L(+)T(−) with the main amplitude on the carbonyl of leucine. Another is mode 849: it describes A(−)F(+)I(−)L(−) displacements with the main amplitude on the carbonyl of the phenylalanine. In Ramachandran space, the involved amino-acids, save isoleucine, find secondary structural expressions in the angular region specific to β-sheet see Fig. 2. Additionally, theory suggests a smaller contribution to the experimentally observed band at 1650 cm⁻¹ due to modes 736 and 738 delocalized as A(+)F(−)I(−)L(+) and A(+)F(+)I(+)L(+), and the threonine specific mode 739 of structure 82_2:50. As one may see in see Fig. 2, the dihedral angles of the terminal residues of this structure occupy the structural region specific to a helix, while the central isoleucine, leucine and proline follow β-sheet architecture.

The computed mode 820 of structure 91_3:09 demonstrates both, strong intensity and relatively low frequency (at 1440 cm⁻¹) and corresponds well with the experimental data. This mode arises from admixing of the NH stretching of the NH₃⁺ terminal with the wags of the CH moieties of the side group of Alanine and Isoleucine. Even more importantly, the NH stretching here is toward the ≡SiO⁻ defect of the silica surface. This offers an explanation for the red-shift of the band at 1440 cm⁻¹ upon binding to silica as reported in the FTIR experimental data: see Fig. 1A. Overall, the observed changes in experimental (see Fig. 1) infrared and Raman responses are subtle, without any clear markers, save that theory predicts a spectral signature of the NH₃⁺ terminal when next to a polar site on silica. This is consistent with the outcome of a previous study where we demonstrated that structural discontinuities of silica do not affect normal modes of surface associated moieties of molecular guests if such moieties are not involved in a direct contact.⁴¹ The results suggest dominance of indirect effects of silica on the structure of the polypeptide, through thermodynamics of interaction with water at the silica interface. To gain further knowledge we use optical spectroscopy which has the capacity to correlate frequency fluctuations over a longer distance range.

Assignment of circular dichroism spectra

To discuss structure according to the observed and computed electronic optical activity, for the first time we describe pertinent transitions considering their NTO pairs, orientation of electric and magnetic transition dipole moments (in respect of each other and in respect to the involved amide units) and distribution of atomic partial charges. This approach is in contrast to the empirical characterisation of optical activity responses onto contributions from helical, sheet and random coil structural motifs.^42,43

In Fig. 4, we present NTO pairs to describe the electronic transitions which may explain the experimental CD spectrum of the AF polypeptide in water. Specifically, to explain the negative shoulder within the spectral range from 210–220 nm, theory suggests NTO pair 20 of the case 82_4:50w and NTO pairs 7 and 15 for the structure 82_3:150w. Pair 20 describes a charge-transfer transition from a superposition which contains an antibonding π orbital of alanine carbonyl , a nonbonding orbital of the phenylalanine carbonyl (n_F) and a single nodal bonding π orbital of the aromatic side group (π_F2) to π_F5 antibonding orbital of the aromatic side group (π_F5): + n_F+ π_F2 → π_F5. The NTO pair 7 accounts the transition from nonbonding orbital of isoleucine carbonyl (n_I) to antibonding π orbital of isoleucine carbonyl mainly: 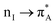. Pair 15 describes mainly charge transfer from the single nodal bonding π orbital of the aromatic side group (π_F2) to a superposition of the antibonding π orbital of the Alanine carbonyl , the antibonding π orbital of the Leucine carbonyl and the 4a1 orbital of several water molecules: . Furthermore, using the computed structures we assign the main negative CD band (as reported by the experiment at 200 nm) to transitions described by NTO pairs 27 and 31 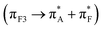of structure 82_4:50w, and transitions described by NTO pairs 22 , 27 and 39 for the case 82_3:150. In Table 1, we list the main transitions for the relevant AF structures in water, while in the ESI,† we provide NTO images of all transitions as numbered in Fig. 4.

Table 1 Electronic components of the most significant optical transitions in the spectral ranges as indicated according to the NTO pairs computed for extracted structures of the AF polypeptide in water: see Fig. 3. We use red and blue fonts to describe electronic contributions of the aromatic side group and water molecules, respectively

210–220 nm		190–200 nm
8:82_4:50w		27:82_4:50w
20:82_4:50w		31:82_4:50w
7:82_3:150w		22:82_3:150w
12:82_3:150w		27:82_3:150w
15:82_3:150w		39:82_3:150w
44:82_4:300w		74:82_4:300w
12: MD3		33: MD3	πL* + nP + πCOO^−* + 8w1a2 → πI* + πL* + πP* + πT*
13: MD3		48: MD3

---

We now compare experimental CD spectral signatures and theoretical predictions for the AF polypeptide in the presence of silica. To explain the negative shoulder within the 210–220 nm spectral region, theory suggests NTO pairs 116 , 118 and 137 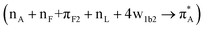for the case 82_2:50 and NTO pairs 19 , 22 and 27 for the structure 82_3:150. Furthermore, we ascribe the main negative feature at 200 nm, to NTO pairs 164 , 165 and 167 of the case 82_2:50; and NTO pairs 41 , 45 and 50 for the structure 82_3:150. In Table 2, we list the main transitions for the relevant AF structures at silica, while in the ESI,† file we provide NTO images for all transitions as numbered in Fig. 4.

Table 2 Electronic components of the most significant optical transitions in the spectral ranges as indicated according to the NTO pairs computed for extracted structures of the AF polypeptide when next to silica: see Fig. 3. We use red and blue fonts to describe electronic contributions of the aromatic side group and water molecules, respectively

210–220 nm		190–200 nm
63:82_2:50		137:82_2:50
74:82_2:50	nL + πF3 → πA* + πF* + πI* + Na^+ + w4a1	164:82_2:50
116:82_2:50		165:82_2:50
118:82_2:50		167:82_2:50
19:82_3:150		41:82_3:150
22:82_3:150		45:82_3:150
25:82_3:150	πF3 → silica	48:82_3:150
27:82_3:150		50:82_3:150

---

In summary, here we show that: firstly, π-bonding orbitals of amide carbonyls do not play a role in optical transitions in the spectral range 190 and 300 nm. Instead, the non bonding electronic component of a carbonyl or a superposition of n and π* components of different amide units contribute to the optical electronic excitation in the spectral range 190–300 nm.

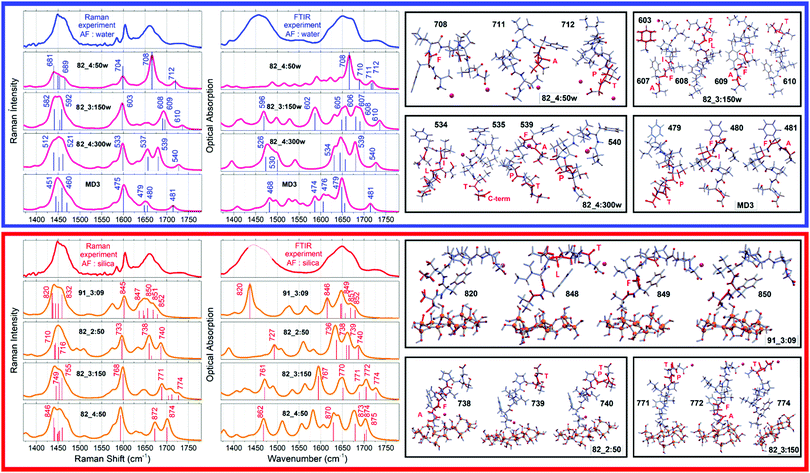
Second, our computed data suggest for transitions in the 190–300 nm spectral range, localized n → π* excitations tend to contribute weakly (due to the relatively small electric transition dipole moment) at the lower energy side of the electronic optical transition edge: from 200 to 220 nm. In polypeptides, we observed that on local n → π* excitation, the magnetic transition dipole moment tends to align parallel or antiparallel to the direction of the corresponding C=O moiety, while the electric transition dipole moment may vary its direction between the C_α–R and C_α–H structural vectors. To support this statement, in the ESI† we image properties for a single amide of methylated variances of alanine to show that the electric component has a weak tendency to co-align with the C=O structural vector while the magnetic vector departs from the amide plane.

Third, charge transfer plays a strong role in higher frequency (spectral range 190–210 nm) transitions. These involve charge transfer between different amide units, or with participation of the C-terminal, or with participation of an aromatic side group: see Tables 1 and 2 and Fig. 4. Particularly strong are the transitions with participation of the aromatic side group. Since charge transfers involve structural components at different positions, the delocalization, transition dipoles and amplitudes are larger. The role of the aromatic side group in CD responses of proteins was noticed and reported very early.⁴⁴ Here, for the peptide under study, we describe the diversity of CD responses from aromatic functional groups due to their involvement in charge transfer transitions; for details, see Fig. 4 and the ESI.†

Fourth, even though electronic absorption of bulk water is reported to become relevant at wavelengths below 177 nm,⁴⁵ while the direct bandgap of amorphous SiO₂ is reported to be about 9.3 eV (ca. 133 nm),^46,47 due to local bonding and defects,^48,49 we may expect participation of local water and silica components in optical transitions at wavelengths longer than 190 nm. Indeed, as in our quantum studies we include proximal water, sodium ions and silica explicitly, our computation results unambiguously demonstrate that electronic delocalizations with such chemical components contributes to the optical properties in the considered spectral range: for example, see NTO 64 and 74 predicated for the case MD3 as shown in Fig. 4. The ESI,† provides more graphical presentations of examples of the participation of water and silica in optical activities predicted for the polypeptide when in water alone and when next to silica.

In this article we present evidence that circular dichroism spectroscopy of polypeptides may report on the chirality of first neighbour water. In particular, since bulk water is not optically active, the observed participation of aqueous states is induced by interactions with chiral moieties of the polypeptide. In this respect, it is important to provide more theoretical details on the nature of aqueous states, including their relative orientation, that might be involved in optical activities and how this may affect a particular spectral range. For example, in the case 82_4:50w, the NTO pairs 4, 18, 32, 41, 130, 138 and 142, as shown in the ESI,† clearly indicate that the role of aqueous states (relative contribution, spatial delocalization, and the nature of electronic components) is larger at the higher frequency side of the spectral range used. Since the optical absorption of bulk water peaks at 8.2 eV (ca. 151 nm)⁴⁵ and such is not optically active, it is obvious that the polypeptide may be considered as a guest to stimulate a density of localized aqueous defects that contribute at the lower frequency side of the main water absorption band. The localization of such states is by hydrogen bonding admixed with the electronic components of the polypeptide backbone and side groups. The relative arrangement of the permitted number of water molecules that coordinate with the local chiral moieties of the polypeptide determines the amplitudes and the relative arrangements of the electric and magnetic transition dipole moments characteristic of the electronic transitions. Understanding this opens up a new research perspective in CD spectroscopy of using polypeptides to probe structure and dynamics.

Discussion

Fitting the observed skeletal (infrared and Raman) and circular dichroism electronic responses we suggest that upon exposure to silica the dominance of 82_4:50w and 82_3:150w structural forms (with probabilities 0.37 and 0.36) in water is replaced with the silica associated 91_3:09 and 82_2:50 cases with probabilities of 0.42 and 0.25, respectively. Here it is important to note the residues of the silica associated 91_3:09 demonstrate larger Φ angles than residues of the aqueous 82_4:50w structure: see Fig. 2. Specifically, the average Φ angles are −99.4° and 80° for the cases, respectively. Results of an early study on a dipeptide⁵⁰ suggest that decreasing of folding along the Φ direction should lead to significantly stronger coupling between amide carbonyls. When coupling is weak, the carbonyls would experience a slightly different environment and we would observe resonances of about the same intensity at slightly different frequencies, according to the differences of the local environments. From this perspective, the computed infrared and Raman properties of the aqueous 82_4:50w case suggest excitonic enhancement of mode 708 as a consequence of the stronger folded character of this structure along the Φ direction. An analogous picture is seen in the case of the aqueous MD3, where the infrared intensity of mode 479 correlates well with a relatively small average Φ angle of −78°.

To understand the sensitivity of electronic responses to backbone structure when in water and next to silica we use the NTO presentation to explore the character of computed optical electronic excitations of the most intense optical activities where relatively long-distance charge transfers do not dominate. For examples, in the case of aqueous systems, we consider NTO pairs 27 of 4:50w, 27 and 39 of 3:150w, and the NTO pair 74 of 4:300w. For comparison, when the polypeptide is next to silica, we consider contributing NTO pairs 19 and 45 of 82_3:150, and NTO 165 of 82_2:50. Exploring the graphical presentations and the tabulated values we observe a tendency in such transitions for a larger delocalization upon excitation for the polypeptide when next to silica: a slightly larger number of backbone electronic terms in the ‘hole’ (destination) part of the NTO, as tabulated. This theoretical prediction of slightly better possible electronic delocalizations for the polypeptide simulated when next to silica also suggests that when next to the mineral interface the polypeptide has a possibility to explore the configurational space of less folded, less constrained structural conformations. Indeed, in the right-side panel in Fig. 2 we suggest a graphical co-alignment of the predicted main structures under the two environments to visualise the anticipated tendency that the polypeptide is less folded when next to the surface.

The importance of the prediction concerns thermodynamics and mechanisms of association of the AF polypeptide with silica. The polypeptide is relatively hydrophobic. Therefore, when in water, structural compacting may help in reducing interactions with solvent. At the same time, the silica surface with its moderate density of polar sites (comparing to such in water), but sufficient to interact with the NH₃⁺ terminal of the polypeptide, would offer possible diversity for the hydrophobic moieties to orient optimally between the relatively nonpolar mineral surface and the (relatively reduced in presence) aqueous counterpart. The described geometry suggests a degree of orientational ordering for the polypeptide when next to the surface. Indeed, in the ESI,† we present relative distances of selected polypeptide moieties in respect to the silica surface, which suggest that when next to silica, the N-terminal tends to orient toward the surface while the other moieties prefer to sample the wider space away from the surface. Quantum computations suggest that for the structures under such arrangement, the electric transition dipole moment vectors of the optical transitions demonstrate a tendency to orient either toward the surface or away, but not parallel in respect to the surface. Consistently, the magnetic transition dipole moment vectors would have a slight tendency to align parallel with the surface. The mild character of orientational tendencies for electric and magnetic induced components agrees with the nature of disordered silica as a high band-gap semiconductor. For example, recently, we reported that structural discontinuities of silica do not affect normal modes of surface associated moieties of molecular guests if such moieties are not involved in a direct contact.⁴⁰

Here, it is interesting to notice that the results of isothermal titration calorimetry for binding of the AF polypeptide to silica nanoparticles are quite comparable to those we reported recently for the LD polypeptide.¹⁷ Specifically, under low ionic environment the polypeptide does not show any thermodynamic tendency to associate with the surface. Under higher ionic strength (0.2 M NaCl), the calorimetry results suggest changes of Enthalpy and Entropy to stimulate and passivate association with the surface, respectively and equally. This is in contradiction with the results of bio-panning experiments, that reported that, when translated as a part of a capsid glycol–protein, the AFILPTG sequence effectively promotes association of phages bearing this sequence with a silica surface.¹² The results of FTIR, Raman and CD experiments as well as MD and DFT simulations confirm a weak tendency for the sequence to associate with silica even with N and C terminal groups. In contrast to the outcome of theoretical studies for the hydrophilic LDHSLHS polypeptide,¹⁷ here the extracted structures suggest that simulations next to a surface with low levels of ionization (AF-91) are more suitable to predict association of the AF system with silica. According to the predictions of MD and simulations of infrared and Raman modes we deduce that a favourable enthalpy of binding for the sequence is likely due to effective association of the NH₃⁺ terminal with the sparsely present ≡SiO⁻ moieties at the surface. Consistently, in the presence of the hydrophobic components of the polypeptide the neighbouring ≡SiOH groups promote more optimal local clusters of water in the presence of amide carbonyls.

Conclusions

Here we explore the interaction of the AFILPTG sequence and its interaction with water and silica. This is an example of structural analysis at a disordered bioinorganic interface, where methods of NMR and X-ray are limited due to line broadening and lack of translation symmetry, respectively. To describe structural possibilities, we develop an approach in which we simulate structural variances with replica exchange and molecular dynamics, use DFT to compute optical responses of anticipated structural cases, and evaluate probabilities of the structures to reproduce infrared, Raman and circular dichroism dispersions as observed experimentally. To review circular dichroism of the hepta-peptide according to the full complexity of its configuration space, we suggest combining natural transition orbital theory with predictions of density functional theory on optical activities, orientation of transition dipole moments and local atomic charges. We do not use the empirical factoring of optical activity responses of proteins in terms of helical/sheet/random contributions, rather offer a rigorous (up to the level of the used theory) description of polypeptide circular dichroism in terms of electronic identities specific to backbone components, side groups, proximal water, sodium cations and silica moieties. Here, for the first time, we report on the chirality of aqueous and hydrated silica states associated with coordination to a polypeptide backbone and associated functional groups. With agreement between theory and experiment, we discuss the role of the NH₃ terminal and hydrophobic moieties of the polypeptide in interaction with a moderately charged silica surface with limited capacity to coordinate aqueous states. With high computing power, the protocol we suggest and test in this study will provide a systematic industrial perspective valuable for biomineral engineering.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Funding from AFOSR FA9550-16-1-0213 and FA9550-20-1-0206 is gratefully acknowledged. The authors thank Dr Joanna Aizenberg, Harvard University, for continued access to the Odyssey/Cannon cluster at Harvard University. The computations in this paper were run on the Odyssey/Cannon cluster supported by the Faculty of Arts and Sciences division, Research Computing Group at Harvard University. The authors are thankful to Dr Fernando R. Clemente (Gaussian Inc., Wallingford, USA) for stimulating discussions.

References

1. O. W. L. Carter, Y. Xu and P. J. Sadler, RSC Adv., 2021, 11, 1939–1951.
2. M. J. Limo, A. Sola-Rabada, E. Boix, V. Thota, Z. C. Westcott, V. Puddu and C. C. Perry, Chem. Rev., 2018, 118, 11118–11193.
3. H. A. Lowenstam, Science, 1981, 211, 1126–1131.
4. H. C. Schroder, X. H. Wang, W. Tremel, H. Ushijima and W. E. G. Muller, Nat. Prod. Rep., 2008, 25, 455–474.
5. C. C. Perry, Biomineralization: chemical and biochemical perspectives, VCH, Cambridge, New York, 1989, 223–256.
6. R. H. Newman and A. L. Mackay, Ann. Bot., 1983, 52, 927–929.
7. J. Arivalagan, T. Yarra, B. Marie, V. A. Sleight, E. DuvernoisBerthet, M. S. Clark, A. Marie and S. Berland, Mol. Biol. Evol., 2017, 34, 66–77.
8. D. O. Wagner and P. Aspenberg, Acta Orthop. Belg., 2011, 82, 393–398.
9. G. P. Smith, Science, 1985, 228, 1315–1317.
10. J. McCafferty, A. Griffiths, G. Winter and D. Chiswell, Nature, 1990, 348, 552–554.
11. S. Donatan, H. Yazici, H. Bermek, M. Sarikaya, C. Tamerler and M. Urgen, Mater. Sci. Eng., C, 2009, 29, 14–19.
12. S. V. Patwardhan, F. S. Emami, R. J. Berry, S. E. Jones, R. R. Naik, O. Deschaume, H. Heinz and C. C. Perry, J. Am. Chem. Soc., 2012, 134, 6244–6256.
13. W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637.
14. N. Qian and T. J. Sejnowski, J. Mol. Biol., 1988, 202, 865–884.
15. M. Torrisi, M. Kaleel and G. Pollastri, bioRxiv, 2018, 289033.
16. B. Zhang, J. Li and Q. Lü, BMC Bioinf., 2018, 19, 293.
17. D. Oliver, M. Michaelis, H. Heinz, V. V. Volkov and C. C. Perry, Phys. Chem. Chem. Phys., 2019, 21, 4663–4672.
18. H. Torii, J. Phys. Chem. A, 2006, 110, 4822–4832.
19. J. Kyte and R. F. Doolittle, J. Mol. Biol., 1982, 157, 105–132.
20. O. V. Krokhin and V. Spicer, Anal. Chem., 2009, 81(22), 9522–9530.
21. Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151.
22. A. Onufriev, A Continuum electrostatics solvent modeling with the generalized born model In Modeling Solvent Environments, Wiley, USA, 2010, pp. 127–165.
23. P. Roach, D. Farrar and C. C. Perry, J. Am. Chem. Soc., 2006, 128, 3939–3945.
24. W. Stober, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69.
25. V. Puddu and C. C. Perry, ACS Nano, 2012, 6, 6356–6363.
26. Z. Wang, A. Pakoulev, Y. Pang and D. Dlott, J. Phys. Chem. A, 2004, 108, 9054–9063.
27. P. K. Gupta and M. Meuwly, Faraday Discuss., 2013, 167, 329–346.
28. A. Sola-Rabada, M. Michaelis, D. Oliver, M. Roe, L. Colombi Ciacchi, H. Heinz and C. C. Perry, Langmuir, 2018, 34, 8255–8263.
29. F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 5725–5734.
30. F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 2647–2658.
31. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
32. M. Feig, J. Karanicolas and C. L. Brooks, J. Mol. Graphics Modell., 2004, 22, 377–395.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone and B. Mennucci, et al., Gaussian 09, revision B.01, 2010.
34. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
36. C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49–56.
37. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
38. T. Koopmans, Physica, 1934, 1, 104–113.
39. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.
40. A. T. Amos and G. G. Hall, Proc. R. Soc. A, 1961, 263, 483–493.
41. V. V. Volkov, D. J. Belton and C. C. Perry, J. Phys. Chem. A, 2018, 122, 4997–5003.
42. P. Manavalan and W. C. Johnson, Anal. Biochem., 1987, 167, 76–85.
43. W. C. Johnson, Proteins, 1990, 7, 205–214.
44. M. C. Manning and R. W. Woody, Biochemistry, 1989, 28, 8609–8613.
45. K. D. Kerr, R. N. Hamm, M. W. Williams, R. D. Birkhoff and L. R. Painter, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 2523–2527.
46. Z. A. Weinberg, G. W. Rubloff and E. Bassous, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 3107.
47. G. L. Tan, M. F. Lemon, D. J. Jones and R. H. French, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205117.
48. D. L. Griscom, J. Non-Cryst. Solids, 1985, 73, 51–77.
49. L. Skuja, B. Guttler, D. Schiel and A. R. Silin, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14296.
50. H. Torii and M. Tasumi, J. Raman Spectrosc., 1998, 29, 81.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02072b

---