Routes involving no free C₂ in a DFT-computed mechanistic model for the reported room-temperature chemical synthesis of C₂

Abstract

Recent lively debates about the nature of the quadruple bonding in the diatomic species C₂ have been heightened by recent suggestions of molecules in which carbon may be similarly bonded to other elements. The desirability of having methods for generating such species at ambient temperatures and in solution in order to study their properties may have been realized by a recent report of the first chemical synthesis of free C₂ itself under mild conditions. The method involved unimolecular fragmentation of an alkynyl zwitterion 2 as generated from the precursor 1, resulting in production and then trapping of free C₂ at ambient temperatures rather than the high temperature gas phase methods normally employed for C₂ generation. Here, alternative mechanisms are proposed for this reaction based on DFT calculations involving bimolecular 1,1- or 1,2-iodobenzene displacement reactions from 2 directly by galvinoxyl radical, or hydride transfer from 9,10-dihydroanthracene to 2. These mechanisms result in the same trapped products as observed experimentally, but unlike that involving unimolecular generation of free C₂, exhibit calculated free energy barriers commensurate with the reaction times observed at room temperatures. The relative energies of the transition states for 1,1 vs. 1,2 substitution provide a rationalisation for the observed isotopic substitution patterns. The same mechanism also provides an energetically facile path to polymeric synthesis of carbon rich species by extending the carbon chain attached to the iodonium group, eventually resulting in formation of amorphous carbon and discrete molecules such as C₆₀.

---

Introduction

The diatomic species C₂ has a long and literally colourful history, one nicely summarised recently.¹ Much of the known chemistry and particularly the spectroscopy relates to the gaseous species at high temperatures, but the very high reactivity has also meant that ambient temperature generation in the condensed phase and the mechanism of subsequent reactions has hitherto been less studied. Interest in this species has been particularly sparked in the last decade by renewed discussion of its chemical bonding in the form of a proposal that it sustains a quadruple bond between the carbons as in ,^2–4 a claim that generated⁵ much stimulating debate and continues to do so unabated.⁶ Most recently, the attention has extended to species with quadruple bond patterns between carbon and other elements such as ⁷ or related main group elements with similar four-fold bond characteristics as in ⁸ or .⁹ Such diverse reports raise the distinct possibility that room temperature/solution studies of species containing quadruple bonds to carbon will become possible and perhaps even routine. In this context then, the recent proposal^10,11 of a room temperature chemical synthesis in the condensed phase on a relatively rapid timescale (∼minutes) of C₂ itself was particularly significant, since this would open an avenue for exploring the reactivity of carbon in this unusual bonding state in new media and a new temperature range. The reaction was thought to proceed at ambient or low temperatures from the transient zwitterionic intermediate 2, formed by treating precursor 1 with a source of fluoride anion. Unimolecular fragmentation of 2 would then produce iodobenzene and free singlet state C₂ (Fig. 1). It should be noted that other reagents that deliver a dicarbon fragment have been reported,¹² although there the mechanism was not thought to involve any free C₂. Likewise dicarbon stabilized by a single phosphine ligand has been characterised¹³ which can undergo, inter alia, an interesting intermolecular C–H activation upon thermolysis. Experiments trapping 2 in solution with either 9,10-dihydroanthracene or galvinoxyl radical (Fig. 2) enabled isolation of products from which participation of free C₂ was inferred.^10,11 The same conclusion also following from detection of polymeric carbon products such as amorphous carbon and even C₆₀. An experiment carried out using solid reagents putatively produced “C₂ gas”, as inferred by using argon to flush any volatile products out of the reagent flask and into a second flask, where they were again observed to be trapped using solid galvinoxyl.

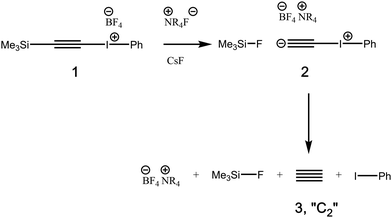Fig. 1 Reaction scheme for proposed^10,11 chemical synthesis of singlet free C₂.

Fig. 2 Trapping reactions for inferring the existence of singlet free C₂.

Further pertinent experimental observations are the reported results^10,11 of isotopic substitution in 2. In dichloromethane solutions, it was asserted that , as apparently formed from labelled 2 and trapped using galvinoxyl, results in a 71 : 29 product ratio in favour of a ¹³C label in the α position of the product rather than β (see Fig. 4). For the experiment conducted without solvent, the isotope distribution was found to be almost equal (52 : 48). The former result was attributed^10,11 to a fast radical pairing between C₂ and galvinoxyl in solution, prior to ejection of iodobenzene from the solvent cage. Changes in the isotope patterns with solvent were thought to arise from differing solvent viscosities.

A fundamental aspect of any ambient temperature reaction occurring on a relatively short time scale is its energetics. These were addressed as matter arising^14,15 from the original synthetic report, in which analysis of the computed thermodynamics of this reaction led to the conclusion that the production of free C₂ and iodobenzene was likely to be highly endoenergic. The energetics of the equilibrium (eqn (1), R = Me, Ph) were in the range of +(43–53) kcal mol⁻¹ using three different estimates, anchored by a calibrated CCSD(T)/Def2-TZVPPD/SCRF = dichloromethane calculation for a simplified model (eqn (1), R = Me) for which ΔG₂₉₈ +47.1 kcal mol⁻¹. Eyring theory tells us that at 298 K, unimolecular reactions with a half-life of respectively 1 minute and 1 hour correspond to free energy barriers of 20.0 or 22.5 kcal mol⁻¹, significantly lower than the energy range predicted above.

In order to demonstrate that the species being trapped really is C₂, one has to exclude the possibility that its putative precursor, the zwitterionic species 2, is itself being trapped by these same reagents (Fig. 3) prior to any release of C₂. Since generation of C₂ by reactions such as these has the potential for much exploitation, it is important to try to establish not only the energetics but also the mechanisms by which the observed products might be forming. Following on from the previous energetic study^14,15 (Fig. 2), the present article reports the results of a computational exploration of the bimolecular reaction mechanism between 2 and the trapping reagents used in the original experimental study (Fig. 3), including the self-reaction of 2 and further similar steps which result in polymerisation giving linear carbon chains.

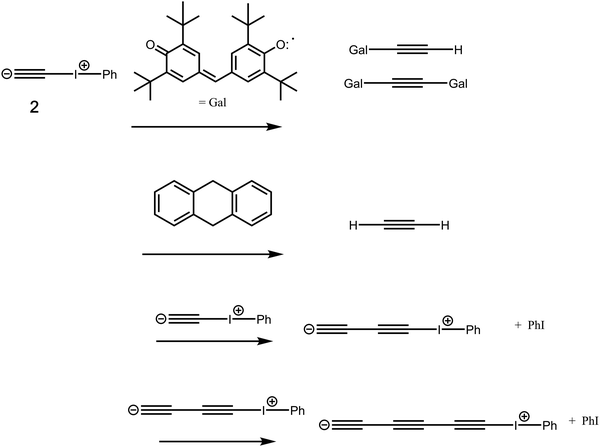Fig. 3 Reactions of the zwitterionic species 2 with the chemical traps galvinoxyl and 9,10-dihydroanthracene and with itself.

Computational details

To study the energetics and mechanism of these reactions, the ωB97XD¹⁶/Def2-SVPD¹⁷/SCRF¹⁸ = dichloromethane solvent density functional procedure was selected¹⁹ as computationally more feasible than coupled-cluster methods such as CCSD(T) for computing large species such as galvinoxyl and for evaluating intrinsic reaction coordinates (IRCs). This DFT method was first calibrated against both the CCSD(T)²⁰/Def2-TZVPPD¹⁷ model and experiment (Table S2).²¹ This revealed that the relative energy of free itself is predicted to be too high^14,15 by ∼28 kcal mol⁻¹ using the ωB97XD/Def2-SVPD/SCRF = DCM method. Transition states were verified using IRC pathways.²² A model 1,2-substitution reaction which is similar to the reactions shown in Fig. 3 and which allows the CCSD(T) level transition state to be located using symmetry alone (C_2h) was selected for calibration (eqn (2)).

Me–I⁺–C≡C⁻ + I–Me → Me–I + ⁻C≡C–I⁺–Me (2)

Results and discussion

A bimolecular mechanistic model avoiding the formation of free C₂ is here proposed. This involves concerted 1,1-substitution directly on 2 by nucleophilic attack from e.g. the galvinoxyl oxygen atom and with iodobenzene acting as a nucleofuge, to form a β-labelled product if isotopic substitution is present in 2 and α-labelled product for 1,2-substitution (Fig. 4). The transition state structures for these two alternatives are shown in Fig. 5. Classical nucleophilic substitution at trigonal²³ and digonal²⁴ carbon is suggested to proceed via a 1,1-mode involving either addition/elimination or a direct S_N2 like structure, but 1,2-modes have apparently never been previously proposed. A similar 1,1-substitution mechanism which avoids liberating the free cation (a species isoelectronic with ) may apply²⁵ when cyanogen chloride or bromide (Cl–C≡N) reacts with benzene in the presence of e.g., aluminium chloride to produce benzonitrile,²⁶ with benzene as nucleophile displacing the chloride nucleofuge directly at carbon.

Fig. 4 Isotopic substitution patterns resulting from competing 1,1- and 1,2-substitution reactions of iodobenzene in 2 by galvinoxyl.

Fig. 5 Calculated (ωB97XD/Def2-SVPD/SCRF = dichloromethane) geometry for reaction of 2 with (a) phenoxyl radical via a 1,1- and (b) a 1,2-substitution, (c) with galvinoxyl via 1,1-substitution and (d) 1,2-substitution. For 3D representations and normal transition mode animations of all transition states, see Table S1.³¹

The issue now is whether either of these alternative mechanisms have overall lower activation free energies than the previously mooted pathway generating C₂ itself, whether unbound or as a “solvent-cage trapped” species. The ωB97XD/Def2-SVPD/SCRF = DCM model predicts the barriers for this bimolecular reaction (eqn (2) and Table S2,²⁷ column 8) to be close to those obtained at the CCSD(T) levels and also that the differences between the more accurate Def2-TZVPPD and the computationally faster Def2-SVPD basis sets are acceptably small (<1 kcal mol⁻¹). It was also possible to compare the free energy of the 1,2-substitution transition states (eqn (2)) with that of free C₂ + two Me–I molecules (Table S2,²⁸ column 7). If a correction of ∼+28 kcal mol⁻¹ noted above is applied to ΔG₂₉₈ using the ωB97XD/Def2-SVPD/SCRF = DCM model,²⁸ the 1,2-substitution reaction of Me–I⁺–C≡C⁻ by Me–I as nucleophile still emerges as ∼10 kcal mol⁻¹ lower in energy than the pathway involving free C₂. Replacing Me–I by phenoxyl radical as a better substituting nucleophile suggests that this 1,2-reaction is now ∼21 kcal mol⁻¹ lower in free energy than generation of free C₂, and that the activation free energy itself (∼21 kcal mol⁻¹) is compatible with a facile room temperature reaction.

The results for increasingly complete models of the galvinoxyl trap are shown in Table 1 for both the 1,1- and 1,2-substitution mechanisms. The reaction between 2 and phenoxyl radical has a slightly lower barrier (ΔG^‡ ∼ 16.9–18.8 kcal mol⁻¹) in the gas phase than in dichloromethane solution (∼19.4–19.6), due to solvent stabilization of the ionic 2. The free energies of the 1,1- and 1,2-substitutions tend to be similar but not identical, which would account for the small variations in isotopic ratios of the final product. Such a model no longer requires stipulating fast radical pairing in a solvent cage to account for unequal isotope ratios in solutions. For the full galvinoxyl model, 1,2-substitution resulting in α-labelled ¹³C-product is computed as slightly lower in free energy, in accord with observation. These transition states also have slightly different dipole moments (1,2 isomer 12.2 D, vs. 1,1-isomer 11.0 D), which suggests that such differences may explain the changes in isotope ratios as a function of solvent observed in the original experiments (cf.Fig. 4). The height of the dichloromethane solution free energy barrier (25.9 kcal mol⁻¹) is now perhaps 3–4 kcal mol⁻¹ higher than expected for a facile room temperature reaction, but the size of the system has thus far precluded full conformational optimisation to identify any conformers with lower energy barriers. The energies of both the 1,1- and 1,2-substitution transition states are lower than the computed combined free energies of the trapping species + free C₂ + iodobenzene by ∼12.3 and 14.3 kcal mol⁻¹ respectively. Bimolecular reaction between free C₂ and any trap would augment that free energy difference because of an additional free energy barrier induced by loss of entropy (see e.g. the entry in Table 1 for the reaction between free C₂ and dichloromethane), reinforcing the conclusion that the route involving bound rather than free C₂ is the more probable mechanism.

Table 1 Computed activation free energies for substitution reactions of 2^a 27

2 + X; X =	ΔΔG^‡ 1,1-substitution	ΔΔG^‡ 1,2-substitution
a ωB97XD/Def2-SVPD/CPCM = dichloromethane model. ΔΔG^‡298 energies in kcal mol^−1 for a standard state of 0.044 M (1 atm). The experimental concentrations range from 0.02–0.033 M. b wB97XD/Def2-TZVPPD/CPCM = dichloromethane model. c Gas phase ωB97XD/Def2-SVPD model. d Branched isomer for C5 chain. e Branched isomer for C7 chain. f CCSD/Def2-TZVPPD/SCRF = dichloromethane model for free singlet C2. g CCSD/Def2-TZVPPD/SCRF = dichloromethane model for free C2 in the lowest energy triplet state.
Phenoxyl	19.4 (19.6)^b {18.8}^c	19.6 (19.6)^b {16.9}^c
2,6-Di-t-butylphenoxyl	24.4	23.7
Galvinoxyl	27.9	25.9
9,10-Dihydroanthracene	31.7	23.8
PhIC2	19.9	15.4
PhIC4	16.9	20.3 (17.8)^d
PhIC6	13.3	24.5 (17.2)^e
PhIC8	11.9	24.1
NH3	32.7	20.9
F^−	35.2	24.3 (25.1)^b
Dichloromethane	38.7	33.3
Dichloromethane + free singlet C2	10.7^f
Dichloromethane + free triplet C2	15.6^g

---

The transition state for reaction of 2 with 9,10-dihydroanthracene shows much greater discrimination between 1,1- and 1,2-substitution, with the latter being clearly favoured (Fig. 6 and Table 1). The former has a small degree of biradicaloid character (〈S²〉 = 0.4129) and is highly asynchronous, tending towards formation of HC≡C˙ and 9,10-dihydroanthracen-9-yl radical as a “hidden intermediate”,²⁹ but which eventually results in hydrogen abstraction from the latter by the former to give the final trapped products. The more stable 1,2-isomer has no biradicaloid character at the equally asynchronous transition state and at this point approximately corresponds to hydride abstraction to form a 9,10-dihydroanthracen-9-ylium cation and a HC≡C⁻ hidden-intermediate ion-pair instead, which then collapses to final observed products. Importantly, a thermally accessible barrier is computed for this reaction (ΔG^‡ ∼ 23.8 kcal mol⁻¹), which again is lower than the combined (corrected) energies of the species involved in unbound C₂ by ∼19.4 kcal mol⁻¹ plus any additional entropic barrier for bimolecular reaction of C₂ (see above).

Fig. 6 Calculated (ωB97XD/Def2-SVPD/SCRF = dichloromethane) geometry for reaction of 2 with (a) 9,10-dihydroanthracene via a 1,1, and (b) a 1,2-substitution.

The next mechanism to be addressed here relates to the observation^10,11 that along with trapping of assumed unbound C₂ itself, other major products are clearly carbon oligomers, including the formation of C₆₀. Can these too arise without the intermediacy of free/unbound C₂? The reaction of 2 with itself to form a new C–C bond provides an obvious route for such a process (Fig. 7 and 8). A 1,2-transition state is clearly lower than the 1,1-mode and hence provides a facile thermal route to formation of a bound C₄ species (ΔG^‡ 15.4 kcal mol⁻¹). The geometry of the former has a novel aspect in having two-fold (C_2h) symmetry, with each molecule of 2 acting as the nucleophile attacking the other and both iodobenzene units apparently acting as the nucleofuge. An IRC (Fig. 5) reveals that this symmetry is initially maintained following the transition state, with apparent elimination of a free C₄ unit, but eventually the energy landscape breaks symmetry to bifurcate and the unit of C₄ is “frustrated” by recombining with one PhI only to form PhIC₄. Such a bifurcating potential energy surface is reminiscent of the dimerization of cyclopentadiene.³⁰ Further low barrier reactions between this product and more of 2 extends the carbon chain to six, this time favouring 1,1-substitution. The process can be repeated to form longer linear or even branched carbon chains (Table 1, footnotes d and e). Eventually these chains will undertake further complex reactions to result in e.g., polymers such as amorphous carbon and C₆₀, the energetics of which will be investigated in future work.

Fig. 7 Calculated (ωB97XD/Def2-SVPD/SCRF = dichloromethane) transition state geometry for reaction of 2 with (a) itself via a 1,1, and (b) a 1,2-substitution, (c) with the product of the previous reaction via 1,1-substitution and (d) ditto, via 1,2-substitution.

Fig. 8 Intrinsic reaction coordinate energy profile for the 1,2-dimerization of 2.

The final transition states investigated are those involving reaction of 2 with a solvent such as dichloromethane, in which the original solution experiments^10,11 were performed. Predominant trapping of 2 by other species such as galvinoxyl would require the barrier for reaction with solvent to be significantly higher than with the trap, especially since the concentration of the solvent is much greater (∼12 M) than that reported for the trapping species (∼0.02–0.033 M). The bimolecular reaction between 2 and dichloromethane involves hydride abstraction to give an acetylide anion and a 1,1-dichloromethylium cation (no biradical character was detected). The transition state (Fig. 9) for 1,2-substitution corresponds to a reaction free energy barrier of 33.3 kcal mol⁻¹, which is high enough to preclude facile reaction of 2 with 12 M solvent, as observed. Contrast this with the free energy barrier calculated for reaction of singlet free C₂ itself with dichloromethane (Fig. 10), which is very much lower (ΔG^‡₂₉₈ 10.7 kcal mol⁻¹ or 15.6 kcal mol⁻¹ for the lowest triplet state of C₂, Table 1). If unbound C₂ were indeed to be generated in dichloromethane solutions at ambient temperatures, a free energy barrier this low would certainly mean its rapid trapping by the solvent.

Fig. 9 Calculated (ωB97XD/Def2-SVPD/SCRF = dichloromethane) transition state geometry for reaction of 2 with dichloromethane.

Fig. 10 Calculated (CCSD/Def2-TZVPPD/SCRF = dichloromethane) transition state geometry for reaction of free singlet C₂ with dichloromethane.

Conclusions

A reaction that can produce the simple diatomic species C₂ under mild conditions would open up a new landscape for the synthesis of carbon-rich species, including C₆₀ itself and generate potential access routes to species in which carbon sustains the hypothesized quadruple bonding pattern. Given the recent report of exactly such a reaction, it appeared desirable to apply quantitative computational techniques as a reality check, not only regarding the energetics of such a process but also to the mechanisms by which it may proceed. These computed mechanisms reveal that ambient temperature routes for reaction of the zwitterion 2 (“bound” C₂) as the active species are lower in energy than those involving unbound or free C₂. Compounds such as 2 serve as potentially useful and potentially selective precursors or synthons for C₂, reacting readily with species such as galvinoxyl or 9,10-dihydroanthracene and less readily with solvents such as dichloromethane, whereas the very high energy free dicarbon species 3 is likely to be less selective.

These low energy bimolecular mechanisms bring into question whether free C₂ as generated by unimolecular fragmentation of 2 actually participates in the solution-phase reactions. It also raises the issue of what is happening in the reported^10,11 experiment where a flask containing solid-state reactants is flushed by argon gas into a second flask containing galvinoxyl. The assumption^10,11 was that the only species sufficiently volatile to be transferred between flasks would be “C₂ gas”, which would then be trapped and crucially that 2 itself was too involatile to be so transferred. An experiment whereby 2, via the aryl group, be covalently anchored to a solid-phase support and placed in the first flask would eliminate any possibility that it is 2 and not C₂ that is being transferred and trapped in the second flask.

The introduction of reagents such as 1 opens the exciting prospect that rational syntheses of carbon rich species are indeed possible and that strategies for increasing the selectivity and scope of these reactions may emerge.

Author contributions

The author performed the calculations and wrote the text.

Data availability

All relevant FAIR (Findable, Accessible, Interoperable, Reusable) datasets are available from a data repository via the master collection DOI: 10.14469/hpc/7616 and datasets cited therein and Table S1²⁷ (a version of Table 1 with 3D interactive/animated models) and Table S2.³²

Conflicts of interest

The author declares no conflicts of interest.

Notes and references

1. T. W. Schmidt, Acc. Chem. Res., 2021, 54, 481–489.
2. S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Nat. Chem., 2012, 4, 195–200.
3. D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, Chem. – Eur. J., 2014, 20, 6220–6232.
4. S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., 2013, 52, 3020–3033.
5. G. Frenking and M. Hermann, Chem. – Eur. J., 2016, 22, 18975–18976.
6. I. Bhattacharjee, D. Ghosh and A. Paul, Chem. Sci., 2020, 11, 7009–7014.
7. A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah and A. K. Guha, Phys. Chem. Chem. Phys., 2020, 22, 24178–24180.
8. L. F. Cheung, T. Chen, G. S. Kocheril, W. Chen, J. Czekner and L. Wang, J. Phys. Chem. Lett., 2020, 11, 659–663.
9. A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah, I. Baruah, L. J. Mazumder, P. P. Sahu and A. K. Guha, Phys. Chem. Chem. Phys., 2021, 23, 9660–9662.
10. K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, M. Kimura, M. Ochiai and M. Uchiyama, ChemRxiv, 2019 DOI:10.26434/chemrxiv.8009633.v1.
11. K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, T. Osawa, M. Kimura, M. Ochiai and M. Uchiyama, Nat. Commun., 2020, 11, 2134.
12. T. Kitamura, M. Hasan Morshed, S. Tsukada, Y. Miyazaki, N. Iguchi and D. Inoue, J. Org. Chem., 2011, 76, 8117–8120.
13. T.-F. Leung, D. Jiang, M.-C. Wu, D. Xiao, W.-M. Ching, G. P. A. Yap, T. Yang, L. Zhao, T.-G. Ong and G. Frenking, Nat. Chem., 2021, 13, 89–93.
14. H. S. Rzepa, ChemRxiv, 2020 DOI:10.26434/chemrxiv.12237980; FAIR data DOI:10.14469/hpc/7185.
15. H. S. Rzepa, Nat. Commun., 2021, 12, 1241.
16. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
17. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
18. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
20. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
21. H. S. Rzepa, Imperial College Research Data Repository, 2020 DOI:10.14469/hpc/7616.
22. H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69.
23. D. K. Nevill and W. F. K. Wang, J. Chem. Soc., Perkin Trans. 2, 1998, 2631–2637.
24. J. O. Edwards, T. E. Erstfeld, K. M. Ibne-Rasa, G. Levey and M. Moyer, Int. J. Chem. Kinet., 1986, 18, 165–180.
25. H. S. Rzepa, Chemistry with a twist (blog), 2020 DOI:10.14469/hpc/7692.
26. P. Karrer and E. Zeller, Helvetica, 1919, 2, 482–486.
27. H. S. Rzepa, Imperial College Research Data Repository, 2020 DOI:10.14469/hpc/7721.
28. H. S. Rzepa, Imperial College Research Data Repository, 2020 DOI:10.14469/hpc/7198.
29. E. Kraka and D. Cremer, Acc. Chem. Res., 2010, 43, 591–601.
30. P. Caramella, P. Quadrelli and L. Toma, J. Am. Chem. Soc., 2012, 124, 1130–1131.
31. H. S. Rzepa, Imperial College Research Data Repository, 2020 DOI:10.14469/hpc/7720.
32. H. S. Rzepa, Imperial College Research Data Repository, 2020 DOI:10.14469/hpc/7719.

---