Open Access Article
Open Access ArticleHow the hydroxylation state of the (110)-rutile TiO2 surface governs its electric double layer properties†
Sebastien
Groh
 a,
Holger
Saßnick‡
b,
Victor G.
Ruiz
b and
Joachim
Dzubiella
*ab
a,
Holger
Saßnick‡
b,
Victor G.
Ruiz
b and
Joachim
Dzubiella
*ab
aApplied Theoretical Physics-Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de; Tel: +49 761 2037627
bResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany
First published on 28th June 2021
Abstract
The hydroxylation state of an oxide surface is a central property of its solid/liquid interface and its corresponding electrical double layer. This study integrated both a reactive force field (ReaxFF) and a non-reactive potential into a hierarchical framework within molecular dynamics (MD) simulations to reveal how the hydroxylation state of the (110)-rutile TiO2 surface affects the electrical double layer properties. The simulation results obtained in the ReaxFF framework have shown that, while water dissociation occurs only at the under-coordinated Ti5c sites on the pristine TiO2 surface, the presence of point defects on the surface facilitates water dissociation at the oxygen vacancy sites, leading to two protonated oxygen bridge atoms for each vacancy site. As a consequence of enhanced water dissociation at the vacancy sites, water dissociation is quenched at the under-coordinated Ti5c sites resulting in two competitive hydroxylation mechanisms on the (110)-TiO2 surface. Using non-reactive MD simulations with hydroxylation states derived from the ReaxFF analysis, we demonstrate that water dissociation at the vacancy sites is a central mechanism governing the structuring of water near the interface. While the structuring of water near the interface is the main contribution to the electric field, water dissociation at the vacancy site enhances the adsorption of the electrolyte ions at the interface. The adsorbed ions lead to an increase of the effective surface charge as well as surface (zeta) potentials which are in the range of experimental observations. Our work provides a hierarchical multiscale simulation approach, covering a series of results with in-depth discussion for atomic/molecular level understanding of water dissociation and its effect on electric double layer properties of TiO2 to advance water splitting.
1 Introduction
Since the discovery by Fujishima and Honda1 of the photocatalytic ability of titanium dioxide, TiO2, this system has been extensively studied for hydrogen fuel production through water splitting.2 Although the anatase TiO2 was found to be the polymorph with the most photocatalytic efficiency, the (110)-rutile surface has become the prototypical oxide surface in surface science, and its interaction with water a model system for the water oxide interface.3 The interaction of water with (110)-rutile TiO2 surfaces has been the subject of numerous computational and experimental studies, ranging from the sub-monolayer and monolayer regimes,4–6 up to the interaction with liquid water.7–10Whereas the dissociation of water molecules on particular surface sites drives the hydroxylation state of the rutile TiO2(110) surface, the quality of the surface, for example the presence of surface defects, defines the nature of these surface sites. On a defect free (110)-rutile TiO2 surface, water can dissociate at the five-fold coordinated titanium site (Ti5c) according to the chemical reaction:
 | (1) |
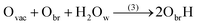 | (2) |
It is clear that the hydroxylation state of the surface is therefore a function of the quality of the surface, and thus on the concentration of oxygen bridge vacancies on the surface before being in contact with water or an aqueous electrolyte. The hydroxylation state of the surface is a critical physical property for photocatalytic properties. It was reported that oxygen bridge vacancies on the surface enhance the hydrophilicity of the surface,25 and improve the photocatalytic activities of (110)-rutile TiO2.26,27
From a modeling perspective, the molecular dynamics (MD) simulation framework is in the numerical world what high resolution electronic microscopy is in the experimental realm, and therefore, microscopic mechanisms can be monitored directly. In addition, macroscopic properties can be obtained by ensemble averaging these microscopic processes using statistical mechanics. Thus, the MD framework is well suited to establish structure–property relationships. Within this idea, numerous in silico experiments in the MD framework were performed to reveal structure–property relationships for the rutile-(110) TiO2/water system.8,28–33
Although the hydroxylation of the surface was (i) explicitly considered in classical, non-reactive MD approaches for modeling charged surfaces,8,33–35 or (ii) dynamically evolving using a reactive force field to analyze electrostatic properties of the rutile-TiO2/water system31 or to quantify the surface reactivity of different TiO2 polymorphs,36 a defect-free titania surface interacting with bulk water or aqueous electrolyte is the common assumption to both classical MD studies and the ones performed using a reactive force field. Recently, it was reported that dissociation kinetics of a water molecule was around 20 times faster on a defective rutile-(101) TiO2 surface than on the defect-free surface.37 However, since the hydroxylation state of the interface results from the collective dissociation of water molecules near the interface, one has to model the interaction of bulk water with a defective surface to physically motivate the structure of the hydroxylation state.
While the electrical double layer properties of a solid surface in contact with a solvent can be derived using a continuum model based on the Poisson–Boltzmann theory, atomistic modeling is a framework capable of establishing relationships between surface chemistry and the electrical double layer properties. Recently, Zhang et al.10 shed light on the microscopic origin of the pH dependency that the Helmholtz capacitance exhibits at the (110)-rutile TiO2 interface. However, no defective surfaces were considered by these authors. Wang et al.9 reported for the first time ab initio MD (AIMD) calculations for a defective (110)-rutile TiO2 surface interacting with bulk water. The authors reported that oxygen bridge vacancies did not enhance water dissociation. In contrast, oxygen bridge vacancies have also been identified in experiments as active sites for protonation of the surface by water molecules in vacuum for protonation of the surface by water molecules in vacuum.15,38–40
In this work, we propose a numerical, hierarchical multiscale methodology involving a specific bridge over two different time scales, which intrinsically predicts the competitive mechanism of water dissociation between the vacancy sites and the undercoordinated Ti surface atoms. This methodology builds a clear bridging approach connecting reactive force field and non-reactive molecular dynamics. Reactive molecular dynamics simulations are initially performed over a few hundred ps to generate an average hydroxylation state of the surface. Subsequent non-reactive MD simulations then use the topology of the hydroxylated surfaces obtained in the reactive calculations to determine the electrical double layer properties over hundred of nanoseconds, based on static structures and non-equilibrium (NEMD) flows to determine effective surface and zeta-potentials, respectively. Based on this hierarchical multiscale scheme, we demonstrate that the electrical double layer properties strongly depend on the hydroxylation state of the surface.
2 Results and discussion
Structural properties of the hydroxylation state of defect-free/defective surfaces
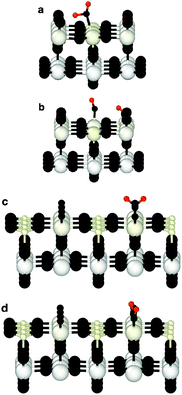
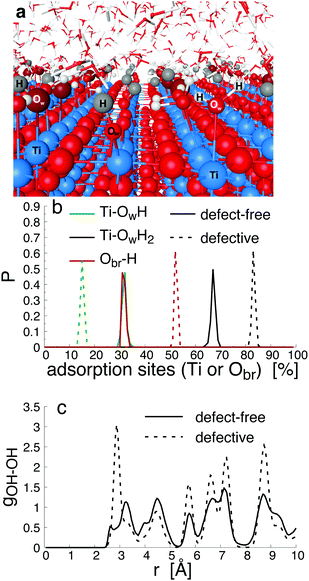
Since bond cleavage and bond formation are explicitly treated in reactive MD simulations such as the ReaxFF framework,41 the hydroxylation state of the (110)-rutile TiO2 surface resulting from dissociation of water on the defect-free surface was already reported in the literature.31 On a defective surface, since dissociation of water at the oxygen vacancy (as given by eqn (2)) and water dissociation at the five-fold coordinated Ti5c (as given by eqn (1)) compete with each other, different hydroxylation states of the surface can effectively be generated by tuning the concentration of oxygen bridge vacancies on the surface (Fig. 2a). In our study, the hydroxylation state of a surface is defined by (i) the amount of hydroxyl groups bonded to undercoordinated Ti5c sites and protonated oxygen bridge atoms resulting from the water dissociation mechanisms at the different sites, and (ii) the distribution of the chemically adsorbed groups on the surface. These two structural properties of the hydroxylated surfaces are the bridging step of the proposed hierarchical multiscale framework. The structural properties of the hydroxylated surface derived in the reactive framework will then be used in a nonreactive framework to model the electrical double layer properties. It should be noted that although MD simulations performed in the ReaxFF framework contain more information on the kinetics occurring at the interface than those conducted in a nonreactive framework, the latter provides a compromise between atomistic description and computational cost allowing for a larger and sufficient sampling of the electrolyte configurations.42 Such strategy disables both intrinsic proton diffusion on the oxygen bridges atoms along the [001] direction21,43 and water assisted proton diffusion.44By increasing the concentration of oxygen vacancies from 0 to 25% (the percentage of oxygen vacancy being defined as the ratio of number of vacancy to the total number of oxygen bridge on the defect-free surface), the amount of dissociated water was monitored, and averaged over the simulation run. The probability density distribution of hydroxyl groups on the surface and water molecules are plotted in Fig. 2b for both the pristine surface and a surface containing 18.75% of oxygen bridge vacancies. On the pristine surface, around 30% of water is dissociated at the Ti5c sites according to eqn (1) resulting in a well balanced amount of hydroxyl groups bonded to undercoordinated Ti5c sites and protonated oxygen bridges. Water molecules are adsorbed at the remaining undercoordinated Ti5c sites (around 70%). Such amount of dissociated water is in agreement with previously reported calculations.31,45,46 On the defective surface, however, the distribution of surface groups is drastically changed as a consequence of two mechanisms for water dissociation. The results reveal that 15% of the available Ti5c sites are bonded to hydroxyl groups. Knowing that these are the signature of a water dissociation mechanism occurring at the Ti5c sites, the remaining 85% are surface Ti5c sites where molecular adsorption of water can occur. Out of the resulting 52% of protonated oxygen bridge atoms, 15% are in consequence a result from the dissociation of water at Ti5c sites, meaning that the remaining 37% result from the dissociation of water molecules occurring at the oxygen bridge vacancies.
To gain a better view on the adsorption pattern of the hydroxyl groups, the in-plane radial distribution function (RDF) between hydroxyl groups (hydroxyl group here refers indifferently to hydroxyl group on Ti5c sites and to protonated oxygen bridge atoms) was calculated, and reported in Fig. 2c. Based on the crystallographic structure of the (110)-rutile TiO2 surface, the first nearest distance between two oxygen bridge atoms (and between two undercoordinated Ti5c atoms) on the surface is, on average, 0.29 nm along the [001] direction. The first and the second nearest distances between an oxygen bridge atom and an undercoordinated Ti5c atom are 0.36 nm and 0.47 nm, respectively. According to Fig. 2c, the first and second nearest neighbouring hydroxyl groups are separated by 0.27 nm and 0.34 nm, respectively, on the defect-free surface. Therefore, the location of the first maximum of the in-plane RDF is correlated to two consecutive protonated oxygen bridge atoms (or two hydroxylated Ti5c), and the second maxima corresponds to the nearest protonated oxygen bridge and hydroxylated Ti5c. On the defective surface, the averaged shortest distance between two hydroxyl groups is about 0.29 nm (Fig. 2c). Since the presence of oxygen vacancies quenched the water dissociation at the undercoordinated Ti5c, the location of the first maxima on the in-plane radial density function between hydroxyl groups is mainly controlled by two nearest protonated oxygen bridge atoms when considering the defective surface containing initially 18.75% of vacancy sites. The second nearest distance between two hydroxyl groups on the defective surface corresponds to the second nearest distance between a protonated oxygen bridge atom and a hydroxylated undercoordinated Ti5c atom.
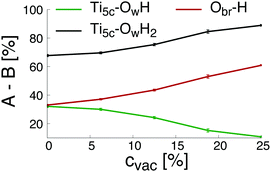
Finally, the changes of the different groups physically and chemically adsorbed on the surface as a function of the initial concentration of oxygen bridge vacancy sites are plotted in Fig. 3. The increase of the initial concentration of oxygen bridge vacancy sites enhances water dissociation at the location of the vacancy sites resulting in an increase of protonated oxygen bridges. Since less oxygen bridges are available to host the remaining protons from water dissociation at the undercoordinated Ti5c sites, the efficiency of the water dissociation mechanism at the undercoordinated Ti5c sites is thus reduced, as illustrated by the decreasing amount of hydroxyl groups bonded to undercoordinated Ti5c sites. As a consequence, molecular adsorption of water is more likely to occur on the defective (110)-rutile TiO2 surface than on the defect-free surface. The variation of the adsorbed groups on the (110)-rutile TiO2 surface as a function of the initial concentration of oxygen bridge vacancy is in agreement with the experimental trends,24 thus confirming that the hydroxylation states modeled in the ReaxFF framework are representative of the experimental observations.
From the structural properties of the interface to a macroscopic definition of the interface
Following Stern's model of the electrical double layer (EDL), the EDL is decomposed in two specific regions: the inner region known as the Stern layer, and the outer part, also called the diffusive layer. In contact to the diffusive region in which mobile ions are treated according to the Poisson–Boltzmann equation in bulk-like water, the Stern layer is the interface region where specific adsorption caused by the partial release of the solvation shell and/or surface complexation caused by the high affinity of attracting counterions can occur. It should be noted that the water structure in the Stern layer is controlled by the interface, and thus the dielectric properties of water in the Stern layer differ drastically from the ones obtained in the bulk water.47–49 In electrokinetic phenomena, the zeta-potential, ζ, is defined as the potential at the location of the shear plane, ySP. Up to the shear plane, the interfacial water and some of the ions of the electrolyte solution bind strongly to the solid, and thus are immobile under the effect of an external and tangential electric field. The zeta-potential is therefore a critical property of the solid/liquid interface since it represents the effective surface charge of the interface. A direct numerical measurement of the zeta-potential for the system (110)-rutile TiO2 surface interacting with aqueous electrolyte was obtained by electro-osmosis experiments.33,35 In such experiments, the zeta-potential is proportional to the flow velocity, v0, and the applied electric field, Ex, according to50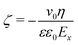 | (3) |
With the knowledge gained from the adsorption of water on defect-free and defective surfaces performed in the ReaxFF framework, three interfacial structures were considered to characterize the EDL in the non-reactive framework, as summarized in Table 1. The interfacial structure labeled MA is representative of the one resulting from the interaction between defect-free (110)-rutile TiO2 surfaces and bulk water with only adsorption of water (adsorption of water molecule at the undercoordinated Ti5c) occurring at the interface. The interfacial structure D is obtained by balanced adsorption of hydroxyl groups on the undercoordinated Ti5c and protonated oxygen bridge atoms on a defect-free surface according to eqn (1). Finally, the interfacial structure H is representative of a highly defective (110)-rutile TiO2 surface containing 25% of oxygen bridge vacancies interacting with bulk water, and assuming that dissociation of water at the vacancy sites leading to two protonated oxygen bridges given by eqn (2) is the only adsorption mechanism. Since these interfaces were obtained assuming different adsorption mechanisms at the interface, they have different hydroxylation states. When considering concentration of approximately 16% of oxygen vacancies, a transition from a (1 × 1) termination to a (1 × 2) reconstruction occurring for a surface maintained at low temperature and in ultra high vacuum was reported both experimentally and theoretically.54 However, their DFT calculations show that the reconstruction does not appear in the phase diagram if an explicit relaxation of the sites around the polaronic Ti3 + site is neglected. This suggests that, in contact with a liquid phase at high temperature, this process is probably in competition with water dissociation occurring at vacancy sites given that both processes happen at similar timescales.55 In addition, it was recently reported protonated oxygen bridges formed at the interface between (110) rutile TiO2 and water without observing a reconstruction of the surface.56 For these reasons, we believe that the assumption of an unreconstructed surface is valid given the experimental and theoretical evidence.
| Surface type | Adsorption mechanism |
|---|---|
| MA | Adsorption of water molecule at the Ti5c |
| D | Adsorption of hydroxyl groups the Ti5c and protons at Obr |
| H | Adsorption and dissociation of water molecule at the Ovac |
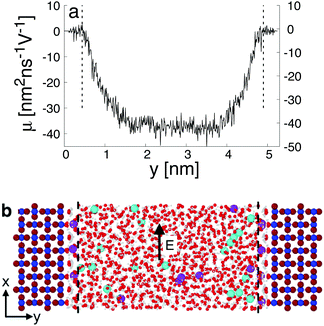
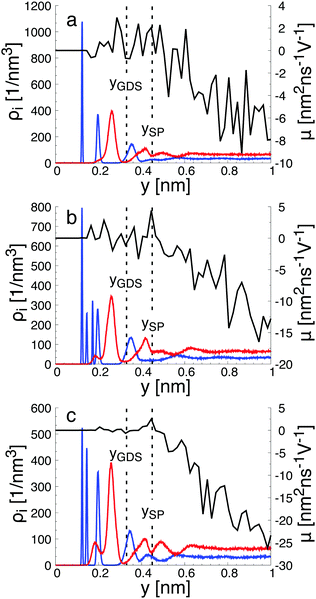
When interacting with an aqueous electrolyte solution, ions are adsorbed at the interfaces leaving a surplus of counterions in the solution. Under the effect of an external electric field applied along a direction parallel to the interface, the surplus of counterions in the aqueous electrolyte solution is moving. Since the water molecules have no net charge, the moving counterions drag their surrounding water molecules resulting in an electro-osmotic flow, expressed by the position-dependent mobility μ(y) = v0(y)/Ex of the aqueous solution. To illustrate such a phenomenon, a representative electro-osmotic mobility profile μ(y) obtained with an interfacial structure type H interacting with a NaCl aqueous solution, averaged over 100 ns, is plotted in Fig. 4. The electro-osmotic mobility can be decomposed in three distinct regions. Up to a distance of 0.48 nm from the interface plane, the electro-osmotic mobility fluctuates around a near zero mean value, suggesting that the aqueous solution is not flowing. In the center region of the slab, between 1.56 nm and 4.84 nm, the aqueous solution is flowing with a constant electro-osmotic mobility around −38 nm2 ns−1 V−1. According to eqn (3), the zeta-potential is then estimated to be around 45 mV. A transient region connecting the immobile aqueous solution and homogeneous flow is visible. The analysis of the MD snapshots extracted from the simulation revealed that some of the Na+-ions are adsorbed in the immobile region. However, spikes in the electro-osmotic mobility are also visible in the immobile region, suggesting that adsorbed Na+-ions are not fully immobile as expected by definition of the shear plane. Using microelectrophoresis cell measurements, the temperature and the pH dependencies of the zeta-potential were quantified at the rutile/aqueous interface for two concentrations of NaCl salt.57 At room temperature, it was found that the zeta-potential decreased from about 40 mV to −70 mV when the pH was increased from 3 to 8. In non-reactive MD simulations, the effect of pH on the interface cannot be modelled directly due to the nondissociative nature of the water model. To model this dependency in the presence of ions, it has been proposed to use a correspondence between solution pH and surface charge density observed in macroscopic titration experiments of rutile powder dominated by (110) surfaces.58 Since our current work focuses on the effect of oxygen bridge vacancies and our setup does not carry a surface charge density, a pH value cannot be either defined nor directly related to the surface charge, and thus a direct comparison of the zeta-potential with experimental values is not available. According to microelectrophoresis experiments, the value of 45 mV that we have obtained in our simulations, corresponds to the zeta potential of the interface at a pH solution of approximately 3 at 298 K and 1 bar, which in turn would correspond to a positive surface charge density according to the relation derived by titration experiments.
From the structural properties of the interface to a macroscopic analysis
To gain a global view of the interface properties, the density profiles as a function of the position along the direction normal to the interfaces were computed from the trajectories as an ensemble average as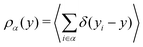 , where δ is the Dirac delta-function, and the sum index i runs over atom types α. The oxygen and hydrogen density profiles are plotted in Fig. 5 for the three representative interfacial microstructures, in addition to the corresponding electro-osmotic flow profiles. For the pristine surface (Fig. 5a), the first maximum visible on the oxygen density profile represents the location of oxygen bridge atoms bonded to the solid. The second maximum located at y = 0.19 nm from the surface in combination with the first maximum visible on the hydrogen density profile are linked to the adsorption of water molecules at the undercoordinated Ti5c sites. Finally, the third maximum of the oxygen density profile together with the second maximum of the hydrogen density profile correspond to the second hydration layer on the (110)-rutile TiO2 surface. By correlating the maxima of the oxygen and hydrogen density profiles with the electro-osmotic mobility profile, the location of the shear plane is found to be at 0.45 nm from the interface. Such location is between the second and the third hydration layer. In addition, the location of the Gibbs dividing surface,59yGDS, obtained numerically by solving the equation
, where δ is the Dirac delta-function, and the sum index i runs over atom types α. The oxygen and hydrogen density profiles are plotted in Fig. 5 for the three representative interfacial microstructures, in addition to the corresponding electro-osmotic flow profiles. For the pristine surface (Fig. 5a), the first maximum visible on the oxygen density profile represents the location of oxygen bridge atoms bonded to the solid. The second maximum located at y = 0.19 nm from the surface in combination with the first maximum visible on the hydrogen density profile are linked to the adsorption of water molecules at the undercoordinated Ti5c sites. Finally, the third maximum of the oxygen density profile together with the second maximum of the hydrogen density profile correspond to the second hydration layer on the (110)-rutile TiO2 surface. By correlating the maxima of the oxygen and hydrogen density profiles with the electro-osmotic mobility profile, the location of the shear plane is found to be at 0.45 nm from the interface. Such location is between the second and the third hydration layer. In addition, the location of the Gibbs dividing surface,59yGDS, obtained numerically by solving the equation 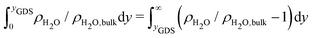 is found to be at 0.34 nm from the surface. This location is between the first and the second hydration layer. The same analysis was performed for the other two interfaces carrying a different hydroxylation state. While our data suggest that the location of the Gibbs dividing surface is independent of the hydroxylation state of the interface, the Gibbs dividing surface underestimates the location of the shear plane. Furthermore, whereas the electro-osmotic mobility for the hydroxylation state representative of a highly defective surface was found to be around −40 nm2 ns−1 V−1, the same quantity for the pristine surface interacting with an aqueous solution of 0.44 nm−2 salt concentration amounts only to −15 nm2 ns−1 V−1. This finding demonstrates that the zeta-potential depends on the hydroxylation state of the (110)-rutile TiO2 surface.
is found to be at 0.34 nm from the surface. This location is between the first and the second hydration layer. The same analysis was performed for the other two interfaces carrying a different hydroxylation state. While our data suggest that the location of the Gibbs dividing surface is independent of the hydroxylation state of the interface, the Gibbs dividing surface underestimates the location of the shear plane. Furthermore, whereas the electro-osmotic mobility for the hydroxylation state representative of a highly defective surface was found to be around −40 nm2 ns−1 V−1, the same quantity for the pristine surface interacting with an aqueous solution of 0.44 nm−2 salt concentration amounts only to −15 nm2 ns−1 V−1. This finding demonstrates that the zeta-potential depends on the hydroxylation state of the (110)-rutile TiO2 surface.
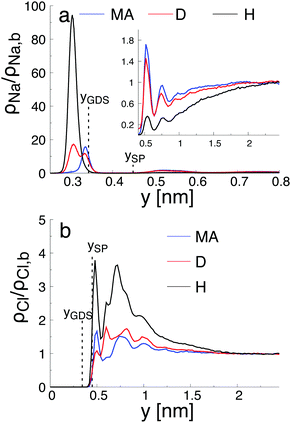
As reported in Fig. 6, the adsorption sites of Na+-ions were analyzed for the different hydroxylation states through the density profile along the direction normal to the interface, and by calculating the survival time correlation function. The latter one is defined by 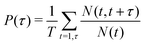 of the adsorbed ions in the immobile region, where N(t,t + τ) is the number of adsorbed Na+-ions in the immobile layer during the time interval [t,t + τ], and N(t) is the total number of Na+-ions in the immobile layer at time t.60 The characteristic decay time (survival time), τr, is obtained by fitting the time correlation function to an exponential decay P(τ) ≈ exp(−τ/τr).34 Based on the maxima of the density profiles (Fig. 6), Na+-ions are adsorbed between the first and the second hydration layers independently of the hydroxylation state of the surface. This finding is in agreement with the adsorption of ions at a generic solid/liquid interface treated by classical MD simulation.61 However, the exact location of the adsorption sites with respect to the interface depends on the hydroxylation state of the surface. Thus, for an interfacial microstructure representative of a highly defective surface healed by a water molecule, Na+-ions adsorb at 0.3 nm from the interface, while Na+-ions adsorb at 0.34 nm from the interface when considering an interface without any hydroxyl groups or protonated oxygen bridge atoms. For an interfacial microstructure representative of a hydroxylation state resulting from the dissociation of 30% of water molecules at the undercoordinated Ti5c atoms, the density profile of Na+-ions is well described by a bimodal distribution with the two maxima located at 0.3 nm and 0.34 nm from the interface. In response to the adsorption of Na+-ions at the interface, Cl−-ions adsorbed near the interface as reported in Fig. 6b. However, although the Na+-ions strongly adsorbed in the region up the shear plane, Cl−-ions systematically adsorbed in the region starting after the shear plane, independently of the hydroxylation state of the surface. From a microscopic perspective, Na+-ions are adsorbed directly above the oxygen bridge atoms on the MA-type of interface, whereas adsorption at bidenate sites between two adjacent oxygen bridge atoms, with at least one of them being protonated, is observed on the H-type of interface.
of the adsorbed ions in the immobile region, where N(t,t + τ) is the number of adsorbed Na+-ions in the immobile layer during the time interval [t,t + τ], and N(t) is the total number of Na+-ions in the immobile layer at time t.60 The characteristic decay time (survival time), τr, is obtained by fitting the time correlation function to an exponential decay P(τ) ≈ exp(−τ/τr).34 Based on the maxima of the density profiles (Fig. 6), Na+-ions are adsorbed between the first and the second hydration layers independently of the hydroxylation state of the surface. This finding is in agreement with the adsorption of ions at a generic solid/liquid interface treated by classical MD simulation.61 However, the exact location of the adsorption sites with respect to the interface depends on the hydroxylation state of the surface. Thus, for an interfacial microstructure representative of a highly defective surface healed by a water molecule, Na+-ions adsorb at 0.3 nm from the interface, while Na+-ions adsorb at 0.34 nm from the interface when considering an interface without any hydroxyl groups or protonated oxygen bridge atoms. For an interfacial microstructure representative of a hydroxylation state resulting from the dissociation of 30% of water molecules at the undercoordinated Ti5c atoms, the density profile of Na+-ions is well described by a bimodal distribution with the two maxima located at 0.3 nm and 0.34 nm from the interface. In response to the adsorption of Na+-ions at the interface, Cl−-ions adsorbed near the interface as reported in Fig. 6b. However, although the Na+-ions strongly adsorbed in the region up the shear plane, Cl−-ions systematically adsorbed in the region starting after the shear plane, independently of the hydroxylation state of the surface. From a microscopic perspective, Na+-ions are adsorbed directly above the oxygen bridge atoms on the MA-type of interface, whereas adsorption at bidenate sites between two adjacent oxygen bridge atoms, with at least one of them being protonated, is observed on the H-type of interface.
The adsorption sites of Na+-ions reported in our study differ drastically from the ones previously reported.34,58,62 Such difference is attributed to the different hydroxylation states of the (110)-rutile TiO2 surface, and thus to the different partial charges of the protonated oxygen bridge atoms. For example, Predota et al.58 reported a tetradenate site between two hydroxylated undercoordinated Ti5c and two bridging oxygens as a possible adsorption site for Na+-ions. Since dissociation of water at the two consecutive undercoordinated Ti5c atoms was not observed in the analysis of the hydroxylation state performed in the reactive framework, such configuration was not introduced in the non-reactive simulation.
By analyzing the survival time correlation function of Na+-ions between the first and the second hydration layers (Fig. S1 in the ESI†), it appears that adsorption on the pristine surface is less stable than adsorption on the surface with protonated oxygen bridge atoms, e.g., the survival time of the Na+-ions between the first and the second hydration layers being different by almost two orders of magnitude. For the interface with protonated oxygen bridge atoms, the survival time of the Na+-ions in the immobile region is in agreement with the one obtained when considering the adsorption of ions to a generic solid/liquid interface.61
We note that our microscopic analysis was obtained using trajectories with a fixed topology of the hydroxylation state, and therefore surface diffusion of protons on the surface was not included. Different mechanisms of surface diffusion of protons are possible, but these mechanisms are assumed to depend on the hydroxylation of the surface. Thus, for an interfacial structure type H with only protonated oxygen bridge atoms and adsorbed water at the undercoordinated Ti5c, protons can diffuse intrinsically along the [001] direction21,43 or the diffusion can be water-assisted with a water molecule from the second hydration shell.44 In the latter case, a water molecule would transfer a proton to an oxygen bridge atom before capturing another proton from a different oxygen bridge atom. Such mechanisms are explicitly included when characterising the hydroxylation state of the solid surface interacting with bulk water in the reactive framework. The feedback of the adsorbed ions on the hydroxylation state, however, is not included, and therefore the survival time of adsorbed Na+-ions is potentially altered by the proton diffusion. In our study, different topologies for each specific state of surface hydroxylation were investigated, and the survival time was found to be independent of the initial configuration. However, further work to reveal the coupling between the survival time of Na+-ions on the surface and the surface diffusion of protons is envisioned.
Comparison of the electrostatic properties of the EDL with diffusive model
To shed light on the relation between the hydroxylation state of the interface and the electrostatic macroscopic properties, the intrinsic electrostatic potential profile was derived by integrating twice the Poisson equation according to: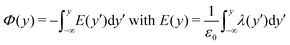 | (4) |
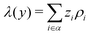 where zi and ρi are the partial charge valencies and the densities of element i, respectively.
where zi and ρi are the partial charge valencies and the densities of element i, respectively.
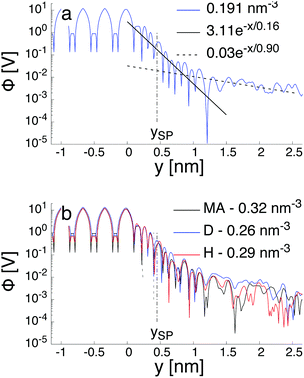
Fig. 7a illustrates the variation of the intrinsic electrostatic potential profile as a function of the distance normal to the interface obtained with the interface of type H in contact with an aqueous solution containing 0.19 nm−3 of NaCl. For symmetry reasons, the electrostatic potential was averaged over the two interfaces of the slab to increase the statistics. The location of the surface, y = 0, is again defined as the location of the undercoordinated Ti5c in contact with water. The location of the shear plane, ySP, derived from the electro-osmosis flow profile is plotted for comparison purposes. As represented in Fig. 7, the electrostatic potential in the aqueous electrolyte can be represented by the superposition of two exponential functions, each of them having a characteristic decay length. In the interfacial region, up to 1.25 nm away from the interface, the decay length is about 0.16 nm. In the bulk liquid, between 1.25 nm and 2.5 nm, the decay length is about 0.9 nm. The origin of the screening of the electrostatic potential in the interfacial region differs from the one in the bulk liquid. The structural ordering of water molecules at the interface leads to the formation of an interfacial dipolar moment. Since the bulk water has no net dipolar moment, an order to disorder transition occurs in the interfacial region. As a consequence, a decrease of the electrostatic potential is observed in the interfacial region with its exponential decay length correlated closely to the dipolar correlation length.63 In the bulk aqueous electrolyte, the origin of the screening is different. Although no surface charge was applied at the TiO2 surface, the adsorption of Na and Cl−-ions at the interface (Fig. 6) causes an effective surface charge, leading to the formation of a diffuse layer.64,65 Therefore, the electrostatic potential can be derived by solving the Poisson–Boltzmann equation (PBE).50 For a planar surface and potentials lower than kBT/e, the linearized PBE is valid, reading d2Φ/d2y = κ−2Φ with κ being the inverse of the Debye screening length. Assuming that Φ0 corresponds to the surface potential and that the potential should vanish at large distances from the interface, the variation of the electrostatic potential in the aqueous electrolyte can be written in the generic form Φ(y) = Φ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−κy). By correlating the generic form of the electrostatic potential with the intrinsic potential, a decay length of 0.9 nm was found. Such a value is in good agreement with the inverse Debye length (
exp(−κy). By correlating the generic form of the electrostatic potential with the intrinsic potential, a decay length of 0.9 nm was found. Such a value is in good agreement with the inverse Debye length (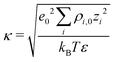 where ρi,0 is the density of ion of type i in the bulk reservoir) obtained for an aqueous solution containing 0.19 nm−3 of NaCl salt (see Fig. S2 in the ESI†).
where ρi,0 is the density of ion of type i in the bulk reservoir) obtained for an aqueous solution containing 0.19 nm−3 of NaCl salt (see Fig. S2 in the ESI†).
However, the definition of the surface potential is subject to interpretation. Since two mechanisms govern the variation of the electrostatic potential in the liquid, one could define in principle, at least, two surface potentials. Assuming a clear definition of the surface, the question of the value for the surface potential arises. Specifically, whether the magnitude of the potential at the location of the surface corresponds to that of the intrinsic potential or to the solution of the linearized PBE. When considering the surface potential as the magnitude of the intrinsic electrostatic potential, the surface potential is around 340 mV and 300 mV at the location of the Gibbs dividing surface and at the location of the shear plane, respectively. However, these surface potentials drop to 20 mV and 17 mV when considering the magnitude of the electrostatic potential obtained for the bulk liquid and extrapolated at the location of the Gibbs dividing surface and the location of the shear plane, respectively. Thus, independently of the definition of the exact location of the effective surface, the intrinsic surface electric potential is more than one order of magnitude higher than the one resulting from the electrolyte contribution. Since the intrinsic potential contains both the contribution of the water ordering at the interface and the one of the electrolyte, one can conclude that the electrolyte contribution is a first order correction to the electric field resulting from the water ordering near the interface. Similar conclusions have been drawn recently also for other interfacial systems in aqueous electrolytes.64–66
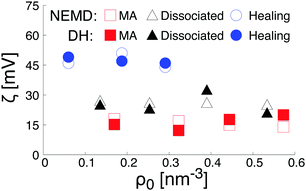
As plotted in Fig. 7b, the total intrinsic electric potential is not significantly altered by a change of the hydroxylation state of the surfaces, assuming the same concentration of salt in the bulk solution. However, although the overall trend of the electrostatic potential in the diffusive region is recovered by double integration of the Poisson equation containing the total partial charges (water and salt), large fluctuations of the electrostatic potential caused by structural fluctuations of water molecules in the bulk water region annihilate any attempts of quantifying the effect of the hydroxylation state on the surface potential resulting from the extrapolation of the far field at the location of the shear plane or the Gibbs dividing surface. Such a difficulty in extracting the surface potential from the total charge density was already reported in the literature.64 To reduce the uncertainty caused by the fluctuation of the bulk water in the diffusive region, we calculated the electrostatic potential therefore also by a double integration of the charge density of the salt only, embedded in a continuum water model with relative permittivity εr. The obtained electrostatic potential was then correlated with the functional form solution of the linearized Poisson–Boltzmann equation. The fitting procedure was validated by a good agreement with theoretical prediction of the screening as a function of the salt concentration (see Fig. S2 in the ESI†). The surface potential caused by the salt was then obtained by evaluating the fit electrostatic potential at the location of the shear plane (Fig. 8). As a consistency check, these zeta-potentials are compared to those calculated from the (non-equilibrium) electro-osmosis calculations in Fig. 8. We indeed see that the variation of the zeta-potential as a function of the salt concentration is independent of the method, even quantitative. While such an agreement is initially surprising, it is somehow natural when considering that the relation between the zeta-potential and the electro-osmosis mobility given by eqn (3) is obtained by double integration of the electric potential.
Finally, the trends in Fig. 8 can be rationalized as follows. According to the data plotted Fig. 6, the density of Na+-ions adsorbed on the surface depends on the hydroxylation of the surface. In addition, the density of adsorbed ions defines the effective charge of the surface. Based on a linearized version of the Grahame equation50 an increase of the surface charge leads to an increase of the surface potential. Thus, at constant salt concentration, the increase of the Na+-ions adsorbed at the interface while changing the hydroxylation state of the surface from a MA-type to a H-type, is in agreement with the increase of the surface potential reported in Fig. 8.
3 Conclusions
In this study, we have proposed a hierarchical multiscale modeling framework to shed light on the role played by the solid surface structure, in particular defects and hydroxylation, on macroscopic properties such as the electric field and the zeta-potential. The structural properties of the water structure near the interface is revealed using molecular dynamics in the framework of a reactive force field. In agreement with experimental findings, competitive mechanisms for water dissociation at the interface was observed in our simulations. While undercoordinated Ti5c sites are the only opportunity for water dissociation on the pristine surface leading to approximatively 30% of water dissociation, the presence of point defects on the surface drastically alters the structure of the hydroxylated surface. When increasing the concentration of point defects on the surface, dissociation occurred at the point defects, changing the mechanism of water dissociation. While the dissociation of a water at an oxygen vacancy site leads to two protonated oxygen bridge atoms, the increasing concentration of protonated oxygen bridge atoms quenched water dissociation at the undercoordinated Ti5c sites. In our hierarchical multiscale framework, the interface structure, such as the amount of dissociation water at the interface, and the distribution of the hydroxyl groups on the surface were used as a bridging link between reactive and non-reactive molecular dynamics frameworks.Using the information gathered from the reactive MD, representative hydroxylated surfaces were built and used as an input setup for the MD simulations in the non-reactive framework to elucidate the critical role played by the hydroxylation state of the surface on the electric potential in the aqueous electrolyte solution when considering the interaction between the surface with a bulk aqueous electrolyte. To this end, both equilibrated MD and non-equilibrium MD calculations were performed to quantify the electric potential. The overall shape of the electric potential in the aqueous electrolyte solution was analyzed, and two main contributions were identified. The structuring of water near the interface was found to be the most significant contribution to the surface potential, while the contribution from the electrolyte resulting from an effective surface charge is a first order correction to it. This result has a significant implication in the theoretical modeling of solid/liquid interfaces. Ionic centric concept embedded in a homogeneous water is the classical way of modeling EDL using Poisson–Boltzmann theory. Since the electrostatic potential profiles near the interface are mainly controlled by the water structure, independently of the ionic concentration and the hydroxylation state of the surface, the variation of the water dielectric properties near the interface must be included in the theoretical modelling of the EDL.
Finally, from a methodological perspective, the idea of hierarchically coupling reactive to non reactive MD simulations allowed us to integrate the physical chemistry properties of surface hydroxylation into longer simulation time scales (up to hundreds of nanoseconds) of the solid/liquid interface to analyze the effects on the EDL interfacial properties. Although the results presented in this work focussed on the (110)-rutile titanium dioxide surface, which is a prototypical oxide in surface science, the methodology that we have used here is completely general and can be applied to a wide range of other materials.
4. Simulation and analysis methods
In this work, three distinct types of calculations were performed: (i) equilibrium MD of the (110)-rutile TiO2/water system in the ReaxFF framework to characterize the hydroxylation state of the surface as a function of the initial concentration of vacancy sites, (ii) non-equilibrium (NEMD) of the (110)-rutile TiO2/aqueous electrolyte system using a non reactive framework with hydroxylation state of the surface motivated by the data gathered in (i) to identify the location of the shear plane and to quantify the magnitude of the zeta potential, and (iii) equilibrium MD using the same setup as in (ii) to quantify the effect of the hydroxylation state on the structural properties near the interface compared the magnitude of the zeta-potential obtained using a Debye–Hückel (DH) approach extrapolated at the location of the shear plane with the ones measure from the NEMD calculations.Hydroxylation state in the ReaxFF framework
The total energy, E, of an atomic system modeled in the ReaxFF framework41 is given as the sum of the partial energies according to:| E = Ebond + Eval + Etor + Eov + Eun + Elp + EvdW + Ecoul | (5) |
Modeling the interaction of (110)-rutile TiO2 with bulk water was performed using a system composed by two parallel blocks of TiO2 separated by water. Since the system is fully symmetric, two identical solid/liquid interfaces are modeled, and thus, the properties reported here are the average over both interfaces. The dimension of each solid block is 5.32 nm × 1.33 nm × 4.59 nm along 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉, 〈110〉, 〈001〉, respectively, and the normal to the interface is along 〈110〉. Thus, each defect-free solid surface interacting with bulk water contains 128 five-fold-coordinated Ti sites and 128 two-fold-coordinated O sites. A distance of 11.18 nm along 〈110〉 separates the two solid surfaces interacting with water. Such a distance is large enough to model bulk like water in the center of the slab, and to prevent interaction between the two surfaces. The liquid region of dimension 5.32 nm × 11.18 nm × 4.59 nm was filled with 9216 water molecules resulting in a bulk water density of about 1 g cm−3. Periodic boundary conditions were applied along 〈
10〉, 〈110〉, 〈001〉, respectively, and the normal to the interface is along 〈110〉. Thus, each defect-free solid surface interacting with bulk water contains 128 five-fold-coordinated Ti sites and 128 two-fold-coordinated O sites. A distance of 11.18 nm along 〈110〉 separates the two solid surfaces interacting with water. Such a distance is large enough to model bulk like water in the center of the slab, and to prevent interaction between the two surfaces. The liquid region of dimension 5.32 nm × 11.18 nm × 4.59 nm was filled with 9216 water molecules resulting in a bulk water density of about 1 g cm−3. Periodic boundary conditions were applied along 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉 and 〈001〉, and fixed boundary condition was applied in the direction normal to the interfaces. Bulk crystal atoms of the solid blocks together with five-fold and six-fold surface titanium atoms were kept immobile. The temperature was maintained constant at 298.15 K by application of a Nosé–Hoover thermostat.71,72 All calculations presented in this work were performed using the software package LAMMPS.73 A time step of 0.25 fs was applied. Following 125 ps of equilibration, 4
10〉 and 〈001〉, and fixed boundary condition was applied in the direction normal to the interfaces. Bulk crystal atoms of the solid blocks together with five-fold and six-fold surface titanium atoms were kept immobile. The temperature was maintained constant at 298.15 K by application of a Nosé–Hoover thermostat.71,72 All calculations presented in this work were performed using the software package LAMMPS.73 A time step of 0.25 fs was applied. Following 125 ps of equilibration, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps were performed, resulting in simulation time of 1 ns. Long-range electrostatic interactions were evaluated using the charge-equilibration scheme with a 1 nm real-space cutoff and a relative precision of 10−6.
000 MD steps were performed, resulting in simulation time of 1 ns. Long-range electrostatic interactions were evaluated using the charge-equilibration scheme with a 1 nm real-space cutoff and a relative precision of 10−6.
Oxygen vacancies were artificially introduced on the surface by randomly removing two-fold-coordinated oxygen bridge sites. Oxygen vacancy concentration of 0, 6.25%, 12.5%, 18.75%, and 25% corresponding to 0, 8, 16, 24, and 32 oxygen vacancy sites per surface, respectively, were considered. Once the oxygen vacancies were introduced on the surface, the local charges around the vacancies were equilibrated using the charge-equilibration scheme of the ReaxFF potential.
EDL properties in the non-reactive framework
The total potential energy, E, of a molecular system modeled in the non-reactive framework is evaluated as the sum of bonded and non-bonded energies according to: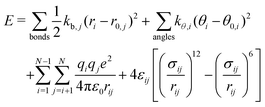 | (6) |
| Surface group | ReaxFF | Non reactive |
|---|---|---|
| Non hydroxylated | ||
| Ti5c | 1.43 | 2.196 |
| O3c | −0.815 | −1.098 |
| O2c | −0.605 | −1.098 |
| Ti6c | 1.589 | 2.196 |
| O3c | −0.815 | −1.098 |
| Water dissociation at Ti5c | ||
| Hydroxyl group adsorbed on Ti5c | ||
| Ti5c | 1.59 | 2.429 |
| O3c | −0.79 | −1.064 |
| Hhydroxyl | 0.38 | 0.527 |
| Ohydroxyl | −0.669 | −0.948 |
| Remaining proton bonded to O2c | ||
| Hhydroxyl | 0.313 | 0.425 |
| O2c | −0.814 | −1.359 |
| Ti6c | 1.55 | 2.131 |
| O3c | −0.77 | −1.077 |
| Water dissociation at Ovac | ||
| H | 0.3506 | 0.4873 |
| Ovac,filled | 0.815 | −1.4794 |
| Ovac,1stneighbours | 0.634 | −1.1509 |
To validate the parameterization of the interatomic potential, the oxygen and hydrogen density profiles obtained for a (110)-rutile TiO2 surface interacting with bulk water were calculated using the parameterization of the nonreactive framework, and compared to their ReaxFF counterparts (Fig. S3 of the ESI†).
Equilibrium MD and NEMD were performed using the same setup of the (110)-rutile TiO2/aqueous electrolyte interface, the difference between the two calculations being the application of an external electric field along a direction parallel to the interface when performing NEMD calculations. A slab geometry system with two parallel (110)-rutile TiO2 walls separated by an aqueous electrolyte was build to model the structure of the rutile-aqueous electrolyte interface. Therefore, two identical interfaces are modelled, and the properties are taken as averages over both interfaces. A representative snapshot of the simulation cell is given in Fig. 4. The dimension of each solid block is 3.25 nm × 1.33 nm × 2.95 nm along 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉, 〈110〉, and 〈001〉, respectively. The normal to the interface is along 〈110〉. Thus, each defect-free solid surface interacting with bulk water contains 50 undercoordinated Ti sites and 50 oxygen bridge sites. A distance of 4.91 nm along 〈110〉 separates the two solid surfaces interacting with the aqueous electrolyte. Such a distance is large enough to model bulk like water in the center of the slab, and to prevent interaction between the two surfaces. The liquid region with the dimensions 3.25 nm × 4.91 nm × 2.95 nm was filled with 1603 water molecules resulting in a bulk water density of about 1 g cm−3. Periodic boundary conditions were applied along 〈
10〉, 〈110〉, and 〈001〉, respectively. The normal to the interface is along 〈110〉. Thus, each defect-free solid surface interacting with bulk water contains 50 undercoordinated Ti sites and 50 oxygen bridge sites. A distance of 4.91 nm along 〈110〉 separates the two solid surfaces interacting with the aqueous electrolyte. Such a distance is large enough to model bulk like water in the center of the slab, and to prevent interaction between the two surfaces. The liquid region with the dimensions 3.25 nm × 4.91 nm × 2.95 nm was filled with 1603 water molecules resulting in a bulk water density of about 1 g cm−3. Periodic boundary conditions were applied along 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉 and 〈001〉, and fixed boundary condition was applied in the direction normal to the interfaces. The long-range Coulombic interactions were calculated with a particle–particle particle-mesh solver. Although non-periodic along the direction normal to the interface, the slab-slab interactions are effectively turned off by considering a periodic system in all three directions with an empty volume between the slabs. The temperature was maintained constant at 298.15 K by applying a Nosé–Hoover thermostat.71,72 A time step of 1 fs was applied. Prior to the production run of 100 ns, an equilibration run of 10 ns was performed. When considering NEMD calculations, the external electric field was applied along 〈
10〉 and 〈001〉, and fixed boundary condition was applied in the direction normal to the interfaces. The long-range Coulombic interactions were calculated with a particle–particle particle-mesh solver. Although non-periodic along the direction normal to the interface, the slab-slab interactions are effectively turned off by considering a periodic system in all three directions with an empty volume between the slabs. The temperature was maintained constant at 298.15 K by applying a Nosé–Hoover thermostat.71,72 A time step of 1 fs was applied. Prior to the production run of 100 ns, an equilibration run of 10 ns was performed. When considering NEMD calculations, the external electric field was applied along 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉. An applied electric field of 0.01 V Å−1 was set.
10〉. An applied electric field of 0.01 V Å−1 was set.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Catarina Cocchi, David Starr, and Marco Favaro for inspiring discussions. The authors acknowledge support for computing facilities provided by the North-German Supercomputing Alliance (HLRN) as well as the High Performance Cluster framework by the state of Baden-Württemberg (bwHPC) and the German Research Foundation (DFG) through grant no. INST 39/963-1 FUGG (bwForCluster NEMO).Notes and references
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- X. Chen, S. Shen, L. Huo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed.
- U. Diebold, J. Chem. Phys., 2017, 147, 040901 CrossRef PubMed.
- P. Lindan, N. Harrison and M. Gillan, Phys. Rev. Lett., 1998, 80, 762–765 CrossRef CAS.
- S. Wendt, J. Matthiesen, R. Schaub, E. Vestergaard, E. Laegsgaard, F. Besenbacher and B. Hammer, Phys. Rev. Lett., 2006, 96, 066107 CrossRef CAS PubMed.
- L. Yang, D.-J. Shu, S.-C. Li and M. Wang, Phys. Chem. Chem. Phys., 2016, 18, 14833–14839 RSC.
- D. Zhang and P. Lindan, J. Chem. Phys., 2003, 118, 4620–4630 CrossRef.
- M. Predota, A. Bandura, P. Cummings, D. Kubicki, D. Wesolowski, A. Chialvo and M. Machesky, J. Phys. Chem. B, 2004, 108, 1204900 Search PubMed.
- H.-L. Wang, Z.-P. Hu and H. Li, Front. Phys., 2018, 13, 138107 CrossRef.
- C. Zhang, J. Hutter and M. Sprik, J. Phys. Chem. Lett., 2019, 10, 3871–3876 CrossRef CAS PubMed.
- L. E. Walle, A. Borg, P. Uvdal and A. Sandell, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235436 CrossRef.
- Z.-T. Wang, Y.-G. Wang, R. Mu, Y. Yoon, A. Dahal, G. Schenter, G. Glezakou, R. Rousseau, I. Lyubinetsky and Z. Dohnálek, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1801–1805 CrossRef CAS PubMed.
- C. Sun, L.-M. Liu, A. Selloni, G. Lu and S. C. Smith, J. Mater. Chem., 2010, 20, 10319–10334 RSC.
- M. Patel, G. Malia, L. Liborio and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045302 CrossRef.
- R. Schaub, P. Thostrup, N. Lopez, E. Laegsgaard, I. Stensgaard, J. Norskovm and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 266104 CrossRef CAS PubMed.
- M. Menetry, A. Markovits and C. Minot, Surf. Sci., 2003, 524, 49–62 CrossRef.
- H. Heydari, M. Elahifard and R. Behjatmanesh-Ardakani, Surf. Sci., 2019, 679, 218–224 CrossRef CAS.
- U. Martinez, L. Vilhelmsen, H. Kristoffersen, J. Stausholm-Moller and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205434 CrossRef.
- B. Lee and D. Trinkle, J. Phys. Chem. C, 2015, 119, 18203–18209 CrossRef CAS.
- T. Zheng, C. Wu, M. Chen, Y. Zhang and P. Cummings, J. Chem. Phys., 2016, 145, 044702 CrossRef PubMed.
- Z. Zhang, O. Bondarchuk, B. Kay, J. White and Z. Dohnalek, J. Phys. Chem. B, 2006, 110, 21840–21845 CrossRef CAS PubMed.
- B. Hammer, S. Wendt and F. Besenbacher, Top. Catal., 2010, 53, 423–430 CrossRef CAS.
- N. Petrik and G. Kimmel, J. Phys. Chem. C, 2015, 119, 23059–23067 CrossRef CAS.
- L. Walle, D. Ragazzon, A. Borg, P. Uvdal and A. Sandell, Surf. Sci., 2014, 621, 77–81 CrossRef CAS.
- T. Watanabe, A. Nakajima, A. Wang, M. Minabe, S. Koizumi, A. Fujishima and K. Hashimoto, Thin Solid Films, 1999, 351, 206–263 CrossRef.
- J. Yan, G. Wu, N. Guan, L. Li, Z. Li and X. Cao, Phys. Chem. Chem. Phys., 2013, 15, 10978–10988 RSC.
- D. Zhang, M. Yang and S. Dong, J. Phys. Chem. C, 2015, 119, 1451–1456 CrossRef CAS.
- M. Predota, M. Cummings and D. Wesolowski, J. Phys. Chem. C, 2007, 111, 3071–3079 CrossRef CAS.
- E. Brandt and A. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18110–18125 CrossRef CAS.
- N. English, Crystals, 2016, 6, 1–7 CrossRef CAS.
- Z. Futera and N. English, J. Phys. Chem. C, 2017, 121, 6701–6711 CrossRef CAS.
- D. Biriuokv, O. Kroutil and M. Predota, Phys. Chem. Chem. Phys., 2018, 20, 23954–23966 RSC.
- D. Biriukov, P. Fibich and M. Predota, J. Phys. Chem. C, 2020, 124, 3159–3170 CrossRef CAS.
- C. Wu, A. Skelton, M. Chen, L. Vlcek and P. Cummings, Langmuir, 2012, 28, 2799–2811 CrossRef CAS PubMed.
- M. Predota, M. Machesky and D. Wesolwski, Langmuir, 2016, 32, 10189–10198 CrossRef CAS PubMed.
- L. Huang, K. Gubbins, L. Li and X. Lu, Langmuir, 2014, 30, 14832–14840 CrossRef CAS PubMed.
- S. Malali and M. Foroutan, Appl. Surf. Sci., 2018, 467, 295–302 CrossRef.
- W. Epling, C. Peden, M. Henderson and U. Diebold, Surf. Sci., 1998, 412, 333–343 CrossRef.
- B. Morgan and G. Watson, Surf. Sci., 2007, 601, 5034–5041 CrossRef CAS.
- F. Xiao, W. Zhou, B. Sun, H. Li, P. Qiao, L. Ren, X. Zhao and H. Fu, Sci. China Mater., 2018, 61, 822–830 CrossRef CAS.
- K. Chenoweth, A. van Duin and W. I. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- L. Scalfi, M. Salanne and B. Rotenberg, Annu. Rev. Phys. Chem., 2021, 72, 189–212 CrossRef CAS PubMed.
- S.-C. Li, Z. Zhang, D. Sheppard, B. Kay, J. White, Y. Du, I. Lyubinetsky, G. Henkelman and Z. Dohnalek, J. Am. Chem. Soc., 2008, 130, 9080–9088 CrossRef CAS PubMed.
- M. Hellstrom, V. Quaranta and J. Behler, Chem. Sci., 2019, 10, 1232–1243 RSC.
- M. Raju, S.-Y. Kim, A. van Duin and K. Fichthorn, J. Phys. Chem. C, 2013, 117, 10558–10572 CrossRef CAS.
- S.-Y. Kim, N. Kumar, P. Person, J. Sofo, A. van Duin and J. Kubicki, Langmuir, 2013, 29, 7838–7846 CrossRef CAS PubMed.
- D. Bonthuis, S. Gekle and R. Netz, Phys. Rev. Lett., 2011, 107, 166102 CrossRef PubMed.
- D. Bonthuis, S. Gekle and R. Netz, Langmuir, 2012, 28, 7679–7694 CrossRef CAS PubMed.
- S. Parez, M. Predota and M. Machesky, J. Phys. Chem. C, 2014, 118, 4818–4834 CrossRef CAS.
- H.-J. Butt, K. Graf and M. Kappl, Physics and chemistry of interfaces, Wiley-CH, 2013 Search PubMed.
- C. Vega and J. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- M. Rami Reddy and M. Berkowitz, Chem. Phys. Lett., 1989, 155, 173 CrossRef.
- S. Dewan, V. Carnevale, A. Banduka, A. Eftekhari-Bafrooei, G. Fiorin, M. Klein and E. Borguet, Langmuir, 2014, 30, 8056–8065 CrossRef CAS PubMed.
- M. Reticcioli, M. Setvin, X. Hao, P. Flauger, G. Kresse, M. Schmid, U. Diebold and C. Franchin, Phys. Rev. X, 2017, 7, 031053 Search PubMed.
- J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986 CrossRef CAS PubMed.
- H. Hussain, G. Tocci, T. Woolcot, X. Torrelles, C. L. Pang, D. S. Humphrey, C. M. Yim, D. C. Grinter, G. Cabail, O. Bikondoa, R. Lindsayo, J. Zegenhagen, A. Michaelides and G. Thornton, Nat. Mater., 2017, 16, 461–467 CrossRef CAS PubMed.
- M. Fedkin, X. Zhou, J. Kubicki, A. Bandura and S. Lvov, Langmuir, 2003, 19, 3797–3804 CrossRef CAS.
- M. Predota, M. Machesky, D. Wesolowski and P. Cummings, J. Phys. Chem. C, 2013, 117, 22852–22866 CrossRef CAS.
- F. Sedlmeier, J. Janecek, C. Sendner, L. Bocquet, R. Netz and D. Horinek, Bioninterphases, 2008, 3, 23–39 CrossRef PubMed.
- P. Liu, E. Harder and B. Berne, J. Phys. Chem. B, 2004, 108, 6595–6602 CrossRef CAS.
- J. Lyklema, S. Rovillard and J. De Coninck, Langmuir, 1998, 14, 5659–5663 CrossRef CAS.
- M. Predota, Z. Zhang, P. Fenter, D. Wesolowski and P. Cummings, J. Phys. Chem. B, 2004, 108, 12061–12072 CrossRef CAS.
- S.-J. Marrink, M. Berkowitz and H. Berendsen, Langmuir, 1993, 9, 3122–3131 CrossRef CAS.
- R. Nikam, X. Xu, M. Ballauff, M. Kanduc and J. Dzubiella, Soft Matter, 2018, 14, 3400–4310 RSC.
- Z. Li, V. G. Ruiz, M. Kanduč and J. Dzubiella, Langmuir, 2020, 36, 13457–13468 CrossRef CAS PubMed.
- R. Nikam, X. Xu, M. Kanduč and J. Dzubiella, J. Phys. Chem., 2020, 153, 044904 CrossRef CAS PubMed.
- S. Monti, A. van Duin, S.-Y. Kim and V. Barone, J. Phys. Chem. C, 2012, 116, 5141–5150 CrossRef CAS.
- A. Bahramian, Fluid Phase Equilib., 2017, 438, 53–55 CrossRef CAS.
- S. Wendt, R. Schaub, J. Matthiesen, E. Vestergaard, E. Wahlstrom, M. Rasmussen, P. Thostrup, L. Molina, E. Laegsgaard, I. Stensgaard, B. Hammer and F. Besenbacher, Surf. Sci., 2005, 598, 226–245 CrossRef CAS.
- P. Kowalski, B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115410 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1697 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02043a |
| ‡ Present address: Institute of Physics, Carl von Ossietzky Universität Oldenburg, 26129 Oldenburg, Germany. |
| This journal is © the Owner Societies 2021 |