Thermally regenerative electrochemically cycled flow batteries with pH neutral electrolytes for harvesting low-grade heat
Received
5th May 2021
, Accepted 14th September 2021
First published on 15th September 2021
Abstract
Harvesting waste heat with temperatures lower than 100 °C can improve the system efficiency and reduce greenhouse gas emissions, yet it has been a longstanding and challenging task. Electrochemical methods for harvesting low-grade heat have aroused research interest in recent years due to the relatively high effective temperature coefficient of the electrolytes (>1 mV K−1) compared with the thermopower of traditional thermoelectric devices. Compared with other electrochemical devices such as the temperature-variation based thermally regenerative electrochemical cycle and temperature-difference based thermogalvanic cells, the thermally regenerative electrochemically cycled flow battery (TREC-FB) has the advantages of providing a continuous power output, decoupling the heat source and heat sink, and recuperating heat, and compatible with stacking for scaling up. However, the TREC-FB suffers from the issue of stable operation due to the challenge of pH matching between catholyte and anolyte solutions with desirable temperature coefficients. In this work, we demonstrate a pH-neutral TREC-FB based on KI/KI3 and K3Fe(CN)6/K4Fe(CN)6 as the catholyte and anolyte, respectively, with a cell temperature coefficient of 1.9 mV K−1 and a power density of 9 μW cm−2. This work also presents a comprehensive model with a coupled analysis of mass transfer and reaction kinetics in a porous electrode that can accurately capture the flow rate dependence of the power density and energy conversion efficiency. We estimate that the efficiency of the pH-neutral TREC-FB can reach nearly 9% of the Carnot efficiency at the maximum power output with a temperature difference of 37 K. Via analysis, we identify that the mass transfer overpotential inside the porous electrode and the resistance of the ion exchange membrane are the two major factors limiting the efficiency and power density, pointing to directions for future improvements.
1. Introduction
Low-grade heat sources (<100 °C) contain more than half of the global energy rejection,1 and therefore the reuse of low-grade waste heat is a promising route to improve the energy efficiency and reduce CO2 emissions. However, due to the distributed nature and the small temperature difference between the heat source and the environment, harvesting low-grade heat has always been a challenging task. In the past few years, electrochemical methods have emerged as a promising alternative to thermoelectrics for converting low-grade heat to electricity. This recent pursuit is driven by the relatively high “effective thermopower” (on the order of 1 to 10 mV K−1)2–5 compared with thermoelectric materials (∼200 μV K−1).6 Several different types of devices have been investigated,7–9 including thermionic capacitors,10,11 thermally charged batteries,12–20 vacuum distillation-concentration redox flow batteries (VD-CRFB),21,22 thermogalvanic cells,23,24 thermally regenerative electrochemical cycles (TREC)25–27 and thermally regenerative electrochemically cycled flow batteries (TREC-FB).28,29 Thermionic capacitors rely on the thermodiffusion of ions, also known as the Soret effect. Driven by a temperature gradient applied between the two electrodes, a concentration gradient of cations and anions is created. If the thermal mobilities of the cations and anions are mismatched, a net charge profile will build up, which further generates an electric field across the device. Although thermionic capacitors have shown giant Seebeck coefficients, the device cannot operate continuously. Heat conduction leakage along with the long thermal charging time has led to low efficiency (0.01%).5,30 Thermally regenerable batteries utilize electrolytes that can be regenerated using heat, including copper–ammonia batteries,12–14 copper–ethylenediamine batteries,15 and copper–acetonitrile batteries.20 The discharge power density of these thermally charged batteries can reach 10 W m−2 K−1 to 100 W m−2 K−1 and they have a high efficiency (15–30% relative to the Carnot limit). These batteries usually involve heat-facilitated dissociation of ligands as the regeneration step once the battery is fully discharged. More recently, VD-CRFBs have been developed utilizing concentration difference induced electromotive forces for energy conversion, with vacuum distillation for regenerating the concentration difference.21,22 VD-CRFBs also showed competitive power density and even higher efficiency than copper ammonia batteries. Thermogalvanic cells, on the other hand, generate electricity continuously as long as there is a temperature difference across the device. Thermogalvanic cells utilize a single redox pair while the two electrodes are kept at different temperatures. The electrode potential of a general redox reaction would depend on the temperature if the O + ne ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R entropy change is nonzero. This temperature dependence is quantified by the temperature coefficient α,4 which is related to the entropy change of the cathodic reaction:where sR and sO are the partial molar entropies of species O and R, and F the Faraday constant. The redox species at each electrode are rebalanced via ionic transport through the electrolyte, enabling thermogalvanic cells to operate continuously similar to thermoelectric devices. Yet the efficiency remained very low (∼0.8% relative to the Carnot efficiency),31 due to the undesirable heat conduction across the device32 and the low ionic conductivity compared with electrons and holes in thermoelectric materials.33
R entropy change is nonzero. This temperature dependence is quantified by the temperature coefficient α,4 which is related to the entropy change of the cathodic reaction:where sR and sO are the partial molar entropies of species O and R, and F the Faraday constant. The redox species at each electrode are rebalanced via ionic transport through the electrolyte, enabling thermogalvanic cells to operate continuously similar to thermoelectric devices. Yet the efficiency remained very low (∼0.8% relative to the Carnot efficiency),31 due to the undesirable heat conduction across the device32 and the low ionic conductivity compared with electrons and holes in thermoelectric materials.33
Compared with thermionic capacitors and thermogalvanic cells operating under a temperature gradient, the TREC is more suitable to harvest a temperature difference in the time-domain, such as the temperature change between the daytime and the nighttime.34 A TREC device is similar to a normal battery with cathode and anode materials and can operate in two modes: (1) electrically assisted,25,33 and (2) charging-free.26 In an electrically assisted device (Fig. 1a), the total temperature coefficient of the cell αCell is the difference between that of the cathode α+ and the anode α−: αCell = α+ − α−, and its sign determines the discharge and charge temperature. If αCell > 0, then the TREC battery needs to be discharged at high temperature and recharged at low temperature (Fig. 1a). The charge and discharge temperatures would be swapped for a negative αCell. In a charging-free TREC, the standard electrode potentials of the cathode and anode redox pairs at room temperature are matched such that the open-circuit voltage is close to zero.26 Either a temperature rise or decrease would generate a nonzero electromotive force, driving electrochemical reactions and generating power at both high or low temperatures. The directions of the electrochemical reactions are opposite at high and low temperatures so that the reactants are regenerated while generating power. The requirement of periodic temperature changes does not match waste heat sources, which are usually continuous. Both electrically-assisted and charging-free devices have high relative efficiency to the Carnot limit (10–30%), depending on the heat recuperating efficiency of 50–85%.25–27
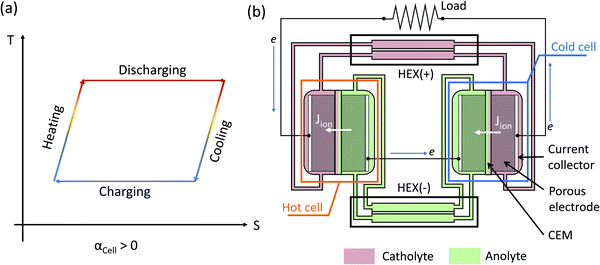 |
| | Fig. 1 (a) Temperature–entropy diagram of the thermally regenerative electrochemical cycle (TREC) for a positive temperature coefficient αCell > 0. If the temperature coefficient of the cell is negative, then the charging takes place at a higher temperature while the discharging is performed at a lower temperature. For a charging-free TREC, both high-temperature and low-temperature reactions can output power, but the directions of the electrochemical reactions are opposite. (b) Schematic of a TREC-FB with αCell > 0. The catholyte (or anolyte) is the electrolyte that is reduced (or oxidized) in the discharging cell, which is the cell operating at a higher temperature for αCell > 0. The flow direction of electrons is indicated by the blue arrow, while the ionic current (Jion) across the cation exchange membrane (CEM) is indicated by the white arrows. Two heat exchangers (HEXs) are implemented for heat recuperation of the catholyte (+) and the anolyte (−). | |
Continuous operation of the TREC can be achieved via the TREC-FB configuration.7,28 A TREC-FB device is composed of two flow batteries working at different temperatures while using pumps to circulate the electrolytes (Fig. 1b). In the example of a TRFB with a positive temperature coefficient, the flow cell at high temperature works as a galvanic cell providing current and the voltage for the cold flow cell responsible for regenerating the reactants. To ensure continuous operation, the redox-active species ideally only exist in the solution, and the electrodes only provide electrons but do not directly participate in the redox reactions. In a TREC-FB, one cell serves as a galvanic cell generating current while providing the electromotive force for the other electrolytic cell to regenerate the redox species. Therefore, the TREC-FB does not need any auxiliary power supplies. Another advantage of the TREC-FB is that heat recuperation can be easily achieved with heat exchangers to pre-heat or pre-cool the regenerated electrolytes. For example, Majumdar demonstrated that a 15% efficiency relative to the Carnot efficiency can be achieved using a TREC-FB based on V3+/V2+ and Fe(CN)63−/Fe(CN)64−.28
However, several challenges need to be resolved before the practical implementation of TRFBs, which has not received significant attention so far. The most important challenge is the difficulty in simultaneously achieving a high value of αCell while ensuring the stability of the electrolytes. Similar to the TREC, the cell temperature coefficient of a TREC-FB is calculated as αCell = α+ − α−. Ideally, achieving a high absolute value of αCell requires not only large absolute values of the temperature coefficients but also opposite signs of the temperature coefficients of the catholyte and the anolyte.
We can understand the routes to high αCell qualitatively using Born's solvation model. According to Born's solvation model,35,36 the entropy change of the reaction O + ne ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R is proportional to the change of squared valence number z2 divided by the ionic radii r:
R is proportional to the change of squared valence number z2 divided by the ionic radii r:
| |  | (2) |
where
s denotes the partial molar entropy of the oxidized species O and the reduced species R, and
F is the Faraday constant. In many redox reactions like Fe
3+ + e
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif)
Fe
2+, the change of the ionic radii is not large enough to affect the sign of
α. For cation redox pairs, the reduced ion species usually has a smaller valence value,
zO2 −
zR2 > 0, giving rise to a positive
α. In contrast, anion redox pairs usually have a negative
α according to Born's solvation model. Born's solvation model also indicates that higher valence ions with smaller radii tend to have relatively large temperature coefficients. However, another factor that needs to be simultaneously considered is the hydrolysis of these redox ions, which affects the stability of the electrolyte solution. For example, metallic cations like V
3+/V
2+ and Fe
3+/Fe
2+ are good candidates for relatively large positive temperature coefficients,
28 but these solutions are only stable in low pH environments.
37,38 Anions like Fe(CN)
63−/Fe(CN)
64−, however, are usually stable in neutral or basic environments. Such a mismatched stable range of pH greatly affects the stability of TREC-FB cells. For example, although pairing cations such as Fe
3+/Fe
2+ and V
3+/V
2+ with Fe(CN)
63−/Fe(CN)
64− can achieve a high value of |
αCell| ∼ 2.7 mV K
−1 and 3.1 mV K
−1,
28 the proton exchange across the ion exchange membrane would gradually shift the pH value on the Fe(CN)
63−/Fe(CN)
64− side, resulting in a complicated decomposition of the Fe(CN)
63−/Fe(CN)
64− ions releasing toxic CN
− once the solution becomes acidic.
39 Such cells can only operate stably until the pH buffer is consumed. In addition to the pH matching problem, it is also preferred that the redox-active species have the same sign of charges. For example, the TREC-FB based on Cu(NH
3)
42+/Cu(NH
3)
2+ and Fe(CN)
63−/Fe(CN)
64− has a high temperature coefficient |
αCell| = 2.9 mV K
−1;
29 however, the different sign of charges between the reactive ion pairs makes it difficult to find the optimal ion exchange membrane to prevent the cross-over of redox active ions.
29
In addition to the challenges of pH matching and electrolyte stability, a comprehensive analysis of coupled mass transfer and electrochemical kinetics is also lacking. For flow batteries, the steady-state current density is determined by the rate of the redox reaction at the electrode surface, which is proportional to the local concentration of redox species at the liquid–electrode interfaces.40 When the mass transfer is slow compared with the redox reaction rate, there could be a large concentration gradient near the electrode, resulting in a concentration overpotential and limiting the maximum current of the cell. When the reactants are depleted locally at the electrode surfaces, the current reaches the limiting current. Clearly, such a mass transfer process and thus the discharging current depend on the flow rate. Another factor that can limit the reaction rate is the polarization of the electrodes, which becomes important when a porous electrode is used in the battery. Consider a cathodic reaction with n electrons transferred from the electrode to the electrolyte. Charge conservation dictates that this amount of extra negative charge needs to be compensated by the ionic current (Fig. 1b). If the ionic conductivity inside the porous electrode is low, there could also be an extra irreversible potential drop as a result of charge redistribution during the relaxation at the steady state. All these kinetic processes described would result in an additional potential drop at the electrode/electrolyte interface, known as the overpotential. However, the analysis of TREC-FBs in the literature either neglected the overpotential41 or assumed an infinitely large mass transfer coefficient.28 In addition, these irreversible losses are usually coupled with the forced convection of electrolytes, dictating the flow rate-dependent power density. It is therefore necessary to comprehensively study the coupled effects of mass transfer and reaction kinetics at different flow rates for optimized performance.
Here we tackle the challenges aforementioned and demonstrated a pH neutral TREC-FB using KI/KI3 as the catholyte and K3Fe(CN)6/K4Fe(CN)6 as the anolyte with all-anionic redox-active ion pairs. The redox reaction of the catholyte between the iodide ion (I−) and triiodide ion (I3−) is a two-electron process:
| | I3− + 2e ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 3I−, E0 = 0.536 V 3I−, E0 = 0.536 V | (3) |
while the redox reaction for the anolyte is written as:
| | Fe(CN)63− + e ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Fe(CN)64−, E0 = 0.37 V Fe(CN)64−, E0 = 0.37 V | (4) |
where
E0 denotes the standard electrode potential with respect to the standard hydrogen electrode (SHE).
42,43 This pairing of electrolytes only involves anions as the redox-active species while sharing the same K
+ counterion, allowing convenient cation exchange without shifting the pH value and preventing the proton-induced decomposition of K
3Fe(CN)
6/K
4Fe(CN)
6. This pH-neutral TREC-FB has a temperature coefficient of 1.9 mV K
−1 and a maximum power density of 9 μW cm
−2 at the high limit of the flow rate. To analyze the energy conversion efficiency and factors affecting the performance of the TREC-FB, we develop a comprehensive porous electrode model for TREC-FBs, which can capture the effect of the flow rate, mass transfer, surface kinetics, and electrode polarization on the power density and efficiency. We also pinpoint the mass transfer inside the porous electrode, membrane resistance, and heat recuperation effectiveness as the key factors for improving the efficiency and power factors in the future. This model can also be applied or extended for analyzing other waste-heat recovering flow batteries.
2. Theoretical model of a TREC-FB with a porous electrode
Fig. 2 shows the geometry of the porous electrode considered in the model. For the convenience of notation, we consider a general half-cell reaction:| | νOO + ne ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) νRR νRR | (5) |
where O denotes the oxidized species and R denotes the reduced species, with n electrons transferred per unit reaction, νO and νR being the stoichiometry numbers. The electrochemical potential of the electrolyte at thermal equilibrium is determined by the concentration of reactants through the Nernst equation:| | 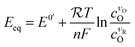 | (6) |
where  is the universal ideal gas constant, ck = Ck/C0 (k = O,R) denotes the dimensionless concentration of species against the standard concentration C0 (1 M), and
is the universal ideal gas constant, ck = Ck/C0 (k = O,R) denotes the dimensionless concentration of species against the standard concentration C0 (1 M), and  is the formal potential with γ the activity coefficients and E0 the standard electrode potential. At equilibrium, the measured electrode potential E is equal to the equilibrium potential Eeq described by the Nernst equation, which is essentially the Gibbs free energy change of the half-reaction. With a finite discharging current, the equilibrium condition is broken, resulting in an additional potential drop known as the overpotential (η = E − Eeq). At a finite current, the concentration would become nonuniform, which further affects the surface kinetics and mass transfer, resulting in a non-uniform profile of the overpotential.
is the formal potential with γ the activity coefficients and E0 the standard electrode potential. At equilibrium, the measured electrode potential E is equal to the equilibrium potential Eeq described by the Nernst equation, which is essentially the Gibbs free energy change of the half-reaction. With a finite discharging current, the equilibrium condition is broken, resulting in an additional potential drop known as the overpotential (η = E − Eeq). At a finite current, the concentration would become nonuniform, which further affects the surface kinetics and mass transfer, resulting in a non-uniform profile of the overpotential.
 |
| | Fig. 2 Schematic of the porous electrode sandwiched between the CEM and the current collector or the channel wall. The flow direction is along the x-axis. | |
This section derives a model to determine the overpotential drop inside the porous media as a combined result of mass transfer, electrode polarization, and surface reaction kinetics. Section 2.1 outlines the mass transfer inside the porous electrode. An empirical mass-transfer relation for interdigitated media is used to consider the local concentration gradient between the mean concentration and the microscopic concentration at the interface between the electrolyte and the fibers of the electrode. In Section 2.2, the extended Butler–Volmer equation and condition of charge neutrality are used as the bridges coupling the effects of local mass transfer, surface reaction kinetics, and electrode polarization. In Section 2.3, we derive the self-consistent equation for determining the discharge current and outline the evaluation of the efficiency.
2.1 Mass transfer in the porous electrode
We start deriving the TREC-FB model by considering the spatial profile of the concentration, which can be obtained by solving the continuity equation:| | 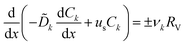 | (7) |
where RV is the rate of reaction, which takes a positive sign for the cathodic reaction, per unit volume. Eqn (7) can be obtained by integrating the two-dimensional equation of mass conservation along the y-direction, with the boundary conditions that the y-components of the ionic diffusion currents at y = 0 and y = L are zero because active species cannot penetrate across the current collector or membrane. The subscript k (= O or R) denotes the redox species, ν the stochiometric number and us the superficial velocity of the electrolyte. ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k, the effective diffusivity inside the porous electrode, can be related to the diffusivity of the bulk solution Dk through
k, the effective diffusivity inside the porous electrode, can be related to the diffusivity of the bulk solution Dk through  , where ε is the porosity and
, where ε is the porosity and  the tortuosity factor of the porous media. The sign of the source term takes + when k = O and − when k = R. By nondimensionalizing the concentration ck = Ck/C0 and the coordinate X = x/L with L the electrode length, eqn (7) can be written as:
the tortuosity factor of the porous media. The sign of the source term takes + when k = O and − when k = R. By nondimensionalizing the concentration ck = Ck/C0 and the coordinate X = x/L with L the electrode length, eqn (7) can be written as:| |  | (8) |
where Pek = usL/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k is the Peclet number of species k and ġk is the normalized rate of generating species k inside the porous electrode:
k is the Peclet number of species k and ġk is the normalized rate of generating species k inside the porous electrode:| |  | (9) |
The concentration profile can be solved analytically with the boundary condition ck(X = 0) = ck0 and  :
:| |  | (10) |
In TREC flow batteries, the superficial velocity of the electrolyte is on the order of 0.1–1 mm s−1, yielding a large Peclet number 103–104, and therefore the mean concentration profile is approximately linear along the flow direction.
At steady-state, the rate of consuming and generating reactants should also be balanced with the flux of reactants from the bulk solution to the electrode surface, and therefore:
| |  | (11) |
where

and

are the mass transfer coefficient,
CsO,R is the mean concentration at the surface of the electrode, and
Ae is the specific electrode area per unit volume, determined by the porosity
ε and fiber diameter
df as
Ae = 4(1 −
ε)/
df.
44 The dimensionless form of
eqn (11) can be written as:
| | | −ζġO = ShO(cO − csO), ζġR = ShR(cR − csR) | (12) |
where

is the Sherwood number of mass transfer,
dH is the hydrodynamic diameter for the porous media, calculated as

, and
ζ =
dH/
AeL2 is a geometric factor of the porous electrode.
45 Mass transfer inside the porous electrode is modeled by the correlation developed by Kinoshita
et al. for flow-through felt electrodes:
46where Re =
ρusdH/
εμ is the Reynolds number.
2.2 Overpotential and current density
This section discusses the modeling of overpotential loss inside the porous electrode. While discharging, mass transfer and surface reaction kinetics dictate that the concentrations of active species at the electrode surface will be different from the mean concentrations outside the mass transfer boundary layer. A local overpotential profile η(x,y) = E(x,y) − Eeq(x) will thus be developed, and it is related to the local current density and surface concentration of reactants through the extended Butler–Volmer equation:| |  | (14) |
where αS is the symmetry factor of the excitation energy barrier, and  is the exchange current density with k0(T) the rate constant calculated through the Arrhenius law:
is the exchange current density with k0(T) the rate constant calculated through the Arrhenius law:| | 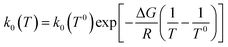 | (15) |
Eqn (14) converges to the original Butler–Volmer equation when CSO = CO and CsR = CR:| |  | (16) |
which is valid when the mass transfer coefficients approach infinity (Sh → ∞).
The current density J is evaluated per unit electrode surface area, and can be related to the volumetric reaction rate through charge balance across the electrode/electrolyte interface:
The charge balance condition in the electrolyte should also be considered along the normal direction to the membrane (
y-axis). For each mole of cathodic reaction happening, the amount of negative charges transferred to the electrolyte is
nFRV per unit volume, which needs to be balanced with the ionic current:
| |  | (18) |
where
ϕl is the local galvanic potential of the liquid phase, and
σeff is the effective ionic conductivity of the electrolyte inside the porous media, estimated as

. Note that
ϕl is regarded as a local mean potential of the liquid electrolyte of a mesoscopic local pore, outside the electric double layer. Namely, the microscopic details of ion transport at the electrode–electrolyte interface are not included in
eqn (18). The approximate equality in
eqn (18) can be made due to the following reasons. The divergence of the ionic current can be expressed as

, since the
x-derivatives are negligible with the length of the electrode much larger than the thickness. Through simple dimensional analysis, the ratio between the ionic conduction current and diffusion current is roughly
ziFϕl/
RTDi, on the order of 10
7, and the ratio between the conduction current and convection current is roughly
zi2Fϕl/
RTvs also on the order of 10
2 due to the slow velocity on the order of 0.1 mm s
−1, and hence it is a fair approximation that the divergence of the ionic current can be estimated by Ohm's law, and
eqn (18) holds.
Now we show that eqn (18) can be related to local overpotential η. At each point (x,y), the local overpotential can be written as η = E − Eeq = ϕs − ϕl − Eeq. The very large electrical conductivity of the electrode makes ϕs approximately uniform in the y-direction. Eeq can also be approximated as uniform due to the small variation of the concentration in the y-direction. Hence, we have 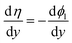 , and eqn (18) becomes
, and eqn (18) becomes
| |  | (19) |
This approximation is also usually adopted in other work modeling vanadium redox flow batteries.
47 Together with
eqn (11), (14), (17) and (19), we can obtain an ordinary differential equation (ODE) describing the electrode polarization:
| |  | (20) |
Using the nondimensionalized coordinate Y = y/H with H the thickness of the porous electrode, and the nondimensionalized overpotential 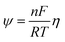 , we can derive the following equivalent ODE:
, we can derive the following equivalent ODE:
| |  | (21) |
where

is the dimensionless exchange current, with
J00 =
nFk0C0. Da
k is the Damköhler number characterizing the ratio between the reaction rate and the mass diffusion rate, defined as Da
k =
k0AeL2/
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k
k.
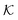
is the dimensionless conductivity
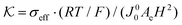
, which can be interpreted as the ratio of the conduction current driven by the “thermal voltage”
RT/
F to the exchange current
J00 at standard concentration. The dimensionless ODE (
eqn (21)) clearly shows that the overpotential is a combined result of mass transfer quantified by the Sherwood number Sh and reaction kinetics characterized by the Damköhler number Da, and the activities of redox species
cO and
cR.
Finally, we consider the boundary conditions for solving the overpotential. At y = H, the ionic current across the membrane should equal the discharging current of the cell, and at y = 0, where the electrode is in contact with either the current collector or the wall of the flow channel, the ionic current should be zero. The boundary condition for solving eqn (20) or (21) can therefore be written as:
| |  | (22) |
where
icell is the discharging current of the TREC-FB and the apparent
A is the electrode area.
For each location x along the flow direction, we solve the ODE (eqn (20)) using the boundary value problem solver bvp4c of Matlab to obtain the overpotential profile η(x,y). In this work, we assume that the electrode is conductive enough and neglect the electric potential variation in the solid phase, and hence the final measured overpotential drop inside the electrode is then taken as the mean value across the entire electrode domain.48 Similarly, the electrochemical potential E(x) of the electrolyte is calculated with the local concentrations CO(x) and CR(x), and we take the electrode potential as the mean value of E(x).48 Rigorously, a full set two-dimensional model coupling hydrodynamics, mass transfer, and electrode polarization should be solved, but we shall see later that the mean-field approach taken in our modeling can already achieve reasonable agreement with experiments and capture the coupled effects of mass transfer, electrochemical kinetics, and electrode polarization.
2.3 Self-consistent solution of the discharging current
After discussing the mass transfer and the overpotential inside the electrolyte, we now solve the total current that can be extracted from the cell. We first consider the discharging cell operating at T1, with the electrode potential of the cathode (+) and the anode (−) expressed as:| | | E±(T1) = E(T0) + α±(T1 − T0) | (23) |
For convenience, the solution to the ODE of the overpotential (eqn (20)) is denoted as η = f(RV), and then the overpotential at the two electrodes for the discharging cell can be written as:| |  | (24) |
where the subscript 1 indicates the discharging cell operating at T1,  the volume of the porous electrode, and n± the electron transfer number for the redox reaction of the catholyte (+) and anolyte (−) correspondingly. The anode will adopt a negative sign when computing the volumetric reaction rate because we define the cathodic reaction as the positive direction. We now clarify how the function f mapping the reaction rate to the overpotential in eqn (24) is constructed. First, the solution is taking a mean-field treatment of the reaction rate
the volume of the porous electrode, and n± the electron transfer number for the redox reaction of the catholyte (+) and anolyte (−) correspondingly. The anode will adopt a negative sign when computing the volumetric reaction rate because we define the cathodic reaction as the positive direction. We now clarify how the function f mapping the reaction rate to the overpotential in eqn (24) is constructed. First, the solution is taking a mean-field treatment of the reaction rate  at each point x along the flow direction, because it is challenging to inversely solve the full profile of J(x,y) with the total current icell. Such a mean-field treatment of
at each point x along the flow direction, because it is challenging to inversely solve the full profile of J(x,y) with the total current icell. Such a mean-field treatment of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) V made it possible to extract the overpotential from eqn (20) and the boundary conditions in eqn (22). At each point x along the flow direction, the overpotential profile as a function of y is solved, and the final measured overpotential η± is taken as the average value of η(x,y) inside the electrode domain.48 In this way, we constructed the function f relating the total current to the overpotential.
V made it possible to extract the overpotential from eqn (20) and the boundary conditions in eqn (22). At each point x along the flow direction, the overpotential profile as a function of y is solved, and the final measured overpotential η± is taken as the average value of η(x,y) inside the electrode domain.48 In this way, we constructed the function f relating the total current to the overpotential.
At a finite discharging current, the voltage for the discharging cell (V1) is therefore
| | | V1(icell) = Voc(T0) + αCell(T1 − T0) − (η1+ − η1−) − icell·Rin | (25) |
where
Voc(
T0) =
E+(
T0) −
E−(
T0) is the open-circuit voltage at the reference temperature, and
Rin =
Rmem +
RΩ is the internal resistance as a combination of the membrane resistance
Rmem and electrical ohmic resistance
RΩ of the electrode and current collector. Note here that we did not lump the overpotential into the internal resistance, since the overpotential loss depends on the discharging current and cannot be simply understood as a resistive component. From the extended Butler–Volmer equation, the sign of the overpotential is the same as the sign of the current and
RV, and thereby
η1− < 0, and the total overpotential for the cell is positive (
η1+ −
η1−) > 0.
The voltage of the charging cell operating at T2 can be computed in the same manner by simply replacing icell→ −icell, because all the chemical reactions are opposite to the discharging cell. The overpotential for the cathode and the anode is:
| |  | (26) |
The voltage of the charging cell at a finite current is:
| | | V2(icell) = Voc(T0) + αcell(T2 − T0) − (η2+ − η2−) + icellRin | (27) |
With the overpotential of all electrodes of the hot and the cold cells, the measured potential for the full TREC-FB can be derived:
| | | V(icell) = V1 − V2 = αCell(T1 − T2) − ηtot(icell) − 2icellRin | (28) |
where
ηtot(
icell) = (
η1+ −
η1−) − (
η2+ −
η2−) is the total overpotential drop of the TREC-FB. Similarly, (
η2+ −
η2−) < 0 and hence the total overpotential drop is positive. In addition, the current is also determined by the load
Rload in the external circuit, and hence the current can be determined by the following equation:
| | 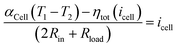 | (29) |
Eqn (29) can be solved self-consistently using a minimization solver of Matlab. Nonetheless, such a mean-field treatment is approximately reasonable as the discharging current is mass-transfer limited, far from depleting the redox-active species. The efficiency
ηE of the TREC-FB system can be determined as:
49| |  | (30) |
where
Ċj =
ρjcp,jQj is the heat capacity rate of the electrolyte
j, with
ρ,
cp, and
Q the density, specific heat and volumetric flow rate, respectively,
εHX,j is the effectiveness of heat recuperation for the electrolyte
j, and
TH = max[
T1,
T2] is the hot cell temperature. The effectiveness of the heat exchangers can be evaluated by the number of transfer units (NTU). Given the heat transfer coefficient of
U, the area
AHX, and the heat capacity rate
Ċ, the NTU is calculated as NTU =
UAHX/
Ċ. The heat recuperation effectiveness is then calculated by
εHX = NTU/(1 + NTU) when the two fluids have similar flow rates. The pump work
Wpump = Δ
p·(
Q+ +
Q−), where Δ
p, the pressure drop along the flow direction inside the porous media, is estimated using the Ergun equation:
50| | 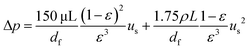 | (31) |
where
μ is the dynamic viscosity of the electrolytes. In our work, the flow rate across the cell is small and the pump work is negligible compared with the output power of the TREC-FB. Besides, the free energy term |
αcell|
icell·
TH and the Joule heating term
icell2Rin are both negligible compared with the heat absorbed by the electrolytes at the current level of a few mA in this work, and hence the relation for the energy efficiency can be simplified as:
| |  | (32) |
In addition to the commonly used energy efficiency ηE and electrode area based power density P, there are also other performance metrics for low-grade harvesting devices, including the efficiency  without heat recuperation, and the power density PHX normalized by the heat exchanger area, as recently proposed by Brogioli and La Mantia.9
without heat recuperation, and the power density PHX normalized by the heat exchanger area, as recently proposed by Brogioli and La Mantia.9 evaluates the intrinsic efficiency, which can be regarded as the baseline without any heat recuperation for improvement. The power density PHX, on the other hand, captures the trade-off between higher efficiency ηE through recuperation, and the penalty due to the larger amount of heat exchange area required. In this work, we will also adopt these indices to provide insights for performance evaluation of the TREC-FB.
evaluates the intrinsic efficiency, which can be regarded as the baseline without any heat recuperation for improvement. The power density PHX, on the other hand, captures the trade-off between higher efficiency ηE through recuperation, and the penalty due to the larger amount of heat exchange area required. In this work, we will also adopt these indices to provide insights for performance evaluation of the TREC-FB.
It is also helpful to establish simple relations between the performance indices ηE,  , and PHX and the temperature drops across the device components. By setting the recuperation effectiveness εHX to zero, we can relate ηE with the intrinsic efficiency
, and PHX and the temperature drops across the device components. By setting the recuperation effectiveness εHX to zero, we can relate ηE with the intrinsic efficiency  :
:
| | 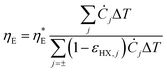 | (33) |
Since the catholyte and the anolyte have similar specific heat, viscosity, and flow rates, we can regard the heat exchangers as having similar effectiveness, and hence we can obtain:
| | 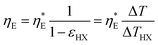 | (34) |
where Δ
THX is the log-mean temperature difference (LMTD) across the counterflow heat exchanger, calculated as Δ
THX = Δ
T/(NTU + 1). In our experiment, we keep the flow cell and the reservoir at the same temperature, but practical implementation usually uses external heat exchangers to couple the device with the reservoirs. In this case, there will be a total temperature drop Δ
T1 from the device to the two reservoirs, and then we will arrive at a simple relation describing the efficiency improvement as a function of temperature drops:
| |  | (35) |
Eqn (35) is similar to the equation

derived by Brogioli and La Mantia (eqn (16) of ref.
9) with Δ
T* = 0. Δ
T* is regarded as the intrinsic temperature difference across a single energy conversion effect. In the TREC-FB considered in this work, both the hot and the cold battery are operating at thermal equilibrium, and the electrolytes entering and leaving the flow cells have the same temperatures, and hence Δ
T* is indeed zero.
Using the expression for heat exchanger power qHX = εHXĊtotΔT = UAHXΔT and eqn (32), we can obtain the power density PHX:
| | | PHX = V(icell)·icell/AHX = ηEUΔTHX(1 − εHX)/εHX | (36) |
where
U is the heat transfer coefficient of the heat exchanger. By expressing the effectiveness as the NTU, together with
eqn (35), we can obtain:
| |  | (37) |
This expression is again aligned with eqn (17) of ref.
9 but with Δ
T* = 0.
Eqn (35) and (37) give a simple evaluation of
ηE and
PHX parametrically with the LMTD across the heat exchanger, once the intrinsic efficiency

is known.
The porous electrode model of TREC-FBs presented here will be used to comprehensively analyze the factors and sources limiting the power density and efficiency in the following sections, including operating factors such as flow rates, heat recuperation effectiveness, and temperature differences, as well as electrolyte and electrode properties such as rate constants and ionic conductivities.
3. Experimental implementation of the TREC-FB
In this section, we describe the experimental details of the TREC-FB testing system. As shown in Fig. 3(a) and (b), the testing system was composed of two flow batteries, two heat exchangers, and a heating box for temperature control. As shown in Fig. 3b, the heating box chamber was built with pink insulation foam and filled with extra ceramic fiber insulation blankets at the top, the bottom, and the backside walls. Heating was performed with a coil heater and a heating plate placed at the bottom of the box. The heating plate consisted of an OMEGA silicone fiberglass heater attached to a piece of aluminum plate. The coil heater and the heating plate were connected in parallel to a programmable power supply (BK precision 9130). A thermocouple was suspended in the chamber to monitor the temperature. Temperature control was achieved via a home-built PID model through LABVIEW.
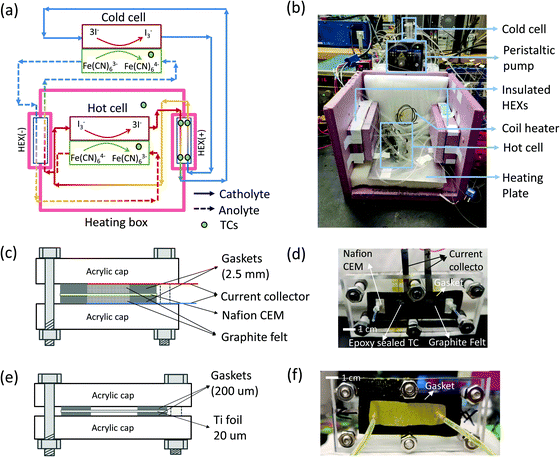 |
| | Fig. 3 TREC-FB experimental testing system. (a) Schematic of the testing system, with the temperature difference between the hot cell and cold cell achieved by a heating box chamber made with thermal insulation foam. (b) Picture of the dissembled heating box chamber showing the structure of the temperature control system. (c) The schematic structure (not to scale) of the flow battery. Two acrylic caps were used as the structure host. The flow channel was created by silicone gaskets and filled with graphite felt as the porous electrode. A Nafion cation exchange membrane (CEM) was sandwiched between the gaskets and porous electrodes to separate the catholyte and anolyte. (d) The picture of the flow battery assembly. An epoxy sealed thermocouple was also inserted into the flow channel to monitor the temperature of the electrolyte. (e) The schematic structure (not to scale) and (f) the picture of the planar heat exchanger. | |
Fig. 3(c) and (d) show the assembly of the flow cell, with the flow channels created by cutting silicone gaskets (2.5 mm thick) filled with graphite felt (AvCarb® G200, with fiber diameter ∼10 μm)51 as the porous electrode. The graphite felt was cut into dimensions of 1.3 cm × 6 cm × 2.5 mm to fit into the flow channel. To improve the hydrophilicity, the graphite felt was heated up to 400 °C in ambient conditions for 24 hours. A Nafion 115 cation exchange membrane was used as the separator between the catholyte and the anolyte to prevent cross-over of negatively charged redox species and short-circuiting. Each porous electrode was in contact with a strip of titanium foil (grade II, 20 μm) as the current collector. A thermocouple coated with epoxy was embedded in the flow channel of the anolyte Fe(CN)63−/Fe(CN)63− to monitor the temperature of the cells. We did not embed the thermocouple into the channel of I3/I− solutions, because the dissolved iodine could penetrate through the thin layer of epoxy coating and corrode the thermocouple junction. The gaskets, electrodes, and membranes were compressed with two pieces of acrylic plate. The heat exchangers were assembled similarly as shown in Fig. 3(e) and (f). At relatively high flow rates (Q = 340 μL min−1), the heat exchanger had a reasonable effectiveness of 90%, calculated from the temperature readings of the four thermocouples embedded inside the flow channels of the heat exchangers. For laminar flow across a narrow gap (2 cm by 200 μm) with one surface insulated, the Nusselt number is approximately a constant ∼5.3.52 The convection heat transfer coefficient h can therefore be estimated as  , with kl the thermal conductivity of the liquid, ∼0.6 W m−1 K−1 of water, and dH the hydraulic diameter of the narrow gap. With 20 μm thick Ti foil as the heat exchanger surface (kTi = 17 W m−1 K−1), the overall heat transfer coefficient U = (2/h + dTi/kTi)−1 = 3996 W m−2 K−1. In this work, the dimension of the heat exchange surface 1.5 cm by 5 cm ensures a high theoretical effectiveness of 99% using the NTU method. Due to the small thermal mass, the heat loss across the tube walls was significant, especially at smaller flow rates even when insulation foam is applied. However, this issue of insulation will be not as severe when the flow rates are scaled up to the order of mL min−1. Therefore, we assume a recuperation effectiveness of 90% to estimate the energy conversion efficiency ηE.
, with kl the thermal conductivity of the liquid, ∼0.6 W m−1 K−1 of water, and dH the hydraulic diameter of the narrow gap. With 20 μm thick Ti foil as the heat exchanger surface (kTi = 17 W m−1 K−1), the overall heat transfer coefficient U = (2/h + dTi/kTi)−1 = 3996 W m−2 K−1. In this work, the dimension of the heat exchange surface 1.5 cm by 5 cm ensures a high theoretical effectiveness of 99% using the NTU method. Due to the small thermal mass, the heat loss across the tube walls was significant, especially at smaller flow rates even when insulation foam is applied. However, this issue of insulation will be not as severe when the flow rates are scaled up to the order of mL min−1. Therefore, we assume a recuperation effectiveness of 90% to estimate the energy conversion efficiency ηE.
A peristaltic pump was used to inject the electrolytes into the flow cells. The anolyte solution contained 0.375 M K3Fe(CN)6 and 0.375 M K4Fe(CN)6 and the catholyte solution contained 0.1 M KI3 and 1 M KI. The catholyte solution was prepared by dissolving 0.1 M iodine (I2) into 1.1 M KI solution. Both the catholyte and anolyte are stable near neutral pH and can be paired without the pH buffer solutions. In addition, the active ions of both solutions are anionic, and therefore can be well separated using a cation exchange membrane.
We used a potentiostat (BioLogic VSP-300) to characterize the cell temperature coefficient αCell, open-circuit voltage and the discharging performance. The current collectors of the anodes (Fe(CN)63−/Fe(CN)63−) of the two cells were connected by a wire, and the current collector of the cathode (I3−/I−) of the hot cell was connected with the working electrode terminal of the potentiostat, and the other cathode of the cold cell served as the counter and reference electrode. Before heating, we maintained the system at room temperature for nearly 20 minutes for equilibration of the temperature and the relaxation of the initial built-in voltage. Then we increased the temperature in a stepwise manner and recorded the open-circuit voltage as shown in Fig. 4a. By linear regression, the cell temperature coefficient was extracted as αcell = 1.9 mV K−1 (Fig. 4b), with only slight deviations from the measurement done by Yu's group due to the difference of electrolyte concentrations.34
 |
| | Fig. 4 Temperature coefficient measurement of the TREC-FB using 0.1 M I2/1 M KI as the catholyte, and 0.375 M K3Fe(CN)6/0.375 M K4Fe(CN)6 as the anolyte. (a) Open circuit voltage (OCV) and temperature difference (ΔT) as a function of time. The vertical black arrow indicates the start time of heating. (b) Temperature coefficient extracted by linear fitting to the relation between the OCV and ΔT. The obtained temperature coefficient of the cell is αcell = 1.9 mV K−1. | |
4. Results and analysis of performance
This section discusses the experimental results of the flow rate-dependent discharging performance of the TREC-FB cell, together with the theoretical analysis pointing to the factors limiting the efficiency and power density. We first discuss the flow-rate dependence of P by comparing the measurement and prediction results. Through analysis using the model with coupled mass transfer and electrochemical kinetics, we identify mass transfer as the bottleneck limiting the power density P and efficiency. We then discuss the heat exchanger size dependence of the metric PHX and comparing with other low-grade heat harvesting techniques.
In Fig. 5a and b, we first compared the measured flow rate dependent voltage and power density Pm at ΔT = 37 °C as a function of discharging current with the modeling results. Good agreement is achieved between the predicted and measured discharging behavior, indicating that our model accurately captures the coupled effect mass transfer, electrode polarization, and reaction kinetics, which has been ignored in previous work. The parameters for the model prediction are summarized in Table 1. Only two parameters, the internal cell resistance Rin = 7.25 Ω and the tortuosity factor 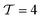 of the media, were fit from the data obtained at 230 μL min−1 (Re ≈ 3 × 10−3). This obtained tortuosity factor agreed reasonably with the literature values of graphite felts around 5.44 For other flow rates tested, we fixed these parameters and directly computed the results as plotted in Fig. 5. In general, the mass transfer overpotential was larger at lower Reynolds numbers and flow rates, thus decreasing the power density. However, the extra amount of heat needed to increase the temperature of the electrolyte also decreased at a smaller flow rate and the efficiency ηE increased at a smaller flow rate (Fig. 5c). We estimated that 9% of ηCarnot can be achieved at 1 μL min−1 at the maximum power output, while the power density can approach 9.5 μW cm−2 at 0.5 mL min−1. To eliminate the effect of the heat exchanger, we have also estimated the intrinsic efficiency
of the media, were fit from the data obtained at 230 μL min−1 (Re ≈ 3 × 10−3). This obtained tortuosity factor agreed reasonably with the literature values of graphite felts around 5.44 For other flow rates tested, we fixed these parameters and directly computed the results as plotted in Fig. 5. In general, the mass transfer overpotential was larger at lower Reynolds numbers and flow rates, thus decreasing the power density. However, the extra amount of heat needed to increase the temperature of the electrolyte also decreased at a smaller flow rate and the efficiency ηE increased at a smaller flow rate (Fig. 5c). We estimated that 9% of ηCarnot can be achieved at 1 μL min−1 at the maximum power output, while the power density can approach 9.5 μW cm−2 at 0.5 mL min−1. To eliminate the effect of the heat exchanger, we have also estimated the intrinsic efficiency  without heat recuperation. At a low flow rate of 1 μL min−1,
without heat recuperation. At a low flow rate of 1 μL min−1, 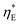 is approximately 1% relative to the Carnot efficiency. In general, simply choosing the operating conditions (temperature difference ΔT and flow rate Q) of the TREC-FB cell cannot simultaneously optimize the power density and efficiency. Fig. 6a and b show the map of the peak power density and the corresponding efficiency as a function of the temperature difference and flow rate. Although increasing temperature differences could simultaneously improve the efficiency and power density, the effect of the flow rate on the power density and efficiency is opposite with nonperfect heat recuperation.
is approximately 1% relative to the Carnot efficiency. In general, simply choosing the operating conditions (temperature difference ΔT and flow rate Q) of the TREC-FB cell cannot simultaneously optimize the power density and efficiency. Fig. 6a and b show the map of the peak power density and the corresponding efficiency as a function of the temperature difference and flow rate. Although increasing temperature differences could simultaneously improve the efficiency and power density, the effect of the flow rate on the power density and efficiency is opposite with nonperfect heat recuperation.
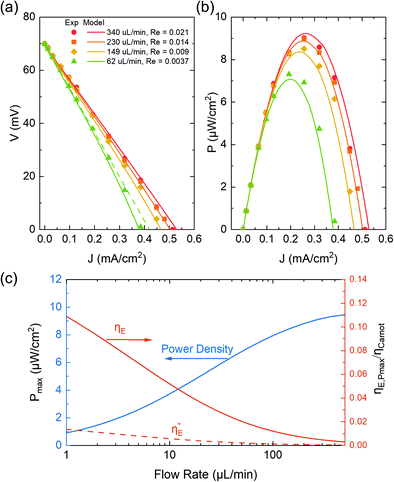 |
| | Fig. 5 (a) Voltage and (b) areal power density as functions of discharge current J at ΔT = 37 °C, with the hot cell kept at 60 °C and the cold cell left at ambient temperature (23 °C). The symbols represent the experimental results and the solid lines are the modeling results. At a small flow rate (62 μL min−1), the current-dependent discharging voltage deviated from the linear relationship as indicated by the dashed green line. (c) The trade-off between the maximum power density and maximum relative efficiency ηE/ηCarnot (on an absolute scale from 0 to 1) as a function of flow rate. The dashed red line indicates the intrinsic efficiency  without any heat recuperation. without any heat recuperation. | |
Table 1 Summary of the parameters used for the theoretical model
| Parameters |
Values |
Reference or method |
| Internal resistance (Rin) |
7.25 Ω |
Fitted to the discharging curve |
| Porosity (ε) |
95% |
Ref. 61 |
Tortuosity ( ) ) |
4.0 |
Fitted to the discharging curve |
| Fiber diameter (df) |
10 μm |
Ref. 51 |
| Density of the catholyte (ρ+) |
1191 kg m−3 |
Measured |
| Density of the anolyte (ρ−) |
1282 kg m−3 |
Measured |
| Kinematic viscosity (ν) |
8 × 10−7 m2 s−1 |
Ref. 52 |
| Diffusivity of KI3 (DO,+) |
7.0 × 10−10 m2 s−1 |
Ref. 34 |
| Diffusivity of KI (DR,+) |
5.4 × 10−9 m2 s−1 |
Ref. 34 |
| Diffusivity of K3Fe(CN)6 (DO,−) |
7.6 × 10−10 m2 s−1 |
Ref. 34 |
| Diffusivity of K4Fe(CN)6 (DR,−) |
6.9 × 10−10 m2 s−1 |
Ref. 34 |
| Rate constant of I3−/I− (k0,+) |
6.7 × 10−5 m s−1 |
Ref. 34 |
| Rate constant of Fe(CN)63−/4− (k0,−) |
0.75 × 10−5 m s−1 |
Ref. 34 |
 |
| | Fig. 6 Map of the (a) power density and (b) absolute efficiency (on an absolute scale) as a function of the temperature difference and flow rate, with the heat recuperation effectiveness fixed at 90%. | |
The effectiveness of heat recuperation is pivotal to improving the energy efficiency of TREC-FB systems. Fig. 7a and b show the map of absolute ηE,Pmax and relative efficiency ηE,Pmax/ηCarnot at the maximum power density, as a function of temperature difference ΔT and heat recuperation effectiveness εHX. Fig. 7b also highlights that the relative efficiency is very sensitive to the heat recuperation effectiveness, especially in the range εHX > 95%. With perfect recuperation, the relative efficiency could reach 50%, but decreases fast below 15% with an εHX of 95%.
 |
| | Fig. 7 (a) Absolute and (b) relative efficiency map on an absolute scale (from 0 to 1) at the maximum power density as a function of heat recuperation effectiveness and temperature difference. The flow rate is fixed at 4 μL min−1 and the cold cell temperature is fixed at TC = 300 K. | |
We further evaluate the effect of heat exchange area AHX on the device efficiency ηE and the power density PHX. Fig. 8a shows the effect of the heat exchanger size on PHX, εHX, ΔTHX and energy efficiency ηE, at a flow rate of 100 μL min−1. A clear trade-off between the efficiency ηE and the power density PHX can be observed with increased AHX. Since the TREC-FB is operating at low-flow rates, the heat exchanger effectiveness can easily reach 90% when AHX is more than a few percent of the electrode area. Given ΔTHX = 5 K as shown in Fig. 8a, PHX and εHX are estimated to be 5.76 W m−2 and 86.5%, respectively. The scaled efficiency ηE/ηCarnot is 0.9% relative to the Carnot limit. Fig. 8b summarizes the flow-rate dependence in the PHX−ηE plot, compared with other techniques in the literature. With increased flow rate, the efficiency decreased because of the larger amount of heat needed to increase the temperature of the electrolytes. PHX also decreased with increased flow rate, because the heat exchanger area needed to keep ΔTHX = 5 K also becomes larger. In Fig. 8b, we also present the flow-rate dependence of the PHX−ηE curve by assuming a fixed LMTD across the heat exchanger ΔTHX = 5 K. Although the power density P of the TREC-FB is higher than TREC systems, it remains uncompetitive compared with other low-grade heat harvesting techniques. In the following discussions, we analyze the bottlenecks for the performance of the TREC-FB.
 |
| | Fig. 8 (a) Effect of the heat exchanger area on the relative efficiency ηE/ηCarnot, power density PHX and recuperation effectiveness εHX. The operating condition of the heat exchanger can be specified by assigning either LMTD ΔTHX or effectiveness εHX. (b) Comparison between the TREC-FB and other techniques. The labels Q300, Q100, Q50, Q10, and Q5 indicate a performance flow rate of 300, 100, 50, 10 and 5 μL min−1, respectively. (c) Power density and efficiency of the TREC-FB as a function of flow rate, compared with other techniques. The efficiency is evaluated at ΔTHX = 5 K. Other literature: thermogalvanic cells (TEC),24,53 thermally regenerative electrochemical cycles (TREC),25–27 vacuum distillation-concentration redox flow battery (VD-CRFB),21,22 vacuum distillation/membrane distillation-reverse electrodialysis (VD/MD-RED),54,55 thermolysis-reverse electrodialysis (TL-RED),56 vacuum distillation/membrane distillation-pressure retarded osmosis (VD/MD-PRO),57,58 thermo-osmosis energy conversion (TOEC),59 and thermally charged batteries including thermally regenerative ammonia batteries (TRAB),12–19 and thermally regenerative copper acetonitrile batteries (CuACN).20 | |
To provide insights for future improvement of the power density and higher efficiency, it is important to understand the factors contributing to the overpotential as an irreversible loss. Such an irreversible loss is especially important when the flow rate is small, manifested in the clear deviation of the voltage drop from the linear voltage–current (V–J) relation at a large discharge current (Fig. 5a). Such a nonlinear V–J curve would result in lower thermodynamic efficiency. By pushing the effective ionic conductivity of the porous electrode σeff → ∞, the nonlinearity of the V–J curve is eliminated. This loss due to the finite ionic conductivity inside the porous electrode is referred to as electrode polarization, as shown in Fig. 9a. The major factor limiting both the power density and the efficiency is the mass transfer-induced overpotential. By further pushing the Sherwood number to infinity, the relative efficiency can increase almost two-fold from 7.5% to 14% (Fig. 9b). Such analysis also shows that optimizing the electrochemical kinetics at the electrode might show negligible improvement in the TRFB performances if the other factors such as mass transfer become the dominant bottleneck.
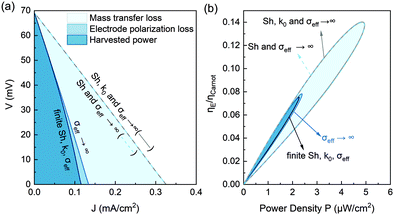 |
| | Fig. 9 (a) Effect of the mass transfer overpotential loss and electrode polarization loss on the discharging voltage (V)–current (J) relation. The model is not sensitive to the electrochemical rate constant in the range of k0 > 0.75 × 10−5 m s−1. The discharging curve is almost unchanged by further letting the rate constant approach k0 → ∞, based on the discharge curve at the nonpolarized and infinite mass transfer limit (Sh → ∞, σeff → ∞). (b) The corresponding relative efficiency versus power density. The efficiency is estimated assuming 90% heat recuperation effectiveness. This figure is estimated at a flow rate of 4 μL min−1 and a temperature difference of ΔT = 37 °C. | |
Finally, the internal resistance (Rin) of the TRFB cells is also a major factor contributing to the loss, which is composed of the electrical ohmic resistance and the membrane resistance. The electrical resistance of the porous electrode and the contact resistance between the current collector and the electrode should not be the major contribution to Rin. We characterized the total electrical Ohmic resistance (RΩ) by measuring the resistance of the cell assembly without the Nafion membrane, showing that the electrical Ohmic resistance is ∼3 Ω. The contact resistance could be further reduced by applying compression to the porous electrode. Since the Nafion membrane has a relatively low ionic conductivity of K+ (3.3 × 10−4 S cm−1),60 the membrane resistance Rmem was estimated to be ∼5 Ω. Adding Rmem and RΩ together, Rin of a single cell was estimated to be around 8 Ω, agreeing with Rin obtained by fitting the experimental discharging curves in Table 1. The fitted Rin value was slightly smaller, which might be attributed to the fact that the electrodes were wetted by the electrolytes, and ionic conduction contributed to the extra conductance. If the membrane conductivity of K+ can be improved close to that of protons H+ (7.8 × 10−2 S cm−1), then the membrane resistance would become negligible compared with the electrical Ohmic resistance. In this case, the power density at high flow rates (340 μL min−1) can increase two-fold from 9 μW cm−2 to 18 μW cm−2. However, the membrane resistance would have a smaller effect at low flow rates due to the limitation of the mass transfer. At a flow rate of 4 μL min−1, the corresponding relative efficiency could be improved from 7.8% to 8.3%, while the power density increased by 14% from 2.2 μW cm−2 to 2.5 μW cm−2. Currently, the power density of the TREC-FB as a continuous heat engine is still too small for practical application. Compared with other techniques for harvesting low-grade heat ($4–6 per Watt), the low power density of the TREC-FB and the high cost of the cation exchange membrane ($500 m−2) prohibit its implementation, especially on a large scale. Developing a membrane-free TREC-FB and improving the temperature coefficients could be effective future routes to reduce the cost per unit power.
5. Conclusions
In summary, we demonstrate a prototype of an all-anionic thermally regenerative flow battery operated with pH-neutral K3Fe(CN)6/K4Fe(CN)6 and KI3/KI electrolytes for the anolyte and catholyte solutions, respectively. A reasonably high-temperature coefficient of the cell αCell = 1.9 mV K−1 and a power density of 9 μW cm−2 at ΔT = 37 °C were measured. Such a cell design is free of the pH-matching issue affecting the stability of the electrolytes and the issue of cross-over of active species since both active ions are anions. Combining experiments with the porous electrode model, this work quantitatively captures the flow-rate dependent discharging behavior, even the nonlinear discharging characteristics at low flow rate or low Reynolds number. The theoretical analysis in this work could also be used to estimate the coupled effects of mass transfer and electrochemical reaction kinetics for other types of flow batteries for harvesting low grade heat, such as the recently developed concentration redox flow batteries21 or copper-acetonitrile nanoslurry flow batteries.15 For the first time, this work comprehensively analyzed the coupled effects of surface kinetics, mass transfer, and electrode polarization on the energy efficiency and power of a TREC-FB for harvesting low-grade heat. At a fixed flow rate and internal resistance, the mass transfer overpotential inside the porous electrode is the major factor limiting both the power density and efficiency. Electrode polarization becomes pronounced at low flow rates and large discharging currents, resulting in the nonlinearity of the discharging voltage–current curves. The surface reaction kinetics characterized by the rate constant, however, does not significantly affect the performance of the system in the case when the mass transfer is the major limiting factor. Future efforts for improving the power density of the TREC-FB include developing pH-matched electrolytes with high temperature coefficients and high concentrations, and membrane-free configurations of the TREC-FB, as well as porous electrodes with highly efficient mass transfer.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
X. Q. acknowledges helpful and productive discussions with Haoran Jiang and Xun Wang. The authors also acknowledge Prof. Evelyn Wang for valuable suggestions in the preparation of this manuscript. The authors gratefully thank John Barton and Fikile Brushett for the advice on mass transfer modeling, and the referees for the helpful suggestions on evaluating device performances. Device modeling was partially performed using the Stampede2 supercomputer through the startup allocation (TG-DMR200043) of Extreme Science and Engineering Discovery Environment (XSEDE).
References
- C. Forman, I. K. Muritala, R. Pardemann and B. Meyer, Renewable Sustainable Energy Rev., 2016, 57, 1568–1579 CrossRef
 .
.
- M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, J. Chem. Phys., 2011, 134, 114513 CrossRef CAS
 .
.
- T. Li, X. Zhang, S. D. Lacey, R. Mi, X. Zhao, F. Jiang, J. Song, Z. Liu, G. Chen, J. Dai, Y. Yao, S. Das, R. Yang, R. M. Briber and L. Hu, Nat. Mater., 2019, 18, 608–613 CrossRef CAS
 .
.
- A. J. deBethune, T. S. Licht and N. Swendeman, J. Electrochem. Soc., 1959, 106, 616 CrossRef CAS
 .
.
- C.-G. Han, X. Qian, Q. Li, B. Deng, Y. Zhu, Z. Han, W. Zhang, W. Wang, S.-P. Feng, G. Chen and W. Liu, Science, 2020, 368, 1091–1098 CrossRef CAS
 .
.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed
 .
.
-
H. L. Chum, Review of thermally regenerative electrochemical systems, Solar Energy Research Institute, 1981 Search PubMed
 .
.
- M. Rahimi, A. P. Straub, F. Zhang, X. Zhu, M. Elimelech, C. A. Gorski and B. E. Logan, Energy Environ. Sci., 2018, 11, 276–285 RSC
 .
.
- D. Brogioli and F. La Mantia, Energy Environ. Sci., 2021, 14, 1057–1082 RSC
 .
.
- H. Wang, D. Zhao, Z. U. Khan, S. Puzinas, M. P. Jonsson, M. Berggren and X. Crispin, Adv. Electron. Mater., 2017, 3, 1700013 CrossRef
 .
.
- X. Wang and S.-P. Feng, Front. Mech. Eng., 2017, 3, 20 CrossRef
 .
.
- F. Zhang, J. Liu, W. Yang and B. E. Logan, Energy Environ. Sci., 2015, 8, 343–349 RSC
 .
.
- F. Zhang, N. LaBarge, W. Yang, J. Liu and B. E. Logan, ChemSusChem, 2015, 8, 1043–1048 CrossRef CAS PubMed
 .
.
- H. Tian, W. Jiang, G. Shu, W. Wang, D. Huo and M. Z. Shakir, J. Electrochem. Soc., 2019, 166, A2814–A2825 CrossRef CAS
 .
.
- M. Rahimi, A. D'Angelo, C. A. Gorski, O. Scialdone and B. E. Logan, J. Power Sources, 2017, 351, 45–50 CrossRef CAS
 .
.
- M. Rahimi, T. Kim, C. A. Gorski and B. E. Logan, J. Power Sources, 2018, 373, 95–102 CrossRef CAS
 .
.
- X. Zhu, M. Rahimi, C. A. Gorski and B. Logan, ChemSusChem, 2016, 9, 873–879 CrossRef CAS PubMed
 .
.
- W. Wang, G. Shu, H. Tian, D. Huo and X. Zhu, J. Power Sources, 2019, 424, 184–192 CrossRef CAS
 .
.
- W. Wang, H. Tian, G. Shu, D. Huo, F. Zhang and X. Zhu, J. Mater. Chem. A, 2019, 7, 5991–6000 RSC
 .
.
- S. Maye, H. H. Girault and P. Peljo, Energy Environ. Sci., 2020, 13, 2191–2199 RSC
 .
.
- I. Facchinetti, R. Ruffo, F. La Mantia and D. Brogioli, Cell Rep. Phys. Sci., 2020, 1, 100056 CrossRef
 .
.
- I. Facchinetti, E. Cobani, D. Brogioli, F. La Mantia and R. Ruffo, ChemSusChem, 2020, 13, 5460–5467 CrossRef CAS
 .
.
- B. Yu, J. Duan, J. Li, W. Xie, H. Jin, R. Liu, H. Wang, L. Huang, B. Hu and J. Zhou, Research, 2019, 2019, 2460953 CAS
 .
.
- R. Hu, B. A. Cola, N. Haram, J. N. Barisci, S. Lee, S. Stoughton, G. Wallace, C. Too, M. Thomas, A. Gestos, M. E. Cruz, J. P. Ferraris, A. A. Zakhidov and R. H. Baughman, Nano Lett., 2010, 10, 838–846 CrossRef CAS
 .
.
- S. W. Lee, Y. Yang, H. W. Lee, H. Ghasemi, D. Kraemer, G. Chen and Y. Cui, Nat. Commun., 2014, 5, 3942 CrossRef CAS
 .
.
- Y. Yang, S. W. Lee, H. Ghasemi, J. Loomis, X. Li, D. Kraemer, G. Zheng, Y. Cui and G. Chen, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17011–17016 CrossRef CAS PubMed
 .
.
- Y. Yang, J. Loomis, H. Ghasemi, S. W. Lee, Y. J. Wang, Y. Cui and G. Chen, Nano Lett., 2014, 14, 6578–6583 CrossRef CAS PubMed
 .
.
- A. D. Poletayev, I. S. McKay, W. C. Chueh and A. Majumdar, Energy Environ. Sci., 2018, 11, 2964–2971 RSC
 .
.
- R. H. Hammond and W. M. R. Jr, Sol. Energy, 1979, 23, 443–449 CrossRef CAS
 .
.
- D. Zhao, H. Wang, Z. U. Khan, J. C. Chen, R. Gabrielsson, M. P. Jonsson, M. Berggren and X. Crispin, Energy Environ. Sci., 2016, 9, 1450–1457 RSC
 .
.
- J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Nat. Commun., 2018, 9, 5146 CrossRef
 .
.
- T. I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3985 CrossRef CAS
 .
.
- C. Gao, S. W. Lee and Y. Yang, ACS Energy Lett., 2017, 2, 2326–2334 CrossRef CAS
 .
.
- Y. Ding, X. Guo, K. Ramirez-Meyers, Y. Zhou, L. Zhang, F. Zhao and G. Yu, Energy Environ. Sci., 2019, 12, 3370–3379 RSC
 .
.
- J. T. Hupp and M. J. Weaver, Inorg. Chem., 1984, 23, 3639–3644 CrossRef CAS
 .
.
- B. Huang, S. Muy, S. Feng, Y. Katayama, Y. C. Lu, G. Chen and Y. Shao-Horn, Phys. Chem. Chem. Phys., 2018, 20, 15680–15686 RSC
 .
.
- K. Post and R. G. Bobins, Electrochim. Acta, 1976, 21, 401–405 CrossRef CAS
 .
.
- H.-H. Huang, Metals, 2016, 6, 23 CrossRef
 .
.
- P. L. Domingo, B. Garcia and J. M. Leal, Can. J. Chem., 1990, 68, 228–235 CrossRef CAS
 .
.
-
A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, Wiley, 2nd edn, 2000 Search PubMed
 .
.
- H. Fathabadi, IEEE Trans. Power Electron., 2019, 34, 8626–8633 Search PubMed
 .
.
- G. Boschloo and A. Hagfeldt, Acc. Chem. Res., 2009, 42, 1819–1826 CrossRef CAS
 .
.
- R. C. M. Jr. and P. A. Rock, Electrochim. Acta, 1969, 13, 969–975 Search PubMed
 .
.
- L. F. Castañeda, F. C. Walsh, J. L. Nava and C. Ponce de León, Electrochim. Acta, 2017, 258, 1115–1139 CrossRef
 .
.
- A. Nakayama, F. Kuwahara and Y. Sano, AlChE J., 2007, 53, 732–736 CrossRef CAS
 .
.
- K. Kinoshita and S. C. Leach, J. Electrochem. Soc., 1982, 129, 1993 CrossRef CAS
 .
.
- J. D. Milshtein, K. M. Tenny, J. L. Barton, J. Drake, R. M. Darling and F. R. Brushetta, J. Electrochem. Soc., 2017, 165, E3265–E3275 CrossRef
 .
.
- J. L. Barton and F. R. Brushett, Batteries, 2019, 5, 25 CrossRef CAS
 .
.
- H. Fathabadi, Renewable Energy, 2019, 133, 118–125 CrossRef CAS
 .
.
- S. Ergun and A. A. Orning, Ind. Eng. Chem., 1949, 41, 1179–1184 CrossRef CAS
 .
.
- E. Griškonis, A. Ilginis, I. Jonuškienė, L. Raslavičius, R. Jonynas and K. Kantminienė, Processes, 2020, 8, 939 CrossRef
 .
.
-
J. P. Holman, Heat Transfer, McGraw-Hill Education, 2009 Search PubMed
 .
.
- L. Zhang, T. Kim, N. Li, T. J. Kang, J. Chen, J. M. Pringle, M. Zhang, A. H. Kazim, S. Fang, C. Haines, D. Al-Masri, B. A. Cola, J. M. Razal, J. Di, S. Beirne, D. R. MacFarlane, A. Gonzalez-Martin, S. Mathew, Y. H. Kim, G. Wallace and R. H. Baughman, Adv. Mater., 2017, 29, 1605652 CrossRef
 .
.
- F. Giacalone, C. Olkis, G. Santori, A. Cipollina, S. Brandani and G. Micale, Energy, 2019, 166, 674–689 CrossRef CAS
 .
.
- M. Micari, A. Cipollina, F. Giacalone, G. Kosmadakis, M. Papapetrou, G. Zaragoza, G. Micale and A. Tamburini, Desalination, 2019, 453, 77–88 CrossRef CAS
 .
.
- F. Giacalone, F. Vassallo, F. Scargiali, A. Tamburini, A. Cipollina and G. Micale, J. Membr. Sci., 2020, 595, 117522 CrossRef CAS
 .
.
- E. Shaulsky, C. Boo, S. Lin and M. Elimelech, Environ. Sci. Technol., 2015, 49, 5820–5827 CrossRef CAS
 .
.
- A. Altaee, P. Palenzuela, G. Zaragoza and A. A. AlAnezi, Appl. Energy, 2017, 191, 328–345 CrossRef CAS
 .
.
- A. P. Straub and M. Elimelech, Environ. Sci. Technol., 2017, 51, 12925–12937 CrossRef CAS
 .
.
- E. A. Sanginov, R. R. Kayumov, L. V. Shmygleva, V. A. Lesnichaya, A. I. Karelin and Y. A. Dobrovolsky, Solid State Ionics, 2017, 300, 26–31 CrossRef CAS
 .
.
- H. R. Jiang, W. Shyy, M. C. Wu, R. H. Zhang and T. S. Zhao, Appl.
Energy, 2019, 233–234, 105–113 CAS
 .
.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Jungwoo
Shin
,
Yaodong
Tu
,
James Han
Zhang
and
Gang
Chen
*
*,
Jungwoo
Shin
,
Yaodong
Tu
,
James Han
Zhang
and
Gang
Chen
*
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R entropy change is nonzero. This temperature dependence is quantified by the temperature coefficient α,4 which is related to the entropy change of the cathodic reaction:
R entropy change is nonzero. This temperature dependence is quantified by the temperature coefficient α,4 which is related to the entropy change of the cathodic reaction:![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R is proportional to the change of squared valence number z2 divided by the ionic radii r:
R is proportional to the change of squared valence number z2 divided by the ionic radii r:
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Fe2+, the change of the ionic radii is not large enough to affect the sign of α. For cation redox pairs, the reduced ion species usually has a smaller valence value, zO2 − zR2 > 0, giving rise to a positive α. In contrast, anion redox pairs usually have a negative α according to Born's solvation model. Born's solvation model also indicates that higher valence ions with smaller radii tend to have relatively large temperature coefficients. However, another factor that needs to be simultaneously considered is the hydrolysis of these redox ions, which affects the stability of the electrolyte solution. For example, metallic cations like V3+/V2+ and Fe3+/Fe2+ are good candidates for relatively large positive temperature coefficients,28 but these solutions are only stable in low pH environments.37,38 Anions like Fe(CN)63−/Fe(CN)64−, however, are usually stable in neutral or basic environments. Such a mismatched stable range of pH greatly affects the stability of TREC-FB cells. For example, although pairing cations such as Fe3+/Fe2+ and V3+/V2+ with Fe(CN)63−/Fe(CN)64− can achieve a high value of |αCell| ∼ 2.7 mV K−1 and 3.1 mV K−1,28 the proton exchange across the ion exchange membrane would gradually shift the pH value on the Fe(CN)63−/Fe(CN)64− side, resulting in a complicated decomposition of the Fe(CN)63−/Fe(CN)64− ions releasing toxic CN− once the solution becomes acidic.39 Such cells can only operate stably until the pH buffer is consumed. In addition to the pH matching problem, it is also preferred that the redox-active species have the same sign of charges. For example, the TREC-FB based on Cu(NH3)42+/Cu(NH3)2+ and Fe(CN)63−/Fe(CN)64− has a high temperature coefficient |αCell| = 2.9 mV K−1;29 however, the different sign of charges between the reactive ion pairs makes it difficult to find the optimal ion exchange membrane to prevent the cross-over of redox active ions.29
Fe2+, the change of the ionic radii is not large enough to affect the sign of α. For cation redox pairs, the reduced ion species usually has a smaller valence value, zO2 − zR2 > 0, giving rise to a positive α. In contrast, anion redox pairs usually have a negative α according to Born's solvation model. Born's solvation model also indicates that higher valence ions with smaller radii tend to have relatively large temperature coefficients. However, another factor that needs to be simultaneously considered is the hydrolysis of these redox ions, which affects the stability of the electrolyte solution. For example, metallic cations like V3+/V2+ and Fe3+/Fe2+ are good candidates for relatively large positive temperature coefficients,28 but these solutions are only stable in low pH environments.37,38 Anions like Fe(CN)63−/Fe(CN)64−, however, are usually stable in neutral or basic environments. Such a mismatched stable range of pH greatly affects the stability of TREC-FB cells. For example, although pairing cations such as Fe3+/Fe2+ and V3+/V2+ with Fe(CN)63−/Fe(CN)64− can achieve a high value of |αCell| ∼ 2.7 mV K−1 and 3.1 mV K−1,28 the proton exchange across the ion exchange membrane would gradually shift the pH value on the Fe(CN)63−/Fe(CN)64− side, resulting in a complicated decomposition of the Fe(CN)63−/Fe(CN)64− ions releasing toxic CN− once the solution becomes acidic.39 Such cells can only operate stably until the pH buffer is consumed. In addition to the pH matching problem, it is also preferred that the redox-active species have the same sign of charges. For example, the TREC-FB based on Cu(NH3)42+/Cu(NH3)2+ and Fe(CN)63−/Fe(CN)64− has a high temperature coefficient |αCell| = 2.9 mV K−1;29 however, the different sign of charges between the reactive ion pairs makes it difficult to find the optimal ion exchange membrane to prevent the cross-over of redox active ions.29
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 3I−, E0 = 0.536 V
3I−, E0 = 0.536 V![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Fe(CN)64−, E0 = 0.37 V
Fe(CN)64−, E0 = 0.37 V![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) νRR
νRR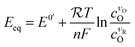
 is the universal ideal gas constant, ck = Ck/C0 (k = O,R) denotes the dimensionless concentration of species against the standard concentration C0 (1 M), and
is the universal ideal gas constant, ck = Ck/C0 (k = O,R) denotes the dimensionless concentration of species against the standard concentration C0 (1 M), and  is the formal potential with γ the activity coefficients and E0 the standard electrode potential. At equilibrium, the measured electrode potential E is equal to the equilibrium potential Eeq described by the Nernst equation, which is essentially the Gibbs free energy change of the half-reaction. With a finite discharging current, the equilibrium condition is broken, resulting in an additional potential drop known as the overpotential (η = E − Eeq). At a finite current, the concentration would become nonuniform, which further affects the surface kinetics and mass transfer, resulting in a non-uniform profile of the overpotential.
is the formal potential with γ the activity coefficients and E0 the standard electrode potential. At equilibrium, the measured electrode potential E is equal to the equilibrium potential Eeq described by the Nernst equation, which is essentially the Gibbs free energy change of the half-reaction. With a finite discharging current, the equilibrium condition is broken, resulting in an additional potential drop known as the overpotential (η = E − Eeq). At a finite current, the concentration would become nonuniform, which further affects the surface kinetics and mass transfer, resulting in a non-uniform profile of the overpotential.

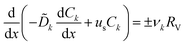
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k, the effective diffusivity inside the porous electrode, can be related to the diffusivity of the bulk solution Dk through
k, the effective diffusivity inside the porous electrode, can be related to the diffusivity of the bulk solution Dk through  , where ε is the porosity and
, where ε is the porosity and  the tortuosity factor of the porous media. The sign of the source term takes + when k = O and − when k = R. By nondimensionalizing the concentration ck = Ck/C0 and the coordinate X = x/L with L the electrode length, eqn (7) can be written as:
the tortuosity factor of the porous media. The sign of the source term takes + when k = O and − when k = R. By nondimensionalizing the concentration ck = Ck/C0 and the coordinate X = x/L with L the electrode length, eqn (7) can be written as:
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k is the Peclet number of species k and ġk is the normalized rate of generating species k inside the porous electrode:
k is the Peclet number of species k and ġk is the normalized rate of generating species k inside the porous electrode:
 :
:

 and
and  are the mass transfer coefficient, CsO,R is the mean concentration at the surface of the electrode, and Ae is the specific electrode area per unit volume, determined by the porosity ε and fiber diameter df as Ae = 4(1 − ε)/df.44 The dimensionless form of eqn (11) can be written as:
are the mass transfer coefficient, CsO,R is the mean concentration at the surface of the electrode, and Ae is the specific electrode area per unit volume, determined by the porosity ε and fiber diameter df as Ae = 4(1 − ε)/df.44 The dimensionless form of eqn (11) can be written as: is the Sherwood number of mass transfer, dH is the hydrodynamic diameter for the porous media, calculated as
is the Sherwood number of mass transfer, dH is the hydrodynamic diameter for the porous media, calculated as  , and ζ = dH/AeL2 is a geometric factor of the porous electrode.45 Mass transfer inside the porous electrode is modeled by the correlation developed by Kinoshita et al. for flow-through felt electrodes:46
, and ζ = dH/AeL2 is a geometric factor of the porous electrode.45 Mass transfer inside the porous electrode is modeled by the correlation developed by Kinoshita et al. for flow-through felt electrodes:46
 is the exchange current density with k0(T) the rate constant calculated through the Arrhenius law:
is the exchange current density with k0(T) the rate constant calculated through the Arrhenius law: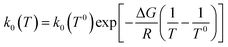


 . Note that ϕl is regarded as a local mean potential of the liquid electrolyte of a mesoscopic local pore, outside the electric double layer. Namely, the microscopic details of ion transport at the electrode–electrolyte interface are not included in eqn (18). The approximate equality in eqn (18) can be made due to the following reasons. The divergence of the ionic current can be expressed as
. Note that ϕl is regarded as a local mean potential of the liquid electrolyte of a mesoscopic local pore, outside the electric double layer. Namely, the microscopic details of ion transport at the electrode–electrolyte interface are not included in eqn (18). The approximate equality in eqn (18) can be made due to the following reasons. The divergence of the ionic current can be expressed as  , since the x-derivatives are negligible with the length of the electrode much larger than the thickness. Through simple dimensional analysis, the ratio between the ionic conduction current and diffusion current is roughly ziFϕl/RTDi, on the order of 107, and the ratio between the conduction current and convection current is roughly zi2Fϕl/RTvs also on the order of 102 due to the slow velocity on the order of 0.1 mm s−1, and hence it is a fair approximation that the divergence of the ionic current can be estimated by Ohm's law, and eqn (18) holds.
, since the x-derivatives are negligible with the length of the electrode much larger than the thickness. Through simple dimensional analysis, the ratio between the ionic conduction current and diffusion current is roughly ziFϕl/RTDi, on the order of 107, and the ratio between the conduction current and convection current is roughly zi2Fϕl/RTvs also on the order of 102 due to the slow velocity on the order of 0.1 mm s−1, and hence it is a fair approximation that the divergence of the ionic current can be estimated by Ohm's law, and eqn (18) holds.
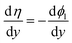 , and eqn (18) becomes
, and eqn (18) becomes

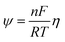 , we can derive the following equivalent ODE:
, we can derive the following equivalent ODE:
 is the dimensionless exchange current, with J00 = nFk0C0. Dak is the Damköhler number characterizing the ratio between the reaction rate and the mass diffusion rate, defined as Dak = k0AeL2/
is the dimensionless exchange current, with J00 = nFk0C0. Dak is the Damköhler number characterizing the ratio between the reaction rate and the mass diffusion rate, defined as Dak = k0AeL2/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k.
k. 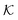 is the dimensionless conductivity
is the dimensionless conductivity 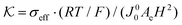 , which can be interpreted as the ratio of the conduction current driven by the “thermal voltage” RT/F to the exchange current J00 at standard concentration. The dimensionless ODE (eqn (21)) clearly shows that the overpotential is a combined result of mass transfer quantified by the Sherwood number Sh and reaction kinetics characterized by the Damköhler number Da, and the activities of redox species cO and cR.
, which can be interpreted as the ratio of the conduction current driven by the “thermal voltage” RT/F to the exchange current J00 at standard concentration. The dimensionless ODE (eqn (21)) clearly shows that the overpotential is a combined result of mass transfer quantified by the Sherwood number Sh and reaction kinetics characterized by the Damköhler number Da, and the activities of redox species cO and cR.


 the volume of the porous electrode, and n± the electron transfer number for the redox reaction of the catholyte (+) and anolyte (−) correspondingly. The anode will adopt a negative sign when computing the volumetric reaction rate because we define the cathodic reaction as the positive direction. We now clarify how the function f mapping the reaction rate to the overpotential in eqn (24) is constructed. First, the solution is taking a mean-field treatment of the reaction rate
the volume of the porous electrode, and n± the electron transfer number for the redox reaction of the catholyte (+) and anolyte (−) correspondingly. The anode will adopt a negative sign when computing the volumetric reaction rate because we define the cathodic reaction as the positive direction. We now clarify how the function f mapping the reaction rate to the overpotential in eqn (24) is constructed. First, the solution is taking a mean-field treatment of the reaction rate  at each point x along the flow direction, because it is challenging to inversely solve the full profile of J(x,y) with the total current icell. Such a mean-field treatment of
at each point x along the flow direction, because it is challenging to inversely solve the full profile of J(x,y) with the total current icell. Such a mean-field treatment of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) V made it possible to extract the overpotential from eqn (20) and the boundary conditions in eqn (22). At each point x along the flow direction, the overpotential profile as a function of y is solved, and the final measured overpotential η± is taken as the average value of η(x,y) inside the electrode domain.48 In this way, we constructed the function f relating the total current to the overpotential.
V made it possible to extract the overpotential from eqn (20) and the boundary conditions in eqn (22). At each point x along the flow direction, the overpotential profile as a function of y is solved, and the final measured overpotential η± is taken as the average value of η(x,y) inside the electrode domain.48 In this way, we constructed the function f relating the total current to the overpotential.

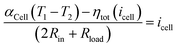

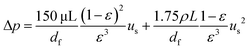

 without heat recuperation, and the power density PHX normalized by the heat exchanger area, as recently proposed by Brogioli and La Mantia.9
without heat recuperation, and the power density PHX normalized by the heat exchanger area, as recently proposed by Brogioli and La Mantia.9 evaluates the intrinsic efficiency, which can be regarded as the baseline without any heat recuperation for improvement. The power density PHX, on the other hand, captures the trade-off between higher efficiency ηE through recuperation, and the penalty due to the larger amount of heat exchange area required. In this work, we will also adopt these indices to provide insights for performance evaluation of the TREC-FB.
evaluates the intrinsic efficiency, which can be regarded as the baseline without any heat recuperation for improvement. The power density PHX, on the other hand, captures the trade-off between higher efficiency ηE through recuperation, and the penalty due to the larger amount of heat exchange area required. In this work, we will also adopt these indices to provide insights for performance evaluation of the TREC-FB. , and PHX and the temperature drops across the device components. By setting the recuperation effectiveness εHX to zero, we can relate ηE with the intrinsic efficiency
, and PHX and the temperature drops across the device components. By setting the recuperation effectiveness εHX to zero, we can relate ηE with the intrinsic efficiency  :
: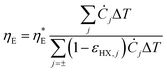
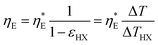

 derived by Brogioli and La Mantia (eqn (16) of ref. 9) with ΔT* = 0. ΔT* is regarded as the intrinsic temperature difference across a single energy conversion effect. In the TREC-FB considered in this work, both the hot and the cold battery are operating at thermal equilibrium, and the electrolytes entering and leaving the flow cells have the same temperatures, and hence ΔT* is indeed zero.
derived by Brogioli and La Mantia (eqn (16) of ref. 9) with ΔT* = 0. ΔT* is regarded as the intrinsic temperature difference across a single energy conversion effect. In the TREC-FB considered in this work, both the hot and the cold battery are operating at thermal equilibrium, and the electrolytes entering and leaving the flow cells have the same temperatures, and hence ΔT* is indeed zero.

 is known.
is known.
 , with kl the thermal conductivity of the liquid, ∼0.6 W m−1 K−1 of water, and dH the hydraulic diameter of the narrow gap. With 20 μm thick Ti foil as the heat exchanger surface (kTi = 17 W m−1 K−1), the overall heat transfer coefficient U = (2/h + dTi/kTi)−1 = 3996 W m−2 K−1. In this work, the dimension of the heat exchange surface 1.5 cm by 5 cm ensures a high theoretical effectiveness of 99% using the NTU method. Due to the small thermal mass, the heat loss across the tube walls was significant, especially at smaller flow rates even when insulation foam is applied. However, this issue of insulation will be not as severe when the flow rates are scaled up to the order of mL min−1. Therefore, we assume a recuperation effectiveness of 90% to estimate the energy conversion efficiency ηE.
, with kl the thermal conductivity of the liquid, ∼0.6 W m−1 K−1 of water, and dH the hydraulic diameter of the narrow gap. With 20 μm thick Ti foil as the heat exchanger surface (kTi = 17 W m−1 K−1), the overall heat transfer coefficient U = (2/h + dTi/kTi)−1 = 3996 W m−2 K−1. In this work, the dimension of the heat exchange surface 1.5 cm by 5 cm ensures a high theoretical effectiveness of 99% using the NTU method. Due to the small thermal mass, the heat loss across the tube walls was significant, especially at smaller flow rates even when insulation foam is applied. However, this issue of insulation will be not as severe when the flow rates are scaled up to the order of mL min−1. Therefore, we assume a recuperation effectiveness of 90% to estimate the energy conversion efficiency ηE.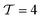 of the media, were fit from the data obtained at 230 μL min−1 (Re ≈ 3 × 10−3). This obtained tortuosity factor agreed reasonably with the literature values of graphite felts around 5.44 For other flow rates tested, we fixed these parameters and directly computed the results as plotted in Fig. 5. In general, the mass transfer overpotential was larger at lower Reynolds numbers and flow rates, thus decreasing the power density. However, the extra amount of heat needed to increase the temperature of the electrolyte also decreased at a smaller flow rate and the efficiency ηE increased at a smaller flow rate (Fig. 5c). We estimated that 9% of ηCarnot can be achieved at 1 μL min−1 at the maximum power output, while the power density can approach 9.5 μW cm−2 at 0.5 mL min−1. To eliminate the effect of the heat exchanger, we have also estimated the intrinsic efficiency
of the media, were fit from the data obtained at 230 μL min−1 (Re ≈ 3 × 10−3). This obtained tortuosity factor agreed reasonably with the literature values of graphite felts around 5.44 For other flow rates tested, we fixed these parameters and directly computed the results as plotted in Fig. 5. In general, the mass transfer overpotential was larger at lower Reynolds numbers and flow rates, thus decreasing the power density. However, the extra amount of heat needed to increase the temperature of the electrolyte also decreased at a smaller flow rate and the efficiency ηE increased at a smaller flow rate (Fig. 5c). We estimated that 9% of ηCarnot can be achieved at 1 μL min−1 at the maximum power output, while the power density can approach 9.5 μW cm−2 at 0.5 mL min−1. To eliminate the effect of the heat exchanger, we have also estimated the intrinsic efficiency  without heat recuperation. At a low flow rate of 1 μL min−1,
without heat recuperation. At a low flow rate of 1 μL min−1,  is approximately 1% relative to the Carnot efficiency. In general, simply choosing the operating conditions (temperature difference ΔT and flow rate Q) of the TREC-FB cell cannot simultaneously optimize the power density and efficiency. Fig. 6a and b show the map of the peak power density and the corresponding efficiency as a function of the temperature difference and flow rate. Although increasing temperature differences could simultaneously improve the efficiency and power density, the effect of the flow rate on the power density and efficiency is opposite with nonperfect heat recuperation.
is approximately 1% relative to the Carnot efficiency. In general, simply choosing the operating conditions (temperature difference ΔT and flow rate Q) of the TREC-FB cell cannot simultaneously optimize the power density and efficiency. Fig. 6a and b show the map of the peak power density and the corresponding efficiency as a function of the temperature difference and flow rate. Although increasing temperature differences could simultaneously improve the efficiency and power density, the effect of the flow rate on the power density and efficiency is opposite with nonperfect heat recuperation. )
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.








