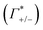Open Access Article
Open Access ArticleCation enrichment in the ion atmosphere is promoted by local hydration of DNA†
Chun Yu
Ma
a,
Simone
Pezzotti
 a,
Gerhard
Schwaab
a,
Gerhard
Schwaab
 a,
Magdalena
Gebala
b,
Daniel
Herschlag
b and
Martina
Havenith
a,
Magdalena
Gebala
b,
Daniel
Herschlag
b and
Martina
Havenith
 *a
*a
aDepartment of Physical Chemistry II, Ruhr-University Bochum, 44780 Bochum, Germany. E-mail: martina.havenith@rub.de
bDepartment of Biochemistry, Stanford University, Stanford, California 94305, USA
First published on 15th September 2021
Abstract
Electrostatic interactions are central to the structure and function of nucleic acids, including their folding, condensation, and interaction with proteins and other charged molecules. These interactions are profoundly affected by ions surrounding nucleic acids, the constituents of the so-called ion atmosphere. Here, we report precise Fourier Transform-Terahertz/Far-Infrared (FT-THz/FIR) measurements in the frequency range 30–500 cm−1 for a 24-bp DNA solvated in a series of alkali halide (NaCl, NaF, KCl, CsCl, and CsF) electrolyte solutions which are sensitive to changes in the ion atmosphere. Cation excess in the ion atmosphere is detected experimentally by observation of cation modes of Na+, K+, and Cs+ in the frequency range between 70–90 cm−1. Based on MD simulations, we propose that the magnitude of cation excess (which is salt specific) depends on the ability of the electrolyte to perturb the water network at the DNA interface: In the NaF atmosphere, the ions reduce the strength of interactions between water and the DNA more than in case of a NaCl electrolyte. Here, we explicitly take into account the solvent contribution to the chemical potential in the ion atmosphere: A decrease in the number of bound water molecules in the hydration layer of DNA is correlated with enhanced density fluctuations, which decrease the free energy cost of ion-hydration, thus promoting further ion accumulation within the DNA atmosphere. We propose that taking into account the local solvation is crucial for understanding the ion atmosphere.
Introduction
Nucleic acids are the most highly charged polyelectrolytes in nature that carry one negatively charged phosphate group per nucleotide residue. Their charge provides a substantial energetic barrier in the form of electrostatic repulsion in processes that require nucleic acid folding or compaction.1,2 Ions, specifically cations, can reduce the electrostatic repulsion between nucleic acids and mitigate electrostatic attraction with oppositely charged molecules such as proteins and aminoglycosides3–6 in a process known as electrostatic screening.1,2,7,8 The vast majority of these ions forms a loosely associated sheath, which is referred to as an ion atmosphere.8–14 Since the ion atmosphere around nucleic acids is crucial to biological processes such as packing, folding, molecular recognition, and enzymatic catalysis,1,2,15–17 dissecting its properties and energetics on a molecular level is essential to understand nucleic acid biology. Despite decades of research, the microscopic nature of the ion atmosphere around double-stranded DNA (dsDNA) and its hydration dynamics is still poorly understood as the nature of the interaction is dynamic rather than static.Recently, several experimental techniques have been proposed to study the size12 and the composition of the ion atmosphere.8,10,11 Experimental techniques like fluorescence, near-infrared, electron paramagnetic resonance, and nuclear magnetic resonance spectroscopies probe local electrostatics around biomolecules.18–21 Ion counting based on Buffer Exchange-Atomic Emission Spectroscopy (BE-AES) allowed a precise determination of the number of cations and anions in the ion cloud around dsDNA.11 Due to charge neutrality, the total charge of the cations and anions is equal in magnitude but opposite to that of the DNA. This implies cation enhancement while anions are depleted. Prior studies found that the accumulation of ions in the atmosphere depends on the salt identity and concentration. Based on these results, ion-pair formation was proposed as the simplest mechanism which would be able to explain the observed anion specificity in cation enrichment.11,22
Elsaesser et al. investigated energy exchange along the hydrated dsDNA via water–phosphate interactions on a fs timescale and pointed out its importance along the DNA backbone.23
In addition to experimental approaches, computational methods have been developed to obtain atomic-level descriptions of the ions in the DNA atmosphere. This includes intermolecular distances between ions and ions/dsDNA and their hydration status.24–26 These simulations proposed the localization of cations in the helical grooves, with a size dependence on this occupancy27–34 and greater accumulation of smaller cations around phosphoryl oxygen atoms forming an ion pair.28,32,35,36 More recently, a combination of ion radius, ion hydration and ion clustering ability was proposed to dictate anion specificity in the cation excess within the DNA atmosphere.37 These previous studies focused on ion–ion interaction or DNA–ion interaction in the ion atmosphere. However, for an overall assessment of the thermodynamics, the contribution of the solvent to the entropic penalty due to ion enrichment is crucial. In the present paper we identify a specific water-related driving force, which is proposed to be at the origin of the anion specific effects.
Experimentally, the characterization of hydration is still a challenge. In the present investigation, we focus on DNA, cation, and anion hydration by a joint THz spectroscopic/Molecular Dynamics (MD) simulation study. More specifically, we investigate the ion atmosphere around 24-bp DNA for distinct prototype electrolytes by THz absorption spectroscopy. Based on our results, we propose a general model to explain the anion specificity in cation enrichment and propose that the role of the local hydration or local thermodynamics is crucial to explain the previously observed effects. While we find no indication for changes in ion–ion interaction (e.g., ion-pairing), the enhanced cation enrichment in the case of NaF compared to NaCl can be instead explained by the distinct number of bound water molecules that interact with the polar/charged groups of the DNA. We show that local solvent density fluctuations around the DNA and, consequently, the local entropic cost contributing to ion hydration free energy in the ion atmosphere is crucial to understand the ion atmosphere.
Results
The experimental measurements were carried out using a Vertex 80v Fourier transform infrared (FTIR) spectrometer from Bruker Co. (USA) with a spectral range of 30–650 cm−1. The THz/FIR absorption coefficients can be described by Lambert–Beer's Law: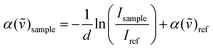 | (1) |
To minimize “etalon effects”, i.e., standing waves due to back reflection from the windows, a reference spectrum was recorded with bulk water, since pure water has a similar index of refraction and thus similar etalon effects, and the spectrum of water is well known (see ESI† for details and ref. 38–40).
We recorded the absorption spectrum of five different electrolytes (CsF, CsCl, KCl, NaF, NaCl) with and without dsDNA.
The dsDNA samples were prepared in 2 mM M-EPPS (M: Na/K/Cs; pH = 7) by titrating MOH with the corresponding sulfonic acid (HEPPS). The equilibration process with the appropriate buffer was carried out using Amicon Ultracel-10K filters from Merck Millipore (MA, USA). DNA-containing samples (500 μL) were spun down to ∼100 μL at 9500 × g in Amicon Ultracel-10 K filters. The sample solutions containing the DNA were taken only after equilibration was fully achieved (after eight rounds of buffer exchange). Only the filtered sample fractions with the DNA and the equilibrated anion/cation concentration were taken into consideration for the spectroscopic experiments on the five electrolyte solutions with DNA. Thus, the total number of ions is not conserved in between the samples with and without DNA, due to cation enrichment and anion depletion in the DNA ion-cloud.
In the case of the bulk electrolyte solutions, the effective absorption change, αeffion(ṽ) compared to bulk water is given as:
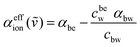 | (2) |
In previous publications, we were able to show that αeffion(ṽ) can be dissected into contributions of the hydrated ions and their hydration shells (see ESI† for details).38–41 Each cation and anion have characteristic spectroscopic fingerprints in the THz range, the so-called rattling modes. These are absorption modes from the hydrated ions. Those of the cations Na+, K+ and Cs+, are found in the low-frequency range (ca. 70–90 cm−1). For anions, the center frequencies of rattling modes lie in the frequency range 180–290 cm−1.38
Assuming additivity, the total absorption coefficient αDNAsample of the filtered fraction with dsDNA can be theoretically dissected into the partial absorption of the solvated dsDNA, the ions in the ion cloud, and of the bulk-electrolyte-like parts. Since we are only interested in the spectroscopic changes upon addition of the dsDNA (at a concentration cDNA and a molar volume ϕDNA), we subtracted the partial absorption due to the bulk-like electrolyte. We therefore define:
| αeffDNA+cloud = αDNAsample − [1 − cDNAϕDNA]αbe | (3) |
We want to note, that due to the buffer exchange procedure used to prepare the sample containing the dsDNA, the number of cations/anions in our sample differs from the number of cations/anions in the bulk electrolyte: Due to the charged dsDNA, we expect that the number of cations will be increased and the number of anions decreased.
The volume exclusion due to a single dsDNA molecule (1.47 × 10−26 m3 or ϕDNA = 8.85 cm3 mmol−1, see ESI† for details) is estimated using the reference atomic volumes of dsDNA in crystal form as reported in ref. 42 Note, that this volume accounts for 0.86% of Vtotal per mM of dsDNA. Therefore, upon addition of 1 mM of DNA, the salt concentration is effectively increased by 4.3 mM salt for a 0.5 M electrolyte solution.
If we further assume that the molar extinction of the solvated dsDNA is concentration independent, we obtain
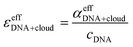
| αeffDNA+cloud = cDNA(εeffDNA + ncloudMεcloud,effM + ncloudXεcloud,effX − [ncloudM,beεbe,effM + ncloudX,beεbe,effX]) | (4) |
Here, εeffDNA, is an effective dsDNA extinction coefficient, that includes the absorption of the solvated DNA, ncloudM/X are the number of cations, M, and anions, X, in the cloud per dsDNA, and ncloudM/X,be are the numbers of cations and anions in the cloud assuming bulk electrolyte concentration. For simplification, we used effective molar extinction coefficients, εcloud,effΓ, (Γ = X, M, be) to account for the molar concentration of the solvated cations/anions in the ion atmosphere or the bulk electrolyte, respectively. εcloud,effΓ can be expressed as the sum of the molar extinction of the effective ion extinction in the bulk electrolyte, εbe,effΓ, and the extinction coefficient difference, ΔεeffΓ, caused by presence of the dsDNA.
| εcloud,effΓ = εbe,effΓ + ΔεeffΓ | (5) |
As a result, we obtain:
| αeffDNA+cloud = cDNA[εeffDNA + (ncloudM − ncloudM,be)ε−effM + (ncloudX − ncloudX,be)ε−effX + ncloudMΔεeffM + ncloudXΔεeffX] | (6) |
 | (7a) |
 | (7b) |
These numbers are directly related to the Γ+ and Γ− values that have been deduced experimentally in previous BE-AES measurements:5,7,8,10,13,14 In addition to the BE-AES measurements, we need to take the DNA-induced dilution effect into account. Since one dsDNA corresponds to an electrolyte volume that contains approximately four anions and cations, respectively, the spectroscopic enrichment factors 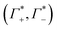 are related to the previously measured enrichment factors Γ+ and Γ−5 by
are related to the previously measured enrichment factors Γ+ and Γ−5 by
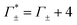 | (8) |
Furthermore, we define an extinction difference Δεhydration = ncloudMΔεeffM + ncloudXΔεeffX that is caused by a change in solvation environment. Thus eqn (6) can be simplified to
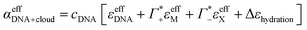 | (9) |
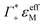 taking into account the cation enrichment in the cloud, (3) a subtractive component
taking into account the cation enrichment in the cloud, (3) a subtractive component 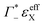 (note, that
(note, that 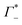 is negative) describing the anion depletion in the ion atmosphere.
is negative) describing the anion depletion in the ion atmosphere.
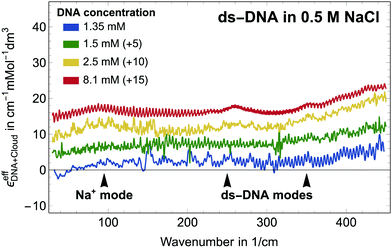
Let us first focus on a solution of dsDNA in NaCl. In Fig. 1 we plot
 | (10) |
All spectra look very similar in their spectral line shape. Therefore, we conclude that αeffDNA+cloud scales approximately linearly with DNA concentration. For all measurements plotted in Fig. 1, an absorption peak is observed at 90 cm−1, independent of the NaCl concentration. By comparison to the low frequency spectra of the bulk electrolytes this band is assigned to the Na+ rattling mode.40,41 A second cation peak is expected around 150 cm−1 for Na+ (aq.).41 However, this is mostly compensated by the anion peak of Cl− around 190 cm−1, which – due to anion depletion – leads to a negative contribution in this difference spectrum in case of NaCl. We note that the narrower absorption bands at 260 cm−1–280 cm−1, 360 cm−1 and 430 cm−1 are observed for all investigated samples, independent of the specific electrolyte, see Fig. 2. We assign these bands, which are absent in the bulk electrolyte, to intramolecular modes of DNA, i.e. αeffDNA = cDNAεeffDNA. Their narrow linewidth of ≈ 100 cm−1 is typical for intramolecular bands, see e.g. the N–C–C–O open/close mode centered at 315 cm−1 for solvated glycine.43
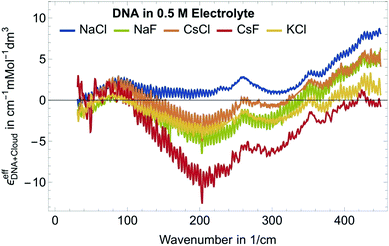
Fig. 2 shows εeffDNA+cloud for dsDNA for five different 0.5 M electrolyte solutions. In all cases we find a peak in the 70–90 cm−1 region which is dominated by the cation rattling bands (see ESI† for details) of Na+, Cs+ and K+. The frequency range 140–300 cm−1 is strongly electrolyte dependent. Here, the anion and cation specific modes both contribute, and the individual contributions are difficult to disentangle.
Furthermore, we observe a decrease of the extinction coefficient around 300 cm−1 and a continuous, almost linear increase in εeffDNA+cloud in the frequency range between 300 and 500 cm−1 compared to the bulk electrolyte. How can we explain this? The observed difference spectra do not only incorporate partial contributions due to cation excess and anion depletion in the ion atmosphere but also reflect changes in the vicinity of DNA. Hydration water of DNA might have distinct absorption spectra compared to bulk water, in particular due to the specific interactions that water molecules form with the charged/polar groups of the DNA. Indeed, in previous studies we observed an increase in the THz intensity beyond 350 cm−1 for aqueous solutions of polar/charged solutes as compared to bulk water.41,43 As discussed in more details in ref. 41 for the case of water hydrating ions, such increase is due to water molecules directly bound to the charged solute, and more specifically arises from the self-correlation terms of water molecules in the 1st hydration layer plus the cross terms between 1st and 2nd hydration layer. Therefore, we attribute the observed general increase in εeffDNA+cloud beyond 350 cm−1 to the spectroscopic nature of the hydration water molecules bound to charged and polar groups within the DNA atmosphere.
Thus, we can dissect the plotted spectra into the following partial contributions:
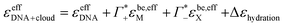 | (11) |
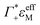 the cation excess in the DNA ion atmosphere,
the cation excess in the DNA ion atmosphere, 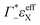 the anion depletion, and Δεhydration the changes in the extinction coefficient of water in the vicinity of DNA compared to bulk water.
the anion depletion, and Δεhydration the changes in the extinction coefficient of water in the vicinity of DNA compared to bulk water.
Γ i denote ion preferential interaction coefficients, i.e. the number of associated ions (either excess or a lack of ions compared to bulk) around 24-bp DNA and is determined according to:
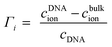 | (12) |
In the absence of DNA aggregation, or ion pair formation within the cloud, αeffDNA+cloud is expected to be proportional to the DNA concentration. This allows to define the effective extinction coefficient 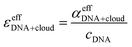 of hydrated dsDNA including the ion cloud. In the following analysis we wanted to focus explicitly on the DNA hydration. If we assume that the ions in the ion atmosphere are fully solvated and thus have the same THz signatures as in the bulk, we can subtract the scaled hydrated cation and anion extinctions
of hydrated dsDNA including the ion cloud. In the following analysis we wanted to focus explicitly on the DNA hydration. If we assume that the ions in the ion atmosphere are fully solvated and thus have the same THz signatures as in the bulk, we can subtract the scaled hydrated cation and anion extinctions 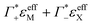 from εeffDNA+cloud yielding:
from εeffDNA+cloud yielding:
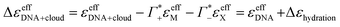 | (13) |
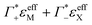 and ΔεeffDNA+cloud for various electrolytes. As an example, we show in Fig. 3B the effect of the subtraction of the ion contribution from εeffDNA+cloud for a solution of 8 mM dsDNA in 0.5 M NaCl.
and ΔεeffDNA+cloud for various electrolytes. As an example, we show in Fig. 3B the effect of the subtraction of the ion contribution from εeffDNA+cloud for a solution of 8 mM dsDNA in 0.5 M NaCl.
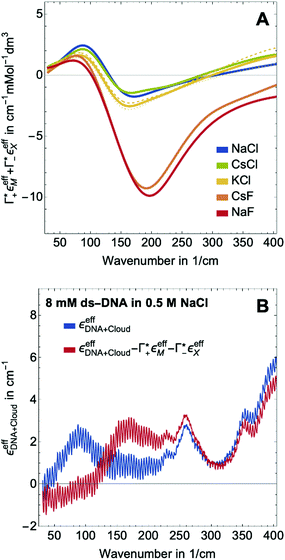 | ||
Fig. 3 (A) Expected contribution of cation enrichment and anion depletion on the millimolar extinction coefficient of dsDNA as deduced from bulk measurements. For KCl no experimental values for Γ were available. Therefore, we took 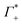 and and 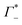 values from NaCl (dotted), from CsCl (dashed), and an average of the two (full line). (B) εeffDNA+cloud (blue, eqn (11)) and ΔεeffDNA+cloud (red, eqn (13)) are compared for 8 mM dsDNA in 0.5 M NaCl solution as an example. For the effect on the remaining salts, see Fig. 5. values from NaCl (dotted), from CsCl (dashed), and an average of the two (full line). (B) εeffDNA+cloud (blue, eqn (11)) and ΔεeffDNA+cloud (red, eqn (13)) are compared for 8 mM dsDNA in 0.5 M NaCl solution as an example. For the effect on the remaining salts, see Fig. 5. | ||
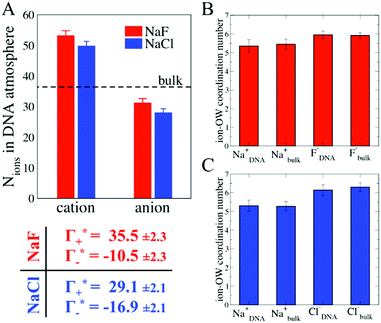
In order to provide a molecular picture for the experimentally observed changes in the DNA atmosphere, we have carried out classical MD simulations. Instead of 24-bp DNA duplexes we used a DNA dodecamer solvated either in a 0.5 M NaF or in a 0.5 M NaCl aqueous solution to reduce complexity. The simulations qualitatively reproduce the two main experimental findings on the composition of the DNA atmosphere: (i) ions are enriched within the DNA atmosphere for both NaF and NaCl, (ii) the enrichment is larger in case of NaF than in case of NaCl. This is illustrated in Fig. 4A, where the average number of ions within the DNA atmosphere in the MD simulations has been quantified for the two electrolytes (see methods for details).
As illustrated in Fig. 4A, the simulations predict that the DNA atmosphere contains more cations and less anions as compared to an equivalent volume in the bulk (black dashed line) for both NaF (red) and NaCl (blue), Moreover, more cations as well as more anions are found within the DNA atmosphere in the system with NaF as compared to the system with NaCl. A theoretical ion count, directly comparable to the experimental count, can be calculated from the MD simulations using the two-partition model introduced in refs. 44 and 45 (see methods). In a nutshell, the count of cations (Γ+) and anions (Γ−) is directly obtained from the average number of ions within the DNA atmosphere (red and blue histograms in Fig. 4A) minus the number of ions found in an equivalent volume in the bulk (black dashed line). We obtain values of Γ+ = 17.0 ± 1.1 and Γ− = −5.0 ± 1.1 for the atmosphere with 0.5 M NaF and values of Γ+ = 13.9 ± 1.0 and Γ− = −8.1 ± 1.0 for the atmosphere with 0.5 M NaCl. The Γ+ and Γ− values in both NaF and NaCl atmospheres satisfy the condition Γ+ − Γ− = |ZMDDNA|, i.e. the difference between the average number of cations and anions in the DNA atmosphere compensates the negative charge of the DNA dodecamer. In our simulations we model a small DNA dodecamer with ZMDDNA = −22, while in the experiments ZEXPDNA = −46. For a comparison the theoretical ion counts are further re-scaled as follows:
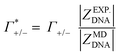 | (14) |
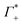 and
and 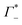 values are reported in the table of Fig. 4A. The predicted values are consistent with the experimental values within error bars, which confirms our model.
values are reported in the table of Fig. 4A. The predicted values are consistent with the experimental values within error bars, which confirms our model.
Discussion
At this point we want to focus on the question why the cation excess Γ+ is anion specific. In a previous paper ion pairing/clustering was suggested as the simplest model consistent with the anion-specific cation excess.11 Here, we carried out a joint THz/MD simulation study, that allows to probe the changes in local hydration around the DNA and the ions.In case of preferred ion pairing, we would expect to see changes in the line shape and/or the center frequencies of the Na+ cation rattling mode in the ion atmosphere of DNA compared to those of the Na+ cation rattling mode in the bulk electrolyte. However, we find no indication in the experimental spectra. The measured bulk spectra for each electrolyte are shown in the ESI† for comparison. Based on a dissection of each spectrum into the anion, cation and hydration contribution, we predict the change in molar extinction due to cation excess and anion depletion as: 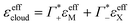 . For further discussion, we subtracted these cation and anion specific spectroscopic features from the recorded spectra, see Fig. 5, using the values of
. For further discussion, we subtracted these cation and anion specific spectroscopic features from the recorded spectra, see Fig. 5, using the values of 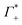 and
and 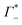 obtained from BE-AES (see Table 1 and Fig. 3A).
obtained from BE-AES (see Table 1 and Fig. 3A).
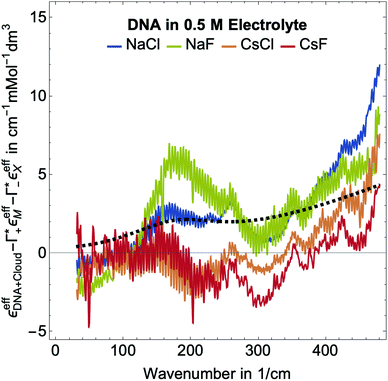 | ||
Fig. 5 Plotted is 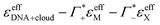 , i.e., the mM extinction coefficient of the hydrated dsDNA after subtraction of the excess cation contribution and depleted anion contribution, as shown in Fig. 3. The KCl spectrum is not shown since experimental Γ+ and Γ− values are not available for this salt. The characteristic cation modes have a positive partial absorption around 70–90 cm−1, see Fig. 3B. When subtracting these contributions by inserting the previously determined Γ values, we can dissect these spectra further. Intramolecular DNA modes are visible at 260 cm−1–280 cm−1, 360 cm−1, 430 cm−1 (intramolecular modes have a smaller linewidth). The increase between 350 cm−1 and 500 cm−1 is taken as spectroscopic signature of bound water. For comparison, we display a scaled bulk water spectrum (black dashed line), which is clearly different in the spectral lineshape. , i.e., the mM extinction coefficient of the hydrated dsDNA after subtraction of the excess cation contribution and depleted anion contribution, as shown in Fig. 3. The KCl spectrum is not shown since experimental Γ+ and Γ− values are not available for this salt. The characteristic cation modes have a positive partial absorption around 70–90 cm−1, see Fig. 3B. When subtracting these contributions by inserting the previously determined Γ values, we can dissect these spectra further. Intramolecular DNA modes are visible at 260 cm−1–280 cm−1, 360 cm−1, 430 cm−1 (intramolecular modes have a smaller linewidth). The increase between 350 cm−1 and 500 cm−1 is taken as spectroscopic signature of bound water. For comparison, we display a scaled bulk water spectrum (black dashed line), which is clearly different in the spectral lineshape. | ||
In Fig. 2, where we plot εeffDNA+cloud, the cation rattling modes around 70–90 cm−1 can be clearly seen. After subtraction of the anion and cation specific modes (Fig. 5) we observe no peaks around 90–100 cm−1 within our experimental uncertainty. Thus, our measurements confirm the cation enrichment and anion depletion factors in the ion atmosphere, as previously measured by Gebala et al.11 The spectral line shape and thus the ionic hydration seems to be unchanged compared to the bulk. Thus, within our experimental uncertainty, the cation and anion hydration are bulk like, which is in contrast to our expectations in case of contact ion pairing. Enhanced contact ion-pairs in the DNA atmosphere compared to the bulk should result in a loss of the hydration shell around Na+/K+/Cs+. Thus, the cation and anion specific molar extinctions should differ from their bulk value. The frequency range 150–300 cm−1 is difficult to disentangle spectroscopically. In a previous study of hydration water around alcohol chains, this was assigned to the spectroscopic signature of the so-called HB-wrap hydration water, i.e. a collective intermolecular hydrogen bond stretch mode of those water molecules in the first hydration shell which form a 2-dimensional hydration hydrogen-bond network.46 The same could hold for part of the water molecules in the hydration shell of DNA. However, since in this frequency range many contributions overlap, an unambiguous assignment is not possible.
As expected, all resonances assigned to intramolecular DNA modes at 260–280 cm−1, 360 cm−1 and 430 cm−1, are still present. For all electrolytes, we observe an increase in absorption beyond 350 cm−1, which is steeper than that of bulk water (see Fig. 5). This feature is typical for water molecules bound to charged and polar species. We want to note here that we observed the same increase for hydration water molecules (denoted bound water) in liquid phase separated droplets, and assigned them to water molecules that strongly interact with polar groups of organic molecules.47 Whereas, the characteristic increase observed is independent of the electrolyte, the magnitude of the slope is electrolyte specific. Furthermore, we observe an increase around 150–160 cm−1, most pronounced for NaCl.
In order to unravel the anion specificity in the molecular mechanism of cation enrichment, in Fig. 6B and C, we discuss the results obtained from the MD simulations of two prototypes, NaF and NaCl, which both have the same electrostatic interaction with the DNA. We first compare the simulated ion coordination number within the DNA atmosphere and in the bulk. This analysis allows us to focus on the effect of ion-pair interactions in the coordination environment of the ions in the two regions, since any contact ion-pair formation is expected to alter the number of coordinating water molecules. Interestingly, we find – on average – for both systems an equivalent number of water molecules coordinating cations and anions in the bulk and in the DNA atmosphere, i.e. contact ion-pair interactions are similar in the two regions. Thus, in the simulations we find no indication for preferred ion pairing in the DNA atmosphere compared to bulk. Instead, we reveal a similar solvation environment for the ions in the DNA atmosphere and in the bulk, for both NaF and NaCl electrolytes. A more detailed analysis of the ion clusters formed around the DNA shows that the ions preferentially form small clusters of hydrated ions, with a most probable total charge of +1, followed by charge values of 0 and +2, see ESI† for details.
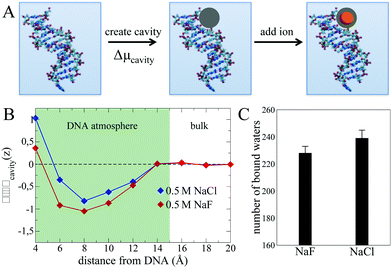
The picture emerging from the MD simulations and THz experiments is that while – as expected-cation enrichment within the DNA atmosphere is driven by electrostatics, the mechanism for the anion specificity is not directly related to contact ion-pairing. In order to further investigate other possibilities, we now adopt the decomposition from ref. 48, and divide the process of solvating an ion within the DNA atmosphere into two steps illustrated in Fig. 6A. The first step consists in creating a cavity within the DNA atmosphere that is large enough to accommodate the ion. This step contributes to the thermodynamics of ion solvation as an energetic penalty, given by the cavitation free energy cost to distort the water H-bond network and to create a cavity (Δμcavity).49 The second step is the insertion of the ion, that is accompanied by a free energy gain due to the interaction of the ion with its coordination environment (including free energy contributions from e.g. solvent reorganization and polarization effects). Despite this second term being the largest when dealing with the hydration of (hydrophilic) ionic species, its contribution to the insertion of an ion from the bulk into the DNA atmosphere is dictated by the difference between the free energy values in the two regions. This difference can be small in cases where a similar coordination environment is achieved by the ions in the two regions, as suggested by our results.
Therefore, we hereafter search for an alternative driving force for explaining the distinct NaCl vs. NaF accumulation within the DNA atmosphere in the Δμcavity term. To this end, we compare in Fig. 6B the Δμcavity profiles as a function of the distance from the DNA in presence of the NaF and NaCl atmospheres. The Δμcavity values are deduced from the simulations by monitoring the fluctuations in the number density of the liquid in a spherical observation volume at various distances from the DNA (see methods section). A spherical observation volume of 3.5 Å radius is adopted, large enough to represent the cavity formed in water by the ions considered in this work. Large/small water density fluctuations result in small/large Δμcavity values.
For both NaF and NaCl systems, the Δμcavity profiles show a well-defined minimum at distances of 5–14 Å, i.e. within the DNA atmosphere. Since Δμcavity is defined as zero in the bulk electrolyte (see caption of Fig. 6B), negative values of Δμcavity imply that it is easier to create a cavity that accommodates the ions within the DNA atmosphere than in the bulk. For small cavities, such as the ones considered here, the free energy cost of cavity formation is well described by the volume-dominated regime of the Lum–Chandler–Weeks theory and it is known to be mostly entropic.49
The predicted minima of Δμcavity within the DNA atmosphere obtained for both NaF and NaCl systems indicate a water-related entropic driving force for ionic excess within the DNA atmosphere. This driving force is unrelated to specific ion–ion configurations and arises from the ability of the ions to enhance density fluctuations within the DNA atmosphere as compared to the bulk. To understand the microscopic mechanism leading to such enhancement, it is important to consider that density fluctuations of water in contact with a surface are larger than in bulk water if water–surface interactions are weak (as in case of hydrophobic interfaces), while they are suppressed by strong water–surface interactions.50,51 Any ion induced enhancement of density fluctuations can be therefore ascribed to the ions affecting the capability of water molecules to interact with the polar sites of the DNA. Such an effect has been extensively investigated in previous studies (see e.g. ref. 8 and 52), showing how the cations compete with water not only for the favourable interaction sites close to the phosphate groups, but also for the interaction sites inside the minor and major groves of the DNA. In this context it is also relevant to consider that halide anions like to be surface species in aqueous systems. However, their speciation at the interface differs due to differences in their polarizability, in the size of their hydration shell and in the anion–water binding energy (see ESI† Fig. S4 for more analyses of size and binding energy for F− and Cl).53–55 In particular, when an aqueous NaX (X = halide) solution is in contact with hydrophobic surfaces (e.g. air) the anions surface propensity was shown to scale in the order F− < Cl− < Br− < I−,55,56 while the order is reversed at hydrophilic surfaces, e.g. Silica and Alumina surfaces, where the ions can interact with the polar groups of the surface.57,58 Therefore, the Cl− and F− anions present in the DNA atmosphere likely populate different areas, with Cl− preferring more hydrophobic surface patches and F− preferring more hydrophilic surface patches. Based on this consideration, one would expect F− to have the largest impact on water density fluctuations, since it can more efficiently influence the amount of bound water molecules interacting with the polar groups of the DNA.
In order to quantify the electrolyte specific change of the DNA hydration motif, we show in Fig. 6C the average number of bound water molecules that interact with DNA in the NaF and NaCl atmosphere as deduced from the MD simulations. Bound water molecules are defined as the water molecules H-bonded to the polar groups of the DNA (see methods for the adopted H-bond definition). As a result, we predict that the number of bound waters is on average smaller for NaF than for NaCl, explaining why larger fluctuations of the water density are recorded in the former compared to the latter case. Ion accumulation within the DNA atmosphere is proposed to be promoted by the capability of the ions to decrease the amount of bound water molecules H-bonded to favourable interaction sites around the DNA, reducing cavitation free energies. As a result, we predict an increased value of Γ+ in a NaF atmosphere compared to a NaCl ion atmosphere, in agreement with previous experiments.11
In order to further test our hypothesis and provide a quantitative experimental measure for the number of bound water molecules interacting with the DNA, we use the steepness of the increase in molar extinction as a measure for the shift in population of water molecules directly bound to the charged/polar groups of the DNA. Thus, we have fitted a slope to the observed εeffDNA+cloud for NaCl and NaF in the frequency range between 380 and 480 cm−1, a frequency range where anion or prominent intramolecular modes are absent. This yields a slope of (0.031 ± 0.002) dm3 mmol−1 and (0.050 ± 0.001) dm3 mmol−1 for NaF and NaCl, respectively. Thus, we find a more rapid increase for NaCl compared to NaF, which we correlate with a higher number of bound water molecules for NaCl compared to NaF. This supports the results of our simulation, which proposes that the number of bound water molecules is increased for NaCl (239) compared to NaF (227).
While we have no simulations for CsF or CsCl, and no ion counting measurements are available for KCl, we applied still the same fit for the other electrolytes. For CsCl, the fit of εeffDNA+cloud in the frequency range between 380 and 480 cm−1 yields a slope of (0.029 ± 0.001) dm3 mmol−1. Thus, by analogy we would expect a similar number of bound water for CsCl as for NaF. Both show a similar cation excess, i.e.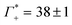 and
and 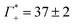 for CsCl and NaF, respectively.
for CsCl and NaF, respectively.
For CsF we observe a steep increase starting from 200 cm−1, which becomes flatter beyond 350 cm−1. Based on the steep increase for frequencies up to 350 cm−1, we would expect a high number of bound water molecules, i.e. a small cation excess, based on the higher frequency part, the slope would be smaller than, and similar to that of CsCl where we propose a small number of bound water, i.e. a larger cation excess. Thus, our qualitative analysis might be restricted due to the large negative partial contribution of the electrolyte in this frequency range or a different molecular mechanism applies.
In summary, while contact ion-pairing is the simplest model to explain the experimentally observed increased cation excess of NaF compared to NaCl, we find here that an extended model is needed, which explicitly includes the free energy contribution of local solvation. We show that the magnitude of cation excess depends on the ability of the electrolyte to perturb the water network at the DNA interface. The cation excess in the ion atmosphere is governed by a competition between cations and the negative charges of the DNA to H-bond surrounding water molecules. Thus, the previously stated correlation with activity can also be explained: While we support the statement that the ion atmosphere composition correlates with the activity, we see this as a consequence of the very same competition between cation-negative charge, cation-water and water-negative charge interaction, but not as a cause. Instead of enhanced contact ion-pairs in the ion atmosphere, we propose that the local changes of DNA hydration, i.e. the number of bound water molecules, are decisive for the observed cation excess and anion depletion. Our results show that ions induced changes in the number of bound water molecules result in enhanced water density fluctuations in the DNA atmosphere, providing an anion-specific free energy stabilization for ions in the surrounding of the DNA, and creating a driving force for ion accumulation.
Materials and methods
Sample preparation
Preparation of electrolyte
In this work, dry NaCl (99.5%) and KCl (99.8%) were purchased from Carl Roth (Karlsruhe, Germany) and VWR Chemical Co. Ltd (USA), respectively. NaF (99.99%), CsCl (99.9%) and CsF (99.9%) were purchased from Sigma-Aldrich Corporation (USA). The aqueous solutions were prepared in ultrapure water without further purification. To monitor the apparent molar volume changes of different solutes and to calculate the salt and water concentrations in the electrolyte solutions, the densities of the solutions were determined with a DMA 58 density meter from Anton Paar GmbH (Graz, Austria). The concentration of the electrolytes prepared was 0.5 M and the electrolytes were used directly in subsequent buffer equilibration.Buffer equilibration
To ensure chemical equilibrium was reached, we employed the same buffer equilibration protocol as in previous studies by centrifugation with a size-selective membrane.11 Lyophilized DNA samples were prepared in 500 μL of 2 mM M-EPPS (M: Na/K/Cs; pH = 7) by titrating MOH with the corresponding sulfonic acid (HEPPS). The DNA solution was pre-concentrated into ∼100 μL by centrifuging with Amicon Ultracel-10 K filters from Merck Millipore (MA, USA) as previously described.11 The subsequent equilibration processes with the appropriate electrolyte were carried out with the same protocol by adding the mass-equivalent pure electrolyte comparing to the flow through (∼400 μL) after each round of buffer exchange. To minimize solvent evaporation, centrifugation was conducted at 4 °C. Equilibration between ions associated with DNA and the bulk ions has been reported to be completed after eight rounds of buffer exchange.11,22 After the buffer exchange, the concentration of 24-bp DNA was determined with a Nanodrop 2000 UV-Vis spectrometer from Thermo Fischer and Scientific (USA) and the pH value of the electrolyte containing dsDNA is 7′′. For further spectroscopic experiments only the sample fraction with the DNA and the equilibrated anion/cation concentration was taken into consideration. Thus, the total number of ions is not conserved in the sample during the preparation process, however the total number of ions is conserved if we would count the number of anions and cations in the sample plus the number of cations and anions in the filtered buffer solution, which was not further used for analysis.Computational methods
Classical MD simulations were carried out using the GROMACS package.59 The SPC/E model60 was chosen for water, while ion parameters that were optimized to reproduce solvation energies were taken from Joung and Cheatham.61 The all-atom ff10 force field was adopted for the DNA.62 This simulation set-up was shown in ref. 63 to provide a realistic description of the ion-counts around the DNA atmosphere in a 0.2–0.7 M concentration range, i.e. at the ion concentration of interest in this work. Electrostatic interactions were computed using a 3D Ewald summation method, with a cut-off of 12 Å for the short-range part of the Coulomb interactions. Lorentz–Berthelot mixing rules were used to model the interactions between all atoms. The DNA dodecamer initial structure for the MD simulations was taken from ref. 64 The DNA was immersed in a pre-equilibrated water cubic box of 130 Å length. The ionic atmosphere consisted either of Na+ and Cl− ions or in Na+ and F− ions, that were added at random positions at least 5.0 Å away from any DNA atom to neutralize the system and reach a desired concentration of ∼0.5 M. A first equilibration run in the NPT ensemble was followed by a second run of 60 ns in the NVT ensemble, with target pressure and temperature of 1 atm and 298 K. After equilibration, NVT simulations runs of 60 ns were performed and used for the analysis. The equations of motions were solved with a time-step of 2 fs (1 fs during the first equilibration run) and stretching motions involving H-atoms were constrained.The theoretical ion-counting is performed from the MD simulations by using the two-partition (domain) approach, introduced by Anderson and Record in a general context,44,45 and successfully employed in ref. 63 for ion-counts in the DNA atmosphere. Within the two-partition formalism, the simulation box is divided in two regions: (i) the DNA atmosphere region accounting for the volume where the ions distribution is affected by the DNA and is non-bulk-like; (ii) the bulk region containing all the volume in the simulation box at a sufficiently large distance from the DNA to recover a bulk-like ions distribution.
The theoretical ion-counts (Γ+/−) are obtained from the number of cations and anions within the DNA atmosphere region (N+/− as reported by the histograms in Fig. 4A):
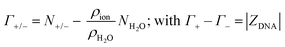 | (15) |
A crucial aspect of this method is that the DNA atmosphere region has to be sufficiently large so that the DNA charge is fully compensated by the number of ions within the atmosphere and the ion distributions in the bulk are not affected by the DNA. This condition is verified in the present model starting from a distance of 15 Å from the DNA surface, as demonstrated by the ion counts in Fig. 4A, that satisfy the condition Γ+ − Γ− = |ZDNA|, and by the cavitation free energy profiles in Fig. 6, that show a bulk-like behaviour for distances from the DNA > 14 Å.
The ions coordination numbers reported in Fig. 4 have been obtained with ion–oxygen distance cut-off values of 3.0, 3.2 and 3.8 Å for F−, Na+ and Cl− respectively. The dependence of the results on the chosen cut-off value has been tested to ensure the robustness of the resulting trends in ions coordination.
The free energy cost to form a cavity as a function of the distance from the DNA, Δμcavity (shown in Fig. 6B), is calculated from the MD simulations by monitoring the probability Pv(0) to find empty volumes, v, within the liquid:49,51,65
| Pv(0) = e−βΔμcavity | (16) |
For the analysis of the bound water molecules, the H-bonds are defined using the standard distance and angle criterion from Luzar and Chandler,66 with O–X distance cut-off of 3.5 Å and H–O–X angle in the 0–30° range. Different criteria have been tested with H–O–X angle in the 0–40° to ensure that our results are not biased by the chosen criterion.
Author contributions
C. Y. Ma carried out the THz measurements, S. Pezzotti carried out MD simulations, M. Gebala provided the dsDNA. All authors discussed the data and contributed new ideas. C. Y. Ma, S. Pezzotti, G. Schwaab analyzed the data. C.Y. Ma, S. Pezzotti, G. Schwaab and M. Havenith wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Havenith acknowledges funding by the ERC Advanced Grant 698437 THz calorimetry. This work is part of the Cluster of Excellence RESOLV (EXC 2033) funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy-EXC 2033-390677874-RESOLV. D. Herschlag is supported by the Grant (NIGMS 1R01GM132899).References
- D. E. Draper, D. Grilley and A. M. Soto, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 221–243 CrossRef CAS PubMed
.
- D. E. Draper, Biophys. J., 2008, 95, 5489–5495 CrossRef CAS PubMed
.
- S. Shazman and Y. Mandel-Gutfreund, PLoS Comput. Biol., 2008, 4, e1000146 CrossRef PubMed
.
- A. Re, T. Joshi, E. Kulberkyte, Q. Morris and C. T. Workman, Methods Mol. Biol., 2014, 1097, 491–521 CrossRef CAS PubMed
.
- K. Hamasaki and A. Ueno, Bioorg. Med. Chem. Lett., 2001, 11, 591–594 CrossRef CAS PubMed
.
- C. Faber, H. Sticht, K. Schweimer and P. Rösch, J. Biol. Chem., 2000, 275, 20660–20666 CrossRef CAS PubMed
.
- C. F. Anderson and M. T. Record Jr, Annu. Rev. Phys. Chem., 1995, 46, 657–700 CrossRef CAS PubMed
.
- J. Lipfert, S. Doniach, R. Das and D. Herschlag, Annu. Rev. Biochem., 2014, 83, 813–841 CrossRef CAS PubMed
.
- K. A. Sharp and B. Honig, Curr. Opin. Struct. Biol., 1995, 5, 323–328 CrossRef CAS PubMed
.
- Y. Bai, M. Greenfeld, K. J. Travers, V. B. Chu, J. Lipfert, S. Doniach and D. Herschlag, J. Am. Chem. Soc., 2007, 129, 14981–14988 CrossRef CAS PubMed
.
- M. Gebala, G. M. Giambaşu, J. Lipfert, N. Bisaria, S. Bonilla, G. Li, D. M. York and D. Herschlag, J. Am. Chem. Soc., 2015, 137, 14705–14715 CrossRef CAS PubMed
.
- R. Das, T. Mills, L. Kwok, G. Maskel, I. Millett, S. Doniach, K. Finkelstein, D. Herschlag and L. Pollack, Phys. Rev. Lett., 2003, 90, 188103 CrossRef CAS PubMed
.
- D. R. Jacobson and O. A. Saleh, Nucleic Acids Res., 2017, 45, 1596–1605 CAS
.
- B. Jayaram and D. Beveridge, Annu. Rev. Biophys. Biomol. Struct., 1996, 25, 367–394 CrossRef CAS PubMed
.
- C. M. Knobler and W. M. Gelbart, Annu. Rev. Phys. Chem., 2009, 60, 367–383 CrossRef CAS PubMed
.
- S.-J. Chen, Annu. Rev. Biophys., 2008, 37, 197–214 CrossRef CAS PubMed
.
- G. C. Wong and L. Pollack, Annu. Rev. Phys. Chem., 2010, 61, 171–189 CrossRef CAS PubMed
.
- B. E. Cohen, T. B. McAnaney, E. S. Park, Y. N. Jan, S. G. Boxer and L. Y. Jan, Science, 2002, 296, 1700–1703 CrossRef CAS PubMed
.
- I. T. Suydam and S. G. Boxer, Biochemistry, 2003, 42, 12050–12055 CrossRef CAS PubMed
.
- M. Y. Berezin, H. Lee, W. Akers and S. Achilefu, Biophys. J., 2007, 93, 2892–2899 CrossRef CAS PubMed
.
- M. A. Voinov and A. I. Smirnov, Electron Paramagn. Reson., 2011, 22, 71–106 CAS
.
- M. Gebala, S. Bonilla, N. Bisaria and D. Herschlag, J. Am. Chem. Soc., 2016, 138, 10925–10934 CrossRef CAS PubMed
.
- Ł. Szyc, M. Yang and T. Elsaesser, J. Phys. Chem. B, 2010, 114, 7951–7957 CrossRef PubMed
.
- O. Liubysh, A. Vlasiuk and S. Perepelytsya, Ukr. J. Phys., 2015, 433–442 CrossRef
.
- M. L. Sushko, D. G. Thomas, S. A. Pabit, L. Pollack, A. V. Onufriev and N. A. Baker, Biophys. J., 2016, 110, 315–326 CrossRef CAS PubMed
.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC
.
- M. Rueda, E. Cubero, C. A. Laughton and M. Orozco, Biophys. J., 2004, 87, 800–811 CrossRef CAS PubMed
.
- A. Savelyev and G. A. Papoian, J. Am. Chem. Soc., 2006, 128, 14506–14518 CrossRef CAS PubMed
.
- S. Y. Ponomarev, K. M. Thayer and D. L. Beveridge, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14771–14775 CrossRef CAS PubMed
.
- P. Várnai and K. Zakrzewska, Nucleic Acids Res., 2004, 32, 4269–4280 CrossRef PubMed
.
- Y. Cheng, N. Korolev and L. Nordenskiöld, Nucleic Acids Res., 2006, 34, 686–696 CrossRef CAS PubMed
.
- A. Savelyev and A. D. MacKerell Jr, J. Phys. Chem. B, 2015, 119, 4428–4440 CrossRef CAS PubMed
.
- A. Savelyev and A. D. MacKerell Jr, J. Phys. Chem. Lett., 2015, 6, 212–216 CrossRef CAS PubMed
.
- A. Savelyev and A. D. MacKerell Jr, J. Chem. Theory Comput., 2015, 11, 4473–4485 CrossRef CAS PubMed
.
- A. Savelyev and G. A. Papoian, J. Phys. Chem. B, 2008, 112, 9135–9145 CrossRef CAS PubMed
.
- G. M. Giambaşu, M. K. Gebala, M. T. Panteva, T. Luchko, D. A. Case and D. M. York, Nucleic Acids Res., 2015, 43, 8405–8415 CrossRef PubMed
.
- H.-T. Xu, N. Zhang, M.-R. Li and F.-S. Zhang, J. Mol. Liq., 2021, 332, 115899 CrossRef CAS
.
- G. Schwaab, F. Sebastiani and M. Havenith, Angew. Chem., Int. Ed., 2019, 58, 3000–3013 CrossRef CAS PubMed
.
- S. Funkner, G. Niehues, D. A. Schmidt, M. Heyden, G. Schwaab, K. M. Callahan, D. J. Tobias and M. Havenith, J. Am. Chem. Soc., 2012, 134, 1030–1035 CrossRef CAS PubMed
.
- D. A. Schmidt, O. Z. R. Birer, S. Funkner, B. P. Born, R. Gnanasekaran, G. W. Schwaab, D. M. Leitner and M. Havenith, J. Am. Chem. Soc., 2009, 131, 18512–18517 CrossRef CAS PubMed
.
- P. Schienbein, G. Schwaab, H. Forbert, M. Havenith and D. Marx, J. Phys. Chem. Lett., 2017, 8, 2373–2380 CrossRef CAS PubMed
.
- K. Nadassy, I. Tomás-Oliveira, I. Alberts, J. Janin and S. J. Wodak, Nucleic Acids Res., 2001, 29, 3362–3376 CrossRef CAS PubMed
.
- F. Sebastiani, C. Y. Ma, S. Funke, A. Bäumer, D. Decka, C. Hoberg, A. Esser, H. Forbert, G. Schwaab and D. Marx, Angew. Chem., Int. Ed., 2021, 60, 3768–3772 CrossRef CAS PubMed
.
- M. T. Record Jr and C. F. Anderson, Biophys. J., 1995, 68, 786–794 CrossRef CAS
.
- M. T. Record Jr, W. Zhang and C. F. Anderson, Adv. Protein Chem., 1998, 51, 281–353 CrossRef CAS
.
- V. Conti Nibali, S. Pezzotti, F. Sebastiani, D. Galimberti, G. Schwaab, M. Heyden, M.-P. Gaigeot and M. Havenith, J. Phys. Chem. Lett., 2020, 11, 4809–4816 CrossRef CAS PubMed
.
- J. Ahlers, E. Adams, V. Bader, S. Pezzotti, K. Winklhofer, J. Tatzelt and M. Havenith, Biophys. J., 2021, 120, 1266–1275 CrossRef CAS PubMed
.
- D. Chandler and P. Varilly, Lectures on Molecular- and Nano-scale Fluctuations in Water, 2011, vol. 176, pp. 75–111 Search PubMed.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS
.
- A. J. Patel, P. Varilly and D. Chandler, J. Phys. Chem. B, 2010, 114, 1632–1637 CrossRef CAS PubMed
.
- S. N. Jamadagni, R. Godawat and S. Garde, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 147–171 CrossRef CAS PubMed
.
- P. Auffinger and E. Westhof, J. Mol. Biol., 2000, 300, 1113–1131 CrossRef CAS PubMed
.
- D. D. Kemp and M. S. Gordon, J. Phys. Chem. A, 2005, 109, 7688–7699 CrossRef CAS PubMed
.
- C.-G. Zhan and D. A. Dixon, J. Phys. Chem. A, 2004, 108, 2020–2029 CrossRef CAS
.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2002, 106, 6361–6373 CrossRef CAS
.
- D. Liu, G. Ma, L. M. Levering and H. C. Allen, J. Phys. Chem. B, 2004, 108, 2252–2260 CrossRef CAS
.
- R. Wang, M. DelloStritto, R. C. Remsing, V. Carnevale, M. L. Klein and E. Borguet, J. Phys. Chem. C, 2019, 123, 15618–15628 CrossRef CAS
.
- A. Tuladhar, S. Dewan, S. Pezzotti, F. S. Brigiano, F. Creazzo, M.-P. Gaigeot and E. Borguet, J. Am. Chem. Soc., 2020, 142, 6991–7000 CrossRef CAS PubMed
.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed
.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed
.
- P. Banás, D. Hollas, M. Zgarbová, P. Jurecka, M. Orozco, T. E. Cheatham III, J. Sponer and M. Otyepka, J. Chem. Theory Comput., 2010, 6, 3836–3849 CrossRef
.
- G. M. Giambaşu, T. Luchko, D. Herschlag, D. M. York and D. A. Case, Biophys. J., 2014, 106, 883–894 CrossRef PubMed
.
- H. R. Drew, R. M. Wing, T. Takano, C. Broka, S. Tanaka, K. Itakura and R. E. Dickerson, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 2179–2183 CrossRef CAS PubMed
.
- A. Serva, M. Salanne, M. Havenith and S. Pezzotti, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2023867118 CrossRef CAS PubMed
.
- A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01963e |
| This journal is © the Owner Societies 2021 |