 Open Access Article
Open Access ArticleVacancy diffusion in palladium hydrides†
Jonathan M.
Polfus
 *ab,
Thijs
Peters
*ab,
Thijs
Peters
 a,
Rune
Bredesen
a and
Ole Martin
Løvvik
a,
Rune
Bredesen
a and
Ole Martin
Løvvik
 *a
*a
aSINTEF Industry, Sustainable Energy Technology, PO Box 124 Blindern, Oslo NO-0314, Norway. E-mail: olemartin.lovvik@sintef.no
bDepartment of Chemistry, Centre for Materials Science and Nanotechnology, University of Oslo, PO Box 1033 Blindern, Oslo N-0315, Norway. E-mail: jonathan.polfus@kjemi.uio.no
First published on 4th June 2021
Abstract
The self-diffusion coefficients of palladium in PdHx (x = 0, 0.25, 0.5, 0.75, 1) were studied using density functional theory to obtain the required thermodynamic and kinetic parameters. The enthalpy of migration decreased from 0.95 eV for Pd to 0.78 eV for PdH. The enthalpy of vacancy formation exhibited a substantial decrease from about 1.1 eV in Pd to 0.4 eV in PdH, which was ascribed to successive filling of antibonding states weakening the Pd–Pd bonds. Concurrently, the Arrhenius pre-exponential was significantly reduced from 4.75 × 10−3 cm2 s−1 for Pd to 5.67 × 10−9 cm2 s−1 for PdH due to softening of the vibrational modes that determine the entropy of vacancy formation and initial/transition state frequencies. A linear correlation between the logarithm of the pre-exponential and the activation energy was interpreted as enthalpy–entropy compensation (Meyer–Neldel rule). The Pd self-diffusion coefficients in the hydrides were within 1 order of magnitude of that in pure palladium above 200 °C for hydrogen pressures up to at least 107 Pa.
1. Introduction
Palladium exhibits fast dissociation kinetics of molecular hydrogen at its surfaces and high bulk diffusivity of atomic hydrogen. Combined, these properties constitute the basis for the functional properties of Pd-based materials in several applications. Most notably, Pd-based alloys have been employed as H2 selective membranes for gas separation and membrane reactors,1 as well as fiber-optic H2 sensors.2 Recently, palladium has also been applied as interfacial electrode layer in electrochemical energy conversion devices based on proton-conducting ceramics,3 and as hydrogen reservoir and gate electrode in a protonic solid-state electrochemical synapse.4Hydrogen absorbs into the octahedral interstitial sites of the fcc structure of palladium and causes expansion of the lattice as well as changes to the electron and phonon band structures.5 However, exposure to hydrogen can as well result in a range of structural and microstructural deterioration processes, including embrittlement, cracking and void formation,6–8 which may be ascribed to several aspects. The Pd–H phase diagram exhibits a miscibility gap below 290 °C between a diluted PdHx phase (α) and a concentrated phase (β, 1 ≥ x ≳ 0.6 at room temperature). Exposure to hydrogen can thus result in phase separation and hysteresis in the absorption/desorption isotherms.9 The presence of hydrogen further leads to increased concentrations of metal vacancies due to favorable interactions with hydrogen interstitials through formation of vacancy–hydrogen clusters.10–12 Despite their abundance, monovacancies do not spontaneously coalesce into larger voids due to the significant loss of configurational entropy that would be associated with clustering.12 Void formation therefore appears to be caused by other factors such as decohesion related to so-called hydrogen-enhanced local plasticity.13
Self-diffusion of palladium is central to most of the afore-mentioned degradation processes and can govern the degradation rate and lifetime of the material or device8,14 Dissolution of hydrogen has been reported to result in hydrogen-induced lattice migration and diffusion creep in palladium.15–17 Lacking still are self-diffusion coefficients of palladium in palladium hydrides, and a deeper understanding of their dependence on temperature and composition. Metal diffusion proceeds according to the vacancy mechanism in palladium, and it is reasonable to expect the same mechanism to dominate in palladium hydrides considering their common fcc arrangement of Pd atoms. The diffusivity follows an Arrhenius behavior and can be expressed as
 | (1) |
 | (2) |
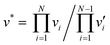 | (3) |
Self-diffusion coefficients of palladium in palladium hydrides are not readily attainable by conventional experimental methods due to the limited stability of the materials at the temperatures required for appreciable diffusion to occur. However, density functional theory (DFT) calculations can be used to directly obtain the required thermodynamic and kinetic parameters according to the above set of equations.20 Accordingly, the present work provides self-diffusion coefficients in palladium hydrides including the underlying contributions from both formation and migration of vacancies, as illustrated in Fig. 1. Furthermore, the study provides detailed insight into the relationship between the self-diffusion coefficients and the physical properties of the materials, notably lattice dynamics and electronic structure.
2. Methods
DFT calculations were performed using the projector augmented wave method implemented in the Vienna ab initio simulation package (VASP) and the generalized gradient approximation due to Perdew, Burke and Ernzerhof (GGA-PBE).21,22 The calculations were carried out with a plane wave cut-off energy of 500 eV and an electronic convergence criterion of 10−6 eV. In addition to Pd and PdH, PdHx (x = 0.25, 0.5, 0.75) were constructed as special quasirandom structures,23 in line with the disordered nature of interstitial hydrogen at ambient and elevated temperatures. A Γ-centered 2 × 2 × 2 Monkhorst–Pack k-point grid was used for the 4 × 4 × 4 supercells containing 256–512 atoms. Migration barriers were calculated using the climbing image nudged elastic band (CI-NEB) method.24 The atomic positions were relaxed until the residual forces were within 0.02 eV Å−1 (0.03 eV Å−1 for selected CI-NEB calculations). Vibrational frequencies were obtained with the finite displacement method and harmonic approximation.The vacancy formation enthalpies ΔHf were determined from vacancy formation energies (ΔEf) and zero-point energy (ZPE) contributions from H and Pd according to
| ΔHf = ΔEf + nΔZPEH + lΔZPEPd | (4) |
 | (5) |
| ΔSfvib = lΔSfv + nΔSfH | (6) |
3. Results and discussion
The optimized lattice parameters showed a linear expansion with hydrogen content according to Vegard's law, from 3.94 Å for Pd to 4.13 Å for PdH (ESI† Fig. S1). The enthalpy of vacancy formation exhibited a strong dependence on composition, decreasing from about 1.1 eV in Pd to 0.4 eV in PdH (Fig. 2(a)). While the zero-point energy contribution to ΔHf was essentially zero from the Pd atoms adjacent to the vacancy, there was a substantial contribution from hydrogen due to its low mass. Notably, the magnitude of ΔZPE increased as a function of hydrogen content, and the total contribution eventually amounted to half of the vacancy formation enthalpy for PdH with six hydrogen atoms adjacent to the vacancy. The vacancies are stabilized by clustering with interstitial hydrogen, but the considered vacancies in PdH0.25 were associated with an average of only one hydrogen atom. These vacancies may therefore be further stabilized by clustering with additional hydrogen atoms. Still, vacancy–hydrogen clustering is less important at higher temperatures where configurational entropy prevails. For instance, vacancy clusters with 1–2 hydrogen atoms were found to predominate above approximately 160 °C in palladium.12 | ||
| Fig. 2 Contributions to the self-diffusion coefficient as a function of PdHx composition: (a) enthalpy of vacancy formation ΔHf and contribution from zero-point energy ΔZPE per H. (b) Enthalpy of migration ΔHm and average bond lengths to nearest Pd and H at the transition state, and minimum distance between Pdnn and adjacent hydrogen atoms. (c) Pre-exponential factor D0 and the contribution from entropy of vacancy formation ΔSfvib and effective frequency v*, with temperature-dependent variables shown for 298 K and 1000 K. The error bars are standard deviations for five different vacancy sites in (a) and the corresponding four transitions states in (b) (ESI†). Lines are guides to the eye. | ||
The origin of the large variation in enthalpy of vacancy formation for PdH0.75 and PdH (Fig. 2(a)) can be understood from the electronic structure of the materials. Fig. 3 shows the electronic density of states of the palladium hydrides and the corresponding Fermi levels. Notably, the Fermi level is shifted to higher energies from PdH0.75, resulting in a destabilization of the system by successive filling of antibonding states, specifically d band Pd t2g–t2g according to previous analysis.25 As these antibonding states are filled, it becomes increasingly easy to form vacancies.
The migration enthalpy ΔHm showed less variation with composition in comparison to the formation enthalpy, ranging from 0.95 eV for Pd to 0.78 eV for PdH (Fig. 2(b)). Moreover, the non-monotonic behavior as a function of hydrogen content indicates at least two competing effects. These can reasonably be ascribed to two structural features with opposite impact on ΔHm: while the distance between the migrating Pd atom and its nearest neighbors at the transition state (PdTS–Pdnn) increases with hydrogen content, the Pdnn atoms are simultaneously pushed closer to adjacent hydrogen atoms, especially for PdH0.5 and PdH0.75 (Fig. 2(b)). The latter aspect is subject to the presence of hydrogen at sites along the direction to which the Pdnn atoms are pushed, and therefore leads to a rather large variation in ΔHm for these compositions. In the case of PdH, the expanded lattice appears to lead to less steric constraints of this kind.
The pre-exponential factor D0 and its major contributions from the effective frequency v* and entropy of vacancy formation ΔSfvib are shown in Fig. 2(c). The entropies of vacancy formation were determined from the vibrational frequencies of the nearest neighbor palladium and hydrogen atoms. On the other hand, the effective frequencies were determined from the vibrational frequencies of nearest neighbor Pd atoms (at the initial and transition state), while hydrogen was considered to be free to rearrange during the migration event.26 The entropy of vacancy formation exhibited a steep decrease for PdH which could be associated with changes in the vibrational entropies of both palladium and hydrogen atoms upon vacancy formation (ESI† Fig. S2). In particular, the contribution to ΔSfvib from Pd switched from positive to negative between PdH0.75 and PdH, most likely due to the weakening of the bulk Pd–Pd bonds as the antibonding states were filled. The contribution to ΔSfvib from the hydrogen atoms was negative for all compositions since the Pd–H bonds were shortened and the vibrational frequencies of hydrogen increased adjacent to the vacancy (ESI† Table S3). The effective frequency showed a limited variation of 1.5 orders of magnitude as a function of hydrogen content. Notably, the effective frequency followed the same trend as ΔHm, which may be understood from the relationship between the bond lengths and dynamics of the palladium atoms at the transition state. Combined, these contributions resulted in a pre-exponential for PdH that is five orders of magnitude lower than for Pd and PdHx up to x = 0.5. The vacancy formation entropy showed relatively little variation with temperature, which translates to a minor non-linearity in the Arrhenius behavior of the diffusion coefficients.
 | ||
| Fig. 4 Correlation between the pre-exponential factor D0 (298.15 K) and activation energy (ΔHf + ΔHm) for PdHx with linear fit. | ||
Correlations between the pre-exponential factor D0 and the enthalpic terms in the activation energy were considered based on the observation of so-called enthalpy–entropy compensation (Meyer–Neldel rule) in a wide range of thermally activated processes. In particular, enthalpy–entropy compensation has been reported for self- and impurity diffusion in metals and on metal surfaces,27,28 hydrogen diffusion in minerals,29 and oxygen diffusion in perovskite oxides.30 As shown in Fig. 4, a linear correlation was obtained between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0 and the activation energy. The correlation with log
D0 and the activation energy. The correlation with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0 was similar for ΔHf while it was not evident for ΔHm. The compensation effect has been largely ascribed to softening of low-frequency modes at the transition state relative to the initial state based on diffusion studies in silicon and aluminum.31 In the present case, however, the change in D0 was mainly determined by the change in the entropy of vacancy formation, which in turn had a significant contribution from the vibrational entropy of hydrogen (ESI† Fig. S2). The contribution to D0 from the relative softening of the vibrational modes at the transition state, i.e., the change in effective frequency, was less pronounced (Fig. 2c and ESI† Table S3).
D0 was similar for ΔHf while it was not evident for ΔHm. The compensation effect has been largely ascribed to softening of low-frequency modes at the transition state relative to the initial state based on diffusion studies in silicon and aluminum.31 In the present case, however, the change in D0 was mainly determined by the change in the entropy of vacancy formation, which in turn had a significant contribution from the vibrational entropy of hydrogen (ESI† Fig. S2). The contribution to D0 from the relative softening of the vibrational modes at the transition state, i.e., the change in effective frequency, was less pronounced (Fig. 2c and ESI† Table S3).
The diffusion coefficients are summarized for the given hydride compositions in the Arrhenius plots in Fig. 5(a). PdH exhibits a distinctly lower activation energy, but also a significantly lower pre-exponential factor than the other compositions, and the resulting diffusivity is higher than that of Pd below 400 °C. The calculated diffusion coefficient of pure palladium is in reasonable agreement with experimental values, although both the pre-exponentials and the activation energies are somewhat different (Fig. 5(a), inset). These discrepancies may be associated with the anomalous non-linear elastic behavior of palladium with a transition at around 600 °C,32 or intrinsic surface errors in the vacancy calculations.33 The obtained enthalpies of formation and migration of vacancies in Pd are in good agreement with similar computational studies.34
 | ||
| Fig. 5 Arrhenius plot of the diffusion coefficients for fixed PdHx compositions (a) and for isobaric conditions (b). The inset in (a) shows a comparison between the calculated self-diffusion coefficient in pure Pd and experimental values from 103Pd impurity diffusion in single- and polycrystalline Pd by Peterson36 and Fillon.37 The shaded regions for PdH0.25 and PdH0.5 in (a) are within the Pd–H miscibility gap. The dotted lines in (b) are guides to the eye. | ||
In evaluating the diffusion coefficients in palladium hydrides, it may be most relevant to consider isobaric conditions. As shown in Fig. 5(b), the considered compositions correspond to a single temperature at the given H2 pressures, outside of the miscibility gap in the Pd–H phase diagram.35 Here, the presence of hydrogen results in an increased diffusion coefficient at all temperatures as long as the hydrogen content is appreciable. The largest difference in diffusivity between Pd and its hydrides is obtained for PdH at the lowest temperatures. For instance, the diffusivity of PdH at 0 °C is the same as that of Pd at 109 °C. Overall, it is reasonable to assert that the self-diffusion coefficients are within 1 order of magnitude of that of pure palladium above 200 °C for hydrogen pressures up to at least 107 Pa (100 bar).
The softening of the vibrational modes of the palladium lattice upon hydride formation is well established, for instance in PdH0.66.38 It may be noted that the calculations of the vibrational frequencies of hydrogen in the disordered structures, i.e., PdH0.25, PdH0.5 and PdH0.75, revealed anharmonicity that may be best described as asymmetry in the potential energy profile for hydrogen (ESI† Fig. S4).5 The disorder resulted in distortion of hydrogen to off-center positions, while hydrogen adjacent to metal vacancies relaxed to well-defined positions with more symmetric potential energy profiles.
Hydrogen embrittlement of palladium reflects the tendency for elastic breakdown and crack formation due to reduced ductility and enhanced localized plasticity in regions saturated with hydrogen.39 The formation of voids has therefore been ascribed to local enrichment of hydrogen that leads to decohesion due to the impaired mechanical properties.13 Accordingly, void formation at grain boundaries may be caused by segregation of hydrogen and vacancy–hydrogen clusters in these regions.8,12 Hydrogen can additionally affect the microstructural features of palladium such as increased dislocation densities,6 presumably influenced by chemical expansion and associated strain. While void formation may be further facilitated by microstrain, abundant monovacancies and clusters,11,12 the present work implies that enhanced vacancy diffusion is not a major factor in void formation.
The detrimental changes in mechanical properties upon hydride formation may be suppressed by addition of alloy elements. For instance, the expanded lattice and increased plasticity of palladium–silver alloys suppress the miscibility gap and internal stresses associated with the α/β phase transition.40,41 At the same time, alloying with Ag leads to filling of the Pd d band,42 and can thereby advance the filling of antibonding states upon hydrogen incorporation. Thus, alloying that leads to improved mechanical properties in relation to the α/β phase transition may also increase the susceptibility of the α-phase towards decohesion in regions locally enriched in hydrogen. Further studies are required for quantitative assessments of the role of alloy elements and the degree of d-band filling on the mechanical properties of palladium hydrides.
4. Conclusions
The self-diffusion coefficients in the palladium hydride system exhibited a complex relationship between the hydrogen content and several concurrent changes in the physical properties of the materials, including bond lengths, unit cell volume, lattice dynamics, and electronic structure. In particular, the overall reduction in the enthalpies of formation and migration of vacancies with increasing hydrogen content was accompanied by a softening of the lattice vibrations that resulted in a significant reduction of the pre-exponential factor. Furthermore, the logarithm of the pre-exponential was determined to correlate linearly with the activation energy of diffusion, which was interpreted as enthalpy–entropy compensation. The resulting self-diffusion coefficients were therefore lower than previous estimates based solely on changes in the vacancy concentration.43Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Research Council of Norway, through the CLIMIT program (Contract No. 281824), and HYDROGEN Mem-Tech AS. Computational resources were provided by Uninett Sigma2 under the projects nn9259k and nn2615k.References
- N. A. Al-Mufachi, N. V. Rees and R. Steinberger-Wilkens, Hydrogen selective membranes: a review of palladium-based dense metal membranes, Renewable Sustainable Energy Rev., 2015, 47, 540–551 CrossRef CAS.
- S. F. Silva, L. Coelho, O. Frazão, J. L. Santos and F. X. Malcata, A review of palladium-based fiber-optic sensors for molecular hydrogen detection, IEEE Sens. J., 2012, 12, 93–102 CAS.
- J. S. Park, H. J. Choi, G. D. Han, J. Koo, E. H. Kang, D. H. Kim, K. Bae and J. H. Shim, High–performance protonic ceramic fuel cells with a PrBa0.5Sr0.5Co1.5Fe0.5O5+δ cathode with palladium–rich interface coating, J. Power Sources, 2021, 482, 229043 CrossRef CAS.
- X. Yao, K. Klyukin, W. Lu, M. Onen, S. Ryu, D. Kim, N. Emond, I. Waluyo, A. Hunt, J. A. del Alamo, J. Li and B. Yildiz, Protonic solid-state electrochemical synapse for physical neural networks, Nat. Commun., 2020, 11, 3134 CrossRef CAS PubMed.
- S. S. Setayandeh, C. J. Webb and E. M. A. Gray, Electron and phonon band structures of palladium and palladium hydride: a review, Prog. Solid State Chem., 2020, 60, 100285 CrossRef CAS.
- Y. Z. Chen, H. P. Barth, M. Deutges, C. Borchers, F. Liu and R. Kirchheim, Increase in dislocation density in cold-deformed Pd using H as a temporary alloying addition, Scr. Mater., 2013, 68, 743–746 CrossRef CAS.
- B. Amin-Ahmadi, D. Connétable, M. Fivel, D. Tanguy, R. Delmelle, S. Turner, L. Malet, S. Godet, T. Pardoen, J. Proost, D. Schryvers and H. Idrissi, Dislocation/hydrogen interaction mechanisms in hydrided nanocrystalline palladium films, Acta Mater., 2016, 111, 253–261 CrossRef CAS.
- T. A. Peters, P. A. Carvalho, J. F. van Wees, J. P. Overbeek, E. Sagvolden, F. P. F. van Berkel, O. M. Løvvik and R. Bredesen, Leakage evolution and atomic-scale changes in Pd-based membranes induced by long-term hydrogen permeation, J. Membr. Sci., 2018, 563, 398–404 CrossRef CAS.
- R. Griessen, N. Strohfeldt and H. Giessen, Thermodynamics of the hybrid interaction of hydrogen with palladium nanoparticles, Nat. Mater., 2016, 15, 311–317 CrossRef CAS PubMed.
- O. Y. Vekilova, D. I. Bazhanov, S. I. Simak and I. A. Abrikosov, First-principles study of vacancy-hydrogen interaction in Pd, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–5 CrossRef.
- R. Nazarov, T. Hickel and J. Neugebauer, Ab initio study of H-vacancy interactions in fcc metals: implications for the formation of superabundant vacancies, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–18 Search PubMed.
- J. M. Polfus, O. M. Løvvik, R. Bredesen and T. Peters, Hydrogen Induced Vacancy Clustering and Void Formation Mechanisms at Grain Boundaries in Palladium, Acta Mater., 2020, 195, 708–719 CrossRef CAS.
- W. Zhong, Y. Cai and D. Tománek, Computer simulation of hydrogen embrittlement in metals, Nature, 1993, 362, 435–437 CrossRef CAS.
- F. Guazzone and Y. H. Ma, Leak Growth Mechanism in Composite Pd Membranes Prepared by the Electroless Deposition Method, AIChE J., 2008, 54, 487–494 CrossRef CAS.
- Z. R. Xu and R. B. Mclellan, Hydrogen enhanced diffusional creep, Acta Mater., 1998, 46, 4543–4547 CrossRef CAS.
- T. B. Flanagan and C. N. Park, Hydrogen-induced rearrangements in Pd-rich alloys, J. Alloys Compd., 1999, 293, 161–168 CrossRef.
- N. Fukumuro, M. Yokota, S. Yae, H. Matsuda and Y. Fukai, Hydrogen-induced enhancement of atomic diffusion in electrodeposited Pd films, J. Alloys Compd., 2013, 580, S55–S57 CrossRef CAS.
- A. D. Leclaire and A. B. Lidiard, LIII. Correlation effects in diffusion in crystals, Philos. Mag. A, 1956, 1, 518–527 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Reaction-rate theory: fifty years after Kramers, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- M. Mantina, Y. Wang, R. Arroyave, L. Q. Chen, Z. K. Liu and C. Wolverton, First-principles calculation of self-diffusion coefficients, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- G. Kresse, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- C. Zhang and A. Alavi, First-principles study of superabundant vacancy formation in metal hydrides, J. Am. Chem. Soc., 2005, 127, 9808–9817 CrossRef CAS PubMed.
- J.-P. Du, W. T. Geng, K. Arakawa, J. Li and S. Ogata, Hydrogen-Enhanced Vacancy Diffusion in Metals, J. Phys. Chem. Lett., 2020, 11, 7015–7020 CrossRef CAS PubMed.
- G. Boisvert, L. J. Lewis and A. Yelon, Many-Body Nature of the Meyer-Neldel Compensation Law for Diffusion, Phys. Rev. Lett., 1995, 75, 469–472 CrossRef PubMed.
- L. Messina, M. Nastar, N. Sandberg and P. Olsson, Systematic electronic-structure investigation of substitutional impurity diffusion and flux coupling in bcc iron, Phys. Rev. B, 2016, 93, 1–18 CrossRef.
- A. G. Jones, Compensation of the Meyer–Neldel Compensation Law for H diffusion in minerals, Geochem., Geophys., Geosyst., 2014, 15, 2616–2631 CrossRef.
- A. V. Berenov, J. L. MacManus-Driscoll and J. A. Kilner, Observation of the compensation law during oxygen diffusion in perovskite materials, Int. J. Inorg. Mater., 2001, 3, 1109–1111 CrossRef CAS.
- S. Gelin, A. Champagne-Ruel and N. Mousseau, Enthalpy-entropy compensation of atomic diffusion originates from softening of low frequency phonons, Nat. Commun., 2020, 11, 1–7 Search PubMed.
- M. Yoshihara and R. B. McLellan, Self-diffusion in the noble metals, Acta Metall., 1981, 29, 1277–1283 CrossRef CAS.
- T. R. Mattsson and A. E. Mattsson, Calculating the vacancy formation energy in metals: Pt, Pd, and Mo, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 1–8 CrossRef.
- S. L. Shang, B. C. Zhou, W. Y. Wang, A. J. Ross, X. L. Liu, Y. J. Hu, H. Z. Fang, Y. Wang and Z. K. Liu, A comprehensive first-principles study of pure elements: vacancy formation and migration energies and self-diffusion coefficients, Acta Mater., 2016, 109, 128–141 CrossRef CAS.
- W. Huang, S. M. Opalka, D. Wang and T. B. Flanagan, Thermodynamic modelling of the Cu-Pd-H system, Comput. Coupling Phase Diagrams Thermochem., 2007, 31, 315–329 CrossRef CAS.
- N. L. Peterson, Isotope Effect in Self-Diffusion in Palladium, Phys. Rev., 1964, 136, 568–574 CrossRef CAS.
- J. Fillon and D. Calais, Autodiffusion dans les alliages concentres fer-palladium, J. Phys. Chem. Solids, 1977, 38, 81–89 CrossRef CAS.
- D. K. Hsu and R. G. Leisure, Elastic constants of palladium and β-phase palladium hydride between 4 and 300 K, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1339–1344 CrossRef CAS.
- W. Zhong, Y. Cai and D. Tománek, Mechanical stability of Pd-H systems: a molecular dynamics study, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 8099–8108 CrossRef PubMed.
- N. I. Timofeev, F. N. Berseneva and V. M. Makarov, New palladium-based membrane alloys for separation of gas mixtures to generate ultrapure hydrogen, Int. J. Hydrogen Energy, 1994, 19, 895–898 CrossRef CAS.
- J. Okazaki, D. A. P. Tanaka, M. A. L. Tanco, Y. Wakui, F. Mizukami and T. M. Suzuki, Hydrogen permeability study of the thin Pd-Ag alloy membranes in the temperature range across the α–β phase transition, J. Membr. Sci., 2006, 282, 370–374 CrossRef CAS.
- I. Coulthard and T. K. Sham, Charge redistribution in Pd-Ag alloys from a local perspective, Phys. Rev. Lett., 1996, 77, 4824–4827 CrossRef CAS PubMed.
- R. B. McLellan and D. Zang, Kinetics of vacancy migration in hydrogenated palladium, Scr. Mater., 1997, 36, 1207–1210 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01960k |
| This journal is © the Owner Societies 2021 |


