Quantum-state-dependent decay rates of electrostatically trapped Rydberg NO molecules

Abstract

Nitric oxide (NO) molecules travelling in pulsed supersonic beams have been prepared in long-lived Rydberg–Stark states by resonance-enhanced two-colour two-photon excitation from the X ²Π_1/2 (v′′ = 0, J′′ = 3/2) ground state, through the A ²Σ⁺ (v′ = 0, N′ = 0, J′ = 1/2) intermediate state. These excited molecules were decelerated from 795 ms⁻¹ to rest in the laboratory-fixed frame of reference, in the travelling electric traps of a transmission-line Rydberg–Stark decelerator. The decelerator was operated at 30 K to minimise effects of blackbody radiation on the molecules during deceleration and trapping. The molecules were electrostatically trapped for times of up to 1 ms, and detected in situ by pulsed electric field ionisation. Measurements of the rate of decay from the trap were performed for states with principal quantum numbers between n = 32 and 50, in Rydberg series converging to the N⁺= 0, 1, and 2 rotational states of NO⁺. For the range of Rydberg states studied, the measured decay times of between 200 μs and 400 μs were generally observed to reduce as the value of n was increased. For some particular values of n deviations from this trend were seen. These observations are interpreted, with the aid of numerical calculations, to arise as a result of contributions to the decay rates, on the order of 1 kHz, from rotational and vibrational channel interactions. These results shed new light on the role of weak intramolecular interactions on the slow decay of long-lived Rydberg states in NO.

---

1 Introduction

Rydberg states of atoms and small molecules, including H₂, N₂, O₂, and NO, are of importance in recombination processes that occur in laboratory, atmospheric, and astrophysical plasmas.^1–6 They are also of interest in studies of chemical dynamics at low temperatures. For example, they can be employed to study ion–molecule reactions, as most recently demonstrated in the case of the H₂⁺ + HD → H₂D⁺ + H reaction, at temperatures as low as 50 mK.^7–10 In this setting the Rydberg electron shields the reaction centre from stray electric fields that would otherwise cause heating. Long-lived Rydberg states of small molecules also offer opportunities for studies of low-energy molecular scattering that are dominated at long range by resonant dipole–dipole interactions,¹¹ and the exploration of the chemistry associated with ultra-long range Rydberg molecules¹² formed of a Rydberg atom or molecule bound to a ground-state atom or molecule through low-energy Rydberg-electron scattering.^13,14 They are also important in tests of molecular quantum mechanics and quantum chemistry, for example, through the precise determination of ionisation and dissociation energies.^15–17 The implementation of general methods for preparing samples of cold molecules in high Rydberg states is of interest in each of these areas, and is also foreseen as a means of producing cold samples of ground-state species following de-excitation.¹⁸ For each of these endeavours a detailed understanding of the lifetimes and decay processes of long-lived Rydberg states is essential.

The large electric dipole moments associated with Rydberg–Stark states of atoms and molecules mean that forces can be exerted on them using inhomogeneous electric fields.^19,20 This has led to the development of the methods of Rydberg–Stark deceleration^21–23 and the implementation of guides,^24–27 beam-splitters,²⁸ decelerators,^29–31 and traps^18,31–36 for atoms and molecules. To implement these experimental techniques it is necessary to prepare Rydberg states with sufficiently long lifetimes, i.e., >10 μs, and small avoided crossing between individual sublevels in the presence of electric fields, that can be traversed diabatically on typical experimental timescales. Both of these requirements can be met in general for small molecules through the preparation of Rydberg states with values of |M_N| ≥ 3 (M_N is the projection of the total angular momentum vector excluding spin, N⃑, onto the z-axis in the laboratory frame of reference).¹⁸ In previous experiments with H₂, the preparation of selected |M_N| = 3 Rydberg–Stark states was achieved by three-photon excitation from the X ¹Σ_g⁺(v = 0, J = 0) ground electronic state using circular polarised vacuum ultraviolet, visible, and infrared laser radiation.^18,37 When these molecules were confined in a cryogenically cooled trap, n-dependent (n is the principal quantum number) decay times on the order of 100 μs, and effects of rotational channel interactions, were observed.³⁸ In the work described here, |M_N| ≥ 3 Rydberg states were prepared in NO by two-photon laser photoexcitation from the ground electronic state with subsequent M_N-mixing arising as a result of intramolecular interactions and effects of static and time-varying electric fields close to the time of photoexcitation.³⁹ Deceleration and trapping of the NO molecules in these long-lived states has permitted studies of slow decay processes over timescales of up to 1 ms that were previously inaccessible.

Studies of the lifetimes, and decay dynamics of high-n, n = 40 to 122, v⁺ = 0 (v⁺ is the vibrational quantum number of the NO⁺ ion core) Rydberg states in NO have been reported previously by Vrakking and Lee.^40,41 This work was performed to aid in the interpretation of excited-state lifetimes observed in ZEKE spectroscopy experiments.⁴² These measurements were performed on timescales of up to ∼1 μs. The results showed that np(0) and nf(2) [n[small script l](N⁺), where [small script l] is the orbital angular momentum quantum number of the Rydberg electron, and N⁺ is the rotational quantum number of NO⁺] Rydberg states in NO have short lifetimes, on the order of ∼1 ns and ∼10 ns, respectively, for this range of values of n in zero-electric-field. This indicated that fast predissociation dominated the decay of these low-[small script l] states. However, when photoexcitation was performed in the presence of sufficiently large electric fields, lifetimes on the order of 100 ns were observed. Calculations reported by Bixon and Jortner⁴³ showed that this lifetime enhancement could be accounted for by considering a combination of electric-field-induced [small script l]-mixing and intramolecular interactions, between each optically accessible short-lived low-[small script l] state and long-lived high-[small script l] states.

Measurements and calculations reported by Goodgame et al.⁴⁴ on the Stark effect in v⁺ = 1 Rydberg states in NO with values of n between 10 and 20, located above the v⁺ = 0 series limit, allowed for the study of intramolecular interactions, and of the lifetimes of the states excited to be estimated from the measured spectral linewidths. For Rydberg states in series converging to excited vibrational states of NO⁺, non-radiative decay by vibrational autoionisation can occur if the interaction between the Rydberg electron and the ion core couples the Rydberg state with the continuum of a lower vibrational series. Rydberg states in the v⁺ = 1 series, that lie above the v⁺ = 0 series limit, can therefore undergo vibrational autoionisation because of coupling to the v⁺ = 0 continuum. From a comparison of calculated and measured spectral linewidths, lifetimes of the low-[small script l] states with v⁺ = 1 and values of n between 10 and 20 were estimated to be between ∼1 ps and ∼50 ps. These lifetimes are dominated by fast non-radiative decay and contain contributions from both predissociation and autoionisation.

Further studies of Rydberg states in NO in electric fields were carried out by Jones et al.⁴⁵ and Patel et al.⁴⁶ to investigate effects of intramolecular interactions on the Stark structure of v⁺ = 0 Rydberg states. These works included laser photoexcitation spectra recorded in electric fields of between 0 and 150 V cm⁻¹, with detection by pulsed electric field ionisation, and by monitoring predissociated fragments by photoionisation. These measurements, combined with the results of numerical calculations, allowed intramolecular couplings of optically accessible np(N⁺) and nf(N⁺) states with neighbouring states to be studied. They also allowed the distribution of np(N⁺) and nf(N⁺) character among the [small script l]-mixed Stark states in the presence of electric fields to be determined. The implementation of two complementary detection methods in these works yielded information on the importance of predissociation in the decay of the states excited, and how this changed in an electric field.

Recently, using a two-dimensional spectroscopy technique based on laser photoexcitation and delayed state-selective electric field ionisation, long-lived Rydberg states in NO were characterised in detail for values of n in the range from 40 to 100.³⁹ States with lifetimes in excess of 10 μs were identified and observed to ionise diabatically. These results indicated that high-|M_N| [small script l]-mixed states with long lifetimes, i.e., states without any short-lived [small script l] ≤ 3 character, were populated upon photoexcitation. That work led to the first experiments to decelerate and electrostatically trap Rydberg NO molecules.⁴⁷ The experiments and calculations reported here build upon these works, and include new high-precision decay-rate measurements for long-lived Rydberg states of different rotational series, and the identification of contributions from weak intramolecular interactions to the measured decay rates.

In the following, the experimental apparatus and techniques are described in Section 2. In Section 3, calculations of the energy-level structure and lifetimes of the Rydberg states in NO in electric fields, and considerations necessary for the implementation of Rydberg–Stark deceleration are discussed. In Section 4, the results of trap decay measurements performed for hydrogenic Rydberg–Stark states with values of n between 32 and 50 are presented and interpreted in terms of the effects of intramolecular rotational and vibrational channel interactions. Finally conclusions are drawn in Section 5.

2 Experiment

A schematic diagram of the apparatus used in the experiments is shown in Fig. 1. A pulsed supersonic beam of NO was generated with a mean longitudinal speed of 810 ms⁻¹. The pulsed valve from which the beam emanated was operated at room temperature at a repetition rate of 25 Hz. After passing through a 2-mm-diameter skimmer, the beam entered the cryogenically cooled region of the apparatus containing a chip-based transmission-line Rydberg–Stark decelerator.^30,33

Fig. 1 Schematic diagram (not to scale) of the chip-based transmission-line Rydberg–Stark decelerator used in the experiments, (a) in the xz-plane, and (b) in the plane perpendicular to the curved decelerator axis close to the detection region. E1 and E2 represent plane metallic electrodes. A1 and A2 are the two detection apertures in electrode E2.

Laser photoexcitation of the NO molecules to Rydberg states was performed between electrodes E1 and E2, as shown in Fig. 1(a), using the n[small script l]X^{+ 1}Σ⁺(v⁺ = 0, N⁺) ← A ²Σ⁺(v′ = 0, N′ = 0, J′ = 1/2) ← X ²Π_1/2(v′′ = 0, J′′ = 3/2) resonance-enhanced two-colour two-photon excitation scheme^39,46,48,49 depicted in Fig. 2. Counter-propagating radiation from a pair of Nd:YAG pumped pulsed dye lasers, with full-width-at-half-maximum (FWHM) spectral widths of 0.17 cm⁻¹, was used for photoexcitation. The frequency-tripled output of the first laser was set to υ₁ = 44193.99 cm⁻¹ (≡226.275 nm), a pulse energy of ∼10 μJ, and linearly polarised in the z dimension to drive the A ²Σ⁺ ← X ²Π_1/2 transition. The frequency-doubled output of the second laser was tuned over the wavenumber range from υ₂ = 30 420 cm⁻¹ to 30 500 cm⁻¹ (≡328.7 nm to 327.8 nm), had a pulse energy of ∼1.6 mJ and was linearly polarised in the y dimension to access np(0) and nf(2) Rydberg states from the intermediate A ²Σ⁺ state. The fundamental wave numbers of the dye lasers were monitored using a fibre-coupled wavelength meter with an absolute accuracy of ±0.005 cm⁻¹. At the time of photoexcitation, gated time-dependent electric potentials could be applied to electrode E1 to enhance population transfer to long-lived [small script l]-mixed hydrogenic Rydberg–Stark states.

Fig. 2 Resonance-enhanced two-colour two-photon excitation scheme employed in the preparation of Rydberg states in NO converging to the lowest vibrational state (v⁺ = 0) of the NO⁺ ion core. Low-n states in the v⁺ = 1 series that are located close to the v⁺ = 0, N⁺ = 0 series limit are also shown. The energies of the levels in this figure were either measured in the experiments,³⁹ or calculated using the methods described in Section 3.1.

After photoexcitation the excited Rydberg molecules travelled for 5.3 μs (∼4 mm) before being loaded into the travelling electric traps of a chip-based transmission-line Rydberg–Stark decelerator.⁴⁷ The decelerator was operated by applying a set of 5 sinusoidally oscillating electric potentials of amplitude V₀ to the segmented centre-conductor electrodes (see Fig. 1), and a constant offset potential of −V₀/2 to electrode E2. Molecules confined in the travelling traps were decelerated from 795 ms⁻¹ to zero mean velocity in the laboratory-fixed frame of reference, over a distance of ∼100 mm, and in a time of ∼250 μs. In each cycle of the experiment the bunch of molecules excited was loaded into a single travelling trap. The curvature of the decelerator in the xz-plane minimised effects of collisions of decelerated and trapped molecules with the trailing component of the molecular beam.³⁴ To minimise blackbody radiation induced transitions during deceleration and trapping the decelerator was enclosed in a heat shield and cooled to 30 K.

The trapped molecules were detected in situ within the decelerator structure by pulsed electric field ionisation (PFI) upon the application of a pulsed potential of +500 V to the side electrodes [see Fig. 1(a)]. The resulting NO⁺ ions were accelerated through the 2-mm-diameter aperture A1 in electrode E2, and collected on a microchannel plate (MCP) detector. Measurements were performed with rapidly switched PFI potentials (rise time ∼50 ns), to detect all Rydberg molecules present in the detection region above A1. To obtain information on the populations of the Rydberg states at the time of ionisation, slowly-rising pulsed potentials could be applied. These had a time-dependence of the form V_Ramp(t) = −V_max[1 − exp(−t/τ)], with the time constant τ = 4.4 μs. When this slowly rising pulsed potential was applied, ionised electrons were accelerated through aperture A1 to the MCP. The shorter flight time of the electrons to the MCP detector (typically <10 ns), than the NO⁺ ions (typically ∼1 μs), permitted the most direct mapping of the detection time of the electrons to the potential applied at the time of ionisation.⁵⁰

The alignment of the apparatus was optimised by performing time-of-flight (TOF) measurements with the decelerator off, and PFI above the on-axis aperture A2 in electrode E2. Decelerated and trapped molecules were detected by PFI above the off-axis aperture A1. PFI at times beyond those for which the trap in the decelerator in which the molecules were confined was brought to rest, allowed studies of the rate of decay of the molecules.

3 Stark effect in Rydberg states of NO

To aid the interpretation of the results of the experiments, calculations of the energy-level structure and lifetimes of the Rydberg states in NO in the presence of externally applied electric fields were performed. The methods used in these calculations follow those reported in ref. 44, 46, 51 and 52, and involved determining the eigenvalues and eigenvectors of the Hamiltonian matrix describing the interaction of the molecule with an external electric field.

Although the J′′ = 1/2 rotational level of the X ²Π_1/2 ground electronic state in NO can be described purely in Hund's angular momentum coupling case (a), excited rotational levels, including the X ²Π_1/2(v′′ = 0, J′′ = 3/2) state used in the laser photoexcitation scheme implemented here, are intermediate cases between Hund's case (a) and Hund's case (b).^53,54 On the other hand, the high Rydberg states of NO, prepared here for deceleration and electrostatic trapping, are most readily described in Hund's case (d).⁴⁴ Calculations of the Stark effect in these Rydberg states were therefore performed in the |n[small script l]N⁺NM_N〉 Hund's-case-(d) basis where n and [small script l] are the principal and orbital angular momentum quantum numbers of the Rydberg electron, respectively, N⁺ is the rotational quantum number of the NO⁺ ion core, N is the total angular momentum quantum number excluding spin , and M_N is the projection of N⃑ onto the z-axis in the laboratory frame of reference. Here this z-axis is defined by the local external electric field vector at the position of the molecule. In this basis, the total Hamiltonian can be expressed as,

H^(d)_tot = H^(d)₀ + H^(d)_Stark, (1)

where H^(d)₀ and H^(d)_Stark are the field-free and Stark Hamiltonians, respectively. H^(d)_Stark contains all contributions arising from the presence of the external electric field.

3.1 Field-free Hamiltonian

For Rydberg states in NO, the field-free Hamiltonian, H^(d)₀ in eqn (1), contains diagonal contributions that represent the energies of the unperturbed Hund's-case-(d) eigenstates. These were calculated using the Rydberg formula. Off-diagonal contributions to H^(d)₀ arise from the interactions of the Rydberg electron with the electric dipole moment, electric quadrupole moment, and electric polarisability of the NO⁺ ion core.^55–57 They also contain contributions from the multi-electron character of NO⁺ which causes sσ–dσ configuration mixing^44,52 (σ represents the λ = 0 projection of the Rydberg electron orbital angular momentum vector onto the internuclear axis).

The general approach used here to construct the matrix H^(d)₀ follows that presented by Goodgame et al.,⁴⁴ which itself is based on the work of Fredin et al.⁵² on the determination of off-diagonal elements of the field-free Hamiltonian from a first order approximation to multichannel quantum defect theory (MQDT). Off diagonal matrix elements arising from the interaction of the Rydberg electron with the electric dipole moment of the NO⁺ ion were calculated using the method described by Bixon and Jortner.⁴³

To construct the Hamiltonian, H^(d)₀, it was separated into a diagonal part, H^(d)_diag, a part that accounts for the interaction of the Rydberg electron with the static electric dipole moment of the NO⁺ ion core, H^(d)_dip, and a part that accounts for the combination of the interaction of the Rydberg electron with the electric quadrupole moment and higher order multipole moments of NO⁺, and the multi-electron character of the molecule, H^(d)_multi, i.e.,

H^(d)₀ = H^(d)_diag + H^(d)_dip + H^(d)_multi. (2)

The Hamiltonian H^(d)_diag is diagonal in the |n[small script l]N⁺NM_N〉 basis with matrix elements given by,

Here, W_v⁺ is the ionisation wavenumber of the Rydberg series converging to the ground electronic state of the NO⁺ cation with vibrational quantum number v⁺. and are the rotational and centrifugal distortion constants for NO⁺. The Rydberg constant adjusted for the reduced mass of NO is R_NO = 109735.31 cm⁻¹, and represents the effective principal quantum number calculated using the Hund's-case-(d) quantum defects . For v⁺ = 0, the rotational constant is B⁺₀ = 1.987825 cm⁻¹, and the centrifugal distortion constant is D⁺₀ = 5.64 × 10⁻⁶ cm⁻¹.⁴⁶

The elements of the Hamiltonian matrix H^(d)_dip are given by,^43,56,57

where e is the electron charge, ε₀ is the vacuum permittivity, μ_NO⁺ is the electric dipole moment of NO⁺ in a coordinate system with its origin at the centre of mass of the molecule, and 〈ν[small script l]|r⁻²|ν′[small script l]′〉 is a radial integral. The angular integral,where the terms in the ( ) and { } parentheses represent Wigner 3J and 6J symbols, respectively, and δ_N,N′ and are Kronecker delta functions. H^(d)_dip leads to interactions between Hund's-case-(d) basis states for which,

Δ[small script l] = ±1; ΔN⁺ = ±1; ΔN= 0; ΔM_N = 0. (6)

The radial integral, in eqn (4), was calculated using the Gilbert-Child⁵⁸ near-threshold approximation with a finite quantum defect such that,

where a_NO is the Bohr radius adjusted for the reduced mass of NO, and . This charge-dipole interaction is strongest between low-[small script l] states, i.e., states with non-zero quantum defects. In these calculations, a static electric dipole moment of NO⁺ of μ_NO⁺ ≃ 0.4 D was used. This was based on the value reported from calculations, at the equilibrium internuclear separation, for the X^{+ 1}Σ⁺ state of the NO⁺ ion.^59–62

The elements of the Hamiltonian matrix H^(d)_multi can be expressed as,⁴⁴

withwhere represents the Hund's-case-(b) to Hund's-case-(d) frame transformation, and are Hund's-case-(b) matrix elements.

For Rydberg states converging to the ¹Σ⁺ state of NO⁺ with Λ⁺ = 0 (Λ⁺ is the projection of the total electron orbital angular momentum vector of the NO⁺ cation onto the internuclear axis), the projection of the total orbital angular momentum vector in the neutral NO molecule onto the internuclear axis is Λ = λ.⁵² With this in mind can be expressed as,^37,44,63,64

Note that the Rydberg-electron spin and spin projection are common to Hund's-case-(b) and Hund's-case-(d) so are not considered in these transformations.⁶³

In NO, the configuration mixing of importance in the work described here occurs predominantly between the sσ ([small script l] = 0, Λ = 0) and dσ ([small script l] = 2, Λ = 0) Hund's-case-(b) basis states, and therefore results in [small script l]-mixing of the Rydberg eigenstates. In Hund's-case-(b), the corresponding matrix elements, that account for these effects of configuration mixing, are,^44,52

where θ_sd = −38.7° is the sσ–dσ mixing angle,⁵² and μ^(b)_{[small script l]Λ} are the Hund's-case-(b) quantum defects. Taking this into account, the complete sets of selection rules for the intramolecular interactions accounted for in H^(d)_multi are,

Δ[small script l] = 0, ±2; ΔN⁺ = ±2; ΔN = 0; ΔM_N = 0, (12)

where the Δ[small script l] = ±2 interactions only occur between basis states with [small script l] = 0 and [small script l]′ = 2, and vice versa. The Hund's-case-(b) quantum defects, μ^(b)_{[small script l]Λ}, used in the calculations are listed in Table 1. To obtain the Hund's-case-(d) quantum defects, , required in the determination of ν in eqn (3), (4), and (8), a frame transformation was performed such that,

Table 1 Hund's-case-(b) quantum defects, μ^(b)_{[small script l]Λ}, for [small script l] ≤ 3 from ref. 46

		Λ
		0	1	2	3
[small script l]	0	0.210
	1	0.7038	0.7410
	2	0.050	−0.053	0.089
	3	0.0182	0.0172	0.00128	0.0057

---

3.2 Stark Hamiltonian

In an electric field F⃑ = (0, 0, F_z), the Hund's-case-(d) Hamiltonian in eqn (2) can be extended to include contributions from the Stark effect. The resulting perturbation, H^(d)_Stark = eF_zz, has matrix elements given by,^37,65where the integral,This perturbation leads to non-zero off diagonal couplings between states, within the same rotational series, for which Δ[small script l] = ±1, i.e., between states for which,

Δ[small script l] = ±1; ΔN⁺ = 0; ΔN = 0, ±1 (not 0 → 0); ΔM_N = 0. (16)

The radial integrals 〈ν[small script l]|r|ν′[small script l]′〉 on the right-hand side of eqn (15) were evaluated using the Numerov method⁶⁶ with a pure Coulomb potential. Stepwise integration was performed inwards from large r to either the inner classical turning point of the Rydberg electron orbit, or the polarisability radius, r_α, of the NO⁺ ion core whichever was encountered first. The polarisability radius, r_α, was taken to be r_α ≃ (α_NO⁺)^1/3,⁶⁶ where α_NO⁺ ≃ 8 a.u. is the electric dipole polarisability of the NO⁺ cation.^67,68

3.3 Lifetime calculations

Using the eigenvectors obtained following diagonalisation of H^(d)_tot, the lifetimes of the Rydberg states in NO in the presence of an electric field could be determined. From the rates of decay by fluorescence, γ_fl(k), and dissociation, γ_dis(k), of each basis state, denoted |k〉 = |n_k[small script l]_kN⁺_kN_kM_Nk〉, the total decay rate of an eigenstate |i〉 of H^(d)_tot is,where c_ik(F_z) = 〈k|i〉^(F_z) are the coefficients of the corresponding eigenvector in the electric field F_z.

The fluorescence rates γ_fl(k) = 1/τ_fl(k) of the basis states were calculated by considering the zero-field lifetimes, τ_{n[small script l]}, of the hydrogenic Rydberg states averaged over all polarisations. The effect of [small script l]-mixing was then accounted for through the dependence of c_ik(F_z) on the field strength. The fluorescence lifetimes can be expressed as,

where A_{n[small script l],n′[small script l]′} are the Einstein A coefficients, and the primes denote states energetically below the |n, [small script l]〉 state. The values of A_{n[small script l],n′[small script l]′} are given by,⁶⁹with ω_{n[small script l],n′[small script l]′} = (E_{n[small script l]} − E_{n′[small script l]′})/ħ, and ħ the reduced Planck constant.

The dissociation rates, γ_dis(k), required in eqn (17) are dependent upon ν_k and [small script l]_k. This dependence can be expressed as,⁴³

where R_dis([small script l]_k) is the dissociation rate parameter for a basis state in the v⁺ = 0 series with [small script l] = [small script l]_k. The dissociation rate parameters for Rydberg states in the v⁺ = 0 series that are available in the literature for values of [small script l] ≤ 4, and were used in the calculations described here, are presented in Table 2. For higher values of [small script l], R_dis([small script l]) was assumed to be zero.

Table 2 Dissociation rate parameters, R_dis([small script l]), for v⁺ = 0 states in NO (see text for details)

[small script l]	R dis([small script l])(s^−1)	Origin
a Arbitrarily partitioned in ref. 43 from [Rdis(0) + Rdis(2)]/2πc ≃ 1500 cm^−1. b From ref. 41 and 43. c From ref. 51 and 70.
0	9.42 × 10^13
1	3.03 × 10^14
2	1.88 × 10^14
3	8.10 × 10^12
4	1.60 × 10^11

---

The calculated lifetimes, τ_0(i) = 1/γ_0(i), of the n = 38, N⁺ = 2 Rydberg states in the v⁺ = 0 series with M_N = 0, 2, and 4 are shown in Fig. 3(a), (b), and (c), respectively. In each panel, the 2N⁺ + 1 = 5 Stark manifolds can be seen. The results of all calculations shown in this figure were obtained for an electric field of 5 V cm⁻¹. In this field sufficient [small script l]-mixing has occurred for the calculated lifetimes to provide a reasonable representation of those of the same states in higher fields, while Stark states with different values of n remain clearly distinguishable allowing for ease of interpretation of the results. For low values of |M_N|, i.e., |M_N| ≤ 2, dissociation represents the dominant contribution to the decay of the excited states and the lifetimes of the states in the different Stark manifolds overlap. For larger values of |M_N|, dissociation plays a less important role, and the manifolds of states decay predominantly by fluorescence and therefore have distinguishable lifetimes.

Fig. 3 Calculated lifetimes of Rydberg–Stark states in NO with n = 38, N⁺ = 2, and v⁺ = 0 for (a) M_N = 0, (b) M_N = 2, and (c) M_N = 4. The wave numbers on the horizontal axis are shown relative to the v⁺ = 0, N⁺ = 0 series limit. All calculations were performed for an electric field of 5 V cm⁻¹.

The high dissociation decay rates of the low-[small script l] ([small script l] ≤ 3) basis states, which are between ∼10⁸ s⁻¹ and ∼5 × 10⁹ s⁻¹ for n = 38, dominate over the fluorescence decay rates (∼10⁴ s⁻¹ for n = 38) of these states. On the other hand, for high-[small script l] basis states ([small script l] ≥ 4) the total decay rates are smaller, with fluorescence rates ranging from ∼10² s⁻¹ to ∼10⁴ s⁻¹ and dissociation rates <3 × 10⁶ s⁻¹. Because of the significant reduction in the dissociation rates as the value of [small script l] increases, only the dissociation of basis states with [small script l] ≤ 4 were considered in calculations. With this in mind, mixed states, with some high-[small script l] character and some low-[small script l] character, can have significantly reduced lifetimes compared to those of the higher-[small script l] states in zero-electric-field. This can be seen in Fig. 3(a), where all possible [small script l] values are present for M_N = 0, with significant low-[small script l] character mixed into all Stark states. The lifetimes of states with M_N = 0 are all <1 μs, i.e., they decay predominately by dissociation even in weak electric fields.

When |M_N| > 0 not all low-[small script l] basis states contribute to the [small script l]-mixed Stark states. However individual low-[small script l] states are not absent from all Stark manifolds with the same value of |M_N|. Contributions from basis states with particular values of N⁺ and [small script l] reduce when |M_N| > |N⁺ − [small script l]|, and are completely absent when |M_N| > N⁺ + [small script l]. Therefore, in the example case with N⁺ = 2, to prevent [small script l] ≤ 3 basis states mixing into at least one of the Stark manifolds populated, it is necessary for |M_N| to be greater than or equal to 2. The effect this has on the lifetimes can be seen in Fig. 3(b and c). When M_N = 2 [Fig. 3(b)], only one of the N⁺ = 2 Stark manifolds has no [small script l] ≤ 3 character. This manifold is easily identifiable as that with lifetimes between ∼10 μs and ∼1 ms. The shorter lifetimes towards the centre of this manifold reflect the presence of an [small script l] = 4 component which still causes some dissociative decay.

For the case in which M_N = 4 [Fig. 3(c)], the Stark manifolds are clearly distinguishable by the lifetimes of their component states. In the manifold with the shortest lifetimes (∼10 ns) the lowest [small script l] basis states present are those for which [small script l] = 2. Whereas, in the manifold with the longest lifetimes (∼1 ms) [small script l] ≥ 6. In between these extreme cases the lowest [small script l] basis state present lies between these values. In these data it is therefore possible to distinguish between manifolds of states that decay predominantly by dissociation and contain low-[small script l] ([small script l] ≤ 3) character, and those with only high-[small script l] ([small script l] ≥ 4) character for which decay by fluorescence dominates. The asymmetry in the lifetimes of the states of the Stark manifolds with [small script l] ≤ 3 character in Fig. 3, arises because the low-[small script l] states are not degenerate with those of higher [small script l] in zero-field.

3.4 Considerations for the implementation of Rydberg–Stark deceleration

An example of a Stark map calculated by diagonalising H^(d)_tot, and encompassing the wavenumber region around the field-free 38(2) state, is displayed in Fig. 4. The energy-level structure for states with M_N = 0, 2, and 4 is displayed in Fig. 4(a), (b), and (c), respectively. The quantum numbers used to label the individual states on the left-hand side of each panel in this figure indicate the dominant character in zero electric field. In this labelling scheme, a distinction is made between non-degenerate low-[small script l] ([small script l] ≤ 3) states, for which the dominant [small script l] character can be determined in weak fields, and high-[small script l] ([small script l] ≥ 4) degenerate states.

Fig. 4 Calculated Stark maps for v⁺ = 0 Rydberg states in NO with (a) M_N = 0, (b) M_N = 2, and (c) M_N = 4. The wave numbers on the vertical axis are shown relative to the v⁺ = 0, N⁺ = 0 series limit.

For Rydberg–Stark deceleration and electrostatic trapping,^18,71 [small script l]-mixed Stark states with positive Stark energy shifts, i.e., low-field-seeking (LFS) states, are required. These states must have lifetimes greater than ∼10 μs, and evolve diabatically through any avoided crossings in the Stark map in the time-dependent electric fields used for deceleration and trapping.¹⁸ These requirements demand that contributions from short-lived, non-degenerate low-[small script l] basis states are minimised. This can be achieved, as seen, e.g., from the data in Fig. 3, by populating states with high values of |M_N|, i.e., |M_N| ≥ 3.¹⁸

The effect of increasing the value of |M_N|, on the Stark energy level structure of the Rydberg states, can be seen in Fig. 4. For M_N = 0 [Fig. 4(a)], basis states with all values of [small script l] are present in the Stark map. Contributions from the low-[small script l] states in this case lead to short lifetimes and large avoided crossings for LFS states. For larger values of |M_N|, e.g., |M_N| = 4 in Fig. 4(c), basis states with [small script l] < |M_N| − N⁺ are absent. The absence of these low-[small script l] states results in longer lifetimes and smaller avoided crossing throughout the Stark map.

Rydberg states with |M_N| ≥ 3 can be selectively populated by resonance-enhanced multi-photon excitation with circularly polarised laser radiation as achieved, e.g., in the case of H₂.¹⁸ They can also be populated by M_N-mixing in collisions and in the presence of time-varying electric fields.^72,73 In this latter case, deceleration and electrostatic trapping acts to filter the long-lived high-|M_N| components of an ensemble of excited molecules. This filtering of long-lived high-|M_N| states occurs because of the finite time required for deceleration, which is only effective for molecules in long-lived Rydberg states, and the requirement to undergo diabatic traversal of avoided crossings in the deceleration fields, that only occurs with high probability for high values of |M_N|.

The two-colour two-photon laser photoexcitation scheme used in the work reported here led to the population of long-lived hydrogenic Rydberg–Stark states in NO through collisions and the effects of time-varying electric fields, as demonstrated previously by state-selective electric field ionisation measurements.³⁹ Although direct measurements of the lifetimes of the states excited were not made previously, the geometry of the apparatus meant that lifetimes in excess of 10 μs were required for the excited molecules to be detected. This observation, in conjunction with the calculated lifetimes in Fig. 3, suggest that hydrogenic Rydberg–Stark states without any low-[small script l] ([small script l] ≤ 3) character, i.e., states with |M_N| ≥ 3, were therefore populated.

4 Results

The methods of Rydberg–Stark deceleration and electrostatic trapping of NO molecules in long-lived Rydberg–Stark states that were employed in the work reported here, have allowed detailed studies of the decay of these excited states on time scales up to 1 ms. Experiments were performed to investigate: (i) the range of values of n and N⁺ of the Rydberg states that could be efficiently decelerated and electrostatically trapped in the apparatus, (ii) the effects of transitions induced by blackbody radiation on the Rydberg state populations in the trap, and (iii) the range of trapping times over which quantum-state-dependent decay rates of the molecules from the trap could be reliably determined. The results of this work, to characterise and validate the measurement methodology are described in the following in Section 4.1. Measurements of quantum-state-dependent decay rates of molecules from the trap are then presented in Section 4.2. The interpretation of these results, in terms of effects of rotational and vibrational channel interactions, are discussed in Sections 4.4 and 4.3, respectively.

4.1 Trap decay measurements

To measure rates of decay of electrostatically trapped Rydberg NO molecules, laser photoexcitation and Rydberg–Stark deceleration were performed as described in Section 2. When the traps in which the molecules were confined were brought to rest, at time t_trap = 0 μs in the following, in situ detection by PFI was performed for times up to t_trap = 1 ms. Examples of the results of such trap decay measurements, for molecules photoexcited on the 38f(2) resonance (υ₂ = 30458.37 cm⁻¹), can be seen in Fig. 5. There are two main components to the decay dynamics observed in these data: (i) at early trapping times a fast reduction in signal is observed, reflecting the decay of the Rydberg states predominantly populated upon photoexcitation, and (ii) at later times this reduction slows down reflecting the presence of some molecules in states with longer lifetimes that remain in the trap at late times.^47,74

Fig. 5 Decay of trapped Rydberg NO molecules, photoexcited on the 38f(2) resonance at υ₂ = 30458.37 cm⁻¹, with (V_Mod = 7.5 V) and without (V_Mod = 0 V) a 50 MHz gated sinusoidal potential applied to the electrode E1 at the time of photoexcitation (see text for details). For both measurements V₀ = 149 V and the data were normalised to the NO⁺ signal recorded at time t_trap = 0 μs.

The data indicated by the open squares in Fig. 5 represent measurements made upon laser photoexcitation in nominally zero electric field, V_Mod = 0 V. However, because the mechanism by which long-lived Rydberg–Stark states are populated close to the time of laser photoexcitation depends on M_N-mixing that occurs in time-varying electric fields, this can be enhanced by applying a rapidly-varying field in the excitation region when the laser radiation is present. The effect of this sinusoidal field modulation, generated by applying a gated sinusoidally oscillating electric potential to electrode E1 (see Fig. 1) with an amplitude of V_Mod = 7.5 V and a frequency of 50 MHz for a time of 50 ns, can be seen by comparing the data recorded with (blue circles) and without (orange open squares) this modulation. The rapid modulation of the field in the excitation region resulted in a factor of ∼30 increase in the NO⁺ signal detected by PFI, compared to photoexcitation performed with V_Mod = 0 V, and hence an increase in the number of molecules in long-lived Rydberg–Stark states that were trapped. The corresponding increase in signal meant that upon the application of this field modulation, molecules could be observed in the trap for times up to 1 ms. Without this field modulation the NO⁺ signal reduced to the level of the background noise after a trapping time of ∼500 μs. The introduction of this field modulation does not change the measured decay time constants from the trap at early times. An exponential function fitted to both sets of data in Fig. 5, for trapping times between 0 and 500 μs, resulted in decay time constants of 366 ± 6 μs and 377 ± 21 μs for the cases with and without the modulation, respectively. From this it is concluded that rapid electric field modulation close to the time of laser photoexcitation leads to the population of Rydberg–Stark states with similar characteristics to those populated as a result of effects of electric field noise, and the presence of ions. In the following, all measurements were therefore performed with the 50 MHz sinusoidal potential, of amplitude V_Mod = 7.5 V, applied at the time of photoexcitation.

To measure quantum-state-dependent decay rates of the trapped molecules single exponential functions were fit to the experimental data, such as that in Fig. 5, over a range of early trapping times to obtain the decay time constant, τ_decay. To validate the fitting procedure, and minimise spurious effects arising from the motion of the molecules in the trap, the range of trapping times over which the fit was performed was tested to ensure the stability of values of τ_decay obtained. This was done for molecules excited on the 38f(2) resonance shown in Fig. 6(a). In Fig. 6(b) the variation in the values of τ_decay obtained for fixed fit start times of 50 μs or 100 μs, and a range of fit end times can be seen. For end times up to ∼350 μs the value of τ_decay remains constant within the the experimental uncertainties. However at later end times the value of τ_decay gradually increases as the experimental data deviates from a single exponential function. This change in the decay time constant at later trapping times reflects the fact that a range of Rydberg–Stark states were populated close to the time of photoexcitation.⁷⁴ Molecules in shorter lived states decay more quickly from the trap, and therefore at later times only molecules in states with longer lifetimes remain. To minimise the effects of these decay dynamics on the values of τ_decay, the fit end time was chosen to be 350 μs for all measurements described below.

Fig. 6 (a) Measured decay of Rydberg NO molecules, excited on the 38f(2) resonance, from the electrostatic trap, with an example of a fitted exponential function encompassing the times from t_trap = 50 μs to 350 μs. (b) The variation in τ_decay associated with fitting between 50 μs (orange circles) or 100 μs (black open-squares) and the fit end times indicated on the horizontal axis. (c) The variation in τ_decay associated with fitting between the fit start times indicated on the horizontal axis, and 350 μs.

Fig. 6(c) shows the values of τ_decay obtained for a range of fit start times. For trapping times ≤50 μs the value of τ_decay varied with the fit start time. This behaviour is a consequence of the motion of the molecules in the trap after it is brought to rest.^32,47 During deceleration the molecules are predominantly located ahead of the electric field minima of the travelling traps.³⁰ After a trap is stopped the molecules oscillate with a period of ∼50 μs, as they evolve to fill it. From these considerations, the start time of the fitting process was therefore set to 50 μs.

To ascertain the range of Rydberg states suitable for decelerating and electrostatically trapping, a laser photoexcitation spectrum, shown in Fig. 7, was recorded with detection after a trapping time of t_trap = 350 μs. The spectral intensities of each of the features in this spectrum reflect the combined contributions from the efficiency with which long-lived LFS hydrogenic Rydberg–Stark states were populated, the deceleration and trap loading efficiencies, and the excited-state decay rates. The reduced spectral intensities at lower values of n reflect the n² dependence of the maximal electric dipole moments of the Rydberg states, that reduce the deceleration and trapping efficiency for lower n states. The spectral intensities in Fig. 7 also reduce for high values of n. This is a consequence of the lower threshold for electric field ionisation during deceleration and trap loading, and the lifetimes of the states.⁴⁷

Fig. 7 Laser photoexcitation spectrum of long-lived Rydberg states in NO recorded after deceleration and trapping for t_trap = 350 μs, with υ₁ = 44193.99 cm⁻¹, and V₀ = 149 V.

The deceleration and trapping efficiency of the NO molecules depends on effects of intramolecular interactions between the optically accessible np(0) or nf(2) states, and nearby [small script l]-mixed hydrogenic Stark states. The resonances associated with transitions to the nf(2) states in Fig. 7 arise because of their close proximity to, and mixing with, the n(2) hydrogenic Stark states.^39,47 Spectral features that arise from mixing of the np(0) states and hydrogenic Stark states are also observed. Despite the np(0) states being shorter lived that the nf(2) states,^40,41 the hydrogenic states populated in both cases are long lived. Two manifolds of [small script l]-mixed hydrogenic Stark states are accessible upon excitation because of mixing with the np(0) states. These are (i) n′(1) (where n′ ≠ n) hydrogenic Stark states that mix because of accidental degeneracies with np(0) states as a result of intramolecular charge-dipole interactions.^39,43 These coincide with resonances denoted np(0) in Fig. 7. And (ii) n(0) hydrogenic Stark states that mix with the [n + 1]p(0) states in the electric field present close to the time of photoexcitation. These states are denoted n(0) in Fig. 7.

The use of state-selective PFI to detect trapped Rydberg NO molecules allowed information on the time-evolution of the excited state populations to be determined. To achieve this PFI was performed by turning off the trapping potentials, and ∼1 μs later applying a slowly-rising ionising potential V_Ramp(t) to the side electrodes of the decelerator. The time-dependence of V_Ramp(t) is shown Fig. 8(a). The electron signal obtained at a trapping time of t_trap = 0 μs, for molecules excited on the 38(2) and 43(2) resonances, are shown in Fig. 8(b)-(i). From these data a distinction between the electron detection times, and hence the ionisation fields of the molecules, can be identified. The maxima in the signals recorded following excitation on the 38(2) and 43(2) resonances, occur at t_Ramp ∼ 5.9 μs [V_Ramp(5.9 μs) ∼ −160 V] and ∼3.3 μs [V_Ramp(3.3 μs) ∼ −110 V], respectively. Since the maximum in the electron signal associated with the 43(2) resonance occurs earlier than that associated with the 38(2) resonance, it is concluded that excitation on the 43(2) resonance leads to ionisation in smaller electric fields. This is expected from the n-dependence of the ionisation field and previous detailed measurements of the electric field ionisation dynamics of long-lived hydrogenic states in NO.³⁹ The widths of the distributions in Fig. 8(b)-(i) reflect the combined effects of a distribution of Stark states present in the trap at the time of PFI, the inhomogeneity of the ionisation field arising as a result of the electrode geometry in the decelerator, and the motion of the molecules in this time-varying inhomogeneous electric field after the trap is switched off. The tails in the electron signals at late times in Fig. 8(b)-(i) are attributed to secondary electron generation following PFI.

Fig. 8 (a) The potential V_Ramp(t) applied to the side electrodes (see Fig. 1) during state-selective PFI. (b) Measured electron signals following excitation of NO molecules on (i) the 38(2) and 43(2) resonances recorded after a trapping time of t_trap = 0 μs, (ii) the 38(2) resonance at t_trap = 0 μs and t_trap = 400 μs, and (iii) the 43(2) resonance at t_trap = 0 μs and t_trap = 400 μs.

The expected ratio of the ionisation fields for LFS hydrogenic Rydberg–Stark states with different values of n was determined from the ionisation field, F_ion(n), of the outermost LFS Stark state,

F_ion(n) = 2F₀/9n⁴, (21)

where F₀ = 2hcR_NO/ea_NO. For the 43(2) and 38(2) states this ratio is F_ion(43)/F_ion(38) = 0.6. This value is comparable to the ratio of the values of V_Ramp(t) at the maxima of the electron distribution for the molecules excited on the 43(2) and 38(2) resonances of V_Ramp(3.3 μs)/V_Ramp(5.9 μs) ∼ 0.7. It is therefore concluded that the molecules trapped in these states predominately undergoing diabatic electric field ionisation.³⁹

Using this state selective PFI detection scheme, information on the evolution of the excited state populations was also obtained by comparing the electron signals recorded when t_trap = 0 μs and 400 μs. This was done for the 38(2) and 43(2) resonances with the results, scaled such that the signal maximum in each case is 1, are shown in Fig. 8(b)-(ii and iii), respectively. For molecules excited on the 43(2) resonance, no significant change in the general form of the electron TOF distribution was observed between t_trap = 0 μs and 400 μs. For molecules excited on the 38(2) resonance this is not the case. Under these conditions when t_trap = 400 μs the maximum of the electron signal occurred at t_Ramp ∼ 4.8 μs [V_Ramp(4.8 μs) ∼ −140 V], i.e., approximately 1.1 μs before that recorded when t_trap = 0 μs. This suggests that the molecules detected at late times in this case are in higher-n states. From the ratio of the corresponding values of V_trap(t), this shift in the maximum of the electron signal is estimated to correspond to a change in n of ∼+2.

By performing numerical particle trajectory calculations assuming diabatic traversal of all avoided crossings between Stark states,⁴⁷ the typical distribution of the maximum electric fields experienced by molecules when trapped was determined. The mean of this distribution was ∼150 V cm⁻¹. As an estimate of the electric field ionisation rates of the trapped NO molecules in the experiments, it can be determined that for hydrogenic Rydberg–Stark states with n = 38, |m| = 4, k = +33 (n = 43, |m| = 4, k = +38), tunnel ionisation would occur at a rate of ∼10⁻³⁰ s⁻¹ (∼10⁻³ s⁻¹) in this field^75,76 (k = n₁ − n₂ is the difference in the parabolic quantum numbers n₁ and n₂ obtained by solving the Schrödinger equation for a pure Coulomb potential in parabolic coordinates⁷⁷). Hence, it is concluded that electric field ionisation arising from the motion of molecules in the trap does not affect the distribution of states with these values of n populated over time.

In a similar vein, for hydrogenic Stark states with n = 38, |m| = 4, k = +33 (n = 43, |m| = 4, k = +38), the Δn = ±1 and ±2 blackbody transitions rates at 30 K are ∼9 × 10² s⁻¹ and ∼4 × 10² s⁻¹ (∼7 × 10² s⁻¹ and ∼3 × 10² s⁻¹), respectively. At this temperature these depopulation rates scale approximately with n⁻². However, because the molecules are trapped ∼2 mm above a 2-mm-diameter aperture in the heat shield surrounding the decelerator (A1 in Fig. 1), the blackbody field that the molecules interact with has a room temperature component. By considering the fractional solid angle subtended by the aperture at the minimum of the trap this corresponds to approximately 0.25, not accounting for modifications in the spectrum arising from the dimensions of the electrode structure. At 300 K the Δn = ±1 and ±2 blackbody depopulation rates, for n = 38, |m| = 4, k = 33 (n = 43, |m| = 4, k = 38), are ∼1 × 10⁴ s⁻¹ and ∼5 × 10³ s⁻¹ (∼7 × 10³ s⁻¹ and ∼3 × 10³ s⁻¹), respectively. Therefore the total Δn = ±1 and ±2 blackbody depopulation rates for these states at the position of the trap are estimated to be below 0.75γ_BB(30 K) + 0.25γ_BB(300 K) and hence ∼3 × 10³ s⁻¹ and ∼1 × 10³ s⁻¹ (∼2 × 10³ s⁻¹ and ∼1 × 10³ s⁻¹), respectively. These blackbody transition rates are similar for both n = 38 and n = 43. Therefore any blackbody-induced changes in the electron distribution, measured by PFI, are not expected to differ for the molecules excited to the 38(2) and 43(2) states. Consequently, the change in the n = 38 electron distribution with trapping time [see Fig. 8(b)-(ii)] is interpreted to reflect the initial population of the Rydberg states close to the time of photoexcitation and before deceleration and trapping. Excited states with longer lifetimes remain in the trap for longer times. Hence if an ensemble of molecules is prepared in a range of states, with different lifetimes, the measured distribution of states populated in the trap will change over time. This behaviour has been discussed previously by Seiler et al. in the interpretation of experiments with electrostatically trapped Rydberg H atoms.⁷⁴ In the case of interest here, this suggests that excitation of the NO molecules on the 38f(2) resonance resulted in the population of at least two Rydberg states with different values of n(N⁺), while excitation on the 43f(2) resonance lead predominantly to the population of states with a single set of values of n(N⁺).

4.2 Decay rate measurements

Measurements of the trap decay time constants, τ_decay, for NO molecules in n(0), n(1), or n(2) Stark states were performed for values of n between 32 and 50. The value of τ_decay was determined from each of these measurements by fitting a single exponential function to the experimental data between t_trap = 50 μs and 350 μs, as described in Section 4.1. The weighted mean and standard deviation of up to 6 separate measurements of τ_decay for each set of values of n(N⁺) were calculated. These values of τ_decay obtained for the n(0), n(1), and n(2) states, with V₀ = 149 V, can be seen in Fig. 9. For reference, the decay time constants of the 38(2) and 43(2) states in this figure were τ_decay = 346.2 ± 3.4 μs and 290.0 ± 4.7 μs, respectively.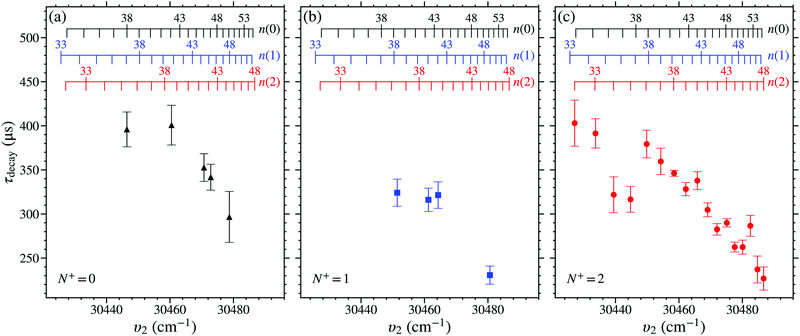

Fig. 9 Measured values of τ_decay, for V₀ = 149 V, of Rydberg–Stark states in NO with (a) N⁺ = 0, (b) N⁺ = 1, and (c) N⁺ = 2.

From the measured trap decay times in Fig. 9 it is seen that there is a general trend for the measured value of τ_decay to decrease with increasing values of n, and therefore also increasing excitation wavenumber, υ₂. This behaviour occurs for states in each N⁺ series studied. For the n(0) and n(1) states this trend is seen for n ≥ 40. For the N⁺ = 2 series, the general reduction in the value of τ_decay with n begins at lower values of n. But for n = 34, 35, 40, 43, 45, and 46, deviations from this general behaviour are observed. For n = 34 and 35 the measured values of τ_decay are shorter than those of the surrounding states that follow the general trend. While, for n = 40, 43, 45, and 46 the measured values of τ_decay are longer.

In the hydrogen atom, the fluorescence lifetimes of [small script l]-mixed Rydberg states scale approximately with n⁴.⁷⁷ Therefore, the observed general reduction in τ_decay with n for long-lived ‘hydrogenic’ Rydberg–Stark states in NO in Fig. 9 indicates that intramolecular interactions with short-lived states must occur. These interactions must in general increase with n. However, for particular values of n at which deviations from this general trend occur, additional contributions from interactions with more energetically localised states must arise.

4.3 Vibrational channel interactions

The general reduction in the measured values of τ_decay as the value of n, and hence υ₂, increase in the data in Fig. 9, occurs because of weak intramolecular interactions with short-lived low-n electronic states in series that converge to the X^{+ 1}Σ⁺(v⁺ = 1, N⁺) state of NO⁺. As can be seen in the energy-level diagram in Fig. 2, n = 7 states in the v⁺ = 1 series lie above, but close to, the v⁺ = 0, N⁺ = 0 series limit. The lifetimes of these states in the v⁺ = 1 series are dominated by fast non-radiative decay processes, i.e., a combination of predissociation and vibrational autoionisation.⁴⁴ Transitions to these states have spectral widths of ∼5 cm⁻¹, and hence they are estimated to have lifetimes of ∼1 ps.⁴⁴ Studies have been reported previously of the Δv⁺ ≠ 0 vibrational channel interactions in NO between Rydberg states in series converging to the v⁺ = 1 series limit, and the v⁺ = 0 continuum that give rise to autoionisation.^44,78 In the case of interest here these same vibrational channel interactions are seen to persist between states with v⁺ = 0 and v⁺ = 1 below both series limits.

To evaluate the effects of these vibrational channel interactions in the experiments here, calculations of τ_decay were performed including contributions from the v⁺ = 0 fluorescence and dissociation decay rates, as described in Section 3.3. In these calculations the interactions between states in the v⁺ = 0 and v⁺ = 1 series were treated semi-empirically. The amount of low-n, v⁺ = 1 character mixed into a v⁺ = 0 Rydberg–Stark state |i〉 was described by the value of a Lorentzian function,

at the off-resonance wavenumber E_i/hc of the Rydberg–Stark states for which the trap decay time was measured. E_v⁺=1/hc is the wavenumber of the peak of the Lorentzian function, Γ_v⁺=1 is the v⁺ = 1 spectral width (Γ_v⁺=1 = 1/2π c τ _v⁺=1 where τ_v⁺=1 ∼ 1 ps), and a_(N⁺) is a scaling factor. In the interpretation of the experimental data in Fig. 9, E_v⁺=1 and a_(N⁺) were chosen to be fit parameters. Their values depended on the dominant N⁺ character of the state |i〉. The total decay rate, γ_tot(i), of the state |i〉 was then considered to be,where γ_v⁺=1 = 1/τ_v⁺=1 is the v⁺ = 1 decay rate, and γ_0(i) is given by eqn (17). The decay time constant of the state |i〉 was then τ_tot(i) = 1/γ_tot(i). This approach allowed the v⁺ = 1 character of the n(N⁺) Stark states prepared in the experiments to be estimated.

Because the data in Fig. 9 were recorded for times greater than 250 μs after laser photoexcitation, the decay rates after this time were calculated using a similar procedure to that employed by Bixon and Jortner.⁴³ This involved considering the population of all accessible short and long lived n(N⁺) Stark states, each of which decay exponentially. The resulting exponential functions were summed,

to give the total Rydberg state population, P(t), where t = 0 μs corresponds to the photoexcitation time. A single exponential function was then fit to the results of these calculations between t = 300 μs and 600 μs, i.e., between the times corresponding to t_trap = 50 to 350 μs. Because the deceleration and trapping process only accepted the outer LFS Rydberg–Stark states, this procedure was implemented for the outer quarter of the Stark manifold for each value of n(N⁺) to obtain the calculated time constant τ_calc.

Calculations of τ_calc were performed using fixed values of the electric field, F_z, and M_N. The value of F_z was taken to be equal to the time-averaged field experienced by the molecules in the electrostatic trap obtained from numerical particle trajectory calculations.⁴⁷ For V₀ = 149 V this field was F_z = 95 V cm⁻¹, and was approximately constant across the range of values of n studied. The values of M_N were restricted to |M_N| > |N⁺ − 3| such that at least one of the 2N⁺ + 1 Stark manifolds, for each n(N⁺), contained no short-lived [small script l] ≤ 3 character, i.e., for N⁺ = 0, 1, and 2, |M_N| ≥ 4, 3, and 2, respectively.

The decay time constants, τ_calc, where first calculated without including effects of vibrational channel interactions (i.e., a_(N⁺) = 0 in eqn (22)). In this case only the intrinsic v⁺ = 0 fluorescence and dissociation decay rates were considered. For the n(2) v⁺ = 0 states, the resulting time constants are shown for M_N = 2 to 5 in Fig. 10(a). From these data it is seen that when only v⁺ = 0 fluorescence and dissociation decay rates were included the value of τ_calc increases with n, as would be expected in an atom. This does not however reflect the general trend observed in the experimental data in Fig. 9.

Fig. 10 (a) Calculated decay time constants, τ_calc, excluding effects of vibrational channel interactions for M_N = 2, 3, 4, and 5 LFS n(2) Rydberg–Stark states in NO. (b) Fraction of v⁺ = 1 (τ_v⁺=1 ∼ 1 ps) character mixed into the n(2) v⁺ = 0 Stark states. The red shaded region represents the uncertainty in the fit parameters (see text for details). (c) Comparison of the experimentally measured values of τ_decay for n(2) states (filled red circles) with calculated values of τ_calc for LFS n(2), M_N = 4 Stark states including effects of vibrational channel interactions (open black squares). The grey shaded region represents the uncertainty in τ_calc resulting from the uncertainty in the fit parameters.

To determine the values of E_v⁺=1 and a_(N⁺) for each N⁺ series, a fit was performed of τ_calc to τ_decay. In this fitting process the reduced chi-squared was minimised in each N⁺ series. For N⁺ = 0 and 1, all measured values of n were used in the fitting process. For N⁺ = 2, the fitting was performed for the data points between n = 36 and 48 where the values of τ_decay change smoothly. The values of τ_decay for the 40(2), 43(2), 45(2), and 46(2) states were not included in the fit because of their deviation from the general trend followed at surrounding values of n. A value of M_N = 4 was used in determining τ_calc because it is the smallest value of M_N for which all N⁺ series considered contain at least one set of Stark states without any short lived low-[small script l] ([small script l] ≤ 3) character. The values of E_v⁺=1 and a_(N⁺) which resulted in the minimum chi-squared, χ²_min, can be seen in Table 3. The uncertainties on these values were calculated by considering the change required in E_v⁺=1 or a_(N⁺) to increase the chi-squared to χ² = χ²_min + 1.

Table 3 Parameters associated with the Lorentzian function in eqn (22), representing the strength of the vibrational channel interactions between the short-lived (τ_v⁺=1 ∼ 1 ps) low-n states with v⁺ = 1 and the high Rydberg states with v⁺ = 0, obtained by minimising the reduced chi-squared of τ_calc with respect to τ_decay for the different N⁺ hydrogenic series separately. The fitting process was performed with the data recorded for V₀ = 149 V. Values of M_N = 4 and F_z = 95 V cm⁻¹ where used in the calculations

N ^+	E v ^+=1/hc (cm^−1)	a (N^+)/10^−6
0	−7 ± 7	0.18 ± 0.08
1	45 ± 10	3.0 ± 0.7
2	31 ± 3	2.0 ± 0.2

---

Comparison of the best-fit values of E_v⁺=1 in Table 3 with the energy-level structure in Fig. 2 shows that the peaks of the Lorentzian functions, which approximately represent the positions of the v⁺ = 1 (τ_v⁺=1 ∼ 1 ps) states mixed into the v⁺ = 0 Stark states, lie close to or above the v⁺ = 0, N⁺ = 0 series limit and are in the vicinity of the calculated energies of the (n = 7)X^{+ 1}Σ⁺(v⁺ = 1, N⁺) states. From the values of E_v⁺=1 and a_(N⁺), in Table 3 and eqn (22) it can be estimated that the fraction of short lived (τ_v⁺=1 ∼ 1 ps) n = 7, v⁺ = 1 character mixed into the n(N⁺) v⁺ = 0 Stark states is between 10⁻¹⁰ and 10⁻⁹. For example, a 10⁻⁹ contribution from a short-lived state with a lifetime of 1 ps, mixed into a long-lived state with a lifetime of 1 ms, yields a total decay rate of 2000 s⁻¹ and a lifetime of 500 μs.

Fig. 10(b) shows the fraction of (n = 7)X^{+ 1}Σ⁺(v⁺ = 1, N⁺) character mixed into the predominantly v⁺ = 0, N⁺ = 2 Rydberg states below the v⁺ = 0, N⁺ = 0 series limit as given by eqn (22). The shaded region corresponds to the range of mixing fractions that arise from the uncertainty in the fit parameters. As can be seen in Fig. 10(b) the fraction of this n = 7, v⁺ = 1 character mixed into the n(2) Stark states increases by approximately a factor of 5 over the wavenumber range studied. In Fig. 10(c) the effects of these vibrational channel interactions on the values of τ_calc for the n(2) states (black squares) can be seen, and these results are compared to the measured values of τ_decay (red circles). The grey shaded region in this panel of Fig. 10 corresponds to the uncertainty in τ_calc arising from the uncertainty in the fit parameters. The calculated decay time constant obtained for the 38(2), M_N = 4 [43(2), M_N = 4] state using this approach was τ_calc = 343 ± 30 μs [τ_calc = 279 ± 35 μs]. It can be seen in Fig. 10(c) that, in contrast to the case in which only v⁺ = 0 fluorescence and dissociation rates were considered [Fig. 10(a)], this type of vibrational channel interaction leads to a dependence of the excited state decay times on the value of n that follows the trend observed in the experiments. The contributions from this interaction to the excited state decay rates are ∼1 kHz.

To further validate this interpretation of the experimental observations as arising from vibrational channel interactions, a two state quantum mechanical model was implemented. To approximate the interaction between a v⁺ = 0 and v⁺ = 1 state, a 2 × 2 Hamiltonian, H_vib, was constructed,

where E_v⁺=0 and E_v⁺=1 represent the energies of the v⁺ = 0 and v⁺ = 1 states, respectively, and I_vib represents the strength of the interaction. Within the harmonic oscillator approximation, Δv⁺ = 1 mixing occurs when an interaction is present that causes the Hund's-case-(b) quantum defects to have a non-zero derivative with respect to the internuclear separation R, when evaluated at the equilibrium internuclear distance R_e, i.e.,^{44,63,79–82}For the Rydberg states of NO the dependence of μ^(b)_{[small script l]Λ} on R arises as a result of the interaction of the Rydberg electron with the R-dependent multipole moments of the NO⁺ ion core.^44,59 The off-diagonal matrix elements associated with this interaction, I_vib in eqn (25), can therefore be estimated by considering the interaction between the |n[small script l]N⁺NM_Nv⁺ = 0〉 and |n′[small script l]′N⁺′N′v⁺′ = 1〉 Hund's-case-(d) basis states. This interaction can be expressed as,⁶³where, for Δv⁺ = 1,with μ_red and ω_e the reduced mass and vibrational frequency of NO⁺, respectively. The units of the coupling given by eqn (27) are introduced through the density of Rydberg states as in the first order approximation to MQDT.^52,80 It is assumed that the values of the Hund's-case-(b) quantum defect at the equilibrium internuclear distance, μ^(b)_{[small script l]Λ}|_R=Re, are small because [small script l] ≥ 4, and hence . The derivatives of the quantum defects, for Λ ≤ 2, were obtained by considering the low-n, R-dependent quantum defects calculated in ref. 59. For Λ ≥ 3, it was assumed that . Values of I_vib were then determined by considering the interactions between states for which v⁺ = 0, N⁺ = 2, and n = 38, and those for which v⁺ = 1, N⁺ = 0 and 4, n = 7, and [small script l] = 4 and 5. Following this approach the interaction strength I_vib was calculated to be between I_vib/hc ≃ 1 × 10⁻³ cm⁻¹ and 5 × 10⁻² cm⁻¹. The effect of this interaction on the v⁺ = 0 and v⁺ = 1 states was then determined by considering that (E_v⁺=1 − E_v⁺=0)/hc ∼ 100 cm⁻¹, and calculating the eigenvalues and eigenvectors of the Hamiltonian in eqn (25). The resulting mixed states contain 10⁻¹⁰ to 10⁻⁷ of the minority component, i.e., the absolute values of the amplitudes of the minority component in the wave functions are 10⁻⁵ to 10^−3.5. These mixing fractions are consistent with those expected from the measured trap decay times. Using this two-state model it can also be estimated that the vibrational channel interaction considered here would give rise to wavenumber shifts of the v⁺ = 0 and v⁺ = 1 states of ∼10⁻⁸ cm⁻¹ to 10⁻⁵ cm⁻¹ (i.e., frequency shifts of ∼100 Hz to 100 kHz).

4.4 Rotational channel interactions

To interpret the trap decay time constants for the individual Rydberg states that deviate from the general trend in Fig. 9, i.e., that τ_decay decreases with increasing n, it is necessary to consider the role of rotational channel interactions between states with v⁺ = 0. As discussed by Bixon and Jortner,⁴³ and in Section 4.1, the hydrogenic Stark states populated by photoexcitation in the experiments here are those that undergo intramolecular interactions with nearby optically accessible np(0) or nf(2) states. These interactions can be induced solely by external electric-fields, as is the case for n(2) states that mix with nf(2) states, or by a combination of intramolecular charge-multipole interactions and external electric-fields, that occur, for example, in the case of n(1) states populated because of accidental degeneracies between np(0) and n′d(1) states (where n′ ≠ n), with the n′d(1) states further mixing with the n′(1) hydrogenic states.

In Fig. 9(c) the measured values of τ_decay for the 40(2), 43(2), and 45(2) Rydberg–Stark states are larger than expected from the behaviour of the surrounding states. These n(2) hydrogenic Stark states are populated because of the effects of mixing with the nf(2) states. However, the charge-quadrupole interactions that couple states for which ΔN⁺ = ±2 and Δ[small script l] = 0 lead to mixing between nf(2) and n′f(0) states, which, in the presence of an electric field also mix with the n′(0) states. This type of interaction with intramolecular and external field contributions leads to the population of n′(0) states upon photoexcitation if they are energetically close to an nf(2) resonance. Hence, because of accidental degeneracies with n′(0) states, photoexcitation on the 40f(2), 43f(2), and 45f(2) resonances leads to the population of both the 40(2) and 44(0), the 43(2) and 48(0), and the 45(2) and 51(0) states, respectively. Since the n′(0) states have longer decay time constants than the n(2) states at a particular excitation wave number (see Fig. 9), trapped molecules in these states have larger values of τ_decay than those excited on resonances where only n(2) states are populated. This increase in the observed decay time constant also depends on the ratio of the n(2) and n′(0) state populations.

Further deviations from the general trend in the values of τ_decay in Fig. 9 are also seen for the 34(2) and 35(2) states. In these cases, charge–dipole interactions that couple states for which ΔN⁺ = ±1 and Δ[small script l] = ±1 lead to mixing of the nf(2) and n′[small script l]′(3) states. These result in the population of n′(3) states, in addition to n(2) states, upon photoexcitation. Consequently, excitation on the 34f(2) and 35f(2) resonances leads to the population of both the 34(2) and 32(3), and the 35(2) and 33(3) states, respectively. The reduced decay time constants observed for n = 34 and 35 in Fig. 9(c), when compared to the surrounding states, suggests that the 32(3) and 33(3) states have shorter lifetimes than the 34(2) and 35(2) states.

The measured decay time constant for the 46(2) state in Fig. 9, is larger than expected from the trend in the surrounding states. In this case the presence of both the optically accessible 46f(2) and 53p(0) states within the laser spectral width, and the increasing overlap of the Stark manifolds at these high values of n complicate the interpretation of this feature. However, based upon similar arguments to those outlined above, an estimate of the states that can be populated in both of these cases can still be made. Although a rigorous treatment, e.g., by combining particle trajectory calculations with MQDT, will be required to determine the relative populations of each Stark state and the efficiency with which each can be decelerated and trapped. In this instance it is considered that:

• The 46(2) Stark states are populated because of electric-field-induced mixing with the 46f(2) states.

• The 50(1) Stark states are almost degenerate with the 46(2) states and can therefore be populated as a result of charge-dipole interactions that (i) couple the 46f(2) states and 50d(1) or 50g(1) states, or (ii) couple the 53p(0) state with the 50s(1) or 50d(1) states. These are then mixed with the hydrogenic 50(1) states in the electric field.

• Finally, 52(0) Stark states can be populated as a result of electric-field-induced mixing with the 53p(0) state.

Since, at a particular excitation wavenumber the N⁺ = 0 Stark states were observed to exhibit longer decay time constants than the N⁺ = 1 and 2 Stark states (see Fig. 9), the presence of 52(0) states is expected to increase the value of τ_decay measured at the wave number associated with the excitation of the 46(2) states when compared to the other surrounding states. This is consistent with the experimental observations.

The dependence of τ_decay on the trap depth was measured for the n(2) states in the range from n = 38 to 44, see Fig. 11. The data in this figure were recorded for three different trap depths with V₀ = 149 V (red circles), V₀ = 125 V (blue open diamonds), and V₀ = 100 V (black triangle). From these data, it is seen that in general τ_decay is insensitive to the value of V₀, and hence the trap depth. This is consistent with the results of calculations for F_z = 95 V cm⁻¹ (V₀ = 149 V) and F_z = 80 V cm⁻¹ (V₀ = 125 V) in which the reduction in the electric field strength caused τ_calc to change by <5 μs over this range of values of n. However, two exceptions to this general trend are seen in Fig. 11. These occur for the 40(2) and 43(2) states where the value of τ_decay increased as the value of V₀ was decreased.

Fig. 11 Measured values of τ_decay, for states in the N⁺ = 2 series. The data were recorded for V₀ = 100 V (black triangle), 125 V (blue open diamonds), and 149 V (red circles).

As discussed above, photoexcitation on the 40f(2) and 43f(2) resonances results in the population of the 40(2) and 44(0), and the 43(2) and 48(0) Stark states, respectively. The increase in τ_decay as V₀ was decreased at these resonances indicates that in these cases the fractions of trapped molecules in the longer lived 44(0), or 48(0), states also increase as V₀ decreases. For states with n > 40 the trapping efficiency is limited by electric field ionisation during deceleration and trapping, with the ionising field scaling with n⁻⁴. For lower values of V₀, the electric field experienced by the molecules during deceleration and trapping is reduced. This leads to an increase in the trapping efficiency for molecules in higher n states, because of reduced loses from electric field ionisation and the resulting increase in the effective volume of the trap. This increase in trap loading efficiency is greater for states with higher values of n. Therefore, for the measurements performed following excitation on the 40f(2) resonance, the trapping efficiency for molecules in the 40(2) states only changes a little between V₀ = 149 V and 125 V, whereas the efficiency of trapping molecules in the near degenerate 44(0) states increases as the values of V₀ is reduced. This results in an increase in the fraction of molecules in the longer-lived 44(0) states present in the trap when V₀ = 125 V, compared with V₀ = 149 V, and therefore τ_decay is observed to increase. The situation is similar for the 43f(2) resonance, where the trapped molecules are in the 43(2) and 48(0) states, and the fraction of molecules in the longer-lived 48(0) states increases as V₀ decreases resulting in an increase in τ_decay.

5 Conclusions

In conclusion, NO molecules have been prepared in high Rydberg states with lifetimes in excess of 100 μs, decelerated to rest in the laboratory-fixed frame of reference in the travelling traps of a transmission-line Rydberg–Stark decelerator and electrostatically trapped. Trapping was performed in a cryogenic environment to minimise the effects of blackbody radiation induced transitions. Measurements, of the decay of the molecules from the trap, were conducted in situ by pulsed electric field ionisation. The long lifetimes of the Rydberg states observed in the experiments are reminiscent of those of Rydberg states in atoms. However, over the timescales of ∼1 ms on which the experiments were performed, molecular effects were seen to play a significant role in the decay of the trapped molecules, and result in a breakdown of n-scaling rules typical of hydrogenic systems. These effects arise because of rotational and vibrational channel interactions which originate from the coupling of the Rydberg electron to the electric dipole, quadrupole, and higher order multipole moments of the NO⁺ ion core. These types of channel interactions have been discussed previously in the literature, in the context of the lifetimes of Rydberg states in ZEKE spectroscopy experiments. However, ZEKE experiments are generally performed on the 1 μs timescale and many of the effects of these interactions are weak. Consequently, the quantum-state-dependence of each of the interaction mechanisms identified here, which typically contribute ∼1 kHz to the excited state decay rates, were not observable. In the experiments reported here, with measurement times of up to 1 ms, these effects are clearly seen. Vibrational channel interactions between Rydberg states in the nX^{+ 1}Σ⁺(v⁺ = 0, N⁺) series, and short-lived (n = 7)X^{+ 1}Σ⁺(v⁺ = 1, N⁺) states, lead to a general reduction in the lifetimes of the nX^{+ 1}Σ⁺(v⁺ = 0, N⁺) Rydberg states with N⁺ = 0, 1, and 2 and values of n > 35 as each series limit is approached. Rotational channel interactions within the v⁺ = 0 series have been identified to specifically affect the decay time constants of some individual Rydberg states.

The effects of molecular interactions on the lifetimes of Rydberg states studied here must be carefully considered when employing general n-scaling rules in the analysis of excited state decay, e.g., following electron–ion recombination. The experimental methods developed and implemented in this work offer opportunities for similar studies with other molecules, e.g., N₂ and O₂, provided schemes for populating long-lived Rydberg states are identified. The results reported here will provide important input for future low-energy collision experiments using Rydberg NO molecules, and the implementation of schemes to exploit the technique of Rydberg–Stark deceleration to prepare cold samples of ground state molecules.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Dr Adam Deller (Max-Planck-Institut für Plasmaphysik) for his contributions to the development of the apparatus used in this work and for valuable discussions. This work was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant No. 683341). MHR is grateful to the Engineering and Physical Sciences Research Council (EPSRC) for support through their Doctoral Training Partnership (Grant No. EP/R513143/1).

References

1. J. P. Morrison, C. J. Rennick, J. S. Keller and E. R. Grant, Phys. Rev. Lett., 2008, 101, 205005.
2. R. Wang, M. Aghigh, K. L. Marroquín, K. M. Grant, J. Sous, F. B. V. Martins, J. S. Keller and E. R. Grant, Phys. Rev. A, 2020, 102, 063122.
3. S. L. Guberman, J. Phys. Chem. A, 2007, 111, 11254.
4. R. Peverall, S. Rosén, J. R. Peterson, M. Larsson, A. Al-Khalili, L. Vikor, J. Semaniak, R. Bobbenkamp, A. Le Padellec, A. N. Maurellis and W. J. van der Zande, J. Chem. Phys., 2001, 114, 6679.
5. A. Giusti, J. Phys. B, 1980, 13, 3867.
6. T. P. Softley, Int. Rev. Phys. Chem., 2004, 23, 1.
7. P. Allmendinger, J. Deiglmayr, O. Schullian, K. Höveler, J. A. Agner, H. Schmutz and F. Merkt, ChemPhysChem, 2016, 17, 3596.
8. P. Allmendinger, J. Deiglmayr, K. Höveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316.
9. V. Zhelyazkova, F. B. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401.
10. K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676.
11. K. Gawlas and S. D. Hogan, J. Phys. Chem. Lett., 2020, 11, 83.
12. R. González-Férez, J. Shertzer and H. R. Sadeghpour, Phys. Rev. Lett., 2021, 126, 043401.
13. C. H. Greene, A. S. Dickinson and H. R. Sadeghpour, Phys. Rev. Lett., 2000, 85, 2458.
14. V. Bendkowsky, B. Butscher, J. Nipper, J. P. Shaffer, R. Löw and T. Pfau, Nature, 2009, 458, 1005.
15. J. Liu, E. J. Salumbides, U. Hollenstein, J. C. Koelemeij, K. S. Eikema, W. Ubachs and F. Merkt, J. Chem. Phys., 2009, 130, 174306.
16. N. Hölsch, M. Beyer, E. J. Salumbides, K. S. Eikema, W. Ubachs, C. Jungen and F. Merkt, Phys. Rev. Lett., 2019, 122, 103002.
17. L. Semeria, P. Jansen, G.-M. Camenisch, F. Mellini, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 124, 213001.
18. S. D. Hogan, C. Seiler and F. Merkt, Phys. Rev. Lett., 2009, 103, 123001.
19. W. H. Wing, Phys. Rev. Lett., 1980, 45, 631.
20. T. Breeden and H. Metcalf, Phys. Rev. Lett., 1981, 47, 1726.
21. D. Townsend, A. L. Goodgame, S. R. Procter, S. R. Mackenzie and T. P. Softley, J. Phys. B, 2001, 34, 439.
22. Y. Yamakita, S. R. Procter, A. L. Goodgame, T. P. Softley and F. Merkt, J. Chem. Phys., 2004, 121, 1419.
23. E. Vliegen, H. J. Wörner, T. P. Softley and F. Merkt, Phys. Rev. Lett., 2004, 92, 033005.
24. P. Lancuba and S. D. Hogan, Phys. Rev. A, 2013, 88, 043427.
25. P. Allmendinger, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. A, 2014, 90, 043403.
26. H. Ko and S. D. Hogan, Phys. Rev. A, 2014, 89, 053410.
27. A. Deller and S. D. Hogan, Phys. Rev. Lett., 2019, 122, 053203.
28. J. Palmer and S. D. Hogan, Phys. Rev. A, 2017, 95, 053413.
29. E. Vliegen and F. Merkt, J. Phys. B, 2006, 39, L241.
30. P. Lancuba and S. D. Hogan, Phys. Rev. A, 2014, 90, 053420.
31. S. D. Hogan, P. Allmendinger, H. Saßmannshausen, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2012, 108, 063008.
32. V. Zhelyazkova, M. Žeško, H. Schmutz, J. A. Agner and F. Merkt, Mol. Phys., 2019, 117, 2980.
33. P. Lancuba and S. D. Hogan, J. Phys. B, 2016, 49, 074006.
34. C. Seiler, S. D. Hogan, H. Schmutz, J. A. Agner and F. Merkt, Phys. Rev. Lett., 2011, 106, 073003.
35. E. Vliegen, S. D. Hogan, H. Schmutz and F. Merkt, Phys. Rev. A, 2007, 76, 023405.
36. S. D. Hogan and F. Merkt, Phys. Rev. Lett., 2008, 100, 043001.
37. C. Seiler, S. D. Hogan and F. Merkt, Phys. Chem. Chem. Phys., 2011, 13, 19000.
38. C. Seiler, PhD thesis, Eidgenössische Technische Hochschule Zürich, 2013.
39. A. Deller and S. D. Hogan, J. Chem. Phys., 2020, 152, 144305.
40. M. J. Vrakking and Y. T. Lee, Phys. Rev. A, 1995, 51, 894.
41. M. J. Vrakking and Y. T. Lee, J. Chem. Phys., 1995, 102, 8818.
42. G. Reiser, W. Habenicht, K. Müller-Dethlefs and E. W. Schlag, Chem. Phys. Lett., 1988, 152, 119.
43. M. Bixon and J. Jortner, J. Chem. Phys., 1996, 105, 1363.
44. A. L. Goodgame, H. Dickinson, S. R. Mackenzie and T. P. Softley, J. Chem. Phys., 2002, 116, 4922.
45. N. J. A. Jones, R. S. Minns, R. Patel and H. H. Fielding, J. Phys. B, 2008, 41, 185102.
46. R. Patel, N. J. Jones and H. H. Fielding, J. Phys. B, 2007, 40, 1369.
47. A. Deller, M. H. Rayment and S. D. Hogan, Phys. Rev. Lett., 2020, 125, 73201.
48. T. Ebata, Y. Anezaki, M. Fujii, N. Mikami and M. Ito, J. Phys. Chem., 1983, 87, 4773.
49. M. Seaver, W. A. Chupka, S. D. Colson and D. Gauyacq, J. Phys. Chem., 1983, 87, 2226.
50. M. G. Littman, M. M. Kash and D. Kleppner, Phys. Rev. Lett., 1978, 41, 103.
51. M. J. Vrakking, J. Chem. Phys., 1996, 105, 7336.
52. S. Fredin, D. Gauyacq, M. Horani, C. Jungen, G. Lefevre and F. Masnou-Seeuws, Mol. Phys., 1987, 60, 825.
53. S. N. Dixit, D. L. Lynch, V. McKoy and W. M. Huo, Phys. Rev. A, 1985, 32, 1267.
54. E. Klisch, S. P. Belov, R. Schieder, G. Winnewisser and E. Herbst, Mol. Phys., 1999, 97, 65.
55. E. E. Eyler and F. M. Pipkin, Phys. Rev. A, 1983, 27, 2462.
56. E. E. Eyler, Phys. Rev. A, 1986, 34, 2881.
57. M. Bixon and J. Jortner, Mol. Phys., 1996, 89, 373.
58. R. D. Gilbert and M. S. Child, Chem. Phys. Lett., 1991, 187, 153.
59. I. Rabadán and J. Tennyson, J. Phys. B, 1997, 30, 1975.
60. M. Fehér and P. A. Martin, Chem. Phys. Lett., 1993, 215, 565.
61. R. Polák and J. Fišer, Chem. Phys., 2004, 303, 73.
62. F. P. Billingsley, Chem. Phys. Lett., 1973, 23, 160.
63. M. S. Child, Theory of Molecular Rydberg States, Cambridge University Press, 2011.
64. C. Jungen and G. Raseev, Phys. Rev. A, 1998, 57, 2407.
65. H. H. Fielding and T. P. Softley, Chem. Phys. Lett., 1991, 185, 199.
66. M. L. Zimmerman, M. G. Littman, M. M. Kash and D. Kleppner, Phys. Rev. A, 1979, 20, 2251.
67. C. Jungen and E. Miescher, Can. J. Phys., 1969, 47, 1769.
68. D. T. Biernacki, S. D. Colson and E. E. Eyler, J. Chem. Phys., 1988, 89, 2599.
69. H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One- and Two-Electron Atoms, Springer, 1957.
70. A. Fujii and N. Morita, J. Chem. Phys., 1995, 103, 6029.
71. S. D. Hogan, EPJ Tech. Instrum., 2016, 3, 1.
72. W. A. Chupka, J. Chem. Phys., 1993, 98, 4520.
73. F. Merkt and R. N. Zare, J. Chem. Phys., 1994, 101, 3495.
74. C. Seiler, J. A. Agner, P. Pillet and F. Merkt, J. Phys. B, 2016, 49, 094006.
75. R. J. Damburg and V. V. Kolosov, J. Phys. B, 1979, 12, 2637.
76. K. Gawlas and S. D. Hogan, Phys. Rev. A, 2019, 99, 013421.
77. T. F. Gallagher, Rydberg Atoms, Cambridge University Press, 1994.
78. R. S. Minns, D. T. Lazenby, F. H. Hall, N. J. Jones, R. Patel and H. H. Fielding, Mol. Phys., 2014, 112, 1808.
79. G. Herzberg and C. Jungen, J. Mol. Spec., 1972, 41, 425.
80. R. W. Field, C. M. Gittins, N. A. Harris and C. Jungen, J. Chem. Phys., 2005, 122, 18314.
81. J. J. Kay, S. L. Coy, B. M. Wong, C. Jungen and R. W. Field, J. Chem. Phys., 2011, 134, 114313.
82. J. Jiang, T. J. Barnum, S. L. Coy and R. W. Field, J. Chem. Phys., 2019, 150, 154305.

---