A photoelectron imaging study of the deprotonated GFP chromophore anion and RNA fluorescent tags

Abstract

Green fluorescent protein (GFP), together with its family of variants, is the most widely used fluorescent protein for in vivo imaging. Numerous spectroscopic studies of the isolated GFP chromophore have been aimed at understanding the electronic properties of GFP. Here, we build on earlier work [A. V. Bochenkova, C. Mooney, M. A. Parkes, J. Woodhouse, L. Zhang, R. Lewin, J. M. Ward, H. Hailes, L. H. Andersen and H. H. Fielding, Chem. Sci., 2017, 8, 3154] investigating the impact of fluorine and methoxy substituents that have been employed to tune the electronic structure of the GFP chromophore for use as fluorescent RNA tags. We present photoelectron spectra following photoexcitation over a broad range of wavelengths (364–230 nm) together with photoelectron angular distributions following photoexcitation at 364 nm, which are interpreted with the aid of quantum chemistry calculations. The results support the earlier high-level quantum chemistry calculations that predicted how fluorine and methoxy substituents tune the electronic structure and we find evidence to suggest that the methoxy substituents enhance internal conversion, most likely from the 2ππ* state which has predominantly Feshbach resonance character, to the 1ππ* state.

---

1 Introduction

Green fluorescent protein (GFP) is a fluorescent protein found in coelenterates, such as the jellyfish Aequorea victoria, which emits green light with a high quantum yield.¹ GFP is often employed as a molecular marker in biology as it may be genetically tagged, non-perturbatively, onto a protein of interest.² The deprotonated GFP chromophore, p-hydroxybenzylidene-2,3-dimethyl-4-imidazolinone (p-HBDI⁻), has been the focus of numerous spectroscopic studies in the gas-phase^3–20 and in solution.^21–30 In 2001, the gas-phase absorption spectrum of p-HBDI⁻ was reported to be very similar to that of the deprotonated form of GFP.³¹ This observation triggered numerous investigations into the electronic structure and dynamics of the isolated chromophore anion aimed at shedding light on the roles of the chromophore and the protein environment in tuning the fluorescence properties.^3–20,32,33 Gas-phase studies have also allowed the higher lying electronically excited states to be characterised,^{6–9,11–16,18} which is difficult in the protein because the UV absorption of the chromophore overlaps with the UV absorption of amino acid residues. Characterising the higher lying electronically excited states is particularly important for understanding their role in UV photoinitiated reactions of GFP, such as decarboxylation and cis–trans isomerisation.^34–39

Substituting methoxy groups and fluorine atoms at the ortho-positions of the phenolate building block of the chromophore (Fig. 1) has been found to tune the pK_a, the ability of the chromophore to bind to specific RNA sequences and the emission wavelength.^40,41 There is only one previous gas-phase study of these biomimetic chromophores, which compared photoelectron spectra of p-HBDI⁻ with those of 3,5-difluoro-p-HBDI⁻ (DF-HBDI⁻) and 3,5-dimethoxy-p-HBDI (DM-HBDI⁻) at 346 nm and 328 nm, and presented XMCQDPT2/aug-cc-pVTZ calculations of their vertical excitation energies (VEEs) and vertical detachment energies (VDEs).¹⁴ From this study it was concluded that the UV photoelectron spectra of p-HBDI⁻ should be interpreted in terms of direct S₀–D₀ photodetachment and indirect detachment via the 3ππ* state which has, predominantly, excited shape resonance character with respect to the D₀ continuum. It was found that the electron withdrawing effect of the fluorine atoms resulted in the VDE being raised from around 2.7 eV for p-HBDI⁻ to 2.95 eV for DF-HBDI⁻. The VDE of DM-HBDI⁻ was found to be similar to that of p-HBDI⁻, which was rationalised in terms of opposing inductive and mesomeric effects of the methoxy groups. In both biomimetic chromophores, the bright excited shape resonance was found to be shifted higher in energy and resonant autodetachment processes evident in the spectra were attributed to nπ*-D₀ and nπ*-D_1n detachment processes. Here, we build on this work and present significantly improved quality photoelectron spectra and photoelectron angular distributions (PADs) of the deprotonated anions of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ following photodetachment over the wavelength range 364–230 nm. This allows us to establish that resonant detachment from the 2ππ* electronically excited state and internal conversion from the 2ππ* state to a lower lying electronically excited state, or S₀, play a role in the electronic relaxation mechanism following UV photoexcitation.

Fig. 1 Structures of the anions of (a) p-HBDI⁻, (b) DF-HBDI⁻, (c) DM-HBDI⁻ (syn rotamer) and (d) DM-HBDI⁻ (anti rotamer).

2 Methods

2.1 Experimental

p-HBDI, DF-HBDI and DM-HBDI were synthesised using reported procedures.^40,42

Anion photoelectron spectra and photoelectron angular distributions were recorded using our electrospray ionisation (ESI) velocity-map imaging (VMI) instrument that has been described in detail elsewhere.⁴³ For the negative ion electrospray, 1 mM solutions of p-HBDI⁻ or DF-HBDI⁻, in methanol, or DM-HBDI⁻, in 9/1 (v/v) methanol/water, were treated with a few drops of ammonia as a base to shift the equilibrium towards the deprotonated anion, enhancing the observed anion signal. Singly-charged anions produced by ESI were mass-selected in a quadrupole mass filter, accumulated in a hexapole ion trap and thermalised using Ar or He gas before being focused into the source region of a VMI photoelectron spectrometer. Wavelengths in the range 364–315 nm were generated by second harmonic generation of the output of a dye laser pumped by a frequency-doubled nanosecond Nd:YAG laser operating at 20 Hz. 230 nm was generated using the third harmonic of the output of the dye laser. The resulting photoelectrons were imaged on a 2D CCD detector coupled to a phosphor screen. Background counts arising from collisions with the detector or from ionization of background gas by the laser were also recorded and subtracted and the resulting images were inverted using the pBASEX method.⁴⁴ The eKE was calibrated using the photodetachment spectrum of I⁻ and the eKE resolution was determined to be ≤5% for the measurements presented here. For a one-photon detachment process with linearly polarised light, the PAD can be expressed as

dσ/dΩ ∝ 1 + β₂P₂(cos θ), (1)

where I(θ) is the probability of photoelectron emission at an angle θ with respect to the laser polarisation, P₂(cos θ) is the second-order Legendre polynomial and β₂ is the asymmetry parameter.⁴⁵ The two limiting values of β₂ are +2 and −1, corresponding to photoelectron emission predominantly parallel and perpendicular to the laser polarisation, respectively.

2.2 Computational

Anion geometries were optimised using density functional theory⁴⁶ (DFT) with the B3LYP functional^47,48 and the 6-311++G(3df,3pd) basis set⁴⁹ within the Gaussian09 program suite.⁵⁰ Vertical detachment energies (VDEs) were calculated using the equation-of-motion coupled-cluster method with single and double excitations for the calculation of ionisation potentials⁵¹ (EOM-IP-CCSD) within the Q-Chem program package.⁵² For p-HBDI⁻ and DF-HBDI⁻, the EOM-IP-CCSD calculations were run with the aug-cc-pVDZ basis set,⁵³ while the smaller 6-311++G(d,p) basis set was used for the rotamers of DM-HBDI⁻ to reduce computational expense.

β ₂ parameters were calculated over the relevant eKE range using ezDyson with the analytical averaging method to provide lab-frame angular distributions from the molecular frame PADs;⁵⁴ the Dyson orbitals for the S₀–D₀ transition were obtained from the EOM-IP-CCSD calculations. The ezDyson calculations presented here use a plane wave instead of a Coulomb wave for the photoelectron wavefunction, which has been demonstrated to yield accurate trends in β₂ parameter for several molecular anions.^55–59 The 6-311++G(d,p) basis set was benchmarked against the previously used aug-cc-pVDZ basis set for the EOM-IP-CCSD and ezDyson calculations (Fig. S5 in the ESI†) for phenolate and p-HBDI⁻. For p-HBDI⁻, the calculated VDEs were lower by ∼0.05 eV and good agreement was found in the ezDyson predicted trends in the photoelectron angular distributions as a function of eKE. Our observation that reducing the number of polarisation functions, whilst maintaining the same number of diffuse functions, has a minimal impact on the calculated angular distributions for these closed-shell anions is in agreement with work reported by Anstöter et al.⁵⁸

3 Results

3.1 Computational

The B3LYP/6-311++G(3df,3pd) structures, EOM-IP-CCSD calculated VDEs and corresponding D₀ hole orbitals are presented in Table 1 for p-HBDI⁻, DF-HBDI⁻ and the rotamers of DM-HBDI⁻. Of the four rotamers of DM-HBDI⁻, the most stable are the syn and anti forms, which are isoenergetic and stabilised relative to the others by two hydrogen-bonding interactions between the phenolate oxygen and hydrogen atoms on the methyl groups, with each hydrogen-bonding interaction stabilising the negative charge by ∼0.15 eV, in excellent agreement with previous EOM-IP-CCSD/aug-cc-pVDZ calculations of the VDEs of the four rotamers of 2,6-dimethoxyphenolate.⁵⁷ The structure of the syn rotamer of DM-HBDI⁻ is in agreement with the MP2/aug-cc-pVTZ optimised geometry obtained in ref. 14. Given that the barriers to interconversion between the rotamers of DM-HBDI⁻ are expected to be small (being largely determined by the strength of the H-bonding interactions) we expect the populations of these rotamers to be determined by the temperature upon thermalisation to 300 K. Therefore, the higher energy rotamers are not expected to contribute strongly to the observed signal as these states are less thermally accessible at 300 K; for example, the population ratio of the 0.06 eV rotamer to the minimum energy rotamer is expected to be 1 : 10 at 300 K. EOM-IP-CCSD VDEs and orbital holes for the D₁ neutral radical states of p-HBDI⁻, DF-HBDI⁻ and the four rotamers of DM-HBDI⁻ are presented in Table S1 in the ESI† and show that, as reported previously for p-HBDI⁻, o-HBDI⁻ and substituted p-HBDI⁻ anions, the D₁ state corresponds to detachment of an electron from a non-bonding orbital localised on the C–O bond of the phenolate moiety and will from now on be referred to as the D_1n state.^14,15 In the case of the planar DMHBDI⁻ rotamer, the D_1n threshold is isoenergetic with the D₁ state, which corresponds to direct detachment from the HOMO−1 π-orbital, with EOM-IP-CCSD/6-311++G(d,p) calculated VDEs of 4.63 eV and 4.64 eV to the D₁ and D_1n states, respectively. The VDEs calculated for p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ (syn and anti rotamers) are in good agreement with the EPT/6-311++G(3df,3pd) and XMCQPDT2 values reported in ref. 14.

Table 1 B3LYP/6-311++G(3df,3pd) optimised structures, EOM-IP-CCSD VDEs and corresponding D₀ hole orbitals for p-HBDI⁻, DF-HBDI⁻ and all possible rotamers of DM-HBDI⁻. For p-HBDI⁻ and DF-HBDI⁻, the EOM-IP-CCSD calculations were carried out using the aug-cc-pVDZ basis set whereas a smaller 6-311++G(d,p) basis set was used for DM-HBDI⁻. The VDEs of the rotamers of DM-HBDI⁻ in Table 1 are given relative to the corresponding local minimum, rather than the global minimum. The D₀ hole orbitals correspond to the Fock orbitals which contribute most strongly (weight >0.95) to the S₀−D₀ detachment transition

Anion	Structure	E rel/eV	D0 VDE/eV	D0 hole
p-HBDI^−		—	2.66
DF-HBDI^−		—	2.93
syn-DM-HBDI^−		0	2.61
anti-DM-HBDI^−		0	2.62
DM-HBDI^− (1 H-bond)		0.06	2.45
DM-HBDI^− (No H-bonds)		0.09	2.31

---

3.2 Photoelectron spectra

The 364–230 nm photoelectron spectra of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ are presented in Fig. 2 as a function of electron binding energy, eBE = hν − eKE, and in Fig. 3 as a function of eKE. The red lines in Fig. 3 mark the high eKE edges of any features with constant eKE in the spectra. Experimental VDEs are determined from maxima in the photoelectron spectra plotted as a function of eBE (marked with blue lines in Fig. 2). It is important to note that, experimentally, the VDE refers to the binding energy of the most intense vibronic band, which depends on the Franck–Condon overlap of the vibrational wavefunctions within the initial and final electronic states. This does not equate directly with the calculated VDE, which is the separation of the electronic potential energy surfaces at the minimum point of the ground state potential. However, in practise, the value of the computational VDE is often similar enough to the experimental VDE for these values to be compared, e.g. for identification of different isomers in a mixture.

Fig. 2 Photoelectron spectra of deprotonated anions of (a) p-HBDI⁻, (b) DF-HBDI⁻ and (c) DM-HBDI⁻ plotted as a function of eBE. The blue lines in (a–c) indicate the experimentally determined VDEs to D₀ and D₁.

Fig. 3 Photoelectron spectra of deprotonated anions of (a) p-HBDI⁻, (b) DF-HBDI⁻ and (c) DM-HBDI⁻ plotted as a function of eKE. The black line in (a) indicates the maximum in the resonant photoelectron signal shown in Fig. S1 in the ESI.† The red lines in (a–c) indicate experimentally determined approximate AEEs for excited states which give rise to resonant autodetachment signals.

Previous high-resolution photoelectron spectra of cryogenically cooled p-HBDI⁻ have shown that the ADE ≈ VDE = 2.73 ± 0.01 eV.¹⁰ There are peaks in the p-HBDI⁻ spectra presented here at 2.74 ± 0.04 eV eBE (Fig. 2a), which is consistent with the high resolution measurement and other measurements of the S₀–D₀ VDE.^5–7,11,13 There are two additional features at 4.3 ± 0.1 eV and 4.9 ± 0.1 eV, consistent with previous measurements of the S₀–D_1n and S₀–D₁ VDEs^6,15 and XMCQDPT2/aug-cc-pVTZ and EOM-IP-CCSD/aug-cc-pVDZ calculations.^14,15

As the wavelength decreases in the range 364–315 nm (3.41–3.94 eV), the S₀–D₀ direct detachment feature broadens on the high eBE side. From the eKE distribution (Fig. 3a), this can mostly be attributed to the presence of an additional feature with constant eKE whose maximum intensity lies at around 0.8 eV eKE, consistent with previous experimental observations.^11,13 Electrons resulting from autodetachment processes from electronically excited states above the detachment threshold commonly give rise to features with constant eKE as a function of wavelength in the photoelectron spectra of anions, and results from the propensity for vibrational energy to be retained on autodetachment.^{5,7,11,13–15,18,57,60–68} To identify the presence of weaker features in the spectra, we subtracted the 364 nm spectrum (which contains predominantly direct detachment signal) from the spectra at all other wavelengths, to produce difference spectra which reveal all features resulting from indirect detachment processes; these are presented in Fig. S1 in the ESI.† These spectra appear to contain an additional weak feature with maximum intensity around 0.7 eV eKE; this feature is visible in the 346 nm difference spectrum (where the intense feature peaking at 0.8 eV eKE is not present). To investigate this observation, vibrationally resolved spectra in the range 364–315 nm were recorded using He collision gas for improved cooling, and are presented in Fig. 4. In the He-thermalised spectrum at 315 nm, there is a clear peak at 1.03 eV which is not obvious in the broader, Ar-thermalised spectra. Difference spectra were also generated for the He-thermalised data set and are presented in Fig. S2 in the ESI.† In place of the broad, almost Gaussian features observed in the difference spectra for the Ar-thermalised data, the difference spectra using He collision gas show clear rising edges for two distinct states, peaking at 0.87 ± 0.05 eV and 1.03 ± 0.05 eV. The slight shift in the maximum of the resonant signal when comparing these two data sets (∼0.87 eV in He compared with ∼0.80 eV in Ar) is attributed to the Ar-thermalised spectra being broadened to higher eBEs (lower eKEs) due to the increased population of higher vibrational levels, as expected at higher temperatures. We note that a recent gas-phase action spectroscopy study by Bieske and coworkers showed that a small fraction of the p-HBDI⁻E-isomer can be formed when using high collision energies with N₂ collision gas, so we cannot rule out the possibility that a contribution from the E-isomer is responsible for this small shift in the spectra of the Ar-thermalised anions.¹⁷

Fig. 4 Photoelectron spectra (black line) of He-thermalised p-HBDI⁻ anions at the specified wavelengths plotted as a function of eKE. The red lines indicate approximate AEEs for excited states which give rise to resonant autodetachment signals.

As a result of the propensity for conserving vibrational energy during autodetachment, indirect photodetachment following resonant photoexcitation of an excited electronic state, S_n, with excess vibrational energy, E_v = hν − E(S_n), where E(S_n) is the adiabatic excitation energy (AEE) of S_n, will result in the emission of electrons with eKE ∼ hν − E(D₀) − E_v ∼ E(S_n) − E(D₀), where E(D₀) is the ADE. Thus, the photoelectrons are emitted with eKE corresponding to the S_n–D₀ energy difference (Fig. 5). Using this approximation, the additional features with maxima at 0.87 eV eKE and 1.03 eV eKE can be attributed to detachment from resonances with AEEs around 3.60 eV (∼344 nm) and 3.76 eV (∼330 nm), respectively. Excited state calculations have been previously carried out for p-HBDI⁻ at the CAM-B3LYP/6-311++G(3df,3pd),¹¹ ADC(2)/aug-cc-pVDZ¹⁵ and XMCQDPT2/aug-cc-pVTZ^12,14 levels of theory, all of which identified a bright ππ* transition (here labelled 3ππ*, see Fig. S9 in the ESI†) between the HOMO and a π*-orbital localised on the phenolate ring (LUMO+1), which has excited shape resonance character with respect to the D₀ continuum, in the energy range of the presented measurements. Experimental observations of indirect detachment signal at wavelengths in the 355–300 nm range has therefore predominantly been assigned to autodetachment from the 3ππ* state.^9,11–16,18 Excited state calculations at the XMCQDPT2/aug-cc-pVTZ^12,14 level for p-HBDI⁻ and m-HBDI⁻ also identified another ππ* transition (here labelled 2ππ*, see Fig. S9 in the ESI†) between a π-orbital localised predominantly on the imidizolinone moiety (HOMO−1) to a π*-orbital which is delocalised across the π-system (the LUMO orbital), which has Feshbach resonance character with respect to the D₀ continuum.^12,14 The results of these quantum chemistry calculations are summarised in Fig. 6. Action spectroscopy measurements of m-HBDI⁻ have observed signal attributable to autodetachment from the 2ππ* state;¹² however, while it has previously been suggested that autodetachment from the 2ππ* state contributes to the broadness of the photoelectron spectra of p-HBDI⁻ in the range 335–302 nm,¹³ the proximity of the 2ππ* and 3ππ* states in p-HBDI⁻ has so far prevented the explicit identification of signal arising from autodetachment from the 2ππ* state. Both AEEs measured here (3.60 eV and 3.76 eV) are in excellent agreement with the XMCQDPT2/aug-cc-pVTZ quantum chemistry calculations that determined the VEE of the 2ππ* Feshbach resonance to be 3.74 eV (332 nm) and the VEE of the 3ππ* excited shape resonance to be 3.78 eV (328 nm).^12,14 Together with anion photoelectron spectroscopy measurements, these quantum chemistry calculations of p-HBDI⁻ demonstrated that the electronically excited state that would make the most intense contribution to the photoelectron spectra in the 346–315 nm range would be the 3ππ* state, given that the 3ππ* state has excited shape resonance character with respect to the D₀ continuum and a significant oscillator strength (0.08).¹⁴ This work also showed that the full widths of the photoelectron spectra in the 346–315 nm range could be reproduced using calculated Franck–Condon profiles of the S₀–D₀ and 3ππ*-D₀ transitions convolved with a Gaussian with a 40 meV HWHM, if the AEE of the S₀-3ππ* transition was taken to lie at 348 nm (3.56 eV). We therefore assign the features with maxima at 0.87 eV eKE and 1.03 eV eKE to the 3ππ* excited shape resonance and the 2ππ* Feshbach resonance, respectively. As noted in the earlier work,¹⁴ the excited shape resonance is considerably brighter than the Feshbach resonance, whose oscillator strength is only 0.02, and autodetachment from the 3ππ* excited shape resonance is the dominant decay channel in this region. Nonetheless, the improved quality of our new spectra allow us to identify the contribution from the Feshbach resonance at 1.03 eV.

Fig. 5 Schematic energy level diagram illustrating direct and indirect electron detachment processes observed in p-HBDI⁻. Thin horizontal black lines represent the vibrational levels of the electronic states of the anion and the blue shaded area represents the electron detachment continuum. Vertical blue arrows represent the eKE of direct and indirect electron detachment processes and the thin horizontal blue lines represent the vibrational energy left in the neutral radical following electron detachment (determined by the propensity for conservation of vibrational energy). The horizontal black arrow represents internal conversion (IC). (a) Direct photodetachment from S₀ to the D₀ continuum gives electrons with eKE, ε₁ ∼ hν − VDE; in this particular example, VDE = ADE. (b) Indirect photodetachment following photoexcitation of S_n with excess vibrational energy, E_v = hν − E(S_n) gives electrons with eKE, ε₂ ∼ E(S_n) − E(D₀). Indirect photodetachment following photoexcitation of S_n and subsequent IC to S₁ gives electrons with eKE, ε₃ ∼ 0.

Fig. 6 XMCQDPT2/aug-cc-pVTZ vertical excitation energies and vertical detachment energies for p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ from ref. 14. The energy region corresponding to the 364–315 nm spectra is shaded in blue. Detachment thresholds are shown in purple and the optically dark 1nπ* states are shown in grey. The 2ππ* states have predominantly Feshbach resonance character with respect to their D₀ continua. The bright excited shape resonance in p-HBDI⁻ is the 3ππ* state but becomes the 4ππ* state in DF-HBDI⁻ and DM-HBDI⁻.

In the spectra of p-HBDI⁻ at 320 nm and 315 nm, there is an extremely weak additional feature at very low eKE (∼0.05 eV). Such a low eKE feature is characteristic of indirect detachment from an electronically excited state lying close to a detachment threshold or thermionic emission from S₀ following internal conversion. Several previous experimental and computational studies of p-HBDI⁻in vacuo have demonstrated that the 1ππ* state (which has shape resonance character with respect to D₀) lies just below the D₀ detachment threshold at ∼2.48 eV (500 nm), with many of the experimental studies finding evidence of vibrational autodetachment (VAD) following direct photoexcitation into the 1ππ* state.^{4,5,12,14,15,17,69–72} However, a recent ion-mobility action spectroscopy study of p-HBDI⁻ in the range 415–550 nm found that VAD is a minor channel with respect to isomerisation and internal conversion to the ground state, suggesting that the low eKE signal observed here could result from a combination of both VAD from the 1ππ* state and thermionic emission processes.¹⁷

For DF-HBDI⁻, there is a peak in all the spectra plotted as a function of eBE (Fig. 2b) around 2.98 ± 0.04 eV attributed to direct S₀–D₀ detachment. This is close to the EOM-IP-CCSD/aug-cc-pVDZ VDE (2.93 eV, Table 1) and values obtained from earlier measurements and EPT calculations.¹⁴ There is an additional peak in the 230 nm spectrum at 4.5 ± 0.1 eV eBE that can be attributed to direct detachment to the D_1n threshold, which is predicted by our EOM-IP-CCSD/aug-cc-pVDZ calculations to lie at 5.06 eV; this value is also in agreement with earlier EPT and XMCQDPT2/aug-cc-pVTZ calculations which place this transition at 4.47 eV.¹⁴ In DFHBDI⁻, the D₁ threshold, which corresponds to the product of direct detachment from the HOMO−1 π-orbital, is predicted to lie very close in energy to D_1n (at 5.18 eV at the EOM-IP-CCSD/aug-cc-pVDZ level of theory and at 4.66 eV according to previous EPT and XMCQDPT2/aug-cc-pVTZ calculations) and therefore likely also contributes to the feature at 4.5 eV.¹⁴ Similar to p-HBDI⁻, the photoelectron spectra are broadened as the wavelength is decreased in the range 364–315 nm. This broadening can be attributed to features with maximum eKEs around 0.4 eV and 0.8 eV (Fig. 3b and Fig. S3, ESI†), corresponding to detachment from resonances with AEEs around 3.4 eV and 3.8 eV, respectively. Given that the electron-withdrawing fluorine substituents are expected to shift the energies of the electronic excited states of p-HBDI⁻, but do not alter the molecular symmetry, it is likely that these resonances are analogous to the 2ππ* and 3ππ* resonances that we observe in the spectra of p-HBDI⁻, with the 2ππ* state lowered in energy as a result of greater stabilisation of the LUMO (which is delocalised across the π-system) relative to the HOMO−1 (which is predominantly localised on the imidazolinone moiety). This is consistent with earlier XMCQDPT2/aug-cc-pVTZ calculations of the VEEs of ππ* excited states lying in the range 3.58–4.20 eV, see Fig. 6.¹⁴

For DM-HBDI⁻, there is a peak in all the spectra plotted as a function of eBE (Fig. 2c) around 2.7 ± 0.04 eV attributed to direct S₀–D₀ detachment. This is close to the EOM-IP-CCSD/aug-cc-pVDZ VDEs for the syn and anti rotamer (2.61 eV and 2.62 eV, Table 1) and significantly higher than the VDEs for the rotamers with fewer hydrogen-bonds, suggesting that the spectra are dominated by contributions from the two lowest energy syn and anti rotamers. This value for the S₀–D₀ VDE is also consistent with those obtained from earlier measurements and EPT and XMCQDPT2/aug-cc-pVTZ calculations, which corresponds to the VDE of the syn rotamer.¹⁴ Despite the potential for population of the singly H-bonded rotamer at 300 K, there is no signal peaking at 2.5 eV eBE which could correspond to direct detachment from this rotamer. The rising edges of the DM-HBDI⁻ spectra are shallower than those of p-HBDI⁻ and DF-HBDI⁻. This could be a result of the spectra containing contributions from both the syn and anti rotamers. However, if there is a large conformational change upon ionisation, this could result in a shift of the maximum Franck–Condon overlap away from the S₀–D₀ origin. Similar observations and interpretations were made for photoelectron spectra of DMPhO⁻ compared with spectra of PhO⁻ and DFPhO⁻.⁵⁷ There is an additional peak in the 230 nm spectrum at 4.3 ± 0.1 eV eBE which is consistent with the EOM-IP-CCSD S₀–D_1n VDEs (Table S1 in the ESI†) (4.48 eV and 4.52 eV for the syn and anti rotamers, respectively); this value is also in agreement with earlier calculations.¹⁴

Similar to p-HBDI⁻ and DF-HBDI⁻, the photoelectron spectra are broadened as the wavelength is decreased in the range 364–315 nm. This broadening can be attributed to features with maximum eKEs around 0.7 eV and 1.0 eV (Fig. 3c and Fig. S4, ESI†), corresponding to detachment from resonances with AEEs around 3.4 eV and 3.7 eV, respectively. Due to the electron withdrawing nature of the methoxy-substituents, the resonances at 3.4 eV and 3.7 eV are likely to correspond to the 2ππ* and 3ππ* states, respectively. This is consistent with earlier XMCQDPT2/aug-cc-pVTZ calculations of the VEEs of ππ* excited states lying in the range 3.60–4.05 eV, see Fig. 6.¹⁴ While our spectra agree with the excited state calculations from ref. 14, which use an optimised geometry similar to the syn rotamer, it is possible that there are small differences between the AEEs of the syn and anti rotamers which likely contributes to the overall broad appearance of the experimental spectra of DMHBDI⁻.

Interestingly, the spectra of DM-HBDI⁻ also have a fairly distinct low eKE feature centred around 0.05 eV eKE that is more pronounced in the 346–315 nm spectra than the 364 nm spectrum. Similarly to the equivalent feature observed in the 315 nm and 320 nm spectra of p-HBDI⁻, this low eKE feature is characteristic of indirect detachment from an electronically excited state lying close to a detachment threshold or thermionic emission from S₀. Experimental studies of 2,6-dimethoxyphenolate and DMHBDI⁻ have demonstrated that the methoxy substituents have a relatively weak effect on the electronic structure of the chromophore due to the competition between the opposing inductive and mesomeric effects, so it is likely that the 1ππ* electronic excited state of DMHBDI⁻ lies close to the detachment threshold as observed for p-HBDI⁻ and as suggested by XMCQDPT2/aug-cc-pVTZ VEE calculations for DMHBDI⁻.^14,57 Given that the shape of the feature at 0.05 eV eKE does not appear exponential (as is typical for thermionic emission^73,74) it seems likely that the feature is a result of VAD from 1ππ*, however, this assignment is tentative as this signal corresponds to the centremost pixels of the photoelectron image which are the most susceptible to the amplification of noise by the pBASEX inversion method.

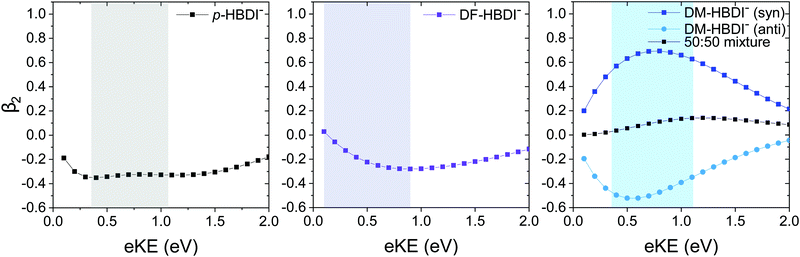
3.3 Photoelectron angular distributions

The 364 nm photoelectron images of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ are presented in Fig. 7 together with the photoelectron spectra and β₂ parameters, plotted as a function of eBE and eKE. ezDyson calculations of the β₂ parameters that characterise direct S₀–D₀ detachment in p-HBDI⁻, DFHBDI⁻ and syn and anti DM-HBDI⁻ are plotted in Fig. 8 as a function of eKE. The two limiting cases of β₂ are +2 and −1, corresponding to photoelectron emission predominantly parallel and perpendicular to the laser polarisation, respectively. In the absence of resonances in the continuum, β₂ < 0 corresponds to photodetachment from an orbital with p or π character and β₂ > 0 corresponds to photodetachment from an orbital with s or σ character.

Fig. 7 364 nm photoelectron images and spectra of p-HBDI⁻ (top), DF-HBDI⁻ (middle) and DM-HBDI⁻ (bottom). β₂ values are averaged over five data points and the error bars are the standard deviation. The photoelectron images have been oriented so that the vertical axis is parallel with the polarisation vector of the laser light.

Fig. 8 Plots of the calculated β₂ anisotropy parameter as a function of eKE for the p-HBDI⁻ anion (left), the DF-HBDI⁻ anion (middle) and the DM-HBDI⁻ anion (right). Calculated using ezDyson with EOM-IP-CCSD/aug-cc-pVDZ Dyson orbitals in the case of p-HBDI⁻ and DF-HBDI⁻, and EOM-IP-CCSD/6-311++G(d,p) Dyson orbitals in the case of DM-HBDI⁻. The shaded regions indicate the eKEs accessible in the 364–315 nm wavelength range.

For p-HBDI⁻, the experimental β₂ value is reasonably constant across the peak in the photoelectron spectrum and has an intensity-weighted average value of −0.15 ± 0.05, consistent with the calculated value of β₂ = −0.35. The anisotropy can be understood qualitatively by considering partial waves of s and p character.⁷⁵ The orientation of the p partial waves with respect to the electric field vector of the light can be calculated by taking the direct products of the irreducible representation of the HOMO with those of the x, y and z axes in the molecular frame. For p-HBDI⁻ (C_s point group), the HOMO and z axis have A′′ symmetry, resulting in p partial waves having A′ symmetry, i.e. perpendicular to the electric field vector of the laser light (β₂ < 0), in agreement with previous measurements.¹³

The PAD of DF-HBDI⁻ is strikingly different to that of p-HBDI⁻. β₂ ∼ 0 on the low eBE edge of the photoelectron spectrum and rises to around 0.4 on the high eBE edge, i.e. the PAD is isotropic on the low eBE edge of the spectrum and becomes increasingly parallel to the electric field vector of the laser light with increasing eBE. This contrasts with our ezDyson calculations which predict the PAD of the direct detachment process to be perpendicular (β₂ < 0) for eKE > 0.1 eV (Fig. 8). The increase in β₂ with increasing eBE can be rationalised in terms of an increasing contribution from autodetachment from a resonance, which is consistent with our observation of contributions to the photoelectron spectra from a resonance with AEE around 3.4 eV (365 nm). This is similar to a previous study of p-HBDI⁻ following photoexcitation in the range 516–282 nm in which resonant autodetachment from the 2ππ* state was found to give rise to a parallel PAD.¹³ Similar PADs are observed for all the photoelectron images of DF-HBDI⁻ following photoexcitation in the range 346–315 nm (Fig. S6, ESI†). At the shortest wavelengths it becomes apparent that the β₂ values become strongly positive at eKEs ≤ 0.5 eV.

For DM-HBDI⁻, the experimental β₂ value is reasonably constant across the peak in the photoelectron spectrum and has an intensity-weighted average value of 0.05 ± 0.05. Isotropic PADs are observed for all the photoelectron images of DM-HBDI⁻ following photoexcitation in the range 346–315 nm (Fig. S7 in the ESI†). The calculated values for the syn and anti rotamers have values of 0.57 and −0.49, respectively, at this wavelength and an average value of 0.04. This suggests that the experimentally observed PAD could be predominantly the result of direct detachment. Nonetheless, given that there is still a weak feature at 0.05 eV which may be attributed to vibrational autodetachment from a vibrationally hot 1ππ* state, or thermionic emission from the ground electronic state, it is possible that there is a weak contribution from autodetachment from the electronic excited state at 3.4 eV in the 364 nm spectrum which may also influence the observed PAD. ezDyson calculations of the β₂ parameters that characterise direct S₀–D₀ detachment in the higher energy rotamers of DM-HBDI⁻, which do not appear to contribute to the presented spectra, are plotted as a function of eKE in S8 in the ESI.†

It is interesting to note the opposing signs of the ezDyson PADs of the syn and anti rotamers of DM-HBDI⁻, which mirrors those for the syn and anti rotamers of 2,6-dimethoxyphenolate anion.⁵⁷ Similar effects have also been observed in para-substituted phenolates.^16,58,76

4 Discussion

From Fig. 6, it is clear that adding methoxy and fluorine substituents has the effect of removing the near degeneracy of the 2ππ* and 3ππ* states, which is reflected in our observation of two clearly distinct constant eKE features, attributed to resonances, in the photoelectron spectra of DF-HBDI⁻ and DM-HBDI⁻, whereas in the photoelectron spectra of p-HBDI⁻ the contribution from the feature at 1.03 eV eKE can only be seen clearly in the He-thermalised data at 315 nm. Our estimates of the AEEs of these features are consistent with the calculated VEEs from ref. 14 giving confidence in the high level calculations. Thus, we assign the features in the DF-HBDI⁻ photoelectron spectra centered around eKEs of 0.4 eV and 0.8 eV, corresponding to AEEs of 3.4 eV and 3.8 eV, as resonant detachment from the 2ππ* and 3ππ* or 4ππ* states (with calculated VEEs of 3.58 eV and 4.02 eV or 4.20 eV). For DM-HBDI⁻, we suggest that the features in the photoelectron spectra centered around eKEs of 0.7 eV and 1.0 eV, corresponding to AEEs of 3.4 eV and 3.7 eV, arise from resonant detachment from the 2ππ* and 3ππ* or 4ππ* states (with calculated VEEs of 3.60 eV and 4.02 eV or 4.08 eV). However, given that the calculated oscillator strengths for the 2ππ* state are zero in the substituted chromophores (compared with 0.02 in p-HBDI⁻), we cannot rule out that the lower eKE resonant signal may arise from 1nπ*-D₀ autodetachment.

Comparing the PADs recorded at 364 nm (3.41 eV) with the ezDyson calculations shows that, for the planar anions, direct detachment from S₀ to the D₀ continuum generates photoelectrons with a distribution predominantly perpendicular to the electric field vector of the laser light and that resonant autodetachment from the 2ππ* state generates photoelectrons with a distribution that is predominantly parallel to the electric field vector of the laser light. Previous work has suggested that the 2ππ* state in p-HBDI⁻, which has predominantly Feshbach resonance character with respect to the D₀ continuum, generates photoelectrons with a distribution that is predominantly parallel to the electric field vector of the laser light.¹³ Our observation of positive β₂ values at eKEs ≤ 0.5 eV in the photoelectron spectra of DF-HBDI⁻ supports this suggestion.

The photoelectron spectra of DM-HBDI⁻ all have a low eKE feature that is characteristic of autodetachment from high lying vibrational states of a lower lying electronically excited state or thermionic emission from S₀. This low eKE feature was previously assigned to detachment from the 1nπ* electronic excited state to the D_1n continuum;¹⁴ however, since the work presented here shows that this feature is also observed in spectra at photon energies significantly below the calculated S₀–D_1n VDE (4.05 eV), it seems likely that it arises from vibrational autodetachment from the 1ππ* state following internal conversion from a higher lying state, or from thermionic emission from S₀. Although this low eKE feature is quite pronounced in the photoelectron spectra of DM-HBDI⁻, there are also low eKE electrons observed in photoelectron spectra of DF-HBDI⁻ and p-HBDI⁻, most notably in the shorter wavelength spectra. Since the photon energies employed in these experiments are far higher than the VEEs of the 1ππ* state, it is unlikely to be populated directly. Thus, it is most likely that these low eKE electrons arise from internal conversion from the 2ππ* state which has, predominantly, Feshbach resonance character with respect to the D₀ continuum and thus a potentially long enough lifetime for internal conversion to the 1ππ* state to compete with autodetachment. It seems that addition of the methoxy substituents enhances the internal conversion process. This could result from a change in molecular geometry or symmetry caused by internal rotations of the methoxy groups of the anion upon electronic excitation. Such a change in geometry and/or point group could change the relative energies and/or symmetries of the electronic states in a way which enables more efficient population transfer to the lower states. The involvement of the 2ππ* state in the electronic relaxation process is consistent with an earlier time-resolved study of the relaxation dynamics of p-HBDI⁻ following UV photoexcitation.¹³

5 Conclusions

Photoelectron spectra and photoelectron angular distributions (PADs) of the deprotonated anions of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻, following photodetachment in the 364–230 nm wavelength range have been presented and interpreted using a combination of previously published¹⁴ and new quantum chemistry calculations. By examining the photoelectron spectra of DF-HBDI⁻ and DM-HBDI⁻ over a wider range of wavelengths an additional resonant photodetachment process via the 2ππ* electronic excited state has been revealed. Analysis of the PADs suggest that indirect detachment via the 2ππ* state, which has Feshbach resonance character with respect to the D₀ continuum, is likely to contribute to the spectra of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻ following UV photoexcitation in the 364–315 nm range. Furthermore, a low eKE feature that is most pronounced in the DM-HBDI⁻ spectra and was previously assigned as 1nπ*-D_1n detachment has been reassigned as detachment from a vibrationally hot 1ππ* state or thermionic emission from S₀, following internal conversion from the 2ππ* state. Although there are low eKE electrons observed in the spectra of p-HBDI⁻, DF-HBDI⁻ and DM-HBDI⁻, this feature is most pronounced in the DM-HBDI⁻ spectra, suggesting that the methoxy substituents enhance the rate of internal conversion from the 2ππ* state relative to electron detachment. Improving our understanding of the competition between the various electronic relaxation processes is important for the rational design of chromophores and fluorescent proteins for new imaging applications; particularly in the case of these small molecular chromophores which are used as fluorescent tags for biological macromolecules such as RNA, without impeding their function.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by EPSRC Grant EP/L005646/1. HHF acknowledges the Leverhulme Trust and the Royal Society for a Royal Society Leverhulme Trust Senior Research Fellowship (SRF/R1/180079). AVB acknowledges support from the Russian Science Foundation (Grant Number 17-13-01276). We are grateful to Dr Michael Parkes for technical support and Dr Frank Otto for computational support.

References

1. J. G. Morin and J. W. Hastings, J. Cell. Physiol., 1971, 77, 313–318.
2. R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544.
3. M. W. Forbes and R. A. Jockusch, J. Am. Chem. Soc., 2009, 131, 17038–17039.
4. M. W. Forbes, A. M. Nagy and R. A. Jockusch, Int. J. Mass Spectrom., 2011, 308, 155–166.
5. Y. Toker, D. B. Rahbek, B. Klærke, A. V. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2012, 109, 128101.
6. D. A. Horke and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515.
7. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
8. C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 865–1356.
9. C. W. West, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Chem. Phys., 2013, 139, 071104.
10. S. H. Deng, X. Y. Kong, G. Zhang, Y. Yang, W. J. Zheng, Z. R. Sun, D. Q. Zhang and X. B. Wang, J. Phys. Chem. Lett., 2014, 5, 2155–2159.
11. C. R. S. Mooney, M. A. Parkes, L. Zhang, H. C. Hailes, A. Simperler, M. J. Bearpark and H. H. Fielding, J. Chem. Phys., 2014, 140, 205103.
12. A. V. Bochenkova, B. Klærke, D. B. Rahbek, J. Rajput, Y. Toker and L. H. Andersen, Angew. Chem., Int. Ed., 2014, 53, 9797–9801.
13. C. W. West, J. N. Bull, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Phys. Chem. B, 2015, 119, 3982–3987.
14. A. V. Bochenkova, C. Mooney, M. A. Parkes, J. Woodhouse, L. Zhang, R. Lewin, J. M. Ward, H. Hailes, L. H. Andersen and H. H. Fielding, Chem. Sci., 2017, 8, 3154–3163.
15. C. McLaughlin, M. Assmann, M. A. Parkes, J. L. Woodhouse, R. Lewin, H. C. Hailes, G. A. Worth and H. H. Fielding, Chem. Sci., 2017, 8, 1621–1630.
16. C. S. Anstöter, C. R. Dean and J. R. R. Verlet, J. Phys. Chem. Lett., 2017, 8, 2268–2273.
17. E. Carrascosa, J. N. Bull, M. S. Scholz, N. J. A. Coughlan, S. Olsen, U. Wille and E. J. Bieske, J. Phys. Chem. Lett., 2018, 9, 2647–2651.
18. A. Henley and H. H. Fielding, Int. Rev. Phys. Chem., 2019, 38, 1–34.
19. W. Zagorec-Marks, M. M. Foreman, J. R. R. Verlet and J. M. Weber, J. Phys. Chem. Lett., 2019, 10, 7817–7822.
20. W. Zagorec-Marks, M. M. Foreman, J. R. R. Verlet and J. M. Weber, J. Phys. Chem. Lett., 2020, 11, 1940–1946.
21. H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. I. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622.
22. N. M. Webber, K. L. Litvinenko and S. R. Meech, J. Phys. Chem. B, 2001, 105, 8036–8039.
23. A. D. Kummer, C. Kompa, H. Niwa, T. Hirano, S. Kojima and M. E. Michel-Beyerle, J. Phys. Chem. B, 2002, 106, 7554–7559.
24. D. Mandal, T. Tahara and S. R. Meech, J. Phys. Chem. B, 2004, 108, 1102–1108.
25. R. Gepshtein, D. Huppert and N. Agmon, J. Phys. Chem. B, 2006, 110, 4434–4442.
26. S. S. Stavrov, K. M. Solntsev, L. M. Tolbert and D. Huppert, J. Am. Chem. Soc., 2006, 128, 1540–1546.
27. K. Y. Chen, Y. M. Cheng, C. H. Lai, C. C. Hsu, M. L. Ho, G. H. Lee and P. T. Chou, J. Am. Chem. Soc., 2007, 129, 4534–4535.
28. J. Kang, G. Zhao, J. Xu and W. Yang, Chem. Commun., 2010, 46, 2868–2870.
29. C. C. Hsieh, P. T. Chou, C. W. Shih, W. T. Chuang, M. W. Chung, J. Lee and T. Joo, J. Am. Chem. Soc., 2011, 133, 2932–2943.
30. Y.-H. Hsu, Y.-A. Chen, H.-W. Tseng, Z. Zhang, J.-Y. Shen, W.-T. Chuang, T.-C. Lin, C.-S. Lee, W.-Y. Hung, B.-C. Hong, S.-H. Liu and P.-T. Chou, J. Am. Chem. Soc., 2014, 136, 11805–11812.
31. S. B. Nielsen, A. Lapierre, J. U. Andersen, U. V. Pedersen, S. Tomita and L. H. Andersen, Phys. Rev. Lett., 2001, 87, 228102.
32. W. J. Glover, A. S. P. Paz, W. Thongyod and C. Punwong, J. Chem. Phys., 2019, 151, 201101.
33. J. W. Park, J. Chem. Theory Comput., 2020, 16, 326–339.
34. J. J. van Thor, T. Gensch, K. J. Hellingwerf and L. N. Johnson, Nat. Struct. Biol., 2002, 9, 37–41.
35. A. F. Bell, D. Stoner-Ma, R. M. Wachter and P. J. Tonge, J. Am. Chem. Soc., 2003, 125, 6919–6926.
36. K. A. Lukyanov, D. M. Chudakov, S. Lukyanov and V. V. Verkhusha, Nat. Rev. Mol. Cell Biol., 2005, 6, 885–890.
37. J. J. van Thor, Chem. Soc. Rev., 2009, 38, 2935–2950.
38. A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2017, 117, 758–795.
39. A. M. Bogdanov, A. Acharya, A. V. Titelmayer, A. V. Mamontova, K. B. Bravaya, A. B. Kolomeisky, K. A. Lukyanov and A. I. Krylov, J. Am. Chem. Soc., 2016, 138, 4807–4817.
40. J. S. Paige, K. Y. Wu and S. R. Jaffrey, Science, 2011, 333, 642–646.
41. M. You and S. R. Jaffrey, Annu. Rev. Biophys., 2015, 44, 187–206.
42. J. B. Greenwood, J. Miles, S. D. Camillis, P. Mulholland, L. Zhang, M. A. Parkes, H. C. Hailes and H. H. Fielding, J. Phys. Chem. Lett., 2014, 5, 3588–3592.
43. A. R. McKay, M. E. Sanz, C. R. S. Mooney, R. S. Minns, E. M. Gill and H. H. Fielding, Rev. Sci. Instrum., 2010, 81, 123101.
44. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989.
45. J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942–943.
46. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997.
47. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
48. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
49. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, G. Ehara, M. K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. E. Montgomery, Jr., J. A. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
51. P. U. Manohar and A. I. Krylov, J. Chem. Phys., 2008, 129, 194105.
52. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
53. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
54. S. Gozem and A. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, e1546.
55. S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540.
56. C. S. Anstöter, C. R. Dean and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2017, 19, 29772–29779.
57. J. L. Woodhouse, A. Henley, M. A. Parkes and H. H. Fielding, J. Phys. Chem. A, 2019, 123, 2709–2718.
58. C. S. Anstöter and J. R. R. Verlet, J. Phys. Chem. A, 2021, 125, 4888–4895.
59. C. S. Anstöter and J. R. R. Verlet, Mol. Phys., 2021, 119, e1821921.
60. R. F. Gunion, M. K. Gilles, M. L. Polak and W. C. Lineberger, Int. J. Mass Spectrom. Ion Process., 1992, 117, 601–620.
61. C. R. S. Mooney, M. A. Parkes, A. Iskra and H. H. Fielding, Angew. Chem., Int. Ed., 2015, 54, 5646–5649.
62. M. A. Parkes, C. Phillips, M. J. Porter and H. H. Fielding, Phys. Chem. Chem. Phys., 2016, 18, 10329–10336.
63. J. Tay, M. A. Parkes, K. Addison, Y. Chan, L. Zhang, H. C. Hailes, P. C. Bulman Page, S. R. Meech, L. Blancafort and H. H. Fielding, J. Phys. Chem. Lett., 2017, 8, 765–771.
64. A. Henley, M. Diveky, A. Patel, M. A. Parkes, J. C. Anderson and H. H. Fielding, Phys. Chem. Chem. Phys., 2017, 19, 31572–31580.
65. J. L. Woodhouse, M. Assmann, M. A. Parkes, H. Grounds, S. J. Pacman, J. C. Anderson, G. A. Worth and H. H. Fielding, Phys. Chem. Chem. Phys., 2017, 19, 22711–22720.
66. M. A. Parkes, J. Crellin, A. Henley and H. H. Fielding, Phys. Chem. Chem. Phys., 2018, 20, 15543–15549.
67. A. Henley, A. M. Patel, M. A. Parkes, J. C. Anderson and H. H. Fielding, J. Phys. Chem. A, 2018, 122, 8222–8228.
68. A. M. Patel, A. Henley, M. A. Parkes, M. Assmann, G. A. Worth, J. C. Anderson and H. H. Fielding, Phys. Chem. Chem. Phys., 2020, 22, 19022–19032.
69. E. Epifanovsky, I. Polyakov, B. Grigorenko, A. Nemukhin and A. I. Krylov, J. Chem. Theory Comput., 2009, 5, 1895–1906.
70. C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 921–927.
71. A. V. Bochenkova and L. H. Andersen, Faraday Discuss., 2013, 163, 297–319.
72. A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771.
73. C. E. Klots, J. Chem. Phys., 1993, 98, 1110–1115.
74. C. E. Klots, J. Chem. Phys., 1994, 100, 1035–1039.
75. A. Sanov and R. Mabbs, Int. Rev. Phys. Chem., 2008, 27, 53–85.
76. C. S. Anstöter, B. F. Curchod and J. R. R. Verlet, Nat. Commun., 2020, 11, 2827.

---

Footnotes

† Electronic supplementary information (ESI) available: Difference spectra; benchmarking calculations; ezDyson calculations for PhO⁻; β₂ parameters for DF-HBDI⁻ from 364–346 nm photoelectron spectra. See DOI: 10.1039/d1cp01901e

‡ Current address: Chemistry, University of Southampton, Highfield, Southampton SO17 1BJ, UK.

---