Open Access Article
Open Access ArticleDirect nonadiabatic quantum dynamics simulations of the photodissociation of phenol
Georgia
Christopoulou
 a,
Thierry
Tran
a,
Thierry
Tran
 ab and
Graham A.
Worth
ab and
Graham A.
Worth
 *a
*a
aDepartment of Chemistry, University College London, London WC1H 0AJ, UK
bDepartment of Chemistry, Imperial College London, Imperial College London, White City Campus, W12 0BZ London, UK. E-mail: g.a.worth@ucl.ac.uk
First published on 5th October 2021
Abstract
Gaussian wavepacket methods are becoming popular for the investigation of nonadiabatic molecular dynamics. In the present work, a recently developed efficient algorithm for the Direct Dynamics variational Multi-Configurational Gaussian (DD-vMCG) method has been used to describe the multidimensional photodissociation dynamics of phenol including all degrees of freedom. Full-dimensional quantum dynamic calculations including for the first time six electronic states (1ππ, 11ππ*, 11πσ*, 21πσ*, 21ππ*, 31ππ*), along with a comparison to an existing analytical 4-state model for the potential energy surfaces are presented. Including the fifth singlet excited state is shown to have a significant effect on the nonadiabatic photodissociation of phenol to the phenoxyl radical and hydrogen atom. State population and flux analysis from the DD-vMCG simulations of phenol provided further insights into the decay mechanism, confirming the idea of rapid relaxation to the ground state through the 1ππ/11πσ* conical intersection.
1 Introduction
Photochemistry is the branch of chemistry that deals with the investigation of chemical reactions, physical behavior and isomerizations which take place under the influence of visible and/or ultraviolet light.1 After a molecule absorbs energy from a photon of light, it is transferred into an excited electronic state and can advance along the potential energy surface (PES) of the excited state. However, the reaction path of the molecule cannot be represented by a single PES but instead at least two are needed, one for the excited electronic state and the second one for the ground electronic state. Once these potential energy surfaces have been obtained, the time-dependent Schrödinger equation (TDSE) can be solved to simulate the photo-excited dynamics, taking into consideration that the Born–Oppenheimer approximation (BOA) breaks down in a region where two PESs cross.Over the years, a wide range of dynamics methods have been established to solve the TDSE. As the number of degrees of freedom increases, the complexity in solving the TDSE scales exponentially. One of the most efficient algorithms, especially for molecules with more than a few degrees of freedom, is the multi-configuration time-dependent Hartree (MCTDH) method and the related multi-layer MCTDH method.2–5 However, a significant bottleneck of MCTDH, like all the grid-based methods, is that before any calculation is conducted, the global potential energy surfaces must be first computed and fit to analytic functions. Thus, on-the-fly molecular dynamics are gaining a lot of interest as they overcome the aforementioned problem by simply calculating the potential in the areas of the configuration space which are reached by the system.
Direct Dynamics variational Multi-configurational Gaussian method (DD-vMCG) is a quantum molecular dynamics method using the on-the-fly approach to calculate the PESs.6–8 This is a purely Gaussian wavepacket (GWP) method, where the basis functions that grid-based methods employ are replaced by multi-dimensional parameterised Gaussian functions, and the wavefunction is represented by a superposition of these GWPs that follow variationally coupled trajectories.9–11
In DD-vMCG, a quantum chemistry program is called to calculate the information required to represent the PESs (energies, gradients and Hessians) along the trajectories followed by the centres of the GWPs. This information is stored in a database. Each time a GWP reaches a new point the database is read in order to check for previously calculated points that are close to the new point. If suitable points exist, instead of performing a quantum chemistry calculation, which is an expensive computational process, the PES are computed by employing a modified Shepard interpolation.12 If no suitable points exist, the quantum chemistry code is called and the new information added to the database. Recently, a more efficient parallel algorithm for DD-vMCG was introduced accompanied with various methodological updates focusing on the interpolation and diabatisation schemes previously employed.13 All the different methods and schemes presented above are included in the Quantics package.14,15
Amino acids are among the essential biomolecules. Aromatic amino acids such as phenylalanine, tryptophan and tyrosine have broad UV absorption cross sections. Nevertheless, the fluorescence quantum yield produced from these molecules is quite small. The existence of fast non-radiative processes, that effectively quench the fluorescence is described in the literature.16–19 Other research studies further show that the non-radiative process is predominantly ultrafast internal conversion where the electronic energy is turned into vibrational energy.17–20 Immediately after the internal conversion, through intermolecular energy transfer this vibrational energy is rapidly dissipated from the highly vibrationally excited molecules to the surrounding molecules prior to chemical reactions occurring. The prevention of photochemical reactions upon UV irradiation is known as photostability.
Phenol (C6H5OH) is the chromophore of the amino acid tyrosine and a major component of other important biomolecules, such as the green fluorescent protein chromophores.21 It has thus been extensively studied by both experimentalists22–25 and theoreticians.26–28 The equilibrium structure of neutral phenol, shown in Fig. 1, belongs to the Cs point group and has 33 normal vibrational modes. An interaction between one of the lone pairs on the oxygen atom and the delocalised electrons in the benzene ring significantly affects the properties of both the –OH group and the ring. The electron density around the ring is increased by the donation of the oxygen's lone pair into the ring system. Thus, the ring is far more reactive compared to benzene itself. As experimental results and computational quantum chemistry calculations show, phenol has a low fluorescence quantum yield attributable not just due to fast internal conversion back to the ground-state, but also due to the dissociative character of the electronic excited state PES.27,29,30 Also, the important coordinates which are fundamentally involved in the dynamics are the O7–H13 distance, the C1–O7–H13 bond angle and the C2–C1–O7–H13 torsion angle as depicted in Fig. 1.
Furthermore, the PES change in character as the O–H stretch increases. The PES of a dark repulsive 1πσ* state (S2 in the Franck–Condon region) of phenol undergoes two conical intersections with other PESs, initially with the strongly absorbing bound 1ππ* state (S1) and further with the ground state 1ππ (S0). The photodissociation dynamics is significantly influenced by these two conical intersections as their shapes and energetics define the branching ratios of photodissociation products and the reaction mechanism for various UV wavelengths. The relative kinetic energy distribution of photofragments is the most direct experimental observable, which is found to be bimodal for excitation ranging from 279.145 to 193 nm, as defined by a wide range of different techniques, such as time-resolved velocity map ion imaging, high-resolution H Rydberg atom translational spectroscopy, and multimass ion imaging.22,23,25,31–35
For molecules with a lot of degrees of freedom, such as phenol, the dissociation lifetime can vary from sub-microseconds to several hundred microseconds.36–38 The dissociation lifetime of phenol is quite short, below a few nanoseconds, but it has a slow dissociation rate of reaction. It was found that the lifetime of a highly vibrationally excited phenol in the S0 state, produced via the internal conversion following the excitation to the S1 band origin, was 62 μs.39 Overall, if the pumping photon energy is chosen to enhance the propensity for 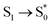 is increased, then the lifetime of the S1 state at the excited Franck–Condon window (including vibrational modes orthogonal to the O–H coordinate) will be reduced and could lead to production of H from S0. However, this increase in O–H fission rate has never been observed in the H transients that are known to be sensitive to decay into H photoproducts along the S2 state. Subsequently, an
is increased, then the lifetime of the S1 state at the excited Franck–Condon window (including vibrational modes orthogonal to the O–H coordinate) will be reduced and could lead to production of H from S0. However, this increase in O–H fission rate has never been observed in the H transients that are known to be sensitive to decay into H photoproducts along the S2 state. Subsequently, an  dissociation mechanism is unlikely to be active.22
dissociation mechanism is unlikely to be active.22
Employing theoretical methods up to the complete active space with perturbation theory (CASPT2) level, Sobolewski and Domcke30 were the first to explore the phenol nonadiabatic dissociation pathways. Their innovative work disclosed that since the 1πσ* character state, a dark and strongly repulsive state, crosses both the S1 and S0 states, the dissociation from the 1ππ* character state involves two seams of conical intersections. Recently, significant efforts have been made to map out the full-dimensional potential energy surfaces for this system. Three full-dimensional coupled potential energy surfaces were reported40 employing the anchor-points reactive potential (ARPR) method to a large number of points determined from multi-configuration quasi-degenerate perturbation theory. Moreover, four full-dimensional coupled PESs based on multi-reference configuration interaction single and double excitation expansions have been reported by Zhu and Yarkony.26,41,42
In the following, the variational multi-configuration Gaussian method and its direct dynamics implementation will be briefly recapped. The methodology employed for the electronic structure and direct dynamics calculations is then discussed in detail. A comparison of direct dynamics calculations performed for the ground and the first three excited states of phenol including all degrees of freedom at a 6-311+G** level of theory is first performed, with the four-state potential energy surfaces generated by employing the Zhu and Yarkony model for phenol26–28 using a comparable level of theory.
The paper thus aims to showcase the ability of DD-vMCG to treat photoexcited dynamics as well as to provide new insights into the excited state photochemistry of phenol. Results for 3-, 4-, 5- and 6-state full-dimensional DD-vMCG calculations are presented. This allows not only a demonstration of the potential of the method, but also the sensitivity of direct dynamics calculations to the electronic structure method used and the number of states included. How many states are required is an important question. While it is possible to have an idea as to how many must be included by an analysis of the critical points (Franck–Condon point, conical intersections, minima, barriers, etc.), it is difficult to have a definitive answer as it is impossible to know where all the critical points are. Thus the ability to run dynamics simulations with a differing number of states is an important property for a method.
2 Theory
2.1 The variational multi-configuration Gaussian method
A brief overview of the key concepts of vMCG is presented here: a detailed description of the method can be found in various publications.7,11,43 The method aims to solve the time-dependent Schrödinger equation for a wavefunction Ψ which depends both on nuclear coordinates, x, and time, t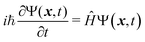 | (1) |
 | (2) |
vMCG is a purely Gaussian wavepacket (GWP) method, i.e. the following ansatz is employed
 | (3) |
Each GWP in the above ansatz is a multi-dimensional parameterised function for the set of coordinates, x, having the following form
| gj(x,t) = exp(xT·ςj·x + ξj·x + ηj) | (4) |
| Λj = {ςj,ξj,ηj} | (5) |
 | (6) |
Equations of motion can be written as follows in a vector notation
| Ȧ = iS−1(H − iτ)A | (7) |
iC![[capital Lambda, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e138.gif) = Y = Y | (8) |
| Hij = 〈gi|Ĥ|gj〉 | (9) |
| Sij = 〈gi|gj〉 | (10) |
 | (11) |
2.2 Direct dynamics
Due to its variational basis, the vMCG method is one of the most promising applications of Gaussian wavepacket dynamics in terms of accuracy and flexibility. In order to solve the EOMs outlined in the previous section, the matrix elements of the Hamiltonian must be evaluated. As shown in eqn (2), the Hamiltonian contains the kinetic and potential energy terms. Assuming that the dynamics run in rectilinear coordinates (e.g. Cartesian or normal modes), the kinetic energy operator has a fairly simple analytic form.11Using a Taylor series to second-order around the geometry at the centre of a GWP, x0, a potential energy surface can be expanded as follows
 | (12) |
The DD-vMCG method makes use of the fact that with the LHA all the required integrals can be obtained analytically using information from standard quantum chemistry calculations (QC) only at the centres of the GWP basis functions. This explains the term on-the-fly which is commonly used to describe the way the potential energy surfaces are obtained during a direct dynamics calculation. However, it is not desirable to run an expensive QC calculation at each step in the propagation. Thus QC calculations are only run when the centre of a GWP has moved significantly away from a previous point. For the integration steps between the QC calculations, Shepard interpolation is used to provide the LHA based on the set of prior QC calculations which are saved in a database.
DD-vMCG thus builds up the potential energy surfaces as the database contains energies, gradients, Hessians and other information calculated on-the-fly through an interface to an external quantum chemistry software package. The idea of reading all the required information from a database instead of performing expensive electronic structure calculations for each point reached by the GWPs has also been applied previously in classical trajectory44,45 and quantum trajectory methods.12 In the simulations here, the maximum displacement of an atom in a new structure compared to the structures already in the database in Cartesian space is used as a distance criterion. This distinguishes structures that are locally mobile. The distance that must be exceeded is referred to as the dbmin parameter and it is user defined at the beginning of the DD-vMCG calculation. Here a value of 0.2 Bohr was used.
To keep the PESs smooth, the database also stores the molecular orbital coefficients from the quantum chemistry calculation. Each new CASSCF calculation then takes the orbitals from the nearest geometry as the initial guess. To obtain the nonadiabatic couplings without discontinuities at surface intersections, the potential matrix is transformed to a diabatic picture. Within the DD-vMCG method, a general on-the-fly diabatisation scheme is provided by the so-called propagation diabatisation.43 This method is based on the propagation of the adiabatic-to-diabatic transformation matrix along the paths followed by the GWPs and is in principle able to handle an arbitrary number of states with unknown number of surface crossings.
The basic idea of the propagation diabatisation method is to use the relationship46
| ∇S = −FS | (13) |
 | (14) |
It should be kept in mind, however, that the integration of eqn (13) is formally path dependent due to couplings with states outside the manifold included in the calculation.47 Here the test used for the correctness of the diabatic surfaces is visual inspection that they are smooth through crossing points. Future work will introduce more rigorous testing, for example using the diabatisation ideas and tools of Adikhari and co-workers.48
3 Methods
3.1 Computational details
All the nuclear dynamics calculations were carried out using the DD-vMCG implementation in the Quantics package.14 PESs were generated using state-average CASSCF with up to 6 states, including the ground (S0) and the lowest singlet excited states (S1–S5). For all the calculations OpenMolcas49 was used at the complete active space self-consistent field (CASSCF) level of theory with 10 electrons in 10 orbitals and a basis set of 6-311+G**. This is denoted as CASSCF(10,10)/6-311+G** and the active space employed is depicted in Fig. 2. | ||
| Fig. 2 Molecular orbitals used for the CASSCF calculation with phenol using 10 electrons in 10 orbitals. | ||
The initial wavepacket was a Gaussian function of width  along all normal coordinates, which were generated from a frequency calculation at the optimised S0 geometry. In the mass-frequency scaled normal mode coordinates used, this corresponds to the exact ground-state vibrational eigenfunction in the harmonic approximation. Calculations were made with a vertical excitation to the S1 state using 20 Gaussian basis functions, with a propagation time of 200 fs and data output every 0.5 fs. The initial wavefunction is constructed with all GWPs centred at the FC point and distributed in momentum space. Only the GWP with no momentum is initially populated, thus providing an exact representation of the vertical excitation. The variational nature of vMCG means that results are not sensitive to the initial momenta of the unpopulated GWPs.
along all normal coordinates, which were generated from a frequency calculation at the optimised S0 geometry. In the mass-frequency scaled normal mode coordinates used, this corresponds to the exact ground-state vibrational eigenfunction in the harmonic approximation. Calculations were made with a vertical excitation to the S1 state using 20 Gaussian basis functions, with a propagation time of 200 fs and data output every 0.5 fs. The initial wavefunction is constructed with all GWPs centred at the FC point and distributed in momentum space. Only the GWP with no momentum is initially populated, thus providing an exact representation of the vertical excitation. The variational nature of vMCG means that results are not sensitive to the initial momenta of the unpopulated GWPs.
With only 20 GWPs, these are not converged calculations, but from our experience provide a qualitatively good solution to the TDSE over the short time-scale of these simulations. It is certainly able to describe the major features of non-adiabatic crossing, such as the bifurcation of the wavepacket, and allows a good description of the potential surfaces by visiting the key regions of configuration space. While the diabatic populations are expected to be reliable, more functions will be required to get reliable quantities such as adiabatic populations and other expectation values that require more sensitive details of the wavepacket.
As a comparison to the surfaces generated using the OpenMolcas quantum chemistry program, DD-vMCG calculations were also carried out employing the PESs for phenol from Zhu and Yarkony26–28 as an external program, referred to as the PESZY potentials. This program provides four full-dimensional coupled diabatic PESs based on multi-reference configuration interaction single and double excitation expansions. For dynamics employing this program, the initial geometry had to be generated with the molecule aligned on the XZ plane. The similar level of theory used in the PESXY surfaces and the OpenMolcas calculations allow a good comparison to be made between the diabatic surfaces generated by the propagation diabatisation procedure and those provided analytically.
Complex absorbing potentials (CAPs) were employed to absorb parts of the wavepacket that dissociate. In grid-based methods, these are required to prevent artificial reflection of the wavepacket from the end of the grid.50,51 In DD-vMCG, CAPs are used as a cut-off point to the dissociative motion as when this occurs, the dissociating atom gains momentum as it initially accelerates away from the parent molecule. As a result, the integrator will rapidly decrease the size of the time step that enables a valid description of the system as a whole. These rapidly changing geometries will additionally lead into a larger number of points requiring electronic structure calculations. At these widely spaced geometries, the electronic structure calculations will take much longer to run, and may eventually fail.
The CAPs are defined as a negative, imaginary potential
| iW = ηΘ(k(x − x0))n | (15) |
Moreover, the flux operator for the dissociating wavepacket can be evaluated using the CAP. The flux is the rate of change of probability density into a defined subspace. If Θ denotes a Heaviside step function projecting onto the sub-space of interest, then the flux has the following form
 | (16) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) = i[H,Θ] = i[H − iW,Θ] = i(HΘ − ΘH) + 2W = i[H,Θ] = i[H − iW,Θ] = i(HΘ − ΘH) + 2W | (17) |
Initially, for all the calculations presented here, a direct dynamics run was conducted with an empty database to seed the database with the energies, gradients, Hessians and nonadiabatic couplings at the Franck–Condon point. A propagation was then run starting from this point and using Hessian updating in the diabatic picture. In a direct dynamics propagation, if one considers a GWP that reaches the same point in configuration space multiple times, each time the database is different as it is built on-the-fly and therefore the extrapolated potential will not be the same. Hence, to get the best representation of the dynamics, multiple sequential propagations were performed until no new points were added to the database.
This protocol of re-running a calculation aiming to add more points in the database is a key feature of DD-vMCG. The final databases were obtained after 3 reruns of the same calculation and contained approximately 2000 points. The final propagation used this database to read all required information without running any further quantum chemistry calculations. For all the re-runs of the same DD-vMCG calculation a recently developed efficient algorithm was employed which uses a local dynamic version of the full database for each GWP each time the code needs to read, sort and analyse the database.13 In the following analysis the results of this final set of calculations were employed.
4 Results
4.1 Potential energy surfaces
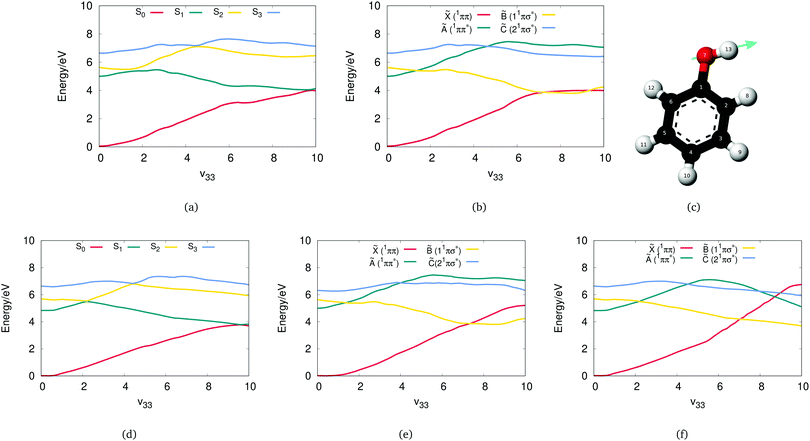
Initially, a study including four states to describe the phenol photodissociation was performed employing the DD-vMCG method including all degrees of freedom. The Zhu and Yarkony26–28 PESXY potential program and OpenMolcas have been employed as external programs for computing the adiabatic energies, gradients and Hessians when needed. The diabatic and adiabatic potential energy surfaces have been calculated from the resulting database along the ν33 vibrational mode, which corresponds to the O–H bond stretch mode.Fig. 3(a) and (b) show the adiabatic and diabatic potential energy surfaces along the O–H stretching coordinate generated from the direct dynamics calculation using OpenMolcas. These curves, as well as those shown in subsequent figures, are obtained from the final database with all the points collected from the simulations and using the Shepard interpolation scheme. They are thus cuts through the multi-dimensional potential functions and not associated with any single trajectory or basis function.
The surfaces are smooth with well defined conical intersections (CIs). The diabatic potentials consist of the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) and three singlet excited states. The first singlet state (Ã) has a ππ* character and is bound along the O–H stretching coordinate, and the second (
) and three singlet excited states. The first singlet state (Ã) has a ππ* character and is bound along the O–H stretching coordinate, and the second (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and third (
) and third (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) states both have πσ* character and are dissociative along the O–H stretching coordinate.
) states both have πσ* character and are dissociative along the O–H stretching coordinate.
The corresponding adiabatic potentials in Fig. 3(a) include three conical intersections. As expected, the first crossing occurs when the first excited 11ππ* state crosses the strong repulsive 1πσ* state. Transfer of the population from the bright state to the dark state can be possible through this conical intersection. An additional conical intersection between the third repulsive excited 1πσ* state and the first 11ππ* state is also seen, which will be shown below to be crucial for the dissociation of phenol. Furthermore, at larger O–H distance, a third conical intersection is occurring when the S1 state, which now has 1πσ* character, crosses the ground state. The role of these conical intersections in the photodissociation of phenol has been extensively studied as it has a great impact on the probability of dissociation.52
Comparing these results with the ones obtained by employing the adiabatic potentials from the PESZY program, the OpenMolcas adiabatic surfaces are a good match to those from PESXY shown in Fig. 3(d). These in turn are a good match to those presented in the original Zhu and Yarkony paper.26 All the conical intersections, S2/S1, S3/S2 and S1/S0, are found at the same positions. To give the scale of the potential cuts in Fig. 3, note that the x-axis in the figure is for the dimensionless normal mode coordinate ν33. One unit along this vibration is equivalent to the O–H bond stretching by approximately 0.1 Å. Thus, given that the equilibrium O–H bond length is 0.96 Å, the S1/S0 intersection is at a bond length of 1.96 Å.
However, the diabatic surfaces generated from the PEXXY adiabatic potentials using the diabatisation scheme of the DD-vMCG method, shown in Fig. 3(e), do not match the ones shown in the Zhu and Yarkony paper and thus new calculations were run where the potential energy matrix elements are obtained directly from the diabatic representation generated by the PESZY program (Fig. 3(f)). One major difference here is that the diabatic potential surfaces from the PESZY model show multiple crossings along the ν33 coordinate, especially the ground state that crosses all the excited states. The differences here depend on how the couplings are defined and connected and also on the potential shifting used in the PESZY model to match experimental data. More specifically, during the construction of the analytical PESs in the PESZY model, the diabatic potential energy functions were forced to match the experimental data by shifting down in energy both the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) diabatic states.
diabatic states.
This comparison demonstrates how the same adiabatic surfaces can be generated by different valid diabatic potentials. DD-vMCG offers a simpler picture of the diabatic PESs of phenol and thus employing the propagation diabatisation scheme to address this complicated problem, is an efficient approach which directly matches the accuracy of the well constructed analytical PESXY potential energy surfaces model for the adiabatic picture.
The number of the excited states that need to be included in quantum dynamical simulations is of great interest as it affects the results by potentially adding new channels. In CASSCF calculations, it can also have the effect of dramatically changing the surfaces calculated. Taking advantage of the flexibility the DD-vMCG method offers, a 3-state problem was therefore selected to examine the photodissociation of phenol as this is the minimal number that will be required to describe the ground-state and 1ππ* and 1πσ* excited-states.
As shown in Fig. 4(c) and (f), the three-state model can describe the two main conical intersections which are both experimentally and theoretically known to be key for the photo-induced hydrogen elimination reaction in phenol. The potential surfaces are, however, not well described. There is a large barrier at around 5 units along the v33 mode not seen in the 4-state calculations above. This is at the place the S2 and S3 surfaces cross, and the missing state is causing problems for the electronic structure. It was, as a result of this barrier, computationally harder to run 3-state direct dynamics calculations: it was difficult to converge and took more integration steps compared to the 4-state calculations.
Including more states during direct dynamics calculations is thus important not only to understand the behaviour of these particular states, such as the positions of possible conical intersections, but also to better define the target states such as the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) for the phenol molecule. The adiabatic (Fig. 4(b)) and diabatic (Fig. 4(e)) cuts of the potential energy surfaces of phenol along the ν33 normal mode are shown for a 5-state CASSCF calculation. Here the extra state (
for the phenol molecule. The adiabatic (Fig. 4(b)) and diabatic (Fig. 4(e)) cuts of the potential energy surfaces of phenol along the ν33 normal mode are shown for a 5-state CASSCF calculation. Here the extra state (![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) ) has a ππ* character and is thus bound along the O–H coordinate. The target states along with their conical intersections are well defined, yet the
) has a ππ* character and is thus bound along the O–H coordinate. The target states along with their conical intersections are well defined, yet the ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) state unexpectedly crosses both the
state unexpectedly crosses both the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) multiple times. As a final step and to better understand the effect of the fifth state, another state has been added (Ẽ) with a ππ* character which is again bound along the O–H coordinate (Fig. 4(a) and (d)). Smooth potential energy surfaces can be observed, with the diabatic states crossing between states as expected. We can observe here that the shape of the lowest three states is significantly affected by adding more states.
multiple times. As a final step and to better understand the effect of the fifth state, another state has been added (Ẽ) with a ππ* character which is again bound along the O–H coordinate (Fig. 4(a) and (d)). Smooth potential energy surfaces can be observed, with the diabatic states crossing between states as expected. We can observe here that the shape of the lowest three states is significantly affected by adding more states.
Finally, a comparison of the vertical excitation energies obtained in this study at the Franck–Condon point employing a CASSCF(10,10)/6-311+G** level of theory and using different state-averaging is presented in Table 1 along with results from prior experimental53,54 and theoretical studies.24,27,55,56 The calculated energies are in agreement with the previous theoretical results and a good match with the experimental values. Theoretical results that have a better agreement with experiment can be achieved with energy optimisation24. For the different state models presented in this comparison, the 6-state model yields the closest values to the experimental data available.
| St. Ave. | St. | Char. | Sym. | ΔE | Experiment | Theory |
|---|---|---|---|---|---|---|
| 3 States | S1 | ππ* | A′ | 4.90 | 4.5153/4.5854 | 4.8255/4.8527/4.8624 |
| S2 | πσ* | A′′ | 5.72 | 5.1253 | 5.3724/5.4827/5.7055 | |
| 4 States | S1 | ππ* | A′ | 4.95 | 4.51/4.58 | 4.82–4.86 |
| S2 | πσ* | A′′ | 5.59 | 5.12 | 5.37–5.70 | |
| S3 | πσ* | A′′ | 6.59 | 6.4256 | ||
| 5 States | S1 | ππ* | A′ | 4.86 | 4.51/4.58 | 4.82–4.86 |
| S2 | πσ* | A′′ | 5.74 | 5.12 | 5.37–5.70 | |
| S3 | πσ* | A′′ | 6.68 | 6.42 | ||
| S1 | ππ* | A′ | 7.59 | |||
| 6 States | S1 | ππ* | A′ | 4.80 | 4.51/4.58 | 4.82–4.86 |
| S2 | πσ* | A′′ | 5.67 | 5.12 | 5.37–5.70 | |
| S3 | πσ* | A′′ | 6.56 | 6.42 | ||
| S1 | ππ* | A′ | 7.61 | |||
| S1 | ππ* | A′ | 7.80 | |||
4.2 State population analysis
The state populations show how the total wavepacket is distributed between the different electronic states included in the calculation over the propagation period. Here, the diabatic state populations as a function of time for the phenol molecule are presented, after vertical excitation to the à and![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states for the 3-, 4-, 5- and 6-state model. The thick black line in all the figures of Fig. 5 corresponds to the total density which reveals the percentage of the dissociation as it decreases due to the dissociating wavepacket being absorbed by the CAP.
states for the 3-, 4-, 5- and 6-state model. The thick black line in all the figures of Fig. 5 corresponds to the total density which reveals the percentage of the dissociation as it decreases due to the dissociating wavepacket being absorbed by the CAP.
 | ||
Fig. 5 Normalised diabatic state populations from DD-vMCG simulations of phenol starting with a vertical excitation to à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states for the 3-, 4-, 5- and 6-state models. states for the 3-, 4-, 5- and 6-state models. | ||
The populations for the 3-state model after excitation to the à (Fig. 5(a)) and to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (Fig. 5(e)) show a small amount of population transfer but no dissociation. The diabatic population results for the 3-state model are thus in agreement with the barrier seen in the PESs along the O–H dissociation, confirming our initial impression that this 3-state model cannot successfully describe the photodissociation dynamics of phenol and more states must be included.
(Fig. 5(e)) show a small amount of population transfer but no dissociation. The diabatic population results for the 3-state model are thus in agreement with the barrier seen in the PESs along the O–H dissociation, confirming our initial impression that this 3-state model cannot successfully describe the photodissociation dynamics of phenol and more states must be included.
Fig. 5(b) and (f) show that employing a 4-state model the diabatic population dynamics are quite different from the 3-state model and including more states than the target ones has a significant effect on the population transfer and the percentage of dissociation: both have considerably increased. Fig. 5(b) depicts the diabatic state populations for the 4-state model after excitation to the à state. The population transfer starts immediately and mostly to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. Approximately 30% of the population remains in the à state at the end of the propagation and the population transfer to the other states is relatively small. The population decay starts at 10 fs and is complete by around 140 fs. Moreover, after excitation to the
state. Approximately 30% of the population remains in the à state at the end of the propagation and the population transfer to the other states is relatively small. The population decay starts at 10 fs and is complete by around 140 fs. Moreover, after excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state (Fig. 5(f)), a faster population transfer mostly to the à state is observed, but also a small amount flowing to the
state (Fig. 5(f)), a faster population transfer mostly to the à state is observed, but also a small amount flowing to the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) state is seen. Density begins to flow into the CAPs after around 10 fs and a steady dissociation continues until the end of the propagation.
state is seen. Density begins to flow into the CAPs after around 10 fs and a steady dissociation continues until the end of the propagation.
In the 5-state model, relaxation from the à state (Fig. 5(c)) shows a similar behaviour to the 4-state model, while the presence of the ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) state increases the total transfer to
state increases the total transfer to ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and also to
and also to ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) . In Fig. 5(g) again the principal population transfer from the
. In Fig. 5(g) again the principal population transfer from the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state is occurring immediately into the à state. After around 140 fs about 15% of the population has been transferred to the à state, with around 10% of the population being transferred to the
state is occurring immediately into the à state. After around 140 fs about 15% of the population has been transferred to the à state, with around 10% of the population being transferred to the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) and
and ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) states. The decrease in total density after excitation to the à state (Fig. 5(c)) takes more time to start and the amount of total dissociation (25%) is also less compared to the case of excitation to the
states. The decrease in total density after excitation to the à state (Fig. 5(c)) takes more time to start and the amount of total dissociation (25%) is also less compared to the case of excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state as depicted in Fig. 5(g) (20 fs, 40%).
state as depicted in Fig. 5(g) (20 fs, 40%).
Moving to the 6-state model, the rate of population transfer is significantly slower compared to the 4- and 5-states models for propagation after vertical excitation to both the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. As well as the slower relaxation from à (Fig. 5(d)), including Ẽ results in a significant reduction in the amount of dissociation that is now close to 10%, which is in accordance with experimental results.25,35,57–60Fig. 5(h) indicates that more time is needed for the density to begin to flow in the CAPs after excitation to the
state. As well as the slower relaxation from à (Fig. 5(d)), including Ẽ results in a significant reduction in the amount of dissociation that is now close to 10%, which is in accordance with experimental results.25,35,57–60Fig. 5(h) indicates that more time is needed for the density to begin to flow in the CAPs after excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state compared to Fig. 5(d). However, the percentage of dissociation is higher reaching approximately 30% at the end of the propagation.
state compared to Fig. 5(d). However, the percentage of dissociation is higher reaching approximately 30% at the end of the propagation.
The difference between the population transfer and dissociation demonstrates the sensitivity of direct dynamics to the electronic structure calculations. The 3-state model, which contains just the target states, is unable to describe the dissociation. It also leads to a significant population returning to the ground-state, particularly after excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, which is not seen in the other models. Presumably the barrier to dissociation is reflecting the outgoing wavepacket back into the equilibrium geometry region.
state, which is not seen in the other models. Presumably the barrier to dissociation is reflecting the outgoing wavepacket back into the equilibrium geometry region.
The 5-state model also gives a poor description of the dynamics. The strong ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) –Ẽ coupling that is present in the 6-state model cannot be reproduced by the 5-state model and leads to a spurious
–Ẽ coupling that is present in the 6-state model cannot be reproduced by the 5-state model and leads to a spurious ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) –
–![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) coupling, with increased population in both the higher states and the ground-state compared to the 4-state and 6-state models. This poor description of the couplings is seen in the incorrect conical intersections depicted in Fig. 4(b) and (e).
coupling, with increased population in both the higher states and the ground-state compared to the 4-state and 6-state models. This poor description of the couplings is seen in the incorrect conical intersections depicted in Fig. 4(b) and (e).
The 4-state model seems to provide a good description, able to model the dissociation, but the 6-state model shows that the inclusion of the ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) and Ẽ states leads to a different realisation of the couplings between the states and a slower population transfer and the rate of dissociation.
and Ẽ states leads to a different realisation of the couplings between the states and a slower population transfer and the rate of dissociation.
4.3 Flux analysis
To unravel the probability of the different decay pathways in order to understand the dynamic mechanism of the photodissociation of phenol, the integral of the flux into each dissociation channel was analysed. It is obtained using eqn (17) by integrating the expectation value of the CAP using the density projected onto each state to give the probability of decay via that channel as a function of time. Here, we only consider the 4- and 6-state models, and look at the integrated flux for the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states as flux was very close to zero for the other states.
states as flux was very close to zero for the other states.
Fig. 6 shows that the flux into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) dissociation channels increases significantly for both the 4- and 6-state models and the dissociation starts to occur after 50 fs – the time to reach the dividing surface into the channel provided by the CAP.
dissociation channels increases significantly for both the 4- and 6-state models and the dissociation starts to occur after 50 fs – the time to reach the dividing surface into the channel provided by the CAP.
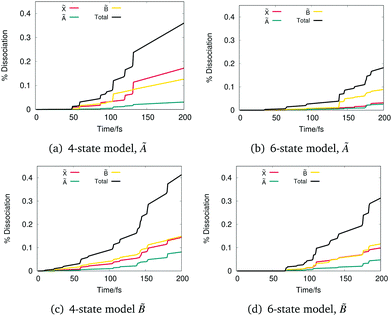 | ||
Fig. 6 Integrated flux as a function of time from DD-vMCG simulations of phenol starting with a vertical excitation to the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states for the 4- and 6-state models. states for the 4- and 6-state models. | ||
After excitation to à for the 4-state model, Fig. 6(a), a first significant rise on the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state is taking place around 100 fs and then the majority of the flux is going into the
state is taking place around 100 fs and then the majority of the flux is going into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state at around 125 fs. For the 6-state model (Fig. 6(b)), the total dissociation is almost half compared to the 4-state model. In this case, the flux distribution into
state at around 125 fs. For the 6-state model (Fig. 6(b)), the total dissociation is almost half compared to the 4-state model. In this case, the flux distribution into ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) is about double the one to
is about double the one to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and to the à state.
and to the à state.
In the case of excitation to ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , in both Fig. 6(c) and (d) the flux distribution into the three target states follows a similar pattern. The amount of flux in both
, in both Fig. 6(c) and (d) the flux distribution into the three target states follows a similar pattern. The amount of flux in both ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) gradually increases with an analogous rate, while in the case of the 6-state model the amount of flux into
gradually increases with an analogous rate, while in the case of the 6-state model the amount of flux into ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) after 175 fs is greater compared to the one into
after 175 fs is greater compared to the one into ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) . It can be noted that after excitation to the
. It can be noted that after excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, there is more energy and thus more dissociation in the à state is possible. Fig. 6(c) shows that the percentage of the total flux going out of à has been doubled compared to Fig. 6(a). In the case of the 6-state model, flux going out of à stays almost the same until 175 fs where it starts to increase, reaching a higher value compared to the one after excitation to the à state.
state, there is more energy and thus more dissociation in the à state is possible. Fig. 6(c) shows that the percentage of the total flux going out of à has been doubled compared to Fig. 6(a). In the case of the 6-state model, flux going out of à stays almost the same until 175 fs where it starts to increase, reaching a higher value compared to the one after excitation to the à state.
In the literature, the dissociation mechanism of phenol is still under discussion. In this study, the timescales are too short for the O–H dissociation through hydrogen tunnelling seen in experiments for excitations at energies below the S1/S2 conical intersection.22,23 The simulations do agree with the main dissociation mechanism at short times being an ultrafast internal conversion from the bright 1ππ* state to the dark 1πσ* state through their conical intersection seam, leading to the formation of the phenoxyl radical after hydrogen dissociation.27,57
Details of the dissociation channels, however, differ according to the model and the energy of excitation. In the 4-state model, excitation to the à state results in a similar proportion exciting through the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) channels, with only a small fraction dissociating along the higher lying à channel. This dissociation pattern is due to the near degeneracy of the
channels, with only a small fraction dissociating along the higher lying à channel. This dissociation pattern is due to the near degeneracy of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à asymptotes in this model. In contrast, in the 6-state model, the
and à asymptotes in this model. In contrast, in the 6-state model, the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) channel is the most important. This channel connects the S1(πσ*) state to the ground state of the phenoxy radical. Excitation to the
channel is the most important. This channel connects the S1(πσ*) state to the ground state of the phenoxy radical. Excitation to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state in both models, however, leads to a similar dissociation with equal amounts in the
state in both models, however, leads to a similar dissociation with equal amounts in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) channels and a lower amount in the Ã.
channels and a lower amount in the Ã.
4.4 Geometry analysis
The geometrical change of phenol on photodissociation can be monitored by looking at the expectation values of the wavepacket for the coordinates as a function of time. This is achieved by calculating the bond length, angle and dihedral angle of interest at the centre of the individual GWPs and averaging them using the normalised Gross Gaussian Populations, | (18) |
In the current work, we focus on the OH dissociation of phenol and thus, the O7–H13 bond length, C1–O7–H13 angle and C2–C1–O7–H13 dihedral angle (see Fig. 1 for atom labeling). These are plotted in Fig. 7 for the dynamics from the 4- and 6-state models after excitation to the à state.
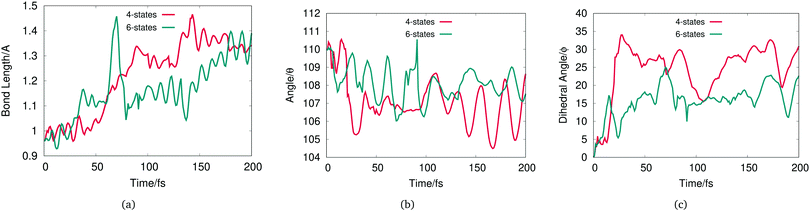 | ||
| Fig. 7 (a) O7–H13 bond length, (b) C1–O7–H13 angle and (c) C2–C1–O7–H13 dihedral angle, averaged over the 20 GWP for the 4-state (red) and 6-state (green) dynamics starting in the à state. | ||
Fig. 7(a) shows that for both the 4- and 6-state dynamics an increase in the phenol OH bond length is observed over time. This shows the bond length is longer in the excited state than in the ground-state. For the 6-state dynamics, the origin of the spike at around 60 fs is due to the fast OH dissociation displayed by some GWP with high population that is subsequently reduced to zero by the effect of the CAP.
The C–O–H angle plotted in Fig. 7(b) barely changes over time for both models with a maximum change of 5 degree compared to the value at initial time. In contrast the dihedral angle displayed in Fig. 7(c) shows a greater change over time. On average, the hydrogen on the hydroxyl group has non-negligible out-of-plane motion and this is more visible on the 4-state dynamics compared to the 6-state results.
Both the 4- and 6-state dynamics have quantitatively a similar number of GWPs displaying O–H bond breaking (8 GWPs for the 4-state and 9 GWPs for the 6-state simulation). By a visual analysis of the geometry change of these GWPs, the dissociation occurs predominantly with in-plane O–H bond stretching for both the 4- and 6-state model. However, the 4-state shows a more visible out-of-plane O–H bond dissociation compared to the 6-state which is confirmed by the results shown on Fig. 7(c).
4.5 Kinetic energy release
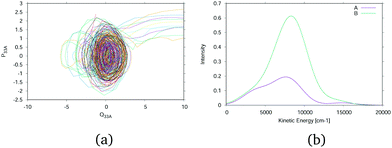
A useful tool for probing the photo-excited dynamics of molecules such as phenol is translation kinetic energy release (TKER) spectroscopy.35 In these, the kinetic energy of the dissociating hydrogen atom is probed using time-of-flight measurements and from conservation of energy arguments information can be gained on the dynamics of the dissociative process.An approximate TKER spectrum can be obtained from the DD-vMCG simulations by analysing the dissociating wavepackets. In Fig. 8(a) the phase space trajectories for the GWPs are plotted in the momentum, coordinate space of the O–H normal mode ν33. This simulation was started in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. A similar plot is obtained when starting in the à state. The initial orbits for the vibrations in the excited-state well are seen, as well as the dissociation of 11 GWPS which move to large distances. Fig. 8(b) shows the spectrum of the kinetic energy of these dissociating GWPs in the direction of the dissociation. This is obtained by the expectation value for each GWP multiplied by the GGP and broadened by the appropriate width for the kinetic energy spread in each. As this is a normal mode the kinetic energy of the recoiling fragment is automatically included. The spectra are shown for calculations starting in both the à and
state. A similar plot is obtained when starting in the à state. The initial orbits for the vibrations in the excited-state well are seen, as well as the dissociation of 11 GWPS which move to large distances. Fig. 8(b) shows the spectrum of the kinetic energy of these dissociating GWPs in the direction of the dissociation. This is obtained by the expectation value for each GWP multiplied by the GGP and broadened by the appropriate width for the kinetic energy spread in each. As this is a normal mode the kinetic energy of the recoiling fragment is automatically included. The spectra are shown for calculations starting in both the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states.
states.
The experimental TKER in Fig. 4 of ref. 25 show two peaks. The first is centred around 200 cm−1 and the second moves to higher kinetic energy with lower wavelength excitation. In the simulations the low energy peak is not seen as it is due to hydrogen atoms that dissociate at longer time scales than the 200 fs of the simulations. The high kinetic energy peaks cannot be directly compared to any of the experimental spectra as the experimental initial conditions used a single excitation frequency whereas the simulations started with a vertical excitation. The placement and width of the peaks are, however, in the correct range and the peak for the simulation starting in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state is at slightly higher kinetic energy, as expected.
state is at slightly higher kinetic energy, as expected.
5 Conclusions
In this paper, the recently improved algorithm for DD-vMCG13 has made possible the study of the full dimensional photodissociation dynamics of phenol. The results of DD-vMCG calculations were analysed by plotting the PESs, the diabatic state populations and the integrated flux.The PESs were presented for models including 3-, 4-, 5- and 6-states calculated using state-averaged CASSCF. The 4-state and 6-state models were the ones with the smoothest PESs and had well defined conical intersections between the ground state and the first three excited states. In contrast, the 3-state model contained a barrier along the O–H dissociation channel, and the 5-state model PES along this channel contained multiple crossings between the upper states.
In the subsequent dynamics calculations, the 3-state model did not show any dissociation as a result of the barrier. The 3-state model was also computationally harder, requiring more integration steps and quantum chemistry calculations than the 6-state model, which would be expected to be a harder computational problem.
Including a fourth state removed the barrier to dissociation. It also allowed a comparison between the surfaces produced by the propagation diabatisation scheme with existing analytical potential energy surfaces from Zhu and Yarkony. At the level of theory used, DD-vMCG with OpenMolcas can reproduce the adiabatic PESs used by Zhu and Yarkony in their fitted diabatic potentials. Interestingly, the DD-vMCG diabatic surfaces are different from those of Zhu and Yarkony, but are also smooth with well defined crossing points. The DD-vMCG diabatic surfaces are in fact simpler, with fewer crossings, and clearly the algorithm is automatically generating surfaces of a comparable accuracy to the detailed fits.
By including, for the first time, more than four states in the study of phenol, we demonstrate the potential need to use models with more states than just the target ones in order to have a better description for the molecule under investigation. It is, however, important to include the correct states. The 5-state model leads to population transfers to the higher lying states and ground-state as not including the Ẽ state, which is strongly coupled with the ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) state, leads to spurious crossings in the PESs, and thus spurious couplings between the states.
state, leads to spurious crossings in the PESs, and thus spurious couplings between the states.
The analysis of the dynamics showed similar behaviour by the 4-state and the 6-state models. However, the 6-state model after excitation to the à state shows slower population transfer and lower dissociation. A more detailed analysis of the flux going into the different channels indicates further that the 6-state model provides results closer to experimental findings, with around 10% of the phenol molecules dissociating almost entirely into the ground-state of the phenoxy radical using the dissociation pathway provided by the conical intersection between the 1ππ and the 1πσ* states.
Finally, an analysis of the geometry changes after excitation to the bright 1ππ state indicate that the O–H bond dissociation takes place predominantly in the plane of the molecule. At the same time, the length of the O–H bond in non-dissociating molecules extends by around 0.3 Å, while the CCOH torsion angle changes to move the hydrogen atom out of plane by 20–30°.
Beyond the successful description of the photodissociation of phenol, this study illustrates the possibilities of the DD-vMCG method as it is capable of capturing the complete quantum picture of the coupled nuclear and electronic motions after photo-excitation into multiple states for a molecule like phenol with 33 vibrational modes. A natural extension of this work will be to perform quantum dynamics simulations with DD-vMCG to the phenoxyl radical in order to further unravel the photodissociation dynamics of phenol.
Conflicts of interest
There are no conflicts to declare.References
- M. Garavelli, Theor. Chem. Acc., 2006, 116, 87–105 Search PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- H. Wang, J. Phys. Chem. A, 2015, 119, 7951–7965 CrossRef CAS PubMed.
- G. A. Worth, P. Hunt and M. A. Robb, J. Phys. Chem. A, 2003, 107, 621–631 CrossRef CAS.
- G. A. Worth, M. A. Robb and I. Burghardt, Faraday Discuss., 2004, 127, 307–323 RSC.
- G. A. Worth, M. A. Robb and B. L. Lasorne, Mol. Phys., 2008, 106, 2077–2091 CrossRef CAS.
- I. Burghardt, M. Nest and G. A. Worth, J. Chem. Phys., 2003, 119, 5364–5378 CrossRef CAS.
- G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508 CrossRef CAS.
- G. W. Richings, I. Polyak, K. E. Spinlove, G. A. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- T. J. Frankcombe, M. A. Collins and G. A. Worth, Chem. Phys. Lett., 2010, 489, 242–247 CrossRef CAS.
- G. Christopoulou, A. Freibert and G. A. Worth, J. Chem. Phys., 2021, 154, 124127 CrossRef CAS PubMed.
- G. A. Worth, K. Giri, G. W. Richings, M. H. Beck, A. Jäckle and H.-D. Meyer, Quantics package, Version 1.1, 2015 Search PubMed.
- G. A. Worth, Comput. Phys. Comm., 2020, 248, 107040 CrossRef.
- M. Robin, Higher excited states of polyatomic molecules, Academic Press, 2012, vol. 3 Search PubMed.
- C. Crespo-Hernández, B. Cohen, P. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- P. Callis, Annu. Rev. Phys. Chem., 1983, 34, 329–357 CrossRef CAS.
- D. Creed, Photochem. Photobiol., 1984, 39, 537–562 CrossRef CAS.
- A. Reuther, H. Iglev, R. Laenen and A. Laubereau, Chem. Phys. Lett., 2000, 325, 360–368 CrossRef CAS.
- K. Nienhaus and G. Nienhaus, J. Phys.: Condens. Matter, 2016, 28, 443001 CrossRef PubMed.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS PubMed.
- R. N. Dixon, T. A. Oliver and M. N. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef PubMed.
- G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S.-I. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2010, 133, 124313 CrossRef CAS PubMed.
- M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318 CrossRef PubMed.
- X. Zhu, C. Malbon and D. R. Yarkony, J. Chem. Phys., 2016, 144, 124312 CrossRef PubMed.
- Z. Lan, W. Domcke, V. Vallet, A. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 283–293 CrossRef PubMed.
- C. P. Schick and P. M. Weber, J. Phys. Chem. A, 2001, 105, 3725–3734 CrossRef CAS.
- A. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- A. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS.
- G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 7984–7993 CrossRef CAS PubMed.
- A. Iqbal, M. S. Y. Cheung, M. G. D. Nix and V. G. Stavros, J. Phys. Chem. A, 2009, 113, 8157–8163 CrossRef CAS PubMed.
- M. Hause, Y. Heidi Yoon, A. Case and F. Crim, J. Chem. Phys., 2008, 128, 104307 CrossRef PubMed.
- A. L. Devine, B. Cronin, M. G. D. Nix and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 184302–184309 CrossRef PubMed.
- M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G. D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706 CrossRef CAS.
- U. Brand, H. Hippler, L. Lindemann and J. Troe, J. Phys. Chem., 1990, 94, 6305–6316 CrossRef CAS.
- E. T. Sevy, M. A. Muyskens, S. M. Rubin, G. W. Flynn and J. T. Muckerman, J. Chem. Phys., 2000, 112, 5829–5843 CrossRef CAS.
- C.-K. Ni, C.-M. Tseng, M.-F. Lin and Y. A. Dyakov, J. Phys. Chem. B, 2007, 111, 12631–12642 CrossRef CAS PubMed.
- C. Lee, Y.-C. Lin, S.-H. Lee, Y.-Y. Lee, C.-M. Tseng, Y.-T. Lee and C.-K. Ni, J. Chem. Phys., 2017, 147, 013904 CrossRef PubMed.
- K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Chem. Sci., 2014, 5, 4661–4680 RSC.
- X. Zhu and D. R. Yarkony, J. Chem. Phys., 2014, 140, 024112 CrossRef PubMed.
- C. Xie, J. Ma, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, J. Am. Chem. Soc., 2016, 138, 7828–7831 CrossRef CAS PubMed.
- G. W. Richings and G. A. Worth, Chem. Phys. Lett., 2017, 683, 606–612 CrossRef CAS.
- J. Ischtwan and M. A. Collins, J. Chem. Phys., 1994, 100, 8080–8088 CrossRef CAS.
- M. A. Collins and D. H. Zhang, J. Chem. Phys., 1999, 111, 9924–9931 CrossRef CAS.
- M. Baer, Chem. Phys. Lett., 1975, 35, 112–118 CrossRef CAS.
- M. Baer, Phys. Rep., 2002, 358, 75–142 CrossRef CAS.
- S. Mukherjee, S. Ravi, K. Naskar, S. Sardar and S. Adhikari, J. Chem. Phys., 2021, 154, 094306 CrossRef CAS PubMed.
- K. Andersson, M. R. A. Blomberg, M. P. Fülscher, G. Karlström, R. Lindh, P. Malmqvist, P. Neogrády, J. Olsen, B. O. Roos, A. J. Sadlej, M. Schütz, L. Seijo, L. Serrano-Andrés, P. E. M. Siegbahn and P. O. Widmark, MOLCAS, Version 4, 1997 Search PubMed.
- C. Leforestier and R. E. Wyatt, J. Chem. Phys., 1983, 78, 2334 CrossRef CAS.
- R. Kosloff and D. Kosloff, J. Comput. Phys., 1986, 63, 363–376 CrossRef.
- X. Xu, K. R. Yang and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 3612–3625 CrossRef CAS PubMed.
- H. Bist, J. Brand and D. Williams, J. Mol. Spectrosc., 1966, 21, 76–98 CrossRef CAS.
- R. C. Fuh, Phenol, Oregon medical laser center technical report, 1995 Search PubMed.
- O. Vieuxmaire, Z. Lan, A. Sobolewski and W. Domcke, J. Chem. Phys., 2008, 129, 224307 CrossRef.
- G. King, A. Devine, M. Nix, D. Kelly and M. Ashfold, Phys. Chem. Chem. Phys., 2008, 10, 6417–6429 RSC.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- A. Sur and P. Johnson, J. Chem. Phys., 1986, 84, 1206–1209 CrossRef CAS.
- T. Ebata, M. Furukawa, T. Suzuki and M. Ito, J. Opt. Soc. Am. B, 1990, 7, 1890–1897 CrossRef CAS.
- M. G. D. Nix, A. L. Devine, R. N. Dixon and M. N. R. Ashfold, Chem. Phys. Lett., 2008, 463, 305–308 CrossRef CAS.
- C. S. M. Allan, B. Lasorne, G. A. Worth and M. A. Robb, J. Phys. Chem. A, 2010, 114, 8713–8729 CrossRef CAS PubMed.
- K. E. Spinlove, G. W. Richings, M. A. Robb and G. A. Worth, Faraday Discuss., 2018, 212, 191–215 RSC.
| This journal is © the Owner Societies 2021 |