Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mobility of bound water in PNIPAM microgels†
Tetyana
Kyrey
 *a,
Judith
Witte
*a,
Judith
Witte
 b,
Jana
Lutzki
b,
Michaela
Zamponi
a,
Stefan
Wellert
b and
Olaf
Holderer
b,
Jana
Lutzki
b,
Michaela
Zamponi
a,
Stefan
Wellert
b and
Olaf
Holderer
 a
a
aForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science at Heinz Maier-Leibnitz Zentrum, Garching, Germany. E-mail: t.kyrey@fz-juelich.de; Fax: +49 89289 10799; Tel: +49 89289 54841
bTechnical University Berlin, Institute of Chemistry, Berlin, Germany
First published on 17th June 2021
Abstract
Polymer–solvent interactions play a crucial role in the stimuli-responsive behaviour of polymer networks. They influence the swelling/deswelling behaviour as well as the dynamics of the polymer chains. Scattering experiments provide insight into the polymer–water interaction of poly(N-isopropylacrylamide) (PNIPAM) microgels cross-linked with N,N′-methylenebisacrylamide (BIS) in dried and humidified state. The water mobility is studied by means of neutron spin-echo spectroscopy and neutron backscattering spectroscopy. The residual water amount has been determined with Karl Fischer titration. For both degrees of humidification, the relaxation time of the water molecules is much larger than that of free water due to the strong interactions with the polymer network and is only weakly depending on temperature and length scale of observation. The possible influence of the water on methyl group rotations is discussed.
1 Introduction
The stimuli-responsive behaviour of poly(N-isopropylacryl-amide)(PNIPAM) polymers as well as its derivatives (microgels, brushes, membranes etc.) attracts unrelenting interest to these systems.1–6 Due to the possibility to change the properties of PNIPAM based systems by variation of temperature, pressure or pH, such polymer systems are promising for an application in medicine, bio-engineering or smart polymer coatings.7–11 However, the numerous applications are strongly dependent on the polymer–solvent interaction. Particularly the polymer–water interaction is of high interest for medical applications aiming at drug delivery or smart polymer coatings where the properties depend on the polymer–solvent interaction.N-Isopropylacrylamide (NIPAM) monomer possess a lower critical solution temperature (LCST) of approximately 305 K in water. It leads to a similar volume phase transition temperature (VPTT) for poly(N-isopropylacrylamide) (PNIPAM) microgel particles.8
In solution, both hydrophilic and hydrophobic domains of PNIPAM are present simultaneously,12i.e. both polymer–polymer as well as polymer–water interactions occur below and above VPTT. However, the interaction of the polymer with solute molecules or with neighboring polymer segments is a very complex and competitive process. Temperature dependent solute interactions occur when interactions of the isopropyl groups of PNIPAM with solution molecules are energetically more favorable for isopropyl groups in a polymer rich environment compared to isopropyl groups in water.
Crossing the critical temperature via temperature increase leads to the phase separation into polymer-rich and water-rich phases. Below the LCST the isopropyl groups of PNIPAM are surrounded by water, whereas above the LCST the stronger hydrophobicity of backbone and side chains result in a dehydration of the polymers.13 PNIPAM undergoes reversible phase transition at the LCST accompanied by (de)hydration of polymer chains. However, the temperature-driven transition mostly occurs via release of bulk-water (free water molecules), but structural changes of the water shell were also observed.14
Previous indirect investigation of PNIPAM solutions demonstrate that hydration numbers (number of H2O molecules bound to one NIPAM monomer) amounts to 8 molecules slightly below LCST.15 Quasi-elastic investigations of local diffusion behaviour of hydration water in highly concentrated PNIPAM solution reveal that the hydration number decreases from 8 to 2 during the phase separation, moreover this number depends on the PNIPAM concentration in solution.16
Similar to the observations in hydration water of proteins at low temperatures below 200 K, the onset of molecular mobility, often called dynamical transition, has been also observed in PNIPAM solutions. Simulations of the dynamical transition in microgels allowed to identify the molecular processes which control the dynamics of PNIPAM and water below the dynamical transition temperature. It was shown that below the dynamical transition temperature PNIPAM dynamics is governed by the rotation of the methyl groups of the side chains.17
Although (de)hydration of PNIPAM hydrogels is studied explicitly, the polymer–water interaction of crosslinked PNIPAM microgels is still not fully understood.
The presence/absence of the water molecules within cross-linked PNIPAM microgels affects their properties in bulk as well as in adsorbed state.
The PNIPAM chain dynamics of microgels in solution obeys rather well Zimm dynamics at large q where density fluctuations do not play the major role any more, but with a significantly higher apparent viscosity than the pure solvent viscosity which would be expected for Zimm dynamics.18,19 This is most probably related to the water–polymer interactions via H-bonds. The presence of bound water molecules was also observed in the near-surface dynamics investigation of the adsorbed batch and feeding microgels with high cross-linker concentration.20
With the questions regarding the role of water in swollen microgels and the remaining bound water in interfacial microgel films of PNIPAM microgels in mind, we present experimental results of polymer/water dynamics of the cross-linked PNIPAM microgels in dried and humidified states by means of neutron spin-echo spectroscopy and backscattering spectroscopy. Investigations have been performed at different temperatures to follow the temperature dependence of proton dynamics within the PNIPAM microgels. Quasi-elastic neutron scattering (QENS) in this case allows investigation of the localized or diffusive motion of the hydration water still present in the sample as a function of temperature. The current water amount within cross-linked microgels in dried state has been estimated with the Karl Fisher titration.
2 Materials and methods
2.1 Materials
N-Isopropylacrylamide (>99%) (NIPAM), N,N′-methylene-bisacrylamide (BIS) (>99.5%) and 2,2′-azobis(2-methyl-propionamidine)dihydrochloride (97%) (AAPH) were purchased from Sigma-Aldrich (Munich, Germany). All chemicals were used as received. A Millipore Milli-Q Plus 185 purification system was used for water purification.Methanol (anhydrous) was purchased from Sigma-Aldrich Chemie GmbH, Germany. HYDRANALTM-Composite 5 (Honeywell FlukaTM) was purchased from Fisher Scientific GmbH, Germany. All chemicals were used without further purification.
PNIPAM microgel particles crosslinked with BIS were synthesized via surfactant-free precipitation polymerization as described in our previous work.19
For neutron experiments 0.192 g of dried microgels were mounted in aluminium sandwich cells (Fig. 1). To measure the humidified sample 0.09 g of purified water (Millipore) has been added in small drops to the dried system. The degree of humidification is still too small to dissolve the microgels, it remains a gel like solid.
2.2 Neutron spin-echo spectroscopy
In order to investigate polymer dynamics neutron spin-echo (NSE) experiments were carried out on the J-NSE21 spectrometer “Phoenix” operated by Jülich Centre for Neutron Science (JCNS) at the research reactor FRM II of the Heinz Maier-Leibnitz Zentrum (MLZ) in Garching, Germany. NSE spectroscopy provides the highest energy resolution in neutron scattering and is used for example to observe thermally driven motion of macromolecules such as polymers in the melt or fluctuations of self assembled membranes in microemulsions. NSE measures the normalized intermediate scattering function S(q, t), the Fourier transform from energy into the time domain of the scattering function S(q,ω) measured e.g. in backscattering spectroscopy, and the Fourier transform from real space to reciprocal space of the van Hove correlation function G(r,t). Here fully incoherent experiments have been conducted with fully protonated samples, where the strong incoherent scattering cross section of the proton is exploited. NSE measures in this case the self correlation function of all protons present in the sample. If the motion of protons of different species is different, such as e.g. the protons bound to the PNIPAM backbone compared to those belonging to water molecules, this will result in different relaxation times of the different species. Fractions with different mobility might be discernible in this way. Measurements were performed at q of 0.5 Å−1 at a wavelength of 6 Å probing Fourier times up to 20 ns. The samples were mounted in a thermostat-controlled sample environment. Aluminum sandwich cells with a neutron path length of 0.3 mm were used. Fig. 1 shows a photograph of the sample cell with sample.The incoherent intermediate scattering function has been obtained from NSE raw data with the standard data reduction software DrSPINE.22 The empty cell has been subtracted from the measured data.
2.3 Backscattering spectroscopy
Quasi-elastic scattering investigation in the energy domain has been performed on backscattering spectrometer SPHERES23,24 operated by Jülich Centre for Neutron Science (JCNS) at the research reactor FRM II of the Heinz Maier-Leibnitz Zentrum (MLZ) in Garching, Germany. Backscattering spectroscopy provides a high resolution in energy space by using monochromator and analyzer crystals in backscattering geometry and thus minimizing the angular error in the Bragg equation. It provides an energy resolution (FWHM of the elastic peak) of about 0.7 μeV. In the present case, where no elastic Bragg peaks are within the investigated q-range, the intensity is also dominated by the incoherent scattering of the protons. Due to a low signal-to-noise ratio of the small-angle detectors, the dynamics in q-range of 0.6–1.7 Å−1 was probed. The largest q in our analysis may contain effects of self shielding and is also associated with a higher uncertainty. Measurements in the energy range of −25 μeV < ħω < 25 μeV were performed in temperature range of 293–323 K, resolution measurement was performed at 3 K.The same sandwich aluminium sample cell and sample as for the NSE experiments were used. The scattering contribution from the empty cell has been subtracted.
2.4 Karl Fischer titration
Volumetric Karl Fischer (KF) titration is an established technique to determine the water content in gaseous, liquid and solid samples. It uses the following chemical reactions:| CH3OH + SO2 + RN → [RNH]SO3CH3 |
| H2O + I2 + [RNH]SO3CH3 + 2RN → [RNH]SO4CH3 + 2[RNH]I |
When all water has reacted, the excess iodine indicates the endpoint of the titration. The water content of the sample is then calculated using the titer, a measure for the amount of water that can react with 1 mL of titrant.
Volumetric KF titration was done with a Metrohm 836 Titrando, equipped with a 803 Ti stand. Prior to the measurements the titer of the titrant was determined. Microgels were dispersed in anhydrous methanol. The microgel dispersion (c = 20 mg mL−1) was placed in the titration vessel and the one-component titrant Hydranal Composite 5 was added with a burette. When the endpoint was indicated by the threshold voltage, the addition of KF titrant stopped automatically. All measurements were carried out at room temperature and averaged over three titrations.
3 Results and discussions
This section contains of four parts: in first, the water content of the freeze dried PNIPAM microgels determined by KF titration is briefly discussed, other subsections are dedicated to the dynamics of the cross-linked PNIPAM microgels in dried and humidified state probed by means of neutron spin-echo spectroscopy and neutron backscattering spectroscopy, respectively.Water content from KF titration experiment
The KF titration experiments leading to a water contents of ∼13.3% on samples stored for some time in a closed vial (as were the samples of the neutron scattering experiments), showed that a significant amount of water has to be expected in such PNIPAM microgels. The experiment has been repeated on PNIPAM microgels which were freeze-dried again to see what might be the minimum achievable water level. The remaining water contents was 3%, which shows on the one hand that the microgels easily take up water from humid air during sample preparation and that a fully water free environment is not achievable. This remaining amount must be strongly bound to the PNIPAM microgel, with the other 10% which have been taken up during handling in different batches of microgels being slightly more loosely bound.Elastic fixed window scans with the backscattering spectrometer
In Fig. 2 elastic fixed window scans of the dried and humidified PNIPAM microgels obtained on the backscattering spectrometer are presented. The Doppler drive of the backscattering spectrometer is at halt in this modus of operation. The elastic intensity I(q, ω ≃ 0) is recorded as a function of temperature. Elastic temperature scans reveal for example phase transitions in the sample. An increase in mean square displacement (MSD) of the protons due to inelastic scattering events is visible as a drop of elastic intensity. In the presented case, the dried PNIPAM microgels shows a rather smooth and continuous intensity drop and hence increase in MSD, while the sample with added water has a sudden intensity drop at 273 K. Here, the solid–liquid phase transition of water occurs. An additional intensity increase is visible when the sample is heated above the VPTT of PNIPAM at around 305 K. The collapse of the PNIPAM with the water expulsion leaves rather rigid polymer clusters behind. | ||
| Fig. 2 Elastic scans of the dried (orange) and humidified (blue) sample obtained in the backscattering experiment in a temperature range of 3–330 K, averaged over the q-range from 0.78–1.27 Å−1. | ||
To eliminate the possible influence of water loss in the sample during the heating/cooling process, the sample mass has been controlled before and after the neutron experiments. No mass change has been observed.
The elastic scans show that the dry microgel contains not enough water to show any collapse transition. The role of the polymer is discussed in the following by further evaluation of the elastic fixed window scans. The mean square displacement, 〈u2〉, calculated from the elastic intensity I(q, ħω ≃ 0) = I(q) as 〈u2〉 = −3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(I(q)/q2) is shown in Fig. 3. The time scale of the MSD corresponds to the time scale provided by the resolution of the instrument and is ≃2 ns in the case of the backscattering spectrometer SPHERES.25 The MSD is plotted up to 270 K, avoiding discontinuity of I(q) at 273 K in the hydrated sample. The MSD up to this point is of the order of <0.6 Å2. It has been determined from a linear fit of the logarithm of the intensity I(q) vs. q2 for q > 0.7 Å−1, i.e. 〈u2〉 = limq→0
ln(I(q)/q2) is shown in Fig. 3. The time scale of the MSD corresponds to the time scale provided by the resolution of the instrument and is ≃2 ns in the case of the backscattering spectrometer SPHERES.25 The MSD is plotted up to 270 K, avoiding discontinuity of I(q) at 273 K in the hydrated sample. The MSD up to this point is of the order of <0.6 Å2. It has been determined from a linear fit of the logarithm of the intensity I(q) vs. q2 for q > 0.7 Å−1, i.e. 〈u2〉 = limq→0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3/q2
3/q2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(I(q, T)/I(q, T = 4 K)) with the temperature dependent elastic intensity I(q, T). The neutron transmission of the sample, relevant to judge the influence of multiple scattering effects, was 0.93.
ln(I(q, T)/I(q, T = 4 K)) with the temperature dependent elastic intensity I(q, T). The neutron transmission of the sample, relevant to judge the influence of multiple scattering effects, was 0.93.
 | ||
| Fig. 3 Mean square displacement, 〈u2〉, from the q-dependent elastic fixed window scans of dried (orange) and humidified (blue) samples. | ||
Multiple scattering effects, which affect the normalized intensity I(q) that it is not approaching 1 for small q, can be taken into account approximately by26I(q)′ = I(q) + sIav2/(1 − Iav) (with s being the probability of a neutron to be scattered again after the first scattering event and Iav the solid angle averaged elastic intensity; for more details, see ref. 26). It turned out to be below 5% in our case and can be neglected for the purposes of the analysis here. For the hydrated sample, the fitted 〈u2〉 at low q deviates from the large q behavior, as it has been observed also for hydrated elastin.25Fig. 3 shows therefore the high-q fit of the MSD.
In the temperature range below 200 K, typically methyl groups are the only mobile component of the sample and methyl group rotations are visible in the time window of ≃1 ns. The point of inflection in the MSD in Fig. 3 is at around 200 K. It is slightly higher than in typical polymers and indicates that the activation energy required for this process is higher than in typical polymers, similar to the arguments by Zorn et al. in ref. 27 for the case of intrinsically microporous polymers. By normalizing to the low temperature intensity the procedure of determining the MSD is sensitive to the parts which start to move at a certain temperature and not to fully immobile parts of the sample. The MSD is therefore mainly attributed to methyl group rotations above 100 K, with harmonic vibrational motion, e.g. of immobile water molecules, playing only a very small role. The variation of the hydration level in a broader range would shed more light on the interesting question of ice formation in such systems.
In Fig. 3 it can be observed that the hydrated sample has a slightly lower MSD as the dried sample. The additional water molecules seem to hinder the rotational methyl group motion rather than provide more flexibility.
Dynamics measured with neutron spin-echo spectroscopy
The neutron spin-echo spectroscopy time range is larger than that of the backscattering spectroscopy and the measured q-value is smaller than the backscattering range (the backscattering q-range is somewhat limited to q ≥ 0.6 Å−1). NSE data collected at 293 K provide quick and rather straightforward insight to the fraction of immobile and mobile protons. The incoherent intermediate scattering function is measured with the fully protonated sample.Fig. 4 shows the intermediate scattering functions of dried and humidified PNIPAM microgels collected at 293 K. Here, the plateau level at large Fourier times allows estimating the fraction of immobile protons, while the decay at short times gives a hint on the mobility and related time scales. For the dried state, it is at the short time limit of the measurement.
 | ||
| Fig. 4 Intermediate scattering function S(q, t) of the dried (top) and humidified (bottom) PNIPAM microgels. | ||
The incoherent intermediate scattering function S(q, t) was fitted as:
| S(q, t) = Aexp(−t/τ) + (1 − A) | (1) |
| Sample | Immobile fraction | τ, ns | Γ, μeV |
|---|---|---|---|
| Dried | 86% ± 1% | 0.12 ± 0.028 | 5.502 ± 1.284 |
| Humidified | 40% ± 3% | 0.198 ± 0.047 | 3.321 ± 0.788 |
In the dried state the plateau of S(q, t) indicates the immobile fraction of protons to be 86%, while the sample humidification leads to a decrease (at least on the time scales of this experiment) of the elastic contribution and thus, the immobile part becomes 40%. This increase of the mobility is caused by the added water (in the humidified sample ratio of the added water and the microgel masses is ≃0.47). However, the water possesses a lower mobility than bulk water, a comparison follows later on in this section. Similar constrains of the water dynamics has been observed for the highly concentrated PNIPAM homopolymer solution.16
The mobile fraction of the dried sample of 14% is in a good agreement with the assumption that this corresponds to the overall water contents. It agrees well with the results of KF titration, where the estimated water amount is 13.3%.
Dynamics from backscattering spectroscopy
While NSE allows an estimation of mobile and immobile contributions to the scattering of the PNIPAM microgels, more insight into the q-dependence has been obtained with backscattering spectroscopy. Dried as well as humidified PNIPAM microgels were probed in q-range of 0.6–1.7 Å−1 in temperature range of 293–325 K. Spectra of the dry and humidified sample at 293 K and q = 0.96 Å−1 are shown in Fig. 5. | ||
| Fig. 5 Normalized QENS spectra S(q, ω) of the dried PNIPAM microgel and the humidified microgel at a single q-value, together with the corresponding fit. Data were collected at 293 K. | ||
The experimentally measured spectra S(q, ω) were modeled as a sum of a δ-function with amplitude A0, accounting for scattering contributions from immobile parts of the sample, and a necessary number of Lorentzians with corresponding amplitudes Ai (i > 0). To adequately describe the experimental data, in our case one Lorentzian function was necessary for the dry microgel, while two Lorentzian functions were required for the humidified one (for comparison of one and two Lorentzian fits of dry microgels see ESI†). This model agrees well with the model used for NSE data analysis, where mobile (corresponding to Ai) and immobile (corresponding to A0) contributions were determined. Including further Lorentzians does neither improve fit quality nor give any complementary information concerning the system behaviour.
Eqn (2) represents the fit function, which is a convolution of the model scattering function with the instrumental resolution R(q, ħω), plus a background contribution b(q).
| S(q,hω) = [A0(q)δ(hω) + A1(q)L1(q,hω) + A2(q)L2(q,hω)] ⊗ R(q,hω) + b(q) | (2) |
The Lorentzians describe the broadening of the peak:
 | (3) |
The resolution function of the backscattering spectrometer R(q, ħω) is determined by fitting the lowest temperature spectrum (3 K) with a series of Gaussian (allowing for some asymmetry of the resolution):
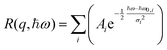 | (4) |
The origin of a purely elastic contribution would come from immobile protons from the backbone, while mobile protons (e.g. from the PNIPAM side-groups and the water) are described by the HWHM of the Lorentzians.
The extracted fitting parameters for dried and humidified PNIPAM microgels are shown in Fig. 6 and 7 for measurements at a temperature of 293 K.
In case of the dried sample only one relaxation process could be observed. The elastic contribution matches well the plateau value of the NSE experiment and has been attributed to the immobile fraction of protons belonging to the polymer. The dynamic component is rather q-independent. It is related to the NSE relaxation time (or inversely relaxation rate with τ = ħ/Γ), which is also included in Fig. 6. The q-average of the relaxation time of the mobile motions is τ1 = 137 ± 6 ps and agrees well with the relaxation time observed with NSE. The q-independence indicates a localized process or in a jump diffusion model corresponds to the time between successive jumps.28
In the case of the humidified microgels, two Lorentzians were needed to describe the spectrum in addition to the elastic contribution. Both Lorentzians have a linewidth within the energy range of the backscattering spectrometer (Fig. 7). The rates of both processes are again q-independent, indicating that both processes are still belonging to localized motions or the high-q limit of a jump diffusion process. The average relaxation times τ1,2 were 63 ± 3 ps and 440 ± 21 ps respectively.
The relaxation time of NSE lies in between τ1 and τ2, probably seeing a combination of both processes there. But the NSE data do not allow for a separation of these two contributions.
The amplitude of the elastic contribution levels again at a value comparable to that observed with NSE of 45% at low q, slightly decreasing towards higher q. It is discussed below in terms of an elastic incoherent structure factor (EISF). The two dynamic processes possess similar amplitudes (33% and 22% respectively). The QENS spectra and a separation of the different contributions of the fit can be found in the ESI.†
The free water has a long range diffusion constant of 2.299 × 10−9 m2 s−1 according to ref. 29. The water relaxation time τ at large q for bulk water at 293 K is 1.25 ps and the jump length yields 1.29 Å according to J. Teixeira et al.30 Bulk water is therefore out of the range of the spectrum of SPHERES.
So both components we observe here are strongly confined and slowed down motion.
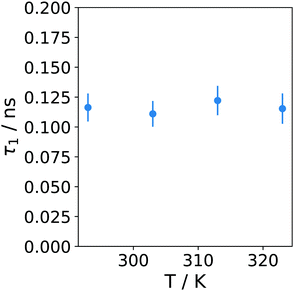
The temperature dependence of the dried microgel is not very pronounced. The amplitudes for the elastic contribution and for the dynamic process are rather constant (see ESI†). The relaxation time τ1 is also rather independent of temperature over the investigated temperature range as is shown in Fig. 8, i.e. the water inside the microgel does not gain in mobility during heating. Although the volume phase transition was not visible in the elastic scan of the dried microgel, this might play a role in the temperature independent mobility.
The humidified sample could only be measured at 293 K and 323 K (see ESI†). The step above the VPTT (which was already visible in the elastic scans of Fig. 2) resulted in a slightly slower motion of the fast component at 323 K and an increase of the elastic contribution to 64% at low q decreasing slightly to 51% at the larger q-values. The volume phase transition is therefore clearly visible, the microgel has a larger immobile proton fraction.
A detailed analysis of the motion of H-atoms involved in the backscattering spectroscopy data would require from an experimental point of view the use of deuterated water and ideally deuterated side groups of the PNIPAM microgel particles for some contrast variation experiments. But some conclusions might be drawn also from the composition and the amplitudes of the different contributions.
With the PNIPAM monomer consisting of C6H11NO (molecular weight 113 g mol−1), a contents of ∼ 13% of water determined with KF titration corresponds roughly to one water molecule per monomer. The mobile fraction of the incoherent scattering (with NSE and backscattering spectroscopy) was also in this range. We can assume therefore to see mainly the water protons in the dried sample as the component described by the Lorentzian component.
The trend of the relaxation time of the dry sample with temperature is also a strong indication that it is not e.g. the methyl group rotation which governs this relaxation. The latter would rather take place at lower relaxation times27 with a decreasing trend with increasing temperature (τ1 ≃ 0.04 ns for 330 K for methyl group rotation in ref. 27), and it might be out of our time window. This more or less constant relaxation time even across the VPTT indicates in our point of view the strong water–polymer interaction of this part of the water in the dried state.
In the humidified sample, water of about half of the original microgel weight was added, i.e. about 3 water molecules (molecular weight 18 g mol−1) per monomer. The humidified sample contained therefore 3–4 water molecules per monomer. Separating the hydrogen atoms of the sample in three groups, namely H of the water molecules, the two CH3 groups of the PNIPAM and the rest of the side chain and backbone, each group has about a third of the protons. In the QENS spectra, the faster component of the first Lorentzian might then represent the water dynamics, the slower component – fluctuations of the side chain, i.e. an onset of softening of the polymer. The elastic fraction is discussed below.
The elastic incoherent structure factor (EISF) is included in the elastic contribution A0 of the relative amplitudes in Fig. 6 and 7. It shows a weak q-dependence, as it would be characteristic for some reorientational diffusion process.28
The Debye–Waller factor, which reduces the scattered intensity, is of the order of 0.97 and plays therefore only a minor role. From the elastic scans, methyl group rotations have been identified as one localized process. Backbone and purely elastic protons would contribute to a q-independent incoherent elastic signal with a fraction celast. The EISF of the methyl group rotations would therefore contribute with a fraction of cMethyl = 1 − celast to the elastic part. The remaining protons of the PNIPAM chain, are assumed to be rather immobile on the time scales of observation with celast. Such that the elastic amplitude is Aelast = [(1 − celast)EISFMethyl + celast] × clocal, where the fraction clocal denotes the fraction of protons contributing to localized scattering, that we account to the protons of the polymer. In this model the water protons are therefore assumed not to contribute to the EISF. The fraction 1 − clocal which is not part of localized motion would then be water which is still undergoing much slower diffusion than bulk water, such that it is within the backscattering time window, but with the possibility to rearrange locally. Fully bulk-like water would be too fast to be seen with backscattering spectroscopy (i.e. would be a too broad Lorentzian) and would be part of the background contribution.
The  describes a rotation in a three-fold potential with a radius of the motion of r = 1.027 Å.27 For the dry sample, the fit of Aelast in Fig. 6 results in clocal = 0.89 in good agreement with the value from NSE, and cMethyl = 0.25. For the hydrated sample, clocal = 0.47 and cMethyl = 0.23. The fraction of cMethyl is therefore roughly the same in both samples in agreement with the picture of the methyl group rotations which should be the same in both samples. The value of cMethyl is lower than expected, corresponding only to 3 protons out of 11, or only one methyl group per side chain. It seems that the two methyl groups have significantly different energy barriers for rotational motion. If one of the methyl groups is hindered to rotate by the water cage surrounding the side chains needs further investigations.
describes a rotation in a three-fold potential with a radius of the motion of r = 1.027 Å.27 For the dry sample, the fit of Aelast in Fig. 6 results in clocal = 0.89 in good agreement with the value from NSE, and cMethyl = 0.25. For the hydrated sample, clocal = 0.47 and cMethyl = 0.23. The fraction of cMethyl is therefore roughly the same in both samples in agreement with the picture of the methyl group rotations which should be the same in both samples. The value of cMethyl is lower than expected, corresponding only to 3 protons out of 11, or only one methyl group per side chain. It seems that the two methyl groups have significantly different energy barriers for rotational motion. If one of the methyl groups is hindered to rotate by the water cage surrounding the side chains needs further investigations.
As mentioned above, contrast variation could shed a more detailed light into this question of the different components of the EISF and the different dynamic processes from an experimental point of view.
4 Conclusion
Neutron scattering provided insight into the molecular proton motion in dried and humidified crosslinked PNIPAM microgels. Titration experiments revealed a remaining water contents in the dried microgel of about 13%.Neutron spin-echo spectroscopy provided the amount of immobile protons on a molecular level by the plateau of the incoherent intermediate scattering function at large Fourier times, which was at a level of 86%, i.e. 14% of mobile protons which we attribute to water still present in the dried sample, but with a reduced mobility compared to bulk water.
Adding water increased the mobility by the expected amount with an immobile fraction of 40% and was also visible as a steep drop in intensity at 273 K in the elastic scans of the backscattering spectrometer. The mobile water fractions in the dried as well as humidified microgel still showed a dynamics much slower than bulk water, and were therefore most probably strongly coupled to the microgel. QENS showed in detail that the remaining water is mobile but still strongly linked to the PNIPAM microgel. The segmental polymer dynamics in swollen microgels (i.e. in solvent), which can also be measured with NSE, shows that a locally higher viscosity is required to explain the segmental motion with Zimm dynamics.19 The strongly confined water fraction inside microgels which as been observed here might be the reason for this observed higher apparent viscosity. Also humidification still leads to a slower water relaxation compared to bulk water, so a significant amount remains linked in some way to the polymer chains of the microgel. The previously reported strong interaction between up to 8 water molecules with the PNIPAM, depending on temperature and PNIPAM concentration, is confirmed by our investigation in the freeze dried samples with the strongly bound remaining water, where also the humidified sample still shows a relatively slow water mobility.15,16
More insight into the interaction of residual water and water in general with the PNIPAM microgels can be obtained, as already mentioned, with contrast variation experiments by partly deuteration. The difficulty might be to obtain well defined starting parameters, since the KF titration showed that a fully water free sample is hardly obtainable, and it is not clear how many of the remaining hydrogen atoms are able to exchange with subsequent D2O rinsing. It would be desirable to also substitute the side groups of the PNIPAM chains in order to get a handle on the influence of methyl group rotations. Contrast variation under controlled conditions is therefore a rather extensive project of its own.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) [Grants HO 5488/2-1 (O. Holderer) and WE 5066/3-1 (S. Wellert)] and Meier-Leibniz Center for the neutron beam time.References
- J. Witte, T. Kyrey, J. Lutzki, A. M. Dahl, J. Houston, A. Radulescu, V. Pipich, L. Stingaciu, M. Kühnhammer, M. U. Witt, R. von Klitzing, O. Holderer and S. Wellert, Soft Matter, 2019, 15, 1053–1064 RSC.
- K. Uhlig, T. Wegener, J. He, M. Zeiser, J. Bookhold, I. Dewald, N. Godino, M. Jaeger, T. Hellweg, A. Fery and C. Duschl, Biomacromolecules, 2016, 17, 1110–1116 CrossRef CAS.
- B.-J. Niebuur, K.-L. Claude, S. Pinzek, C. Cariker, K. N. Raftopoulos, V. Pipich, M.-S. Appavou, A. Schulte and C. M. Papadakis, ACS Macro Lett., 2017, 6, 1180–1185 CrossRef CAS.
- S. Nouhi, M. S. Hellsing, V. Kapaklis and A. R. Rennie, J. Appl. Crystallogr., 2017, 50, 1066–1074 CrossRef CAS PubMed.
- P. S. Mohanty, S. Nöjd, K. V. Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef PubMed.
- J. Witte, P. Krause, T. Kyrey, A. M. Dahl, J. Luzki, B. V. K. J. Schmidt, M. Ganeva, A. Koutsioubas, O. Holderer and S. Wellert, Macromolecules, 2020, 53(5), 1819–1830 CrossRef CAS.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2012, 64, 18–23 CrossRef.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS.
- E. S. Gil and S. M. Hudson, Prog. Polym. Sci., 2004, 29, 1173–1222 CrossRef CAS.
- M. R. Islam and M. J. Serpe, Chem. Commun., 2013, 49, 2646–2648 RSC.
- C. M. Nolan, M. J. Serpe and L. A. Lyon, Macromol. Symp., 2005, 227, 285–294 CrossRef CAS.
- R. Pelton, J. Colloid Interface Sci., 2010, 348, 673–674 CrossRef CAS PubMed.
- M. H. Futscher, M. Philipp, P. Müller-Buschbaum and A. Schulte, Sci. Rep., 2017, 7, 17012 CrossRef PubMed.
- K. Mochizuki and B.-A. Dor, J. Phys. Chem. Lett., 2017, 7, 1360–1364 CrossRef PubMed.
- H. Kogure, S. Nanami, Y. Masuda, Y. Toyama and K. Kubota, Colloid Polym. Sci., 2005, 283, 1163–1171 CrossRef CAS.
- M. Philipp, K. Kyriakos, L. Silvi, W. Lohstroh, W. Petry, J. K. Krüger, C. M. Papadakis and P. Müller-Buschbaum, J. Phys. Chem. B, 2014, 118, 4253–4260 CrossRef CAS PubMed.
- L. Tavagnacco, E. Chiessi, M. Zanatta, A. Orecchini and E. Zaccarelli, J. Phys. Chem. Lett., 2019, 10, 870–876 CrossRef CAS PubMed.
- S. Maccarrone, C. Scherzinger, O. Holderer, P. Lindner, M. Sharp, W. Richtering and D. Richter, Macromolecules, 2014, 47, 5982–5988 CrossRef CAS.
- T. Kyrey, J. Witte, A. Feoktystov, V. Pipich, B. Wu, S. Pasini, A. Radulescu, M. U. Witt, M. Kruteva, R. von Klitzing, S. Wellert and O. Holderer, Soft Matter, 2019, 15, 6536–6546 RSC.
- J. Witte, T. Kyrey, J. Lutzki, A. M. Dahl, M. Kühnhammer, R. V. Klitzing, O. Holderer and S. Wellert, ACS Appl. Polym. Mater., 2021, 3, 976–985 CrossRef CAS.
- S. Pasini, O. Holderer, T. Kozielewski, D. Richter and M. Monkenbusch, Rev. Sci. Instrum., 2019, 90, 043107 CrossRef CAS PubMed.
- P. Zolnierczuk, O. Holderer, S. Pasini, T. Kozielewski, L. Stingaciu and M. Monkenbusch, J. Appl. Crystallogr., 2019, 52(5), 1022–1034 CrossRef CAS PubMed.
- H. Maier-Leibnitz Zentrum, Journal of Large-Scale Research Facilities, 2015, 1, A30 CrossRef.
- J. Wuttke, M. Budwig, A. Drochner, H. Kämmerling, F.-J. Kayser, H. Kleines, V. Ossovyi, L. C. Pardob, M. Pragerc, D. Richter, G. J. Schneider, H. Schneider and S. Staringer, Rev. Sci. Instrum., 2012, 83, 075109 CrossRef PubMed.
- K. Kämpf, D. Demuth, M. Zamponi, J. Wuttke and M. Vogel, J. Chem. Phys., 2020, 152, 245101 CrossRef PubMed.
- R. Zorn, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 572, 874–881 CrossRef CAS.
- R. Zorn, W. Lohstroh, M. Zamponi, W. J. Harrison, P. M. Budd, M. Böhning and A. Schönhals, Macromolecules, 2020, 53, 6731–6739 CrossRef CAS.
- J. P. Embs, F. Juranyi and R. Hempelmann, Zeitschrift für Physikalische Chemie, 2010, 224, 5–32 CrossRef CAS.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- J. Teixeira, M.-C. Bellissent-Funel, S.-H. Chen and A.-J. Dianoux, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1913 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01823j |
| This journal is © the Owner Societies 2021 |