Open Access Article
Open Access ArticleElectronic excitation spectra of cerium oxides: from ab initio dielectric response functions to Monte Carlo electron transport simulations†
Andrea
Pedrielli
ab,
Pablo
de Vera
a,
Paolo E.
Trevisanutto
c,
Nicola M.
Pugno
bd,
Rafael
Garcia-Molina
 e,
Isabel
Abril
e,
Isabel
Abril
 f,
Simone
Taioli
f,
Simone
Taioli
 *ag and
Maurizio
Dapor
*a
*ag and
Maurizio
Dapor
*a
aEuropean Centre for Theoretical Studies in Nuclear Physics and Related Areas (ECT*-Bruno Kessler Foundation) and Trento Institute for Fundamental Physics and Applications (TIFPA-INFN), Trento, Italy. E-mail: taioli@ectstar.eu; dapor@ectstar.eu
bLaboratory of Bio-Inspired, Bionic, Nano, Meta Materials & Mechanics, Department of Civil, Environmental and Mechanical Engineering, University of Trento, Italy
cBruno Kessler Foundation, Trento, Italy
dSchool of Engineering and Materials Science, Queen Mary University of London, UK
eDepartamento de Física, Centro de Investigación en Óptica y Nanofísica, Universidad de Murcia, Spain
fDepartament de Física Aplicada, Universitat d'Alacant, Spain
gPeter the Great St. Petersburg Polytechnic University, Russia
First published on 6th August 2021
Abstract
Nanomaterials made of cerium oxides CeO2 and Ce2O3 have a broad range of applications, from catalysts in automotive, industrial or energy operations to promising materials to enhance hadrontherapy effectiveness in oncological treatments. To elucidate the physico-chemical mechanisms involved in these processes, it is of paramount importance to know the electronic excitation spectra of these oxides, which are obtained here through high-accuracy linear-response time-dependent density functional theory calculations. In particular, the macroscopic dielectric response functions ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) of both bulk CeO2 and Ce2O3 are derived, which compare remarkably well with the available experimental data. These results stress the importance of appropriately accounting for local field effects to model the dielectric function of metal oxides. Furthermore, we reckon the energy loss functions Im(−1/
of both bulk CeO2 and Ce2O3 are derived, which compare remarkably well with the available experimental data. These results stress the importance of appropriately accounting for local field effects to model the dielectric function of metal oxides. Furthermore, we reckon the energy loss functions Im(−1/![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ) of the materials, including the accurate evaluation of the momentum transfer dispersion from first-principles calculations. In this respect, by using Mermin-type parametrization we are able to model the contribution of different electronic excitations to the dielectric loss function. Finally, from the knowledge of the electron inelastic mean free path, together with the elastic mean free path provided by the relativistic Mott theory, we carry out statistical Monte Carlo (MC) electron transport simulations to reproduce the major features of the reported experimental reflection electron energy loss (REEL) spectra of cerium oxides. The good agreement with REEL experimental data strongly supports our approach based on MC modelling, whose main inputs were obtained using ab initio calculated electronic excitation spectra in a broad range of momentum and energy transfers.
) of the materials, including the accurate evaluation of the momentum transfer dispersion from first-principles calculations. In this respect, by using Mermin-type parametrization we are able to model the contribution of different electronic excitations to the dielectric loss function. Finally, from the knowledge of the electron inelastic mean free path, together with the elastic mean free path provided by the relativistic Mott theory, we carry out statistical Monte Carlo (MC) electron transport simulations to reproduce the major features of the reported experimental reflection electron energy loss (REEL) spectra of cerium oxides. The good agreement with REEL experimental data strongly supports our approach based on MC modelling, whose main inputs were obtained using ab initio calculated electronic excitation spectra in a broad range of momentum and energy transfers.
1 Introduction
Cerium oxides are inner transition metal oxides with promising applications ranging from fuel cells1 to catalysis for hydrogen and water splitting,2,3 coating technologies,4 glass-polishing tools,5 electrochromic devices,6 and locomotive industries.7 Ceria-based materials have also received increasing attention owing to the higher abundance of cerium among the rare-earth family elements, their relatively narrow band gap, which makes them active in the visible region of the light spectrum (near violet), and their stability under irradiation as well as their large adsorption capacity.Recently, cerium dioxide (CeO2) and dicerium trioxide (Ce2O3) nanoparticles (NPs) have been proposed also as possible enhancers of the relative biological effectiveness (RBE) in hadrotherapy for cancer treatment.8,9 In this technique, irradiation by protons or heavier ions is aimed to destroy tumor cells within well localized tumour regions. The use of high-Z materials (such as gold, platinum, gadolinium, and iron nanoparticles) in radiation therapy, with high concentration near the tumour region, has been shown to enhance the RBE due to an increase in both direct and indirect damage.10–17 However, while some of these NPs can be toxic for humans, high-Z ceramic oxides, such as CeO2, might offer a viable biocompatible alternative to enhance localized dose and biodamage in radiotherapy.9 Furthermore, ceria nanoparticles are also being investigated as possible radioprotectors in healthy cells,18 thus making this material more promising for hadrontherapy.
Besides these remarkable applications, the study of cerium-based oxides CeO2 and Ce2O3 is of fundamental interest to understand the electronic and optical properties of materials that exhibit strong electron correlation, which is affected by the presence of highly localized 4f states. Indeed, while in experiments both oxides show insulator behaviours in their ground state,19–21 density functional theory (DFT) predicts correctly a non-magnetic insulator state only for CeO2, while wrongly a metallic one for Ce2O3.22,23 The latter failure represents a known shortcoming of DFT to describe highly-localized orbitals24 in antiferromagnetic materials that exhibit Mott insulating behaviour. The inaccurate description of ceria by first-principles DFT is due to the presence of multiple-valence states of cerium within the oxides, showing competing divalent and trivalent characteristics.24 In this respect, ceria represents a challenging problem for DFT.
To open the fundamental gap one relies on approaches based either on DFT with hybrid density functionals using a fraction of nonlocal Fock exchange,23,25,26 which is able to describe better than DFT in the local density (LDA) (or in the generalized gradient correction GGA) approximation the electronic properties of ceria without applying any explicit localization constraints to the 4f bands, or on more rigorous many-body perturbation theory, such as GW,27 in general aiming at a trade-off between accuracy and computational cost.
Finally, a more phenomenological way to correct DFT failure in this respect is based on the so-called DFT+U method28 (or also on the GW+U approximation,29,30 where the GW correction27,31,32 is applied on top of LDA+U), in which the addition of an Hubbard correction increases the effective Coulomb repulsion Ueff = U − J by the sum of the strong on-site Coulomb interaction of localized electrons U and the strength of the exchange interaction J.33 Within this framework, the localization of the 4f states in CeO2 and Ce2O3 can be achieved, resulting in band gap opening. Indeed, the introduction of an Hubbard correction Ueff shifts the Ce 4f states, and enhances the stability of the ground state reproducing correctly the insulating behaviour for all oxidation states. This makes the use of the Hubbard correction a valid approach for treating systems with multiple-valence states.
Several studies have reported the structural, electronic and optical properties of cerium oxides using first-principles calculations.19,20,22,34 However, to the best of our knowledge, significant differences between computer simulations and experimental results persist, particularly in the assessment of the optical properties.19,35 Here we focus our study on the ab initio calculations of the electronic band structure and of the dielectric response of bulk Ce(+IV)O2 and Ce(+III)2O3, which are characterised by the two known oxidation states of cerium in solids, using the time-dependent density functional theory method (TDDFT)36 in linear response (LR) approximation.37
We adopt an interacting all-electron approach not plagued by the presence of pseudopotentials (that deal implicitly with the core and explicitly with chemically active valence states), the only approximation being the interaction potential among electrons. The macroscopic dielectric function ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) (q, W), or the closely related energy loss function ELF(q, W), where q and W are the momentum and energy transfers, respectively, is used to describe the material excitation spectrum and, thus, the inelastic interactions between charged particles and the medium constituents.38,39 In particular, we show that the inclusion of local field effects (LFE) overcomes the discrepancy between first-principles calculations and experimental measurements.
(q, W), or the closely related energy loss function ELF(q, W), where q and W are the momentum and energy transfers, respectively, is used to describe the material excitation spectrum and, thus, the inelastic interactions between charged particles and the medium constituents.38,39 In particular, we show that the inclusion of local field effects (LFE) overcomes the discrepancy between first-principles calculations and experimental measurements.
The ELF, conveniently weighted and integrated, provides the electron inelastic scattering cross-section,39,40 which is used, along with the elastic scattering cross-section derived from the relativistic Mott theory,41 as an input to a Monte Carlo (MC) routine to model the transport of charged particles within these solids and predict the reflection electron energy loss (REEL) spectra in particular.42–49 REEL spectroscopy is an analysis technique that uses an electron beam impinging with kinetic energy lower than 2 keV into thin films. Primary electrons penetrate a few nanometers into the material surface, lose their energy via inelastic collisions and some of them are eventually backscattered to the spectrometer,50 resulting in spectra that are typically characterised by a number of structures attributed to both collective (plasmons) and single-electron excitations and can be directly benchmarked against the available experimental data. Here, the agreement between the simulated and the measured REELS is used to validate the TDDFT-calculated electronic excitation spectra of cerium oxides in a broad energy and momentum transfer region.
This paper is organized as follows. In Section 2 we summarize the theoretical methods used to perform the ab initio calculations of the dielectric function and the MC strategy. In Section 3 we discuss first the electronic and optical properties of cerium oxides, such as the ELF in momentum–energy space. Furthermore, a detailed analysis of the excitation spectra is carried out using the Mermin Energy-Loss Function-Generalized Oscillator Strength (MELF-GOS) approach.51–54 Finally, the REEL spectra are obtained by applying our MC method and compared with experimental measurements. Atomic units are used throughout this work except otherwise stated.
2 Theoretical and computational methods
Here we provide the fundamentals of the methodology used to obtain the atomic structures and the excitation spectra of bulk CeO2 and Ce2O3. These properties are required to obtain reliable cross-sections needed to simulate the main interactions that affect the electron transport through these materials.We stress that this work is aimed at the numerical assessment of the electron excitation spectra and of the ELF, where both collective excitations, such as plasmons, and high-energy single-electron excitations play a main role. We point out that the electron–hole (e–h) interactions are more relevant in the assessment of absorption spectra and determine the optical band gap (the on-set energy value in the ELF), while they have minor influence on the ELF lineshape and on the assessment of the inelastic cross-sections. Thus, we decided to use TDDFT within the adiabatic local density approximation (ALDA) kernel, where e–h interactions are missing.
In principle, to calculate the excitation spectra of solids one could perform GW calculations (that usually open the fundamental band gap with respect to the DFT ground state calculations) in conjunction with the Bethe–Salpeter Equation (BSE), which is a Dyson-type equation for the two-particle Green's function, to include the excitonic effects. However, in view of the minor effects that e–h interactions have on the ELF lineshapes, of the much higher computational cost of GW + BSE with respect to TDDFT simulations, and finally of the good accuracy of the results attainable already at the level of the random phase approximation (RPA) (i.e. without electron–hole correlation terms in the kernel), we have chosen to use TDDFT to determine the ELF spectra of ceria solids.
At odds, the use of G0W0 many-body corrections (without the excitonic effects provided by BSE) could possibly result in a blue-shift of the ELF and thus in worsening the numerical simulation results. Therefore, being our main concern the accurate determination of the d and f state energies and the interpretation of the electron excitation spectra, related to the ELF, rather than a better estimation of the fundamental band gap, we decided to use the LDA+U functional.
Here, we compare our numerical results with the REELS experimental measurements and we obtain a very good agreement. This is a confirmation of the correctness of this approach for the observables we are interested in.
2.1 Material structure
The DFT+U method28 has been employed to optimize both the cell volume and atomic positions of the cerium oxides by using the ELK code suite55 (where the Hubbard correction Ueff was applied to the 4f orbitals of Ce). On the one hand, CeO2 is characterised by a face centered cubic fluorite-type structure, belonging to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m point group. The primitive cell of CeO2 (inset in Fig. 1) has a crystal basis defined by two oxygen atoms, which in lattice coordinates are positioned at (0.25, 0.25, 0.25) and (0.75, 0.75, 0.75), respectively, and one cerium atom, centered at (0, 0, 0).
m point group. The primitive cell of CeO2 (inset in Fig. 1) has a crystal basis defined by two oxygen atoms, which in lattice coordinates are positioned at (0.25, 0.25, 0.25) and (0.75, 0.75, 0.75), respectively, and one cerium atom, centered at (0, 0, 0).
On the other hand, Ce2O3 has a trigonal geometry, belonging to the P3![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 1 point group. The primitive cell (inset in Fig. 2) includes three oxygen atoms at the crystallographic positions (0, 0, 0), (1/3, 2/3, 0.642), and (2/3, 1/3, 0.3574) in lattice coordinates, respectively, and two cerium atoms centered at (1/3, 2/3, 0.2459) and (1/3, 2/3, 0.754).
1 point group. The primitive cell (inset in Fig. 2) includes three oxygen atoms at the crystallographic positions (0, 0, 0), (1/3, 2/3, 0.642), and (2/3, 1/3, 0.3574) in lattice coordinates, respectively, and two cerium atoms centered at (1/3, 2/3, 0.2459) and (1/3, 2/3, 0.754).
We report in Table 1 the lattice constants of the optimized cells. The motivations to fix the value of Ueff = 5 eV, which delivers good agreement with experimental data, will be discussed further below.
2.2 Dielectric response
The microscopic dielectric function of the materials depends on the bare Coulomb potential vC and the polarization function χ(q, W) through:58| ε(q, W) = 1 − vC(q)χ(q, W). | (1) |
| χ−1(q, W) = χ0−1(q, W) − vC(q) − fxc(q, W), | (2) |
 | (3) |
For periodic crystals one can exploit the translational symmetry, and the microscopic dielectric function can be conveniently written in reciprocal space, i.e. εG,G′(q, W) = ε(q + G, q + G′, W), where G and G′ are the reciprocal lattice vectors, and q is the transferred momentum vector in the first Brillouin zone (1BZ). Using this notation, εG,G′(q, W) is also often called the dielectric matrix. It can be shown63,64 that the experimentally measurable macroscopic dielectric function ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) and the microscopic one ε are related by the following expression:
and the microscopic one ε are related by the following expression:
 | (4) |
The dielectric response function has been obtained using the LR-TDDFT implementation of the ELK code suite55 on top of the ground state obtained by the DFT+U method. ELK uses an all-electron full-potential linearized augmented-plane-wave (FP-LAPW) approach. The Hubbard correction has been treated in the fully localised limit (FLL). To deal with the antiferromagneticity of Ce2O3, we included both spin polarization and spin–orbit coupling. The local spin density approximation (LSDA) exchange correlation functional65 has been used for the ground state calculations alongside the ALDA approximation for the time dependent exchange correlation functional. We also checked the convergence with respect to the number of k-points in the 1BZ, finding well converged results for a 10 × 10 × 10 k-point grid for CeO2 and for a 8 × 8 × 8 k-point grid for Ce2O3. A total of 50 empty bands for each atom have been used to obtain converged results up to 120 eV.
To perform the extension of the dielectric function in the optical limit (i.e.q = 0) to finite momenta the transferred momentum has been selected along the [111], [110], and [211] directions in the reciprocal space for CeO2 and along the [001], [110], and [100] directions for Ce2O3, respectively, with the modulus set to 6 Å−1 in the reciprocal space. Such an extension to finite momenta is necessary to carry out the accurate calculation of observables, such as the inelastic mean free path (IMFP) that depends critically on the momentum dispersion (see Section 2.4).
2.3 Energy loss function
To describe the propagation of charged particles through matter using the dielectric formalism,38–40 one relies on the material energy loss function ELF, which is related to the macroscopic dielectric function as follows: | (5) |
Thus, to extend the excitation energy range beyond the valence regime, we propose to use the MELF-GOS model,51–54 which implements a numerically effective and accurate method to compute the ELF over the entire Bethe surface (i.e., the momentum and energy transfer plane) by including both valence and inner shell electronic excitations. In short, the derivation of the ELF within the MELF-GOS framework is based on a fitting procedure, whereby the optical-limit ab initio (or measured) energy-loss spectrum of the target material is equated to a zero-momentum-transfer functional form which, for the valence (outer) contribution, can be written as a sum of Mermin-type ELFs:67,68
 | (6) |
 | (7) |
 | (8) |
 | (9) |
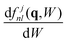 are the analytical non-relativistic hydrogenic GOSs that are obtained using an effective nuclear charge for each inner shell identified by the atomic quantum numbers (n, l) of the target j-th constituent with stoichiometric weight αj. In eqn (9), Wjth,nl is the ionization energy of the orbital, and
are the analytical non-relativistic hydrogenic GOSs that are obtained using an effective nuclear charge for each inner shell identified by the atomic quantum numbers (n, l) of the target j-th constituent with stoichiometric weight αj. In eqn (9), Wjth,nl is the ionization energy of the orbital, and  is the target atomic or molecular number density.
is the target atomic or molecular number density.
2.4 Monte Carlo simulations of electron transport
In the MC approach the interaction between the incident electron beam and a cerium oxide target is simulated by treating the electrons as point particles that follow classical trajectories within the material. This is a viable representation at high enough energy.69 Electron trajectories are determined by the elastic and inelastic interactions, which are assessed using quantum mechanical methods. The occurrence of either an elastic or inelastic scattering event at kinetic energy T is assessed by comparing a random number uniformly distributed in the range [0, 1] with the relevant probabilities pel(T) = Λel(T)/Λtot(T) and pinel(T) = Λinel(T)/Λtot(T), where Λtot(T) = Λinel(T) + Λel(T).42Λel/inel = λ−1el/inel(T) is the inverse mean free path for the elastic or inelastic scattering.Once the type of collision has been chosen, the angular deviation of the electron trajectory after an elastic collision, given by the scattering angle θ, can be evaluated by equating the elastic scattering cumulative probability
 | (10) |
In a similar way, the energy loss W due to an inelastic scattering event of an electron with kinetic energy T can be reckoned by equating the inelastic scattering cumulative probability distribution:
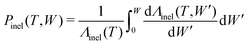 | (11) |
The main quantity to account for inelastic events that electrons with kinetic energy T undergo when moving through a medium characterised by an ELF is the differential inverse inelastic mean free path (DIIMFP):
 | (12) |
 , result from energy and momentum conservation in the interaction process.
, result from energy and momentum conservation in the interaction process.
From the knowledge of the DIIMFP one can reckon the IMFP to be used in the MC simulation of electron transport through the cerium oxides by calculating the following inelastic scattering cross-section:
 | (13) |
We notice that the dielectric formalism in our implementation includes the exchange–correlation effects only within the probed solid system at the mean field level in the local density approximation (LDA), as the ELF is derived by using the time-dependent extension of the “static” DFT LDA functional to include (non-local) energy-dependent interactions. Nevertheless, exchange–correlation interaction is also experienced between the electrons of the impinging primary beam and the system itself. We point out that the electron exchange, arising from the indistinguishability of the primary and target electrons, is not included in the dielectric formalism (i.e., only the direct scattering amplitude is considered) as given by eqn (12). Indeed, the electron DIIMFP is assessed within the first Born approximation neglecting both relativistic and exchange effects between the primary and the target electrons. In principle, the electron exchange interaction can be included by means of the Born–Ochkur exchange factor.70,71 However, this correction only affects the calculated IMFP at energies of the primary beam lower than those analysed here (<500 eV) (see ref. 70 and 71). Also the backscattered electrons recorded in the REELS measurements are characterised by a kinetic energy large enough (>1550 eV) to neglect the exchange interaction.
The elastic scattering is accounted for by means of the Mott theory,41 which generalizes the screened Rutherford scattering model also at low kinetic energy of the colliders and for high-Z materials. This approach provides the differential elastic scattering cross-section (DESCS) for an electron being scattered at an angle θ when impinging on a central potential as follows:42
 | (14) |
However, in condensed matter the central symmetry of atomic systems is lost, and thus we must generalize to some extent the Mott theory to take into account the presence of bonded interactions among neighbours in the periodic unit cell. Condensed phase effects can be achieved by allowing interference between the direct fm(θ) and spin–flip gm(θ) scattering amplitudes of the mth-atom and those of the neighbouring nth-atom. These interference terms account for multiple scattering events among the scattered waves modifying eqn (14) as follows:
 | (15) |
Finally, by integrating over the solid angle, one obtains the total elastic scattering cross-section as:
 | (16) |
3 Results and discussion
In the following, the main features of the electronic excitation spectra of CeO2 and Ce2O3 will be discussed. First, the band structure, and the total and partial density of states (DOS) of electrons will be analyzed, which serves to set up the Hubbard parameter Ueff for the TDDFT calculations. These DOS will be then useful to interpret the dielectric properties of cerium oxides. Finally, the electron inelastic scattering cross-sections will be obtained from the complex dielectric functions, and will be used to perform the MC simulations of REEL spectra.3.1 Band structures and DOS of bulk CeO2 and Ce2O3
Ground state DFT calculations have been carried out, aiming particularly to check the dependence of the electronic band structure on different values of the Hubbard correction Ueff. After a number of tests carried out on the total density of states (DOS) (see Fig. S1 and S2 of the ESI†) and on the ELF in the optical limit (see Fig. S5 of the ESI†), Ueff was set to 5 eV. This value has been fixed so that (i) the localized 4f band blueshifts with respect to plane LDA and opens the fundamental gap, particularly in the case of Ce2O3 for which LDA wrongly predicts a metallic character; (ii) the optical ELF calculated with this value of Ueff is in fair agreement with the experimental data available for CeO2.In CeO2 the fundamental gap occurs between the top of the valence band with O2p character and the bottom of the conduction band formed by the localized Ce4f orbitals. This can be observed in the bottom panel of Fig. 1, where we plot the total DOS of bulk CeO2 along with the relevant band gaps (the Fermi level is set to the origin of the energy axis). In particular, in the top panel of Fig. 1 we show the contribution to the total DOS of cerium (dashed lines in the top panel) and oxygen (continuous lines in the top panel), respectively, along with the projection on the relevant angular momenta (PDOS). This analysis shows clearly the hybridization between different symmetry orbitals of O and Ce. In particular, a deeper occupied band (below −10 eV in Fig. 1) is mainly formed by Ce5p mixed with O2s, while O2p and Ce4f hybridize between −5 eV and 0 eV. Above the valence band, between 0 eV and 5 eV, there is a localized Ce4f–O2p narrow band and beyond that we find a conduction band mainly of Ce5d nature with a mixture of several O and Ce levels at larger energies between 5 eV and 15 eV (see also Fig. S3 of the ESI†).
In Table 2 we also report, in comparison with other theoretical and experimental data, the gaps between the O2p valence band and the 4f states and between the O2p valence band and the Ce5d conduction band with the exclusion of the 4f states. The latter is more affected by the fine tuning of Ueff. Plain DFT values show the typical underestimation of the fundamental gap (2.05 eV) with respect to experimental measurements (ranging from 3.3 to 3.6 eV77–79), slightly improved to 2.35 eV by adding the Hubbard correction Ueff.
The full band structure of CeO2 calculated using DFT+U is given in Fig. S3 of the ESI† for reference. Both conduction (above 4 eV) and valence (below −1 eV) bands show some significant dispersion, while the 4f states between 0.8 and 2 eV have a smaller bandwidth. From the band plot analysis it turns out that CeO2 is an indirect gap insulator. While the relative values of the orbital energy gaps are underestimated by our DFT+U approach, the emergence of localized 4f states is correctly predicted as in previous studies using hybrid functionals.19,23
In the case of Ce2O3, the addition of the Hubbard correction is critical in the simulation of the electronic band structure and DOS as this material is wrongly predicted to be a metal by DFT-LDA. In fact, the Ce atom in Ce2O3 displays a +3 oxidation state, where one electron is expected to populate the 4f band leading to a possible ferromagnetic or antiferromagnetic ground state. By switching on the Hubbard correction we obtain the localization of the 4f states, with redshift of the latter bands by increasing the Ueff value from 5 to 6 eV (see a plot of the DOS of bulk Ce2O3 for Ueff = 5 and 6 eV in Fig. S2 of the ESI†) and with blueshift of the conduction bands at higher energies. The gaps between different bands are reported in Table 3.
| Method | U eff | Band gap | Band gap | Band gap |
|---|---|---|---|---|
| O2p → Ce4f | O2p → Ce5d | Ce4f → Ce4f, 5d | ||
| LSDA+U | 5 | 1.1 | 3.95 | 2.04 |
| LSDA+U | 6 | 1.7 | 3.97 | 2.59 |
In Fig. 2 we show the total (TDOS, bottom panel) and projected (PDOS, top panel) DOS of Ce2O3. The full band structure calculated using DFT+U is given in Fig. S4 of the ESI† for reference. From the analysis of the PDOS we notice that the Ce4f band splits into two subbands, a very narrow occupied band, and a narrow and intense empty band that overlaps with the empty Ce5d band above the Fermi level (the origin of the energy axis), respectively. The DOS is also characterised by a valence band mainly of O2p nature, a deeper occupied band mainly of Ce5p origin, and an outer conduction band above 10 eV which is a mixture of high energy states from all constituents. The almost localized nature of the 4f band can be seen in Fig. S4 of the ESI,† where a flat band around −1 eV from the Fermi level appears. At variance, the other conduction bands show a large dispersion owing to the hybridization of the Ce4f, 5d states with O2p orbitals. Finally, we notice that also Ce2O3 is an indirect gap insulator, being found at the top of the valence band at the Γ-point and the bottom of the conduction band at the K-point.
3.2 The excitation spectrum of bulk CeO2
The excitation spectrum of bulk materials is determined by the real (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1) and imaginary (
1) and imaginary (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2) parts of the complex macroscopic dielectric function (see eqn (4)). The former informs about the screening capacity of the material to electric fields, while the latter provides the spectrum of possible electronic transitions between occupied and empty states. They are directly connected to the optical refractive index and extinction coefficient (see Fig. S10 and eqn (S1) of the ESI†), so they can be straightforwardly checked against experimental optical determinations for q → 0. Particularly,
2) parts of the complex macroscopic dielectric function (see eqn (4)). The former informs about the screening capacity of the material to electric fields, while the latter provides the spectrum of possible electronic transitions between occupied and empty states. They are directly connected to the optical refractive index and extinction coefficient (see Fig. S10 and eqn (S1) of the ESI†), so they can be straightforwardly checked against experimental optical determinations for q → 0. Particularly, ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 can be correlated with the PDOS obtained in Section 3.1, which allows identifying the origin of the different excitations. The latter are in turn connected to the structure of the ELF, and this identification may be relevant for the assessment of the quality of the obtained spectra (see Sections 3.2 and 3.3 below) and the calculation of the inelastic mean free path.68
2 can be correlated with the PDOS obtained in Section 3.1, which allows identifying the origin of the different excitations. The latter are in turn connected to the structure of the ELF, and this identification may be relevant for the assessment of the quality of the obtained spectra (see Sections 3.2 and 3.3 below) and the calculation of the inelastic mean free path.68
Fig. 3 shows the real (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1, top panel) and imaginary (
1, top panel) and imaginary (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2, bottom panel) parts of the macroscopic dielectric function in the optical limit (q → 0), respectively, in comparison with experimental data.20,21,80,81 We notice how the inclusion of LFE in the description of the macroscopic dielectric function is critical to reproduce the experimental measurements, in particular in the flattening of the third major peak between 15–20 eV in
2, bottom panel) parts of the macroscopic dielectric function in the optical limit (q → 0), respectively, in comparison with experimental data.20,21,80,81 We notice how the inclusion of LFE in the description of the macroscopic dielectric function is critical to reproduce the experimental measurements, in particular in the flattening of the third major peak between 15–20 eV in ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1 and between 20–25 eV for
1 and between 20–25 eV for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2.
2.
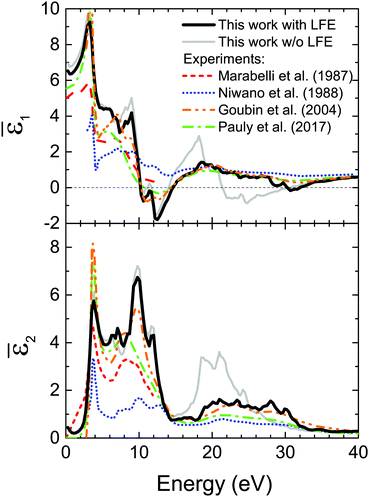 | ||
Fig. 3 Top panel: Comparison between the real part (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1) of the experimental dielectric function of bulk CeO220,21,80,81 and our calculation. Bottom panel: Comparison between the imaginary part ( 1) of the experimental dielectric function of bulk CeO220,21,80,81 and our calculation. Bottom panel: Comparison between the imaginary part (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2) of the experimental dielectric function of bulk CeO220,21,80,81 and our calculation. Both 2) of the experimental dielectric function of bulk CeO220,21,80,81 and our calculation. Both ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1 and 1 and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 are calculated along the [111] direction of the momentum transfer, taking afterwards the q → 0 limit. The inclusion of LFE improves the agreement with experimental data, flattening in particular the features in the range of 15–30 eV. 2 are calculated along the [111] direction of the momentum transfer, taking afterwards the q → 0 limit. The inclusion of LFE improves the agreement with experimental data, flattening in particular the features in the range of 15–30 eV. | ||
The features seen in Fig. 3 for ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 can be understood on the basis of the PDOS shown in the top panel of Fig. 1. The first peak around 3 eV corresponds to the transition from the O2p valence band to the Ce4f localized states, with a fundamental band gap of 2.35 eV. The second gap extracted from Fig. 1 is of 5.2 eV, above which three main structures can be seen in the
2 can be understood on the basis of the PDOS shown in the top panel of Fig. 1. The first peak around 3 eV corresponds to the transition from the O2p valence band to the Ce4f localized states, with a fundamental band gap of 2.35 eV. The second gap extracted from Fig. 1 is of 5.2 eV, above which three main structures can be seen in the ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 spectrum of Fig. 3 below 15 eV. These peaks correspond to the superposition of the PDOS of the O2p occupied levels with that of the Ce5d empty levels. The next peaks above 15 eV correspond to a mix of transitions from the O2p band to the top part of the conduction band (being an hybridization of s, p, d and f states, labelled the “conduction band (others)” in Fig. 1) and from the Ce5p band to the conduction Ce5d band, as previously noted.19 The former presents an approximate onset of 14.12 eV (a dip in the PDOS of the conduction band should be noted in Fig. 1 around 14 eV), while the latter has a gap of 16.8 eV (see Fig. 1), approximately corresponding to the structures observed in Fig. 3. This assignment is in agreement with previous studies.20,21,82,83 Transitions with Δl = ±1 are allowed, despite the angular momentum selection rule, owing to the hybridization between p, d and f orbitals of O and Ce (see top panel of Fig. 1).
2 spectrum of Fig. 3 below 15 eV. These peaks correspond to the superposition of the PDOS of the O2p occupied levels with that of the Ce5d empty levels. The next peaks above 15 eV correspond to a mix of transitions from the O2p band to the top part of the conduction band (being an hybridization of s, p, d and f states, labelled the “conduction band (others)” in Fig. 1) and from the Ce5p band to the conduction Ce5d band, as previously noted.19 The former presents an approximate onset of 14.12 eV (a dip in the PDOS of the conduction band should be noted in Fig. 1 around 14 eV), while the latter has a gap of 16.8 eV (see Fig. 1), approximately corresponding to the structures observed in Fig. 3. This assignment is in agreement with previous studies.20,21,82,83 Transitions with Δl = ±1 are allowed, despite the angular momentum selection rule, owing to the hybridization between p, d and f orbitals of O and Ce (see top panel of Fig. 1).
The optical ELF of CeO2 is shown in Fig. 4. The top panel depicts the TDDFT results using the ALDA kernel or random phase approximation (RPA), with and without the inclusion of LFE. Both ALDA and RPA give similar results, while LFE plays a crucial role in reducing the intensity of the optical ELF, bringing it closer to the experimental data.20,21,80,81 The ALDA calculation including LFE is compared to the recorded data in the bottom panel, where a broadening to the calculated ELF has been applied in order to account for the finite lifetime of the electronic excitations and the experimental resolution. To take into account the electron–electron and phonon dephasing, we have added an absolute Lorentzian width equal to 0.2 eV, a Lorentzian with quadratic energy dependence multiplied by a factor of 6 × 10−4 and a Gaussian with a width of σ = 0.2 eV. The calculations agree well with the experimental data below 40 eV, except for intensities of the peaks reported in ref. 81. We notice that the agreement between our calculations and the experimental findings by Goubin et al.20 is remarkable in the entire energy range. Above 40 eV, the calculations overestimate the experiments, although they reproduce very well their shape.
 | ||
| Fig. 4 Optical energy-loss function of CeO2 under different approximations. Top panel: calculations using ALDA and RPA approximations, with and without the LFE. Bottom panel: optical ELF obtained within ALDA and LFE applying peak broadening, in comparison to different sets of experimental data.20,21,80,81 | ||
The discrepancy found between our calculations and experiments at the larger energies in Fig. 4 can be rationalised in light of the f- and ps-sum rules,84 which serve to check the accuracy of an optical ELF. The former gives the effective number of electrons per unit cell participating in the electronic excitations:
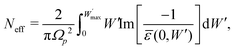 | (17) |
 , which should converge to the atomic number as
, which should converge to the atomic number as  . The latter sum-rule states that the ELF should fulfill the following equation:
. The latter sum-rule states that the ELF should fulfill the following equation: | (18) |
Note that, since we are dealing with all-electron simulations, in principle the inclusion of high-energy transitions above 120 eV is possible. However, the extension of the simulations in the energy axis well beyond the value of 120 eV cannot be typically achieved at an affordable computational cost from first-principles calculations. In this respect, this extension of the energy range (including the Ce and O core levels) has been performed by means of the atomic GOS within the MELF-GOS model, while at intermediate energies between valence and core excitations, a Mermin function fitting to the atomic X-ray data by Henke et al.85 has been carried out.
The structures observed in the ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 spectrum can be translated to those seen in the optical ELF, where the peaks are generally shifted to larger energies as compared to
2 spectrum can be translated to those seen in the optical ELF, where the peaks are generally shifted to larger energies as compared to ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2, as ELF = Im(−1/
2, as ELF = Im(−1/![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ) =
) = ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2/(
2/(![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 12 +
12 + ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 22) (see Fig. 3 and 4 for a comparison between energy peaks) and typically
22) (see Fig. 3 and 4 for a comparison between energy peaks) and typically ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1 decreases with an increase in the energy transfer. Additionally, plasmon excitations can be found by searching for the conditions
1 decreases with an increase in the energy transfer. Additionally, plasmon excitations can be found by searching for the conditions ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1 ≈ 0 and
1 ≈ 0 and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 ≪ 1. According to our calculations, only the excitations around 12–14 eV and 32 eV could have collective or plasmon-like character. While several authors21,82,86 attribute the first peak to plasmon excitation, this is not entirely evident from our simulations, even though the inclusion of LFE lowers the minimum of
2 ≪ 1. According to our calculations, only the excitations around 12–14 eV and 32 eV could have collective or plasmon-like character. While several authors21,82,86 attribute the first peak to plasmon excitation, this is not entirely evident from our simulations, even though the inclusion of LFE lowers the minimum of ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 in correspondence to
2 in correspondence to ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1 ≈ 0 (see Fig. 3), resulting in a maximum of the ELF.
1 ≈ 0 (see Fig. 3), resulting in a maximum of the ELF.
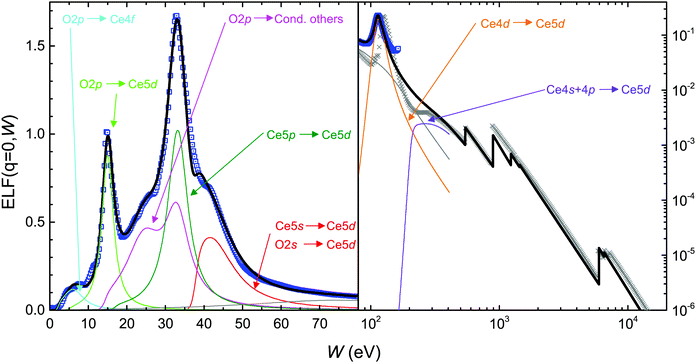
Following the trends in the band gaps and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 features obtained from the PDOS analysis, we fitted the first-principles optical ELF of CeO2 with 11 Mermin ELFs assigned to particular transitions, see Fig. 5. However, two of the Mermin functions (7 and 11, shown by a gray line) were intended to act as a “baseline” to obtain a smooth crossover between the valence and core levels and, thus, have not been assigned to any particular transition to fulfill the sum rules. Note that for the larger energies (Ce5s, O2s and larger energy excitations, including those described by GOS), threshold energies have been taken from atomic binding energies from the X-Ray Data Booklet,87 see Table 4. The individual contributions to the Mermin function fitting of the first-principles optical ELF are depicted by thin solid lines in Fig. 5 and the corresponding parameters are given in Table S1 in the ESI.† Each Mermin function or group of functions has been assigned to particular transitions, as indicated in Table 4. The assignment has been made with the purpose of fulfilling the individual f-sum rules, i.e. that the effective number of electrons Neff coming from each interband transition is close to the number of electrons expected in such transition Nexp.
2 features obtained from the PDOS analysis, we fitted the first-principles optical ELF of CeO2 with 11 Mermin ELFs assigned to particular transitions, see Fig. 5. However, two of the Mermin functions (7 and 11, shown by a gray line) were intended to act as a “baseline” to obtain a smooth crossover between the valence and core levels and, thus, have not been assigned to any particular transition to fulfill the sum rules. Note that for the larger energies (Ce5s, O2s and larger energy excitations, including those described by GOS), threshold energies have been taken from atomic binding energies from the X-Ray Data Booklet,87 see Table 4. The individual contributions to the Mermin function fitting of the first-principles optical ELF are depicted by thin solid lines in Fig. 5 and the corresponding parameters are given in Table S1 in the ESI.† Each Mermin function or group of functions has been assigned to particular transitions, as indicated in Table 4. The assignment has been made with the purpose of fulfilling the individual f-sum rules, i.e. that the effective number of electrons Neff coming from each interband transition is close to the number of electrons expected in such transition Nexp.
| Mermin | Transition | W th (eV)a | N exp | N eff |
|---|---|---|---|---|
| a Threshold energies derived from the PDOS except otherwise stated. b The Mermin functions 1–4 describe the excitations of the outermost valence electrons, located in a band of mainly O2p origin, but which also contains the valence electrons Ce6s, 5d, and 4f, see Fig. 1. c From ref. 87. | ||||
| 1 | O2p → Ce4f | 2.35 | ||
| 2 | O2p → Ce5d (plasmon-like) | 5.20 | ||
| 3–4 | O2p → cond. (others) | 14.12 | ||
| 1–4 | O2p, Ce6s, 5d, 4fb | 12b | 8.08 | |
| 5 | Ce5p → 5d (plasmon-like) | 16.80 | 6 | 6.13 |
| 6 | Ce5s, O2s → Ce5d | 37.80c | 6 | 5.91 |
| 7 | Not assigned | 5.32 | ||
| 8–9 | Ce4d → 5d | 100.68c | 10 | 10.87 |
| 10 | Ce4s, 4p → 5d | 206.53c | 8 | 7.89 |
| 11 | Not assigned | 6.39 | ||
| GOS | Atomic shells | |||
| O K | O1s | 543.10c | 4 | 3.48 |
| Ce M | Ce3s, 3p, 3d | 883.80c | 18 | 14.23 |
| Ce L | Ce2s, 2p, 4f | 5723.00c | 8 | 4.53 |
| Ce K | Ce1s | 40443.00c | 2 | 1.07 |
| Total | 74 | 73.89 | ||
To this respect, two further aspects should be taken into account. First, the Mermin functions 1 to 4 are associated with transitions from the occupied O2p band, as this is the main hybridization of the valence band. However, this being the outermost band, it also hosts the valence electrons from Ce6s, 5d, 4f, and so the total expected number of electrons there should be 12. Second, the hydrogenic GOS systematically underestimates the number of inner-shell electrons (see Table 4) as a consequence of Pauli's exclusion principle. Indeed, as the inner-shell electrons cannot be promoted to occupied outer-shells, they lose some amount of GOS. At the same time, the outer-shell electrons cannot fall into the occupied inner shells, thus losing some amount of negative GOS, resulting in a larger effective number of electrons.50 In CeO2 the number of core electrons in the O K, Ce K, L, M shells is 32, while we find ≈23. Thus, the remaining electrons are relocated in the outer shells in order to fulfil the total f-sum rule. These missing electrons are located in the unassigned “baseline” Mermin functions (7 and 11), so they do not affect much the electron count in the other assigned contributions.
Despite some underestimation in the number of electrons in a few shells (e.g. of the 12 O2p and Ce4f, 5d and 6s electrons, only 8.08 electrons were found, see Table 4), the assignment of the levels is rather satisfactory for most of the transitions. The ∼4 electrons missing from the O2p and Ce6s, 5d, 4f bands (Mermin functions 1 to 4) are contained in the seventh not assigned Mermin function (see Table 4), which possibly may represent a large energy tail of these transitions. The fulfilment of the total f- and ps-sum rules is remarkable, with errors of −0.15% and +0.36%, respectively. Particularly, the effective number of electrons in our fitting corresponding to the Ce5p → 5d (dark green line in Fig. 6) and Ce5s, O2s → Ce5d transitions (red line) is very close to the expected number of electrons. This reveals an underestimation in the f-sum rule of the experimental ELFs20,21,80,81 in the range of 30–70 eV, which may reveal some degree of experimental uncertainty. The Mermin functions corresponding to the Ce4d → 5d (orange line) and Ce4s, 4p → 5d transitions (purple line) also deliver an effective number of electrons remarkably close to the expected ones.
Finally, to determine the inelastic scattering cross-sections within the dielectric approach,39,40,42 we need to assess the dependence of the ELF in both the energy and momentum space (the so-called Bethe surface). We report in Fig. S6 of the ESI† the energy and momentum dependent ELF of bulk CeO2 calculated according to eqn (4) and (5) in the range of 0–6 Å−1 along the [111] direction in the reciprocal-space for energies up to 120 eV. We notice that the agreement between MELF-GOS and TDDFT results is reasonable at low energy and finite momentum, while the peak at 120 eV shows a momentum dispersion that does not increase in energy (see Fig. S6 of the ESI†). We assessed the dependence on the direction of the momentum transfer of the ELF of bulk CeO2, finding a small difference between the [111], [110], and [211] orientations (see Fig. S7 of the ESI† showing this dependence). Therefore, we used the ELF in the [111] direction for the Monte Carlo simulations of the REEL spectrum.
3.3 The excitation spectrum of bulk Ce2O3
To identify the electronic transitions of bulk Ce2O3 we followed an approach similar to that of CeO2, based on the MELF-GOS fit. The first-principles real (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 1) and imaginary (
1) and imaginary (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2) parts of the macroscopic dielectric function, together with the resulting ELF in the [001] (solid lines) and the equivalent [110] and [100] directions (dashed lines) are shown in Fig. 6, taking the q → 0 limit. Although there is a small difference in the crystal direction, it will be seen that it is not as significant to affect the REEL Monte Carlo simulations.
2) parts of the macroscopic dielectric function, together with the resulting ELF in the [001] (solid lines) and the equivalent [110] and [100] directions (dashed lines) are shown in Fig. 6, taking the q → 0 limit. Although there is a small difference in the crystal direction, it will be seen that it is not as significant to affect the REEL Monte Carlo simulations.
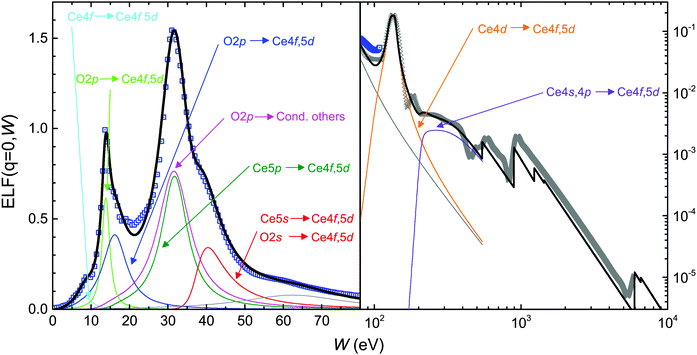
From the combined analysis of the PDOS (see Fig. 2) and of Fig. 6 we can argue that the first shoulder in ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2 around 5 eV corresponds to the Ce4f → Ce4f, 5d transition, with a gap of 2.04 eV. The next two peaks correspond to transitions from the O2p band to the narrow Ce4f band, and from the O2p band to the wider Ce5d band, with a threshold of 3.83 eV. The first peak above 13 eV corresponds to another O2p transition to the top of the conduction band, composed of a mixture of states, with an approximated threshold of 13.06 eV (notice the dip in the TDOS at this energy in Fig. 2). The other peaks above 13 eV can be attributed to transitions from the Ce5p band to the Ce4f, 5d band, with a threshold of 15.10 eV. The O2s → Ce4f, 5d transitions can be found at higher energies.
2 around 5 eV corresponds to the Ce4f → Ce4f, 5d transition, with a gap of 2.04 eV. The next two peaks correspond to transitions from the O2p band to the narrow Ce4f band, and from the O2p band to the wider Ce5d band, with a threshold of 3.83 eV. The first peak above 13 eV corresponds to another O2p transition to the top of the conduction band, composed of a mixture of states, with an approximated threshold of 13.06 eV (notice the dip in the TDOS at this energy in Fig. 2). The other peaks above 13 eV can be attributed to transitions from the Ce5p band to the Ce4f, 5d band, with a threshold of 15.10 eV. The O2s → Ce4f, 5d transitions can be found at higher energies.
The optical ELF of bulk Ce2O3 is fitted using the MELF-GOS model following the above assignments and band gaps, and we report its low (<70 eV) and high (up to 10 keV) energy structure in Fig. 7. As seen from Table 5, a number of 17.12 electrons are missing from the inner shells, which are relocated among the outer shells. The first Mermin function (cyan curve) represents the Ce4f (occupied) → Ce4f, 5d (empty) transition. The transitions from the O2p band (also containing the outermost Ce4f, 5d, 4s electrons) can be separated in three distinguishable contributions. The green line corresponds to the transition from the O2p levels to the narrow empty band of Ce4f character with a threshold of 3.83 eV, and possibly having a plasmon-like character, as suggested by the results in Fig. 6. The blue line represents the transition to the wider Ce5d band with a threshold of 3.83 eV, and finally the magenta line indicates the transition to the upper part of the conduction band with an approximate threshold of 13.06 eV. A test of the f-sum rule by integrating all the 1–4 Mermin functions delivers 20.68 electrons, comparable to the expected value of 20.
| Mermin | Transition | W th (eV) | N exp | N eff |
|---|---|---|---|---|
| a Threshold energies derived from the PDOS except otherwise stated. b The Mermin functions 1–4 describe the excitations of the outermost valence electrons, located in a band of mainly O2p origin, but which also contains the valence electrons Ce6s, 5d, and 4f, see Fig. 1. c From ref. 87. | ||||
| 1 | Ce4f → 4f, 5d | 2.04 | ||
| 2 | O2p → Ce4f, 5d | 3.83 | ||
| (plasmon-like) | ||||
| 3 | O2p → Ce4f, 5d | 3.83 | ||
| 4 | O2p → cond. (other) | 13.06 | ||
| 1–4 | O2p, Ce6s, Ce5d, Ce4fb | 20b | 20.68 | |
| 5 | Ce5p → 4f, 5d | 15.10 | 12 | 12.16 |
| (plasmon-like) | ||||
| 6 | Ce5s, O2s → Ce4f, 5d | 37.8c | 10 | 10.10 |
| 7 | Not assigned | 11.81 | ||
| 8–9 | Ce4d → 4f, 5d | 100.68c | 20 | 24.47 |
| 10 | Ce4s, 4p → 4f, 5d | 206.53c | 16 | 15.98 |
| GOS | Atomic shells | |||
| O K | O1s | 543.68c | 6 | 5.22 |
| Ce M | Ce3s, 3p, 3d | 883.80c | 36 | 28.47 |
| Ce L | Ce2s, 2p | 5723.00c | 16 | 9.06 |
| Ce K | Ce1s | 40443.00c | 4 | 2.13 |
| Total | 140 | 140.19 | ||
As in the case of CeO2, the Ce5s, O2s → Ce4f, 5d transition (red line) is located at higher energies with a threshold of 37.8 eV (from ref. 87). The f-sum rule test delivers 10.10 electrons of the 10 electrons expected. A seventh Mermin function (gray line) has not been assigned, and recovers a major part (11.81 of 17.12) of the electrons missing from the inner shells. Finally, we identify the transitions Ce4d → Ce5d lying above 10.6 eV (orange line, 24.47 electrons of the 20 expected, containing also some of the electrons missing from the inner shells) and Ce4s, 4p → Ce5d (purple line, 15.98 electrons of the 16 expected). We notice the satisfactory fulfillment of the total f-sum rule with an error of 0.14%, and of the ps-sum rule with an error of 0.70%.
The energy and momentum dependent ELF of bulk Ce2O3 along the [110] direction in reciprocal-space from 0 to 6 Å−1 is provided in the bottom panel of Fig. S6 of the ESI.† We also checked the dependence on the direction of the momentum transfer of the ELF of bulk Ce2O3, finding a difference between the [001], [110], and [100] orientations (depicted in Fig. S8 of the ESI†) without significant effects on the MC simulations of REEL spectra. Thus, we used the ELF structure in the specific direction [110] for the momentum transfer in MC simulations.
3.4 Electron transport in the cerium oxides
The description of the inelastic interactions of charged particles moving through bulk solids in terms of the DIIMFP (see eqn (12)) and IMFP (see eqn (13)) is one of the inputs to carry out charge transport MC simulations. We thus calculated the latter observables for bulk CeO2. We plot the IMFP in Fig. 8, alongside the experimental data obtained for CeO2 on Ni (circles) and Au (squares) substrates.88 While the agreement between calculations and experimental measurements is remarkable, we stress the crucial importance of including the semicore 4d → 5d transitions and deeper inner-shell excitations (those beyond 100 eV) in the assessment of the IMFP. Indeed, using only the ab initio data limited to 100 eV (the typical energy range affordable for TDDFT calculations) we notice a discrepancy up to 25% higher with respect to the experimental data (see the difference between the orange dot-dot-dashed and solid black curves around 120 eV in Fig. 8). | ||
| Fig. 8 Comparison of the ab initio IMFP of bulk CeO2 and Ce2O3 calculated in this work with TPP-2M formula predictions and experimental data for CeO2 obtained with respect to Ni and Au substrates.88 | ||
The IMFP of bulk Ce2O3 is also reported as a blue dot-dashed line in Fig. 8, showing no significant differences with that of CeO2. It should be noted that, despite the resemblance of the IMFP of both oxides, they present some differences (not shown here explicitly) in their DIIMFP, eqn (12), arising from their diverse electronic excitation spectra (see Fig. 5, 7 and Fig. S6, ESI†).
Typically, elastic scattering occurs between electrons and the massive ionic constituents of the target, and results only in the deflection of electron trajectories. While in principle relativistic first-principles quantum mechanical calculations based on the formal theory of scattering47,49 can be used to calculate the DESCS,66 the computational cost to include a large number of atoms required to carry out accurate relativistic simulations in a solid is prohibitive. Thus, we use the expression of the Mott's cross-section (see eqn (14) and (15)) within the cluster method, by which we carve out a portion of the material (which can be as small as one atom) and reckon the DESCS only dealing with a molecular cluster surrounded by empty space. This approximation, which can be made more accurate by increasing the cluster size until the DESCS ceases to vary, can be drastic at times but works in our case. However, the exclusion (inclusion) of multiple scattering effects in the calculation of the DESCS reckoned by using eqn (14) and (15) leads to negligible discrepancies. Thus, using eqn (14), we have calculated the DESCSs of CeO2 and Ce2O3 at different primary beam kinetic energies.
The REEL spectra of the materials under investigation have been computed by our MC approach, where the electron trajectories ensemble is set to reach statistical significance and low noise of the simulated data (≈109 trajectories). We remind that the REEL spectrum probes the dielectric response of materials in the longitudinal direction (along the momentum transfer), being a purely longitudinal field a condition of propagation of the plasmon. Furthermore, the microscopic components of the transverse induced field are negligible in the optical limit.
In Fig. 9 we report the REEL spectra of bulk CeO2 (red line) and Ce2O3 (blue line), and we also compare our simulations with the available experimental data,21 finding good agreement by reproducing all the main features of the experimental spectrum. These simulated REEL spectra have been obtained using the ELF of CeO2 and Ce2O3 along the [111] and [110] directions in the reciprocal space, respectively. However, we noticed a negligible dependence on the momentum transfer direction of the REEL spectra (see Fig. S7 and S8 of the ESI,† where we compare the calculated Bethe surfaces along different orientations of the momentum transfer). The REEL spectra are both normalized with respect to the area under the curves. We remind that surface effects, such as the presence of surface plasmons, are not included in our bulk simulations, while they may affect the measurements. This can explain e.g. the discrepancy of the brighter experimental peak intensity near the elastic peak with our simulations.
 | ||
| Fig. 9 Comparison between the REEL spectra of bulk CeO2 (red line) and Ce2O3 (blue line) simulated by MC compared with the directly measured spectrum (black line).21 Spectra are normalized with respect to the area under the curves. Zero-loss peak is found at the extreme right of the spectrum. The primary beam impinges the material with an incident angle equal to 60° with respect to the surface's normal. | ||
The overall satisfactory agreement with the experimental data makes us confident that both the simulated dispersion law with the momentum transfer and the MELF-GOS extension to very high energy are indeed accurate. We stress again the need for including the Ce4d transitions and LFE in the calculation of the dielectric response to achieve good accuracy of the REEL spectra. We notice that the experimental spectrum21 shows features reproduced in both our simulated REEL spectra of CeO2 and Ce2O3 bulk structures, thus experimental determinations seem more consistent with polycrystalline samples possibly mixing these two stable allotropic forms of cerium oxide.
The REEL spectra are characterised by a number of structured peaks, due to plasmon-like losses and single electron intraband and interband transitions. In particular, the REEL spectral lineshape of CeO2 in Fig. 9 (red line) shows three major structures below the elastic zero-energy loss peak of backscattered electrons (extreme right of the plot). According to our previous analysis of both the PDOS and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) 2, the first peak found at ≈3.7 eV from the elastic peak can be attributed to the interband transition from the O2p valence band to the localized Ce4f narrow band, the second peak around 15 eV to a plasmon-like excitation from O2p → Ce5d reflecting the PDOS of Ce5d conduction band, and finally, the third broader loss structure at 32.5 eV from the elastic peak can be attributed to the Ce5p → 5d interband transition.
2, the first peak found at ≈3.7 eV from the elastic peak can be attributed to the interband transition from the O2p valence band to the localized Ce4f narrow band, the second peak around 15 eV to a plasmon-like excitation from O2p → Ce5d reflecting the PDOS of Ce5d conduction band, and finally, the third broader loss structure at 32.5 eV from the elastic peak can be attributed to the Ce5p → 5d interband transition.
Analogously, the REEL spectrum of bulk Ce2O3 reflects the previous analysis of the peaks found in the PDOS and in the ELF, showing a lineshape with orbital characters similar to CeO2. Interestingly, the experimental REELS21 shows three structures (a first peak around 1595 eV, a shoulder around 1598–1590 eV, and a second peak at 1575 eV), which are revealed to distinctly correspond to CeO2 (red dashed line) and Ce2O3 (blue dotted line), respectively. Thus, the current approach demonstrates how first principles-based simulations may help in characterizing and identifying the features observed in experimental determinations. Finally, we notice that the REEL spectra are almost independent of the chosen direction of the momentum transfer.
4 Conclusions
In this work, we have computed the dielectric response functions of cerium oxides, which are materials with potential applications ranging from radiotherapy to catalysis industry, using linear response TDDFT on the top of ground state calculations based on DFT+U, adding the Hubbard correction to deal with the presence of 4f localized states. We found excellent agreement with most of the experimental determinations, showing in particular that an accurate assessment of the optical properties must include LFE.We also performed also assignment of the different features of the spectra in terms of interband transitions, which allowed checking the accuracy of the results further by means of sum rules. The information collected via numerical simulations based on first-principles was extended to higher energies by the MELF-GOS model to include core-level excitations. We stress that the inclusion of the interband transitions from the 4d levels of Ce and of the innermost Ce and O shells, as well as of the LFE into the dielectric response of these oxides is of paramount importance for calculating accurately the IMFP of electrons in their motion through the medium.
Furthermore, the ELF calculations of both bulk CeO2 and Ce2O3 have also been performed by considering the full energy-momentum dispersion at finite values of momentum transfer. The inelastic collision parameters, directly obtainable from the ELF, along with the elastic scattering ones, are essential ingredients to feed a MC routine and follow the trajectory of electrons within the solid. In this respect, we were able to reproduce (or predict) in remarkably good agreement with the available experimental data the major REEL spectral features of bulk CeO2 and Ce2O3.
Our work, based on a statistical MC method performed with high-accuracy ab initio inputs, paves the way towards a thorough understanding of the electron transport and optical properties of cerium oxides, which can drive appropriate design of materials, also in terms of nanoparticle shapes, with potential disruptive impact on enhancing the local radiation damage in cancer cure treatments and catalysis applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Bruno Kessler Foundation (FBK) for providing unlimited access to the KORE computing facility. A. P. acknowledges Fondazione Caritro and DICAM (University of Trento) for the financial support under the CARITRO project High-Z ceramic oxide nanosystems for mediated proton cancer therapy. A. P. also acknowledges fruitful discussion with the ELK code developers. This project has received funding from the European Union's Horizon 2020 Research and Innovation programme under the Marie Sklodowska-Curie grant agreement no. 840752 NanoEnHanCement of P. d. V., as well as from the Spanish Ministerio de Economía y Competitividad and the European Regional Development Fund (Project no. PGC2018-096788-B-I00), from the Fundación Séneca (Project no. 19907/GERM/15) and from the Conselleria d'Educació, Investigació, Cultura i Esport de la Generalitat Valenciana (Project no. AICO/2019/070).Notes and references
- C. Sun, R. Hui and J. Roller, J. Solid State Electrochem., 2010, 14, 1125–1144 CrossRef CAS.
- G. H. Gunasekar, J. Shin, K.-D. Jung, K. Park and S. Yoon, ACS Catal., 2018, 8, 4346–4353 CrossRef CAS.
- O. Matz and M. Calatayud, ACS Omega, 2018, 3, 16063–16073 CrossRef CAS PubMed.
- J. Tang, Z. Han, Y. Zuo and Y. Tang, Appl. Surf. Sci., 2011, 257, 2806–2812 CrossRef CAS.
- X. Feng, D. C. Sayle, Z. L. Wang, M. S. Paras, B. Santora, A. C. Sutorik, T. X. T. Sayle, Y. Yang, Y. Ding, X. Wang and Y.-S. Her, Science, 2006, 312, 1504–1508 CrossRef CAS.
- N. Özer, Sol. Energy Mater. Sol. Cells, 2001, 68, 391–400 CrossRef.
- J. Kašpar, P. Fornasiero and M. Graziani, Catal. Today, 1999, 50, 285–298 CrossRef.
- S. McKinnon, S. Guatelli, S. Incerti, V. Ivanchenko, K. Konstantinov, S. Corde, M. Lerch, M. Tehei and A. Rosenfeld, Phys. Med., 2016, 32, 1584–1593 CrossRef PubMed.
- A. Briggs, S. Corde, S. Oktaria, R. Brown, A. Rosenfeld, M. Lerch, K. Konstantinov and M. Tehei, Nanomedicine, 2013, 9, 1098–1105 CrossRef CAS PubMed.
- S. Jain, D. Hirst and J. O'Sullivan, Br. J. Radiol., 2012, 85, 101–113 CrossRef CAS PubMed.
- E. Porcel, S. Liehn, H. Remita, N. Usami, K. Kobayashi, Y. Furusawa, C. L. Sech and S. Lacombe, Nanotechnology, 2010, 21, 085103 CrossRef PubMed.
- L. Sancey, F. Lux, S. Kotb, S. Roux, S. Dufort, A. Bianchi, Y. Crémillieux, P. Fries, J.-L. Coll, C. Rodriguez-Lafrasse, M. Janier, M. Dutreix, M. Barberi-Heyob, F. Boschetti, F. Denat, C. Louis, E. Porcel, S. Lacombe, G. Le Duc, E. Deutsch, J.-L. Perfettini, A. Detappe, C. Verry, R. Berbeco, K. T. Butterworth, S. J. McMahon, K. M. Prise, P. Perriat and O. Tillement, Br. J. Radiol., 2014, 87, 20140134 CrossRef CAS.
- J. C. Polf, L. F. Bronk, W. H. P. Driessen, W. Arap, R. Pasqualini and M. Gillin, Appl. Phys. Lett., 2011, 98, 193702 CrossRef.
- J.-K. Kim, S.-J. Seo, H.-T. Kim, K.-H. Kim, M.-H. Chung, K.-R. Kim and S.-J. Ye, Phys. Med. Biol., 2012, 57, 8309–8323 CrossRef PubMed.
- Z. Kuncic and S. Lacombe, Phys. Med. Biol., 2018, 63, 02TR01 CrossRef.
- J. Schuemann, A. F. Bagley, R. Berbeco, K. Bromma, K. T. Butterworth, H. L. Byrne, B. D. Chithrani, S. H. Cho, J. R. Cook, V. Favaudon, Y. H. Gholami, E. Gargioni, J. F. Hainfeld, F. Hespeels, A.-C. Heuskin, U. M. Ibeh, Z. Kuncic, S. Kunjachan, S. Lacombe, S. Lucas, F. Lux, S. McMahon, D. Nevozhay, W. Ngwa, J. D. Payne, S. Penninckx, E. Porcel, K. M. Prise, H. Rabus, S. M. Ridwan, B. Rudek, L. Sanche, B. Singh, H. M. Smilowitz, K. V. Sokolov, S. Sridhar, Y. Stanishevskiy, W. Sung, O. Tillement, N. Virani, W. Yantasee and S. Krishnan, Phys. Med. Biol., 2020, 65, 21RM02 CrossRef CAS.
- I. Kempson, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2021, 13, e1656 Search PubMed.
- B. W. Swartz, PhD thesis, Doctoral dissertation, East Carolina University, 2015.
- M. El Khalifi, F. Picaud and M. Bizi, Anal. Methods, 2016, 8, 5045–5052 RSC.
- F. Goubin, X. Rocquefelte, M.-H. Whangbo, Y. Montardi, R. Brec and S. Jobic, Chem. Mater., 2004, 16, 662–669 CrossRef CAS.
- N. Pauly, F. Yubero, J. P. Espinós and S. Tougaard, Appl. Opt., 2017, 56, 6611 CrossRef CAS PubMed.
- N. V. Skorodumova, R. Ahuja, S. I. Simak, I. A. Abrikosov, B. Johansson and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115108 CrossRef.
- P. J. Hay, R. L. Martin, J. Uddin and G. E. Scuseria, J. Chem. Phys., 2006, 125, 034712 CrossRef PubMed.
- S. Fabris, S. de Gironcoli, S. Baroni, G. Vicario and G. Balducci, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 041102 CrossRef.
- J. Graciani, A. M. Márquez, J. J. Plata, Y. Ortega, N. C. Hernández, A. Meyer, C. M. Zicovich-Wilson and J. F. Sanz, J. Chem. Theory Comput., 2011, 7, 56–65 CrossRef CAS.
- L. Brugnoli, A. M. Ferrari, B. Civalleri, A. Pedone and M. C. Menziani, J. Chem. Theory Comput., 2018, 14, 4914–4927 CrossRef CAS PubMed.
- F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys., 1998, 61, 237–312 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- H. Jiang, R. I. Gomez-Abal, P. Rinke and M. Scheffler, Phys. Rev. Lett., 2009, 102, 126403 CrossRef PubMed.
- H. Jiang, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125115 CrossRef.
- P. Umari, O. Petrenko, S. Taioli and M. M. De Souza, J. Chem. Phys., 2012, 136, 181101 CrossRef CAS PubMed.
- S. Taioli, P. Umari and M. De Souza, Phys. Status Solidi B, 2009, 246, 2572–2576 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- J. A. Aguiar, Q. M. Ramasse, M. Asta and N. D. Browning, J. Phys.: Condens. Matter, 2012, 24, 295503 CrossRef CAS.
- D. Tian, C. Zeng, Y. Fu, H. Wang, H. Luo, C. Xiang, Y. Wei, K. Li and X. Zhu, Solid State Commun., 2016, 231–232, 68–79 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- S. Botti, A. Schindlmayr, R. D. Sole and L. Reining, Rep. Prog. Phys., 2007, 70, 357–407 CrossRef.
- J. Lindhard, Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddelelser, 1954, 28(8), 1–57 Search PubMed.
- R. H. Ritchie, Phys. Rev., 1959, 114, 644–654 CrossRef.
- R. H. Ritchie, Phys. Rev., 1957, 106, 874–881 CrossRef CAS.
- N. F. Mott, Proc. R. Soc. London, Ser. A, 1929, 124, 425–442 CAS.
- M. Dapor, Transport of Energetic Electrons in Solids. Computer Simulation with Applications to Materials Analysis and Characterization, Springer Nature Switzerland AG, 3rd edn, 2020 Search PubMed.
- M. Azzolini, O. Y. Ridzel, P. S. Kaplya, V. Afanasev, N. M. Pugno, S. Taioli and M. Dapor, Comput. Mater. Sci., 2020, 173, 109420 CrossRef.
- M. Azzolini, M. Angelucci, R. Cimino, R. Larciprete, N. M. Pugno, S. Taioli and M. Dapor, J. Phys.: Condens. Matter, 2018, 31, 055901 CrossRef PubMed.
- M. Azzolini, T. Morresi, K. Abrams, R. Masters, N. Stehling, C. Rodenburg, N. M. Pugno, S. Taioli and M. Dapor, J. Phys. Chem. C, 2018, 122, 10159–10166 CrossRef CAS.
- M. Azzolini, T. Morresi, G. Garberoglio, L. Calliari, N. M. Pugno, S. Taioli and M. Dapor, Carbon, 2017, 118, 299–309 CrossRef CAS.
- S. Taioli and S. Simonucci, Annu. Rep. Comput. Chem., 2015, 11, 191–310 Search PubMed.
- S. Taioli, S. Simonucci, L. Calliari, M. Filippi and M. Dapor, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085432 CrossRef.
- S. Taioli, S. Simonucci, L. Calliari and M. Dapor, Phys. Rep., 2010, 493, 237–319 CrossRef CAS.
- R. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, Springer, Boston, MA, 1996 Search PubMed.
- I. Abril, R. Garcia-Molina, C. D. Denton, F. J. Pérez-Pérez and N. R. Arista, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 357–366 CrossRef CAS.
- S. Heredia-Avalos, R. Garcia-Molina, J. M. Fernández-Varea and I. Abril, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 052902 CrossRef.
- R. Garcia-Molina, I. Abril, I. Kyriakou and D. Emfietzoglou, Energy Loss of Swift Protons in Liquid Water: Role of Optical Data Input and Extension Algorithms, in Radiation Damage in Biomolecular Systems, ed. G. Gómez-García Tejedor and M. C. Fuss, Springer Netherlands, Dordrecht, 2012, pp. 239–261 Search PubMed.
- R. Garcia-Molina, I. Abril, I. Kyriakou and D. Emfietzoglou, Surf. Interface Anal., 2017, 49, 11–17 CrossRef CAS.
- http://elk.sourceforge.net/ .
- L. Gerward, J. Staun Olsen, L. Petit, G. Vaitheeswaran, V. Kanchana and A. Svane, J. Alloys Compd., 2005, 400, 56–61 CrossRef CAS.
- H. Bärnighausen and G. Schiller, J. Less-Common Met., 1985, 110, 385–390 CrossRef.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- A. A. Shukri, F. Bruneval and L. Reining, Phys. Rev. B, 2016, 93, 035128 CrossRef.
- H.-C. Weissker, J. Serrano, S. Huotari, E. Luppi, M. Cazzaniga, F. Bruneval, F. Sottile, G. Monaco, V. Olevano and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085104 CrossRef.
- A. Seidu, A. Marini and M. Gatti, Phys. Rev. B, 2018, 97, 125144 CrossRef CAS.
- O. A. Paredes-Mellone, J. Koskelo, S. A. Ceppi and G. E. Stutz, Phys. Status Solidi B, 2020, 257, 1900780 CrossRef CAS.
- S. L. Adler, Phys. Rev., 1962, 126, 413–420 CrossRef.
- N. Wiser, Phys. Rev., 1963, 129, 62–69 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef PubMed.
- S. Taioli, P. E. Trevisanutto, P. de Vera, S. Simonucci, I. Abril, R. Garcia-Molina and M. Dapor, J. Phys. Chem. Lett., 2020, 12, 487–493 CrossRef PubMed.
- N. D. Mermin, Phys. Rev. B: Solid State, 1970, 1, 2362–2363 CrossRef.
- P. de Vera and R. Garcia-Molina, J. Phys. Chem. C, 2019, 123, 2075–2083 CrossRef CAS.
- D. Liljequist and H. Nikjoo, Radiat. Phys. Chem., 2014, 99, 45–52 CrossRef CAS.
- J. M. Fernandez-Varea, R. Mayol, D. Liljequist and F. Salvat, J. Phys.: Condens. Matter, 1993, 5, 3593–3610 CrossRef CAS.
- P. de Vera, I. Abril and R. Garcia-Molina, Phys. Chem. Chem. Phys., 2021, 23, 5079–5095 RSC.
- A. Jablonski, F. Salvat and C. J. Powell, J. Phys. Chem. Ref. Data, 2004, 33, 409–451 CrossRef CAS.
- J. B. Furness and I. E. McCarthy, J. Phys. B: At. Mol. Phys., 1973, 6, L204–L207 CrossRef CAS.
- Y. Jiang, J. B. Adams and M. van Schilfgaarde, J. Chem. Phys., 2005, 123, 064701 CrossRef PubMed.
- Z. Yang, T. K. Woo, M. Baudin and K. Hermansson, J. Chem. Phys., 2004, 120, 7741–7749 CrossRef CAS.
- E. Wuilloud, B. Delley, W. D. Schneider and Y. Baer, Phys. Rev. Lett., 1984, 53, 202–205 CrossRef CAS.
- S. Guo, H. Arwin, S. N. Jacobsen, K. Järrendahl and U. Helmersson, J. Appl. Phys., 1995, 77, 5369–5376 CrossRef CAS.
- A. Pfau and K. Schierbaum, Surf. Sci., 1994, 321, 71–80 CrossRef CAS.
- J.-F. Jerratsch, X. Shao, N. Nilius, H.-J. Freund, C. Popa, M. V. Ganduglia-Pirovano, A. M. Burow and J. Sauer, Phys. Rev. Lett., 2011, 106, 246801 CrossRef PubMed.
- F. Marabelli and P. Wachter, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 1238–1243 CrossRef CAS.
- M. Niwano, S. Sato, T. Koide, T. Shidara, A. Fujimori, H. Fukutani, S. Shin and M. Ishigame, J. Phys. Soc. Jpn., 1988, 57, 1489–1496 CrossRef CAS.
- G. Strasser, G. Rosina, E. Bertel and P. Netzer, Surf. Sci., 1985, 152–153, 765–775 CrossRef CAS.
- J. Pflüger, J. Fink, W. Weber, K. P. Bohnen and G. Crecelius, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1155–1163 CrossRef.
- D. Y. Smith and E. Shiles, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 4689–4694 CrossRef CAS.
- B. Henke, E. Gullikson and J. Davis, At. Data Nucl. Data Tables, 1993, 54, 181–342 CrossRef CAS.
- J. Bloch, N. Shamir, M. H. Mintz and U. Atzmony, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 2462–2469 CrossRef CAS.
- G. Williams, X-ray properties of the elements, ed. A. C. Thompson, X-Ray Data Booklet, Lawrence Berkeley National Laboratory, University of California, Berkley, California, 2009, https://xdb.lbl.gov/ Search PubMed.
- M. Krawczyk, M. Holdynski, W. Lisowski, J. Sobczak and A. Jablonski, Appl. Surf. Sci., 2015, 341, 196–202 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Several figures cited in the text, including the band structure, ELF, and optical properties of cerium oxides, convergence tests, etc. See DOI: 10.1039/d1cp01810h |
| This journal is © the Owner Societies 2021 |