Molecular properties affecting the hydration of acid–base clusters

Abstract

In the atmosphere, water in all phases is ubiquitous and plays important roles in catalyzing atmospheric chemical reactions, participating in cluster formation and affecting the composition of aerosol particles. Direct measurements of water-containing clusters are limited because water is likely to evaporate before detection, and therefore, theoretical tools are needed to study hydration in the atmosphere. We have studied thermodynamics and population dynamics of the hydration of different atmospherically relevant base monomers as well as sulfuric acid–base pairs. The hydration ability of a base seems to follow in the order of gas-phase base strength whereas hydration ability of acid–base pairs, and thus clusters, is related to the number of hydrogen binding sites. Proton transfer reactions at water–air interfaces are important in many environmental and biological systems, but a deeper understanding of their mechanisms remain elusive. By studying thermodynamics of proton transfer reactions in clusters containing up to 20 water molecules and a base molecule, we found that that the ability of a base to accept a proton in a water cluster is related to the aqueous-phase basicity. We also studied the second deprotonation reaction of a sulfuric acid in hydrated acid–base clusters and found that sulfate formation is most favorable in the presence of dimethylamine. Molecular properties related to the proton transfer ability in water clusters are discussed.

---

1 Introduction

Atmospheric aerosol particles influence human health and global climate. Airborne particles act as condensation nuclei for clouds and can also directly absorb or scatter incoming radiation, forming a significant but highly uncertain effect on Earth's radiation balance.¹ New-particle formation (NPF) from atmospheric vapors is a significant source of ultrafine particles, but the participating vapors as well as the molecular-level mechanisms are not fully resolved.^2,3 In the present-day atmosphere that contains high levels of sulfur, sulfuric acid is a key precursor vapor and has been shown to be linked to NPF events in various environments. However, sulfuric acid-driven NPF requires additional stabilizing compounds in order to yield particle formation rates similar to those observed in the atmosphere.⁴ These compounds include atmospheric bases, organic compounds and ions.^5–7 In addition, water can act a stabilizer but, due to its weak binding ability, it cannot be a main driver of NPF. In the upper troposphere, pure sulfuric acid–water clustering may occur as the low temperature stabilizes clusters and other compounds are scarce.⁸ Water can also participate in particle growth, but it is unlikely to be a major contributor due to its relatively high saturation vapor pressure and small molecular volume.⁹

Because water evaporates rapidly from ions under the high-vacuum conditions in mass spectrometers, its connection to cluster formation is difficult to observe directly.^10,11 The ability of sulfuric acid–base clusters to absorb water is believed to be dependent on either the basicity of the base compound or the number of available hydrogen binding sites in the cluster.^12–15 Yang et al. have used tandem mass spectrometry coupled to a temperature-controlled ion trap to study water uptake of positively charged sulfuric acid–base clusters.¹⁶ They synthesized the hydrated clusters by mass-selecting dry clusters and storing them in an ion trap held at 180 K with a small partial pressure of water vapor. Based on the vibrational spectra, they showed that the binding of water molecules is most favorable for clusters containing base compounds with more NH groups. Thus the hydration ability of a cluster correlates much stronger with the number of hydrogen bond donors than the strength of the base.¹⁷ With similar methods, Kreinbihl et al. showed that hydration of ammonium bisulfate clusters has complex temperature dependence and that water can also insert into a bisulfate-bisulfate hydrogen bond.¹⁸ Also in negative ion photoelectron spectroscopy studies of bisulfate-oxidized organic compound complex, it has been found that the hydrated cluster stability is directly connected to the total number of the hydrogen bonds formed.^19,20

Several studies have used ion mobility spectrometry to probe water uptake by sulfuric acid–dimethylamine (SA–DMA) nanoclusters. Ouyang et al. produced SA–DMA clusters using electrospray ionization (ESI) and investigated their water uptake through a coupled differential mobility analyzer-atmospheric pressure drift tube ion mobility spectrometer (DT-IMS).²¹ They observed that as relative humidity (RH) increased, the electrical mobility of the nanoclusters decreased, indicating water uptake by the clusters. Based on thermal stability measurements, hydrated clusters are stabilized under ambient conditions by the presence of water molecules. Similar work by Thomas et al. using the same differential mobility analyzer-DT-IMS technique to study charged SA–DMA clusters showed modest water uptake by both positive and negative polarities.²² For the RH range studied (3–30%), they estimated that typically fewer than 10, and possibly fewer than 5, water molecules adsorbed to the nanocluster surface.

Water uptake by larger sulfuric acid–base particles has also been studied. Using a hygroscopicity tandem differential mobility analyzer (HTDMA), Hu et al. investigated the hygroscopic growth of several alkylaminium sulfate salts.²³ Unlike ammonium sulfate, ethylammonium, diethylammonium, and triethylammonium sulfate particles do not show deliquescence but instead exhibit a monotonic diameter increase with relative humidity. Notably, all particle sizes studied (diameters 40, 100, and 150 nm) for all salts showed increased hygroscopic growth compared to ammonium sulfate, and the hygroscopicity of the particles was not affected by the number of ethyl groups. Ambient measurements suggest that ammonium sulfate is the major form of sulfate in atmospheric particles, but reactions of gaseous amines on particle surfaces can lead to displacement of ammonia. Calculations of hygroscopic growth of triethylammonium sulfate–ammonium sulfate mixed particles using the Zdanovskii–Stokes–Robinson (ZSR) mixing rule suggest that growth occurs at low RH and is monotonic like triethylammonium sulfate. These results indicate that the displacement of ammonia by amines in atmospheric particles will greatly enhance their hygroscopicity.

Here we investigate the molecular properties that impact the hydration ability of a base molecule or an acid–base heterodimer. Using a relatively large number of water molecules in a cluster (up to 20), we have studied the protonation of a base molecule as well as sulfate formation in a water cluster. We have estimated how different stable acid–base particles hydrate in atmospheric conditions. To gain insights into how varying molecular properties affect to the role of water, we have studied sulfuric acid together with ammonia, dimethylamine, guanidine and trimethylamine oxide, which cover a wide range of structural properties (e.g. number of available hydrogen-bonds, volatilities, dipole moments, gas-phase basicities, and aqueous-phase basicities).^24–27

2 Computational details

We studied heterodimers of sulfuric acid (SA) with ammonia (AMM), dimethylamine (DMA), guanidine (GUA) and trimethylamine oxide (TMAO), where heterodimers were hydrated with 0–20 water molecules. Monomer hydration was also studied. To find the global minimum energy cluster structures, we explored the potential energy surface of all the acid–base–water clusters using a systematic configurational sampling technique.²⁸ To create the initial cluster structures, we used 3000 random guesses and 100 exploration loops, with a scout limit of 4 in the ABCluster program,^29,30 and for each building block combination we saved 2000 of the lowest energy structures that were subsequently optimized by the tight-binding method GFN2-xTB with a very tight optimization criteria.³¹ Based on the electronic energies, radius of gyration, and dipole moments, we separated different conformers, which were then optimized using the ωB97X-D/6-31+G* level of theory.^32,33 Based on the obtained electronic energies, we selected structures with a maximum of N kcal mol⁻¹ from the lowest electronic energy (where N is the number of molecules in the cluster). For remaining structures, the ωB97X-D/6-31++G** level of theory was used for final optimization and vibrational frequency calculation using Gaussian 16 RevA.03.^34,35 We selected 2–5 of the lowest Gibbs free energy structures, for which we performed single point energy calculations using the highly accurate DLPNO-CCSD(T)/aug-cc-pVTZ level of theory with tight pair natural orbital criteria, tight self consistent field criteria, and integration grid 4 as implemented in Orca version 4.2.1.^36–41 For each clusters we identified the global minimum Gibbs free energy structure at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G** level.⁴² Calculated thermochemical data are further used to study population dynamics of water clusters by Atmospheric Cluster Dynamics Code (ACDC).⁴³ Enthalpies and entropies for the minimum energy clusters are available in the ESI.† The ACDC code is available from the authors upon request.

3 Results and discussion

3.1 Hydration of monomers

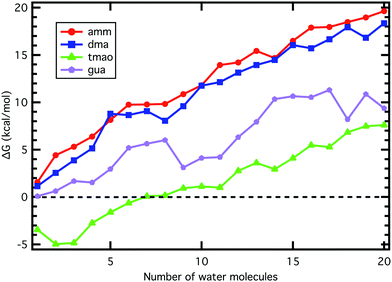
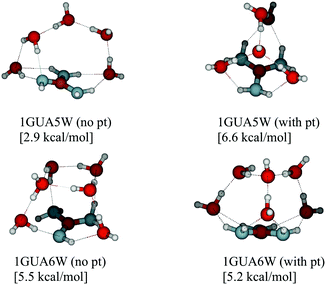
Acid and base molecules may exist in the atmosphere as isolated monomers or they may be clustered with water molecules. The hydration ability is dependent on the molecular properties of a monomeric compound as well as the environment (RH and T). Possible monomeric properties affecting hydration ability can be studied by calculating thermochemistry of clusters and the environmental effects can be accounted by cluster dynamics simulations.

3.1.1 Thermodynamics of monomer hydration. Fig. 1 shows the Gibbs free binding energies of a base monomer with 1–20 water molecules at 298 K. The first addition of a water molecule to monomeric AMM, DMA and GUA is slightly endergonic, with Gibbs free reaction energy of 1.6, 1.1 and 0.1 kcal mol⁻¹ respectively, whereas the interaction between water and TMAO is thermodynamically favorable by −3.5 kcal mol⁻¹. The favorable interaction between TMAO and water is due the zwitterionic structure of TMAO, which allows the polar water molecule to stabilize the partial charges of TMAO by forming hydrogen bonds. Also the addition of a second water to TMAO is favorable by −1.5 kcal mol⁻¹, but the third addition is slightly unfavorable by 0.1 kcal mol⁻¹. The hydration ability of monomers follows an order of TMAO > GUA > DMA ≥ AMM, which is the same as the order of gas phase basicities.

Fig. 1 Gibbs free binding energies of hydrated base monomers up to 20 water molecules at 298 K.

The majority of water addition reactions to any of the base monomers are endergonic, as shown by the increased ΔG value as a function of water molecule number in Fig. 1. There are a few exceptions where the addition free energy is favorable, for instance, the formation of 1GUA9W and 1GUA18W clusters. This can be either a result of an additional stabilization effect in cluster structure such as increased number of hydrogen bonds (see Fig. 2) or an artifact caused by locating a wrong global minimum structure.

Fig. 2 Molecular structures of 1GUA8W and 1GUA9W. 1GUA9W is more stable than 1GUA8W because it is able to form a multiple ring structures, which results from a large number of hydrogen bonds and cluster symmetry.

3.1.2 Proton transfer in water clusters. Proton transfer reactions taking place in water interfaces rather than in bulk liquid are participating in many important phenomena such as acidification of the ocean, energy transduction across biomembranes, and aerosol chemistry.^44–47 However, the interfacial proton transferring mechanisms are not completely understood.^48,49 Base molecules have an ability to accept a proton from water and form protonated base cation (BH⁺) and hydroxide anion in water clusters. We studied whether the proton transfer reaction is thermodynamically favorable in clusters containing 1–20 water molecules. For AMM, DMA, and TMAO, we were able to locate the structures containing BH⁺ starting from clusters containing 9, 3, and 2 water molecules, respectively. However, even 20 water molecules was not enough to make the proton transfer reaction favorable. In the case of GUA the proton transfer reaction is favorable for clusters having six or more water molecules (see Fig. 3).

Fig. 3 Molecular structures of 1GUA5W and 1GUA6W with and without proton transfer reaction with their Gibbs free binding energies at 298 K. For 1GUA6W the global minimum structure is the one with proton transfer whereas for 1GUA5W that structure is a local minimum.

Our results indicate that the ability of a base to accept a proton in a small water cluster has a stronger connection to the aqueous phase than gas-phase basicity as GUA is the strongest base in aqueous phase but TMAO is the strongest one in gas phase. However, the total hydration ability is likely to be connected to the gas-phase base strength.

3.1.3 Hydration distribution of monomers. In order to study whether hydration occurs under atmospherically relevant conditions, we have simulated the hydration distributions using Atmospheric Cluster Dynamics Code.⁴³Fig. 4 shows that at 273 K when relative humidity is 100%, AMM, DMA, and GUA mainly exist as dry monomers and the concentrations of hydrated monomers are at least two orders of magnitude lower than the dry monomer. In the case of TMAO, the 1TMAO1W and 1TMAO2W complexes have higher steady-state concentrations compared to the dry monomer. Water molecules are capable of stabilizing the zwitterionic bond in TMAO's structure, and therefore, TMAO is more likely to be found from water complexes in the atmosphere rather than as an isolated dry monomer.

Fig. 4 Hydration distributions of ammonia, dimethylamine, trimethylamine oxide, and guanidine monomers at 273 K at [base] = 10⁷ cm⁻³ and RH = 100%.

3.2 Water and self stabilization

Ions can have a remarkable role in stabilizing atmospheric particle formation but, unlike neutral compounds, they are unlikely to exist as isolated monomers in the gas phase. Here we have investigated whether a water cluster or a homomolecular base cluster offers a better stabilizing environment for a protonated base. This has been done by studying the strength of cation–base and cation–water interactions, and comparing the ability of a surrounding base or water cluster to stabilize the protonated base. Additionally, we have compared the interactions between a neutral base with a surrounding base cluster or a water cluster and discussed properties related those results.

3.2.1 Interaction strength. As Table 1 shows, the protonated base BH⁺ is more stabilized in the base environment BH⁺B_n than in water environment BH⁺W_n, when n is 2–6. The reason is likely to be related to the higher polarizabilities of base compounds compared to water, which allows them to distribute the charge of proton for a wider area. The difference between the stabilizing effect of a base and water environment is most significant for TMAO for which Gibbs free binding energies for 1TMAOH⁺nTMAO are from 26.4 to 47.6 kcal mol⁻¹ more negative than for 1TMAOH⁺nW. For GUA, the self-stabilization of the protonated base compared to water is 11.5–28.1 kcal mol⁻¹ larger. For protonated AMM and DMA, the larger stabilization base environment decreases compared to water environment and in the case of DMA, the 1DMAH⁺6W cluster is thermodynamically slightly more stable than 1DMAH⁺6DMA. This is because the interactions between DMA molecules (or AMM molecules) are weaker than between water molecules, and when the number of those interactions increases when n increases, they impact the stability more than the strength of direct interactions between protonated base and base or water. It should be noted that even though protonated TMAO and GUA are thermodynamically more stable in a base environment, the abundance of water vapor in the atmosphere is many orders of magnitude higher than that of bases, which ultimately affects to the concentrations of cationic clusters.

Table 1 Calculated Gibbs free binding energies (kcal mol⁻¹) at 298 K for 2–6-components neutral and protonated clusters containing only base molecules (left) or one base and 1–5 water molecules (right)

n	Base environment		Water environment
	AMM	AMM(+)	AMM	AMM(+)
2	3.7	−19.1	1.6	−13.4
3	8.0	−31.8	4.4	−22.7
4	11.9	−38.1	5.3	−27.7
5	16.2	−41.2	6.4	−32.5
6	21.1	−40.3	8.1	−33.5

---

n	Base environment		Water environment
	DMA	DMA(+)	DMA	DMA(+)
2	3.9	−15.7	1.1	−9.5
3	5.5	−24.6	2.5	−16.2
4	5.8	−23.0	3.9	−18.1
5	12.8	−21.5	5.1	−20.5
6	16.9	−18.5	8.8	−22.0

---

n	Base environment		Water environment
	TMAO	TMAO(+)	TMAO	TMAO(+)
2	−3.6	−33.9	−3.5	−7.5
3	−4.1	−46.4	−5.0	−10.5
4	−6.1	−46.1	−4.8	−13.5
5	−7.1	−53.6	−2.7	−14.0
6	−16.2	−60.4	−1.6	−12.8

---

n	Base environment		Water environment
	GUA	GUA(+)	GUA	GUA(+)
2	−2.2	−19.5	0.1	−8.0
3	−3.1	−31.9	0.6	−12.8
4	−10.5	−39.2	1.7	−16.6
5	−10.9	−46.8	1.5	−18.7
6	−13.2	−48.4	2.9	−20.6

---

The comparison of base–base and base–water interactions in Table 1 shows that neutral AMM and DMA interact stronger with water than themselves. For ammonia the AMM–W interaction is 2.1 kcal mol⁻¹ more favorable than AMM–AMM and for dimethylamine the interaction with water is 2.8 kcal mol⁻¹ more favorable than with itself. TMAO and GUA interact stronger with themselves than with water, with Gibbs free energy difference of 0.1 and 2.3 kcal mol⁻¹ in 2-component clusters, respectively. The difference in base–base and base–water interaction strengths might be related to the fact that AMM and DMA have smaller dipole moments than water, whereas TMAO and GUA have larger dipole moments, making them capable of forming stronger dipole–dipole interactions with themselves than with water.

Base–base interactions are thermodynamically unfavorable for ammonia and dimethylamine, meaning that the Gibbs free binding energies are increasingly positive for nAMM (from 3.7 to 21.1 kcal mol⁻¹) and nDMA clusters (from 3.9 to 16.9 kcal mol⁻¹), when the number of base molecules n increases from 2 to 6 (see Table 1). For trimethylamine oxide and guanidine, the Gibbs free binding energy is increasingly negative for nTMAO (from −3.6 to −16.2 kcal mol⁻¹) and nGUA (from −2.2 to −13.2 kcal mol⁻¹) clusters, when the number of base molecules n increases from 2 to 6, meaning that the intermolecular interactions between base molecules are favorable. It should be noted that even though the Gibbs free energies for the formation of TMAO or GUA homoclusters are slightly negative, it does not mean that they would have meaningful concentrations under atmospheric conditions. Favorable interactions in TMAO and GUA homoclusters might be correlated with their low vapor pressures and high dipole moments, whereas positive free energies of AMM and DMA homoclusters could be related their high volatility and low dipole moments. Water–water interactions are stronger than those for AMM or DMA but weaker than those for TMAO or GUA, and water is moderately volatile with a medium dipole moment.

3.3 Cluster hydration

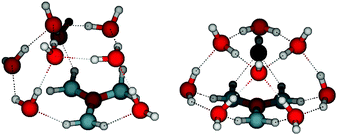
The hydration ability of clusters has shown to be related to the number of available hydrogen binding sites. As can be seen in Fig. 5, if a base molecule can form at least two hydrogen bonds, a water molecule can bridge the acid and base molecules while the acid and base still have one direct interaction. In the case of TMAO, which can form only one hydrogen bond, water is hydrogen bonded just with SA, and the direct SA–TMAO interaction remains.

Fig. 5 Heterodimers of sulfuric acid with ammonia, dimethylamine, guanidine and trimethylamine oxide (top, left to right) and hydrated structures of sulfuric acid with ammonia, dimethylamine, guanidine and trimethylamine oxide complexes (bottom, left to right).

3.3.1 Thermodynamics of cluster hydration. Fig. 6 shows the Gibbs free binding energies of sulfuric acid–base heterodimers with 1–20 water molecules at 298 K. From non-hydrated acid–base pairs, the SA–TMAO complex is thermodynamically the most stable with ΔG of −21.8 kcal mol⁻¹ and the SA–GUA complex is next with a ΔG value of −20.4 kcal mol⁻¹. The SA–DMA complex has moderate stability with a ΔG of −13.2 kcal mol⁻¹ and SA–AMM is the least stable with a ΔG of −6.4 kcal mol⁻¹. When hydration occurs, the Gibbs free binding energy of hydrated SA–GUA complexes becomes 5 kcal mol⁻¹ lower than that of hydrated SA–TMAO complexes. Also the difference between the stabilities of hydrated SA–DMA and SA–AMM complexes is significantly lower than that of dry complexes. This indicates that clusters containing GUA and AMM are more likely to be hydrated than clusters containing TMAO or DMA.

Fig. 6 Hydration free energies of sulfuric acid–base complexes at 298 K.

The more favorable reaction energies of an addition of a water molecule to the SA–GUA and SA–AMM clusters compared to SA–TMAO or SA–DMA clusters can be assumed to be related to the availability of hydrogen binding sites. For instance, in acid–base clusters having six water molecules, we found that there are 25 hydrogen bonds in SA–GUA and 23 in SA–AMM clusters whereas SA–DMA has 21 and SA–TMAO 20 hydrogen bonds. In clusters containing 12 water molecules, there are 25, 23, 21 and 20 hydrogen bonds in SA clusters with GUA, AMM, DMA and TMAO, respectively. For H-bond definition we have used default settings in Molden, i.e., H-bond length can be from 1.50 to 3.15 Å and H-bond angle can be from 145 to 215°. It should be noted that the same H-bond parameters for different systems might not an appropriate choice in some cases, but rather they should be separately defined for each system.⁵⁰ Thus, we additionally viewed the structures to make sure that the results make sense chemically. Global minimum structures of acid–base clusters with 6 and 12 water molecules are shown in Fig. 7.

Fig. 7 Molecular structures of SA clusters with AMM, DMA, TMAO and GUA, respectively, with 6 (top) and 12 (bottom) water molecules.

While it is thought that water can participate in aerosol particle formation, particle formation rates from acid–base chemistry have been shown to have a minimal dependence on relative humidity.^51,52 Olenius et al. showed that hydration has maximum of an order of magnitude effect on the particle formation rates of sulfuric acid with ammonia or methylamine and negligible effect in the case of dimethylamine or trimethylamine.¹⁴ As the particle formation of SA with GUA or TMAO is at the kinetic limit, hydration cannot increase the particle formation rates notably. However it is also possible that particle formation under high relative humidity is suppressed and that option cannot be excluded in this study but further studies are needed.

3.3.2 Sulfate formation in water clusters. It is known that the isolated sulfate SO₄²⁻ dianion is unstable and three water molecules are required for its stabilization,⁵³ and 12 water molecules is needed to form the first solvation shell.^54,55 Here the second deprotonation of a sulfuric acid molecule in hydrated acid–base clusters has been investigated. In the case of DMA, sulfate formation seems to be thermodynamically favored when the cluster has at least 13 water molecules. In SA–GUA clusters, the second protonation becomes favorable when the number of water molecules is 15 and in SA–AMM and SA–TMAO clusters when the number of water molecules is 16. Interestingly DMA makes the sulfate formation reaction occur with the lowest number of water molecules. As the free energy differences between minimum energy clusters containing bisulfate or sulfate are in many cases less than 1 kcal mol⁻¹, and the potential energy surface of a large cluster is very complicated, meaning that there might be lower energy configurations, it is possible that this observation is just a computational artefact. However, the OH group of bisulfate interacts with water molecules in small SA–DMA clusters, which is required for a second proton transfer to occur, whereas that is not a case in AMM, TMAO or GUA containing clusters (see Fig. 8).

Fig. 8 Molecular structures of SA clusters with AMM, DMA, TMAO and GUA, respectively, with 4 water molecules. Notable is the interaction between water and OH group of a bisulfate in DMA cluster.

Fig. 9 shows the molecular structures of acid–base pairs in a cluster with 20 water molecules, where the second proton transfer reaction from bisulfate to water has occurred and SO₄²⁻ has formed. Sulfate is one of the most kosmotropic Hofmeister ions, having an order-making effect on water structure.^56–58 Indeed it can be seen that in all cluster structures, SO₄²⁻ locates on the center of the cluster, maximising the number of hydrogen bonds. Similar results have found experimentally in photoelectron studies by Wang et al.⁵⁹ It is notable that there is no direct interaction between the sulfate and the protonated base in a hydrated cluster structure, but one or more water molecules bridge them. Also, the protonated base cation seems to prefer to be located on the surface of a cluster. These kinds of structural effects are likely to stabilize the hydrated cluster in which the proton transfer reactions have occurred.

Fig. 9 Molecular structures of SA clusters with AMM, DMA, TMAO and GUA, respectively, with 20 water molecules, where SO₄²⁻ ion has been formed.

3.4 Estimation of a stable particle hydration

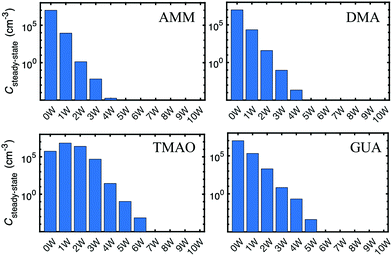
We have simulated population dynamics of acid–base particle hydration, with an assumption that acid–base system does not evaporate. This was done to estimate abilities of “stable particles” to hydrate. Hydration free energies of non-evaporating acid–base clusters are given in Fig. 10.

Fig. 10 Hydration free energies of “stable particles” containing sulfuric acid and base at 298 K.

We have simulated the hydration distributions of stable acid–base particles with conditions where the total particle concentration is 10⁵ cm⁻³, temperature is 273 K, and relative humidity is 100%. Steady-state concentrations for dry and hydrated acid–base particles are given in Fig. 11. In the case of SA–AMM and SA–DMA particles, hydrated particles (2–3 water molecules in the case of AMM and 1–3 in the case of DMA) have slightly higher concentrations than dry particles. This implies that SA–AMM and SA–DMA particles could slightly grow via water additions, which could possibly affect particle composition.⁶⁰ In the case of SA–TMAO particles, dry particles have the highest steady-state concentration and those with one water molecule have almost an order of magnitude lower concentration. The concentrations of more hydrated particles decrease gradually. This indicates that SA–TMAO particles are unlikely to absorb water in atmospheric conditions and their hygroscopic growth factor is very low. For SA–GUA particles, the concentrations of hydrated particles are significantly higher than that of dry particles. Particles having 2–4 water molecules have up to three orders of magnitude higher concentrations than dry particles. Also particles with 5–6 water molecules have concentrations similar than dry particles. This implies that atmospheric SA–GUA particles are highly hydrated and their hygroscopic growth factor is high. This is most likely related to the large number of possible hydrogen binding sites in SA–GUA structure and to the absence of sterical blocks such as bulky alkyl groups.

Fig. 11 Hydration distributions of stable sulfuric acid particles with ammonia, dimethylamine, trimethylamine oxide, and guanidine at 273 K at [particle] = 10⁵ cm⁻³ and RH = 100%.

4 Conclusions

In this paper we have studied the hydration of monomers and heterodimers up to 20 water molecules. Previous quantum chemical studies have often modeled up to 4 or 5 water molecules,^13–15,61 which limit the study of proton transfer reactions. Here we have discussed connections of aqueous-phase base strength and proton transfer reactions as well as sulfate formation from heterodimer bisulfate ion in water clusters. Our results indicate that the ability of a base to accept a proton in a water cluster is related to the aqueous-phase basicity whereas the ability of a base molecule to hydrate is connected to the gas-phase base strength. Especially TMAO is very likely to be hydrated due to its zwitterionic character.

The ability of a cluster to be hydrated is related to the number of possible hydrogen binding sites, meaning that SA–GUA clusters are likely to be strongly hydrated. However, although the effective evaporation rates might vary as a function of relative humidity, we do not think high RH can increase the SA–GUA particle formation rates as that occur at the kinetic limit even at room temperature and low monomer concentrations.⁶² However, it would be interesting to see what the effect of relative humidity is to SA–TMAO particle formation as the TMAO monomer is likely to be highly hydrated but SA–TMAO cluster does not need water molecules to stabilize it. In that case, it is possible that the presence of high relative humidity would decrease the particle formation rates from SA and TMAO.

By uptake of water vapor, aerosol particles can act as cloud condensation nuclei and thus impact cloud properties. As clouds have an overriding global relevance by regulating Earth's radiative balance, it is clear that understanding how different acid–base particles have different abilities to absorb water is essential. In addition of hygroscopic growth, the absorption of water might lead an aerosol particle to change its chemical composition, morphology, phase or reactivity. Thus it is important to understand what molecular properties have impacts on the hydration ability. While highly accurate quantum chemical calculations are limited to studies of relatively small systems, further studies such as molecular dynamics simulations could assist in understanding how properties of aerosol particles change when particle is hydrated. In addition, laboratory studies are needed to supplement theoretical findings.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding from the U.S. National Science Foundation under Grant No. CHE-1710580 and computational resources from the CSC-IT Center for Science in Espoo, Finland.

Notes and references

1. IPCC (Intergovernmental Panel on Climate Change), Climate change 2013: The Physical Science Basis, 2013.
2. R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011.
3. M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. M. Donahue, C. George, A. H. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, T. F. Mentel, A. Monod, A. S. H. Prévôt, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, Atmos. Chem. Phys., 2009, 9, 5155–5236.
4. M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petäjä, M. Sipilä, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Järvinen, M. Äijälä, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkilä, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin, J. Duplissy, H. Vehkamäki, J. Bäck, A. Kortelainen, I. Riipinen, T. Kurtén, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V.-M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946.
5. J. Almeida, S. Schobesberger, A. Kürten, I. K. Ortega, O. Kupiainen-Määttä, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi and M. Breitenlechner, et al. , Nature, 2013, 502, 359–363.
6. K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kürten, S. Ehrhart, A. Franchin and T. Nieminen, et al. , Nat. Commun., 2016, 7, 11594.
7. J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639.
8. F. Arnold and R. Fabian, Nature, 1980, 283, 55–57.
9. V. Vaida, J. Chem. Phys., 2011, 135, 020901.
10. S. Schobesberger, H. Junninen, F. Bianchi, G. Lönn, M. Ehn, K. Lehtipalo, J. Dommen, S. Ehrhart, I. K. Ortega, A. Franchin, T. Nieminen, F. Riccobono, M. Hutterli, J. Duplissy, J. Almeida, A. Amorim, M. Breitenlechner, A. J. Downard, E. M. Dunne, R. C. Flagan, M. Kajos, H. Keskinen, J. Kirkby, A. Kupc, A. Kürten, T. Kurtén, A. Laaksonen, S. Mathot, A. Onnela, A. P. Praplan, L. Rondo, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Sipilä, A. Tomé, G. Tsagkogeorgas, H. Vehkamäki, D. Wimmer, U. Baltensperger, K. S. Carslaw, J. Curtius, A. Hansel, T. Petäjä, M. Kulmala, N. M. Donahue and D. R. Worsnop, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17223–17228.
11. J. N. Smith, D. C. Draper, S. Chee, M. Dam, H. Glicker, D. Myers, A. E. Thomas, M. J. Lawler and N. Myllys, J. Aerosol Sci., 2020, 105733.
12. B. R. Bzdek, J. W. DePalma and M. V. Johnston, Acc. Chem. Res., 2017, 50, 1965–1975.
13. N. T. Tsona, H. Henschel, N. Bork, V. Loukonen and H. Vehkamäki, J. Phys. Chem. A, 2015, 119, 9670–9679.
14. T. Olenius, R. Halonen, T. Kurtén, H. Henschel, O. Kupiainen-Määttä, I. K. Ortega, C. N. Jen, H. Vehkamäki and I. Riipinen, J. Geophys. Res.: Atmos., 2017, 122, 7103–7118.
15. H. Henschel, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 1886–1896.
16. Y. Yang, S. E. Waller, J. J. Kreinbihl and C. J. Johnson, J. Phys. Chem. Lett., 2018, 9, 5647–5652.
17. Y. Yang and C. J. Johnson, Faraday Discuss., 2019, 217, 47–66.
18. J. J. Kreinbihl, N. C. Frederiks and C. J. Johnson, J. Chem. Phys., 2021, 154, 014304.
19. G.-L. Hou, W. Lin and X.-B. Wang, Commun. Chem., 2018, 1, 1–8.
20. G.-L. Hou and X.-B. Wang, Acc. Chem. Res., 2020, 779–785.
21. H. Ouyang, S. He, C. Larriba-Andaluz and C. J. Hogan, J. Phys. Chem. A, 2015, 119, 2026–2036.
22. J. M. Thomas, S. He, C. Larriba-Andaluz, J. W. DePalma, M. V. Johnston and C. J. Hogan Jr., Phys. Chem. Chem. Phys., 2016, 18, 22962–22972.
23. D. Hu, C. Li, H. Chen, J. Chen, X. Ye, L. Li, X. Yang, X. Wang, A. Mellouki and Z. Hu, J. Environ. Sci., 2014, 26, 37–43.
24. N. Myllys, T. Ponkkonen, S. Chee and J. Smith, Atmosphere, 2020, 11, 35.
25. N. Myllys, J. Kubečka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Atmos. Chem. Phys., 2019, 19, 9753–9768.
26. N. Myllys, S. Chee, T. Olenius, M. Lawler and J. N. Smith, J. Phys. Chem. A, 2019, 123, 2420–2425.
27. S. Chee, K. Barsanti, J. N. Smith and N. Myllys, Atmos. Chem. Phys. Discuss., 2021, 2021, 1–27.
28. J. Kubečka, V. Besel, T. Kurtén, N. Myllys and H. Vehkamäki, J. Phys. Chem. A, 2019, 123, 6022–6033.
29. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
30. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
31. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
32. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
33. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
34. N. Myllys, J. Elm and T. Kurtén, Comput. Theor. Chem., 2016, 1098, 1–12.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision A.03, 2016.
36. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
37. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
38. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
39. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
40. D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
42. N. Myllys, J. Elm, R. Halonen, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 621–630.
43. M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355.
44. O. Hoegh-Guldberg, P. J. Mumby, A. J. Hooten, R. S. Steneck, P. Greenfield, E. Gomez, C. D. Harvell, P. F. Sale, A. J. Edwards and K. Caldeira, et al. , Science, 2007, 318, 1737–1742.
45. S. Enami, H. Mishra, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. A, 2012, 116, 6027–6032.
46. A. Ravishankara, Science, 1997, 276, 1058–1065.
47. M. Kumar and J. S. Francisco, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12401–12406.
48. H. Mishra, S. Enami, R. J. Nielsen, M. R. Hoffmann, W. A. Goddard and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10228–10232.
49. S. Biswas, H. Kwon, K. C. Barsanti, N. Myllys, J. N. Smith and B. M. Wong, Phys. Chem. Chem. Phys., 2020, 22, 26265–26277.
50. D. Herschlag and M. M. Pinney, Biochemistry, 2018, 57, 3338–3352.
51. M. L. Dawson, M. E. Varner, V. Perraud, M. J. Ezell, R. B. Gerber and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18719–18724.
52. A. Kürten, C. Li, F. Bianchi, J. Curtius, A. Dias, N. M. Donahue, J. Duplissy, R. C. Flagan, J. Hakala, T. Jokinen, J. Kirkby, M. Kulmala, A. Laaksonen, K. Lehtipalo, V. Makhmutov, A. Onnela, M. P. Rissanen, M. Simon, M. Sipilä, Y. Stozhkov, J. Tröstl, P. Ye and P. H. McMurry, Atmos. Chem. Phys., 2018, 18, 845–863.
53. X.-B. Wang, J. B. Nicholas and L.-S. Wang, J. Chem. Phys., 2000, 113, 10837–10840.
54. L. C. Smeeton, J. D. Farrell, M. T. Oakley, D. J. Wales and R. L. Johnston, J. Chem. Theory Comput., 2015, 11, 2377–2384.
55. M. Kulichenko, N. Fedik, K. V. Bozhenko and A. I. Boldyrev, J. Phys. Chem. B, 2019, 123, 4065–4069.
56. F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 24, 247–260.
57. M. Cacace, E. Landau and J. Ramsden, Q. Rev. Biophys., 1997, 30, 241–277.
58. J. T. OBrien, J. S. Prell, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 8248–8249.
59. X.-B. Wang, X. Yang, J. B. Nicholas and L.-S. Wang, Science, 2001, 294, 1322–1325.
60. H. Chen, S. Chee, M. J. Lawler, K. C. Barsanti, B. M. Wong and J. N. Smith, Aerosol Sci. Technol., 2018, 52, 1120–1133.
61. F. R. Rasmussen, J. Kubečka, V. Besel, H. Vehkamäki, K. V. Mikkelsen, M. Bilde and J. Elm, J. Phys. Chem. A, 2020, 124, 5253–5261.
62. N. Myllys, T. Ponkkonen, M. Passananti, J. Elm, H. Vehkamäki and T. Olenius, J. Phys. Chem. A, 2018, 122, 4717–4729.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01704g

---