Role of the carrier density in the transport mechanisms of polycrystalline ZnO films

Abstract

The transport processes occurring in polycrystalline ZnO have been investigated by measuring the resistivity as a function of temperature in ZnO films with different n-doping levels, obtained by varying the oxygen pressure during the deposition process. These films show an electrical resistivity spanning about two orders of magnitude, from 4 to 8 × 10⁻² Ω cm at room temperature, corresponding to low and high levels of n-type doping, respectively. The present results indicate a relevant role of the carrier density in determining the dominant transport mechanisms in these samples by showing that the picture characterizing a highly n-doped ZnO sample, where an intra-grain mechanism and a grain-boundary mechanism dominate the high temperature and low temperature transport processes, respectively, is thoroughly overturned in lightly n-doped samples, where a grain-boundary mechanism and an intra-grain mechanism govern the charge transport in the same temperature regimes, respectively. Moreover, the present results indicate a critical role of the conditions limiting the occurrence of the Mott variable range hopping regime. They show indeed that an incomplete check of such conditions can result in erroneous conclusions about the prevalent transport mechanisms.

---

1. Introduction

Zinc oxide is one of the largely studied II–VI semiconductors, highly attractive for potential applications in fields such as optoelectronics, spintronics, and photovoltaics. It generally shows an n-type character due to shallow-donor native or unintentional dopants like Zn interstitials (Zn-int) or H-defects,¹ respectively, whose concentration can be heavily affected by the growth conditions.²

According to a general behaviour of semiconducting materials, the ZnO resistivity should follow a temperature dependence of the form ρ = ρ₀ exp(T₀/T)^p, where the p-value is characteristic of the relevant transport mechanism. In ZnO, Arrhenius thermally activated processes (p = 1), where carriers are thermally excited from impurity levels into the conduction band (CB), and variable range hopping processes (Mott VRH, p = 1/4; Efros–Shklovskii VRH, p = 1/2) are often considered to fit values of resistivity as a function of temperature, ρ(T), in high and low temperature ranges, respectively.^3–6

In the case of polycrystalline ZnO, further kinds of transport processes have to be considered due to possible grain boundary (GB) effects. In particular, the ZnO surface reactivity and n-type nature, which implies a noticeable presence of electrons in the CB, induce the formation of O²⁻-like, negatively charged defects at the grain boundary surfaces.⁷ Such defects produce a depletion layer of electrons close to the surface and a buildup of negative charge at grain boundaries. This gives rise to a band bending in the bulk region near the GB, inducing a potential barrier between the grains (V_b) that can inhibit inter-grain electronic transport. Thus, in polycrystalline ZnO, the conduction mechanisms can be affected by processes that control the intra-grain electron transport, ig processes, having the same features as the above single-crystal processes, and inter-grain transport through the GB barriers, gb processes. In the latter processes, the current can flow between grains by thermionic emission (TE) over the potential barriers or, alternatively, by thermally-assisted quantum-mechanical tunneling (TAT) of electrons through the V_b barriers. In a given T-range, the ig or gb process requiring the largest activation energy may be the “bottle-neck” process that governs the conduction mechanisms.

In previous studies, following Petritz's model for TE,^8,9 Orton and Powell discussed polycrystalline and powdered semiconductors,¹⁰ whereas Roth focused on ZnO films.¹¹ In the latter case, the experimental findings were described in terms of TE at high T, whereas, at low T, tunneling processes were invoked. In highly n-doped ZnO films Vai followed the Roth approach at high T and an Arrhenius type activation for the low T regime.¹²

In a recent study, we investigated transport processes in polycrystalline heavily n-type doped ZnO, Co-doped ZnO and Co-doped and hydrogenated ZnO.¹³ The achieved results showed that, in pristine ZnO, Arrhenius thermally activated ig processes, which arise from mobile electrons in the CB, excited to this band from shallow donor states D (D-CB process), dominate at high-temperature (HT), whereas TAT gb processes control the electron transport at low temperature (LT). The same study also gave two interesting suggestions. First, it raised the attention to the need for a systematic analysis of the different ways in which the n-type carrier density (N) can affect the ZnO transport processes. For instance, obviously, a high N value can favour the ig D-CB process. Less evident effects regard the occurrence of ig processes following the Mott VRH mechanism as well as gb processes like the TE one, where the N value can affect the conditions limiting the occurrence of both mechanisms, as will be illustrated in detail in a next section. Finally, N affects the formation of the above O₂⁻ surface defects and, therefore, the height of the V_b barriers that control the GB transport processes. Moreover, the same study highlighted the relevance of a careful check of the conditions that have to be satisfied for the occurrence of Mott VRH processes.

The above issues have motivated the present study, where transport processes were investigated in the case of polycrystalline ZnO thin films with largely different N values. By varying the O₂ partial pressure in the deposition process (a procedure that is expected to affect the concentration of donor Zn interstitials), we obtained semiconducting films with electrical resistivity spanning about two orders of magnitude at room temperature (RT). Moreover, the resistivity ratio ρ* = ρ(20 K)/ρ(300 K) for each sample was found to be larger than a factor of 10. We also carefully considered the conditions for the validity of the Mott VRH processes and compared our results with those of recently published studies.

2. Experimental

Thin ZnO films S1, S2, S3, and S4 were deposited by pulsed laser deposition, using a Nd:YAG laser, operating at λ = 355 nm, a fluence of 2 J cm⁻² and 10 Hz repetition rate. These films were grown on optically transparent Al₂O₃(001) single crystals at a substrate temperature of 500 °C. The O₂ partial pressure was 1 × 10⁻⁵ mbar for S1, 10⁻³ mbar for S2, 10⁻² mbar for S3, and 10⁻¹ mbar for S4. XRD spectra, according to previous reports,^14–21 exhibit only the presence of (00l) reflections, indicating a c-axis oriented structure without appreciable secondary phases. In line four-probe dc resistance vs. T measurements were carried out by means of a Keithley current source and a high-impedance Keithley voltmeter, with the probe insert fitted into a closed-cycle refrigerator system operating in the 20–300 K range. The carrier concentration was estimated by measuring the Hall voltage, in the van der Pauw configuration at RT, and the thickness with an alpha-step profilometer. Finally, fitting of experimental data to models was carried out by means of the standard nonlinear least-squares method, based on iterative Levenberg–Marquardt (LM) algorithms. Such a technique minimizes the sum of the squares of the errors between the model function and the data points by a combination of two numerical algorithms, the gradient (steepest) descent method, when the model parameters are far from their optimal value, and the Gauss–Newton method (on assuming the least squares function locally quadratic in the parameters) when the parameters are close to their optimal value.

3. Results and discussion

3.1 ZnO films with different carrier densities

The resistivities of the ZnO samples as a function of temperature, T, in the range 300–20 K are shown in Fig. 1. Samples S1, S2, S3, and S4 corresponding to N values of 1 × 10¹⁹ cm⁻³, 3 × 10¹⁸ cm⁻³, 4.5 × 10¹⁷ cm⁻³, and 2.2 × 10¹⁷ cm⁻³, respectively, exhibit an increasing resistivity at decreasing T, according to a general semiconducting behavior. Sample S1 represents a highly n-doped sample. The S3 and S4 samples can be considered as lightly n-doped ZnO and the S2 sample corresponds to a somewhat intermediate n-doping level.

Fig. 1 Resistivity (ρ) as a function of temperature (T) for samples S1, S2, S3, and S4.

Let us focus on the conductivity σ(ρ⁻¹) as a function of T⁻¹ of the S1 and S3 samples, representatives of the high and low doping levels, see Fig. 2(a) and (b), respectively. The shapes of the curves suggest the occurrence of different thermally activated processes in HT and LT regimes. A natural, first attempt for the investigation of the σ behaviour in the whole temperature range has been performed by using the following equation:^13,22,23

σ = pe^−E1/kT + qe^−E2/kT (1)

where p and q are temperature-independent conductivity parameters, Ei are thermal activation energies describing, in principle, the electronic conduction in the HT (E1) and LT (E2) regimes, k is the Boltzmann's constant, and T is the temperature. The results of the fitting procedure are summarized in Table 1, where E1 and E2 values are reported, together with the corresponding T-ranges of validity, in the first two rows of the table.

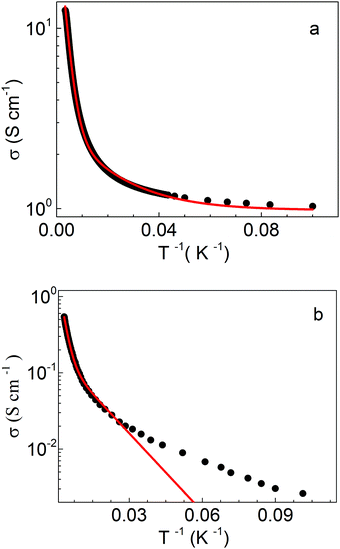Fig. 2 Conductivity (σ) as a function of T⁻¹ for the S1 (a) and S3 (b) samples; the solid line indicates the fit with eqn (1).

Table 1 Activation energies derived from conductivity data fitting to eqn (1) for the S1 and S3 samples are reported in the two upper rows of the table together with their validity temperature range. The fit results for the S3 sample achieved by applying eqn (3) (describing a TE process, see the text) are given in the third row. Finally, the fourth row reports the results of data fitting to eqn (1) achieved in a previous study on a highly n-doped ZnO sample

Sample	E1 (meV)	E2 (meV)	E1 T range (K)	E2 T range (K)
S1	36.0 ± 0.4	4.6 ± 0.6	300–141	141–20
S3	45 ± 2	7.0 ± 0.4	300–133	133–38
S3 (TE)	37.0 ± 0.9	—	300–143	—
ZnO (ref. 13)	36.0 ± 0.4	4.6 ± 0.4	300–170	170–20

---

For sample S1, a satisfactory fit is obtained in the whole range of temperatures. The activation energies and the features of the σ curve closely resemble those found for the highly n-doped ZnO sample investigated in our previous study (bottom row in the table).¹³ Thus, the same conclusions apply here: two different thermally activated processes govern the charge transport in the HT and LT regimes, respectively. The first one refers to an intra-grain conduction process which arises from mobile electrons in the CB, D-CB process. The second one refers instead to an inter-grain TAT charge transport overcoming the V_b barriers at GBs. We anticipate that, in the following discussion, the role of N in the predominance of these two processes will be clarified.

In the case of sample S3, the shape of the σ(T⁻¹) curve still suggests the occurrence of two processes in the HT and LT regimes; however, the data are not satisfactorily fitted by eqn (1) in the whole T range, as clearly shown at LT. The following sections focus therefore on such a lightly doped sample.

3.1.1 Lightly doped S3 film – high temperature regime. In principle, the analysis of the S3 σ(T⁻¹) data in the HT regime should consider three possible transport mechanisms. The first one refers to the above ig D-CB process. The other two processes, the TE and TAT ones, refer instead to a gb charge transport. The E1 value estimated by eqn (1) may be compatible with the occurrence of a D-CB mechanism. However, a useful indication on the main transport mechanism is obtained by applying a simple criterion to determine the occurrence of a TE process, which is based on the so-called E₀₀ tunneling parameter:²⁴

E₀₀ = 18.5 × 10⁻¹² (N/(m*ε))^1/2 eV (2)

where N is the carrier density, ε the relative dielectric constant, and m* the reduced electron effective mass of a given semiconductor. For E₀₀ < kT a TE process is the relevant charge transport mechanism. This condition is satisfied for T > T*, with T* being such that E₀₀ = kT.

In the case of the ZnO samples, m* has a value of 0.24 and ε is equal to 8.5.¹¹ An S3 E₀₀ value of 7.95 meV indicates that TE is the prevalent mechanism for T > 95.5 K. For comparison, the estimation of the same parameters in the other samples gives: S1 E₀₀ = 41 meV (T* = 492 K), S2 E₀₀ = 20.5 meV (T* = 246 K), and S4 E₀₀ = 5.55 meV (T* = 66 K).

The indication given by the E₀₀ parameter for the S3 sample is also confirmed considering that in lightly doped materials the TE over the GB can be described by a thermally activated conductivity of the form:^10,11

σ = σ₀T^−1/2 exp(−E/kT) (3)

The fit results for the S3 sample (see Fig. 3) indicate the occurrence of the TE mechanism in the 300–143 K range, with TE being ruled out in the LT range.

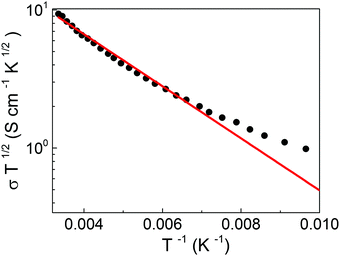Fig. 3 σT ^1/2 as a function of T⁻¹ for the S3 sample; the fit with eqn (3) (solid line) indicates the occurrence of the TE mechanism in the 300–143 K range (see text).

3.1.2 Lightly doped S3 film – low temperature regime. At low temperatures, having excluded the TE mechanism, two kinds of thermally activated processes requiring small activation energies can be considered: (i) intra-grain conduction controlled by the “hopping” of electrons between localized impurity states, which can be described by the Mott or Efros models, and (ii) inter-grain TAT.

First, we analyze our data in the framework of the Mott model. The basic mechanism of the model is a phonon-assisted tunneling between localized impurity states governed by a competition between tunneling and activation; thus, the optimal hopping distance and the activation energy are temperature dependent, which results in a non-Arrhenius behavior. To calculate the hopping conductance, Miller and Abrahams introduced the so-called resistor network model.²⁵ First, starting from electron wave functions, they calculated the hopping probability between impurity sites i and j with the absorption or emission of a phonon and then the number of i → j transitions per unit time. In the absence of an electric field there is a detailed balance and this number is exactly equal to the number of reverse transitions. However, in the presence of a weak electric field an imbalance occurs and a current appears proportional to the variation of the electrochemical potential between hopping sites i and j. Consequently, by introducing an effective resistance R_ij of a given transition, the whole problem is reduced to calculating the effective resistance of a network of random resistors, where each element connects an impurity i, j pair with a resistance given by

R_ij = R₀ exp(2r_ij/ξ + ε_ij/kT) (4)

where r_ij is the distance between sites i and j, ε_ij is the activation energy for hopping between localized impurity states, ξ is the electron localization length,²⁷k is the Boltzmann's constant, T is the temperature and the prefactor R₀ is generally assumed to be independent of T. The dominant conduction paths are thus dictated by minimization of R_ij. At a suitable T, charge carriers readily acquire sufficient thermal energy to hop between adjacent sites regardless of ε_ij, taking the path with the lowest r_ij. In this case, the conduction results from a nearest-neighbor hopping (NNH) and the temperature dependence of the network conductivity is described by a simple Arrhenius law, where E_a is an activation energy related to ε_ij.

σ ∼ exp(−E_a/kT) (5)

However, Mott pointed out that the exponential dependence of the resistances on the site energies cannot be ignored at low T,²⁶ where charge carriers may hop farther in order to find paths with lower activation energy (i.e. the exponent of eqn (4) may be minimized at relatively high r_ij). Indeed, at low T hopping occurs between the states whose energies are concentrated near the Fermi level. Because of the factor exp(ε_ij)/kT in the expression for the resistance R_ij, only the states within the narrow band near the Fermi level are important and hence the density of states in this band can be considered as constant. In this case, variable-range hopping (VRH) occurs and the temperature dependence of σ assumes the form:²⁸

σ = σ₀ exp[−(T_M/T)^1/4] (6)

where

σ₀ = 3e²ν_ph[ξg(E_F)/(8πkT)]^1/2; (7)

T_M = 18/(kg(E_F)ξ³) (8)

where g(E_F) is the density of states near the Fermi energy E_F, ν_ph is the phonon frequency (∼10⁻¹³ s⁻¹) and T_M is the so called Mott temperature.

For the Mott theory to be valid, two conditions have to be fulfilled:

(a) the electrons must hop a mean distance R greater than the localization length ξ, i.e. R/ξ > 1.

(b) the mean hopping energy difference between sites (W) has to be larger than kT, i.e. W/kT > 1.

These quantities can be calculated by the Mott relations:

R/ξ = (3/8)(T_M/T)^1/4 (9)

W/kT = (1/4)(T_M/T)^1/4 (10)

where the T_M value is estimated by fitting σ(T) data with eqn (6).

The applicability of the model critically depends on the impurity concentration and, therefore, on the carrier density N. In fact, as N approaches a critical value where electronic states start to overlap (i.e. the localization character is lost and an impurity band forms) the semiconductor undergoes the Anderson transition from an insulator to a metal. Moreover, T_M can be related to N by assuming a 3D free electron gas approximation. In such a way, g(E_F) = 3N/2E_F and eqn (8) leads to:

T_M = 32E_F/3Nkξ³ (11)

Thus, the carrier density N plays a key role in the conditions governing the occurrence of the TE process, through the E₀₀ parameter, and of the Mott VRH mechanism through eqn (9)–(11).

The S3 conductivity data have been analyzed in the framework of the Mott model by plotting ln(σT^1/2) vs. T^−1/4. The resulting fit, see Fig. 4a, shows that the conductivity follows eqn (6) for T below 100 K. The T_M evaluated from the slope of the linear regime, 1.2 × 10⁵ K, has been used for the estimation of R/ξ and W/kT, see Table 2. Both parameters show that the above two limiting conditions are fully satisfied. Thus, the Mott VRH mechanism controls the LT transport in the S3 sample, whereas the TE mechanism is responsible of the charge transport in the HT regime.

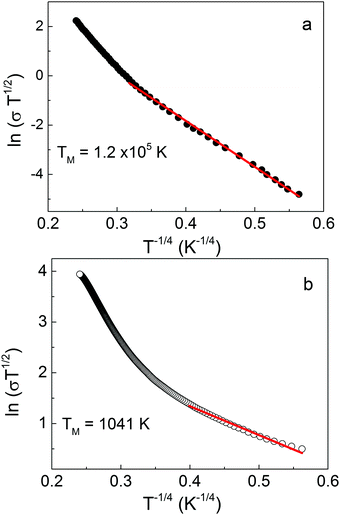Fig. 4 ln (σT^1/2) as a function of T^−1/4 for the S3 (a) and S1 (b) samples; solid line: fit with eqn (6).

Table 2 Mott and electrical parameters for the S1, S2, S3, and S4 samples (see the text)

Sample	N (cm^−3)	ρ (Ω cm) (300 K)	T M (K)	R/ξ	W/kT
S1	1 × 10^19	0.08	1.04 × 10^3	>1 (T < 15 K)	>1 (T < 10 K)
S2	3 × 10^18	0.32	0.85 × 10^5	>1 (T < 88 K)	>1 (T < 88 K)
S3	0.45 × 10^18	1.84	1.2 × 10^5	>1 (T < 100 K)	>1 (T < 100 K)
S4	0.22 × 10^18	4.0	1.2 × 10^5	>1 (T < 96 K)	>1 (T < 96 K)

---

3.2 Highly doped and lightly doped sample comparison

For a complete comparison of the transport processes between the S1 and S3 samples, the S1 conductivity has been plotted in terms of the Mott model. The resulting fit, see Fig. 4b, gives a quite lower T_M (1.04 × 10³ K) with R/ξ and W/kT parameters such that the Mott regime could hold only below 10 K, see Table 2. The overall results achieved here for the highly n-doped S1 sample compare well with those found for a similar sample investigated in our previous study.¹³ There and here, in the LT regime, both the TE and Mott processes have been ruled out, thus permitting describing the transport behavior in terms of the TAT mechanism. At HT, the S1 E₀₀ parameter reported above rules out the TE mechanism in favour of the D-CB one, in agreement with our previous results. The transport processes occurring in the S1 (high N) and S3 (low N) samples in the HT and LT regimes are summarized in Table 3.

Table 3 Synoptic table reporting the different transport processes occurring at low T and high T for the S1 (high N) and S3 (low N) samples: donor to CB electron excitation (D-CB), Mott variable range hopping (Mott VRH), thermionic emission (TE), and thermally assisted tunneling (TAT). Note the reversed order of the high T and low T symbols in the high N and low N rows

	Intra-grain (ig)		Inter-grain (gb)
	D-CB	Mott VRH	TE	TAT
S1 – high N	High T			Low T
S3 – low N		Low T	High T

---

Thus, a major indication arising from the S1 and S3 comparison is that the picture describing the transport processes in the highly n-doped sample, where an ig (D-CB) mechanism dominates the HT range and a gb (TAT) mechanism controls the LT one, is thoroughly overturned in the lightly n-doped sample, where gb (TE) and ig (Mott-VRH) mechanisms govern the HT and LT processes, respectively. Such results also indicate the Mott limiting conditions as a valuable tool for identifying the dominant transport mechanism among possible competitors.

The analysis performed for the S1 and S3 samples, extended to the S2 and S4 ones, leads to similar conclusions. Namely, the S2 and S4 E₀₀ values are equal to 20.5 meV and 5.55 meV, which would require T values higher than 246 K and 66 K for the occurrence of the TE mechanism, respectively. Thus, in the HT regime, the S4 sample, having an N value close to the S3 one, has an identical behavior. Instead, the S2 sample, with an intermediate N density among the S1 and S3 ones, is expected to combine, in the same regime, a D-CB mechanism with the TE one.

Regarding the LT regime, the results of the Mott model analysis for the S2 and S4 samples are given in Table 2. Let us summarize that for S1 the Mott law is satisfied for T < 10 K (T_M = 1041 K), for S2 when T < 88 K (T_M = 0.85 × 10⁵ K), for S3 when T < 100 K (T_M = 1.2 × 10⁵ K), and for S4 when T < 96 K (T_M = 1.23 × 10⁵ K). Thus, substantially, the Mott model holds for all the samples except for S1. According to (11)T_M decreases on increasing N and it eventually vanishes at a critical value, N_c, for the semiconductor to metal transition. The N_c value can be determined by using the Mott theory:²⁶

N_c^1/3a* = C (12)

where a* is the donor Bohr radius, and the constant C varies from 0.18 to 0.376, depending on the adopted theoretical model. For ZnO, a* = 1.2 nm, and N_c spans from 4.8 × 10¹⁸ cm⁻³ (C = 0.18) to 2.2 × 10¹⁹ cm⁻³ (C = 0.376). By considering the former as a safe N_c value, S1 has a carrier concentration slightly larger than the critical value, whereas S2, S3, and S4 have lower values in agreement with the occurrence of the Mott VRH mechanism.

The ξ value is generally taken to be equal to the effective Bohr radius of the shallow donors which, in ZnO, is about 2 nm for most shallow donors.²⁹ Instead, we have calculated such values for each sample by using the well-known Fermi gas relationships for E_F and g(E_F); by inserting the fitted T_M values into eqn (8) the ξ values are obtained, see Table 4.

Table 4 Electrical and Mott parameters for selected literature results; the last four rows refer to the films of the present paper

	ρ (Ω cm)	N (cm^−3)	VRH validity range (K)	T M (K)	g (EF) (J^−1 m^−3)	ξ (nm)	W/kT	R/ξ	Ref.
a Parameters calculated assuming the free electron gas approximation.
ZnO film ann.	0.04	5 × 10^18	T < 30 K	1101	1.1 × 10^50	0.2	W/kT > 1	R/ξ > 1	Kumar
					4.4 × 10^45 ^a	6.8^a	T < 3 K	T < 20 K	Ref. 5
ZnO film 2	1.7	n.a.	25 < T < 80	65	2.5 × 10^48	2	W/kT > 1	R/ξ > 1	Lien
							never	never	Ref. 4
ZnO film 4	2.01	n.a.	25 < T < 80	854	1.9 × 10^47	2	W/kT > 1	R/ξ > 1
							T < 3 K	T < 15 K
ZnO film 5	5.9	n.a.	25 < T < 80	10 400	1.6 × 10^46	2	W/kT > 1	R/ξ > 1
							T < 40 K	T < 80 K
ZnO film 6	11.3	n.a.	25 < T < 80	23 600	6.9 × 10^45	2	W/kT > 1	R/ξ > 1
							T < 80 K	T < 80 K
ZnO film 7	26	n.a.	25 < T < 80	15 200	1.1 × 10^46	2	W/kT > 1	R/ξ > 1
							T < 60 K	T < 80 K
ZnO film 3	3.2	10^18	30 < T < 90	1250	1.3 × 10^47	2	W/kT > 1	R/ξ > 1	Huang
					2.58 × 10^45 ^a	7.8^a	T < 5 K	T < 25 K	Ref. 3
ZnO film 4	11.4	6 × 10^17	30 < T < 90	5820	2.8 × 10^46	2	W/kT > 1	R/ξ > 1
					2.2 × 10^45 ^a	4.95^a	T < 23 K	T < 90 K
ZnO film 5	26	2 × 10^17	30 < T < 90	34 500	4.7 × 10^45	23.1^a	W/kT > 1	R/ξ > 1
					1.5 × 10^45 ^a		T < 90 K	T < 90
ZnO film 6	48	2 × 10^16	30 < T < 90	108 000	1.5 × 10^45	2	W/kT > 1	R/ξ > 1
					0.75 × 10^45 ^a	2.74^a	T < 90 K	T < 90 K
ZnO film	0.19	n.a.	n.a.	7.42	6 × 10^45	n.a.	Never	Never	Singh
									Ref. 32
ZnO H: film	0.01	5 × 10^19	n.a.	26 843	2 × 10^49	n.a.	N > Nc	n.a.
ZnO bulk	300	n.a.	n.a.	3 × 10^8	n.a.	88	n.a.	R/ξ > 1	Singh
								T < 300 K	Ref. 31
ZnO film	8.1	7 × 10^18	T < 300	2.14 × 10^5	4.9 × 10^45	1.1	W/kT > 1	R/ξ > 1	Thimsen
		μ = 0.1			T F = 170 K		T < 300 K	T < 300 K	Ref. 30
ZnO film S1	0.08	1 × 10^19	T < 40 K	1041	5.5 × 10^45	6.45	W/kT > 1	R/ξ > 1	S1
					T F = 163 K		T < 10 K	T < 15 K
ZnO film S2	0.32	3 × 10^18	T < 88 K	85 500	3.72 × 10^45	1.69	W/kT > 1	R/ξ > 1	S2
							T < 88 K	T < 88 K
ZnO film S3	1.84	4.5 × 10^17	T < 100 K	1.2 × 10^5	1.98 × 10^45	1.86	W/kT > 1	R/ξ > 1	S3
							T < 100 K	T < 100 K
ZnO film S4	4.0	2.2 × 10^17	T < 96 K	1.2 × 10^5	1.57 × 10^45	2.01	W/kT > 1	R/ξ > 1	S4
							T < 96 K	T < 96 K

---

Let us note that, in our samples, the ξ value is comparable to the donor Bohr radius of the ZnO shallow donors when the Mott VRH model is valid, whereas there is a threefold increase of ξ for S1, where N > N_c. Let us also recall that, according to (11), T_M is expected to vanish at N_c, where the ξ is predicted to diverge, indicating the entrance into the metallic regime.

The above results indicate that the applicability of the Mott theory, devoted to insulators, to ZnO critically depends on the N value that, in this material, can be largely modulated by donor doping as well as by the growth conditions from the insulator to the metallic case. When the samples are grown at high T (>500 °C) and in the presence of O₂ (p > 10⁻⁴ mbar), ξ is small, N is low and T_M is large. The transport mechanism at low T is the VRH one. In the case of sample growth in a high vacuum (and high T), the formation of defects like Zn-int induces a strong donor doping increasing the N in excess of 10¹⁸ cm⁻³. In such a case a metallic character appears since the electrons are no more confined to their hydrogenic orbital but are delocalized on several atoms. In this case ξ is large and T_M is small; the VRH does not apply.

3.3 Relevance of the Mott conditions

The usefulness of the Mott limiting conditions clearly appears when they are applied to several results taken from the literature, see Table 4. Indeed, most of the previous studies report only T_M extracted from data fitting with eqn (6). Other relevant parameters, such as ξ, R/ξ, and W/kT, are rarely calculated and discussed in relation to the T-range of validity. In order to perform a homogeneous comparison, when N is reported, we have estimated the Mott parameters by using the ξ value obtained assuming the 3D free electron gas approximation. Such values are reported in Table 4 labelled with ‘a’. In the case of Lien's films,⁴ we observe that, among the samples with higher resistivity, only the film 6 sample meets the Mott conditions in the whole reported validity range of 25–80 K. Although R/ξ > 1 also for films 5 and 7, the condition W/kT > 1 holds only for T < 60 K (film 7) and T < 40 K (film 5). Similarly, the Mott conditions are fulfilled only for the Huang samples 5 and 6, whereas for sample 4 the validity is restricted to T < 23 K.³

In other cases, the samples are not immediately comparable to ours. For instance, Thimsen's as-grown nanocrystalline films, even though showing a large N, have a large resistivity and a small mobility; in such a case the validity conditions are met in the full T-range.³⁰ For Singh's ZnO films,³¹ the only reported parameters, T_M larger than 10⁸ K and ξ of about 88 nm, are hard to reconcile with the Mott theory. In the case of hydrogenated ZnO films reported by Singh,³² the high N value (>N_c), extrapolated from a graph, would suggest a T_M well below the high reported value. Finally, for easier comparison, our results are also reported in the last rows of Table 4. Our samples S2, S3, and S4 suggest that the Mott VRH regime is valid below 100 K when N < N_c. In this case, the results of Table 4 indicate a ξ value approaching the hydrogenic radius of ZnO donors of 2 nm and a DOS at E_F close to 10⁴⁵ J⁻¹ m⁻³.

The case of high N pertains to our S1 sample, the ZnO film of Kumar, samples 1 and 2 of Lien, 3 of Huang, and 1 of Singh.³² In all of these cases the validity conditions are fulfilled below ∼10 K only, where R/ξ > 1 and W/kT > 1. Furthermore, T_M is below 2000–3000 K and ξ is more than three times the hydrogenic Bohr radius: for example 6.45 nm for our S1 sample, 6.8 nm for Kumar's sample, and 7.8 nm for the more metallic film of Huang.

4. Summary and conclusions

In the present study, the effects of carrier density on processes governing the charge transport in polycrystalline ZnO have been investigated by measuring the resistivity as a function of temperature in samples showing an electrical resistivity spanning about two orders of magnitude at room temperature. As a clear evidence of a significant role played by the carrier density in such processes, our results show that the picture describing charge transport in highly n-doped ZnO, where an intra-grain (D-CB) mechanism and a grain-boundary (TAT) mechanism control the HT and LT regimes, respectively, is thoroughly overturned in lightly n-doped samples, where a grain-boundary (TE) mechanism and an intra-grain (Mott VRH) mechanism govern the same regimes, respectively.

Moreover, the present results indicate a critical role of the conditions limiting the occurrence of the Mott VRH regime showing that an incomplete check of such conditions can result in erroneous conclusions about the prevalent transport mechanisms.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. A. Janotti and C. G. Van de Walle, Fundamentals of zinc oxide as a semiconductor, Rep. Prog. Phys., 2009, 72, 126501.
2. Ü. Özgür, Ya. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, A comprehensive review of ZnO materials and devices, J. Appl. Phys., 2005, 98, 041301.
3. Y.-L. Huang, S.-P. Chiu, Z.-X. Zhu, Z.-Q. Li and J.-J. Lin, Variable-range-hopping conduction processes in oxygen deficient polycrystalline ZnO films, J. Appl. Phys., 2010, 107, 063715.
4. C.-C. Lien, C.-Y. Wu, Z.-Q. Li and J.-J. Lin, Electrical conduction processes in ZnO in a wide temperature range 20–500 K, J. Appl. Phys., 2011, 110, 063706.
5. R. Kumar and N. Khare, Temperature dependence of conduction mechanism of ZnO and Co-doped ZnO thin films, Thin Solid Films, 2008, 516, 1302.
6. Y. Natsume, H. Sakata, T. Hirayama and H. Yanagida, Low-temperature conductivity of ZnO films prepared by chemical vapor deposition, J. Appl. Phys., 1992, 72, 4203.
7. D. D’Agostino, C. Di Giorgio, F. Bobba, A. Di Trolio, P. Alippi, A. M. Cucolo and A. Amore Bonapasta, Effects of cobalt substitution on ZnO surface reactivity and electronic structure, J. Mater. Chem. C, 2019, 33, 8364.
8. R. L. Petritz, Theory of photoconductivity in semiconductor films, Phys. Rev., 1956, 104, 1508.
9. J. Y. W. Seto, The electrical properties of polycrystalline silicon films, J. Appl. Phys., 1975, 46, 5247.
10. J. W. Orton and M. J. Powell, The Hall effect in polycrystalline and powdered semiconductors, Rep. Prog. Phys., 1980, 43, 1263.
11. A. P. Roth and D. F. Williams, Properties of zinc oxide films prepared by the oxidation of diethyl zinc, J. Appl. Phys., 1981, 52, 6685.
12. A. T. Vai, V. L. Kuznetsov, H. Jain, D. Slocombe, N. Rashidi, M. Pepper and P. P. Edwards, The Transition to the Metallic State in Polycrystalline n-type Doped ZnO Thin Films, Z. Anorg. Allg. Chem., 2014, 640, 1054.
13. A. Di Trolio, A. Amore Bonapasta, C. Barone, A. Leo, G. Carapella, S. Pagano, A. Polimeni and A. M. Testa, Transport mechanisms in Co-doped ZnO (ZCO) and H-irradiated ZCO polycrystalline thin films, Phys. Chem. Chem. Phys., 2021, 23, 2368.
14. A. Di Trolio, C. Veroli, A. M. Testa and D. Fiorani, Ferromagnetism above room temperature in Mn-doped ZnO thin films, Superlattices Microstruct., 2009, 46, 101.
15. A. Di Trolio, R. Larciprete, S. Turchini and N. Zema, Bulk sensitive X-ray absorption and magnetic circular dichroism investigation of Mn- and Co-doped ZnO thin films, Appl. Phys. Lett., 2010, 97, 052505.
16. G. Ciatto, A. Di Trolio, E. Fonda, P. Alippi, A. M. Testa and A. Amore Bonapasta, Evidence of Cobalt-Vacancy Complexes in Zn_1−x CoxO Dilute Magnetic Semiconductors, Phys. Rev. Lett., 2011, 107, 127206.
17. A. Di Trolio, P. Alippi, G. Ciatto, G. Scavia, M. Valentini and A. Amore Bonapasta, The effect of Co doping on the conductive properties of ferromagnetic Zn_1−xCo_xO films, J. Mater. Chem. C, 2015, 3, 10188.
18. A. Di Trolio, P. Alippi, E. M. Bauer, G. Ciatto, M. H. Chu, G. Varvaro, A. Polimeni, M. Capizzi, M. Valentini, F. Bobba, C. Di Giorgio and A. Amore Bonapasta, Ferromagnetism and conductivity in hydrogen irradiated Co-doped ZnO thin films, ACS Appl. Mater. Interfaces, 2016, 8, 12925.
19. D. D’Agostino, C. Di Giorgio, A. Di Trolio, A. Guarino, A. M. Cucolo, A. Vecchione and F. Bobba, Piezoelectricity and charge trapping in ZnO and Co-doped ZnO thin films, AIP Adv., 2017, 7, 055010.
20. A. Di Trolio, M. Polichetti, A. Polimeni and A. M. Testa, Local magneto-optical response of H⁺ irradiated Zn_1−xCo_xO thin films, Eur. Phys. J.-Spec. Top., 2019, 228(3), 683.
21. G. Varvaro, A. Di Trolio, A. Polimeni, A. Gabbani, F. Pineider, C. de Julián Fernández, G. Barucca, P. Mengucci, A. Amore Bonapasta and A. M. Testa, Giant magneto-optical response in H⁺ irradiated Zn_1−xCo_xO thin films, J. Mater. Chem. C, 2019, 7, 78–85.
22. S.-P. Chiu, Y.-H. Lin and J.-J. Lin, Electrical conduction mechanisms in natively doped ZnO nanowires, Nanotechnology, 2009, 20, 015203.
23. L.-T. Tsai, S.-P. Chiu, J. G. Lu and J.-J. Lin, Electrical conduction mechanisms in natively doped ZnO nanowires(II), Nanotechnology, 2010, 21, 145202.
24. C. R. Crowell and V. Rideout, Normalized thermionic-field (T-F) emission in metal-semiconductor (Schottky) barriers, Solid-State Electron., 1969, 12, 89.
25. A. Miller and E. Abrahams, Impurity conduction at low concentrations, Phys. Rev., 1960, 120, 745.
26. N. F. Mott and E. A. Davis, Electronic Processes in Non-Crystalline Materials, Clarendon, Oxford, 2nd edn, 1979.
27. P. W. Anderson, Absence of Diffusion in Certain Random Lattices., Phys. Rev., 1958, 109, 1492.
28. W. N. Shafarman, D. W. Koon and T. G. Castner, dc conductivity of arsenic-doped silicon near the metal-insulator transition, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 1216.
29. M. D. McCluskey and S. J. Jokela, Defects in ZnO, J. Appl. Phys., 2009, 106, 071101.
30. E. Thimsen, M. Johnson, X. Zhang, A. J. Wagner, K. A. Mkhoyan, U. R. Kortshagen and E. S. Aydil, High electron mobility in thin films formed via supersonic impact deposition of nanocrystals synthesized in nonthermal plasmas, Nat. Commun., 2014, 5, 5822.
31. S. Singh and M. S. R. Rao, Optical and electrical resistivity studies of isovalent and aliovalent 3d transition metal ion doped ZnO, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045210.
32. A. Singh, S. Chaudhary and D. K. Pandya, Hydrogen incorporation induced metal-semiconductor transition in ZnO:H thin films sputtered at room temperature, Appl. Phys. Lett., 2013, 102, 172106.

---