Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
C14H10 polycyclic aromatic hydrocarbon formation by acetylene addition to naphthalenyl radicals observed†
Jeehyun
Yang
 a,
Mica C.
Smith
a,
Mica C.
Smith
 b,
Matthew B.
Prendergast
b,
Matthew B.
Prendergast
 b,
Te-Chun
Chu
b,
Te-Chun
Chu
 b and
William H.
Green
b and
William H.
Green
 *b
*b
aDepartment of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: whgreen@mit.edu
First published on 15th June 2021
Abstract
The formation of polycyclic aromatic hydrocarbons (PAHs) during combustion has a substantial impact on environmental pollution and public health. The hydrogen-abstraction-acetylene-addition (HACA) mechanism is expected to be a significant source of larger PAHs containing more than two rings. In this study, the reactions of 1-naphthalenyl and 2-naphthalenyl radicals with acetylene (C2H2) are investigated using VUV photoionization time-of-flight mass spectrometry at 500 to 800 K, 15 to 50 torr, and reaction times up to 10 ms. Our experimental conditions allow us to probe the Bittner–Howard and modified Frenklach HACA routes, but not routes that require multiple radicals to drive the chemistry. The kinetic measurements are compared to a temperature-dependent kinetic model constructed using quantum chemistry calculations and accounting for chemical-activation and fall-off effects. We measure significant quantities of C14H10 (likely phenanthrene and anthracene), as well as 2-ethynylnaphthalene (C12H8), from the reaction of the 2-naphthalenyl radical with C2H2; these results are consistent with the predictions of the kinetic model and the HACA mechanism, but contradict a previous experimental study that indicated no C14H10 formation in the 2-naphthalenyl + C2H2 reaction. In the 1-naphthalenyl radical + C2H2 reaction system, the primary product measured is C12H8, consistent with the predicted formation of acenaphthylene via HACA. The present work provides direct experimental evidence that single-radical HACA can be an important mechanism for the formation of PAHs larger than naphthalene, validating a common assumption in combustion models.
1 Introduction
The chemical mechanisms of polycyclic aromatic hydrocarbon (PAH) formation, growth, and partitioning into the particulate phase are not well understood despite their importance in accurately predicting the impact of PAHs on the environment. PAHs are molecules containing fused aromatic rings that are known to be produced in fuel-rich regions of combustion engines, industrial process streams, and interstellar media.1 Several PAHs are also classified as mutagenic and carcinogenic substances.2 Many experimental flame studies have linked PAHs with the formation of soot, a byproduct of combustion that decreases its efficiency and contributes to air pollution when emitted into the atmosphere.3 PAHs are also undesirable side products in many other industrial processes. Previous theoretical calculations have helped elucidate some of the complex chemistry involved, identifying several key mechanisms that are likely to be significant under combustion-relevant conditions.4–6A prevailing mechanism that rationalizes the formation of larger PAHs from 1- and 2-ringed aromatics is the hydrogen-abstraction-acetylene-addition (HACA) mechanism: an aromatic radical formed via hydrogen abstraction adds to acetylene (C2H2) to form a larger vinylic radical adduct.3,7–9 HACA can proceed via several different routes. The vinylic radical can add sequentially to another C2H2 to produce a larger conjugated intermediate for which ring closure is possible, or the vinylic radical can isomerize (e.g. to form a vinyl-substituted aryl radical), and then that isomer can add the second C2H2. At higher temperatures, the vinylic radical adduct rapidly undergoes H-atom loss to form an ethynyl-substituted aromatic species, which can undergo HACA again (by attack by a second H atom) to add a second C2H2 molecule. While a wealth of evidence exists from both indirect flame experiments and theoretical calculations linking the HACA mechanisms to PAH growth, few experimental studies have directly investigated the chemical kinetics of HACA.3,4,10 The chemistry of radical species derived from the simplest six-membered aromatic hydrocarbon, benzene, has previously been investigated using quadrupole mass spectrometry and cavity ringdown spectroscopy to measure the temperature-dependent rate of the reaction of phenyl radicals with C2H2.11–13 Recent investigations using photoionization mass spectrometry to probe phenyl radical (C6H5) reactions with C2H2 in the 500–800 K range have revealed an ion signal with a mass-to-charge ratio of 128 (m/z = 128) consistent with naphthalene, which is rationalized via the HACA mechanism with sequential H-atom loss and C2H2 addition.14,15
Combustion models commonly assume that naphthalene (C10H8), the simplest PAH, follows the HACA mechanism, in a manner similar to benzene, to form larger three-ring PAHs, an assumption that is corroborated by theoretical calculations.4,16 Hydrogen abstraction from naphthalene produces two distinct C10H7 radicals: 1-naphthalenyl and 2-naphthalenyl radicals. Sequential addition of C2H2 to these radicals can lead to different products. Theoretical investigations indicate that 1-naphthalenyl radical reactions with C2H2 preferentially form acenaphthylene (C12H8) via a C12H9 intermediate with a five-membered ring. On the other hand, the reaction of 2-naphthalenyl with C2H2 is expected to produce a vinylic adduct that can live long enough to undergo intramolecular hydrogen transfer followed by addition to a second C2H2 molecule and ring-closing to form either phenanthrene or anthracene (C14H10).4,10 These pathways of “two-to-three-ring” PAH growth compete with the β-scission pathways leading to loss of a hydrogen atom and formation of ethynylnaphthalene. At combustion temperatures and pressures, theory predicts acenaphthylene and ethynylnaphthalene isomers to be the major stable products of the naphthalene HACA mechanism,.4 But at lower temperatures the Bittner–Howard9 and modified Frenklach pathways17,18 are predicted to be significant for 2-naphthalenyl radical, leading to formation of significant amounts of phenanthrene and anthracene. (Both of these stable C14H10 species are commonly observed in flames.)
Only a few experimental investigations have been conducted to test these theoretical predictions. The reaction of 1-naphthalenyl + C2H2 was investigated in a shock tube experiment at temperatures above 950 K,19 and the kinetics of the 2-naphthalenyl + C2H2 reaction was measured using cavity ring-down spectroscopy following laser photolysis of bromonaphthalene at 303 to 448 K.20 The temperature-dependent rate coefficients for these reactions were in agreement with theoretical predictions.19,20 A product detection study for 1-naphthalenyl and 2-naphthalenyl reactions with C2H2 was recently conducted at temperatures up to 1500 K using mass spectrometry to monitor products formed in a silicon carbide micro-reactor.21 Both radical isomer reactions led to products at m/z = 152, corresponding to acenaphthylene or ethynylnaphthalene, but surprisingly, no product formation at m/z = 178 corresponding to phenanthrene or anthracene, was observed.21
Recent theoretical calculations have been reported suggesting that addition of acetylene to 2-naphthalenyl radical at temperatures around 800 K will lead to formation of phenanthrene and anthracene.22 At around 800 K, the formation and branching of major stable products (including phenanthrene, anthracene, acenaphthylene, and ethynylnaphthalene) are expected to be highly sensitive to temperature. In order to reconcile previous investigations of the reaction mechanisms for growth from naphthalenyl radicals to three-ring species, direct experimental measurements of the time-resolved product distributions are needed.
In the current work, we perform direct measurements of the 1-naphthalenyl and 2-naphthalenyl radical reactions with C2H2 to test the validity of a kinetic model recently developed within our group.22 Vacuum-ultraviolet photoionization time-of-flight mass spectrometry (VUV-PI-TOF-MS) is used to measure the time-dependent product formation at 500 to 800 K and 15 to 50 torr. Products from the first and second C2H2 addition are observed and the results compared with the kinetic model from Chu et al.22 Potential explanations for the observed kinetic behavior are discussed.
2 Experimental
For both the 1- and 2-naphthalenyl + C2H2 reactions, experiments were conducted at temperatures between 500 K and 800 K and total gas pressures between 15 torr and 50 torr. Experiments were carried out in a vacuum ultraviolet photoionization time-of-flight mass spectrometry (VUV-PI-TOF-MS) apparatus previously described in literature23,24 and only briefly described here. The apparatus features a bow-tie shaped quartz flow reactor enclosed in a stainless steel high-vacuum chamber (pressure: 10−5–10−8 torr) equipped with two quartz windows to allow laser access for photolysis of the radical precursor. The reactor includes two wide outer sections (inner diameter = 36 mm; length = 295 mm each) and a narrower middle section (inner diameter = 16 mm; length = 400 mm). The wider sections of the reactor enable measurements with laser absorption spectroscopy, which has been used in some studies; however, the present work only focuses on VUV-PI-TOF-MS. A pinhole (diameter = 300 ± 25 μm) was laser drilled into the middle section of the reactor to allow the escape of gases from the reactor into the high-vacuum chamber.6 A skimmer was used to sample the gas passing through the pinhole, producing a supersonic molecular beam containing the gas-phase species, which then underwent photoionization. The cations produced are detected by reflectron time-of-flight mass spectrometry.The radical precursors 1-iodonaphthalene (obtained from Sigma Aldrich, 97% purity) and 2-iodonaphthalene (obtained from Oakwood Chemicals, >98% purity) were degassed with several freeze–pump–thaw cycles using liquid nitrogen. Samples of 1-iodonaphthalene and 2-iodonaphthalene were analyzed by proton NMR to assess potential contamination by the opposing isomer. No significant peak of opposing isomer was found from each precursor, and it is reasonable to conclude that opposing isomer contamination is less than 0.5% (The H-NMR analysis can be found in Fig. S1 and S2 in the ESI†). Control experiments were also performed using 1-bromonaphthalene (Sigma Aldrich, 97% purity) and 2-bromonaphthalene (Sigma Aldrich, 97% purity) instead of each corresponding iodonaphthalene.
Throughout each experiment, a mixture of radical precursor (usually 1- or 2-iodonaphthalene), excess C2H2 (Airgas, ≥99.5%), and helium bath gas (Airgas, >99.999%) flowed continuously through the reactor. The gas mixture was created by bubbling a stream of helium with a backing pressure of 10 psig through the liquid iodonaphthalene in a heated bubbler at 70 °C. The resulting gas stream was then combined with the C2H2 stream (that was passed through an activated carbon filter to remove residual acetone) and a small flow of helium containing seven calibration gases (obtained from Airgas: propylene, 80.00 ppm; 1,3-butadiene, 97.27 ppm; benzene, 88.00 ppm; furan, 97.52 ppm; cyclohexane, 100.2 ppm; toluene, 80.00 ppm; and n-heptane, 99.97 ppm; analytical uncertainty ±2%) used to calibrate the time-of-flight mass spectrometer response.23 The pressure inside the reactor was controlled by a butterfly valve on the reactor outlet to a Roots type blower (Leybold). Flow rates were controlled using mass flow controllers (MKS Instruments, USA). The lines between the bubbler and the reactor inlet were heated to >70 °C to prevent condensation. The total flow rate was adjusted during experiments so the gas in the reactor was completely refreshed every 1 s. The quartz reactor was heated to temperatures from 500 to 800 K with Nichrome ribbon wire wrapped around the exterior of the tube. Two K-type thermocouples inside the reactor were used to control the experimental temperature. The gas temperature profile throughout the length of the reactor was characterized prior to experiments with a thermocouple extended inside the reactor, and found to be constant within ±2% (2 standard deviations) in the main sampling region (center ±5 cm).
In each experiment, a pulsed 266 nm Nd:YAG laser (Spectra-Physics Quanta-Ray, fourth harmonic) with a repetition rate of approximately 1 Hz was directed co-axially along the reactor to generate 1- or 2-naphthalenyl radicals from the radical precursor in the flowing gas mixture, initiating the radical chemistry. The reaction products were monitored using VUV-PI-TOF-MS to probe the molecular beam of gas sampled from the reactor as mentioned above. The VUV ionizing radiation was produced by a pulsed 355 nm Nd:YAG laser (Quantel Brilliant, third harmonic) focused into a stainless steel cell containing 90 torr of Xe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar (1
Ar (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) gas.25,26 The resulting 118.2 nm (10.49 eV) light was directed through an off-axis MgF2 lens through a small hole to physically separate the VUV radiation from the remaining 355 nm light.25,27 The VUV beam then intersected with the molecular beam of sampled gas, producing ions that were collected and focused into a reflectron time-of-flight mass spectrometer (Kore Technology). The resulting mass spectrum was averaged over 150 photolysis laser shots, and the peak at each m/z of interest was integrated to obtain the signal intensity. Changes in signal intensity with reaction time were measured by varying the time delay between the photolysis laser pulse and the VUV photoionization laser pulse. Several spectra were also collected before the photolysis pulse for a background subtraction, so changes in 266 nm laser dependent signal can be analyzed for kinetic information. Additional corrections were made for signals originating from the natural abundance of 13C; assuming that m/z = 152 signal entirely originated from C12H8 and there was no iodo compounds interference by HCCI and C2H2I. In the case of the m/z = 153 signal, which was attributed to both C12H9 radicals and the 13C isotopologue of C12H8 (the mass spectrometer resolution was not high enough to distinguish these two species), the processed signal intensity for C12H9 (Sexptm/z=153) reported in the figures here was calculated as
10) gas.25,26 The resulting 118.2 nm (10.49 eV) light was directed through an off-axis MgF2 lens through a small hole to physically separate the VUV radiation from the remaining 355 nm light.25,27 The VUV beam then intersected with the molecular beam of sampled gas, producing ions that were collected and focused into a reflectron time-of-flight mass spectrometer (Kore Technology). The resulting mass spectrum was averaged over 150 photolysis laser shots, and the peak at each m/z of interest was integrated to obtain the signal intensity. Changes in signal intensity with reaction time were measured by varying the time delay between the photolysis laser pulse and the VUV photoionization laser pulse. Several spectra were also collected before the photolysis pulse for a background subtraction, so changes in 266 nm laser dependent signal can be analyzed for kinetic information. Additional corrections were made for signals originating from the natural abundance of 13C; assuming that m/z = 152 signal entirely originated from C12H8 and there was no iodo compounds interference by HCCI and C2H2I. In the case of the m/z = 153 signal, which was attributed to both C12H9 radicals and the 13C isotopologue of C12H8 (the mass spectrometer resolution was not high enough to distinguish these two species), the processed signal intensity for C12H9 (Sexptm/z=153) reported in the figures here was calculated as
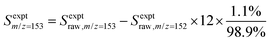 | (1) |
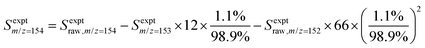 | (2) |
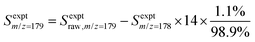 | (3) |
The mass spectrometric signal intensities corresponding to the calibration gases were recorded and were found to be constant over the reaction time studied apart from the benzene signal at m/z = 78 that overlaps with products formed during the reaction (standard deviation ≤5.05%); experiments were performed with and without the calibration mixture to confirm its insignificant effect on the C10H7 + C2H2 reaction system. The calibration gas signals were averaged over all delay times and the response factor (Ri) for the time-of-flight mass spectrometer was determined using their VUV photoionization cross sections at 10.49 eV (listed in ESI†) and known concentrations.23Ri values at each m/z (excluding one outlier for propylene, as well as the Ri value for m/z = 78 that contained interference from side reactions) were averaged to obtain the average response factor R. This response factor was used to determine expected integrated mass signals for reaction products predicted from the kinetic model, as described in the following section.
An unexpectedly large m/z = 154 signal (bigger than expected from the 13C satellite) was formed in the 2-iodonaphthalene + C2H2 experiments indicating the expected C12H9 (m/z = 153) product was picking up an H atom from an unknown source. Removing the C2H2 revealed the same sort of thing: in addition to the expected m/z = 127 signals from C10H7 and from I atom, an unexpectedly large signal was seen at m/z = 128 suggesting C10H8 formation. From these observations and several control experiments, we are confident that a reaction happened inside the pinhole in the reactor wall leading to the mass spectrometer (see Fig. S3 and the discussion in the ESI†). In prior work by Buras et al.,24 a similar phenomenon was observed when phenyl iodide was photolyzed: not just C6H5 (m/z = 77) was formed, but also an unexpectedly large amount of m/z = 78 suggesting the phenyl radical was picking up an H atom somewhere. The excess m/z = 154 signal tracks the computed concentration of C12H9. We hypothesize that some fraction of the very reactive aryl and vinylic radicals being sampled abstract H atoms in a wall reaction occurring at or inside the pinhole, so this is an artefact of our reactor sampling system. This is discussed further below.
3 Kinetic modeling
To model experimentally measured reaction rates and product branching ratios, we constructed an elementary-step reaction mechanism containing the reactions involved in the 1-naphthalenyl + C2H2 and 2-naphthalenyl + C2H2 systems recently computed at the G3(MP2,CC) level of theory by Chu et al.22 This model chemistry included several new species and pathways in addition to the previously reported potential energy surface from Kislov et al.4 An accurate model for the present experiments required inclusion of several side reactions not discussed by Chu et al. or Kislov et al., but fortunately values for many of the rate coefficients of the side reactions (involving e.g. vinyl radicals and iodine atoms) were presented previously in the literature.19,28,29The full reaction mechanism with rate coefficients and thermochemical parameters and their sources is given in CHEMKIN format in the ESI.† A few of the rate coefficients were newly-estimated in this present work, see Table S1 in the ESI.† We simulated the experiments modeling the reactor as isobaric, isothermal, and well-mixed (homogeneous), using the model simulator included in the Reaction Mechanism Generator (RMG) suite package.30 Sensitivity analysis was done using the Reaction Mechanism Generator (RMG) suite package.30 Rate of Production analysis (ROP) was done using the Reaction Mechanism Simulator (RMS).31
In our apparatus the mass spec signals did not show perfectly sharp changes when the time delay between the photolysis and photoionization laser pulses was varied, but instead had a finite rise time of several hundred microseconds. As discussed by Middaugh et al.23 this was due to several factors, most importantly diffusion of molecules across the thin gap between the photolyzed region and the pinhole, and also velocity dispersion in the pinhole and in the molecular beam. Following Middaugh et al. we modeled this by including a first-order sampling rate. This sampling rate was fitted to the experimentally observed rise time of the m/z = 127 signal, which was predominantly due to I atoms formed on a nanosecond timescale by the photolysis pulse. The inferred sampling rate (ks) from the fits varied from 1200–1800 s−1. There was slightly higher uncertainty in the sampling analysis for this system than in previous experiments made using this apparatus, because there were some other species contributing to the m/z = 127 signal in the mass spectra, most importantly C10H7. This was discussed in detail in the ESI.†
The chemical kinetics of this low-temperature system mostly follows the Bittner–Howard9 and modified Frenklach routes.17,18 Different from the Frenklach route that is important in high-temperature systems,7,8,32 these lower-temperature routes only require one radical that can add first one and then a second C2H2 to form larger PAHs, so reaction rates of the low-temperature routes are first order in radical concentration. However, in the experiments there are some second-order disproportionations and recombination reactions that noticeably affect the measurements. In order to account for the second-order reactions in the simulations, one needs an estimate of the absolute radical concentration formed by the photolysis flash. We obtained that value from the amplitude of the m/z = 127 signal, using the known photoionization cross-section of I atom and various calibrations. The uncertainty in this estimate of the initial radical concentration, due in part to other species contributing to the m/z = 127 signal, and also due to the reactions of I atom, was discussed in the ESI† (Fig. S4). Because the second-order reactions are much slower than the first-order reactions at the reaction conditions of interest, this uncertainty in the absolute radical concentration does not affect the main findings of this work.
The resulting model predicted time-dependent concentration of each species j (with molecular weight m/z = i), Cmodelj(t), were summed over and converted to a value that can be compared to the experimentally measured and processed ion signal intensity at m/z = i (Sexpti(t)) using eqn (4)
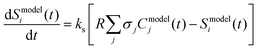 | (4) |
| m/z | Species | PICS (Mb) | 2σ Uncertainty (Mb) | Ref. |
|---|---|---|---|---|
| a Assumed with a 50% uncertainty. b Assumed to have the same PICS as 2,3-dihydro-2-naphthalenyl radical. c Assumed to have the same PICS as 2-propenyl radical. d Assumed to have the same PICS as C4H5I. | ||||
| 152 | Acenaphthylene | 54 | ±27a | 36 |
| 152 | (1-,2-)Ethynylnapthalene | 54 | ±27a | 36 |
| 153 | C12H9 RSR species | 24 | ±12a | 36 |
| 153 | C12H9 non-RSR species | 5 | ±3a | 33 |
| 154 | (1-,2-)Vinylnaphthalene | 61 | ±31a | 36 |
| 154 | C2H3I | 50 | ±15 | 28 |
| 178 | Phenanthrene | 30 | ±15a | 37 and 38 |
| 178 | Anthracene | 31 | ±16a | 37 and 38 |
We can classify radicals into resonance-stabilized radicals and non-resonance-stabilized radicals. Resonance-stabilized radicals (RSR) are free radicals that are stabilized by delocalizaion (resonance). The benzyl radical (C7H7) is one example. Non-resonance-stabilized radicals are those where in all the important Lewis structures the radical remains on the same atom, i.e. the SOMO is not conjugated with a π system or free electron pair or empty valence orbital. The phenyl radical (C6H5) is one example of a non-resonance-stabilized radical: although there is a lot of resonance in the π system of phenyl, the SOMO is in the plane of the ring, orthogonal to the π orbitals, so it is not conjugated. For C12H9 non-resonance-stabilized radicals (non-RSR), their PICS were assumed to be same as that of 2-propenyl radical that is also a non-RSR: 5 Mb.33 Radicals that have one electron in their HOMO are expected to have lower PICS than closed-shell molecules that have two electrons in their HOMO since the electron is ejected from lower occupancy. For example, Xu and Pratt's model expects the PICS of radical species to be half that of the analogous closed-shell species.34 However, aromatic (RSR) have been observed to have higher PICS compared to non-RSR, e.g. the benzyl radical PICS = 25.5 Mb.35 For this reason, C12H9 RSR PICS were assumed to be the same as that of 2,3-dihydro-2-naphthalenyl radical (24 Mb), which is also a RSR.36
The amplitude of the integrated mass signals measured in the experiment can vary daily with the reactor alignment, the laser pulse energies, and other instrument parameters. In order to correct for these variations, the experimentally observed integrated mass signals for each m/z were normalized to the experimentally observed integrated mass signals at m/z = 127 (mainly I atom) recorded at the time after photolysis when the m/z = 127 integrated mass signal reached its peak. This normalizing process was based on the assumption that the peak intensity was unchanged throughout each experimental set (i.e. different delay times but otherwise same experimental conditions, measured on the same day). These normalized integrated MS signals were compared with model-predicted integrated MS signals that also were normalized to those of model-predicted I-atom signal intensity, i.e. we are comparing predicted and experimental product yields per radical introduced. This procedure not only corrects for experimental variations, but also removes the uncertainty in the response factor R.
4 Results and discussion
4.1 Time-of-flight mass spectrometry
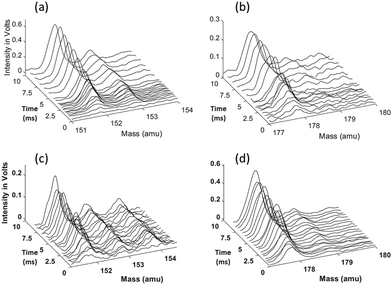
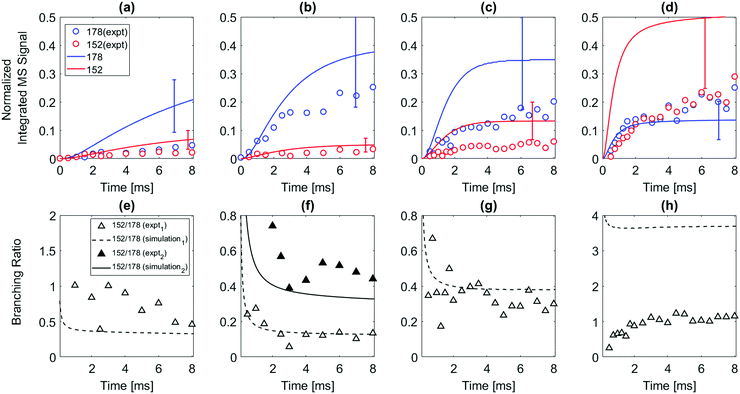
The 1- and 2-naphthalenyl radicals (C10H7, m/z = 127) are generated within the flow reactor by photolysis of 1-iodonaphthalene (C10H7I, m/z = 254), and separately 2-iodonaphthalene, and react with excess C2H2 to form products detected by VUV-PI-TOF-MS (PI energy = 10.49 eV). Fig. 1 shows representative mass spectra acquired after photolysis of the iodinated radical precursors in the presence of (C2H2).The m/z = 152 ion signal shown in Fig. 1 is attributed to C12H8 isomers following C2H2 addition to naphthalenyl radicals and subsequent H-atom loss. The m/z = 153 signal is assigned to the C10H7 + C2H2 adduct (C12H9) isomers and the 13C isotopologues of C12H8. The m/z = 178 raw signals are due to C14H10 isomers and can be rationalized by a HACA mechanism with a total of two C2H2 additions.
Ion signals with m/z = 42, 54, 68, 84, 92, and 100 correspond to the calibration mixture described in the Experimental section and do not exhibit a noticeable change in signal intensity with reaction time (i.e. delay between photolysis and photoionization lasers).
Time-dependent signals at m/z = 52 (C4H4), 53 (C4H5), 78 (C6H6), and 79 (C6H7) are likely the result of side reactions detailed by Smith et al.28 Time-dependent signals at m/z = 126, 128, 154, 179, and 180 were also measured. The small signal at m/z = 126 rises immediately after photolysis, suggesting either C10H6+ is formed by dissociative ionization of the C10H7 after photolysis of C10H7I, or a minor photolysis mechanism forming naphthyne (C10H6) followed by its photoionization. The signal at m/z = 128 can be attributed to several sources: (i) the 13C isotopologue of C10H7, (ii) naphthalene (C10H8), and (iii) hydrogen iodide (HI). The m/z = 154 signal can be attributed to 13CC11H9, 13C2C10H8, C12H10, and plausibly C2H3I from C2H3 + I recombination (after C2H2 + H).28 The m/z = 179 signal is attributed to the convolution of the 13CC13H10 isotopologue of the C14H10 products and the 13CC3H3I isotopologue of the C4H3I products. The observed m/z = 180 signal is predominantly attributed to C4H5I from C4H5 + I, and also partially to vinyl radical (C2H3) recombination with the C12H9 radicals. Since the formation of C14H11 is predicted to be minor based on the model prediction, the contribution to this signal from C14H11 + H should be negligible.
All the major reaction products observed in the mass spectra (Fig. 1) are predicted by the model for both the 1-naphthalenyl + C2H2 and 2-naphthalenyl + C2H2 reaction systems, except for the signal at m/z = 178 observed from 1-naphthalenyl + C2H2. These observed mass spectra and the predictions of the kinetic model are explained further in the following sections.
4.2 Naphthalenyl + acetylene reaction kinetics
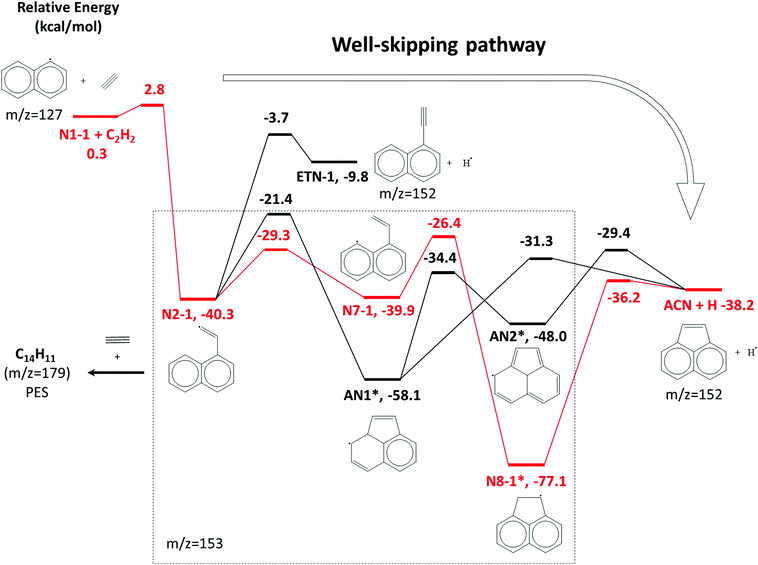 | ||
| Scheme 1 A part of the C12H9 potential energy scheme from Chu et al.22 The primary reaction pathway for 1-naphthalenyl + C2H2 predicted by the kinetic model under the experimental conditions in this work is shown in red lines. The asterisks indicate C12H9 RSR species. | ||
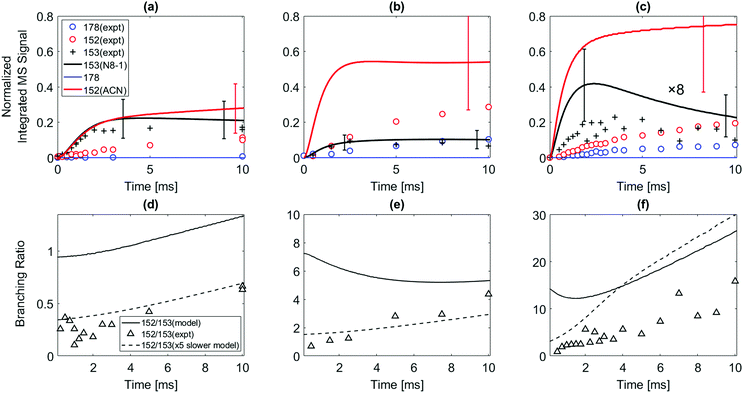
The model predicts an increasing product branching ratio of acenaphthylene (m/z = 152) to N8-1 (m/z = 153) with increasing temperature, consistent with the experimental data shown in Fig. 2d–f. This behavior is attributed to the increased rate of well-skipping reaction at higher temperatures (1-naphthalenyl radical + C2H2 → ACN + H, shown in Scheme 1), which favors ACN formation over N8-1 formation. At every set temperature condition, the initial steep increase of ACN observed in the experiments up until 2 ms (Fig. 2a–c) is attributed to rapid well-skipping reactions as assessed by the Rate Of Production (ROP) analysis shown in Fig. S12 (ESI†), up to 0.5 ms. This steep increase is followed by relatively slow formation of acenaphthylene through disproportionation reactions (N8-1 + I → ACN + HI). At 700 K, the steep increase is followed by relatively flat line, which indicates no significant acenaphthylene formation after the well-skipping reaction is exhausted (due to consumption of the initial C10H7 radical). At 800 K, the steep increase due to well-skipping reaction is followed by gradual increase due to disproportionation with I atom (N8-1 + I → ACN + HI). The switch in mechanism is easy to see in Fig. 2f where the product branching ratio of m/z = 152 to 153 stays relatively flat up until 2 ms and then gradually increases after 2 ms as the disproportionation reaction becomes more important than the well-skipping reaction of the initial reactants C10H7 + C2H2.
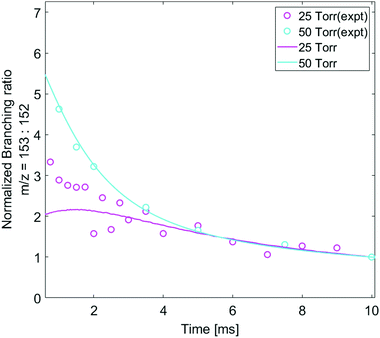
The pressure dependence of the observed and predicted 1-naphthalenyl + C2H2 product branching ratio was investigated at 25 and 50 torr. As shown in Fig. 3, up until 2 ms, the observed product branching ratio of m/z = 153 to 152 increases from 25 to 50 torr. This behavior might be attributed to increased collisional stabilization into m/z = 153 product well (predominantly N8-1) at higher pressure, which decreases the probability of well-skipping to acenaphthylene product. The m/z = 153 radical then slowly dissociates to yield m/z = 152 on a longer time scale. However, the observed pressure dependence is not as strong as predicted by the model. Discrepancies between the model and the experimental data will be discussed in a later section.
The model predicts most of the m/z = 152 signal observed when 2-naphthalenyl reacts with acetylene is due to 2-ethynylnaphthalene. According to ROP analysis (see Fig. S13, ESI†), at the conditions of these experiments, up until 600 K, the formation of m/z = 152 (2-ethynylnaphthalene) is predominantly due to disproportionation between I atom and the radical adduct, N2-2 (i.e. N2-2 + I → 2-ethynylnaphthalene + HI). However, it has to be noted that this I atom involved reaction is estimated. Without this disproportionation reaction with I atom, the model predicts formation of m/z = 152 at temperatures ≤600 K would be negligible. The formation of 2-ethynylnaphthalene is not sensitive to disproportionation above 700 K. As in the case of 1-naphthalenyl + C2H2, an initial sharp increase followed by slow increase in m/z = 152 formation can be observed in the model prediction for the 2-naphthalenyl + C2H2 system above 700 K. According to ROP analysis in Fig. S13 (ESI†), above 700 K most of the 2-ethynylnaphthalene product observed is due to β-scission of the initial adduct (N2-2). At the very shortest times, before much N2-2 has accumulated, the direct chemically activated pathway is also important.
In the model prediction, most of the m/z = 178 product is phenanthrene and anthracene (with a predicted branching ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 500 K and 1
1 at 500 K and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at higher T). At all the conditions of the present experiments, the ROP analysis (see Fig. S15 and S16 of ESI†) shows that the formation of m/z = 178 is predominantly due to second acetylene additions to N2-2, N8-2, and N11-2 directly forming m/z = 178 plus H atom; see Scheme 2. Phenanthrene formation in the model is predominantly determined by N2-2 + acetylene well-skipping reaction at every temperature. Anthracene formation is mostly attributed to N2-2 + acetylene well-skipping reaction up to 600 K, but at temperatures above 700 K, N11-2 + acetylene well-skipping reaction becomes more important for Anthracene formation. In the model prediction, for temperatures ≥700 K, most of radical adducts (i.e. N2-2, N8-2, and N11-2) are consumed within 3 ms, leading to the flattening in the profiles (Fig. 4c and d).
1 at higher T). At all the conditions of the present experiments, the ROP analysis (see Fig. S15 and S16 of ESI†) shows that the formation of m/z = 178 is predominantly due to second acetylene additions to N2-2, N8-2, and N11-2 directly forming m/z = 178 plus H atom; see Scheme 2. Phenanthrene formation in the model is predominantly determined by N2-2 + acetylene well-skipping reaction at every temperature. Anthracene formation is mostly attributed to N2-2 + acetylene well-skipping reaction up to 600 K, but at temperatures above 700 K, N11-2 + acetylene well-skipping reaction becomes more important for Anthracene formation. In the model prediction, for temperatures ≥700 K, most of radical adducts (i.e. N2-2, N8-2, and N11-2) are consumed within 3 ms, leading to the flattening in the profiles (Fig. 4c and d).
When the temperature increases from 500 to 600 K, the model predicts that the product branching ratio of m/z = 152 to m/z = 178 decreases as shown in Fig. 4e and f. This behavior is due to increased rate of well-skipping reaction to form three-ring PAHs (i.e. phenanthrene and anthracene). (At these low temperatures, the main pathway to m/z = 152 is radical disproportionation with I atom, which is much less sensitive to temperature.) However, from 700 to 800 K, when the temperature is high enough for significant β-scission of N2-2, the model predicts that the branching ratio shifts to favor m/z = 152 formation over m/z = 178 as shown in Fig. 4g and h. At high temperatures, the three radical adducts N2-2, N8-2, and N11-2 rapidly interconvert, so they are partially equilibrated. As the temperature increases, fewer of these radical adducts are collisionally stabilized, and also the β-scission of thermalized N2-2 to m/z = 152 + H becomes more important. This explains why the yield of m/z = 178 drops in the model (and less dramatically in the experimental data) as temperature increases from 700 K to 800 K, Fig. 4. Different acetylene concentration was also tested as shown in Fig. 4f. While maintaining all the other experimental condition same, only acetylene concentration was reduced from 3 × 1016 molecules per cm3 to 1 × 1016 molecules per cm3 compensating with additional helium. As expected from the model prediction, this results in increased branching ratio of m/z = 152 to m/z = 178 due to decreased rate of second acetylene addition to m/z = 153 (forming m/z = 178). The experimental data (black triangles) show reasonable agreement with the model prediction (solid black line).
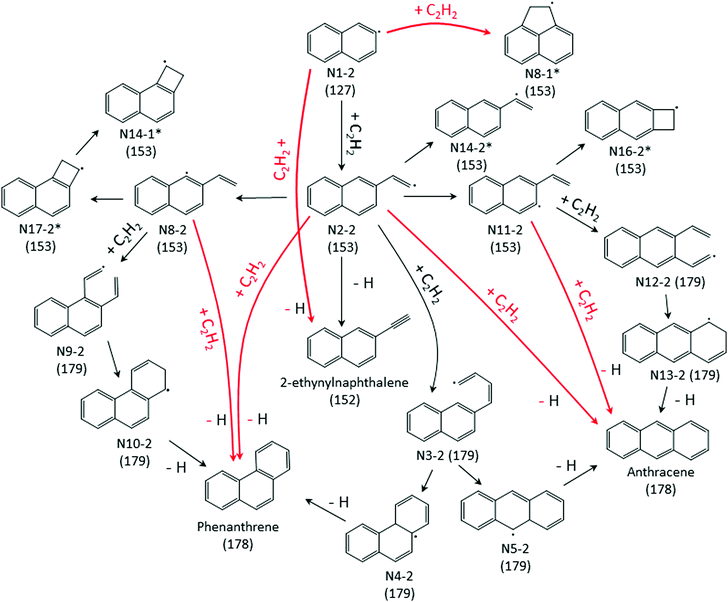
While the m/z = 153 signal from 1-naphthalenyl radical + C2H2 is mostly predicted in the model to be resonance stabilized radical, N8-1, under every experimental condition in this study, there are at least six different C12H9 isomers predicted from the model of 2-naphthalenyl radical + C2H2, as shown in Fig. 5. As discussed further in later section, these model predicted C12H9 isomers can be categorized into two different species types: non-resonance stabilized radicals (non-RSR) and resonance stabilized radicals (RSR). As shown in Fig. 5a, the model suggests initial formation of C12H9 non-RSR species (N2-2, N8-2, and N11-2), followed by the appearance of C12H9 RSR species (N17-2, N16-2, and N14-2). When C12H9 non-RSR species are formed, these species go through various reactions depending on the temperature conditions: (i) disproportionation reaction with I atom, (ii) isomerization into C12H9 RSR species, (iii) second acetylene addition to form anthracene or phenanthrene, and (iv) β-scission reaction to form 2-ethynylnaphthalene. When the temperature is lower than 600 K, (i) and (iii) are dominant in the system. However, at temperatures ≥700 K, (ii) and (iv) become more important. According to ROP analysis at 700 K (see Fig. S16, ESI†), C12H9 non-RSR species are predicted to be formed and then rapidly consumed through second acetylene addition in early time scale, while a portion of non-RSR species isomerize to relatively stable RSR species. It has to be noted that although the amplitude of the blue dashed line (model predicted RSR species) in Fig. 5 a is comparable to red dashed line (model predicted non-RSR species), considering RSR species’ high PICS (about 5 times larger than that of non-RSR species) the actual concentration of RSR species would be more than 5 times lower than that of non-RSR species. This is because the isomerization from non-RSR species to RSR species is more than an order of magnitude slower compared to non-RSR species consumption rate. At higher temperature like 800 K, fast equilibrium between non-RSR and RSR species takes place. At the same time, non-RSR species are continuously consumed through increased rate of β-scission and partially through second acetylene addition, which results in the decrease of C12H9 at later time scale. The experimentally observed mass signal at m/z = 153 shows reasonable agreement with the model-predicted RSR species signal as shown in Fig. 5a at later time scale. However, it is surprising that the measured m/z = 153 signal is much lower than expected at short times (<2 ms). At these times one would expect (and the model indicates) that there should be a fairly high concentration of the newly formed non-RSR adducts. This discrepancy, which might indicate C12H9 non-RSR adducts (N2-2, N11-2, and N8-2) have an unusually small PICS, is discussed further below.
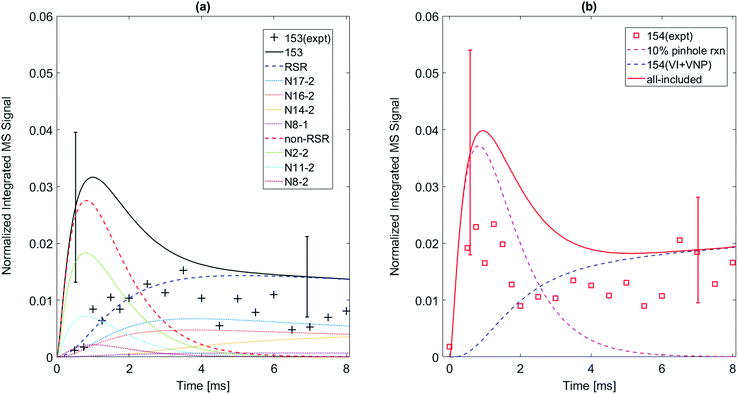 | ||
| Fig. 5 Model predictions (solid) vs. experimental data for m/z = 153 and m/z = 154 formed when 2-naphthalenyl radical is formed in an C2H2/He mixture at 700 K, P = 15 torr. Uncertainties in the predictions due to estimated PICS are shown as error bars. (a) Several isomeric C12H9 radicals are predicted to contribute significantly to the m/z = 153 signal, see Scheme 2. Most of the observed m/z = 153 signal is from long-lived resonantly stabilized radicals (N17-2, N16-2, N14-2, N8-1); their sum is the blue-dashed RSR curve. The model over-predicts signals from short-lived reactive non-stabilized m/z = 153 radicals (N2-2, N11-3, N8-2); their sum is the red-dashed “non-RSR” curve. This discrepancy may be due to low PICS of those radicals or fragmentation of their parent ions. (b) The early peak in the m/z = 154 signal (magenta dashed curve) is attributed to products from the m/z = 153 non-RSR formed in the pinhole (see text). The blue-dashed curve is the model's prediction of signal from stable m/z = 154 species (vinyl iodide, vinyl naphthalene) formed by slower secondary reaction sequences. | ||
The product distribution formed when 2-naphthalenyl radical is mixed with C2H2 was measured at a total gas pressure of 15 torr and 25 torr, with the pressure increased by adding more helium. As shown in Fig. S5 (ESI†), no significant pressure-dependent product branching ratio is observed.
4.3 Discrepancies between the model predictions and the experimental data
While the main observations (e.g. that 1-naphthalenyl + C2H2 primarily forms acenaphthylene, while 2-naphthalenyl + C2H2 primarily forms either C14H10 PAHs or 2-ethynylnaphthalene depending on the reaction conditions) are in concord with expectations and theoretical calculations, there are also several discrepancies between the model and the experimental data, discussed in detail below.For discrepancy (i), we consider two possible explanations: (i.1) error in the estimated PICS of acenaphthylene (54 Mb, ref. 36) or (i.2) the model overpredicts the rate coefficient for the well-skipping reaction 1-naphthalenyl radical + C2H2 → acenaphthylene + H. For explanation (i.1) to resolve the discrepancy, the estimated PICS of acenaphthylene in the literature would need to be about a factor of 3 too high, i.e. the true PICS would have to be around 18 Mb. This is possible, sometimes molecules have unexpectedly low photoionization cross-sections. The current model predicts m/z = 153 pretty well, suggesting that the uncertain estimated PICS for those isomeric radicals are not too far off. Changing the assumed PICS of acenaphthylene brings the model into much better agreement with the data (Fig. S17, ESI†), but there is still a discrepancy at long times at 800 K: experimentally the normalized m/z = 152 signal continues to grow, but the model predicts that the 152 growth should be much slower at long times right after 2 ms.
Considering alternative explanation (i.2) instead: as shown in Fig. S19a and b (ESI†), reducing the rate of the well-skipping reaction (1-naphthalenyl radical + C2H2 → ACN + H) by a factor of 5 significantly improves the agreement between the model prediction and the experimental data at temperatures ≤700 K. Reducing the rate of this well-skipping reaction also significantly improves agreement between the model and the experimental data on the branching ratio of m/z = 152 to 153 as shown in Fig. 2d–f, although at 800 K, the model is still over-predicting the branching ratio of m/z = 152 to 153 at longer timescale. A factor of 5 error in the computed rate coefficient is not impossible; it could be due to errors in the calculated reaction barriers or due to the Modified Strong Collision approximation that was used to calculate the pressure-dependent rate coefficients in Chu et al.22 Previous work by Allen et al.39 showed that this approximation often introduces errors of about a factor of 3 in calculated rate coefficients for chemically-activated reactions, so a factor of 5 error would not be surprising. However, explanation (i.2) is not sufficient to fully resolve the discrepancy: at 800 K, the adjusted model still over-predicts the rate of chemically-activated formation of acenaphthylene. But adjusting this one rate coefficient significantly improves the predicted product branching ratio between 152 and 153 in every experiment.
We conclude it is likely that discrepancy (i) is mainly due to combined effects of both uncertainties in PICS of acenaphthylene and errors in the well-skipping reaction's rate coefficient.
Discrepancy (ii) is the unexpected appearance of m/z = 178 signal from the experiments using 1-iodonaphthalene as a precursor at longer times, as can be observed in Fig. 2. Although m/z = 178 species such as phenanthrene and anthracene are predicted (and observed) to be major products from 2-naphthalenyl, none of the theoretical studies predict significant m/z = 178 formation from 1-naphthalenyl. However, m/z = 178 signals were not observed from experiments that use 1-bromonaphthalene as a precursor, which indicates that m/z = 178 peak is a result of iodine-dependent secondary chemistry. For more detailed discussion of this unexpected peak, which we believe is C4H3I, see the ESI.†
Discrepancy (iii): while the model and experiment are qualitatively in concord for the 2-naphthalenyl + C2H2 case, there are several quantitative discrepancies between the model predictions and measurements of the major products at m/z = 152 and m/z = 178 at certain temperatures. For example, at 500 and 700 K, the model over-predicts the formation of m/z = 178 about a factor of 3–4, and over-predicts the formation of m/z = 152 about a factor of 2–3. At 800 K, the model predicts the formation of m/z = 178 well up to 3 ms, but under-estimates it at longer time scale. In the case of m/z = 152 formation at 800 K, the model over-estimates the formation of m/z = 152 about a factor of 2–3 over time. One of course would not expect the model predictions to perfectly match the experimental data even if we knew the PICS to perfect accuracy, since the rate coefficients used in the model are somewhat uncertain. Here we consider whether modest variations in some of the rate coefficients, within their uncertainties, would be enough to resolve these quantitative discrepancies.
We computed the sensitivity of the main m/z = 152 and 178 species to all of the rate coefficients in the model (Fig. S24 and S25, ESI†). The most sensitive five reactions are
| N2-2 + C2H2 → Phenanthrene + H | (5) |
| N2-2 + C2H2 → Anthracene + H | (6) |
| N11-2 + C2H2 → Anthracene + H | (7) |
| N2-2 → 2-ethynylnaphthalene + H | (8) |
| N2-2 + I → 2-ethynylnaphthalene + HI | (9) |
They each have normalized sensitivities 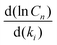 with magnitudes in the range of 0.3–0.8. The sensitivities for different products have different signs, and their magnitudes vary with temperature. There is no way to modify just one of the rate coefficients to resolve the discrepancies in m/z = 152 and m/z = 178 at all the temperatures. However, we find that there are combinations of reasonable modifications within the expected uncertainties of the rate coefficients that mostly resolve the discrepancies. For example, if one reduces I atom involved disproportionation rate coefficient (reaction (9)) by half, reduces β-scission rate coefficient (reaction (8)) by a factor of 5, and reduces well-skipping reaction rate coefficient (reaction (5)) by a factor of 5, the model is in pretty good agreement with the m/z = 152 and m/z = 178 data (see Fig. S26, ESI†).
with magnitudes in the range of 0.3–0.8. The sensitivities for different products have different signs, and their magnitudes vary with temperature. There is no way to modify just one of the rate coefficients to resolve the discrepancies in m/z = 152 and m/z = 178 at all the temperatures. However, we find that there are combinations of reasonable modifications within the expected uncertainties of the rate coefficients that mostly resolve the discrepancies. For example, if one reduces I atom involved disproportionation rate coefficient (reaction (9)) by half, reduces β-scission rate coefficient (reaction (8)) by a factor of 5, and reduces well-skipping reaction rate coefficient (reaction (5)) by a factor of 5, the model is in pretty good agreement with the m/z = 152 and m/z = 178 data (see Fig. S26, ESI†).
We note that this by no means a firm determination of the rate coefficients for these 5 reactions – there are too many model parameters and too few experimental data to allow a unique determination of the model parameters (and keep in mind that there are a large number of uncertain PICS) and several other moderately sensitive rate coefficients in the model, not just these 5 most sensitive reactions. However, the fact that modest adjustment of a few rate coefficients can bring the model into much better agreement suggests that quantitative discrepancy (iii) is not indicating a fundamental problem, but is more a reflection of our imperfect knowledge of the values of the model parameters.
Discrepancy (iv): while small adjustment of the 5 most sensitive rate coefficients can resolve most of discrepancies for m/z = 152 and m/z = 178, it doesn't resolve the discrepancy between the model and the data on m/z = 178 at 700 and 800 K at long times (>4 ms). According to our model, the C14H10 formation chemistry should essentially be over by this time, so the model trajectory is quite flat at long times. We hypothesize that the additional 178 signal growing in at long times (Fig. 5c and d) is not C14H10, but instead is C4H3I formed by some unknown secondary iodine chemistry, as is seen in the 1-naphthalenyl + C2H2 experiments (see Section 4.3.1). To test this hypothesis, we repeated the 2-naphthalenyl + C2H2 experiment using 2-bromonaphthalene instead of 2-iodonaphthalene as the precursor. The results are shown in Fig. S21b and S27, and discussed more in the ESI.† In the iodine-free system, we still observe m/z = 178 formation at short times from the expected hydrocarbon chemistry (e.g.reactions (5)–(7) above). But in the absence of any source of iodine, we no longer see the extra m/z = 178 growth at long times, consistent with the hypothesis.
Discrepancy (v): the model prediction for m/z = 153 at 700 K matched the experimental data fairly well for times >3 ms, but predicted a strong signal at shorter times which was not observed. As previously mentioned in Section 4.2.2, this could happen if the C12H9 non-RSR species had an unusually small PICS, while their RSR isomers have normal PICS. According to the model, the very reactive non-RSR C12H9 species are formed first but are quickly consumed, while the stabler RSR isomers have long lifetimes. This hypothesis is consistent with the experimental observation in Fig. 5a. Similar data on m/z = 153 at other experimental conditions are presented in the ESI.† As you can see from Fig. 5a, the model predicts that most of the m/z = 153 signal at early times (<3 ms) is due to C12H9 non-RSR species, where there is a model-data discrepancy (since the model assumes a normal PICS for all non-RSR radicals). However, after 3 ms, the model predicts most of the m/z = 153 signal is due to C12H9 RSR species, and at those times the model shows reasonable agreement with experimentally observed m/z = 153 signals. So, we conclude it is likely that discrepancy (v) is mainly due to the unusually small PICS of C12H9 non-RSR species. The unexpectedly low PICS is unfortunate, since it means we cannot directly observe time-dependent behavior of C12H9 non-RSR species which are predicted to be important at early times (<3 ms). However, we can observe the time-behavior of C12H9 non-RSR species indirectly, taking advantage of a side-reaction discussed in the following section.
4.4 The effect of side reactions
The chemical kinetic analysis of the time-dependent product signal is affected by side reactions that perturb measured signal intensities. The side reactions and how they are addressed are described in the following section.Wall reactions are typically assumed to occur before the reactants and products reach the pinhole, and thus would influence the chemistry inside the reactor by acting as an additional sink for radicals. As the concentration of radicals decreases due to reactions with the wall, the stable product formed by the wall reaction is expected to gradually increase and then reach a plateau.24 However, the time behavior of both m/z = 154 and m/z = 128 in this study differs from the expected behavior for typical wall reaction: the signal rises and peaks at early reaction times, decreases with a time constant of 1–2 ms, and then increases at longer time scale again before stabilizing. This is not consistent with a wall reaction forming a stable product. (Note m/z = 154 is a stable closed shell hydrocarbon C12H10 which should have a long lifetime at our reaction conditions.) Hence, we hypothesize the observed behavior in Fig. 5b results from wall reactions within the pinhole in the reactor wall – referred to here as “pinhole reactions”, distinct from the typical wall reaction described above. The stable products formed in the pinhole reactions such as C12H10 rapidly flow out of the pinhole, and they do not diffuse back into the main reactor volume. Note the concentration of the stable m/z = 154 species in the main reactor volume is clearly much lower than it is inside the pinhole, otherwise the m/z = 154 signal would not decrease so rapidly.
We assume that the observed m/z = 154 signal shown in Fig. 5b can be attributed to some fraction of C12H9 radicals (m/z = 153) undergoing pinhole reactions. To estimate the effect of pinhole reactions on the kinetic model, we analyze the predicted concentrations of m/z = 153 products and compare their time behavior to the experimentally observed m/z = 154 signal. An agreeable fit is obtained by assuming that C12H9 resonance-stabilized radical (RSR) isomers leave the reactor without undergoing a pinhole reaction, while 10% of the much more reactive non-resonance-stabilized radicals (C12H9 non-RSR species) capture H atom at the pinhole and produce the signal at m/z = 154. This assumption is reasonable since RSR species are much less reactive than non-RSR species.15 The pinhole reaction product is assumed to be vinylnaphthalene (C12H10) under all tested experimental conditions (500–800 K; 15 and 25 torr) for the 2-naphthalenyl + C2H2 chemical mechanism (other conditions can be found in ESI†). As shown in Fig. 5b, the computed m/z = 154 signal intensity that accounts for pinhole reactions of 10% C12H9 non-RSRs can explain this early peak of m/z = 154 at around 1 ms. In the case of 1-naphthalenyl + C2H2, this behavior is not observed and easily rationalized because the m/z = 153 is predicted to be predominantly N8-1, a RSR.
This pinhole reaction assumption can be used to infer the behavior of non-RSR species at early reaction times. The initial increase of m/z = 154 intensity is attributed to reactions of the C12H9 non-RSRs in the pinhole when their concentration is high. Soon, C12H9 non-RSR concentration decreases through β-scission to form 2-ethynylnapthalene, or second acetylene addition to form phenanthrene or anthracene, consistent with the decrease of m/z = 154 as shown in Fig. 5b. The m/z = 154 signal seen at longer times (≥3 ms) after the C12H9 non-RSR concentration has decayed, is primarily due to products of secondary reactions occurring in the main reactor volume: recombination of C12H9 RSR isomers with H-atom and the recombination C2H3 + I → C2H3I.
4.5 Comparison with previous experimental study of the naphthalenyl + C2H2 reaction
There has been one previous fairly direct experiment that selectively formed 2-naphthalenyl radical in the presence of C2H2.21 In sharp contrast with the present work, the prior experiment failed to detect any C14H10 (e.g. phenanthrene, anthracene) formation, but we observe C14H10 (m/z = 178) as one of the major products.The yield of C14H10 is expected to strongly depend on several aspects of the reaction conditions: radical concentration, temperature, acetylene concentration, reaction time, and pressure. High radical concentrations are needed to drive the high-temperature Frenklach mechanism.7,8,32 The low-temperature Bittner–Howard mechanism9 relies on pressure to trap the initial radical adduct and a high acetylene concentration to react with that radical before it beta-scissions.
In the prior experiment, the 2-naphthalenyl radical was generated by pyrolysis of 2-iodonaphthalene, but in the present work the radical was generated by photolysis. (Also in the present work we did a control experiment using 2-bromonaphthalene as the radical precursor instead of 2-iodonaphthalene.) Photolysis generates approximately the same radical concentration in every experiment, mostly set by the number of photons in the flash, but in the pyrolysis experiment the radical concentration depends strongly on the temperature. As a consequence, the pyrolysis experiments become very challenging at low temperature, since only very small concentrations of radicals and products are generated. Lifshitz et al.29 reported the rate coefficient of 1-iodonaphthalene dissociation at 1000 K to be 4.84 s−1 at 1000 K. Assuming that the dissociation of 2-iodonaphthalene has a similar rate, this implies <0.1% of it dissociated to form radicals during the 0.1 ms timescale40–42 of Parker's experiments. Parker et al.21 say that they did not detect C14H10 “from room temperature to 1500 K”. But since the pyrolysis rate coefficient drops very rapidly with temperature, at room temperature the radical formation rate in Parker et al.'s21 apparatus must have been near zero. Because of the very small radical concentrations produced pyrolytically at low temperatures, we doubt that Parker et al.21 had sufficient signal-to-noise to measure products of radical reactions in the 500–800 K range of the experiments reported here. The lowest temperature data published by Parker et al.21 was measured at 1000 K.
Although one would expect problems at lower temperatures, at 1000 K, Parker et al.'s21 pyrolysis experiment definitely had enough sensitivity to detect C14H10 if it was a significant minor product. Indeed, in earlier work in the same apparatus, Parker et al.14 observed the analogous reaction of phenyl radical adding two C2H2's to form naphthalene, and measured that about 5% of the phenyl radicals followed this path rather than stopping after adding one C2H2. One would expect 2-naphthalenyl radical would behave similarly at 1000 K, with a few percent of the initial adduct adding a second C2H2 to form C14H10. We see both reaction pathways as being competitive at our conditions at 800 K (e.g. see Fig. 4d). The yield of C14H10 is expected to drop with temperature, but it remains an unresolved mystery why it apparently dropped very sharply from 800 to 1000 K, so C14H10 could not be detected at all in the higher temperature experiments. Eyeballing the Parker et al.21 data, it appears their experiment sets an upper bound on m/z = 178 signal of about 1% of their measured m/z = 152 (C12H8) product at 1000 K.
In contrast, the current measurements on 1-naphthalenyl + C2H2 are in reasonable concord with the prior experiments by Parker et al.21 and also by Lifshitz et al.29 The experiments and the models all agree that over a broad range of reaction conditions the major stable product from 1-napthalenyl + C2H2 is C12H8, primarily the isomers acenaphthalene and 1-ethynylnaphthalene.
5 Conclusions
Modelers expect 2-naphthalenyl radical will sequentially add 2 C2H2's in a HACA process to form the 3-ring C14H10 aromatics phenanthrene or anthracene, either via a stable intermediate 2-ethynylnaphthalene (the Frenklach mechanism7,8,32) at high temperature or via a reactive C12H9 radical adduct (e.g. the Bittner–Howard mechanism9 or the modified Frenklach mechanism17,18) at lower temperatures. There have been many modeling studies on this system over several decades, most recently by Chu et al.22 Phenanthrene and anthracene are often observed as products in real-world systems with high concentrations of acetylene and aromatics. However, this observation does not prove the hypothesized reaction mechanisms since many reactions are occurring in those systems, and there are usually no attempt to measure the naphthalenyl radicals. In the present work, for the first time, formation of C14H10 as a major product was observed in a direct experiment starting with 2-naphthalenyl radical, more or less consistent with model predictions.Here we report the first direct measurement of the time-dependent kinetic behavior and product distributions for the reactions of 1-naphthalenyl and 2-naphthalenyl radicals with C2H2, using VUV-PI-TOF-MS (PI energy = 10.49 eV) from 500 to 800 K and 15 to 50 torr. The reaction of 1-naphthalenyl radical with C2H2 led to product signal at m/z = 153, corresponding to a C12H9 radical intermediate, N8-1 in the model prediction; m/z = 152, corresponding to stable acenaphthylene (C12H8) in the model prediction; and m/z = 178, which was not expected in the model prediction, likely C4H3I based on the result from the control experiment. In the reaction of 2-naphthalenyl radical with C2H2, the main products are m/z = 152, corresponding to 2-ethynylnaphthalene (C12H8) in the model prediction; and m/z = 178, corresponding to phenanthrene and anthracene (C14H10) in the model prediction. Other products were observed at m/z = 153, corresponding to isomeric (C12H9) radicals in the model prediction; and m/z = 154, corresponding to the product formed after non-resonance stabilized radical isomers captured H-atom on the walls of the pinhole or at longer timescales from secondary chemistry (C12H10) as well as C2H3I formed from side reactions involving I atom. The experiments were compared with a model of the temperature-dependent kinetics constructed using ab initio quantum calculations by Chu et al.22 The model qualitatively described the 1-naphthalenyl radical + C2H2 temperature-dependent product branching ratio, but overpredicted the rate of production of m/z = 152 at every experimental condition. Furthermore, the model couldn't account for the formation of m/z = 178 (C4H3I) at temperature above 700 K. For 2-naphthalenyl radical + C2H2, the model predicted the product branching ratio between m/z = 152 and 178 fairly well at the temperature between 600 and 700 K; underpredicted at 500 K; and overpredicted at 800 K. However, the model captured qualitative temperature dependent behavior of product branching ratio for both reaction systems (1-naphthalenyl + C2H2 and 2-naphthalenyl + C2H2). As discussed in some detail here, inaccurate model parameters, errors in PICS, and mechanism truncation error may be responsible for the discrepancies between the model prediction and the experimental data. This work provides direct experimental evidence for formation of significant yields of tricyclic C14H10 PAHs from sequential addition of 2 acetylene molecules to 2-naphthalenyl radicals, in contrast with a recent report that suggested C14H10 products are not formed below 1500 K.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge SABIC and the FAA for financial support. We gratefully acknowledge Matt Johnson's help with RMG and RMS usage. We thank Prof. Alexander Mebel and Dr Istvan Lengyel for providing detailed theoretical calculations used to construct the kinetic model, and Yoshinaga Kosuke for H-NMR analysis. We thank Dr Musahid Ahmed and Dr Wenchao Lu for providing mass-spec data of supplementary 2-iodonaphthalene + C2H2 experiment at various photon energy.Notes and references
- M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. S. Gillette and S. J. Clemett, Science, 1999, 283, 1135–1138 CrossRef CAS.
- G. Grimmer, Environmental Carcinogens: Polycyclic Aromatic Hydrocarbons, CRC Press, 1983 Search PubMed.
- H. Richter and J. Howard, Prog. Energy Combust. Sci., 2000, 26, 565–608 CrossRef CAS.
- V. V. Kislov, A. I. Sadovnikov and A. M. Mebel, J. Phys. Chem. A, 2013, 117, 4794–4816 CrossRef CAS PubMed.
- A. M. Mebel, Y. Georgievskii, A. W. Jasper and S. J. Klippenstein, Proc. Combust. Inst., 2017, 36, 919–926 CrossRef CAS.
- T.-C. Chu, PhD thesis, Massachusetts Institute of Technology, 2020.
- M. Frenklach and H. Wang, Symp. (Int.) Combust., [Proc.], 1991, 23, 1559–1566 CrossRef.
- M. Frenklach, D. W. Clary, W. C. Gardiner and S. E. Stein, Symp. (Int.) Combust., [Proc.], 1985, 20, 887–901 CrossRef.
- J. D. Bittner and J. B. Howard, Symp. Combust. Proc., 1981, 18, 1105–1116 CrossRef.
- M. Frenklach, R. I. Singh and A. M. Mebel, Proc. Combust. Inst., 2019, 37(1), 969–976 CrossRef CAS.
- A. Fahr and S. Stein, Symp. (Int.) Combust., [Proc.], 1989, 22, 1023–1029 CrossRef.
- T. Yu and M. C. Lin, J. Am. Chem. Soc., 1993, 115, 4371–4372 CrossRef CAS.
- T. Yu, M. C. Lin and C. F. Melius, Int. J. Chem. Kinet., 1994, 26, 1095–1104 CrossRef CAS.
- D. S. N. Parker, R. I. Kaiser, T. P. Troy and M. Ahmed, Angew. Chem., 2014, 53, 7740–7744 CrossRef CAS PubMed.
- T.-C. Chu, Z. J. Buras, M. C. Smith, A. B. Uwagwu and W. H. Green, Phys. Chem. Chem. Phys., 2019, 21, 22248–22258 RSC.
- M. Frenklach and A. M. Mebel, Phys. Chem. Chem. Phys., 2020, 22, 5314–5331 RSC.
- N. W. Moriarty, N. J. Brown and M. Frenklach, J. Phys. Chem. A, 1999, 103, 7127–7135 CrossRef CAS.
- M. Frenklach, N. W. Moriarty and N. J. A. Brown, Symp. Combust. Proc., 1998, 27, 1655–1661 CrossRef.
- A. Lifshitz, C. Tamburu and F. Dubnikova, J. Phys. Chem. A, 2009, 113, 10446–10451 CrossRef CAS.
- J. Park, H. M. T. Nguyen, Z. F. Xu and M. C. Lin, J. Phys. Chem. A, 2009, 113, 12199–12206 CrossRef CAS PubMed.
- D. S. N. Parker, R. I. Kaiser, B. Bandyopadhyay, O. Kostko, T. P. Troy and M. Ahmed, Angew. Chem., 2015, 54, 5421–5424 CrossRef CAS PubMed.
- T.-C. Chu, M. C. Smith, J. Yang, M. Liu and W. H. Green, Int. J. Chem. Kinet., 2020, 52, 752–768 CrossRef CAS.
- J. E. Middaugh, Z. J. Buras, M. Matrat, T.-C. Chu, Y.-S. Kim, I. M. Alecu, A. K. Vasiliou, C. F. Goldsmith and W. H. Green, Rev. Sci. Instrum., 2018, 89, 074102 CrossRef.
- Z. J. Buras, T.-C. Chu, A. Jamal, N. W. Yee, J. E. Middaugh and W. H. Green, Phys. Chem. Chem. Phys., 2018, 20, 13191–13214 RSC.
- S. E. Van Bramer and M. V. Johnston, Appl. Spectrosc., 1992, 46, 255–261 CrossRef CAS.
- M. P. McCann, C. H. Chen and M. G. Payne, J. Chem. Phys., 1988, 89, 5429–5441 CrossRef CAS.
- Z. J. Buras, PhD thesis, Massachusetts Institute of Technology, 2018.
- M. C. Smith, G. Zhu, Z. J. Buras, T.-C. Chu, J. Yang and W. H. Green, J. Phys. Chem. A, 2020, 124, 2871–2884 CrossRef CAS PubMed.
- A. Lifshitz, C. Tamburu and F. Dubnikova, J. Phys. Chem. A, 2008, 112, 925–933 CrossRef CAS PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- M. S. Johnson, H. Pang, X. Dong and W. H. Green, Reaction Mechanism Simulator, https://github.com/ReactionMechanismGenerator/ReactionMechanismSimulator.jl.
- H. Wang and M. Frenklach, J. Phys. Chem., 1994, 98, 11465–11489 CrossRef CAS.
- J. C. Robinson, N. E. Sveum and D. M. Neumark, Chem. Phys. Lett., 2004, 383, 601–605 CrossRef CAS.
- H. Xu and S. T. Pratt, J. Chem. Phys., 2013, 139, 214310 CrossRef.
- Z. Zhou, M. Xie, Z. Wang and F. Qi, Rapid Commun. Mass Spectrom., 2009, 23, 3994–4002 CrossRef CAS.
- Y. Y. Li, J. Z. Yang and Z. J. Cheng, Edited by JiuZhong Yang and Combustion Team, Photonionization Cross Section Database (Version 2.0), 2017, http://flame.nsrl.ustc.edu.cn/database/.
- G. Malloci, G. Mulas and C. Joblin, Astron. Astrophys., 2004, 426, 105–117 CrossRef CAS.
- H. W. Jochims, H. Baumgartel and S. Leach, Astron. Astrophys., 1996, 314, 1003–1009 CAS.
- J. W. Allen, C. F. Goldsmith and W. H. Green, Phys. Chem. Chem. Phys., 2012, 14, 1131–1155 RSC.
- P. Chen, S. D. Colson, W. A. Chupka and J. A. Berson, J. Phys. Chem., 1986, 90, 2319–2321 CrossRef CAS.
- P. Chen, J. B. Pallix, W. A. Chupka and S. D. Colson, J. Chem. Phys., 1986, 86, 516–520 CrossRef.
- Q. Guan, K. N. Urness, T. K. Ormond, D. E. David, G. B. Ellison and J. W. Daily, Int. Rev. Phys. Chem., 2014, 33, 447–487 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01565f |
| This journal is © the Owner Societies 2021 |