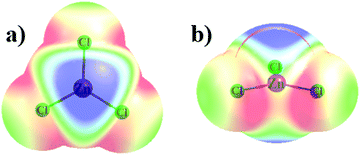Anion⋯anion (MX₃⁻)₂ dimers (M = Zn, Cd, Hg; X = Cl, Br, I) in different environments

Abstract

The possibility that MX₃⁻ anions can interact with one another is assessed via ab initio calculations in gas phase as well as in aqueous and ethanol solution. A pair of such anions can engage in two different dimer types. In the bridged configuration, two X atoms engage with two M atoms in a rhomboid structure with four equal M–X bond lengths. The two monomers retain their identity in the stacked geometry which contains a pair of noncovalent M⋯X interactions. The relative stabilities of these two structures depend on the nature of the central M atom, the halogen substituent, and the presence of solvent. The interaction and binding energies are fairly small, generally no more than 10 kcal mol⁻¹. The large electrostatic repulsion is balanced by a strong attractive polarization energy.

---

Introduction

The idea that ions of like charge can engage in stable complexes with one another has recently become a subject of intense scrutiny. Despite the obvious strong Coulombic repulsions which ought to hold these ions apart, there is an accumulating body of experimental data that supports the existence of such ion–ion complexes^1–9 in the context of ionic liquids and crystal solids. The explanation that has been offered in some cases concerns the ability of H-bonds to act as a glue between the two anions if they are drawn close enough together. A balance is achieved between long and short-range interactions, as well as directional and non-directional contacts between ions in ionic liquids.²

In comparison to cation-cation contacts, less data is available concerning the analogous anion–anion complexes. Such anion–anion interactions have been observed recently by Ganatra et al.¹⁰ in ionic liquids composed of mixtures of alkali halides/sodium acetate with sodium salt of butyric acid. The presence of anion–anion interactions was rationalized therein as the hydrophobic interaction between non-polar moieties (of high polarizability) which constitute the anions.¹⁰ Theoretical simulations of Miranda and co-workers treated the anion–anion interactions between aspartate dimers.¹¹ Complexes studied there had positive interaction energies in the gas phase but these quantities turned negative in aqueous solution due to hydration of the monomers which considerably reduced the anion–anion repulsion. In the gas phase it was found that the high energy barrier prevented the dissociation of subunits.¹¹ So far, similar results of metastable anion–anion complexes were also achieved by other researchers in the field of theoretical chemistry,^12–15 including works published by our own group.^16,17 Experimentally characterized structures containing anion–anion interactions have occurred in the literature for some time.^18–30 As an example, the work of Chesman et al. noted five crystal structures of salts consisting of functionalized methanide anions. It was suggested that three of them are stabilized by π–π stacking interactions between anions while in the remaining two the anion–anion attraction results from the presence of hydrogen-bonding interactions.²¹

The possibility of stacking interactions between a pair of anions motivated us to search for analogous inorganic systems, containing transition metal, without the assistance of any hydrogen bonds. The Cambridge Structural Database (CSD)³¹ shows 8 hits for searching criteria comprising trihalogenated transition metals in subunits of charge −1, linked to each other by intermolecular contacts shorter than the sum of vdW radii. Surprisingly, within the abovementioned group of crystalline solids discovered in the CSD survey it is only mercury that fits this description^20,32–38 where the Hg atom is engaged in unusual Hg⋯X (X = Cl, Br, I) interactions which stabilize anion–anion stacked polymeric chains. This particular type of interaction involving elements from the 12th group (Zn, Cd, Hg) with an electron-rich center has been introduced in literature very recently and baptized as spodium bond.³⁹ It has been earlier shown that this noncovalent interaction has a complicated nature which incorporates both coulombic forces and some degree of covalency.⁴⁰

The goal of the current work is a detailed investigation of the intriguing interanion stabilization in these crystal structures. We consider first whether such interactions between pairs of anions can be stabilizing, and how the nature and strength of each such interaction might be affected by the surrounding environment. To what specific forces can the attraction be attributed? How is the interaction affected by the identity of the central M atom and the three halogen ligands of the MX₃⁻ unit? The calculations confirm the experimental observation of two very different modes of binding of each pair of anions, and proceed to assess their relative stability, and their interconversion process.

Methods

Full optimization of the (MX₃⁻)₂ dimers (M = Zn, Cd, Hg; X = Cl, Br, I) as well as the isolated MX₃⁻ monomers were performed at the MP2/aug-cc-pVDZ level of theory.^41–43 The pseudopotential-containing aug-cc-pVDZ-PP basis set was used for metal and iodine atoms in order to incorporate relativistic effects.^44,45 The accuracy of the energies was tested against calculations at a higher level, namely CCSD(T)/aug-cc-pVDZ(-PP)^43–47 and MP2/aug-cc-pVQZ(-PP).^43–45 Harmonic frequency analysis verified optimized geometries represent true minima on the potential energy surfaces with no imaginary frequencies. Calculations were carried out in the gas phase and solution. The chosen solvents water (ε = 78.4) and ethanol (ε = 25.3) were simulated by the PCM (polarizable continuum model).⁴⁸ The interaction energy (E_int) of each complex was computed as the difference in total electronic energy between the fully optimized complex and its constituents in the geometries adopted within the complex, while the binding energy (E_b) takes as its reference the doubled value of the total electronic energy for the corresponding monomer in its fully optimized isolated state. The basis set superposition error (BSSE) was corrected via the counterpoise procedure introduced by Boys and Bernardi.⁴⁹ As the Gaussian package does not allow the calculation of BSSE corrections within the context of solvent, the corrections were taken from the calculations in the gas phase for systems in their solvent geometry. Single-point calculations at the MP2/aug-cc-pVQZ and CCSD(T)/aug-cc-pVDZ levels were performed for the MP2/aug-cc-pVDZ optimized geometry. Calculations were carried out with the Gaussian 16, Rev. C.01 code.⁵⁰ The MEP (molecular electrostatic potential) measures were assessed based on the values of its extrema on the 0.001 a.u. isodensity surface by the MultiWFN program.^51,52 MEP maps were visualized by the VMD software.⁵³ The AIM (atoms-in-molecules) method was engaged to elucidate bond paths and their topological properties by means of the AIMAll program.⁵⁴ Decomposition of the interaction energies was carried out through the LMOEDA protocol⁵⁵ realized in GAMESS-US (version 2020-R2) software.⁵⁶ Energy barriers were quantified by the QST2 approach of the Synchronous Transit-Guided Quasi-Newton (STQN) method.⁵⁷ The Cambridge Structural Database (CSD) supported the current study by providing X-ray structures similar to those studied in this work.³¹

Results

Monomers

The MX₃⁻ anions are planar units with D_3h symmetry in the gas phase, but with some small inequalities of the three M–X bond lengths in solution, in which the anions were not precisely planar. Optimized r(M–X) bond lengths are compiled in Table S1 (ESI†), where they may be seen to be between 2.2 and 2.8 Å. Not surprisingly these bond lengths are commensurate with the size of the atoms: Zn < Cd ≈ Hg and Cl < Br < I.

Consideration of the topography of the molecular electrostatic potential (MEP) surrounding each monomer offers clues as to the preference for the way in which the two might approach one another. The MEP shown in Fig. 1 is illustrated for ZnCl₃⁻ as representative of all MX₃⁻ anions where the least and most negative regions are indicated by blue and red colors, respectively. The blue area immediately above the central Zn atom corresponds to what has come to be known as a π-hole, although since the species involved is an anion, the potential in this area is negative. The value of V_s,max, the potential at a maximum of the MEP on an isodensity surface, is listed in Table 1 not only in the gas phase, but in both ethanol and aqueous solvent. It might also be observed that the potential surrounding the Cl atoms is most negative in the ZnCl₃ plane.

Fig. 1 MEP of ZnCl₃⁻ at the M06-2X/aug-cc-pVDZ level on a surface corresponding to 1.5 × vdW atomic radii from the (a) top and (b) side. Blue (−82 kcal mol⁻¹) and red (−107 kcal mol⁻¹) colors refer to least and most negative regions, respectively.

Table 1 MEPs of π-holes (global maxima, kcal mol⁻¹) of MX₃⁻ monomers, calculated at the MP2/aug-cc-pVDZ level of theory. Values of V_s,max along extensions of the MX bond are displayed in parentheses

Isolated molecule	Water	Ethanol	Gas
ZnCl3^−	−32.0 (−91.2)	−37.7 (−91.3)	−56.5 (−89.8)
ZnBr3^−	−38.4 (−83.3)	−39.9 (−83.1)	−56.6 (−81.6)
ZnI3^−	−35.5 (−72.1)	−40.0 (−72.2)	−56.7 (−71.6)
CdCl3^−	−7.2 (−94.2)	−10.2 (−93.7)	−44.9 (−89.1)
CdBr3^−	−7.3 (−84.7)	−9.1 (−84.2)	−45.9 (−80.9)
CdI3^−	−3.9 (−75.2)	−14.4 (−72.6)	−47.8 (−70.9)
HgCl3^−	−23.9 (−89.2)	−27.5 (−88.5)	−61.4 (−101.5)
HgBr3^−	−32.7 (−81.5)	−31.5 (−74.6)	−61.5 (−78.4)
HgI3^−	−27.8 (−67.4)	−36.6 (−68.9)	−61.9 (−68.8)

---

There are several trends apparent in the data in Table 1. First considering the gas phase data, V_max is least negative for Cd, followed by Zn and then by Hg with the most negative π-hole. The nature of the X halogen substituent has little effect on these quantities. Immersion of these anions in a polar medium makes each of these π-holes much less negative, particularly in water. Nonetheless, Cd retains its position as least negative π-hole followed now by Hg and then Zn. Within the context of solution, the nature of the X substituent plays a larger role, wherein Cl leaves the π-hole less negative than Br or I, although this pattern is not consistent throughout the set.

In addition to the π-holes above the M atoms, there are also secondary maxima near the X atoms, along the extensions of the M–X bonds. As shown by the parenthetical quantities in Table 1, these maxima are much more negative than the M π-hole, and so do not represent any sort of strong competition for a Lewis base. These secondary maxima, with σ-hole characteristics, are least negative for X = I and most negative for F.

Dimers

1. CSD survey. A critical survey of relevant crystallographic structures deposited in the Cambridge Structural Database (CSD) indicates that (MX₃)²⁻ anion···anion interactions fall into one of two distinct types of structural motif. In the first kind of structure (349 hits in CSD), two halogens bridge the two metal (Zn, Cd or Hg) atoms, forming a four-membered ring (which can be planar or slightly puckered). A diagram of this “bridging” structure is displayed in Fig. 2 for the (Hg₂Cl₆)²⁻ system, with refcode: BETPAR. The coordination of the Hg atom can be categorized as a deformed tetrahedron. Such geometries are not part of polymeric systems. For example, the r(Hg-Cl) bonds involving the bridging Cl atoms (Cl1 and Cl2 in Fig. 2) are quite different than those involving the other peripheral Cl atoms. As may be seen by the statistical data in Table 2, there are quite a number of bridging structures, especially for M = Hg.

Fig. 2 Example of bridged structure of (Hg₂Cl₆)²⁻, refcode: BETPAR.

Table 2 Detailed results of CSD survey (number of hits)

Atom	Cl	Br	I
	Bridged
Zn	51	11	2
Cd	8	7	39
Hg	91	39	101
	Stacked
Hg	4	3	1

---

Another structural motif is less common, wherein each MX₃⁻ unit is stacked above another. As illustrated in Fig. 3 for (HgCl₃)⁻₂, this stacking places each Hg directly above a Cl atom of the neighboring unit, such that each dimer contains a pair of Hg⋯Cl direct interactions. This stacked arrangement occurs far less often with only 8 instances, all of which involve Hg, as indicated in Table 2.^20,32–38 An essential difference between the stacked systems and bridged structures is the lack of a covalent bond between the two MX₃ units in the former, leaving the central Hg atom in its quasi-D_3h geometry. These stacked arrangement are also generally part of an extended polymeric geometry in a long (MX₃)_n chain.

Fig. 3 Example of stacked structure of (HgCl₃⁻)₂ (part of polymeric chain), refcode: TAGCAF.

2. Bridged structures. Geometry optimizations were carried out for bridged structures, as illustrated in Fig. 4, in vacuo as well as in ethanol and aqueous solution. The key geometric parameters of the bridged M₂X₆²⁻ systems are collected in Table 3. Each M atom is surrounded by four halogen X atoms. Two of these are bridging atoms X_b which are part of the four-membered ring, and the two peripheral atoms are labeled X_a. As may be seen in Table 3, the M–X bond lengths are what one would expect for covalent bonds, with r(M–X_b) slightly longer than r(M–X_a). The four-membered ring at its core contains 4 equivalent M–X bonds, but the overall ring is not quite square, with θ(X_b–M–X_b) angles slightly different than 90°. The strain within the ring reduces the θ(X_b–M–X_b) angles to be smaller than the tetrahedral angle, which is compensated by the larger θ(X_a–M–X_a) angles. A measure of the overall deviation of the coordination from a pure tetrahedron can be assessed by summing the three θ(X–M–X) angles involving one of the X atoms (see description under Table 3). This sum reported in the last column of Table 3 is roughly 10–20° larger than the 328.5° of a true tetrahedron.

Fig. 4 Structure of model bridged anions (M₂X₆)²⁻ (M = Zn, Cd, Hg; X = Cl, Br, I) in two projections. Bond lengths for (Zn₂Cl₆)²⁻ in water.

Table 3 Structural parameters (distances in Å, angles in degrees) in bridged (M₂X₆)²⁻ (M = Zn, Cd, Hg; X = Cl, Br, I) complexes calculated at the MP2/aug-cc-pVDZ level of theory

	M–Xa	∑Cov (%)	M–Xb	∑Cov (%)	θ(Xa–M–Xa)	θ(Xb–M–Xb)	∑X–M–X^a
a Sum of θ(Xa–M–Xa) and two of θ(Xa–M–Xb) angles.
	Vacuum
(Zn2Cl6)^2−	2.241	100	2.380	106	114.7	91.4	339
(Zn2Br6)^2−	2.376	98	2.513	104	114.7	94.3	338
(Zn2I6)^2−	2.576	99	2.709	104	114.9	95.2	338
(Cd2Cl6)^2−	2.438	99	2.575	105	114.6	89.2	334
(Cd2Br6)^2−	2.563	97	2.697	102	114.8	91.9	339
(Cd2I6)^2−	2.747	97	2.878	102	114.9	94.4	339
(Hg2Cl6)^2−	2.438	104	2.625	112	120.8	88.0	342
(Hg2Br6)^2−	2.560	102	2.735	109	119.5	90.9	341
(Hg2I6)^2−	2.737	101	2.892	107	118.0	93.9	339
	Ethanol
(Zn2Cl6)^2−	2.242	100	2.382	106	120.5	93.9	340
(Zn2Br6)^2−	2.384	99	2.513	104	118.3	95.6	338
(Zn2I6)^2−	2.579	99	2.713	104	117.5	98.1	337
(Cd2Cl6)^2−	2.492	101	2.617	106	108.5	89.6	337
(Cd2Br6)^2−	2.600	98	2.762	105	126.3	93.7	342
(Cd2I6)^2−	2.785	98	2.947	104	125.4	93.8	342
(Hg2Cl6)^2−	2.524	108	2.704	116	113.0	87.2	340
(Hg2Br6)^2−	2.580	102	2.856	113	138.2	87.9	348
(Hg2I6)^2−	2.788	103	2.993	110	120.4	96.3	339
	Water
(Zn2Cl6)^2−	2.242	100	2.384	106	121.1	93.9	340
(Zn2Br6)^2−	2.378	98	2.518	104	119.3	95.3	336
(Zn2I6)^2−	2.581	99	2.722	104	117.1	96.8	338
(Cd2Cl6)^2−	2.496	101	2.636	107	120.6	89.4	342
(Cd2Br6)^2−	2.660	101	2.761	105	119.5	92.5	340
(Cd2I6)^2−	2.819	100	2.960	105	122.0	92.3	347
(Hg2Cl6)^2−	2.464	105	2.822	121	135.8	86.8	347
(Hg2Br6)^2−	2.622	104	2.860	113	126.8	87.2	344
(Hg2I6)^2−	2.759	102	2.981	110	114.2	114.3	333

---

Analysis of the electron density topology of these bridged complexes by the AIM protocol provides some information about the internal bonding. The resulting AIM molecular diagrams are provided in Fig. S1 (ESI†). As delineated in Table S2 (ESI†), the electron densities at the M–X bond critical points lie in the range between 0.03 and 0.07 a.u. which would place them solidly in the noncovalent category, despite their short length. This characterization is supported by the positive Laplacians of roughly 0.01–0.02 a.u.

3. Stacked complexes. The search of the CSD database alluded to earlier had yielded 8 crystals in which planar MX₃⁻ units were stacked above one another. Full optimizations of this sort of dimer led to true minima of the type exhibited in Fig. 5, whose structural details are reported in Table 4. The planarity of the individual MX₃⁻ units is obvious from the angle sums of 360° in the last column of the Table. In each case, one X_b atom of one unit lies directly above the M atom of another, directly along its C₃ axis. Whereas bridged structures are present in all three environments tested, stacked geometries are only present in solution, with no such minima in vacuo. Table 5 allows a comparison of the stabilities of the two complex types in the solution media in which both exist. The positive values in the upper portion of Table 5 indicate that the bridged dimer is preferred for M = Zn, while it is the stacked structure that is the more stable for the heavier Hg; Cd lies intermediate between these two extremes. There is also a shift from stacked toward bridged as the X atom becomes heavier, with (HgI₃⁻)₂ showing the most extreme preference for stacked. With respect to solvent, the shift from ethanol to the more polar water pushes the equilibrium toward the stacked geometry. The data in Table 4 indicate a near equivalence in the various M–X bond lengths, whether X_a or X_b. In other words, the direct interaction of X_b with the M atom of the neighboring unit has very little effect upon this bond length, which is in turn very close to the sum of covalent radii. The interunit M⋯X_b distances are considerably longer, by more than 1 A. These distances are slightly shorter than the sum of the vdW radii, on the order of 90% ∑r_vdW.

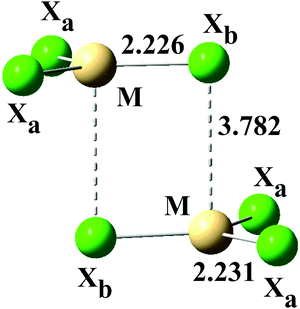Fig. 5 Structure of model stacked anions (MX₃⁻)₂ (M = Zn, Cd, Hg; X = Cl, Br, I). Bond lengths for (ZnCl₃)₂⁻ in water.

Table 4 Structural parameters (distances in Å, angles in degrees) in stacked (MX₃⁻)₂ dimers calculated at the MP2/aug-cc-pVDZ level of theory

	M–Xa	∑Cov (%)	M–Xb	∑Cov (%)	M⋯Xb	∑Cov (%)	∑vdW (%)	M-Xb⋯M	∑X–M–X
Ethanol
(ZnCl3^−)2	2.227	99	2.225	99	3.781	169	90	93.2	360
(ZnBr3^−)2	2.358	97	2.360	98	3.809	157	90	90.5	360
(ZnI3^−)2	2.559	98	2.564	98	4.093	157	92	87.8	360
(CdCl3^−)2	2.496	101	2.493	101	3.731	152	87	89.2	360
(CdBr3^−)2	2.613	99	2.606	99	3.850	146	89	96.0	360
(CdI3^−)2	2.784	98	2.787	98	4.012	142	89	85.2	360
(HgCl3^−)2	2.510	107	2.469	106	3.621	155	85	81.6	359
(HgBr3^−)2	2.573	102	2.535	101	3.689	146	86	90.1	359
(HgI3^−)2	2.792	103	2.782	103	3.944	146	88	79.2	359
Water
(ZnCl3^−)2	2.231	100	2.226	99	3.782	169	90	93.5	360
(ZnBr3^−)2	2.362	98	2.362	98	3.815	158	90	90.6	360
(ZnI3^−)2	2.566	98	2.565	98	3.987	153	90	87.0	359
(CdCl3^−)2	2.503	102	2.502	102	3.737	152	87	87.9	360
(CdBr3^−)2	2.624	99	2.648	100	3.830	145	88	85.7	360
(CdI3^−)2	2.823	100	2.786	98	4.030	142	89	82.8	359
(HgCl3^−)2	2.524	108	2.474	106	3.616	155	85	80.2	359
(HgBr3^−)2	2.622	104	2.618	104	3.769	150	87	87.8	360
(HgI3^−)2	2.796	103	2.752	102	3.928	145	87	82.7	358

---

Table 5 Relative energy (kcal mol⁻¹)^a of stacked dimer versus bridged structure

	Water	Ethanol
a Gibbs free energy differences in parentheses.
(ZnCl3^−)2	4.58 (3.37)	5.52 (4.40)
(ZnBr3^−)2	2.68 (3.63)	4.00 (6.31)
(ZnI3^−)2	0.42 (1.12)	0.47 (1.11)
(CdCl3^−)2	1.18 (0.54)	2.56 (1.02)
(CdBr3^−)2	0.91 (0.74)	2.23 (3.47)
(CdI3^−)2	−6.59 (−8.16)	−0.07 (−1.60)
(HgCl3^−)2	−4.80 (−5.94)	−6.29 (−6.05)
(HgBr3^−)2	−4.00 (−5.53)	−4.90 (−5.12)
(HgI3^−)2	−6.26 (−4.36)	−8.08 (−7.44)

---

As each MX₃⁻ unit retains its structural integrity in the stacked dimers, it is possible to evaluate both their interaction and binding energies, which are displayed in Table 6 at three different levels of theory. As a reminder, the interaction energy takes as its reference point the monomers in the geometry they adopt within the complex, so can be considered a pure measure of the interaction itself. In any case, there is little geometrical deformation of the subunits so E_int is only very slightly more exothermic than is E_b. The energetics of dimerization are more favourable in water than in ethanol, with all quantities negative in the former solvent. Dimerization is favoured with the larger X atoms I > Br > Cl, as well as for the larger M atoms Hg > Cd > Zn. The greater exothermicity of formation of stacked complexes with Hg is consistent with the CSD survey where it is only this M atom which engages in such arrangements (see Table 2). It is lastly important to point out the parallel nature of the MP2 (combined with aug-cc-pVDZ and aug-cc-pVQZ basis sets) energetic trends with those extracted via the more reliable CCSD(T) approach. When the BSSE correction is considered these trends become less coherent in the ethanol solvent. The reason for these discrepancies are due to the computational package limitation which does not give possibility of direct calculations of this correction in solvent (see details in the Method section).

Table 6 Interaction and binding energies (kcal mol⁻¹) of stacked dimers calculated at the MP2/aug-cc-pVDZ (I), MP2/aug-cc-pVQZ (II) and CCSD(T)/aug-cc-pVDZ (III) levels. Values corrected for BSSE are given in parentheses

	E int			E b
	I	II	III	I	II	III
Water
(ZnCl3^−)2	−2.18 (−0.90)	−1.99 (−1.68)	−2.04 (−0.57)	−2.14 (−0.87)	−1.98 (−1.67)	−2.00 (−0.53)
(ZnBr3^−)2	−3.81 (−1.30)	−4.32 (−2.63)	−3.36 (−0.64)	−3.76 (−1.25)	−4.29 (−2.60)	−3.31 (−0.58)
(ZnI3^−)2	−5.35 (−2.35)	−7.16 (−4.47)	−4.42 (−1.23)	−5.34 (−2.34)	−6.96 (−4.27)	−4.36 (−1.07)
(CdCl3^−)2	−2.93 (−1.50)	−2.83 (−2.46)	−2.71 (−1.04)	−2.90 (−1.47)	−2.69 (−2.33)	−2.68 (−1.06)
(CdBr3^−)2	−4.74 (−1.95)	−5.14 (−3.68)	−4.17 (−1.13)	−4.70 (−1.91)	−5.10 (−3.65)	−4.12 (−1.08)
(CdI3^−)2	−6.25 (−2.91)	−8.36 (−5.58)	−5.34 (−2.05)	−6.02 (−2.68)	−7.23 (−4.45)	−5.28 (−1.99)
(HgCl3^−)2	−4.74 (−1.88)	−4.09 (−3.33)	−4.12 (−0.99)	−4.71 (−1.85)	−3.92 (−3.16)	−4.06 (−0.93)
(HgBr3^−)2	−6.11 (−2.00)	−6.13 (−4.08)	−5.11 (−0.75)	−6.05 (−1.94)	−6.13 (−4.08)	−5.08 (−0.72)
(HgI3^−)2	−8.44 (−3.49)	−10.00 (−6.43)	−6.99 (−1.69)	−8.22 (−3.27)	−9.85 (−6.28)	−6.26 (−0.96)
Ethanol
(ZnCl3^−)2	−0.46 (0.82)	−0.26 (0.05)	−0.33 (1.14)	−0.37 (0.90)	−0.29 (0.02)	−0.18 (1.29)
(ZnBr3^−)2	−2.11 (0.42)	−2.63 (−0.94)	−1.66 (1.08)	−2.04 (0.48)	−2.56 (−0.87)	−1.60 (1.15)
(ZnI3^−)2	−3.41 (−0.58)	−5.32 (−2.63)	−2.56 (0.55)	−3.35 (−0.52)	−5.27 (−2.58)	−2.49 (0.61)
(CdCl3^−)2	−1.25 (0.15)	−1.14 (−0.78)	−1.01 (0.60)	−1.18 (0.21)	−1.00 (−0.63)	−0.98 (0.63)
(CdBr3^−)2	−2.86 (−0.41)	−3.11 (−1.66)	−2.41 (0.25)	−2.83 (−0.37)	−3.03 (−1.57)	−2.39 (0.26)
(CdI3^−)2	−4.62 (−1.23)	−6.34 (−3.55)	−3.62 (0.10)	−4.52 (−1.13)	−6.19 (−3.40)	−3.55 (0.17)
(HgCl3^−)2	−2.98 (−0.10)	−2.27 (−1.50)	−2.25 (0.81)	−2.85 (−0.06)	−2.12 (−1.35)	−2.21 (0.84)
(HgBr3^−)2	−4.90 (−0.91)	−4.68 (−2.63)	−3.96 (0.27)	−4.81 (−0.82)	−4.54 (−2.49)	−3.91 (0.31)
(HgI3^−)2	−7.48 (−2.16)	−8.79 (−5.22)	−5.76 (−0.07)	−6.86 (−1.54)	−8.13 (−4.56)	−5.24 (0.44)

---

One window into the fundamental nature of the interaction in the stacked dimers is opened with a LMOEDA decomposition of the total interaction energy. The data in Table 7 show first a strongly repulsive electrostatic term, not surprising in light of the close approach of the two anions. There is also a smaller complementary repulsion resulting from the overlap of the electron clouds of the two species. The polarization component furnishes the lion's share of the attractive force, with smaller increments arising from exchange and dispersion. Although of opposite sign, the magnitudes of E_es and E_pol both diminish for larger X atoms and grow larger along with the size of the central M atom. Reducing the polarity of the solvent from water to ethanol reduces these quantities, but only by a relatively small amount.

Table 7 LMOEDA/MP2/aug-cc-pVDZ decomposition of the interaction energy of stacked complexes into electrostatic (E_es), repulsion (E_rep), exchange (E_ex), polarization (E_pol) and dispersion (E_disp) components. All quantities in kcal mol⁻¹

	E es	E rep	E ex	E pol	E disp	E int
Water
(ZnCl3^−)2	178.66	6.90	−4.55	−178.86	−3.11	−0.95
(ZnBr3^−)2	165.37	11.50	−7.47	−166.19	−4.43	−1.23
(ZnI3^−)2	153.62	16.60	−10.86	−155.48	−5.92	−2.04
(CdCl3^−)2	213.66	7.93	−4.96	−214.22	−3.78	−1.36
(CdBr3^−)2	205.06	12.26	−7.60	−208.30	−5.08	−2.17
(CdI3^−)2	192.03	16.79	−10.73	−195.30	−6.35	−3.55
(HgCl3^−)2	225.07	13.11	−8.07	−226.73	−5.37	−1.99
(HgBr3^−)2	210.70	17.56	−11.21	−212.89	−6.39	−2.23
(HgI3^−)2	192.09	22.19	−13.91	−195.79	−7.80	−3.23
Ethanol
(ZnCl3^−)2	173.96	6.76	−4.45	−172.67	−3.04	0.56
(ZnBr3^−)2	161.54	11.65	−7.57	−161.00	−4.40	0.21
(ZnI3^−)2	152.85	15.44	−10.40	−152.76	−5.75	−0.62
(CdCl3^−)2	203.72	7.71	−4.80	−203.07	−3.67	−0.11
(CdBr3^−)2	187.79	10.53	−6.54	−187.89	−4.34	−0.44
(CdI3^−)2	183.33	18.45	−11.84	−184.80	−6.63	−1.49
(HgCl3^−)2	214.09	12.88	−7.97	−214.56	−5.23	−0.77
(HgBr3^−)2	197.04	15.24	−9.51	−197.94	−5.86	−1.04
(HgI3^−)2	190.15	25.08	−16.00	−192.69	−8.74	−2.20

---

The AIM diagrams of these stacked dimers in Fig. S2 (ESI†) show a pair of clear inter-unit bond M⋯X bond paths in each case. The values of the various properties of the bond critical point are compiled in Table S3 (ESI†), not only for the latter M⋯X bond, but also others of interest, e.g. the internal M–X bond. The density of the inter-anion M⋯X bond critical point is rather small, less than 0.01 a.u., much smaller than the internal M–X bonds. When viewed in concert with the positive Laplacian and the very small values of H, this interaction can be classified as noncovalent.

Given the comparable energies of the stacked and bridged structures in solvent where both are present, it is natural to inquire about the process that would transform one to the other. This process was explored for the MCl₃⁻ systems in some depth and the energetics are displayed in Table 8.

Table 8 Relative energies (kcal mol⁻¹) between different geometries of MCl₃⁻ dimers in water and ethanol solvents

Complex	Bridged	TS	Stacked
	Water
(ZnCl3^−)2	0.00	14.75	4.58
(CdCl3^−)2	0.00	6.99	1.18
(HgCl3^−)2	0.00	1.86	−4.80
	Ethanol
(ZnCl3^−)2	0.00	11.92	5.52
(CdCl3^−)2	0.00	4.59	2.56
(HgCl3^−)2	0.00	4.73	−6.29

---

Taking the transition from bridged to stacked (ZnCl₃⁻)₂ in water in the first row as an example, the stacked dimer is higher in energy than bridged by 4.58 kcal mol⁻¹. The conversion must overcome an energy barrier of 14.75 kcal. This same transformation is exoergic for (HgCl₃⁻)₂ as the stacked dimer is more stable by 4.80 kcal mol⁻¹. Nonetheless, there is a small energy barrier of 1.86 kcal mol⁻¹ that the system must overcome for this transition to occur. In summary, as the M atom grows larger, the bridged → stacked conversion reverses from endoergic to exoergic, and the barrier rapidly diminishes. Replacement of the aqueous solvent by ethanol lowers the transition barrier for the two lighter metal atoms, but raises the barrier for (HgCl₃⁻)₂, even though the transition from bridged to stacked becomes more exoergic. These trends in the conversion process can be visualized more easily in Fig. 6 which also presents a schematic diagram of the geometry of the transition state. The transition state involves a stretch of one of the M–Cl_b bonds which is reduced again as the system settles into the stacked geometry. The magnitude of this stretching in the TS is provided in Table 9 which lists an interatomic distance between 4.2 and 4.5 Å.

Fig. 6 Energetics of conversion from bridged to stacked configurations of (MCl₃⁻) dimers in water and ethanol solvents.

Table 9 Distances between M and Cl_b (Å) in optimized structures

Complex	Bridged	TS	Stacked
	Water
(ZnCl3^−)2	2.384	4.253	3.782
(CdCl3^−)2	2.636	4.500	3.737
(HgCl3^−)2	2.822	4.170	3.616
	Ethanol
(ZnCl3^−)2	2.382	4.350	3.781
(CdCl3^−)2	2.617	4.380	3.731
(HgCl3^−)2	2.704	4.516	3.621

---

Discussion

It might be surprising at first sight that anions can come together to form stable and metastable dimers, especially since the maximum in the MEP of the Lewis acid is clearly negative. But the systems discussed here fall into an ever enlarging category of anion⋯anion dimers which are either stable in their own right, or metastable in the sense that their dissociation requires surmounting an energy barrier. The largest subset of systems of this type are held together by H-bonds,^15,58–72 but there have also been a number of halogen-bonded dianion complexes.^{12,24,73–78} Recent work has extended this growing list to pnicogen⁷⁹ and triel bonds,⁸⁰ as well as those involving metal atoms.^16,17 The general finding is that such anion–anion complexes are stable in polar solvent but only metastable in the gas phase.

In terms of overall stability, many of these complexes have fairly large binding energies. Considering water as a solvent, for example, the binding energy of CN⁻ with the various MCl₃⁻ anions, where M is a Group 2 atom ranges up to 20 kcal mol⁻¹ (ref. 17) and lies in a similar range for Group 12 atoms Zn, Cd, or Hg.¹⁶ Pnicogen bonds between anions are even larger in magnitude, more than 20 kcal mol⁻¹ for the ZCl₄⁻ series, with Z = P, As or Sb.⁷⁹ In the cases examined here, it is not a small and compact CN⁻ base that is interacting with the Lewis acid, but rather a pair of MCl₃⁻ units with one another. Instead of a single strong N⋯CN bond, the interactions in these stacked dimers are dependent upon a pair of much weaker M⋯X interactions. It is therefore sensible to note the smaller total interaction energies here.

Focusing on the electrostatic component of the interactions here, E_es is large and positive, highly repulsive. It is the other components, chiefly polarization, which are responsible for the small cumulative attractions. This characteristic also differentiates these dual spodium bonded systems with some of the other anion–anion interactions. E_es is very small for the Group 2 complexes, and its sign depends on the specific central M atom.¹⁷ The electrostatic energy is quite attractive for the Group 12 analogues, in the 40–100 kcal mol⁻¹ range¹⁶ and is further magnified to even larger negative quantities up to 111 kcal mol⁻¹ for the pnicogen-bonded anion pairs.⁷⁹ As a second issue leading to the large positive coulombic repulsions here, the minima surrounding the X atoms of MX₃⁻ are not directed at the M atom below. These minima instead lie in the MX₃ plane, as is evident in Fig. 1, which would weaken any potential stabilizing interaction with the M π-hole.

Conclusions

MX₃⁻ ions can engage with one another in one of two different modes, despite their strong mutual coulombic repulsion. In the bridged structures, the bonding is largely covalent, with four equivalent short M–X bonds within a four-membered rhomboid ring. Each M atom is tetracoordinated and the bridging X atoms are covalently bonded to two M atoms. The bonding scenario is rather different in the stacked geometries where each MX₃ unit largely retains its native D_3h structure, which is held to the MX₃ unit beneath it by a pair of noncovalent M⋯X bonds. The latter stacked structure does not represent a stable minimum in the gas phase, but occurs with an energy comparable to that of the bridged configuration in ethanol and aqueous solution. In fact, it is the noncovalently bonded stacked geometry that is preferred over bridged for the heavier HgCl₃⁻ dimers in either solvent. The overall energetics of formation of the noncovalently bonded stacked dimers are roughly thermoneutral. The binding energies are consistently exothermic in aqueous solution, albeit by only a few kcal mol⁻¹, and E_b is smaller in magnitude in ethanol. There is a trend toward more exothermic stacking for heavier M atoms: Zn < Cd < Hg and for larger X atoms as well: Cl < Br < I.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology and by the US National Science Foundation under Grant No. 1954310. A generous allotment of computer time from the Wroclaw Supercomputer and Networking Center is acknowledged.

References

1. T. Niemann, P. Stange, A. Strate and R. Ludwig, ChemPhysChem, 2018, 19, 1691–1695.
2. T. Niemann, A. Strate, R. Ludwig, H. J. Zeng, F. S. Menges and M. A. Johnson, Angew. Chem., Int. Ed., 2018, 57, 15364–15368.
3. T. Niemann, D. Zaitsau, A. Strate, A. Villinger and R. Ludwig, Sci. Rep., 2018, 8, 14753.
4. A. Strate, V. Overbeck, V. Lehde, J. Neumann, A. M. Bonsa, T. Niemann, D. Paschek, D. Michalik and R. Ludwig, Phys. Chem. Chem. Phys., 2018, 20, 5617–5625.
5. I. A. Charushnikova, N. N. Krot and V. P. Perminov, Radiochemistry, 2020, 62, 9–17.
6. W.-Y. Wen, K. Miyajima and A. Otsuka, J. Phys. Chem., 1971, 75, 2148–2157.
7. W.-Y. Wen and K. Nara, J. Phys. Chem., 1967, 71, 3907–3914.
8. I. A. Charushnikova, M. S. Grigor'ev, A. M. Fedoseev, A. A. Bessonov and K. A. Lysenko, Radiochemistry, 2020, 62, 161–169.
9. R. Maurice, P. D. Dau, M. Hodee, E. Renault and J. K. Gibson, Eur. J. Inorg. Chem., 2020,(47), 4465–4476.
10. S. H. Ganatra, V. R. Shaikh, A. S. Ujjankar, S. D. Khobragade, P. A. Tomar and K. J. Patil, J. Mol. Liq., 2020, 315, 113654.
11. M. O. Miranda, D. J. R. Duarte and I. Alkorta, ChemPhysChem, 2020, 21, 1052–1059.
12. D. Quinonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939–27950.
13. I. Iribarren, M. M. Montero-Campillo, I. Alkorta, J. Elguero and D. Quinonero, Phys. Chem. Chem. Phys., 2019, 21, 5796–5802.
14. R. Prohens, A. Portell, M. Font-Bardia, A. Bauza and A. Frontera, Chem. Commun., 2018, 54, 1841–1844.
15. I. Alkorta, I. Mata, E. Molins and E. Espinosa, Chem. – Eur. J., 2016, 22, 9226–9234.
16. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
17. W. Zierkiewicz, R. Wysokinski, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
18. T. R. Griffiths and M. C. R. Symons, Trans. Faraday Soc., 1960, 56, 1752–1761.
19. P. L. Goggin, P. King, D. M. Mcewan, G. E. Taylor, P. Woodward and M. Sandstrom, J. Chem. Soc., Dalton Trans., 1982, 875–882,  10.1039/dt9820000875.
20. P. Biscarini, L. Fusina, G. Nivellini and G. Pelizzi, J. Chem. Soc., Dalton Trans., 1977, 664–668,  10.1039/dt9770000664.
21. A. S. R. Chesman, J. L. Hodgson, E. I. Izgorodina, A. Urbatsch, D. R. Turner, G. B. Deacon and S. R. Batten, Cryst. Growth Des., 2014, 14, 1922–1932.
22. Y. H. Kim, S. Rhim, J. J. Park and J. Kang, J. Inclusion Phenom. Macrocyclic Chem., 2012, 74, 317–323.
23. P. Kumar, M. K. Cabaj and P. M. Dominiak, Crystals, 2019, 9, 668.
24. T. Maxson, A. S. Jalilov, M. Zeller and S. V. Rosokha, Angew. Chem., Int. Ed., 2020, 59, 17197–17201.
25. Y. V. Nelyubina, M. Y. Antipin and K. A. Lyssenko, Russ. Chem. Rev., 2010, 79, 167–187.
26. R. Zangi, J. Chem. Phys., 2012, 136, 184501.
27. F. Zapata, L. Gonzalez, A. Bastida, D. Bautista and A. Caballero, Chem. Commun., 2020, 56, 7084–7087.
28. D. Braga and F. Grepioni, Chem. Commun., 1998, 911–912,  10.1039/a708438b.
29. M. K. Cerreta and K. A. Berglund, J. Cryst. Growth, 1987, 84, 577–588.
30. Q. He, P. Y. Tu and J. L. Sessler, Chem, 2018, 4, 46–93.
31. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
32. L. A. Bengtsson, B. Noren and H. Stegemann, Acta Chem. Scand., 1995, 49, 391–398.
33. R. H. Fenn, Acta Crystallogr., 1966, 20, 20–23.
34. P. Ghosh and A. Chakravorty, Indian J. Chem. A, 2013, 52, 1247–1250.
35. D. Grdenic, M. Sikirica and I. Vickovic, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1977, 33, 1630–1632.
36. V. V. Gritsenko, O. A. Dyachenko, G. V. Shilov, R. N. Lyubovskaya, T. V. Afanaseva, R. B. Lyubovskii and M. K. Makova, Russ. Chem. Bull., 1992, 41, 697–703.
37. T. S. Lobana, S. A. Mbogo, W. R. Mcwhinnie, W. C. Patalinghug and A. H. White, J. Organomet. Chem., 1990, 390, 29–34.
38. T. G. Takhirov, O. A. Dyachenko, L. O. Atovmyan, E. I. Zhilyaeva and R. N. Lyubovskaya, J. Struct. Chem., 1990, 31, 712–719.
39. A. Bauze, I. Alkorta, J. Elguero, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2020, 59, 17482–17487.
40. T. Xia, D. Li and L. J. Cheng, Chem. Phys., 2020, 539, 110978.
41. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
42. C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 0618–0622.
43. D. E. Woon and T. H. Dunning, J. Phys. Chem., 1993, 98, 1358–1371.
44. K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
45. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
46. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Phys. Chem., 1987, 87, 5968–5975.
47. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Headgordon, Chem. Phys. Lett., 1989, 157, 479–483.
48. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
49. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
51. T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323.
52. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
53. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
54. T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019.
55. P. Su and H. Li, J. Phys. Chem., 2009, 131, 014102.
56. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Phys. Chem., 2020, 152, 154102.
57. C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454.
58. S. R. Kass, J. Am. Chem. Soc., 2005, 127, 13098–13099.
59. I. Mata, I. Alkorta, E. Molins and E. Espinosa, ChemPhysChem, 2012, 13, 1421–1424.
60. I. Mata, I. Alkorta, E. Molins and E. Espinosa, Chem. Phys. Lett., 2013, 555, 106–109.
61. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2014, 119, 183–194.
62. F. Weinhold and R. A. Klein, Angew. Chem., Int. Ed., 2014, 53, 11214–11217.
63. G. Frenking and G. F. Caramori, Angew. Chem., Int. Ed., 2015, 54, 2596–2599.
64. E. M. Fatila, E. B. Twum, A. Sengupta, M. Pink, J. A. Karty, K. Raghavachari and A. H. Flood, Angew. Chem., Int. Ed., 2016, 55, 14057–14062.
65. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
66. F. Weinhold, Inorg. Chem., 2018, 57, 2035–2044.
67. R. Barbas, R. Prohens, A. Bauzá, A. Franconetti and A. Frontera, Chem. Commun., 2019, 55, 115–118.
68. D. A. Cullen, M. G. Gardiner and N. G. White, Chem. Commun., 2019, 55, 12020–12023.
69. N. G. White, CrystEngComm, 2019, 21, 4855–4858.
70. W. Zhao, B. Qiao, J. Tropp, M. Pink, J. D. Azoulay and A. H. Flood, J. Am. Chem. Soc., 2019, 141, 4980–4989.
71. L. M. Azofra, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2020, 124, 2207–2214.
72. L. M. Azofra, J. Elguero and I. Alkorta, Phys. Chem. Chem. Phys., 2020, 22, 11348–11353.
73. G. Wang, Z. Chen, Z. Xu, J. Wang, Y. Yang, T. Cai, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 610–620.
74. C. Wang, Y. Fu, L. Zhang, D. Danovich, S. Shaik and Y. Mo, J. Comput. Chem., 2018, 39, 481–487.
75. Z. Zhu, G. Wang, Z. Xu, Z. Chen, J. Wang, J. Shi and W. Zhu, Phys. Chem. Chem. Phys., 2019, 21, 15106–15119.
76. J. M. Holthoff, E. Engelage, R. Weiss and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 11150–11157.
77. K. Ghosh, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 1429–1438.
78. Y. Li, L. Meng and Y. Zeng, ChemPlusChem, 2021, 86, 232–240.
79. S. Scheiner, R. Wysokiński, M. Michalczyk and W. Zierkiewicz, J. Phys. Chem. A, 2020, 124, 4998–5006.
80. R. Wysokiński, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 4818–4828.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01502h

---