Nanoporous gold electrodes modified with self-assembled monolayers for electrochemical control of the surface charge

Abstract

The electrochemical behaviour of nanoporous gold modified with self-assembled monolayers is investigated with regard to its point of zero charge (pzc) and proton transfer reaction. Due to their high surface-to-volume ratio and conductivity, nanoporous electrodes represent promising materials for numerous applications, including the immobilization of biomolecules in biotechnology and biosensing. Therefore, the fundamental understanding and controllability of the surface state of the electrode is essential. To achieve a precise surface charge control, nanoporous gold (npAu) is modified with self-assembled monolayers (SAMs) of different lengths (3-mercaptopropionic acid (MPA) and 16-mercaptohexadecanoic acid (MHDA)). Cyclic voltammetry and impedance spectroscopy are used to determine the pzc. The most distinct pzc, and thus the most precise charge control, is found for the long-chain MHDA. Subsequently, the proton transfer reaction was investigated as a function of pH and scan rate. The observed protonation/deprotonation reaction was qualitatively well in line with the literature for planar gold electrodes, albeit the fraction of electrochemical controllable SAMs increased by a factor of 10 compared to planar electrodes indicating attractive application potential.

---

1 Introduction

Nanoporous gold (npAu) is a promising carrier material for the immobilization of biomolecules and as enzyme electrodes (e.g. 3rd generation biosensors) due to the high surface-to-volume ratio and conductivity as well as the free-standing structure.^1,2 To facilitate the binding of biomolecules, the surface of this porous structure can be modified with self-assembled monolayers (SAMs)³ consisting of a thiol group, which binds spontaneously to the gold surface, a carbon chain and a functional head group.⁴ The functional group can be chosen according to the desired applications. With electrochemical control over the protonation state of the head group of the monolayer, the binding process of biomolecules, which possess an exposed polar group, may be controlled independently of the type of biomolecule and enabling new applications and more flexibility.^5,6 Moreover, precise surface charge control is of high interest for various research fields way beyond biochemical applications, e.g. for the wettability of the porous structure.⁷ The electrochemical control of the proton transfer reaction at the head group of SAMs has already been the subject of numerous theoretical and experimental studies.^8–13 However, it has also been shown that SAMs on polycrystalline surfaces exhibit a significantly different behaviour compared to single crystals¹⁴ as their final ordering differs greatly, which influences the overall (electro-)chemical behavior.^15,16 This makes it impossible to directly transfer the available knowledge from the planar Au to porous substrates which exhibit very rough and strongly curved surfaces with high defect concentrations.¹⁶

Nanoporous metal electrodes, although very promising for several application fields, are not directly accessible for many experimental techniques, such as microscopy (SEM and TEM) and spectroscopy (XPS and Raman), making the precise analysis of surface modifications hard to achieve. Therefore, electrochemical techniques such as cyclic voltammetry (CV) or impedance spectroscopy (EIS) become worthwhile as they take advantage of the large surface area. Apparently, for analysis, the peculiarities of these porous electrodes have to be taken into account, which have already been the focus of a number of publications including the development of equivalent electrical circuits (EEC) for (nano-)porous samples.^17–19 The surface modification of npAu with SAMs for biotechnological applications has recently been the subject of several publications indicating the high interest in this research field.^2,20,21 However, no comprehensive study is available on the surface charge control of (nano-)porous electrodes modified with SAMs which is, however, essential for further applications.

Here, we present a strategy first to gain basic information on the surface conditions and second to control the proton transfer of npAu electrodes modified with different SAM molecules. As a case study, 16-mercaptohexadecanoic acid (MHDA) and 3-mercaptopropionic-acid (MPA) are chosen as SAMs, which differ only in the length of their carbon chain. While the electron transfer is easier through short-chain SAMs, MHDA is known to form a smoother and denser monolayer, which is identified as essential for precise charge control. Finally, by adjusting the morphology of the npAu as well as the experimental parameters, a successful electrochemical control of the proton transfer is demonstrated under conditions suitable for future applications, e.g. in biotechnology.

2 Experimental

2.1 Chemicals

3-Mercaptopropionic acid (HSCH₂CH₂CO₂H, MPA), 16-mercaptphexadecanioc acid (HS(CH₂)₁₅CO₂H, MHDA), both >99%, and 1 M perchloric acid HClO₄ (>99%) were from Sigma Aldrich. Potassium hydroxide (KOH, ≥85%), sodium chloride (NaCl, ≥99.5%), sodium hydroxide (NaOH, ≥99%), monopotassium phosphate KH₂PO₄ (≥99%) and dipotassium phosphate K₂HPO₄ (≥99%) were from Carl Roth. All chemicals, apart from MHDA, were dissolved or diluted, respectively, to the desired concentration in high purity water (ROTIPURAN, Carl Roth). MHDA was dissolved in ethanol (Carl Roth, ≥99.5%). 50 mM potassium phosphate buffer (KPi) was prepared by titrating 50 mM KH₂PO₄ and 50 mM K₂HPO₄ to pH 8.0.

2.2 Sample preparation

Nanoporous gold was prepared from an AuAg (25at%75at%) master alloy by the potential controlled dealloying of platelets with a weight of (50 ± 5) mg (approx. 6 mm × 4 mm × 150 mm) in 0.1 M HClO₄, followed by the electrochemical reduction of the primary oxide²² (for details see our previous publication²³). In the ESI† (Fig. S1), the current versus time curve during dealloying is shown exemplarily. To investigate the influence of the pore size, one of the samples was thermally coarsened at 350 °C for 3 h in a vacuum oven. To determine the electrochemically active surface area, the dependence of the double layer capacitance on the scan rate was used. The specific surface area and the pore size were subsequently calculated following the study by Lakshmanan et al.²⁴ yielding 10 m² g⁻¹ and 15–20 nm for the as-dealloyed samples (in good agreement with the literature²⁵) and 0.6 m² g⁻¹ and 300 nm for the coarsened sample, respectively. MPA and MHDA were applied by the immersion of npAu samples for 60 h in 5 mM aqueous (for MPA) and ethanol (for MHDA) solutions, respectively. After SAM modification, the samples were thoroughly rinsed with water to remove unbound molecules. To assess the stability of the SAMs under the applied conditions, cyclic voltammetry (CV) in strong alkaline conditions (1 M KOH) was performed after the respective measurements.

2.3 Electrochemical measurements

All electrochemical measurements were performed in a three-electrode setup, controlled by an Autolab PGSTAT128N potentiostat with an electrochemical impedance spectroscopy (EIS) module (FRA32M) using the NOVA 1.11 software for fitting electrical equivalent circuits (EEC). A commercial Ag/AgCl (3 M KCl with 3 M KNO₃ salt bridge) was used as the reference, versus which all potentials are given hereafter. A carbon cloth served as the counter electrode for CV. For EIS, a capacitance (1 mF) was connected parallel to the reference electrode to reduce the reference electrode impedance in the high frequency regime and a coiled Pt-wire was used as the counter electrode. To determine the pzc, spectra were recorded in 10 mM HClO₄ at frequencies between 100 kHz and 1 mHz with a peak amplitude of 10 mV. The applied potential was varied in 50 mV steps between −200 mV and a sample-specific positive limit, which was chosen in order to avoid oxidation. Protonation/deprotonation of freshly prepared MHDA samples was studied in 100 mM NaCl. The pH of the solution was adjusted by titrating 10 mM NaOH assisted by magnetic stirring. The pH was monitored by using a commercial pH electrode (WTW pH3110). CVs were then recorded at a rate of 5 mV s⁻¹ between 0 mV and a sample-specific negative limit, avoiding hydrogen evolution. At pH 9, also, EIS spectra were recorded at applied potentials between +150 and −800 mV. Between spectra recording, the potential was slowly swept to the next step with a scan rate of 0.5 mV s⁻¹. To investigate the protonation/deprotonation reaction in more detail, a fresh npAu sample was first coarsened and then modified with MHDA. For CV, the sample was immersed in 50 mM KPi (pH 8.0). CVs were then recorded at scan rates of 0.1, 1, 2, 4, and 6 mV s⁻¹ between +250 mV and −1000 mV.

3 Results

3.1 Determination of the point of zero charge

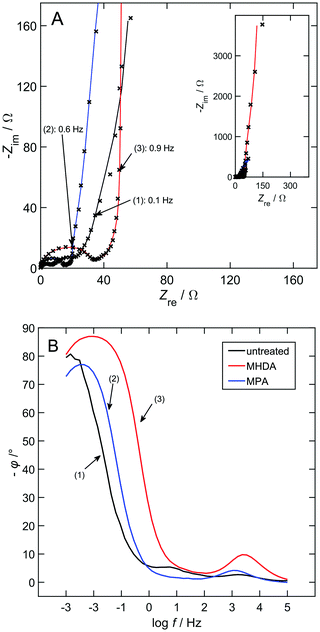
To gain basic information on the chemical surface state of the samples, the point of zero charge was determined by means of electrochemical impedance spectroscopy. Impedance spectra of the three sample types (unmodified, MPA, and MHDA) in the double layer regime at +150 mV are shown in Fig. 1. The acidic electrolyte (10 mM HClO₄) was chosen to ensure that no acid–base reaction occurs at the head group. EEC fits were chosen according to the transmission-line model of de Levie¹⁸ and Keiser¹⁷ for porous electrodes. Within this model, porous electrodes can be described by pore electrolyte resistances in parallel interfacial impedances in the pores; the electrolyte resistance outside of the pores is described by an additional resistor in series. As it can be assumed that all electrodes are in blocking conditions during the whole measurement, the interfacial impedance only consists of a capacitance. The resulting EEC for all samples is composed of a truncated transmission-line of 5 resistor–capacitor (RC) elements and the electrolyte resistance. Due to consistency, the number of RC elements was kept constant for all fits. This causes slight variations in the fit quality²⁶ for all samples because the surface roughness and the pore morphology change with different surface modifications (as explained in more detail in the Discussion section).

Fig. 1 EIS measurements on unmodified npAu ((1) black), npAu/MPA ((2) blue) and npAu/MHDA ((3) red) samples in 10 mM HClO₄ at an applied potential of +150 mV. Black crosses represent the measured data, and solid lines represent the EEC fits. (A) The Nyquist representation of the negative imaginary part (−Z_im) vs. the real part of the impedance (Z_re); the main figure shows a section, and the inset shows the whole dataset. (B) The corresponding bode phase plot showing the phase angle φ as a function of the logarithmic frequency (log f).

All spectra in Fig. 1 show three distinct frequency regimes, starting with the high frequency regime on the left (at low Z_re values), which shows a semicircle for all samples, the sample-dependent mid frequency regime and the low frequency regime with a steep increase. The semicircle at high frequencies is caused by the contact resistance,²⁷ which is excluded from further analysis. In the mid-frequency regime, samples modified with SAMs clearly show a different trend than the unmodified npAu indicating a changed (apparent) pore shape, probably from a convex to a cylindrical shape according to Keiser et al.¹⁷ At low frequencies (high Z_re values), a purely capacitive behavior would be expected,¹⁹ exhibiting a phase angle of 90° (see Fig. 1B). This may, however, deviate for porous materials caused by the pore size distribution.²⁶ In Fig. 1B, the unmodified npAu and npAu/MPA samples reach a phase angle of approximately 80°, and the npAu/MHDA sample reaches up to 87° indicating an enhanced capacitive behaviour.

To check for the undesired desorption of SAMs during the EIS measurement, after the respective measurements, CVs were performed in 1 M KOH. Depending on the structure of SAM molecules and the morphology of the substrate surface, it is known from the literature⁴ that SAMs desorb from gold substrates either reductively and/or oxidatively. For detailed studies of SAMs on npAu, the reader is referred to our preceding publication²³ as well as the studies by Hakamada et al.¹⁶ and Chu et al.²⁸ For all measurements, a pronounced oxidation peak, which results from the oxidative desorption of SAMs, was observable in the first cycle indicating that SAMs have been stable for the duration of the previous measurements. Exemplarily, Fig. S2 in the ESI† shows the desorption of MHDA and MPA after the determination of the pzc.

Fig. 2 shows the interfacial capacitances of the three sample types as a function of applied potential, obtained from the summed-up transmission line capacitances of the EEC fit. The spectra considered for this calculation were limited to the frequency regime dominated by the double layer capacitance following the literature.²⁹ For comparison, the effective capacitance C_eff = −1/(2πfZ_im) for the three sample types was calculated at a frequency lying in the plateau in the low-frequency regime, shown as grey dotted lines in Fig. 2. For all samples and potentials, these values coincide well, indicating the reliability of both methods. As expected, SAM modification decreases the capacitance (3-fold for MPA and 7-fold for MHDA at +150 mV). For the unmodified npAu (Fig. 2(a)), no capacitance minimum was found and thus no pzc could be determined. This can be explained well by considering the particular surface structure of npAu compared to the planar gold (for details, see the Discussion section). For npAu/MPA (Fig. 2(b)), the lowest capacitance (and thus the pzc) lies between +150 mV and +250 mV. The lack of a clear minimum is most likely caused by pinholes left in the SAM.¹¹ For the smoother npAu/MHDA (Fig. 2(c)), the overall change in capacitance is small, but a minimum is found around +100 mV, which fits well to the literature results for 11-mercaptoundecanoic acid on Au(111).¹⁴ The pzc of SAMs is mostly influenced by the dipole moment perpendicular to the surface,¹⁴ which can be assumed to be smaller in the less-ordered MPA, compared to MHDA.⁴ Summarizing the above findings, MHDA seems more suitable for the precise control of the surface state and hence, it was chosen for further studies.

Fig. 2 Interfacial capacitance C as a function of applied potential U for (a) unmodified npAu, (b) npAu/MPA, and (c) npAu/MHDA samples in 10 mM HClO₄. Grey dotted lines indicate the effective capacitance C_eff and the black crosses indicate the values obtained from the EEC fit.

3.2 pH-dependent proton transfer reaction for npAu/MHDA

To investigate the protonation/deprotonation reaction, a MHDA-modified sample was scanned in 100 mM NaCl, adjusted to different pH-values by titrating 10 mM NaOH. For the sake of clarity, the CV in Fig. 3 is separated into A, the negative scan with the protonation reaction, and B, the positive scan with the deprotonation reaction. For reference, the whole CV at pH 8.6 is inserted in the inset in B. The protonation appears as a distinct peak between −500 mV and −700 mV and the deprotonation peak between −200 mV and 0 mV, both dependent on the pH as expected. According to theory,⁹ the fraction of protonated molecules at the peak position is 1/2, and at more negative potential they are fully protonated. In the reverse scan, the process is also reversed ending in the fully deprotonated state at potentials higher than those of the deprotonation peak. In Fig. 3A, the pH dependence of the peak potential and also of the peak current is clearly visible (see the inset in Fig. 3A), with a minimum at pH 8.6 which, interestingly, correlates well with the literature for planar electrodes.¹⁴ The peak potential of the protonation peak shifts with pH by −45 mV per pH unit. This deviates from a theoretically expected value of −59 mV per pH unit,¹¹ which is most likely caused by concentration differences of the electrolyte and, thus, varying pH values in the pores.

Fig. 3 Cyclic voltammetry of npAu/MHDA in 100 mM NaCl with a scan rate of 5 mV s⁻¹ for a given pH (see legend). For the sake of clarity, only the cathodic scan in A and the anodic scan in B are shown. Arrows indicate the scan direction. Inset in A: dependence of the peak current of the protonation peak as a function of pH. Inset in B: complete cycle at pH 8.6 for comparison.

From the inset of Fig. 3B, it is obvious that the deprotonation peak is significantly broader than the protonation peak, almost exhibiting a double peak shape. This has been observed in simulations¹² as well and is dependent on the diffuse layer potential and can be expected to be more pronounced for a large concentration of surface acid groups. Worthwhile to mention is the underlying slope in the cathodic current (Fig. 3) which is presumably caused by the onset of hydrogen evolution.³⁰

At pH 9.0 (close to the highest peak current in Fig. 3A), protonation was investigated in more detail by using EIS (see Fig. 4). The acid–base reaction is non-faradaic but formally can be described similar to faradaic impedance.¹⁰ The phase angle φ shows a clear dip around −400 mV corresponding to protonation. This potential is shifted from −600 mV to −400 mV, compared to the corresponding peak potential in CV (Fig. 3A) which is most likely caused by the slow distribution of the electrolyte in solution. The time elapsed during the EIS measurement is significantly longer than that for CV, giving the system more time for equilibration. The overall EIS measurement, including all EIS spectra and the potential sweep between each measurement point, took approx. 3 h, whereas one cycle in CV in Fig. 3A only took 6 min. Thus, it can be assumed that EIS data points were recorded in the well equilibrated state whereas concentration gradients in the pores are likely during CV.

Fig. 4 Change of the phase angle φ during the EIS measurement of npAu/MHDA at pH 9.0 in 0.1 M NaCl (the pH was adjusted with NaOH) as a function of applied potential. The arrows indicate the scan direction. The potential was scanned with 0.5 mV s⁻¹ from one measurement step to the next.

At potentials far away from the protonation reaction, the phase angle should reach 90°. This can be observed at the higher potential edge. At the lower potential edge, however, the phase angle only increases up to 72°, which can be attributed to the onset of hydrogen evolution. After the reverse scan (deprotonation), the phase angle (and also the calculated interfacial capacitance) is fully recovered to the initial value, indicating a completely reversible process without the SAM desorption.

3.3 Scan rate dependent proton transfer reaction for npAu/MHDA

The findings above reveal a successful control of the protonation of SAMs on nanoporous gold and a clear dependence on the pH was observed. However, several impediments, such as the early onset of hydrogen evolution and the potentially uneven distribution of the pH in pores, have been observed which hinder further in-depth analysis. To respond to these obstacles, the following adjustments were made in the sample preparation and the whole setup. First, the npAu sample was coarsened up to 300 nm which should facilitate the electrolyte exchange in the pores. Second, the electrolyte was exchanged from 100 mM NaCl to 50 mM KPi (pH 8.0) as the aim of the subsequent study was not to measure the pH dependence anymore, but rather to provide as stable conditions in the solution as possible and to represent conditions which might also be suitable for further biotechnological applications.

In Fig. 5, the cyclic voltammogram of npAu/MHDA in 50 mM KPi (pH 8.0) at varying scan rates is shown. The protonation peak lies in the range of −300 to −400 mV, depending on the scan rate. However, the peak position in Fig. 3A at the respective pH is at −600 mV. As outlined earlier, the peak position in Fig. 3A might be influenced by an uneven distribution of electrolyte in the pores. The npAu sample in Fig. 5 was coarsened significantly, which enhances the diffusion in the pores. Therefore, the electrolyte was most likely better distributed in the pores during the CV, explaining the shifted peak potential. This assumption is supported by the EIS measurements of the phase angle (Fig. 4) for which also a better distribution of the electrolyte prevailed owing to a long equilibration time. In fact, the phase angle dip, which corresponds to the peak in the protonation reaction, lies at −400 mV (Fig. 4) and, therefore, nicely fits with the protonation peak in Fig. 5.

Fig. 5 Cyclic voltammetry of npAu/MHDA in 50 mM KPi buffer at pH 8.0 with varying scan rates (see the legend). Inset: Laviron plot, overpotential E − E_1/2versus scan rate for the protonation/deprotonation reaction.

Interestingly, the difference in peak width is less pronounced as for the same measurement in NaCl which is probably caused by the difference in ionic strength and hence the interactions between the ions.

The steep increase of the current at potentials more negative than −900 mV is caused by hydrogen evolution. This reaction is shifted significantly compared to hydrogen evolution in Fig. 3. This later onset of the hydrogen evolution reaction after coarsening is attributed to the annealing-induced reduction of surface defect concentrations as smoother surfaces are known to catalyse the hydrogen reaction less efficiently.

The acid–base reaction can formally be described as the one-electron transfer faradaic reaction and hence from the protonation peak, the overall charge transfer can roughly be estimated to be 2 mC by the integration of the CV current. The total active surface area was determined by the dependence of the double layer capacitance on the applied scan rate to be 200 cm². Assuming 10¹⁷ adsorption sites and a SAM surface coverage of 0.5 ML,²³ it can be concluded that approximately 10% of SAM molecules take part in the protonation reaction. From the Laviron plot (see the inset in Fig. 5), which is the representation of the overpotential versus scan rate, the proton transfer frequency can be estimated as follows:³¹

giving f_p = 0.3 s⁻¹, with ν being the intercept of a linear extrapolation at E − E_1/2 = 0 and F the faradaic constant, T the temperature in Kelvin and R the gas constant.

4 Discussion

The objective of the present study was to gain detailed insights into the controllability of the surface state of npAu modified with SAMs. Hence, in the following, the results are discussed with respect to the peculiarities of npAu and how its behaviour differs from that of planar electrodes. Moreover, the focus is drawn to conclusions relevant for the binding of biomolecules and general biotechnological applications.

4.1 Surface characteristics

The point of zero charge, defined as the potential at which no net charge accumulates at the interface, is highly dependent on the structure of the surface. At the corresponding potential, the interfacial capacitance exhibits a minimum and the sharpness of the peak can be used to gain information on the controllability of the surface charge.

Interestingly, as shown in Fig. 2(a), no pzc could be detected for the unmodified npAu. This can be well explained from the literature as it is known that the pzc strongly depends on the crystal plane orientation,³² varying in a potential range of 300 mV, and also the surface roughness (low coordination atoms and defects) influences the pzc.³³ Different surface states can be considered as different capacitors connected in parallel, together creating the total interfacial capacitance. Thus, when the pzc of one surface condition is reached, there are still charges accumulating at other sites of the rough surface causing the absence of a sharp pzc.

Comparing the EIS data for npAu/MHDA and npAu/MPA, it can be concluded that MHDA forms a denser and smoother surface. This has also been observed by Patel et al.³⁴ The van der Waals interactions between the long hydrocarbon chains seem to have the ability to shield some of the structural defects from the npAu surface. In particular, this smoothing may also explain the higher phase angle compared to the unmodified npAu (Fig. 1B), similar to coarsening.³⁵ This tendency is also qualitatively similar to flat surfaces,³⁶ showing that longer chain SAMs arrange in better order.

The results for the pzc-determination of the npAu modified with MPA (2(b)) and MHDA (2(c)) can also be interpreted by considering the ordering of the SAM. The npAu/MPA sample exhibits a minimum in capacitance and hence, in the region of pzc between +150 mV and +250 mV, the npAu/MHDA sample exhibits a sharper minimum with a pzc at +100 mV. The monolayer of MPA is more likely to exhibit pinholes where ions from the electrolyte can still reach the substrate, while the long MHDA molecules can be expected to have the most smoothing, passivating effect.^36,37

The more precise pzc for npAu/MHDA clearly reveals that long chains are favorable to control the surface charge on porous surfaces because they suppress side-effects caused by the rough surface. This stands in contrary to conclusions drawn for planar gold electrodes¹² where highly ordered long chains appear to be less suitable as the long chains also suppress acid–base reactions on the head group due to the large diffusive layer (the dielectric layer between the metallic surface and the ionisable head group). Based on these findings, the focus of the subsequent study lies on MHDA due to the better control of the surface charge.

4.2 Control of the proton transfer reaction

In the following, the issue of how the nanoporous structure influences the protonation/deprotonation reaction will be addressed. The small dimensions in the pores, which result in the close proximity of opposing interfaces/SAM molecules, different ordering and slow electrolyte diffusion, potentially alter the reaction kinetics.

The pH-dependent analysis of the protonation/deprotonation reaction was done in NaCl, which is a commonly used supporting electrolyte. The protonation as well as the reverse deprotonation reaction could be well resolved for the npAu sample modified with MHDA (Fig. 3 and 4). The pH at which the maximum peak current I_peak is observed lies near the pH reported for planar gold (see the inset of Fig. 3A), indicating that the reaction is indeed qualitatively similar to planar gold. However, the potential at which the peak was observed was shifted significantly compared to planar gold, which could have been caused by the inhomogeneous distribution of the electrolyte (varying the pH in pores). The small pore diameter of the dealloyed npAu (approx. 10 nm) is reduced due to SAM modification by about 4 nm.³⁸ This also leads to an increased pore resistance in the EEC fit (not shown). Although pore wetting of the dry sample upon immersion is rather fast, the only driving force for diffusion when changing the pH is the gradient in the ion concentration which makes it likely that the distribution was still inhomogeneous during CV. This slow diffusion in the bulk porous structure is a common phenomenon known in the literature.³⁹ As mentioned above, for this reason, several improvements were made, namely that the sample was coarsened and the electrolyte was changed to 50 mM KPi. At this point, it might be important to mention that all adjustments made are also in favor of possible applications in biotechnology as the KPi buffer (or generally phosphate buffers) is very common for biomolecules and the coarsened structure might be necessary to geometrically fit biomolecules in the internal surface.

The CV of the coarsened npAu sample modified with MHDA (Fig. 5) exhibits the well defined protonation and deprotonation reaction. From the overall charge transfer during the protonation reaction, it can be estimated that 10% of molecules participate in the reaction and are electrochemically controllable, which is 10 times more than what has been reported by Luque et al.¹² for planar electrodes. They argue that only those head groups that are closer to the surface (caused by disordering) can participate in the reaction. This, most likely, also explains the higher percentage observed in the present study as the intrinsic surface roughness and curvature cause more head groups to be sufficiently close to the surface. Additionally, the relatively slow scan rates of 0.1 to 6 mV s⁻¹ (compared to rates in the V s⁻¹ range for planar electrodes) may also contribute as the protonation reaction is known to be a very slow process for long-chain molecules.³⁶

The high protonation yield highlights the advantages of npAu as the substrate material as the surface charge of a significantly higher fraction of molecules can be controlled electrochemically. The charge transfer frequency was estimated to be 0.3 s⁻¹ from the Laviron plot (inset in Fig. 5). This value corresponds very well with the value obtained by Smiljanic et al.³⁶ for the same SAMs (MHDA) on planar gold. This implies that the kinetics of the electron transfer for the protonation reaction from the npAu to the head group of the SAM is comparable to that from the planar gold. However, as a significantly higher fraction of molecules can be controlled electrochemically, the overall controllability of the reaction is higher for nanoporous substrates which is especially interesting for potential binding of biomolecules.

5 Conclusions

Nanoporous electrodes have intrinsic properties, such as a high number of structural defects, that prevent the direct transfer of the established knowledge from planar electrodes. In this study, a procedure was successfully established to monitor and control the surface charge of SAMs on nanoporous gold particularly aiming at biotechnological applications. The substrate was functionalized with SAMs, exemplarily using MHDA and MPA. The MHDA-modified npAu exhibited the most distinct pzc (at +100 mV) which indicates that long-chain SAMs are best suited for precise surface charge control because of the smoothing effect. The proton transfer reaction was subsequently investigated, first as a function of pH (in 100 mM NaCl), revealing a peak current maximum at pH 8.6 which fits well with the literature on flat surfaces, underlining the smoothing effect of long-chain SAMs on the porous substrate. Secondly, after adjustment of the substrate material and experimental setup, the same reaction was investigated as a function of scan rate (in 50 mM KPi) yielding a proton transfer frequency of 0.3 s⁻¹. Approximately 10% of surface groups can be electrochemically protonated/deprotonated which is 10 times more than that for planar electrodes. As an outlook, this strategy will be useful for a wide range of application fields including pore wetting for fluid transport and the immobilization of biomolecules for future applications facilitating the immobilization of biomolecules as the electrochemical controllable surface charge may be utilized as the switching or stirring mechanism. In this context, it may be interesting to further investigate the influence of the chain length and, if possible, to further increase the fraction of the electrochemically protonated SAMs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Lead Project (LP-03) Porous Materials @ Work at TU Graz. It was performed in the framework of the interuniversity cooperation of TU Graz and Uni Graz on natural sciences (NAWI Graz).

References

1. K. J. Stine, Biochem. Insights, 2017, 10, 1–12.
2. X. Xiao, P. Si and E. Magner, Bioelectrochemistry, 2016, 109, 117–126.
3. N. Mameka, L. Lührs, S. Heissler, H. Gliemann and C. Wöll, ACS Appl. Nano Mater., 2018, 1, 6613–6621.
4. C. Vericat, M. E. Vela, G. Benitez, P. Carro and R. C. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834.
5. D. Jambrec, M. Gebala, F. LaMantia and W. Schuhmann, Angew. Chem., Int. Ed., 2015, 54, 15064–15068.
6. F. Fixe, R. Cabeça, V. Chu, D. M. F. Prazeres, G. N. M. Ferreira and J. P. Conde, Appl. Phys. Lett., 2003, 83, 1465–1467.
7. Y. Xue, J. Markmann, H. Duan, J. Weissmüller and P. Huber, Nat. Commun., 2014, 5, 1–8.
8. C. Smith and H. White, Langmuir, 1993, 9, 1–3.
9. H. S. White, J. D. Peterson, Q. Cui and K. J. Stevenson, J. Phys. Chem. B, 1998, 102, 2930–2934.
10. W. R. Fawcett, M. Fedurco, Z. Kováčová and Z. Borkowska, J. Electroanal. Chem., 1994, 368, 265–274.
11. I. Burgess, B. Seivewright and R. B. Lennox, Langmuir, 2006, 22, 4420–4428.
12. A. M. Luque, W. H. Mulder, J. J. Calvente, A. Cuesta and R. Andreu, Anal. Chem., 2012, 84, 5778–5786.
13. A. M. Luque, W. H. Mulder, J. J. Calvente and R. Andreu, J. Electroanal. Chem., 2018, 819, 145–151.
14. P. Ramírez, R. Andreu, Á. Cuesta, C. J. Calzado and J. J. Calvente, Anal. Chem., 2007, 79, 6473–6479.
15. E. Boubour and R. B. Lennox, Langmuir, 2000, 16, 4222–4228.
16. M. Hakamada, M. Takahashi, T. Furukawa, K. Tajima, K. Yoshimura, Y. Chino and M. Mabuchi, Phys. Chem. Chem. Phys., 2011, 13, 12277–12284.
17. H. Keiser, K. Beccu and M. Gutjahr, Electrochim. Acta, 1976, 21, 539–543.
18. R. de Levie, Electrochim. Acta, 1963, 8, 751–780.
19. S. Cattarin, D. Kramer, A. Lui and M. M. Musiani, J. Phys. Chem. C, 2007, 111, 12643–12649.
20. A. Sharma, J. K. Bhattarai, S. S. Nigudkar, S. G. Pistorio, A. V. Demchenko and K. J. Stine, J. Electroanal. Chem., 2016, 782, 174–181.
21. M. Hakamada, M. Takahashi and M. Mabuchi, Gold Bull., 2011, 45, 9–15.
22. H.-J. Jin, S. Parida, D. Kramer and J. Weissmüller, Surf. Sci., 2008, 602, 3588–3594.
23. E. Hengge, E.-M. Steyskal, R. Bachler, A. Dennig, B. Nidetzky and R. Würschum, Beilstein J. Nanotechnol., 2019, 10, 2275–2279.
24. C. Lakshmanan, R. Viswanath, S. Polaki and R. Rajaraman, AIP Conference Proceedings, Melville, NY, 2015, p. 140033 ff.
25. T. Krekeler, A. V. Straßer, M. Graf, K. Wang, C. Hartig, M. Ritter and J. Weissmüller, Mater. Res. Lett., 2017, 5, 314–321.
26. H.-K. Song, Y.-H. Jung, K.-H. Lee and L. H. Dao, Electrochim. Acta, 1999, 44, 3513–3519.
27. J. Landesfeind, D. Pritzl and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A1773–A1783.
28. Y. Chu, B. Seo and J. Kim, Bull. Korean Chem. Soc., 2010, 31, 3407–3410.
29. B. Ter-Ovanessian, C. Alemany-Dumont and B. Normand, J. Appl. Electrochem., 2013, 44, 399–410.
30. T. D. Tran, M. T. T. Nguyen, H. V. Le, D. N. Nguyen, Q. D. Truong and P. D. Tran, Chem. Commun., 2018, 54, 3363–3366.
31. A. L. Eckermann, D. J. Feld, J. A. Shaw and T. J. Meade, Coord. Chem. Rev., 2010, 254, 1769–1802.
32. T. Doneux, M. Steichen, A. D. Rache and C. Buess-Herman, J. Electroanal. Chem., 2010, 649, 164–170.
33. K. M. Dickinson, K. E. Hanson and R. A. Fredlein, Electrochim. Acta, 1992, 37, 139–141.
34. D. A. Patel, A. M. Weller, R. B. Chevalier, C. A. Karos and E. C. Landis, Appl. Surf. Sci., 2016, 387, 503–512.
35. R. G. Kelly, A. J. Young and R. C. Newman, Electrochemical impedance: Analysis and interpretation, ASTM International, 1993.
36. M. Smiljanić, C. Adam and T. Doneux, J. Electroanal. Chem., 2018, 815, 238–245.
37. S. Campuzano, M. Pedrero, C. Montemayor, E. Fatás and J. M. Pingarrón, J. Electroanal. Chem., 2006, 586, 112–121.
38. J. F. Smalley, S. W. Feldberg, C. E. Chidsey, M. R. Linford, M. D. Newton and Y.-P. Liu, J. Phys. Chem., 1995, 99, 13141–13149.
39. M. D. Scanlon, U. Salaj-Kosla, S. Belochapkine, D. MacAodha, D. Leech, Y. Ding and E. Magner, Langmuir, 2011, 28, 2251–2261.

---

Footnote

† Electronic supplementary information (ESI) available: Current vs. time curve for the dealloying process (Fig. S1) and CV of SAM modified npAu in 1 M KOH to investigate the stability (Fig. S2). See DOI: 10.1039/d1cp01491a

---