Ion association in hydrothermal aqueous NaCl solutions: implications for the microscopic structure of supercritical water

Abstract

Knowledge of the microscopic structure of fluids and changes thereof with pressure and temperature is important for the understanding of chemistry and geochemical processes. In this work we investigate the influence of sodium chloride on the hydrogen-bond network in aqueous solution up to supercritical conditions. A combination of in situ X-ray Raman scattering and ab initio molecular dynamics simulations is used to probe the oxygen K-edge of the alkali halide aqueous solution in order to obtain unique information about the oxygen's local coordination around the ions, e.g. solvation-shell structure and the influence of ion pairing. The measured spectra exhibit systematic temperature dependent changes, which are entirely reproduced by calculations on the basis of structural snapshots obtained via ab initio molecular dynamics simulations. Analysis of the simulated trajectories allowed us to extract detailed structural information. This combined analysis reveals a net destabilizing effect of the dissolved ions which is reduced with rising temperature. The observed increased formation of contact ion pairs and occurrence of larger polyatomic clusters at higher temperatures can be identified as a driving force behind the increasing structural similarity between the salt solution and pure water at elevated temperatures and pressures with drawback on the role of hydrogen bonding in the hot fluid. We discuss our findings in view of recent results on hot NaOH and HCl aqueous fluids and emphasize the importance of ion pairing in the interpretation of the microscopic structure of water.

---

1 Introduction

Hot aqueous (hydrothermal) fluids are of crucial importance in numerous chemical technologies (e.g., for hazardous waste treatment,^1,2 recycling of composite materials and polymers,^3,4 biomass gasification,⁵ or nanomaterial fabrication⁶) and in many heat and mass transport processes in the Earth's crust and mantle. One of these processes is the formation of magma as hydrothermal fluids disrupt bonds in the minerals thereby significantly lowering the melting temperature.^7,8 The vast majority of ore deposits originated from the action of hydrothermal fluids. This is because hydrothermal water is very efficient in permeating rocks and dissolving and transporting metals due to the high temperature and the substantial amount of dissolved salts resulting in complexation of metals with anionic ligands and/or water molecules.^9,10 Thus, the structural changes in the properties of water and aqueous solution with temperature and their causes have been a long-standing research topic.^11–13 Here, ion–solvent interaction and the strongly enhanced ion pairing is of particular interest.^14,15 The temperature and pressure dependent changes in ion hydration in aqueous liquids affect metal complex formation, mineral solubility and phase equilibria.^16,17 Sodium chloride (NaCl) is the most abundant solute in seawater and in most natural hydrothermal fluids.¹⁸ For instance, analysis of fluid inclusions indicated a salinity of up to 30 wt% NaCl in the ore-forming fluids of lead–zinc deposits.¹⁹ Even in the Earth's upper mantle, NaCl is a major component of hydrous fluids as revealed by brine inclusions in diamonds.²⁰ Therefore, the binary system H₂O–NaCl has widely been studied^21,22 as a first approximation and a representative model for Cl-rich fluids in many geological environments and in chemical reactors such as for supercritical water oxidation.²³ Numerous theoretical approaches have addressed the structural properties of the H₂O–NaCl binary as function of temperature,^24–26 with the results of several studies pointing towards the formation of larger polyatomic NaCl clusters in the solution due to the decreasing dielectric constant of water with rising temperature.^{16,17,27–31}

Several X-ray and neutron diffraction studies have been performed, on a variety of different salt solution and at a large range of different experimental conditions.^12,32–34 However, X-ray spectroscopy studies on ions comprised of elements with a low atomic number (Z) or the surrounding water itself are scarce owing to the limitations imposed by the sample environment,^35,36 in contrast to ions with high-Z elements, which can be and have been extensively investigated at high pressures and temperatures using X-ray absorption spectroscopy (XAS).^37–42 Hence, most previous X-ray spectroscopic studies of aqueous NaCl solutions were at relatively low temperature and pressure conditions. Generally, they indicate a destabilizing effect of the dissolved ions on the water structure, which is largely limited to the first hydration shell⁴³ and weakened at an increased temperature of 90 °C.⁴⁴

In order to achieve relevant conditions to study hydrothermal NaCl aqueous solution we exploit bulk sensitive X-ray Raman scattering spectroscopy (XRS) at the oxygen K-edge. The detailed interpretation of spectral fingerprints related to changes in the water network structure requires spectral calculations based on structural simulations for a variety of thermodynamic conditions. It is the combination between experiment and theory that is capable to retrieve solid information on the local water structure which can hardly be obtained by discussion of bare spectral changes in the experiment. Thus we used in this study XRS spectroscopy in combination with state-of-the-art modeling of the spectroscopic data based on structures obtained from ab initio MD simulations. This approach was utilized to investigate the influence of NaCl on the water structure in aqueous solutions at elevated temperatures and pressures of up to 600 °C and 120.6 MPa, respectively. Furthermore, we compared our findings with the results of similar studies on pure water and discuss them in the scope of earlier work on hydrothermal NaOH and HCl solution.³⁶

2 Experiment and modelling

2.1 Experimental

We exploited XRS spectroscopy to study the oxygen K-edge of aqueous NaCl solutions at hydrothermal conditions by means of a resistively heated diamond anvil cell (DAC). XRS is a non-resonant inelastic X-ray scattering⁴⁵ technique, which utilizes hard X-rays as a bulk sensitive probe to investigate absorption edges of elements with low atomic numbers in complex, highly-absorbing sample environments (for example see ref. 35, 36, 46–49 and 50 as well as references therein). Thus, it allows measuring the oxygen K-edge XRS spectrum of aqueous solutions under extreme thermodynamic conditions not accessible by soft X-ray techniques. Performing XRS measurements at low absolute values of momentum transfer, the transitions probed are dominated by dipole excitations and thus XRS provides similar information as XAS but with the advantage of providing a bulk sensitive probe free of saturation effects. The combination of XRS measurements with state of the art calculations of the system under investigation yields detailed structure information and is applicable for a variety of different systems, i.e. crystalline and amorphous solids, fluids or gases.

Aqueous solutions of 1.9 and 2.0 molal NaCl were prepared using double-distilled water and NaCl (ultrapure, Alfa, >99.0%). In order to expose the sample to high temperature T and high pressure p conditions, we used the gasketless Bassett-type hydrothermal diamond anvil cell (HDAC)⁵¹ employed by Schmidt and Seward,⁵² with the modification of a larger cylindrical recess in one of the diamond culets to enclose the sample (see ref. 35). The recess was machined using an UV femtosecond pulsed laser ablation system. The diameter of the recess was 0.5 mm and the depth 0.11 mm. Omitting the gasket increased the measured intensity significantly owing to the larger accessible solid angle. The temperature was measured with thermocouples attached to each diamond anvil with an overall error of uppermost ±1 °C.⁵³ The pressure was calculated from the fluid bulk density and the known temperature using appropriate correlation functions.⁵⁴ The density was determined from the actual NaCl concentration of the solution and the measured liquid–vapor homogenization temperature, the latter via visual observation of the disappearance of a vapor bubble contained in the sample volume.^35,51 The actual concentration of the samples was higher than that of the stock solution due to water evaporation during transfer of a small droplet into the sample chamber of the diamond-anvil cell. It was measured via cryoscopy before each temperature run using the equation for the freezing point depression of aqueous NaCl solutions by Bodnar.⁵⁵ The actual concentrations were 2.63 ± 0.25 molal NaCl. The temperature was increased along the liquid–vapor curve up to a homogenization temperature of 470 °C at which the vapour disappears. This leads to an increase of temperature along an isochore and thus to more drastic pressure changes. Therefore, at 400 °C a maximum pressure of about 26 MPa was reached while at 500 °C and 600 °C pressures of 63 MPa and 120.6 MPa were generated, respectively. The experimental conditions for each measured spectrum, in terms of applied temperature, pressure and resulting density are listed in Table 1 in section Further information.

The XRS experiments were performed at beamline P01 of PETRA III using the XRS spectrometer⁵⁶ and at beamline ID20 of ESRF exploiting the large-solid-angle XRS spectrometer.⁵⁷ At beamline P01 spectra were measured with an overall energy resolution of 0.85 eV at a momentum transfer of (2.4 ± 0.3) Å⁻¹ using an array of 12 spherically bend Si analyzer crystals at a fixed analyzer energy of 9.7 keV exploiting the Si(660) reflection in forward scattering. Energy loss spectra were collected by scanning the incident energy using the Si(311) monochromator. The beam was focused to a size of 50 μm × 50 μm (v × h) at the sample position. At beamline ID20 the incident energy was tuned via a combination of a Si(111) high heat-load and a Si(311) channel cut monochromator at a fixed analyzer energy of 9.7 keV with an overall energy resolution of 0.75 eV the Si(660) analyzers were used to acquire XRS spectra at a momentum transfer of (2.7 ± 0.3) Å⁻¹. The beam size was set to 70 μm × 50 μm (v × h).

The oxygen K-edges were extracted using the XRStools⁵⁸ program package. Details for data reduction in XRS experiments can be found in ref. 58 and 59. XRStools was also used for the further data reduction of the extracted spectra, i.e. the sum of spectra from all analyzers for each energy loss scan, namely the consistency check of single spectra before merging several scans, the background subtraction and the normalization to the area between 525 eV and 575 eV. The final spectra are obtained by summing up at least three single spectra at the same pressure, temperature conditions.

2.2 Theory

2.2.1 Molecular dynamics simulations. Ab initio MD (AiMD) simulations were conducted using the QUICKSTEP module of the CP2K code.⁶⁰ Electronic structure calculations were performed in the framework of Kohn–Sham density functional theory using a mixed Gaussian and plane wave approach.⁶¹ The exchange–correlation functional was treated by the BLYP method.^62,63 Core electrons (1s for O and Na; 1s, 2s and 2p for Cl) were included into the pseudocores of Goedecker–Teter–Hutter pseudopotentials.⁶⁴ As basis sets we employed double-zeta valence plus polarization basis sets.⁶⁵

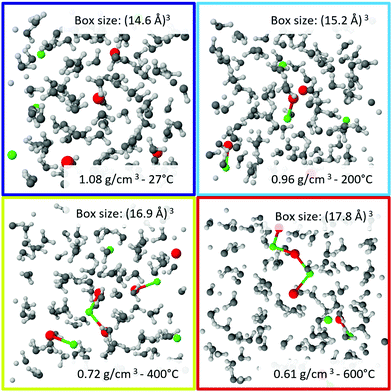
To closely match the experimental conditions, the simulation cells contained 100 H₂O molecules and 4 or 5 Na and Cl atoms, which corresponds to a concentration of approximately 2.2 molal and 2.8 molal, respectively. Simulation cell lengths and temperatures were chosen to match experimental densities and temperatures. Initial structures were obtained from previous unpublished ab initio MD simulations at 727 °C and various densities, in which the original cells contained 100 H₂O and 10 NaCl. For lower concentrations the number of Na and Cl atoms was subsequently reduced. Each of these simulation boxes was equilibrated for a few tens of picoseconds at 727 °C. For the present simulations densities and temperatures were adopted to the desired conditions and equilibration runs of about 10 ps were performed. Temperature was controlled by canonical sampling through velocity rescaling, CSVR.⁶⁶ The equations of state were integrated with a time step of 0.5 fs. All simulations were performed using periodic boundary conditions and in the canonical ensemble (constant number of particles, volume and temperature, NVT). After equilibration production runs of 20 ps were performed. From each of the trajectories 100 snapshots taken at equal time intervals were extracted for the calculation of theoretical XRS spectra and further analysis. The thermodynamic conditions of each performed simulation are listed in section Further information in Table 1.

2.2.2 Spectral calculations. The oxygen K-edge spectra were calculated with the ERKALE code⁶⁷ for all individual snapshots extracted from the MD simulations as discussed above. We used the ERKALE code to calculate XRS spectra within the transition potential approximation (TPA) within density functional theory using the revised Perdew–Burke–Ernzerhof functional.^68,69 We applied Dunning's augmented correlation consistent polarized valence double zeta basis set⁷⁰ for all atoms in the system but the excited oxygen site for which the IGLO-III basis set⁷¹ was used. Furthermore, after convergence of the self-consistent field, the basis set of the excited atom was augmented with diffuse functions to improve the description of virtual orbitals. In order to obtain a uniform energy scale for calculations of each MD snapshot, the energy value of the first TPA transition was set to the total energy difference of the first core-excited state and the ground state.⁶⁷ This provides a reliable energy scale to compare spectra of the individual snapshots. Typically about 600 simulated spectra of the oxygen K-edge were calculated at each p/T condition. For each single calculation, a spherical cluster with approximately 30 water molecules was randomly chosen from the simulated trajectory to calculate the K-edge spectrum for the central water molecule. Convergence in terms of cluster size proved to be reached. Finally, all individual spectra were merged to obtain an oxygen K-edge spectrum based on a statistical average of the structural snapshots. For each p/T condition the corresponding final spectra were shifted on the energy scale to match the experimental pre-edge onset in order to enable comparison with the experimental data. The momentum transfer was set to a value of 2.65 Å⁻¹ for all calculations. A Gaussian broadening scheme^72,73 with a full width at half-maximum that increase linearly from 0.4 eV to 10 eV between 535 eV and 545 eV was further applied to account for finite lifetime effects and instrumental broadening.

In order to compare the calculated spectra of the aqueous NaCl solutions with those of pure water from ref. 35 and 36, we used the same procedure as described above utilizing the MD trajectories published in ref. 36.

2.2.3 Structural analysis. For a comprehensive analysis of the AiMD simulations, several structural parameters were extracted from the generated trajectories to characterize the local water network and quantify relative changes. A hydrogen bond between two water molecules was determined following the definition of A. Luzar and D. Chandler in ref. 74. This defines a structural arrangement of two water molecules as a hydrogen bond when the two oxygen atoms are less than 3.5 Å apart and the hydrogen-donor–acceptor angle is less or equal to 30°. Furthermore, to quantify the deviation from a perfect tetrahedral structure in the water network upon increasing temperature or the addition of salt, we used the definition in ref. 75 which involves a central molecule and its four closest neighboring water molecules to determine the degree of deviation in terms of distance and angle. These two parameters are evaluated by the formulas

Δ_d = max{|r^loc_i|}_i − min{|r^loc_i|}_i

where r̂^loc_k = r^loc_k/|r^loc_k| are vectors pointing from the excited oxygen atom to one of the four closest neighbouring oxygen atoms. The parameters are calculated for each water molecule and then averaged. Here Δ_a corresponds to the summed absolute deviation from the tetragonal O–O(central)–O-angle of 109.5° and Δ_d to the difference in distance of the closest and uttermost of the four nearest oxygen atoms. This way, the two calculated parameters Δ_a and Δ_d are zero for a perfect tetrahedron but increase when the O–O(central)–O angles are not equal to 109.5° and the distance between the nearest and farthest neighbor changes, respectively. Both parameters are useful to quantitatively investigate deviation from the tetrahedral structure by variation of an external parameter. Additionally, ions were classified as being in a contact pair bond or a larger cluster if their distance to adjacent ions is smaller than 3.75 Å, which is the first minimum of the radial Na–Cl distribution function as extracted from our MD simulations. Furthermore, the structural properties of bulk and hydration shell water were determined using the definition that every water molecule outside the first coordination shell with the radius 3.40 Å and 3.93 Å for Na⁺ and Cl⁻, respectively, is considered as bulk water as those distances correspond to the first minimum of the ion-oxygen radial distribution functions of the two ions. In the language used in this paper, the terms water structure or water network are used in reference to the introduced parameter describing the local symmetry and bonding properties of water molecules as seen from the oxygen site.

2.3 Analysis of the oxygen K-edge in aqueous solutions

The oxygen K-edge of water and aqueous solutions exhibits three well-distinct features, which are depicted in Fig. 1b: the pre-edge, main-edge and post-edge at around 535 eV, 537 eV and 541 eV, respectively. In recent decades, substantial efforts have been made to relate the absolute and relative intensities of these spectral features to the local structure of the absorbing/scattering atom. Even though some details are still debated, in particular those related to the interpretation of the pre-edge, the following picture emerges from the literature.^73,75–78 It is assumed that the intensity of the pre-edge feature is anti-correlated to the number of hydrogen bonded water molecules and correlated to a deviation from a tetrahedral structure. Hence, the pre-edge feature of e.g. hydrothermal fluids is highly pronounced at higher temperatures at which the tetrahedral network is extremely distorted and hydrogen bonding is strongly suppressed³⁵ or even absent.⁷⁹ The main-edge feature is largely associated with localized excitations, hence, comparing different ice phases, the intensity of this feature rises with increasing density as more water molecules approach the first shell even tough the amount of hydrogen-bonds stays the same.^73,76 Furthermore, an increase of main-edge intensity is observed when the structural arrangement of the water network is disturbed by e.g. temperature. The correlation of the post-edge feature is contrary to the correlation of the pre-edge feature. Gain in spectral weight in the post-edge region implies an increase in the number of hydrogen bonded molecules and a stronger orientation of the molecules into a tetrahedral structure. This more ordered, tetrahedral structure forms a well defined potential well for a shape resonance.⁷⁸ The correlation can be observed, for instance, in the XRS spectra of different ice phases.⁷³ The change in intensity between post-edge to main and pre-edge can also be understood in terms of excitations becoming more localized in disordered systems as discussed for low- and high-density amorphous ice,⁷⁶ a picture which may be adopted to fluids in the supercritical regime.

Fig. 1 The measured and calculated XRS spectra of the aqueous NaCl solution (H₂O + NaCl) (a and c) and pure water (b and d) in a temperature range from 20 °C to 600 °C. The spectra of pure water were taken from our previous study ref. 35 and 36. The approximate position of the different spectral features are indicated in (b) by I (pre-edge), II (main-edge) and III (post-edge). The integrated intensities of the pre-edge (e) and post-edge (f) feature of the measured (small dots with lines) and calculated (triangle symbols) spectra as a function of density (see text for details). Isochoric temperature changes i.e. higher pressures are indicated by a black border color. The density values are rounded to the second decimal place and the corresponding pressure values are listed in Table 1.

Table 1 The experimental conditions at each measured spectrum of the aqueous salt solution as well as the thermodynamic conditions of the performed AiMD simulations. The densities are rounded to the second decimal place. For the sake of completeness, the values are also listed for the spectra taken from the previous studies. A plot of the temperature applied in the experiment and the resulting density is shown in Fig. 5(d)

Sample	°C	g cm^−3	MPa
H2O + NaCl(Exp.)	25	1.09	0.1
H2O + NaCl(Exp.)	100	1.05	0.1
H2O + NaCl(Exp.)	200	0.96	1.4
H2O + NaCl(Exp.)	300	0.86	7.8
H2O + NaCl(Exp.)	400	0.72	25.4
H2O + NaCl(Exp.)	500	0.60	62.7
H2O + NaCl(Exp.)	600	0.60	120.6
H2O + NaCl(Theo.)	25	1.09
H2O + NaCl(Theo.)	100	1.04
H2O + NaCl(Theo.)	200	0.96
H2O + NaCl(Theo.)	300	0.86
H2O + NaCl(Theo.)	400	0.72
H2O + NaCl(Theo.)	500	0.62
H2O + NaCl(Theo.)	600	0.62
H2O(Exp.)	20	1	0.1
H2O(Exp.)	200	0.86	1.6
H2O(Exp.)	370	0.45	21
H2O(Exp.)	400	0.54	48
H2O(Exp.)	600	0.45	134
H2O(Theo.)	20	1
H2O(Theo.)	200	0.86
H2O(Theo.)	400	0.54
H2O(Theo.)	600	0.45

---

3 Results

The XRS spectra of the aqueous NaCl solution (H₂O + NaCl) measured at different temperatures are shown in Fig. 1a. Additional spectra from our first attempt confirm the presented findings (see Further information, Fig. 6). The spectra exhibit a more pronounced pre-edge feature with rising temperature together with a shift to lower energy loss values. Latter is likewise observable for the main-edge but with hardly any change in the spectral intensity. In contrast to the pre-edge, the post-edge is dominant at ambient temperature but loses intensity when the temperature is increased. Similar spectral changes can be identified in the XRS spectra of pure water (see Fig. 1b), which were taken from our previous study ref. 35 and 36. The experimental conditions of the shown spectra of pure water are also listed in Table 1. The induced spectral changes due to the generated pressures are negligible compared to the more drastic changes with increasing temperature.⁸⁰

A qualitative analysis based on the described relationship between the intensity of the different spectral features and the local structure shows a general reduction in the total number of hydrogen-bonded molecules with decreasing density, accompanied by a general loss of the tetrahedral order, for both aqueous NaCl solutions and pure water.

The computed XRS spectra of the oxygen K-edge are shown in Fig. 1c and d for the case of aqueous NaCl solutions and pure water, respectively, and are in good overall agreement with the experiment. Specifically, the relative changes with temperature are adequately reproduced by theory. A selection of snapshots at different temperatures, which were used for the calculation, are shown in Fig. 2.

Fig. 2 Snapshots from the AiMD trajectory showing ion clusters of different size at several temperature steps. Sodium is shown in red and chlorine in green. Oxygen and hydrogen are depicted in grey and light grey, respectively, for better clarity. Ion pairs and ion clusters are indicated with a drawn connection between the ions.

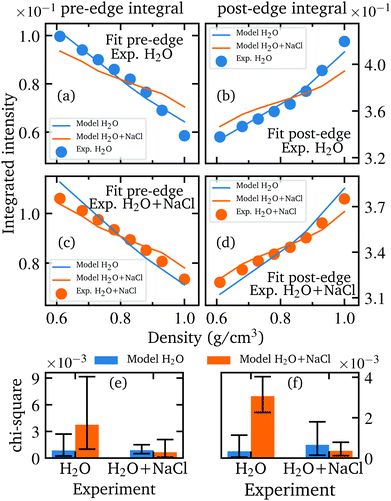
A well-established analysis scheme of previous XRS studies consists of using either the peak intensity or the integrated intensity of spectral features to quantify the variation of spectral features with density and to assess the consistency of the calculations with the experiment.^{35,36,73,78,81,82} Following this analysis scheme, we integrated the spectral features with the most significant changes, namely the pre-edge and the post-edge. The integrated intensities of the measured and calculated spectra are plotted as function of density in Fig. 1e and f. Using the composite trapezoidal rule, the pre-edge was integrated in a range from 532.5 eV to 535.5 eV and the post-edge from 538.5 eV to 543.5 eV. The error is determined by calculating several integrals with a slight deviation of the integration limits by 0.2 eV and then evaluating the standard deviation of the mean value. This estimation gave a much larger error than a strict evaluation via error propagation of the statistical uncertainties. The integrated values of the calculated spectra are further scaled by a constant factor to compensate the discrepancy in the absolute intensities between theory and experiment. The integrated values of the pre-edge were scaled by 1.015 and 0.965 for pure water and aqueous sodium chloride solution, respectively, and the values of the post-edge were scaled by 1.066 and 1.068, respectively. As mentioned in our previous study, the use of the scaling factor highlights the difficulty of core-level simulations for liquids to achieve a perfect agreement between experimentally recorded and calculated intensities on an absolute scale.³⁶ This allows a thorough comparison of the relative changes with density. At densities below 0.75 g cm⁻³, the integrated intensities of the NaCl solution approach those of the pure water. Comparing experiment and theory, the variation of pre-edge and post-edge intensities is well described by the calculations, with exception of a slight overestimation of the pre-edge intensity for water at the lowest density. A χ² test verifies that the two models are not interchangeable to reproduce the systematic changes of the integrated pre- and post-edge intensities as a function of density (further elaborated in section Further information).

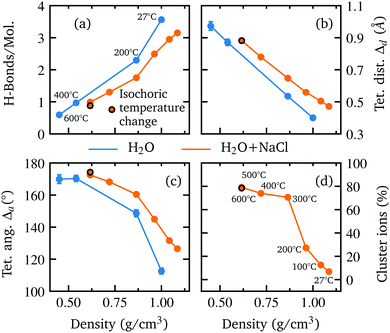
The good agreement of the calculated and measured spectral changes together with the result of the χ² test justify the use of the underlying model to extract detailed structural information on the hydrogen bond network. The extracted number of hydrogen bonded molecules and the introduced parameters to quantify the deviation from tetrahedral order Δ_a and Δ_d are shown in Fig. 3 as a function of density. Water and the aqueous NaCl solution show the same trends with density, but a reduced number of hydrogen bonded molecules is observed along with larger deviation from a tetrahedral structure in the case of the NaCl solution. This is in accordance with the integrated intensities displayed in Fig. 1(e and f), which are higher (lower) for the pre-(post-)edge of the spectrum of the salt solution.

Fig. 3 Comparison of the averaged structural parameters of the aqueous NaCl solution (orange) with those of pure water (blue) as extracted from the AiMD simulations. The extracted number of H-bonds per molecule (a), the deviation from tetrahedrality in terms of distance Δ_d (b) and angle Δ_a (c) and the percentage of ions being part of an ion cluster (d) are shown as function of density. The orange markers with black border color correspond to an isochoric temperature change.

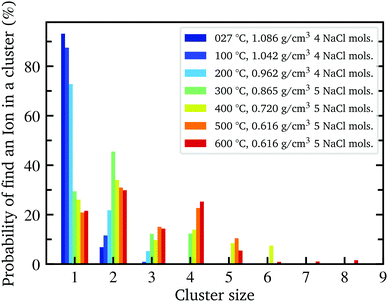
With decreasing density, however, all determined parameters of the aqueous NaCl solution approach those of pure water at similar densities. According to the results of the MD simulation, the number of hydrogen bonded molecules per water molecule decreases in the NaCl solution from 3.13 at ambient conditions to 0.87 at the lowest density of 0.62 g cm⁻³ (600 °C) in contrast to pure water, where at the highest density on average 3.56 hydrogen bonds per molecule are found and only 0.67 average bonds per molecule persist at the highest temperature (600 °C) owing to the lower density of 0.45 g cm⁻³. The calculated angular deviation from the tetrahedral structure can be used to evaluate the mean angle deviation of the four closest neighbouring molecules by dividing its value by 6 (the number of unique combinations of these nearest neighbors with the central water molecule) yielding a value of 18.76° and 21.08° at the highest densities and 28.32° and 29.05° at the lowest density (600 °C) for pure water and the aqueous sodium chloride solution, respectively. Furthermore, we determined the percentage of ions which are part of an ion pair bond or a larger ion cluster. At ambient conditions, just 7% of ions are associated. This number increases rapidly to 70% at 0.86 g cm⁻³ (300 °C) followed by a flatter rise up to 78% at the lowest density of 0.62 g cm⁻³ (600 °C). A detailed depiction of the cluster distribution is given in section Further information, Fig. 7 revealing larger ion clusters as the predominant form at higher temperatures.

4 Discussion

The observed spectral changes upon addition of NaCl, both in theory and experiment, in combination with the extracted structural parameters reveal a net destabilizing effect of hydrated ions on the water structure at room temperature confirming findings of previous work, which exploited optical Raman and X-ray absorption spectroscopy.^44,83–86 Following the goal of this study to investigate the structural changes with increasing temperature, the analysis shows that this destabilizing effect is not equally pronounced over the entire density range. Both the integrated spectral intensities as well as the theoretical determined parameters exhibit a weakening of this effect as they approach the values of pure water with increasing temperature. Comparing the increasing similarity of the two systems with the formation of contact ion pairs in the system, it becomes apparent that these two phenomena are directly related. The observation of the formation of contact ion pairs and larger ion clusters at higher temperatures is in accordance to earlier experimental studies^38,87–89 and simulations^90,91 of NaCl aqueous solutions and other aqueous salt solutions. The formation of contact ion pairs and larger ion clusters is a response to the decrease of the dielectric constant of water with increasing temperature thus reducing the ion–water interaction and increasing the ion–ion interaction,^15,92 consequently, lowering the ions' influence on the water structure. For instance, a neutron diffraction study on nickel sulfate dissolved in heavy water at ambient and elevated temperatures reveals a significant weakening of the first hydration shell structure of the Ni²⁺ ions at higher temperatures which might be explained by enhanced ion pairing of nickel and sulphate ions.⁹³ From an entropic point of view ion association is also favored because the entropy loss due to the electrostriction by water molecules is smaller for ion pairs than for free ions.¹³ This leads to clusters with a size of at least three ions as the predominant form at temperatures above 400 °C and to even larger clusters with a maximum size of eight ions which occasionally occur at even higher temperatures²⁸ (see Further information, Fig. 7). In agreement with MD simulations, we observe a significant amount of ion pairs, more than has been inferred from conductivity measurements on dilute NaCl solutions up to 0.1 molal.^28,94,95 According to Sherman et al. the determination of the associated ions based on structural criteria is independent of the lifetime of the clusters, thus taking into account transient ion pairs that are not detectable in conductivity experiments due to their short lifetime.⁹⁰ However, the influence of such short-lived ion pairs on the water structure still affects the measured XRS signal as the structural average on the atto-second time scale is probed.

In order to further study and verify the correlation of the formation of contact ion pairs and larger ion clusters with the increase of structural similarities between pure water and the salt solution, we calculated the difference between the two systems in terms of the integrated experimental pre- and post edge intensities, respectively, as a function of density. This way, the evolution of the theoretically derived parameter with decreasing density (increasing temperature) can directly be compared with an experimentally determined quantity which depends on the local structure environment of the absorbing atom. Beforehand, the integrated experimental intensities of the two systems were interpolated onto the same uniform density grid because naturally both measurements could not be performed at the exact same densities. Furthermore, the y-axis was flipped for a better comparison with the variation of the number ions being in a contact pair bond or a larger ion cluster. As depicted in Fig. 4, we observe a significant correlation of the increasing percentage of clustered ions in the system with the decreasing difference of the integrated spectral intensities of the two fluids for both, the pre- and post-edge. This indicates that the formation of contact ion pairs is the driving force for the observed spectral changes of the two systems and thus presumably responsible for the increasing structural similarity as derived from the MD simulations.

Fig. 4 The percentage of ions in a cluster as a function of density (orange, right y-axis) together with the absolute difference between the integrated experimental pre and post edge intensities (green/red on the left side, see Fig. 1(e and f)) of aqueous NaCl solution and pure water, calculated in the density regime where both experiments overlap. For a better comparison with the evolution of the fraction of cluster ions in the system, the y-axis of the integrated differences is flipped upside down.

With the release of water from the coordination shells of the pairing ions, more bulk water is probed and the two systems become more alike with decreasing density in terms of both spectral and structural differences.^29,90 This indicates that the perturbation of the water network is largely limited to the first coordination shell of Na⁺ and Cl⁻.^83,96 This is further supported by the MD simulation result because a separate structural analysis of the water molecules within the first hydration shell of the ions and the bulk water (see Fig. 5(a–c)) shows a strongly disturbed first shell, while the bulk water of the solution rather resembles the structure of pure water.

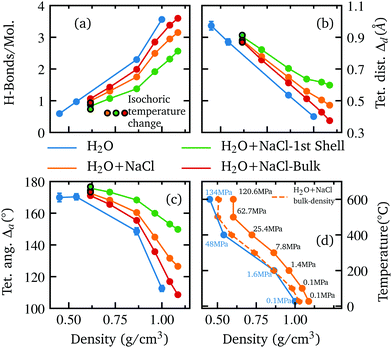Fig. 5 The extracted number of H-bonds per molecule (a) and the deviation from tetrahedrality in terms of distance Δ_d (b) and angle Δ_a (c) are shown as function of density, determined separately for pure water (blue) the whole aqueous NaCl solution (orange), the water molecules inside the first coordination shell of ions (green) and the remaining bulk water molecules (red). Results for pure water and the aqueous NaCl solution from Fig. 3 are shown for reference. The isochoric temperature change at the highest temperature is indicated by a black border color. The plot in the lower right (d) shows the experimental conditions i.e. the relationship between the applied temperature and the density of the sample for each measured spectrum in this work (orange, solid line) and as a function of the determined bulk density (orange, dashed line). The same relationship is also shown for the spectra used from the previous work on pure water (blue, solid line). The corresponding pressure is given next to each data point.

Although the direct influence of the ions on the water structure decreases with rising temperature, the occupied volume by the ions and ion clusters still leads to less available space for the bulk water and thus to a slightly higher density compared to pure water at the same temperature (see Fig. 5(d) for calculated bulk densities). The resulting influence on the water structure becomes apparent when comparing the two systems as a function of bulk density and temperature (see Further information, Fig. 8). In terms of bulk density, the extracted parameter for the systems become nearly identical for smaller densities than approximately 0.875 g cm⁻³i.e. when the influence of the ions decreases rapidly due to ion clustering. However, as the corresponding temperature of each bulk density value is higher than the respective temperature of the corresponding pure water density, an apparent stabilization effect is observed at higher temperatures for some parameters, as the number of hydrogen bonds is slightly higher in the salt solution and the deviation of tetrahedral order in terms of distance is less pronounced.

A recent study³⁶ on hydrothermal aqueous solution also combined XRS experiments with AiMD calculations to investigate sodium hydroxide and hydrochloric acid. Similarly, the ions in the two solutions exhibit an overall destabilising effect at ambient conditions, followed by a net stabilizing effect on the water structure at higher temperatures. This indicates, to a certain extent, a general tendency of saline solutions to stabilize the water structure at hydrothermal conditions regardless of the pH value of the solution or how the ions incorporate into the water structure, as e.g. the addition of hydrogen in HCl solutions leads to the formation of Eigen and Zundel structural motifs.⁹⁷ At higher temperatures the NaOH solution exhibits a stronger stabilization of the water structure compared to the NaCl solution as more hydrogen bonded molecules persist and the water network resembles closer to a tetrahedral structure. This can be related to the strong hydration shells surrounding not only the Na⁺ cation but likewise the OH anion as can be inferred from the comparison of calculated XRS spectra of water molecules belonging to the bulk and to the hydration shells of Na⁺ and OH⁻ while the stabilization via Cl⁻ hydration was found to be weaker. A neutron diffraction study⁹⁸ supports this view reporting a strong hydrogen bond of the OH⁻ to the neighbouring water molecules exceeding the Coulomb interaction of the Na⁺ counter ion in the competition for the orientation of the surrounding common water molecules. Moreover, a comparison of Na⁺ and Cl⁻ in a recent high-pressure XRD study³⁴ reveals a more rigid hydration shell surrounding the Na⁺ and withstanding even pressures up to 1700 MPa, while the hydration shell of Cl⁻ is highly altered. In conjunction with our study, this might point towards a stronger stabilizing influence of the OH⁻ ion at higher temperatures compared to the smaller bulk density increasing effects of the Cl⁻ ion. It should be noted, however, that the different concentrations of the aqueous salt solutions in the previous and this study must be considered in a direct comparison.

Waluyo et al.⁴⁴ performed an X-ray absorption spectroscopy study on a 4 molal aqueous NaCl solution and pure water at 4 °C and 90 °C. They observed an overall destabilization of the water structure by the dissolved ions but a reduced effect at the elevated temperature, consistent with our results. This observation was attributed to the conversion from a low density liquid (LDL) to a high density liquid (HDL)⁹⁹ triggered by temperature and by the addition of ions. According to this hypothesis, the Na⁺ and Cl⁻ ions have less influence on the water structure at higher temperature as most of the water molecules already exist as HDL. Consequently, only a small remaining fraction of LDL species can be perturbed and interconverted to HDL by the presence of ions. Our analysis of 2.63 molal NaCl aqueous solution suggests that ion pair formation contributes significantly to the observed decrease in perturbation at elevated temperatures, as the number of clustered ions nearly doubles between room temperature and 90 °C.

5 Summary and outlook

We studied the microscopic structure of aqueous NaCl solutions by means of XRS spectroscopy and ab initio MD simulations in a temperature range from 25 °C to 600 °C and compared our results with previously published XRS data on pure water.³⁵ We found a net destabilizing effect of the dissolved ions on the water network at room temperature, which decreases with rising temperature as the increased formation of ion pairs and larger clusters mitigate the ions' influence on the water structure. Hence, we observe increasing similarities in the microscopic structure of aqueous NaCl solution and pure water with increasing temperature both in our simulated trajectory and in the spectral fingerprints in the experimental data. Calculated XRS spectra based on structures generated from simulated trajectories entirely reproduce the observed experimental changes with increasing temperature. Furthermore, this was also confirmed by the χ² analysis of the two different systems, which indicated that the models were non-interchangeable. This good agreement enabled us to extract detailed structural information from the simulated systems. Exploiting the structural information of the MD simulations, we find that the destabilizing effect of the dissolved ions on the water structure under ambient conditions results in less hydrogen-bound molecules and a larger deviation from a tetrahedral structure. Noteworthy, these structural changes are consistent in a comparison with a qualitative and quantitative analysis of the different spectral features as we observe an increase of spectral intensity in the pre-edge region accompanied by spectral loss of the post-edge.

We find that ion association is the most prominent driving force to control the structure of aqueous solutions at elevated temperature. The experimental evidence of strong ion association at higher temperatures and the resulting formation of large polyatomic clusters is highly important for geochemical processes because assumptions in previous theoretical studies claim that those clusters may contribute significantly to the hydrothermal transport of metals by forming metal bearing complexes and thus to the formation of ore deposits.¹⁶

An analysis of the extracted parameters as a function of temperature indicates a slight stabilizing effect at higher temperatures because the occupied volume of the ions in the solution leads to a higher bulk density compared to pure water at the same temperature. Comparing those findings with the determined parameters of our previous study on aqueous sodium hydroxide solutions, a stronger stabilization of the water structure at high temperature is observed in the case of NaOH, probably due to the strong hydration shells surrounding the OH⁻ ions in contrast to the rather weak hydration of the chloride ions. Measurements with a variety of concentrations and different ion combinations would give further insight on how electrolytes affect the water structure. Furthermore, experiments conducted under conditions that correspond not only to the temperature but also to the pressure during the formation of ore deposits could further enhance the understanding of this highly relevant geochemical processes. This unique XRS data set on aqueous NaCl solution will allow understanding the role of hydrogen bonding and bare van der Waals interaction for aqueous systems under supercritical conditions by direct comparison with calculated spectra based on new molecular dynamics approaches recently discussed.⁷⁹

6 Further information

A comparison between first experiments performed at ID20 and the experiments performed at P01 with our improved HDAC set-up is shown in Fig. 6. Although the improvement in data quality is enormous, the integrated intensities nevertheless indicate a reproducibility of the measurement results.

Fig. 6 The spectra of the oxygen K-edge at different temperatures measured with our improved HDAC set-up at the P01 beamline of DESY (a) and during our preliminary experiments at ID20 (b). The improvements are due to the reduced use of cement to fix the diamonds onto the seats resulting in less absorption in the sample environment. Corresponding integrated intensities of the pre-edge (c) and post-edge (d) as a function of density. Data points with a black border color underwent isochoric temperature change, i.e., are at significantly higher pressure. The corresponding pressure for each data point is listed in plot (d).

We performed a χ² test in order to prove the significance of the calculated spectra and to ensure that the spectra calculated for instance on the basis of the AiMD simulations of the aqueous sodium chloride solution agree best with the experimentally measured spectra of the salt solutions and not equally well with the spectra of pure water which would weaken any conclusive analysis. This was achieved by performing a fit using the integrated pre- and post-edge intensities of the calculated and measured spectra with the previously mentioned scaling factor as fit parameter. In more detail, the evolution of the integrated intensities of the pre- and post-edge were scaled for each model (H₂O and H₂O + NaCl) onto the integrated experimental intensities of each sample to find the minimum χ² value for each combination of simulated model and measured sample. In particularly, this verifies the agreement of the relative changes between the theoretical and experimental data. Before performing the fit, the integrated pre-edge and post-edge intensities of each model as well as the experimental values were interpolated in the overlapping density range of the measured densities of pure water and aqueous NaCl solution to the same uniform density grid because naturally neither the measurements nor the simulations could be performed at the same densities. The best fit results of each combination and the resulting Chi-square values are depicted in Fig. 9 and confirm that the respective models reproduce best the density behaviour of the respective measurements and are not interchangeable. A necessity of this analysis is to perform the experiment under several different conditions depending on canonical parameters such as pressure and temperature. Otherwise, a conclusive fit is not feasible and the agreement of the theoretical model with the experimental data cannot be sufficiently verified.

In order to further investigate the structural differences of the water network in the aqueous sodium chloride solution and in pure water, the structural parameters determined as a function of bulk density and temperature are shown in Fig. 8 in addition to the comparison as function of density as depicted in the main text. Moreover, the detailed distribution of the ion cluster sizes in the trajectory of the simulated aqueous sodium chloride solution at different temperature and densities is shown in Fig. 7.

Fig. 7 Distribution of NaCl cluster sizes for each simulated temperature. A cluster size of one stands for a fully dissociated ion and is therefore not a cluster, but has been included for the sake of completeness.

Fig. 8 A depiction of the parameters discussed in the main text for pure water (blue, from Fig. 3 as reference) and for the aqueous NaCl solution (orange) as a function of bulk density (left) and temperature (right). Shown are the extracted number of H-bonds per molecule (a and b) and the deviation from tetrahedrality in terms of distance Δ_d (c and d) and angle Δ_a (e and f). The isochoric temperature change at the highest temperature is indicated by a black border color in the plots on the left side. The temperature axis on the right side is reversed for all plots to allow a better comparison with the parameters as a function of bulk density.

Fig. 9 Best fit results and corresponding χ² values for the pre-edge (left side) and post-edge (right side) for H₂O and H₂O + NaCl. Best fit results of the interpolated integrated values of the calculated oxygen K-edge spectra of the two models (solid lines, blue: water, orange: aqueous NaCl) to the experimental values of H₂O (a and b) and H₂O + NaCl (c and d) (dots, same color code). The computed χ² values for the pre-edge (left, e) and post-edge (right, f): the two figures depict the χ² values of the two different theoretical models (height of the bar) when fitted to the experimental data (on the x-axis). The error is estimated by calculating χ² for the upper and lower error limits of the integrated values and summing up the smallest and highest χ² values.

Author contributions

M. E., C. Schmidt, C. Sternemann, C. J. S., M. T. and M. W. designed research; M. E., C. Schmidt, C. Sternemann, C. J. S., S. J., R. S., C. A., H. G., M. S. and M. W. performed research; C. Schmidt and M. W. prepared the sample environment; S. J. performed AiMD simulations; M. E. and C. J. S. calculated spectra; M. E., C. Sternemann, C. J. S., M. T. and M. W. analyzed data; and M. E., C. Schmidt, C. Sternemann, C. J. S. and S. J. wrote the paper with contributions from all co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge PETRA III (beamline P01, proposal number 20180388) and the ESRF (beamline ID20, proposal number ES-863) for providing synchrotron radiation and beamline support. M. E., C. Ste., and M. T. would like to thank the BMBF (05KP16PE1) for financial support. R. S. and C. A. acknowledge funding by the German Research Foundation (DFG) via STE 1079/2-1 and STE 1079/4-1 (FOR2125, CarboPaT), respectively. M. T. acknowledges funding by the DFG under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV. M. E., C. Ste. and M. W. also acknowledge the German Research Foundation (DFG) via STE 1079/6-1 (M. E., C. Ste.) and WI 2000/22-1 (M. W.) for financial support. The recess in the diamond anvil was machined by Josefine Buhk (GFZ Potsdam). S. J. gratefully acknowledges the Gauss Centre for Supercomputing e.V. for providing computing time (project ID CHPO15) through the John von Neumann Institute for Computing (NIC) on the JUWELS supercomputer at Jülich Super-computing Centre (JSC). We acknowledge the computing time provided on the Linux HPC cluster at Technical University Dortmund (LiDO3), partially funded in the course of the Large-Scale Equipment Initiative by the DFG as project 271512359.

References

1. P. A. Marrone, M. Hodes, K. A. Smith and J. W. Tester, J. Supercrit. Fluids, 2004, 29, 289–312.
2. J. Sánchez-Oneto, J. R. Portela, E. Nebot and E. Martínez de la Ossa, J. Hazard. Mater., 2007, 144, 639–644.
3. J. A. Onwudili, E. Yildirir and P. T. Williams, Waste Biomass Valorization, 2013, 4, 87–93.
4. R. Morales Ibarra, M. Sasaki, M. Goto, A. T. Quitain, S. M. García Montes and J. A. Aguilar-Garib, J. Mater. Cycles Waste Manage., 2015, 17, 369–379.
5. A. Kruse, J. Supercrit. Fluids, 2009, 47, 391–399.
6. P. W. Dunne, A. S. Munn, C. L. Starkey, T. A. Huddle and E. H. Lester, Philos. Trans. R. Soc., A, 2015, 373, 20150015.
7. P. E. van Keken, Earth Planet. Sci. Lett., 2003, 215, 323–338.
8. C. E. Manning, Earth Planet. Sci. Lett., 2004, 223, 1–16.
9. J. W. Hedenquist and J. B. Lowenstern, Nature, 1994, 370, 519–527.
10. B. W. D. Yardley and R. J. Bodnar, Geochem. Perspect., 2014, 3, 1–127.
11. P. Postorino, R. H. Tromp, M. A. Ricci, A. K. Soper and G. W. Neilson, Nature, 1993, 366, 668–670.
12. P. H. De Jong and G. W. Neilson, J. Chem. Phys., 1997, 107, 8577–8585.
13. N. Akiya and P. E. Savage, Chem. Rev., 2002, 102, 2725–2750.
14. O. A. Karim and J. A. McCammon, J. Am. Chem. Soc., 1986, 108, 1762–1766.
15. Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621.
16. E. H. Oelkers and H. C. Helgeson, Geochim. Cosmochim. Acta, 1993, 57, 2673–2697.
17. D. M. Sherman, Geofluids, 2010, 10, 41–57.
18. E. Roedder, Fluid inclusions, De Gruyter, 1984.
19. D. L. Leach, R. D. Taylor, D. L. Fey, S. F. Diehl and R. W. Saltus, A deposit model for Mississippi Valley-type lead-zinc ores: Chapter A in mineral deposit models for resource assessment, U.S. geological survey technical report, 2010.
20. O. Klein-BenDavid, E. S. Izraeli, E. Hauri and O. Navon, Geochim. Cosmochim. Acta, 2007, 71, 723–744.
21. A. K. Soper, G. W. Neilson, J. E. Enderby and R. A. Howe, J. Phys. C: Solid State Phys., 1977, 10, 1793–1801.
22. S. Cummings, J. E. Enderby, G. W. Neilson, J. R. Newsome, R. A. Howe, W. S. Howells and A. K. Soper, Nature, 1980, 287, 714–716.
23. M. D. Bermejo and M. J. Cocero, AIChE J., 2006, 52, 3933–3951.
24. P. T. Cummings and A. A. Chialvo, J. Phys.: Condens. Matter, 1996, 8, 9281–9287.
25. A. A. Chialvo, P. T. Cummings and H. D. Cochran, Int. J. Thermophys., 1996, 17, 147–156.
26. M. T. Reagan, J. G. Harris and J. W. Tester, J. Phys. Chem. B, 1999, 103, 7935–7941.
27. S. T. Cui and J. G. Harris, Chem. Eng. Sci., 1994, 49, 2749–2763.
28. H. Shen, T. Hao, J. Wen, R. R. Tan and F. S. Zhang, Mol. Simul., 2015, 41, 1488–1494.
29. S. J. Fowler and D. M. Sherman, Geochim. Cosmochim. Acta, 2020, 277, 243–264.
30. C. Zhang, F. Giberti, E. Sevgen, J. J. de Pablo, F. Gygi and G. Galli, Nat. Commun., 2020, 11, 1–9.
31. L. A. Patel, T. J. Yoon, R. P. Currier and K. A. Maerzke, J. Chem. Phys., 2021, 154, 064503.
32. J. E. Enderby, Ion solvation via neutron scattering, 1995.
33. K. Yamanaka, M. Yamagami, T. Takamuku, T. Yamaguchi and H. Wakita, J. Phys. Chem., 1993, 97, 10835–10839.
34. T. Yamaguchi, N. Fukuyama, K. Yoshida and Y. Katayama, J. Phys. Chem. Lett., 2021, 12, 250–256.
35. C. J. Sahle, C. Sternemann, C. Schmidt, S. Lehtola, S. Jahn, L. Simonelli, S. Huotari, M. Hakala, T. Pylkkänen, A. Nyrow, K. Mende, M. Tolan, K. Hämäläinen and M. Wilke, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6301–6306.
36. C. J. Sahle, J. Niskanen, C. Schmidt, J. Stefanski, K. Gilmore, Y. Forov, S. Jahn, M. Wilke and C. Sternemann, J. Phys. Chem. B, 2017, 121, 11383–11389.
37. S. L. Wallen, B. J. Palmer and J. L. Fulton, J. Chem. Phys., 1998, 108, 4039–4046.
38. T. M. Seward, C. M. Henderson and J. M. Charnock, Chem. Geol., 2000, 167, 117–127.
39. A. Filipponi, S. De Panfilis, C. Oliva, M. A. Ricci, P. D'Angelo and D. T. Bowron, Phys. Rev. Lett., 2003, 91, 19–22.
40. G. S. Pokrovski, B. R. Tagirov, J. Schott, E. F. Bazarkina, J. L. Hazemann and O. Proux, Chem. Geol., 2009, 259, 17–29.
41. M. Wilke, C. Schmidt, J. Dubrail, K. Appel, M. Borchert, K. Kvashnina and C. E. Manning, Earth Planet. Sci. Lett., 2012, 349-350, 15–25.
42. M. Elbers, C. Sternemann, K. Julius, M. Paulus, G. Surmeier, N. König, J. Nase, J. Bolle, R. Wagner, T. Irifune and M. Tolan, High Press. Res., 2020, 40, 194–204.
43. L. Å. Näslund, D. C. Edwards, P. Wernet, U. Bergmann, H. Ogasawara, L. G. Pettersson, S. Myneni and A. Nilsson, J. Phys. Chem. A, 2005, 109, 5995–6002.
44. I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 140, 244506.
45. W. Schülke, Electron Dynamics by Inelastic X-Ray Scattering, Oxford Univ. Press, 2007.
46. J. P. Rueff and A. Shukla, Rev. Mod. Phys., 2010, 82, 847–896.
47. S. K. Lee, P. J. Eng and H. K. Mao, Rev. Mineral. Geochem., 2014, 78, 139–174.
48. C. Weis, C. Sternemann, V. Cerantola, C. J. Sahle, G. Spiekermann, M. Harder, Y. Forov, A. Kononov, R. Sakrowski, H. YavaÅŸ, M. Tolan and M. Wilke, Sci. Rep., 2017, 7, 1–10.
49. S. Petitgirard, C. J. Sahle, C. Weis, K. Gilmore, G. Spiekermann, J. S. Tse, M. Wilke, C. Cavallari, V. Cerantola and C. Sternemann, Geochem. Perspect. Lett., 2018, 9, 32–37.
50. C. Sternemann and M. Wilke, High Pressure Res., 2016, 36, 275–292.
51. C. Schmidt and K. Rickers, Am. Mineral., 2003, 88, 288–292.
52. C. Schmidt and T. M. Seward, Chem. Geol., 2017, 467, 64–75.
53. C. Schmidt, Geochim. Cosmochim. Acta, 2009, 73, 425–437.
54. M. Steele-MacInnis, P. Lecumberri-Sanchez and R. J. Bodnar, Comput. Geosci., 2012, 49, 334–337.
55. R. J. Bodnar, Geochim. Cosmochim. Acta, 1993, 57, 683–684.
56. D. Ketenoglu, G. Spiekermann, M. Harder, E. Oz, C. Koz, M. C. Yagci, E. Yilmaz, Z. Yin, C. J. Sahle, B. Detlefs and H. Yavaş, J. Synchrotron Radiat., 2018, 25, 537–542.
57. S. Huotari, C. J. Sahle, C. Henriquet, A. Al-Zein, K. Martel, L. Simonelli, R. Verbeni, H. Gonzalez, M. C. Lagier, C. Ponchut, M. Moretti Sala, M. Krisch and G. Monaco, J. Synchrotron Radiat., 2017, 24, 521–530.
58. C. J. Sahle, A. Mirone, J. Niskanen, J. Inkinen, M. Krisch and S. Huotari, J. Synchrotron Radiat., 2015, 22, 400–409.
59. H. Sternemann, C. Sternemann, G. T. Seidler, T. T. Fister, A. Sakko and M. Tolan, J. Synchrotron Radiat., 2008, 15, 162–169.
60. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. Vande Vondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
61. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
62. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
63. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
64. S. Goedecker and M. Teter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
65. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
66. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
67. J. Lehtola, M. Hakala, A. Sakko and K. Hämäläinen, J. Comput. Chem., 2012, 33, 1572–1585.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
69. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
70. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
71. W. Kutzelnigg, U. Fleischer and M. Schindler, The IGLO-Method: Ab-initio Calculation and Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities, Springer, Berlin/Heidelberg, 1990, vol. 23, pp. 165–262.
72. J. D. Smith, C. D. Cappa, B. M. Messer, W. S. Drisdell, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2006, 110, 20038–20045.
73. T. Pylkkänen, V. M. Giordano, J. C. Chervin, A. Sakko, M. Hakala, J. A. Soininen, K. Hämäläinen, G. Monaco and S. Huotari, J. Phys. Chem. B, 2010, 114, 3804–3808.
74. A. Luzar and D. Chandler, Phys. Rev. Lett., 1996, 76, 928–931.
75. J. Niskanen, C. J. Sahle, K. Gilmore, F. Uhlig, J. Smiatek and A. Föhlisch, Phys. Rev. E, 2017, 96, 1–8.
76. J. S. Tse, D. M. Shaw, D. D. Klug, S. Patchkovskii, G. Vankó, G. Monaco and M. Krisch, Phys. Rev. Lett., 2008, 100, 1–4.
77. A. Nilsson and L. G. Pettersson, Chem. Phys., 2011, 389, 1–34.
78. J. Niskanen, M. Fondell, C. J. Sahle, S. Eckert, R. M. Jay, K. Gilmore, A. Pietzsch, M. Dantz, X. Lu, D. E. McNally, T. Schmitt, V. Vaz da Cruz, V. Kimberg, F. Gel'mukhanov and A. Föhlisch, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4058–4063.
79. P. Schienbein and D. Marx, Angew. Chem., 2020, 59, 18578–18585.
80. H. Fukui, S. Huotari, D. Andrault and T. Kawamoto, J. Chem. Phys., 2007, 127, 134502.
81. I. Juurinen, T. Pylkkänen, K. O. Ruotsalainen, C. J. Sahle, G. Monaco, K. Hämälainen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2013, 117, 16506–16511.
82. G. Lelong, L. Cormier, L. Hennet, F. Michel, J. P. Rueff, J. M. Ablett and G. Monaco, Inorg. Chem., 2021, 60, 798–806.
83. Q. Sun, Vib. Spectrosc., 2012, 62, 110–114.
84. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370.
85. I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. Pettersson and A. Nilsson, The structure of water in the hydration shell of cations from X-ray Raman and small angle X-ray scattering measurements, 2011.
86. Y. L. Jeyachandran, F. Meyer, A. Benkert, M. Bär, M. Blum, W. Yang, F. Reinert, C. Heske, L. Weinhardt and M. Zharnikov, J. Phys. Chem. B, 2016, 120, 7687–7695.
87. J. K. Fogo, S. W. Benson and C. S. Copeland, J. Chem. Phys., 1954, 22, 212–216.
88. T. M. Seward, C. M. Henderson, J. M. Charnock and T. Driesner, Geochim. Cosmochim. Acta, 1999, 63, 2409–2418.
89. C. Schmidt, Geochim. Cosmochim. Acta, 2014, 145, 281–296.
90. D. M. Sherman and M. D. Collings, Geochem. Trans., 2002, 3, 102–107.
91. G. V. Bondarenko, Y. E. Gorbaty, A. V. Okhulkov and A. G. Kalinichev, J. Phys. Chem. A, 2006, 110, 4042–4052.
92. J. P. Brodholt, Chem. Geol., 1998, 151, 11–19.
93. I. Howell and G. W. Neilson, J. Chem. Phys., 1996, 104, 2036–2042.
94. A. S. Quist and W. L. Marshall, J. Phys. Chem., 1968, 72, 684–703.
95. C. E. Manning, Rev. Mineral. Geochem., 2013, 76, 135–164.
96. A. P. Gaiduk and G. Galli, J. Phys. Chem. Lett., 2017, 8, 1496–1502.
97. J. M. Heuft and E. J. Meijer, Phys. Chem. Chem. Phys., 2006, 8, 3116–3123.
98. A. Botti, F. Bruni, S. Imberti, M. A. Ricci and A. K. Soper, J. Chem. Phys., 2004, 120, 10154–10162.
99. C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr and T. M. Weiss, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214–15218.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01490k

---