 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fracto-eutectogels: SDS fractal dendrites via counterion condensation in a deep eutectic solvent†
Lauren
Matthews‡
 ab,
Silvia
Ruscigno
a,
Sarah E.
Rogers
ab,
Silvia
Ruscigno
a,
Sarah E.
Rogers
 c,
Paul
Bartlett
c,
Paul
Bartlett
 a,
Andrew J.
Johnson
d,
Robert
Sochon
d and
Wuge H.
Briscoe
a,
Andrew J.
Johnson
d,
Robert
Sochon
d and
Wuge H.
Briscoe
 *a
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: wuge.briscoe@bristol.ac.uk
bBristol Centre for Functional Nanomaterials, HH Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK
cISIS Muon and Neutron Source, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX11 0QX, UK
dGlaxoSmithKline, St George's Avenue, Weybridge, KT13 0DE, UK
First published on 4th May 2021
Abstract
Glyceline, a deep eutectic solvent comprising glycerol and choline chloride, is a green nonaqueous solvent with potential industrial applications. Molecular mechanisms of surfactant self-assembly in deep eutectic solvents are expected to differ from those in their constituent polar components and are not well understood. Here we report the observation of self-assembled SDS fractal dendrites with dimensions up to ∼mm in glyceline at SDS concentrations as low as cSDS ∼ 0.1 wt%. The prevalence of these dendritic fractal aggregates led to the formation of a gel phase at SDS concentrations above ≥1.9 wt% (the critical gelation concentration cCGC). The gel microscopic structure was visualised using polarised light microscopy (PLM); rheology measurements confirmed the formation of a colloidal gel, where the first normal stress difference was negative and the elastic modulus was dominant. Detailed nano-structural characterisation by small-angle neutron scattering (SANS) further confirmed the presence of fractal aggregates. Such SDS aggregation or gelation has not been observed in water at such low surfactant concentrations, whereas SDS has been reported to form lamellar aggregates in glycerol (a component of glyceline). We attribute the formation of the SDS fractal dendrites to the condensation of counterions (i.e. the choline ions) around the SDS aggregates – a diffusion-controlled process, leading to the aggregate morphology observed. These unprecedented results shed light on the molecular mechanisms of surfactant self-assembly in deep eutectic solvents, important to their application in industrial formulation.
1. Introduction
Deep eutectic solvents (DES)1,2 are green, non-volatile, and they are good solvents for many inorganic and organic species.3,4 Their green credentials are of interest in many industrial applications ranging from electroplating5–9 to personal care products. DES have also been shown to improve rates and enantioselectivities of lipase-catalysed biotransformation processes.10–14Self-assembly of surfactants and particles in DES is of particular interest due to their ubiquity in industrial formulations and applications. Raghuwanshi et al. investigated self-assembly of gold nanoparticles in reline (a DES comprising choline chloride and urea in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) for green energy applications.15–18 Hammons et al. probed the aggregation of silica particles in reline and ethaline (1
2 molar ratio) for green energy applications.15–18 Hammons et al. probed the aggregation of silica particles in reline and ethaline (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 choline chloride:ethylene glycol).19–21 The self-assembly behaviour of amphiphiles in various DES has also been studied. Bryant et al. reported that phospholipids (1,2-dipalmitoyl-sn-glycero-3-phosphocholine, DPPC; 1,2-distearoyl-sn-glycero-3-phosphocholine, DSPC; 1,2-dimyristoyl-sn-glycero-3-phosphocholine, DMPC; and egg-PC – 16-22 carbon tails with phosphocholine headgroups) formed lamellar (Lα) phases and vesicles22 in reline, similar to aqueous systems.
2 choline chloride:ethylene glycol).19–21 The self-assembly behaviour of amphiphiles in various DES has also been studied. Bryant et al. reported that phospholipids (1,2-dipalmitoyl-sn-glycero-3-phosphocholine, DPPC; 1,2-distearoyl-sn-glycero-3-phosphocholine, DSPC; 1,2-dimyristoyl-sn-glycero-3-phosphocholine, DMPC; and egg-PC – 16-22 carbon tails with phosphocholine headgroups) formed lamellar (Lα) phases and vesicles22 in reline, similar to aqueous systems.
Surfactant self-assembly has also been investigated in both reline and glyceline (comprising choline chloride and glycerol in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio).23–25 It has been found that the interfacial self-assembly behaviour of surfactants in the DES is similar to that in aqueous systems. Using surface tensiometry, Sanchez-Fernandez et al. reported that cationic surfactants dodecyl/tetradecyl/hexadecyltrimethyl ammonium bromide (C12/C14/C16TAB) displayed a critical micelle concentration (CMC) in glyceline of 22.0, 3.9, and 0.9 mM, respectively.26 Anionic sodium dodecyl sulfate (SDS) was shown to have a CMC of 2.0 mM in reline27 and 3.9 mM in glyceline.28 X-Ray reflectivity (XRR) showed surfactant monolayer formation at the air–reline interface similar to that the air–water interface.27,28
2 molar ratio).23–25 It has been found that the interfacial self-assembly behaviour of surfactants in the DES is similar to that in aqueous systems. Using surface tensiometry, Sanchez-Fernandez et al. reported that cationic surfactants dodecyl/tetradecyl/hexadecyltrimethyl ammonium bromide (C12/C14/C16TAB) displayed a critical micelle concentration (CMC) in glyceline of 22.0, 3.9, and 0.9 mM, respectively.26 Anionic sodium dodecyl sulfate (SDS) was shown to have a CMC of 2.0 mM in reline27 and 3.9 mM in glyceline.28 X-Ray reflectivity (XRR) showed surfactant monolayer formation at the air–reline interface similar to that the air–water interface.27,28
However, surfactant self-assembly in the bulk DES solution has shown different behaviours compared to in water or in the individual solvents constituting the DES. For instance, Ruiz-Olles et al. observed that 1,3:2,4-dibenzylidene-D-sorbitol (DBS) formed a ‘eutectogel’ in a range of DES comprising a binary mixture of choline chloride with glycerol, xylitol, sorbitol, or urea.29 For DBS in reline, SEM and TEM revealed nanofibrillar structures forming an entangled network with a dominant elastic modulus (G′), characteristic of a gel, with a gelation concentration, c = 4 w/v% at 82 °C.
Here, we report gelation of SDS in glyceline at room temperature (RT ∼ 25 °C) at low surfactant concentrations, i.e. cSDS ∼ 1.9 wt%. Surprisingly, the gel phase comprised complex interpenetrating networks of dendritic fractal aggregates of size some hundreds of μm – thus termed a “fracto-eutectogel”. For comparison, SDS forms globular micelles in water under the same condition, whilst SDS lamellar gels in glycerol (a glyceline constituent hydrogen-bonding rich solvent) have been reported recently.30 The microscopic structure of this fracto-eutectogel was visualised with polarising light microscopy (PLM) and its nanostructure studied with small-angle neutron scattering (SANS). Rheology measurements provided complementary information on the gel mechanical properties. The unprecedented observation of the microscopic fractal structures as a result of SDS self-organisation in glyceline points to different molecular interactions in DES compared to aqueous systems or single-component hydrogen-bonding rich solvents.
2. Materials and methods
2.1 Materials
Protonated sodium dodecyl sulfate (h-SDS) (Sigma-Aldrich, >98.0%) was recrystallised three times from ethanol, and its purity was checked with 1H NMR. h-Glycerol (Fisher Scientific, >98.0%) and d-glycerol (Sigma–Aldrich, >98.0% and >98.0 atom%D) were used as received. h-Choline chloride (Sigma–Aldrich, >98.0%) and d9-trimethyl-choline chloride (Sigma-Aldrich, >98.0% and >98.0 atom%D) were used as received. h-/d-glyceline was prepared by mixing h-/d-choline chloride and h-/d-glycerol in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio in a shaker incubator (Stuart SI505) at 550 rpm at 60 °C for two hours (2 h). The gel-like phase was prepared by adding a designated amount of h-SDS to h- or d-glyceline, then incubating the mixture in the shaker incubator at 550 rpm at 60 °C for 2 h before equilibrating at room temperature overnight. All the samples were kept sealed from moisture before measurements, due to hygroscopicity of both choline chloride and glycerol. In a further study, we have examined the effect of water addition systematically (manuscript in preparation).
2 molar ratio in a shaker incubator (Stuart SI505) at 550 rpm at 60 °C for two hours (2 h). The gel-like phase was prepared by adding a designated amount of h-SDS to h- or d-glyceline, then incubating the mixture in the shaker incubator at 550 rpm at 60 °C for 2 h before equilibrating at room temperature overnight. All the samples were kept sealed from moisture before measurements, due to hygroscopicity of both choline chloride and glycerol. In a further study, we have examined the effect of water addition systematically (manuscript in preparation).
2.2 Surface tensiometry
Equilibrium surface tension measurements were carried out in ambient conditions with the Wilhelmy plate method using a Krüss K100 tensiometer, with the platinum plate cleaned by flaming between measurements. Due to the relatively high viscosity of h-glyceline (∼380 cP), the samples were left to equilibrate for 30 minutes to allow for diffusion of surfactants to the air–liquid interface.2.3 Viscometry and oscillation rheology
All rheological measurements were performed using a rotational rheometer (Malvern Panalytical Kinexus Pro) in a cone-plate geometry (CP 4/20) to minimise the wall-depletion effect observed in oscillation measurements.31 Viscometry measurements were carried out with the shear rate,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , decreasing from 100 s−1 to 0.001 s−1 and each measurement was run for 3 minutes or until it reached a steady state equilibrium. Oscillation rheology measurements involved first characterising the linear viscoelastic region while changing the deformation, γ, (or the strain rate) applied, at a constant frequency ω = 1 Hz. A strain value was then selected from this linear region, typically γ = 0.012%, for frequency sweep measurements.
, decreasing from 100 s−1 to 0.001 s−1 and each measurement was run for 3 minutes or until it reached a steady state equilibrium. Oscillation rheology measurements involved first characterising the linear viscoelastic region while changing the deformation, γ, (or the strain rate) applied, at a constant frequency ω = 1 Hz. A strain value was then selected from this linear region, typically γ = 0.012%, for frequency sweep measurements.
2.4 Polarised light microscopy (PLM)
PLM was carried out using an Olympus BX53-P microscope, where the polarisers were crossed at 90° with respect to each other and images were captured using Stream software. PLM measurements were carried out under ambient conditions, using 10, 20, and 40× magnifications. A 530 nm first order waveplate was placed in the optical patch to improve the contrast in some cases.2.5 Small-angle neutron scattering (SANS)
SANS measurements were made using quartz cells with a 2 mm path length with a 0.5 h integration time on the Loq32 small-angle diffractometer at the ISIS Pulsed Neutron Source (STFC Rutherford Appleton Laboratory, Didcot, UK). Loq utilizes neutrons with wavelengths λ = 2–10 Å and the data were collected in the q range of 0.008–1.6 Å−1, corrected for the detector efficiency, sample transmission, and background scattering and converted to scattering cross-section data (∂Σ/∂Ω vs. q) using MantidPlot.33 The data were then converted to an absolute scale (cm−1) using the scattering intensity from a standard sample (a solid blend of hydrogenous and perdeuterated polystyrene).342.6 SANS data analysis
The SANS data at 25 °C were fitted using two different models. The first was a lamellar paracrystal stack model (Fig. 8b), in which individual SDS lamellae stacks in solution were treated as being independent of each other, with the lamellae considered as a whole rather than separate headgroup and tail layers. The general scattering intensity for the lamellar systems is described as35–38 | (1) |
The second model used to fit data at 25 °C was a mass fractal model (Fig. 8c) describing the scattering from fractal-like aggregates in solution39
| I(q) ∼ P(q)S(q) | (2) |
| P(q) = F(qr)2 | (3) |
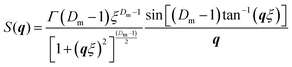 | (4) |
3. Results and discussion
3.1 Surface tensiometry measurements of SDS in glyceline
The surface tension, γ, vs. ln(cSDS) plots in water, glycerol, and glyceline at room temperature (RT ∼ 25 °C) are shown in Fig. 1, with the data for glycerol from ref. 30 included for comparison. The critical micelle concentration, CMC, pure solvent surface tension, γ0, minimum surface tension, γmin, and the headgroup area, AHG, at ∼CMC determined from the surface excess are summarised in Table 1. All three curves show SDS adsorption at the air–liquid interface and an apparent CMC at RT, indicative of SDS surface activity and self-assembly in these solvents. | ||
| Fig. 1 Surface tension, γ, vs. ln(cSDS) for SDS at the air–water (red circles), air–glycerol (blue circles), and air–glyceline (green circles) interfaces at room temperature (RT). The surface tensions of the pure solvents, γ0, are indicated by the horizontal dashed lines. The curve corresponding to SDS at the air–glycerol interface is taken from ref. 30. | ||
| Solvent | γ 0 (mN m−1) | γ min (mN m−1) | CMC (mM) | Γ (10−6 mol m−2) | A HG (Å2) |
|---|---|---|---|---|---|
| Water | 72.8 ± 0.1 | 38.3 ± 0.1 | 8.1 ± 0.1 | 3.82 ± 0.25 | 43.5 ± 0.9 |
| Glycerol | 64.0 ± 0.1 | 46.0 ± 0.1 | 11.7 ± 0.1 | 1.66 ± 0.38 | 46.0 ± 0.5 |
| Glyceline | 63.5 ± 0.1 | 34.2 ± 0.1 | 5.4 ± 0.2 | 4.29 ± 0.59 | 38.7 ± 0.3 |
The cohesive energy and the related Gordon parameter, G = γ0/Vm1/3 where Vm is the molecular volume, of a solvent has previously been used to gauge the solvophobic effect in driving self-assembly,40,41 with a higher G value indicative of a more pronounced solvophobic effect and hence promoting amphiphile self-assembly more strongly.40,42 Glyceline has a lowest surface tension value compared to water and glycerol (Table 1). This would point to the lowest cohesive energy density of glyceline among the three solvents, as measured by the Gordon parameter.40,42 The calculated G values for the three solvents are listed in Table 2. However, the CMC of SDS in glyceline is the lowest of the three solvents at 5.4 mM (vs. 8.1 and 11.7 mM in water and glycerol, respectively), also with the lowest γmin (Table 1).
The Hildebrand solubility parameter, δH ∼ (CED)1/2 where CED is the cohesive energy density, is another measure of cohesion. The δH values for the three solvents are compared in Table 2, and it shows a different trend to G and cannot be reconciled with the observed CMC (Table 1). This suggests that the self-assembly behaviour of SDS in DES glyceline cannot be readily predicted by the Gordon parameter or the Hildebrand solubility parameter, which have been widely used to gauge the cohesive energy and the solvophobic effect in pure solvents.
3.2 The formation of a gel in glyceline
Fig. 2 shows a series of glyceline samples in inverted glass vials containing SDS at different concentrations, cSDS = 0.1–5.3 wt% (i.e. 5–220 mM; 0.9–37.0 CMC; cf.Table 3). At 60 °C, all the samples were transparent and fluid (Fig. 2a); however, when cooled to RT ∼ 25 °C, an opaque phase formed. At cSDS ≥1.9 wt%, the sample could hold its weight upon inversion (Fig. 2b). In contrast, SDS in aqueous solutions formed transparent fluid phases consistent with globular micellar solutions.43–45 For comparison, opaque SDS gel phases have been observed in glycerol,30 with a critical gelation SDS concentration of cCGC ∼ 2 wt% (or 110 mM) below a critical gelation temperature of TGC ∼ 45 °C.30 The observation of SDS gelation in glyceline suggests interpenetrated networks of aggregates at RT, which would break up at elevated temperatures. Such an SDS-in-glyceline gel (or in other DES), at low SDS concentrations, has not been previously reported in the literature to our knowledge.| Sample no. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c SDS (wt%) | 0.1 | 0.3 | 0.6 | 1.2 | 1.9 | 2.5 | 2.9 | 3.4 | 3.9 | 4.4 | 4.8 | 5.3 |
| Modulus | Regime/phase | Modulus vs. cSDS slope (Pa) |
|---|---|---|
| G′(γ) | Liquid | 54.7 |
| Gel | 701.3 | |
| G′′(γ) | Liquid | 29.8 |
| Gel | 214.8 | |
| G′(ω) | Liquid | 389.5 |
| Gel | 3122.5 | |
| G′′(ω) | Liquid | 230.6 |
| Gel | 937.0 |
3.3 Rheological properties of the fracto-eutectogel
A representative plot of shear stress, σ, as a function of shear rate,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , of the SDS-in-glyceline gel (5.3 wt%, ∼53 CMC) is shown in Fig. 3a, displaying shear thinning behaviour with a non-linear stress-rate (σ–
, of the SDS-in-glyceline gel (5.3 wt%, ∼53 CMC) is shown in Fig. 3a, displaying shear thinning behaviour with a non-linear stress-rate (σ–![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) relationship. The magnitude of σ (<100 Pa) is consistent with a weak physical gel that can be disturbed by the applied shear, indicated by the presence of an inflection point at
) relationship. The magnitude of σ (<100 Pa) is consistent with a weak physical gel that can be disturbed by the applied shear, indicated by the presence of an inflection point at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 5 s−1 in the σ–
∼ 5 s−1 in the σ–![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) plot. This behaviour is similar to previously reported gel phases consisting of fibrillar aggregates.46–51Fig. 3b shows the variation of the shear viscosity, η, with cSDS at two different shear rates (taken from linear fits before and after the inflection point). At the lower shear rate (0–5 s−1; LSR), ηLSR increased linearly with cSDS, in contrast to the constant ηHSR at the higher shear rate (5–100 s−1;HSR). This suggests that the 3D structure in the gel phase was broken up at the HSR into smaller aggregates, manifesting in a constant viscosity value over the cSDS range.
plot. This behaviour is similar to previously reported gel phases consisting of fibrillar aggregates.46–51Fig. 3b shows the variation of the shear viscosity, η, with cSDS at two different shear rates (taken from linear fits before and after the inflection point). At the lower shear rate (0–5 s−1; LSR), ηLSR increased linearly with cSDS, in contrast to the constant ηHSR at the higher shear rate (5–100 s−1;HSR). This suggests that the 3D structure in the gel phase was broken up at the HSR into smaller aggregates, manifesting in a constant viscosity value over the cSDS range.
The behaviour of the first normal stress difference, N1, (Fig. 3a, inset) is different from that expected of fibrillar dispersions, for which N1 would typically increase with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) due to fibrous aggregates becoming elongated in the direction of the applied shear.52–54 Here, N1 decreased with
due to fibrous aggregates becoming elongated in the direction of the applied shear.52–54 Here, N1 decreased with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (for
(for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > ∼0.05 s−1), indicating that the aggregates became shorter in the direction of the applied shear. The decreasing N1 with
> ∼0.05 s−1), indicating that the aggregates became shorter in the direction of the applied shear. The decreasing N1 with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) can be attributed to hydrodynamic friction between individual aggregates,55,56 implying the presence of globular aggregates. Unlike the shear thickening behaviour often observed in colloidal dispersions due to shear-induced aggregation,57,58 the shear thinning and N1 behaviour observed in this study suggest that, while the aggregates showed hydrodynamic friction, there was no flocculation-induced shear thickening, a behaviour observed in some colloidal gels.59,60
can be attributed to hydrodynamic friction between individual aggregates,55,56 implying the presence of globular aggregates. Unlike the shear thickening behaviour often observed in colloidal dispersions due to shear-induced aggregation,57,58 the shear thinning and N1 behaviour observed in this study suggest that, while the aggregates showed hydrodynamic friction, there was no flocculation-induced shear thickening, a behaviour observed in some colloidal gels.59,60
The elastic and viscous moduli (G′ and G′′, respectively) are shown as a function of the deformation (or strain, γ, Fig. 4a) to demonstrate the viscoelastic behaviour of the 5.3 wt% SDS-in-glyceline gel in response to an applied deformation. The presence of a linear viscoelastic region (LVER) at small deformations (γ ∼ 0.001–0.1%) shows that the structure of the gel was unaffected by small strains.
A previous report showed that the magnitude of G′(γ) and G′′(γ) of an SDS-in-glycerol gel was an order of magnitude higher than that observed here.30 The MacKintosh model, assuming the system consisting of a semiflexible network,61 relates the bending modulus, κ, of the constituent fibres to the gel elastic modulus,  . The estimated κ values using this model are plotted against cSDS in Fig. 5, showing a linear relationship, with a maximum κ value of ∼50 Pa, which was lower than that observed for the SDS-in-glycerol gel (κ ∼ 140 Pa).
. The estimated κ values using this model are plotted against cSDS in Fig. 5, showing a linear relationship, with a maximum κ value of ∼50 Pa, which was lower than that observed for the SDS-in-glycerol gel (κ ∼ 140 Pa).
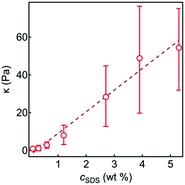 | ||
| Fig. 5 The bending modulus, κ, as a function of cSDS with a linear guideline. κ was determined from the MacKintosh model61 using the plateau G′ values from the amplitude sweep measurements. The dashed line is a guide for the eye. | ||
The behaviour of G′(γ) and G′′(γ) beyond the LVER shows the sensitivity of the gel network to the applied deformation, as both moduli decreased by two orders of magnitude, possibly due to the breakup of the larger aggregates into smaller ones. The gel appeared elastic at low deformations (γ < 0.2%), with G′(γ) > G′′(γ); however, a crossover point is observed at γ* ∼ 0.3%, above which G′′(γ) > G′(γ), indicating a transition to a more liquid-like phase.
The values of the LVER elastic and viscous moduli as a function of cSDS are shown in Fig. 4b. As cSDS increased, a transition from a liquid-like to a solid-like material can be observed at cSDS ∼ 1.2 wt% (the slopes of the G′/G′′ vs. cSDS plots before and after the transiton are listed in Table 4). This concentration can be deemed (as similarly defined in ref. 30) a critical gelation concentration, cCGC, consistent with the macroscopic observations in the inverted vial test (Fig. 2).
The gel structure appeared to be more sensitive to the magnitude of deformation than the speed at which it was applied. Fig. 4c shows the variation of G′ and G′′ at low strain (γ < 0.2%) as a function of the shear frequency, ω, for the 5.3 wt% SDS-in-glyceline gel. Over the ω range measured, the elastic modulus remained dominant (i.e. G′ > G′′) with no crossover, indicating a solid-like behaviour. Whilst the gel showed sensitivity to strains, γ, the moduli were less sensitive to the frequency, ω. The absence of the G′(ω)–G′′(ω) crossover would suggest that the system was not comprised of fibrillar aggregates62 – and instead more likely of globular aggregates. The magnitudes of the two moduli (G′ ∼ 12.5 kPa and G′′ ∼ 4 kPa) are quite high compared to surfactant-based gels of elongated wormlike micelles63–66 (in the range of 10–100 Pa). However, these values are comparable to those of the SDS-in-glycerol gel (G′ ∼ 27 kPa and G′′ ∼ 11 kPa).30
The dependence of G′ and G′′ (at a high frequency ω = 10 Hz) on cSDS is shown in Fig. 4d, with a similar transition (cf. Table 4) observed compared to the amplitude sweep data (Fig. 4b). Whilst the G′(ω) and G′′(ω) magnitude increased with cSDS, there was no crossover and the elastic modulus remained dominant (G′(ω) > G′′(ω)) even in the liquid regime. The lack of a crossover arises from the lower sensitivity of globular aggregates to the speed at which the deformation is applied, without structural changes observed in the globular aggregates. This again suggests that the structure of the gel consisted of particulates, akin to a colloidal gel.67
3.4 Microscopic structure of the ordered surfactant mesophase
Polarised light microscopy (PLM) revealed an anisotropic mesophase at room temperature at SDS concentrations (cSDS > 1.9 wt%) (Fig. 6), consisting of dendritic feather-like aggregates of some μm in length scale with no particular alignment. The dendritic fractal68,69 morphology (seen in detail in Fig. 6c, d) exhibits a central fibre that supports secondary fibres, which in turn support tertiary fibres, and so on. A fibre order parameter, nf, can be defined as the fibre position away from the parent or central fibre, where the parent fibre nf = 1. As nf increases, both the fibre length and the diameter generally decrease (Fig. 7b). It is conceivable that the fibres grew sequentially: first the growth of the parent fibres, then the secondary fibres and the tertiary fibres. The detailed mechanism – whether the parent and child fibres grow simultaneously, or the parent grows first and then stops to allow the children to grow – is unclear. | ||
| Fig. 6 PLM images of the dendritic feather-like aggregates present in SDS in glyceline at RT at magnifications of 10× (a), 20× (b and c), and 40× (d), with the cSDS indicated. | ||
3.5 Gel nanostructure from SANS
Fig. 8 shows the SANS scattering profiles at different cSDS, with the data fitted to a mass fractal model (Fig. 8c) and, for cSDS = 1.2, 2.7, and 5.3 wt%, also a lamellar paracrystal model (Fig. 8b). The appearance of a Bragg peak at q ∼ 0.30 Å−1 at the higher SDS concentrations (cSDS = 1.2, 2.7 and 5.3 wt%), corresponding to d ∼ 2π/q ∼ 20.9 Å, suggests the formation of an ordered mesophase. There was no plateau observed in the low-q region of the SANS scattering profiles at any cSDS, indicating the presence of a large structure or mesophase in the gel whose size was not accessible in the q-range of the SANS measurement.The coherence length, Lc, which is indicative of the disorder of the meso-structure, can be obtained from analysing the broadening of the Bragg peaks using the Scherrer equation70–76
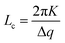 | (5) |
The Lcvs. cSDS behaviour (Fig. 9) appears different at low cSDS (1.2 wt%) compared to the two higher cSDS samples (2.7 and 5.3 wt%), implying different structural orders. The Lc value at the two higher cSDS converged to Lc ∼ 140 Å at T = 40 °C.
 | ||
| Fig. 9 The coherence length, Lc, calculated using the Scherrer equation, with the full-width half maximum (FWHM) determined through a Gaussian peak analysis. | ||
As only one Bragg peak is present in the scattering profile, it cannot ascertain the exact mesophase type; this peak could also arise from the presence of solid SDS crystallites. Complementary X-ray reflectivity (XRR) measurements at the air-glyceline interface (Fig. S1, ESI†) showed the presence of a second Bragg peak at q ∼ 0.6 Å−1, consistent with the nα = 1, 2 peaks of a lamellar phase or surfactant crystal. A recent study has similarly shown the presence of aggregates with a lamellar structure in SDS-in-glycerol gel,30 and thus the obtained SANS profile was fitted to a lamellar paracrystal stack model (Fig. 8b). The fits to 5.3, 2.7, and 1.2 wt% h-SDS in d-glyceline are shown in Fig. 8 with the fitting parameter values in Table 5. The reduced intensity and number of Bragg peaks observed in this study – as compared in glycerol in the previous study30 – could be attributed to the presence of choline chloride in glyceline, which could disrupt the structural order of the SDS lamellar phase.
| Lamellar paracrystal stack parameters | c SDS (wt%) | ||
|---|---|---|---|
| 1.2 | 2.7 | 5.3 | |
| t L (Å) | 20.0 | 20.0 | 20.0 |
| n Layers | 57.7 | 57.7 | 57.7 |
| d-Spacing (Å) | 20.4 | 20.4 | 20.4 |
| σ d (Å) | 0.012 | 0.012 | 0.013 |
| ρ SDS (10−6 Å−2) | 0.43 | 0.43 | 0.40 |
| ρ Gly (10−6 Å−2) | 5.85 | 5.84 | 5.50 |
| σ t | 1.0 | 1.0 | 1.0 |
| χ 2 | 4.4 | 3.8 | 3.8 |
The thickness, tL, and the d-spacing of the lamellar phase show a close agreement, tL ∼ d ∼ 20 Å (cf.Fig. 8b), indicating that the lamellar sheets consisted solely of SDS bilayers. A full SDS bilayer of thickness of two SDS lengths would give tL ∼ 35–45 Å; however, smaller SDS lamellar spacing has been reported, tL ∼ 25–28 Å77,78 in the presence of additives, such as a co-solvent. The smaller value reported here, tL ∼ 20 Å, could arise from a tilted SDS bilayer or interpenetration of the tails. The high polydispersity of the lamellar thickness implies polymorphisms with different SDS packing and conformations, leading to different d-spacing. We acknowledge that, along with the large thickness polydispersity, the presence of a single Bragg peak and the relatively small fitted tL value could mean the paracrystal lamellar model might not best describe data.
Fractal models were also trialled to fit the SANS data – to capture the structural features at larger length scales. Of these, the mass fractal model39 was found to best fit the SANS profiles at 25 °C (Fig. 8a, c and Table 6). The fitted radii, r, of the aggregates decreased with increasing cSDS, a feature also evident from PLM (Fig. S2, ESI†), where larger aggregates were more noticeable at lower cSDS. This could be due to the growth of the aggregates being stunted by the number of aggregates forming, suggesting that the growth mechanism is that all fibre orders (nf = 1, 2, and 3) grow simultaneously.79
| c SDS (wt%) | r (Å) | D m | χ 2 |
|---|---|---|---|
| 0.1 | 20.0 | 3.37 | 4.9 |
| 0.3 | 145.6 | 2.30 | 6.9 |
| 0.6 | 128.5 | 2.65 | 4.5 |
| 1.2 | 88.5 | 2.97 | 4.4 |
| 2.7 | 77.5 | 2.91 | 3.0 |
| 5.3 | 56.5 | 2.95 | 3.4 |
The fractal dimension, Dm, is related to the Hausdorff dimension,80,81 which is a mathematical description of scale invariances that appear identical when viewed over a range of scales. Mass fractals typically have Dm ∼ 2–3; for instance broccoli has a Dm ∼ 1.8 and cauliflower a Dm ∼ 1.9.82Dm ∼ 2 is indicative of smoother aggregates and Dm ∼ 3 is from rougher aggregates, with Dm > 2 implying three dimensional fractals.83,84Table 5 shows Dm ∼ 2.8–3 across the cSDS studied, indicating very rough mass fractal aggregates of similar Dm to that reported of human lungs.85
The fractal dimension can also be estimated directly from a power law fit to the low-q data of the scattering profile,39i.e. ∼ qD−6 (Table 7). This yielded lower Dm values (1.5–2.8) compared to those obtained through the fitting to the SANS profiles of the higher cSDS. This difference could be due to the sensitivity of the mass fractal model regarding the dimensionality of the interfacial region between the cluster and solvent bulk, as opposed to the cluster itself, as noted by Mildner and Hall.39
| c SDS (wt%) | D m |
|---|---|
| 0.1 | 2.6 ± 0.7 |
| 0.3 | 2.8 ± 0.6 |
| 0.6 | 2.6 ± 0.2 |
| 1.2 | 1.9 ± 0.1 |
| 2.7 | 1.5 ± 0.1 |
| 5.3 | 1.5 ± 0.2 |
4. Summary, further discussions and proposed gelation mechanism
We have observed the formation of a gel in glyceline, a deep eutectic solvent (DES), at an SDS critical gelation concentration as low as cCGC ∼ 1.9 wt% (i.e. 12.7 CMC). PLM revealed that the gel phase comprised fractal dendritic aggregates of ∼mm in size, consistent with the SANS data fitted using a mass fractal model. At comparable cSDS, SDS would form spherical micellar aggregates in water as expected from its packing parameter of ∼ 0.25.86,87 At much higher concentrations and at higher T (> 80 °C), SDS would form lamellar or hexagonal phases (cSDS ∼ 75 and 45 wt%, respectively).43,44 The formation of dendritic fractal aggregates has not been reported, and we term it a fracto-eutectogel.The dendritic aggregates oriented anisotropically and their hierarchical structures might be considered as comprising parent and child fibres. The fibre length and diameters of the fibres decreased with increasing fibre order, nf, implying that the growth of the parent fibre preceded the child fibres. Rheology measurements confirmed relatively weak interactions of the network entanglement, akin to a physical colloidal gel. The negative first normal stress difference, N1, and elastic properties of the gel phase were consistent with a colloidal gel comprising globular aggregates in solution.
Dendrites are fern-like or tree-like fractals common in nature, such as hoarfrost,88 and have been widely studied. The driving force for dendrite formation is related to the Mullins–Sekerka instability.89–92 It describes the progression of a solid front, or the dendrite tip, in a liquid medium, where the cooled solid advances into a warm, or undercooled, medium.93,94 For growth to occur, the interface must be warmed to the temperature of the liquid, typically as a result of latent heat released by kinks along an otherwise smooth surface.95,96 The growth of fractals, and dendritic patterns in particular, is driven by surface tension anisotropy as proposed by Gruber and Mullins,97 where the surface tension of perturbed surfaces deviates from that of unperturbed planar surfaces.98,99
SANS measurements showed the formation of a bulk mesophase at all cSDS studied, well described by a mass fractal model with a fractal dimension Dm = 2.8–3.0 in the gel phase (or a smaller value using the power law fit to the low q SANS data), confirming the PLM visualization. This contrasts with SDS self-assembly in aqueous systems,43,44,78 forming globular aggregates at comparable cSDS.
The morphological details of the fracto-eutectogel are also quite unusual for non-aqueous systems. For example, an SDS-in-glycerol gel30 has been recently reported at comparable cSDS at RT, comprising fibrous networks of lamellar building blocks. Here, a lamellar model could well capture the Bragg peaks in the SANS data (Fig. 8), suggesting lamellar packing of SDS in the dendritic fractal aggregates as observed in hydrated crystalline systems.100 Surfactants are known to form hydrated crystals below the Krafft point101 and crystallisation of inorganic ions in DES has also been reported.102,103 Gelation and crystallisation are often viewed as two competing processes.104,105 However, the crystal engineering approach to forming supramolecular gels has been reported.106,107 For instance, anthracenyl groups of cholesteryl 4-(2-anthryloxy)butanoate (CAB) forms a stacked helical arrangement, leading to a thermally reversible gel network;107,108 inulin gels comprise networks of small crystallites.109
The contrast between the observation in glyceline (choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol in 1
glycerol in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio) here and in glycerol30 points to the pivotal role of choline chloride in facilitating the formation of fractal aggregates. We note that a critical gelation temperature, TGC, exists, above which SDS forms cylindrical aggregates.
2 ratio) here and in glycerol30 points to the pivotal role of choline chloride in facilitating the formation of fractal aggregates. We note that a critical gelation temperature, TGC, exists, above which SDS forms cylindrical aggregates.
The role of choline chloride in the self-assembly of such aggregates may be explained by the counterion condensation theory,110 commonly used to describe polyelectrolyte systems but also extended to other systems.111–113 In our system, the parent fibre grows in one dimension into a rod-like shape and simultaneously choline ions are diffusing to the fibre surface through counterion condensation (Fig. 10). The condensed choline ions lead to certain points along the fibre that radiate heat more effectively, causing kinking along the otherwise flat rod surface as a result of Mullins–Sekerka instability.89–92 Due to the bridging effect of the condensed choline ions, this leads to increased growth at the kink sites, resulting in branching and dendritic growth95,96 (Fig. 10f). Such a counterion condensation effect is more favourable in glyceline due to its lower dielectric constant (εGlyceline ∼ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 114vs. 78.3115 and 42.5116 for water and glycerol, respectively), due to stronger attractions between opposite ions and, in turn, a stronger bridging effect. Such cation-bridging has been observed;117–119 for instance, SDS and caesium dodecyl sulfate formed hemicylinders bridged with Na+/Cs+ counterions at the water-graphite interface.119
114vs. 78.3115 and 42.5116 for water and glycerol, respectively), due to stronger attractions between opposite ions and, in turn, a stronger bridging effect. Such cation-bridging has been observed;117–119 for instance, SDS and caesium dodecyl sulfate formed hemicylinders bridged with Na+/Cs+ counterions at the water-graphite interface.119
At cSDS > 1.9 wt%, jamming of the fractal aggregates – rather than their interpenetration – would lead to a colloidal gel, consistent with the rheological observations, which indicate a structure closer to a colloidal gel rather than an entangled fibrillar network.
Fractal aggregates exist already at low SDS concentration (cSDS ∼ 0.1 wt%) evident from PLM observations (Fig. S3 in ESI†) with the constituent fibres appearing thicker possibly due to a smaller number of nucleation sites at the lower SDS concentration.
The SDS Krafft point in glycerol, a component of glyceline, is Tk > 30 °C,120 below which crystallisation of surfactants is favoured over self-assembly.121 Surface tensiometry measurements (Fig. 1) however points to SDS surface activity and thus self-assembly tendency at RT. Addition of salt has been shown to alter the Krafft point of ionic surfactants,122–124 and the presence of choline chloride could thus suppress the Krafft point, giving rise to the self-assembly tendency of SDS observed at RT.
Further experimental work would be required to fully validate the proposed formation mechanism for the fracto-eutectogel of SDS in glyceline. For instance, use of cationic, zwitterionic, and a nonionic surfactants (e.g. DTAB, cocobetaine, and C5E12 respectively) would inform whether the cationic choline ion would stabilise the different types of headgroup. Our results have fundamental implications to gelation and self-assembly important in application of DES as green solvents.
Author contributions
Lauren Matthews: data curation, formal analysis, methodology, investigation, validation, visualisation, writing – original draft. Silvia Ruscigno: data curation, investigation. Sarah E. Rogers: resources, methodology, investigation. Paul Bartlett: funding acquisition, conceptualisation, supervision. Andrew J. Johnson: resources, project administration, supervision. Robert Sochon: funding acquisition, conceptualisation, resources, project administration, supervision. Wuge H. Briscoe: funding acquisition, conceptualisation, resources, methodology, formal analysis, validation, supervision, project administration, writing – reviewing and editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We acknowledge the ISIS Muon and Neutron Source for the awarded beamtime under experiment number: RB1810629, and the Diamond Light Source for the awarded beamtime under experiment number SI20171-2. We thank A. Seddon (Bristol Physics) for use of the polarising light microscope (PLM). We thank A. Slastanova, J. Rawle, and H. Stockdale for their help with the XRR experiments, and Ż. Przybyłowicz, and S. Michel for their help with the SANS experiments. L.M. was supported by a studentship jointly funded through the Engineering and Physical Science Research Council (the Bristol Centre for Functional Nanomaterials (EPSRC, EP/L016648/1)) and GlaxoSmithKline. SasView, originally developed under NSF award DMR-0520547, contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement No 654000.References
- A. P. Abbott, G. Capper, D. L. Davies, H. L. Munro, R. K. Rasheed and V. Tambyrajah, Preparation of novel, moisture-stable, Lewis-acidic ionic liquids containing quaternary ammonium salts with functional side chains, Chem. Commun., 2001, 2010 RSC
.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Deep Eutectic Solvents (DESs) and Their Applications, Chem. Rev., 2014, 114(21), 11060 CrossRef CAS PubMed
.
- K. R. Seddon, Ionic liquids - A taste of the future, Nat. Mater., 2003, 2(6), 363 CrossRef CAS PubMed
.
- R. D. Rogers and K. R. Seddon, Ionic liquids - Solvents of the future?, Science, 2003, 302(5646), 792 CrossRef PubMed
.
- A. P. Abbott, M. Azam, G. Frisch, J. Hartley, K. S. Ryder and S. Saleem, Ligand exchange in ionic systems and its effect on silver nucleation and growth, Phys. Chem. Chem. Phys., 2013, 15(40), 17314 RSC
.
- A. P. Abbott, G. Capper, B. G. Swain and D. A. Wheeler, Electropolishing of stainless steel in an ionic liquid, Trans. Inst. Met. Finish., 2005, 83(1), 51 CrossRef CAS
.
- A. P. Abbott, K. El Ttaib, G. Frisch, K. J. McKenzie and K. S. Ryder, Electrodeposition of copper composites from deep eutectic solvents based on choline chloride, Phys. Chem. Chem. Phys., 2009, 11(21), 4269 RSC
.
- A. P. Abbott, K. El Ttaib, G. Frisch, K. S. Ryder and D. Weston, The electrodeposition of silver composites using deep eutectic solvents, Phys. Chem. Chem. Phys., 2012, 14(7), 2443 RSC
.
- A. P. Abbott, K. J. McKenzie and K. S. Ryder, Electropolishing and Electroplating of Metals Using Ionic Liquids Based on Choline Chloride, ACS Symp. Ser., 2007, 975, 186 CrossRef CAS
.
- N. Guajardo, C. R. Muller, R. Schrebler, C. Carlesi and P. D. de Maria, Deep Eutectic Solvents for Organocatalysis, Biotransformations, and Multistep Organocatalyst/Enzyme Combinations, ChemCatChem, 2016, 8(6), 1020 CrossRef CAS
.
- J. T. Gorke, F. Srienc and R. J. Kazlauskas, Hydrolase-catalyzed biotransformations in deep eutectic solvents, Chem. Commun., 2008, 1235 RSC
.
- J. Gorke, F. Srienc and R. J. Kazlauskas, ORGN 299-Deep eutectic solvents: Alternative reaction media for hydrolase-catalyzed reactions, Abstracts of Papers of the American Chemical Society, 2008, 236 Search PubMed
.
- J. Gorke, F. Srienc and R. Kazlauskas, Toward Advanced Ionic Liquids. Polar, Enzyme-friendly Solvents for Biocatalysis, Biotechnol. Bioprocess Eng., 2010, 15(1), 40 CrossRef CAS
.
- P. D. de Maria and Z. Maugeri, Ionic liquids in biotransformations: from proof-of-concept to emerging deep-eutectic-solvents, Curr. Opin. Chem. Biol., 2011, 15(2), 220 CrossRef PubMed
.
- V. S. Raghuwanshi, M. Ochmann, F. Polzer, A. Hoell and K. Rademann, Self-assembly of gold nanoparticles on deep eutectic solvent (DES) surfaces, Chem. Commun., 2014, 50(63), 8693 RSC
.
- V. Raghuwanshi, M. Ochmann, F. Polzer, A. Hoell and K. Rademann, Growth mechanisms of self-assembled gold nanoparticles in Deep Eutectic Solvent, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, C891 Search PubMed
.
- V. S. Raghuwanshi, M. Ochmann, A. Hoell, F. Polzer and K. Rademann, Deep Eutectic Solvents for the Self-Assembly of Gold Nanoparticles: A SAXS, UV-Vis, and TEM Investigation, Langmuir, 2014, 30(21), 6038 CrossRef CAS PubMed
.
- M. O'Neill, V. S. Raghuwanshi, R. Wendt, M. Wollgarten, A. Hoell and K. Rademann, Gold Nanoparticles in Novel Green Deep Eutectic Solvents: Self-Limited Growth, Self-Assembly & Catalytic Implications, Z. Phys. Chem., 2015, 229(1-2), 221 CrossRef
.
- J. A. Hammons, F. Zhang and J. Ilaysky, Extended hierarchical solvent perturbations from curved surfaces of mesoporous silica particles in a deep eutectic solvent, J. Colloid Interface Sci., 2018, 520, 81 CrossRef CAS PubMed
.
- J. A. Hammons, J. Ustarroz, T. Muselle, A. A. J. Torriero, H. Terryn, K. Suthar and J. Ilavsky, Supported Silver Nanoparticle and Near-Interface Solution Dynamics in a Deep Eutectic Solvent, J. Phys. Chem. C, 2016, 120(3), 1534 CrossRef CAS
.
- J. A. Hammons, T. Muselle, J. Ustarroz, M. Tzedaki, M. Rats, A. Hubin and H. Terryn, Stability, Assembly, and Particle/Solvent Interactions of Pd Nanoparticles Electrodeposited from a Deep Eutectic Solvent, J. Phys. Chem. C, 2013, 117(27), 14381 CrossRef CAS
.
- S. J. Bryant, R. Atkin and G. G. Warr, Spontaneous vesicle formation in a deep eutectic solvent, Soft Matter, 2016, 12(6), 1645 RSC
.
- A. Sanchez-Fernandez, G. L. Moody, L. C. Murfin, T. Arnold, A. J. Jackson, S. M. King, S. E. Lewis and K. J. Edler, Self-assembly and surface behaviour of pure and mixed zwitterionic amphiphiles in a deep eutectic solvent, Soft Matter, 2018, 14(26), 5525 RSC
.
- M. Pal, R. K. Singh and S. Pandey, Evidence of Self-Aggregation of Cationic Surfactants in a Choline Chloride plus Glycerol Deep Eutectic Solvent, ChemPhysChem, 2015, 16(12), 2538 CrossRef CAS PubMed
.
- M. Pal, R. Rai, A. Yadav, R. Khanna, G. A. Baker and S. Pandey, Self-Aggregation of Sodium Dodecyl Sulfate within (Choline Chloride plus Urea) Deep Eutectic Solvent, Langmuir, 2014, 30(44), 13191 CrossRef CAS PubMed
.
- A. Sanchez-Fernandez, T. Arnold, A. J. Jackson, S. L. Fussell, R. K. Heenan, R. A. Campbell and K. J. Edler, Micellization of alkyltrimethylammonium bromide surfactants in choline chloride: glycerol deep eutectic solvent, Phys. Chem. Chem. Phys., 2016, 18(48), 33240 RSC
.
- T. Arnold, A. J. Jackson, A. Sanchez-Fernandez, D. Magnone, A. E. Terry and K. J. Edler, Surfactant Behavior of Sodium Dodecylsulfate in Deep Eutectic Solvent Choline Chloride/Urea, Langmuir, 2015, 31(47), 12894 CrossRef CAS PubMed
.
- A. Sanchez-Fernandez, O. S. Hammond, K. J. Edler, T. Arnold, J. Doutch, R. M. Dalgliesh, P. Li, K. Ma and A. J. Jackson, Counterion binding alters surfactant self-assembly in deep eutectic solvents, Phys. Chem. Chem. Phys., 2018, 20(20), 13952 RSC
.
- J. Ruiz-Olles, P. Slavik, N. K. Whitelaw and D. K. Smith, Self-Assembled Gels Formed in Deep Eutectic Solvents: Supramolecular Eutectogels with High Ionic Conductivity, Angew. Chem., Int. Ed., 2019, 58(13), 4173 CrossRef CAS PubMed
.
- L. Matthews, Ż. Przybyłowicz, S. E. Rogers, P. Bartlett, A. J. Johnson, R. Sochon and W. H. Briscoe, The curious case of SDS self-assembly in glycerol: Formation of a lamellar gel, J. Colloid Interface Sci., 2020, 572, 384 CrossRef CAS PubMed
.
-
H. A. Barnes, A Handbook of Elementary Rheology, The University of Wales Institute of Non-Newtonian Fluid Mechanics, Aberystwyth, UK, 1st edn, 2000 Search PubMed
.
- R. K. Heenan, J. Penfold and S. M. King, SANS at pulsed neutron sources: Present and future prospects, J. Appl. Crystallogr., 1997, 30, 1140 CrossRef CAS
.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal and M. A. Gigg,
et al., Mantid—Data analysis and visualization package for neutron scattering and μ SR experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156 CrossRef CAS
.
- G. D. Wignall and F. S. Bates, Absolute Calibration of Small-Angle Neutron-Scattering Data, J. Appl. Crystallogr., 1987, 20, 28 CrossRef CAS
.
- J. Berghausen, J. Zipfel, P. Lindner and W. Richtering, Influence of water-soluble
polymers on the shear-induced structure formation in lyotropic lamellar phases, J. Phys. Chem. B, 2001, 105(45), 11081 CrossRef CAS
.
- M. Bergstrom, J. S. Pedersen, P. Schurtenberger and S. U. Egelhaaf, Small-angle neutron scattering (SANS) study of vesicles and lamellar sheets formed from mixtures of an anionic and a cationic surfactant, J. Phys. Chem. B, 1999, 103(45), 9888 CrossRef
.
- A. Caille, X-Ray Scattering by Smectic-a Crystals, C. R. Seances Acad. Sci., Ser. B, 1972, 274(14), 891 CAS
.
- F. Nallet, R. Laversanne and D. Roux, Modeling X-Ray or Neutron-Scattering Spectra of Lyotropic Lamellar Phases - Interplay between Form and Structure Factors, J. Phys. II, 1993, 3(4), 487 CrossRef CAS
.
- D. F. R. Mildner and P. L. Hall, Small-Angle Scattering from Porous Solids with Fractal Geometry, J. Phys. D: Appl. Phys., 1986, 19(8), 1535 CrossRef
.
- T. L. Greaves and C. J. Drummond, Ionic liquids as amphiphile self-assembly media, Chem. Soc. Rev., 2008, 37(8), 1709 RSC
.
- C. M. Hansen, Universality of Solubility Parameter, Ind. Eng. Chem. Prod. Res. Dev., 1969, 8(1), 2 CrossRef CAS
.
- H. S. Salehi, M. Ramdin, O. A. Moultos and T. J. H. Vlugt, Computing solubility parameters of deep eutectic solvents from Molecular Dynamics simulations, Fluid Phase Equilib., 2019, 497, 10 CrossRef CAS
.
- P. Kekicheff, Phase-Diagram of Sodium Dodecyl-Sulfate Water-System 2. Complementary Isoplethal and Isothermal Phase Studies, J. Colloid Interface Sci., 1989, 131(1), 133 CrossRef CAS
.
- P. Kekicheff, C. Grabiellemadelmont and M. Ollivon, Phase-Diagram of Sodium Dodecyl-Sulfate Water-System 1. A Calorimetric Study, J. Colloid Interface Sci., 1989, 131(1), 112 CrossRef CAS
.
- R. A. Abdel-Rahem, Influence of Glycerol and Temperature on the Phase Behavior and Micellization of CTAB and SDS in Aqueous Solutions, J. Dispersion Sci. Technol., 2013, 34(7), 932 CrossRef CAS
.
- B. Arenas-Gomez, C. Garza, Y. Liu and R. Castillo, Alignment of worm-like micelles at intermediate and high shear rates, J. Colloid Interface Sci., 2020, 560, 618 CrossRef CAS PubMed
.
- J. das Neves, M. V. da Silva, M. P. Goncalves, M. H. Amaral and M. F. Bahia, Rheological properties of vaginal hydrophilic polymer gels, Curr. Drug Delivery, 2009, 6(1), 83 CrossRef CAS PubMed
.
- J. Y. Kim, J. Y. Song, E. J. Lee and S. K. Park, Rheological properties and microstructures of Carbopol gel network system, Colloid Polym. Sci., 2003, 281(7), 614 CrossRef CAS
.
- V. Kobelev and K. S. Schweizer, Dynamic yielding, shear thinning, and stress rheology of polymer-particle suspensions and gels, J. Chem. Phys., 2005, 123(16), 164903 CrossRef PubMed
.
- J. R. Mitchell, The Rheology of Gels, J. Texture Stud., 1980, 11(4), 315 CrossRef CAS
.
- F. K. Oppong, L. Rubatat, B. J. Frisken, A. E. Bailey and J. R. de Bruyn, Microrheology and structure of a yield-stress polymer gel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73(4), 041405 CrossRef PubMed
.
- H. de Cagny, M. Fazilati, M. Habibi, M. M. Denn and D. Bonn, The yield normal stress, J. Rheol., 2019, 63(2), 285 CrossRef CAS
.
- J. Y. Lee, J. J. Magda, H. Hu and R. G. Larson, Cone angle effects, radial pressure profile, and second normal stress difference for shear-thickening wormlike micelles, J. Rheol., 2002, 46(1), 195 CrossRef CAS
.
- T. Shikata, S. J. Dahman and D. S. Pearson, Rheooptical Behavior of Wormlike Micelles, Langmuir, 1994, 10(10), 3470 CrossRef CAS
.
- C. D. Cwalina and N. J. Wagner, Material properties of the shear-thickened state in concentrated near hard-sphere colloidal dispersions, J. Rheol., 2014, 58(4), 949 CrossRef CAS
.
- Y. F. Lee, Y. Luo, S. C. Brown and N. J. Wagner, Experimental test of a frictional contact model for shear thickening in concentrated colloidal suspensions, J. Rheol., 2020, 64, 267 CrossRef CAS
.
- T. Chatterjee, M. Linsen, V. V. Ginzburg, D. A. Saucy, A. I. Nakatani and A. K. Van Dyk, Influence of the first normal stress differences on model hydrophobically modified ethoxylated urethane-thickened waterborne paints brush drag, Prog. Org. Coat., 2019, 135, 582 CrossRef CAS
.
- T. Chatterjee, A. K. Van Dyk, V. V. Ginzburg and A. I. Nakatani, Formulation-Controlled Positive and Negative First Normal Stress Differences in Waterborne Hydrophobically Modified Ethylene Oxide Urethane (HEUR)-Latex Suspensions, ACS Macro Lett., 2017, 6(7), 716 CrossRef CAS
.
- P. Hebraud, Normal and tangential stress fluctuations during jamming, Rheol. Acta, 2009, 48(8), 845 CrossRef CAS
.
- C. O. Osuji and D. A. Weitz, Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system, Soft Matter, 2008, 4(7), 1388 RSC
.
- F. C. Mackintosh, J. Kas and P. A. Janmey, Elasticity of Semiflexible Biopolymer Networks, Phys. Rev. Lett., 1995, 75(24), 4425 CrossRef CAS PubMed
.
- B. A. Schubert, E. W. Kaler and N. J. Wagner, The microstructure and rheology of mixed cationic/anionic wormlike micelles, Langmuir, 2003, 19(10), 4079 CrossRef CAS
.
- D. P. Acharya, D. Varade and K. Aramaki, Effect of temperature on the rheology of wormlike micelles in a mixed surfactant system, J. Colloid Interface Sci., 2007, 315(1), 330 CrossRef CAS PubMed
.
- P. A. Hassan, S. J. Candau, F. Kern and C. Manohar, Rheology of wormlike micelles with varying hydrophobicity of the counterion, Langmuir, 1998, 14(21), 6025 CrossRef CAS
.
- R. Kumar, G. C. Kalur, L. Ziserman, D. Danino and S. R. Raghavan, Wormlike micelles of a C22-tailed zwitterionic betaine surfactant: From viscoelastic solutions to elastic gels, Langmuir, 2007, 23(26), 12849 CrossRef CAS PubMed
.
- H. Rehage and H. Hoffmann, Viscoelastic Surfactant Solutions – Model Systems for Rheological Research, Mol. Phys., 1991, 74(5), 933 CrossRef CAS
.
- A. G. Marangoni and S. S. Narine, The influence of microstructure on the macroscopic rheological properties of soft materials, Scanning, 1999, 21(2), 120 Search PubMed
.
- P. Wasik, A. M. Seddon, H. Wu and W. H. Briscoe, Dendritic surface patterns from Benard-Marangoni instabilities upon evaporation of a reactive ZnO nanofluid droplet: A fractal dimension analysis, J. Colloid Interface Sci., 2019, 536, 493 CrossRef CAS PubMed
.
-
B. B. Mandelbrot, The fractal geometry of nature, W. H. Freeman, San Francisco, 1983 Search PubMed
.
- P. Bestimmung Scherrer, der Grose und der inneren Struktur von Kolloidteilchen mittels Rontgenstrahlen, Nachr. Ges. Wiss. Goettingen, Math.-Phys. Kl., 1918, 98 Search PubMed
.
- A. L. Patterson, The Scherrer formula for X-ray particle size determination, Phys. Rev., 1939, 56(10), 978 CrossRef CAS
.
- L. Fox, J. Slastanova, A. Taylor, N. Wlodek, M. Bikondoa, O. Richardson and R. M. Briscoe, W. H. Interactions between PAMAM dendrimers and DOPC lipid multilayers: Membrane thinning and structural disorder, Biochim. Biophys. Acta, Gen. Subj., 2021, 1865, 129542 CrossRef CAS PubMed
.
- L. J. Fox, L. Matthews, H. Stockdale, S. Pichai, T. Snow, R. M. Richardson and W. H. Briscoe, Structural changes in lipid mesophases due to intercalation of dendritic polymer nanoparticles: Swollen lamellae, suppressed curvature, and augmented structural disorder, Acta Biomater., 2020, 104, 198 CrossRef CAS PubMed
.
- T. G. Dane, P. T. Cresswell, G. A. Pilkington, S. Lilliu, J. E. Macdonald, S. W. Prescott, O. Bikondoa, C. F. J. Faul and W. H. Briscoe, Oligo(aniline) nanofilms: from molecular architecture to microstructure, Soft Matter, 2013, 9(44), 10501 RSC
.
- T. G. Dane, P. T. Cresswell, O. Bikondoa, G. E. Newby, T. Arnold, C. F. J. Faul and W. H. Briscoe, Structured oligo(aniline) nanofilms via ionic self-assembly, Soft Matter, 2012, 8(10), 2824 RSC
.
- B. Sironi, T. Snow, C. Redeker, A. Slastanova, O. Bikondoa, T. Arnold, J. Klein and W. H. Briscoe, Structure of lipid multilayers via drop casting of aqueous liposome dispersions, Soft Matter, 2016, 12(17), 3877 RSC
.
- R. Guo, M. E. Compo, S. E. Friberg and K. Morris, The coupling action of a hydrotrope and structure transition from lamellar liquid crystal to bicontinuous microemulsion, J. Dispersion Sci. Technol., 1996, 17(5), 493 CrossRef CAS
.
- P. Kekicheff, B. Cabane and M. Rawiso, Macromolecules Dissolved in a Lamellar Lyotropic Mesophase, J. Colloid Interface Sci., 1984, 102(1), 51 CrossRef CAS
.
- T.-Y. Chen, E. M. Woo and S. Nagarajan, Periodic Fractal-Growth Branching to Nano-Structured Grating Aggregation in Phthalic Acid, Sci. Rep., 2020, 10(1), 4062 CrossRef CAS
.
- F. Hausdorff, Dimension and outer dimension, Mathematische Annalen, 1919, 79, 157 CrossRef
.
- C. M. Sorensen, Light scattering by fractal aggregates: A review, Aerosol Sci. Technol., 2001, 35(2), 648 CrossRef CAS
.
- S. H. Kim Fractal dimensions of a green broccoli and a white cauliflower, arXiv preprint cond-mat/0411597 2004.
- X. Gu and D. F. R. Mildner, Determination of porosity in anisotropic fractal systems by neutron scattering, J. Appl. Crystallogr., 2018, 51, 175 CrossRef CAS
.
- J. Teixeira, Small-Angle Scattering by Fractal Systems, J. Appl. Crystallogr., 1988, 21, 781 CrossRef
.
- K. L. Uahabi and M. Atounti, New approach to the calculation of fractal dimension of the lungs, Annals of the University of Craiova-Mathematics and Computer Science Series, 2017, 44(1), 78 Search PubMed
.
- G. B. Ray, I. Chakraborty, S. Ghosh and S. P. Moulik, A critical and comprehensive assessment of interfacial and bulk properties of aqueous binary mixtures of anionic surfactants, sodium dodecylsulfate, and sodium dodecylbenzenesulfonate, Colloid Polym. Sci., 2007, 285(4), 457 Search PubMed
.
- C. Tanford, Micelle Shape and Size, J. Phys. Chem., 1972, 76(21), 3020 CrossRef CAS
.
- L. Makkonen, A model of hoarfrost formation on a cable, Cold Reg. Sci. Technol., 2013, 85, 256 CrossRef
.
- W. W. Mullins and R. F. Sekerka, Morphological Stability of a Particle Growing by Diffusion or Heat Flow, J. Appl. Phys., 1963, 34(2), 323 CrossRef CAS
.
- W. W. Mullins and R. F. Sekerka, Stability of a Planar Interface During Solidification of a Dilute Binary Alloy, J. Appl. Phys., 1964, 35(2), 444 CrossRef
.
- R. C. Brower, D. A. Kessler, J. Koplik and H. Levine, Geometrical models of interface evolution, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29(3), 1335 CrossRef CAS
.
- B. Caroli, C. Caroli and B. Roulet, The Mullins-Sekerka instability in directional solidification of thin samples, J. Cryst. Grow., 1986, 76(1), 31 CrossRef CAS
.
- J. S. Langer, Instabilities and pattern formation in crystal growth, Rev. Mod. Phys., 1980, 52(1), 1 CrossRef CAS
.
- P. K. Galenko and D. V. Alexandrov, From atomistic interfaces to dendritic patterns, Philos. Trans. R. Soc., A, 2018, 376(2113), 20170210 CrossRef PubMed
.
- H. Brune, C. Romainczyk, H. Röder and K. Kern, Mechanism of the transition from fractal to dendritic growth of surface aggregates, Nature, 1994, 369(6480), 469 CrossRef CAS
.
- Y. Sawada, A. Dougherty and J. P. Gollub, Dendritic and Fractal Patterns in Electrolytic Metal Deposits, Phys. Rev. Lett., 1986, 56(12), 1260 CrossRef CAS PubMed
.
- E. E. Gruber and W. W. Mullins, On the theory of anisotropy of crystalline surface tension, J. Phys. Chem. Solids, 1967, 28(5), 875 CrossRef CAS
.
- S. R. Coriell and R. F. Sekerka, The effect of the anisotropy of surface tension and interface kinetics on morphological stability, J. Cryst. Grow., 1976, 34(2), 157 CrossRef CAS
.
- G. Radnoczi, T. Vicsek, L. M. Sander and D. Grier, Growth of fractal crystals in amorphous GeSe2 films, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35(9), 4012 CrossRef CAS PubMed
.
- M. Ambrosi, P. Lo Nostro, L. Fratoni, L. Dei, B. W. Ninham, S. Palma, R. H. Manzo, D. Allemandi and P. Baglioni, Water of hydration in coagels, Phys. Chem. Chem. Phys., 2004, 6(7), 1401 RSC
.
- K. Shinoda, N. Yamaguchi and A. Carlsson, Physical meaning of the Krafft point: observation of melting phenomenon of hydrated solid surfactant at the Krafft point. The, J. Phys. Chem., 1989, 93(20), 7216 CrossRef CAS
.
- E. Ahmed, J. Breternitz, M. F. Groh and M. Ruck, Ionic liquids as crystallisation media for inorganic materials, CrystEngComm, 2012, 14(15), 4874 RSC
.
- J. Potticary, C. Hall, V. Hamilton, J. F. McCabe and S. R. Hall, Crystallization from Volatile Deep Eutectic Solvents, Cryst. Growth Des., 2020, 20(5), 2877 CrossRef CAS
.
- I. Kapoor, E.-M. Schön, J. Bachl, D. Kühbeck, C. Cativiela, S. Saha, R. Banerjee, S. Roelens, J. J. Marrero-Tellado and D. D. Díaz, Competition between gelation and crystallisation of a peculiar multicomponent liquid system based on ammonium salts, Soft Matter, 2012, 8(12), 3446 RSC
.
- D. J. Adams, K. Morris, L. Chen, L. C. Serpell, J. Bacsa and G. M. Day, The delicate balance between gelation and crystallisation: structural and computational investigations, Soft Matter, 2010, 6(17), 4144 RSC
.
- P. Dastidar, Supramolecular gelling agents: can they be designed?, Chem. Soc. Rev., 2008, 37(12), 2699 RSC
.
- Y. C. Lin, B. Kachar and R. G. Weiss, Liquid-crystalline solvents as mechanistic probes. Part 37. Novel family of gelators of organic fluids and the structure of their gels, J. Am. Chem. Soc., 1989, 111(15), 5542 CrossRef CAS
.
- Y. C. Lin and R. G. Weiss, Liquid-crystalline solvents as mechanistic probes. 24. A novel gelator of organic liquids and the properties of its gels, Macromolecules, 1987, 20(2), 414 CrossRef CAS
.
- A. Bot, U. Erle, R. Vreeker and W. G. M. Agterof, Influence of crystallisation conditions on the large deformation rheology of inulin gels, Food Hydrocolloids, 2004, 18(4), 547 CrossRef CAS
.
- G. S. Limiting Manning, Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. The, J. Chem. Phys., 1969, 51(3), 924 CrossRef CAS
.
- G. S. Manning, Counterion condensation theory constructed from different models, Phys. A, 1996, 231(1), 236 CrossRef CAS
.
- G. S. Manning, Electrostatic free energy of the DNA double helix in counterion condensation theory, Biophys. Chem., 2002, 101–102, 461 CrossRef CAS PubMed
.
- G. S. Manning, Counterion condensation on charged spheres, cylinders, and planes, J. Phys. Chem. B, 2007, 111(29), 8554 CrossRef CAS PubMed
.
- A. Faraone, D. V. Wagle, G. A. Baker, E. C. Novak, M. Ohl, D. Reuter, P. Lunkenheimer, A. Loidl and E. Mamontov, Glycerol Hydrogen-Bonding Network Dominates Structure and Collective Dynamics in a Deep Eutectic Solvent, J. Phys. Chem. B, 2018, 122(3), 1261 CrossRef CAS
.
- D. G. Archer and P. Wang, The Dielectric Constant of Water and Debye–Hückel Limiting Law Slopes, J. Phys. Chem. Ref. Data, 1990, 19(2), 371 CrossRef CAS
.
- A. Wolfson, C. Dlugy and Y. Shotland, Glycerol as a green solvent for high product yields and selectivities, Environ. Chem. Lett., 2007, 5(2), 67 CrossRef CAS
.
- M. O. de la Cruz, L. Belloni, M. Delsanti, J. P. Dalbiez, O. Spalla and M. Drifford, Precipitation of highly charged polyelectrolyte solutions in the presence of multivalent salts, J. Chem. Phys., 1995, 103(13), 5781 CrossRef
.
- J. A. Schellman and N. Parthasarathy, X-ray diffraction studies on cation-collapsed DNA, J. Mol. Biol., 1984, 175(3), 313 CrossRef CAS
.
- N. R. Tummala and A. Striolo, Hydrogen-bond dynamics for water confined in carbon tetrachloride-acetone mixtures, J. Phys. Chem. B, 2008, 112(34), 10675 CrossRef CAS PubMed
.
- H. Khan, J. M. Seddon, R. V. Law, N. J. Brooks, E. Robles, J. T. Cabral and O. Ces, Effect of glycerol with sodium chloride on the Krafft point of sodium dodecyl sulfate using surface tension, J. Colloid Interface Sci., 2019, 538, 75 CrossRef CAS PubMed
.
- T. Gu and J. Sjöblom, Surfactant structure and its relation to the Krafft point, cloud point and micellization: Some empirical relationships, Colloids Surf., 1992, 64(1), 39 CrossRef CAS
.
- Y. Moroi, N. Ikeda and R. Matuura, Anionic surfactants with methylviologen or cupric ions as divalent cationic gegenion: Solubility and micelle formation, J. Colloid Interface Sci., 1984, 101(1), 285 CrossRef CAS
.
- K. Tsujii and J. Mino, Krafft point depression of some zwitterionic surfactants by inorganic salts, J. Phys. Chem., 1978, 82(14), 1610 CrossRef CAS
.
- K. Tsujii, N. Saito and T. Takeuchi, Krafft points of anionic surfactants and their mixtures with special attention to their applicability in hard water, J. Phys. Chem., 1980, 84(18), 2287 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01370j |
| ‡ Current address: ESRF, The European Synchrotron, Grenoble 38043, France. |
| This journal is © the Owner Societies 2021 |






