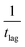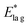Open Access Article
Open Access ArticleLow temperature aging in a molecular glass: the case of cis-methyl formate
Andrew
Cassidy
 *a,
Mads R. V.
Jørgensen
*a,
Mads R. V.
Jørgensen
 bc,
Artur
Glavic
bc,
Artur
Glavic
 d,
Valeria
Lauter
d,
Valeria
Lauter
 e,
Oksana
Plekan
e,
Oksana
Plekan
 f and
David
Field
f and
David
Field
 a
a
aCenter for Interstellar Catalysis and Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, Aarhus C, Denmark. E-mail: amc@phys.au.dk
bCenter of Materials Crystallography, iNano & Department of Chemistry, Aarhus University, Langelandsgade 140, Aarhus C, Denmark
cMAX IV Laboratory, Lund University, Fotongatan 2, Lund, Sweden
dLaboratory for Neutron and Muon Instrumentation, Paul Scherrer Institut, 5232 Villigen PSI, Switzerland
eNeutron Scattering Division, Oak Ridge National Lab, Oak Ridge, TN 37831, USA
fSincrotrone Trieste S.C.P.A., Area Science Park, Strada Statale 14, km 163.5, I-34149 Basovizza, Trieste, Italy
First published on 19th July 2021
Abstract
Glassy films of cis-methyl formate show spontaneous dipole orientation on deposition from the vacuum, the so-called ‘spontelectric effect’, creating surface potentials and electric fields within the films. We follow the decay of these fields, and their accompanying dipole orientation, on the hours timescale at deposition temperatures between 40 K and 55 K. Our data trace the low temperature ‘secondary decay’ mechanism, at tens of degrees below the glass transition temperature of 90 K. We show that secondary decay is due to molecular rotation, with associated activation energies lying between 0.1 and 0.2 eV. Diffusion is absent, as established from published neutron reflectivity data. Using an analytical model for the spontelectric effect, data are placed on a quantitative footing, showing that angular motion in excess of 50° reproduces the observed values of activation energies. Exploitation of the spontelectric effect is new in the study of glass aging and is shown here to give insight into the elusive processes which take place far from the molecular glass transition temperature.
Introduction
A very great array of materials have a glassy structure, in which constituents are arranged with little local or long-range order and in which species are kinetically trapped out of equilibrium. These materials are solids in the sense that they display resistance to deformation but, like liquids, they lack a crystalline lattice. Glasses tend by their nature to be metastable. Individual constituents in molecular glasses, in their search for a lower energy state, can move by both diffusion and rotation, leading to aging. There is a very extensive literature in the area of glass relaxation, extending over many decades, recently partly reviewed in ref. 1 for network glasses. The numerous techniques involved, for example scanning calorimetry, dielectric relaxation, inelastic neutron scattering and NMR, may be found summarized in ref. 1. The processes of relaxation and physical aging are difficult to follow experimentally. Despite its importance, for example in the lifetimes of electronics and the shelf-life of drugs, mechanisms of aging have remained in some respects elusive.2–6 Even the definition of a glass is far from fully agreed, according to some authors.1As a liquid is cooled, it loses its viscosity. The temperature at which the liquid is too viscous to flow, on any useful laboratory timescale, is the empirical definition of the glass transition temperature, Tg.1 The particular aspect addressed in the present work is the mechanisms at play, which lead to structural relaxation in a deeply supercooled molecular glass at low temperature well below Tg. Almost all glassy materials possess the potential for secondary relaxation.7 The materials for consideration here are prepared at cryo-temperatures, some tens of degrees below Tg. Note that we study a molecular glass, as opposed to recently much-studied metallic glasses8–10 or network glasses.1 Our work may shed some light on the origin of the so-called ‘shadow glass transition’ identified in metallic glasses, as this relates to deeply supercooled processes.9 At all events we show unequivocally that low temperature structural relaxation is described by rotation of molecules about their fixed positions in the glass.11 The current work rests on published experimental data for cis-methyl formate, henceforth cis-MF.11 Material is in the form of a thin film, laid down by condensation from the gas. Tg is ∼90 K for cis-MF11 and we study so-called “secondary” structural changes in cis-MF deposited at temperatures between 40 K and 55 K, between 0.45–0.6 × Tg. The material is a few to a few tens of nm thick, corresponding to a few tens to several hundred monolayers (ML).
The special handle which we have on this system stems from the electrical characteristics of such films. It turns out that on deposition onto a sufficiently cold surface, that is, at deposition temperatures, Td, ≤90 K, the molecular dipoles of this species spontaneously orient. In this connection, cis-MF evaporates from the substrate at 137 K. Spontaneous orientation at Td ≤ 90 K leads to a potential on the surface of the film, a phenomenon known as the ‘spontelectric effect’. This effect is a general phenomenon and cis-MF is only one species among many, both crystalline and glassy, which exhibit the spontelectric effect.12–15 Note that the presence of spontaneous molecular orientation implies that the structure of the material is to some extent organized and demonstrates long-range interaction between discrete molecular species. Moreover, it remains organized, but more weakly, even after relaxation, subsequent to deposition at low temperature. Thus, following film formation, the surface potential on cis-MF is metastable and slowly decays in magnitude for Td = 40 K to 55 K to a new but stable value, where stable signifies unchanging over a period of many hours. The temporal decay of the surface potential on cis-MF films follows the decay of average orientation of the constituent molecules and therefore allows us to monitor the molecular rotation. Changes of a few hundredths of a degree in average angle of dipole orientation with time are readily observable, where this net rotational motion constitutes the so-called ‘secondary relaxation process’. Thus, the time decay of electric fields in spontelectric films of cis-MF provides a means to probe relaxation pathways in a deeply cooled glass, providing real-time measurement of molecular relaxation.
For Td > 55 K, the surface potential remains unchanged on a laboratory timescale up to Td = 77.5 K.11 For films formed with Td ≥ 80 K, decay of orientation once again takes place, but now towards zero orientation on a long time scale. The highest value of Td at which a surface potential can be detected is 90 K, coinciding with Tg. X-ray scattering measurements show that cis-MF crystallises at deposition temperatures of 90 K, very close to Tg.11 Thus crystallization corresponds to a loss of molecular orientation, in the case of cis-MF. Neutron scattering data show that relaxation at Td > 77.5 K is attended by diffusion.11 This is accompanied by molecular rotation. For Td > 77.5 K, we therefore encounter the ‘primary relaxation process’. At Td = 80 K, the lower limit of measurement, self-diffusion causes a translational motion of 0.15 nm in 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds. Neutron data at lower temperatures show that diffusion can be ruled out as a contributory mechanism to decay. Therefore at deeply supercooled temperatures, <55 K, studied here, diffusion is absent and net molecular rotation, relative to the normal to the film, is the sole cause of secondary relaxation.
000 seconds. Neutron data at lower temperatures show that diffusion can be ruled out as a contributory mechanism to decay. Therefore at deeply supercooled temperatures, <55 K, studied here, diffusion is absent and net molecular rotation, relative to the normal to the film, is the sole cause of secondary relaxation.
Qualitative studies of aging in cis-MF glasses, exploiting the spontelectric effect, have already been described.11 Relevant data are presented here in Fig. 1 and Table 1. In the present work, we place our interpretation of these low-temperature studies, for Td ≤ 55 K, on a firm analytical and quantitative basis. The rate of aging, measured by the rate of decay of surface potential, is observed to decrease with increasing Td, between 40 K and 55 K corresponding to an increasing activation energy for the aging process over this temperature range. This increase may be reproduced by an established theoretical model for the spontelectric state and involves only molecular rotational motion. This generates a striking physical picture, in which low temperature aging occurs through molecules swinging on average through angles of ∼50° from their steady state orientation, in order to effect the secondary aging process.
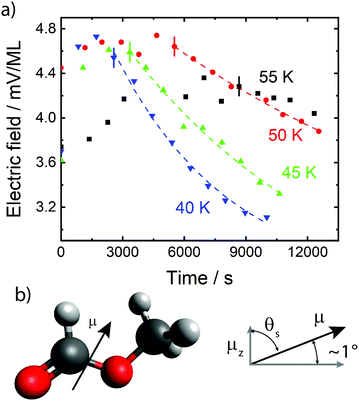 | ||
| Fig. 1 (a) Electric fields per ML in thin films of cis-MF, measured as a function of time, for deposition temperatures, Td, as shown, using the electron beam technique described in the text. Using 1 ML = 0.244 nm,17 maximum fields are ∼2 × 107 V m−1. Offset times described in the main text are indicated with short vertical lines. Dashed lines are exponential fits to the data, yielding activation energies (see text). (b) Schematic indicating the orientation of the dipole moment from negative to positive, μ;, of cis-MF and the definition of μ;z or the positive vector component of the dipole moment pointing towards the film–vacuum interface. | ||
| T d/K | t lag/s | /s−1 | /eV | k 1st/s−1 | E*/eV |
|---|---|---|---|---|---|
| Column 1: deposition temperature. Column 2: lag period before onset of decay of orientation. Column 3: values of the first order decay constant, in s−1, obtained from 1/tlag. Column 4: the activation energy, in eV, associated with the values of rate coefficients in column 3. Column 5: values of the first order decay constant, in s−1, for Espont or, equally, the degree of orientation, 〈μz〉/μ, obtained by fitting to data for decay of orientation in Fig. 1. Column 6: the activation energy, in eV, associated with rotational motion sufficient to lead to decay of orientation. | |||||
| 40 | 2564 | 3.90 × 10−4 | 0.112 | 1.78 × 10−4 | 0.115 |
| 45 | 3348 | 2.98 × 10−4 | 0.127 | 8.94 × 10−5 | 0.132 |
| 50 | 5520 | 1.81 × 10−4 | 0.143 | 5.80 × 10−5 | 0.148 |
| 55 | 8672 | 1.15 × 10−4 | 0.160 | — | — |
Experimental data
The technique of surface potential measurement has been described in detail in ref. 13. Briefly, films of cis-MF were prepared by standard background dosing techniques, on a polycrystalline gold substrate, cooled with a closed-cycle He cryostat. The surface potential was measured by interrogating the film with a low energy electron beam, with an energy resolution of ∼1.5 meV, formed by photoionization of Ar at threshold (78.67 nm), using light from the ASTRID storage ring at Aarhus University. The maximum beam current was 200 fA, to avoid surface charging on the timescale of any experiment. The surface potential was measured by applying a bias potential to the target material and adjusting this bias in order to null the current. The value of the bias yields the potential on the film surface. The onset of current, of 2–3 fA, was detected by an ammeter connected to the back side of the film. Electric fields inferred in cis-MF films, and their time dependence, are shown in Fig. 1, for Td = 40 K, 45 K, 50 K and 55 K. Data are presented in Fig. 1, as a function of time and each data point in Fig. 1a represents a surface potential measurement recorded as the film thickness was increased. Since there are no substrate or epitaxial influences on the spontelectric effect, we do not anticipate any thickness effects.16Analytical model
To progress, we need now to go more deeply into the nature of the spontelectric effect. We define a degree of dipole orientation as the average component of the dipole moment in the z-direction, normal to the plane of the film, divided by the total dipole moment of the species in the solid, that is, 〈μz〉/μ. Components in the x–y plane average to zero.For cis-MF, the positive end of the molecular dipole moment protrudes from the film surface, see Fig. 1b.17 Dipole orientation gives rise to a polarization electric field in the film in the z-direction, Espont, proportional to 〈μz〉/μ. There is no free charge in the system and therefore Espont is constant. The value of Espont is given by the measured surface potential divided by the known thickness of the film.13
A mean-field model for the spontelectric state is described in detail elsewhere.13 We use atomic units throughout. Briefly, the mean field Hamiltonian for the system, HMF, is given by the energy of interaction of the average dipole in an effective field in the film. We write:
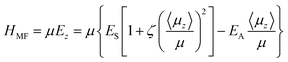 | (1) |
As incoming molecules are added, the film initializes itself in a dipole-oriented configuration, corresponding to a balance between the short range and long-range terms in HMF and thermal agitation. The system is therefore seen as composed of an array of dipoles bathed in a mean field, Ez, with order opposed by thermal motions. This leads to a degree of dipole alignment represented by some value of 〈μz〉/μ, determined by the requirement for consistency of eqn (1) with the standard Langevin equation.18
This analysis yields:
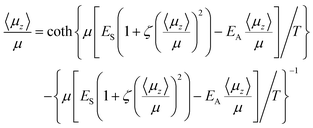 | (2) |
The model embodied in eqn (1) and (2) has been shown to reproduce the values and temperature dependence of observed spontelectric fields in solid films of nitrous oxide, nitrous oxide diluted in xenon, cis-MF and CClxFy (x + y = 4).13,20–22 The model also underpins a description of the observed deposition temperature dependence of Stark shifts in IR spectra of films of N2O,23cis-MF,20 and CO24 and in Stark shifts of Wannier–Mott excitons in vacuum-ultraviolet spectra in solid ammonia films.25 This proving ground for the model involves the constraint that, in the absence of a phase change,22,25 the parameters ES, EA and ζ are independent of Td. In the present case, fitting to experimental values of Espont and 〈μz〉/μ for Td = 40, 45, 50 and 55 K is achieved by relaxing this constraint for ζ. Thus ES and EA are held constant at the values which satisfy data for the variation of spontelectric field and degree of dipole orientation of cis-MF between 57 K and 89–90 K, namely ES = 1.206 × 107 V m−1, EA = 1.148 × 109 V m−1. However ζ is allowed to vary between 40 K and 55 K, and no longer assumes the invariant value of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 assigned by the fit to data between 57 K and 89 K. The parameter ζ governs frustration of molecular rotation within the solid film, and determines, as mentioned, the tendency of orientation to be locked in position. The energy required to overcome this locking is related to the energy barrier to rotational motion. This barrier must be overcome in order for structural relaxation to take place in films with Td ≤ 55 K, shown in Fig. 1, given that loss of polarization arises through collective loss of orientation of the molecular dipoles. A certain temperature dependent proportion of molecules have sufficient energy to rotate through any specified angle. For a great enough angle, we propose that molecules are able to overcome the activation barrier to decay into a less oriented state, where this barrier is a function of Td. Such a decay is governed by an exponential behaviour with time, as observed in Fig. 1. Data yield values of the activation energy barriers as a function of Td, as evaluated below, and given in Table 1. We also show that ζ, essentially measuring the resistance to rotation of any dipole in relation to another, and also a function of Td, (Table 2), must be related to the rate of decay of polarization and, via this, to the associated barriers, in a manner dictated by the spontelectric model outlined above.
500 assigned by the fit to data between 57 K and 89 K. The parameter ζ governs frustration of molecular rotation within the solid film, and determines, as mentioned, the tendency of orientation to be locked in position. The energy required to overcome this locking is related to the energy barrier to rotational motion. This barrier must be overcome in order for structural relaxation to take place in films with Td ≤ 55 K, shown in Fig. 1, given that loss of polarization arises through collective loss of orientation of the molecular dipoles. A certain temperature dependent proportion of molecules have sufficient energy to rotate through any specified angle. For a great enough angle, we propose that molecules are able to overcome the activation barrier to decay into a less oriented state, where this barrier is a function of Td. Such a decay is governed by an exponential behaviour with time, as observed in Fig. 1. Data yield values of the activation energy barriers as a function of Td, as evaluated below, and given in Table 1. We also show that ζ, essentially measuring the resistance to rotation of any dipole in relation to another, and also a function of Td, (Table 2), must be related to the rate of decay of polarization and, via this, to the associated barriers, in a manner dictated by the spontelectric model outlined above.
| T d/K | 〈μ〉/μ | ζ | Angle to plane of film 90° − θS | |θM− θS|lag | |θM− θS| |
|---|---|---|---|---|---|
Column 1: temperature of deposition. Column 2: average degree of orientation in the steady state. Column 3: values of ζ obtained by fitting to values of orientation shown in column 2, using eqn (2). Column 4: average angle of molecules to the plane of the film corresponding to values of 〈μ〉/μ, given by 90° − cos−1〈μ〉/μ = 90° − θS in eqn (3) and (4). Column 5: threshold angular excursions of molecules in the solid film, (Fig. 2 and eqn (4)), calculated to match 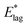 in column 4 of Table 1. The first figure represents excursions in the upper hemisphere and the second in the lower hemisphere, save for ∼1° in the latter, see text. Column 6: threshold angular excursions of molecules in the solid film, (Fig. 2 and eqn (4)) representing the gateway to secondary decay, calculated to match E*; in column 6 of Table 1. in column 4 of Table 1. The first figure represents excursions in the upper hemisphere and the second in the lower hemisphere, save for ∼1° in the latter, see text. Column 6: threshold angular excursions of molecules in the solid film, (Fig. 2 and eqn (4)) representing the gateway to secondary decay, calculated to match E*; in column 6 of Table 1. |
|||||
| 40 | 0.01846 | 8532 | 1.057° | 50.4°, 51.6° | 51. 5°, 52.6° |
| 45 | 0.01758 | 9635 | 1.007° | 50.6°, 51.7° | 51.7°, 52.8° |
| 50 | 0.01804 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275 275 |
1.034° | 51.8°, 53.0° | 53.1°, 54.3° |
| 55 | 0.01523 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
0.873° | 49.9°, 51.0° | — |
Understanding the variation of the spontelectric field vs. time
The data in Fig. 1 show that at early times, molecules reorganize to increase the degree of dipole orientation, 〈μz〉/μ. Whilst the system feels its way through configuration space towards some critical configuration leading to decay, there is a ∼30% increase in 〈μz〉/μ. Orientation then settles down to a maximum value, which is maintained for ∼1000 seconds for Td = 40 K up to ∼4000 seconds for Td = 55 K. Following a total time after the beginning of the experiment, tlag, the orientation decays. The inverse of tlag is taken as the rate coefficient for attainment of a gateway to decay, as we describe below.We now set out to estimate the activation energy barriers to rotational motion from our experimental data. We calculate the barrier to overcome molecular locking for each film separately, where each film in Fig. 1, with its distinct Td, is treated as a separate system. There are two independent sources for activation energies, the values of tlag and the measured rate coefficients of decay (Fig. 1 and Table 1). Values of tlag and its inverse are shown in columns 2 and 3 of Table 1. We express 1/tlag as 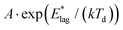 . The standard interpretation of the pre-exponential factor, A, is of a frequency factor representing the number of attempts, unhindered by an energy barrier, to perform the relevant process. Since we deal here with rotation, we have chosen A to be 5 × 1010 s−1, based upon a period of free rotation of MF estimated from values of the moment of inertia and rotational constants.26 In this connection, systematic errors in values of
. The standard interpretation of the pre-exponential factor, A, is of a frequency factor representing the number of attempts, unhindered by an energy barrier, to perform the relevant process. Since we deal here with rotation, we have chosen A to be 5 × 1010 s−1, based upon a period of free rotation of MF estimated from values of the moment of inertia and rotational constants.26 In this connection, systematic errors in values of 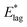 , while dominated by uncertainty in A, turn out to be somewhat insensitive to the choice of A. For example A = 5 × 1012 s−1, a figure more appropriate to a vibrationally driven system, would yield values of
, while dominated by uncertainty in A, turn out to be somewhat insensitive to the choice of A. For example A = 5 × 1012 s−1, a figure more appropriate to a vibrationally driven system, would yield values of 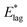 which are only 12% larger.
which are only 12% larger.
Turning to the second source of values of activation energy, data showing decay of orientation in Fig. 1 have been fit using Espont(t) = Espont(t0)·exp(−t/τ) + a constant, the latter value discussed below. Here, t is the elapsed time after tlag, Espont(t0) is the spontelectric field at the time of the start of decay, and τ is the decay constant, used to calculate the first order rate coefficient for the exponential decay process. We did attempt to fit the data with stretched exponentials, following Espont(t) = Espont(t0)·exp(−t/τ)β + a constant, as dynamics in supercooled glasses usually follow a stretched function, but these fits resulted in β values very close to 1. Hence, we used the normal exponential function to fit the data, meaning β = 1 throughout. This may be related to the short timescales over which aging is reported here.31 The resulting fits are shown as dashed lines in Fig. 1 and relevant values are shown in Table 1, column 5. The corresponding values of E*, shown in column 6 follow directly, where we have assumed the same pre-exponential factor of 5 × 1010 s−1, as above. Note that we have not fitted the data for 55 K, since results, while showing decay, are insufficient to ascribe a reliable value of k1st.
We suggest that the lag time before decay of orientation arises through essentially similar, though not identical, physical processes to the decay itself. There is a clear tendency for the rate coefficients associated with the lag time to be larger than those for decay, by factors of 2.19, 3.33 and 3.12 for 40 K, 45 K and 50 K respectively. This is reflected in the differences in E* arising in the two sets of data in Table 1. These results support the hypothesis that dynamical events associated with the search for candidate configurations, which seed decay, and the mechanism of decay itself, follow similar but not identical pathways.
The electric fields in Fig. 1 do not decay to zero but rather to a constant value, as just noted. We find that the residual fields, at long time, average to 2.3 ± 0.3 mV per ML. Given that the layer spacing, s, is 0.244 nm,13 this is equivalent to a residual spontelectric field of 9.2 ± 1.2 × 106 V m−1 and, recalling that Espont = 〈μz〉/μ〈EA〉, using EA = 1.148 × 109 V m−1, the residual orientation is 0.008. This is equivalent to an average angle to the horizontal plane of the film for a cis-MF molecular dipole of 0.46°. This may be compared to the steady-state angles to the horizontal, 90° − θS, before decay, in Table 2, column 4, of 1.057°, 1.007°, 1.034° and 0.873° for 40 K, 45 K, 50 K and 55 K respectively, where θ is given by cos−1〈μz〉/μ.
We now seek to make contact with the spontelectric model by establishing the relationship between activation energies 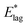 , E*; and ζ. The torque on an average molecule, displaced from its steady state angle, θS, is proportional to the angular acceleration via the molecular moment of inertia, I. This torque is due to the net electric field on the dipole, given by the difference between Ez (eqn (1)) for 〈μz〉/μ in the steady state and that engendered by some arbitrary rotation through an angle |θ − θS|. Thus the angular acceleration, Q, becomes (μ;/I)[Ez(θ)sin
, E*; and ζ. The torque on an average molecule, displaced from its steady state angle, θS, is proportional to the angular acceleration via the molecular moment of inertia, I. This torque is due to the net electric field on the dipole, given by the difference between Ez (eqn (1)) for 〈μz〉/μ in the steady state and that engendered by some arbitrary rotation through an angle |θ − θS|. Thus the angular acceleration, Q, becomes (μ;/I)[Ez(θ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ; − Ez(θS)sin
θ; − Ez(θS)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θS] and the work done by the dipole against the field, that is, the energy required to achieve an angular displacement |θ; − θS|, may be written as the integral of Q·I over θ. Using eqn (1) and cos−1〈μz〉/μ = θ, the product Q·I is given by
θS] and the work done by the dipole against the field, that is, the energy required to achieve an angular displacement |θ; − θS|, may be written as the integral of Q·I over θ. Using eqn (1) and cos−1〈μz〉/μ = θ, the product Q·I is given by
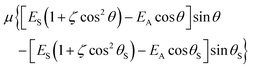 | (3) |
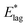 or E* in Table 1. Essentially, we propose that configurations associated with θM become the gateway to subsequent decay of the orientation, within the glassy structure, to some new value of orientation, the events reflected in the data in Fig. 1. Thus every molecule which undergoes angular motion |θM− θS| ultimately undergoes decay of orientation. In this model, a specific physical environment is associated with secondary decay. This carries with it the requirement that values of |θM− θS| should be very similar for different values of Td. This is based on the very similar average orientations for Td between 40 K and 55 K, which requires that the average environment of any species changes little over this temperature range.
or E* in Table 1. Essentially, we propose that configurations associated with θM become the gateway to subsequent decay of the orientation, within the glassy structure, to some new value of orientation, the events reflected in the data in Fig. 1. Thus every molecule which undergoes angular motion |θM− θS| ultimately undergoes decay of orientation. In this model, a specific physical environment is associated with secondary decay. This carries with it the requirement that values of |θM− θS| should be very similar for different values of Td. This is based on the very similar average orientations for Td between 40 K and 55 K, which requires that the average environment of any species changes little over this temperature range.
The definite integral of (3), equal to 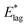 or E*, may be written:
or E*, may be written:
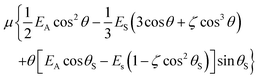 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275 (Table 2), as illustrative examples. Given a desired value of activation energy, or work expended, on the vertical axis, one may read off the corresponding rotation angle from values on the horizontal axis. In Fig. 2, a molecule oriented in the plane of the film is represented by 90° and thus a 50° twist corresponds to an angle on the horizontal axis of Fig. 2 of 40° or 140°. These latter values can be seen by inspection to correspond to values of activation energy for 40 K and 50 K in Table 1.
275 (Table 2), as illustrative examples. Given a desired value of activation energy, or work expended, on the vertical axis, one may read off the corresponding rotation angle from values on the horizontal axis. In Fig. 2, a molecule oriented in the plane of the film is represented by 90° and thus a 50° twist corresponds to an angle on the horizontal axis of Fig. 2 of 40° or 140°. These latter values can be seen by inspection to correspond to values of activation energy for 40 K and 50 K in Table 1.
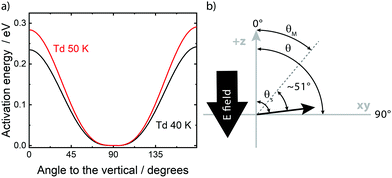 | ||
| Fig. 2 (a) The activation energy per eV as a function of the angle to the vertical, θM, of a cis-MF moiety in the glassy solid, expressed in degrees, with 90° representing the plane of the film. The upper curve, red, is for films with Td = 50 K and the lower, black, for Td = 40 K. Results in Table 2 suggest rotation through ±∼51°, from an initial value, 90° − θS of ∼1°, in either sense. Thus the observed activation energies (Table 1) translate into an angle of ca. 40° or 140° (Table 2). See text for details. (b) Schematic illustration defining the angles described in the text. | ||
Angular motions are the result of random fluctuations in the environment of any species and may occur in either sense. There is some small asymmetry around θS, arising from the form of eqn (3), since molecules are at an average angle of ∼1° to the plane of the film. Excursions involving purely the upper hemisphere require marginally lower |θM− θS|, such that the energy change equals any specified value. This arises since the direction of the dipole relative to the spontelectric field reverses as the molecule rotates through the plane of the film. Thus, net resistance to angular motion is a little greater in upper hemisphere motion. This gives rise to two sets of values of |θM− θS|, in columns 5 and 6 of Table 2, representing the slightly asymmetrical nature of the motion.
Table 2 shows values of |θM− θS| derived from both 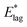 derived from values of tlag, and E*;, derived from the decays shown in Fig. 1. Results demonstrate that values of |θM− θS| are indeed very similar for different values of Td, as the model requires. In Fig. 3a and b, we compare observed and predicted values of
derived from values of tlag, and E*;, derived from the decays shown in Fig. 1. Results demonstrate that values of |θM− θS| are indeed very similar for different values of Td, as the model requires. In Fig. 3a and b, we compare observed and predicted values of 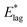 and E*;, respectively. Results demonstrate how the spontelectric model may reproduce the temperature dependence of energy barriers for the secondary relaxation process in this glassy material. This provides a quantitative affirmation that the secondary aging process arises through rotation of constituent molecules about their fixed positions.
and E*;, respectively. Results demonstrate how the spontelectric model may reproduce the temperature dependence of energy barriers for the secondary relaxation process in this glassy material. This provides a quantitative affirmation that the secondary aging process arises through rotation of constituent molecules about their fixed positions.
 | ||
Fig. 3 (a) Black points: values of 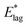 , (eV), Table 1, column 4, derived from tlag. Red points: values of , (eV), Table 1, column 4, derived from tlag. Red points: values of 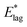 , determined from eqn (4), corresponding to an average value of upper hemisphere rotation of 50.7°, column 6, Table 2. Error bars in the experimental values of , determined from eqn (4), corresponding to an average value of upper hemisphere rotation of 50.7°, column 6, Table 2. Error bars in the experimental values of 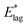 arise from uncertainties in the estimation of the lag time. Error bars in the calculated values of arise from uncertainties in the estimation of the lag time. Error bars in the calculated values of 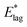 are those associated with random errors in parameters in eqn (1)–(4), that is, ES, EA, ζ, θS and θM. (b) Blue points: values of E*, (eV), Table 1, column 6. Green points: values of E*, determined from eqn (4), corresponding to an average upper hemisphere values of 52.1° from |θM− θS| derived from values in column 5 of Table 2. Error bars in the experimental values of E* arise from uncertainties in the fits shown in Fig. 1. Error bars in the calculated values of E*;: as in (a). are those associated with random errors in parameters in eqn (1)–(4), that is, ES, EA, ζ, θS and θM. (b) Blue points: values of E*, (eV), Table 1, column 6. Green points: values of E*, determined from eqn (4), corresponding to an average upper hemisphere values of 52.1° from |θM− θS| derived from values in column 5 of Table 2. Error bars in the experimental values of E* arise from uncertainties in the fits shown in Fig. 1. Error bars in the calculated values of E*;: as in (a). | ||
We also note that higher values of Td (>55 K) may be fit individually with specific values of ζ, to yield larger values for the lag in decay or time constants for the decay of the spontelectric field in cis-MF. For example at Td = 60 K, ζ = 1.77 × 104 fits experimental measurement of the spontelectric field precisely, rather than the global vale of 1.45 × 104 used to fit all higher temperature data. A value of ζ = 1.77 × 104 gives E*; = 0.248 eV and a rate coefficient for decay of 8 × 10−11 s−1, a factor of 4 × 10−5 times smaller than that for 50 K. Moving to 65 K, matching both the spontelectric field and the degree of orientation involves ζ = 2.2 × 104 and yields decay rates of the order of 10−14 s−1 to 10−15 s−1. Thus, our results are consistent with the observation that films are essentially stable for Td ≥ 60 K.
Discussion
The above analysis, for Td ≪ Tg, yields an image of molecules of cis-MF which, at any time, have some probability of leaking, through angular excursions of |θM − θS|, into an unstable configuration. This configuration becomes a gateway to subsequent decay of dipole orientation. Only a very tiny fraction of the total number of rotational motions, per second per molecule, achieve this large displacement angle of >50°, necessary for decay of polarization. The fraction of angular excursions which lead to decay of dipole orientation is of the order of k1st/A lying between ∼2 × 10−15 at Td = 40 K and ∼6 × 10−16 at Td = 50 K, given a pre-exponential factor A = 5 × 1010 s−1. Moreover, this secondary process of decay, in contrast to the primary process, which is found above 80 K,11 does not remove the alignment altogether. Rather, it establishes a new, more weakly polarized spontelectric state, decaying from an initial value of ∼2.3 × 107 V m−1 to a field of ∼8 × 106 V m−1, as estimated above.We note that the spontelectric model involves feedback between all the species in a film, through which each species talks to every other, via the spontelectric field permeating the medium. Thus the secondary relaxation mechanism propagates through the film, rendering it homogeneous on the timescale of the decay of the orientation. All molecules relax effectively as one, percolating through the potential landscape together, although any secondary relaxation mechanism may be initiated locally. The small but consistent differences in activation energy barriers measured using the lag time and the decay rate for the spontelectric field (Table 1) may help to clarify the process of relaxation. Local initiation of aging should occur via the lowest energy barrier, assessed experimentally using the lag times to field decay while the barrier to homogeneous rendering of the field decay on a global scale may be better assessed through the exponential rate of field decay.
We have found above that ζ is larger at higher values of Td (Table 1), indicating that rotational motion is effectively more hindered at higher Td. Rates of decay of molecular orientation are correspondingly lower at higher Td, cutting through the normal expectation that rates of thermally activated processes will increase at higher temperatures. This feature highlights a fundamental difference between an organized crystal structure and a glass. The potential landscape of a glass is of a large number of wells with a broad distribution of depths, separated by energy barriers with a distribution of heights. Locally, a structure may reside in any of these wells. As Td progresses from 40 K to 55 K, so molecules explore more of this space as the glass forms and they can therefore come to occupy deeper wells. Thus barriers blocking molecular rotations, 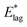 or E*;, are higher for higher Td, as shown explicitly in Table 1, resulting in slower secondary relaxation. Still more stable films, formed at higher Td, do not undergo observable secondary relaxation, in agreement with our estimates for Td = 60 K or 65 K. Films laid down at higher temperature than 55 K have relaxed during growth and species already reside in deeper wells, such that decay is not detectable on laboratory timescales.
or E*;, are higher for higher Td, as shown explicitly in Table 1, resulting in slower secondary relaxation. Still more stable films, formed at higher Td, do not undergo observable secondary relaxation, in agreement with our estimates for Td = 60 K or 65 K. Films laid down at higher temperature than 55 K have relaxed during growth and species already reside in deeper wells, such that decay is not detectable on laboratory timescales.
Our observations are in accord with the formation of ‘ultra-stable’ glasses, as distinct from ordinary glasses. These have been observed to form if Td falls within a critical temperature window, when grown, as here, via deposition from the gas phase. This window has been reported to lie between 0.8 to 0.91Tg.8,27–30 Here we find that the critical window for ultra-stable cis-MF glasses lies between 60 K and 75 K, that is, 0.66Tg to 0.83Tg with Tg = 90 K. In this connection, neutron scattering experiments11 show that molecular diffusion increases in rate as Td approaches Tg. Dipole ordering is not possible in the material that results from either deposition or annealing above 90 K.13 Neutron reflectivity data demonstrated that molecular translation, and accompanying rotation, and, in the case of cis-MF, that crystallisation are the mechanisms by which films depolarise when Td approaches Tg,11 giving a qualitative image of the physics underlying the Curie effect in spontelectrics. The present work complements this in showing that secondary relaxation takes place, at lower temperature, through molecular rotation, without translational motion.
Conclusions
The key message of the current work is that the depolarisation in spontelectric cis-MF is a proxy for the secondary relaxation mechanism for glassy solids, occurring at temperatures tens of degrees below the glass transition temperature. Decay of the spontelectric field acts as a probe of molecular dynamics, showing how films with Td < 60 K relax to a more stable glass through molecular rotation on timescales of hours, while films with Td ≥ 60 K are stable.Author contributions
AC designed the experiments, collected data, and performed data analysis on SP measurements; DF performed analysis on the SP data using the analytical model; AG, VL, MJ and OP collected data. All authors contributed to drafting the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AC and MRVJ are grateful for the support of the Danish National Research Foundation (Center for Interstellar Catalysis, DNRF150 and Center for Materials Crystallography, DNRF93 respectively). We thank the Danish Agency for Science, Technology and Innovation for funding the instrument centre DanScatt. This research is supported by the experiment that used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory.Notes and references
- M. Micoulaut, Relaxation and physical aging in network glasses: a review, Rep. Prog. Phys., 2016, 79, 066504 CrossRef PubMed.
- S. R. Forrest and M. E. Thompson, Introduction:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Organic Electronics and Optoelectronics, Chem. Rev., 2007, 107, 923–925 CrossRef CAS.
Organic Electronics and Optoelectronics, Chem. Rev., 2007, 107, 923–925 CrossRef CAS. - G. Tan, F. Wu, C. Zhan, J. Wang, D. Mu, J. Lu and K. Amine, Solid-State Li-Ion Batteries Using Fast, Stable, Glassy Nanocomposite Electrolytes for Good Safety and Long Cycle-Life, Nano Lett., 2016, 16, 1960–1968 CrossRef CAS PubMed.
- W. Brütting, S. Berleb and A. G. Mückl, Device physics of organic light-emitting diodes based on molecular materials, Org. Electron., 2001, 2, 1–36 CrossRef.
- M. Alomari, F. H. Mohamed, A. W. Basit and S. Gaisford, Personalised dosing: Printing a dose of one's own medicine, Int. J. Pharm., 2015, 494, 568–577 CrossRef CAS PubMed.
- E. S. Zarie, V. Kaidas, D. Gedamu, Y. K. Mishra, R. Adelung, F. H. Furkert, R. Scherließ, H. Steckel and B. Groessner-Schreiber, Solvent Free Fabrication of Micro and Nanostructured Drug Coatings by Thermal Evaporation for Controlled Release and Increased Effects, PLoS One, 2012, 7, e40746 CrossRef CAS PubMed.
- J. D. Stevenson and P. G. Wolynes, A universal origin for secondary relaxations in supercooled liquids and structural glasses, Nat. Phys., 2010, 6, 62–68 Search PubMed.
- H. B. Yu, M. Tylinski, A. Guiseppi-Elie, M. D. Ediger and R. Richert, Suppression of β;-Relaxation in Vapor-Deposited Ultrastable Glasses, Phys. Rev. Lett., 2015, 115, 185501 CrossRef CAS PubMed.
- E. Ma, Tuning order in disorder, Nat. Mater., 2015, 14, 547–552 CrossRef CAS PubMed.
- Q. Yang, S.-X. Peng, Z. Wang and H.-B. Yu, Shadow glass transition as a thermodynamic signature of β; relaxation in hyper-quenched metallic glasses, Nat. Sci. Rev., 2020, 7, 1896–1905 CrossRef CAS.
- A. Cassidy, M. R. V. Jørgensen, A. Glavic, V. Lauter, O. Plekan and D. Field, A mechanism for ageing in a deeply supercooled molecular glass, Chem. Commun., 2021, 57, 6368–6371 RSC.
- R. Balog, P. Cicman, N. C. Jones and D. Field, Spontaneous Dipole Alignment in Films of N2O, Phys. Rev. Lett., 2009, 102, 073003 CrossRef PubMed.
- D. Field, O. Plekan, A. Cassidy, R. Balog, N. C. Jones and J. Dunger, Spontaneous electric fields in solid films: spontelectrics, Int. Rev. Phys. Chem., 2013, 32, 345–392 Search PubMed.
- O. Plekan, A. Cassidy, R. Balog, N. C. Jones and D. Field, A new form of spontaneously polarized material, Phys. Chem. Chem. Phys., 2011, 13, 21035–21044 RSC.
- I. K. Gavra, A. N. Pilidi and A. A. Tsekouras, Spontaneous polarization of vapor-deposited 1-butanol films and its dependence on temperature, J. Chem. Phys., 2017, 146, 104701 CrossRef PubMed.
- A. Cassidy, O. Plekan, R. Balog, J. Dunger, D. Field and N. C. Jones, Electric Field Structures in Thin Films: Formation and Properties, J. Phys. Chem. A, 2014, 118, 6615–6621 CrossRef CAS PubMed.
- O. Plekan, A. Cassidy, R. Balog, N. C. Jones and D. Field, Spontaneous electric fields in films of cis-methyl formate, Phys. Chem. Chem. Phys., 2012, 14, 9972–9976 RSC.
- C. Kittel, Introduction to Solid State Physics, Wiley India Pvt. Limited, 7th edn, 2007 Search PubMed.
- S. A. Blair and A. J. Thakkar, Relating polarizability to volume, ionization energy, electronegativity, hardness, moments of momentum, and other molecular properties, J. Chem. Phys., 2014, 141, 074306 CrossRef PubMed.
- M. Roman, S. Taj, M. Gutowski, M. R. S. McCoustra, A. C. Dunn, Z. G. Keolopile, A. Rosu-Finsen, A. M. Cassidy and D. Field, Non-linear and non-local behaviour in spontaneously electrical solids, Phys. Chem. Chem. Phys., 2018, 20, 5112–5116 RSC.
- A. Cassidy, O. Plekan, J. Dunger, R. Balog, N. C. Jones, J. Lasne, A. Rosu-Finsen, M. R. S. McCoustra and D. Field, Investigations into the nature of spontelectrics: nitrous oxide diluted in xenon, Phys. Chem. Chem. Phys., 2014, 16, 23843–23853 RSC.
- A. Cassidy, M. R. V. Jørgensen, A. Rosu-Finsen, J. Lasne, J. H. Jørgensen, A. Glavic, V. Lauter, B. B. Iversen, M. R. S. McCoustra and D. Field, Dipole-Oriented Molecular Solids Can Undergo a Phase Change and Still Maintain Electrical Polarization, J. Phys. Chem. C, 2016, 120, 24130–24136 CrossRef CAS.
- J. Lasne, A. Rosu-Finsen, A. Cassidy, M. R. S. McCoustra and D. Field, Spontaneously electrical solids in a new light, Phys. Chem. Chem. Phys., 2015, 17, 20971–20980 RSC.
- J. Lasne, A. Rosu-Finsen, A. Cassidy, M. R. S. McCoustra and D. Field, Spontaneous electric fields in solid carbon monoxide, Phys. Chem. Chem. Phys., 2015, 17, 30177–30187 RSC.
- A. Cassidy, R. L. James, A. Dawes and D. Field, Crystallites and Electric Fields in Solid Ammonia, ChemistryOpen, 2020, 9, 983–990 CrossRef CAS PubMed.
- J. Demaison, L. Margulès, I. Kleiner and A. G. Császár, Equilibrium structure in the presence of internal rotation: A case study of cis-methyl formate, J. Mol. Spectrosc., 2010, 259, 70–79 CrossRef CAS.
- K. Ishii and H. Nakayama, Structural relaxation of vapor-deposited molecular glasses and supercooled liquids, Phys. Chem. Chem. Phys., 2014, 16, 12073–12092 RSC.
- K. L. Ngai, L.-M. Wang and H.-B. Yu, Relating Ultrastable Glass Formation to Enhanced Surface Diffusion via the Johari–Goldstein β;-Relaxation in Molecular Glasses, J. Phys. Chem. Lett., 2017, 8, 2739–2744 CrossRef CAS PubMed.
- Y. Z. Chua, M. Tylinski, S. Tatsumi, M. D. Ediger and C. Schick, Glass transition and stable glass formation of tetrachloromethane, J. Chem. Phys., 2016, 144, 244503 CrossRef CAS PubMed.
- S. F. Swallen, K. L. Kearns, M. K. Mapes, Y. S. Kim, R. J. McMahon, M. D. Ediger, T. Wu, L. Yu and S. Satija, Organic Glasses with Exceptional Thermodynamic and Kinetic Stability, Science, 2007, 315, 353–356 CrossRef CAS PubMed.
- Z. W. Wu, W. Kob, W. H. Wang and L. Xu, Stretched and compressed exponentials in the relaxation dynamics of a metallic glass-forming melt, Nat. Commun., 2018, 9, 5334 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |