Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ionisation of PF3: absolute partial electron ionisation cross sections and the formation and reactivity of dication states†
Lilian K.
Ellis-Gibbings
 *a,
William G.
Fortune
*a,
William G.
Fortune
 a,
Bridgette
Cooper
a,
Bridgette
Cooper
 b,
Jonathan
Tennyson
b,
Jonathan
Tennyson
 b and
Stephen D.
Price
b and
Stephen D.
Price
 *a
*a
aDepartment of Chemistry, University College London, London WC1H 0AJ, UK. E-mail: l.ellis-gibbings@ucl.ac.uk; s.d.price@ucl.ac.uk
bDepartment of Physics and Astronomy, University College London, London WC1E 6BT, UK
First published on 26th April 2021
Abstract
Absolute partial electron ionisation cross sections, and precursor-specific partial electron ionisation cross sections, for the formation of cations from phosphorus trifluoride (PF3) are reported over the electron energy range 50–200 eV. The absolute values are determined by the measurement of cross sections relative to the formation of PF3+ using 2D ion–ion coincidence time-of-flight mass spectrometry and subsequent scaling using binary encounter-Bethe calculations of the total ionisation cross section. This new dataset significantly augments the partial ionisation cross sections for electron ionization of PF3 found in literature, addressing previous discrepancies in the branching ratios of product ions, and provides the first values for the precursor-specific cross sections. Comparisons to calculated cross sections from the literature are encouraging, although there are discrepancies for individual ions. The coincidence experiments indicate that double and triple ionisation generate approximately 20% of the cationic ionisation products at 200 eV electron energy. One dissociative dication state, dissociating to PF2+ + F+, is clearly identified as the lowest triplet state of PF32+ and five different dications (PF32+, PF22+, PF2+, P2+ and F2+) are detected in the mass spectra. The dication energetics revealed by the experiments are supported by a computational investigation of the dication's electronic structure. The cross sections reported will allow more accurate modelling of the role of the ionization of PF3 in energetic environments. A first investigation of the bimolecular reactivity of metastable states of PF32+ is also reported. In collisions with Ar, O2 and CO dissociative single electron transfer dominates the product ion yield, whereas collision-induced dissociation of the dication is important following collisions with Ne. Consideration of the energetics of these processes indicates that the reactant dication beam contains ions in both the ground singlet state and the first excited triplet state. The deduction regarding the longevity of the triplet state is supported by metastable signals in the coincidence spectra. Weak signals corresponding to the formation of ArF+ are detected following PF32+ collisions with Ar, and experimental and computational considerations indicate this new chemical bond is formed via a collision complex.
1 Introduction
Phosphorus trifluoride (PF3) is a molecule commonly used both in research laboratories and in industry, with particular applications in metal–ligand chemistry.1,2 In addition, phosphorus and fluorine containing compounds are often used in plasma-assisted surface modification3 and PF+ and PF2+ have both been investigated for their contributions to the chemistry in interstellar clouds.4 Thus, the electron ionisation, and subsequent fragmentation, of PF3 are of interest to both materials chemists and astrochemists. Previous studies have revealed significant ion yields involving chemical bond formation following collisions between fluorinated dications and neutral molecules,5–9 and so the potential formation of long-lived dications following electron ionisation of PF3, as investigated in this study, could therefore allow access to new bond-forming ion chemistry.The ionisation and subsequent chemistry of PF3 in electron-rich environments can only be well-modelled if there is an understanding of the ionic electronic states populated and reliable cross sections are available to characterize their formation and behaviour. Indeed, electron ionisation of molecules, and the production of cations, have long been recognised as a primary route for the formation of plasmas,10 dose deposition in radiotherapy,11 and the formation of species in planetary atmospheres12 and the interstellar medium.13 Generating usable and reliable partial ionisation cross sections to characterize the consequences of electron ionisation of PF3, and qualitative data exploring the properties of the dications formed following multiple ionisation of this molecule, are the aims of this study.
The yield of cations following a given electron-molecule collision is quantified by the total ionisation cross section, which is a function of the incident electron energy. Partial ionisation cross sections (PICS) involve a decomposition of the total ionisation cross section into cross sections for forming individual product ions. PICS allow, for example, modelling of the abundance of different ions in electron rich environments. Precursor-specific partial ionisation cross sections (PS-PICS) quantify the proclivity for forming an individual ion via a given level of ionisation (single, double, triple,…) as a function of electron energy. Data on relative, and in some cases absolute, PS-PICS have been extracted from experiment for several molecules.14–17 However, in the electron collision energy range of concern in this paper (50–200 eV) there have been a limited number of computational approaches to generating PICS or PS-PICS for complex molecules, and certainly no established algorithms are available to the non-specialist.18–22 In this paper we recognise that relative PICS and PS-PICS are relatively routine to measure experimentally with the appropriate apparatus, whilst total ionisation cross sections can be calculated robustly and routinely. Hence, we present a route to generating absolute PICS and PS-PICS, important data for modellers, by developing a methodology for placing the experimental relative cross sections on an absolute scale using a computational determination of the total ionisation cross section. We apply this approach in a study of the electron ionisation of PF3.
Previous studies of electron scattering from PF3 have included the calculation of the total elastic and total inelastic (ionisation and excitation) cross sections (0.15 to 5000 eV),23 measurement and calculation of elastic differential cross sections between 2.0–200 eV,24 measurement and calculation of integral and differential vibrational cross sections (2.0-10 eV),25 measurement of ion appearance energies and relative ion intensities at 70 eV,26,27 measurement of experimental absolute total scattering cross sections (0.5 to 370 eV)28 and calculations of partial differential ionisation cross sections at 100 eV and 200 eV.29 Photoionisation of PF3 has also been investigated.30 Of particular relevance to the cross sections determined in the current study are the theoretical studies of Vinodkumar et al.23 and Kumar.29 Vinodkumar et al.,23 over the energy range 15–5000 eV, used the spherical complex optical potential (SCOP) method to calculate various elastic and inelastic cross sections, including the total ionisation cross section of PF3. Kumar29 used the Jain–Khare semi-empirical approach to calculate partial ionisation cross sections for the production of cations from ionisation of PF3 at electron energies from threshold to 1000 eV.
This paper reports values of the PICS and PS-PICS for PF3 following electron ionisation (50–200 eV). Coincidence mass spectrometry measurements provide relative PICS as well as relative PS-PICS.17 The binary encounter Bethe (BEB) method is then used to calculate the absolute total ionisation cross section of PF3, to which the experimental relative cross sections are then robustly normalized. For molecules where an experimental determination of the absolute total ionisation cross section is available, a normalization of relative experimental PICS with the absolute total ionisation cross section to yield absolute PICS (the nomenclature commonly used for these scaled experimental data, and adopted here) has been performed in the past.31,32 However, the procedure illustrated in this paper, exploiting the modern computational facility to determine robust total ionisation cross sections routinely, allows the extension of this scaling procedure to larger and more reactive/unstable species; these species are often those of interest in many energised environments. In addition, this work extends this procedure to generate absolute values for the PS-PICS as well as the PICS.
2 Methodology
2.1 Experimental details
Relative PICS and PS-PICS are determined from coincidence mass spectrometry experiments. The coincidence time-of-flight mass spectrometer (TOF-MS) used in these experiments has been described in detail before,15,33 and is of the Wiley–McLaren design.34 Ions are formed in the, initially field-free, source region of the TOF-MS, at the intersection of a pulsed electron beam and an effusive gas jet. The gas jet and the electron beam are oriented in a mutually perpendicular arrangement and both are perpendicular to the principal axis of the TOF-MS. The electron pulses are 30 ns long and have a frequency of 50 kHz. The energy calibration and spread of the electron beam is determined via calibration to the Ar double ionisation threshold, giving an observed kinetic energy spread of ∼0.5 eV. An effusive flow of PF3 is introduced into the experiment via a hypodermic needle, giving a typical pressure of 10−6 torr in the vacuum chamber as recorded via an ion gauge. Following the passage of the electron pulse across the source region, a pulser applies a voltage to the repeller plate of the TOF-MS, accelerating cations into the second (acceleration) field of the MS and then on into the drift tube. Ions with a kinetic energy up to 11.5 eV perpendicular to the TOF axis will hit, and are detected by, a microchannel plate stack at the end of the drift tube. As most dicationic kinetic energy releases are less than 9 eV in total,35 the vast majority of monocation pairs formed by dicationic fragmentations are collected. The arrival times of ions at the detector are recorded by a time to digital converter (TDC), started by the application of the voltage to the repeller plate. The TDC is capable of recording multiple “stop” signals for an individual electron pulse. These arrival times are classified as one of: (i) single ion detections, (ii) pairs or (iii) triples of ions. As has been discussed before in the literature,36 extraction of relative PS-PICS from these coincidence data requires the ion detection efficiency of the apparatus. The detection efficiency is determined via recording reference spectra of CF4 for which PS-PICS are available.16,37 The relative PICS we determine from our dataset do not depend on the ion detection efficiency.38 At least three sets of experiments, generating three determinations of the relative PICS and PS-PICS, are carried out at each incident electron energy with the results then averaged. Each experiment lasts 6–8 hours and involves approximately 109 data acquisition cycles.Bimolecular reactions of the parent dication PF32+ with target gases Ar, Ne, CO, and O2 have been investigated in a separate crossed-beam apparatus. These experiments identify collision products, and provide information on relative reaction cross sections, at selected collision energies. The operation of this experiment has been described in detail in the literature.39,40 In brief, ions are generated from PF3 in a purpose built low-pressure ion source. Here, electron collisions (200 eV) with the precursor molecule generate the full range of ionised species (parent ions and fragments). The pressure in the source is closely controlled and maintained at a low enough pressure to minimize dication losses due to collisions with neutral species. Ions from the source are accelerated into a velocity filter (crossed electric and magnetic fields) where the dication projectile is selected by its m/z value. The purity of the resulting beam is >99% with minimal contamination from other ions which are weakly transmitted by the mass filter. The selected projectile ion (PF32+ in this study) is then electrostatically decelerated to the desired laboratory collision energy (4 V [8 eV] in the lab frame). The selected and decelerated ion beam is crossed perpendicularly with an effusive gas jet of the target gas in the collision region of the experiment. The pressure in the collision region is also carefully controlled to maintain single collision conditions, with pressures below 5 × 10−6 torr as measured by an ion gauge remote from the collision region. The charged collision products are periodically accelerated from the collision region, perpendicular to the direction of the dication beam, into a TOF-MS by applying an appropriate voltage across the collision region. At the end of the TOF-MS the ions extracted are detected by a multichannel plate detector.
To ensure spectra are able to distinguish between the products of the desired collisions and those with any background gas in the vacuum chamber, or any products from the metastable decay of the projectile dication, spectra are recorded both with and without the collision gas present.41 This procedure involves subtracting the appropriately normalized contribution from a series (at least two) of “gas-off” spectra from the relative ion intensities from interspersed (again at least two) “gas on” spectra to give values for the corrected relative product ion intensities at a given collision energy. At least three such determinations are performed at each collision energy for each collision gas. The standard deviations of the individual relative ion intensities across each determination are used in further error processing.
The determination of accurate relative product ion intensities from the above spectra is complicated by the variation in the velocity of the different product ions in the direction of the dication beam, transverse to the TOF axis.42 As noted above, the dication beam is directed perpendicular to the principal axis of the TOF and as such the velocity of the detected ions in the direction of the dication beam translates into a velocity transverse to the axis of the TOF. The more translationally energetic the ion the smaller the volume of the collision region that is imaged onto the TOF-MS detector, resulting in differences in the detection efficiency of different ions as a function of their velocity. In an extension of the procedure used to correct for these discrimination effects,42 a SimIon43 simulation of the extraction region and TOF system allows an assessment of this geometric discrimination as a function of ion velocity. This simulation assumes dication and product beam diameters of 4 mm, as determined from previous simulations of the beam path. Testing shows increasing or decreasing this diameter by 1 mm changes the final cross section by up to 8% across the collision energy range used here, and this has been included in our estimate of the uncertainties of the relative intensities. The lengths of the cylindrical volumes of the dication and product beams extracted onto the MCP, and hence the relative detection efficiencies, are determined, as described in detail in the literature, from the geometries of the TOF and the kinetic energies of the different ions.42 Estimates of the typical kinetic energy release in the various classes of dication reactions are used to determine the product ion velocities.42 As shown by Burnside and Price,42 using the above procedure for product ions derived from the dication, the ratio of the recorded intensities of the different products can be reliably transformed to yield relative reaction cross sections, which clearly quantify the branching between the different reaction pathways. The ions derived from the neutral collision partner have a very different laboratory frame velocity distribution, and spatial distribution, to those derived from the dication,42 and as such the relative intensities of these products cannot be easily compared with the products derived from the dication.
The PF3 used in this study was synthesised in-house.44 In brief, PCl3 was added dropwise onto ZnF2 suspended in acetonitrile under controlled vacuum conditions. The presence of the acetonitrile allowed good control of the temperature of the reaction mixture. The gaseous PF3 product resulting from this procedure was then trapped at liquid nitrogen temperatures and subsequently purified. See ESI† for further details of the synthesis of PF3. The product was purified several times by trap-to-trap distillation. Traces of Cl containing contaminants are seen in the ionisation mass spectrum. However, such contaminants do not affect the partial cross sections we extract due both to the fact the associated mass peaks do not interfere with those of PF3 and the fact that the impurities are at a very low level. Additionally, very weak signals are also present due to traces of the acetonitrile solvent. These contaminants from the synthesis, and any air/water present as background gas in the apparatus, contribute significantly less than 1% of the ion counts in any of the ion peaks of interest in any mass spectrum.
2.2 Data processing: coincidence TOF-MS
The data processing and analysis of the coincidence mass spectra are laid out in full here. A ‘singles’ mass spectrum is generated as a histogram of the flight times of ion arrivals in the TOF-MS where only a single ion is detected following a repeller plate pulse. The mass scale of this mass spectrum, and the associated coincidence spectra, is calibrated by recording a mass spectrum of a reference gas (e.g. Ar) under the same experimental conditions. A baseline correction is applied to the summed counts associated with each mass spectral peak, to remove the small background present due to detector noise and stray ions. This procedure yields the ion intensities I[X+] in the singles spectrum. Further corrections are made, where necessary, if there is a potential contribution from an ion from the background gas to a mass peak of interest. For example, in the case of PF32+, with a mass of 44, any contribution from CO2+ is evaluated using the intensities of unmasked signals from CO2 and the associated partial ionisation cross sections.14 Due to the low levels of impurities in our gas sample, as described above, such corrections are small.‘Pairs’ and ‘triples’ are events where two or three ions are detected in coincidence, respectively, following one pulse of the repeller plate. The flight times associated with each of these individual events are stored and subsequently processed offline. To begin this processing, all the detected ion pairs are plotted in a 2D histogram (a ‘pairs’ spectrum) using the TOF of the lightest ion (tA) and the TOF of the heavier ion (tB) as the two ordinates. The number of counts (intensities) in each of the peaks in the pairs spectrum, peaks which correspond to different dissociation reactions of PF32+/3+, are evaluated to yield the number of counts for a given ion in the pairs spectrum P2[X+]. It is important to note that the pairs spectrum, although dominated by dissociative double ionisation events, also involves a contribution from higher levels of ionisation. For example, pairs are detected from triple ionisation where one species is a dication and the other a monocation (P3[X+]). Some monocation pairs also result from triple ionisation where the third ion is not detected as the experimental ion detection efficiency is less than unity. Such events contribute to the values of P2. Indeed, the imperfect ion detection efficiency of the apparatus allows ions from dissociative multiple ionisation to contribute to the singles spectrum. These contributions are included explicitly in the data reduction described in the next section.
To process the triples, the time of flight range corresponding to the mass of one ion (ion A) which could potentially contribute to the spectrum (tA) is selected (e.g. P+) and then a 2D histogram is generated of all ions (tB and tC) that are detected in coincidence with an ion in the time window for ion A. This process is then repeated for all potential combinations of possible triples. Evaluation of the intensities of the peaks in these triples spectra yields T[X+]. Very small ion signals are visible in the triples spectra which can be attributed to quadruple (or higher) ionisation. However, since these signals are very weak the contribution of quadruple and higher ionisation is neglected in the subsequent analysis.
Both the pairs and triples spectra contain a contribution from false coincidences. The number of false coincidences is kept low by operating at low ion count rates. As has been described before in the literature, we use an ion-autocorrelation function to evaluate the contribution of false counts (at most 1–2%) in each peak in the triples or pairs spectra, and hence correct our values of Pn[X+] or T[X+] for false coincidences.33 Conversely, a source of missing counts in the coincidence histograms is the deadtime of the TOF-MS discrimination circuitry, which is unable to process a second ion arrival within 32 ns of a first ion. This dead-time results in reduced counts for pairs or triples involving ions with the same mass (e.g. F+ + F+). We can readily correct for these losses by extrapolation of a one-dimensional ion–ion coincidence (tB − tA) spectrum for the reaction of interest to the tB − tA = 0 limit, as detailed in earlier work.45 In the data reported here, such a deadtime correction is applied to the F+ + F+ pair and the triples 3F+, 2F+ + P+ and 2F+ + PF+.
Additional signal losses arise for ion pairs and triples where the transverse kinetic energy release of an ion is sufficient (∼11.5 eV) for the ion to miss the detector.46 Such losses are readily apparent in the shape of the peaks in the pairs or triples spectrum which become “hollowed” in the centre. These losses are corrected for quantitatively, on a peak by peak basis, by determining the counts required to give the expected flat-topped peak in a one-dimensional tB − tA spectrum.45 However, we should note that losses of highly energetic ions from single ionization events (>11.5 eV), ions which miss the detector, cannot be quantified. However, such fragment ions are expected to be a very minor component of the yield from single ionisation, as evidenced by the excellent agreement of previous datasets from our apparatus with other experiments where complete collection of fragment ions is demonstrated.15,47
2.3 Data reduction: coincidence TOF-MS
Relative PICS and relative precursor-specific PICS are extracted from the corrected ion intensities in the singles, pairs and triples spectra: I[X+], P2[X+], P3[X+], T[X+]. The instrumental ion detection efficiency f is necessary to extract the PS-PICS and is determined, as noted above, via calibration spectra45 recorded with CF4,16,37 prior to the PF3 experiments. Using this methodology the value of f for the experiments involved in this study was found to be 0.25, a value in accord with previous determinations for our apparatus.48An example of the relationship between the detected ion intensities in the singles mass spectra I[X+] and the detection efficiency f is shown by eqn (1), where Nn is the number of X+ ions formed via ionising events involving the loss of n electrons from a PF3 molecule. Similar equations can be constructed for pairs and triples P2[X+], P3[X+], T[X+], as shown in the literature.14 Using the equations constructed for the ion intensities in the various spectra (singles, pairs, triples), the required relative cross sections can be determined. For example, relative PICS σr[X+/2+, E] are the cross sections for forming the fragment ion (X+, X2+) from any level of ionisation relative to the cross section of formation for the parent monocation (PF3+) as a function of electron energy E, as shown in eqn (2).
| I[X+] = fN1[X+] + f(1 − f)N2[X+] + f(1 − f)Npairs3[X+] + f(1 − f)2Ntriples3[X+] | (1) |
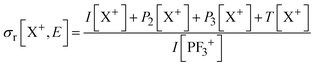 | (2) |
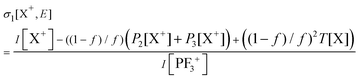 | (3) |
It is possible to determine the kinetic energy release (KER) of each dicationic dissociation reaction detected in the pairs spectrum. This determination is performed by generating a TOF difference spectrum for the dissociation of interest, a histogram of intensity against (tB − tA) as discussed above.33 Such a difference spectrum, for a given dication dissociation channel, has a characteristic square shape with a width determined by the KER of the associated dissociation. By optimizing the fit of a Monte Carlo simulation of the difference spectrum, incorporating an electrostatic model of the TOF-MS and various parameters characterizing the dissociation, to the experimental difference spectrum, the value of the KER can be estimated.33 The KER and the energies of the dissociation products Efrag relative to the ground state of PF3, can then be summed to provide an estimate of the energy of the dicationic precursor state Ep(X2+) responsible for the dissociation (eqn (4)). In this procedure the dissociation products are assumed to be formed in their ground electronic states, and rovibrational excitation of the products is neglected. Thus, Ep(X2+) provides a lower limit on the energy of the dicationic precursor state.
| Ep(X2+) = KER + Efrag | (4) |
2.4 BEB calculations
Total electron impact ionisation cross sections have been computed using the binary-encounter Bethe (BEB) method of Kim and Rudd49 as implemented in the new Quantemol electron collisions (QEC) expert system.50,51 QEC is a graphical user interface that wraps Molpro,52 for generating molecular orbitals and properties, and UKRmol+53 to generate a variety of molecule-electron scattering cross sections. BEB is a semi-empirical method, simply requiring the occupation, binding and average kinetic energies of the electrons in the occupied orbitals of the target molecule. BEB has a track-record of generating reliable predictions for total ionisation cross sections. Thus, for example, a recent data compilation of electron collision cross sections for NF3 and CH4 by Song et al.54,55 chose to recommend the BEB cross section in preference to several experimental determinations. As part of the present study all-electron BEB calculations were performed using Hartree–Fock target wavefunctions and three different Gaussian basis sets for the PF3 target; specifically, the 3-21G, 6-21G and cc-pVDZ basis sets. The calculation using the 6-21G basis set gave larger cross sections than the other two basis sets, this difference arising primarily from differences in the generated orbital kinetic energies. Additionally, the cc-pVDZ basis set uses higher order spherical harmonics, with up to d orbital functions for the P atom, allowing for more realistic molecular orbitals. Hence, here we adopt the value given by the largest basis set employed (cc-pVDZ) with an uncertainty estimate obtained using the difference between this and the results of the 6-21G calculations. A further increase in the size of the basis set did not result, given the BEB methodology, in a significant increase in the accuracy of the calculated cross section with respect to the marked increase in computational cost.In order to normalize the relative PICS and PS-PICS determined in our experiment, to the BEB function representing the total ionisation cross section B(E) as a function of the electron energy E, the following procedure was developed. We define:
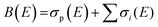 | (5) |
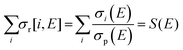 | (6) |
| B(E) = σp(E) + S(E)σp(E) = σp(E)(1 + S(E)) | (7) |
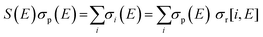 | (8) |
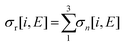 | (9) |
2.5 Electronic structure calculations
Electronic structure calculations using Gaussian16 (Rev. A03)56 have been used to support the experimental findings. Relevant equilibrium geometries, and adiabatic and vertical ionisation energies, were determined for the neutral, cation and dicationic states of PF3. These quantities were calculated, for the lowest lying states of appropriate multiplicity, for each of the charge states. Stationary points were located using the MP2 algorithm with a cc-pVTZ basis set and verified as minima by frequency analysis. The energetics of these stationary points were then determined using single-point CCSD(T) calculations with the same basis set, and corrected for zero-point energies using the vibrational data from the MP2 geometry optimizations. This methodology has been successfully used in the past, by several groups, to determine dication geometries and energetics.57 Along with the geometries of an isolated PF32+ ion, the geometries of [Ar–PF3]2+ complexes were also investigated.3 Results and discussion
As outlined above, relative PICS and PS-PICS of PF3 were determined using the mass spectral data generated by the coincidence TOF-MS. Similarly, mass spectra revealing the product ions generated following bimolecular collisions of PF32+ and the neutral species Ar, Ne, O2, and CO were collected using the crossed beam apparatus.3.1 Electron ionisation of PF3
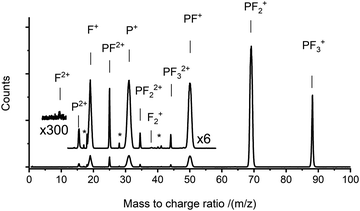
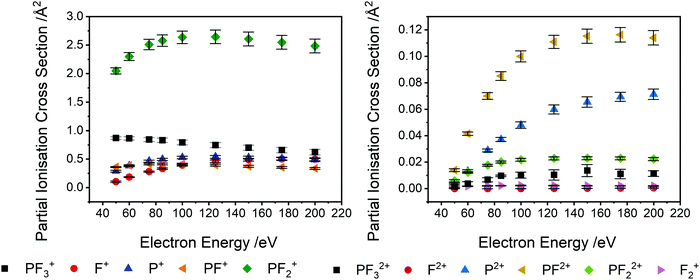
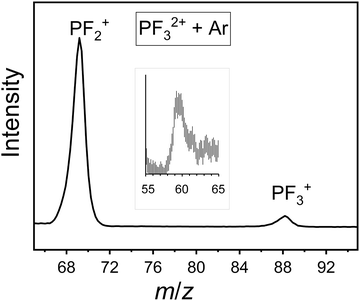
TOF-MS coincidence spectra were recorded following electron ionisation of PF3 at electron energies between 50 eV and 200 eV. From the coincidence data at an individual electron energy, singles spectra (e.g.Fig. 1) and pairs spectra (e.g.Fig. 2) are assembled. These spectra were analysed, as described above, to produce the relative PICS for each ion (Fig. 3) and the relative PS-PICS (Fig. 4), where appropriate. Several coincidence spectra (typically of duration 7 hours) were recorded at each electron kinetic energy and the relative cross sections at a given electron energy averaged to give final values of σr[X+/2+, E] and σn[X+/2+, E] for each electron energy investigated. These relative values are then normalized to the BEB model, again as described above, to produce absolute values of the cross sections. As noted above, these absolute cross sections are of significantly more value for modellers than the relative values.The ions present in the PF3 singles TOF-MS are: PF3+, F+, PF+, P+, PF2+, PF2+, P2+, PF22+, PF32+, F2+, and F2+. To the best of our knowledge the literature reports no previous observations of F2+, and F2+ following ionisation of PF3. The results of the BEB calculation of the total ionisation cross section are compared to previous calculations available in the literature in Fig. 5 and the resulting absolute PICS are compared to available calculations in Fig. 6 and 7.
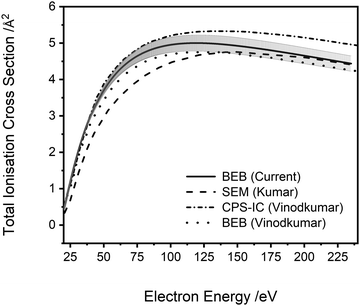 | ||
| Fig. 5 Total ionisation cross sections. BEB (current) calculation (cc-pVDZ), solid line, error shaded. SEM (Kumar)29 semi-empirical modified Jain–Khare method, long dash line. CPS-IC (Vinodkumar)23 complex scattering potential ionisation contribution method, dot-dash line. BEB (Vinodkumar),23 dotted line. See text for details. | ||
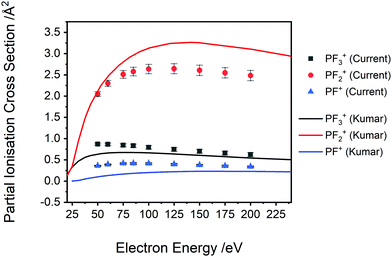 | ||
| Fig. 6 Comparison between the current normalized experimental PICS to the SEM calculated PICS of Kumar29 for PF3+, PF2+ and PF+. See text for details. | ||
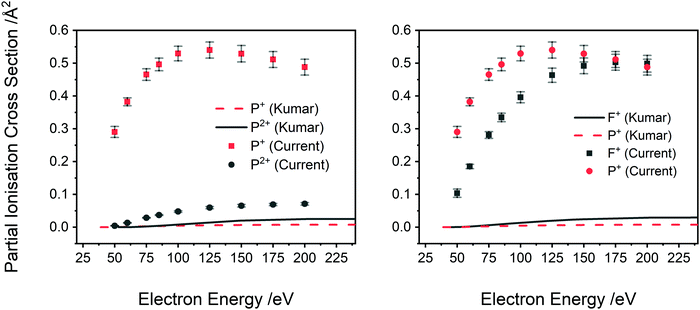 | ||
| Fig. 7 Comparison of the current absolute PICS, normalized to the BEB model, to the calculated PICS of Kumar.29 Left: Ions P2+ and P+, right: ions F+ and P+. Lines indicate calculation and points experiment. See text for details. | ||
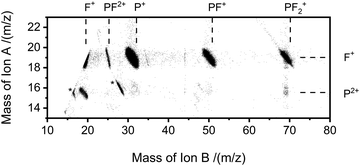
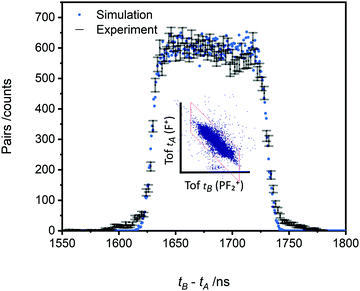
The pairs spectra (e.g.Fig. 2) reveal the charge-separating dissociations generate the following pairs of ions: F+ + F+, F+ + P2+, PF2+ + F+, P+ + F2+, P+ + F+, PF22+ + F+, PF+ + F+ and PF2+ + F+. These ions pairs result from double or triple ionisation of PF3 in a single electron-molecule collision. In addition to the peaks in the pair spectrum, which correspond to rapid dissociation of the PF32+/3+ multiply charged ions, there is a clear signature of a slower, metastable, dissociation (Fig. 2): a tail extending to low tB and high tA from the peak for the PF2+ + F+ pair. Such a tail reveals that some dissociations forming PF2+ + F+ occur on the timescale of tens of nanoseconds when the metastable PF32+ ion has moved out of the source region of the TOF-MS. The ion triples PF+ + F+ + F+, F+ + F+ + F+ and P+ + F+ + F+ are also detected on the triples spectrum.
Table 1 lists the partial ionisation cross sections (PICS) we determine, following the normalization of the relative cross sections extracted from the experiment to the calculated total ionisation cross section. As described above, the quoted uncertainties reflect the combination of the estimated uncertainties from the calculation and the relative experimental values. The PICS are shown graphically in Fig. 3. It is worth noting that the most abundant ion produced via electron ionisation, in the energy range investigated is PF2+, rather than the parent ion, PF3+. Production of the P+ ion is far more significant than that of the F+ ion in the lower half of the energy range, where single ionisation dominates. F+ production increases, relative to P+, with increasing collision energy, as there is a significant contribution to the F+ yield by multiple ionisation above 85 eV (Fig. 4). Production of P+ by single ionisation can involve the production of three F atoms or F2 + F. The cross section for the production of the PF2+ dication is found to be of the same order of magnitude as the generation of PF+ and F+. The cross sections for formation of PF32+ and PF22+ are also non-negligible. This efficient dication formation stimulated our further study of the bimolecular reactivity of PF32+, described below.
| Energy | 50 eV | 60 eV | 75 eV | 85 eV |
|---|---|---|---|---|
| BEB total | 370(2) | 419(3) | 464(4) | 481(4) |
| PF3+ | 87(2) | 87(3) | 84(3) | 83(3) |
| F2+ | 3(2) × 10−3 | — | 1(2) × 10−3 | — |
| P2+ | 0.45(6) | 1.3(1) | 2.9(1) | 3.7(2) |
| F+ | 10(1) | 18.5(7) | 28(1) | 33(1) |
| PF2+ | 1.4(3) | 4.1(2) | 7.0(3) | 8.5(3) |
| P+ | 29(2) | 38(1) | 47(2) | 50(2) |
| PF22+ | 0.6(1) | 1.24(6) | 1.77(7) | 2.02(8) |
| F2+ | 0.13(1) | 0.18(1) | 0.22(2) | 0.23(1) |
| PF32+ | 0.2(1) | 0.4(2) | 0.7(2) | 0.97(6) |
| PF+ | 36.0(8) | 39(1) | 42(2) | 42(2) |
| PF2+ | 204(5) | 230(7) | 251(9) | 258(10) |
| Energy | 100 eV | 125 eV | 150 eV | 175 eV | 200 eV |
|---|---|---|---|---|---|
| BEB total | 495(4) | 500(4) | 493(5) | 480(5) | 465(5) |
| PF3+ | 79(3) | 75(3) | 70(3) | 66(3) | 62(3) |
| F2+ | 4(3) × 10−3 | 1.5(3) × 10−2 | 2.6(7) × 10−2 | 4.3(3) × 10−2 | 5.9(7) × 10−2 |
| P2+ | 4.8(2) | 6.0(3) | 6.6(4) | 6.9(3) | 7.1(4) |
| F+ | 40(2) | 46(2) | 49(2) | 50(2) | 50(3) |
| PF2+ | 9.9(4) | 11.1(5) | 11.5(6) | 11.6(6) | 11.4(6) |
| P+ | 53(2) | 54(3) | 53(3) | 51(2) | 49(2) |
| PF22+ | 2.2(1) | 2.3(1) | 2.3(1) | 2.3(1) | 2.2(1) |
| F2+ | 0.24(3) | 0.24(3) | 0.22(2) | 0.22(1) | 0.21(2) |
| PF32+ | 1.0(2) | 1.0(4) | 1.4(5) | 1.1(4) | 1.1(2) |
| PF+ | 41(2) | 40(2) | 38(2) | 36(2) | 34(2) |
| PF2+ | 264(11) | 264(12) | 261(12) | 255(12) | 248(12) |
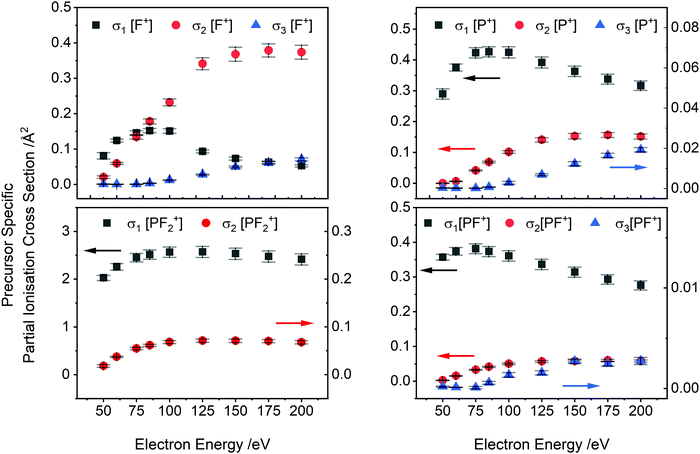
PS-PICS were determined for each ion detected and are tabulated in the ESI† (Table SI1). Selected PS-PICS are shown graphically in Fig. 4 revealing, as noted above, that double ionisation is responsible both for the majority of the F+ ions generated above 75 eV and for a sizable proportion of the P+ and PF+ production. The PS-PICS also reveal a significant proportion of the F+ ions detected are formed by triple ionisation, above 150 eV, though the contribution to other ion yields from triple ionisation is small.
Prior to a comparison of our derived cross sections to those found in literature, we note the important contribution of multiple ionisation to the ion yields in this system. In many treatments of electron ionisation, single ionisation (one electron in, two electrons out) is considered the only channel and multiple ionisation is neglected. Our dataset allows the determination of the ion yield of the single, double, and triple ionisation channels. At low energies single ionisation is certainly dominant: we see that at 50 eV electron energy single ionisation accounts for 98% of ions produced. As the electron energy increases the contribution of multiple ionisation to the ion yield increases as well. At 100 eV, single ionisation produces 87% of ions, while double and triple ionisation contribute 12% and <1% respectively. At 150 eV, single ionisation produces 81% of ions, with 17% and <2% due to double and triple ionisation respectively. At 200 eV, the maximum energy studied here, the maximum contribution of higher order ionisation also occurs, with 79%, 18% and <3% of ions produced by single, double or triple ionisation respectively. In these energy ranges, and potentially at higher ionization energy as well, the likelihood of an electron-PF3 collision removing 2 or more electrons is up to 20%. These figures should be noted in relevant models. As in previous work, where PS-PICS (relative or absolute) have been determined for a variety of small molecules, we see that considering just single ionisation in a description of the consequences of electron-molecule collisions is a poor description of the ion yield above the double ionisation energy.16,33,58,59
There have been several previous investigations of the electron ionisation of PF3. However, no previous experimental determinations of the PICS following electron-PF3 collisions are available in the literature. The appearance energies and relative intensities of ions following electron-PF3 collisions were reported in 1975.27 This early study did not detect the weak signals from F2+ and F2+ ions revealed in the current work, undoubtedly due to the greater sensitivity of modern instrumentation. The branching ratios between the monocationic products (F+, P+, PF+, PF2+ and PF3+) following electron ionisation at 70 eV were reported in an early mass spectrometric study by Torgerson and Westmore.60 These ratios differ to those reported here, notably underestimating the relative yields of lower mass fragments and the highest intensity fragment, PF2+, by up to 50%, and overestimating the relative yields of dications by up to 600%. It appears likely in the earlier work that the apparatus may have discriminated against ions with high kinetic energy, leading to the under-reporting of the yields of atomic and low mass fragments. Such discrimination in early mass spectrometric investigations of dissociative ionisation has been noted before.33,45,58,59 The appearance energies reported by Torgerson et al.,27 are for ionic products generated at or below 40 eV, and are not accessible in the current study.
A comparison of the results of the current study to previous theoretical determinations of the ionisation cross sections of PF3 is possible. As noted above, Vinodkumar et al.23 used the SCOP method to calculate elastic and inelastic electron scattering cross sections and from these data extracted the total ionisation cross section.61 Vinodkumar et al. compare the cross section they extract to a total ionisation cross section calculated using the BEB method. Fig. 5 clearly shows that there is good general agreement (within 10%) between the various calculated total ionisation cross sections, including that from the current work, particularly given the differences in methodology and basis sets. This uncertainty is well-represented by the uncertainty estimates on our BEB calculation, evaluated as described above.
Partial ionisation cross sections, directly comparable to the work here, have been calculated by Kumar using the Jain-Khare semi-empirical method (SEM).29 Kumar considered the formation of PF3+, PF2+, PF+, PF32+, PF22+, P+, PF2+, F+, and P2+ over electron energies from threshold to 1000 eV. No calculated values are available for the F2+ and F2+ ions.
A comparison of Kumar's calculated PICS29 with our absolute PICS are shown in Fig. 6 and 7. For the higher intensity cations (Fig. 6), the SEM method generates PICS in fair agreement with the experimental values but overestimates the yield of the PF2+ cation and underestimates the PICS for PF3+ and PF+. Fig. 7 shows that the SEM calculations dramatically underestimate the PICS for P+, F+ and P2+ as well as reversing the relative intensities of F+ and P2+ with respect to P+. The calculation of the PICS by Kumar29 uses the experimental differential optical oscillator strengths, extracted from (e,2e) spectra, reported by Au et al.62 The optical oscillator strengths (from the (e,2e) data) for P2+ formation are clearly less than that for P+,62 supporting our experimental data in ratio order if not in intensity (Fig. 7 right). In contrast, the current experimental findings indicating F+ has lower yield than P+ for all electron energies below 175 eV are not supported by the oscillator strengths. The reported oscillator strengths62 and calculated29 PICS report values for F+ that surpass those for P+ above 70 eV. Considering the good agreement of previous relative cross sections derived from our apparatus with experimental work from other groups, the ratio of F+ to P+ in our data is expected to be reliable. One cause for the disagreement could be that losses of the translationally energetic atomic fragment ions in the experimental spectra used for the extraction of the oscillator strengths could then have skewed the calculations. The fair agreement in the PICS for the heavier monocations, where ion losses due to translational energy effects are likely to be far less serious, support this conclusion.
As noted above, the data we record in the pairs spectrum allows for the determination of the kinetic energy release of the charge-separating dissociation reactions following multiple ionisation; data of interest to ionospheric and plasma kinetic modelling.63 The tB–tA data for the PF2+ + F+ pair, and the associated Monte Carlo simulation, used to determine the kinetic energy release for this channel are shown in Fig. 8. The simulation reveals a KER of 3.4 ± 0.5 eV (at 75 eV ionising energy) for the formation of PF2+ and F+. The pairs spectra indicate the threshold for PF2+ + F+ production is below 50 eV, the lowest electron energy accessed in this work. The “square” form of the tB–tA peak is readily modelled with a single KER indicating a single dissociation pathway dominates the formation of this ion pair.
As discussed above, Ep(PF32+), the energy of the dissociative dication precursor state forming the PF2+ + F+ pair, can be estimated from the KER. From heats of formation and ionisation energies64 we determine the energy of the PF2+ + F+ asymptote, relative to the ground state of PF3, as Efrag = 32.0 eV, assuming ionic formation in their vibrationless ground electronic states. Combining with the measured KER results in Ep(PF32+) = 35.4 ± 0.5 eV.
3.2 Computational investigation of PF32+
To attempt to associate the precursor energy extracted above with a specific state of PF32+ we have investigated the electronic structure of the dication computationally. The methodology employed has been discussed in Section 2.5. The geometries and energetics of the PF30/+/2+ minima revealed by our calculations are listed in Table 2. The values for the PF3 neutral can be used to assess the reliability and accuracy of our methodology. These values agree satisfactorily with higher level calculations and experimental data within a few tenths of a degree and a few hundredths of an angstrom.65–67| PF3 charge | Multiplicity | Symmetry | r(P–F)/Å | θ(FPF)/° | AIE/eV | VIE/eV |
|---|---|---|---|---|---|---|
| 0 | 1 | C 3v | 1.58 | 97.7 | — | — |
| 1+ | 2 | C 3v | 1.51 | 109.1 | 11.2 | 11.8 |
| 2+ | 1 | D 3h | 1.46 | 120.0 | 30.2 | 33.6 |
| 2+ | 3 | C 3v | 1.55 | 103.7 | 35.3 | 35.3 |
Early consideration of the ground-state geometry of PF3+ involved some debate about the relative stability of D3h and C3v structures, before the pyramidal geometry was confirmed.68 Theoretical work from 197366 indicated a C3v structure with a bond length of 1.57 Å and a F–P–F angle of 109° in reasonable agreement with our calculated values. More recent higher-level calculations generated a bond length of 1.50 Å and a F–P–F angle of 108.6°.69 The adiabatic ionisation energy (AIE) and vertical ionisation energy (VIE) of PF3 have been calculated by Aarons et al.66 using a range of Hartree–Fock and Koopmans’ theorem approximations. Their values for the AIE ranged from 10.52 eV to 11.85 eV, while the VIE encompassed 11.19 eV to 12.32 eV. Early experimental work gave a value of 11.57 eV for the AIE,70 whilst a data evaluation by Lias64 recommends 11.38 eV for the AIE. The value of 11.38 eV arises from experimental work determining the appearance energy of the parent cation.26 Again, these energetic values compare favourably with those calculated in this work (Table 2).
The calculations reveal the ground state of PF32+, a closed shell singlet, is of a D3h geometry. The lowest lying triplet dication state, calculated to lie 35.3 eV above the neutral, is in excellent agreement with the dication state energy determined from our experiments (35.4 ± 0.5 eV) hinting strongly that the triplet dication state is the source of the PF2+ + F+ pair, particularly given that the singlet ground state of PF32+ lies markedly lower in energy (Table 2). The other ion pairs we detect in our coincidence spectra, such as P+ + F+ and PF+ + F+, exhibit complex coincidence peak shapes indicating multiple dissociation pathways and energy dependencies. Hence no attempt to extract the KER of these dissociation reactions was made.
3.3 Bimolecular collisions of PF32+
Mass spectra following bimolecular collisions between PF32+ and the neutral species Ar, Ne, CO and O2 were recorded as described above. Fig. 9 shows product ion peaks from a representative raw (“collision gas on”) mass spectrum for the PF32+/Ar collision system. Such spectra are processed as described above, and in the literature,42 to reveal the product ions that result from bimolecular collisions (Table 3) by subtracting the, appropriately normalized, signals in mass spectra recorded with the collision gas off from those recorded with the collision gas on.| Target | T CM/eV | Product ions from neutral | Product ions from dication |
|---|---|---|---|
| Ne | 1.5 | — | F+, PF22+, PF2+, PF3+ |
| Ar | 2.5 | Ar+, [ArF+] | F+, PF22+, PF+, PF2+, PF3+ |
| O2 | 2.1 | O2+, O+ | F+, P+, PF22+, F2+, PF+, PF2+, PF3+ |
| CO | 1.9 | C+, O+, CO+ | F+, PF+, PF2+, PF3+ |
As described above, the relative reactive cross sections, for the channels generating ions derived from the dication, can be derived by consideration of the detection efficiency of these products in our transverse experimental geometry as described by Burnside.42 Such an analysis allows us to correctly compare the fluxes into these product channels for a given collision system. The results of this analysis are presented in Table 4 for interactions with Ar, O2 and CO. The product ion signals for the Ne collision system are too weak to robustly support this additional processing and are discussed separately.
| Target | Ar | Ar | O2 | CO |
|---|---|---|---|---|
| T cm | 2.2 eV | 2.5 eV | 2.1 eV | 1.9 eV |
| F+ | 1(0.3) | 1(0.3) | 1(0.3) | 2(1) |
| F2+ | 1(0.5) | 8(0.3) | * | — |
| PF+ | 34(34) | 17(16) | 0.1(1) | * |
| PF2+ | 100(14) | 55(7) | 100(14) | 100(21) |
| PF3+ | 6(1) | 2(0.5) | 10(2) | 19(4) |
Table 4 shows that formation of PF2+ is the dominant product channel following collisions with Ar, O2 and CO. PF3+ is a minor product in all the collision systems. A PF+ signal is observed following collisions with Ar, but there is a large uncertainty in the relative intensity of this signal due to the subtraction of comparable PF+ signals in the “gas-off” spectra due to traces of this ion in the dication beam. Traces of F+ are detected in all the collision systems. F2+ formation is detected in the Ar collision systems, which are those having the highest collision energy.
The majority of product ions observed following collisions of PF32+ with Ar, O2 and CO (Tables 3 and 4), result from single electron transfer. Although, the formation of PF22+ following collisions with Ar and O2 clearly originates from a collision-induced neutral loss (collision-induced dissociation) channel. This collision-induced channel is very weak in comparison with the electron transfer processes. For this reason the relative reaction cross sections for PF22+ production were not included in Table 4. Similar collision-induced processes involving F atom loss from fluorinated dications have been previously observed for CF32+, SiF32+ and SF42+.8,71 Using the dicationic energetics reported in Table 2, we can determine (using literature values for the ionisation energies of the neutral targets64) that single-electron transfer populating the ground state of the monocation from the ground state of the dication is exoergic for Ar (3.1 eV), CO (4.8 eV) and O2 (6.8 eV) readily accounting for our observation of PF3+ signals in these collision systems. Indeed, these exoergicities show that routes to the formation of PF3+ will lie in or near the favoured (2–6 eV) exoergicity reaction window for efficient electron transfer for all three dication-neutral collision systems.5 In addition to PF3+ formation, it is clear from our data (Table 4) that dissociative electron transfer (DET) is in fact the major product channel following these collisions: PF2+ is the major product derived from the dication. In a DET process the nascent, and energised, PF3+* product of an initial electron transfer step subsequently dissociates into a daughter ion (e.g. PF2+ + F).5 Accessing the asymptotes for forming PF3+ with sufficient internal excitation to allow dissociation to PF2+ and PF+ requires an extra 4.6 and 9.1 eV of internal energy to be deposited in the nascent PF3+*. This additional energetic burden makes these dissociative processes endothermic for collisions of the ground state of PF32+ with Ar, and well-outside the reaction window for collisions with CO. It is important to note in the considerations of the energetics of these reactions that, in this collision energy regime, it has been shown that the long-range nature of the dicationic electron transfer process means that the translational energy of the collision system does not efficiently couple into the chemical energetics.5 Thus, it is well established for this class of reactions, that processes with exoergicities outside the reaction window (2–6 eV exoergicity) are strongly disfavoured.5 Yet, despite the unfavourable energetics for reactions involving the dicationic ground state, formation of PF2+ is the dominant reactive process in PF32+ collision systems involving Ar, CO and O2. This observation clearly indicates that excited states of PF32+ must be present in the reactant dication beam. Indeed, the extra electronic excitation of the lowest lying triplet state of the dication (5.1 eV, Table 2) is sufficient to place dissociative electron transfer to form PF2+ firmly in the reaction window for collisions with Ar and CO, and provide access to PF3+* states above the dissociation asymptote to PF2+ in collisions with O2. Thus, if the lowest triplet state of PF32+ is a significant component of our dication beam, along with the ground singlet state, we can satisfactorily rationalise the bimolecular reactivity we observe. Thus, similarly to our ionisation experiments, we have good evidence that the lowest lying triplet state of PF32+ is efficiently populated in electron-PF3 collisions in our ion source and the metastable vibrational levels of this state are a significant component of our dication beam. The triplet state appears to result in the bulk of the DET processes whilst the presence of the singlet ground state is signposted by the formation of PF3+ by non-dissociative electron transfer. The lower ionisation energy of O2 will allow for more efficient access of the dissociative manifold of PF3+ states in the PF32+/O2 collisions, explaining the wider range of dissociative products in this collision system. Indeed, this extra energy available in the PF32+/O2 collision system also allows access to dissociative states of O2+, resulting in the O+ ions we observe.72–75
The formation of PF+, a minor channel, appears more significant in the more energetic collisions with Ar than with the molecules (CO, O2), where the collision energy is lower. This observation strongly indicates that the formation of PF+ is via a collision-induced fragmentation process, rather than electron transfer, perhaps fragmentation to PF+ + F+ + F.
Considering the PF32+/Ne collision system (Table 3), the product ion yields here are very low and no clear Ne+ signals are detected. The absence of Ne+ shows electron transfer is very weak in this collision system in accord with the endothermic energetics (exoergicity = −2.7 eV) where even the extra internal energy of the triplet dication only allows access to the very edge of the reaction window. Inefficient electron transfer from the triplet dication state is likely the source of the very weak PF3+ signals, as our experimental geometry will make the detection of the small number of corresponding Ne+ ions very inefficient. The traces of F+, PF2+ and PF22+ ions in this collision system almost certainly result from collision-induced charge separation or neutral loss.8,71,76
As shown in Fig. 9 we see weak signals corresponding to ArF+ following collisions of PF32+ with Ar. This weak ArF+ signal exhibits a tail to longer flight times, the tail linking to the PF2+ peak. Such tails have been observed before77 in our experiments and are associated with the metastable decay of dicationic collision complexes. Such a feature here is consistent with the decay of [Ar–PF3]2+ to ArF+ + PF2+. Indeed, collision complexes have been identified as a key intermediate in the pathways to many bond-forming products generated in dication neutral collisions and ArF+ has been observed before as a product following collisions of fluorinated dications with argon.78 Supporting this mechanistic deduction is the fact our computational methodology identifies energetically accessible local minima corresponding to [Ar–PF3]2+ on both the triplet and singlet surfaces. The geometries and energetics of these collision complexes are given in the ESI.† In other studies of dicationic bond-forming reactivity, where the operation of a mechanism involving dicationic complexation has been unambiguously demonstrated,72 similar computational investigations have identified local minima corresponding to the corresponding collision complex.
In summary, where exoergic, dissociative single electron transfer from the neutral collision partner to PF32+ dominates the ion yield in bimolecular collisions. The reactivity and energetics hint strongly that the first excited metastable triplet state of the dication is responsible for the bulk of the reactivity observed, with a minor contribution from the ground singlet state of the dication. When electron transfer is energetically disfavoured, weak collision-induced dissociation processes give some product ion flux. A small signal from a bond-forming process generating ArF+ is observed from the PF32+/Ar collision system. Metastable features in the mass spectrum, and supporting calculations, implicate the involvement of a collision complex on the pathway to generating ArF+.
4 Conclusions
Absolute partial electron ionisation cross sections, and precursor-specific partial electron ionisation cross sections, for the formation of cations from phosphorus trifluoride (PF3) are reported over the electron energy range 50–200 eV. The absolute values are determined by the measurement of cross sections relative to the formation of PF3+ using 2D ion–ion coincidence time-of-flight mass spectrometry and subsequent scaling using binary encounter-Bethe (BEB) calculations of the total ionisation cross section. This new dataset significantly augments the partial ionisation cross sections for electron ionization of PF3 found in literature, addressing previous discrepancies in the branching ratios of product ions, and provides the first values for the precursor-specific cross sections. Comparisons to calculated cross sections from the literature are encouraging, although there are discrepancies for individual ions. The coincidence experiments indicate that double and triple ionisation generate approximately 20% of the cationic ionisation products at 200 eV electron energy. One metastable dication state, dissociating to PF2+ + F+, is clearly identified as the lowest triplet state of PF32+ and five different dications (PF32+, PF22+, PF2+, P2+ and F2+) are detected in the mass spectra. The cross sections reported will allow more accurate modelling of the role of the ionization of PF3 in energetic environments. A first investigation of the bimolecular reactivity of metastable states of PF32+ is also reported. In collisions with Ar, O2 and CO dissociative single electron transfer dominates the product ion yield, whereas collision-induced dissociation of the dication is responsible for the small ion yields following collisions with Ne. Consideration of the energetics of these processes indicates the reactant dication beam contains ions in both the ground singlet state and the first excited triplet state. The deduction regarding the longevity of the triplet state is supported by metastable signals in the coincidence spectra. Weak signals corresponding to the formation of ArF+ are detected following PF32+ collisions with Ar, and experimental and computational considerations indicate this new chemical bond is formed via a collision complex.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BC thanks STFC for funding her fellowship ST/R005133/1 “Integrated software for electron-molecule collisions”. We thank Willow Farr for help with the BEB calculations and Prof Andrea Sella for providing the PF3 sample. SP and LE-G thank the Leverhulme Trust (RPG-2017-309) for funding the work at UCL.References
- M. P. Mitoraj and A. Michalak, Inorg. Chem., 2010, 49, 578–582 CrossRef CAS PubMed.
- R. M. Bligh-Smith, H. G. M. Edwards and V. Fawcett, Spectrochim. Acta, Part A, 1987, 43, 1069–1073 CrossRef.
- Z. J. Han, A. T. Murdock, D. H. Seo and A. Bendavid, 2D Mater., 2018, 5, 032002 CrossRef.
- A. Filippi, G. Occhiucci and M. Speranza, Inorg. Chem., 1997, 36, 3936–3946 CrossRef CAS.
- S. D. Price, J. D. Fletcher, F. E. Gossan and M. A. Parkes, Int. Rev. Phys. Chem., 2017, 36, 145–183 Search PubMed.
- S. D. Price, M. Manning and S. R. Leone, J. Am. Chem. Soc., 1994, 116, 8673–8680 CrossRef CAS.
- J. F. Lockyear, K. Douglas, S. D. Price, M. Karwowska, K. J. Fijalkowski, W. Grochala, M. Remeš, J. Roithová and D. Schröder, J. Phys. Chem. Lett., 2010, 1, 358–362 CrossRef CAS.
- Y. Y. Lee, S. R. Leone, P. Champkin, N. Kaltsoyannis and S. D. Price, J. Chem. Phys., 1997, 106, 7981–7994 CrossRef CAS.
- N. Tafadar and S. D. Price, Int. J. Mass Spectrom., 2003, 223–224, 547–560 CrossRef CAS.
- B. M. Smirnov, Theory of Gas Discharge Plasma, 2015, vol. 84 Search PubMed.
- I. El Naqa, P. Pater and J. Seuntjens, Phys. Med. Biol., 2012, 57, R75–R97 CrossRef CAS PubMed.
- R. G. Harrison and H. Tammet, Space Sci. Rev., 2008, 137, 107–118 CrossRef CAS.
- I. W. M. Smith, Annu. Rev. Astron. Astrophys., 2011, 49, 29–66 CrossRef CAS.
- S. J. King and S. D. Price, Int. J. Mass Spectrom., 2008, 272, 154–164 CrossRef CAS.
- N. A. Love and S. D. Price, Phys. Chem. Chem. Phys., 2004, 6, 4558–4565 RSC.
- M. R. Bruce and R. A. Bonham, Int. J. Mass Spectrom. Ion Process., 1993, 123, 97–100 CrossRef CAS.
- K. M. Douglas and S. D. Price, Int. J. Mass Spectrom., 2011, 303, 147–153 CrossRef CAS.
- M. S. Pindzola and F. Robicheaux, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 2142–2145 CrossRef CAS PubMed.
- Y.-K. Kim and J.-P. Desclaux, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 012708 CrossRef.
- V. Saksena, M. S. Kushwaha and S. P. Khare, Phys. B, 1997, 233, 201–212 CrossRef CAS.
- H. Deutsch, K. Becker, S. Matt and T. D. Märk, Int. J. Mass Spectrom., 2000, 197, 37–69 CrossRef CAS.
- A. Jain and K. L. Baluja, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 202–218 CrossRef CAS PubMed.
- M. Vinodkumar, C. Limbachiya, H. Desai and P. C. Vinodkumar, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 1–9 CrossRef.
- N. Hishiyama, M. Hoshino, F. Blanco, G. García and H. Tanaka, J. Chem. Phys., 2017, 147, 224308 CrossRef CAS PubMed.
- N. Hishiyama, M. Hoshino, F. Blanco, G. García and H. Tanaka, J. Chem. Phys., 2018, 148, 084313 CrossRef CAS PubMed.
- R. Rüede, H. Troxler, C. Beglinger and M. Jungen, Chem. Phys. Lett., 1993, 203, 477–481 CrossRef.
- F. Torgerson and J. B. Westmore, Can. J. Chem., 1975, 53, 933–938 CrossRef.
- C. Szmytkowski, M. Piotrowicz, A. Domaracka, Ł. Kłosowski, E. Ptasińska-Denga and G. Kasperski, J. Chem. Phys., 2004, 121, 1790–1795 CrossRef CAS PubMed.
- R. Kumar, J. Appl. Math. Phys., 2015, 03, 1671–1678 CrossRef.
- I. Powis, J. Chem. Phys., 1993, 99, 3436–3443 CrossRef CAS.
- K. Gluch, P. Scheier, W. Schustereder, T. Tepnual, L. Feketeova, C. Mair, S. Matt-Leubner, A. Stamatovic and T. D. Märk, Int. J. Mass Spectrom., 2003, 228, 307–320 CrossRef CAS.
- N. Endstrasser, F. Zappa, A. Mauracher, A. Bacher, S. Feil, D. K. Bohme, P. Scheier, M. Probst and T. D. Märk, Int. J. Mass Spectrom., 2009, 280, 65–71 CrossRef CAS.
- S. J. King and S. D. Price, J. Chem. Phys., 2007, 127, 174307 CrossRef PubMed.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- D. M. Curtis and J. H. D. Eland, Int. J. Mass Spectrom. Ion Process., 1985, 63, 241–264 CrossRef CAS.
- S. Harper, P. Calandra and S. D. Price, Phys. Chem. Chem. Phys., 2001, 3, 741–749 RSC.
- M. R. Bruce, L. Mi, C. R. Sporleder and R. A. Bonham, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 5773–5794 CrossRef CAS.
- M. D. Ward, S. J. King and S. D. Price, J. Chem. Phys., 2011, 134, 024308 CrossRef PubMed.
- S. D. Price, J. Chem. Soc., Faraday Trans., 1997, 93, 2451–2460 RSC.
- N. Lambert, D. Kearney, N. Kaltsoyannis and S. D. Price, J. Am. Chem. Soc., 2004, 126, 3658–3663 CrossRef CAS PubMed.
- D. Kearney and S. D. Price, Phys. Chem. Chem. Phys., 2003, 5, 1575–1583 RSC.
- P. W. Burnside and S. D. Price, Int. J. Mass Spectrom., 2006, 249–250, 279–288 CrossRef.
- D. A. Dahl, Int. J. Mass Spectrom., 2000, 200, 3 CrossRef CAS.
- G. Brauer, Handbuch der präparativen anorganischen chemie, Ferdinand Enke Verlag, 1960 Search PubMed.
- P. Calandra, C. S. S. O’Connor and S. D. Price, J. Chem. Phys., 2000, 112, 10821–10830 CrossRef CAS.
- S. J. King and S. D. Price, Int. J. Mass Spectrom., 2008, 277, 84–90 CrossRef CAS.
- B. G. Lindsay, R. Rejoub and R. F. Stebbings, J. Chem. Phys., 2003, 118, 5894–5900 CrossRef CAS.
- M. A. Parkes, K. M. Douglas and S. D. Price, Int. J. Mass Spectrom., 2019, 438, 97–106 CrossRef CAS.
- Y.-K. Kim and M. E. Rudd, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 3954–3967 CrossRef CAS PubMed.
- B. Cooper, M. Tudorovskaya, S. Mohr, A. O’Hare, M. Hanicinec, A. Dzarasova, J. D. Gorfinkiel, J. Benda, Z. Mašín, A. F. Al-Refaie, P. J. Knowles and J. Tennyson, Atoms, 2019, 7, 97–108 CrossRef CAS.
- V. Graves, B. Cooper and J. Tennyson, J. Chem. Phys., 2021, 154, 114104 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- Z. Mašín, J. Benda, J. D. Gorfinkiel, A. G. Harvey and J. Tennyson, Comput. Phys. Commun., 2020, 249, 107092 CrossRef.
- M.-Y. Song, J.-S. Yoon, H. Cho, G. P. Karwasz, V. Kokoouline, Y. Nakamura, J. R. Hamilton and J. Tennyson, J. Phys. Chem. Ref. Data, 2017, 46, 043104 CrossRef.
- M.-Y. Song, J.-S. Yoon, H. Cho, Y. Itikawa, G. P. Karwasz, V. Kokoouline, Y. Nakamura and J. Tennyson, J. Phys. Chem. Ref. Data, 2015, 44, 023101 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. D. Fletcher, M. A. Parkes and S. D. Price, Mol. Phys., 2015, 113, 2125–2137 CrossRef CAS.
- J. D. Fletcher, M. A. Parkes and S. D. Price, J. Chem. Phys., 2013, 138, 184309 CrossRef PubMed.
- S. D. Price, Phys. Chem. Chem. Phys., 2003, 5, 1717–1729 RSC.
- P. W. Harland, D. W. H. Rankin and J. C. J. Thynne, Int. J. Mass Spectrom. Ion Phys., 1974, 13, 395–410 CrossRef CAS.
- C. Limbachiya, M. Vinodkumar, M. Swadia and A. Barot, Mol. Phys., 2014, 112, 101–106 CrossRef CAS.
- J. W. Au, G. Cooper and C. E. Brion, Chem. Phys., 1997, 215, 397–418 CrossRef CAS.
- J. Lilensten, C. Simon Wedlund, M. Barthélémy, R. Thissen, D. Ehrenreich, G. Gronoff and O. Witasse, Icarus, 2013, 222, 169–187 CrossRef CAS.
- P. J. Linstrom and W.G. Mallard (eds.), NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg (MD), http://webbook.nist.gov. Retrieved 2020 Search PubMed.
- J. Breidung and W. Thiel, J. Phys. Chem. A, 2019, 123, 5600–5612 CrossRef CAS PubMed.
- L. Aarons, M. Guest, M. Hall and I. Hillier, J. Chem. Soc., Faraday Trans. 2, 1972, 643–647 Search PubMed.
- S. A. Rogers, S. D. Price and S. R. Leone, J. Chem. Phys., 1993, 98, 280–289 CrossRef CAS.
- R. P. Tuckett and P. J. Knowles, Chem. Phys. Lett., 1996, 261, 486–494 CrossRef CAS.
- S. Creve and M. T. Nguyen, Chem. Phys. Lett., 1997, 273, 199–204 CrossRef CAS.
- J. P. Maier and D. W. Turner, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 711–719 RSC.
- N. Tafadar, N. Kaltsoyannis and S. D. Price, Int. J. Mass Spectrom., 1999, 192, 205–214 CrossRef CAS.
- S. Armenta Butt and S. D. Price, Phys. Chem. Chem. Phys., 2020, 22, 8391–8400 RSC.
- D. Ascenzi, P. Franceschi, P. Tosi, D. Bassi, M. Kaczorowska and J. N. Harvey, J. Chem. Phys., 2003, 118, 2159–2163 CrossRef CAS.
- M. A. Parkes, J. F. Lockyear, S. D. Price, D. Schröder, J. Roithová and Z. Herman, Phys. Chem. Chem. Phys., 2010, 12, 6233–6243 RSC.
- C. L. Ricketts, S. M. Harper, S. W.-P. Hu and S. D. Price, J. Chem. Phys., 2005, 123, 134322 CrossRef PubMed.
- S. D. Price, M. Manning and S. R. Leone, Chem. Phys. Lett., 1993, 214, 553–558 CrossRef CAS.
- P. W. Burnside, PhD thesis, University College London, 2007.
- J. Berkowitz and W. A. Chupka, Chem. Phys. Lett., 1970, 7, 447–450 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01328a |
| This journal is © the Owner Societies 2021 |